User:Tohline/H BookTiledMenu

From VistrailsWiki
Jump to navigation Jump to search


Tiled Menu

Whitworth's (1981) Isothermal Free-Energy Surface
|   Tiled Menu   |   Tables of Content   |  Banner Video   |  Tohline Home Page   |

[Preamble by Joel E. Tohline — Circa 2020]  In an effort to serve ongoing research activities of the astrophysics community, this media-wiki-based hypertext book (H_Book) reviews what is presently understood about the structure, stability, and dynamical evolution of (Newtonian) self-gravitating fluids. In the context of this review, the "dynamical evolution" categorization generally will refer to studies that begin with an equilibrium configuration that has been identified — via a stability analysis — as being dynamically (or, perhaps, secularly) unstable then, using numerical hydrodynamic technique, follow the development to nonlinear amplitude of deformations that spontaneously develop as a result of the identified instability.

As is reflected in our choice of the overarching set of Principle Governing Equations, our focus is on studies of compressible fluid systems — those that obey a barotropic equation of state. But, in addition, chapters are included that review what is known about the structure and stability of self-gravitating incompressible (uniform-density) fluid systems because: (a) in this special case, the set of governing relations is often amenable to a closed-form, analytic solution; and (b) most modern computationally assisted studies of compressible fluid systems — both in terms of their design and in the manner in which results have been interpreted — have been heavily influenced by these, more classical, studies of incompressible fluid systems.

As the layout of the following tiled menu reflects, this review is broken into three major topical areas based primarily on geometrical considerations:

  • Studies of configurations that are — at least initially — spherically symmetric.
  • Two-dimensional configurations — such as rotationally flattened spheroidal-like or toroidal-like structures; or infinitesimally thin, but nonaxisymmetric, disk-like structures.
  • Configurations that require a full three-dimensional treatment — most notably, "spinning" ellipsoidal-like structures; or binary systems.

This is very much a living review. The chosen theme encompasses an enormous field of research that, because of its relevance to the astrophysics community, over time is continuing to expand at a healthy pace. As a consequence the review is incomplete now, and it will always be incomplete, so please bear with me. On any given day/week/month I will turn my attention to a topic that seems particularly interesting to me and I will begin writing a new chapter or I will edit/expand the contents of an existing tiled_menu chapter. This necessarily means that all chapters are incomplete while, in practice, some are much more polished than others. Hopefully steady forward progress is being made and the review will indeed be viewed as providing a service to the community.

Context

Global Energy
Considerations
Principal
Governing
Equations
(PGEs) 		Continuity Euler 1st Law of
Thermodynamics 		Poisson

 

Equation
of State
(EOS) 		Ideal Gas Total Pressure
 

Bond, Arnett, & Carr
(1984)

Spherically Symmetric Configurations

(Initially) Spherically Symmetric Configurations

 

Whitworth's (1981) Isothermal Free-Energy Surface Structural
Form
Factors 		Free-Energy
of
Spherical
Systems
One-Dimensional
PGEs


Equilibrium Structures

1D STRUCTURE

 

Spherical Structures Synopsis Scalar
Virial
Theorem
Hydrostatic
Balance
Equation

LSU Key.png

<math>~\frac{dP}{dr} = - \frac{GM_r \rho}{r^2}</math>

Solution
Strategies

 

Uniform-Density
Sphere

 

Isothermal
Sphere

LSU Key.png

<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\psi}{d\xi} \biggr) = e^{-\psi}</math>

via
Direct
Numerical
Integration

 

Isolated
Polytropes 		Lane
(1870)

LSU Key.png

<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H^n</math>

Known
Analytic
Solutions 		via
Direct
Numerical
Integration 		via
Self-Consistent
Field (SCF)
Technique

 

Zero-Temperature
White Dwarf 		Chandrasekhar
Limiting
Mass
(1935)

 

Virial Equilibrium
of
Pressure-Truncated
Polytropes
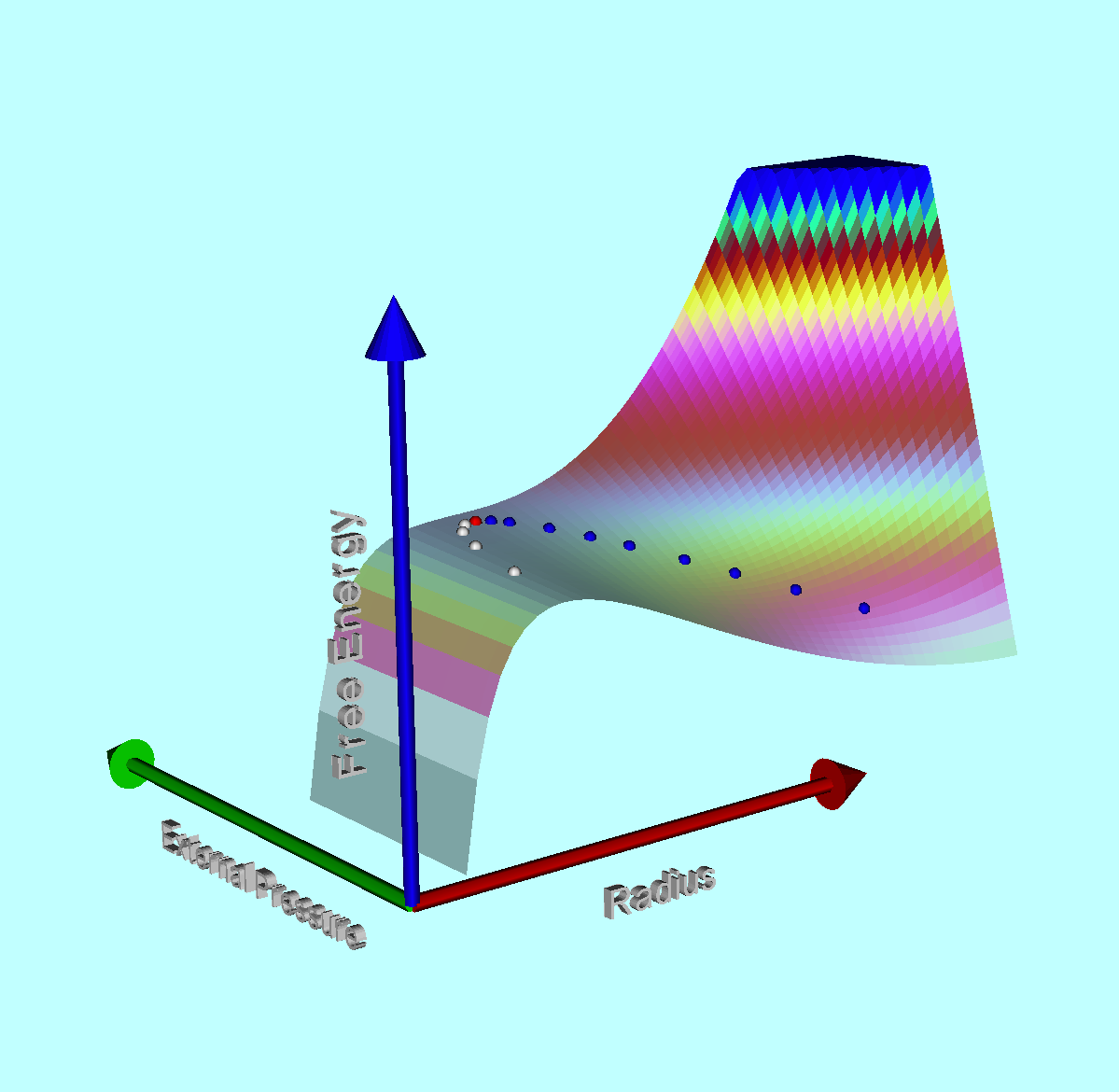
Pressure-Truncated
Configurations 		Bonnor-Ebert
(Isothermal)
Spheres
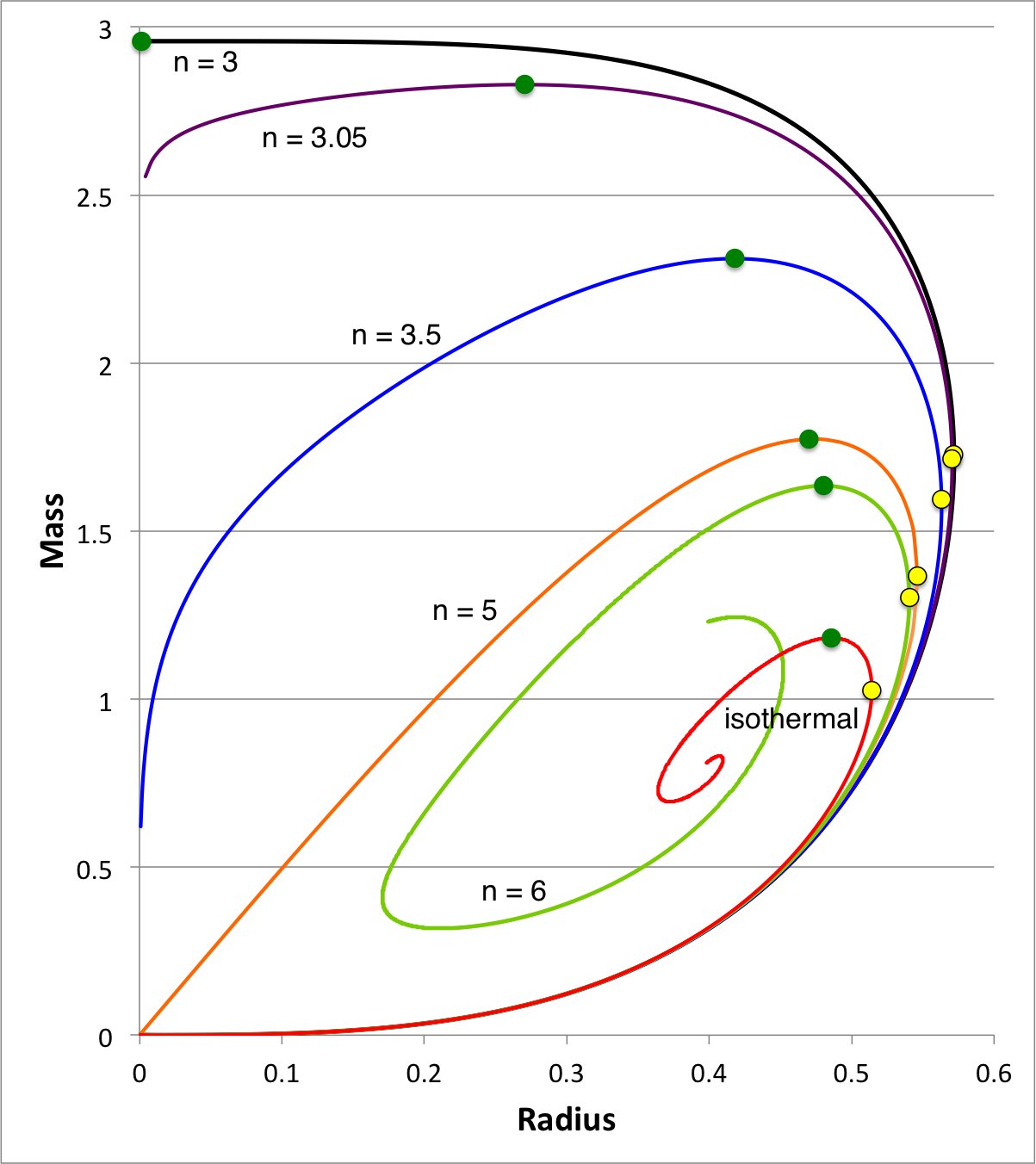
(1955 - 56) 		Polytropes Equilibrium
Sequence
Turning-Points

♥ 		Equilibrium sequences of Pressure-Truncated Polytropes Turning-Points
(Broader Context)

 

Free Energy
of
Bipolytropes

(nc, ne) = (5, 1)
Composite
Polytropes
(Bipolytropes) 		Milne
(1930) 		Schönberg-
Chandrasekhar
Mass
(1942) 		Analytic

(nc, ne) = (5, 1) 		Analytic

(nc, ne) = (1, 5)

 

Stability Analysis

1D STABILITY

 

Synopsis: Stability of Spherical Structures Variational
Principle
Radial
Pulsation
Equation 		Example
Derivations
&
Statement of
Eigenvalue
Problem 		(poor attempt at)
Reconciliation 		Relationship
to
Sound Waves

 

Jeans (1928) or Bonnor (1957)
Ledoux & Walraven (1958)
Rosseland (1969)

 

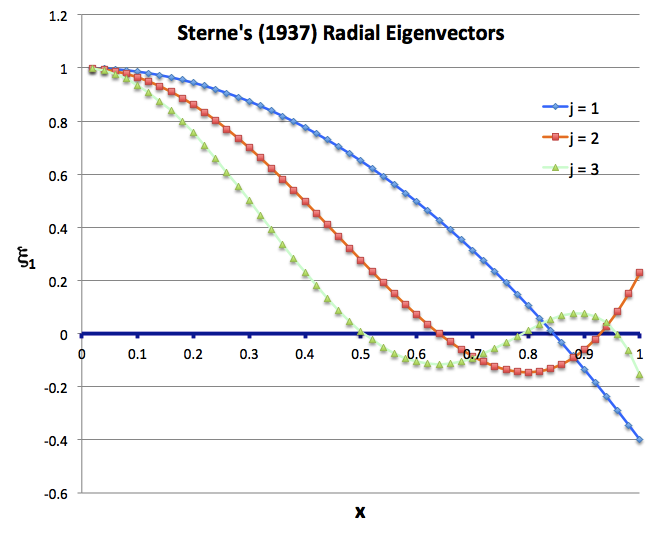
Uniform-Density
Configurations 		Sterne's
Analytic Sol'n
of
Eigenvalue
Problem
(1937) 		Sterne's (1937) Solution to the Eigenvalue Problem for Uniform-Density Spheres

 

Pressure-Truncated
Isothermal
Spheres

LSU Key.png

<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[4 - \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_\mathrm{g}}\biggr)\xi^2 - \alpha \xi \biggl( \frac{d\psi}{d\xi} \biggr) \biggr] \frac{x}{\xi^2} </math>

where:    <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c}</math>     and,     <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math>

via
Direct
Numerical
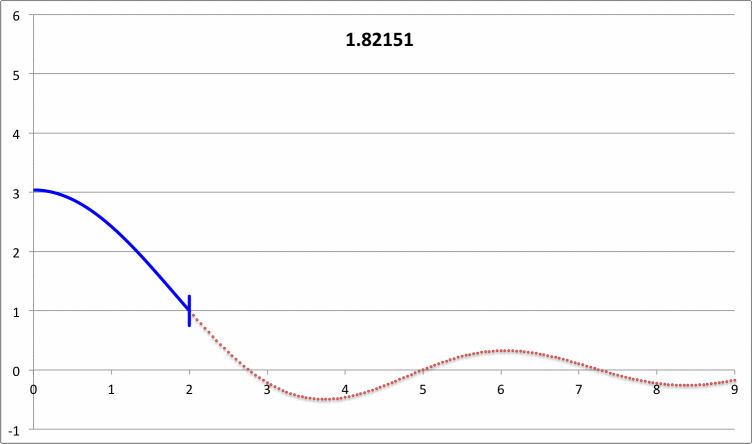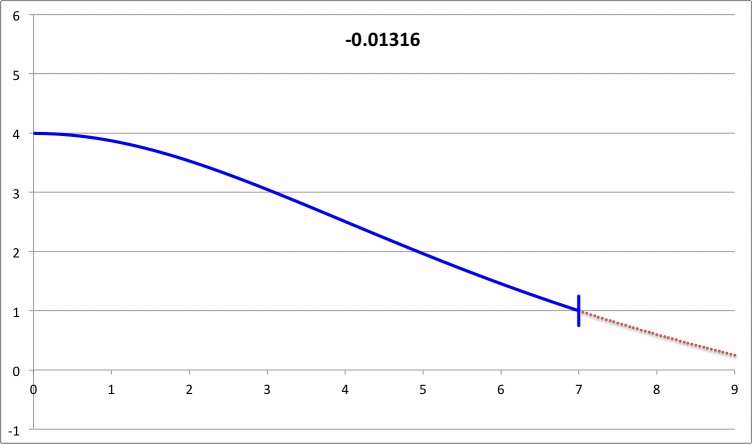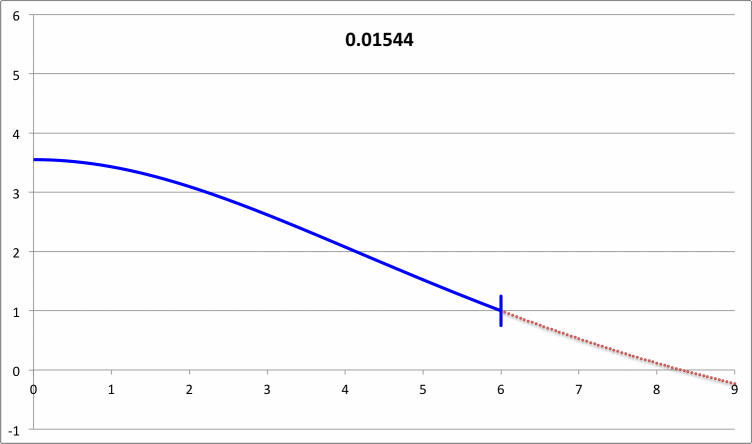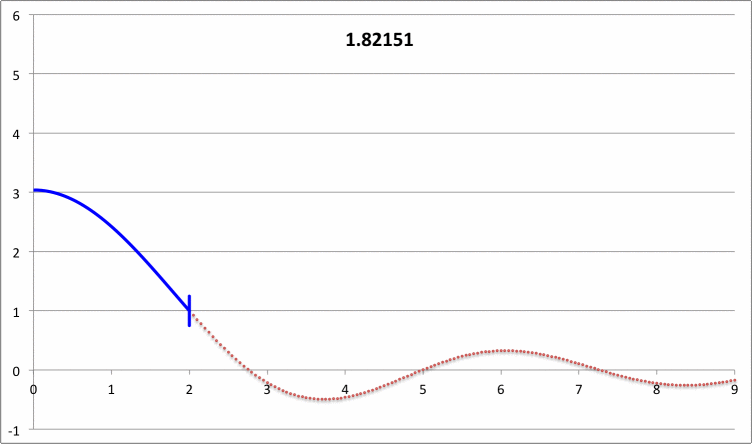
Integration 		Fundamental-Mode Eigenvectors


Yabushita's
Analytic Sol'n
for
Marginally Unstable
Configurations
(1974)

<math>~\sigma_c^2 = 0 \, , ~~~~\gamma_\mathrm{g} = 1</math>

 and  

<math>~x = 1 - \biggl( \frac{1}{\xi e^{-\psi}}\biggr) \frac{d\psi}{d\xi} </math>

 

Polytropes

LSU Key.png

<math>~0 = \frac{d^2x}{d\xi^2} + \biggl[ 4 - (n+1) Q \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + (n+1) \biggl[ \biggl( \frac{\sigma_c^2}{6\gamma_g } \biggr) \frac{\xi^2}{\theta} - \alpha Q\biggr] \frac{x}{\xi^2} </math>

where:    <math>~Q(\xi) \equiv - \frac{d\ln\theta}{d\ln\xi} \, ,</math>    <math>~\sigma_c^2 \equiv \frac{3\omega^2}{2\pi G\rho_c} \, ,</math>     and,     <math>~\alpha \equiv \biggl(3 - \frac{4}{\gamma_\mathrm{g}}\biggr)</math>

Isolated
n = 3
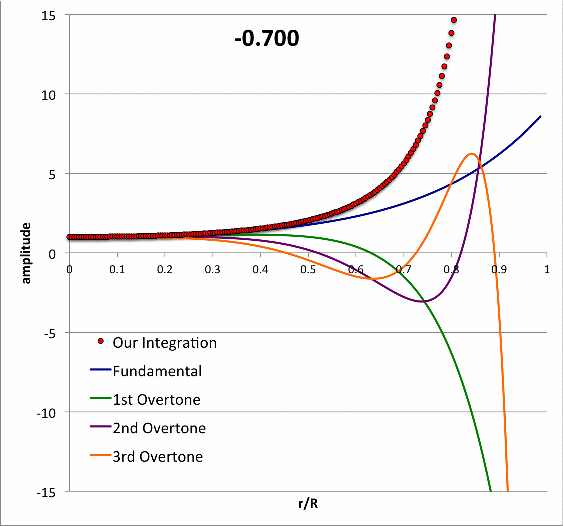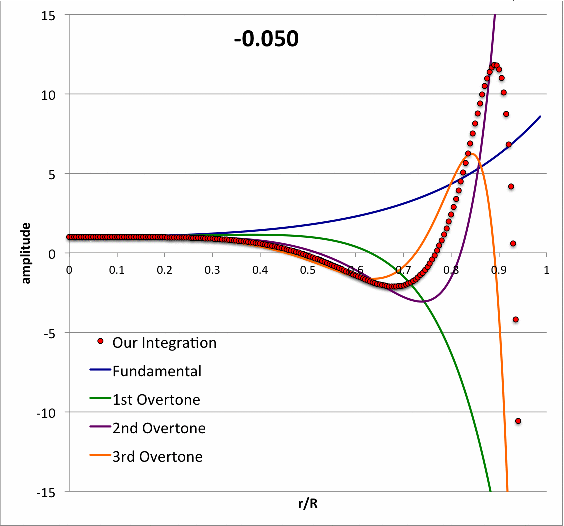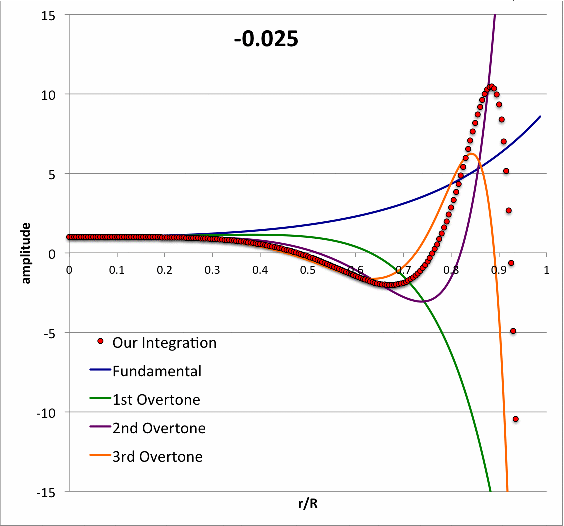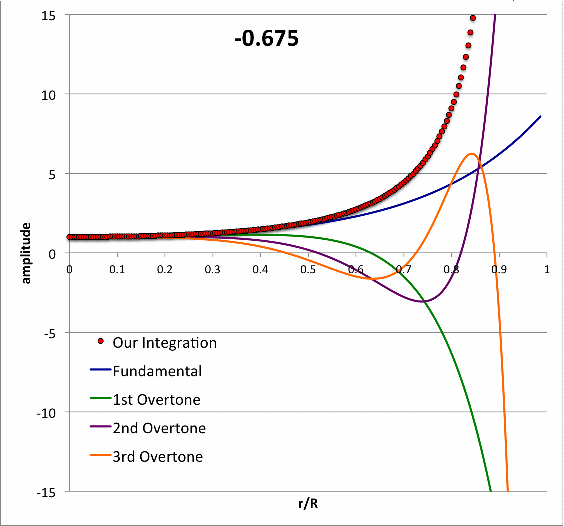
Polytrope 		Schwarzschild's Modal Analysis Pressure-Truncated
n = 5
Configurations


Exact
Demonstration
of
B-KB74
Conjecture 		Exact
Demonstration
of
Variational
Principle 		Pressure-Truncated
n = 5
Polytropes
Our Analytic Sol'n
for
Marginally Unstable
Configurations
(2017)
♥

<math>~\sigma_c^2 = 0 \, , ~~~~\gamma_\mathrm{g} = (n+1)/n</math>

 and  

<math>~x = \frac{3(n-1)}{2n}\biggl[1 + \biggl(\frac{n-3}{n-1}\biggr) \biggl( \frac{1}{\xi \theta^{n}}\biggr) \frac{d\theta}{d\xi}\biggr] </math>

 

BiPolytropes Murphy & Fiedler
(1985b)

(nc, ne) = (1,5) 		Our
Broader
Analysis

 

Nonlinear Dynamical Evolution

1D DYNAMICS

 

Free-Fall
Collapse

 

Collapse of
Isothermal
Spheres 		via
Direct
Numerical
Integration 		Similarity
Solution

 

Collapse of
an Isolated
n = 3
Polytrope

 

Two-Dimensional Configurations (Axisymmetric)

(Initially) Axisymmetric Configurations

 

Storyline

 

PGEs
for
Axisymmetric
Systems


Axisymmetric Equilibrium Structures

2D STRUCTURE

 

Constructing
Steady-State
Axisymmetric
Configurations 		Axisymmetric
Instabilities
to Avoid 		Simple
Rotation
Profiles 		Hachisu Self-Consistent-Field
[HSCF]
Technique 		Solving the
Poisson Equation

 

Using
Toroidal Coordinates
to Determine the
Gravitational
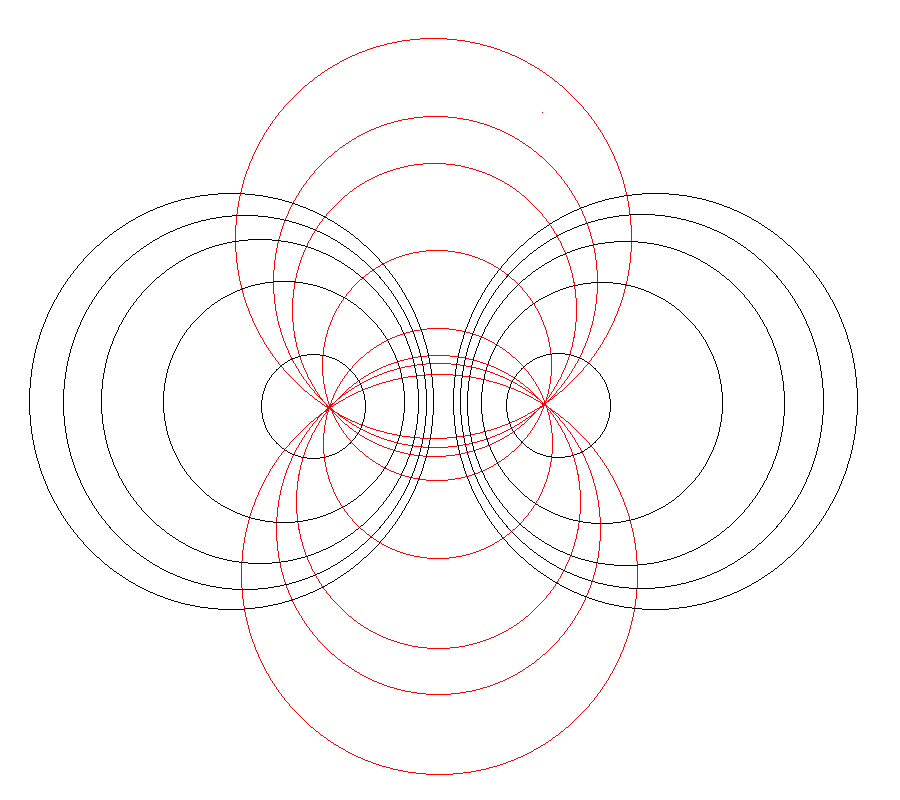
Potential 		Apollonian Circles Attempt at
Simplification

♥ 		Wong's
Analytic Potential
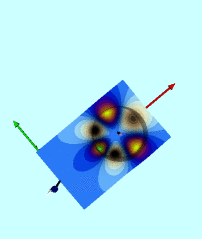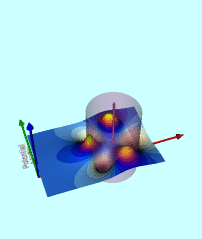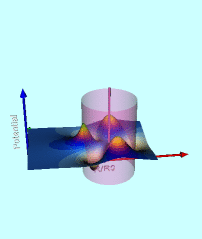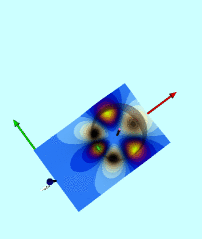
(1973) 		n = 3 contribution to potential

Spheroidal & Spheroidal-Like

Uniform-Density
(Maclaurin)
Spheroids 		Maclaurin's
Original Text
&
Analysis
(1742)
Our Construction of Maclaurin's Figure 291Pt2
 Maclaurin
Spheroid
Sequence

 

Rotationally
Flattened
Isothermal
Configurations 		Hayashi, Narita
& Miyama's
Analytic Sol'n
(1982) 		Review of
Stahler's (1983)
Technique

 

Rotationally
Flattened
Polytropes 		Example
Equilibria

 

Rotationally
Flattened
White Dwarfs 		Ostriker
Bodenheimer
& Lynden-Bell
(1966) 		Example
Equilibria

Toroidal & Toroidal-Like

Definition: anchor ring
Massless
Polytropic
Configurations 		Papaloizou-Pringle
Tori
(1984) 		Pivoting PP Torus

 

Self-Gravitating
Incompressible
Configurations 		Dyson
(1893) 		Dyson-Wong
Tori

 

Self-Gravitating
Compressible
Configurations 		Ostriker
(1964)

 

Stability Analysis

2D STABILITY

 

Sheroidal & Spheroidal-Like

Linear
Analysis
of
Bar-Mode
Instability 		Bifurcation
from
Maclaurin
Sequence 		Traditional
Analyses

 

 

The equilibrium models are calculated using the polytrope version (Bodenheimer & Ostriker 1973) of the Ostriker and Mark (1968) self-consistent field (SCF) code … the equilibrium models rotate on cylinders and are completely specified by <math>~n</math>, the total angular momentum, and the specific angular momentum distribution <math>~j(m_\varpi)</math>. Here <math>~m_\varpi</math> is the mass contained within a cylinder of radius <math>~\varpi</math> centered on the rotation axis. The angular momentum distribution is prescribed in several ways: (1) imposing strict uniform rotation; (2) using the same <math>~j(m_\varpi)</math> as that of a uniformly rotating spherical polybrope of index <math>~n^'</math> (see Bodenheimer and Ostriker 1973); and (3) using <math>~j(m_\varpi) \propto m_\varpi</math>, which we refer to as <math>~n^' = L</math>, <math>~L</math> for "linear."

 

Toroidal & Toroidal-Like

Defining the
Eigenvalue Problem

 

(Massless)
Papaloizou-Pringle
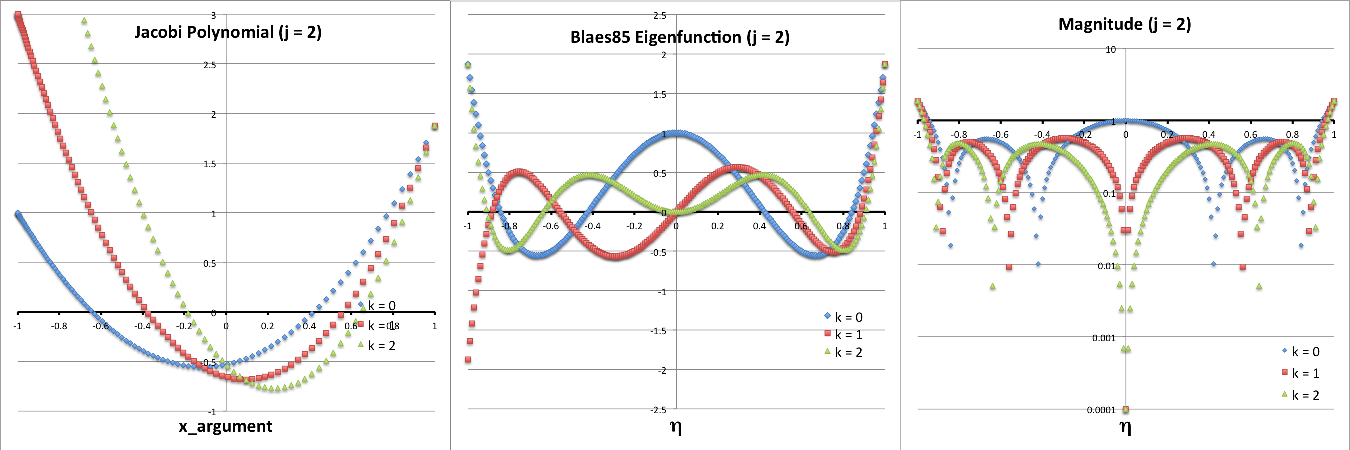
Tori 		Analytic Analysis
by
Blaes
(1985)
N1.5j2 Combinedsmall.png

 

Self-Gravitating
Polytropic
Rings 		Numerical Analysis
by
Tohline & Hachisu
(1990)
PP torus instability
 Thick
Accretion
Disks
(WTH94)

 

Nonlinear Dynamical Evolution

Sheroidal & Spheroidal-Like

2D DYNAMICS

 

Free-Fall
Collapse
of an
Homogeneous
Spheroid

 

Nonlinear
Development of
Bar-Mode 		Initially
Axisymmetric
& Differentially
Rotating
Polytropes 		Cazes Model A Simulation

 

Two-Dimensional Configurations (Nonaxisymmetric Disks)

Infinitesimally Thin, Nonaxisymmetric Disks

 

2D STRUCTURE

 

Constructing
Infinitesimally Thin
Nonaxisymmetric
Disks

 

Three-Dimensional Configurations

(Initially) Three-Dimensional Configurations

 

Equilibrium Structures

3D STRUCTURE

Special numerical techniques must be developed "to build three-dimensional compressible equilibrium models with complicated flows." To date … "techniques have only been developed to build compressible equilibrium models of nonaxisymmetric configurations for a few systems with simplified rotational profiles, e.g., rigidly rotating systems (Hachisu & Eriguchi 1984; Hachisu 1986), irrotational systems (Uryū & Eriguchi 1998), and configurations that are stationary in the inertial frame (Uryū & Eriguchi 1996)."

— Drawn from §1 of Ou (2006), ApJ, 639, 549

Ellipsoidal & Ellipsoidal-Like

Constructing
Ellipsoidal
& Ellipsoidal-Like
Configurations

 

Steady-State
2nd-Order
Tensor Virial
Equations
Uniform-Density
Incompressible
Ellipsoids 		The
Gravitational
Potential

(Ai coefficients) 		Jacobi
Ellipsoids 		Riemann
S-Type
Ellipsoids 		Type I
Riemann
Ellipsoids 		Riemann
meets
COLLADA
&
Oculus Rift S

 

A Gauge Theory
of
Riemann Ellipsoids 		Nuclear
Wobbling Motion

 

Compressible
Analogs of
Riemann Ellipsoids 		Ferrers
Potential
(1877) 		Thoughts
&
Challenges

 

Binary Systems

  • S. Chandrasekhar (1933), MNRAS, 93, 539: The equilibrium of distorted polytropes. IV. the rotational and the tidal distortions as functions of the density distribution
  • S. Chandrasekhar (1963), ApJ, 138, 1182: The Equilibrium and the Stability of the Roche Ellipsoids
 

Roche's problem is concerned with the equilibrium and the stability of rotating homogeneous masses which are, further, distorted by the constant tidal action of an attendant rigid spherical mass.

 

Stability Analysis

3D STABILITY

Ellipsoidal & Ellipsoidal-Like

 

Binary Systems

Nonlinear Evolution

3D DYNAMICS

 

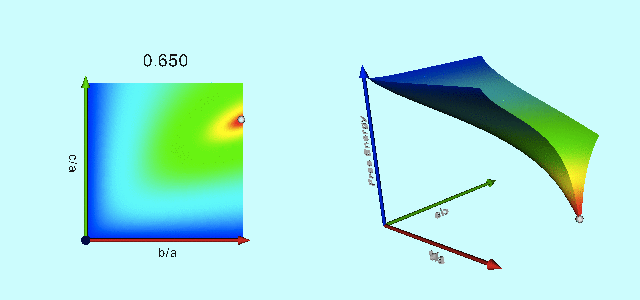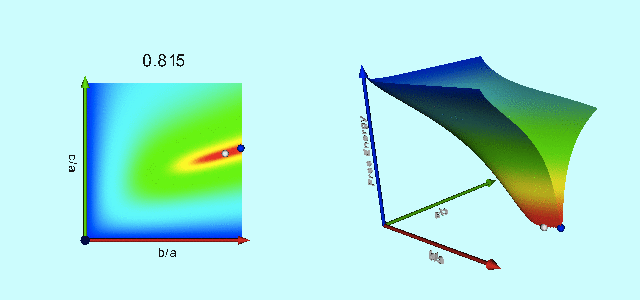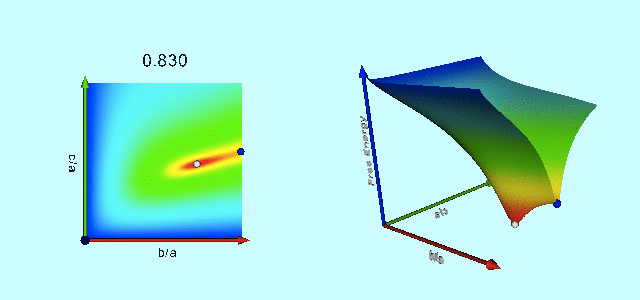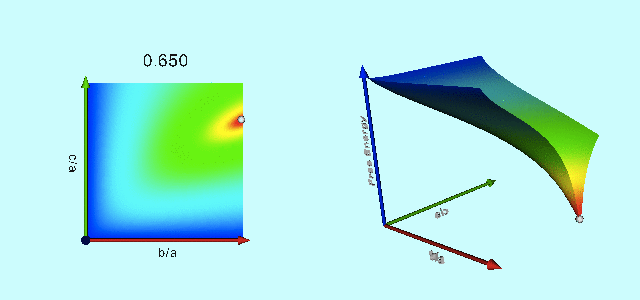
Animation related to Fig. 3 from Christodoulou1995 Free-Energy
Evolution
from the Maclaurin
to the Jacobi
Sequence
Fission
Hypothesis 		"Fission"
Simulations
at LSU

 

Secular

Dynamical

See Also

Whitworth's (1981) Isothermal Free-Energy Surface

© 2014 - 2021 by Joel E. Tohline
|   H_Book Home   |   YouTube   |
Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS |
Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation

Retrieved from "https://www.vistrails.org//index.php?title=User:Tohline/H_BookTiledMenu&oldid=22129"