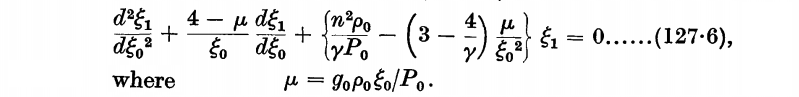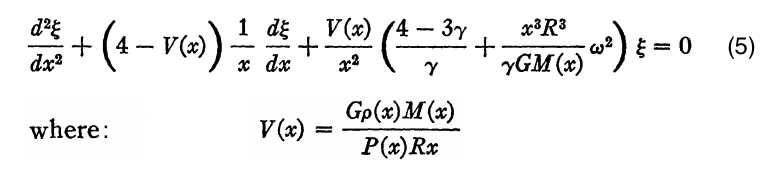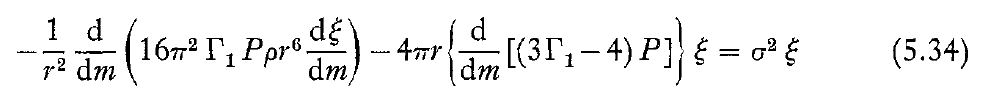User:Tohline/SSC/Perturbations
Spherically Symmetric Configurations (Stability — Part II)

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Suppose we now want to study the stability of one of the spherically symmetric, equilibrium structures that have been derived elsewhere. The identified set of simplified, time-dependent governing equations will tell us how the configuration will respond to an applied radial (i.e., spherically symmetric) perturbation that pushes the configuration slightly away from its initial equilibrium state.
Very useful reviews of this topic include:
- A book titled, The Pulsation Theory of Variable Stars, by S. Rosseland, 1969 (New York: Dover Publications, Inc.) … first published at the Clarendon Press, Oxford, in 1949.
- An Annual Reviews article titled, Pulsation Theory by Christy (1965) and Cox (1967)
Assembling the Key Relations
Governing Equations
After combining the Euler equation with the Poisson equation in essentially the manner outlined by the "structural solution strategy" we have called Technique 1, the relevant set of time-dependent governing equations is:
Equation of Continuity
<math>\frac{d\rho}{dt} = - \rho \biggl[\frac{1}{r^2}\frac{d(r^2 v_r)}{dr} \biggr]
= -\rho \biggl[ \frac{dv_r}{dr} + \frac{2v_r}{r} \biggr] </math>
Euler + Poisson Equations
<math>\frac{dv_r}{dt} = - \frac{1}{\rho}\frac{dP}{dr} - \frac{GM_r}{r^2} </math>
Adiabatic Form of the
First Law of Thermodynamics
<math>~\frac{d\epsilon}{dt} + P \frac{d}{dt} \biggl(\frac{1}{\rho}\biggr) = 0</math>
where,
<math>v_r \equiv \frac{dr}{dt}</math> ,
and, as before, the mass enclosed inside radius <math>r</math> is,
<math>M_r \equiv \int_0^r dm_r = \int_0^r 4\pi r^2 \rho dr</math> .
Consistent Lagrangian Formulation
The (Lagrangian) time derivatives in these equations define how a given physical parameter — for example, <math>~\rho</math>, <math>~v_r</math>, or <math>~\epsilon</math> — should vary with time in a (Lagrangian) fluid element that is not fixed in space but, rather, is moving along with the flow. However, the radial derivatives describe the spatial variation of various physical parameters as measured at fixed locations in space; that is, as written, the radial derivatives do not track conditions as viewed by a (Lagrangian) fluid element that is moving along with the flow because the position <math>r</math> of each (Lagrangian) fluid element is itself changing with time. A proper Lagrangian representation of the spatial derivatives can be formulated in the case of one-dimensional, spherically symmetric flows by using <math>~M_r</math> (or, equivalently, <math>~m_r</math>) instead of <math>~r</math> as the independent variable. Making the substitution,
<math>~\frac{d}{dr} = \frac{dM_r}{dr}\frac{d}{dM_r} = 4\pi \rho r^2 \frac{d}{dM_r} \, ,</math>
in the first two equations above gives, respectively,
<math>\frac{d\rho}{dt} = - 4\pi \rho^2 r^2 \frac{dv_r}{dM_r} - \frac{2\rho v_r}{r} \, ,</math>
and,
<math>\frac{dv_r}{dt} = - 4\pi r^2 \frac{dP}{dM_r} - \frac{GM_r}{r^2} \, .</math>
Supplemental Relations
As has been discussed elsewhere, in any analysis of time-dependent flows, the principal governing equations must be supplemented by adopting an equation of state for the gas and by specifying initial conditions. Here, initial conditions will be given by the structural properties — for example, <math>~\rho</math><math>(M_r)~</math> and <math>~P</math><math>(M_r)~</math> — of one of our derived, spherically symmetric equilibrium structures — for example, a uniform-density sphere or an <math>~n = 1</math> polytrope. We will adopt an ideal gas equation of state and, specifically, the relation,
<math>~P = (\gamma_\mathrm{g} - 1)\epsilon \rho </math>.
As a result, the adiabatic form of the <math>1^\mathrm{st}</math> law of thermodynamics can be written as,
<math> \rho \frac{dP}{dt} - \gamma_\mathrm{g} P \frac{d\rho}{dt} = 0 . </math>
Summary Set of Nonlinear Governing Relations
In summary, the following three one-dimensional ODEs define the physical relationship between the three dependent variables <math>~\rho</math>, <math>~P</math>, and <math>~r</math>, each of which should be expressible as a function of the two independent (Lagrangian) variables, <math>~t</math> and <math>~M_r</math>:
Equation of Continuity
<math>\frac{d\rho}{dt} = - 4\pi \rho^2 r^2 \frac{d}{dM_r}\biggl(\frac{dr}{dt}\biggr) - \frac{2\rho}{r} \biggl(\frac{dr}{dt}\biggr) </math>
,
Euler + Poisson Equations
<math>\frac{d^2 r}{dt^2} = - 4\pi r^2 \frac{dP}{dM_r} - \frac{GM_r}{r^2} </math>
Adiabatic Form of the
First Law of Thermodynamics
<math>
\rho \frac{dP}{dt} - \gamma_\mathrm{g} P \frac{d\rho}{dt} = 0 .
</math>
The Eigenvalue Problem
Here we adopt a notation and presentation very similar to what can be found in §38 of [KW94]. In particular, we will use <math>~m</math> rather than the more cumbersome <math>~M_r</math> to tag each (Lagrangian) mass shell, both initially and at all later times. As is customary in perturbation studies throughout the field of physics, we will assume that the pressure <math>~P(m,t)</math>, density <math>~\rho(m,t)</math>, and radial position <math>~r(m,t)</math> of each mass shell at any time <math>~t</math> can be written in the form,
|
<math>~P(m,t)</math> |
<math>~=</math> |
<math>~P_0(m) + P_1(m,t) = P_0(m) \biggl[1 + p(m) e^{i\omega t} \biggr] \, ,</math> |
|
<math>~\rho(m,t)</math> |
<math>~=</math> |
<math>~\rho_0(m) + \rho_1(m,t) = \rho_0(m) \biggl[1 + d(m) e^{i\omega t} \biggr] \, ,</math> |
|
<math>~r(m,t)</math> |
<math>~=</math> |
<math>~r_0(m) + r_1(m,t) = r_0(m) \biggl[1 + x(m) e^{i\omega t} \biggr] \, ,</math> |
where the subscript "1" denotes the variation of any variable away from its initial value (subscript 0) as drawn from the derived structure of the selected initial equilibrium model. These expressions encompass the hypothesis that, when perturbations away from the initial equilibrium state are sufficiently small — that is, <math>~|p|</math>, <math>~|d|</math>, and <math>~|x|</math> all <math>~\ll 1</math> — the perturbation can be treated as a product of functions that are separable in <math>~m</math> and <math>~t</math>, and that in general the time-dependent component can be represented by an exponential with an imaginary argument. The task is to solve a linearized version of the coupled set of key relations for the "eigenfunctions" <math>~p_i(m)</math>, <math>~d_i(m)</math>, and <math>~x_i(m)</math> associated with various characteristic "eigenfrequencies" <math>~\omega_i</math> of the underlying equilibrium model.
Linearizing the Key Equations
Adiabatic form of the First Law of Thermodynamics
Plugging the perturbed expressions for <math>~P(m,t)</math> and <math>~\rho(m,t)</math> into the adiabatic form of the First Law of Thermodynamics, we obtain,
|
<math>~(i\omega) \rho_0(m) \biggl[1 + d(m) e^{i\omega t} \biggr]P_0(m) p(m) e^{i\omega t} - \gamma_\mathrm{g}(i\omega) P_0(m) \biggl[1 + p(m) e^{i\omega t} \biggr] \rho_0(m) d(m) e^{i\omega t}</math> |
<math>~=</math> |
<math>~0</math> |
|
<math>~\Rightarrow ~~~~~ (i\omega) \rho_0(m)P_0(m) e^{i\omega t} \biggl\{\biggl[1 + d(m) e^{i\omega t} \biggr] p(m) - \gamma_\mathrm{g} \biggl[1 + p(m) e^{i\omega t} \biggr] d(m) \biggr\}</math> |
<math>~=</math> |
<math>~0 \, .</math> |
Because we are seeking solutions that will be satisfied throughout the configuration — that is, for all mass shells <math>~m</math> — the expression inside the curly brackets must be zero. Hence,
<math> ~p(m) - \gamma_\mathrm{g} d(m) + (1 - \gamma_\mathrm{g} ) d(m)p(m) e^{i\omega t} =0 \, . </math>
Also, because we are only examining deviations from the initial equilibrium state in which <math>~|d(m)|</math> and <math>~|p(m)|</math> are both <math>\ll 1</math>, then the third term on the left-hand-side of this equation, which contains a product of these two small quantities, must be much smaller than the first two terms. As is standard in perturbation theory throughout physics, for our stability analysis, we will drop this "quadradic" term and keep only terms that are linear in the small quantities. This leads to the following algebraic relationship between <math>~d(m)</math> and <math>~p(m)</math>:
<math> ~p = \gamma_\mathrm{g} d \, . </math>
Continuity Equation
Adopting the same approach, we will now "linearize" each term in the continuity equation:
|
<math> ~\frac{d\rho}{dt} </math> |
<math> \rightarrow </math> |
<math> (i\omega)\rho_0 d~e^{i\omega t} </math> |
|
<math> \frac{\rho}{r} </math> |
<math> \rightarrow </math> |
<math> \frac{\rho_0}{r_0} \biggl[1 + d e^{i\omega t} \biggr] \biggl[1 + x e^{i\omega t} \biggr]^{-1} \approx \frac{\rho_0}{r_0} \biggl[1 + d ~e^{i\omega t} \biggr]\biggl[1 - x~ e^{i\omega t} \biggr] \approx \frac{\rho_0}{r_0} \biggl[1 + (d - x) ~e^{i\omega t} \biggr]
</math> |
|
<math> \frac{dr}{dt} </math> |
<math> \rightarrow </math> |
<math> (i\omega) r_0 x~e^{i\omega t} </math> |
|
<math> ~\rho^2 r^2 </math> |
<math> \rightarrow </math> |
<math> \rho_0^2 r_0^2 \biggl[1 + d e^{i\omega t} \biggr]^2 \biggl[1 + x e^{i\omega t} \biggr]^2 \approx \rho_0^2 r_0^2 \biggl[1 + 2d ~e^{i\omega t} \biggr]\biggl[1 + 2x~ e^{i\omega t} \biggr] \approx \rho_0^2 r_0^2 \biggl[1 + 2(d + x) ~e^{i\omega t} \biggr] </math> |
|
<math> \frac{d}{dm}\biggl(\frac{dr}{dt}\biggr) </math> |
<math> \approx </math> |
<math> \frac{d}{dm}\biggl[(i\omega) r_0 x~e^{i\omega t}\biggr] = (i\omega) e^{i\omega t} \biggl[x\frac{dr_0}{dm} + r_0\frac{dx}{dm} \biggr] = (i\omega) e^{i\omega t} \biggl[\frac{x}{4\pi r_0^2 \rho_0} + r_0\frac{dx}{dm} \biggr] </math> |
In the last step of this last expression we have made use of the fact that, in the initial, unperturbed equilibrium model, <math>dr_0/dm = 1/(4\pi r_0^2 \rho_0)</math>. Combining all of these terms and linearizing the combined expression further, the linearized continuity equation becomes,
|
<math>~(i\omega)\rho_0 d~e^{i\omega t}</math> |
<math>~\approx</math> |
<math>~- \frac{2\rho_0}{r_0} \biggl[1 + (d - x) ~e^{i\omega t} \biggr] (i\omega) r_0 x~e^{i\omega t} - 4\pi \rho_0^2 r_0^2 \biggl[1 + 2(d + x) ~e^{i\omega t} \biggr](i\omega) e^{i\omega t} \biggl[\frac{x}{4\pi r_0^2 \rho_0} + r_0\frac{dx}{dm} \biggr]</math> |
|
<math>~\Rightarrow ~~~ \rho_0 d </math> |
<math>~\approx</math> |
<math>~- 3\rho_0 x - 4\pi \rho_0^2 r_0^3 \frac{dx}{dm}</math> |
|
<math>~\Rightarrow ~~~ 4\pi \rho_0 r_0^3 \frac{dx}{dm} </math> |
<math>~\approx</math> |
<math>~- 3 x - d \, ,</math> |
or,
<math> r_0 \frac{dx}{dr_0} \approx - 3 x - d , </math>
where, to obtain this last expression, we have switched back from differentiation with respect to <math>~m</math> to differentiation with respect to <math>~r_0</math>.
Euler + Poisson Equations
Finally, linearizing each term in the combined "Euler + Poisson" equation gives:
|
<math> \frac{d^2r}{dt^2} </math> |
<math> \rightarrow </math> |
<math> \frac{d}{dt}\biggl[(i\omega) r_0 x~e^{i\omega t}\biggr] = - \omega^2 r_0 x~e^{i\omega t} </math> |
|
<math> r^2 \frac{dP}{dm} </math> |
<math> \rightarrow </math> |
<math> r_0^2 \biggl[1 + x~ e^{i\omega t} \biggr]^2 \biggl\{\frac{dP_0}{dm} \biggl[1 + p~ e^{i\omega t} \biggr] + P_0~e^{i\omega t} \frac{dp}{dm} \biggr\} \approx r_0^2 \frac{dP_0}{dm} \biggl[1 + (2x+p)~ e^{i\omega t} \biggr] + P_0 r_0^2~e^{i\omega t} \frac{dp}{dm} </math> |
|
<math> \frac{Gm}{r^2} </math> |
<math> \rightarrow </math> |
<math> \frac{Gm}{ r_0^2} \biggl[1 + x~ e^{i\omega t} \biggr]^{-2} \approx \frac{Gm}{ r_0^2} \biggl[1 -2 x~ e^{i\omega t} \biggr] \, . </math> |
Hence, the combined linearized relation is,
<math>
- \omega^2 r_0 x~e^{i\omega t} \approx -4\pi \biggl\{r_0^2 \frac{dP_0}{dm} \biggl[1 + (2x+p)~ e^{i\omega t} \biggr] + P_0 r_0^2~e^{i\omega t} \frac{dp}{dm} \biggr\} - \frac{Gm}{ r_0^2} \biggl[1 -2 x~ e^{i\omega t} \biggr]
</math>
<math>
\Rightarrow ~~~~~ e^{i\omega t} \biggl\{(2x + p)4\pi r_0^2 \frac{dP_0}{dm}-2x \frac{Gm}{r_0^2} + 4\pi P_0 r_0^2 \frac{dp}{dm} -\omega^2 r_0 x \biggr\} \approx - 4\pi r_0^2 \frac{dP_0}{dm} - \frac{Gm}{r_0^2}
</math>
<math>
\Rightarrow ~~~~~ 4\pi P_0 r_0^2 \frac{dp}{dm} \approx (4x + p)g_0 + \omega^2 r_0 x \, ,
</math>
where, in order to obtain this last expression we have made use of the fact that, in the unperturbed equilibrium configuration,
<math>
g_0(m) \equiv \frac{Gm}{r_0^2} = - 4\pi r_0^2 \frac{dP_0}{dm} = - \frac{1}{\rho_0} \frac{dP_0}{dr_0} \, .
</math>
Switching back from differentiation with respect to <math>~m</math> to differentiation with respect to <math>~r_0</math>, the "Euler + Poisson" combined linearized relation can alternatively be written as,
<math>
\frac{P_0}{\rho_0} \frac{dp}{dr_0} \approx (4x + p)g_0 + \omega^2 r_0 x .
</math>
Summary Set of Linearized Equations
In summary, the following three linearized equations describe the physical relationship between the three dimensionless perturbation amplitudes <math>~p(r_0)</math>, <math>~d(r_0)</math> and <math>~x(r_0)</math>, for various characteristic eigenfrequencies, <math>~\omega</math>:
|
Linearized Linearized Linearized |
It is customary to combine these three relations to obtain a single, second-order ODE in terms of the fractional displacement, <math>~x</math> as follows. Using the third expression to replace <math>~d</math> by <math>~p</math> in the first expression, then differentiating the first expression with respect to <math>~r_0</math> generates,
|
<math>~\frac{d}{dr_0} \biggl[ r_0 \frac{dx}{dr_0}\biggr]</math> |
<math>~=</math> |
<math>~- \frac{d}{dr_0}\biggl[ 3 x + \frac{p}{\gamma_\mathrm{g}} \biggr]</math> |
|
<math>~\Rightarrow ~~~~~ r_0 \frac{d^2x}{dr_0^2} + 4 \frac{dx}{dr_0}</math> |
<math>~=</math> |
<math>~- \frac{1}{\gamma_\mathrm{g}} \frac{dp}{dr_0} \, .</math> |
Similarly, replacing <math>~p</math> by <math>~d</math> in the second expression, then using the first expression to eliminate <math>~d</math> gives,
|
<math>~\frac{P_0}{\rho_0} \frac{dp}{dr_0}</math> |
<math>~=</math> |
<math>~\biggl[4x + \gamma_\mathrm{g}\biggl( -3x -r_0\frac{dx}{dr_0} \biggr) \biggr] g_0 + \omega^2 r_0 x </math> |
|
<math>~\Rightarrow ~~~~~ \frac{1}{\gamma_\mathrm{g}} \frac{dp}{dr_0}</math> |
<math>~=</math> |
<math>~- \frac{dx}{dr_0} \biggl(\frac{r_0 g_0 \rho_0}{P_0}\biggr) + \biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] \biggl(\frac{r_0 \rho_0}{\gamma_\mathrm{g} P_0} \biggr) x \, .</math> |
Finally, then, combining these two expressions gives the desired 2nd-order ODE, which we will henceforth refer to as the,
LAWE: Linear Adiabatic Wave (or Radial Pulsation) Equation
|
<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 </math> |
After deriving this equation in his review article titled, Pulsating Stars (see related information, below),
Cox (1974) offers the following immediate observation: If the motion following a perturbation were homolgous — that is, if <math>~x \equiv \delta r/r_0</math> were constant in space — then the terms involving the first and second derivatives of <math>~x</math> would vanish. These terms therefore arise solely from differential expansion or compression of the configuration's layers. For the idealized case of homologous oscillations, the governing linearized equation becomes,
<math>~\omega^2 = (3\gamma_g - 4) \frac{g_0}{r_0} \, .</math>
The physical interpretation of this relation is that stable oscillatory motion <math>~(\omega^2 > 0)</math> is possible only for <math>~\gamma_g > 4/3 \, .</math> Otherwise, for <math>~\gamma_g < 4/3 \, ,</math> "the motion will be aperiodic on a time scale which is seen to be of the general order of magnitude of the … free-fall time … [and] this behaviour corresponds to dynamical instability …"
Boundary Conditions
Two boundary conditions must accompany the derived, 2nd-order ODE. It is customary to establish one of these conditions at the center of the spherically symmetric configuration, and the other at the surface.
Inner Boundary
In order for the solution to be physically reasonable, the eigenfunction, <math>~x(r_0)</math>, must be "regular" at the center of the configuration. This demand will be met if the function's first derivative goes to zero at the center, that is, if,
<math>~\frac{dx}{dr_0} = 0</math> at <math>~r_0 = 0 \, .</math>
Outer Boundary
Set the Surface Pressure Fluctuation to Zero
Using the above "Linearized Adiabatic Form of the First Law of Thermodynamics" to replace the fractional density variation, <math>~d</math>, in favor of the fractional pressure variation, <math>~p</math> in the above "Linearized Equation of Continuity", gives,
|
<math>~p</math> |
<math>~=</math> |
<math>~-\gamma_g \biggl( 3 x + r_0 \frac{dx}{dr_0} \biggr) \, .</math> |
Ledoux & Pekeris (1941; see additional discussion below) suggest that an adequate outer boundary condition is provided by setting the fractional pressure fluctuation, <math>~p</math>, to zero at the surface. Leaning on this just-derived relation, therefore, they recommend (see their equation 4) imposing the following surface boundary constraint on the fractional radial variation, <math>~x</math>:
|
<math>~-\gamma_g \biggl( 3 x + r_0 \frac{dx}{dr_0} \biggr)</math> |
<math>~=</math> |
<math>~0</math> at <math>~r_0 = R \, .</math> |
Ensure Finite-Amplitude Fluctuations
Here we follow the discussion provided by J. P. Cox (1967); specifically, the relevant discussion begins in the middle of p. 21, in association with Cox's equation (3.7). Text drawn directly from J. P. Cox (1967) is presented here in green.
At the surface <math>~(r_0 = R)</math> of our oscillating, spherically symmetric configuration we must require, in general, that all relative pulsation variables … be finite. The specific surface condition can be obtained most generally from the above derived,
Linearized Euler + Poisson Equations
<math>
\frac{P_0}{\rho_0} \frac{dp}{dr_0} = (4x + p)g_0 + \omega^2 r_0 x .
</math>
Multiplying through by <math>~(R\rho_0/P_0)</math> and remembering that
<math>g_0 = - \frac{1}{\rho_0} \frac{dP_0}{dr_0} \, ,</math>
this relation assumes the form of equation (3.7) in J. P. Cox (1967), namely,
|
<math>~R \frac{dp}{dr_0}</math> |
<math>~=</math> |
<math>~- \frac{R}{P_0} \frac{dP_0}{dr_0}\biggl[(4x + p) + \frac{\omega^2 r_0 x}{g_0} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{R}{\lambda_p}\biggl[(4x + p) + \frac{\omega^2 r_0 x}{g_0} \biggr] \, ,</math> |
where, as is highlighted by Cox in association with his equation (2.42'),
<math>~\lambda_p \equiv -\biggl(\frac{d\ln P_0}{dr_0} \biggr)^{-1} \, ,</math>
is the (equilibrium) pressure scale height of the configuration. (Note that, the pressure scale height is often represented by the variable, <math>~H</math>, instead of <math>~\lambda_p</math>.)
Since <math>~R/\lambda_p \gg 1</math> at the photosphere for most stars (and <math>~R/\lambda_p = \infty</math> if <math>~P/\rho</math> is assumed to vanish at the surface), a reasonable surface boundary condition would be to force the terms inside the square brackets on the right-hand side of this expression to sum to zero, that is, for the pressure fluctuation to obey the relation,
|
<math>~p</math> |
<math>~=</math> |
<math>~-\biggl(4 + \frac{\omega^2 r_0 }{g_0} \biggr)x </math> |
|
|
<math>~=</math> |
<math>~-\biggl( 4 + \frac{\omega^2 R^3}{GM_\mathrm{tot}}\biggr) x</math> at <math>~r_0 = R \, .</math> |
This boundary condition prevents <math>~dp/dr_0</math> from having a large (or infinite) value at <math>~r_0 = R</math> and also requires that <math>~p</math> be finite at <math>~r_0 = R</math> even if <math>~P_0 = 0</math> here. This is the surface boundary condition specified in two key review articles on this subject — one by R. F. Christy (1965; see discussion below) and another, almost a decade later, by J. P. Cox (1974; see additional discussion below).
Christy (1965) and Cox (1967) also point out that, by calling upon the above "Linearized Adiabatic Form of the First Law of Thermodynamics" to replace the fractional pressure variation, <math>~p</math>, in favor of the fractional density variation, <math>~d</math>; then using the above "Linearized Equation of Continuity" to replace <math>~d</math> in favor of the fractional radial displacement, <math>~x</math>, the same boundary condition may be written as,
|
<math>~- \gamma_g d</math> |
<math>~=</math> |
<math>~\biggl( 4 + \frac{\omega^2 R^3}{GM_\mathrm{tot}}\biggr) x</math> |
|
<math>~\Rightarrow ~~~~~ 3 x + r_0 \frac{dx}{dr_0}</math> |
<math>~=</math> |
<math>~\biggl( 4 + \frac{\omega^2 R^3}{GM_\mathrm{tot}}\biggr) \frac{x}{\gamma_g}</math> |
|
<math>~\Rightarrow ~~~~~ r_0 \frac{d\ln x}{dr_0}</math> |
<math>~=</math> |
<math>~\frac{1}{\gamma_g} \biggl( 4 - 3\gamma_g + \frac{\omega^2 R^3}{GM_\mathrm{tot}}\biggr) </math> at <math>~r_0 = R \, ,</math> |
which, as Cox (1967) summarizes (see following his equation 3.9), gives the logarithmic slope <math>~d\ln x/dr_0</math> of the relative pulsation amplitude <math>~x</math> at <math>~r_0 = R</math> in terms of <math>~\gamma_g</math> and the dimensionless frequency <math>~\omega^2R^3/GM_\mathrm{tot}</math> and assures that both <math>~x</math> and <math>~dx/dr_0</math> are finite at <math>~r_0 = R</math>. This is the boundary condition conventionally used in connection with the adiabatic wave equation.
Ignore Atmospheric Inertia
Here we echo the discussion presented in §38.1 of [KW94], where an alternative boundary condition at the surface of our spherically symmetric, oscillating configuration is recommended; text drawn verbatim from this reference is shown here in green. We simplify the atmosphere by assuming its mass <math>~m_a</math> to be comprised in a thin layer at <math>~r_0 = R(t)</math>, which follows the changing <math>~R</math> during the oscillations and provides the outer boundary condition at each moment by its weight. This amounts to ignoring the inertia of this very thin, nearly massless layer and is accomplished, in practice, by setting to zero the second time-derivative on the left-hand side of the above "Euler + Poisson Equation". Hence, the pressure, <math>~P_b</math>, at the base of the outermost (atmospheric) layer of the oscillating configuration is described, at all times, by,
|
<math>~\cancelto{0}{\frac{d^2 r}{dt^2}}</math> |
<math>~\approx</math> |
<math>~- 4\pi r^2 \frac{dP}{dM_r} - \frac{GM_r}{r^2}</math> |
|
<math>~\Rightarrow ~~~~~ \frac{GM_\mathrm{tot}}{4\pi R^4}</math> |
<math>~\approx</math> |
<math>~- \frac{dP}{dM_r} </math> |
|
|
<math>~\approx</math> |
<math>~- \frac{\Delta P}{\Delta M_r} = - \frac{(0 - P_b)}{m_a} = \frac{P_b}{m_a} \, .</math> |
Appreciating that <math>~R</math> and <math>~P_b</math> are the only time-varying quantities in this expression, perturbing then linearizing the expression gives (at <math>~r_0 = R</math>),
|
<math>~(P_b)_0[1 + p e^{i\omega t}]</math> |
<math>~=</math> |
<math>~\frac{GM_\mathrm{tot} m_a}{4\pi R_0^4}\biggl[ 1 + x e^{i\omega t} \biggr]^{-4}</math> |
|
<math>~\Rightarrow ~~~~~ 1 + p e^{i\omega t}</math> |
<math>~\approx</math> |
<math>~1 -4 x e^{i\omega t} </math> |
|
<math>~\Rightarrow ~~~~~ p + 4x</math> |
<math>~=</math> |
<math>~0</math> at <math>~r_0 = R \, .</math> |
This is identical to the boundary condition presented as equation (38.12) in [KW94]. Combining this condition with the above "linearized adiabatic form of the first law of thermodynamics" allows us to write, as well,
|
<math>~ \gamma_g d + 4x</math> |
<math>~=</math> |
<math>~0</math> at <math>~r_0 = R \, ;</math> |
and, in combination with the above "linearized continuity equation", to also conclude that,
|
<math>~ r_0 \frac{dx}{dr_0}</math> |
<math>~=</math> |
<math>~-3x + \frac{4x}{\gamma_g}</math> |
|
<math>~ \Rightarrow ~~~~~ \biggl( \frac{r_0}{x} \biggr) \frac{dx}{dr_0}</math> |
<math>~=</math> |
<math>~\frac{1}{\gamma_g} (4-3\gamma_g )</math> at <math>~r_0 = R \, .</math> |
This matches the boundary condition, as presented in equation (38.13) of [KW94].
Implications
First Case: If the surface pressure fluctuation is set to zero, we have just deduced that, at the surface of the configuration,
<math>~3 x + r_0 \frac{dx}{dr_0} =0 \, .</math>
This implies that,
|
<math>~\frac{d\ln x}{d\ln r_0}</math> |
<math>~=</math> |
<math>~-3</math> |
|
<math>~\Rightarrow ~~~~ d\ln x</math> |
<math>~=</math> |
<math>~-3d\ln r_0</math> |
|
<math>~\Rightarrow ~~~~ \ln x </math> |
<math>~=</math> |
<math>~\ln C_0 - 3\ln r_0</math> |
|
<math>~\Rightarrow ~~~~ x </math> |
<math>~=</math> |
<math>~\frac{C_0}{r_0^3} \, .</math> |
It is customary to normalize the radial eigenfunction, <math>~x</math>, in such a way that it goes to unity at the surface. Therefore, in order to satisfy this "first case" boundary condition, at the surface of the oscillating configuration, the eigenfunction must display the behavior,
<math>~x = \biggl( \frac{R}{r_0}\biggr)^{3} \, .</math>
Second Case: If, instead, we insist that the first derivative of the surface pressure fluctuation be zero, then, as we have just deduced,
|
<math>~\biggl( 4 - 3\gamma_g + \frac{\omega^2 r_0}{g_0}\biggr) \frac{x}{\gamma_g}-r_0 \frac{dx}{dr_0}</math> |
<math>~=</math> |
<math>~0</math> at <math>~r_0 = R \, .</math> |
But, rearranging terms in the full linear adiabatic wave equation, we see that, throughout the entire structure (including the surface),
|
<math>~ \biggl(\frac{g_0 \rho_0 }{P_0 r_0} \biggr)\biggl[\biggl(4 - 3\gamma_\mathrm{g} + \frac{\omega^2 r_0}{g_0} \biggr) \frac{x}{\gamma_\mathrm{g}} - r_0 \frac{dx}{dr_0}\biggr]</math> |
<math>~=</math> |
<math>~- \biggl[ \frac{d^2x}{dr_0^2} + \biggl(\frac{4}{r_0}\biggr)\frac{dx}{dr_0} \biggr] \, .</math> |
Since, according to the "second case" surface boundary condition, the term inside the square brackets on the left-hand side of this expression must be zero at the surface, it must also be true that the term inside the square brackets on the right-hand side is zero. That is, the "second case" boundary condition will be satisfied if,
|
<math>~\frac{d^2x}{dr_0^2} + \biggl(\frac{4}{r_0}\biggr)\frac{dx}{dr_0} </math> |
<math>~=</math> |
<math>~0</math> at <math>~r_0 = R </math> |
|
<math>~\Rightarrow ~~~~~\frac{1}{r_0^4} \cdot \frac{d}{dr_0}\biggl[ r_0^4\frac{dx}{dr_0} \biggr]</math> |
<math>~=</math> |
<math>~0</math> |
|
<math>~\Rightarrow ~~~~~r_0^4\frac{dx}{dr_0} </math> |
<math>~=</math> |
<math>~C_0</math> |
|
<math>~\Rightarrow ~~~~~dx </math> |
<math>~=</math> |
<math>~C_0 r_0^{-4} dr_0</math> |
|
<math>~\Rightarrow ~~~~~x </math> |
<math>~=</math> |
<math>~C_1 - \biggl(\frac{C_0}{3} \biggr) r_0^{-3} </math> at <math>~r_0 = R \, .</math> |
Again, given that it is customary to normalize the radial eigenfunction, <math>~x</math>, such that it goes to unity at the surface, the eigenfunction must display the behavior,
<math>~x = 1 + \frac{C_0}{3}\biggl(\frac{1}{R^3} - \frac{1}{r_0^3} \biggr) \, ,</math>
at the surface of the oscillating configuration in order to satisfy this "second case" boundary condition.
Third Case: If we follow the lead of [KW94] and choose to establish a surface boundary condition that effectively ignores the inertia of the configuration's atmosphere, then, as we have just determined,
|
<math>~\frac{d\ln x}{d \ln r_0}</math> |
<math>~=</math> |
<math>~- 3 + \frac{4}{\gamma_g} </math> at <math>~r_0 = R \, .</math> |
As in the "first case" discussed above, this constraint leads to a power-law <math>~x(r_0)</math> behavior at the surface. Specifically, this "third case" boundary condition — along with the convention that <math>~x \rightarrow 1</math> at the surface — demands an eigenfunction whose behavior at the surface is,
<math>~x = \biggl( \frac{R}{r_0}\biggr)^{3-4/\gamma_g} \, .</math>
What Makes This an Eigenvalue Problem?
Our own study of radial oscillations in spherically symmetric, self-gravitating fluids has fostered the following appreciation. Generally, with knowledge only of the boundary condition at the center of the configuration and an associated power-series expansion that provides a description of the displacement function, <math>x(r_0)</math>, near the center — see, for example, the expansion that is appropriate for polytropic or for isothermal spheres — the LAWE can be straightforwardly integrated (numerically) from the center, outward to (or at least very near to) the surface for practically any specified value of the (square of the) oscillation frequency, <math>~\omega^2</math>. As a result, integration from the center, outward, can very naturally generate a continuous spectrum of displacement functions, if the integration is unconstrained by specification of an outer boundary condition. This is illustrated, for example, by Figure 2 in our discussion of oscillating n = 3 polytropes. Typically, at low frequencies, the displacement function exhibits no, or only a few, radial nodes; but the number of radial nodes that reside within the volume of the configuration steadily grows as the specified frequency increases.
The continuous spectrum is transformed into a discrete spectrum of oscillation modes when the outward integration is forced to generate a displacement function whose behavior at the configuration's surface matches a specific surface boundary condition. For example, as described above, if the aim is to ensure that there are no pressure fluctuations at the surface throughout an oscillation, then the only physically relevant displacement functions are the ones whose logarithmic radial derivative at the surface is negative three. And each of these relevant displacement functions — now, an eigenfunction — will be associated with a discrete value the oscillation frequency — the associated eigenfrequency. Understanding this interplay between a derived solution to the LAWE and the imposed boundary condition helps clarify why this is an eigenvalue problem.
Classic Papers that Derive & Use this Relation
Eddington (1926)
To our knowledge, a derivation of this governing 2nd-order ODE was first presented by A. S. Eddington (1926) in a book titled, The Internal Constitution of the Stars. (This entire book has been digitally scanned and is now available online.) The derived expression, which appears on p. 188 as equation (127.6) of Eddington's book, is presented in the following, framed image.
| Pulsation equation extracted† from p. 188 of A. S. Eddington (1926) "The Internal Constitution of the Stars"(Cambridge: Cambridge University Press) |
|---|
| †Mathematical expressions have been displayed here, as a single digital image, with a layout that is modified from the original publication. |
The similarity between Eddington's expression and the governing 2nd-order ODE that we have derived is immediately apparent. Specifically, simply after inserting Eddington's definition of his composite variable, <math>~\mu</math>, and making the substitutions,
<math>~\xi_1 \rightarrow x \, ,</math> <math>\xi_0 \rightarrow r_0 \, ,</math> and <math>n^2 \rightarrow \omega^2 \, ,</math>
Eddington's pulsation equation becomes,
|
<math>~ \frac{d^2 x}{dr_0^2} + \biggl[ \frac{4}{r_0} - \frac{g_0 \rho_0}{P_0} \biggr] \frac{dx}{dr_0} + \frac{\rho_0}{\gamma P_0} \biggl\{\omega^2 + \biggl(4 - 3\gamma\biggr) \frac{g_0 }{r_0} \biggr\}x </math> |
<math>~=</math> |
<math>~0 \, ,</math> |
which exactly matches our derived governing relation.
Ledoux and Pekeris (1941)
Historically, by the 1940s, the expression just derived was a relatively familiar one to astrophysicists. For example, the opening paragraph of a 1941 paper by Ledoux & Pekeris (1941, ApJ, 94, 124), reads:
|
Paragraph extracted from P. Ledoux & C. L. Pekeris (1941)
"Radial Pulsations of Stars"
ApJ, vol. 94, pp. 124-135 © American Astronomical Society |
If we divide their equation (1) through by <math>~Xr = \Gamma_1 P r</math> and recognize that,
<math> \frac{dX}{dr} = \frac{dX}{dm}\frac{dm}{dr} = - \Gamma_1 g_0 \rho \, , </math>
we obtain,
<math> \frac{d^2\xi}{dr^2} + \biggl[ \frac{4}{r} - \frac{g_0 \rho}{P} \biggr] \frac{d\xi}{dr} +\frac{\rho}{\Gamma_1 P} \biggl[ \sigma^2 + (4 - 3\Gamma_1) \frac{g_0}{r} \biggr] \xi = 0 \, . </math>
This is clearly the same <math>2^\mathrm{nd}</math>-order, ordinary differential equation as the one we have derived, but with a more general definition of the adiabatic exponent that allows consideration of a situation where the total pressure is a sum of both gas and radiation pressure.
Schwarzschild (1941)
In the same volume of The Astrophysical Journal, Schwarzschild (1941) published work on "Overtone Pulsations for the Standard [Stellar] Model." The following excerpt has been drawn from the first page of this article.
|
Paragraph extracted from M. Schwarzschild (1941)
"Overtone Pulsations for the Standard Model"
ApJ, vol. 94, pp. 245 - 252 © American Astronomical Society |
|
3A. S. Eddington (1930), The Internal Constitution of the Stars, pp. 188 and 192. |
The similarity between Schwarzschild's "pulsation equation" and the governing 2nd-order ODE that we have derived is immediately apparent; for example, the eigenfrequency, <math>~\omega</math>, is the same in both,
<math>~\xi_1 \leftrightarrow x</math> and <math>\xi_0 \leftrightarrow r_0 \, .</math>
But the two equations are not exactly the same. To show this, we begin by comparing the last term on the lefthand-side in both expressions and presume that Schwarzschild's <math>~u</math> is related to the state variables in our equation as,
<math>u = \frac{\gamma_g P_0}{\rho_0} \, .</math>
Restricting the discussion to only polytropic equations of state — that is, <math>~P_0 = K\rho_0^{(n+1)/n}</math> — we can write,
|
<math>~u</math> |
<math>~=</math> |
<math>~\gamma_g K\rho_0^{1/n} \, ,</math> |
which means that,
|
<math>~\frac{du}{d\xi_0}</math> |
<math>~=</math> |
<math>~\biggl( \frac{\gamma_g K}{n} \biggr) \rho_0^{(1-n)/n} \frac{d\rho_0}{d\xi_0} = \biggl( \frac{\gamma_g}{n+1} \biggr) \frac{1}{\rho_0} \frac{dP_0}{d\xi_0} = - \biggl( \frac{\gamma_g}{n+1} \biggr) g_0 \, ,</math> |
where the last step results from recalling that, by our definition above, the unperturbed gravitational acceleration is,
<math>g_0 = - \frac{1}{\rho_0} \frac{dP_0}{dr_0} \, .</math>
Hence, when considering polytropic configurations, the following substitutions are appropriate between the two equations:
<math>\frac{du}{d\xi_0} \leftrightarrow - \biggl( \frac{\gamma_g}{n+1} \biggr) g_0 </math> and <math>\frac{1}{u} \frac{du}{d\xi_0} \leftrightarrow - \frac{1}{(n+1)} \frac{g_0 \rho_0}{P_0} \, .</math>
Making these substitutions into Schwarzschild's pulsation equation gives,
|
<math> \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \frac{4}{(n+1)}\biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 - \biggl( \frac{4a\gamma_g}{n+1} \biggr)\frac{g_0}{r_0} \biggr] x = 0 \, . </math> |
Appreciating that, in Schwarzschild's expression, <math>~a \equiv - (4-3\gamma_g)/\gamma_g</math>, we see that our expression matches his if and only if <math>~n=3</math>. This is, indeed, precisely the "standard model" that Schwarzschild was considering.
In a separate chapter that discusses the radial oscillations of n =3 polytropes, we provide a much more in-depth review of this published investigation by Schwarzshild.
Review Article by Christy (1966)
In the review by R. F. Christy (1966) titled, Pulsation Theory, this key 2nd-order ODE appears as equation (5) in the form shown by the following boxed-in (slightly edited) excerpt:
|
Pulsation Equation extracted† from R. F. Christy (1966)
"Pulsation Theory"
Annual Review of Astronomy & Astrophysics®, vol. 4, pp. 353 - 392 © Annual Reviews |
|---|
|
†Mathematical expressions displayed here, as a single digital image, with presentation order & layout modified from the original publication.
®Copyright 2015 Annual Reviews. All rights reserved. The Annual Reviews logo, and other Annual Reviews products referenced herein are either registered trademarks or trademarks of Annual Reviews. All other marks are the property of their respective owner and/or licensor. |
Correspondence with our derived equation becomes clear by appreciating that Christy's <math>~x \equiv r_0/R</math> and that,
<math>GM(x) = g_0 r_0^2 \, ,</math>
hence,
<math>V(x) \rightarrow \frac{g_0 \rho_0 r_0}{P_0} \, .</math>
Making these substitutions and multiplying Christy's equation through by <math>~R^{-2}</math> gives,
|
<math>~ \frac{d^2\xi}{dr_0^2} + \biggl[ \frac{4}{r_0} - \frac{g_0 \rho_0}{P_0} \biggr]\frac{d\xi}{dr_0} + \frac{\rho_0}{\gamma_g P_0 } \biggl[(4-3\gamma_g)\frac{g_0}{r_0} + \omega^2 \biggr] \xi </math> |
<math>~=</math> |
<math>~ 0\, . </math> |
Review Article by Cox (1974)
In an excellent review of "Pulsating Stars", J. P. Cox (1974, Reports on Progress in Physics, 37, 563) presents a full derivation of, what he refers to as, the adiabatic wave equation. It appears as equation (5.34) in the form displayed in the following boxed-in image:
|
Adiabatic Wave Equation extracted† from J. P. Cox (1974)
"Pulsating Stars"
Reports on Progress in Physics, vol. 37, pp. 563 - 698 © IOP Publishing |
|---|
| †Equation displayed here, as a single digital image, exactly as it appears in the original publication. |
Recognizing the correspondence with our derived expression requires, first, switching the independent variable from <math>~m</math> to <math>~r_0</math> via the relation identified, above, namely,
|
<math>~ \frac{d}{dm} </math> |
<math>~=</math> |
<math>~ \frac{1}{4\pi \rho_0 r_0^2} \cdot \frac{d}{dr_0} \, , </math> |
to obtain,
|
<math>~ \sigma^2 \xi </math> |
<math>~=</math> |
<math>~ - \frac{1}{(4\pi \rho_0 r_0^4)}\frac{d}{dr_0}\biggl[ (4\pi \Gamma_1 P_0 r_0^4) \frac{d\xi}{dr_0} \biggr] - \frac{1}{\rho_0 r_0} \biggl\{ \frac{d}{dr_0} [ (3\Gamma_1-4)P_0] \biggr\} \xi </math> |
|
|
<math>~=</math> |
<math>~ - \frac{\Gamma_1 P_0 }{\rho_0 }\frac{d^2 \xi}{dr_0^2} - \frac{\Gamma_1 }{(\rho_0 r_0^4)} \biggl[4P_0 r_0^3 + r_0^4\frac{dP_0}{dr_0} \biggr] \frac{d\xi}{dr_0} + \frac{(4-3\Gamma_1)}{\rho_0 r_0} \biggl[ \frac{dP_0}{dr_0} \biggr] \xi </math> |
|
<math>~\Rightarrow ~~~~ 0</math> |
<math>~=</math> |
<math>~ - \frac{\Gamma_1 P_0 }{\rho_0 }\biggl\{ \frac{d^2 \xi}{dr_0^2} + \biggl[\frac{4}{r_0} + \frac{1}{P_0}\frac{dP_0}{dr_0} \biggr] \frac{d\xi}{dr_0} \biggr\} - \biggl\{ \sigma^2 - \frac{(4-3\Gamma_1)}{\rho_0 r_0} \biggl[ \frac{dP_0}{dr_0} \biggr] \biggr\} \xi \, . </math> |
Then, using the definition of <math>~g_0</math>, also as provided above, to facilitate the substitution,
<math>~\frac{dP_0}{dr_0} \rightarrow - g_0 \rho_0 \, ,</math>
gives,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{d^2 \xi}{dr_0^2} + \biggl[\frac{4}{r_0} - \frac{g_0 \rho_0}{P_0}\biggr] \frac{d\xi}{dr_0} + \frac{\rho_0 }{\Gamma_1 P_0 }\biggl\{ \sigma^2 + \frac{(4-3\Gamma_1)g_0}{r_0} \biggr\} \xi \, , </math> |
which, apart from the adoption of different variable names, exactly matches our derived expression.
Bonnor (1957)
In a paper titled, "Jeans' Formula for Gravitational Instability," Bonnor (1957, MNRAS, 117, 104) carried out a linear perturbation analysis, preferring to examine the development of Eulerian fluctuations in the matter density rather than the development of Lagrangian position displacements. Here we show the relationship between his approach to a perturbation analysis and the one that we have focused on, above.
Linearized Equations on a Static Background
First, we examine how Bonnor's (1957) linearized Euler equation (2.7) was derived from the nonlinear Euler equation, numbered (2.1) in his paper.
|
Bonnor's (1957, MNRAS, 117, 104) Derivation |
||
|---|---|---|
|
Original nonlinear Euler Equation |
<math>~\rightarrow</math> |
Linearized Euler Equation |
As has been made clear in our introductory discussions, the
Eulerian Representation
of the Euler Equation,
<math>~\frac{\partial\vec{v}}{\partial t} + (\vec{v}\cdot \nabla) \vec{v}= - \frac{1}{\rho} \nabla P - \nabla \Phi</math>
can be counted among the principal set of equations that govern the dynamics of self-gravitating fluids. Accepting that he uses the boldface variable <math>~\mathbf{u}</math> instead of <math>~\vec{v}</math> to represent the fluid velocity, we see that the lefthand side of Bonnor's equation (2.1) exactly matches the lefthand side of the Euler equation, as we have presented it. The term on the righthand side of Bonnor's equation (2.1) that involves a gradient in the gas pressure also matches ours. What remains is to recognize that, in Bonnor's paper,
|
<math>~\mathbf{F}</math> |
<math>~=</math> |
<math>~- \nabla\Phi \, .</math> |
This is confirmed by Bonnor's equation (2.6), which presents another one of our identified set of principal governing equations, namely the
in terms of the vector, <math>~\mathbf{F}</math>, specifically,
|
<math>~\nabla\cdot\mathbf{F}</math> |
<math>~= - \nabla^2\Phi =</math> |
<math>~-4\pi G \rho \, .</math> |
As we have done in our development of the eigenvalue problem, Bonnor (1957) began the process of linearizing the Euler equation by writing each physical variable in terms of its initial, unperturbed value (denoted by subscript "0") plus a "small quantity." For example, he wrote,
|
<math>~\mathbf{u}</math> |
<math>~=</math> |
<math>~\mathbf{u}_0 + \mathbf{u} \, ,</math> |
|
<math>~\mathbf{F}</math> |
<math>~=</math> |
<math>~\mathbf{F}_0 + \mathbf{F}_1 </math> … and we, furthermore, will write … <math>~\mathbf{F}_0 = -\nabla \Phi_0</math> and <math>~\mathbf{F}_1 = - \nabla \Phi_1 \, ,</math> |
|
<math>~\rho</math> |
<math>~=</math> |
<math>~\rho_0 + w \, ,</math> |
|
<math>~\rho</math> |
<math>~=</math> |
<math>~P_0 + q \, .</math> |
[For future reference, notice that the perturbation variable names that we introduced for density and pressure — see above — are different from the ones used by Bonner. They are related via the expressions, <math>(\rho_0 d e^{i\omega t}) \leftrightarrow w</math> and <math>(P_0 p e^{i\omega t}) \leftrightarrow q</math>.] He also initially assumed, as have we, that the unperturbed system is in hydrostatic balance, so,
|
<math>~\mathbf{u}_0</math> |
<math>~=</math> |
<math>~0 \, ,</math> |
|
<math>~\mathbf{F}_0</math> |
<math>~=</math> |
<math>~\frac{1}{\rho_0} \nabla P_0 \, .</math> |
Notice that — confusion notwithstanding — Bonnor did not affix a subscript to the variable being used to represent the velocity perturbation, at least not initially. So, after setting <math>~\mathbf{u}_0 = 0</math>, the generic velocity vector, <math>~\mathbf{u}</math>, on the lefthand side of his equation (2.1) becomes the small in magnitude velocity perturbation, <math>~\mathbf{u}</math>, on the lefthand side of his equation (2.7); and, in his equation (2.7), the <math>~(\mathbf{u}\cdot \nabla)\mathbf{u}</math> term disappears altogether because it involves the product of two quantities that are both small in magnitude. Although details of the derivation are not presented in Bonnor's (1957) paper, it is reasonable to assume that he took the following steps in linearizing the righthand side of equation (2.1):
|
RHS of equation (2.1) |
<math>~\rightarrow</math> |
<math>~\mathbf{F}_0 + \mathbf{F}_1 - \frac{1}{(\rho_0 + w)} \nabla(P_0 + q) </math> |
|
|
<math>~=</math> |
<math>~\mathbf{F}_0 + \mathbf{F}_1 - \frac{1}{\rho_0} \biggl(1 + \frac{w}{\rho_0} \biggr)^{-1}\nabla(P_0 + q) </math> |
|
|
<math>~\approx</math> |
<math>~\mathbf{F}_0 + \mathbf{F}_1 - \frac{1}{\rho_0} \biggl(1 - \frac{w}{\rho_0} \biggr)\nabla(P_0 + q) </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \mathbf{F}_0 - \frac{1}{\rho_0}\nabla P_0 \biggr] + \mathbf{F}_1 - \frac{1}{\rho_0} \nabla q + \biggl(\frac{w}{\rho_0^2} \biggr)\nabla P_0 + \biggl(\frac{w}{\rho_0^2} \biggr)\nabla q</math> |
|
|
<math>~\approx</math> |
<math>~ \mathbf{F}_1 - \frac{1}{\rho_0} \nabla q + \biggl(\frac{w}{\rho_0^2} \biggr)\nabla P_0 \, .</math> |
As is shown in the following framed image, if the discussion is restricted only to fluctuations in the radial coordinate direction of a spherically symmetric configuration, in which case <math>~\nabla \rightarrow \partial/\partial r</math>, this expression exactly matches the righthand side of the linearized Euler equation, derived and presented as equation (12) by James H. Jeans in 1902 (Philosophical Transactions of the royal Society of London. Series A, 199, 1).
|
Linearized Euler Equation as Derived and Presented by Jeans (1902) |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
The correspondence between the righthand-sides of equation (12) from Jeans (1902) and our derived expression [using Bonnor's (1957) variable notation] is clear after accepting the following variable mappings:
The lefthand side of equation (12) from Jeans (1902) also matches the lefthand side of Bonnor's (1957) linearized Euler equation, although this may not be immediately apparent because the variable "u" has been assigned different meanings in the two publications. In Bonnor's paper, <math>~u = \hat{\mathbf{e}}_r \cdot \mathbf{u}</math> is the perturbed velocity in the radial-coordinate direction; while, in the paper by Jeans, <math>~u</math> is the radial displacement itself. Hence,
|
Now, in order to morph this last expression into the expression found on the righthand side of Bonnor's equation (2.7), as reprinted above, we need to draw upon the result obtained, above, from linearizing the adiabatic form of the First Law of Thermodynamics. After shifting to Bonnor's variable notation (as clarified in earlier remarks), the relevant result is,
<math>\frac{q}{P_0} \approx \gamma_g \frac{w}{\rho_0} \, .</math>
In addition, we appreciate that,
<math>\gamma_g = \biggl( \frac{d\ln P}{d\ln \rho} \biggr)_0 = \frac{\rho_0}{P_0}\cdot \biggl( \frac{dP}{d\rho} \biggr)_0 \, .</math>
Hence (see also Bonnor's equation 3.7),
<math>q \approx w \biggl( \frac{dP}{d\rho} \biggr)_0 \, ,</math>
which allows us to write the righthand side of the linearized Euler equation as,
|
RHS of equation (2.1) |
<math>~\approx</math> |
<math>~ \mathbf{F}_1 - \frac{1}{\rho_0} \biggl\{ \nabla \biggl[ w \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] - \biggl(\frac{w}{\rho_0} \biggr)\nabla P_0\biggr\} \, .</math> |
But, given the adopted barotropic equation of state, we can also write,
<math>\nabla P_0 = \biggl(\frac{dP}{d\rho} \biggr)_0 \nabla\rho_0 \, ,</math>
in which case,
|
RHS of equation (2.1) |
<math>~\approx</math> |
<math>~ \mathbf{F}_1 - \biggl\{\frac{1}{\rho_0} \nabla \biggl[ w \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] - \biggl(\frac{w}{\rho_0^2} \biggr)\biggl(\frac{dP}{d\rho} \biggr)_0 \nabla\rho_0\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \mathbf{F}_1 - \biggl\{ \frac{1}{\rho_0} \nabla \biggl[ w \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] + w\biggl(\frac{dP}{d\rho} \biggr)_0 \nabla\biggl(\frac{1}{\rho_0} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \mathbf{F}_1 - \nabla \biggl[ \frac{w}{\rho_0} \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] \, .</math> |
This precisely matches the righthand side of the linearized Euler equation derived and presented as equation (2.7) by Bonnor — see the reprinted equation, above.
Reconciliation
It is instructive to explicitly demonstrate that the linearized "Euler + Poisson" equation that we derived and highlighted in our brief summary subsection, above, namely,
|
<math> \frac{P_0}{\rho_0} \frac{dp}{dr_0} = (4x + p)g_0 + \omega^2 r_0 x \, , </math> |
conveys the same physics as Bonnor's (1957) linearized Euler equation when applied to a spherically symmetric system, namely,
|
<math>\frac{\partial v_r}{\partial t}</math> |
<math>~=</math> |
<math>~ \hat{\mathbf{e}}_r \cdot \mathbf{F}_1 - \frac{d}{d r_0} \biggl[ \frac{w}{\rho_0} \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] \, .</math> |
Step #1: We recognize that, after linearization, <math>~\partial v_r/\partial t = d^2 r/dt^2</math>. So, drawing on our earlier detailed handling of the "Euler + Poisson" equations, we can make the replacement,
|
<math> \frac{\partial v_r}{\partial t} </math> |
<math> \rightarrow </math> |
<math> - ~\omega^2 r_0 x~e^{i\omega t} \, . </math> |
Step #2: As we have already recognized, swapping between our perturbation notation and Bonnor's leads to the replacement,
|
<math> w \biggl( \frac{dP}{d\rho} \biggr)_0 </math> |
<math> \rightarrow </math> |
<math> P_0 p e^{i\omega t} \, . </math> |
Hence,
|
<math> \frac{d}{d r_0} \biggl[ \frac{w}{\rho_0} \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] </math> |
<math> \rightarrow </math> |
<math> \frac{d}{d r_0} \biggl[ \biggl( \frac{P_0 p}{\rho_0}\biggr) e^{i\omega t} \biggr] </math> |
|
|
<math>~=</math> |
<math> e^{i\omega t} \biggl\{ \frac{p}{\rho_0} \frac{d P_0}{d r_0} + P_0 p \frac{d}{d r_0} \biggl( \frac{1}{\rho_0}\biggr) + \frac{P_0}{\rho_0} \frac{d p}{d r_0} \biggr\} </math> |
|
|
<math>~=</math> |
<math> e^{i\omega t} \biggl\{ \biggl[ \frac{1}{\rho_0} \frac{d P_0}{d r_0} \biggr] (p - d) + \frac{P_0}{\rho_0} \frac{d p}{d r_0} \biggr\} </math> |
|
|
<math>~=</math> |
<math> e^{i\omega t} \biggl[ (d - p) g_0 + \frac{P_0}{\rho_0} \frac{d p}{d r_0} \biggr] \, . </math> |
where we have, again, used the relationship,
|
<math>\nabla P_0 = \biggl( \frac{dP}{d\rho} \biggr)_0 \nabla \rho_0 = \biggl( \frac{P_0 p}{\rho_o d} \biggr) \nabla \rho_0 </math> |
<math>~~~~\Rightarrow~~~~</math> |
<math>~ \frac{d}{dr_0} \biggl( \frac{1}{\rho_0}\biggr) = - \frac{1}{\rho_0^2}\frac{d\rho_0}{dr_0} =- \biggl( \frac{d}{P_0 p} \biggr) \biggl[\frac{1}{\rho_0}\frac{dP_0}{dr_0} \biggr] \, .</math> |
Step #3: Implementing these first two substitutions, Bonnor's linearized Euler equation becomes,
|
<math>- ~\omega^2 r_0 x</math> |
<math>~=</math> |
<math>~ e^{-i\omega t}\hat{\mathbf{e}}_r \cdot \mathbf{F}_1 - \biggl[ (d - p) g_0 + \frac{P_0}{\rho_0} \frac{d p}{d r_0} \biggr] </math> |
|
<math>\Rightarrow ~~~~ \frac{P_0}{\rho_0} \frac{d p}{d r_0} </math> |
<math>~=</math> |
<math>~ e^{-i\omega t}\hat{\mathbf{e}}_r \cdot \mathbf{F}_1 + (p - d) g_0 + \omega^2 r_0 x\, .</math> |
Step #4: In order to map Bonnor's <math>~\mathbf{F}_1</math> to our perturbation notation, we back up to expressions for the gravitational acceleration, as a whole, which establish that, for spherically symmetric systems,
|
<math>~\hat{\mathbf{e}}_r \cdot \mathbf{F}</math> |
<math>~=</math> |
<math>~-~\frac{Gm}{r^2}</math> |
|
<math>~\Rightarrow~~~\hat{\mathbf{e}}_r \cdot \biggl[ \mathbf{F}_0 + \mathbf{F}_1 \biggr]</math> |
<math>~=</math> |
<math>~-~\frac{Gm}{r^2}</math> |
Dimensionless Expression
Let's write this governing, 2nd-order ODE and the key physical variables as dimensionless expressions. First, multiply through by <math>~R^2</math> and define the dimensionless radius as,
<math>
\chi_0 \equiv \frac{r_0}{R}
</math>
to obtain,
<math>
\frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0} - \biggl(\frac{R g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{R^2 \rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{R \chi_0} \biggr] x = 0 .
</math>
Now normalize <math>~P_0</math> to <math>~P_c</math> and <math>~\rho_0</math> to <math>~\rho_c</math> to obtain,
<math>
\frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0} - \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_c}{P_0}\biggr) \biggl(\frac{R g_0 \rho_c}{P_c}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_c}{P_0}\biggr) \biggl(\frac{R^2 \rho_c}{\gamma_\mathrm{g} P_c} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{R \chi_0} \biggr] x = 0 \, .
</math>
The characteristic time for dynamical oscillations in spherically symmetric configurations (SSC) appears to be,
<math>
\tau_\mathrm{SSC} \equiv \biggl[ \frac{R^2 \rho_c}{P_c} \biggr]^{1/2} ,
</math>
and the characteristic gravitational acceleration appears to be,
<math>
g_\mathrm{SSC} \equiv \frac{P_c}{R \rho_c} .
</math>
So we can write,
<math>
\frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0} - \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_0}{P_c}\biggr)^{-1} \biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_0}{P_c}\biggr)^{-1} \biggl(\frac{1}{\gamma_\mathrm{g}} \biggr)\biggl[\tau_\mathrm{SSC}^2 \omega^2 + (4 - 3\gamma_\mathrm{g})\biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \frac{1}{\chi_0} \biggr] x = 0 .
</math>
This is the governing relation that we will use to analyze the stability against radial pulsations of spherically symmetric, self-gravitating configurations.
Complementary Approach
Looking back at the set of three, coupled, linearized equations — but using <math>~\Delta</math> to denote the density fluctuation, rather than <math>~d</math>, in order to avoid confusion with the differentiation operators,
|
Linearized Linearized Linearized |
let's combine them into a 2nd-order ODE that governs the eigenfunction of the density perturbation, <math>~\Delta</math>, rather than of the radial displacement, <math>~x</math>. We begin by using the second equation to obtain an expression for <math>~x</math>:
|
<math>~ x</math> |
<math>~=</math> |
<math>~(4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] \, .</math> |
From this, we determine that,
|
<math>~ (4g_0 + \omega^2 r_0)\frac{dx}{dr_0}</math> |
<math>~=</math> |
<math>~\frac{d}{dr_0} \biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] + (4g_0 + \omega^2 r_0)\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr]\frac{d}{dr_0}(4g_0 + \omega^2 r_0)^{-1} </math> |
|
|
<math>~=</math> |
<math>~\frac{P_0}{\rho_0} \frac{d^2p}{dr_0^2} + \frac{dp}{dr_0} \cdot \frac{d}{dr_0} \biggl( \frac{P_0}{\rho_0} \biggr) -p \frac{dg_0}{dr_0} - g_0\frac{dp}{dr_0} - (4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] \biggl[ \omega^2 + 4\frac{dg_0}{dr_0}\biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{P_0}{\rho_0} \frac{d^2p}{dr_0^2} + \frac{dp}{dr_0} \biggl\{ -g_0 + \frac{d}{dr_0} \biggl( \frac{P_0}{\rho_0} \biggr) - (4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \biggr] \biggl[ \omega^2 + 4\frac{dg_0}{dr_0}\biggr] \biggr\} + p \biggl\{ (4g_0 + \omega^2 r_0)^{-1}\biggl[ g_0 \biggr] \biggl[ \omega^2 + 4\frac{dg_0}{dr_0}\biggr] -\frac{dg_0}{dr_0} \biggr\} </math> |
Next, we substitute this expression for <math>~x</math> into the first equation — gradually replacing <math>~p</math> with <math>~\gamma_g \Delta</math>, as well — and carry out the differentiation:
|
<math>~ -\Delta - 3\biggl\{(4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - \gamma_g \Delta g_0 \biggr] \biggr\} </math> |
<math>~=</math> |
<math>~r_0 \frac{d}{dr_0} \biggl\{(4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] \biggr\} </math> |
|
<math>~ \Rightarrow~~- \Delta \biggl[ \frac{g_0}{r_0} (4 - 3\gamma_g)+ \omega^2 \biggr] - \frac{3P_0}{r_0 \rho_0} \frac{dp}{dr_0} </math> |
<math>~=</math> |
<math>~ \frac{d}{dr_0} \biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] - (4g_0 + \omega^2 r_0)^{-1} \biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr]\frac{d}{dr_0} \biggl[(4g_0 + \omega^2 r_0) \biggr] </math> |
See Also
- The History of Radial Stellar Pulsation Theory by A. Gautschy (2003)
- Part I of Spherically Symmetric Configurations: Simplified Governing Equations
- Wave Equation
- Sound Waves and Gravitational Instability — class notes provided online by David H. Weinberg (The Ohio State University)

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |