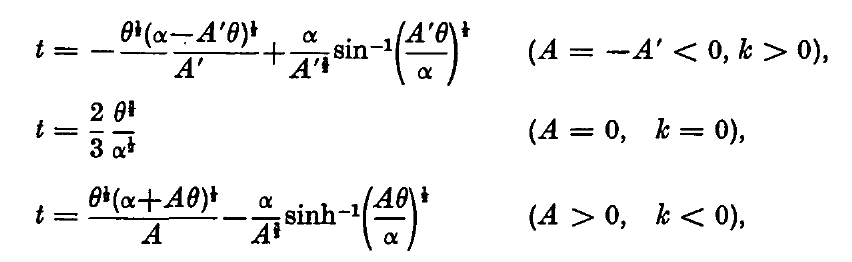User:Tohline/SSC/FreeFall
Free-Fall
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
| Free-Fall Collapse |
|---|
In our broad study of the "dynamics of self-gravitating fluids," we are interested in examining how, in a wide variety of physical systems, initially unbalanced forces or exponentially growing instabilities can lead to the development of fluid motions and structural changes that are of nonlinear amplitude. We begin, here, by discussing the free-fall collapse of a spherically symmetric, uniform-density configuration. In the scheme of things, this is a simple example, but it proves to be powerfully illustrative.
To our knowledge, the solution to this free-fall problem in the context of star formation research first appeared in print in a paper by Chris Hunter (1962, ApJ, 136, 594) titled, The Instability of the Collapse of a Self-Gravitating Gas Cloud. A few years later, this solution appeared — with a reference to Hunter's derivation — in an article by L. Mestel (1965, Quarterly Journal of the Royal Astronomical Society, 6, 161) that discussed a broad range of theoretical problems related to star formation, and it appeared again in the introductory paragraph of a classic paper by C. C. Lin, Leon Mestel, and Frank Shu (1965, ApJ, 142, 143) titled, "The Gravitational Collapse of a Uniform Spheroid." While the primary purpose of this work by Lin, Mestel & Shu (1965; hereafter, LMS65) was to depart from the assumption of spherical symmetry and examine the amplification of spheroidal distortions during a collapse, the solution to the simpler, spherically symmetric free-fall collapse problem is so clearly and succinctly written that we have decided to reprint, here, the paper's introductory paragraph.
As is briefly discussed in a later subsection of this chapter, the same 2nd-order ODE that leads to the spherically symmetric, free-fall collapse model derived by Hunter (1962) also appears in discussions of relativistic cosmologies. Indeed, as is detailed below, the parametric <math>~r(t)</math> solution presented as equations (2) & (3) in LMS65 appeared in print — as far as we have been able to ascertain, for the first time — more than thirty years earlier in a paper by William H. McCrea and Edward A. Milne (1934) Quart. J. Math. Oxford, 5, 73 titled, Newtonian Universes and the Curvature of Space. In the context of early cosmological discussions, however, the focus was usually on model solutions that describe pressure-free "Hubble flow" expansion, rather than free-fall collapse.
In the subsections that follow, we show how equation (1) of LMS65 arises from our generic set of principal governing equations; how their parametric solution in the form of equations (2) and (3) is derived; and elaborate on the physical relevance of this seemingly simplistic problem to the broad study of self-gravitating fluids.
Assembling the Key Relations
We begin with the set of time-dependent governing equations for spherically symmetric systems, namely,
Equation of Continuity
<math>\frac{d\rho}{dt} + \rho \biggl[\frac{1}{r^2}\frac{d(r^2 v_r)}{dr} \biggr] = 0 </math>
Euler Equation
<math>\frac{dv_r}{dt} = - \frac{1}{\rho}\frac{dP}{dr} - \frac{d\Phi}{dr} </math>
Adiabatic Form of the
First Law of Thermodynamics
<math>~\frac{d\epsilon}{dt} + P \frac{d}{dt} \biggl(\frac{1}{\rho}\biggr) = 0</math>
Poisson Equation
<math>\frac{1}{r^2} \biggl[\frac{d }{dr} \biggl( r^2 \frac{d \Phi}{dr} \biggr) \biggr] = 4\pi G \rho \, .</math>
By definition, an element of fluid is in "free fall" if its motion in a gravitational field is unimpeded by pressure gradients. The most straightforward way to illustrate how such a system evolves is to set <math>~P = 0</math> in all of the governing equations. In doing this, the continuity equation and the Poisson equation are unchanged; the equation formulated by the first law of thermodynamics becomes irrelevant; and the Euler equation becomes,
<math>~\frac{dv_r}{dt} = - \frac{d\Phi}{dr} \, ,</math>
or, recognizing that <math>~v_r = dr/dt</math>,
<math>~\frac{d^2r}{dt^2} = - \frac{d\Phi}{dr} \, .</math>
Analytic Model of the Collapse of a Uniform-Density Sphere
Our primary objective in this chapter is to show how a mathematical model of the free-fall collapse of a uniform-density sphere — specifically, the model presented in the introduction of LMS65, as reprinted above — can be derived from our standard, principal set of governing equations. As it turns out, much of the calculus underpinning this derivation can be developed in the context of a simpler physical model, namely, the radial free-fall of a massless particle in a point-mass potential. This is not a continuum fluids problem nor a self-gravitating problem, so the continuity equation and the Poisson equation are superfluous. But the nonlinear dynamics associated with free-fall in a time-invariant, point-mass potential mirrors the dynamics embodied by the Euler equation in the context of the collapse of a self-gravitating, homogeneous fluid sphere. So we begin by discussing this simpler, "single particle in a point-mass potential" problem. This is followed by a derivation of the model of the free-fall collapse of a "uniform-density sphere" presented by LMS65, as viewed from an inertial frame of reference. Then, using techniques described by Goldreich & Weber (1980), we show how the same model can be derived as a similarity solution when viewed from a non-inertial, spherically symmetric coordinate system whose radial coordinate is undergoing an appropriately accelerated collapse.
Single Particle in a Point-Mass Potential
Suppose we examine the free-fall of a single (massless) particle, located a distance <math>~|\vec{r}|</math> from an immovable point-like object of mass, <math>~M</math>. The particle will feel a distance-dependent acceleration due to a gradient in the gravitational potential of the form,
<math>~\frac{d\Phi}{dr} = \frac{GM}{r^2} \, ,</math>
and the Euler equation, as just derived, serves to describe the particle's governing equation of motion, namely,
<math>~\ddot{r} = - \frac{GM}{r^2} \, ,</math>
where we have used dots to denote differentiation with respect to time (see also equation 1 from LMS65, reprinted above). If we multiply this equation through by <math>~2\dot{r} = 2dr/dt</math>, we have,
|
<math>~2\dot{r} \frac{d\dot{r}}{dt}</math> |
<math>~=</math> |
<math>~- \frac{2GM}{r^2} \cdot \frac{dr}{dt} </math> |
|
<math>~\Rightarrow ~~~ d(\dot{r}^2)</math> |
<math>~=</math> |
<math>~2GM \cdot d(r^{-1}) \, ,</math> |
which integrates once to give,
|
<math>~\dot{r}^2</math> |
<math>~=</math> |
<math>~\frac{2GM}{r} - k \, , </math> |
where, as an integration constant, <math>~k</math> is independent of time.
|
Role of Integration Constant |
|---|
|
Within the context of this particular physical problem, the constant, <math>~k</math>, should be used to specify the initial velocity, <math>~v_i</math>, of the particle that begins its collapse from the radial position, <math>~r_i</math>. Specifically, <math>~k = \frac{2GM}{r_i} - v_i^2 \, .</math> Without this explicit specification, it should nevertheless be clear that, in order to ensure that <math>~\dot{r}^2</math> is positive — and, hence, <math>~\dot{r}</math> is real — the constant must be restricted to values, <math>~k \leq \frac{2GM}{r_i} \, .</math> |
Taking the square root of both sides of our derived "kinetic energy" equation, we can write,
|
<math>~\frac{dr}{dt}</math> |
<math>~=</math> |
<math>~\pm \biggl[ \frac{2GM}{r} - k \biggr]^{1/2} </math> |
|
<math>~\Rightarrow~~~ dt </math> |
<math>~=</math> |
<math>~ \pm \biggl[ \frac{2GM}{r} - k \biggr]^{-1/2} dr \, .</math> |
As has been shown by McCrea & Milne (1934), this function can be integrated in closed form to give an analytic prescription for <math>~t(r)</math>. Equation (17) in the McCrea & Milne (1934) paper presents the function to be integrated as,
|
<math>~t</math> |
<math>~=</math> |
<math>~\int\limits_0^\theta \frac{\theta^{1/2} d\theta}{(\alpha + A\theta)^{1/2}} \, ,</math> |
which can be straightforwardly obtained from our expression after adopting the positive root of the "kinetic energy" equation and setting,
<math>~r \rightarrow \theta \, ,</math> <math>~2GM \rightarrow \alpha \, ,</math> and <math>~k \rightarrow A' = -A \, .</math>
The results obtained assuming three different ranges/values for the constant, <math>~k</math>, are presented at the end of §4 of McCrea & Milne (1934) and are reprinted here in an effort to fully acknowledge this early contribution.
|
W. H. McCrea and E. A. Milne |
|---|
In the following subsections, we will rederive these algebraic, <math>~t(r)</math> solutions in the context of three separate, physically interesting scenarios, all of which involve infall, so we will adopt the velocity root having only the negative sign.
Falling from rest at a finite distance …
In this case, we set <math>~v_i = 0</math> in the definition of <math>~k</math>, so,
|
<math>~\frac{dr}{dt}</math> |
<math>~=</math> |
<math>~- ~\biggl[\frac{2GM}{r} - \frac{2GM}{r_i}\biggr]^{1/2} = \biggl(\frac{2GM}{r_i}\biggr)^{1/2} \biggl[\frac{r_i}{r}-1 \biggr]^{1/2} \, , </math> |
and the relevant expression to be integrated is,
|
<math>~dt </math> |
<math>~=</math> |
<math>~ - \biggl(\frac{2GM}{r_i} \biggr)^{-1/2} \biggl[ \biggl( \frac{r_i}{r} \biggr) - 1 \biggr]^{-1/2} dr \, .</math> |
Following LMS65, we see that this equation can be straightforwardly integrated by first making the substitution,
<math>~\cos^2\zeta \equiv \frac{r}{r_i} \, ,</math>
which also means,
<math>~dr = - 2r_i \sin\zeta \cos\zeta d\zeta \, .</math>
The relevant integral is, therefore,
|
<math>~\int_0^t dt </math> |
<math>~=</math> |
<math>~+ \biggl(\frac{2r_i^3}{GM} \biggr)^{1/2} \int_0^\zeta \cos^2\zeta d\zeta \, ,</math> |
where the limits of integration have been set to ensure that <math>~r/r_i = 1</math> at time <math>~t=0</math>. After integration, we have,
|
<math>~ t </math> |
<math>~=</math> |
<math>~ \biggl(\frac{2r_i^3}{GM} \biggr)^{1/2} \biggl[ \frac{\zeta}{2} + \frac{1}{4}\sin(2\zeta) \biggr] \, .</math> |
The physically relevant portion of this formally periodic solution is the interval in time from when <math>~r/r_i = 1 ~ (\zeta = 0)</math> to when <math>~r/r_i \rightarrow 0</math> for the first time <math>~(\zeta = \pi/2)</math>. The particle's free-fall comes to an end at the time associated with <math>~\zeta = \pi/2</math>, that is, at the so-called "free-fall time,"
|
<math>~\tau_\mathrm{ff} </math> |
<math>~\equiv</math> |
<math>~ \biggl(\frac{2r_i^3}{GM} \biggr)^{1/2} \biggl[ \frac{\zeta}{2} + \frac{1}{4}\sin(2\zeta) \biggr]_{\zeta=\pi/2} = \biggl(\frac{\pi^2 r_i^3}{8GM} \biggr)^{1/2} \, .</math> |
In summary, then, the solution, <math>~r(t)</math>, to this simplified but dynamically relevant problem is provided by the following pair of analytically prescribable parametric relations (see also equations 2 & 3 from LMS65, reprinted above):
|
Parametric <math>~r(t)</math> Solution | ||||||
|---|---|---|---|---|---|---|
|
We note, as well, that the radially directed velocity is,
|
<math>~v_r = \frac{dr}{dt} </math> |
<math>~=</math> |
<math>~ - \biggl(\frac{2GM}{r_i} \biggr)^{1/2} \biggl[ \frac{1}{\cos^2\zeta} - 1 \biggr]^{1/2} </math> |
|
|
<math>~=</math> |
<math>~ - \biggl(\frac{2GM}{r_i} \biggr)^{1/2} \tan\zeta \, , </math> |
which formally becomes infinite in magnitude when <math>~\zeta \rightarrow \pi/2</math>, that is, when <math>~t \rightarrow \tau_\mathrm{ff}</math>.
It is worth demonstrating that the parametric solution derived here is identical to the solution published by McCrea & Milne (1934) — reprinted above — for the case, <math>~k > 0</math>, namely,
|
<math>~t</math> |
<math>~=</math> |
<math>~- \frac{\theta^{1/2} (\alpha - A' \theta)^{1/2}}{A'} + \frac{\alpha}{(A')^{3/2}} \sin^{-1} \biggl( \frac{A' \theta}{\alpha} \biggr)^{1/2} </math> |
|
|
<math>~=</math> |
<math>~\frac{\alpha}{(A')^{3/2}} \biggl[ - \biggl(\frac{A' \theta}{\alpha} \biggr)^{1/2} \biggl(1 - \frac{A' \theta}{\alpha} \biggr)^{1/2} + \sin^{-1} \biggl( \frac{A' \theta}{\alpha} \biggr)^{1/2} \biggr] \, .</math> |
After reversing the substitutions detailed above, that is, after setting,
<math>~\theta \rightarrow r \, ,</math> <math>~ \alpha \rightarrow 2GM \, ,</math> and <math>~A' \rightarrow k \, ,</math>
and remembering that, for this particular model example, we have set <math>~v_i = 0 ~\Rightarrow ~ k = 2GM/r_i</math>, the key dimensionless ratio in the McCrea & Milne expression becomes,
|
<math>~\biggl(\frac{A' \theta}{\alpha} \biggr)</math> |
<math>~=</math> |
<math>~\frac{r}{r_i} = \cos^2\zeta \, ,</math> |
and the pre-factor on the righthand side becomes,
|
<math>~\biggl[\frac{\alpha^2}{(A')^3} \biggr]^{1/2}</math> |
<math>~=</math> |
<math>~\biggl[\frac{r_i^3}{2GM} \biggr]^{1/2} = \frac{2}{\pi} \tau_\mathrm{ff} \, .</math> |
Hence, the McCrea & Milne solution becomes,
|
<math>~\frac{t}{\tau_\mathrm{ff}}</math> |
<math>~=</math> |
<math>~\frac{2}{\pi} \biggl[ -\cos\zeta \sin\zeta + \sin^{-1} (\cos\zeta) \biggr]</math> |
|
|
<math>~=</math> |
<math>~\frac{2}{\pi} \biggl[ -\frac{1}{2}\sin(2\zeta) + \biggl(\frac{\pi}{2} - \zeta \biggr) \biggr]</math> |
|
<math>\Rightarrow ~~~ 1 - \frac{t}{\tau_\mathrm{ff}}</math> |
<math>~=</math> |
<math>~\frac{2}{\pi} \biggl[\zeta +\frac{1}{2}\sin(2\zeta) \biggr] \, .</math> |
We see that, by shifting the defined zero-point in time in this last expression such that <math>~t \rightarrow (\tau_\mathrm{ff} - t)</math>, which also reverses the sign on time, we have exact agreement between the solution that we have derived — designed to match the one published by Lin, Mestel, & Shu in 1965 — and the result for <math>~k > 0</math> that was published by McCrea & Milne in 1934.
Falling from rest at infinity …
In this case, we set <math>~k= 0</math>, so the relevant expression to be integrated is,
|
<math>~dt </math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{2GM}{r} \biggr]^{-1/2} dr = - (2GM)^{-1/2} r^{1/2} dr \, .</math> |
Upon integration, this gives,
|
<math>~t + C_0 </math> |
<math>~=</math> |
<math>~ - \frac{2}{3}(2GM)^{-1/2} r^{3/2} \, ,</math> |
where, <math>~C_0</math> is an integration constant. In this case, it is useful to simply let <math>~t=0</math> mark the time at which <math>~r = 0</math> — hence, also, <math>~C_0 = 0</math> — so at all earlier times (<math>~t</math> intrinsically negative) we have,
|
<math>~- t </math> |
<math>~=</math> |
<math>~ \biggl( \frac{2r^3}{9GM} \biggr)^{1/2} </math> |
|
<math>~\Rightarrow ~~~ r </math> |
<math>~=</math> |
<math>~ \biggl( \frac{9}{2} \cdot GMt^2 \biggr)^{1/3} \, .</math> |
It is straightforward to demonstrate that this derived solution is identical to the solution published by McCrea & Milne (1934) — reprinted above — for the case, <math>~k = 0</math>, namely,
|
<math>~t</math> |
<math>~=</math> |
<math>~ \frac{2}{3} \frac{\theta^{3/2}}{\alpha^{1/2}} = \biggl( \frac{4\theta^3}{9\alpha} \biggr)^{1/2} \, .</math> |
After reversing the substitutions detailed above, that is, after setting,
<math>~\theta \rightarrow r \, ,</math> and <math>~ \alpha \rightarrow 2GM \, ,</math>
the McCrea & Milne solution becomes,
|
<math>~t </math> |
<math>~=</math> |
<math>~ \biggl( \frac{2r^3}{9GM} \biggr)^{1/2} \, .</math> |
Aside from reversing the sign on time, we have exact agreement between the solution that we have derived and the result for <math>~k = 0</math> that was published by McCrea & Milne in 1934.
Falling from a finite distance with an initially nonzero velocity …
Here, we examine the case in which <math>~0 < r_i < \infty</math> and <math>~0 < v_i^2 < GM/r_i</math>, in which case, the constant <math>~k</math> is a nonzero, positive number. The relevant expression to be integrated is,
|
<math>~ dt</math> |
<math>~=</math> |
<math>~ - k^{-1/2}\biggl[ \frac{a}{r} - 1 \biggr]^{-1/2} dr \, ,</math> |
where,
<math>~ a \equiv \frac{2GM}{k} \, .</math>
Using Wolfram Mathematica's online integrator, we find,
|
<math>~- \int \biggl[ \frac{a}{r} - 1 \biggr]^{-1/2} dr</math> |
<math>~=</math> |
<math>~ r ( ar^{-1} -1 )^{1/2} + \frac{a}{2} \tan^{-1} \biggl[ \frac{(2r-a)(ar^{-1} - 1)^{1/2}}{2(r-a)} \biggr] \, .</math> |
Hence, we find,
|
<math>~k^{1/2}(t + C_0)</math> |
<math>~=</math> |
<math>~ r ( ar^{-1} -1 )^{1/2} + \frac{a}{2} \tan^{-1} \biggl[ \frac{(2r-a)(ar^{-1} - 1)^{1/2}}{2(r-a)} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ r ( ar^{-1} -1 )^{1/2} + \frac{a}{2} \tan^{-1} \biggl[ \frac{(ar^{-1}-2)(ar^{-1} - 1)^{1/2}}{2(ar^{-1}-1)} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ r ( ar^{-1} -1 )^{1/2} + \frac{a}{2} \tan^{-1} \biggl[ \frac{(ar^{-1}-2)}{2(ar^{-1}-1)^{1/2}} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ r k^{-1/2}( akr^{-1} -k )^{1/2} + \frac{a}{2} \tan^{-1} \biggl[ \frac{(akr^{-1}-2k)}{2k^{1/2}(akr^{-1}-k)^{1/2}} \biggr] \, .</math> |
Let's determine the constant, <math>~C_0</math>. When <math>~t = 0</math>, we can write,
|
<math>~[akr^{-1} - k]_{t=0}</math> |
<math>~=</math> |
<math>~ \frac{2GM}{r_i} - \biggl[\frac{2GM}{r_i} - v_i^2 \biggr] = v_i^2 \, .</math> |
Hence,
|
<math>~C_0</math> |
<math>~=</math> |
<math>~ r_i k^{-1}v_i + \biggl(\frac{a}{2k^{1/2}} \biggr) \tan^{-1} \biggl[ \frac{(v_i^2-k)}{2k^{1/2}v_i} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ GMk^{-3/2} \biggl\{ 2[\eta(1-\eta)]^{1/2} + \tan^{-1} \biggl[ \biggl( \eta - \frac{1}{2} \biggr) [ \eta(1-\eta)]^{-1/2} \biggr] \biggr\} \, , </math> |
where, in this last expression,
<math>\eta \equiv \frac{v_i^2 r_i}{2GM} \, .</math>
(This last expression needs to be checked for errors, as it has been rather hastily derived.)
Relationship to Kepler's 3rd Law
It is useful to note a relationship between Kepler's 3rd law and the free-fall problem, as introduced here in the context of the motion of a single (massless) particle that falls from rest toward a point-like object of mass, <math>~M</math>. According to Kepler's 3rd law, when a massless particle orbits a point-like object of mass, <math>~M</math>, the particle's orbital period, <math>~P_\mathrm{orb}</math>, is related to the semi-major axis, <math>~a_\mathrm{orb}</math>, of its elliptical orbit via the algebraic expression,
<math>~P^2_\mathrm{orb} = \frac{4\pi a_\mathrm{orb}^3}{GM} \, .</math>
This relation works for orbits of any eccentricity,
<math>~e \equiv \biggl[ 1 - \frac{b_\mathrm{orb}^2}{a_\mathrm{orb}^2} \biggr]^{1/2} \, ,</math>
where, <math>~b_\mathrm{orb}</math> is the semi-minor axis of the orbit, the extremes being: <math>~e = 0 ~(b_\mathrm{orb} = a_\mathrm{orb})</math> for a circular orbit, and <math>~e = 1 ~(b_\mathrm{orb} = 0)</math> for a purely radially directed (in-fall) trajectory.
In the context of our current discussion, it should be clear that a particle that "free-falls" from rest at an initial distance, <math>~r_i</math>, from a point mass object will follow a trajectory synonymous with a Keplerian orbit having eccentricity, <math>~e=1</math>. The particle's initial position coincides with the apo-center of this orbit and the point mass object is located at the peri-center (as well as at one focus) of the orbit, so the semi-major axis is <math>~a_\mathrm{orb} = r_i/2</math>. We also recognize that the particle will move from the apo-center to the peri-center of its orbit — completing its "free-fall" onto the point-mass object — in a time, <math>~\tau = P_\mathrm{orb}/2</math>. From Kepler's 3rd law, we therefore deduce that,
<math>~\tau = \frac{1}{2} \biggl[ \frac{4\pi (r_i/2)^3}{GM} \biggr]^{1/2} = \biggl( \frac{\pi r_i^3}{8GM} \biggr)^{1/2} \, ,</math>
which precisely matches the free-fall time, <math>~\tau_\mathrm{ff}</math>, derived above.
Uniform-Density Sphere
Now, let's consider the (pressure-free) collapse, from rest, of a uniform-density sphere of total mass <math>~M_\mathrm{tot}</math> and radius, <math>~R(t)</math>. If we use a subscript "0" to label the radius of the sphere at time <math>~t=0</math>, then the initial mass-density throughout the sphere is,
<math>~\rho_0 = \frac{3M_\mathrm{tot}}{4\pi R_0^3} \, .</math>
If we not only assume that the total mass of this configuration remains constant but that all of the mass remains fully enclosed within the surface of radius, <math>~R(t)</math>, throughout the collapse (the validity of this second assumption will be critically assessed shortly), then at all points across the surface of the configuration, the acceleration will be given — analogous to the single-particle case, above — by,
<math>~\frac{d\Phi}{dR} = \frac{GM_\mathrm{tot}}{R^2} \, ,</math>
and the equation of motion for the surface is, as before,
|
<math>~\ddot{R}</math> |
<math>~=</math> |
<math>~- \frac{GM_\mathrm{tot}}{R^2} \, .</math> |
As in the single-particle case, above, this 2nd-order ODE can be integrated once to generate a "kinetic energy" equation,
|
<math>~\dot{R}^2</math> |
<math>~=</math> |
<math>~\frac{2GM_\mathrm{tot}}{R} - k(R_i, v_i) \, , </math> |
and integrated a second time to give the following parametric relationship between the sphere's radius, and time:
| |||||||||
It is important to notice, from this result, that the timescale for collapse, <math>~\tau_\mathrm{ff}</math>, depends only on the density of the configuration in its initial state. It is important to realize, as well, that the derived parametric solution that gives the ratio <math>~R/R_0</math> as a function of time applies for all positions within the sphere. In this more general way of interpreting the solution, <math>~R</math> represents any radial position, <math>~R_0</math> represents the value of that <math>~R</math> at time <math>~t=0</math>, and the relevant mass is the mass interior to that position, <math>~M_R</math>, rather than the configuration's total mass. This works because, for spherically symmetric configurations, the acceleration only depends on the mass interior to each position. The ultimate result is that the free-fall collapse of an initially uniform-density sphere proceeds homologously. This happens because, independent of <math>~R</math>, the timescale for collapse only depends on <math>~\rho_0</math> and, by design, <math>~\rho_0</math> is independent of <math>~R</math>. This is just a restatement of the behavior emphasized by LMS65, as reprinted above: "… a uniform sphere contracts homologously, and so stays uniform."
Because the pressure-free collapse of an initially uniform-density sphere proceeds in an homologous fashion, the mass interior to any radial shell remains constant. This fully justifies the assumption of constant mass that was made earlier in this derivation.
The expression for the time-dependent velocity that was obtained, above, in the context of a particle falling from rest at a finite distance can also be generalized here to the case of a collapsing uniform-density sphere. A radial shell initially at any position, <math>~R_i \le R_0</math>, within the sphere will enclose a mass, <math>M_i = 4\pi \rho_0 R_i^3/3</math>. Hence the radially directed velocity of that shell at any time, <math>~t</math> (specified via the parameter, <math>~\zeta</math>), will be,
|
<math>~v_r</math> |
<math>~=</math> |
<math>~ - \biggl(\frac{2GM_i}{R_i} \biggr)^{1/2} \tan\zeta = - R_i \biggl[ \biggl(\frac{8\pi G\rho_0}{3} \biggr)^{1/2} \tan\zeta \biggr] </math> |
|
|
<math>~=</math> |
<math>~ - R \biggl[ \biggl(\frac{8\pi G\rho_0}{3} \biggr)^{1/2} \frac{\sin\zeta}{\cos^3\zeta} \biggr] \, .</math> |
Because everything inside the square brackets of this last expression is independent of space, the expression tells us that, at any time during the collapse, the radially directed velocity is linearly proportional to the radial coordinate of the shell.
Knowing the velocity field, we can use the continuity equation to determine the variation with time of the configuration's density. Specifically,
|
<math>~\frac{d\ln\rho}{dt}</math> |
<math>~=</math> |
<math>~- \nabla\cdot \vec{v} = - \frac{1}{R^2} \frac{d}{dR} \biggl( R^2 v_r \biggr) \, ,</math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \biggl(\frac{8\pi G\rho_0}{3} \biggr)^{1/2} \frac{\sin\zeta}{\cos^3\zeta} \biggr] \frac{1}{R^2} \frac{d}{dR} \biggl( R^3 \biggr)</math> |
|
<math>~=</math> |
<math>~ 3\biggl[ \biggl(\frac{8\pi G\rho_0}{3} \biggr)^{1/2} \frac{\sin\zeta}{\cos^3\zeta} \biggr] \, ,</math> |
so we can write,
|
<math>~d\ln\rho</math> |
<math>~=</math> |
<math>~\frac{3\pi}{2\tau_\mathrm{ff}} \biggl(\frac{\sin\zeta}{\cos^3\zeta}\biggr) dt \, . </math> |
But, from the function, <math>~t(\zeta)</math>, we deduce that,
|
<math>~dt</math> |
<math>~=</math> |
<math>~\biggl( \frac{2\tau_\mathrm{ff}}{\pi} \biggr) d[\zeta + \sin\zeta\cos\zeta] = \biggl( \frac{4\tau_\mathrm{ff}}{\pi} \biggr) \cos^2\zeta ~d\zeta \, .</math> |
Hence,
|
<math>~d\ln\rho</math> |
<math>~=</math> |
<math>~6\tan\zeta ~d\zeta </math> |
|
|
<math>~=</math> |
<math>~- 6 d\ln(\cos\zeta) </math> |
|
|
<math>~=</math> |
<math>~d\ln(\cos^{-6}\zeta) \, ,</math> |
which, upon integration, gives,
|
<math>~\ln\rho -~ \mathrm{constant}</math> |
<math>~=</math> |
<math>~\ln(\cos^{-6}\zeta) </math> |
|
|
<math>~=</math> |
<math>~\ln\biggl(\frac{R}{R_0} \biggr)^{-3} \, .</math> |
Because <math>~\rho \rightarrow \rho_0</math> when <math>~R \rightarrow R_0</math>, the constant of integration must be <math>~\ln\rho_0</math>, giving us, finally,
|
<math>~\frac{\rho}{\rho_0}</math> |
<math>~=</math> |
<math>~\biggl(\frac{R}{R_0} \biggr)^{-3} \, .</math> |
Finally we note that, given this quantified relationship between <math>~\rho</math> and <math>~R</math> along with an appreciation that the governing equation of motion applies to any radial position within the homogeneous sphere, we can rewrite the "acceleration" and "kinetic energy" equations as,
|
Pressure-Free Collapse of an Homogeneous Sphere |
||||||
|
We will refer back to this pair of dynamical equations in our briefly discuss relativistic cosmologies, below.
Homologous Collapse in an Accelerated Reference Frame
As we have shown, the free-fall collapse from rest of an initially uniform-density sphere occurs in an homologous fashion: During the collapse, the system maintains the same radial density (specifically, uniform density) profile; at all times the magnitude of the radial velocity of each spherical shell of material is linearly proportional to the shell's distance from the center; and all mass shells hit the center at precisely the same time, that is, at <math>~t = \tau_\mathrm{ff}</math>. This evolutionary behavior is reminiscent of the behavior that is displayed by the self-similar model that Goldreich & Weber (1980, ApJ, 238, 991) developed to describe the near-homologous collapse of stellar cores; an accompanying chapter contains our review of this work. Two key differences are that, in the Goldreich & Weber work, the underlying density distribution resembles that of an <math>~n = 3</math> polytrope, rather than an <math>~n=0</math> (i.e., uniform density) polytrope; and the dynamical equations incorporate a noninertial, radially collapsing coordinate system. Here we investigate what might be learned by mapping the classic free-fall problem onto a Goldreich & Weber-type noninertial coordinate frame.
Adaptation from Goldreich & Weber (1980)
We begin with the set of governing equations, derived by Goldreich & Weber (1980), that result from expressing the vorticity-free velocity flow-field, <math>~\vec{v}</math>, in terms of a stream function, <math>~\psi</math>, viz.,
<math>~\vec{v} = \nabla\psi ~~~~~\Rightarrow~~~~~v_r = \nabla_r\psi </math> and <math>~\nabla\cdot \vec{v} = \nabla_r^2 \psi \, ;</math>
and from adopting a dimensionless radial coordinate that is defined by normalizing the inertial coordinate vector, <math>~\vec{r}</math>, to a time-varying length, <math>~a(t)</math>, viz.,
<math>~\vec\mathfrak{x} \equiv \frac{1}{a(t)} \vec{r} \, .</math>
As is described in detail in an accompanying discussion, the continuity equation, the Euler equation, and the Poisson equation become, respectively,
|
Because Goldreich & Weber were modeling the collapse of a stellar core that is initially in (or nearly in) hydrostatic balance and obeys a <math>~\gamma = 4/3</math> gas law, they supplemented this set of dynamical equations with an <math>~n=3</math>, polytropic equation of state,
<math>~H = 4\kappa \rho^{1/3} \, ,</math>
to relate the key state variables to one another. Here, in our study of free-fall collapse, it is appropriate for us to simply set <math>~H = 0</math>, not only initially but at all times.
Following the lead of Goldreich & Weber (1980) — again, see our accompanying discussion — we adopt a stream function of the form,
|
<math>~\psi</math> |
<math>~=</math> |
<math>~\frac{1}{2}a \dot{a} \mathfrak{x}^2 \, ,</math> |
which, when acted upon by the various relevant operators, gives,
|
<math>~\nabla_\mathfrak{x}\psi</math> |
<math>~=</math> |
<math>~a \dot{a} \mathfrak{x} \, ,</math> |
|
<math>~\nabla^2_\mathfrak{x}\psi</math> |
<math>~=</math> |
<math>~ \biggl( \frac{1}{2}a \dot{a} \biggr) \frac{1}{\mathfrak{x}^2} \frac{d}{d\mathfrak{x}} \biggl[\mathfrak{x}^2 \frac{d}{d\mathfrak{x}} \mathfrak{x}^2 \biggr] = 3 a \dot{a} \, , </math> |
|
<math>~\frac{d\psi}{dt}</math> |
<math>~=</math> |
<math>~\mathfrak{x}^2 \biggl[ \frac{1}{2}\dot{a}^2 + \frac{1}{2}a\ddot{a} \biggr] \, .</math> |
Hence, the radial velocity profile is,
|
<math>~v_r = a^{-1}\nabla_\mathfrak{x} \psi</math> |
<math>~=</math> |
<math>~\dot{a}\mathfrak{x} \, ; </math> |
and the continuity equation gives,
|
<math>~\frac{d\ln \rho}{dt} </math> |
<math>~=</math> |
<math>-~ \frac{3\dot{a}}{a} \, .</math> |
Because we are hoping to identify a similarity solution, it will be advantageous to rewrite the mass density as a product of two functions: One that depends only on time, <math>~\rho_c(t)</math>, and one that reflects spatial variations, <math>f(\mathfrak{x})</math>. Specifically, we will write,
|
<math>~\rho </math> |
<math>~=</math> |
<math>~\rho_c f \, .</math> |
(Because, here, we are modeling the homologous collapse of a uniform-density sphere, this step isn't formally necessary. Ultimately, for example, we expect to find that <math>~f=1</math>, reflecting the system's spatial homogeneity. But rewriting the density in this fashion will make the analogy with Goldreich & Weber's (1980) derivation clearer.) Plugging this new expression into the continuity equation gives,
|
<math>~\cancelto{0}{\frac{d\ln f}{dt}} + \frac{d\ln \rho_c}{dt} </math> |
<math>~=</math> |
<math>~- \frac{d\ln a^3}{dt} \, ,</math> |
which means that the product, <math>~a^3 \rho_c</math>, is independent of time. Hence, if <math>~a_i</math> and <math>~\rho_0</math> are, respectively, the system's scale length and density initially, we can write,
<math>\frac{\rho_c}{\rho_0} = \biggl( \frac{a}{a_i}\biggr)^{-3} \, .</math>
As written, each term in the Euler equation has units of velocity-squared. Goldreich & Weber (1980) chose to normalize the Euler equation by dividing through by the square of the (time-varying) sound speed. This is not a good choice in our examination of the free-fall problem because we are altogether ignoring the effects of pressure. Instead, an appropriate normalization would seem to be,
<math>v_\mathrm{norm}^2 \equiv 4\pi G\rho_c a^2 \, .</math>
Adopting this normalization, the dimensionless gravitational potential is,
|
<math>~\sigma</math> |
<math>~\equiv</math> |
<math>~\frac{\Phi }{4\pi G\rho_c a^2} \, ,</math> |
and (remembering to set <math>~H = 0</math>) the Euler equation becomes,
|
<math>~ - \sigma </math> |
<math>~=</math> |
<math>~\biggl( \frac{1}{4\pi G\rho_c a^2} \biggr) \biggl\{ \mathfrak{x}^2 \biggl[ \frac{1}{2}\dot{a}^2 + \frac{1}{2}a\ddot{a} \biggr] - \frac{1}{2} ( \dot{a} \mathfrak{x} )^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{a}{4\pi G\rho_0 a_i^3 } \biggr)~ \mathfrak{x}^2 \biggl[\frac{1}{2} ( a \ddot{a} )\biggr]
</math> |
|
<math>~\Rightarrow~~~ \frac{\sigma}{\mathfrak{x}^2} </math> |
<math>~=</math> |
<math>~ - \biggl(\frac{4\tau_\mathrm{ff}^2}{3\pi^2 a_i^3} \biggr) a^2 \ddot{a} \, ; </math> |
and the dimensionless Poisson equation is,
|
<math>~a^{-2} \nabla_\mathfrak{x}^2 [ 4\pi G \rho_c a^2 \sigma] </math> |
<math>~=</math> |
<math>~4\pi G \rho_c f </math> |
|
<math>~\Rightarrow~~~\nabla_\mathfrak{x}^2 \sigma </math> |
<math>~=</math> |
<math>~f \, . </math> |
As was argued by Goldreich & Weber (1980), because everything on the lefthand side of the scaled Euler equation depends only on the dimensionless spatial coordinate, <math>~\mathfrak{x}</math>, while everything on the righthand side depends only on time — via the parameter, <math>~a(t)</math> — both expressions must equal the same (dimensionless) constant. If, following Goldreich & Weber, we call this constant, <math>~\lambda/6</math>, the terms on the lefthand side lead us to conclude that, to within an additive constant, the dimensionless gravitational potential is,
|
<math>~\sigma</math> |
<math>~=</math> |
<math>~\frac{\lambda}{6} ~\mathfrak{x}^2 \, .</math> |
From the terms on the righthand side we conclude, furthermore, that the differential equation governing the time-dependent variation of the scale length, <math>~a</math>, is,
|
<math>~ a^2 \ddot{a} </math> |
<math>~=</math> |
<math>~-~\frac{\lambda}{6}\biggl(\frac{3\pi^2 a_i^3}{4\tau_\mathrm{ff}^2 } \biggr) \, . </math> |
Discussion
Upon further assessment of the term on its righthand side, this last expression can be rewritten as,
|
<math>~ a^2 \ddot{a} </math> |
<math>~=</math> |
<math>~-~\lambda G\biggl( \frac{4\pi}{3}\rho_0 a_i^3 \biggr) = ~-~\lambda GM_i \, , </math> |
where, <math>~M_i</math> is independent of time and is the mass associated with the initial scale length, <math>~a_i</math>. Except that <math>~a</math> appears in place of <math>~R</math>, we see that this identically matches the equation of motion for the collapsing, uniform-density sphere presented above if we set <math>~\lambda = 1</math>. Therefore, for a system of any initial size, <math>~a_i</math>, that collapses from rest with an initial (uniform) density, <math>~\rho_0</math>, this equation can be straightforwardly integrated twice using the above sequence of steps to give the following parametric relationship between time and the system's instantaneous scale length at that time:
| |||||||||
Also, when we plug our derived functional expression for the dimensionless gravitational potential, <math>~\sigma</math>, into the dimensionless Poisson equation, we find,
|
<math>~\nabla_\mathfrak{x}^2 \biggl[ \frac{\lambda}{6}\mathfrak{x}^2 \biggr] </math> |
<math>~=</math> |
<math>~f </math> |
|
<math>~\Rightarrow~~~\biggl( \frac{\lambda}{6} \biggr) \frac{1}{\mathfrak{x}^2} \frac{d}{d\mathfrak{x}}\biggl[ \mathfrak{x}^2 \frac{d}{d\mathfrak{x}}\mathfrak{x}^2 \biggr] </math> |
<math>~=</math> |
<math>~f </math> |
|
<math>~\Rightarrow~~~\lambda</math> |
<math>~=</math> |
<math>~f \, ,</math> |
so the proper physical solution is, <math>~f = 1</math>, as expected. This means that, to within an additive constant, the gravitational potential will depend inversely on the time-dependent scale length, <math>~a</math>, and quadratically on the dimensionless — and time independent — radial coordinate, <math>\mathfrak{x}</math>, via the relation,
|
<math>~\Phi</math> |
<math>~=</math> |
<math>~4\pi G \rho_c a^2 \biggl( \frac{1}{6} ~\mathfrak{x}^2 \biggr) </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{2\pi G \rho_0 a_i^3}{3 a} \biggr)\mathfrak{x}^2 = \biggl( \frac{ G M_i}{2 a} \biggr)\mathfrak{x}^2 \, .</math> |
This expression for the gravitational potential looks a bit peculiar because it is zero at the center of the configuration and is otherwise everywhere positive. Customarily, a constant is subtracted from this function in order to ensure that it is everywhere negative and properly normalized to the expected value at the surface of the sphere. For example, in a separate discussion of the internal properties of isolated, uniform-density spheres that are in hydrostatic balance, the derived gravitational potential is,
|
<math>~\Phi(r)</math> |
<math>~=</math> |
<math>~- \frac{3G M}{2R} \biggl[ 1 - \frac{1}{3} \biggl(\frac{r}{R} \biggr)^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{G M}{2R} \biggl(\frac{r}{R} \biggr)^2 - \frac{3G M}{2R} \, . </math> |
We could subtract the quantity, <math>~[3GM_i/(2a)]</math>, from our derived expression for the potential of a free-falling homogeneous sphere in order for it to reflect this more familiar normalization, but this doesn't make a lot of sense because the quantity being subtracted — while constant in space — varies with time.
Relationship to Relativistic Cosmologies
NOTE: Frieman, Turner & Huterer (2008, ARAA, 46, 385 - 432) provide an excellent, very readable review of dark matter and dark energy in the context of various cosmologies.
Einstein's General Theory of Relativity generates the following "Friedmann equations" describing the (pressure-free) evolution of homogeneous, isotropic cosmologies in terms of the time-dependent scale length of the universe, <math>~\mathcal{R}(t)</math>:
|
Evolution of Homogeneous, Isotropic Cosmologies | ||||||
|---|---|---|---|---|---|---|
|
It is instructive to compare these dynamical relations with the analogous pair of equations that we derived, above, in the context of a Newtonian (and flat space) description of the free-fall collapse of a uniform-density sphere having a time-dependent radius, <math>~R(t)</math>:
|
Newtonian Description of Pressure-Free Collapse | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
If we set Einstein's cosmological constant, <math>~\Lambda</math>, to zero in the first set of equations, we see that the cosmological equations are mathematically identical to their Newtonian counterparts. (Apparently, this mathematical overlap was first discussed in back-to-back papers in the Quarterly Journal of Mathematics Oxford by Milne (1934) and McCrea & Milne (1934).) This tight analogy can help us understand the physical origin of the various terms that appear in the set of relativistic equations, or vise versa.
It is clear, for example, that the Newtonian equations that have been derived here in an effort to quantitatively describe the dynamical collapse of a uniform-density sphere could just as well be used to describe the dynamical expansion of a uniform-density sphere. To achieve expansion (in the absence of a cosmological constant), however, the velocity <math>~v_i</math> that appears in our definition of the integration constant, <math>~k</math>, must be nonzero and positive. Also, in order to successfully achieve an homogeneous expansion, the magnitude of <math>~v_i</math> that is assigned to fluid elements at different locations throughout the sphere must be linearly proportional to the radial coordinate of each fluid element.
Furthermore, it is clear that the "Hubble parameter," <math>~H</math>, is a (time-dependent) parameter giving the ratio of the instantaneous collapse/expansion velocity relative to the instantaneous scale length of the universe; and that the constant, <math>~K</math>, in part, relates to the "initial" collapse/expansion velocity imparted to the system.
The Collapse of Initially Centrally Condensed Spheres
Here we examine the free-fall collapse from rest of an initially (mildly) centrally condensed configuration. We will use the variable, <math>~r_i</math>, to identify the (time-dependent) radial location of a Lagrangian mass shell, and label the shell's initial location with, <math>~0 \le r_{0,i} \le R</math>. After specifying the configuration's iinitial radial density distribution, <math>~\rho_{0,i}(r)</math>, the time-independent mass enclosed within each Lagrangian shell can be straightforwardly determined via the integral,
|
<math>~M_{0,i}</math> |
<math>~=</math> |
<math>~4\pi \int_0^{r_{0,i}} r^2 \rho_{0,i}(r) dr \, .</math> |
As Tohline (1982) has shown — see his §3.2 — at any time,
<math>~0 < t < \tau_{ffc} \equiv \biggl[ \frac{3\pi}{32G\rho_c} \biggr]^{1 / 2} \, ,</math>
the radial location and the density of each Lagrangian mass shell is given by the following set of key expressions:
|
Key Relations Defining Free-Fall Collapse of Nonuniform Configurations | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
where, separately for each mass shell, time is referenced parametrically through <math>~\zeta_i</math> via the relation,
|
So, from a Lagrangian perspective, the relationship between time and the parameter, <math>~\zeta</math>, has the same functional form for each individual mass shell; but, for each individual shell, time is scaled to a different free-fall time,
|
<math>~\tau_{ffi}</math> |
<math>~\equiv</math> |
<math>~ \biggl(\frac{\pi}{2} \biggr)\frac{\tau_{ffc}}{A_{0,i}} = \tau_{ffc}\biggl[ \frac{\rho_c}{{\bar\rho}_i} \biggr]^{1 / 2} \, , </math> |
where, <math>~{\bar\rho}_i</math> is the mean density of material interior to each mass shell at the onset of collapse.
The expression for the time-dependent velocity of each mass shell can also be straightforwardly obtained from the above Lagrangian-perspective derivation that was presented in the context of an initially uniform-density configuration. We find that, for each individual mass shell,
|
<math>~v_i</math> |
<math>~=</math> |
<math>~ - \biggl(\frac{2GM_{0,i}}{r_{0,i}} \biggr)^{1/2} \tan\zeta_i </math> |
|
|
<math>~=</math> |
<math>~ - \frac{R}{\tau_{ffc}}\biggl[ \frac{3\pi}{32G \rho_c R^2} \biggr]^{1 / 2} \biggl(\frac{2GM_\mathrm{tot}}{R} \biggr)^{1/2} \biggl[\frac{M_{0,i}}{M_\mathrm{tot}} \biggl(\frac{r_{0,i}}{R}\biggr)^{-1} \biggr]^{1/2}\tan\zeta_i </math> |
|
|
<math>~=</math> |
<math>~ - \frac{R}{\tau_{ffc}}\biggl[ \biggl( \frac{\pi^2}{4}\biggr) \frac{3M_\mathrm{tot} }{4\pi \rho_c R^3} \biggr]^{1 / 2} \biggl[\frac{M_{0,i}}{M_\mathrm{tot}} \biggl(\frac{r_{0,i}}{R}\biggr)^{-1} \biggr]^{1/2}\tan\zeta_i \, . </math> |
Here are the steps that we have followed in order to determine how the radial profile of various physical parameters varies with time during a free-fall collapse for each of several example initial configurations.
- Specify analytically the density profile, <math>~\rho_{0}(r)</math> of the configuration initially, that is, at time, <math>~t = 0</math>; segment the configuration into N separate radial shells and catalog the discrete value of the density, <math>~\rho_{0,i}</math>, and corresponding radius, <math>~r_{0,i}</math>, of each shell.
- Appropriately integrate over the <math>~\rho_{0}(r)</math> distribution to determine an analytic function for <math>~M_{0}(r)</math> and, in turn, for <math>~A_0(r)</math> and <math>~d\ln A_0/d\ln r</math>; evaluate these three functions at each of the N separate radial shells and catalog the sets of discrete values of <math>~M_{0,i}, A_{0,i}</math> and the corresponding logarithmic derivative of <math>~A_{0,i}</math>.
- Develop a numerical algorithm — based, for example, on a standard Newton-Raphson method — that will find the principal root <math>~(\zeta_i)</math> of the following expression for any chosen value of the dimensionless time (usually within the range), <math>~0 < t/\tau_{ffi} < 1</math>:
|
<math>~\zeta_i + \frac{1}{2} \sin(2\zeta_i) - \frac{t}{\tau_{ffc}} \biggl[ A_{0,i}\biggr] </math> |
<math>~=</math> |
<math>~0 \, .</math> |
- Set a value of the integration time; use the root-finding algorithm to determine the value of <math>~\zeta_i</math> for all N discrete shells; by plugging each value of <math>~\zeta_i</math> into the above set of key relations, determine the radial location, <math>~r_i(t)</math>, the density, <math>~\rho_i(t)</math>, and the velocity, <math>~v_i(t)</math>, of each discrete shell at the specified time; then, for example, a plot of <math>~\rho_i(r_i(t))</math> provides the desired density profile at the specified time. A plot of <math>~M(r(t))</math> can also be straightforwardly generated by relying on the (time-independent) function, <math>~M_{0,i}</math>, and the subscript, <math>~i</math>, to identify how much mass is enclosed inside the (time-dependent) radial location of each Lagrangian mass shell.
- Repeat step #4, using a number of different values of the time, as desired, in order to generate a smooth depiction of the density profile's, the velocity profile's, or the mass profile's evolution.
Example Density Profiles Examined by Tohline (1982)
By way of illustration, Tohline (1982) adopted several density profiles parameterized by the integer index, <math>~m</math>, of the form,
|
<math>~ \frac{\rho_{0,i}}{\rho_c} </math> |
<math>~=</math> |
<math>~1 - \biggl(\frac{r_{0,i}}{R}\biggr)^m \, .</math> |
In this case, we have,
|
<math>~M_{0,i}</math> |
<math>~=</math> |
<math>~4\pi R^3 \rho_c \int_0^{r_{0,i}} \biggl( \frac{r}{R}\biggr)^2 \biggl[1 - \biggl(\frac{r}{R}\biggr)^m \biggr] \frac{dr}{R} </math> |
|
|
<math>~=</math> |
<math>~\frac{4\pi R^3 \rho_c}{3} \biggl( \frac{r_{0,i}}{R}\biggr)^3 \biggl[1 - \frac{3}{m+3} \biggl(\frac{r_{0,i}}{R}\biggr)^{m} \biggr] </math> |
|
<math>~\Rightarrow~~~ A_{0,i}^2 </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{3\pi }{16 \rho_c r_{0,i}^3 } \biggr] \frac{4\pi R^3 \rho_c}{3} \biggl( \frac{r_{0,i}}{R}\biggr)^3 \biggl[1 - \frac{3}{m+3} \biggl(\frac{r_{0,i}}{R}\biggr)^{m} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\biggl(\frac{\pi}{2}\biggr)^2 \biggl[1 - \frac{3}{m+3} \biggl(\frac{r_{0,i}}{R}\biggr)^{m} \biggr] </math> |
|
<math>~\Rightarrow~~~ \frac{d\ln A_{0,i}}{d\ln r_{0,i}} = \frac{r_{0,i}}{A_{0,i}} \biggl[ \frac{d A_{0,i}}{d r_{0,i}} \biggr] </math> |
<math>~=</math> |
<math>~ r_{0,i}\biggl[1 - \frac{3}{m+3} \biggl(\frac{r_{0,i}}{R}\biggr)^{m} \biggr]^{-1 / 2} \frac{d }{d r_{0,i}} \biggl[1 - \frac{3}{m+3} \biggl(\frac{r_{0,i}}{R}\biggr)^{m} \biggr]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{r_{0,i}}{2} \biggl[1 - \frac{3}{m+3} \biggl(\frac{r_{0,i}}{R}\biggr)^{m} \biggr]^{-1 }\biggl[- \frac{3m}{R(m+3)} \biggl(\frac{r_{0,i}}{R}\biggr)^{m-1} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ -\frac{3m}{2(m+3)} \biggl[1 - \frac{3}{m+3} \biggl(\frac{r_{0,i}}{R}\biggr)^{m} \biggr]^{-1 }\biggl(\frac{r_{0,i}}{R}\biggr)^{m} \, . </math> |
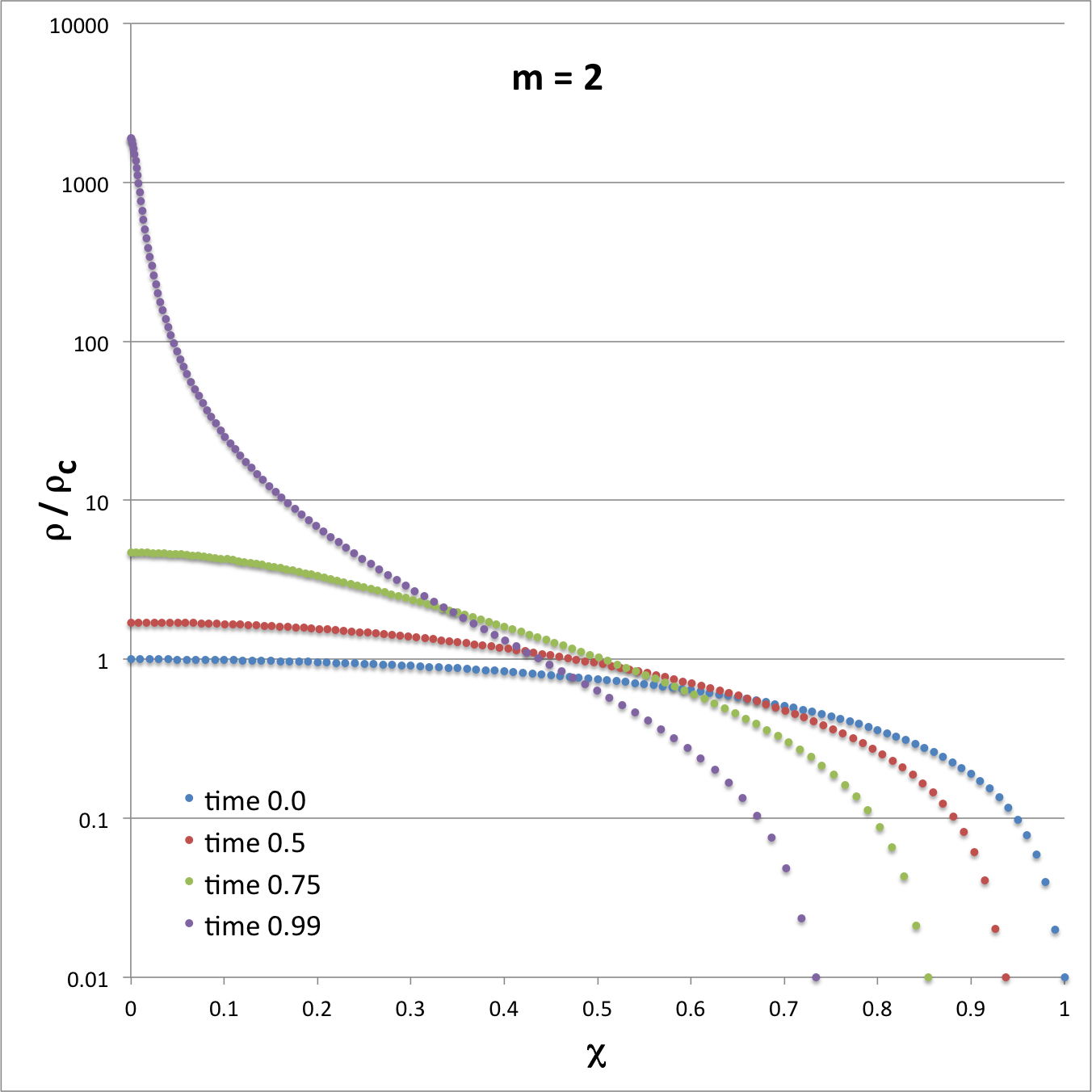
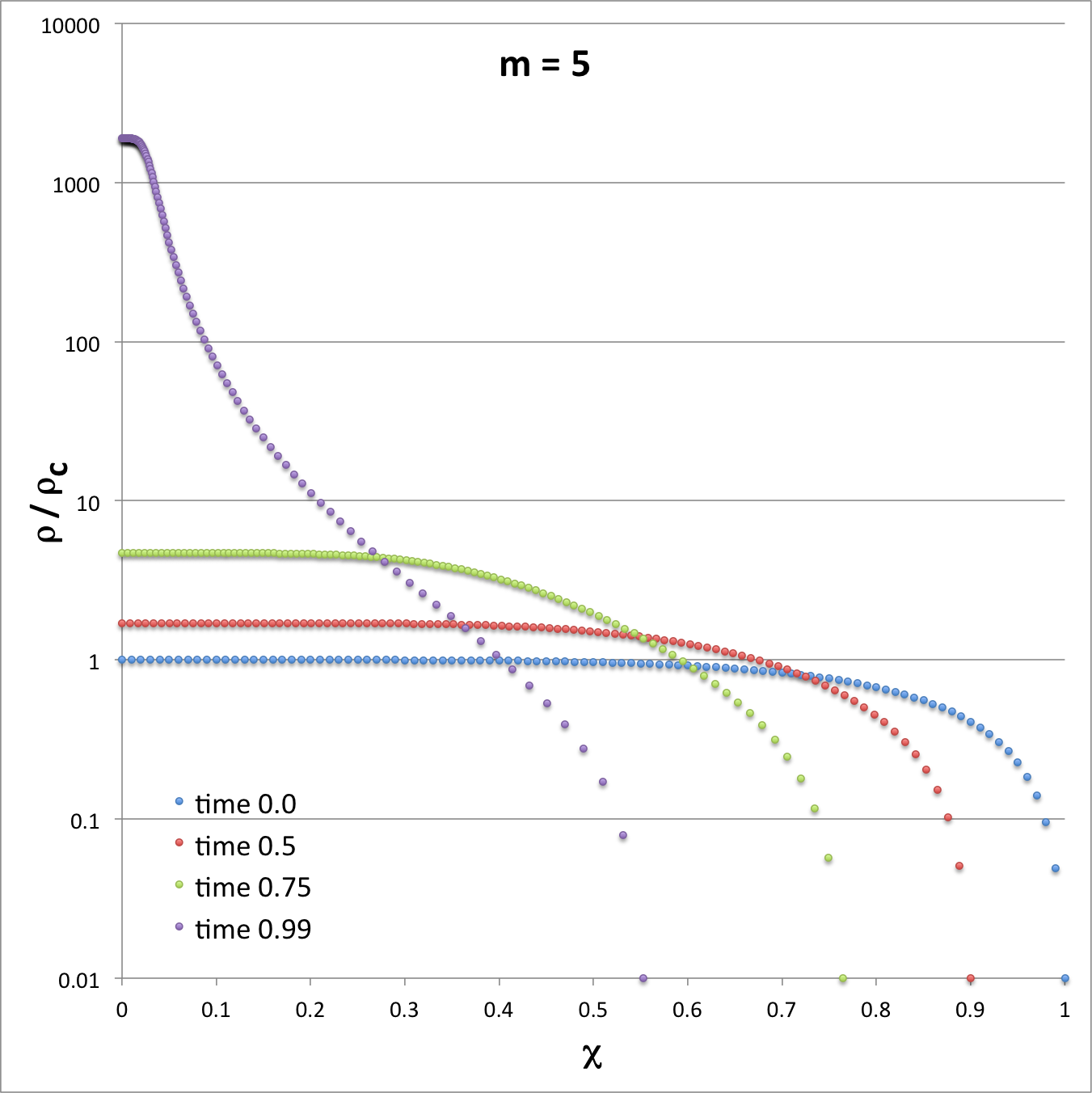
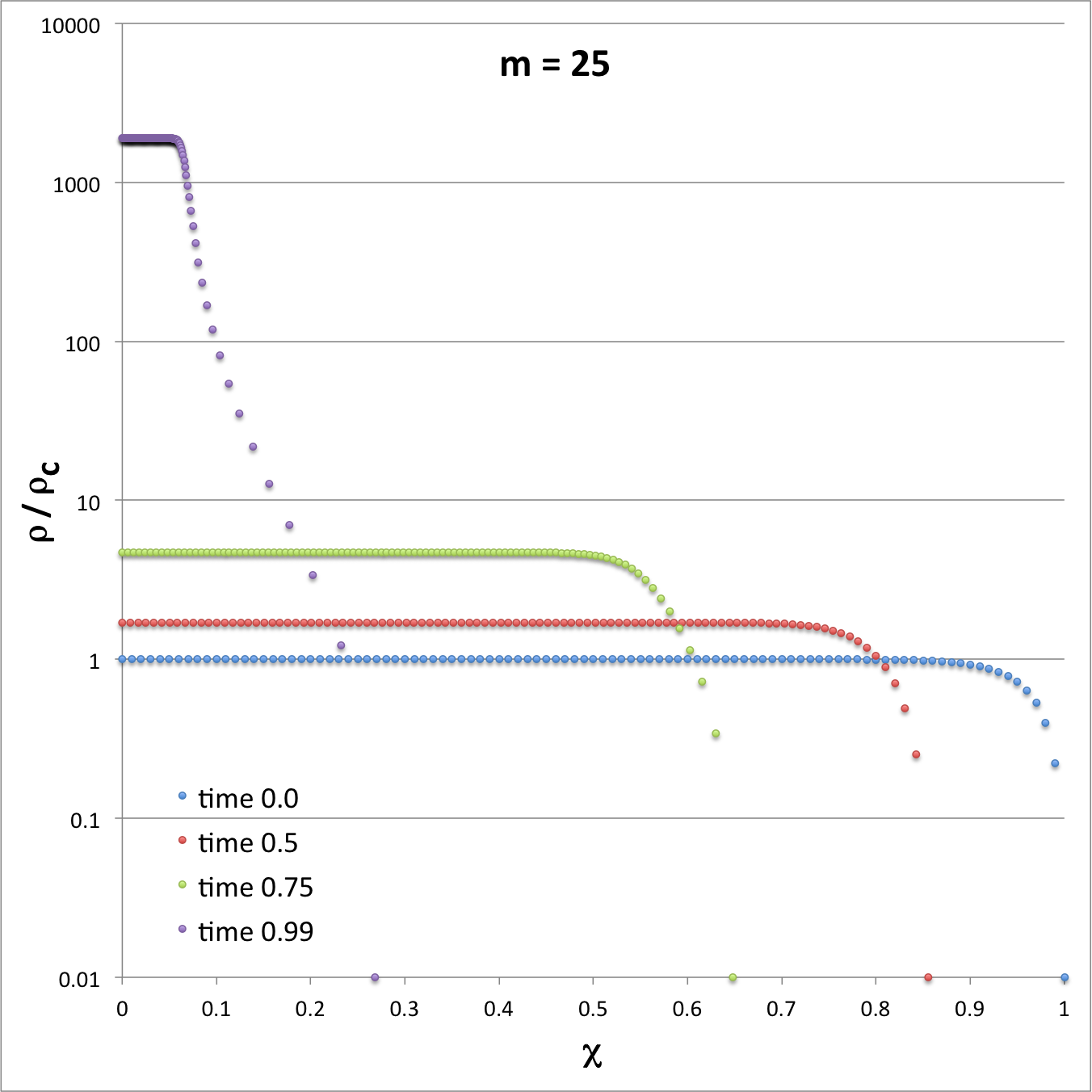
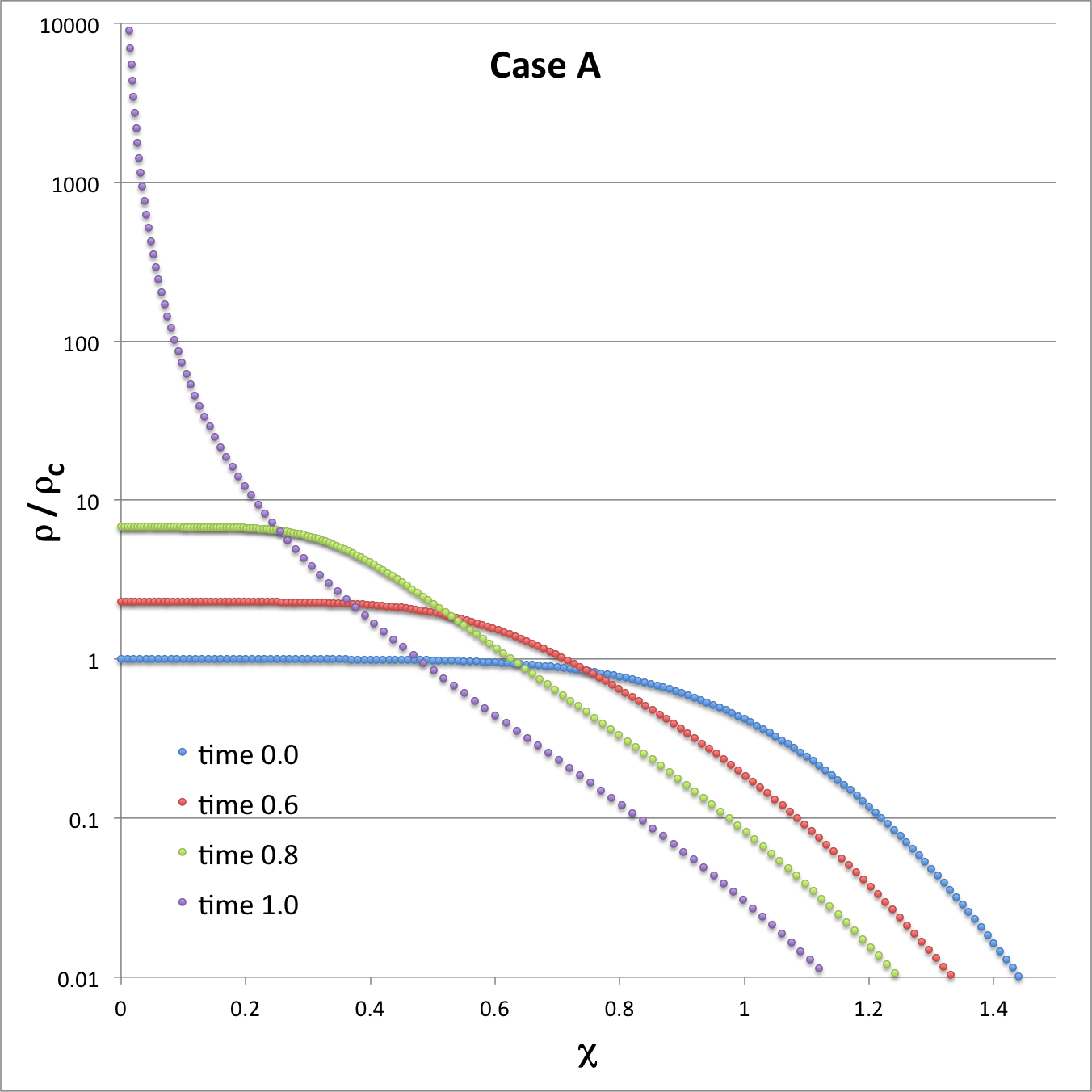
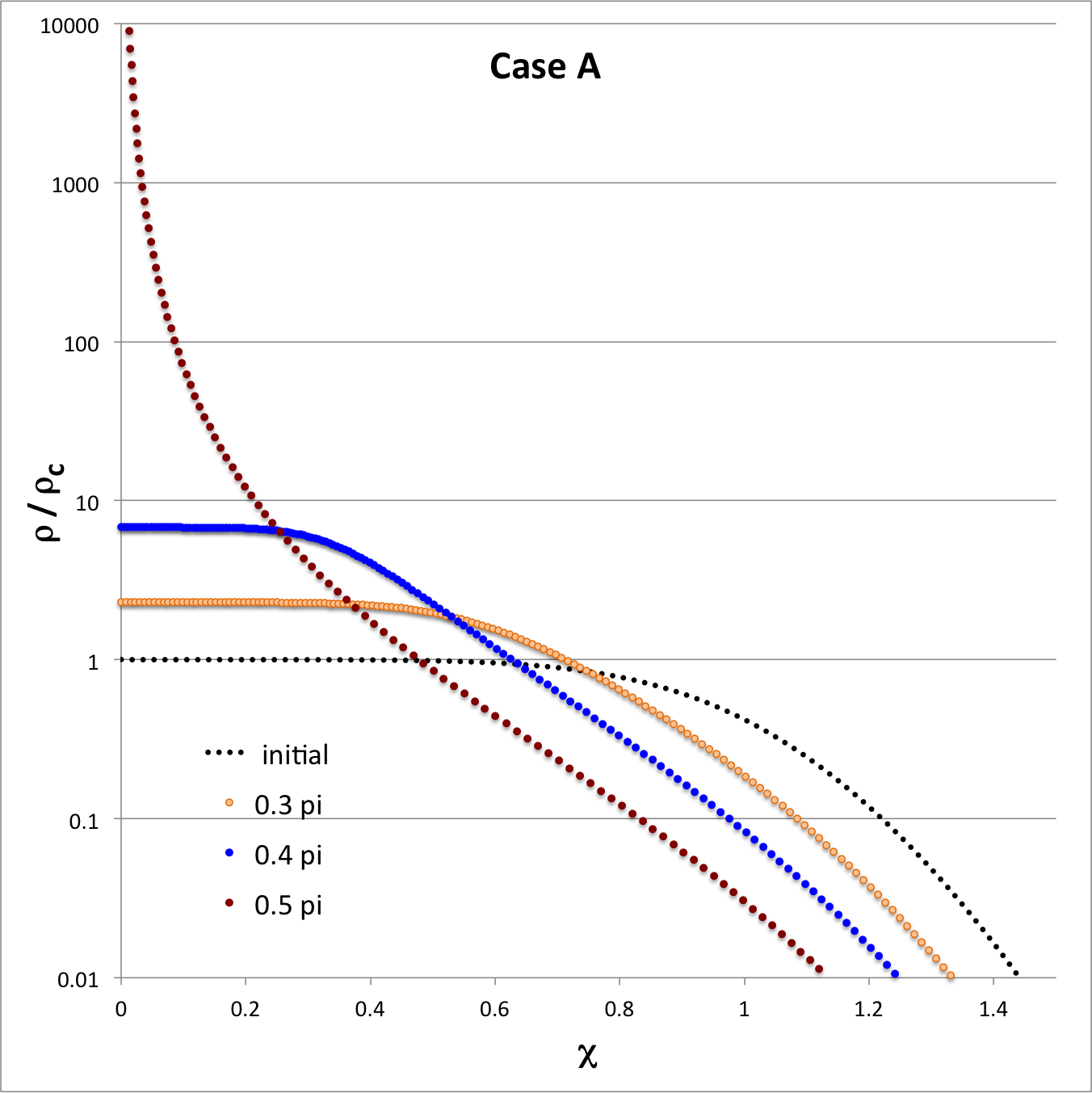
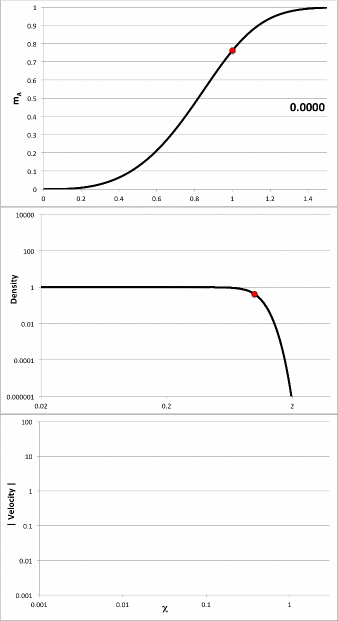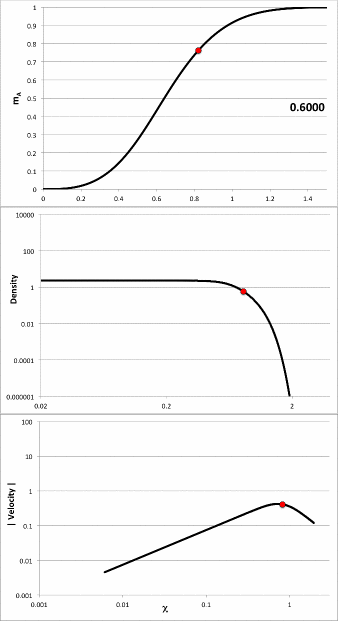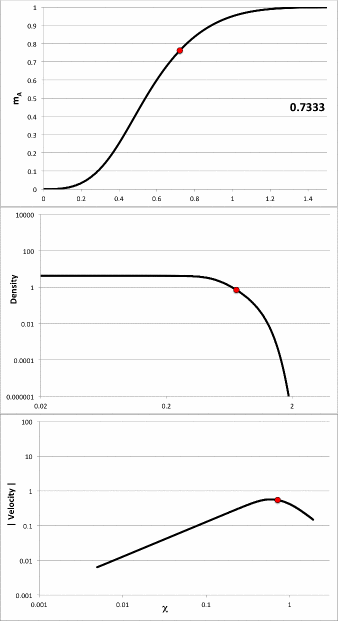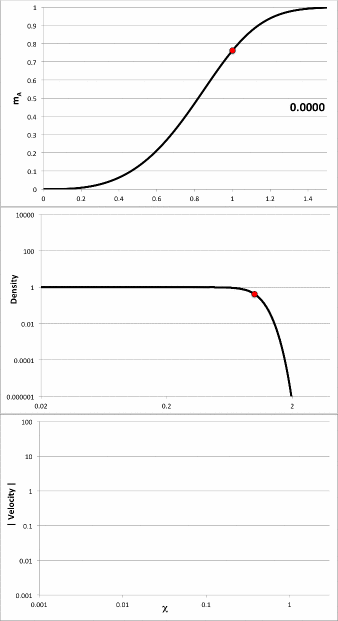
Using these functional expressions — and guided by Tohline's (1982) presentation — we have modeled the early free-fall collapse of configurations whose initial density profiles are defined by setting the index, m = 2, 5, and 25. In three of the four panels of the following composite Figure 1 we have used semi-log plots to show how the density profile varies with time for each of these three models at four times: <math>~t/\tau_{ffc} = 0.0, 0.5, 0.75, 0.99</math>; they replicate the three panels that appear in Figure 3 of Tohline (1982). [The fourth figure panel similarly displays the evolutionary behavior of the model labeled "Case A" that has subsequently been studied by Coughlin (2017); see further discussion, below.] As the images illustrate, there is inevitably a run-away collapse of the central core, even for configurations that are initially only mildly centrally condensed,
| Composite Figure 1 | |
|---|---|
|
In large measure, the three panels labeled, respectively, m = 2, m = 5, and m = 25, are intended to replicate the three panels that appear in Figure 3 of Tohline (1982). For comparison, the fourth panel displays in a similar fashion the early evolutionary behavior of the model labeled Case A that has been studied by Coughlin (2017). |
|
Example Mass Profiles Examined by Coughlin (2017)
Approach
Via an independent analysis, Coughlin (2017) has also examined the free-fall collapse of initially (mildly) centrally condensed, spherically symmetric configurations. When viewed from a Lagrangian frame of reference — see the paragraph accompanying his equation (16) — he concludes that,
|
<math>~ \frac{r_i(t)}{r_{0,i}} </math> |
<math>~=</math> |
<math>~1 - f^2(\xi_i) \, ,</math> |
where, in his derivation, time is referenced parametrically through <math>~\xi_i</math> via the relation,
|
<math>~\xi_i</math> |
<math>~=</math> |
<math>~t \biggl[ \frac{2GM_{0,i}}{r^3_i(t)}\biggr]^{1 / 2} \, .</math> |
While Coughlin does not provide an explicit expression for the function, <math>~f(\xi_i)</math>, he shows — see his equation (11) — that it must satisfy the following nonlinear differential equation:
|
<math>~ \frac{df}{d\xi_i} </math> |
<math>~=</math> |
<math>~ \frac{1 - f^2}{2 + 3\xi_i f} \, . </math> |
Relationship to Tohline's Approach
A comparison between the expression for <math>~r_i(t)/r_{0,i}</math> that appears in Coughlin's (2017) derivation and the one published by Tohline (1982) suggests that,
<math>~f = \sin\zeta_i \, .</math>
Similarly, an inspection of the two, separately derived, expressions for time suggests that,
|
<math>~\xi_i = t \biggl[ \frac{2GM_{0,i} }{r^3_i(t)} \biggr]^{1 / 2}</math> |
<math>~=</math> |
<math>~t \biggl[ \frac{8\pi G \rho_c}{3}\biggr]^{1 / 2} \biggl[ \frac{3M_{0,i}}{4\pi \rho_c r^3_{0,i}}\biggr]^{1 / 2} \biggl[ \frac{r_{0,i}}{r_i(t)}\biggr]^{3 / 2}</math> |
|
|
<math>~=</math> |
<math>~t \biggl[ \frac{A_{0,i} }{\tau_{ffc}}\biggr] \biggl[ \frac{1}{\cos^3\zeta_i}\biggr]</math> |
|
|
<math>~=</math> |
<math>~\biggl[ \zeta_i + \frac{1}{2} \sin(2\zeta_i) \biggr] \biggl[ \frac{1}{\cos^3\zeta_i}\biggr] \, .</math> |
Let's see whether these explicit expressions for <math>~f(\zeta_i)</math> and <math>~\xi_i(\zeta_i)</math> satisfy Coughlin's nonlinear ODE.
Given that,
<math>~\frac{df}{d\zeta_i} = \frac{d\xi_i}{d\zeta_i} \cdot \frac{df}{d\xi_i} ~~~\Rightarrow ~~~ \biggl[ \frac{df}{d\xi_i} \biggr]^{-1} = \biggl[ \frac{df}{d\zeta_i} \biggr]^{-1} \frac{d\xi_i}{d\zeta_i} \, ,</math>
we can rewrite the ODE as,
|
<math>~ (1-f^2)\biggl[ \frac{df}{d\zeta_i} \biggr]^{-1} \frac{d\xi_i}{d\zeta_i} </math> |
<math>~=</math> |
<math>~ 2 + 3\xi_i f \, . </math> |
After adopting our proposed parameter mapping, we find that,
|
<math>~\frac{d\xi_i}{d\zeta_i}</math> |
<math>~=</math> |
<math>~ \frac{3\sin\zeta_i }{\cos^4\zeta_i}\biggl[ \zeta_i + \frac{1}{2} \sin(2\zeta_i) \biggr] + \frac{1}{\cos^3\zeta_i} \biggl[1 + \cos(2\zeta_i) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{3\sin\zeta_i }{\cos^4\zeta_i}\biggl[ \zeta_i + \sin\zeta_i \cos\zeta_i \biggr] + \frac{2}{\cos\zeta_i} \, . </math> |
Hence, the left-hand side of the rewritten ODE becomes,
|
LHS |
<math>~=</math> |
<math>~ \cos^2 \zeta_i \biggl[\cos\zeta_i \biggr]^{-1} \biggl\{ \frac{2}{\cos\zeta_i} +\frac{3\sin\zeta_i }{\cos^4\zeta_i}\biggl[ \zeta_i + \sin\zeta_i \cos\zeta_i \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 2 +\frac{3\sin\zeta_i }{\cos^3\zeta_i}\biggl[ \zeta_i + \sin\zeta_i \cos\zeta_i \biggr] \, . </math> |
It is easy to see that, after adopting the prescribed parameter mapping, the right-hand side of this ODE presents exactly the same expression. We conclude, therefore, that the pair of functions, <math>~f</math> and <math>~\xi_i</math>, introduced by Coughlin (2017) may be straightforwardly expressed in terms of Tohline's (1982) parameter, <math>~\zeta_i</math>, as follows:
|
Models A, B, & D, with Focus on Case A
By way of illustration, Coughlin (2017) examined the pressure-free collapse of configurations having the following three initial mass profiles (see his equations 28, 29, & 30):
|
<math>~M_{0,A}</math> |
<math>~=</math> |
<math>~M_\mathrm{tot} \tanh \biggl(\frac{r_{0,i}}{R_C}\biggr)^3 \, ;</math> |
|
<math>~M_{0,B}</math> |
<math>~=</math> |
<math>~M_\mathrm{tot} \biggl[ 1 - e^{-(r_{0,i}/R_C )^3} \biggr] \, ;</math> |
|
<math>~M_{0,D}</math> |
<math>~=</math> |
<math>~M_\mathrm{tot} \biggl(\frac{2}{\pi}\biggr) \tan^{-1} \biggl[ \frac{\pi}{2} \biggl(\frac{r_{0,i}}{R_C}\biggr)^3\biggr] \, ,</math> |
where, in all three cases, "<math>~R_C</math> should be interpreted as a scale length over which the density decreases appreciably." Adopting the shorthand notation,
<math>~\chi \equiv \frac{r_{0,i}}{R_C} \, ,</math> and <math>~a \equiv \frac{3M_\mathrm{tot}}{4\pi\rho_c R^3_C} \, ,</math>
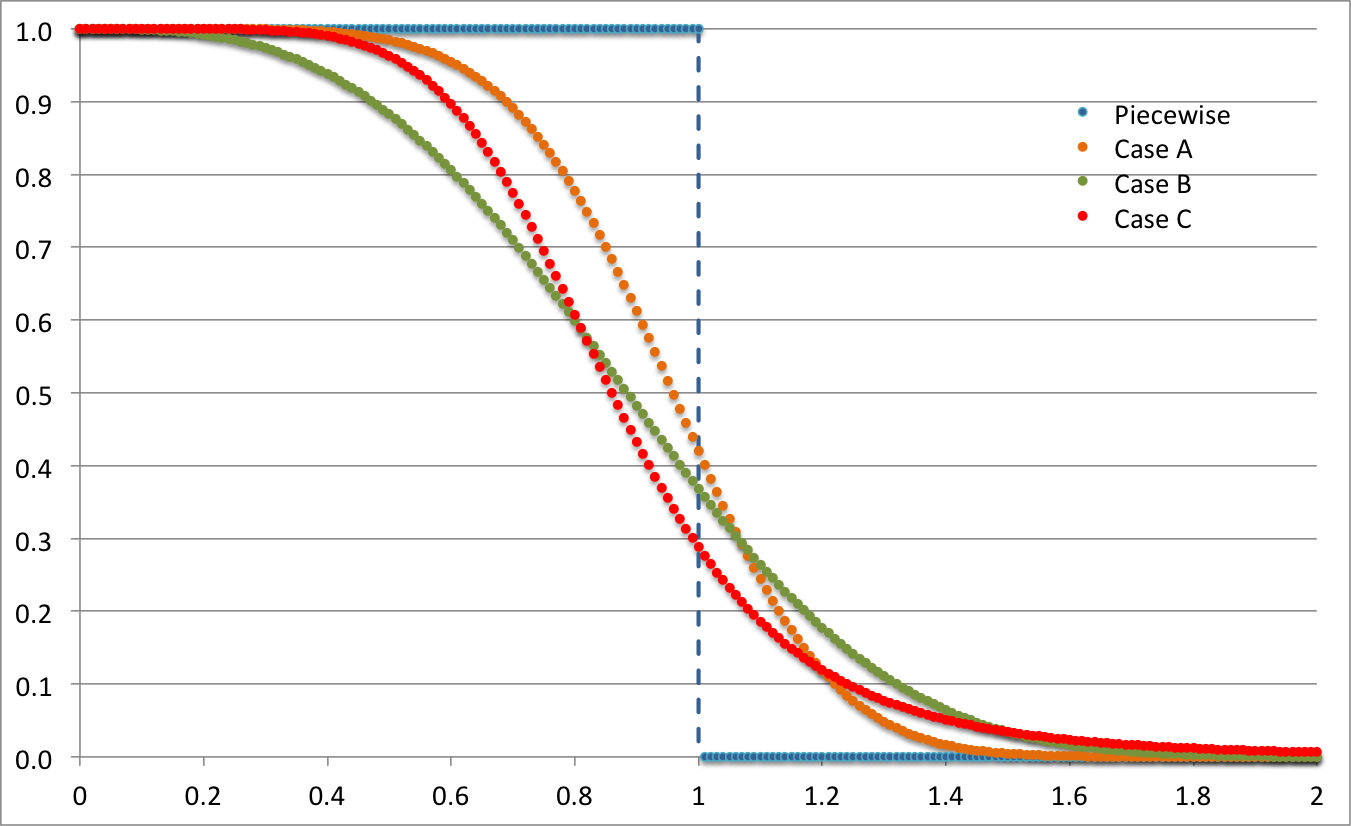
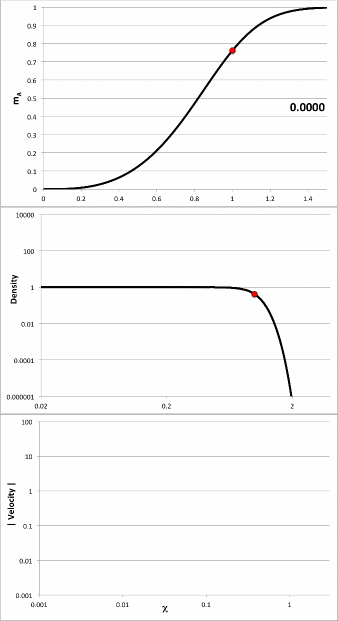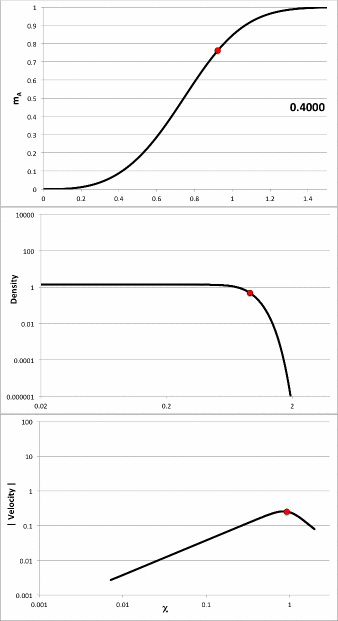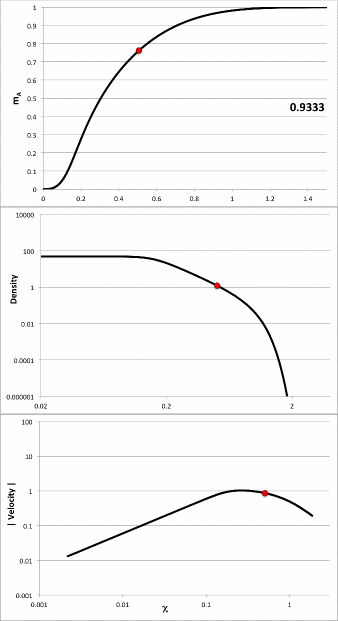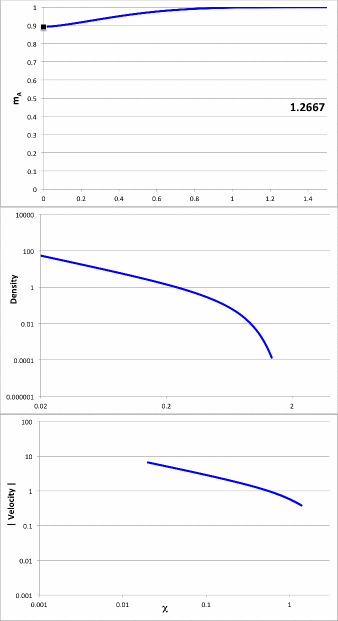
we have deduced that the mathematical expressions that define the corresponding initial density profiles, <math>~\rho_{0,i}</math>, are as recorded in the left-hand portion of composite Figure 2. The right-hand portion of this composite figure presents a plot of <math>~\rho_{0,i}/\rho_c</math> versus <math>~0 \le \chi \le 2</math> for all three of these initial models, in addition to a piecewise constant description of a uniform-density sphere of radius, <math>~R_C</math>; this diagram has been constructed to replicate Figure 2 from Coughlin (2017).
| Composite Figure 2 | ||
|---|---|---|
|
Coughlin's (2017) Example Density Profiles† |
Plot Constructed to Replicate Figure 2 of Coughlin (2017) |
|
|
Case A |
<math>~\frac{\rho_{0,i}}{\rho_c} = \frac{a}{\cosh^2(\chi^3)} </math> |
|
|
Case B |
<math>~\frac{\rho_{0,i}}{\rho_c} = a e^{-\chi^3} </math> |
|
|
Case D |
<math>~\frac{\rho_{0,i}}{\rho_c} = a \biggl[ 1+ \biggl(\frac{\pi}{2} \chi^3\biggr)^2\biggr]^{-1} </math> |
|
|
†As stated in the paragraph that follows his equation (27), Coughlin set the leading coefficient, <math>~a = 1</math>, in all three cases. |
||
We have deduced, as well, that the corresponding functional forms of the coefficient, <math>~A_{0,i}</math>, are:
|
<math>~A^2_{0,i}</math> |
<math>~=</math> |
<math>~ \frac{3\pi M_{0,i}}{16 \rho_c r_{0,i}^3 } = a \biggl(\frac{\pi}{2}\biggr)^2 \chi^{-3} \biggl[ \frac{M_{0,i}}{M_\mathrm{tot}} \biggr] \, , </math> |
that is, for the three example cases,
|
Case A: |
<math>~A^2_{0,A}</math> |
<math>~=</math> |
<math>~ a \biggl(\frac{\pi}{2}\biggr)^2 \biggl[ \frac{\tanh \chi^3}{\chi^3} \biggr] </math> |
<math>~\Rightarrow</math> |
<math>~\frac{d\ln A_{0,A}}{d\ln \chi} = - \frac{3}{2}\biggl[ 1 - \frac{\chi^3}{ \sinh (\chi^3) \cdot \cosh (\chi^3)} \biggr] \, ; </math> |
|
Case B: |
<math>~A^2_{0,B}</math> |
<math>~=</math> |
<math>~ a \biggl(\frac{\pi}{2}\biggr)^2 \chi^{-3} \biggl[ 1 - e^{-\chi^3} \biggr] </math> |
<math>~\Rightarrow</math> |
<math>~\frac{d\ln A_{0,B}}{d\ln \chi} = -\frac{3}{2} \biggl[ 1 - \chi^3 e^{-\chi^3}(1 - e^{-\chi^3})^{-1} \biggr] \, ; </math> |
|
Case D: |
<math>~A^2_{0,D}</math> |
<math>~=</math> |
<math>~ a \biggl(\frac{\pi}{2}\biggr) \chi^{-3} \tan^{-1} \biggl[ \frac{\pi \chi^3}{2} \biggr] </math> |
<math>~\Rightarrow</math> |
<math>~\frac{d\ln A_{0,D}}{d\ln \chi} = -\frac{3}{2}\biggl\{ 1 - \biggr(\frac{\pi \chi^3}{2}\biggr) \biggl[1 + \biggl(\frac{\pi \chi^3}{2}\biggr)^2 \biggr]^{-1} \biggl[\tan^{-1}\biggl( \frac{\pi \chi^3}{2}\biggr) \biggr]^{-1} \biggr\} \, . </math> |
Plugging these functional expressions into the above-defined set of Lagrangian evolution equations and following the above-defined set of modeling steps, we have modeled the early free-fall collapse of these three models. Guided by Coughlin's (2017) presentation, we will focus our discussion on the evolution of the model whose initial density profile has been labeled, "Case A."
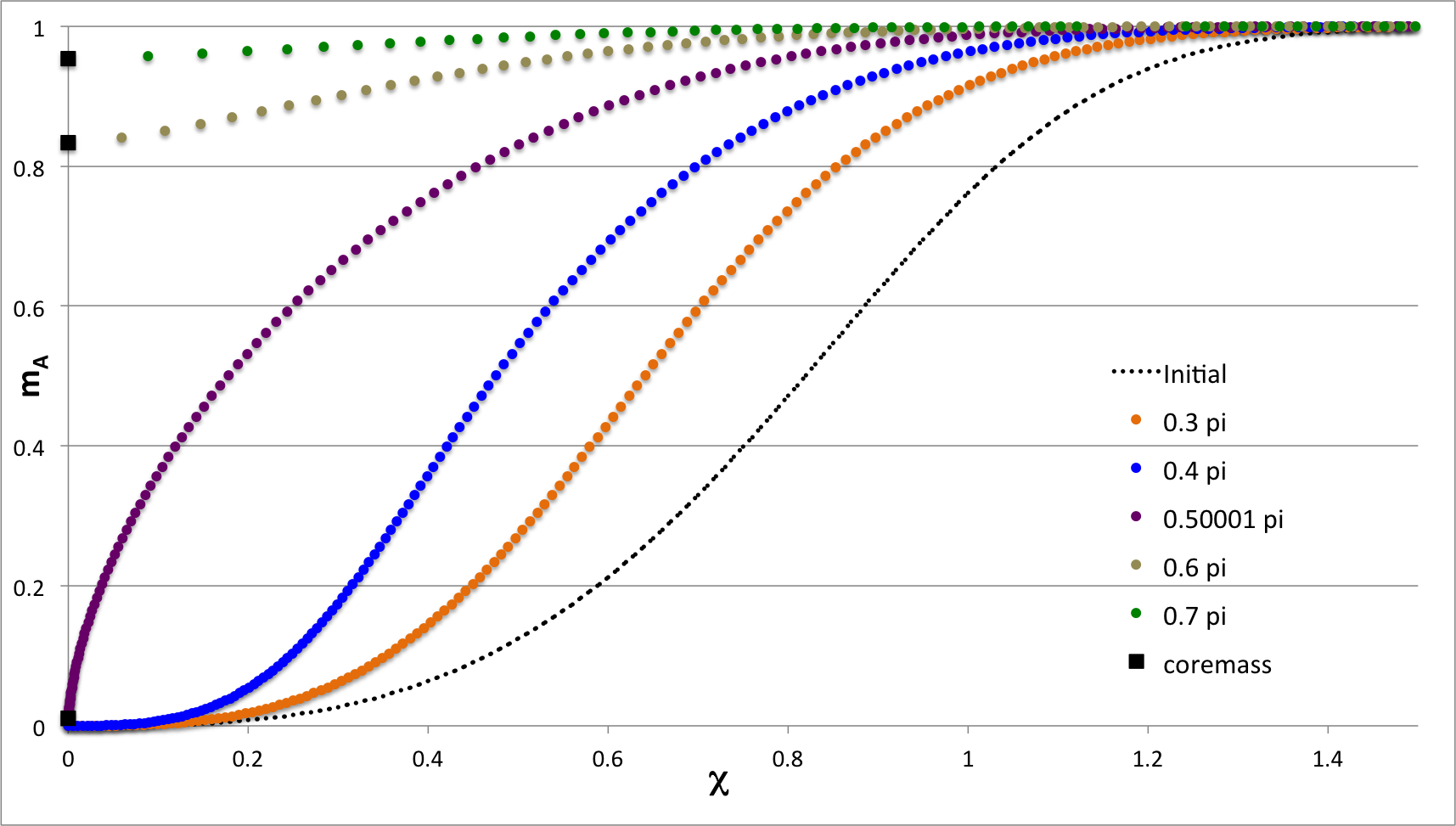
The right-hand panel of our composite Figure 3 shows how the radial density profile changes over time during the initial free-fall collapse of Coughlin's "Case A" model. This panel also has been included in our composite Figure 1, above to facilitate comparison with similar segments of the model evolutions presented by Tohline (1982). The left-hand panel of our composite Figure 3 presents a plot that is largely intended to replicate the left-most panel in Coughlin's (2017) Figure 3. It presents a plot of the model's mass profile — normalized to the total mass — at time <math>~t = 0</math> (dashed black curve) and at the following five evolutionary times:
<math>~\biggl(\frac{\pi}{2} \biggr) \frac{t}{\tau_{ffc}} = 0.3\pi, 0.4\pi, 0.5\pi, 0.6\pi, 0.7\pi \, .</math>
|
Composite Figure 3: Time-Evolution of "Case A" from Coughlin (2017) |
|
|---|---|
|
Left: Radial mass profile initially (dashed black curve) and at five additional evolution times, as annotated; this plot has been constructed to replicate the left-most panel in Figure 3 of Coughlin (2017). Right: Semi-log plot of the radial density profile initially (dashed black curve) and at three additional evolution times, as annotated. This same plot is displayed in composite Figure 1, above, to aid in comparison with models presented by Tohline (1982); it also can appropriately be compared with the middle panel from Figure 3 of Coughlin (2017), which presents three of the same density profiles, but on a log-log plot. |
|
These time-evolving mass profiles — interspersed among others from our analysis of Coughlin's "Case A" evolution — have also been displayed as an animation sequence in our composite Figure 4. Actually, they appear as the top segment of two separate animations — one on the left, the other on the right of the figure — along with the time-evolving density profile (middle segment) and the time-evolving velocity profile (bottom segment). In these animated diagrams, the density is scaled to the model's intial central density, <math>~\rho_c</math>, and, following Coughlin (2017) — see one of the paragraphs following shortly after his equation (27) — the velocity is everywhere, and at all times, normalized to,
|
<math>~v_C</math> |
<math>~\equiv</math> |
<math>~ \biggl[ \frac{2GM_C}{R_C} \biggr]^{1 / 2} = a\biggl(\frac{\pi}{2}\biggr) \frac{R_C}{\tau_{ffc}} \, . </math> |
These additional "density profile" and "velocity profile" panels present evolutionary information that, for the most part, may be extracted, respectively, from the middle panel and the right-most panel in Coughlin's (2017) Figure 3; in order to accommodate large dynamic ranges, the density profiles and velocity profiles are presented as log-log plots.
| Composite Figure 4 | |
|---|---|
|
Animation of Case A Evolution: Radial profiles of (top) mass, (middle) density & (bottom) velocity |
|
|
In both animation sequences, the red circular marker identifies the radial location of the Lagrangian mass shell that was initially located at <math>~\chi = 1</math>; in the animation on the right the red marker disappears after this mass shell has fallen into, and become part of the central core. After one initial central free-fall (blue curves in animation on the right), a black square marker appears on the vertical axis in the top panel to identify the mass of the central, point-mass core. |
|
The animation that appears in the left-hand column of our composite Figure 4 loops back and forth between the initial state, <math>~t = 0 \tau_{ffc}</math>, and (nearly) one central free-fall time, <math>~t = 0.9999\tau_{ffc}</math>. It provides a focus on the behavior of the free-fall collapse and, in particular, illustrates the run-away development of a centrally condensed structure, as highlighted earlier in the model evolutions presented by Tohline. Each loop of the animation that appears in the right-hand column of composite Figure 4 also proceeds from the initial state to one initial free-fall time (drawn as solid black curve segments), but then it continues to display (as solid blue curve segments) evolution through the first free-fall time and formation of a point-mass core, and — see the discussion that follows — into a phase where continued accretion of matter onto the core results in a rapid increase of the core's mass.
Accretion Onto a Point-Mass Core
The mathematical model that has been used, above, to describe the development of nonlinear structure in configurations that undergo free-fall collapse must break down as <math>~t \rightarrow \tau_{ffc}</math> because the volume enclosing the central-most mass shell shrinks to zero — concomitantly, the central density formally climbs to infinity — while the inward-directed radial velocity remains nonzero. At the very least, in the central region of the collapsing configuration it is physically unreasonable to ignore the effects of pressure (and/or general relativity) as <math>~t \rightarrow \tau_{ffc}</math>.
As Coughlin (2017) has suggested, however, it may not be unreasonable to consider that <math>~\tau_{ffc}</math> marks the point in time when a central point mass core forms and to continue to use this mathematical model to represent the behavior of the "envelope" material as it continues to free-fall toward the core. We acknowledge that this point of view can provide additional insight especially if the extended examination is confined to regions well outside the core. It is with this in mind that the animation sequence on the right-hand side of our composite Figure 4 has been extended to times, <math>~(\pi/2)t/\tau_{ffc} > 0.5\pi</math>; at these later times, the accretion envelope profiles are depicted by solid blue curve segments.
As the evolution proceeds past the initial free-fall time, the radius of a larger and larger number of mass shells will shrink to zero and, under the scenario just outlined, must be considered part of the central point-mass core. Presumably, as Coughlin has illustrated, the above-developed free-fall model can continue to be used to estimate how rapidly the core mass grows. Suppose that, at times <math>~t > \tau_{ffc}</math>, we want to determine the mass of the central core. This reduces to determining at what time <math>~\zeta_i \rightarrow \tfrac{\pi}{2}</math> for each mass shell; or, for a given time, <math>~t/\tau_{ffc}</math>, determining for which mass shell,
|
<math>~A_{0,i} </math> |
<math>~=</math> |
<math>~\biggl[ \biggl(\frac{2}{\pi}\biggr) \frac{t}{\tau_{ffc}} \biggl]^{-1} \, .</math> |
For "Case A", for example, after setting the coefficient, <math>~a=1</math>, this is equivalent to determining the root, <math>~\chi</math>, of the equation,
|
<math>~\biggl(\frac{\pi}{2}\biggr)^2 \biggl[ \frac{\tanh \chi^3}{\chi^3} \biggr]</math> |
<math>~=</math> |
<math>~\biggl[ \biggl(\frac{2}{\pi}\biggr) \frac{t}{\tau_{ffc}} \biggl]^{-2}</math> |
|
<math>~\Rightarrow ~~~ 0</math> |
<math>~=</math> |
<math>~\biggl[ \frac{t}{\tau_{ffc}} \biggl]^{2} \tanh \chi^3 - \chi^3 \, .</math> |
The core masses that have been determined in this fashion at times, <math>~t/\tau_{ffc} > 1</math>, have been marked by the small, black squares along the vertical axis in the the left panel of our composite Figure 3 and in the top panel of the animation sequence that appears on the right-hand side of our composite Figure 4.
See Also
- Lecture notes by Pettini — see the official Institute of Astronomy (Cambridge) page on Pettini
- C. Hunter (1962, ApJ, 136, 594): The Instability of the Collapse of a Self-Gravitating Gas Cloud
- L. Mestel (1965, Quarterly Journal of the Royal Astronomical Society, 6, 161): Problems of Star Formation — I
- D. Lynden-Bell & J. P. S. Lemos (1988, MNRAS, 233, 197 - 208): On Penston's Self-Similar Solution for Cold Collapse
- E. Coughlin (2017, ApJ, 835, article id. 40): Spherically Symmetric Cold Collapse: The Exact Solutions and a Comparison with Self-Similar Solutions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |