User:Tohline/ThreeDimensionalConfigurations/EFE Energies
Properties of Homogeneous Ellipsoids (2)
In addition to pulling from §53 of Chandrasekhar's EFE, here, we lean heavily on the papers by M. D. Weinberg & S. Tremaine (1983, ApJ, 271, 586) (hereafter, WT83) and by D. M. Christodoulou, D. Kazanas, I. Shlosman, & J. E. Tohline (1995a, ApJ, 446, 472) (hereafter, Paper I).

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Sequence-Defining Dimensionless Parameters
A Riemann sequence of S-type ellipsoids is defined by the value of the dimensionless parameter,
|
<math>~f</math> |
<math>~\equiv</math> |
<math>~\frac{\zeta}{\Omega} = </math> constant, |
[ EFE, §48, Eq. (31) ]
[ WT83, Eq. (5) ]
[ Paper I, Eq. (2.1) ]
where, <math>~\zeta</math> is the system's vorticity as measured in a frame rotating with angular velocity, <math>~\Omega</math>. Alternatively, we can use the dimensionless parameter,
|
<math>~x</math> |
<math>~\equiv</math> |
<math>~\biggl[\frac{ab}{a^2 + b^2} \biggr]f \, ,</math> |
or,
|
<math>~\Lambda</math> |
<math>~\equiv</math> |
<math>~-\biggl[\frac{ab}{a^2 + b^2} \biggr] \Omega f = -\Omega x \, .</math> |
[ WT83, Eq. (4) ]
Conserved Quantities
Algebraic expressions for the conserved energy, <math>~E</math>, angular momentum, <math>~L</math>, and circulation, <math>~C</math>, are, respectively,
|
<math>~E</math> |
<math>~=</math> |
<math>~\frac{1}{2}v^2 + \frac{1}{2}(a^2 + b^2)(\Lambda^2 + \Omega^2) - 2ab\Lambda\Omega - 2I </math> |
|
|
<math>~\rightarrow</math> |
<math>~\cancelto{0}{\frac{1}{2}v^2} + \frac{1}{2} [(a+bx)^2 + (b+ax)^2]\Omega^2 - 2I \, ,</math> |
[ 1st expression — EFE, §53, Eq. (239) ]
[ 2nd expression — Paper I, Eq. (2.7) ]
where — see an accompanying discussion for the definitions of <math>~A_1</math>, <math>~A_2</math>, and <math>~A_3</math>,
|
<math>~I</math> |
<math>~=</math> |
<math>~A_1a^2 + A_2b^2 + A_3c^2 \, ;</math> |
[ 1st expression — EFE, §53, Eq. (239) ]
[ 2nd expression — Paper I, Eq. (2.8) ]
|
<math>~\frac{5L}{M}</math> |
<math>~=</math> |
<math>~(a^2 + b^2)\Omega - 2ab\Lambda</math> |
|
|
<math>~=</math> |
<math>~ (a^2 + b^2 + 2abx)\Omega \, ;</math> |
[ 1st expression — EFE, §53, Eq. (240) ]
[ 2nd expression — Paper I, Eq. (2.5) ]
|
<math>~\frac{5C}{M}</math> |
<math>~=</math> |
<math>~(a^2 + b^2)\Lambda - 2ab\Omega</math> |
|
|
<math>~=</math> |
<math>~- [2ab + (a^2 + b^2)x ]\Omega \, .</math> |
[ 1st expression — EFE, §53, Eq. (241) ]
[ 2nd expression — Paper I, Eq. (2.6) ]
If we rewrite the expression for the system's free energy in terms of <math>~L</math> (and x) instead of <math>~\Omega</math> (and x), we have,
|
<math>~E</math> |
<math>~=</math> |
<math>~\frac{1}{2} \biggl(\frac{5L}{M}\biggr)^2 \frac{(a+bx)^2 + (b+ax)^2}{(a^2 + b^2 + 2abx)^2} - 2I \, ,</math> |
[ Paper I, Eq. (3.4) ]
Note that, based on the units chosen in Paper I, <math>~M = 5</math>, and <math>~abc = 15/4</math>.
Aside: Chandra's Notation
According to equation (107) in §21 of EFE, it appears as though,
|
<math>~A_i - A_j</math> |
<math>~=</math> |
<math>~- (a_i^2 - a_j^2)A_{ij} \, .</math> |
And, according to equation (105) in §21 of EFE, it appears as though,
|
<math>~B_{ij}</math> |
<math>~=</math> |
<math>~A_j - a_i^2A_{ij} \, .</math> |
So, for example,
|
<math>~A_{12} </math> |
<math>~=</math> |
<math>~-\biggl[ \frac{A_1 - A_2}{a_1^2 - a_2^2} \biggr] \, ,</math> |
and,
|
<math>~B_{12} </math> |
<math>~=</math> |
<math>~A_2 + a_1^2\biggl[ \frac{A_1 - A_2}{a_1^2 - a_2^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{(a_1^2 - a_2^2)A_2 + a_1^2(A_1 - A_2)}{a_1^2 - a_2^2} </math> |
|
|
<math>~=</math> |
<math>~\frac{a_1^2A_1 - a_2^2A_2 }{a_1^2 - a_2^2} \, .</math> |
Free Energy Surface(s)
Scope
Consider a self-gravitating ellipsoid having the following properties:
- Semi-axis lengths, <math>~(x,y,z)_\mathrm{surface} = (a,b,c)</math>, and corresponding volume, <math>~4\pi/(3abc)</math> ; and consider only the situations <math>0 \le b/a \le 1</math> and <math>0 \le c/a \le 1</math> ;
- Total mass, <math>~M</math> ;
- Uniform density, <math>~\rho = (3 M)/(4\pi abc) </math> ;
- Figure is spinning about its c axis with angular velocity, <math>~\Omega</math> ;
- Internal, steady-state flow exhibiting the following characteristics:
- No vertical (z) motion;
- Elliptical (x-y plane) streamlines everywhere having an ellipticity that matches that of the overall figure, that is, <math>~e = (1-b^2/a^2)^{1/2}</math> ;
- The velocity components, <math>~v_x</math> and <math>~v_y</math>, are linear in the coordinate and, overall, characterized by the magnitude of the vorticity, <math>~\zeta</math> .
Such a configuration is uniquely specified by the choice of six key parameters: <math>~a</math>, <math>~b</math>, <math>~c</math>, <math>~M</math>, <math>~\Omega</math>, and <math>~\zeta</math> .
Free Energy of Incompressible, Constant Mass Systems
We are interested, here, in examining how the free energy of such a system will vary as it is allowed to "evolve" as an incompressible fluid — i.e., holding <math>~\rho</math> fixed — through different ellipsoidal shapes while conserving its total mass. Following Paper I, we choose to set <math>~M = 5</math> — which removes mass from the list of unspecified key parameters — and we choose to set <math>~\rho = \pi^{-1}</math>, which is then reflected in a specification of the semi-axis, <math>~a</math>, in terms of the pair of dimensionless axis ratios, <math>~b/a</math> and <math>~c/a</math>, namely,
|
<math>~a^3</math> |
<math>~=</math> |
<math>~\frac{3Ma^2}{4\pi(bc)\rho} = \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1}\, .</math> |
Moving forward, then, a unique ellipsoidal configuration is identified via the specification of four, rather than six, key parameters — <math>~b/a</math>, <math>~c/a</math>, <math>~\Omega</math>, and <math>~x</math> — and the free energy of that configuration is given by the expression,
|
<math>~E\biggl(\frac{b}{a}, \frac{c}{a}, \Omega, x\biggr)</math> |
<math>~=</math> |
<math>~\frac{a^2}{2} \biggl[\biggl(1+\frac{b}{a} \cdot x\biggr)^2 + \biggl(\frac{b}{a}+x\biggr)^2\biggr]\Omega^2 - 2I </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{2/3} \biggl\{\frac{1}{2} \biggl[\biggl(1+\frac{b}{a} \cdot x\biggr)^2 + \biggl(\frac{b}{a}+x\biggr)^2\biggr]\Omega^2 - \frac{2I}{a^2}\biggr\} \, ,</math> |
where,
|
<math>~x</math> |
<math>~\equiv</math> |
<math>~\biggl[\frac{(b/a)}{1 + (b/a)^2} \biggr]\frac{\zeta}{\Omega} \, ,</math> |
|
<math>~\frac{I}{a^2}</math> |
<math>~=</math> |
<math>~\biggl[A_1 + A_2\biggl(\frac{b}{a}\biggr)^2 + A_3\biggl(\frac{c}{a}\biggr)^2 \biggr] \, ,</math> |
and the functional behavior of the coefficients, <math>~A_1</math>, <math>~A_2</math>, and <math>~A_3</math>, are given by the expressions provided in an accompanying discussion.
Alternatively, replacing <math>~\Omega</math> in favor of <math>~L</math>, we have,
|
<math>~E\biggl(\frac{b}{a}, \frac{c}{a}, L, x\biggr)</math> |
<math>~=</math> |
<math>~\frac{L^2}{2a^2} \biggl[ \biggl(1+\frac{b}{a}\cdot x \biggr)^2 + \biggl(\frac{b}{a}+x \biggr)^2 \biggr] \biggl[ 1 + \biggl(\frac{b}{a}\biggr)^2 + 2\biggl(\frac{b}{a}\biggr)x \biggr]^{-2} - 2I </math> |
|
|
<math>~=</math> |
<math>~\frac{L^2}{2} \biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{-2/3} \biggl[ \biggl(1+\frac{b}{a}\cdot x \biggr)^2 + \biggl(\frac{b}{a}+x \biggr)^2 \biggr] \biggl[ 1 + \biggl(\frac{b}{a}\biggr)^2 + 2\biggl(\frac{b}{a}\biggr)x \biggr]^{-2} </math> |
|
|
|
<math>~- 2\biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{2/3} \biggl[A_1 + A_2\biggl(\frac{b}{a}\biggr)^2 + A_3\biggl(\frac{c}{a}\biggr)^2 \biggr]\, .</math> |
Adopted Evolutionary Constraints
Conserve Only L
Let's fix the total angular momentum, <math>~L</math>, of a triaxial configuration and examine how the configuration's free energy varies as we allow it to contort through different triaxial shapes — that is, as its pair of axis ratios varies, always maintaining <math>~\tfrac{b}{a} < 1</math> — and as we vary <math>~x</math>, which characterizes the fraction of angular momentum that is stored in internal spin versus overall figure rotation. The desired free-energy function, <math>~E(\tfrac{b}{a},\tfrac{c}{a}, x)|_L</math>, has just been defined, but visualizing its behavior is difficult because, in this situation, the free energy is a warped, three-dimensional surface draped across the four-dimensional domain, <math>~(\tfrac{b}{a},\tfrac{c}{a}, x, E_L)</math>.
Acknowledging that we are primarily interested in identifying extrema of this free-energy function, the discussion presented in §3.2 of Paper I shows us how to reduce the dimensionality of this problem by one. There, it is shown that, as long as <math>~\tfrac{b}{a} \ne 1</math>, extrema exist in the <math>~x</math>-coordinate direction — that is, <math>~\partial E_L/\partial x = 0</math> — only if <math>~x = 0.</math> For a given choice of <math>~L</math>, therefore, the relevant two-dimensional free-energy surface is defined by the expression,
|
<math>~E\biggl(\frac{b}{a}, \frac{c}{a}, x=0\biggr)\biggr|_L</math> |
<math>~=</math> |
<math>~\frac{L^2}{2} \biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{-2/3} \biggl[ 1 + \biggl(\frac{b}{a}\biggr)^2\biggr]^{-1} </math> |
|
|
|
<math>~ - 2\biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{2/3} \biggl[A_1 + A_2\biggl(\frac{b}{a}\biggr)^2 + A_3\biggl(\frac{c}{a}\biggr)^2 \biggr]\, .</math> |
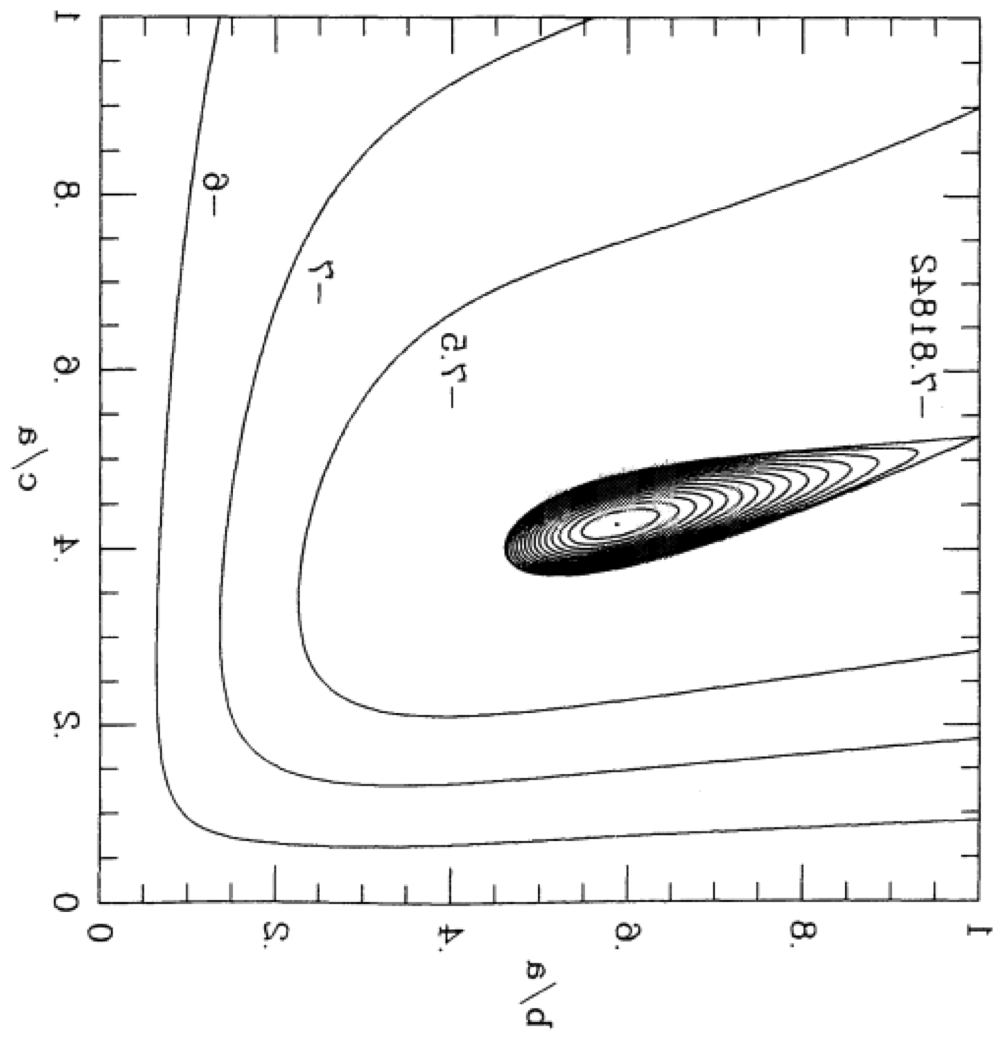
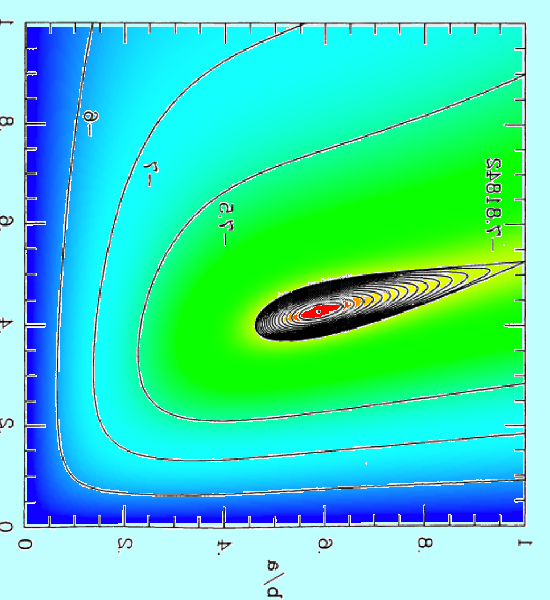
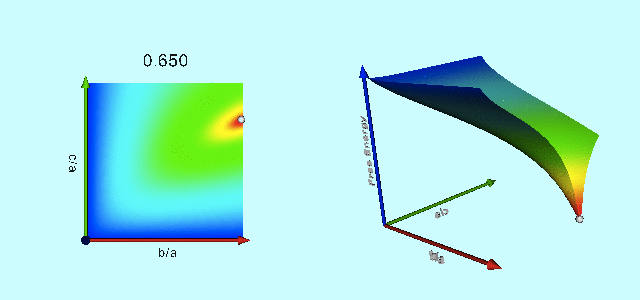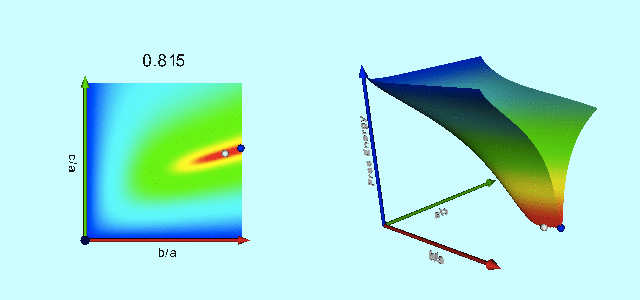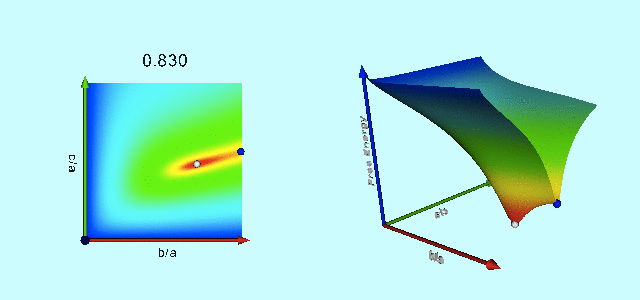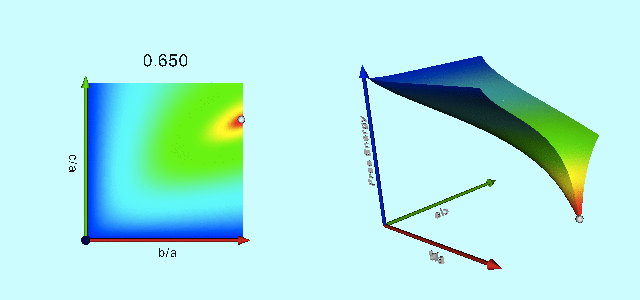
Figure 3 of Paper I presents a black-and-white contour plot of this <math>~E_L</math> function for the specific case of <math>~L = 4.71488</math>, which, for reference, is the total angular momentum of an equilibrium Maclaurin spheroid having an eccentricity, <math>~e = 0.85</math> (see Table 1, below). We have digitally extracted this black-and-white contour plot from p. 477 of the (PDF-formatted) Paper I publication and have reprinted it as the left-hand panel of our Figure 1. Note that we have flipped the plot horizontally and rotated it by 90° so that the orientation of the axis pair, <math>~(\tfrac{b}{a},\tfrac{c}{a})</math>, conforms with the orientation of a related, information-rich diagram presented by Chandrasekhar (1965) — see also our accompanying discussion of equilibrium sequence plots.
| Figure 1: Free-Energy Surface Projected onto the <math>~(\tfrac{b}{a},\tfrac{c}{a})</math> Plane | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| |||||||||
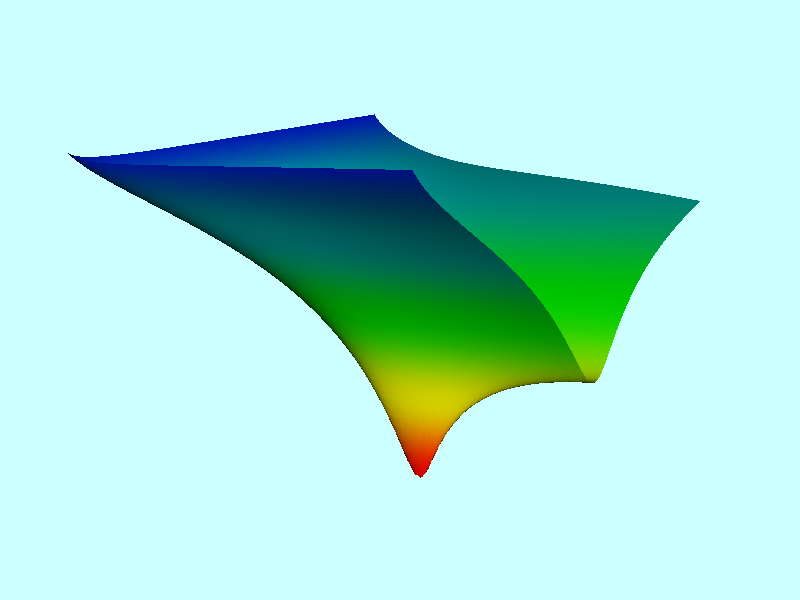
In our Figure 2, this same <math>~E_L</math> function has been displayed as a warped, two-dimensional free-energy surface draped across the three-dimensional <math>~(\tfrac{b}{a},\tfrac{c}{a},E)</math> domain, where depth as well as color has been used to tag energy values. The two-dimensional, colored contour plot presented in the right-hand panel of our Figure 1 results from the projection of this free-energy surface onto the <math>~(\tfrac{b}{a},\tfrac{c}{a})</math> plane; it reproduces in quantitative detail the black-and-white contour plot that we have extracted from Paper I. In an effort to (qualitatively) illustrate this agreement, we have digitally "pasted" the black-and-white contour plot from Paper I onto our colored contour plot and presented the combined image in the middle panel of our Figure 1.
Our Figure 2 image of the free-energy surface helps illuminate the description of this surface that appears in the caption of Fig. 3 from Paper I. Quoting from that figure caption: "The [equilibrium] Maclaurin spheroid sits on a saddle point <math>~[(\tfrac{b}{a},\tfrac{c}{a}) = (1.0,0.52678); E_0 = -7.81842]</math>, while a global minimum with <math>~E_0 = -7.83300</math> exists at <math>~(\tfrac{b}{a},\tfrac{c}{a}) = (0.588,0.428)</math>."
Animation
The animation sequence presented, below, as Figure 3 displays the warped free-energy surface (right) in conjunction with its projection onto the <math>~(\tfrac{b}{a},\tfrac{c}{a})</math> plane (left) for configurations having nineteen different total angular momentum values, <math>~L</math>, as detailed in column 5 of Table 1. The four-digit number that tags each frame of this animation sequence identifies the eccentricity (column 1 of Table 1) of the Maclaurin spheroid that is associated with each selected value of <math>~L</math>. In each frame of the animation, the equilibrium configuration associated with that Maclaurin spheroid is identified by the extremum of the free energy that appears along the right-hand edge <math>~(\tfrac{b}{a} = 1)</math> of the warped surface. For values of <math>~e < 0.81267</math> — corresponding to <math>~L < 4.23296</math> — the Maclaurin spheroid (marked by a small white circle/sphere) sits at the location of the absolute minimum of the free-energy surface and the configuration is stable. But for all larger values of the eccentricity/angular momentum, the Maclaurin spheroid (marked by a small dark-blue circle/sphere) is associated with a saddle point of the free-energy surface — that is, the configuration is in equilibrium, but it is (secularly) unstable — and the absolute energy minimum shifts off-axis to the location of a Jacobi ellipsoid (marked by a small white circle/sphere) having the same total angular momentum. As Paper I points out, evolution from the unstable axisymmetric equilibrium configuration to the stable triaxial configuration occurs along the narrow valley/canyon connecting the two extrema of the free energy.
| Table 1: Parameter Values Associated with Each Frame
of the Figure 3 Animation |
|||||||
| Maclaurin Spheroid | <math>~L^\dagger</math> | Jacobi Ellipsoids | |||||
| <math>~e</math> | <math>~\frac{c}{a}</math> | <math>~E_L</math> | <math>~E_\mathrm{plot}^\ddagger</math> | <math>~\frac{b}{a}</math> | <math>~\frac{c}{a}</math> | <math>~E_\mathrm{Jac}</math> | |
| 0.650 | 0.7599342 | -8.9018255 | 0.0 | 2.8270256 | --- | --- | --- |
| 0.675 | 0.7378177 | -8.8165100 | 0.0 | 2.9985043 | --- | --- | --- |
| 0.700 | 0.7141428 | -8.7216343 | 0.0 | 3.1820090 | --- | --- | --- |
| 0.725 | 0.6887489 | -8.6155943 | 0.0 | 3.3796768 | --- | --- | --- |
| 0.750 | 0.66143783 | -8.4963506 | 0.0 | 3.5942337 | --- | --- | --- |
| 0.775 | 0.6319612 | -8.3612566 | 0.0 | 3.8292360 | --- | --- | --- |
| 0.790 | 0.6131068 | -8.2711758 | 0.0 | 3.9819677 | --- | --- | --- |
| 0.795 | 0.6066094 | -8.2394436 | 0.0 | 4.0351072 | --- | --- | --- |
| 0.800 | 0.6000000 | -8.2067933 | 0.0 | 4.0894508 | --- | --- | --- |
| 0.805 | 0.5932748 | -8.1731817 | 0.0 | 4.1450581 | --- | --- | --- |
| 0.810 | 0.5864299 | -8.1385621 | 0.0 | 4.2019932 | --- | --- | --- |
| 0.815 | 0.5794610 | -8.1028846 | 0.0064 | 4.2603252 | 0.880967 | 0.545588 | -8.102934 |
| 0.820 | 0.5723635 | -8.0660955 | 0.0524 | 4.3201286 | 0.797543 | 0.516311 | -8.066596 |
| 0.825 | 0.5651327 | -8.0281369 | 0.1116 | 4.3814839 | 0.744298 | 0.496028 | -8.029578 |
| 0.830 | 0.5577634 | -7.9889461 | 0.1665 | 4.4444785 | 0.702967 | 0.479341 | -7.991848 |
| 0.835 | 0.5502499 | -7.9484555 | 0.2140 | 4.5092074 | 0.668439 | 0.464724 | -7.953367 |
| 0.840 | 0.5425864 | -7.9065917 | 0.2551 | 4.5757737 | 0.638420 | 0.451485 | -7.914095 |
| 0.845 | 0.5347663 | -7.8632747 | 0.2912 | 4.6442903 | 0.611646 | 0.439241 | -7.873990 |
| 0.850 | 0.5267827 | -7.8184175 | 0.3232 | 4.7148806 | 0.587337 | 0.427750 | -7.833003 |
| †Here, the units of angular momentum are as used in Paper I. In order to convert to units of <math>~L</math> as used in EFE (see, for example, Table I, in Chapter 5, §32), multiply by <math>~[2^2/(3\cdot 5^{10})]^{1/6} = 0.0717585</math>. | |||||||
| ‡<math>~E_\mathrm{plot}</math> is a normalized value of <math>~E_L</math> that has been used for plotting purposes. It's definition is: <math>E_\mathrm{plot} = 0.25*\biggl\{ \log_{10}\biggl[0.0001 + \frac{(E_L + |E_\mathrm{Jac}|)}{|E_\mathrm{Jac}|} \biggr] + 4\biggr\}</math> | |||||||
PROPERTIES OF VARIOUS MACLAURIN SPHEROIDS
eccenL covera omega2 ellChandra L
0.815 5.7946096D-01 3.7625539D-01 3.0571438D-01 4.2603252D+00
0.820 5.7236352D-01 3.8058727D-01 3.1000578D-01 4.3201286D+00
0.825 5.6513273D-01 3.8489420D-01 3.1440854D-01 4.3814839D+00
0.830 5.5776339D-01 3.8917054D-01 3.1892894D-01 4.4444785D+00
0.835 5.5024994D-01 3.9341001D-01 3.2357378D-01 4.5092074D+00
0.840 5.4258640D-01 3.9760569D-01 3.2835048D-01 4.5757737D+00
0.845 5.3476630D-01 4.0174986D-01 3.3326712D-01 4.6442903D+00
0.850 5.2678269D-01 4.0583395D-01 3.3833257D-01 4.7148806D+00
0.855 5.1862800D-01 4.0984835D-01 3.4355656D-01 4.7876802D+00
0.860 5.1029403D-01 4.1378236D-01 3.4894980D-01 4.8628384D+00
0.865 5.0177186D-01 4.1762394D-01 3.5452411D-01 4.9405200D+00
0.870 4.9305172D-01 4.2135955D-01 3.6029264D-01 5.0209081D+00
0.875 4.8412292D-01 4.2497391D-01 3.6626999D-01 5.1042063D+00
0.880 4.7497368D-01 4.2844972D-01 3.7247248D-01 5.1906420D+00
0.885 4.6559102D-01 4.3176729D-01 3.7891846D-01 5.2804708D+00
0.890 4.5596052D-01 4.3490417D-01 3.8562861D-01 5.3739810D+00
0.895 4.4606614D-01 4.3783459D-01 3.9262639D-01 5.4714996D+00
0.900 4.3588989D-01 4.4052888D-01 3.9993856D-01 5.5733994D+00
0.905 4.2541157D-01 4.4295266D-01 4.0759585D-01 5.6801086D+00
0.910 4.1460825D-01 4.4506586D-01 4.1563375D-01 5.7921218D+00
0.915 4.0345384D-01 4.4682147D-01 4.2409362D-01 5.9100155D+00
0.920 3.9191836D-01 4.4816395D-01 4.3302405D-01 6.0344667D+00
0.925 3.7996710D-01 4.4902713D-01 4.4248265D-01 6.1662784D+00
0.930 3.6755952D-01 4.4933139D-01 4.5253852D-01 6.3064134D+00
0.935 3.5464771D-01 4.4897998D-01 4.6327550D-01 6.4560401D+00
0.940 3.4117444D-01 4.4785386D-01 4.7479681D-01 6.6165969D+00
0.945 3.2707033D-01 4.4580450D-01 4.8723156D-01 6.7898831D+00
0.950 3.1224990D-01 4.4264348D-01 5.0074442D-01 6.9781934D+00
PROPERTIES OF JACOBI ELLIPSOIDS THAT HAVE THE SAME ANGULAR MOMENTA (L) AS THE ABOVE MACLAURIN SPHEROIDS
e b/a c/a A1 A2 A3 omega2 a L_C L energy
0.815 0.880967 0.545588 0.474189 0.557354 0.968456 0.371826 1.983364 0.305714 4.260325 -8.102934
0.820 0.797543 0.516311 0.441622 0.589410 0.968968 0.366634 2.088279 0.310006 4.320129 -8.066596
0.825 0.744298 0.496028 0.419233 0.611283 0.969484 0.361394 2.165672 0.314409 4.381484 -8.029578
0.830 0.702967 0.479341 0.400927 0.629069 0.970004 0.356104 2.232633 0.318929 4.444479 -7.991848
0.835 0.668439 0.464724 0.384983 0.644489 0.970527 0.350761 2.293990 0.323574 4.509207 -7.953367
0.840 0.638420 0.451485 0.370620 0.658325 0.971055 0.345362 2.351945 0.328350 4.575774 -7.914095
0.845 0.611646 0.439241 0.357403 0.671009 0.971588 0.339905 2.407740 0.333267 4.644290 -7.873990
0.850 0.587337 0.427750 0.345063 0.682812 0.972126 0.334386 2.462170 0.338333 4.714881 -7.833003
0.855 0.564969 0.416851 0.333417 0.693915 0.972668 0.328802 2.515795 0.343557 4.787680 -7.791082
0.860 0.544173 0.406427 0.322334 0.704450 0.973216 0.323150 2.569038 0.348950 4.862838 -7.748172
0.865 0.524676 0.396390 0.311717 0.714514 0.973770 0.317425 2.622239 0.354524 4.940520 -7.704210
0.870 0.506269 0.386673 0.301490 0.724181 0.974329 0.311624 2.675686 0.360293 5.020908 -7.659127
0.875 0.488788 0.377221 0.291594 0.733511 0.974895 0.305741 2.729638 0.366270 5.104206 -7.612848
0.880 0.472100 0.367988 0.281979 0.742554 0.975467 0.299772 2.784332 0.372472 5.190642 -7.565289
0.885 0.456097 0.358937 0.272604 0.751348 0.976047 0.293710 2.840003 0.378918 5.280471 -7.516357
0.890 0.440687 0.350033 0.263435 0.759930 0.976635 0.287549 2.896880 0.385629 5.373981 -7.465947
0.895 0.425792 0.341249 0.254440 0.768329 0.977230 0.281283 2.955205 0.392626 5.471500 -7.413941
0.900 0.411344 0.332556 0.245593 0.776572 0.977835 0.274902 3.015230 0.399939 5.573399 -7.360207
0.905 0.397284 0.323929 0.236868 0.784683 0.978449 0.268398 3.077231 0.407596 5.680109 -7.304592
0.910 0.383556 0.315345 0.228242 0.792685 0.979073 0.261762 3.141512 0.415634 5.792122 -7.246923
0.915 0.370112 0.306780 0.219694 0.800598 0.979708 0.254980 3.208416 0.424094 5.910016 -7.187000
0.920 0.356903 0.298209 0.211202 0.808442 0.980356 0.248041 3.278337 0.433024 6.034467 -7.124589
0.925 0.343885 0.289608 0.202744 0.816240 0.981017 0.240927 3.351732 0.442483 6.166278 -7.059417
0.930 0.331013 0.280950 0.194298 0.824010 0.981692 0.233621 3.429144 0.452539 6.306413 -6.991160
0.935 0.318242 0.272206 0.185842 0.831774 0.982384 0.226102 3.511226 0.463276 6.456040 -6.919428
0.940 0.305523 0.263344 0.177348 0.839558 0.983094 0.218342 3.598775 0.474797 6.616597 -6.843746
0.945 0.292805 0.254325 0.168790 0.847385 0.983825 0.210310 3.692789 0.487232 6.789883 -6.763530
0.950 0.280029 0.245105 0.160133 0.855288 0.984579 0.201966 3.794537 0.500744 6.978193 -6.678040
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |