User:Tohline/ThreeDimensionalConfigurations/JacobiEllipsoids
Jacobi Ellipsoids

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
General Coefficient Expressions
As has been detailed in an accompanying chapter, the gravitational potential anywhere inside or on the surface, <math>~(a_1,a_2,a_3) ~\leftrightarrow~(a,b,c)</math>, of an homogeneous ellipsoid may be given analytically in terms of the following three coefficient expressions:
|
<math> ~A_1 </math> |
<math> ~= </math> |
<math>~2\biggl(\frac{b}{a}\biggr)\biggl(\frac{c}{a}\biggr) \biggl[ \frac{F(\theta,k) - E(\theta,k)}{k^2 \sin^3\theta} \biggr] \, , </math> |
|
<math> ~A_3 </math> |
<math> ~= </math> |
<math> ~2\biggl(\frac{b}{a}\biggr) \biggl[ \frac{(b/a) \sin\theta - (c/a)E(\theta,k)}{(1-k^2) \sin^3\theta} \biggr] \, , </math> |
|
<math> ~A_2 </math> |
<math> ~= </math> |
<math>~2 - (A_1+A_3) \, ,</math> |
where, <math>~F(\theta,k)</math> and <math>~E(\theta,k)</math> are incomplete elliptic integrals of the first and second kind, respectively, with arguments,
|
<math>~\theta = \cos^{-1} \biggl(\frac{c}{a} \biggr)</math> |
and |
<math>~k = \biggl[\frac{1 - (b/a)^2}{1 - (c/a)^2} \biggr]^{1/2} \, .</math> |
| [ EFE, Chapter 3, §17, Eq. (32) ] | ||
Equilibrium Conditions for Jacobi Ellipsoids
Pulling from Chapter 6 — specifically, §39 — of Chandrasekhar's EFE, we understand that the semi-axis ratios, <math>~(\tfrac{b}{a},\tfrac{c}{a})</math> associated with Jacobi ellipsoids are given by the roots of the equation,
|
<math>~a^2 b^2 A_{12}</math> |
<math>~=</math> |
<math>~c^2 A_3 \, ,</math> |
| [ EFE, §39, Eq. (4) ] | ||
and the associated value of the square of the equilibrium configuration's angular velocity is,
|
<math>~\frac{\Omega^2}{\pi G \rho}</math> |
<math>~=</math> |
<math>~2B_{12} \, ,</math> |
| [ EFE, §39, Eq. (5) ] | ||
where,
|
<math>~A_{12}</math> |
<math>~\equiv</math> |
<math>~-\frac{A_1-A_2}{(a^2 - b^2)} \, ,</math> |
| [ EFE, §21, Eq. (107) ] | ||
|
<math>~B_{12}</math> |
<math>~\equiv</math> |
<math>~A_2 - a^2A_{12} \, .</math> |
| [ EFE, §21, Eq. (105) ] | ||
Taken together, we see that, written in terms of the two primary coefficients, <math>~A_1</math> and <math>~A_3</math>, the pair of defining relations for Jacobi ellipsoids is:
| |||||||||
Roots of the Governing Relation
Constraint on Axis-Ratio Relationship
To simplify notation, here we will set,
|
<math>~\chi \equiv \frac{b}{a}</math> |
and |
<math>~\upsilon \equiv \frac{c}{a} \, ,</math> |
in which case the governing relation is,
|
<math>~f_J</math> |
<math>~=</math> |
<math>~\frac{\chi^2}{1-\chi^2} \biggl[ 2(1-A_1)-A_3\biggr]-\upsilon^2 A_3 =0 \, .</math> |
Our plan is to employ the Newton Raphson method to find the root(s) of the <math>~f_J = 0</math> relation, typically holding <math>~\upsilon</math> fixed and using the Newton-Raphson technique to identify the corresponding "root" value of <math>~\chi</math>. Using this approach, the Newton Raphson technique requires specification of, not only the function, <math>~f_J</math>, but also its first derivative,
|
<math>~f_J^'</math> |
<math>~=</math> |
<math>~\frac{df_J}{d\chi} \, .</math> |
Let's determine the requisite expression, using a prime superscript to indicate differentiation with respect to <math>~\chi</math>.
|
<math>~f_J^'</math> |
<math>~=</math> |
<math>~ \biggl[ 2(1-A_1)-A_3\biggr]\biggl[ \frac{2\chi}{(1-\chi^2)^2} \biggr] -\frac{\chi^2}{1-\chi^2} \biggl[ 2A_1^'+A_3^'\biggr] -\upsilon^2 A_3^' \, , </math> |
where, given that <math>~\theta</math> does not depend on <math>~\chi</math>,
|
<math> ~A_1^' </math> |
<math> ~= </math> |
<math>~\frac{2\upsilon}{\sin^3\theta} \cdot \frac{d}{d\chi}\biggl\{ \frac{\chi}{k^2} \biggl[ F(\theta,k) - E(\theta,k) \biggr] \biggr\} </math> |
|
|
<math> ~= </math> |
<math>~\frac{2\upsilon}{k^3 \sin^3\theta} \cdot \biggl\{ [ F - E ] [k - 2\chi k^' ] +\chi k [ F^' - E^' ]\biggr\} \, , </math> |
|
<math> ~A_3^' </math> |
<math> ~= </math> |
<math> ~\frac{2}{\sin^3\theta} \cdot \frac{d}{d\chi}\biggl\{ \frac{\chi}{(1-k^2)} \biggl[ \chi \sin\theta - \upsilon E(\theta,k)\biggr] \biggr\} </math> |
|
|
<math> ~= </math> |
<math> ~\frac{2}{(1-k^2)^2\sin^3\theta} \biggl\{ \biggl[ \chi \sin\theta - \upsilon E\biggr]\biggl[ (1-k^2) +2\chi kk^' \biggr] + \chi(1-k^2) \biggl[ \sin\theta - \upsilon E^'\biggr] \biggr\}\, , </math> |
|
<math>~k^'</math> |
<math>~=</math> |
<math>~ \frac{d}{d\chi}\biggl[\frac{1 - \chi^2}{1 - \upsilon^2} \biggr]^{1/2} = \frac{-\chi}{(1 - \chi^2)^{1/2}(1 - \upsilon^2)^{1/2}} \, , </math> |
|
<math>~F^'</math> |
<math>~=</math> |
<math>~ \frac{\partial F(\theta,k)}{\partial k} \cdot k^' \, , </math> |
|
<math>~E^'</math> |
<math>~=</math> |
<math>~ \frac{\partial E(\theta,k)}{\partial k} \cdot k^' \, . </math> |
Now, according to online WolframResearch documentation — see, in particular, the subsection titled, "Representations of Derivatives" —
|
<math>~\frac{\partial F(z|m)}{\partial m}</math> |
<math>~=</math> |
<math>~ \frac{E(z|m)}{2(1-m)m} - \frac{F(z|m)}{2m} - \frac{\sin(2z)}{4(1-m)\sqrt{1-m\sin^2(z)}} \, , </math> |
and,
|
<math>~\frac{\partial E(z|m)}{\partial m}</math> |
<math>~=</math> |
<math>~\frac{E(z|m) - F(z|m)}{2m} \, ,</math> |
where, <math>~z~\leftrightarrow~\theta</math>, and,
<math>~m \equiv k^2 ~~~~\Rightarrow~~~~\frac{dm}{dk} = 2k \ .</math>
Hence, we have,
|
<math>~F^'</math> |
<math>~=</math> |
<math>~ \biggl[\frac{\partial F(z|m)}{\partial m} \cdot \frac{dm}{dk}\biggr] k^' </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{E(\theta,k)}{2(1-k^2)k^2} - \frac{F(\theta,k)}{2k^2} - \frac{\sin(2\theta)}{4(1-k^2)\sqrt{1-k^2\sin^2\theta}} \biggr] 2kk^' \, , </math> |
|
<math>~E^'</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{\partial E(z|m)}{\partial m} \cdot \frac{dm}{dk}\biggr] k^' </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ E(\theta,k) - F(\theta,k) \biggr] \frac{k^'}{k} \, . </math> |
This, then, gives us all of the expressions necessary to specify the derivative, <math>~f_J^'</math> analytically.
|
Table 1: Double-Precision Evaluations
Related to Table IV in EFE, Chapter 6, §39 (p. 103) |
|---|
b/a c/a omega2 angmom 5L/M fJ fJderiv
1.00 0.582724 3.742297785D-01 3.037510987D-01 4.232965627D+00 0.000000000D+00 0.000000000D+00
0.96 0.570801 3.739782202D-01 3.039551227D-01 4.235808832D+00 1.377942479D-06 1.636908401D-01
0.92 0.558330 3.731876801D-01 3.046006837D-01 4.244805137D+00 -6.821687132D-07 1.676406830D-01
0.88 0.545263 3.717835971D-01 3.057488283D-01 4.260805266D+00 8.533280272D-07 1.715558312D-01
0.84 0.531574 3.696959199D-01 3.074667323D-01 4.284745355D+00 -4.622993727D-08 1.754024874D-01
0.80 0.517216 3.668370069D-01 3.098368632D-01 4.317774645D+00 2.805300664D-08 1.791408327D-01
0.76 0.502147 3.631138118D-01 3.129555079D-01 4.361234951D+00 3.221800126D-07 1.827219476D-01
0.72 0.486322 3.584232032D-01 3.169377270D-01 4.416729718D+00 3.274773094D-08 1.860866255D-01
0.68 0.469689 3.526490289D-01 3.219229588D-01 4.486202108D+00 1.202999164D-08 1.891636215D-01
0.64 0.452194 3.456641138D-01 3.280805511D-01 4.572012092D+00 2.681560312D-07 1.918668912D-01
0.60 0.433781 3.373298891D-01 3.356184007D-01 4.677056841D+00 1.037186290D-08 1.940927000D-01
0.56 0.414386 3.274928085D-01 3.447962894D-01 4.804956583D+00 1.071021385D-07 1.957166395D-01
0.52 0.393944 3.159887358D-01 3.559412795D-01 4.960269141D+00 8.098003093D-08 1.965890756D-01
0.48 0.372384 3.026414267D-01 3.694732246D-01 5.148845443D+00 1.255768368D-07 1.965308751D-01
0.44 0.349632 2.872670174D-01 3.859399647D-01 5.378319986D+00 1.329168636D-08 1.953277019D-01
0.40 0.325609 2.696779847D-01 4.060726774D-01 5.658882201D+00 -9.783004411D-08 1.927241063D-01
0.36 0.300232 2.496925963D-01 4.308722159D-01 6.004479614D+00 1.044268276D-07 1.884168286D-01
0.32 0.273419 2.271530240D-01 4.617497270D-01 6.434777459D+00 -4.469279448D-08 1.820477545D-01
0.28 0.245083 2.019461513D-01 5.007767426D-01 6.978643856D+00 7.996820889D-08 1.731984783D-01
0.24 0.215143 1.740514751D-01 5.511400218D-01 7.680488329D+00 1.099319693D-07 1.613864645D-01
0.20 0.183524 1.436093757D-01 6.180687545D-01 8.613182979D+00 5.068010978D-08 1.460685065D-01
0.16 0.150166 1.110438660D-01 7.109267615D-01 9.907218635D+00 -2.170751250D-08 1.266576761D-01
0.12 0.115038 7.728058393D-02 8.487699974D-01 1.182815219D+01 3.613784147D-09 1.025686850D-01
0.08 0.078166 4.416740942D-02 1.079303624D+00 1.504078558D+01 3.319018649D-08 7.332782508D-02
0.04 0.039688 1.541513490D-02 1.582762691D+00 2.205680933D+01 -6.674246644D-09 3.882477311D-02
|
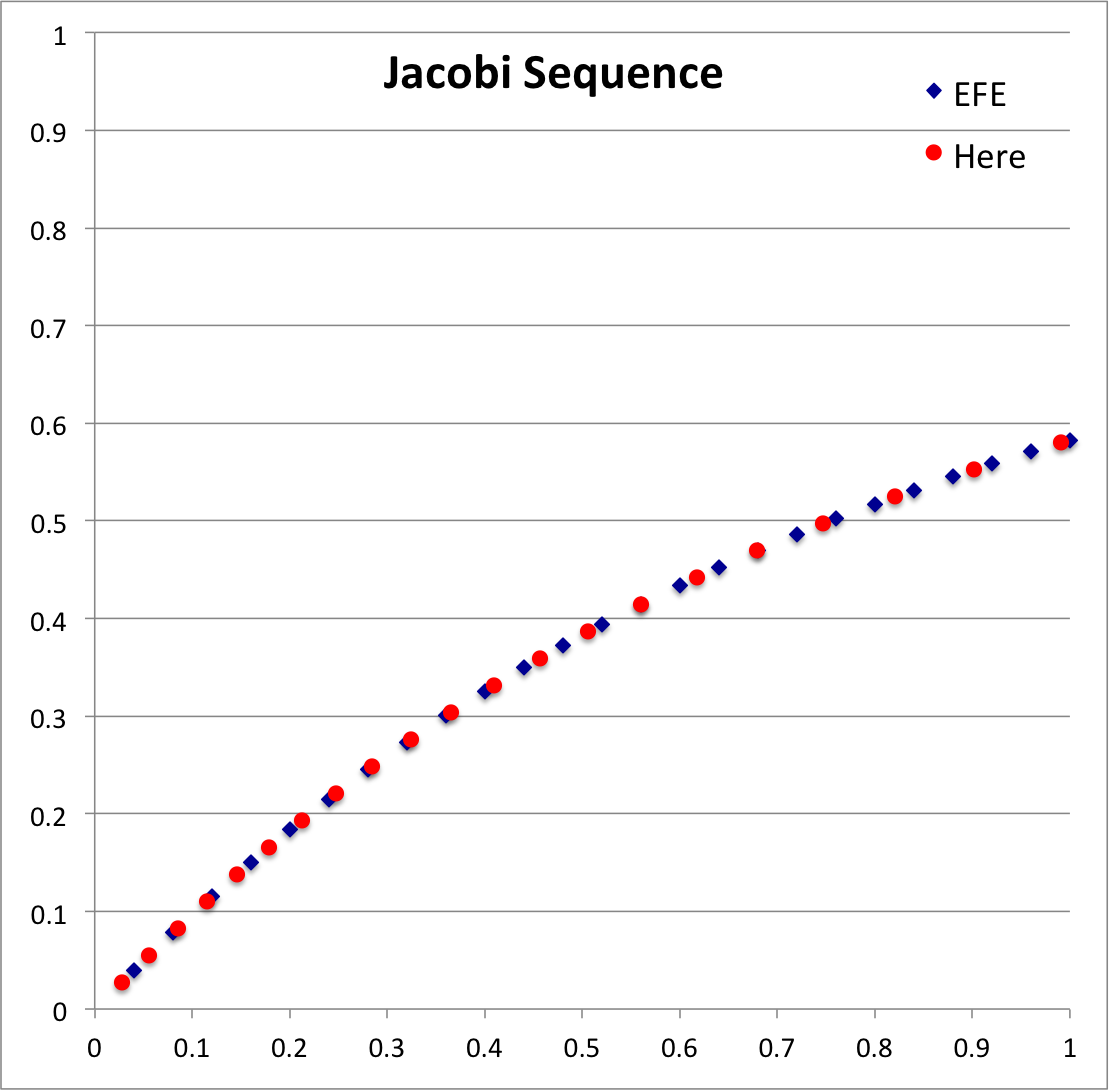
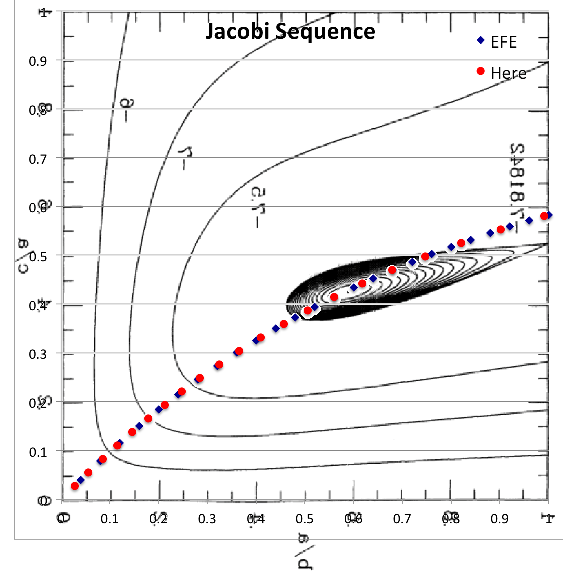
With regard to our Table 1 (immediately above): Given each pair of axis ratios, <math>~(\tfrac{b}{a},\tfrac{c}{a})</math> — copied from Table IV of EFE (see columns 1 and 2 of our Table 1) — and the corresponding coefficient values, <math>~A_1</math>, <math>~A_2</math>, and <math>~A_3</math>, as tabulated in Table 2 of our accompanying discussion, we calculated corresponding values of <math>~\Omega^2</math> (column 3) and total angular momentum (column 4) in the units used in EFE's Table IV, as well as (column 5) the total angular momentum in units used by Christodoulou, et al. (1995, ApJ, 446, 472) — see our related discussion of these physical quantities. We also have tabulated associated values of the function, <math>~f_J</math>, (column 6) and its first derivative, <math>~f_J^'</math>, (column 7) as defined immediately above. Notice that <math>~f_J</math> is very nearly zero in all cases, which indicates that each axis-ratio pair indeed identifies a configuration that lies along the Jacobi sequence.
|
Table 2: Jacobi Sequence |
|---|
b/a c/a A1 A2 A3 omega2 a 5L/M 0.990699 0.580000 0.512818 0.518962 0.968220 0.374217 1.868761 4.233113 0.901558 0.552381 0.481786 0.549836 0.968378 0.372621 1.960046 4.251259 0.820783 0.524762 0.450993 0.580215 0.968792 0.368424 2.057217 4.299402 0.747135 0.497143 0.420459 0.610088 0.969452 0.361716 2.161309 4.377683 0.679613 0.469524 0.390210 0.639442 0.970348 0.352587 2.273548 4.486951 0.617393 0.441905 0.360273 0.668258 0.971469 0.341129 2.395412 4.628802 0.559798 0.414286 0.330684 0.696516 0.972800 0.327439 2.528716 4.805667 0.506257 0.386667 0.301483 0.724187 0.974329 0.311620 2.675723 5.020964 0.456291 0.359048 0.272719 0.751241 0.976040 0.293786 2.839307 5.279337 0.409492 0.331429 0.244450 0.777636 0.977914 0.274062 3.023190 5.587020 0.365507 0.303810 0.216744 0.803324 0.979931 0.252593 3.232298 5.952388 0.324034 0.276190 0.189686 0.828246 0.982067 0.229546 3.473314 6.386811 0.284807 0.248571 0.163376 0.852329 0.984295 0.205118 3.755577 6.906010 0.247591 0.220952 0.137939 0.875480 0.986581 0.179549 4.092599 7.532311 0.212179 0.193333 0.113527 0.897587 0.988885 0.153130 4.504785 8.298565 0.178382 0.165714 0.090333 0.918505 0.991162 0.126229 5.024664 9.255452 0.146026 0.138095 0.068601 0.938044 0.993355 0.099316 5.707871 10.486253 0.114948 0.110476 0.048654 0.955953 0.995393 0.073010 6.659169 12.140357 0.084989 0.082857 0.030927 0.971879 0.997194 0.048162 8.105501 14.522397 0.055982 0.055238 0.016051 0.985298 0.998651 0.026008 10.663879 18.396951 0.027738 0.027619 0.005032 0.995331 0.999637 0.008539 16.979084 26.660547 |
With regard to our Table 2 (immediately above): Here we specified twenty-one values of the axis ratio, <math>~\tfrac{c}{a}</math>, (column 2) and used our Newton-Raphson-based root finder to identify corresponding values of the companion axis ratio, <math>~\tfrac{b}{a}</math>, (column 1) that satisfies the governing relation, <math>~f_J = 0</math>.
Angular Momentum Constraint
Alternatively, let's choose a value for the system's total angular momentum, <math>~L > 4.23296</math>, and solve for the axis-ratio pair that identifies that configuration's location along the Jacobi sequence. We'll adopt the units used by Christodoulou et al (1995), that is, <math>~G = 1</math>, <math>~\pi \rho = 1</math> and <math>~M = 5</math>, hence,
|
<math>~a^3</math> |
<math>~=</math> |
<math>~\frac{3Ma^2}{4\pi(bc)\rho} = \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1}\, .</math> |
Given that the relationship between <math>~L</math> and <math>~\Omega</math> in equilibrium Jacobi ellipsoids is,
|
<math>~L</math> |
<math>~=</math> |
<math>~a^2\biggl[1 + \biggl(\frac{b}{a}\biggr)^2\biggr]\Omega </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{2/3} \biggl[1 + \biggl(\frac{b}{a}\biggr)^2\biggr]\Omega </math> |
the constraint on <math>~\Omega^2</math> given above implies that,
|
<math>~L^2 \biggl[ \frac{4}{15}\biggl(\frac{b}{a}\biggr) \biggl(\frac{c}{a}\biggr) \biggr]^{4/3} \biggl[1 + \biggl(\frac{b}{a}\biggr)^2\biggr]^{-2}</math> |
<math>~=</math> |
<math>~2\biggl\{2 - (A_1+A_3) - \biggl[ \frac{2(1-A_1)-A_3}{1 - (b/a)^2} \biggr] \biggr\} \, .</math> |
Or, again adopting the shorthand notation,
|
<math>~\chi \equiv \frac{b}{a}</math> |
and |
<math>~\upsilon \equiv \frac{c}{a} \, ,</math> |
we seek roots of the function,
|
<math>~f_L</math> |
<math>~\equiv</math> |
<math>~L^2 - \biggl[ \frac{3^4\cdot 5^4}{2^5} \biggr]^{1/3}\chi^{-4/3} \upsilon^{-4/3}(1 + \chi^2)^{2} \biggl\{[2 - (A_1+A_3)] - \biggl[ 2(1-A_1)-A_3\biggr](1-\chi^2)^{-1} \biggr\} = 0 \, .</math> |
As above, we will hold <math>~\upsilon</math> fixed and use the Newton-Raphson technique to identify the corresponding "root" value of <math>~\chi</math>. Hence, we need to specify, not only the function, <math>~f_L</math>, but also its first derivative,
|
<math>~f_L^'</math> |
<math>~\equiv</math> |
<math>~\frac{\partial f_L}{\partial \chi} \, .</math> |
|
|
<math>~=</math> |
<math>~- \biggl[ \frac{3^4\cdot 5^4}{2^5} \biggr]^{1/3}\upsilon^{-4/3} \frac{\partial}{\partial \chi} \biggl\{ \chi^{-4/3} (1 + \chi^2)^{2} [2 - (A_1+A_3)] - \chi^{-4/3} (1 + \chi^2)^{2}(1-\chi^2)^{-1}[ 2(1-A_1)-A_3] \biggr\}</math> |
|
|
<math>~=</math> |
<math>~- \biggl[ \frac{3^4\cdot 5^4}{2^5} \biggr]^{1/3}\upsilon^{-4/3} \biggl\{ -\frac{4}{3}\chi^{-7/3} (1 + \chi^2)^{2}[2 - (A_1+A_3)] +4\chi^{-1/3} (1 + \chi^2)[2 - (A_1+A_3)] -\chi^{-4/3} (1 + \chi^2)^{2}(A_1^'+A_3^') </math> |
|
|
|
<math>~ + \frac{4}{3} \chi^{-7/3} (1 + \chi^2)^{2}(1-\chi^2)^{-1}[ 2(1-A_1)-A_3] - 4\chi^{-1/3} (1 + \chi^2)(1-\chi^2)^{-1}[ 2(1-A_1)-A_3] </math> |
|
|
|
<math>~ - 2 \chi^{-1/3} (1 + \chi^2)^{2}(1-\chi^2)^{-2}[ 2(1-A_1)-A_3] - \chi^{-4/3} (1 + \chi^2)^{2}(1-\chi^2)^{-1}[ -2A_1^'-A_3^'] \biggr\}</math> |
|
|
<math>~=</math> |
<math>~- \biggl[ \frac{3\cdot 5^4}{2^5} \biggr]^{1/3}\upsilon^{-4/3} \chi^{-7/3} (1 + \chi^2)\biggl\{ [12\chi^2-4(1 + \chi^2)][2 - (A_1+A_3)] -3\chi (1 + \chi^2)(A_1^'+A_3^') + 3\chi (1 + \chi^2)(1-\chi^2)^{-1}[ 2A_1^' + A_3^'] </math> |
|
|
|
<math>~ + (1-\chi^2)^{-2}\{ 4 (1 + \chi^2)(1-\chi^2)[ 2(1-A_1)-A_3] - 12\chi^{2} (1-\chi^2)[ 2(1-A_1)-A_3] - 6 \chi^{2} (1 + \chi^2)[ 2(1-A_1)-A_3] \} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~- \biggl[ \frac{3\cdot 5^4}{2^5} \biggr]^{1/3}\upsilon^{-4/3} \chi^{-7/3} (1 + \chi^2)\biggl\{ [8\chi^2-4]A_1 + 3\chi (1 + \chi^2)(1-\chi^2)^{-1} [ (1+\chi^2)A_1^' + \chi^2A_3^' ] </math> |
|
|
|
<math>~ + 2(1-\chi^2)^{-2} [ 2-2A_1-A_3] [ (4\chi^2-2)(1-\chi^2)^{2} + 2 (1 + \chi^2)(1-\chi^2) - 6\chi^{2} (1-\chi^2) - 3 \chi^{2} (1 + \chi^2) ] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~- \biggl[ \frac{3\cdot 5^4}{2^5} \biggr]^{1/3}\upsilon^{-4/3} \chi^{-7/3} (1 + \chi^2)\biggl\{ 3\chi (1 + \chi^2)(1-\chi^2)^{-1} [ (1+\chi^2)A_1^' + \chi^2A_3^' ] </math> |
|
|
|
<math>~+[8\chi^2-4]A_1 + 2(1-\chi^2)^{-2} [ 2-2A_1-A_3] [ - \chi^2 - 9\chi^4 + 4\chi^6 ] \biggr\} </math> |
What values of <math>~L</math> should we choose? In association with our discussion of warped free-energy surfaces, we'd like to specify the eccentricity, <math>~e</math>, of a Maclaurin spheroid and adopt the angular momentum of that configuration. According to our accompanying discussion of the properties of Maclaurin spheroids,
|
<math>~L_\mathrm{Mac}^2</math> |
<math>~=</math> |
<math>~2^2a^4\Omega^2</math> |
|
|
<math>~=</math> |
<math>~2^3a^4 [ A_1 -A_3(1-e^2)]_\mathrm{Mac} </math> |
|
|
<math>~=</math> |
<math>~2^3 \biggl[\frac{3\cdot 5}{2^2}(1-e^2)^{-1/2} \biggr]^{4/3} [ A_1 -A_3(1-e^2)]_\mathrm{Mac} </math> |
|
|
<math>~=</math> |
<math>~ [2\cdot 3^4\cdot 5^4]^{1/3} (1-e^2)^{-2/3} \biggl\{ \frac{1}{e^2} \biggl[\frac{\sin^{-1}e}{e} - (1-e^2)^{1/2} \biggr](1-e^2)^{1/2} -\frac{2}{e^2} \biggl[(1-e^2)^{-1/2} -\frac{\sin^{-1}e}{e} \biggr](1-e^2)^{3/2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ [2\cdot 3^4\cdot 5^4]^{1/3} (1-e^2)^{-2/3} \biggl\{ \frac{1}{e^2} \biggl[\frac{\sin^{-1}e}{e} \biggr](1-e^2)^{1/2} +\frac{2}{e^2} \biggl[\frac{\sin^{-1}e}{e} \biggr](1-e^2)^{3/2} -\frac{1}{e^2} \biggl[ (1-e^2)^{1/2} \biggr](1-e^2)^{1/2} -\frac{2}{e^2} \biggl[(1-e^2)^{-1/2} \biggr](1-e^2)^{3/2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ [2\cdot 3^4\cdot 5^4]^{1/3} (1-e^2)^{-2/3} \biggl\{ \frac{1}{e^2} \biggl[\frac{\sin^{-1}e}{e} \biggr](1-e^2)^{1/2} \biggl[3-2e^2\biggr] -\frac{3(1-e^2)}{e^2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ [2\cdot 3^4\cdot 5^4]^{1/3} \frac{(1-e^2)^{1/3} }{e^2} \biggl\{ \biggl[\frac{\sin^{-1}e}{e} \biggr](1-e^2)^{-1/2} \biggl[3-2e^2\biggr] - 3 \biggr\} \, . </math> |
Note, for example, that if <math>~e = 0.85</math>, the square-root of this expression gives, <math>~L_\mathrm{Mac} = 4.7148806</math>, which matches the angular momentum that was used by Christodoulou et al (1995) to generate their Figure 3.
Sequence Plots
| Jacobi Sequence: (blue) Points defined by data in Table IV of EFE, Chapter 6, §39 (p. 103); (red) points generated here from above-defined roots of the governing relation. |
Figure 2 extracted† from p. 902 of S. Chandrasekhar (1965)
"The Equilibrium and the Stability of the Riemann Ellipsoids. I"
ApJ, vol. 142, pp. 890-921 © American Astronomical Society |
| †Original figure has been annotated (maroon-colored text and arrow added) for clarification. | |
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |