Reconciling Eulerian versus Lagrangian Perspectives

Adopting the Perturbation Notation^† of P. Ledoux & Th. Walraven (1958)

Eulerian

Lagrangian

<math>~\hat{e}_r r</math>	<math>~\rightarrow</math>	<math>~\hat{e}_r [r_0 + \delta r(r) e^{i\sigma t}] </math>
<math>~\hat{e}_r v</math>	<math>~\rightarrow</math>	<math>~\hat{e}_r [0 + v_r^'(r) e^{i\sigma t}] = \hat{e}_r[i\sigma \delta r(r) e^{i\sigma t} ]</math>
<math>~\rho</math>	<math>~\rightarrow</math>	<math>~\rho_0 + \rho^'(r) e^{i\sigma t} </math>
<math>~P</math>	<math>~\rightarrow</math>	<math>~P_0 + P^'(r) e^{i\sigma t} </math>
<math>~\Phi</math>	<math>~\rightarrow</math>	<math>~\Phi_0 + \Phi^'(r) e^{i\sigma t} </math>

<math>~\hat{e}_r r</math>	<math>~\rightarrow</math>	<math>~\hat{e}_r [r_0 + \delta r(m) e^{i\sigma t}] </math>
<math>~\hat{e}_r v</math>	<math>~\rightarrow</math>	<math>~\hat{e}_r [0 + \delta v_r(m) e^{i\sigma t}] = \hat{e}_r[ i\sigma \delta r(m) e^{i\sigma t}]</math>
<math>~\rho</math>	<math>~\rightarrow</math>	<math>~\rho_0 + \delta \rho(m) e^{i\sigma t} </math>
<math>~P</math>	<math>~\rightarrow</math>	<math>~P_0 + \delta P(m) e^{i\sigma t} </math>
<math>~\Phi</math>	<math>~\rightarrow</math>	<math>~\Phi_0 + \delta \Phi(m) e^{i\sigma t} </math>

^†See especially the following clarifying comments from, respectively, §43 (p. 432) and §55 (p. 452) of Ledoux & Walraven (1958):

The time derivatives of Eulerian coordinates have no meaning; hence, the (components of) <math>~\vec{r}</math> must be treated as Lagrangian coordinates in the definition,

Consistent with this understanding, we shall always denote a perturbation of <math>~\mathbf{r}</math> by <math>~\delta\mathbf{r}</math> but for all dependent variables <math>~\psi</math> we shall distinguish between the local or Eulerian perturbations <math>~\psi^'</math> and the Lagrangian perturbations <math>~\delta\psi</math> taken in following the motion.

Introduction

Eulerian Approach

In a related discussion, we have shown that, from a standard Eulerian perspective, the perturbation and linearization of the principal governing equations leads to an equation of continuity (EOC), equation of motion (EOM), and Poisson equation of the form,

<math>~- \nabla\cdot \vec{v}</math>	<math>~=</math>	<math>~ \frac{\partial}{\partial t}\biggl( \frac{\rho_1}{\rho_0} \biggr) + \vec{v} \cdot \frac{\nabla\rho_0}{\rho_0} \, ; </math>
<math>~\frac{\partial \vec{v}}{\partial t}</math>	<math>~=</math>	<math>~ - \nabla\Phi_1 - \nabla\biggl[ \frac{\rho_1}{\rho_0}\biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] \, ; </math>
<math>~\nabla^2\Phi_1</math>	<math>~=</math>	<math>~ 4\pi G \rho_1 \, . </math>

The standard Eulerian approach to combining these expressions is to take the time-derivative of the EOC, take the divergence of the EOM (and combine with the Poisson equation), then add the two to obtain,

<math>~ \frac{\partial^2}{\partial t^2}\biggl( \frac{\rho_1}{\rho_0} \biggr) + \frac{\nabla\rho_0}{\rho_0} \cdot \frac{\partial \vec{v}}{\partial t} - 4\pi G \rho_1 - \nabla^2 \biggl[ \frac{\rho_1}{\rho_0}\biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] </math>

After defining the fractional Eulerian density variation as,

<math>~s \equiv \frac{\rho_1}{\rho_0} \, ,</math>

this becomes what we have referred to elsewhere as the Eulerian Wave Equation.

Lagrangian Approach

In another related discussion, we have shown that, from a standard Lagrangian perspective, the perturbation and linearization of the principal governing equations leads to an equation of continuity (EOC), and equation of motion (EOM) already combined with the Poisson equation of the form,

<math>~d</math>	<math>~=</math>	<math>~- 3x - r_0 \biggl(\frac{dx}{dr_0}\biggr) \, ;</math>
<math>~\frac{\gamma P_0}{\rho_0} \biggl[ \frac{d}{dr_0}\biggl(d \biggr) \biggr]</math>	<math>~=</math>	<math>~\omega^2 r_0 x + g_0\biggl[ 4x + \gamma d \biggr] \, .</math>

The standard Lagranian approach to combining these expressions is to take the radial-derivative of the EOC, then substitute the EOC's expression for <math>~d</math> as well as its radial derivative into the EOM to obtain,

<math>~- \frac{\gamma P_0}{\rho_0} \biggl[ 4\biggl(\frac{dx}{dr_0}\biggr) + r_0 \frac{d^2x}{dr_0^2} \biggr]</math>

<math>~\omega^2 r_0 x + g_0\biggl\{ 4x - \gamma \biggl[ 3x + r_0 \biggl(\frac{dx}{dr_0}\biggr) \biggr] \biggr\} \, ,</math>

which, after rearrangement of terms, gives what we have referred to elsewhere as the Adiabatic Wave (or Radial Pulsation) Equation.

Rosseland's Approach

Rosseland's approach is to take the total time-derivative of the EOM — even before linearizing any of the governing equations — then combine it strategically with the EOC and (integrated) Poisson equation to obtain,

<math>~\frac{d^2v_r}{dt^2}</math>	<math>~=</math>	<math>~ - \frac{1}{\rho} \frac{\partial }{\partial r} \biggl[ \frac{dP}{dt} \biggr] + \biggl\{ - \frac{d}{dt}\biggl( \frac{\partial\Phi}{\partial r}\biggr) + \biggl( \frac{\partial \Phi}{\partial r}\biggr) \frac{2v_r}{r} \biggr\} + \frac{2v_r}{r} \biggl[ \frac{dv_r}{dt} \biggr] </math>
	<math>~=</math>	<math>~ \frac{1}{\rho} \frac{\partial }{\partial r} \biggl[ \gamma_g P \nabla\cdot \vec{v}\biggr] + \frac{4gv_r}{r} + \cancelto{\mathrm{small}}{\frac{2v_r}{r} \biggl[ \frac{dv_r}{dt} \biggr]} \, . </math>

By recognizing that <math>~\vec{v} = 0</math> in the initial equilibrium state and, therefore, that after perturbing the system, <math>~v_r</math> is a "small quantity," this equation is already linearized because every term contains one factor of <math>~v_r</math>. Actually, as indicated, the last term on the right-hand-side can be dropped because it is of order <math>~(v_r)^2</math>.

Approach by Ledoux and Walraven

Note: It also might prove valuable to look at the arguments presented in §2.6 of Ledoux's Chapter 10, pp. 499-574 of Stellar Structure (1965)

P. Ledoux & Th. Walraven (1958) discuss linearization of the principal governing equations and stellar pulsation primarily from an Eulerian perspective. Focusing on §57 (pp. 455 - 458) of their Handbuch der Physik article — which falls under the major heading, "Radial oscillations of a gaseous sphere under its own gravitation" — we note, first that they use <math>~\delta r</math> to denote the radial displacement and use primes to identify all Eulerian perturbations. Then, in separating out the spatial and time dependences, they use the notation (see their equation 57.14),

<math>~\delta r</math>	<math>~\rightarrow</math>	<math>~\delta r e^{i\sigma t} \, ,</math>
<math>~v^'</math>	<math>~\rightarrow</math>	<math>~i \sigma \delta r e^{i\sigma t} \, ,</math>
<math>~\rho^'</math>	<math>~\rightarrow</math>	<math>~\rho^'(r) e^{i\sigma t} \, ,</math>
<math>~p^'</math>	<math>~\rightarrow</math>	<math>~p^'(r) e^{i\sigma t} \, ,</math>
<math>~\Phi^'</math>	<math>~\rightarrow</math>	<math>~\Phi^'(r) e^{i\sigma t} \, .</math>

According to their derivations, the linearized equation of continuity (EOC), equation of motion (EOM), and Poisson equation — see, repectively, their equations 57.15, 57.16 (with nonadiabatic effects set to zero), and 57.21 — are,

<math>~\rho^' + \frac{1}{r^2}\frac{\partial}{\partial r} \biggl( r^2 \rho \delta r \biggr)</math>	<math>~=</math>	<math>~0 \, ,</math>
<math>~- \sigma^2 \delta r</math>	<math>~=</math>	<math>~- \frac{\partial \Phi^'}{\partial r} + \frac{\rho^'}{\rho^2} \frac{\partial p}{\partial r} - \frac{1}{\rho}\frac{\partial p^'}{\partial r} \, ,</math>
<math>~\nabla^2 \Phi^'</math>	<math>~=</math>	<math>~4\pi G \rho^' \, .</math>

Next, with the aim of writing each of the three terms on the right-hand-side of the EOM in terms of the displacement, <math>~\delta r</math>, Ledoux and Walraven do the following: (1) By combining the EOC with the Poisson equation they obtain the perturbation in the gravitational acceleration, namely (see their equation 57.22),

<math>~\frac{1}{r^2} \frac{\partial}{\partial r} \biggl( r^2 \frac{\partial\Phi^'}{\partial r} \biggr) </math>	<math>~=</math>	<math>~- \frac{1}{r^2}\frac{\partial}{\partial r} \biggl( 4\pi G r^2 \rho \delta r \biggr) </math>
<math>~\Rightarrow ~~~~~ \frac{\partial\Phi^'}{\partial r} </math>	<math>~=</math>	<math>~- 4\pi G \rho \delta r \, .</math>

(2) The pressure fluctuation is obtained by using the adiabatic form of the 1^st law of thermodynamics to relate <math>~P</math> to <math>~\rho</math>, replacing the Lagrangian time derivatives with their Eulerian counterparts, then using the linearized EOC to provide an expression for the density fluctuation in terms of the radial displacement. Specifically (see their equations 56.15 and 57.19 with nonadiabatic terms set to zero),

<math>~\frac{dP}{dt}</math>	<math>~=</math>	<math>~\biggl( \frac{\gamma P}{\rho}\biggr) \frac{d\rho}{dt}</math>
<math>~\Rightarrow ~~~~~ \frac{\partial p^'}{\partial t} + v^' \frac{\partial p}{\partial r}</math>	<math>~=</math>	<math>~\biggl( \frac{\gamma P}{\rho}\biggr) \biggl[ \frac{\partial \rho^'}{\partial t} + v^' \frac{\partial \rho}{\partial r} \biggr] </math>
<math>~\Rightarrow ~~~~~ p^'+ \delta r \frac{\partial p}{\partial r}</math>	<math>~=</math>	<math>~\biggl( \frac{\gamma P}{\rho}\biggr) \biggl[ \rho^' + \delta r \frac{\partial \rho}{\partial r} \biggr] </math>
	<math>~=</math>	<math>~\biggl( \frac{\gamma P}{\rho}\biggr) \biggl[ - \frac{1}{r^2}\frac{\partial}{\partial r} \biggl( r^2 \rho \delta r \biggr) + \delta r \frac{\partial \rho}{\partial r} \biggr] </math>
	<math>~=</math>	<math>~- \gamma P \biggl[ \frac{1}{r^2}\frac{\partial}{\partial r} \biggl( r^2 \delta r \biggr) \biggr] </math>

With these substitutions, the linearized EOM (tentatively) takes the form,

<math>~\sigma^2 \rho\delta r - \rho \frac{\partial \Phi^'}{\partial r} - \frac{\partial p^'}{\partial r} </math>	<math>~=</math>	<math>~ - \frac{\rho^'}{\rho} \frac{\partial p}{\partial r}</math>
<math>~ \Rightarrow ~~~~~ \rho \delta r \biggl[ \sigma^2 + 4\pi G \rho \biggr] + \frac{\partial }{\partial r}\biggl\{ \gamma P \biggl[ \frac{1}{r^2}\frac{\partial}{\partial r} \biggl( r^2 \delta r \biggr) \biggr] +\delta r \frac{\partial p}{\partial r} \biggr\} </math>	<math>~=</math>	<math>~ \frac{1}{\rho} \frac{\partial p}{\partial r} \biggl[ \frac{1}{r^2}\frac{\partial}{\partial r} \biggl( r^2 \rho \delta r \biggr)\biggr]</math>
<math>~ \Rightarrow ~~~~~ \rho \delta r \biggl[ \sigma^2 + 4\pi G \rho \biggr] + \frac{\partial }{\partial r}\biggl\{ \gamma P \biggl[ \frac{1}{r^2}\frac{\partial}{\partial r} \biggl( r^2 \delta r \biggr) \biggr] \biggr\} </math>	<math>~=</math>	<math>~ \frac{1}{\rho} \frac{\partial p}{\partial r} \biggl[ \frac{1}{r^2}\frac{\partial}{\partial r} \biggl( r^2 \rho \delta r \biggr)\biggr] - \frac{\partial}{\partial r} \biggl[ \delta r \frac{\partial p}{\partial r} \biggr]</math>
	<math>~=</math>	<math>~ \frac{1}{\rho} \frac{\partial p}{\partial r} \biggl[ \frac{2\rho \delta r}{r} + \frac{\partial}{\partial r}(\rho \delta r)\biggr] + \biggl\{ \frac{1}{\rho} \frac{\partial p}{\partial r} \biggl(\frac{2\rho\delta r}{r} \biggr) - \frac{1}{r^2}\frac{\partial}{\partial r}\biggl[ r^2 \delta r \frac{\partial p}{\partial r} \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ \frac{1}{\rho} \frac{\partial p}{\partial r} \biggl(\frac{4\rho\delta r}{r} \biggr) +\frac{1}{\rho} \frac{\partial p}{\partial r} \biggl[ \frac{\partial}{\partial r}(\rho \delta r)\biggr] - \frac{1}{r^2}\frac{\partial}{\partial r}\biggl[ r^2 \delta r \frac{\partial p}{\partial r} \biggr] </math>
<math>~ \Rightarrow ~~~~~ \rho \delta r \biggl[ \sigma^2 + \frac{4Gm(r)}{r^3}\biggr] + \frac{\partial }{\partial r}\biggl\{ \gamma P \biggl[ \frac{1}{r^2}\frac{\partial}{\partial r} \biggl( r^2 \delta r \biggr) \biggr] \biggr\} </math>	<math>~=</math>	<math>~ -\rho\delta r(4\pi G \rho) +\frac{1}{\rho} \frac{\partial p}{\partial r} \biggl[ \frac{\partial}{\partial r}(\rho \delta r)\biggr] - \frac{1}{r^2}\frac{\partial}{\partial r}\biggl[ r^2 \delta r \frac{\partial p}{\partial r} \biggr] </math>
	<math>~=</math>	<math>~ -\rho\delta r \biggl[\frac{1}{r^2} \frac{\partial}{\partial r} \biggl( r^2 \frac{\partial\Phi}{\partial r}\biggr) \biggr] +\frac{1}{\rho} \frac{\partial p}{\partial r} \biggl[ \frac{\partial}{\partial r}(\rho \delta r)\biggr] - \frac{1}{r^2}\frac{\partial}{\partial r}\biggl[ r^2 (\rho \delta r )\frac{1}{\rho}\frac{\partial p}{\partial r} \biggr] </math>
	<math>~=</math>	<math>~ -\rho\delta r \biggl[\frac{1}{r^2} \frac{\partial}{\partial r} \biggl( r^2 \frac{\partial\Phi}{\partial r}\biggr) \biggr] - \frac{\partial \Phi}{\partial r} \biggl[ \frac{\partial}{\partial r}(\rho \delta r)\biggr] + \frac{1}{r^2}\frac{\partial}{\partial r}\biggl[ r^2 (\rho \delta r )\frac{\partial \Phi}{\partial r} \biggr] </math>
	<math>~=</math>	<math>~ 0 \, . </math>

This matches equation (57.23) of Ledoux & Walraven, if all nonadiabatic terms are set to zero.

Separate Analyses of Homogeneous Sphere

In an accompanying discussion, we have reviewed T. E. Sterne's (1937, MNRAS, 97, 582) study of radial pulsation modes in the homogeneous sphere. He solved the eigenvalue problem as defined by the

Adiabatic Wave (or Radial Pulsation) Equation

<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 </math>

and, hence, as established via a Lagrangian formulation of the problem. The eigenvectors and eigenvalues that Sterne derived for the first two or three radial modes have also appeared — usually in the context of separate, re-derivations — in other publications: See, for example, §38.2 (pp. 402-403) of [KW94].

After finishing that review, we became aware that a separate study of radial pulsation modes in the homogeneous sphere has been published by S. Rosseland (1969) In his book titled, The Pulsation Theory of Variable Stars (see, specifically his § 3.2, beginning on p. 27). Rosseland solved an eigenvalue problem as defined by the relation,

<math>~\frac{\partial}{\partial r} \biggl( \gamma P_0 \nabla\cdot \vec{\xi}\biggr) + \biggl( \omega^2 + \frac{4g_0}{r}\biggr) \rho_0 \xi</math>

(see his equation 2.23 on p. 20, with the adiabatic condition being enforced by setting the right-hand-side equal to zero), where,

<math>~\vec\xi = \mathbf{\hat{e}}_r \xi(r) \, .</math>

Rosseland derived this expression in an earlier section of his book via an Eulerian formulation of the problem. Realizing that, for a spherically symmetric system,

<math>\nabla\cdot \vec\xi = \frac{1}{r^2}\frac{\partial}{\partial r}\biggl(r^2 \xi\biggr) = \frac{\partial \xi}{\partial r} + \frac{2\xi}{r} \, ,</math>

as is demonstrated in and accompanying discussion, this relation can be rewritten in the more familiar form of a 2^nd-order ODE, namely,

<math>~P_0 \frac{\partial^2 \xi}{\partial r^2} + \biggl[ \frac{2P_0}{r}- \rho_0 g_0 \biggr] \frac{\partial \xi}{\partial r} + \biggl[ \biggl( \frac{\omega^2\rho_c}{\gamma} + \frac{4\rho_c g_0}{\gamma r}\biggr) \biggl(\frac{\rho_0}{\rho_c}\biggr) - \biggl(\frac{2\rho_c g_0 }{r}\biggr)\biggl(\frac{\rho_0}{\rho_c}\biggr) - \frac{2P_0}{r^2} \biggr] \xi </math>

Here we will repeat the setup and solution of both eigenvalue problems in an effort to reconcile differences. As we have explained elsewhere, an equilibrium, homogeneous, self-gravitating sphere has the following structural properties:

<math> \frac{g_0}{g_\mathrm{SSC}} = 2\chi_0 \, , </math>

where,

<math>P_c = \frac{3G}{8\pi}\biggl( \frac{M^2}{R^4} \biggr) </math> and <math>\rho_c = \frac{3M}{4\pi R^3} \, ,</math>

and the characteristic gravitational acceleration is defined as,

<math> g_\mathrm{SSC} \equiv \frac{P_c}{R \rho_c} \, . </math>

In addition, it will be useful to recognize that the square of the characteristic time for dynamical oscillations in spherically symmetric configurations (SSC) is,

<math> \tau_\mathrm{SSC}^2 \equiv \frac{R^2 \rho_c}{P_c} = \frac{2R^3}{G M} \, . </math>

Lagrangian Reformulation

Quite generally, we can rewrite the Lagrangian-formulated wave equation as,

<math> \biggl(\frac{P_0}{P_c}\biggr)\frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0}\biggl(\frac{P_0}{P_c}\biggr) - \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{1}{\gamma_\mathrm{g}} \biggr)\biggl[\tau_\mathrm{SSC}^2 \omega^2 + (4 - 3\gamma_\mathrm{g})\biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \frac{1}{\chi_0} \biggr] x = 0 . </math>

Note that we are convinced that this expression is error-free because, for example, when the structural properties of an equilibrium, <math>~n=1</math> polytrope are plugged into it, as is demonstrated in an accompanying discussion, we obtain exactly the same 2^nd-order ODE as published by Murphy & Fiedler (1985). For an homogeneous sphere, in particular, this expression can be rewritten as follows.

<math>~0</math>	<math>~=</math>	<math>~ ( 1-\chi_0^2 )\frac{d^2x}{d\chi_0^2} + \biggl[\frac{4(1-\chi_0^2)}{\chi_0} - 2\chi_0 \biggr] \frac{dx}{d\chi_0} + \frac{1}{\gamma_\mathrm{g}} \biggl[2\biggl(\frac{\omega^2 R^3}{GM}\biggr) + 2(4 - 3\gamma_\mathrm{g}) \biggr] x </math>
	<math>~=</math>	<math>~ ( 1-\chi_0^2 )\frac{d^2x}{d\chi_0^2} + \frac{1}{\chi_0}\biggl[4 - 6\chi_0^2 \biggr] \frac{dx}{d\chi_0} + \mathfrak{F} x \, , </math>

where,

<math>~\mathfrak{F} \equiv \frac{2}{\gamma_\mathrm{g}} \biggl[\biggl(\frac{\omega^2 R^3}{GM}\biggr) + (4 - 3\gamma_\mathrm{g}) \biggr] \, .</math>

This expression precisely matches equation (2) of Sterne (1937).

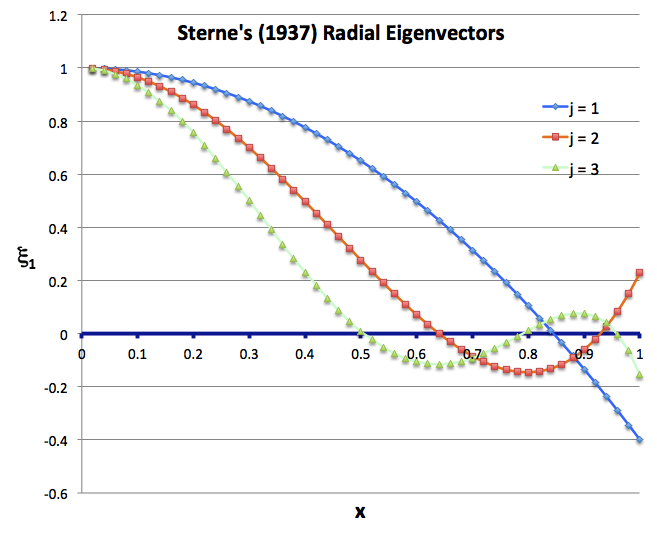
Drawing from Sterne's presentation, the following table details the eigenfunctions for the four lowest radial modes that satisfy this wave equation.

Sterne's (1937) Eigenfunctions for Homogeneous Sphere
Mode	Eigenvector	Square of Eigenfrequency: <math>~3\omega^2/(4\pi G\rho)</math>
<math>~j</math>	Eigenvector	<math>~\gamma[3+j(2j+5)] - 4</math>
<math>~0</math>	<math>~x = 1</math>	<math>~3\gamma-4</math>
<math>~1</math>	<math>~x = 1 -\frac{7}{5} \chi_0^2</math>	<math>~10\gamma-4</math>
<math>~2</math>	<math>~x = 1 -\frac{18}{5} \chi_0^2 + \frac{99}{35} \chi_0^4</math>	<math>~21\gamma-4</math>
<math>~3</math>	<math>~x = 1 -\frac{33}{5} \chi_0^2 + \frac{429}{35} \chi_0^4 - \frac{143}{21} \chi_0^6</math>	<math>~36\gamma-4</math>

Eulerian Reformulation

Using the same characteristic time scale and gravitational acceleration, we can similarly rewrite the Eulerian-formulated expression as,

<math>~ \biggl(\frac{P_0}{P_c}\biggr) \frac{\partial^2 \xi}{\partial \chi_0^2} + \biggl[ \frac{2}{\chi_0}\biggl(\frac{P_0}{P_c}\biggr) - \frac{g_0 }{g_\mathrm{SSC}}\biggl(\frac{\rho_0}{\rho_c}\biggr) \biggr] \frac{\partial \xi}{\partial \chi_0} + \biggl\{ \biggl[\frac{\omega^2\tau_\mathrm{SSC}^2}{\gamma} + \frac{2}{\chi_0 } \biggl(\frac{2}{\gamma } - 1\biggr)\frac{g_0}{g_\mathrm{SSC}}\biggr] \biggl(\frac{\rho_0}{\rho_c}\biggr) - \frac{2}{\chi_0^2} \biggl(\frac{P_0}{P_c}\biggr) \biggr\} \xi </math>

Note that we are convinced that this expression is error-free because, for example, when the structural properties of an equilibrium, "linear stellar model" are plugged into it, we obtain exactly the same 2^nd-order ODE as published by R. Stothers & J. A. Frogel (1967, ApJ, 148, 305) — see their equation (2). For an homogeneous sphere, in particular, this expression can be rewritten as follows.

<math>~0</math>	<math>~=</math>	<math>~ ( 1-\chi_0^2 ) \frac{\partial^2 \xi}{\partial \chi_0^2} + \biggl[ \frac{2( 1-\chi_0^2 )}{\chi_0} - 2\chi_0\biggr] \frac{\partial \xi}{\partial \chi_0} + \biggl\{ \frac{1}{\gamma}\biggl[2\biggl( \frac{\omega^2 R^3}{GM} \biggr) + 4\biggl(2 - \gamma\biggr) \biggr] - \frac{2}{\chi_0^2} ( 1-\chi_0^2 ) \biggr\} \xi </math>
	<math>~=</math>	<math>~ ( 1-\chi_0^2 ) \frac{\partial^2 \xi}{\partial \chi_0^2} + \frac{1}{\chi_0}\biggl[ 2 - 4\chi_0^2\biggr] \frac{\partial \xi}{\partial \chi_0} + \biggl\{ \frac{2}{\gamma}\biggl[\biggl( \frac{\omega^2 R^3}{GM} \biggr) + \biggl(4 - 3\gamma\biggr) +\gamma\biggr] - \frac{2}{\chi_0^2} ( 1-\chi_0^2 ) \biggr\} \xi </math>
	<math>~=</math>	<math>~ ( 1-\chi_0^2 ) \frac{\partial^2 \xi}{\partial \chi_0^2} + \frac{1}{\chi_0}\biggl[ 4 - 6\chi_0^2 - 2(1-\chi_0^2) \biggr] \frac{\partial \xi}{\partial \chi_0} + \biggl\{ \mathfrak{F} + \biggl(4 - \frac{2}{\chi_0^2} \biggr) \biggr\} \xi \, . </math>
	<math>~=</math>	<math>~ ( 1-\chi_0^2 ) \frac{\partial^2 \xi}{\partial \chi_0^2} + \frac{1}{\chi_0}\biggl[ 4 - 6\chi_0^2 \biggr] \frac{\partial \xi}{\partial \chi_0} + \mathfrak{F} \xi - \frac{1}{\chi_0}\biggl[ 2(1-\chi_0^2) \biggr] \frac{\partial \xi}{\partial \chi_0} + \biggl(4 - \frac{2}{\chi_0^2} \biggr) \xi </math>

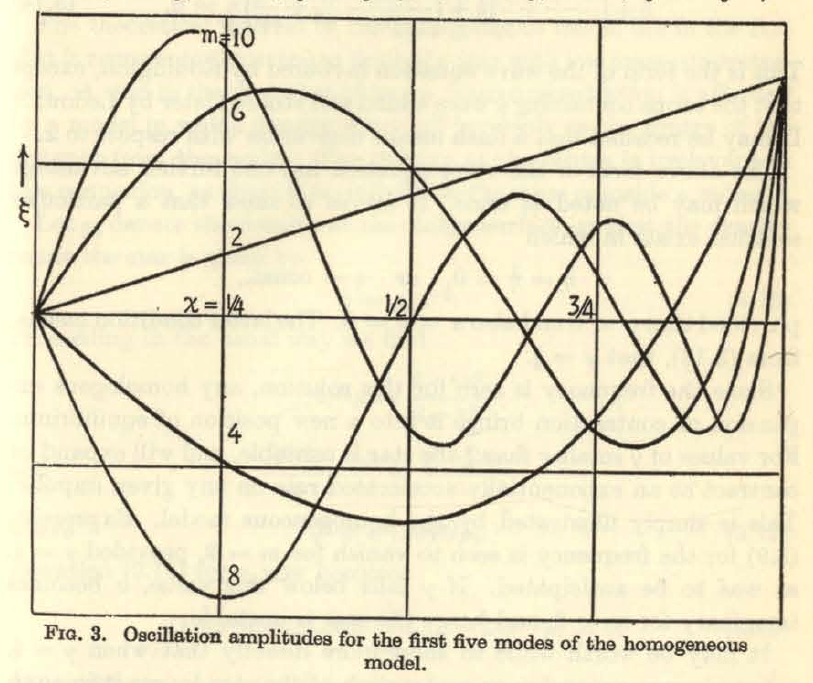
Drawing from Rosseland's presentation (see his p. 29), the following table details the eigenfunctions for the three lowest radial modes that satisfy this wave equation; a virtually identical summary can be found in §6.5 (see especially Figure 6.1 on p. 140) of [ST83].

Rosseland's (1964) Eigenfunctions for Homogeneous Sphere Figure in the right-most column extracted from p. 29 of Rosseland (1964) "The Pulsation Theory of Variable Stars" (New York: Dover Publications, Inc.)
Mode	Eigenvector		Square of Eigenfrequency: <math>~3\sigma^2/(4\pi G\rho)</math>
<math>~m</math>	As Published	Rewritten	<math>~\frac{m}{2}(m+1)\gamma - 4</math>
<math>~2</math>	<math>~\xi = -2\chi_0</math>	<math>~-\frac{1}{2}\biggl( \frac{\xi}{\chi_0}\biggr) = 1</math>	<math>~3\gamma - 4</math>
<math>~4</math>	<math>~\xi = -\frac{20}{3}\chi_0 + \frac{28}{3}\chi_0^3</math>	<math>~-\frac{3}{20}\biggl( \frac{\xi}{\chi_0}\biggr) = 1- \frac{7}{5}\chi_0^2</math>	<math>~10\gamma-4</math>
<math>~6</math>	<math>~\xi = -14\chi_0 + \frac{252}{5} \chi_0^3 - \frac{198}{5} \chi_0^5</math>	<math>~-\frac{1}{14}\biggl( \frac{\xi}{\chi_0}\biggr) = 1 - \frac{18}{5} \chi_0^2 + \frac{99}{35} \chi_0^4</math>	<math>~21\gamma-4</math>

Reconciliation by Rosseland

Rosseland (1969) points out that these two different formulations can be reconciled by adopting the following dependent coordinate substitution (see his equation 3.11):

<math>~x \rightarrow \frac{\xi}{\chi_0} \, .</math>

This means that the derivatives that appear in the above Lagrangian formulation should be replaced by the expressions,

<math>~\frac{dx}{d\chi_0} \rightarrow \biggl(\frac{1}{\chi_0}\biggr)\frac{d\xi}{d\chi_0} - \frac{\xi}{\chi_0^2} \, ,</math>

and,

<math>~\frac{d^2x}{d\chi_0^2} \rightarrow \biggl(\frac{1}{\chi_0}\biggr)\frac{d^2\xi}{d\chi_0^2} - \biggl( \frac{2}{\chi_0^2} \biggr) \frac{d\xi}{d\chi_0} + \frac{2\xi}{\chi_0^3} \, .</math>

Doing this, we have,

<math>~0</math>	<math>~=</math>	<math>~ ( 1-\chi_0^2 )\biggl[ \biggl(\frac{1}{\chi_0}\biggr)\frac{d^2\xi}{d\chi_0^2} - \biggl( \frac{2}{\chi_0^2} \biggr) \frac{d\xi}{d\chi_0} + \frac{2\xi}{\chi_0^3} \biggr] + \frac{1}{\chi_0}\biggl[4 - 6\chi_0^2 \biggr] \biggl[ \biggl(\frac{1}{\chi_0}\biggr)\frac{d\xi}{d\chi_0} - \frac{\xi}{\chi_0^2} \biggr] + \mathfrak{F} \biggl( \frac{\xi}{\chi_0} \biggr) </math>
	<math>~=</math>	<math>~\biggl( \frac{1}{\chi_0}\biggr) \biggl\{ ( 1-\chi_0^2 )\biggl[ \frac{d^2\xi}{d\chi_0^2} - \biggl( \frac{2}{\chi_0} \biggr) \frac{d\xi}{d\chi_0} + \frac{2\xi}{\chi_0^2} \biggr] + \biggl[4 - 6\chi_0^2 \biggr] \biggl[ \biggl(\frac{1}{\chi_0}\biggr)\frac{d\xi}{d\chi_0} - \frac{\xi}{\chi_0^2} \biggr] + \mathfrak{F} \xi \biggr\} </math>
	<math>~=</math>	<math>~\biggl( \frac{1}{\chi_0}\biggr) \biggl\{ ( 1-\chi_0^2 )\frac{d^2\xi}{d\chi_0^2} + \frac{1}{\chi_0} \biggl[4 - 6\chi_0^2 \biggr] \frac{d\xi}{d\chi_0} + \mathfrak{F} \xi -\biggl( \frac{2}{\chi_0} \biggr) ( 1-\chi_0^2 )\frac{d\xi}{d\chi_0} + \biggl[4\chi_0^2 -2 \biggr] \frac{\xi}{\chi_0^2} \biggr\} \, , </math>

which, indeed, matches the expression derived via Rosseland's Eulerian formulation.

Rosseland's Derivation of the Wave Equation

Here we step through a derivation of the wave equation as has been presented by S. Rosseland (1969) in chapter 2 of his book titled, The Pulsation Theory of Variable Stars (see, especially his §§ 2.1 & 2.2, pp. 15-20), dropping all terms that account for nonadiabatic effects.

We begin with the set of principal governing equations that provides the foundation for practically all of our discussions in this H_Book, namely, the

Equation of Continuity

<math>\frac{d\rho}{dt} + \rho \nabla \cdot \vec{v} = 0</math>

Euler Equation

<math>\frac{d\vec{v}}{dt} = - \frac{1}{\rho} \nabla P - \nabla \Phi</math>

Adiabatic Form of the
First Law of Thermodynamics

<math>~\frac{d\epsilon}{dt} + P \frac{d}{dt} \biggl(\frac{1}{\rho}\biggr) = 0</math> .

Poisson Equation

<math>\nabla^2 \Phi = 4\pi G \rho</math>

Because we are considering only spherically symmetric configurations, we will implement operators that reflect structural variations only in the radial coordinate. Specifically, following a parallel discussion of the principal governing equations that are appropriate for spherically symmetric configurations, we have the,

Equation of Continuity

<math>\frac{d\rho}{dt} + \rho \biggl[\frac{1}{r^2}\frac{\partial (r^2 v_r)}{\partial r} \biggr] = \frac{d\rho}{dt} + \rho \biggl[ \frac{\partial v_r}{\partial r} + \frac{2v_r}{r} \biggr] = 0 </math>

Euler Equation

Adiabatic Form of the
First Law of Thermodynamics

<math>~\frac{d\epsilon}{dt} + P \frac{d}{dt} \biggl(\frac{1}{\rho}\biggr) = 0</math>

Poisson Equation

<math>\frac{1}{r^2} \biggl[\frac{d }{dr} \biggl( r^2 \frac{d \Phi}{dr} \biggr) \biggr] = 4\pi G \rho </math>

Step 1:

Following Rosseland, we adopt as a supplemental relation what we have referred to elsewhere as,

Form B
of the Ideal Gas Equation of State,

<math>~P = (\gamma_\mathrm{g} - 1)\epsilon \rho </math>

where, for our purposes, we assume that <math>~\gamma_\mathrm{g}</math> is independent of space and time. Plugging the function, <math>~\epsilon(P,\rho)</math>, that is defined by this equation of state into the adiabatic form of the 1^st law of thermodynamics leads to the relations (see, respectively, Rosseland's equations 2.8 and 2.9),

<math>~\frac{\gamma_g P}{\rho} \frac{d\rho}{dt} \, ,</math>

and,

<math>~\biggl( \frac{\rho}{\rho_0}\biggr)^{\gamma_g} \, ,</math>

where <math>~P_0</math> and <math>~\rho_0</math> are independent of time. We note for later use that, when the equation of continuity — as written in its original vector-operator form — is combined with this last differential form of the 1^st law of thermodynamics, we can write,

<math>~- \gamma_g P \nabla\cdot \vec{v} \, .</math>

Step 2:

As we have shown in a separate discussion of how to construct equilibrium, spherically symmetric configurations, the Poisson equation can be integrated once to give an expression for the gravitational acceleration (see, also, Rosseland's equation 2.16) of the form,

<math>~g \equiv \frac{d\Phi}{dr}</math>

As is quite customary in this field of research, Rosseland substitutes <math>~g</math> for the radial gradient of the gravitational potential in the Euler equation — that is, he writes,

<math>~- \frac{1}{\rho} \frac{\partial P}{\partial r} - g \, ,</math>

(see his equation 2.14 with nonadiabatic terms set to zero) — and, in so doing, considers that the Poisson equation has been solved. This reduces the number of governing equations (as well as the number of unknown structural variables) to three. Then Rosseland proceeds to point out that, when the radial pulsation of a spherically symmetric configuration is viewed from a Lagrangian perspective — that is, while riding along with a fluid element — the mass enclosed inside the radial position of each fluid element, <math>~M_r</math>, does not change with time. Hence, the Lagrangian time-derivative of the gravitational acceleration is (see Rosseland's equation 2.17),

<math>~GM_r \frac{d}{dt}\biggl(\frac{1}{r^2}\biggr) = - \frac{2GM_r}{r^3} \frac{dr}{dt} = - \frac{2gv_r}{r} \, .</math>

Step 3:

Next, Rosseland takes the Lagrangian time-derivative of the Euler equation, which gives (see Rosseland's equation 2.15 with nonadiabatic terms set to zero),

<math>~\frac{d^2v_r}{dt^2}</math>	<math>~=</math>	<math>~- \frac{d}{dt}\biggl[\frac{1}{\rho} \frac{\partial P}{\partial r}\biggr] - \frac{dg}{dt} </math>
	<math>~=</math>	<math>~\frac{1}{\rho^2}\frac{d\rho}{dt} \biggl(\frac{\partial P}{\partial r}\biggr) - \frac{1}{\rho} \frac{d}{dt}\biggl[\frac{\partial P}{\partial r}\biggr] - \frac{dg}{dt} </math>
	<math>~=</math>	<math>~- \frac{1}{\rho}\biggl(\frac{\partial P}{\partial r}\biggr)\biggl[ \frac{\partial v_r}{\partial r} + \frac{2v_r}{r} \biggr] - \frac{1}{\rho} \frac{d}{dt}\biggl[\frac{\partial P}{\partial r}\biggr] + \frac{2gv_r}{r} \, .</math>

But, from the Euler equation, itself, we can write,

<math>~- \frac{1}{\rho} \biggl( \frac{\partial P}{\partial r} \biggr)</math>

Hence,

<math>~\frac{d^2v_r}{dt^2}</math>	<math>~=</math>	<math>~\biggl[ \frac{dv_r}{dt} + g \biggr] \biggl[ \frac{\partial v_r}{\partial r} + \frac{2v_r}{r} \biggr] - \frac{1}{\rho} \frac{d}{dt}\biggl[\frac{\partial P}{\partial r}\biggr] + \frac{2gv_r}{r} </math>
	<math>~=</math>	<math>~\biggl[ \frac{dv_r}{dt} +g\biggr]\frac{\partial v_r}{\partial r} - \frac{1}{\rho} \frac{d}{dt}\biggl[\frac{\partial P}{\partial r}\biggr] + \frac{4gv_r}{r} + \frac{2v_r}{r} \biggl[ \frac{dv_r}{dt} \biggr] \, . </math>

Step 4:

Finally, Rosseland sets out to swap the order of the time- and space-derivatives in the term,

<math>~\frac{d}{dt}\biggl[\frac{\partial P}{\partial r}\biggr] \, .</math>

But, whereas the partial time derivative commutes with the partial radial derivative, the total time derivative does not commute with the spatial derivative. Generically, however, for any scalar variable, <math>~q</math>, we can swap between total and partial time derivatives via the operator relation,

<math>~\frac{dq}{dt} = \frac{\partial q}{\partial t} + v_r \frac{\partial q}{\partial r} \, .</math>

Hence, if <math>~q</math> is replaced by <math>~P</math>, we can write,

<math>~ v_r \biggl(\frac{\partial P}{\partial r}\biggr) = \frac{dP}{dt} - \frac{\partial P}{\partial t}\, ;</math>

while, if <math>~q</math> is replaced by <math>~\partial P/\partial r</math>, we have,

<math>~\frac{d}{dt}\biggl( \frac{\partial P}{\partial r} \biggr)</math>	<math>~=</math>	<math>~\frac{\partial }{\partial t}\biggl( \frac{\partial P}{\partial r} \biggr) + v_r \frac{\partial }{\partial r} \biggl( \frac{\partial P}{\partial r} \biggr)</math>
	<math>~=</math>	<math>~\frac{\partial }{\partial r}\biggl( \frac{\partial P}{\partial t} \biggr) + \frac{\partial }{\partial r} \biggl[ v_r \biggl( \frac{\partial P}{\partial r} \biggr)\biggr] - \biggl( \frac{\partial P}{\partial r} \biggr)\frac{\partial v_r}{\partial r} \, ,</math>

where, in making this last step, we have swapped the order of the partial derivatives in the first term on the right-hand side. Combining these two relations and incorporating the form of Euler's equation that was highlighted in step #3 gives,

<math>~\frac{d}{dt}\biggl( \frac{\partial P}{\partial r} \biggr)</math>	<math>~=</math>	<math>~\frac{\partial }{\partial r}\biggl( \frac{\partial P}{\partial t} \biggr) + \frac{\partial }{\partial r} \biggl[ \frac{dP}{dt} - \frac{\partial P}{\partial t} \biggr] + \rho \biggl[ \frac{dv_r}{dt} + g \biggr]\frac{\partial v_r}{\partial r} </math>
	<math>~=</math>	<math>~ \frac{\partial }{\partial r} \biggl[ \frac{dP}{dt} \biggr] + \rho \biggl[ \frac{dv_r}{dt} + g \biggr]\frac{\partial v_r}{\partial r} \, .</math>

Inserting this into the equation found at the end of step #3, then inserting the expression for <math>~dP/dt</math> derived in step #1 gives,

<math>~\frac{d^2v_r}{dt^2}</math>	<math>~=</math>	<math>~ - \frac{1}{\rho} \frac{\partial }{\partial r} \biggl[ \frac{dP}{dt} \biggr] + \frac{4gv_r}{r} + \frac{2v_r}{r} \biggl[ \frac{dv_r}{dt} \biggr] </math>
	<math>~=</math>	<math>~ \frac{1}{\rho} \frac{\partial }{\partial r} \biggl[ \gamma_g P \nabla\cdot \vec{v}\biggr] + \frac{4gv_r}{r} + \frac{2v_r}{r} \biggl[ \frac{dv_r}{dt} \biggr] \, . </math>

This matches Rosseland's equation (2.18) with the nonadiabatic terms set to zero.

Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |

Linearizing the Key Relations

Continuity Equation

Lagrangian Perspective

Eulerian Perspective

<math>~- \rho \nabla\cdot\vec{v}</math>

<math>~\frac{\partial\rho}{\partial t}</math>

<math>~- \rho \nabla\cdot\vec{v} - \vec{v}\cdot \nabla\rho</math>

Spherically Symmetric Initial Configurations & Purely Radial Perturbations

<math>~- \frac{\rho}{r^2} \frac{\partial}{\partial r} \biggl( r^2 v_r \biggr)</math>

<math>~\frac{\partial\rho}{\partial t}</math>

<math>~- \frac{\rho}{r^2} \frac{\partial}{\partial r} \biggl( r^2 v_r \biggr) - v_r \frac{\partial \rho}{\partial r}</math>

In an interval of time, <math>~dt = \partial t</math>, a fluid element initially at position <math>~r_0</math> moves to position, <math>~r = r_0 + r_1 = r_0(1 + \xi)</math>. [For later reference, note that <math>~\xi</math> can be a function of <math>~r_0</math> as well as of <math>~t</math>.] On the righthand side of the expression, the radial coordinate will be handled as follows: From the Lagrangian perspective, <math>~r \rightarrow r_0 (1+ \xi)</math>, while from the Eulerian perspective, we want to stay at the original coordinate location, so <math>~r \rightarrow r_0</math>. From both perspectives,

<math>~v_r = \frac{\partial ( r_0 \xi )}{\partial t} = r_0 \frac{\partial \xi}{\partial t} \, .</math>

Riding with the fluid element (Lagrangian perspective), <math>~\rho \rightarrow (\rho_0 + \rho_L) = \rho_0(1+s_L)</math>, while at a fixed coordinate location (Eulerian perspective), <math>~\rho \rightarrow (\rho_0 + \rho_E) = \rho_0(1 + s_E)</math>. Finally, in maintaining a Lagrangian perspective, we will need to ensure that the same element of mass is being tracked as we "ride along" with the fluid element to its new position. For radial perturbations associated with a spherically symmetric configuration, this means that the differential mass in each spherical shell, <math>~dm = 4\pi r^2 \rho dr</math>, must remain constant; that is,

<math>~4\pi r_0^2 \rho_0 dr_0</math>	<math>~=</math>	<math>~4\pi r^2 \rho dr</math>
	<math>~=</math>	<math>~4\pi [r_0(1+\xi)]^2 \rho_0(1+s_L) dr</math>
	<math>~=</math>	<math>~4\pi r_0^2 \rho_0 \biggl(1+2\xi + \cancelto{\scriptstyle\text{small}}{\xi^2} + \cdots \biggr) (1+s_L) dr</math>
	<math>~\approx</math>	<math>~4\pi r_0^2 \rho_0 \biggl(1+2\xi + s_L + 2\cancelto{\scriptstyle\mathrm{small}}{\xi s_L} \biggr) dr</math>
<math>~\Rightarrow~~~ \frac{d}{dr}</math>	<math>~\approx</math>	<math>~(1+2\xi + s_L ) \frac{d}{dr_0} \, .</math>

<math>~\frac{d}{dt}\biggl[\rho_0(1+s_L)\biggr]</math>	<math>~=</math>	<math>~- \biggl\{ \frac{\rho_0(1+\cancelto{}{s_L})}{[r_0(1+\cancelto{}{\xi})]^2} \biggr\}(1+2\cancelto{}{\xi s_L}) \frac{\partial}{\partial r_0} \biggl\{ [r_0(1+\cancelto{}{\xi})]^2 v_r \biggr\}</math>
<math>~\Rightarrow~~~ \frac{d s_L}{dt}</math>	<math>~=</math>	<math>~- \biggl[\frac{2v_r}{r_0} + \frac{\partial v_r}{\partial r_0} \biggr] - \frac{1}{\rho_0} \frac{d\rho_0}{dt}</math>

<math>~\frac{\partial}{\partial t}\biggl[\rho_0(1+s_E)\biggr]</math>	<math>~=</math>	<math>~- \frac{\rho_0(1+\cancelto{\mathrm{small}}{s_E})}{r_0^2} \frac{\partial}{\partial r_0} \biggl( r_0^2 v_r \biggr) - v_r \frac{\partial [\rho_0(1+\cancelto{\mathrm{small}}{s_E})] }{\partial r_0}</math>
<math>~\Rightarrow~~~ \frac{\partial s_E}{\partial t}</math>	<math>~=</math>	<math>~- \biggl[\frac{2v_r}{r_0} + \frac{\partial v_r}{\partial r_0} \biggr] - \frac{v_r}{\rho_0} \frac{\partial \rho_0 }{\partial r_0}</math>

Note: The last term that appears on the righthand side of the two expressions appears to be different. But if, as we are assuming here, <math>~\rho_0</math> has no explicit time dependence but may be considered to be a function of the radial coordinate, <math>~r_0</math>, then the two terms are the same. This is because, quite generically for any scalar function <math>~q</math>, the total time-derivative (Lagrangian perspective) differs from the partial time-derivative (Eulerian perspective) via the expression, <math>dq/dt - \partial q /\partial t = \vec{v}\cdot \nabla q</math>. In our case, <math>~\partial \ln \rho_0/\partial t = 0</math>, so <math>~d\ln\rho_0/dt = \vec{v}\cdot \nabla \ln \rho_0</math>.

<math>~s_L ~~\rightarrow~~ \Delta_L(r_0) e^{i\omega t}</math> … and … <math>~s_E ~~\rightarrow~~ \Delta_E(r_0) e^{i\omega t}</math>

<math>~\xi ~~\rightarrow~~ x(r_0) e^{i\omega t}</math> <math>\Rightarrow</math> <math>~v_r ~~\rightarrow~~ (i\omega)r_0 x(r_0) e^{i\omega t}</math>

<math>~e^{i\omega t} \biggl[ (i\omega)\Delta_L + \frac{d\Delta_L}{dt} \biggr]</math>	<math>~=</math>	<math>~- e^{i\omega t} \biggl[ 2(i\omega)x + (i\omega)x + (i\omega)r_0 \frac{\partial x}{\partial r_0} \biggr]</math>
<math>~\Rightarrow ~~~r_0 \frac{\partial x}{\partial r_0} </math>	<math>~=</math>	<math>~- \Delta_L -3 x - \frac{1}{(i\omega)} \biggl[ v_r \frac{\partial\Delta_L}{\partial r_0} \biggr]</math>
	<math>~=</math>	<math>~- \Delta_L - x \biggl[3 + \cancelto{\scriptstyle\mathrm{small}}{\frac{\partial\Delta_L}{\partial \ln r_0} }\biggr]</math>

<math>~e^{i\omega t} (i\omega)\Delta_E </math>	<math>~=</math>	<math>~- e^{i\omega t} \biggl[ 2(i\omega)x + (i\omega)x + (i\omega)r_0 \frac{\partial x}{\partial r_0} \biggr] - \biggl[\frac{1}{\rho_0} \frac{\partial \rho_0}{\partial r_0} \biggr](i\omega)r_0 x e^{i\omega t}</math>
<math>~\Rightarrow ~~~r_0 \frac{\partial x}{\partial r_0} </math>	<math>~=</math>	<math>~- \Delta_E - x \biggl[3 + \frac{\partial \ln\rho_0}{\partial \ln r_0} \biggr] </math>

User:Tohline/SSC/Perspective Reconciliation

Contents