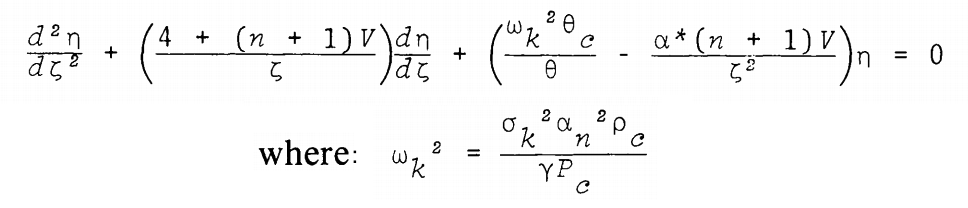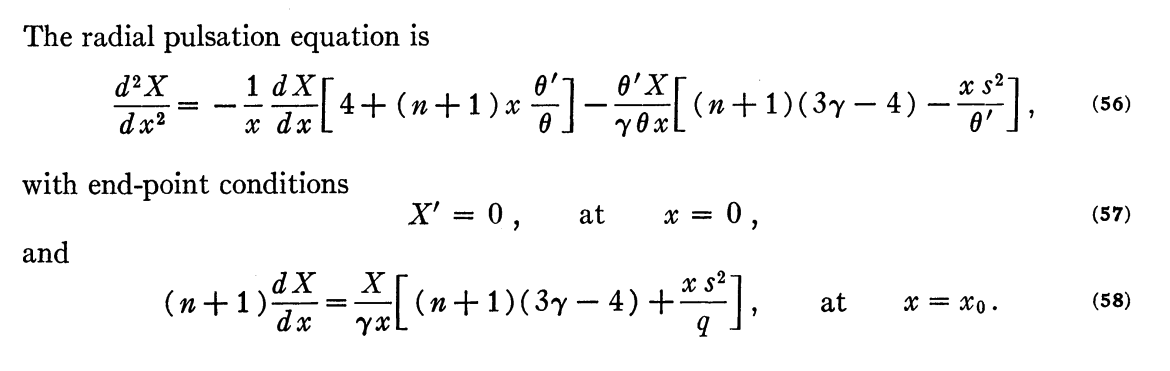Radial Oscillations of Polytropic Spheres

Groundwork

Adiabatic (Polytropic) Wave Equation

In an accompanying discussion, we derived the so-called,

Adiabatic Wave (or Radial Pulsation) Equation

<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 </math>

whose solution gives eigenfunctions that describe various radial modes of oscillation in spherically symmetric, self-gravitating fluid configurations. If the initial, unperturbed equilibrium configuration is a polytropic sphere whose internal structure is defined by the function, <math>~\theta(\xi)</math>, then

<math>~r_0</math>	<math>~=</math>	<math>~a_n \xi \, ,</math>
<math>~\rho_0</math>	<math>~=</math>	<math>~\rho_c \theta^{n} \, ,</math>
<math>~P_0</math>	<math>~=</math>	<math>~K\rho_0^{(n+1)/n} = K\rho_c^{(n+1)/n} \theta^{n+1} \, ,</math>
<math>~g_0</math>	<math>~=</math>	<math>~\frac{GM(r_0)}{r_0^2} = \frac{G}{r_0^2} \biggl[ 4\pi a_n^3 \rho_c \biggl(-\xi^2 \frac{d\theta}{d\xi}\biggr) \biggr] \, ,</math>

where,

<math>~\biggl[\frac{(n+1)K}{4\pi G} \cdot \rho_c^{(1-n)/n} \biggr]^{1/2} \, .</math>

Hence, after multiplying through by <math>~a_n^2</math>, the above adiabatic wave equation can be rewritten in the form,

<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - \frac{g_0}{a_n}\biggl(\frac{a_n^2 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{d\xi} + \biggl(\frac{a_n^2\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{a_n\xi} \biggr] x </math>

In addition, given that,

<math>~4\pi G \rho_c \biggl(-\frac{d \theta}{d\xi} \biggr) \, ,</math>

and,

<math>~\frac{(n+1)}{(4\pi G\rho_c)\theta} = \frac{a_n^2 \rho_c}{P_c} \cdot \frac{\theta_c}{\theta}\, ,</math>

we can write,

<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4 - (n+1)V(\xi)}{\xi} \biggr] \frac{dx}{d\xi} + \biggl[\omega^2 \biggl(\frac{a_n^2 \rho_c }{\gamma_g P_c} \biggr) \frac{\theta_c}{\theta} - \biggl(3-\frac{4}{\gamma_g}\biggr) \cdot \frac{(n+1)V(x)}{\xi^2} \biggr] x </math>

where we have adopted the function notation,

<math>~\equiv</math>

<math>~- \frac{\xi}{\theta} \frac{d \theta}{d\xi} \, .</math>

As can be seen in the following framed image, this is the form of the polytropic wave equation published by J. O. Murphy & R. Fiedler (1985b, Proc. Astron. Soc. Australia, 6, 222), at the beginning of their discussion of "Radial Pulsations and Vibrational Stability of a Sequence of Two Zone Polytropic Stellar Models."

Polytropic Wave Equation extracted^† from J. O. Murphy & R. Fiedler (1985b)

"Radial Pulsations and Vibrational Stability of a Sequence of Two Zone Polytropic Stellar Models"

Proceeding of the Astronomical Society of Australia, vol. 6, pp. 222 - 226 © Astronomical Society of Australia

^†Equations displayed here, as a single digital image, with layout modified from the original publication.

It is also the same as the radial pulsation equation for polytropic configurations that appears as equation (56) in the detailed discussion of "The Oscillations of Gas Spheres" published by H M. Hurley, P. H. Roberts, & K. Wright (1966, ApJ, 143, 535); hereafter, we will refer to this paper as HRW66. The relevant set of equations from HRW66 has been extracted as a single digital image and reprinted, here, as a boxed-in image.

Radial Pulsation Equation as Presented^† by M. Hurley, P. H. Roberts, & K. Wright (1966)

"The Oscillations of Gas Spheres"

The Astrophysical Journal, vol. 143, pp. 535 - 551 © American Astronomical Society

^†Set of equations and accompanying text displayed here, as a single digital image, exactly as they appear in the original publication.

In order to make clearer the correspondence between our derived expression and the one published by HRW66, we will rewrite the HRW66 radial pulsation equation: (1) Gathering all terms on the same side of the equation; (2) making the substitution,

<math>\theta^' \rightarrow -\frac{\theta V}{x} \, ;</math>

and (3) reattaching a "prime" to the quantity, <math>~s</math>, to emphasize that it is a dimensionless frequency.

ASIDE: In their equation (46), HRW66 convert the eigenfrequency, <math>~s</math> — which has units of inverse time — to a dimensionless eigenfrequency, <math>~s^'</math>, via the relation,

<math>~s = \biggl( \frac{4\pi G \rho_c}{1+n} \biggr)^{1/2} s^' ~~~~~~~\cdots\cdots~~~~~~~(46)</math>

Then, immediately following equation (46), they state that they will "omit the prime on <math>~s</math> henceforward." As a result, the dimensionless eigenfrequency that appears in their equations (56) and (58) is unprimed. This is unfortunate as it somewhat muddies our efforts, here, to demonstrate the correspondence between the HRW66 polytropic radial pulsation equation and ours. In our subsequent manipulation of equation (56) from HRW66 we reattach a prime to the quantity, <math>~s</math>, to emphasize that it is a dimensionless frequency. But this prime on <math>~s</math> should not be confused with the prime on <math>~\theta</math> (HRW66 equation 56) or with the prime on <math>~X</math> (HRW66 equation 57), both of which denote differentiation with respect to the radial coordinate.

With these modifications, the HRW66 radial pulsation equation becomes,

<math>~0</math>	<math>~=</math>	<math> ~\frac{d^2 X}{dx^2} + \biggl[\frac{4 - (n+1)V }{x}\biggr]\frac{dX}{dx} - \frac{V}{\gamma x^2}\biggl[\frac{x^2 (s^')^2}{\theta V} + (3\gamma -4)(n+1) \biggr]X </math>
	<math>~=</math>	<math> ~\frac{d^2 X}{dx^2} + \biggl[\frac{4 - (n+1)V }{x}\biggr]\frac{dX}{dx} + \biggl[-\frac{(s^')^2 }{\gamma \theta } - \biggl(3 -\frac{4}{\gamma}\biggr)\frac{(n+1)V}{x^2} \biggr]X \, . </math>

The correspondence with our derived expression is complete, assuming that,

<math>~(s^')^2</math>	<math>~=</math>	<math>~-\omega^2 \biggl(\frac{a_n^2 \rho_c }{P_c} \biggr) \theta_c</math>
	<math>~=</math>	<math>~-\omega^2 \biggl[\frac{n+1 }{4\pi G \rho_c} \biggr] \, .</math>

As has been explained in the above "ASIDE," this is exactly the factor that HRW66 use to normalize their eigenfrequency, <math>~s</math>, and make it dimensionless <math>~(s^')</math>. It is clear, as well, that HRW66 have adopted a sign convention for the square of their eigenfrequency that is the opposite of the sign convention that we have adopted for <math>~\omega^2</math>. That is, it is clear that,

<math>~s^2 ~~\leftrightarrow~~ - \omega^2 \, .</math>

Boundary Conditions

As we have pointed out in the context of a general discussion of boundary conditions associated with the adiabatic wave equation, the eigenfunction, <math>~x</math>, will be suitably well behaved at the center of the configuration if,

which, in the context of our present discussion of polytropic configurations, leads to the inner boundary condition,

This is precisely the inner boundary condition specified by HRW66 — see their equation (57), which has been reproduced in the above excerpt from HWR66.

As we have also shown in the context of this separate, general discussion of boundary conditions associated with the adiabatic wave equation, the pressure fluctuation will be finite at the surface — even if the equilibrium pressure and/or the pressure scale height go to zero at the surface — if the radial eigenfunction, <math>~x</math>, obeys the relation,

<math>~\biggl( 4 - 3\gamma_g + \frac{\omega^2 R^3}{GM_\mathrm{tot}}\biggr) \frac{x}{\gamma_g}</math> at <math>~r_0 = R \, .</math>

Or, given that, in polytropic configurations, <math>~r_0 = a_n\xi</math>,

<math>~\frac{x}{\gamma_g} \biggl[ 4 - 3\gamma_g + \frac{\omega^2 (a_n \xi_1)^3}{GM_\mathrm{tot}}\biggr] </math> at <math>~\xi = \xi_1 \, ,</math>

where, the subscript "1" denotes equilibrium, surface values. As can be deduced from our above summary of the properties of polytropic configurations,

<math>~GM_\mathrm{tot}</math>

<math>~4\pi G a_n^3 \rho_c (-\xi_1^2 \theta_1^') \, .</math>

Hence, for spherically symmetric polytropic configurations, the surface boundary condition becomes,

<math>~\frac{dx}{d\xi}</math>	<math>~=</math>	<math>~\frac{x}{\gamma_g \xi} \biggl[ 4 - 3\gamma_g + \omega^2 \biggl( \frac{1}{4\pi G \rho_c } \biggr) \frac{\xi}{(-\theta^')}\biggr] </math> at <math>~\xi = \xi_1 \, ,</math>
<math>~\Rightarrow ~~~~~(n+1)\frac{dx}{d\xi}</math>	<math>~=</math>	<math>~\frac{x}{\gamma_g \xi} \biggl[ (n+1)(4 - 3\gamma_g) + \omega^2 \biggl( \frac{1+n}{4\pi G \rho_c } \biggr) \frac{\xi}{(-\theta^')}\biggr] </math>
	<math>~=</math>	<math>~-\frac{x}{\gamma_g \xi} \biggl[ (n+1)(3\gamma_g-4) - \omega^2 \biggl( \frac{1+n}{4\pi G \rho_c } \biggr) \frac{\xi}{(-\theta^')}\biggr] </math> at <math>~\xi = \xi_1 \, .</math>

Adopting notation used by HRW66, specifically, as demonstrated above,

<math>~-\omega^2 \biggl( \frac{1+n}{4\pi G \rho_c } \biggr) \rightarrow (s^')^2 \, , </math>

and, from equation (50) of HRW66,

<math>~-\theta^' \rightarrow q </math> at <math>~\xi = \xi_1 \, ,</math>

this outer boundary condition becomes,

<math>~-\frac{x}{\gamma_g \xi} \biggl[ (n+1)(3\gamma_g-4) + \frac{\xi (s^')^2}{q}\biggr] </math> at <math>~\xi = \xi_1 \, .</math>

With the exception of the leading negative sign on the right-hand side, this expression is identical to the outer boundary condition identified by equation (58) of HRW66 — see the excerpt reproduced above.

Overview

The eigenvector associated with radial oscillations in isolated polytropes has been determined numerically and the results have been presented in a variety of key publications:

P. LeDoux & Th. Walraven (1958, Handbuch der Physik, 51, 353) —
R. F. Christy (1966, Annual Reviews of Astronomy & Astrophysics, 4, 353) — Pulsation Theory
M. Hurley, P. H. Roberts, & K. Wright (1966, ApJ, 143, 535) — The Oscillations of Gas Spheres
J. P. Cox (1974, Reports on Progress in Physics, 37, 563) — Pulsating Stars

Tables

Quantitative Information Regarding Eigenvectors of Oscillating Polytropes <math>~(\Gamma_1 = 5/3)</math>
<math>~n</math>	<math>~\frac{\rho_c}{\bar\rho}</math>	Excerpts from Table 1 of Hurley, Roberts, & Wright (1966) <math>~s^2 (n+1)/(4\pi G\rho_c)</math>	Excerpts from Table 3 of J. P. Cox (1974) <math>~\sigma_0^2 R^3/(GM)</math>	<math>\frac{(n+1) \mathrm{Cox74}}{3 \mathrm{HRW66}} \cdot \frac{\bar\rho}{\rho_c}</math>
<math>~0</math>	<math>~1</math>	<math>~1/3</math>	<math>~1</math>	<math>~1</math>
<math>~1</math>	<math>~3.30</math>	<math>~0.38331</math>	<math>~1.892</math>	<math>~0.997</math>
<math>~1.5</math>	<math>~5.99</math>	<math>~0.37640</math>	<math>~2.712</math>	<math>~1.002</math>
<math>~2</math>	<math>~11.4</math>	<math>~0.35087</math>	<math>~4.00</math>	<math>~1.000</math>
<math>~3</math>	<math>~54.2</math>	<math>~0.22774</math>	<math>~9.261</math>	<math>~1.000</math>
<math>~3.5</math>	<math>~153</math>	<math>~0.12404</math>	<math>~12.69</math>	<math>~1.003</math>
<math>~4.0</math>	<math>~632</math>	<math>~0.04056</math>	<math>~15.38</math>	<math>~1.000</math>

Numerical Integration from the Center, Outward

Here we show how a relatively simple, finite-difference algorithm can be developed to numerically integrate the governing LAWE from the center of a polytropic configuration, outward to its surface.

Drawing from our above discussion, the LAWE for any polytrope of index, <math>~n</math>, may be written as,

<math>~0 </math>	<math>~=</math>	<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4 - (n+1)V(\xi)}{\xi} \biggr] \frac{dx}{d\xi} + \biggl[\omega^2 \biggl(\frac{a_n^2 \rho_c }{\gamma_g P_c} \biggr) \frac{\theta_c}{\theta} - \biggl(3-\frac{4}{\gamma_g}\biggr) \cdot \frac{(n+1)V(x)}{\xi^2} \biggr] x </math>
	<math>~=</math>	<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - \frac{(n+1)}{\theta} \biggl(- \frac{d\theta}{d\xi} \biggr)\biggr] \frac{dx}{d\xi} + \frac{(n+1)}{\theta} \biggl[ \frac{\sigma_c^2}{6\gamma_g} - \frac{\alpha}{\xi } \biggl(- \frac{d\theta}{d\xi} \biggr) \biggr] x </math>

where,

<math>~\sigma_c^2</math>

<math>~\equiv</math>

<math>~\frac{3\omega^2}{2\pi G\rho_c} \, .</math>

Following a parallel discussion, we begin by multiplying the LAWE through by <math>~\theta</math>, obtaining a 2^nd-order ODE that is relevant at every individual coordinate location, <math>~\xi_i</math>, namely,

<math>~\theta_i {x_i}</math>

<math>~- \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \frac{x_i'}{\xi_i} - (n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} - \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] x_i </math>

Now, using the general finite-difference approach described separately, we make the substitutions,

<math>~\approx</math>

<math>~ \frac{x_+ - x_-}{2 \Delta_\xi} \, ; </math>

and,

<math>~\approx</math>

<math>~\frac{x_+ - 2x_i + x_-}{\Delta_\xi^2} \, ,</math>

which will provide an approximate expression for <math>~x_+ \equiv x_{i+1}</math>, given the values of <math>~x_- \equiv x_{i-1}</math> and <math>~x_i</math>. Specifically, if the center of the configuration is denoted by the grid index, <math>~i=1</math>, then for zones, <math>~i = 3 \rightarrow N</math>,

<math>~\theta_i \biggl[ \frac{x_+ - 2x_i + x_-}{\Delta_\xi^2} \biggr]</math>	<math>~=</math>	<math>~- \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \biggl[ \frac{x_+ - x_-}{2 \xi_i \Delta_\xi} \biggr] - (n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} - \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] x_i </math>
<math>~\Rightarrow ~~~ \theta_i \biggl[ \frac{x_+ }{\Delta_\xi^2} \biggr] + \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \biggl[ \frac{x_+ }{2 \xi_i\Delta_\xi} \biggr]</math>	<math>~=</math>	<math>~ -\theta_i \biggl[ \frac{- 2x_i + x_-}{\Delta_\xi^2} \biggr] - \biggl[4\theta_i - (n+1)\xi_i (- \theta^')_i\biggr] \biggl[ \frac{- x_-}{2 \xi_i \Delta_\xi} \biggr] - (n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} - \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] x_i </math>
<math>~\Rightarrow ~~~ x_+ \biggl[2\theta_i +\frac{4\Delta_\xi \theta_i}{\xi_i} - \Delta_\xi (n+1)(- \theta^')_i\biggr] </math>	<math>~=</math>	<math>~ x_- \biggl[\frac{4\Delta_\xi \theta_i}{\xi_i} - \Delta_\xi (n+1)(- \theta^')_i - 2\theta_i\biggr] + x_i\biggl\{4\theta_i - 2\Delta_\xi^2(n+1)\biggl[ \frac{\sigma_c^2}{6\gamma_g} - \frac{\alpha}{\xi_i } (- \theta^')_i\biggr] \biggr\} </math>
	<math>~=</math>	<math>~ x_- \biggl[\frac{4\Delta_\xi \theta_i}{\xi_i} - \Delta_\xi (n+1)(- \theta^')_i - 2\theta_i\biggr] + x_i\biggl\{4\theta_i - \frac{\Delta_\xi^2(n+1)}{3}\biggl[ \frac{\sigma_c^2}{\gamma_g} - 2\alpha \biggl(- \frac{3\theta^'}{\xi}\biggr)_i\biggr] \biggr\} \, .</math>

In order to kick-start the integration, we will set the displacement function value to <math>~x_1 = 1</math> at the center of the configuration <math>~(\xi_1 = 0)</math>, then we will draw on the derived power-series expression to determine the value of the displacement function at the first radial grid line, <math>~\xi_2 = \Delta_\xi</math>, away from the center. Specifically, we will set,

<math>~ x_1 \biggl[ 1 - \frac{(n+1) \mathfrak{F} \Delta_\xi^2}{60} \biggr] \, ,</math>

where,

<math>~ \mathfrak{F} </math>

<math>~\equiv</math>

<math>~ \biggl[ \frac{\sigma_c^2}{\gamma_g} - 2\alpha\biggr]\, .</math>

Related Discussions

Radial Oscillations of Uniform-density sphere
Radial Oscillations of Isolated Polytropes
- Setup
- n = 1: Attempt at Formulating an Analytic Solution
- n = 3: Numerical Solution to compare with M. Schwarzschild (1941)
- n = 5: Attempt at Formulating an Analytic Solution

In an accompanying Chapter within our "Ramblings" Appendix, we have played with the adiabatic wave equation for polytropes, examining its form when the primary perturbation variable is an enthalpy-like quantity, rather than the radial displacement of a spherical mass shell. This was done in an effort to mimic the approach that has been taken in studies of the stability of Papaloizou-Pringle tori.

<math>~n=3</math> … M. Schwarzschild (1941, ApJ, 94, 245), Overtone Pulsations of the Standard Model: This work is referenced in §38.3 of [KW94]. It contains an analysis of the radial modes of oscillation of <math>~n=3</math> polytropes, assuming various values of the adiabatic exponent.

<math>~n=2</math> … C. Prasad & H. S. Gurm (1961, MNRAS, 122, 409), Radial Pulsations of the Polytrope, n = 2

<math>~n=\tfrac{3}{2}</math> … D. Lucas (1953, Bul. Soc. Roy. Sci. Liege, 25, 585) … Citation obtained from the Prasad & Gurm (1961) article.

<math>~n=1</math> … L. D. Chatterji (1951, Proc. Nat. Inst. Sci. [India], 17, 467) … Citation obtained from the Prasad & Gurm (1961) article.

Composite Polytropes … M. Singh (1968, MNRAS, 140, 235-240), Effect of Central Condensation on the Pulsation Characteristics

Summary of Known Analytic Solutions … R. Stothers (1981, MNRAS, 197, 351-361), Analytic Solutions of the Radial Pulsation Equation for Rotating and Magnetic Star Models

Interesting Composite! … C. Prasad (1948, MNRAS, 108, 414-416), Radial Oscillations of a Particular Stellar Model

User:Tohline/SSC/Stability/Polytropes

Contents

Radial Oscillations of Polytropic Spheres

Groundwork

Adiabatic (Polytropic) Wave Equation

Boundary Conditions

Overview

Tables

Numerical Integration from the Center, Outward

Related Discussions

Navigation menu

Search