User:Tohline/SSC/Stability/n5PolytropeLAWE
Radial Oscillations of n = 5 Polytropic Spheres

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Background
General Form of the LAWE for Spherical Polytropes
In an accompanying discussion, we derived the so-called,
Adiabatic Wave (or Radial Pulsation) Equation
|
<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 </math> |
whose solution gives eigenfunctions that describe various radial modes of oscillation in spherically symmetric, self-gravitating fluid configurations. Because this widely used form of the radial pulsation equation is not dimensionless but, rather, has units of inverse length-squared, we have found it useful to also recast it in the following dimensionless form:
<math>
\frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0} - \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_0}{P_c}\biggr)^{-1} \biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_0}{P_c}\biggr)^{-1} \biggl(\frac{1}{\gamma_\mathrm{g}} \biggr)\biggl[\tau_\mathrm{SSC}^2 \omega^2 + (4 - 3\gamma_\mathrm{g})\biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \frac{1}{\chi_0} \biggr] x = 0 ,
</math>
where,
<math>~g_\mathrm{SSC} \equiv \frac{P_c}{R\rho_c} \, ,</math> and <math>~\tau_\mathrm{SSC} \equiv \biggl[\frac{R^2 \rho_c}{P_c}\biggr]^{1/2} \, .</math>
In a separate discussion, we showed that specifically for isolated, polytropic configurations, this linear adiabatic wave equation (LAWE) can be rewritten as,
|
<math>~0 </math> |
<math>~=</math> |
<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4 - (n+1)V(\xi)}{\xi} \biggr] \frac{dx}{d\xi} + \biggl[\frac{\omega^2}{\gamma_g \theta} \biggl(\frac{n+1 }{4\pi G \rho_c} \biggr) - \biggl(3-\frac{4}{\gamma_g}\biggr) \cdot \frac{(n+1)V(x)}{\xi^2} \biggr] x </math> |
|
|
<math>~=</math> |
<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - \frac{(n+1)}{\theta} \biggl(- \frac{d\theta}{d\xi}\biggr)\biggr] \frac{dx}{d\xi} + \frac{(n+1)}{\theta}\biggl[\frac{\sigma_c^2}{6\gamma_g } - \frac{\alpha}{\xi} \biggl(- \frac{d\theta}{d\xi}\biggr)\biggr] x \, ,</math> |
where we have adopted the dimensionless frequency notation,
|
<math>~\sigma_c^2</math> |
<math>~\equiv</math> |
<math>~\frac{3\omega^2}{2\pi G \rho_c} \, .</math> |
Specifically for n=5 Configurations
Here we focus on an analysis of the specific case of isolated, <math>~n=5</math> polytropic configurations, whose unperturbed equilibrium structure can be prescribed in terms of analytic functions. Our hope — as yet unfulfilled — is that we can discover an analytically prescribed eigenvector solution to the governing LAWE.
From our discussion of the equilibrium structure of isolated, <math>~n=5</math> polytropes, we know that,
|
<math>~\theta</math> |
<math>~=</math> |
<math>~\biggl( 1 + \frac{\xi^2}{3} \biggr)^{-1/2} =3^{1/2} ( 3 + \xi^2 )^{-1/2}\, .</math> |
Hence, we know as well that,
|
<math>~\frac{d\theta}{d\xi}</math> |
<math>~=</math> |
<math>~- \frac{\xi}{3}\biggl( 1 + \frac{\xi^2}{3} \biggr)^{-3/2} = - 3^{1/2}\xi ( 3 + \xi^2 )^{-3/2} \, .</math> |
The LAWE therefore becomes,
|
<math>~0 </math> |
<math>~=</math> |
<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - \frac{(n+1)}{\theta} \biggl(- \frac{d\theta}{d\xi}\biggr)\biggr] \frac{dx}{d\xi} + \frac{(n+1)}{\theta}\biggl[\frac{\sigma_c^2}{6\gamma_g } - \frac{\alpha}{\xi} \biggl(- \frac{d\theta}{d\xi}\biggr)\biggr] x </math> |
|
|
<math>~=</math> |
<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - \frac{6}{\theta} \biggl(- \frac{d\theta}{d\xi}\biggr)\biggr] \frac{dx}{d\xi} + \biggl[\frac{\sigma_c^2}{\gamma_g } \cdot \frac{1}{\theta} - \frac{6\alpha}{\xi} \cdot \frac{1}{\theta} \biggl(- \frac{d\theta}{d\xi}\biggr)\biggr] x</math> |
|
|
<math>~=</math> |
<math>~\frac{d^2x}{d\xi^2} + \biggl[4 - \frac{6\xi^2}{(3+\xi^2)} \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[\frac{\sigma_c^2}{3^{1/2} \gamma_g } \cdot (3+\xi^2)^{1/2} - \frac{6\alpha}{(3+\xi^2)}\biggr)\biggr] x \, .</math> |
Or,
| LAWE for <math>~n=5</math> Polytropes | |||
|---|---|---|---|
|
Numerical Integration of LAWE
By numerically integrating the above LAWE using the algorithm outlined in a separate chapter, we have examined the properties of the displacement function that describes radial modes of oscillation in pressure-truncated, n = 5, polytropic configurations. Our brief description, here, of these modes parallels the more detailed description of radial oscillation modes in truncated isothermal spheres that has been presented in a separate chapter.
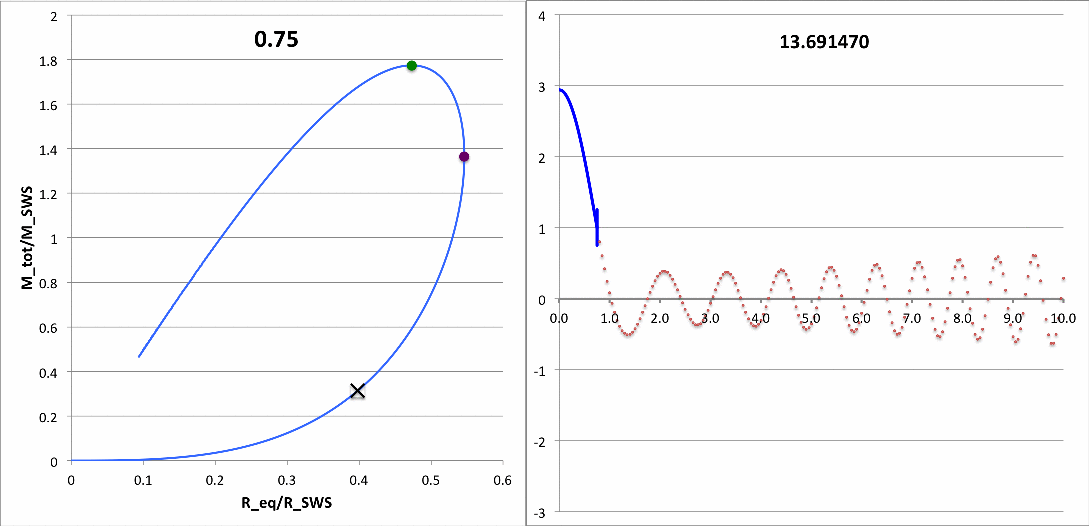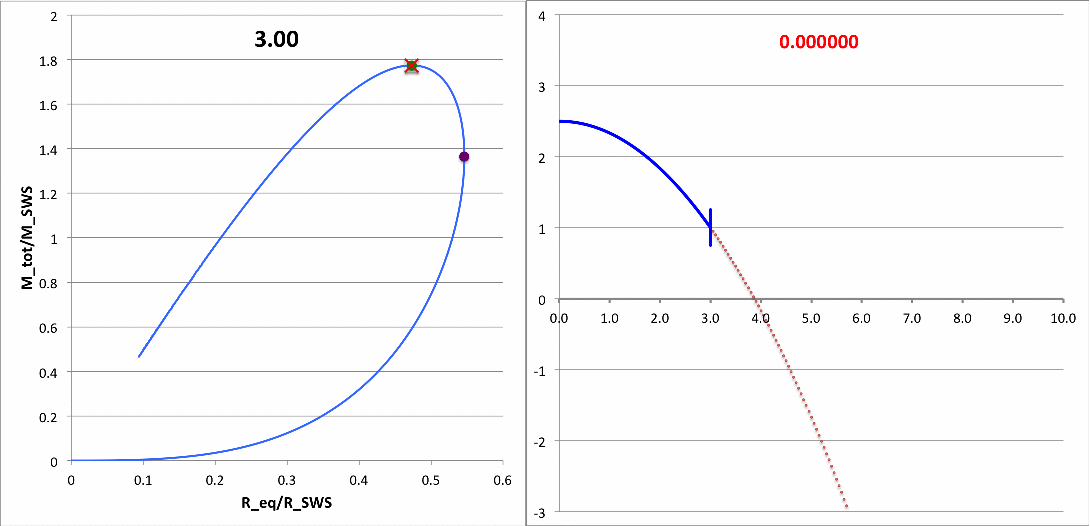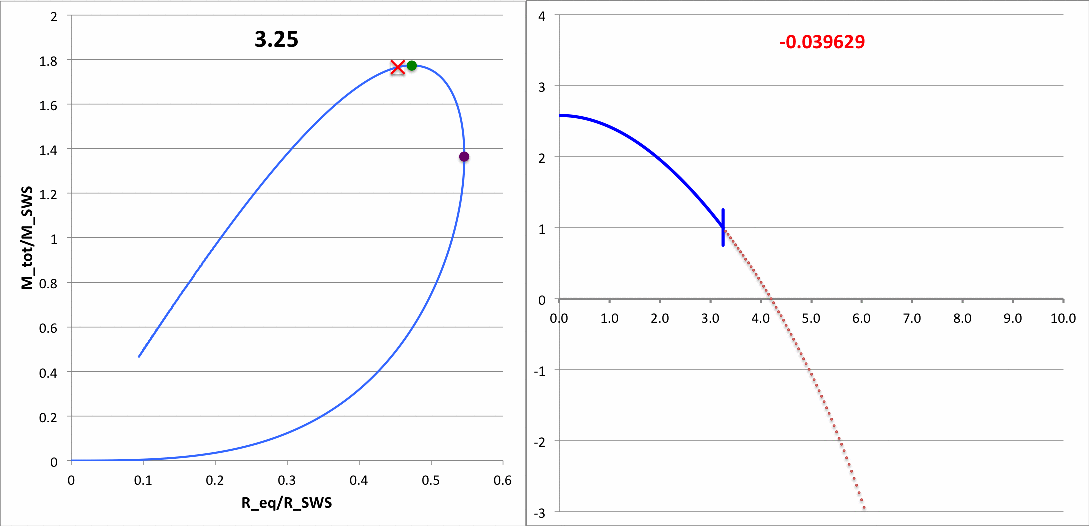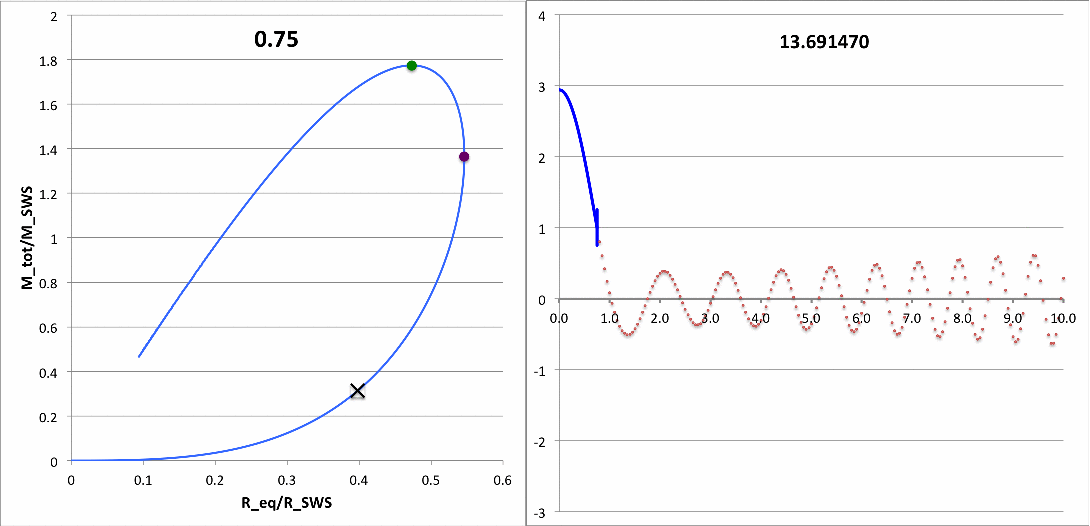
The animation sequence that appears in the right panel of Composite Display 1 shows how our numerically derived displacement function, <math>~x(\xi)</math>, varies with radius — from the center of the n=5 polytropic sphere, out to <math>~\xi = 10</math> — for sixteen different values of the square of the eigenfrequency, <math>~\sigma_c^2</math>, as denoted at the top of each animation frame. The segment of the <math>~x(\xi)</math> curve that has been drawn in blue identifies the eigenfunction that corresponds to the specified value of the eigenfrequency. In each frame, the radial location at which the blue segment terminates simultaneously identifies: (a) the radius at which the logarithmic derivative of the displacement function, <math>~d\ln x/d\ln\xi </math>, is negative three; and (b) the radius, <math>~\tilde\xi</math>, at which the n = 5 polytropic configuration has been truncated. As displayed here, in every frame, the <math>~x(\xi)</math> function has been normalized such that the displacement amplitude is unity at the truncated configuration's surface.
The left panel of Composite Display 1 is also animated and has been provided in support of the animation on the right. Specifically, the number written at the top of each left-panel frame quantitatively identifies the radial location, <math>~\tilde\xi</math>, of the surface of the relevant truncated polytropic configuration; and, on each frame, "×" marks the location of that truncated configuration on the mass-radius equilibrium sequence.
Each full loop through the left-panel animation sequence can be viewed as evolution along the equilibrium sequence from <math>~\tilde\xi = 0.75</math> to <math>~\tilde\xi = 5</math>, then back again. During this evolution, the "×" marker moves through both turning points along the sequence: the maximum radius configuration — at <math>~\tilde\xi= \sqrt{3}</math> — and the maximum mass configuration — at <math>~\tilde\xi= 3</math>. Notice that <math>~\sigma_c^2</math> is positive for all models having <math>~\tilde\xi < 3</math> while it is negative for all models having <math>~\tilde\xi > 3</math>. Hence, models having <math>~\tilde\xi > 3</math> are dynamically unstable and, as best we have been able to determine via these numerical integrations, the transition from stable to unstable models — that is, the marginally unstable model — occurs at <math>~\tilde\xi = 3</math>. (Via an analytic analysis, we prove, below, that this association is precise.) For emphasis, the "×" marker (left panel) and the numerical value recorded for <math>~\sigma_c^2</math> (right panel) have been colored red for models that are not stable.
Search for Analytic Solutions to the LAWE
Eureka Moment
Note from J. E. Tohline on 3/6/2017: Yesterday evening, after I finished putting together the above animation sequence using an Excel workbook, I noticed that the eigenfunction of the fundamental mode for the marginally unstable model <math>~(\sigma_c^2 = 0)</math> resembles a parabola. In an effort to see how well a parabola fits at least the central portion of this eigenfunction, I returned to my Excel spreedsheet and, in a brute-force manner, began to search for the pair of coefficients that would provide a best fit. What I discovered was that a parabola with the following formula fits perfectly!
| Fundamental Mode Eigenfunction when <math>~\sigma_c^2 = 0</math> and <math>~\gamma = 6/5 ~\Rightarrow~\alpha=- 1/3</math> |
|---|
|
<math>~x = x_0 \biggl[ 1 - \frac{\xi^2}{15} \biggr]</math> |
For the specific normalization used in the above animation sequence, <math>~x_0 = \tfrac{5}{2}</math>. Let's demonstrate that this eigenvector provides a solution to the LAWE for <math>~n=5</math> polytropes; for simplicity, we will set <math>~x_0 = 1</math>:
|
<math>~\frac{dx}{d\xi} = -\frac{2\xi}{15} \, ;</math> |
and |
<math>~\frac{d^2x}{d\xi^2} = -\frac{2}{15} \, .</math> |
|
<math>~\Rightarrow ~~~ (3+\xi^2) \frac{d^2x}{d\xi^2} + \biggl[12 - 2\xi^2 \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + \biggl[ \cancelto{0}{\frac{\sigma_c^2}{3^{1/2} \gamma_g }} \cdot (3+\xi^2)^{3/2} + 2\biggr] x </math> |
<math>~=</math> |
<math>~ -\frac{2}{15}(3+\xi^2) -\frac{2}{15} \biggl[12 - 2\xi^2 \biggr] + 2\biggl[1 - \frac{\xi^2}{15}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl( - \frac{6}{15} - \frac{24}{15} + 2\biggr) +\xi^2 \biggl( -\frac{2}{15} + \frac{4}{15} - \frac{2}{15} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ 0 \, . </math> |
Q. E. D. I don't think that anyone has previously appreciated that the LAWE in this case admits to an analytic eigenvector solution.
Now, let's see how the boundary condition comes into play. We see that the logarithmic derivative of the parabolic eigenfunction is,
|
<math>~\frac{d\ln x}{d\ln \xi}</math> |
<math>~=</math> |
<math>~\frac{\xi}{x} \cdot \frac{dx}{d\xi}</math> |
|
|
<math>~=</math> |
<math>~- \frac{2\xi^2}{15} \biggl[ 1 - \frac{\xi^2}{15}\biggr]^{-1}</math> |
|
|
<math>~=</math> |
<math>~- \frac{2\xi^2}{(15-\xi^2)} \, .</math> |
We desire a surface boundary condition that gives, <math>~d\ln x/d\ln\xi = -3</math>. This will only happen when,
|
<math>~- \frac{2\xi^2}{(15-\xi^2)}</math> |
<math>~=</math> |
<math>~-3</math> |
|
<math>~\Rightarrow ~~~2\xi^2</math> |
<math>~=</math> |
<math>~3(15 - \xi^2)</math> |
|
<math>~\Rightarrow ~~~\xi</math> |
<math>~=</math> |
<math>~3 \, .</math> |
Hence, although the parabolic eigenfunction provides an accurate solution to the <math>~n=5</math> LAWE throughout the entire configuration — that is, for all <math>~\xi</math> — the desired surface boundary condition will only be satisfied if the polytrope is truncated at <math>~\xi_\mathrm{surf} = 3</math>. The parabolic eigenfunction is therefore only physically relevant to the model that sits at the point along the equilibrium sequence that is associated with the <math>~P_\mathrm{max}</math> turning point.
Let's express the parabolic displacement function, <math>~x</math>, as a function of the Lagrangian mass coordinate, instead of as a function of <math>~\xi</math>. Drawing upon our accompanying discussion where we have used <math>~\tilde\xi</math> to denote the truncation edge, we know that,
|
<math>~r_\xi(\xi)</math> |
<math>~=</math> |
<math>~\xi \biggl\{ \biggl[ \frac{4\pi}{2^5\cdot 3}\biggr]^{1/2} \tilde\xi^{-6} \biggl( 1+\frac{\tilde\xi^2}{3} \biggr)^{3}\biggr\} \, . </math> |
and that,
|
<math>~ r_\xi (m_\xi) </math> |
<math>~=</math> |
<math>~\tilde{r}_\mathrm{edge} \biggl[\frac{3^2m_\xi^{2/3}}{\tilde{C} - 3 m_\xi^{2/3}}\biggr]^{1/2} \, , </math> |
where,
|
<math>~\tilde{C}</math> |
<math>~\equiv</math> |
<math>~ \frac{3^2}{\tilde\xi^2}\biggl( 1 + \frac{\tilde\xi^2}{3} \biggr) \, . </math> |
|
<math>~\tilde{r}_\mathrm{edge}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{\pi}{2^3\cdot 3}\biggr]^{1/2} {\tilde\xi}^{-6} \biggl(1+\frac{\tilde\xi^2}{3}\biggr)^3 \, . </math> |
By equating <math>~r_\xi(\xi)</math> with <math>~r_\xi(m_\xi)</math>, we find,
|
<math>~\xi \biggl\{ \biggl[ \frac{4\pi}{2^5\cdot 3}\biggr]^{1/2} \tilde\xi^{-6} \biggl( 1+\frac{\tilde\xi^2}{3} \biggr)^{3}\biggr\} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{\pi}{2^3\cdot 3}\biggr]^{1/2} {\tilde\xi}^{-6} \biggl(1+\frac{\tilde\xi^2}{3}\biggr)^3 \biggl[\frac{3^2m_\xi^{2/3}}{\tilde{C} - 3 m_\xi^{2/3}}\biggr]^{1/2} </math> |
|
<math>~\Rightarrow ~~~ \xi </math> |
<math>~=</math> |
<math>~ \biggl[\frac{3^2m_\xi^{2/3}}{\tilde{C} - 3 m_\xi^{2/3}}\biggr]^{1/2} \, . </math> |
This means that,
|
<math>~x</math> |
<math>~=</math> |
<math>~ x_0 \biggl\{1 - \frac{1}{15} \biggl[\frac{3^2m_\xi^{2/3}}{\tilde{C} - 3 m_\xi^{2/3}}\biggr] \biggr\} \, ; </math> |
and, specifically for the critical case of <math>~\tilde\xi = 3</math>, in which case, <math>~\tilde{C} = 4</math>,
|
<math>~x</math> |
<math>~=</math> |
<math>~ x_0 \biggl\{1 - \frac{1}{15} \biggl[\frac{3^2m_\xi^{2/3}}{4 - 3 m_\xi^{2/3}}\biggr] \biggr\} \, . </math> |
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Setup Using Lagrangian Radial Coordinate
Individual Terms
From our accompanying discussion, we have, for pressure-truncated, <math>~n=5</math> polytropic spheres
|
<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{norm}} </math> |
<math>~=~</math> |
<math>~\biggl[ \frac{4\pi}{(n+1)^n}\biggr]^{1/(n-3)} \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} </math> |
|
|
<math>~=~</math> |
<math>~\biggl[ \frac{4\pi}{2^5\cdot 3^5}\biggr]^{1/2} \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{-2} \, , </math> |
which matches the expression derived in an ASIDE box found with our introduction of the Lane-Emden equation, and
|
<math> ~\frac{P_\mathrm{e}}{P_\mathrm{norm}} </math> |
<math>~=~</math> |
<math>~\biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{(n+1)/(n-3)} \tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} </math> |
|
|
<math>~=~</math> |
<math>~\biggl[ \frac{2^3\cdot 3^3}{4\pi}\biggr]^{3} \tilde\theta^{6}( -\tilde\xi^2 \tilde\theta' )^{6} \, , </math> |
where,
|
<math>~R_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} \biggr]^{1/(n-3)} = \biggl( \frac{G}{K} \biggr)^{5/2} M_\mathrm{tot}^{2} \, ,</math> |
|
<math>~P_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}} \biggr]^{1/(n-3)} = \frac{K^{10}}{G^{9} M_\mathrm{tot}^{6} } \, ,</math> |
and, from our more detailed analysis,
|
<math> ~{\tilde\theta}_5 = 3^{1 / 2} \biggl( 3 + {\tilde\xi}^2\biggr)^{-1/2} </math> |
and |
<math> ~\biggl(- {\tilde\xi}^2 {\tilde\theta}^'_5\biggr) = 3^{1 / 2} {\tilde\xi}^3 \biggl( 3 + {\tilde\xi}^2\biggr)^{-3/2} \, . </math> |
Hence,
|
<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{norm}} </math> |
<math>~=~</math> |
<math>~\biggl[ \frac{4\pi}{2^5\cdot 3^5}\biggr]^{1/2} \tilde\xi \biggl[ 3^{1 / 2} {\tilde\xi}^3 \biggl( 3 + {\tilde\xi}^2\biggr)^{-3/2} \biggr]^{-2} </math> |
|
|
<math>~=~</math> |
<math>~\biggl[ \frac{4\pi}{2^5\cdot 3^5}\biggr]^{1/2} \tilde\xi \biggl[ 3^{-1} {\tilde\xi}^{-6} \biggl( 3 + {\tilde\xi}^2\biggr)^{3} \biggr] </math> |
|
|
<math>~=~</math> |
<math>~ \biggl[ \frac{4\pi}{2^5\cdot 3^7}\biggr]^{1/2} {\tilde\xi}^{-5} \biggl( 3 + {\tilde\xi}^2\biggr)^{3} \, ,
</math> |
|
<math> ~\frac{P_\mathrm{e}}{P_\mathrm{norm}} </math> |
<math>~=~</math> |
<math>~\biggl[ \frac{2^3\cdot 3^3}{4\pi}\biggr]^{3} \biggl[ 3^{1 / 2} \biggl( 3 + {\tilde\xi}^2\biggr)^{-1/2} \biggr]^{6} \biggl[ 3^{1 / 2} {\tilde\xi}^3 \biggl( 3 + {\tilde\xi}^2\biggr)^{-3/2} \biggr]^{6} </math> |
|
|
<math>~=~</math> |
<math>~\biggl[ \frac{2^3\cdot 3^3}{4\pi}\biggr]^{3} \biggl[ 3^{3} \biggl( 3 + {\tilde\xi}^2\biggr)^{-3} \biggr] \biggl[ 3^{3} {\tilde\xi}^{18} \biggl( 3 + {\tilde\xi}^2\biggr)^{-9} \biggr] </math> |
|
|
<math>~=~</math> |
<math>~\biggl[ \frac{2^3\cdot 3^5}{4\pi}\biggr]^{3} {\tilde\xi}^{18} \biggl( 3 + {\tilde\xi}^2\biggr)^{-12} \, . </math> |
Now, given that the structural form-factors for <math>~n=5</math> configurations are,
|
<math>~\mathfrak{f}_M</math> |
<math>~=</math> |
<math>~ ( 1 + \ell^2 )^{-3/2} = 3^{3 / 2} (3 + {\tilde\xi}^2)^{-3 / 2} </math> |
|
<math>~\mathfrak{f}_W</math> |
<math>~=</math> |
<math>~ \frac{5}{2^4} \cdot \ell^{-5} \biggl[ \ell \biggl( \ell^4 - \frac{8}{3}\ell^2 - 1 \biggr)(1 + \ell^2)^{-3} + \tan^{-1}(\ell ) \biggr] </math> |
|
<math>~\mathfrak{f}_A</math> |
<math>~=</math> |
<math>~ \frac{3}{2^3} \ell^{-3} [ \tan^{-1}(\ell ) + \ell (\ell^2-1) (1+\ell^2)^{-2} ] \, , </math> |
we understand that the central density is,
|
<math>~\rho_c = \frac{\bar\rho}{ {\tilde\mathfrak{f}}_M }</math> |
<math>~=</math> |
<math>~ \biggl[3^{3 / 2} (3 + {\tilde\xi}^2)^{-3 / 2} \biggr]^{-1} \biggl[ \frac{3 M_\mathrm{tot}}{4 \pi R_\mathrm{eq}^3} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{3}{4\pi}\biggr) \biggl[ \frac{2^5\cdot 3^6}{4\pi}\biggr]^{ 3 / 2} (3 + {\tilde\xi}^2)^{3 / 2} M_\mathrm{tot} \biggl[ R_\mathrm{norm} {\tilde\xi}^{-5} \biggl( 3 + {\tilde\xi}^2\biggr)^{3} \biggr]^{-3}
</math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{2^{5}\cdot 3^{20}}{\pi^5}\biggr]^{ 1 / 2} {\tilde\xi}^{15} (3 + {\tilde\xi}^2)^{-15 / 2} M_\mathrm{tot} R^{-3}_\mathrm{norm} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{2^{5}\cdot 3^{20}}{\pi^5}\biggr]^{ 1 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} M_\mathrm{tot}^{-5} \biggl( \frac{G}{K} \biggr)^{-15/2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{2\cdot 3^{4}}{\pi}\biggr]^{ 5 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2} \, . </math> |
Now let's derive the prescription for the Lagrangian radial coordinate in the context of pressure-truncated, <math>~n=5</math> polytropes.
|
<math>~r_0 \equiv a_5 \xi</math> |
<math>~=</math> |
<math>~\biggl[\frac{3K}{2\pi G} \biggr]^{1 / 2} \rho_c^{-2/5} \xi</math> |
|
|
<math>~=</math> |
<math>~\biggl[\frac{3K}{2\pi G} \biggr]^{1 / 2} \xi \biggl\{ \biggl[ \frac{2\cdot 3^{4}}{\pi}\biggr]^{ 5 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2} \biggr\}^{-2/5} </math> |
|
|
<math>~=</math> |
<math>~\biggl[\frac{3K}{2\pi G} \biggr]^{1 / 2} \biggl[ \frac{\pi}{2\cdot 3^{4}}\biggr] \biggl( \frac{G^3M_\mathrm{tot}^2}{K^3} \biggr) \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi </math> |
|
|
<math>~=</math> |
<math>~ R_\mathrm{norm} \biggl[ \frac{\pi}{2^3\cdot 3^{7}}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi </math> |
Also,
|
<math>~m_0 \equiv M(r_0)</math> |
<math>~=</math> |
<math>~\biggl[ 4\pi a_n^3 \rho_c \biggl(-\xi^2 \frac{d\theta}{d\xi}\biggr) \biggr] \, ,</math> |
|
|
<math>~=</math> |
<math>~2^2\pi \biggl\{ R_\mathrm{norm} \biggl[ \frac{\pi}{2^3\cdot 3^{7}}\biggr]^{1 / 2} \tilde\xi^{-6} (3 + {\tilde\xi}^2)^{3} \biggr\}^3 \biggl\{ \biggl[ \frac{2\cdot 3^{4}}{\pi}\biggr]^{ 5 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2} \biggr\} \biggl\{ 3^{1 / 2} \xi^3 \biggl( 3 + \xi^2\biggr)^{-3/2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 3^{1 / 2} \biggl[ 2^4 \pi^2\biggr]^{1 / 2} \biggl[ \frac{\pi^3}{2^9\cdot 3^{21}}\biggr]^{1 / 2} \biggl[ \frac{2^5\cdot 3^{20}}{\pi^5}\biggr]^{ 1 / 2} \biggl\{ \tilde\xi^{-6} (3 + {\tilde\xi}^2)^{3} \biggr\}^3 \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2} R_\mathrm{norm}^3 \biggl\{ \xi^3 ( 3 + \xi^2 )^{-3/2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \tilde\xi^{-3} (3 + {\tilde\xi}^2)^{3 / 2} \biggr\} M_\mathrm{tot} \biggl\{ \xi^3 ( 3 + \xi^2 )^{-3/2} \biggr\} \, . </math> |
Hence,
|
<math>~g_0 = \frac{Gm_0}{r_0^2}</math> |
<math>~=</math> |
<math>~ \frac{GM_\mathrm{tot}}{R_\mathrm{norm}^2} \biggl\{ \tilde\xi^{-3} (3 + {\tilde\xi}^2)^{3 / 2} \biggr\} \biggl\{ \xi^3 ( 3 + \xi^2 )^{-3/2} \biggr\} \biggl\{ \biggl[ \frac{\pi}{2^3\cdot 3^{7}}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi \biggr\}^{-2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{GM_\mathrm{tot}}{R_\mathrm{norm}^2}\biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr] \biggl[ \tilde\xi (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{9} \xi ( 3 + \xi^2 )^{-3/2} \, ; </math> |
|
<math>~\frac{g_0 }{r_0} </math> |
<math>~=</math> |
<math>~ \frac{GM_\mathrm{tot}}{R_\mathrm{norm}^3}\biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr] \biggl\{ \tilde\xi^{9} (3 + {\tilde\xi}^2)^{-9 / 2} \biggr\} \biggl\{ \biggl[ \frac{\pi}{2^3\cdot 3^{7}}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi \biggr\}^{-1} \xi ( 3 + \xi^2 )^{-3/2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{GM_\mathrm{tot}}{R_\mathrm{norm}^3}\biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr]^{3/2} \biggl[ \tilde\xi (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} ( 3 + \xi^2 )^{-3/2} \, ; </math> |
|
<math>~\frac{\rho_0}{P_0} = \frac{\rho_0}{K\rho_0^{1+1/n}} </math> |
<math>~=</math> |
<math>~ \biggl[K^5 \rho_c \theta^5 \biggr]^{-1/5} </math> |
|
|
<math>~=</math> |
<math>~ \theta^{-1} \biggl\{ K^5 \biggl[ \frac{2\cdot 3^{4}}{\pi}\biggr]^{ 5 / 2} \biggl[{\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{15} \biggl( \frac{K^3}{G^3M_\mathrm{tot}^2} \biggr)^{5/2}\biggr\}^{-1/5} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ 3^{-1} ( 3 + \xi^2 ) \biggr]^{1/2} \biggl\{ \biggl[ \frac{\pi}{2\cdot 3^{4}}\biggr]^{1 / 2} \cancelto{\mathrm{mistake}}{\biggl[{\tilde\xi}^{-3} (3 + {\tilde\xi}^2)^{3 / 2} \biggr]^{-3} } \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1/2}\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1 / 2} \biggl[ \frac{\pi}{2\cdot 3^{5}}\biggr]^{1 / 2} \cancelto{\mathrm{mistake}}{\biggl[ {\tilde\xi} (3 + {\tilde\xi}^2)^{-1 / 2} \biggr]^{9} } ( 3 + \xi^2 )^{1 / 2} \, ; </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ 3^{-1} ( 3 + \xi^2 ) \biggr]^{1/2} \biggl\{ \biggl[ \frac{\pi}{2\cdot 3^{4}}\biggr]^{1 / 2} \biggl[{\tilde\xi}^{-3} (3 + {\tilde\xi}^2)^{3 / 2} \biggr] \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1/2}\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1/2}\biggl[ \frac{\pi}{2\cdot 3^{5}}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{{\tilde\xi}^2 } \biggr]^{3 / 2} ( 3 + \xi^2 )^{1/2} </math> |
|
<math>~\frac{g_0\rho_0}{P_0} </math> |
<math>~=</math> |
<math>~ \biggl( \frac{G^3M_\mathrm{tot}^2}{K^5} \biggr)^{1/2}\biggl[ \frac{\pi}{2\cdot 3^{5}}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{{\tilde\xi}^2 } \biggr]^{3 / 2} ( 3 + \xi^2 )^{1/2} </math> |
|
|
|
<math>~ \times ~ \biggl( \frac{G^2M_\mathrm{tot}^2}{R_\mathrm{norm}^4} \biggr)^{1 / 2}\biggl[ \frac{2^6\cdot 3^{14}}{\pi^2}\biggr]^{1 / 2} \biggl[ \frac{(3 + {\tilde\xi}^2)}{{\tilde\xi}^2 } \biggr]^{-9 / 2} \xi ( 3 + \xi^2 )^{-3/2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{G^5 M_\mathrm{tot}^4}{K^5} \biggr)^{1 / 2} R_\mathrm{norm}^{-2} \biggl[ \frac{{\tilde\xi}^2 }{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[ \frac{2^5\cdot 3^{9}}{\pi}\biggr]^{1 / 2} \xi ( 3 + \xi^2 )^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{K^5}{G^5 M_\mathrm{tot}^4} \biggr)^{1 / 2} \biggl[ \frac{{\tilde\xi}^2 }{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[ \frac{2^5\cdot 3^{9}}{\pi}\biggr]^{1 / 2} \xi ( 3 + \xi^2 )^{-1} \, . </math> |
The Wave Equation
Starting from our Key Adiabatic Wave Equation
The adiabatic wave equation therefore becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x </math> |
|
|
<math>~=</math> |
<math>~ \frac{d^2x}{dr_0^2} + \frac{1}{R_\mathrm{norm}} \biggl\{ \biggl[ \frac{2^7\cdot 3^{7}}{\pi} \biggr]^{1 / 2} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{3} \frac{1}{\xi} - \biggl[ \frac{{\tilde\xi}^2 }{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[ \frac{2^5\cdot 3^{9}}{\pi}\biggr]^{1 / 2} \xi ( 3 + \xi^2 )^{-1} \biggr\} \frac{dx}{dr_0} </math> |
|
|
|
<math>~ + \frac{(4 - 3\gamma_\mathrm{g})}{\gamma_g R_\mathrm{norm}^2} \biggl[ \frac{\pi}{2\cdot 3^{5}}\biggr]^{1 / 2} \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{-3/2} ( 3 + \xi^2 )^{1 / 2} \biggl\{ \frac{R_\mathrm{norm}^3}{GM_\mathrm{tot}} \biggl[\frac{\omega^2}{(4 - 3\gamma_\mathrm{g})} \biggr] + \biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr]^{3/2} \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{15/2} ( 3 + \xi^2 )^{-3/2} \biggr\} x </math> |
|
|
<math>~=</math> |
<math>~ \frac{d^2x}{dr_0^2} + \frac{1}{R_\mathrm{norm}} \biggl[ \frac{2^3\cdot 3^{7}}{\pi} \biggr]^{1 / 2} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[ \frac{4}{\xi} - \frac{6 \xi}{ ( 3 + \xi^2 )} \biggr] \frac{dx}{dr_0} </math> |
|
|
|
<math>~ + \frac{6(4 - 3\gamma_\mathrm{g})}{\gamma_g R_\mathrm{norm}^2} ( 3 + \xi^2 )^{1 / 2} \biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr] \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{6} \biggl\{ \frac{R_\mathrm{norm}^3}{GM_\mathrm{tot}} \biggl[\frac{\omega^2}{(4 - 3\gamma_\mathrm{g})} \biggr] \biggl[ \frac{2^3\cdot 3^{7}}{\pi}\biggr]^{-3/2} \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{-15/2} + ( 3 + \xi^2 )^{-3/2} \biggr\} x </math> |
|
|
<math>~=</math> |
<math>~ \frac{d^2x}{dr_0^2} + \frac{1}{R_*} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{3} \biggl[ \frac{4}{\xi} - \frac{6 \xi}{ ( 3 + \xi^2 )} \biggr] \frac{dx}{dr_0} + \frac{6}{\gamma_g R_*^2} \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{6} \biggl\{ \frac{\omega^2 R_*^3}{GM_\mathrm{tot}} \biggl[ \frac{{\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{-15/2}( 3 + \xi^2 )^{1 / 2} + \frac{(4 - 3\gamma_\mathrm{g})}{( 3 + \xi^2 ) } \biggr\} x </math> |
where,
<math>R_* \equiv R_\mathrm{norm} \biggl[ \frac{\pi}{2^3 \cdot 3^7} \biggr]^{1/2} \, .</math>
Recognizing that,
|
<math>~r_0</math> |
<math>~=</math> |
<math>~ R_* \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi \, , </math> |
we can write,
|
<math>~0</math> |
<math>~=</math> |
<math>~\frac{1}{R_*^2} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)} \biggr]^{6} \biggl\{ \frac{d^2x}{d\xi^2} + \biggl[ \frac{4}{\xi} - \frac{6 \xi}{ ( 3 + \xi^2 )} \biggr] \frac{dx}{d\xi} + \frac{6}{\gamma_g } \biggl[\sigma^2 ( 3 + \xi^2 )^{1 / 2} + \frac{(4 - 3\gamma_\mathrm{g})}{( 3 + \xi^2 ) } \biggr] x \biggr\} \, , </math> |
where,
|
<math>~\sigma^2</math> |
<math>~\equiv</math> |
<math>~ \frac{\omega^2 R_*^3}{GM_\mathrm{tot}} \biggl( \frac{3 + {\tilde\xi}^2}{{\tilde\xi}^2} \biggr)^{15/2} = \frac{\sigma_c^2}{2\cdot 3^{3/2}}\, .</math> |
Finally, if — because we are specifically considering the case of <math>~n=5</math> — we set <math>~\gamma_\mathrm{g} = 1 + 1/n = 6/5</math>, we have,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{d^2x}{d\xi^2} + \biggl[ \frac{4}{\xi} - \frac{6 \xi}{ ( 3 + \xi^2 )} \biggr] \frac{dx}{d\xi} + \biggl[\frac{5\sigma_c^2}{2\cdot 3^{3/2}} ( 3 + \xi^2 )^{1 / 2} + \frac{2}{( 3 + \xi^2 ) }\biggr] x </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{( 3 + \xi^2 ) } \biggl\{ ( 3 + \xi^2 )\frac{d^2x}{d\xi^2} + \biggl[ \frac{2(6 - \xi^2) }{ \xi} \biggr] \frac{dx}{d\xi} + \biggl[\frac{5\sigma_c^2}{2\cdot 3^{3/2}} ( 3 + \xi^2 )^{3 / 2} + 2 \biggr] x \biggr\} \, , </math> |
which matches exactly the form of the LAWE derived above, if in that expression, <math>~\gamma_g</math> is also forced to align with our specification of the polytropic index, that is, if <math>~\gamma_g = (n+1)/n = 6/5</math> and, in turn, <math>~\alpha = (3-4/\gamma) = -1/3</math>.
Starting from the HRW66 Radial Pulsation Equation
More directly, if we begin with the HRW66 radial pulsation equation that is already tuned to polytropic configurations, the wave equation appropriate to <math>~n=5</math> polytropes is,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{d^2 X}{d\xi^2} + \biggl[ \frac{4}{\xi} - \frac{6 (-\theta^'_5)}{\theta_5} \biggr]\frac{d X}{d\xi} + \frac{5(-\theta_5^') }{6\theta_5 \xi} \bigg[ \frac{\xi (s^')^2}{\theta^'_5} + \frac{12}{5} \biggr] X </math> |
|
|
<math>~=</math> |
<math>~ \frac{d^2 X}{d\xi^2} + \biggl[ \frac{4}{\xi} - \frac{6 \xi}{(3 + \xi^2)} \biggr]\frac{d X}{d\xi} + \frac{1}{(3 + \xi^2)} \bigg[ -\frac{5(s^')^2(3 + \xi^2)^{3 / 2}}{2 \cdot 3^{3 / 2}} + 2 \biggr] X </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{(3+\xi^2)} \biggl\{ (3+\xi^2)\frac{d^2 X}{d\xi^2} + \biggl[ \frac{2(6-\xi^2)}{\xi}\biggr]\frac{d X}{d\xi} + \bigg[ -\frac{5(s^')^2}{2 \cdot 3^{3 / 2}} \cdot (3 + \xi^2)^{3 / 2} + 2 \biggr] X \biggr\} \, , </math> |
which is identical to the brute-force derivation just presented, allowing for the mapping,
<math>\sigma^2 ~~ \Leftrightarrow ~~ -\frac{(s^')^2}{2 \cdot 3^{3 / 2}} \, .</math>
Finally, remembering that the HRW66 dimensionless frequency definition is,
|
<math>~(s^')^2</math> |
<math>~=</math> |
<math>~-\omega^2 \biggl[\frac{n+1 }{4\pi G \rho_c} \biggr] \, ,</math> |
we recognize that, specifically for the case of <math>~n=5</math>, we can make the substitution, <math>~(s^')^2 \rightarrow -\sigma_c^2</math>, in which case the LAWE becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~\frac{1}{(3+\xi^2)} \biggl\{ (3+\xi^2)\frac{d^2 X}{d\xi^2} + \biggl[ \frac{2(6-\xi^2)}{\xi}\biggr]\frac{d X}{d\xi} + \bigg[ \frac{5\sigma_c^2}{2 \cdot 3^{3 / 2}} \cdot (3 + \xi^2)^{3 / 2} + 2 \biggr] X \biggr\} \, , </math> |
which matches exactly the form of the LAWE derived above, if in that expression, <math>~\gamma_g</math> is also forced to align with our specification of the polytropic index, that is, if <math>~\gamma_g = (n+1)/n = 6/5</math> and, in turn, <math>~\alpha = (3-4/\gamma) = -1/3</math>.
New Independent Variable
Guided by our conjecture regarding the proper shape of the radial eigenfunction, let's switch the dependent variable to,
|
<math>~u \equiv 1 + \frac{3}{\xi^2}</math> |
<math>~\Rightarrow</math> |
<math>~3 + \xi^2 = \frac{3u}{(u-1)} \, ,</math> |
and |
<math>~\xi = 3^{1 / 2} (u-1)^{-1 / 2} \, .</math> |
This implies that,
|
<math>~\frac{d}{d\xi}</math> |
<math>~~~\rightarrow ~~~</math> |
<math>~-\frac{2}{\sqrt{3}}(u-1)^{3 / 2} \frac{d}{du} \, ,</math> |
and,
|
<math>~\frac{d^2}{d\xi^2}</math> |
<math>~~~\rightarrow ~~~</math> |
<math>~\frac{4}{3}(u-1)^3 \frac{d^2}{du^2} + 2(u-1)^{2} \frac{d}{du} \, .</math> |
Hence, the governing wave equation becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~( 3 + \xi^2 )\frac{d^2x}{d\xi^2} + \biggl[ \frac{2(6 - \xi^2) }{ \xi} \biggr] \frac{dx}{d\xi} + \biggl[5\sigma^2 ( 3 + \xi^2 )^{3 / 2} + 2 \biggr] x </math> |
|
|
<math>~=</math> |
<math>~\frac{3u}{(u-1)} \biggl[\frac{4}{3}(u-1)^3 \frac{d^2x}{du^2} + 2(u-1)^{2} \frac{dx}{du}\biggr] + 4(2u-3)(u-1)\frac{dx}{du} + \biggl\{ 5\sigma^2 \biggl[ \frac{3u}{(u-1)} \biggr]^{3 / 2} + 2 \biggr\} x </math> |
|
|
<math>~=</math> |
<math>~4u(u-1)^2 \frac{d^2x}{du^2} + (14u-12)(u-1)\frac{dx}{du} + \biggl\{ 5\sigma^2 \biggl[ \frac{3u}{(u-1)} \biggr]^{3 / 2} + 2 \biggr\} x \, . </math> |
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
If we assume that <math>~\sigma^2 = 0</math>, then the governing relation is,
|
<math>~0</math> |
<math>~=</math> |
<math>~4u(u-1)^2 \frac{d^2x}{du^2} + (14u-12)(u-1)\frac{dx}{du} + 2 x \, . </math> |
Now, again, guided by our conjecture, let's guess an eigenfunction of the form:
First Guess (n5)
|
<math>~x</math> |
<math>~=</math> |
<math>~ A^3 (u - 1)^{1 / 2} (A u - 1 )^{-1 / 2} \, , </math> |
in which case,
|
<math>~\frac{dx}{du}</math> |
<math>~=</math> |
<math>~ \frac{A^3}{2} \biggl[ (u - 1)^{-1 / 2} (A u - 1 )^{-1 / 2} - A(u - 1)^{1 / 2} (A u - 1 )^{-3 / 2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{A^3(A-1)}{2} \biggr] (u-1)^{-1 / 2} (Au-1)^{-3 / 2} \, ; </math> |
|
<math>~\frac{d^2x}{du^2}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{A^3(A-1)}{2} \biggr] \biggl\{ -\frac{1}{2}(u-1)^{-3 / 2} (Au-1)^{-3 / 2} -\frac{3A}{2} (u-1)^{-1 / 2} (Au-1)^{-5 / 2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -\frac{1}{2} \biggl[ \frac{A^3(A-1)}{2} \biggr] (u-1)^{-3 / 2} (Au-1)^{-5 / 2}\biggl[ (Au-1) +3A (u-1)\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{A^3(A-1)}{4} \biggr] (u-1)^{-3 / 2} (Au-1)^{-5 / 2}\biggl[(3A+1) - 4Au \biggr] \, . </math> |
So the governing relation becomes:
|
<math>~0</math> |
<math>~=</math> |
<math>~4u(u-1)^2 \biggl\{ \biggl[ \frac{A^3(A-1)}{4} \biggr] (u-1)^{-3 / 2} (Au-1)^{-5 / 2}\biggl[(3A+1) - 4Au \biggr] \biggr\} </math> |
|
|
|
<math>~ + (14u-12)(u-1) \biggl\{ \biggl[ \frac{A^3(A-1)}{2} \biggr] (u-1)^{-1 / 2} (Au-1)^{-3 / 2} \biggr\} + 2 A^3 (u - 1)^{1 / 2} (A u - 1 )^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~u(u-1)^{1 / 2} A^3(A-1) (Au-1)^{-5 / 2}\biggl[(3A+1) - 4Au \biggr] </math> |
|
|
|
<math>~ + (7u-6)(u-1)^{1 / 2} A^3(A-1) (Au-1)^{-3 / 2} + 2 A^3 (u - 1)^{1 / 2} (A u - 1 )^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~(u-1)^{1 / 2} \biggl\{ uA^3(A-1) (Au-1)^{-5 / 2}\biggl[(3A+1) - 4Au \biggr] + (7u-6) A^3(A-1) (Au-1)^{-3 / 2} + 2 A^3 (A u - 1 )^{-1 / 2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ u(A-1) \biggl[(3A+1) - 4Au \biggr] + (7u-6) (A-1) (Au-1) + 2 (A u - 1 )^{2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ - 4u^2 A(A-1) + u(A-1) (3A+1) + (7u-6) [A(A-1)u +1 - A] + 2 (A^2u^2 - 2Au +1) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ u^2 \biggl[ - 4A(A-1) +7A(A-1) +2A^2 \biggr] + u\biggl[ (A-1) (3A+1) - 7(A-1) -6A(A-1) - 4A \biggr] + 2(3A-2) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ Au^2 \biggl[ 5A-3 \biggr] + u\biggl[ 3A^2-2A-1-7A+7 -6A^2+6A -4A \biggr] + 2(3A-2) \biggr\} \, . </math> |
|
|
<math>~=</math> |
<math>~A^3(u-1)^{1 / 2} (Au-1)^{-5 / 2} \biggl\{ Au^2 \biggl[ 5A-3 \biggr] + u\biggl[ -3A^2 -7A +6\biggr] + 2(3A-2) \biggr\} \, . </math> |
Second Guess (n5)
|
<math>~x</math> |
<math>~=</math> |
<math>~ (u - 1)^{b / 2} (A u - 1 )^{-a / 2} \, , </math> |
in which case,
|
<math>~\frac{dx}{du}</math> |
<math>~=</math> |
<math>~ \frac{b}{2}(u-1)^{b/2-1} (A u - 1 )^{-a / 2} - \frac{aA}{2}(u - 1)^{b / 2} (A u - 1 )^{-a / 2-1} </math> |
|
|
<math>~=</math> |
<math>~x \biggl[ \frac{b}{2}(u-1)^{-1} - \frac{aA}{2} (A u - 1 )^{-1} \biggr] </math> |
|
<math>~\Rightarrow ~~~ \frac{(u-1)}{x} \frac{dx}{du}</math> |
<math>~=</math> |
<math>~ (A u - 1 )^{-1} \biggl[ \frac{b}{2} (A u - 1 ) - \frac{aA}{2} (u-1) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{1 }{2(A u - 1 )} \biggl[ b (A u - 1 ) - aA (u-1) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1 }{2(A u - 1 )} \biggl[ (aA - b) + A(b - a)u \biggr] \, ; </math> |
and,
|
<math>~\frac{d^2x}{du^2}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{b}{2}(u-1)^{-1} - \frac{aA}{2} (A u - 1 )^{-1} \biggr]\frac{dx}{du} + x \frac{d}{du}\biggl[ \frac{b}{2}(u-1)^{-1} - \frac{aA}{2} (A u - 1 )^{-1} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ x\biggl[ \frac{b}{2}(u-1)^{-1} - \frac{aA}{2} (A u - 1 )^{-1} \biggr]^2 + x \biggl[ -\frac{b}{2}(u-1)^{-2} + \frac{aA^2}{2} (A u - 1 )^{-2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{x}{4(u-1)^2 (Au-1)^2} \biggl\{ \biggl[ b(Au-1) - aA (u - 1 ) \biggr]^2 + \biggl[ 2aA^2 (u-1)^{2} -2b (A u - 1 )^{2} \biggr] \biggr\} </math> |
|
<math>~\Rightarrow ~~~ \frac{(1-u)^2}{x}\frac{d^2x}{du^2}</math> |
<math>~=</math> |
<math>~ \frac{1}{4 (Au-1)^2} \biggl\{ \biggl[ b(Au-1) - aA (u - 1 ) \biggr]^2 + \biggl[ 2aA^2 (u-1)^{2} -2b (A u - 1 )^{2} \biggr] \biggr\} </math> |
Hence, the governing wave equation becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~2u \biggl\{ \frac{(u-1)^2}{x} \frac{d^2x}{du^2} \biggr\} + (7u-6)\biggl\{ \frac{(u-1)}{x} \frac{dx}{du} \biggl\} + 1 </math> |
|
|
<math>~=</math> |
<math>~ \frac{2u}{4 (Au-1)^2} \biggl\{ \biggl[ (aA - b) + A(b - a)u \biggr]^2 + \biggl[ 2aA^2 (u-1)^{2} -2b (A u - 1 )^{2} \biggr] \biggr\} </math> |
|
|
|
<math>~ + \frac{(7u-6) }{2(A u - 1 )} \biggl[ (aA - b) + A(b - a)u \biggr] + 1 </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{4 (Au-1)^2} \biggl\{ 2u\biggl[ (aA - b)^2 + 2(aA - b)A(b - a)u + A^2(b - a)^2u^2 \biggr] + 2u\biggl[ 2aA^2 (u^2 - 2u + 1) -2b (A^2 u^2 - 2Au + 1 ) \biggr] </math> |
|
|
|
<math>~ + 2(A u - 1 )(7u-6) \biggl[ (aA - b) + A(b - a)u \biggr] + 4 (Au-1)^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{4 (Au-1)^2} \biggl\{ 2u\biggl[ (aA - b)^2 + 2(aA - b)A(b - a)u + A^2(b - a)^2u^2 \biggr] + 2u\biggl[ 2A^2(a-b)u^2 + 4A(b - aA) u + 2(aA^2 -b) \biggr] </math> |
|
|
|
<math>~ + 2\biggl[7Au^2 - (6A+7)u +6 \biggr]\biggl[ (aA - b) + A(b - a)u \biggr] + (4A^2u^2-8Au + 4) \biggr\} </math> |
If <math>~b=a</math>,
|
<math>~0</math> |
<math>~=</math> |
<math>~ 2u\biggl[ (aA - b)^2 \biggr] + 2u\biggl[ 4A(b - aA) u + 2(aA^2 -b) \biggr] </math> |
|
|
|
<math>~ + 2\biggl[7Au^2 - (6A+7)u +6 \biggr]\biggl[ (aA - b) \biggr] + (4A^2u^2-8Au + 4) </math> |
|
|
<math>~=</math> |
<math>~ 2a^2u (A - 1)^2 + 2au [ 4A(1 - A) u + 2(A^2 -1) ] </math> |
|
|
|
<math>~ + 2a(A - 1) \biggl[7Au^2 - (6A+7)u +6 \biggr] + (4A^2u^2-8Au + 4) </math> |
|
|
<math>~=</math> |
<math>~ 2Au^2 [4a (1 - A) + 7a(A - 1) + 2A] + 2u [ a^2 (A - 1)^2 + 2a(A^2 -1) - a(A - 1) (6A+7) - 4A] + 4[ 3a(A-1) + 1] </math> |
This should then match the "first guess" algebraic condition if we set <math>~a=1</math>. Let's see.
|
<math>~0</math> |
<math>~=</math> |
<math>~ 2Au^2 [4 (1 - A) + 7(A - 1) + 2A] + 2u [ (A - 1)^2 + 2(A^2 -1) - (A - 1) (6A+7) - 4A] + 4[ 3(A-1) + 1] </math> |
|
|
<math>~=</math> |
<math>~ 2Au^2 [4 - 4A + 7A - 7 + 2A] + 2u [ (A^2 - 2A + 1) + 2A^2 -2 + (1-A ) (6A+7) -4A] + 4[ 3A-2] </math> |
|
|
<math>~=</math> |
<math>~ 2Au^2 [5A - 3] + 2u [ - 3A^2 - 7A + 6 ] + 4[ 3A-2] \, . </math> |
And we see that this expression does match the one derived earlier.
Going back a bit, before setting <math>~a=1</math>, we have the expression:
|
<math>~0</math> |
<math>~=</math> |
<math>~ 2Au^2 [4a (1 - A) + 7a(A - 1) + 2A] + 2u [ a^2 (A - 1)^2 + 2a(A^2 -1) - a(A - 1) (6A+7) - 4A] + 4[ 3a(A-1) + 1] </math> |
|
|
<math>~=</math> |
<math>~ 2Au^2 [ 3aA -3a + 2A] + 2u [ a^2 (A - 1)^2 + 2a(A^2 -1) - a(6A^2+A-7) - 4A] + 4[ 3a(A-1) + 1] </math> |
|
|
<math>~=</math> |
<math>~ 2Au^2 [ 3a(A - 1) + 2A] + 2u [ a^2 (A - 1)^2 + a( -4A^2-A+5) - 4A] + 4[ 3a(A-1) + 1] \, . </math> |
Now, in order for all three expressions inside the square-bracket pairs to be zero, we need, first,
|
<math>~3a(A - 1) + 2A</math> |
<math>~=</math> |
<math>~0</math> |
|
<math>~\Rightarrow ~~~ a</math> |
<math>~=</math> |
<math>~\frac{2A}{3(1-A)} \, ;</math> |
and, third, by simple visual comparison with the first expression,
|
<math>~3a(A-1) + 1</math> |
<math>~=</math> |
<math>~3a(A-1) + 2A</math> |
|
<math>~\Rightarrow A</math> |
<math>~=</math> |
<math>~\frac{1}{2} </math> |
|
<math>~\Rightarrow ~~~ a</math> |
<math>~=</math> |
<math>~\frac{2}{3} \, ;</math> |
which forces the second expression to the value,
|
<math>~a^2 (A - 1)^2 + a( -4A^2-A+5) - 4A</math> |
<math>~=</math> |
<math>~\biggl(\frac{2}{3}\biggr)^2 \biggl(-\frac{1}{2} \biggr)^2 + \frac{2}{3}\biggl[ -1-\frac{1}{2} +5 \biggr] - 2</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{9} + \frac{7}{3} - 2</math> |
|
|
<math>~=</math> |
<math>~\frac{4}{9} \, ,</math> |
which is not zero. Hence our pair of unknown parameters — <math>~a </math> and <math>~A</math> — do not simultaneously satisfy all three conditions. (Not really a surprise.)
Setup Using Lagrangian Mass Coordinate
Alternative Terms
Let's change the independent coordinate from <math>~r_0</math> to <math>~m_0</math>. In particular, the derivative operation will change as follows:
|
<math>~\frac{d}{dr_0}</math> |
<math>~~\rightarrow~~</math> |
<math>~\biggl( \frac{dm_0}{dr_0} \biggr)\frac{d}{dm_0} = \biggl( \frac{dm_0}{d\xi} \cdot \frac{d\xi}{dr_0} \biggr)\frac{d}{dm_0} \, ,</math> |
so what is the expression for the leading coefficient? From above, we have,
|
<math>~r_0</math> |
<math>~=</math> |
<math>~ R_* \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi </math> |
|
<math>~\Rightarrow ~~~ \xi</math> |
<math>~=</math> |
<math>~ \frac{1}{R_*} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)}\biggr]^{3} r_0 \, . </math> |
Also, from above, we know that,
|
<math>~m_0</math> |
<math>~=</math> |
<math>~ M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2} \biggl\{ \xi^3 ( 3 + \xi^2 )^{-3/2} \biggr\} </math> |
|
<math>~\Rightarrow ~~~ \frac{dm_0}{d\xi}</math> |
<math>~=</math> |
<math>~ M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2} \biggl\{ 3\xi^2 ( 3 + \xi^2 )^{-3/2} - 3 \xi^4 ( 3 + \xi^2 )^{-5/2}\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2} 3\xi^2 (3 + \xi^2)^{-5/2} \biggl\{ ( 3 + \xi^2 ) - \xi^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2} 3^2\xi^2 (3 + \xi^2)^{-5/2} </math> |
|
<math>~\Rightarrow ~~~ \frac{dm_0}{dr_0}</math> |
<math>~=</math> |
<math>~ M_\mathrm{tot} \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3 / 2} 3^2\xi^2 (3 + \xi^2)^{-5/2} \frac{1}{R_*} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)}\biggr]^{3} </math> |
|
|
<math>~=</math> |
<math>~ \frac{M_\mathrm{tot} }{R_*} \biggl[ \frac{ {\tilde\xi}^2}{(3 + {\tilde\xi}^2)}\biggr]^{3 / 2} 3^2\xi^2 (3 + \xi^2)^{-5/2} \, . </math> |
To simplify expressions, let's borrow from an accompanying derivation and define,
<math>\tilde{C} \equiv \frac{3^2}{{\tilde\xi}^2} \biggl( 1 + \frac{ {\tilde\xi}^2}{3} \biggr) = 3 \biggl[ \frac{( 3 + {\tilde\xi}^2 )}{ {\tilde\xi}^2} \biggr] \, .</math>
Then we have,
|
<math>~\frac{m_0}{M_\mathrm{tot}}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{\tilde{C}}{ 3}\biggr]^{3 / 2} \biggl[ \frac{\xi^2}{ ( 3 + \xi^2 )} \biggr]^{3/2} </math> |
|
<math>~\Rightarrow ~~~\biggl[ \frac{ 3}{\tilde{C}}\biggr] \biggl[\frac{m_0}{M_\mathrm{tot}}\biggr]^{2 / 3}</math> |
<math>~=</math> |
<math>~ \frac{\xi^2}{ ( 3 + \xi^2 )} </math> |
|
<math>~\Rightarrow ~~~( 3 + \xi^2 )\biggl[ \frac{ 3}{\tilde{C}}\biggr] \biggl[\frac{m_0}{M_\mathrm{tot}}\biggr]^{2 / 3}</math> |
<math>~=</math> |
<math>~ \xi^2 </math> |
|
<math>~\Rightarrow ~~~3 m_*</math> |
<math>~=</math> |
<math>~ \xi^2 (1-m_*) </math> |
|
<math>~\Rightarrow ~~~\xi^2 </math> |
<math>~=</math> |
<math>~ \frac{3m_*}{(1-m_*)} \, , </math> |
where,
<math>~m_* \equiv \biggl[ \frac{ 3}{\tilde{C}}\biggr] \biggl[\frac{m_0}{M_\mathrm{tot}}\biggr]^{2 / 3} \, .</math>
In summary:
|
<math>~ \frac{\xi^2}{ ( 3 + \xi^2 )} = m_* \, ; </math> |
while, |
<math>~ \frac{ {\tilde\xi}^2}{ ( 3 + {\tilde\xi}^2 )} = \frac{3}{\tilde{C}} \, ; </math> |
|
<math>~r_0</math> |
<math>~=</math> |
<math>~ R_* \biggl[ \frac{(3 + {\tilde\xi}^2)}{ {\tilde\xi}^2}\biggr]^{3} \xi = R_* \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} \biggr[ \frac{3m_*}{ (1-m_*) }\biggr]^{1 / 2} \, ; </math> |
|
<math>~\frac{g_0\rho_0}{P_0} </math> |
<math>~=</math> |
<math>~ \frac{6}{R_*} \biggl[ \frac{ {\tilde\xi}^2 }{ (3 + {\tilde\xi}^2) }\biggr]^{9} \frac{\xi}{ ( 3 + \xi^2 )} = \frac{6}{R_*} \biggl[ \frac{ 3 }{ \tilde{C} }\biggr]^{9} \frac{m_*}{ \xi } = \frac{6}{R_*} \biggl[ \frac{ 3 }{ \tilde{C} }\biggr]^{9} m_* \biggl[ \frac{(1-m_*)}{3m_*} \biggr]^{1 / 2} \, ; </math> |
|
<math>~\frac{g_0 }{r_0} </math> |
<math>~=</math> |
<math>~ \frac{GM_\mathrm{tot}}{R_*^3} \biggl[ \frac{ {\tilde\xi}^2 }{ (3 + {\tilde\xi}^2)}\biggr]^{15/2} \frac{1}{\xi^3} \biggl[ \frac{ \xi^2 }{ ( 3 + \xi^2 ) }\biggr]^{3/2} = \frac{GM_\mathrm{tot}}{R_*^3} \biggl[ \frac{3 }{ \tilde{C} }\biggr]^{15/2} (1-m_*)^{3 / 2} \, ; </math> |
|
<math>~\frac{\rho_0}{\gamma_g P_0} </math> |
<math>~=</math> |
<math>~ \frac{6R_* }{\gamma_g GM_\mathrm{tot} }\biggl( \frac{ 3}{ \tilde{C} } \biggr)^{9 / 2} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \, . </math> |
So, the wave equation may be written as,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x </math> |
|
|
<math>~=</math> |
<math>~ \frac{d^2x}{dr_0^2} + \biggl\{ \frac{4}{R_*} \biggl( \frac{ 3}{ \tilde{C} }\biggr)^{3} \biggr[ \frac{ (1-m_*) }{3m_*}\biggr]^{1 / 2} - \frac{6}{R_*} \biggl[ \frac{ 3 }{ \tilde{C} }\biggr]^{9} m_* \biggl[ \frac{(1-m_*)}{3m_*} \biggr]^{1 / 2} \biggr\} \frac{dx}{dr_0} </math> |
|
|
|
<math>~ + \frac{6R_* }{\gamma_g GM_\mathrm{tot} }\biggl( \frac{ 3}{ \tilde{C} } \biggr)^{9 / 2} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \biggl\{ \omega^2 + (4 - 3\gamma_\mathrm{g})\frac{GM_\mathrm{tot}}{R_*^3} \biggl[ \frac{3 }{ \tilde{C} }\biggr]^{15/2} (1-m_*)^{3 / 2} \biggr\} x </math> |
|
|
<math>~=</math> |
<math>~ \frac{d^2x}{dr_0^2} + \frac{1}{R_*} \biggl( \frac{ 3}{ \tilde{C} }\biggr)^{3} \biggl\{ 4 - 6\biggl[ \frac{ 3 }{ \tilde{C} }\biggr]^{6} m_* \biggr\} \biggr[ \frac{ (1-m_*) }{3m_*}\biggr]^{1 / 2}\frac{dx}{dr_0} </math> |
|
|
|
<math>~ + \frac{6(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \cdot \frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{3} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \biggl\{\sigma^2 + (1-m_*)^{3 / 2} \biggr\} x </math> |
|
|
<math>~=</math> |
<math>~\frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{3} \biggl\{ R_*^2 \biggl( \frac{ \tilde{C} }{3 }\biggr)^{3} \frac{d^2x}{dr_0^2} + R_* \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] \biggr[ \frac{ (1-m_*) }{3m_*}\biggr]^{1 / 2}\frac{dx}{dr_0} </math> |
|
|
|
<math>~ + \frac{6(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \cdot \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{3} \biggl[ \frac{1}{3m_*(1-m_*)}\biggr]^{1 / 2} \biggl\{ [ 3m_*(1-m_*) ]^{1 / 2} R_*^2 \biggl( \frac{ \tilde{C} }{3 }\biggr)^{3} \frac{d^2x}{dr_0^2} + R_* \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*) \frac{dx}{dr_0} </math> |
|
|
|
<math>~ + \frac{18(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \cdot m_*^{1 / 2} \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\} \, , </math> |
where,
<math>~\sigma^2 \equiv (4 - 3\gamma_\mathrm{g})^{-1} \frac{R_*^3}{GM_\mathrm{tot}} \biggl[ \frac{ \tilde{C} }{3 } \biggr]^{15/2} \omega^2 \, .</math>
Now, let's look at the differential operators, after defining.
<math>~c_0 \equiv 3^{1 / 2} R_* \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} ~~~~\Rightarrow ~~~~R_* = c_0 3^{-1 / 2} \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{-3} \, .</math>
We find,
|
<math>~dr_0</math> |
<math>~=</math> |
<math>~ c_0 ~d[ m_*^{1 / 2} (1-m_*)^{-1 / 2} ] </math> |
|
|
<math>~=</math> |
<math>~ c_0 ~\biggl[\frac{1}{2} ~m_*^{-1 / 2}( 1 - m_*)^{-1 / 2} + \frac{1}{2} ~m_*^{1 / 2} (1 - m_*)^{-3 / 2} \biggr] dm_* </math> |
|
|
<math>~=</math> |
<math>~ \frac{c_0}{2} ~m_*^{-1 / 2}( 1 - m_*)^{-3 / 2}~ dm_* </math> |
|
<math>~\frac{d}{dr_0}</math> |
<math>~=</math> |
<math>~ \frac{2}{c_0} ~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{d}{dm_*} </math> |
|
<math>~\Rightarrow ~~~ R_*\frac{dx}{dr_0}</math> |
<math>~=</math> |
<math>~ \frac{2}{3^{1 / 2}}\biggl( \frac{ \tilde{C} }{ 3}\biggr)^{-3} ~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{dx}{dm_*} \, . </math> |
Also,
|
<math>~\frac{d^2}{dr_0^2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{2}{c_0} \biggr)^{2}~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{d}{dm_*} \biggl[ m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{d}{dm_*} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2}{c_0} \biggr)^{2}~m_* ( 1 - m_*)^{3 }~ \frac{d^2}{dm_*^2} +\biggl( \frac{2}{c_0} \biggr)^{2}~m_*^{1 / 2}( 1 - m_*)^{3 / 2} \biggl[ \frac{1}{2} m_*^{-1 / 2}( 1 - m_*)^{3 / 2} - \frac{3}{2} m_*^{1 / 2}( 1 - m_*)^{1 / 2}~ \biggr] ~ \frac{d}{dm_*} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2}{c_0} \biggr)^{2}~m_* ( 1 - m_*)^{3 }~ \frac{d^2}{dm_*^2} +\frac{1}{2} \biggl( \frac{2}{c_0} \biggr)^{2}~ ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{d}{dm_*} </math> |
|
<math>~\Rightarrow ~~~ R_*^2 \biggl( \frac{ \tilde{C} }{3 }\biggr)^{3} \frac{d^2x}{dr_0^2}</math> |
<math>~=</math> |
<math>~ \biggl[\frac{2^2}{3} \biggl(\frac{ \tilde{C} }{3} \biggr)^{-3} \biggr] \biggl[ ~m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} +\frac{1}{2} ~ ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{dx}{dm_*} \biggr] </math> |
So, the wave equation becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~\frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{3} \biggl[ \frac{1}{3m_*(1-m_*)}\biggr]^{1 / 2} \biggl\{ [ 3m_*(1-m_*) ]^{1 / 2} \biggl[\frac{2^2}{3} \biggl(\frac{ \tilde{C} }{3} \biggr)^{-3} \biggr] \biggl[ ~m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} +\frac{1}{2} ~ ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{dx}{dm_*} \biggr] </math> |
|
|
|
<math>~ + \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*) \biggl[ \frac{2}{3^{1 / 2}}\biggl( \frac{ \tilde{C} }{ 3}\biggr)^{-3} ~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{dx}{dm_*} \biggr] + \frac{18(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \cdot m_*^{1 / 2} \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{1 }{R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \biggl[ \frac{1}{3m_*(1-m_*)}\biggr]^{1 / 2} \biggl\{ [ 3m_*(1-m_*) ]^{1 / 2} \biggl[\frac{2^2}{3} \biggr] \biggl[ ~m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} +\frac{1}{2} ~ ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{dx}{dm_*} \biggr] </math> |
|
|
|
<math>~ + \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*) \biggl[ \frac{2}{3^{1 / 2}} ~m_*^{1 / 2}( 1 - m_*)^{3 / 2}~ \frac{dx}{dm_*} \biggr] + \frac{18(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} m_*^{1 / 2} \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{2 }{3R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \biggl\{ 2m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} + ( 1 - m_*)^{2} ( 1 - 4m_*) \frac{dx}{dm_*} </math> |
|
|
|
<math>~ + \biggl[ 4 - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*)^2 \frac{dx}{dm_*} + \frac{9(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2}\biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{2 }{3R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \biggl\{ 2m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} </math> |
|
|
|
<math>~ + \biggl[ 5 - 4m_* - 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*)^2 \frac{dx}{dm_*} + \frac{9(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2}\biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{2 }{3R_*^2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \biggl\{ 2m_* ( 1 - m_*)^{3 }~ \frac{d^2x}{dm_*^2} + (5 - \mathcal{A} m_*) (1-m_*)^2 \frac{dx}{dm_*} + \mathcal{B} \biggl[ \frac{\sigma^2}{(1-m_*)^{1 / 2}} + (1-m_*) \biggr] x \biggr\} \, , </math> |
where,
|
<math>~\mathcal{A}</math> |
<math>~\equiv</math> |
<math>~4 + 6\biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} \, ,</math> |
|
<math>~\mathcal{B}</math> |
<math>~\equiv</math> |
<math>~\frac{3^{5/2}(4 - 3\gamma_\mathrm{g}) }{\gamma_g } \biggl( \frac{ \tilde{C} }{ 3}\biggr)^{3} \, .</math> |
Try Again
This time, let's adopt the notation used in a related chapter in our Ramblings appendix. Specifically, the parametric relationship between <math>~m_\xi</math> and <math>~r_\xi</math> in pressure-truncated, <math>~n=5</math> polytropes is,
|
<math>~m_\xi \equiv \frac{m_0}{ M_\mathrm{tot} } = \frac{M_r(\xi)}{M_\mathrm{tot}}</math> |
<math>~=</math> |
<math>~ \biggl(\frac{\xi}{\tilde\xi}\biggr)^3 \biggl(3 + \xi^2 \biggr)^{-3/2} \biggl(3 + {\tilde\xi}^2 \biggr)^{3/2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{( 3+\tilde\xi^2)}{ {\tilde\xi}^2} \biggr]^{3 / 2}\biggl[ \frac{( 3+\xi^2)}{ {\xi}^2} \biggr]^{- 3 / 2} \, ,</math> |
|
<math>~r_\xi \equiv \frac{r_0}{R_\mathrm{norm}} = \biggl(\frac{\xi}{\tilde\xi} \biggr) \frac{R_\mathrm{eq}}{R_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\xi \biggl\{ \biggl[ \frac{4\pi}{2^5\cdot 3}\biggr]^{1/2} \tilde\xi^{-6} \biggl( 1+\frac{\tilde\xi^2}{3} \biggr)^{3}\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{\pi}{2^3\cdot 3^7}\biggr]^{1/2} \biggl[ \frac{( 3+\tilde\xi^2)}{ {\tilde\xi}^2} \biggr]^{3} \xi \, . </math> |
And we are in the fortunate situation of being able to eliminate <math>~\xi</math> to obtain the direct relation,
|
<math>~ r_\xi (m_\xi) </math> |
<math>~=</math> |
<math>~\tilde{r}_\mathrm{edge} \biggl[\frac{3^2m_\xi^{2/3}}{\tilde{C} - 3 m_\xi^{2/3}}\biggr]^{1/2} \, , </math> |
where,
|
<math>~\tilde{C}</math> |
<math>~\equiv</math> |
<math>~ \frac{3^2}{\tilde\xi^2}\biggl( 1 + \frac{\tilde\xi^2}{3} \biggr) = 3 \biggl[ \frac{( 3+\tilde\xi^2)}{ {\tilde\xi}^2} \biggr] \, , </math> |
|
<math>~\tilde{r}_\mathrm{edge}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{\pi}{2^3\cdot 3}\biggr]^{1/2} {\tilde\xi}^{-6} \biggl(1+\frac{\tilde\xi^2}{3}\biggr)^3 = \biggl[ \frac{\pi}{2^3\cdot 3^7}\biggr]^{1 / 2} \biggl[ \frac{\tilde{C}}{ 3} \biggr]^{3} \, . </math> |
If we furthermore define,
<math>m_* \equiv \frac{3}{\tilde{C}} \cdot m_\xi^{2 / 3} \, ,</math>
then,
|
<math>~ r_\xi (m_*) </math> |
<math>~=</math> |
<math>~ 3^{1 / 2} \tilde{r}_\mathrm{edge} \biggl[\frac{m_*}{1-m_*}\biggr]^{1/2} \, . </math> |
Hence,
|
<math>~ \frac{dr_0}{R_\mathrm{norm}} = dr_\xi </math> |
<math>~=</math> |
<math>~3^{1 / 2} \tilde{r}_\mathrm{edge} \biggl\{ \frac{1}{2} (1-m_*)^{- 1 / 2} m_*^{-1 / 2} + \frac{1}{2}m_*^{1 / 2}(1-m_*)^{-3 / 2} \biggr\} dm_* </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{3^{1 / 2}}{2} \biggr) \tilde{r}_\mathrm{edge} m_*^{-1 / 2} (1-m_*)^{-3 / 2} dm_* </math> |
|
<math>\Rightarrow ~~~ R_\mathrm{norm} \cdot \frac{d}{dr_0} </math> |
<math>~=</math> |
<math>~ \frac{1}{ \tilde{r}_\mathrm{edge}} \biggl( \frac{2}{3^{1 / 2}} \biggr) m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{d}{dm_*} \, . </math> |
We therefore also have,
|
<math>~ R^2_\mathrm{norm} \cdot \frac{d^2}{dr_0^2} </math> |
<math>~=</math> |
<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2^2}{3} \biggr) m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{d}{dm_*}\biggl[ m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{d}{dm_*}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2^2}{3} \biggr) m_*^{1 / 2} (1-m_*)^{3 / 2} \biggl\{ \biggl[ m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{d^2}{dm_*^2}\biggr] + \biggl[ \frac{1}{2} m_*^{-1 / 2} (1-m_*)^{3 / 2} + \frac{3}{2}m_*^{1 / 2} (1-m_*)^{1 / 2}\biggr] \frac{d}{dm_*} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{ \biggl[ 2m_* (1-m_*)^{3} \frac{d^2}{dm_*^2}\biggr] + \biggl[ (1-m_*)^{3 } + 3m_* (1-m_*)^{2}\biggr] \frac{d}{dm_*} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{ 2m_* (1-m_*)^{3} \frac{d^2}{dm_*^2} + (1-m_*)^{2} ( 1 + 2m_* ) \frac{d}{dm_*} \biggr\} \, . </math> |
So the wave equation may be written,
|
<math>~0</math> |
<math>~=</math> |
<math>~ R_\mathrm{norm}^2 \cdot \frac{d^2x}{dr_0^2} + \biggl[\frac{4R_\mathrm{norm}}{r_0} - \biggl(\frac{g_0 \rho_0 R_\mathrm{norm}}{P_0}\biggr) \biggr] R_\mathrm{norm} \cdot \frac{dx}{dr_0} + \biggl(\frac{\rho_0 R_\mathrm{norm}}{\gamma_\mathrm{g} P_0} \biggr)\biggl[R_\mathrm{norm} \omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0 R_\mathrm{norm}}{r_0} \biggr] x </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{ 2m_* (1-m_*)^{3} \frac{d^2x}{dm_*^2} + (1-m_*)^{2} ( 1 + 2m_* ) \frac{dx}{dm_*} \biggr\} </math> |
|
|
|
<math>~ +\frac{1}{ \tilde{r}_\mathrm{edge}} \biggl( \frac{2}{3^{1 / 2}} \biggr) \biggl\{ \frac{4}{r_\xi} - \biggl[\frac{6R_\mathrm{norm}}{R_*} \biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{9} m_* \biggl[ \frac{(1-m_*)}{3m_*} \biggr]^{1 / 2} \biggr] \biggr\} m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{dx}{dm_*} </math> |
|
|
|
<math>~ + \frac{6R_* R_\mathrm{norm}}{\gamma_g GM_\mathrm{tot} }\biggl( \frac{ 3}{ \tilde{C} } \biggr)^{9 / 2} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \biggl\{ R_\mathrm{norm} \omega^2 + (4 - 3\gamma_\mathrm{g}) \frac{GM_\mathrm{tot} R_\mathrm{norm}}{R_*^3} \biggl[ \frac{3 }{ \tilde{C} }\biggr]^{15/2} (1-m_*)^{3 / 2} \biggr\} x \, . </math> |
Keeping in mind that,
<math>~\frac{R_*}{R_\mathrm{norm}} = \biggl[ \frac{\pi}{2^3 \cdot 3^7} \biggr]^{1 / 2} = {\tilde{r}}_\mathrm{edge} \biggl( \frac{3}{\tilde{C}} \biggr)^3 \, ,</math>
we therefore have,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{ 2m_* (1-m_*)^{3} \frac{d^2x}{dm_*^2} + (1-m_*)^{2} ( 1 + 2m_* ) \frac{dx}{dm_*} \biggr\} </math> |
|
|
|
<math>~ +\frac{1}{ \tilde{r}_\mathrm{edge}} \biggl( \frac{2}{3^{1 / 2}} \biggr) \biggl\{ 4 \biggl[3^{1 / 2} \tilde{r}_\mathrm{edge} \biggl[\frac{m_*}{1-m_*}\biggr]^{1/2} \biggr]^{-1} - 6 \biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{9} \biggl[{\tilde{r}}_\mathrm{edge} \biggl( \frac{3}{\tilde{C}} \biggr)^3 \biggr]^{-1} m_* \biggl[ \frac{(1-m_*)}{3m_*} \biggr]^{1 / 2} \biggr\} m_*^{1 / 2} (1-m_*)^{3 / 2} \frac{dx}{dm_*} </math> |
|
|
|
<math>~ + 6 \biggl( \frac{ 3}{ \tilde{C} } \biggr)^{9 / 2} \biggl[{\tilde{r}}_\mathrm{edge} \biggl( \frac{3}{\tilde{C}} \biggr)^3 \biggr]^{-2} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \biggl\{ \biggl[ \frac{R_*^3}{\gamma_g GM_\mathrm{tot} } \biggr] \omega^2 + \frac{(4 - 3\gamma_\mathrm{g})}{\gamma_g} \biggl[ \frac{3 }{ \tilde{C} }\biggr]^{15/2} (1-m_*)^{3 / 2} \biggr\} x </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{ 2m_* (1-m_*)^{3} \frac{d^2x}{dm_*^2} + (1-m_*)^{2} ( 1 + 2m_* ) \frac{dx}{dm_*} \biggr\} </math> |
|
|
|
<math>~ +\frac{1}{ \tilde{r}_\mathrm{edge}^2} \biggl( \frac{2^3}{3} \biggr) \biggl[ 1 - \frac{3}{2} \biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* \biggr] (1-m_*)^{2} \frac{dx}{dm_*} + \frac{6}{ {\tilde{r}}_\mathrm{edge}^2 } \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \biggl[ \frac{3}{(1-m_*)}\biggr]^{1 / 2} \frac{(4 - 3\gamma_\mathrm{g})}{\gamma_g} \biggl[ \sigma^2 + (1-m_*)^{3 / 2} \biggr] x </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{ {\tilde{r}}^2_\mathrm{edge}} \biggl( \frac{2}{3} \biggr) \biggl\{ 2m_* (1-m_*)^{3} \frac{d^2x}{dm_*^2} + \biggl[ 5 - 6 \biggl( \frac{ 3 }{ \tilde{C} }\biggr)^{6} m_* + 2m_* \biggr] (1-m_*)^{2} \frac{dx}{dm_*} + 3^{5 / 2} \biggl( \frac{3 }{ \tilde{C} }\biggr)^{6} \frac{(4 - 3\gamma_\mathrm{g})}{\gamma_g} \biggl[ \frac{\sigma^2 }{(1-m_*)^{1 / 2}} + (1-m_*) \biggr] x \biggr\} \, , </math> |
where, as before,
<math>\sigma^2 \equiv \biggl( \frac{ \tilde{C} }{3 } \biggr)^{15/2} \biggl[ \frac{R_*^3}{(4 - 3\gamma_g) GM_\mathrm{tot} } \biggr] \omega^2 \, .</math>
Take Another Approach Using Logarithmic Derivatives
Change Independent Variable
Returning to the LAWE for n = 3 polytropes, as given, above, and repeated here,
| LAWE for <math>~n=5</math> Polytropes | |||
|---|---|---|---|
|
let's make the substitution,
|
<math>~u \equiv (3 + \xi^2)^{1/2}</math> |
<math>~\Rightarrow</math> |
<math>~\xi^2 = u^2-3 \, .</math> |
We must therefore also make the operator substitution,
|
<math>~\frac{d}{d\xi}</math> |
<math>~=</math> |
<math>~\frac{du}{d\xi} \cdot \frac{d}{du}</math> |
|
|
<math>~=</math> |
<math>~\biggl[ \xi (3+\xi^2)^{-1/2} \biggr] \frac{d}{du} = \biggl[ 1 - \frac{3}{u^2} \biggr]^{1/2} \frac{d}{du}</math> |
|
<math>~\Rightarrow~~~ \frac{1}{\xi} \cdot \frac{dx}{d\xi}</math> |
<math>~=</math> |
<math>~\frac{1}{u}\cdot \frac{dx}{du} \, ;</math> |
and,
|
<math>~\frac{d^2}{d\xi^2}</math> |
<math>~=</math> |
<math>~\biggl[ 1 - \frac{3}{u^2} \biggr]^{1/2} \frac{d}{du} \biggl\{ \biggl[ 1 - \frac{3}{u^2} \biggr]^{1/2} \frac{d}{du} \biggr\}</math> |
|
|
<math>~=</math> |
<math>~\biggl[ 1 - \frac{3}{u^2} \biggr]^{1/2} \biggl\{ \frac{3}{u^3} \biggl[ 1 - \frac{3}{u^2} \biggr]^{-1/2} \frac{d}{du} + \biggl[ 1 - \frac{3}{u^2} \biggr]^{1/2} \frac{d^2}{du^2}\biggr\}</math> |
|
|
<math>~=</math> |
<math>~ \frac{3}{u^3} \frac{d}{du} + \biggl[ 1 - \frac{3}{u^2} \biggr] \frac{d^2}{du^2}</math> |
|
<math>~\Rightarrow ~~~ \frac{d^2x}{d\xi^2}</math> |
<math>~=</math> |
<math>~ \frac{3}{u^3} \frac{dx}{du} + \biggl[ 1 - \frac{3}{u^2} \biggr] \frac{d^2x}{du^2} \, .</math> |
The rewritten LAWE is therefore,
|
<math>~0</math> |
<math>~=</math> |
<math>~u^2 \biggl\{ \frac{3}{u^3} \frac{dx}{du} + \biggl[ 1 - \frac{3}{u^2} \biggr] \frac{d^2x}{du^2} \biggr\} + 2\biggl[9 - u^2 \biggr] \frac{1}{u} \cdot \frac{dx}{du} + \biggl[\Omega^2 u^3 - 6\alpha \biggr] x </math> |
|
|
<math>~=</math> |
<math>~(u^2-3) \frac{d^2x}{du^2} + (21 - 2u^2 ) \frac{1}{u} \cdot \frac{dx}{du} + (\Omega^2 u^3 - 6\alpha ) x \, ,</math> |
where we have adopted the shorthand notation,
<math>~\Omega^2 \equiv \frac{\sigma_c^2}{3^{1/2} \gamma_g } \, .</math>
Look at Logarithmic Derivative
Multiplying through by <math>~(u^2/x)</math> gives,
|
<math>~0</math> |
<math>~=</math> |
<math>~(u^2-3) \frac{u^2}{x} \cdot \frac{d^2x}{du^2} + (21 - 2u^2 ) \frac{d\ln x}{d\ln u} + (\Omega^2 u^5 - 6\alpha u^2 ) \, .</math> |
Now, in the context of a separate derivation, we showed that, quite generally we can make the substitution,
|
<math>~\frac{u^2}{x} \cdot \frac{d^2x}{du^2} </math> |
<math>~=</math> |
<math>~ \frac{d}{d\ln u} \biggl[ \frac{d\ln x}{d\ln u} \biggr] + \biggl[ \frac{d\ln x}{d\ln u}-1 \biggr]\cdot \frac{d\ln x}{d\ln u} \, . </math> |
Hence, if we assume that the displacement function can be expressed as a power-law in <math>~u</math>, such that,
<math>\frac{d\ln x}{d\ln u} = c_0 \, ,</math>
then the LAWE for <math>~n=5</math> polytropes simplifies as follows,
|
<math>~0</math> |
<math>~=</math> |
<math>~(u^2-3) c_0(c_0-1) + (21 - 2u^2 ) c_0 + (\Omega^2 u^5 - 6\alpha u^2 ) \, .</math> |
This polynomial equation will be satisfied if, simultaneously, we set:
- <math>\Omega^2 = 0 \, ;</math>
- <math>c_0^2 -3c_0 -6\alpha = 0 </math> <math>~\Rightarrow</math> <math>c_0 = \frac{3}{2}\biggl[1 \pm \biggl(1+\frac{8\alpha}{3} \biggr)^{1/2} \biggl]\, ;</math>
- <math>~\alpha = 20/3 \, .</math>
This gives us some hope that a more general solution of the following form will work:
|
<math>~x</math> |
<math>~=</math> |
<math>~u^{c_0} \biggl[ a + bu + cu^2 + du^3 + \cdots\biggr] \, .</math> |
This means that, for example,
|
<math>~\frac{dx}{du}</math> |
<math>~=</math> |
<math>~ c_0 u^{c_0-1} \biggl[ a + bu + cu^2 + du^3 \biggr] + u^{c_0} \biggl[ b + 2cu + 3du^2 \biggr] </math> |
|
<math>~\Rightarrow ~~~\frac{d\ln x}{d\ln u}</math> |
<math>~=</math> |
<math>~ \frac{c_0(a + bu + cu^2 + du^3) + bu + 2cu^2 + 3du^3}{a + bu + cu^2 + du^3} </math> |
and,
|
<math>~\frac{d^2x}{du^2}</math> |
<math>~=</math> |
<math>~ c_0(c_0-1) u^{c_0-2} \biggl[ a + bu + cu^2 + du^3 \biggr] + 2c_0 u^{c_0-1} \biggl[ b + 2cu + 3du^2 \biggr] + u^{c_0} \biggl[ 2c + 6du \biggr] </math> |
|
<math>~\Rightarrow~~~ \frac{u^2}{x} \cdot \frac{d^2x}{du^2}</math> |
<math>~=</math> |
<math>~ \frac{c_0(c_0-1) ( a + bu + cu^2 + du^3 ) + 2c_0 ( bu + 2cu^2 + 3du^3 ) + ( 2cu^2 + 6du^3 ) }{ a + bu + cu^2 + du^3} </math> |
So the LAWE becomes,
|
<math>~- (\Omega^2 u^5 - 6\alpha u^2 ) (a + bu + cu^2 + du^3)</math> |
<math>~=</math> |
<math>~(u^2-3) [c_0(c_0-1) ( a + bu + cu^2 + du^3 ) + 2c_0 ( bu + 2cu^2 + 3du^3 ) + ( 2cu^2 + 6du^3 )] + (21 - 2u^2 ) [c_0(a + bu + cu^2 + du^3) + bu + 2cu^2 + 3du^3] \,. </math> |
This is cute, but I don't see any way that this approach will provide an avenue to cancel the <math>~\Omega^2 u^5</math> term.
Yet Another Guess
Let's try,
|
<math>~x</math> |
<math>~=</math> |
<math>~e^{a + b\ln\xi + c(\ln\xi)^2} \, ,</math> |
and examine the specific case of <math>~\sigma_c^2 = 0</math>, and, <math>~\gamma = (n+1)/n = 6/5 ~~\Rightarrow~~ \alpha = (3-20/6) = -1/3</math>. Under these conditions, the LAWE for <math>~n=5</math> polytropes becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~(3+\xi^2) \frac{d^2x}{d\xi^2} + \biggl[12 - 2\xi^2 \biggr] \frac{1}{\xi} \cdot \frac{dx}{d\xi} + 2x </math> |
|
|
<math>~=</math> |
<math>~(3+\xi^2) \frac{\xi^2}{x} \cdot \frac{d^2x}{d\xi^2} + \biggl[12 - 2\xi^2 \biggr] \frac{\xi}{x} \cdot \frac{dx}{d\xi} + 2\xi^2 \, . </math> |
And the derivatives give,
|
<math>~\frac{dx}{d\xi}</math> |
<math>~=</math> |
<math>~x \frac{d}{d\xi}\biggl[ a + b\ln\xi + c(\ln\xi)^2 \biggr]</math> |
|
|
<math>~=</math> |
<math>~x \biggl[ \frac{b}{\xi}+ \frac{2c\ln\xi}{\xi} \biggr]</math> |
|
<math>~\Rightarrow ~~~ \frac{\xi}{x} \cdot \frac{dx}{d\xi}</math> |
<math>~=</math> |
<math>~b + 2c\ln\xi \, ;</math> |
and,
|
<math>~\frac{d^2x}{d\xi^2}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{b}{\xi}+ \frac{2c\ln\xi}{\xi} \biggr] \frac{dx}{d\xi} + x \frac{d}{d\xi}\biggl[ \frac{b}{\xi}+ \frac{2c\ln\xi}{\xi} \biggr]</math> |
|
<math>~\Rightarrow ~~~ \frac{\xi^2}{x} \cdot \frac{d^2x}{d\xi^2}</math> |
<math>~=</math> |
<math>~ \xi \biggl[ \frac{b}{\xi}+ \frac{2c\ln\xi}{\xi} \biggr] \frac{\xi}{x} \cdot \frac{dx}{d\xi} + \xi^2 \frac{d}{d\xi}\biggl[ \frac{b+ 2c\ln\xi}{\xi} \biggr]</math> |
|
|
<math>~=</math> |
<math>~ \biggl[ b + 2c\ln\xi \biggr]^2 + \xi \frac{d}{d\xi}\biggl[ b+ 2c\ln\xi \biggr] + (b+ 2c\ln\xi) \xi^2 \biggl[ - \frac{1}{\xi^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ (b + 2c\ln\xi )^2 + 2c- (b+ 2c\ln\xi) </math> |
|
|
<math>~=</math> |
<math>~[ b^2 + 2c - b] + [4bc - 2c] \ln\xi+4c^2 (\ln\xi)^2 \, . </math> |
Hence the "fundamental mode" LAWE becomes,
|
<math>~0</math> |
<math>~=</math> |
<math>~(3+\xi^2) \biggl[ ( b^2 + 2c - b ) + (4bc - 2c) \ln\xi+4c^2 (\ln\xi)^2 \biggr] + (12 - 2\xi^2 ) \biggl[ b + 2c\ln\xi \biggr] \, . + 2\xi^2 </math> |
Now, this expression cannot be satisfied for arbitrary <math>~\xi</math>. But, here we seek a solution only at the surface for the specific model, <math>~\xi = 3</math>. Plugging this value into the expression gives,
|
<math>~0</math> |
<math>~=</math> |
<math>~12 \biggl[ ( b^2 + 2c - b ) + (4bc - 2c) \ln 3+4c^2 (\ln 3)^2 \biggr] + (12 - 18 ) \biggl[ b + 2c\ln 3 \biggr] + 18 </math> |
|
|
<math>~=</math> |
<math>~2 \biggl[ ( b^2 + 2c - b ) + (4bc - 2c) \ln 3+4c^2 (\ln 3)^2 \biggr] -\biggl[ b + 2c\ln 3 \biggr] + 3 \, . </math> |
It appears as though one perfectly satisfactory solution is, <math>~c = 0</math>, in which case, we need,
|
<math>~0</math> |
<math>~=</math> |
<math>~2 b^2 - 3b + 3 </math> |
|
<math>~\Rightarrow~~~b</math> |
<math>~=</math> |
<math>~ \frac{3}{4}\biggl[1 \pm \sqrt{1-\frac{8}{3} } \biggr] \, . </math> |
Thus, <math>~b</math> is an complex number.
Related Discussions
- Radial Oscillations of Uniform-density sphere
- Radial Oscillations of Isolated Polytropes
- Setup
- n = 1: Attempt at Formulating an Analytic Solution
- n = 3: Numerical Solution to compare with M. Schwarzschild (1941)
- n = 5: Attempt at Formulating an Analytic Solution
- In an accompanying Chapter within our "Ramblings" Appendix, we have played with the adiabatic wave equation for polytropes, examining its form when the primary perturbation variable is an enthalpy-like quantity, rather than the radial displacement of a spherical mass shell. This was done in an effort to mimic the approach that has been taken in studies of the stability of Papaloizou-Pringle tori.
- <math>~n=3</math> … M. Schwarzschild (1941, ApJ, 94, 245), Overtone Pulsations of the Standard Model: This work is referenced in §38.3 of [KW94]. It contains an analysis of the radial modes of oscillation of <math>~n=3</math> polytropes, assuming various values of the adiabatic exponent.
- <math>~n=2</math> … C. Prasad & H. S. Gurm (1961, MNRAS, 122, 409), Radial Pulsations of the Polytrope, n = 2
- <math>~n=\tfrac{3}{2}</math> … D. Lucas (1953, Bul. Soc. Roy. Sci. Liege, 25, 585) … Citation obtained from the Prasad & Gurm (1961) article.
- <math>~n=1</math> … L. D. Chatterji (1951, Proc. Nat. Inst. Sci. [India], 17, 467) … Citation obtained from the Prasad & Gurm (1961) article.
- Composite Polytropes … M. Singh (1968, MNRAS, 140, 235-240), Effect of Central Condensation on the Pulsation Characteristics
- Summary of Known Analytic Solutions … R. Stothers (1981, MNRAS, 197, 351-361), Analytic Solutions of the Radial Pulsation Equation for Rotating and Magnetic Star Models
- Interesting Composite! … C. Prasad (1948, MNRAS, 108, 414-416), Radial Oscillations of a Particular Stellar Model

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |