User:Tohline/Appendix/Ramblings/Nonlinar Oscillation

Radial Oscillations in Pressure-Truncated n = 5 Polytropes

Summary Joel E. Tohline (May, 2017) "… a static configuration close to an extremum of the [mass-radius equilibrium] curve may be considered as a perturbed state of a model of the same mass situated on the other side of the extremum. The difference of the two models approximately represents the eigenfunction of the neutral mode. Let there exist two Models 1 and 2 for a mass <math>~M</math> in the vicinity of an extremum; then the eigenfunction <math>~\mathfrak{x}</math> is <math>~\mathfrak{x} = r_2(m_\xi) - r_1(m_\xi) \, ,</math> where <math>~m_\xi</math> is the Lagrangian coordinate and <math>~r_1, r_2</math> Eulerian coordinates of the Models 1 and 2." --- Adapted from §6 of G. S. Bisnovatyi-Kogan & S. I. Blinnikov (1974)   In this Chapter, we focus on pressure-truncated, n = 5 polytropic configurations and demonstrate, entirely via analytical means, that the above-referenced conjecture by G. S. Bisnovatyi-Kogan & S. I. Blinnikov (1974) (hereafter, B-KB74) is correct. Internal Structural Profile of Individual Static Configurations:  When an n = 5 polytropic configuration is embedded in a hot, tenuous external medium of pressure, <math>~P_e</math>, its equilibrium radius will vary with its mass as displayed in Figure 1; the upper portion of this analytically defined equilibrium sequence is shown immediately below, on the right. The location along this sequence of a particular equilibrium (static) configuration — tagged by the subscript index, i — is uniquely identified by the value of a single model parameter:  the dimensionless truncation radius, <math>~{\tilde\xi}_i</math>. The model's normalized total mass is, <math> ~m_\mathrm{tot} \equiv \frac{M_\mathrm{tot}}{M_\mathrm{SWS} } </math> <math>~=~</math> <math> \biggl( \frac{3 \cdot 5^3}{4\pi} \biggr)^{1/2} \biggl( \frac{{\tilde\xi}^2}{3}\biggr)^{3 / 2} \biggl(1+\frac{ {\tilde\xi}^2}{3} \biggr)^{- 2} \, , </math> and the model's internal structural profile is prescribed precisely by the analytic expression, <math>~r_i(m_\xi)</math> <math>~=</math> <math>~\biggl[ \frac{3^2 \cdot 5}{2^2 \pi} \biggr]^{1 / 2} \biggl[ \frac{\tilde{C}_i - 3}{\tilde{C}_i} \biggr] \biggl[ \tilde{C}_i~m_\xi^{-2/3} -3 \biggr]^{-1 / 2} \, ,</math>     where,     <math>~\tilde{C}_i</math> <math>~\equiv</math> <math>~ \frac{3^2}{\tilde\xi_i^2}\biggl( 1 + \frac{\tilde\xi_i^2}{3} \biggr) \, . </math> In this expression the fractional mass, <math>~0 \le m_\xi \le 1</math>, has been employed as the Lagrangian radial coordinate. Note that, at the location of the (maximum-mass) extremum, <math>~{\tilde\xi}_i = 3</math> and, hence, <math>~{\tilde{C}}_i = 4</math> and <math>~m_\mathrm{tot} = m_\mathrm{max} \equiv [3^4\cdot 5^3/(2^{10}\pi)]^{1 / 2}</math>. Static Configurations of Equal Mass Near an Extremum:   In the figure displayed here, on the right, two models with the same total mass and lying near the sequence extremum have been identified. We use the (always real and positive) parameter, <math>~\mu \equiv \biggl[ 1 - \biggl( \frac{m_\mathrm{tot}}{m_\mathrm{max}} \biggr)^2 \biggr]^{1 / 2} \, ,</math> to quantify how close the mass of a given pair of models is to the limiting mass. As depicted here, Model 1 (Model 2) necessarily has a dimensionless truncation radius that is greater (less) than 3; as we demonstrate below, the precise values of the <math>~({\tilde\xi}_1, {\tilde\xi}_2)</math> parameter pair that are associated with a given choice of <math>~\mu</math> can be determined analytically as roots of the quartic equation that, itself, defines the mass-radius equilibrium sequence. The Nonlinear Displacement Function, <math>~\mathfrak{x}</math>:  The (nonlinear) displacement that will map the radial location of every mass shell within Model 1 into the corresponding radial location of every mass shell within Model 2 is given precisely by the expression, <math>~\mathfrak{x} = r_2(m_\xi) - r_1(m_\xi) \, .</math> It is clear, therefore, that the (nonlinear, static-model) eigenfunction referenced in the above B-KB74 quote is definable analytically for pressure-truncated, n = 5 polytropic configurations. In what follows we have found it useful to reference, as well, the corresponding nonlinear fractional displacement function, <math>~x_\mathrm{BKB74} = \frac{\Delta r}{r} \equiv \frac{\mathfrak{x}}{2\langle r \rangle} = \frac{r_2(m_\xi) - r_1(m_\xi)}{r_2(m_\xi) + r_1(m_\xi)} \, .</math> Eigenfunction of the Neutral Mode:  In a separate chapter, we have proven that the fundamental mode of radial oscillation associated with the maximum-mass model along the equilibrium sequence has an eigenfrequency that is precisely zero — that is, the model at the extremum of the sequence is marginally unstable [dynamically] — and it has a radial eigenfunction that is defined by the expression, <math>~x_P \equiv \frac{\delta r}{r}</math> <math>~=</math> <math>~\frac{2A_0}{5} \biggl[ \frac{10 -9~m_\xi^{2/3}}{4 -3~m_\xi^{2/3}} \biggr] \, ,</math> where, <math>~A_0</math> is an arbitrary, overall scaling coefficient. This is what B-KB74 refer to as the "eigenfunction of the neutral mode." Comparison:  By plotting one function on top of the other, in the righthand panel of Figure 2, below — see, also, the animation displayed here on the left — we illustrate that, as conjectured by B-KB74, the nonlinear fractional displacement function, <math>~x_\mathrm{BKB74} </math>, does very accurately represent the exact eigenfunction of the neutral mode for small values of the parameter, <math>~\mu</math>. The validity of this conjecture can be demonstrated even more quantitatively by expanding the function, <math>~x_\mathrm{BKB74} </math>, as a power series in <math>~\mu</math>. To lowest order, we find that, <math>~x_\mathrm{BKB74} </math> <math>~=</math> <math>~ \biggl( \frac{1}{2 \cdot 3} \biggr)^{1 / 2}\mu \biggl[ \frac{10 -9~m_\xi^{2/3}}{4 -3~m_\xi^{2/3}} \biggr] + \mathcal{O}(\mu^2) \, . </math> Especially after setting <math>~A_0 = [5^2/(2^3\cdot 3)]^{1 / 2}\mu</math>, it is clear that <math>~x_\mathrm{BKB74} </math> more and more accurately matches <math>~x_P</math>, as <math>~\mu \rightarrow 0</math>.

[Comment by Joel Tohline on 24 August 2016]  Over the past few weeks, I have been putting together a powerpoint presentation that summarizes what I've learned, especially over the last several years, about turning points — and their relative positioning with respect to points of dynamical instability — along equilibrium sequences. One key finding, which is illustrated in Figure 3 of that discussion, is that the transition from stable to unstable systems along the n = 5 sequence occurs after, rather than at, the pressure maximum of the sequence. This means that, in the immediate vicinity of the pressure maximum, two stable equilibrium configurations exist with the same <math>~(K, M_\mathrm{tot}, P_e) </math> but different radii. Perhaps this means that, in the absence of dissipation, and without the need for a driving mechanism, a permanent oscillation between these two states can be activated.

Upon further thought, it occurred to me that a careful examination of the internal structure of both models — especially relative to one another — might reveal what the eigenvector of that (nonlinear) oscillation might be. In support of this idea, I point to the discussion of "Turning-Points and the Onset of Instability" found in §6.8 of [ST83] — specifically, on p. 149 in the paragraph that follows eq. (6.8.11) — where we find the following statement: "… the eigenfunction at a critical point is simply the Lagrangian displacement <math>~\xi</math> that carries an equilibrium configuration on the low-density side of the critical point into an equilibrium configuration on the high-density side."

See related arguments made by:

• Bisnovatyi-Kogan & Blinnikov (1974) — see especially their §6 — as we have briefly reviewed in an introductory paragraph
• Stahler (1983), as we have briefly reviewed in a separate chapter

Revised Attack

Equilibrium Structural Properties

As we have detailed in an accompanying chapter, some basic properties of pressure-truncated, <math>~n = 5</math> polytropic configurations are:

<math>~\theta</math>	<math>~=</math>	<math>~\biggl(1 + \frac{\xi^2}{3}\biggr)^{- 1 / 2} = \biggl(1 + \ell^2\biggr)^{- 1 / 2} \, ,</math>
<math>~\frac{d\theta}{d\xi}</math>	<math>~=</math>	<math>~- \frac{\xi}{3} \biggl(1 + \frac{\xi^2}{3}\biggr)^{- 3 / 2} = - \frac{\ell}{3^{1 / 2}}\biggl(1 + \ell^2\biggr)^{- 3 / 2} \, ,</math>
<math>~\ell^2 \equiv \frac{\xi^2}{3}</math>	<math>~\Rightarrow</math>	<math>~\xi^2 = 3\ell^2 \, ,</math>
<math> ~\frac{M_\mathrm{tot}}{M_\mathrm{SWS} } </math>	<math>~=~</math>	<math> \biggl( \frac{n^3}{4\pi} \biggr)^{1/2} \theta^{(n-3)/2} (- \xi^2 \theta^') = \biggl( \frac{5^3}{4\pi} \biggr)^{1/2} \theta (- \xi^2 \theta^') </math>
	<math>~=~</math>	<math> \biggl( \frac{3 \cdot 5^3}{4\pi} \biggr)^{1/2} \ell^3 (1+\ell^2)^{- 2} \, , </math>
<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{SWS} } </math>	<math>~=~</math>	<math> \biggl( \frac{n}{4\pi} \biggr)^{1/2} \xi \theta^{(n-1)/2} = \biggl( \frac{5}{4\pi} \biggr)^{1/2} \xi \theta^{2} </math>
	<math>~=~</math>	<math> \biggl( \frac{3 \cdot 5}{4\pi} \biggr)^{1/2} \ell (1+\ell^2)^{-1} \, , </math>
<math>~M_\mathrm{SWS}</math>	<math>~\equiv</math>	<math>~\biggl( \frac{n+1}{nG} \biggr)^{3/2} K^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} = \biggl( \frac{6}{5G} \biggr)^{3/2} K^{5 / 3} P_\mathrm{e}^{- 1 / 6} \, ,</math>
<math>~R_\mathrm{SWS}</math>	<math>~\equiv</math>	<math>~ \biggl( \frac{n+1}{nG} \biggr)^{1/2} K^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} = \biggl( \frac{6}{5G} \biggr)^{1/2} K^{5/6} P_\mathrm{e}^{- 1 / 3} \, ,</math>
<math>~0</math>	<math>~=~</math>	<math> \biggl( \frac{M}{M_\mathrm{SWS}} \biggr)^2 - 5 \biggl( \frac{M}{M_\mathrm{SWS}} \biggr)\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr) + \frac{2^2 \cdot 5 \pi}{3} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^4 \, . </math>

This last expression can either be viewed as a quadratic equation whose solution provides an analytic expression for m(r), or a quartic equation whose solution provides an analytic expression for r(m).

Roots of Quadratic Equation

Solving the quadratic equation, we find that,

<math>~\frac{M}{M_\mathrm{SWS}}</math>

<math>~=</math>

<math>~ \frac{5}{2}\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr) \biggl\{ 1 \pm \biggl[ 1 - \frac{2^4\pi}{3\cdot 5}\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^2 \biggr]^{1 / 2} \biggr\} \, . </math>

As has been summarized in Table 3 of an accompanying discussion, two extrema exist with the following coordinates:

• Maximum radius:     <math>\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}}, \frac{M}{M_\mathrm{SWS}} \biggr)

= [ r_\mathrm{max}, m_\mathrm{crit} ] \equiv \biggl[ \biggl( \frac{3\cdot 5}{2^4 \pi} \biggr)^{1 / 2} , \biggl( \frac{3\cdot 5^3}{2^6 \pi} \biggr)^{1 / 2} \biggr]</math>

• Maximum mass:     <math>\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}}, \frac{M}{M_\mathrm{SWS}} \biggr)

= [r_\mathrm{crit}, m_\mathrm{max} ] \equiv \biggl[ \biggl( \frac{3^2\cdot 5}{2^6 \pi} \biggr)^{1 / 2} , \biggl( \frac{3^4\cdot 5^3}{2^{10} \pi} \biggr)^{1 / 2} \biggr]</math>

Roots of Quartic Equation

Analytic Solution

Here we will adopt the shorthand notation,

<math>~\chi \equiv \frac{R_\mathrm{eq}}{R_\mathrm{SWS}}</math>      and      <math>~m \equiv \frac{M}{M_\mathrm{SWS}} \, .</math>

Drawing from the Wikipedia discussion of the quartic function, we will think in terms of the generic quartic form,

<math>~0</math>

<math>~=</math>

<math>~a\chi^4 + b\chi^3 + c\chi^2 + d\chi + e \,.</math>

Relating this to our specific quartic function, we should make the following assignments:

<math>~a</math>	<math>~=</math>	<math>~\frac{2^2 \cdot 5 \pi}{3} </math>
<math>~b</math>	<math>~=</math>	<math>~0</math>
<math>~c</math>	<math>~=</math>	<math>~0</math>
<math>~d</math>	<math>~=</math>	<math>~-5m</math>
<math>~e</math>	<math>~=</math>	<math>~m^2</math>

We need to evaluate the following expressions:

<math>~p</math>	<math>~\equiv</math>	<math>~\frac{8ac-3b^2}{8a^2}</math>
	<math>~=</math>	<math>~0</math>
<math>~q</math>	<math>~\equiv</math>	<math>~\frac{b^3 - 4abc + 8a^2d}{8a^3} </math>
	<math>~=</math>	<math>~\frac{d}{a} = - \frac{3m}{2^2 \pi} </math>
<math>~\Delta_0</math>	<math>~\equiv</math>	<math>~c^2 - 3bd + 12ae</math>
	<math>~=</math>	<math>~12ae = 2^4 \cdot 5~\pi m^2</math>
<math>~\Delta_1</math>	<math>~\equiv</math>	<math>~2c^3 - 9bcd + 27b^2e+27ad^2 - 72ace</math>
	<math>~=</math>	<math>~27ad^2 = 3^3 \cdot 5^2 m^2 \cdot \frac{2^2 \cdot 5 \pi}{3} = 2^2 \cdot 3^2 \cdot 5^3 ~\pi m^2</math>

Note that the discriminant is,

<math>~\Delta</math>	<math>~=</math>	<math>~ 256a^3 e^3 - 192a^2bde^2 - 128a^2c^2e^2 + 144a^2 c d^2e - 27a^2d^4 </math>
		<math>~ + 144 a b^2c e^2 - 6ab^2d^2e - 80 abc^2de + 18abcd^3 + 16ac^4e </math>
		<math>~ - 4ac^3 d^2 - 27b^4e^2 + 18b^3cde - 4b^3d^3 - 4b^2c^3e + b^2c^2d^2 </math>
	<math>~=</math>	<math>~ 256a^3 e^3 - 27a^2d^4 </math>
	<math>~=</math>	<math>~ 2^8\biggl( \frac{2^2 \cdot 5 \pi}{3} \biggr)^3 m^6 - 3^3\biggl( \frac{2^2 \cdot 5 \pi}{3} \biggr)^2 5^4 m^4 </math>
	<math>~=</math>	<math>~ \biggl( \frac{2^{14} \cdot 5^3 \pi^3}{3^3} \biggr) m^6 - \biggl( 2^4 \cdot 3 \cdot 5^6 \pi^2 \biggr) m^4 </math>
	<math>~=</math>	<math>~ - \biggl( 2^4 \cdot 3 \cdot 5^6 \pi^2 \biggr) m^4 \biggl[1 - \biggl( \frac{1}{2^4 \cdot 3 \cdot 5^6 \pi^2 m^4} \biggr) \biggl( \frac{2^{14} \cdot 5^3 \pi^3}{3^3} \biggr) m^6 \biggr] </math>
	<math>~=</math>	<math>~ - \biggl( 2^4 \cdot 3 \cdot 5^6 \pi^2 \biggr) m^4 \biggl[1 - \biggl( \frac{2^{10} \pi}{3^4\cdot 5^3} \biggr) m^2 \biggr] \, , </math>

and it will be negative (or, in the limit, zero) as long as <math>~m \le m_\mathrm{max}</math>, where, as defined above, <math>~m_\mathrm{max} \equiv [3^4\cdot 5^3/(2^{10}\pi)]^{1 / 2}</math>. Because the discriminant is always negative (or, at most, zero), then our quartic equation has two distinct real roots and two complex conjugate non-real roots.

Furthermore note that,

<math>~\Delta_1^2 - 4\Delta_0^3</math>	<math>~=</math>	<math>~ (2^2 \cdot 3^2 \cdot 5^3 ~\pi m^2)^2 - 2^2(2^4 \cdot 5~\pi m^2 )^3 = (2^4 \cdot 3^4 \cdot 5^6 ~\pi^2 m^4) \biggl[1 - \frac{(2^{14} \cdot 5^3~\pi^3 m^6 )}{2^4 \cdot 3^4 \cdot 5^6 ~\pi^2 m^4}\biggr] </math>
	<math>~=</math>	<math>~ (2^4 \cdot 3^4 \cdot 5^6 ~\pi^2 m^4) \biggl[1 - \biggl(\frac{2^{10} ~\pi}{3^4 \cdot 5^3 }\biggr) m^2\biggr] \, , </math>

and it will never be negative, as long as <math>~m \le m_\mathrm{max}</math>.

For a given value of <math>~m</math>, then, the pair of real roots is:

<math>~\chi_\pm</math>

<math>~=</math>

<math>~ -\frac{b}{4a} + S \pm \frac{1}{2}\biggl[ -4S^2 - 2p - \frac{q}{S} \biggr]^{1/2} \, , </math>

where,

<math>~S</math>	<math>~\equiv</math>	<math>~ \frac{1}{2}\biggl[- \frac{2p}{3} + \frac{1}{3a}\biggl(Q + \frac{\Delta_0}{Q}\biggr) \biggr]^{1/2} \, , </math>
<math>~Q</math>	<math>~\equiv</math>	<math>~ \biggl[ \frac{\Delta_1 + \sqrt{\Delta_1^2 - 4\Delta_0^3}}{2} \biggr]^{1/3} \, . </math>

Let's work through these expressions.

<math>~Q</math>	<math>~=</math>	<math>~(2 \cdot 3^2 \cdot 5^3 ~\pi m^2)^{1 / 3} \biggl\{ 1 + \biggl[1 - \biggl( \frac{m}{m_\mathrm{max}}\biggr)^2\biggr]^{1 / 2} \biggr\}^{1/3} \, , </math>
<math>~S^2</math>	<math>~=</math>	<math>~ \frac{1}{2^2 \cdot 3a}\biggl(Q + \frac{\Delta_0}{Q}\biggr) </math>
	<math>~=</math>	<math>~ \frac{Q}{2^4 \cdot 5 \pi} + \frac{m^2}{Q} \, , </math>
<math>~\chi_\pm</math>	<math>~=</math>	<math>~ S \pm \frac{1}{2}\biggl[\frac{1}{S}\biggl( \frac{3m}{2^2\pi} \biggr) -4S^2 \biggr]^{1/2} </math>
	<math>~=</math>	<math>~ S \pm \biggl( \frac{3m}{2^4\pi ~S} \biggr)^{1 / 2} \biggl[1 - \frac{2^4\pi ~S^3}{3m} \biggr]^{1/2} </math>
	<math>~=</math>	<math>~ S \biggl\{1 \pm \biggl[\frac{3m}{2^4\pi ~S^3} - 1 \biggr]^{1/2} \biggr\} \, . </math>

Check at Maximum Mass

As a check, recognize that the two roots should be identical, and given by (see above definition) <math>~r_\mathrm{crit} = [3^2 \cdot 5/(2^6\pi)]^{1 / 2}</math>, when <math>~m = m_\mathrm{max}</math>. Let's see …

<math>~Q\biggr|_{m_\mathrm{max}}</math>	<math>~=</math>	<math>~\biggl[ 2 \cdot 3^2 \cdot 5^3 ~\pi \biggl( \frac{3^4\cdot 5^3}{2^{10}\pi}\biggr)\biggr]^{1 / 3} = \biggl[ \frac{3^6\cdot 5^6}{2^{9}} \biggr]^{1 / 3} = \frac{3^2\cdot 5^2}{2^{3}} </math>
<math>~\Rightarrow ~~~ S^2 \biggr|_{m_\mathrm{max}}</math>	<math>~=</math>	<math>~ \frac{1}{2^4 \cdot 5 \pi} \biggl(\frac{3^2\cdot 5^2}{2^{3}}\biggr) + \biggl( \frac{3^4\cdot 5^3}{2^{10}\pi}\biggr)\biggl(\frac{2^{3}}{3^2\cdot 5^2}\biggr) = \frac{3^2\cdot 5}{2^{6} \pi} = r_\mathrm{crit}^2 </math>
<math>~\Rightarrow~~~ \chi_\pm\biggr|_{m_\mathrm{max}}</math>	<math>~=</math>	<math>~ r_\mathrm{crit} \biggl\{1 \pm \biggl[\frac{3}{2^4\pi }\biggl( \frac{3^4\cdot 5^3}{2^{10}\pi}\biggr)^{1 / 2}\biggl( \frac{2^{6} \pi}{3^2\cdot 5} \biggr)^{3 / 2} - 1 \biggr]^{1/2} \biggr\} = r_\mathrm{crit} \, , </math>

Q.E.D.

In Terms of the Limiting Mass

Because it will be useful to us later, let's rewrite the expression for <math>~\chi_\pm</math> in terms of the new parameter,

<math>~\mu \equiv \biggl[ 1 - \biggl( \frac{m}{m_\mathrm{max}} \biggr)^2 \biggr]^{1 / 2}</math>       <math>~\Rightarrow</math>       <math>~m^2 =

m_\mathrm{max}^2(1-\mu^2) = \frac{3^4\cdot 5^3}{2^{10} \pi}(1-\mu^2) \, ,</math>

which will be small — and always positive — in the vicinity of the limiting mass. For <math>~S</math> and <math>~Q</math> we have,

<math>~Q^3</math>	<math>~=</math>	<math>~(2 \cdot 3^2 \cdot 5^3 ~\pi m^2)(1+\mu) </math>
	<math>~=</math>	<math>~\biggl[ \frac{3^2\cdot 5^2}{2^{3}} \biggr]^{3} (1-\mu^2)(1+\mu) \, . </math>
<math>~S^2</math>	<math>~=</math>	<math>~ \frac{Q}{2^4 \cdot 5 \pi}\biggl[1 + \frac{2^4\cdot 5\pi ~m^2}{Q^2} \biggr] </math>
	<math>~=</math>	<math>~ \frac{1}{2^4 \cdot 5 \pi}\biggl[ \frac{3^2\cdot 5^2}{2^{3}} \biggr] (1-\mu^2)^{1 / 3}(1+\mu)^{1 / 3} \biggl[1 + \frac{2^4\cdot 5\pi }{Q^2} \cdot \frac{3^4\cdot 5^3}{2^{10} \pi}(1-\mu^2)\biggr] </math>
	<math>~=</math>	<math>~ \biggl[ \frac{3^2\cdot 5}{2^{7}~\pi} \biggr] (1-\mu^2)^{1 / 3}(1+\mu)^{1 / 3} \biggl[1 + \frac{3^4\cdot 5^4}{2^{6} } \cdot \frac{(1-\mu^2)}{Q^2}\biggr] </math>
	<math>~=</math>	<math>~ \biggl( \frac{r_\mathrm{crit}^2}{2} \biggr) (1-\mu^2)^{1 / 3}(1+\mu)^{1 / 3} \biggl[ 1 + (1-\mu^2)^{1 / 3} (1+\mu)^{- 2 / 3} \biggr] </math>
<math>~\Rightarrow ~~~ \biggl( \frac{S}{r_\mathrm{crit}}\biggr)^2</math>	<math>~=</math>	<math>~ (1-\mu^2)^{1 / 3}(1+\mu)^{1 / 3} \biggl[ \frac{1 + (1-\mu^2)^{1 / 3} (1+\mu)^{- 2 / 3}}{2} \biggr] </math>
	<math>~=</math>	<math>~ (1-\mu^2)^{1 / 3}(1+\mu)^{-1 / 3} \biggl[ \frac{(1+\mu)^{2 / 3} + (1-\mu^2)^{1 / 3} }{2} \biggr] </math>
	<math>~=</math>	<math>~ (1-\mu^2)^{1 / 3} \biggl[ \frac{(1+\mu)^{1 / 3} + (1-\mu)^{1 / 3} }{2} \biggr] \, . </math>

This means that,

<math>~\frac{3m}{2^4\pi ~S^3} </math>	<math>~=</math>	<math>~ \frac{3m}{2^4\pi } \biggl\{ \biggl( \frac{r_\mathrm{crit}^2}{2} \biggr) (1-\mu^2)^{1 / 3}(1+\mu)^{1 / 3} \biggl[ 1 + (1-\mu^2)^{1 / 3} (1+\mu)^{- 2 / 3} \biggr] \biggr\}^{-3 / 2} </math>
	<math>~=</math>	<math>~ \frac{3}{2^4\pi } \biggl[ \frac{3^4\cdot 5^3}{2^{10} \pi} \biggr]^{ 1 / 2} \biggl( \frac{2}{r_\mathrm{crit}^2} \biggr)^{3 / 2} (1-\mu^2)^{1 / 2} \biggl\{ (1-\mu^2)^{-1 / 2}(1+\mu)^{- 1 / 2} \biggl[ 1 + (1-\mu^2)^{1 / 3} (1+\mu)^{- 2 / 3} \biggr]^{-3 / 2} \biggr\} </math>
	<math>~=</math>	<math>~ (1+\mu)^{- 1 / 2} \biggl[ \frac{1 + (1-\mu^2)^{1 / 3} (1+\mu)^{- 2 / 3}}{2} \biggr]^{-3 / 2} </math>
	<math>~=</math>	<math>~ \biggl[ \frac{(1+\mu)^{1 / 3} + (1-\mu)^{1 / 3} }{2} \biggr]^{- 3 / 2} \, . </math>

Hence, utilizing the shorthand notation,

<math>~u^2(\mu) \equiv \biggl[ \frac{(1+\mu)^{1 / 3} + (1-\mu)^{1 / 3} }{2} \biggr]^{-1} \, ,</math>

we have,

<math>~\biggl(\frac{\chi}{r_\mathrm{crit}}\biggr)_\pm</math>	<math>~=</math>	<math>~ \frac{S}{r_\mathrm{crit}} \biggl\{1 \pm \biggl[\frac{3m}{2^4\pi ~S^3} - 1 \biggr]^{1/2} \biggr\} </math>
	<math>~=</math>	<math>~ \frac{(1-\mu^2)^{1 / 6}}{u} \biggl[1 \pm (u^3 - 1 )^{1/2} \biggr] \, . </math>

Approximation Near the Limiting Mass

When <math>~m</math> is near <math>~m_\mathrm{max}</math>, we know that <math>~0 \le \mu \ll 1</math>. So, drawing on the binomial expansion, we have,

<math>~ \frac{(1+\mu)^{1 / 3} + (1-\mu)^{1 / 3} }{2} </math>	<math>~=</math>	<math>~\frac{1}{2} \biggl[ 1+ \frac{1}{3}\mu + \frac{1}{2}\biggl(\frac{1}{3}\biggr) \biggl(\frac{1}{3}-1\biggr) \mu^2 + \cdots + 1 - \frac{1}{3}\mu + \frac{1}{2}\biggl(\frac{1}{3}\biggr) \biggl(\frac{1}{3}-1\biggr) \mu^2 + \cdots \biggr] </math>
	<math>~=</math>	<math>~\frac{1}{2} \biggl\{ 2 - \biggl(\frac{2}{3^2}\biggr) \mu^2 + 2\biggl[ \frac{1}{3\cdot 2^3} \biggl(\frac{1}{3}\biggr) \biggl(\frac{1}{3}-1\biggr) \biggl(\frac{1}{3}-2\biggr) \biggl(\frac{1}{3}-3\biggr)\biggr]\mu^4 + \cdots \biggr\} </math>
	<math>~=</math>	<math>~ 1 - \biggl(\frac{1}{3^2}\biggr) \mu^2 + \biggl[ \frac{1}{2^3 \cdot 3^2 } \biggl(-\frac{2}{3}\biggr) \biggl(- \frac{5}{3}\biggr) \biggl(- \frac{8}{3}\biggr)\biggr]\mu^4 + \cdots </math>
	<math>~=</math>	<math>~ 1 - \biggl(\frac{\mu}{3}\biggr)^2 - \biggl[ \frac{2\cdot 5}{3^5 } \biggr]\mu^4 + \cdots </math>

Hence,

<math>~\frac{(1-\mu^2)^{1 / 6}}{u}</math>	<math>~=</math>	<math>~\biggl[ 1 - \frac{\mu^2}{6} + \frac{1}{2}\biggl(\frac{1}{6}\biggr) \biggl(\frac{1}{6}-1\biggr)\mu^4 + \mathcal{O}(\mu^6)\biggr] \biggl[ 1 - \biggl( \frac{\mu^2}{3^2} + \frac{2\cdot 5 \mu^4}{3^5 } \biggr) + \mathcal{O}(\mu^6) \biggr]^{1 / 2} </math>
	<math>~=</math>	<math>~\biggl[ 1 - \frac{\mu^2}{2\cdot 3} - \biggl(\frac{5}{2^3\cdot 3^2}\biggr)\mu^4 + \mathcal{O}(\mu^6) \biggr] \biggl[ 1 - \frac{1}{2}\biggl( \frac{\mu^2}{3^2} + \frac{2\cdot 5 \mu^4}{3^5 } \biggr) - \biggl( \frac{\mu^4}{2^3\cdot 3^4} \biggr)+ \mathcal{O}(\mu^6) \biggr] </math>
	<math>~=</math>	<math>~\biggl[ 1 - \frac{\mu^2}{2\cdot 3} - \biggl(\frac{5}{2^3\cdot 3^2}\biggr)\mu^4 + \mathcal{O}(\mu^6) \biggr] \biggl[ 1 - \frac{\mu^2}{2 \cdot 3^2} - \biggl( \frac{43}{2^3 \cdot 3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^6) \biggr] </math>
	<math>~=</math>	<math>~ 1 - \frac{\mu^2}{2\cdot 3} - \biggl(\frac{5}{2^3\cdot 3^2}\biggr)\mu^4 - \biggl[ 1 - \frac{\mu^2}{2\cdot 3} \biggr] \biggl[ \frac{\mu^2}{2 \cdot 3^2} \biggr] - \biggl( \frac{43}{2^3 \cdot 3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^6) </math>
	<math>~=</math>	<math>~ 1 - \biggl[ \frac{\mu^2}{2\cdot 3} + \frac{\mu^2}{2 \cdot 3^2} \biggr] + \biggl[ \frac{1}{2^2 \cdot 3^3} - \frac{5}{2^3\cdot 3^2} - \frac{43}{2^3 \cdot 3^5 } \biggr]\mu^4 + \mathcal{O}(\mu^6) </math>
	<math>~=</math>	<math>~ 1 - \biggl(\frac{2}{3^2}\biggr) \mu^2 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^6) \, ; </math>

and,

<math>~u^3</math>	<math>~=</math>	<math>~ \biggl[ 1 - \biggl( \frac{\mu^2}{3^2} + \frac{2\cdot 5 \mu^4}{3^5 } \biggr) + \mathcal{O}(\mu^6) \biggr]^{-3 / 2} </math>
	<math>~=</math>	<math>~ 1 + \frac{3}{2} \biggl( \frac{\mu^2}{3^2} + \frac{2\cdot 5 \mu^4}{3^5 } \biggr) + \frac{1}{2} \biggl( -\frac{3}{2}\biggr) \biggl( -\frac{3}{2} - 1\biggr) \biggl( \frac{\mu^2}{3^2} \biggr)^2 + \mathcal{O}(\mu^6) </math>
	<math>~=</math>	<math>~ 1 + \biggl( \frac{\mu^2}{2 \cdot 3}\biggr) + \biggl(\frac{5 }{3^4 } + \frac{5}{2^3 \cdot 3^3} \biggr)\mu^4 + \mathcal{O}(\mu^6) </math>
	<math>~=</math>	<math>~ 1 + \biggl( \frac{\mu^2}{2 \cdot 3}\biggr) + \biggl( \frac{55}{2^3 \cdot 3^4} \biggr) \mu^4 + \mathcal{O}(\mu^6) \, . </math>

Therefore the two real roots of the quartic equation are,

<math>~\biggl(\frac{\chi}{r_\mathrm{crit}}\biggr)_\pm</math>	<math>~=</math>	<math>~ \frac{(1-\mu^2)^{1 / 6}}{u} \biggl\{1 \pm \biggl[u^3 - 1 \biggr]^{1/2} \biggr\} </math>
	<math>~=</math>	<math>~\biggl[ 1 - \biggl(\frac{2}{3^2}\biggr) \mu^2 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^6) \biggr] \biggl\{1 \pm \biggl[\biggl( \frac{\mu^2}{2 \cdot 3}\biggr) + \biggl( \frac{55}{2^3 \cdot 3^4} \biggr) \mu^4 + \mathcal{O}(\mu^6) \biggr]^{1/2} \biggr\} </math>
	<math>~=</math>	<math>~\biggl[ 1 - \biggl(\frac{2}{3^2}\biggr) \mu^2 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 \biggr] \biggl\{1 \pm \biggl( \frac{\mu^2}{2 \cdot 3}\biggr)^{1 / 2} \biggl[1 + \biggl( \frac{5\cdot 11}{2^2 \cdot 3^3} \biggr) \mu^2 + \mathcal{O}(\mu^4) \biggr]^{1/2} \biggr\} </math>
	<math>~=</math>	<math>~\biggl[ 1 - \biggl(\frac{2}{3^2}\biggr) \mu^2 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 \biggr] \biggl\{1 \pm \biggl( \frac{\mu^2}{2 \cdot 3}\biggr)^{1 / 2} \biggl[1 + \biggl( \frac{5\cdot 11}{2^3 \cdot 3^3} \biggr) \mu^2 + \mathcal{O}(\mu^4) \biggr] \biggr\} </math>
	<math>~=</math>	<math>~\biggl[ 1 - \biggl(\frac{2}{3^2}\biggr) \mu^2 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 \biggr] \biggl[ 1 \pm \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu \pm \biggl( \frac{5^2 \cdot 11^2}{2^7 \cdot 3^7} \biggr)^{1 / 2} \mu^3 + \mathcal{O}(\mu^5) \biggr] </math>
	<math>~=</math>	<math>~ \biggl[1 - \biggl(\frac{2}{3^2}\biggr) \mu^2- \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 \biggr] ~\pm~ \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu \biggl[1 - \biggl(\frac{2}{3^2}\biggr) \mu^2 \biggr] ~\pm~ \biggl( \frac{5^2 \cdot 11^2}{2^7 \cdot 3^7} \biggr)^{1 / 2} \mu^3 + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ 1 ~\pm~ \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu - \biggl(\frac{2}{3^2}\biggr) \mu^2 ~\pm~ \biggl[ \biggl( \frac{5^2 \cdot 11^2}{2^7 \cdot 3^7} \biggr)^{1 / 2} - \biggl(\frac{2}{3^5}\biggr)^{1 / 2} \biggr]\mu^3 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ 1 ~\pm~ \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu - \biggl(\frac{2}{3^2}\biggr) \mu^2 ~\pm~ \biggl( \frac{7^2}{2^7 \cdot 3^7} \biggr)^{1 / 2}\mu^3 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^5) \, . </math>

An Excel-spreadsheet check appears to indicate that this expansion is correct, to the specified order.

Identifying Equal-Mass Pairs

Determining the Relevant Values of <math>~\tilde\xi</math>

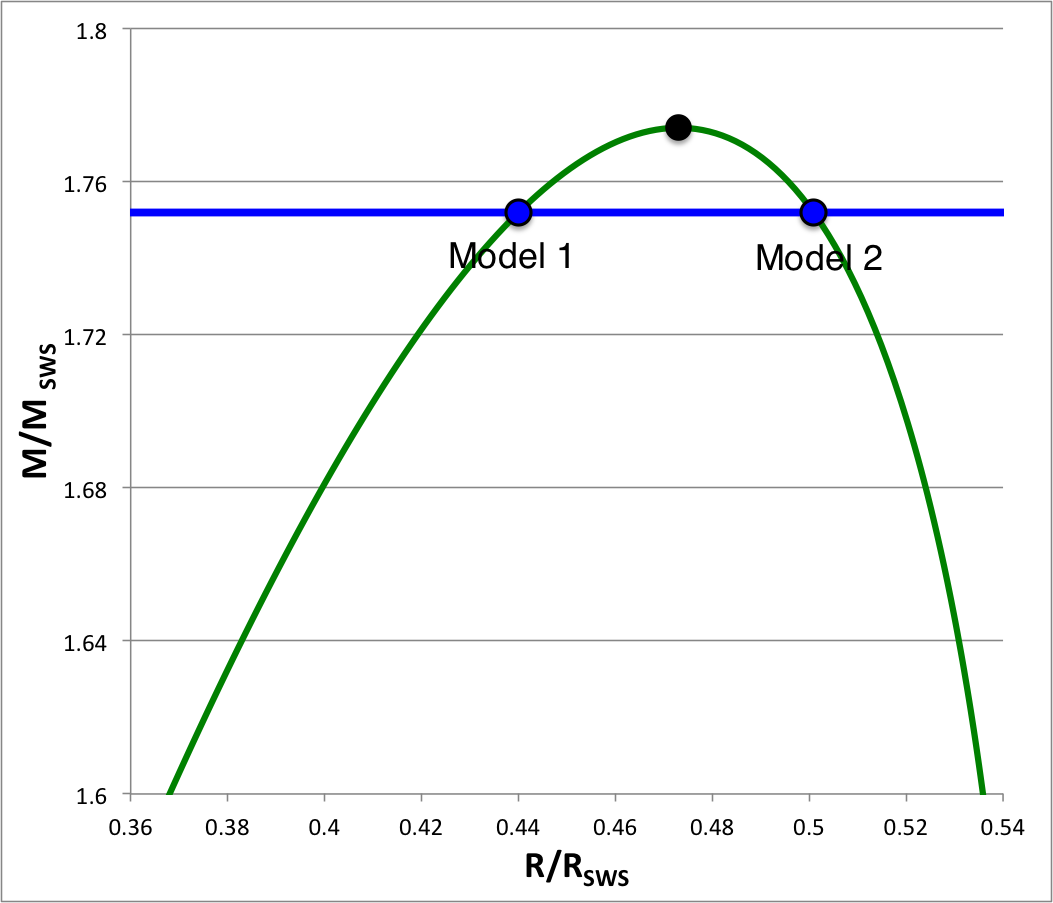
Figure 1:   n = 5 Mass-Radius Sequence

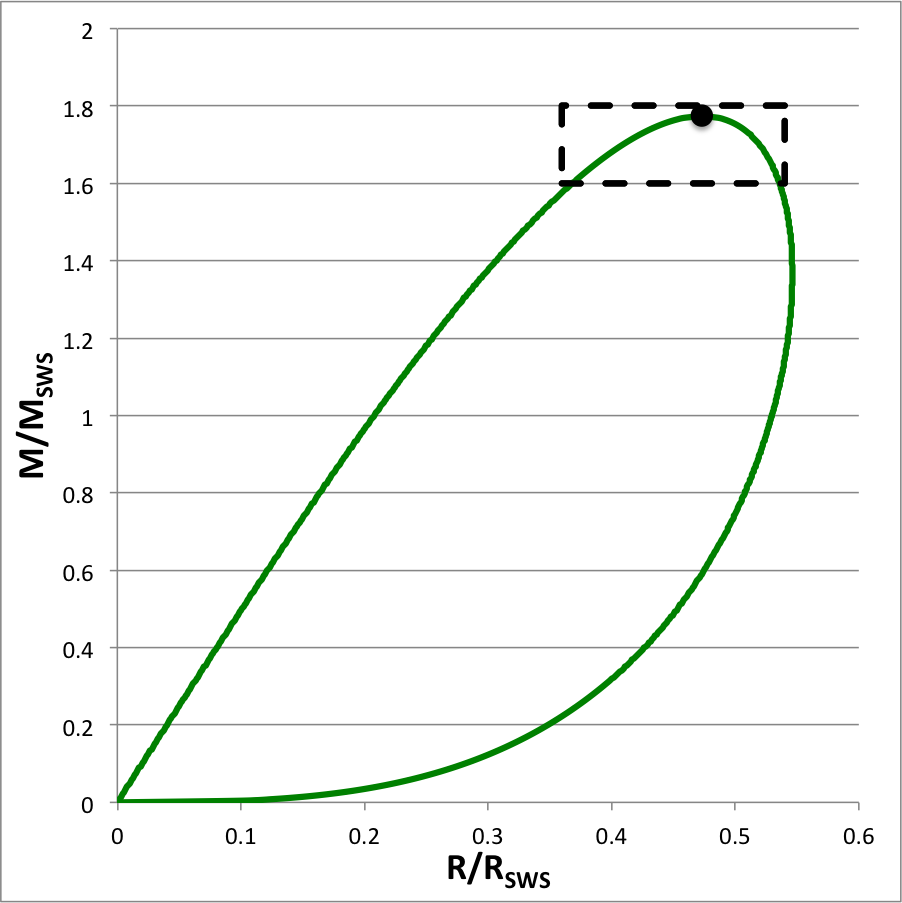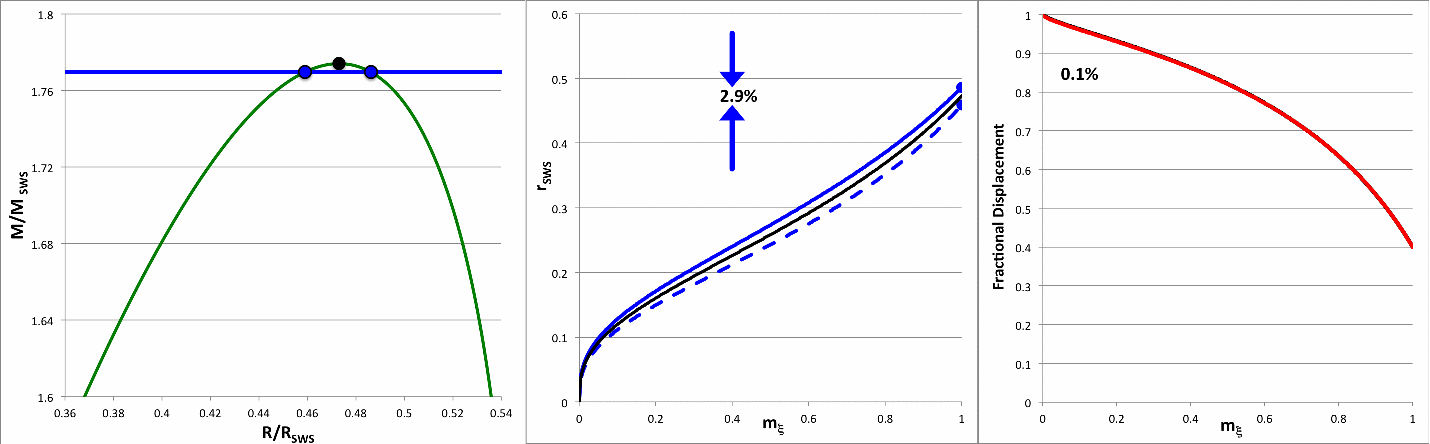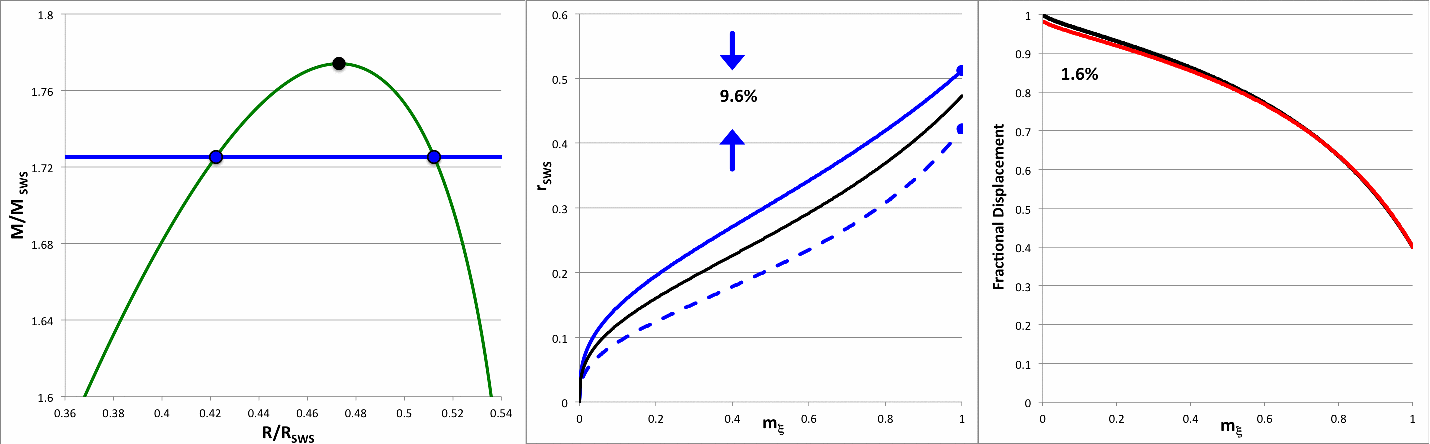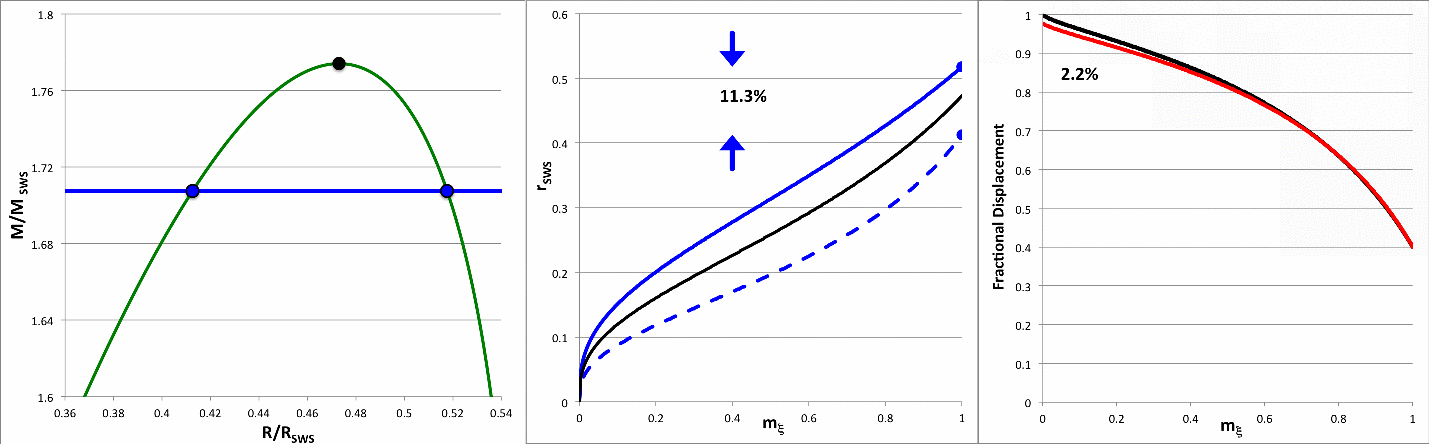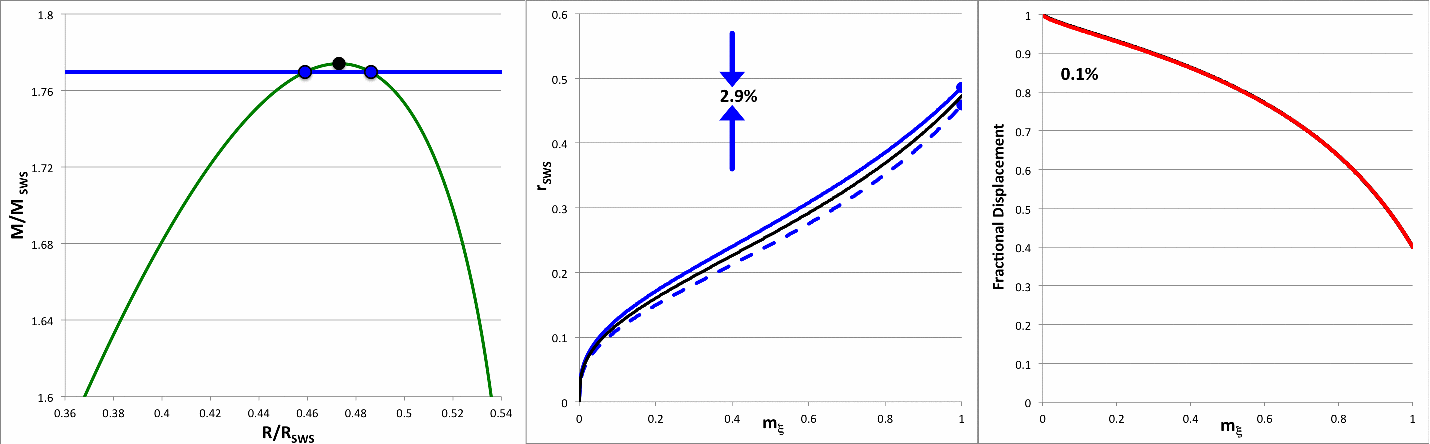
The mass-radius relationship for pressure-truncated, n = 5 polytropic configurations is displayed as a green solid curve, here on the right, in Figure 1. This sequence can be constructed either: (a) by choosing various values of the radius (between zero and the above-specified maximum radius) and, for each choice, determining the two corresponding values of the equilibrium mass from the pair of roots of the quadratic equation; or (b) by choosing various values of the mass (between zero and the above-specified maximum mass) and, for each choice, using the two real roots of the quartic equation to determine the two corresponding values of the equilibrium radius. The green curve shown in Figure 1 is identical to the orange-dashed curve, labeled n = 5, that is nested among six other polytropic equilibrium sequences in the righthand panel of Figure 3 in an accompanying discussion.

Here we are interested in comparing the relative distribution of mass inside various pairs of models that have identical total masses. We therefore will focus on method "b". Specifically, given any value of the mass, <math>~M/M_\mathrm{SWS} < m_\mathrm{max}</math>, the roots of the quartic equation will give us the equilibrium radii of the two configurations that have the same, specified mass. As examples, the second column of Table 1 lists ten separate values of the normalized mass that lie within the region of parameter space that is identified by the black-dashed rectangle drawn in Figure 1; Column three lists the corresponding value of <math>~\mu</math>; and columns four and five of Table 1 give values of the corresponding pair of equilibrium radii, <math>~\chi_\pm</math>.

In each case, from these two values of the dimensionless radius, we can, in turn, determine the corresponding pair of values of <math>~\ell_\pm</math> via the expression,

<math>~\chi_\pm</math>	<math>~=</math>	<math>~\biggl( \frac{3 \cdot 5}{4\pi} \biggr)^{1/2} \ell_\pm (1+\ell_\pm^2)^{-1} </math>
<math>~\Rightarrow ~~~0</math>	<math>~=</math>	<math>~\ell_\pm^2-\biggl( \frac{3 \cdot 5}{4\pi \chi^2_\pm} \biggr)^{1/2} \ell_\pm +1 \, . </math>

But this is a quadratic equation, meaning that for <math>~\chi_+</math> there are two viable roots for <math>~\ell_+</math>, and for <math>~\chi_-</math> there are two viable roots for <math>~\ell_-</math>. We will deal with this by referring to the "plus" root as the "high" value, and by referring to the "minus" root as the "low" value. Specifically,

<math>~\xi_\pm\biggr|_\mathrm{high} = \sqrt{3} \ell_\pm\biggr|_\mathrm{high}</math>	<math>~=</math>	<math>~\sqrt{3} \biggl( \frac{3 \cdot 5}{2^4\pi \chi^2_\pm} \biggr)^{1/2} \biggl[ 1 + \biggl( 1 - \frac{2^4\pi \chi^2_\pm}{3 \cdot 5} \biggr)^{1 / 2} \biggr] \, , </math>
<math>~\xi_\pm\biggr|_\mathrm{low} = \sqrt{3} \ell_\pm\biggr|_\mathrm{low}</math>	<math>~=</math>	<math>~\sqrt{3} \biggl( \frac{3 \cdot 5}{2^4\pi \chi^2_\pm} \biggr)^{1/2} \biggl[ 1 - \biggl( 1 - \frac{2^4\pi \chi^2_\pm}{3 \cdot 5} \biggr)^{1 / 2} \biggr] \, . </math>

This seems to work because, if we plug in a single value for <math>~\chi_\pm</math> — for example, the degenerate case of <math>~\chi_\pm = r_\mathrm{crit}</math> — we get the pair of values of <math>~\xi</math> along the equilibrium sequence where the equilibrium radius has this selected value. Specifically, when <math>~\chi_\pm = r_\mathrm{crit}</math>, we find that, <math>~\xi_\mathrm{high} = 3</math> and <math>~\xi_\mathrm{low} = 1</math>. Given that we are particularly interested in examining the region of parameter space that lies near the marginally unstable case — as identified by the black-dashed rectangle drawn in Figure 1 — columns six and seven of Table 1 list only values of <math>~\xi_\pm</math> that correspond to the "high" roots.

 

Table 1:   Selected Pairings
Pairing (N)	<math>~m \equiv \frac{M}{M_\mathrm{SWS}}</math>	<math>~\mu \equiv \biggl[ 1 - \biggl( \frac{m}{m_\mathrm{max}} \biggr)^2 \biggr]^{1 / 2}</math>	<math>~\chi_+ = \biggl(\frac{R_\mathrm{eq}}{R_\mathrm{SWS}}\biggr)_+</math>	<math>~\chi_- = \biggl(\frac{R_\mathrm{eq}}{R_\mathrm{SWS}}\biggr)_-</math>	"high" roots		<math>~\Delta{\tilde{C}}_2</math>	<math>~\Delta{\tilde{C}}_1</math>	% Profile Difference <math>~\frac{1}{2}\biggl(\chi_+ - \chi_-\biggr) \biggl[ \frac{2^6 \pi}{3^2\cdot 5} \biggr]^{1 / 2}</math>
					<math>~\xi_+</math>	<math>~\xi_-</math>
A (11)	<math>~\biggl( \frac{3^4\cdot 5^3}{2^{10} \pi} \biggr)^{1 / 2}</math>	<math>~0</math>	<math>~\biggl( \frac{3^2\cdot 5}{2^6 \pi} \biggr)^{1 / 2}</math> (degenerate)		<math>~3</math> (degenerate)		<math>~0</math> (degenerate)		<math>~0</math>
B (12)	1.7696424	0.070666	0.486212	0.458911	2.833124	3.180242	0.121273	-0.110139	2.9%
C (14)	1.7607720	0.122245	0.495129	0.447886	2.718303	3.321996	0.217999	-0.184462	5.0%
D (16)	1.7519016	0.157619	0.500918	0.439985	2.642460	3.425043	0.288919	-0.232797	6.4%
E (18)	1.7430312	0.186263	0.505407	0.433378	2.582586	3.512395	0.349376	-0.270482	7.6%
F (20)	1.7341608	0.210935	0.509128	0.427533	2.532015	3.590722	0.403816	-0.301962	8.6%
G (22)	1.7252904	0.232903	0.512327	0.422206	2.487708	3.663068	0.454266	-0.329263	9.5%
H (24)	1.7164200	0.252871	0.515138	0.417261	2.447976	3.731126	0.501855	-0.353509	10.3%
I (26)	1.7075496	0.271282	0.517648	0.412612	2.411770	3.795950	0.547286	-0.375401	11.1%
J (28)	1.6986793	0.288433	0.519913	0.408203	2.378383	3.858252	0.591032	-0.395409	11.8%
NOTE:  The mass of a given configuration pair has been specified according to the expression, <math>~\frac{M}{M_\mathrm{SWS}} = \biggl( \frac{3^4\cdot 5^3}{2^{10} \pi} \biggr)^{1 / 2}\biggl[1 - \frac{(N-11)}{400}\biggr] \, ,</math> where, N is the integer that appears inside the parentheses in the first column of this table.

Approximation Near the Maximum Mass

We can rewrite the expression for the "high" roots of <math>~\xi_\pm</math> as,

<math>~\epsilon_\pm \equiv 3 - \xi_\pm\biggr|_\mathrm{high} </math>	<math>~=</math>	<math>~3 - \sqrt{3} \biggl( \frac{3 \cdot 5}{2^4\pi \chi^2_\pm} \biggr)^{1/2} \biggl[ 1 + \biggl( 1 - \frac{2^4\pi \chi^2_\pm}{3 \cdot 5} \biggr)^{1 / 2} \biggr] </math>
	<math>~=</math>	<math>~3 - 2 \biggl( \frac{\chi_\pm}{r_\mathrm{crit}} \biggr)^{-1} \biggl\{ 1 + \biggl[ 1 - \frac{3}{4} \biggl( \frac{\chi_\pm}{r_\mathrm{crit}} \biggr)^2 \biggr]^{1 / 2} \biggr\} \, . </math>

As desired, <math>~\epsilon_\pm \rightarrow 0</math> when <math>~\chi_\pm/r_\mathrm{crit} \rightarrow 1</math>. Ultimately, we expect to find that,

<math>~\Delta C_2</math>	<math>~=</math>	<math>~\tilde{C}_2 - 4</math>
	<math>~=</math>	<math>~ 3 \biggl( \frac{\tilde\xi_+^2}{3}\biggr)^{-1} \biggl[1 + \biggl( \frac{\tilde\xi_+^2}{3}\biggr)\biggr] - 4 </math>
	<math>~=</math>	<math>~ 3\biggl[ \frac{3 + (3-\epsilon_+)^2}{ (3-\epsilon_+)^2 } \biggr] - 4 </math>
	<math>~=</math>	<math>~ \frac{9 - (3-\epsilon_+)^2}{ (3-\epsilon_+)^2 } </math>
	<math>~=</math>	<math>~ \frac{6\epsilon_+ - \epsilon_+^2}{ 9 -6\epsilon_+ + \epsilon_+^2 } \, . </math>

And, similarly,

<math>~\Delta C_1</math>	<math>~=</math>	<math>~\tilde{C}_1 - 4</math>
	<math>~=</math>	<math>~ \frac{6\epsilon_- - \epsilon_-^2}{ 9 -6\epsilon_- + \epsilon_-^2 } \, . </math>

Now, let's work through power-series expansions for each. For <math>~\epsilon_+</math> we need,

<math>~\biggl( \frac{\chi_+}{r_\mathrm{crit}} \biggr)^{-1} </math>	<math>~=</math>	<math>~ \biggl\{ 1 ~+ \biggl[\biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu - \biggl(\frac{2}{3^2}\biggr) \mu^2 ~+~ \biggl( \frac{7^2}{2^7 \cdot 3^7} \biggr)^{1 / 2}\mu^3 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^5) \biggr] \biggr\}^{-1} </math>
	<math>~=</math>	<math>~ 1 ~- \biggl[\biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu - \biggl(\frac{2}{3^2}\biggr) \mu^2 + \biggl( \frac{7^2}{2^7 \cdot 3^7} \biggr)^{1 / 2}\mu^3 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^5) \biggr] </math>
		<math>~ + \biggl[\biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu - \biggl(\frac{2}{3^2}\biggr) \mu^2 + \biggl( \frac{7^2}{2^7 \cdot 3^7} \biggr)^{1 / 2}\mu^3 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^5) \biggr]^2 </math>
		<math>~ - \biggl[\biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu - \biggl(\frac{2}{3^2}\biggr) \mu^2 + \biggl( \frac{7^2}{2^7 \cdot 3^7} \biggr)^{1 / 2}\mu^3 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^5) \biggr]^3 </math>
		<math>~ + \biggl[\biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu - \biggl(\frac{2}{3^2}\biggr) \mu^2 + \biggl( \frac{7^2}{2^7 \cdot 3^7} \biggr)^{1 / 2}\mu^3 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^5) \biggr]^4 </math>
	<math>~=</math>	<math>~ 1 ~- \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu + \biggl(\frac{2}{3^2}\biggr) \mu^2 - \biggl( \frac{7^2}{2^7 \cdot 3^7} \biggr)^{1 / 2}\mu^3 + \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^5) </math>
		<math>~ + \biggl[ \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu \biggr]^2 \biggl\{ 1 - \biggl[ \biggl(\frac{2^3}{3^3}\biggr)^{1 / 2} \mu - \biggl( \frac{7^2}{2^6 \cdot 3^6} \biggr)^{1 / 2}\mu^2 + \biggl( \frac{2^5 \cdot 5^2}{3^{9} } \biggr)^{1 / 2} \mu^3 + \mathcal{O}(\mu^4)\biggr] \biggr\}^2 </math>
		<math>~ - \biggl[ \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu \biggr]^3 \biggl\{1 - \biggl[ \biggl(\frac{2^3}{3^3}\biggr)^{1 / 2} \mu - \biggl( \frac{7^2}{2^6 \cdot 3^6} \biggr)^{1 / 2}\mu^2 + \biggl( \frac{2^5 \cdot 5^2}{3^{9} } \biggr)^{1 / 2} \mu^3 + \mathcal{O}(\mu^4)\biggr] \biggr\}^3 </math>
		<math>~ + \biggl[ \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu \biggr]^4 \biggl\{1 - \biggl[ \biggl(\frac{2^3}{3^3}\biggr)^{1 / 2} \mu - \biggl( \frac{7^2}{2^6 \cdot 3^6} \biggr)^{1 / 2}\mu^2 + \biggl( \frac{2^5 \cdot 5^2}{3^{9} } \biggr)^{1 / 2} \mu^3 + \mathcal{O}(\mu^4)\biggr] \biggr\}^4 </math>
	<math>~=</math>	<math>~ 1 ~- \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu + \biggl(\frac{2}{3^2}\biggr) \mu^2 - \biggl( \frac{7^2}{2^7 \cdot 3^7} \biggr)^{1 / 2}\mu^3 + \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 </math>
		<math>~ + \frac{\mu^2}{2 \cdot 3} \biggl\{ 1 - \biggl[ \biggl(\frac{2^3}{3^3}\biggr)^{1 / 2} \mu - \biggl( \frac{7^2}{2^6 \cdot 3^6} \biggr)^{1 / 2}\mu^2 + \mathcal{O}(\mu^3)\biggr] \biggr\}^2 </math>
		<math>~ -\biggl( \frac{1}{2 \cdot 3}\biggr)^{3 / 2}\mu^3 \biggl\{1 - \biggl[ \biggl(\frac{2^3}{3^3}\biggr)^{1 / 2} \mu + \mathcal{O}(\mu^2)\biggr] \biggr\}^3 +\biggl( \frac{1}{2 \cdot 3}\biggr)^{2}\mu^4 + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ 1 ~- \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu + \biggl(\frac{2}{3^2}\biggr) \mu^2 - \biggl( \frac{7^2}{2^7 \cdot 3^7} \biggr)^{1 / 2}\mu^3 + \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 </math>
		<math>~ + \frac{\mu^2}{2 \cdot 3} \biggl\{ 1 - \biggl(\frac{2^5}{3^3}\biggr)^{1 / 2} \mu + \biggl[ \frac{7 + 2^3 \cdot 3^2}{2^2\cdot 3^3} \biggr] \mu^2 \biggr\} </math>
		<math>~ -\biggl( \frac{1}{2 \cdot 3}\biggr)^{3 / 2}\mu^3 + 3\biggl(\frac{2^3}{3}\biggr)^{1 / 2}\biggl( \frac{1}{2 \cdot 3}\biggr)^{3 / 2}\mu^4 +\biggl( \frac{1}{2 \cdot 3}\biggr)^{2}\mu^4 + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ 1 ~- \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu + \biggl[ \biggl(\frac{2}{3^2}\biggr) + \frac{1}{2 \cdot 3} \biggr] \mu^2 - \biggl[\biggl( \frac{7^2}{2^7 \cdot 3^7} \biggr)^{1 / 2} + \biggl(\frac{2^3}{3^5}\biggr)^{1 / 2} + \biggl( \frac{1}{2 \cdot 3}\biggr)^{3 / 2} \biggr] \mu^3 </math>
		<math>~ + \biggl[ \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr) + \biggl( \frac{79}{2^3 \cdot 3^4} \biggr) + \biggl( \frac{5}{2^2 \cdot 3^2}\biggr)\biggr] \mu^4 + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ 1 ~- \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu + \biggl( \frac{7}{2 \cdot 3^2} \biggr) \mu^2 - \biggl(\frac{139^2}{2^7 \cdot 3^7}\biggr)^{1 / 2} \mu^3 + \biggl( \frac{23\cdot 29}{2^3 \cdot 3^5} \biggr) \mu^4 + \mathcal{O}(\mu^5) </math>

And we need,

<math>~\biggl( \frac{\chi_+}{r_\mathrm{crit}} \biggr)^{2} </math>	<math>~=</math>	<math>~ \biggl\{ 1 ~+ \biggl[\biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu - \biggl(\frac{2}{3^2}\biggr) \mu^2 ~+~ \biggl( \frac{7^2}{2^7 \cdot 3^7} \biggr)^{1 / 2}\mu^3 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^5) \biggr] \biggr\}^{2} </math>
	<math>~=</math>	<math>~ 1 ~+ 2 \biggl[\biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu - \biggl(\frac{2}{3^2}\biggr) \mu^2 + \biggl( \frac{7^2}{2^7 \cdot 3^7} \biggr)^{1 / 2}\mu^3 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^5) \biggr] </math>
		<math>~ + \biggl[\biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu - \biggl(\frac{2}{3^2}\biggr) \mu^2 + \biggl( \frac{7^2}{2^7 \cdot 3^7} \biggr)^{1 / 2}\mu^3 - \biggl( \frac{2^2 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^5) \biggr]^2 </math>
	<math>~=</math>	<math>~ 1 ~+ \biggl( \frac{2}{3}\biggr)^{1 / 2}\mu - \biggl(\frac{2^2}{3^2}\biggr) \mu^2 + \biggl( \frac{7^2}{2^5 \cdot 3^7} \biggr)^{1 / 2}\mu^3 - \biggl( \frac{2^3 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^5) </math>
		<math>~ + \biggl[\biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu\biggr]^2 \biggl\{1 + \biggl[ - \biggl(\frac{2^3}{3^3}\biggr)^{1 / 2} \mu + \biggl( \frac{7^2}{2^6 \cdot 3^6} \biggr)^{1 / 2}\mu^2 - \biggl( \frac{2^5 \cdot 5^2}{3^{9} } \biggr)^{1 / 2} \mu^3 + \mathcal{O}(\mu^4) \biggr] \biggr\}^2 </math>
	<math>~=</math>	<math>~ 1 ~+ \biggl( \frac{2}{3}\biggr)^{1 / 2}\mu - \biggl(\frac{2^2}{3^2}\biggr) \mu^2 + \biggl( \frac{7^2}{2^5 \cdot 3^7} \biggr)^{1 / 2}\mu^3 - \biggl( \frac{2^3 \cdot 5}{3^5 } \biggr)\mu^4 </math>
		<math>~ + \biggl( \frac{\mu^2}{2 \cdot 3}\biggr) \biggl[ 1 - \biggl(\frac{2^5}{3^3}\biggr)^{1 / 2} \mu + \biggl( \frac{7^2}{2^4 \cdot 3^6} \biggr)^{1 / 2}\mu^2 + \biggl(\frac{2^3}{3^3}\biggr) \mu^2 \biggr] + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ 1 ~+ \biggl( \frac{2}{3}\biggr)^{1 / 2}\mu - \biggl(\frac{2^2}{3^2}\biggr) \mu^2 + \biggl( \frac{7^2}{2^5 \cdot 3^7} \biggr)^{1 / 2}\mu^3 - \biggl( \frac{2^3 \cdot 5}{3^5 } \biggr)\mu^4 </math>
		<math>~ + \biggl( \frac{\mu^2}{2 \cdot 3}\biggr) - \biggl( \frac{1}{2 \cdot 3}\biggr)\biggl(\frac{2^5}{3^3}\biggr)^{1 / 2} \mu^3 + \biggl( \frac{1}{2 \cdot 3}\biggr)\biggl[ \biggl( \frac{7^2}{2^4 \cdot 3^6} \biggr)^{1 / 2} + \biggl(\frac{2^6}{3^6}\biggr)^{1 / 2} \biggr]\mu^4 + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ 1 ~+ \biggl( \frac{2}{3}\biggr)^{1 / 2}\mu + \biggl[ \biggl( \frac{1}{2 \cdot 3}\biggr) - \biggl(\frac{2^2}{3^2}\biggr) \biggr] \mu^2 + \biggl[ \biggl( \frac{7^2}{2^5 \cdot 3^7} \biggr)^{1 / 2} - \biggl( \frac{1}{2 \cdot 3}\biggr)\biggl(\frac{2^5}{3^3}\biggr)^{1 / 2} \biggr] \mu^3 </math>
		<math>~ + \biggl( \frac{1}{2 \cdot 3}\biggr)\biggl[ \biggl( \frac{7^2}{2^4 \cdot 3^6} \biggr)^{1 / 2} + \biggl(\frac{2^6}{3^6}\biggr)^{1 / 2} \biggr]\mu^4 - \biggl( \frac{2^3 \cdot 5}{3^5 } \biggr)\mu^4 + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ 1 ~+ \biggl( \frac{2}{3}\biggr)^{1 / 2}\mu - \biggl(\frac{5}{2\cdot 3^2}\biggr)\mu^2 - \biggl(\frac{41^2}{2^5 \cdot 3^7}\biggr)^{1 / 2} \mu^3 - \biggl( \frac{203}{2^3 \cdot 3^5 } \biggr) \mu^4 + \mathcal{O}(\mu^5) </math>

Hence,

<math>~\biggl[ 1 - \frac{3}{4} \biggl( \frac{\chi_+}{r_\mathrm{crit}} \biggr)^2 \biggr]^{1 / 2}</math>	<math>~=</math>	<math>~ \biggl\{ 1 - \frac{3}{4} \biggl[ 1 ~+ \biggl( \frac{2}{3}\biggr)^{1 / 2}\mu - \biggl(\frac{5}{2\cdot 3^2}\biggr)\mu^2 - \biggl(\frac{41^2}{2^5 \cdot 3^7}\biggr)^{1 / 2} \mu^3 - \biggl( \frac{203}{2^3 \cdot 3^5 } \biggr) \mu^4 + \mathcal{O}(\mu^5) \biggr] \biggr\}^{1 / 2} </math>
	<math>~=</math>	<math>~\frac{1}{2} \biggl\{ 1-3 \biggl[ \biggl( \frac{2}{3}\biggr)^{1 / 2}\mu - \biggl(\frac{5}{2\cdot 3^2}\biggr)\mu^2 - \biggl(\frac{41^2}{2^5 \cdot 3^7}\biggr)^{1 / 2} \mu^3 - \biggl( \frac{203}{2^3 \cdot 3^5 } \biggr) \mu^4 + \mathcal{O}(\mu^5) \biggr] \biggr\}^{1 / 2} </math>
	<math>~=</math>	<math>~\frac{1}{2} \biggl\{ 1- \biggl[ \biggl( 2\cdot 3\biggr)^{1 / 2}\mu - \biggl(\frac{5}{2\cdot 3}\biggr)\mu^2 - \biggl(\frac{41^2}{2^5 \cdot 3^5}\biggr)^{1 / 2} \mu^3 - \biggl( \frac{203}{2^3 \cdot 3^4 } \biggr) \mu^4 + \mathcal{O}(\mu^5) \biggr] \biggr\}^{1 / 2} </math>
	<math>~=</math>	<math>~\frac{1}{2} \biggl\{ 1- \frac{1}{2} \biggl[ \biggl( 2\cdot 3\biggr)^{1 / 2}\mu - \biggl(\frac{5}{2\cdot 3}\biggr)\mu^2 - \biggl(\frac{41^2}{2^5 \cdot 3^5}\biggr)^{1 / 2} \mu^3 - \biggl( \frac{203}{2^3 \cdot 3^4 } \biggr) \mu^4 \biggr] </math>
		<math>~ - \frac{1}{2^3} \biggl[ \biggl( 2\cdot 3\biggr)^{1 / 2}\mu - \biggl(\frac{5}{2\cdot 3}\biggr)\mu^2 - \biggl(\frac{41^2}{2^5 \cdot 3^5}\biggr)^{1 / 2} \mu^3 \biggr]^2 </math>
		<math>~ - \frac{1}{2^4} \biggl[ \biggl( 2\cdot 3\biggr)^{1 / 2}\mu - \biggl(\frac{5}{2\cdot 3}\biggr)\mu^2 \biggr]^3 - \frac{5}{2^7} \biggl[ \biggl( 2\cdot 3\biggr)^{1 / 2}\mu \biggr]^4 + \mathcal{O}(\mu^5) \biggr\} </math>
	<math>~=</math>	<math>~\frac{1}{2} \biggl\{ 1- \biggl( \frac{3}{2}\biggr)^{1 / 2}\mu + \biggl(\frac{5}{2^2 \cdot 3}\biggr)\mu^2 + \biggl(\frac{41^2}{2^7 \cdot 3^5}\biggr)^{1 / 2} \mu^3 + \biggl( \frac{203}{2^4 \cdot 3^4 } \biggr) \mu^4 </math>
		<math>~ - \biggl( \frac{3}{2^2}\biggr) \mu^2 \biggl[1 - \biggl(\frac{5^2}{2^3\cdot 3^3}\biggr)^{1 / 2} \mu - \biggl(\frac{41^2}{2^6 \cdot 3^6}\biggr)^{1 / 2} \mu^2 \biggr]^2 </math>
		<math>~ - \biggl( \frac{3^3}{2^5}\biggr)^{1 / 2} \mu^3 \biggl[ 1 - \biggl(\frac{5^2}{2^3\cdot 3^3}\biggr)^{1 / 2} \mu \biggr]^3 - \biggl( \frac{3^2\cdot 5}{2^5} \biggr) \mu^4 + \mathcal{O}(\mu^5) \biggr\} </math>
	<math>~=</math>	<math>~\frac{1}{2} \biggl\{ 1 - \biggl( \frac{3}{2}\biggr)^{1 / 2}\mu + \biggl[ \biggl(\frac{5}{2^2 \cdot 3}\biggr) - \biggl( \frac{3}{2^2}\biggr)\biggr] \mu^2 + \biggl[ \biggl(\frac{2^2 \cdot 3^4 \cdot 5^2}{2^7\cdot 3^5}\biggr)^{1 / 2} - \biggl( \frac{2^2 \cdot 3^8}{2^7 \cdot 3^5}\biggr)^{1 / 2} + \biggl(\frac{41^2}{2^7 \cdot 3^5}\biggr)^{1 / 2} \biggr] \mu^3 </math>
		<math>~ + \biggl[ \biggl( \frac{3^2\cdot 57}{2^5 \cdot 3^4}\biggr) - \biggl( \frac{3^5\cdot 5}{2^5 \cdot 3^4} \biggr) + \biggl( \frac{2\cdot 203}{2^5 \cdot 3^4 } \biggr) \biggr]\mu^4 \biggr\} + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ \frac{1}{2}\biggl\{ 1 - \biggl( \frac{3}{2}\biggr)^{1 / 2}\mu - \biggl(\frac{1}{3}\biggr) \mu^2 - \biggl( \frac{31^2}{2^7 \cdot 3^5}\biggr)^{1 / 2} \mu^3 - \biggl( \frac{296}{2^5 \cdot 3^4} \biggr) \mu^4 \biggr\} + \mathcal{O}(\mu^5) \, , </math>

and, finally,

<math>~\epsilon_+ </math>	<math>~=</math>	<math>~3 - 2 \biggl( \frac{\chi_+}{r_\mathrm{crit}} \biggr)^{-1} \biggl\{ 1 + \biggl[ 1 - \frac{3}{4} \biggl( \frac{\chi_+}{r_\mathrm{crit}} \biggr)^2 \biggr]^{1 / 2} \biggr\} </math>
	<math>~=</math>	<math>~3 - 2 \biggl\{ 1 ~- \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu + \biggl( \frac{7}{2 \cdot 3^2} \biggr) \mu^2 - \biggl(\frac{139^2}{2^7 \cdot 3^7}\biggr)^{1 / 2} \mu^3 + \biggl( \frac{23\cdot 29}{2^3 \cdot 3^5} \biggr) \mu^4 + \mathcal{O}(\mu^5) \biggr\} \biggl\{ 1 + \frac{1}{2}\biggl[ 1 - \biggl( \frac{3}{2}\biggr)^{1 / 2}\mu - \biggl(\frac{1}{3}\biggr) \mu^2 - \biggl( \frac{31^2}{2^7 \cdot 3^5}\biggr)^{1 / 2} \mu^3 - \biggl( \frac{296}{2^5 \cdot 3^4} \biggr) \mu^4 + \mathcal{O}(\mu^5) \biggr] \biggr\} </math>
	<math>~=</math>	<math>~3 - 3 \biggl\{ 1 ~- \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu + \biggl( \frac{7}{2 \cdot 3^2} \biggr) \mu^2 - \biggl(\frac{139^2}{2^7 \cdot 3^7}\biggr)^{1 / 2} \mu^3 + \biggl( \frac{23\cdot 29}{2^3 \cdot 3^5} \biggr) \mu^4 + \mathcal{O}(\mu^5) \biggr\} \biggl\{ 1 - \biggl( \frac{1}{2\cdot 3}\biggr)^{1 / 2}\mu - \biggl(\frac{1}{3^2}\biggr) \mu^2 - \biggl( \frac{31^2}{2^7 \cdot 3^7}\biggr)^{1 / 2} \mu^3 - \biggl( \frac{296}{2^5 \cdot 3^5} \biggr) \mu^4 + \mathcal{O}(\mu^5) \biggr\} </math>
	<math>~=</math>	<math>~3 - 3 \biggl\{ \biggl[ 1 ~- \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu + \biggl( \frac{7}{2 \cdot 3^2} \biggr) \mu^2 - \biggl(\frac{139^2}{2^7 \cdot 3^7}\biggr)^{1 / 2} \mu^3 + \biggl( \frac{23\cdot 29}{2^3 \cdot 3^5} \biggr) \mu^4 \biggr] </math>
		<math>~- \biggl( \frac{1}{2\cdot 3}\biggr)^{1 / 2}\mu \biggl[ 1 ~- \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu + \biggl( \frac{7}{2 \cdot 3^2} \biggr) \mu^2 - \biggl(\frac{139^2}{2^7 \cdot 3^7}\biggr)^{1 / 2} \mu^3 \biggr] </math>
		<math>~- \biggl(\frac{1}{3^2}\biggr) \mu^2 \biggl[ 1 ~- \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu + \biggl( \frac{7}{2 \cdot 3^2} \biggr) \mu^2 \biggr] - \biggl(\frac{31^2}{2^7 \cdot 3^7}\biggr)^{1 / 2} \mu^3 \biggl[ 1 ~- \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu \biggr] - \biggl( \frac{296}{2^5 \cdot 3^5} \biggr) \mu^4 \biggr\} + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ \biggl( \frac{3}{2}\biggr)^{1 / 2}\mu - \biggl( \frac{7}{2 \cdot 3} \biggr) \mu^2 + \biggl(\frac{139^2}{2^7 \cdot 3^5}\biggr)^{1 / 2} \mu^3 - \biggl( \frac{23\cdot 29}{2^3 \cdot 3^4} \biggr) \mu^4 + \biggl( \frac{3}{2}\biggr)^{1 / 2}\mu \biggl[ 1 ~- \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu + \biggl( \frac{7}{2 \cdot 3^2} \biggr) \mu^2 - \biggl(\frac{139^2}{2^7 \cdot 3^7}\biggr)^{1 / 2} \mu^3 \biggr] </math>
		<math>~+ \biggl(\frac{1}{3}\biggr) \mu^2 \biggl[ 1 ~- \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu + \biggl( \frac{7}{2 \cdot 3^2} \biggr) \mu^2 \biggr] + \biggl(\frac{31^2}{2^7 \cdot 3^5}\biggr)^{1 / 2} \mu^3 \biggl[ 1 ~- \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu \biggr] + \biggl( \frac{296}{2^5 \cdot 3^4} \biggr) \mu^4 + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ \biggl[\biggl( \frac{3}{2}\biggr)^{1 / 2} + \biggl( \frac{3}{2}\biggr)^{1 / 2} \biggr] \mu - \biggl[ \biggl( \frac{7}{2 \cdot 3} \biggr) + \biggl( \frac{1}{2}\biggr) \biggr] \mu^2 + \biggl[ \biggl(\frac{139^2}{2^7 \cdot 3^5}\biggr)^{1 / 2} + \biggl( \frac{7^2}{2^3 \cdot 3^3} \biggr)^{1 / 2}\biggr] \mu^3 - \biggl[ \biggl( \frac{23\cdot 29}{2^3 \cdot 3^4} \biggr) + \biggl(\frac{139^2}{2^8 \cdot 3^6}\biggr)^{1 / 2}\biggr] \mu^4 </math>
		<math>~ + \biggl(\frac{1}{3}\biggr) \mu^2 ~ + \biggl[ \biggl(\frac{31^2}{2^7 \cdot 3^5}\biggr)^{1 / 2} - \biggl(\frac{1}{3}\biggr) \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2} \biggr] \mu^3 + \biggl[ \biggl(\frac{1}{3}\biggr) \biggl( \frac{7}{2 \cdot 3^2} \biggr) - \biggl(\frac{31^2}{2^7 \cdot 3^5}\biggr)^{1 / 2} \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2} + \biggl( \frac{296}{2^5 \cdot 3^4} \biggr) \biggr]\mu^4 + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ \biggl[\biggl( \frac{3}{2}\biggr)^{1 / 2} + \biggl( \frac{3}{2}\biggr)^{1 / 2} \biggr] \mu + \biggl[ \biggl(\frac{1}{3}\biggr) -\biggl( \frac{7}{2 \cdot 3} \biggr) - \biggl( \frac{1}{2}\biggr) \biggr] \mu^2 + \biggl[ \biggl(\frac{139^2}{2^7 \cdot 3^5}\biggr)^{1 / 2} + \biggl( \frac{7^2}{2^3 \cdot 3^3} \biggr)^{1 / 2} + \biggl(\frac{31^2}{2^7 \cdot 3^5}\biggr)^{1 / 2} - \biggl(\frac{1}{3}\biggr) \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2} \biggr] \mu^3 </math>
		<math>~ + \biggl[ \biggl(\frac{1}{3}\biggr) \biggl( \frac{7}{2 \cdot 3^2} \biggr) - \biggl(\frac{31^2}{2^7 \cdot 3^5}\biggr)^{1 / 2} \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2} + \biggl( \frac{296}{2^5 \cdot 3^4} \biggr) -\biggl( \frac{23\cdot 29}{2^3 \cdot 3^4} \biggr) - \biggl(\frac{139^2}{2^8 \cdot 3^6}\biggr)^{1 / 2}\biggr] \mu^4 + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ 6^{1 / 2} \mu - \biggl(\frac{4}{3}\biggr)\mu^2 + \biggl[ \frac{5\cdot 23}{(2^5 \cdot 3^5)^{1 / 2}} \biggr] \mu^3 - \biggl(\frac{191}{2\cdot 3^4}\biggr) \mu^4 + \mathcal{O}(\mu^5) \, . </math>

Similarly we have determined that, for <math>~\epsilon_-</math>,

<math>~\biggl( \frac{\chi_-}{r_\mathrm{crit}} \biggr)^{-1} </math>

<math>~=</math>

<math>~ 1 ~+ \biggl( \frac{1}{2 \cdot 3}\biggr)^{1 / 2}\mu + \biggl[ \frac{7}{2 \cdot 3^2} \biggr] \mu^2 + \biggl(\frac{139^2}{2^7 \cdot 3^7}\biggr)^{1 / 2} \mu^3 + \biggl[ \frac{23\cdot 29}{2^3 \cdot 3^5} \biggr] \mu^4 + \mathcal{O}(\mu^5) \, , </math>

and,

<math>~\biggl( \frac{\chi_-}{r_\mathrm{crit}} \biggr)^{2} </math>

<math>~=</math>

<math>~ 1 ~- \biggl( \frac{2}{3}\biggr)^{1 / 2}\mu + \biggl[ - \biggl(\frac{5}{2\cdot 3^2}\biggr) \biggr] \mu^2 + \biggl(\frac{41^2}{2^5 \cdot 3^7}\biggr)^{1 / 2} \mu^3 + \biggl[- \biggl( \frac{203}{2^3 \cdot 3^5 } \biggr) \biggr] \mu^4 + \mathcal{O}(\mu^5) \, , </math>

and,

<math>~\biggl[ 1 - \frac{3}{4} \biggl( \frac{\chi_-}{r_\mathrm{crit}} \biggr)^2 \biggr]^{1 / 2}</math>

<math>~=</math>

<math>~\frac{1}{2} \biggl\{ 1 + \biggl( \frac{3}{2}\biggr)^{1 / 2}\mu - \biggl(\frac{1}{3}\biggr) \mu^2 + \biggl( \frac{31^2}{2^7 \cdot 3^5}\biggr)^{1 / 2} \mu^3 - \biggl( \frac{296}{2^5 \cdot 3^4} \biggr) \mu^4 \biggr\} + \mathcal{O}(\mu^5) \, , </math>

and,

<math>~\epsilon_-</math>

<math>~=</math>

<math>~ - 6^{1 / 2} \mu - \biggl(\frac{4}{3}\biggr)\mu^2 - \biggl[ \frac{5\cdot 23}{(2^5 \cdot 3^5)^{1 / 2}} \biggr] \mu^3 - \biggl(\frac{191}{2\cdot 3^4}\biggr) \mu^4 + \mathcal{O}(\mu^5) \, . </math>

Inferred Displacement Function

ASIDE:  The various "shorthand" variables that have been introduced throughout this chapter should be viewed as consistent with one another in the following sense. We understand that, in each pairing of models, one will be associated with a value of <math>~\tilde\xi > 3</math> and the other will be associated with a value of <math>~\tilde\xi < 3</math>. The model having the smaller value of <math>~\tilde\xi</math>, and that has been tagged with the "plus" subscript <math>~(\xi_+)</math>, also corresponds to the model that: Has the larger equilibrium radius <math>~(\chi_+)</math> — that is, <math>~\chi_+/r_\mathrm{crit} > 1</math>; Has the larger value of <math>~\tilde{C}</math> — that is, <math>~\tilde{C} > 4</math>; In connection with the Delta Profiles, is tagged with the subscript "2"; hence, <math>~\tilde{C}_2 > 4</math>; Has a positive value of the small parameter, <math>~\epsilon</math> — that is, <math>~\epsilon_+ > 0</math>, whereas, <math>~\epsilon_- < 0</math>.

Foundation

From our discussion, below, for any value of the truncation radius, <math>~\tilde\xi</math>, the fractional mass <math>~(0 \le m_\xi \le 1)</math> that lies interior to <math>~\xi</math> is given by the expression,

<math>~m_\xi \equiv \frac{M(\xi)}{M_\mathrm{tot}}</math>	<math>~=</math>	<math>~ \biggl(\frac{\xi}{\tilde\xi}\biggr)^3 \biggl(1 + \frac{\xi^2}{3}\biggr)^{-3/2} \biggl(1 + \frac{\tilde\xi^2}{3}\biggr)^{3/2} </math>
	<math>~=</math>	<math>~\biggl(\frac{\tilde{C}}{3}\biggr)^{3 / 2} \xi^3 \biggl(3 + \xi^2\biggr)^{-3/2} \, , </math>

where,

<math>~\tilde{C} \equiv \frac{3^2}{\tilde\xi^2}\biggl( 1 + \frac{\tilde\xi^2}{3} \biggr)</math>

<math>~\Rightarrow</math>

<math>~ {\tilde\xi}^2 = \frac{9}{\tilde{C} - 3} \, . </math>

And, when normalized to <math>~R_\mathrm{SWS}</math>, the corresponding radius is,

<math>~r_\mathrm{SWS}(\xi)</math>	<math>~=</math>	<math>~\biggl(\frac{\xi}{\tilde\xi} \biggr) \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} </math>
	<math>~=</math>	<math>~\biggl(\frac{\xi}{\tilde\xi} \biggr) \biggl\{ \frac{3\cdot 5}{2^2 \pi} \biggl[ \frac{ \tilde\xi^2/3}{(1+ \tilde\xi^2/3)^{2}} \biggr] \biggr\}^{1/2}</math>
	<math>~=</math>	<math>~\xi\biggl[ \frac{3^2 \cdot 5}{2^2 \pi} \biggr]^{1 / 2} (3+{\tilde\xi}^2)^{-1} </math>
	<math>~=</math>	<math>~\xi\biggl[ \frac{3^2 \cdot 5}{2^2 \pi} \biggr]^{1 / 2} \biggl[ \frac{\tilde{C} - 3}{3\tilde{C}} \biggr] \, .</math>

Now, this works fine in the sense that, for any choice of <math>~\tilde\xi</math>, and therefore <math>~\tilde{C}</math>, this pair of parametric relations can be used to generate a plot of <math>~r_\mathrm{SWS}</math> versus <math>~m_\xi</math> that correctly displays how the mass enclosed within a given radius varies with radial location throughout the spherical configuration. But, in order to compare one of these configurations to another, we really need to identify how this function varies across a Lagrangian mass grid that is the same for both configurations. The easiest way to accomplish this is to derive an expression for <math>~r_\mathrm{SWS}</math> that is directly a function of <math>~m_\xi</math>. Fortunately, this can be done analytically. First, we invert the mass expression to find,

<math>~m_\xi^{2/3}</math>	<math>~=</math>	<math>~\biggl(\frac{\tilde{C}}{3}\biggr) \xi^2 (3 + \xi^2)^{-1} </math>
<math>~\Rightarrow ~~~ 3 + \xi^2</math>	<math>~=</math>	<math>~ m_\xi^{-2/3}\biggl(\frac{\tilde{C}}{3}\biggr)\xi^2 </math>
<math>~\Rightarrow ~~~ \xi^2\biggl[ 1 - m_\xi^{-2/3}\biggl(\frac{\tilde{C}}{3}\biggr) \biggr]</math>	<math>~=</math>	<math>~ -3 </math>
<math>~\Rightarrow ~~~ \xi^2</math>	<math>~=</math>	<math>~ 3^2 [ \tilde{C}~m_\xi^{-2/3} -3 ]^{-1} \, . </math>

Inserting this into the radial equation, then, gives,

<math>~r_\mathrm{SWS}(m_\xi)</math>

<math>~=</math>

<math>~\biggl[ \frac{3^2 \cdot 5}{2^2 \pi} \biggr]^{1 / 2} \biggl[ \frac{\tilde{C} - 3}{\tilde{C}} \biggr] \biggl[ \tilde{C}~m_\xi^{-2/3} -3 \biggr]^{-1 / 2} \, .</math>

Analytic, Marginally Unstable Eigenfunction

In terms of <math>~\xi</math>, we know that the eigenfunction of the marginally unstable model — see also a more general discussion — is,

<math>~x_P = \frac{\delta r}{r_0}</math>

<math>~=</math>

<math>~1 - \frac{\xi^2}{15} \, .</math>

We can now rewrite this eigenfunction in terms of the fractional mass, <math>~m_\xi</math>. Specifically, given that <math>~\tilde{C} = 4</math> in the marginally unstable configuration, we find that,

<math>~x_P </math>	<math>~=</math>	<math>~1 - \frac{3}{5} \biggl[ 4~m_\xi^{-2/3} -3 \biggr]^{-1} </math>
	<math>~=</math>	<math>~\frac{2}{5} \biggl[ \frac{10~m_\xi^{-2/3} -9}{4~m_\xi^{-2/3} -3} \biggr] </math>
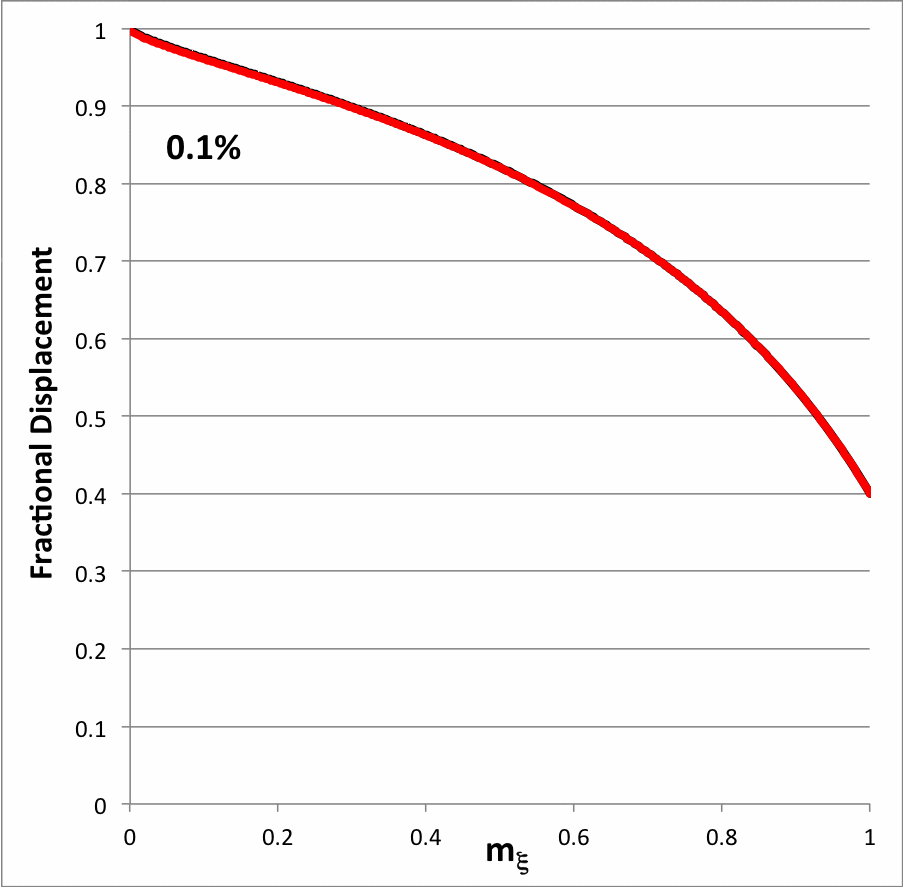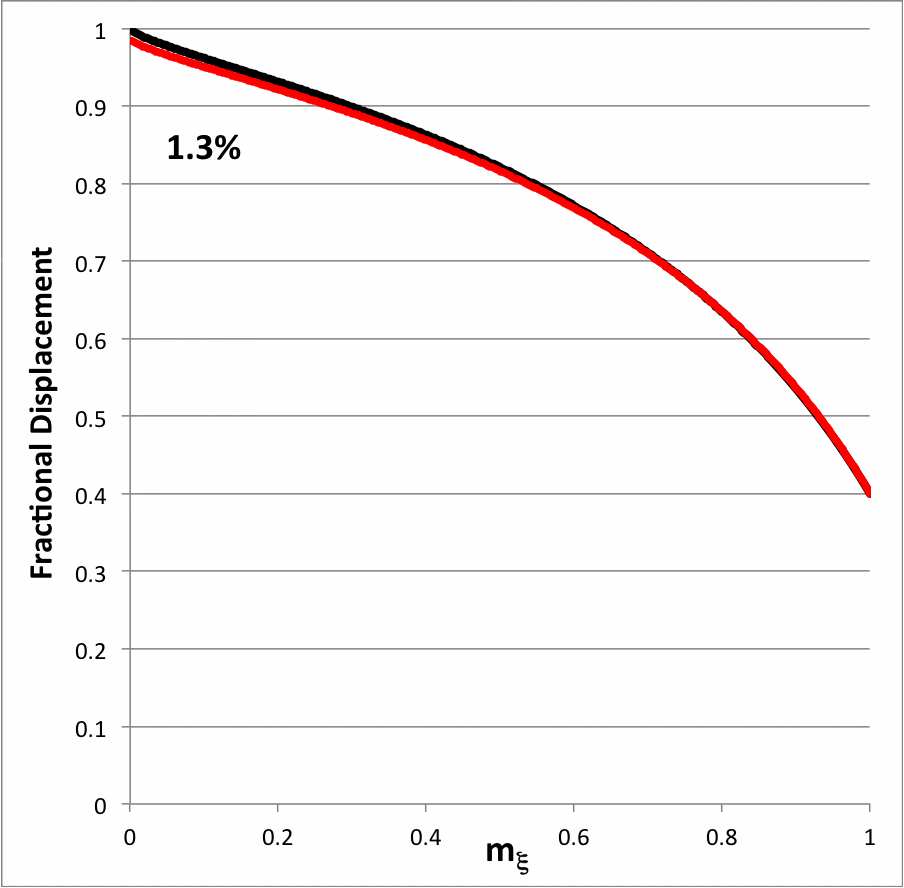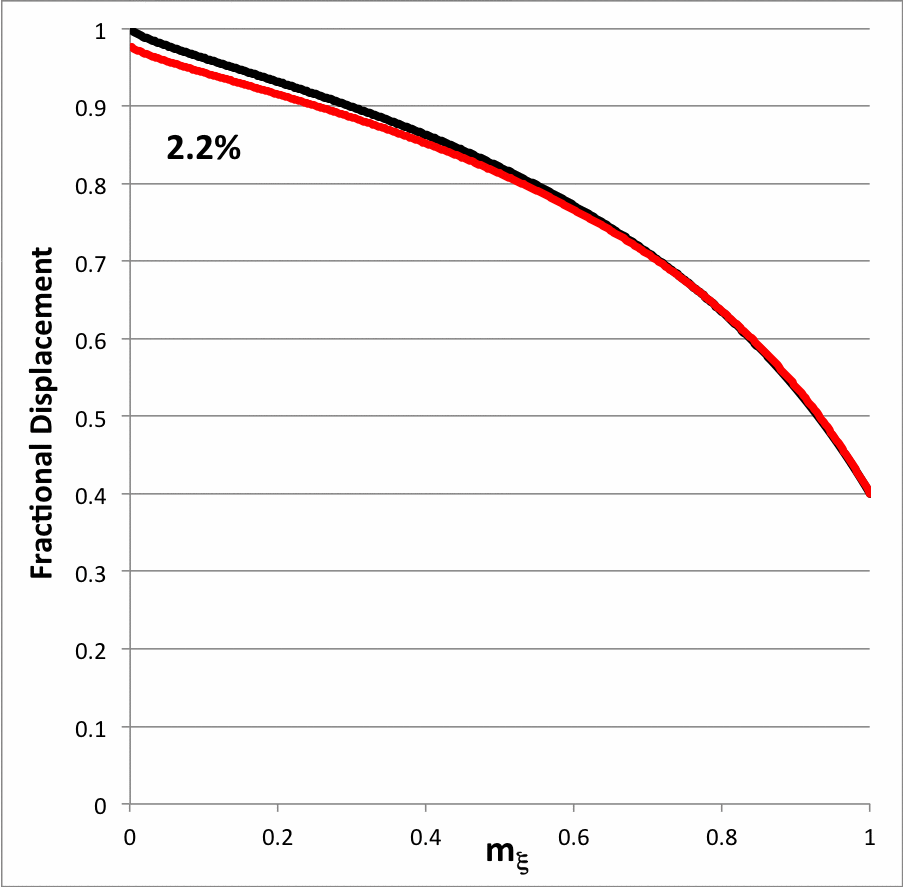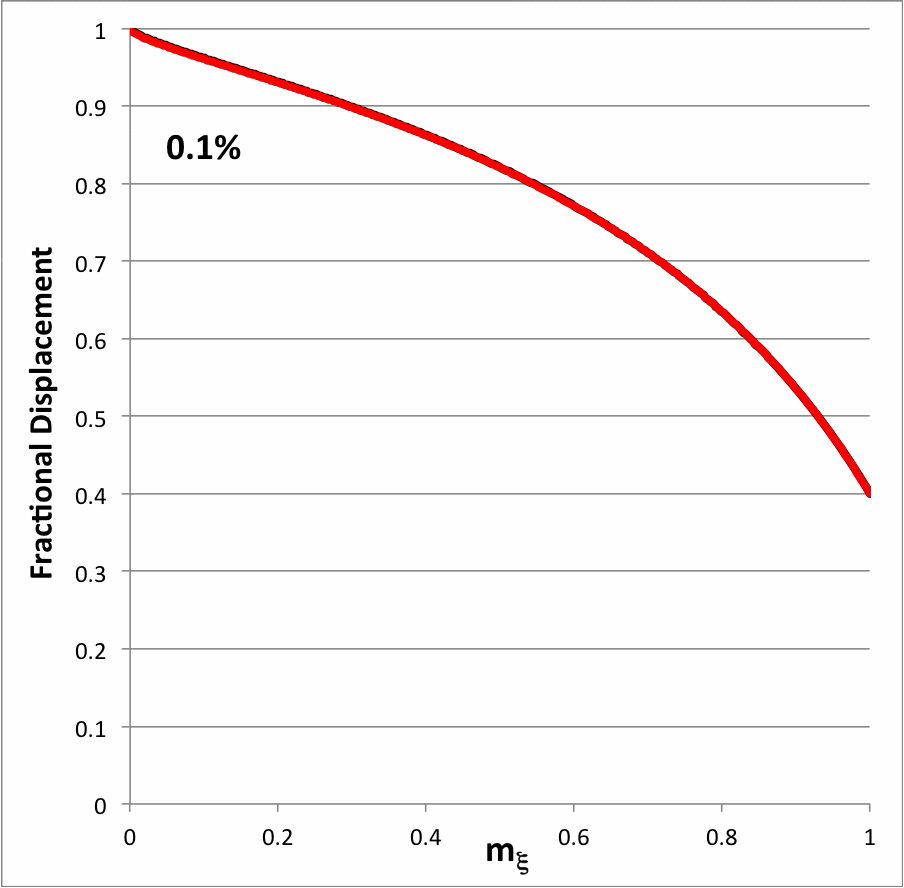
	<math>~=</math>	<math>~\frac{2}{5} \biggl[ \frac{10 -9~m_\xi^{2/3}}{4 -3~m_\xi^{2/3}} \biggr] \, .</math>

It is important to remember that, although the leading factor of this expression is <math>~\tfrac{2}{5}</math>, in general the overall amplitude of this eigenfunction can be set arbitrarily. In order to allow for this, we will introduce an overall scaling factor, <math>~A_0</math>, and write,

<math>~x_P </math>

<math>~=</math>

<math>~\frac{2A_0}{5} \biggl[ \frac{10 -9~m_\xi^{2/3}}{4 -3~m_\xi^{2/3}} \biggr] \, .</math>

Then our originating expression for <math>~x_P</math> is retrieved by setting <math>~A_0 = 1</math>, in which case the amplitude of the eigenfunction is unity at the center <math>~(m_\xi = 0)</math> and it is <math>~\tfrac{2}{5}</math> at the surface <math>~(m_\xi = 1)</math>.

Delta Profiles

Layout

Next, let's define a fractional difference in configuration profiles.

<math>~\mathfrak{x} </math>	<math>~\equiv</math>	<math>~ \frac{\tfrac{1}{2}\Delta r_\mathrm{SWS}}{\langle r_\mathrm{SWS} \rangle} = \frac{ \tfrac{1}{2} [r_2(m_\xi) - r_1(m_\xi) ]}{\tfrac{1}{2} [ r_2(m_\xi) + r_1(m_\xi)]}</math>
	<math>~=</math>	<math>~ \biggl\{\biggl[ \frac{\tilde{C}_2 - 3}{\tilde{C}_2} \biggr] \biggl[ \tilde{C}_2~m_\xi^{-2/3} -3 \biggr]^{-1 / 2} - \biggl[ \frac{\tilde{C}_1 - 3}{\tilde{C}_1} \biggr] \biggl[ \tilde{C}_1~m_\xi^{-2/3} -3 \biggr]^{-1 / 2} \biggr\} \biggl\{\biggl[ \frac{\tilde{C}_2 - 3}{\tilde{C}_2} \biggr] \biggl[ \tilde{C}_2~m_\xi^{-2/3} -3 \biggr]^{-1 / 2} + \biggl[ \frac{\tilde{C}_1 - 3}{\tilde{C}_1} \biggr] \biggl[ \tilde{C}_1~m_\xi^{-2/3} -3 \biggr]^{-1 / 2} \biggr\}^{-1} </math>
	<math>~=</math>	<math>~ \biggl\{ \tilde{C}_1 ( \tilde{C}_2 - 3 ) \biggl[ \tilde{C}_1~m_\xi^{-2/3} -3 \biggr]^{1 / 2} - \tilde{C}_2 ( \tilde{C}_1 - 3 ) \biggl[ \tilde{C}_2~m_\xi^{-2/3} -3 \biggr]^{1 / 2} \biggr\} \biggl\{ \tilde{C}_1 ( \tilde{C}_2 - 3 ) \biggl[ \tilde{C}_1~m_\xi^{-2/3} -3 \biggr]^{1 / 2} + \tilde{C}_2 ( \tilde{C}_1 - 3 ) \biggl[ \tilde{C}_2~m_\xi^{-2/3} -3 \biggr]^{1 / 2} \biggr\}^{-1} </math>
	<math>~=</math>	<math>~ \biggl\{ \tilde{C}_1 ( \tilde{C}_2 - 3 ) \biggl[ \tilde{C}_1 -3~m_\xi^{2/3} \biggr]^{1 / 2} - \tilde{C}_2 ( \tilde{C}_1 - 3 ) \biggl[ \tilde{C}_2 -3 ~m_\xi^{2/3}\biggr]^{1 / 2} \biggr\} \biggl\{ \tilde{C}_1 ( \tilde{C}_2 - 3 ) \biggl[ \tilde{C}_1 -3~m_\xi^{2/3} \biggr]^{1 / 2} + \tilde{C}_2 ( \tilde{C}_1 - 3 ) \biggl[ \tilde{C}_2 -3~m_\xi^{2/3} \biggr]^{1 / 2} \biggr\}^{-1} \, . </math>

Next, let's define,

<math>~\Delta C_i \equiv {\tilde{C}}_i - 4 </math>      <math>~\Rightarrow</math>      <math>~\tilde{C}_i = \Delta C_i + 4 \, ,</math>

in which case,

<math>~\mathfrak{x} </math>	<math>~=</math>	<math>~ \biggl\{ (\Delta C_1 + 4) ( \Delta C_2 + 1 ) \biggl[ \Delta C_1 + 4 -3~m_\xi^{2/3} \biggr]^{1 / 2} - ( \Delta C_2 + 4) ( \Delta C_1 + 1 ) \biggl[ \Delta C_2 + 4 -3 ~m_\xi^{2/3}\biggr]^{1 / 2} \biggr\} </math>
		<math>~\times \biggl\{ (\Delta C_1 + 4) ( \Delta C_2 + 1 ) \biggl[ \Delta C_1 + 4 -3~m_\xi^{2/3} \biggr]^{1 / 2} + ( \Delta C_2 + 4 ) ( \Delta C_1 + 1 ) \biggl[ \Delta C_2 + 4 -3~m_\xi^{2/3} \biggr]^{1 / 2} \biggr\}^{-1} \, . </math>

Now define,

<math>~\beta \equiv (4 -3~m_\xi^{2/3})^{-1 / 2} \, ,</math>

in which case,

<math>~\mathfrak{x} </math>	<math>~=</math>	<math>~ \biggl\{ (1 + \Delta C_1/4 ) (1 + \Delta C_2 ) (1 + \beta^2 \Delta C_1 )^{1 / 2} - (1 + \Delta C_2/4 ) (1+ \Delta C_1 ) ( 1+\beta^2 \Delta C_2 )^{1 / 2} \biggr\} </math>
		<math>~\times \biggl\{ (1 + \Delta C_1/4) (1 + \Delta C_2 ) ( 1 + \beta^2\Delta C_1 )^{1 / 2} + (1 + \Delta C_2/4 ) (1 + \Delta C_1) ( 1 + \beta^2\Delta C_2 )^{1 / 2} \biggr\}^{-1} </math>
	<math>~=</math>	<math>~ \biggl\{ \biggl[ 1 + \frac{\Delta C_1}{4} + \Delta C_2 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr](1 + \beta^2 \Delta C_1 )^{1 / 2} - \biggl[ 1 + \frac{\Delta C_2}{4} + \Delta C_1 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] ( 1+\beta^2 \Delta C_2 )^{1 / 2} \biggr\} </math>
		<math>~\times \biggl\{ \biggl[ 1 + \frac{\Delta C_1}{4} + \Delta C_2 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] ( 1 + \beta^2\Delta C_1 )^{1 / 2} + \biggl[ 1 + \frac{\Delta C_2}{4} + \Delta C_1 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] ( 1 + \beta^2\Delta C_2 )^{1 / 2} \biggr\}^{-1} \, . </math>

Original Manipulation

Given that we are only interested in examining configurations very near <math>~m_\mathrm{max}</math> for which, <math>~|\Delta C_i| \ll 1</math>, we draw guidance from the binomial expansion and make the substitution,

<math>~(1 + \beta^2 \Delta C_i)^{1 / 2}</math>

<math>~=</math>

<math>~ \biggl[ 1 + \frac{\beta^2 \Delta C_i}{2} - \frac{\beta^4 (\Delta C_i)^2 }{8} + \cdots \biggr] </math>

This gives,

<math>~\mathfrak{x} </math>	<math>~=</math>	<math>~ \biggl\{ \biggl[ 1 + \frac{\Delta C_1}{4} + \Delta C_2 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] \biggl[ 1 + \frac{\beta^2 \Delta C_1}{2} - \frac{\beta^4 (\Delta C_1)^2 }{8} + \cdots \biggr] </math>
		<math>~ - \biggl[ 1 + \frac{\Delta C_2}{4} + \Delta C_1 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] \biggl[ 1 + \frac{\beta^2 \Delta C_2}{2} - \frac{\beta^4 (\Delta C_2)^2 }{8} + \cdots \biggr] \biggr\} </math>
		<math>~\times \biggl\{ \biggl[ 1 + \frac{\Delta C_1}{4} + \Delta C_2 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] \biggl[ 1 + \frac{\beta^2 \Delta C_1}{2} - \frac{\beta^4 (\Delta C_1)^2 }{8} + \cdots \biggr] </math>
		<math>~ + \biggl[ 1 + \frac{\Delta C_2}{4} + \Delta C_1 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] \biggl[ 1 + \frac{\beta^2 \Delta C_2}{2} - \frac{\beta^4 (\Delta C_2)^2 }{8} + \cdots \biggr] \biggr\}^{-1} </math>
	<math>~\approx</math>	<math>~ \biggl\{ \biggl[ 1 + \frac{\Delta C_1}{4} + \Delta C_2 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] +\biggl[ 1 + \frac{\Delta C_1}{4} + \Delta C_2 \biggr] \biggl[ \frac{\beta^2 \Delta C_1}{2} \biggr] - \biggl[ \frac{\beta^4 (\Delta C_1)^2 }{8} \biggr] </math>
		<math>~ - \biggl[ 1 + \frac{\Delta C_2}{4} + \Delta C_1 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] - \biggl[ 1 + \frac{\Delta C_2}{4} + \Delta C_1 \biggr] \biggl[ \frac{\beta^2 \Delta C_2}{2} \biggr] + \biggl[ \frac{\beta^4 (\Delta C_2)^2 }{8} \biggr] \biggr\} </math>
		<math>~\times \biggl\{ \biggl[ 1 + \frac{\Delta C_1}{4} + \Delta C_2 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] +\biggl[ 1 + \frac{\Delta C_1}{4} + \Delta C_2 \biggr] \biggl[ \frac{\beta^2 \Delta C_1}{2} \biggr] - \biggl[ \frac{\beta^4 (\Delta C_1)^2 }{8} \biggr] </math>
		<math>~ + \biggl[ 1 + \frac{\Delta C_2}{4} + \Delta C_1 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] + \biggl[ 1 + \frac{\Delta C_2}{4} + \Delta C_1 \biggr] \biggl[ \frac{\beta^2 \Delta C_2}{2} \biggr] - \biggl[ \frac{\beta^4 (\Delta C_2)^2 }{8} \biggr] \biggr\}^{-1} </math>
	<math>~=</math>	<math>~ \biggl\{ \biggl[ \frac{\Delta C_1}{4} + \Delta C_2 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] - \biggl[ \frac{\Delta C_2}{4} + \Delta C_1 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] </math>
		<math>~ +\biggl[ 1 + \frac{\Delta C_1}{4} + \Delta C_2 \biggr] \biggl[ \frac{\beta^2 \Delta C_1}{2} \biggr] - \biggl[ 1 + \frac{\Delta C_2}{4} + \Delta C_1 \biggr] \biggl[ \frac{\beta^2 \Delta C_2}{2} \biggr] + \biggl[ \frac{\beta^4 (\Delta C_2)^2 }{8} \biggr] - \biggl[ \frac{\beta^4 (\Delta C_1)^2 }{8} \biggr] \biggr\} </math>
		<math>~\times \biggl\{ \biggl[ 2 + \frac{\Delta C_1}{4} + \Delta C_2 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] + \biggl[ \frac{\Delta C_2}{4} + \Delta C_1 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] </math>
		<math>~ + \biggl[ 1 + \frac{\Delta C_2}{4} + \Delta C_1 \biggr] \biggl[ \frac{\beta^2 \Delta C_2}{2} \biggr] +\biggl[ 1 + \frac{\Delta C_1}{4} + \Delta C_2 \biggr] \biggl[ \frac{\beta^2 \Delta C_1}{2} \biggr] - \biggl[ \frac{\beta^4 (\Delta C_1)^2 }{8} \biggr] - \biggl[ \frac{\beta^4 (\Delta C_2)^2 }{8} \biggr] \biggr\}^{-1} </math>
	<math>~=</math>	<math>~ \biggl\{ \biggl[ \frac{3}{4}- \frac{\beta^2}{2}\biggr] \biggl( \Delta C_2 - \Delta C_1\biggr) + \frac{\beta^4}{8}\biggl[ (\Delta C_2)^2 - (\Delta C_1)^2 \biggr] + \frac{\beta^2}{2}\biggl[ \biggl( \frac{\Delta C_1}{4} + \Delta C_2 \biggr)\Delta C_1 - \biggl(\frac{\Delta C_2}{4} + \Delta C_1 \biggr)\Delta C_2 \biggr] \biggr\} </math>
		<math>~\times \biggl\{ 2 + \biggl(\frac{5}{4} + \frac{\beta^2}{2} \biggr) \biggr( \Delta C_1 + \Delta C_2\biggr) </math>
		<math>~ + \frac{\Delta C_1 \cdot \Delta C_2}{2} + \biggl[ \frac{\Delta C_2}{4} + \Delta C_1 \biggr] \biggl[ \frac{\beta^2 \Delta C_2}{2} \biggr] +\biggl[ \frac{\Delta C_1}{4} + \Delta C_2 \biggr] \biggl[ \frac{\beta^2 \Delta C_1}{2} \biggr] - \biggl[ \frac{\beta^4 (\Delta C_1)^2 }{8} \biggr] - \biggl[ \frac{\beta^4 (\Delta C_2)^2 }{8} \biggr] \biggr\}^{-1} </math>
	<math>~\approx</math>	<math>~ \frac{1}{16}\biggl\{ (6-4\beta^2) \biggl( \Delta C_2 - \Delta C_1\biggr) + (\beta^4- \beta^2)\biggl[ (\Delta C_2)^2 - (\Delta C_1)^2 \biggr] \biggr\}\biggl\{ 1 + \biggl( \frac{5 + 2\beta^2}{8} \biggr) \biggr( \Delta C_1 + \Delta C_2\biggr) \biggr\}^{-1} </math>

Again, employing the binomial expansion to approximate the numerator, we have,

<math>~\mathfrak{x} </math>	<math>~\approx</math>	<math>~ \frac{1}{16}\biggl\{ (6-4\beta^2) \biggl( \Delta C_2 - \Delta C_1\biggr) + (\beta^4- \beta^2)\biggl[ (\Delta C_2)^2 - (\Delta C_1)^2 \biggr] \biggr\}\biggl\{ 1 - \biggl( \frac{5 + 2\beta^2}{8} \biggr) \biggr( \Delta C_1 + \Delta C_2\biggr) \biggr\} </math>
	<math>~\approx</math>	<math>~ \frac{1}{16}\biggl\{ (6-4\beta^2) \biggl( \Delta C_2 - \Delta C_1\biggr) + (\beta^4- \beta^2)\biggl[ (\Delta C_2)^2 - (\Delta C_1)^2 \biggr] - (6-4\beta^2) \biggl[ (\Delta C_2)^2 - (\Delta C_1)^2 \biggr] \biggl( \frac{5 + 2\beta^2}{8} \biggr) \biggr\} </math>
	<math>~\approx</math>	<math>~ \frac{1}{16}\biggl\{ (6-4\beta^2) ( \Delta C_2 - \Delta C_1 ) + \frac{1}{8}\biggl[ (\Delta C_2)^2 - (\Delta C_1)^2 \biggr] (8\beta^4- 8\beta^2) - \frac{1}{8}\biggl[ (\Delta C_2)^2 - (\Delta C_1)^2 \biggr] (30 -8\beta^2 -8\beta^4) \biggr\} </math>
	<math>~\approx</math>	<math>~ \frac{1}{16}\biggl\{ (6-4\beta^2) ( \Delta C_2 - \Delta C_1 ) + \frac{1}{8}\biggl[ (\Delta C_2)^2 - (\Delta C_1)^2 \biggr] (16\beta^4 - 30 ) \biggr\} </math>
	<math>~\approx</math>	<math>~ \frac{1}{8}( \Delta C_2 - \Delta C_1 )\biggl[ (3-2\beta^2) + \frac{1}{8}\biggl( \Delta C_2 + \Delta C_1 \biggr) (8\beta^4 - 15 ) \biggr] \, . </math>

Compare this result with an earlier derivation that kept only the lowest-order term:

	<math>~\approx</math>	<math>~\frac{1}{2} \biggl[ (1 + \Delta C_1/4 + \Delta C_2 + \beta^2 \Delta C_1/2 ) - (1 + \Delta C_2/4 + \Delta C_1 +\beta^2 \Delta C_2/2 ) \biggr] </math>
	<math>~=</math>	<math>~\frac{1}{2} \biggl[ \Delta C_1/4 + \Delta C_2 + \beta^2 \Delta C_1/2 - \Delta C_2/4 - \Delta C_1 -\beta^2 \Delta C_2/2 \biggr] </math>
	<math>~=</math>	<math>~\frac{1}{2} \biggl[ \frac{1}{4}(\Delta C_1 - \Delta C_2) - (\Delta C_1 - \Delta C_2) + \frac{\beta^2}{2}( \Delta C_1 - \Delta C_2) \biggr] </math>
	<math>~=</math>	<math>~\frac{1}{8} (\Delta C_1 - \Delta C_2) [2\beta^2 -3] </math>
	<math>~=</math>	<math>~\frac{1}{8} (\Delta C_2 - \Delta C_1) \biggl[ \frac{10-9m_\xi^{2 / 3}}{4-3m_\xi^{2 / 3}} \biggr] \, . </math>

New Approach

We begin with the derived expression for <math>~\mathfrak{r}</math>,

<math>~\mathfrak{x} </math>

<math>~=</math>

<math>~ \biggl\{ \tilde{C}_1 ( \tilde{C}_2 - 3 ) \biggl[ \tilde{C}_1 -3~m_\xi^{2/3} \biggr]^{1 / 2} - \tilde{C}_2 ( \tilde{C}_1 - 3 ) \biggl[ \tilde{C}_2 -3 ~m_\xi^{2/3}\biggr]^{1 / 2} \biggr\} \biggl\{ \tilde{C}_1 ( \tilde{C}_2 - 3 ) \biggl[ \tilde{C}_1 -3~m_\xi^{2/3} \biggr]^{1 / 2} + \tilde{C}_2 ( \tilde{C}_1 - 3 ) \biggl[ \tilde{C}_2 -3~m_\xi^{2/3} \biggr]^{1 / 2} \biggr\}^{-1} \, , </math>

and define,

<math>~\delta \equiv \Delta C_2 - \Delta C_1</math>

and

<math>~\Sigma \equiv \Delta C_2 + \Delta C_1 \, .</math>

Then, on the whiteboard, I have shown that,

<math>~ 4\beta \biggl\{ \tilde{C}_1 ( \tilde{C}_2 - 3 ) \biggl[ \tilde{C}_1 -3~m_\xi^{2/3} \biggr]^{1 / 2} \biggr\} </math>	<math>~=</math>	<math>~ \biggl[16 + 10\Sigma + 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl[1 + \frac{1}{2}(\Sigma -\delta) \beta^2\biggr]^{1 / 2} </math>
	<math>~=</math>	<math>~ \biggl[16 + 10\Sigma + 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{1 + \frac{\beta^2}{2^2}(\Sigma -\delta) - \frac{\beta^4}{2^5}(\Sigma -\delta)^2 + \frac{\beta^6}{2^7}(\Sigma -\delta)^3 + \cdots \biggr\} </math>

and,

<math>~ 4\beta \biggl\{ \tilde{C}_2 ( \tilde{C}_1 - 3 ) \biggl[ \tilde{C}_2 -3 ~m_\xi^{2/3}\biggr]^{1 / 2}\biggr\} </math>	<math>~=</math>	<math>~ \biggl[16 + 10\Sigma - 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl[1 + \frac{1}{2}(\Sigma +\delta) \beta^2\biggr]^{1 / 2} </math>
	<math>~=</math>	<math>~ \biggl[16 + 10\Sigma - 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{1 + \frac{\beta^2}{2^2}(\Sigma +\delta) - \frac{\beta^4}{2^5}(\Sigma +\delta)^2 + \frac{\beta^6}{2^7}(\Sigma +\delta)^3 + \cdots \biggr\} \, . </math>

Hence, the numerator and denominator of the expression for <math>~\mathfrak{r}</math> are, respectively,

Numerator	<math>~=</math>	<math>~ \biggl[16 + 10\Sigma + 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{1 + \frac{\beta^2}{2^2}(\Sigma -\delta) - \frac{\beta^4}{2^5}(\Sigma -\delta)^2 + \frac{\beta^6}{2^7}(\Sigma -\delta)^3 + \cdots \biggr\} </math>
		<math>~ - \biggl[16 + 10\Sigma - 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{1 + \frac{\beta^2}{2^2}(\Sigma +\delta) - \frac{\beta^4}{2^5}(\Sigma +\delta)^2 + \frac{\beta^6}{2^7}(\Sigma +\delta)^3 + \cdots \biggr\} </math>
	<math>~=</math>	<math>~ \biggl[16 + 10\Sigma + 6\delta + (\Sigma^2 - \delta^2)\biggr] - \biggl[16 + 10\Sigma - 6\delta + (\Sigma^2 - \delta^2)\biggr] </math>
		<math>~ + \biggl[16 + 10\Sigma + 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{\frac{\beta^2}{2^2}(\Sigma -\delta) \biggr\} - \biggl[16 + 10\Sigma - 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{\frac{\beta^2}{2^2}(\Sigma +\delta) \biggr\} </math>
		<math>~ + \biggl[16 + 10\Sigma + 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{ - \frac{\beta^4}{2^5}(\Sigma -\delta)^2 \biggr\} - \biggl[16 + 10\Sigma - 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{ - \frac{\beta^4}{2^5}(\Sigma +\delta)^2 \biggr\} </math>
		<math>~ + \biggl[16 + 10\Sigma + 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{ \frac{\beta^6}{2^7}(\Sigma -\delta)^3 \biggr\} - \biggl[16 + 10\Sigma - 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{ \frac{\beta^6}{2^7}(\Sigma +\delta)^3 \biggr\} + \cdots </math>
	<math>~=</math>	<math>~ 12\delta + \frac{\beta^2}{2^2} \biggl\{ 12\delta \Sigma - 2\delta \biggl[16 + 10\Sigma + (\Sigma^2 - \delta^2)\biggr] \biggr\} </math>
		<math>~ - \frac{\beta^4}{2^5} \biggl\{ \biggl[16 + 10\Sigma + (\Sigma^2 - \delta^2)\biggr] \biggl[ (\Sigma -\delta)^2 - (\Sigma +\delta)^2 \biggr] + 6\delta \biggl[(\Sigma -\delta)^2 +(\Sigma +\delta)^2 \biggr] \biggr\} </math>
		<math>~ + \frac{\beta^6}{2^7} \biggl\{ \biggl[16 + 10\Sigma + (\Sigma^2 - \delta^2)\biggr] \biggl[ (\Sigma -\delta)^3 - (\Sigma +\delta)^3 \biggr] + 6\delta \biggl[(\Sigma -\delta)^3 +(\Sigma +\delta)^3 \biggr] \biggr\} + \cdots </math>
	<math>~=</math>	<math>~ \delta \biggl\{ 12 - 8\beta^2 \biggl[ 1 + \frac{1}{4} \Sigma + \frac{1}{16} \biggl(\Sigma^2 - \delta^2 \biggr)\biggr] + \frac{\beta^4 }{2^3} \biggl[ 16\Sigma + 7\Sigma^2 -3 \delta^2 + \Sigma(\Sigma^2 - \delta^2) \biggr] \biggr\} </math>
		<math>~ + \frac{\beta^6\delta}{2^6} \biggl\{ 6\Sigma^3 + 18\delta^2\Sigma -\biggl[16 + 10\Sigma + \Sigma^2 - \delta^2\biggr] \biggl[3\Sigma^2 +\delta^2 \biggr] \biggr\} + \cdots </math>
	<math>~=</math>	<math>~ \delta \biggl\{ 12 - 8\beta^2 \biggl[ 1 + \frac{1}{4} \Sigma + \frac{1}{16} \biggl(\Sigma^2 - \delta^2 \biggr)\biggr] + \frac{\beta^4 }{2^3} \biggl[ 16\Sigma + 7\Sigma^2 -3 \delta^2 + \Sigma(\Sigma^2 - \delta^2) \biggr] </math>
		<math>~ + \frac{\beta^6}{2^6} \biggl[ -48\Sigma^2 - 16\delta^2 + 8\delta^2\Sigma - 24\Sigma^3 - 3\Sigma^4 +2\delta^2\Sigma^2 +\delta^4 \biggr] \biggr\} + \cdots </math>
	<math>~=</math>	<math>~ \delta \biggl\{ \biggl[12 - 8\beta^2 \biggr] -2 \Sigma\biggl[\beta^2 - \beta^4 \biggr] + \delta^2\biggl[ \frac{\beta^2}{2} - \frac{3\beta^4}{2^3} -\frac{16\beta^6}{2^6}\biggr] + \Sigma^2\biggl[- \frac{\beta^2}{2} + \frac{7\beta^4}{2^3} - \frac{48\beta^6}{2^6}\biggr] </math>
		<math>~ + \frac{\beta^4 }{2^3} \biggl[ \Sigma(\Sigma^2 - \delta^2) \biggr] + \frac{\beta^6}{2^6} \biggl[ 8\delta^2\Sigma - 24\Sigma^3 - 3\Sigma^4 +2\delta^2\Sigma^2 +\delta^4 \biggr] \biggr\} + \cdots </math>

and,

Denominator	<math>~=</math>	<math>~ \biggl[16 + 10\Sigma + 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{1 + \frac{\beta^2}{2^2}(\Sigma -\delta) - \frac{\beta^4}{2^5}(\Sigma -\delta)^2 + \frac{\beta^6}{2^7}(\Sigma -\delta)^3 + \cdots \biggr\} </math>
		<math>~ + \biggl[16 + 10\Sigma - 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{1 + \frac{\beta^2}{2^2}(\Sigma +\delta) - \frac{\beta^4}{2^5}(\Sigma +\delta)^2 + \frac{\beta^6}{2^7}(\Sigma +\delta)^3 + \cdots \biggr\} </math>
	<math>~=</math>	<math>~ \biggl[16 + 10\Sigma + 6\delta + (\Sigma^2 - \delta^2)\biggr] + \biggl[16 + 10\Sigma - 6\delta + (\Sigma^2 - \delta^2)\biggr] </math>
		<math>~ +\biggl[16 + 10\Sigma + 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{\frac{\beta^2}{2^2}(\Sigma -\delta) \biggr\} + \biggl[16 + 10\Sigma - 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{\frac{\beta^2}{2^2}(\Sigma +\delta) \biggr\} </math>
		<math>~ + \biggl[16 + 10\Sigma + 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{ - \frac{\beta^4}{2^5}(\Sigma -\delta)^2 \biggr\} + \biggl[16 + 10\Sigma - 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{ - \frac{\beta^4}{2^5}(\Sigma +\delta)^2 \biggr\} </math>
		<math>~ +\biggl[16 + 10\Sigma + 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{ \frac{\beta^6}{2^7}(\Sigma -\delta)^3 \biggr\} + \biggl[16 + 10\Sigma - 6\delta + (\Sigma^2 - \delta^2)\biggr] \biggl\{ \frac{\beta^6}{2^7}(\Sigma +\delta)^3 \biggr\} + \cdots </math>
	<math>~=</math>	<math>~ 2\biggl[16 + 10\Sigma + (\Sigma^2 - \delta^2)\biggr] + \frac{\beta^2 \Sigma}{2}\biggl[16 + 10\Sigma + (\Sigma^2 - \delta^2)\biggr] -3 \beta^2 \delta^2 </math>
		<math>~ - \frac{\beta^4}{2^4} \biggl[16 + 10\Sigma + (\Sigma^2 - \delta^2)\biggr] (\Sigma^2 + \delta^2) + \frac{3\beta^4 \delta^2 \Sigma}{2^2} </math>
		<math>~ + \frac{\beta^6}{2^7} \biggl[16 + 10\Sigma + (\Sigma^2 - \delta^2)\biggr]\biggl\{ (\Sigma -\delta)^3 + (\Sigma +\delta)^3 \biggr\} + \frac{\beta^6}{2^7} \biggl[6\delta \biggr] \biggl\{ (\Sigma -\delta)^3 - (\Sigma +\delta)^3\biggr\} + \cdots </math>
	<math>~=</math>	<math>~ 32 + \biggl[20 + 8\beta^2\biggr] \Sigma + \biggl[ (2+ 5 \beta^2 - \beta^4 )\Sigma^2 - ( 2 + 3 \beta^2 + \beta^4 )\delta^2 \biggr] </math>
		<math>~ + \frac{\beta^2 \Sigma}{2}\biggl[(\Sigma^2 - \delta^2)\biggr] - \frac{5\beta^4\Sigma}{2^3} (\Sigma^2 + \delta^2) + \frac{3\beta^4 \delta^2 \Sigma}{2^2} - \frac{\beta^4}{2^4} \biggl[ (\Sigma^2 - \delta^2)\biggr] (\Sigma^2 + \delta^2) + \frac{\beta^6 \Sigma}{2^6} \biggl[16 + 10\Sigma + (\Sigma^2 - \delta^2)\biggr] (\Sigma^2 + 3\delta^2 ) - \frac{3\beta^6 \delta^2}{2^5} ( 3\Sigma^2 + \delta^2) + \cdots </math>

To lowest order in smallness <math>~(\delta~\mathrm{or}~\Sigma)</math>, then, we have,

<math>~\mathfrak{r}</math>	<math>~\approx</math>	<math>~ \delta \biggl[ \biggl(12 - 8\beta^2 \biggr) -2 \Sigma\biggl(\beta^2 - \beta^4 \biggr) \biggr] \biggl[ 32 + \biggl(20 + 8\beta^2\biggr) \Sigma \biggr]^{-1} + \mathcal{O}(\delta^3~\mathrm{or}~\delta\Sigma^2) </math>
	<math>~\approx</math>	<math>~ \frac{\delta}{32} \biggl[ \biggl(12 - 8\beta^2 \biggr) -2 \Sigma\biggl(\beta^2 - \beta^4 \biggr) \biggr] \biggl[ 1 - \biggl(\frac{5}{8} + \frac{1}{4}\beta^2\biggr) \Sigma \biggr] + \mathcal{O}(\delta^3~\mathrm{or}~\delta\Sigma^2) </math>
	<math>~\approx</math>	<math>~ \frac{\delta}{32} \biggl[ \biggl(12 - 8\beta^2 \biggr) -2 \Sigma\biggl(\beta^2 - \beta^4 \biggr) - \biggl(12 - 8\beta^2 \biggr)\biggl(\frac{5}{8} + \frac{1}{4}\beta^2\biggr) \Sigma \biggr] + \mathcal{O}(\delta^3~\mathrm{or}~\delta\Sigma^2) </math>
	<math>~=</math>	<math>~ \frac{\delta}{32} \biggl\{ 4(3 - 2\beta^2) + \Sigma\biggl[ \biggl(2\beta^4 - 2\beta^2 \biggr) + \biggl(8\beta^2 -12\biggr)\biggl(\frac{5}{8} + \frac{1}{4}\beta^2\biggr) \biggr] \biggr\} + \mathcal{O}(\delta^3~\mathrm{or}~\delta\Sigma^2) </math>
	<math>~=</math>	<math>~ \frac{\delta}{32} \biggl\{ 4(3 - 2\beta^2) + \Sigma\biggl[ \biggl(2\beta^4 - 2\beta^2 \biggr) + 5\beta^2 + 2\beta^4 - \frac{15}{2} -3\beta^2 \biggr] \biggr\} + \mathcal{O}(\delta^3~\mathrm{or}~\delta\Sigma^2) </math>
	<math>~=</math>	<math>~ \frac{\delta}{32} \biggl[ 4(3 - 2\beta^2) - \frac{\Sigma}{2} \biggl(15- 8\beta^4 \biggr) \biggr] + \mathcal{O}(\delta^3~\mathrm{or}~\delta\Sigma^2) \, . </math>

This matches the result derived earlier.

Near the Maximum Mass

We seek a power-series expression for,

<math>~\Delta C_2</math>

<math>~=</math>

<math>~ \biggl(1-\frac{\epsilon_+}{3}\biggr)^{-2} -1 \, , </math>

and,

<math>~\Delta C_1</math>

<math>~=</math>

<math>~ \biggl(1-\frac{\epsilon_-}{3}\biggr)^{-2} -1 \, . </math>

Via the binomial expansion, we can write,

<math>~ \biggl(1-\frac{\epsilon_\pm}{3}\biggr)^{-2} - 1 </math>

<math>~=</math>

<math>~ \biggl( \frac{2}{3}\biggr)\epsilon_\pm + \biggl( \frac{1}{3} \biggr) \epsilon_\pm^2 + \biggl(\frac{2^2}{3^3} \biggr) \epsilon_\pm^3 + \biggl( \frac{5}{3^4} \biggr)\epsilon_\pm^4 + \mathcal{O}(\epsilon_\pm^5) \, . </math>

So, given that,

<math>~\epsilon_\pm</math>

<math>~=</math>

<math>~ \pm 6^{1 / 2} \mu - \biggl(\frac{4}{3}\biggr)\mu^2 \pm \biggl[ \frac{5\cdot 23}{(2^5 \cdot 3^5)^{1 / 2}} \biggr] \mu^3 - \biggl(\frac{191}{2\cdot 3^4}\biggr) \mu^4 + \mathcal{O}(\mu^5) \, , </math>

we have,

<math>~\Delta C_2</math>	<math>~=</math>	<math>~ \frac{2}{3} \biggl\{ 6^{1 / 2} \mu - \biggl(\frac{4}{3}\biggr)\mu^2 + \biggl[ \frac{5\cdot 23}{(2^5 \cdot 3^5)^{1 / 2}} \biggr] \mu^3 - \biggl(\frac{191}{2\cdot 3^4}\biggr) \mu^4 \biggr\} </math>
		<math>~ + \frac{1}{3} \biggl\{ 6^{1 / 2} \mu - \biggl(\frac{4}{3}\biggr)\mu^2 + \biggl[ \frac{5\cdot 23}{(2^5 \cdot 3^5)^{1 / 2}} \biggr] \mu^3 \biggr\}^2 </math>
		<math>~ + \frac{2^2}{3^3} \biggl\{ 6^{1 / 2} \mu - \biggl(\frac{4}{3}\biggr)\mu^2 \biggr\}^3 + \frac{5}{3^4} \biggl\{ 6^{1 / 2} \mu \biggr\}^4 + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ \biggl( \frac{2^2}{3^2} \biggr)^{1 / 2} (2\cdot 3)^{1 / 2} \mu - \biggl( \frac{2}{3} \biggr) \biggl(\frac{2^2}{3}\biggr)\mu^2 + \biggl( \frac{2}{3} \biggr) \biggl[ \frac{5\cdot 23}{(2^5 \cdot 3^5)^{1 / 2}} \biggr] \mu^3 - \biggl( \frac{2}{3} \biggr) \biggl(\frac{191}{2\cdot 3^4}\biggr) \mu^4 </math>
		<math>~ + \frac{6}{3} \mu^2 \biggl\{ 1 - (2\cdot 3)^{-1 / 2} \biggl(\frac{2^2}{3}\biggr)\mu + (2\cdot 3)^{-1 / 2} \biggl[ \frac{5\cdot 23}{(2^5 \cdot 3^5)^{1 / 2}} \biggr] \mu^2 \biggr\}^2 </math>
		<math>~ + \frac{2^2}{3^3} (2\cdot 3)^{3 / 2} \mu^3 \biggl[ 1 - (2\cdot 3)^{-1 / 2}\biggl(\frac{2^2}{3}\biggr)\mu \biggr]^3 + \frac{5}{3^4} \biggl[ (2\cdot 3)^{2} \mu^4 \biggr] + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ \biggl( \frac{2^3}{3} \biggr)^{1 / 2}\mu - \biggl(\frac{2^3}{3^2}\biggr)\mu^2 + \biggl[ \frac{5\cdot 23}{(2^3 \cdot 3^7)^{1 / 2}} \biggr] \mu^3 - \biggl(\frac{191}{3^5}\biggr) \mu^4 </math>
		<math>~ + 2 \mu^2 \biggl\{ 1 + \biggl[ - \biggl(\frac{2^3}{3^3}\biggr)^{1 / 2}\mu + \biggl( \frac{5\cdot 23}{2^3 \cdot 3^3} \biggr) \mu^2 \biggr] \biggr\}^2 </math>
		<math>~ + \biggl( \frac{2^7}{3^3} \biggr)^{1 / 2} \mu^3 \biggl[ 1 - \biggl(\frac{2^3}{3^3}\biggr)^{1 / 2} \mu \biggr]^3 + \biggl( \frac{2^2 \cdot 5}{3^2} \biggr) \mu^4 + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ \biggl( \frac{2^3}{3} \biggr)^{1 / 2}\mu + 2\mu^2 - \biggl(\frac{2^3}{3^2}\biggr)\mu^2 + \biggl[ \frac{5\cdot 23}{(2^3 \cdot 3^7)^{1 / 2}} \biggr] \mu^3 - \biggl(\frac{2^7}{3^3}\biggr)^{1 / 2} \mu^3 + \biggl( \frac{2^7}{3^3} \biggr)^{1 / 2} \mu^3 </math>
		<math>~ + \biggl( \frac{5\cdot 23}{2 \cdot 3^3} \biggr) \mu^4 + \biggl(\frac{2^4}{3^3}\biggr) \mu^4 - \biggl(\frac{191}{3^5}\biggr) \mu^4 - \biggl( \frac{2^{10}}{3^4} \biggr)^{1 / 2} \mu^4 + \biggl( \frac{2^2 \cdot 5}{3^2} \biggr) \mu^4 + \mathcal{O}(\mu^5) </math>
	<math>~=</math>	<math>~ \biggl( \frac{2^3}{3} \biggr)^{1 / 2}\mu + \biggl[ 2 - \biggl(\frac{2^3}{3^2}\biggr) \biggr]\mu^2 + \biggl[ \frac{5\cdot 23}{(2^3 \cdot 3^7)^{1 / 2}} \biggr] \mu^3 + \biggl[ \frac{5\cdot 23}{2 \cdot 3^3} + \frac{2^4}{3^3} - \frac{191}{3^5} - \frac{2^{5}}{3^2} + \frac{2^2 \cdot 5}{3^2} \biggr] \mu^4 + \mathcal{O}(\mu^5) \, . </math>
	<math>~=</math>	<math>~ \biggl( \frac{2^3}{3} \biggr)^{1 / 2}\mu + \biggl(\frac{10}{9}\biggr) \mu^2 + \biggl[ \frac{5\cdot 23}{(2^3 \cdot 3^7)^{1 / 2}} \biggr] \mu^3 + \biggl( \frac{293}{2 \cdot 3^5} \biggr) \mu^4 + \mathcal{O}(\mu^5) \, . </math>

Similarly, we have deduced that,

<math>~\Delta C_1</math>

<math>~=</math>

<math>~ - \biggl( \frac{2^3}{3} \biggr)^{1 / 2}\mu + \biggl(\frac{10}{9}\biggr) \mu^2 - \biggl[ \frac{5\cdot 23}{(2^3 \cdot 3^7)^{1 / 2}} \biggr] \mu^3 + \biggl( \frac{293}{2 \cdot 3^5} \biggr) \mu^4 + \mathcal{O}(\mu^5) \, . </math>

Hence,

<math>~\Delta C_2 + \Delta C_1</math>	<math>~=</math>	<math>~\biggl[ \biggl( \frac{2^3}{3} \biggr)^{1 / 2}\mu + \biggl(\frac{10}{9}\biggr) \mu^2 + \biggl[ \frac{5\cdot 23}{(2^3 \cdot 3^7)^{1 / 2}} \biggr] \mu^3 + \biggl( \frac{293}{2 \cdot 3^5} \biggr) \mu^4 + \mathcal{O}(\mu^5) \biggr] </math>
		<math>~ + \biggl[ - \biggl( \frac{2^3}{3} \biggr)^{1 / 2}\mu + \biggl(\frac{10}{9}\biggr) \mu^2 - \biggl[ \frac{5\cdot 23}{(2^3 \cdot 3^7)^{1 / 2}} \biggr] \mu^3 + \biggl( \frac{293}{2 \cdot 3^5} \biggr) \mu^4 + \mathcal{O}(\mu^5) \biggr] </math>
	<math>~=</math>	<math>~ \biggl(\frac{20}{9}\biggr) \mu^2 + \biggl( \frac{293}{3^5} \biggr) \mu^4 + \mathcal{O}(\mu^6) \, , </math>

and,

<math>~\Delta C_2 - \Delta C_1</math>	<math>~=</math>	<math>~\biggl[ \biggl( \frac{2^3}{3} \biggr)^{1 / 2}\mu + \biggl(\frac{10}{9}\biggr) \mu^2 + \biggl[ \frac{5\cdot 23}{(2^3 \cdot 3^7)^{1 / 2}} \biggr] \mu^3 + \biggl( \frac{293}{2 \cdot 3^5} \biggr) \mu^4 + \mathcal{O}(\mu^5) \biggr] </math>
		<math>~ - \biggl[ - \biggl( \frac{2^3}{3} \biggr)^{1 / 2}\mu + \biggl(\frac{10}{9}\biggr) \mu^2 - \biggl[ \frac{5\cdot 23}{(2^3 \cdot 3^7)^{1 / 2}} \biggr] \mu^3 + \biggl( \frac{293}{2 \cdot 3^5} \biggr) \mu^4 + \mathcal{O}(\mu^5) \biggr] </math>
	<math>~=</math>	<math>~ \biggl( \frac{2^5}{3} \biggr)^{1 / 2}\mu + \biggl[ \frac{5\cdot 23}{(2 \cdot 3^7)^{1 / 2}} \biggr] \mu^3 + \mathcal{O}(\mu^5) \, , </math>

so we have,

<math>~\mathfrak{x}</math>	<math>~\approx</math>	<math>~ \frac{1}{8}( \Delta C_2 - \Delta C_1 )\biggl[ (3-2\beta^2) + \frac{1}{8}\biggl( \Delta C_2 + \Delta C_1 \biggr) (8\beta^4 - 15 ) \biggr] </math>
	<math>~\approx</math>	<math>~ \frac{1}{8}\biggl\{ \biggl( \frac{2^5}{3} \biggr)^{1 / 2}\mu + \biggl[ \frac{5\cdot 23}{(2 \cdot 3^7)^{1 / 2}} \biggr] \mu^3 \biggr\} \biggl\{ (3-2\beta^2) + \frac{1}{8}\biggl[ \biggl(\frac{20}{9}\biggr) \mu^2 + \biggl( \frac{293}{3^5} \biggr) \mu^4 \biggr] (8\beta^4 - 15 ) \biggr\} </math>
	<math>~=</math>	<math>~ \biggl\{ \biggl( \frac{1}{2 \cdot 3} \biggr)^{1 / 2}\mu + \biggl[ \frac{5\cdot 23}{(2 \cdot 3)^{7 / 2}} \biggr] \mu^3 \biggr\} \biggl\{ (3-2\beta^2) + \biggl[ \biggl(\frac{5}{18}\biggr) \mu^2 + \biggl( \frac{293}{2^3 \cdot 3^5} \biggr) \mu^4 \biggr] (8\beta^4 - 15 ) \biggr\} </math>
	<math>~=</math>	<math>~\biggl( \frac{\mu^2}{2 \cdot 3} \biggr)^{1 / 2} (3-2\beta^2) \biggl[ 1 + \biggl( \frac{5\cdot 23}{6^3} \biggr) \mu^2 \biggr] \biggl\{ 1 + \biggl[ \biggl(\frac{5}{18}\biggr) \mu^2 + \biggl( \frac{293}{2^3 \cdot 3^5} \biggr) \mu^4 \biggr] \frac{(8\beta^4 - 15 )}{(3-2\beta^2)} \biggr\} </math>

Finally, remembering that,

<math>~\beta</math>	<math>~\equiv</math>	<math>~(4 -3~m_\xi^{2/3})^{-1 / 2}</math>
<math>~\Rightarrow ~~~ (3-2\beta^2)</math>	<math>~=</math>	<math>~\frac{3(4 -3~m_\xi^{2/3}) - 2}{(4 -3~m_\xi^{2/3})} = \biggl[ \frac{10 -9~m_\xi^{2/3}}{4 -3~m_\xi^{2/3} } \biggr] \, ,</math>

and defining an overall normalization,

<math>~\mathfrak{x}_\mathrm{norm}</math>	<math>~\equiv</math>	<math>~\biggl(\frac{5}{2} \biggr) \mathfrak{x}\biggr|_{\beta = 1}</math>
	<math>~=</math>	<math>~\frac{5}{2}~\biggl( \frac{\mu^2}{2 \cdot 3} \biggr)^{1 / 2} \biggl[ 1 + \biggl( \frac{5\cdot 23}{6^3} \biggr) \mu^2 \biggr] \biggl\{ 1 -7 \biggl[ \biggl(\frac{5}{18}\biggr) \mu^2 + \biggl( \frac{293}{2^3 \cdot 3^5} \biggr) \mu^4 \biggr]\biggr\} \, , </math>

such that the normalized amplitude is always <math>~\tfrac{2}{5}</math> at the surface — that is, at <math>~m_\xi = 1</math> and, hence, at <math>~\beta = 1</math> — we have,

<math>~x_\mathfrak{x} \equiv \frac{\mathfrak{x}}{\mathfrak{x}_\mathrm{norm}}</math>

<math>~\approx</math>

<math>~\frac{2}{5} \biggl[ \frac{10 -9~m_\xi^{2/3}}{4 -3~m_\xi^{2/3} } \biggr] \biggl\{ 1 + \biggl[ \biggl(\frac{5}{18}\biggr) \mu^2 + \biggl( \frac{293}{2^3 \cdot 3^5} \biggr) \mu^4 \biggr] \frac{(8\beta^4 - 15 )}{(3-2\beta^2)} \biggr\}\biggl\{ 1 -7 \biggl[ \biggl(\frac{5}{18}\biggr) \mu^2 + \biggl( \frac{293}{2^3 \cdot 3^5} \biggr) \mu^4 \biggr]\biggr\}^{-1} \, . </math>

To leading order — in which case,

<math>~\mathfrak{x}_\mathrm{norm} = \biggl( \frac{5^2}{2^3\cdot 3} \biggr)^{1 / 2} \mu \, ,</math>

— this exactly matches the analytically derived eigenfunction for the marginally unstable model, namely,

<math>~x_P</math>

<math>~=</math>

<math>~\frac{2}{5} \biggl[ \frac{10 -9~m_\xi^{2/3}}{4 -3~m_\xi^{2/3} } \biggr] \, . </math>

Summary

Function Plots

The solid green curve in Figure 1 shows how the equilibrium mass varies with radius for pressure-truncated, n = 5 polytropic spheres, if the polytropic constant and the externally applied pressure are held fixed. The portion of this mass-radius equilibrium sequence that lies inside the black-dashed rectangular box has been displayed again as a (static) solid green curve in the left-most panel of Figure 2. As in Figure 1, the solid black circular marker identifies the configuration along the equilibrium sequence that has the maximum mass,

<math>~m_\mathrm{max} \equiv \frac{M}{M_\mathrm{SWS}}\biggr|_\mathrm{max}</math>

<math>~=</math>

<math>~\biggl[\frac{3^4\cdot 5^3}{2^{10} \pi} \biggr]^{1 / 2} \, .</math>

Other parameter values associated with this maximum-mass model are given in the row of Table 1 that is labeled, "Pairing A" — for example, <math>~{\tilde\xi}_\pm = 3</math> and <math>~\tilde{C} = 4 \Rightarrow \Delta \tilde{C} = 0</math>. The (static) solid black curve in the middle panel of Figure 2 provides a quantitative description of the internal structural profile of this maximum-mass model. It displays how the radius of each mass shell varies with the integrated mass that lies internal to that shell; specifically, the black curve in the middle panel of Figure 2 displays the function,

<math>~r(m_\xi)</math>

<math>~=</math>

<math>~\biggl[ \frac{3^2 \cdot 5}{2^6 \pi} \biggr]^{1 / 2} \biggl[ 4m_\xi^{-2/3} -3 \biggr]^{-1 / 2} \, ,</math>

where the fractional mass, <math>~0 \le m_\xi \le 1</math>, is being employed as the Lagrangian radial coordinate. Notice that, when <math>~m_\xi = 1</math>, this expression gives the configuration's equilibrium radius as tabulated in the third column of the row of Table 1 that is labeled "Pairing A". As has been explained, above, the eigenfunction associated with the fundamental mode of radial oscillation for this maximum-mass model is given precisely by the expression,

<math>~x_P(m_\xi) </math>

<math>~=</math>

<math>~\frac{2}{5} \biggl[ \frac{10 -9~m_\xi^{2/3}}{4 -3~m_\xi^{2/3}} \biggr] \, .</math>

This function has been plotted as a (static) black solid curve in the right-most panel of Figure 2; note that, although its overall normalization is arbitrary, here the eigenfunction has been normalized such that the fractional radial displacement, <math>~x = \delta r/r</math>, is two-fifths at the surface <math>~(m_\xi = 1)</math> of the configuration and unity at the center <math>~(m_\xi = 0)</math>.

As an animation sequence, Figure 2 loops repeatedly through nine separate frames. In the left-most panel of each animation frame, the solid-blue horizontal line identifies a specific value of the equilibrium configuration's mass <math>~(M/M_\mathrm{SWS} < m_\mathrm{max})</math>, and the two solid-blue circular markers identify where — that is, at what two values of equilibrium radii — the horizontal line intersects the equilibrium sequence. The nine separate values of the configuration mass that are highlighted by the animation (and the values of the pair of radii that are associated with each) are given in column 2 (and, respectively, in columns 3 & 4) of Table 1; they are labeled as "Pairing B" through "Pairing J". Note that, for each value of the mass, the pair of values of the equilibrium radii were obtained by analytically identifying the pair of real roots of the quartic equation that defines the mass-radius relationship. For each specified mass, Table 1 also lists (columns 5 & 6) the corresponding values of the pair of dimensionless truncation radii, <math>~{\tilde\xi}_\pm</math>, and (columns 7 & 8) the corresponding values of the pair shifted parameters, <math>~\Delta C_2</math> and <math>~\Delta C_1</math>.

In the middle panel of each frame of the animation sequence, we have displayed in a quantitatively precise manner how the internal structural profiles of the relevant pair of equilibrium models compares with the structural profile of the limiting-mass model. Specifically, the solid blue (dashed blue) curve shows how the radius of each mass shell varies with the integrated mass that lies internal to that shell in the case of the model that has the larger (smaller) equilibrium radius, as defined by the function,

<math>~r_i(m_\xi)</math>

<math>~=</math>

<math>~\biggl[ \frac{3^2 \cdot 5}{2^2 \pi} \biggr]^{1 / 2} \biggl[ \frac{\tilde{C}_i - 3}{\tilde{C}_i} \biggr] \biggl[ \tilde{C}_i~m_\xi^{-2/3} -3 \biggr]^{-1 / 2} \, ,</math>

where,

<math>~\tilde{C}_i \equiv \frac{3^2}{\tilde\xi_i^2}\biggl( 1 + \frac{\tilde\xi_i^2}{3} \biggr)</math>

<math>~\Rightarrow</math>

<math>~ {\tilde\xi}_i^2 = \frac{9}{\tilde{C}_i - 3} \, . </math>

Notice that, as it should, this generalized expression for <math>~r_i(m_\xi)</math> reduces to the expression (shown above) that applies specifically to the maximum-mass model when <math>~{\tilde\xi}_i = 3 \Rightarrow {\tilde{C}}_i = 4</math>. The percentage that is stamped on the center panel of each animation frame — varying from 2.9% to 12% — provides a measure of the degree to which this pair of (blue) profiles departs from the profile of the maximum-mass model; as documented in column 9 of Table 1, each percentage value is determined by dividing one-half the difference in the surface radii of the (blue) model pair by the radius of the (black) limiting-mass model.

References:

• G. S. Bisnovatyi-Kogan & S. I. Blinnikov (1974) [see also here]:  If one wants to know from a stability analysis the answer to only one question — whether the model is stable or not — then the most straightforward procedure is to use the third, static method (Zeldovich 1963; Dmitrie & Kholin 1963). For the application of this method, one needs to construct only equilibrium, stationary models, with no further calculation. Generally the static analysis gives no information about the shape of the modes of oscillation, but, in the vicinity of critical points, where instability sets in, this method makes it possible to find the eigenfunction of the mode which becomes unstable at the critical point.
• §6.8 of [ST83] [see also here]:  Upon further thought, it occurred to me that a careful examination of the internal structure of both models — especially relative to one another — might reveal what the eigenvector of that (nonlinear) oscillation might be. In support of this idea, I point to the discussion of "Turning-Points and the Onset of Instability" found in §6.8 of [ST83] — specifically, on p. 149 in the paragraph that follows eq. (6.8.11) — where we find the following statement: "… the eigenfunction at a critical point is simply the Lagrangian displacement <math>~\xi</math> that carries an equilibrium configuration on the low-density side of the critical point into an equilibrium configuration on the high-density side."
• Stahler (1983) [see also here]:  Referencing Bisnovatyi-Kogan & Blinnikov (1974), Stahler points out that, in principle, the marginally unstable, radial-oscillation eigenvector that is associated with each an equilibrium-sequence turning point … can be computed as the zero-frequency displacement connecting neighboring equilibria. Such an analysis would, presumably, reveal the same eigenfunction that was derived by Yabushita (1975) — that is, the function defined above as, <math>~x_Y(\xi)</math>. But, as far as we are aware, such an analysis has never been completed.

Conjecture posed by G. S. Bisnovatyi-Kogan & S. I. Blinnikov (1974) — see the opening paragraph of their § 6:

… a static configuration close to an extremum of the mass-radius equilibrium curve may be considered as a perturbed state of a model of the same mass situated on the other side of the extremum. The difference of the two models approximately represents the eigenfunction of the neutral mode. Let there exist two Models 1 and 2 for a mass <math>~M</math> in the vicinity of an extremum; then the eigenfunction <math>~\mathfrak{x}</math> is <math>~\mathfrak{x} = r_2(m_\xi) - r_1(m_\xi) \, ,</math> where <math>~m_\xi</math> is the Lagrangian coordinate and <math>~r_1, r_2</math> Eulerian coordinates of the Models 1 and 2.

For each specified value of the truncated configuration's total mass, <math>~m</math>, measured relative to the maximum-allowed mass,

<math>~\mu \equiv \biggl[ 1 - \biggl( \frac{m}{m_\mathrm{max}} \biggr)^2 \biggr]^{1 / 2}</math>       <math>~\Rightarrow</math>       <math>~m^2 =

m_\mathrm{max}^2(1-\mu^2) = \frac{3^4\cdot 5^3}{2^{10} \pi}(1-\mu^2) \, ,</math>

there will be a pair of equilibrium states, whose identifying truncation radii, <math>~(\tilde{C}_1, \tilde{C}_2)</math>, are determined analytically as roots of a quartic equation. Ten such pairings are identified in Table 1.

As shown above, we can define a (nonlinear) displacement function as the fractional difference between the radial profiles of this pair of equal-mass states,

<math>~\mathfrak{x}(m_\xi) </math>	<math>~\equiv</math>	<math>~ \frac{\tfrac{1}{2}\Delta r_\mathrm{SWS}}{<r_\mathrm{SWS}>} = \frac{ \tfrac{1}{2} [r_2(m_\xi) - r_1(m_\xi) ]}{\tfrac{1}{2} [ r_2(m_\xi) + r_1(m_\xi)]}</math>
	<math>~=</math>	<math>~ \biggl\{ \tilde{C}_1 ( \tilde{C}_2 - 3 ) \biggl[ \tilde{C}_1 -3~m_\xi^{2/3} \biggr]^{1 / 2} - \tilde{C}_2 ( \tilde{C}_1 - 3 ) \biggl[ \tilde{C}_2 -3 ~m_\xi^{2/3}\biggr]^{1 / 2} \biggr\} \biggl\{ \tilde{C}_1 ( \tilde{C}_2 - 3 ) \biggl[ \tilde{C}_1 -3~m_\xi^{2/3} \biggr]^{1 / 2} + \tilde{C}_2 ( \tilde{C}_1 - 3 ) \biggl[ \tilde{C}_2 -3~m_\xi^{2/3} \biggr]^{1 / 2} \biggr\}^{-1} \, . </math>

Or, in terms of the shifted parameters,

<math>~\Delta C_i \equiv {\tilde{C}}_i - 4 </math>      <math>~\Rightarrow</math>      <math>~\tilde{C}_i = \Delta C_i + 4 \, ,</math>

<math>~\mathfrak{x}[\beta(m_\xi)] </math>	<math>~=</math>	<math>~ \biggl\{ \biggl[ 1 + \frac{\Delta C_1}{4} + \Delta C_2 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr](1 + \beta^2 \Delta C_1 )^{1 / 2} - \biggl[ 1 + \frac{\Delta C_2}{4} + \Delta C_1 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] ( 1+\beta^2 \Delta C_2 )^{1 / 2} \biggr\} </math>
		<math>~\times \biggl\{ \biggl[ 1 + \frac{\Delta C_1}{4} + \Delta C_2 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] ( 1 + \beta^2\Delta C_1 )^{1 / 2} + \biggl[ 1 + \frac{\Delta C_2}{4} + \Delta C_1 + \frac{\Delta C_1 \cdot \Delta C_2}{4} \biggr] ( 1 + \beta^2\Delta C_2 )^{1 / 2} \biggr\}^{-1} \, , </math>

where,

<math>~\beta \equiv (4 -3~m_\xi^{2/3})^{-1 / 2} \, .</math>

The conjecture is that this nonlinear displacement function, <math>~\mathfrak{x}</math>, should match the analytically specified radial oscillation eigenfunction, <math>~x_P</math>, in the limit of <math>~m/m_\mathrm{max} \rightarrow 1</math>.

This is an excerpt from a related discussion:  Referencing Bisnovatyi-Kogan & Blinnikov (1974), Stahler points out that, in principle, the marginally unstable, radial-oscillation eigenvector that is associated with each of these turning points … can be computed as the zero-frequency displacement connecting neighboring equilibria. Such an analysis would, presumably, reveal the same eigenfunction that was derived by Yabushita (1975) — that is, the function defined above as, <math>~x_Y(\xi)</math>. As far as we are aware, such an analysis has never been completed.

Animation

Figure 2:   Structural properties of Model Pairs having the same Equilibrium Masses

---

Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
|   Go Home   |

---

Review of Internal Structure

Run of Mass

According to Chandrasekhar (Chapter IV, equation 67, p.97), the mass interior to <math>~\xi</math> is,

<math>~M(\xi)</math>

<math>~=</math>

<math>~4\pi a_n^3 \rho_c (-\xi^2 \theta^') \, .</math>

For a pressure-truncated polytrope, the total mass is,

<math>~M_\mathrm{tot}</math>

<math>~=</math>

<math>~4\pi a_n^3 \rho_c (-\tilde\xi^2 \tilde\theta^') \, ,</math>

which means that, as a function of <math>~\xi</math> in a pressure-truncated polytrope, the relative mass is,

<math>~m_\xi \equiv \frac{M(\xi)}{M_\mathrm{tot}}</math>	<math>~=</math>	<math>~\biggl[4\pi a_n^3 \rho_c (-\xi^2 \theta^') \biggr] \biggl[ 4\pi a_n^3 \rho_c (-\tilde\xi^2 \tilde\theta^') \biggr]^{-1}</math>
	<math>~=</math>	<math>~\frac{(-\xi^2 \theta^')}{(-\tilde\xi^2 \tilde\theta^')} \, .</math>

Thus, for an <math>~n = 5</math> system we have,

<math>~m_\xi</math>	<math>~=</math>	<math>~ \biggl(\frac{\xi}{\tilde\xi}\biggr)^2 \biggl[ \frac{\xi }{ 3}\biggl(1 + \frac{\xi^2}{3}\biggr)^{-3/2} \biggr] \biggl[ \frac{\tilde\xi }{ 3}\biggl(1 + \frac{\tilde\xi^2}{3}\biggr)^{-3/2} \biggr]^{-1}</math>
	<math>~=</math>	<math>~ \biggl(\frac{\xi}{\tilde\xi}\biggr)^3 \biggl(1 + \frac{\xi^2}{3}\biggr)^{-3/2} \biggl(1 + \frac{\tilde\xi^2}{3}\biggr)^{3/2} \, ;</math>

and, for the configuration at the pressure maximum <math>~(\tilde\xi = 3)</math>, in particular, we have,

<math>~m_0</math>

<math>~=</math>

<math>~\biggl(\frac{2\xi}{3}\biggr)^3 \biggl(1 + \frac{\xi^2}{3}\biggr)^{-3/2} \, .</math>

Corresponding Lagrangian Radial Coordinate

For any pressure-truncated polytrope, the fractional radial-coordinate running through the equilibrium configuration is,

<math>~\frac{r(\xi)}{R_\mathrm{eq}}</math>	<math>~=</math>	<math>~\frac{\xi}{\tilde\xi}</math>
<math>~\Rightarrow~~~ r(\xi)</math>	<math>~=</math>	<math>~\biggl(\frac{\xi}{\tilde\xi}\biggr) R_\mathrm{eq}</math>
<math>~\Rightarrow~~~r_\xi \equiv \frac{r(\xi)}{R_\mathrm{norm}}</math>	<math>~=</math>	<math>~\biggl(\frac{\xi}{\tilde\xi}\biggr) \biggl[ \frac{4\pi}{(n+1)^n}\biggr]^{1/(n-3)} \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} \, . </math>

For <math>~n=5</math> configurations, this means,

<math>~r_\xi</math>	<math>~=</math>	<math>~\biggl(\frac{\xi}{\tilde\xi}\biggr) \biggl[ \frac{4\pi}{2^5\cdot 3^5}\biggr]^{1/2} \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{-2} </math>
	<math>~=</math>	<math>~\xi \biggl\{ \biggl[ \frac{4\pi}{2^5\cdot 3^5}\biggr]^{1/2} \tilde\xi^{-4} \biggl[ \frac{\tilde\xi}{3} \biggl( 1+\frac{\tilde\xi^2}{3} \biggr)^{-3/2}\biggr]^{-2} \biggr\} </math>
	<math>~=</math>	<math>~\xi \biggl\{ \biggl[ \frac{4\pi}{2^5\cdot 3}\biggr]^{1/2} \tilde\xi^{-6} \biggl( 1+\frac{\tilde\xi^2}{3} \biggr)^{3}\biggr\} \, ; </math>

and, for the configuration at the pressure maximum <math>~(\tilde\xi = 3)</math>, in particular, this gives,

<math>~r_0</math>	<math>~=</math>	<math>~\xi \biggl\{ \biggl[ \frac{4\pi}{2^5\cdot 3}\biggr]^{1/2} \biggl(\frac{2}{3}\biggr)^6\biggr\} </math>
	<math>~=</math>	<math>~\xi \biggl[ \frac{2^9 \pi}{3^{13}}\biggr]^{1/2} </math>

Exploration

n = 5 Mass-Radius Relation

So, for any <math>~\tilde\xi</math> configuration, the parametric relationship between <math>~m_\xi</math> and <math>~r_\xi</math> in pressure-truncated, <math>~n=5</math> polytropes is,

<math>~m_\xi</math>	<math>~=</math>	<math>~ \biggl(\frac{\xi}{\tilde\xi}\biggr)^3 \biggl(1 + \frac{\xi^2}{3}\biggr)^{-3/2} \biggl(1 + \frac{\tilde\xi^2}{3}\biggr)^{3/2} \, ,</math>
<math>~r_\xi</math>	<math>~=</math>	<math>~\xi \biggl\{ \biggl[ \frac{4\pi}{2^5\cdot 3}\biggr]^{1/2} \tilde\xi^{-6} \biggl( 1+\frac{\tilde\xi^2}{3} \biggr)^{3}\biggr\} \, . </math>

And this can be inverted analytically in the case of <math>~\tilde\xi = 3</math>. Specifically,

<math>~m_0</math>	<math>~=</math>	<math>~\biggl(\frac{2\xi}{3}\biggr)^3 \biggl(1 + \frac{\xi^2}{3}\biggr)^{-3/2} </math>
<math>~\Rightarrow~~~ m_0^{2/3}</math>	<math>~=</math>	<math>~\biggl(\frac{2^2\xi^2}{3^2}\biggr) \biggl(1 + \frac{\xi^2}{3}\biggr)^{-1} </math>
<math>~\Rightarrow~~~ 2^2\xi^2 </math>	<math>~=</math>	<math>~ 3^2\biggl(1 + \frac{\xi^2}{3}\biggr) m_0^{2/3} </math>
<math>~\Rightarrow~~~ \xi^2 (2^2 - 3 m_0^{2/3}) </math>	<math>~=</math>	<math>~ 3^2m_0^{2/3} </math>
<math>~\Rightarrow~~~ \xi^2 </math>	<math>~=</math>	<math>~ \frac{3^2m_0^{2/3}}{(2^2 - 3 m_0^{2/3})} \, . </math>

Hence, the radius-mass relationship in the configuration at the <math>~P_\mathrm{max}</math> turning point is,

<math>~ r_0 (m_0) </math>

<math>~=</math>

<math>~\biggl[ \frac{2^9 \pi}{3^{13}}\biggr]^{1/2} \biggl[\frac{3^2m_0^{2/3}}{2^2 - 3 m_0^{2/3}}\biggr]^{1/2} \, . </math>

Actually, the inversion can be performed analytically for any choice of <math>~\tilde\xi</math> to obtain,

<math>~ r_\xi (m_\xi) </math>

<math>~=</math>

<math>~\tilde{r}_\mathrm{edge} \biggl[\frac{3^2m_\xi^{2/3}}{\tilde{C} - 3 m_\xi^{2/3}}\biggr]^{1/2} \, , </math>

where,

<math>~\tilde{C}</math>	<math>~\equiv</math>	<math>~ \frac{3^2}{\tilde\xi^2}\biggl( 1 + \frac{\tilde\xi^2}{3} \biggr) \, . </math>
<math>~\tilde{r}_\mathrm{edge}</math>	<math>~\equiv</math>	<math>~\biggl[ \frac{\pi}{2^3\cdot 3}\biggr]^{1/2} {\tilde\xi}^{-6} \biggl(1+\frac{\tilde\xi^2}{3}\biggr)^3 \, . </math>

Finite Difference Representation of Radial Eigenfunction

Preamble

<math>~\tilde{C}</math>	<math>~\equiv</math>	<math>~ \frac{3^2}{\tilde\xi^2}\biggl( 1 + \frac{\tilde\xi^2}{3} \biggr) \, , </math>
<math>~\tilde{r}_\mathrm{edge}</math>	<math>~\equiv</math>	<math>~ \biggl[ \frac{\pi}{2^3\cdot 3}\biggr]^{1/2} \biggl[ \frac{1}{ {\tilde\xi}^{2} }\biggl(1+\frac{\tilde\xi^2}{3}\biggr) \biggr] ^3 </math>
	<math>~=</math>	<math>~ \biggl[ \frac{\pi}{2^3\cdot 3}\biggr]^{1/2} \biggl[ \frac{\tilde{C} }{ 3^2 }\biggr] ^3 </math>
	<math>~=</math>	<math>~ \biggl[ \frac{\pi}{2^3\cdot 3^{13}}\biggr]^{1/2} {\tilde{C}}^3 \, . </math>

Note that when <math>~\tilde\xi = 3</math>,

<math>~\tilde{C}_3</math>	<math>~=</math>	<math>~ 4 \, , </math>
<math>~\tilde{r}_{e3}</math>	<math>~=</math>	<math>~ \biggl[ \frac{2^9\pi }{3^{13} } \biggr]^{1 / 2} \, . </math>

Conjectures

A first-cut examination of the structure of the radial eigenfunction associated with the <math>~P_\mathrm{max}</math> turning point is given by simply subtracting one <math>~r_\xi(m_\xi)</math> profile from another at the same applied external pressure. (The specific choices of the two appropriate values of <math>~\tilde\xi</math> are discussed in the subsection titled, "Configuration Pairing", which follows.) The answer appears to be,

<math>~[ \Delta r_\xi ]_{21} = [r_\xi (m_\xi)]_2 - [r_\xi (m_\xi)]_1 </math>	<math>~=</math>	<math>~ [\tilde{r}_\mathrm{edge}]_2 \biggl[\frac{3^2m_\xi^{2/3}}{\tilde{C}_2 - 3 m_\xi^{2/3}}\biggr]^{1/2} - [\tilde{r}_\mathrm{edge}]_1 \biggl[\frac{3^2m_\xi^{2/3}}{\tilde{C}_1 - 3 m_\xi^{2/3}}\biggr]^{1/2} </math>
	<math>~=</math>	<math>~ \biggl[ \frac{\pi}{2^3\cdot 3^{13}}\biggr]^{½} \biggl\{ {\tilde{C}_2}^3 \biggl[\frac{3^2m_\xi^{2/3}}{\tilde{C}_2 - 3 m_\xi^{2/3}}\biggr]^{1/2} - {\tilde{C}_1}^3 \biggl[\frac{3^2m_\xi^{2/3}}{\tilde{C}_1 - 3 m_\xi^{2/3}}\biggr]^{1 / 2} \biggr\} </math>
	<math>~=</math>	<math>~ \biggl[ \frac{\pi}{2^3\cdot 3^{13}}\biggr]^{1 / 2} \biggl\{ {\tilde{C}_2}^3 \biggl[\frac{3^2m_\xi^{2/3}/\tilde{C}_1 }{\tilde{C}_2/\tilde{C}_1 - 3 m_\xi^{2/3}/\tilde{C}_1 }\biggr]^{1 / 2} - {\tilde{C}_1}^3 \biggl[\frac{3^2m_\xi^{2/3}/\tilde{C}_1 }{1 - 3 m_\xi^{2/3}/\tilde{C}_1 }\biggr]^{1 / 2} \biggr\} </math>
	<math>~=</math>	<math>~ \biggl[ \frac{\pi}{2^3\cdot 3^{13}}\biggr]^{1 / 2} \biggl\{ {\tilde{C}_2}^3 \biggl[\frac{3/u }{\tilde{C}_2/\tilde{C}_1 - 1/u }\biggr]^{1 / 2} - {\tilde{C}_1}^3 \biggl[\frac{3/u }{1 - 1/u }\biggr]^{1 / 2} \biggr\} </math>
	<math>~=</math>	<math>~ {\tilde{C}_1}^3 \biggl[ \frac{\pi}{2^3\cdot 3^{12}}\biggr]^{1 / 2} \biggl\{ k_{21}^3 \biggl[\frac{1 }{k_{21} u - 1 }\biggr]^{1 / 2} - \biggl[\frac{1 }{u - 1 }\biggr]^{1 / 2} \biggr\} \, , </math>

where,

<math>~u \equiv \tilde{C}_1/(3 m_\xi^{2/3}) \, ,</math>

<math>~k_{21} \equiv \frac{ \tilde{C}_2 }{ \tilde{C}_1 } \, .</math>

After examining the form of this last expression, it is clear that we can also write,

<math>~[r_\xi (m_\xi)]_1</math>

<math>~=</math>

<math>~ {\tilde{C}_1}^3 \biggl[ \frac{\pi}{2^3\cdot 3^{12}}\biggr]^{1 / 2} \biggl[\frac{1 }{u - 1 }\biggr]^{1 / 2} \, , </math>

in which case, the lopsided fractional eigenfunction takes the form,

<math>~\frac{[ \Delta r_\xi ]_{21} }{[r_\xi (m_\xi)]_1} </math>

<math>~=</math>

<math>~ k_{21}^3 \biggl[\frac{u - 1 }{k_{21} u - 1 }\biggr]^{1 / 2} - 1 \, . </math>

And the centered fractional eigenfunction is,

<math>~\frac{[ \Delta r_\xi ]_{32} }{[r_\xi (m_\xi)]_1} </math>	<math>~=</math>	<math>~ \biggl\{ k_{31}^3 \biggl[\frac{u - 1 }{k_{31} u - 1 }\biggr]^{1 / 2} - 1 \biggr\} - \biggl\{ k_{21}^3 \biggl[\frac{u - 1 }{k_{21} u - 1 }\biggr]^{1 / 2} - 1 \biggr\} </math>
	<math>~=</math>	<math>~ k_{31}^3 \biggl[\frac{u - 1 }{k_{31} u - 1 }\biggr]^{1 / 2} - k_{21}^3 \biggl[\frac{u - 1 }{k_{21} u - 1 }\biggr]^{1 / 2} \, . </math>

Configuration Pairing

Setup

Now, let's identify two <math>~n=5</math> equilibrium states that sit very near the <math>~P_\mathrm{max}</math> turning point on the two separate branches of the equilibrium sequence and that have identical external pressures. We know from separate discussions that, in both cases,

<math> ~\frac{P_\mathrm{e}}{P_\mathrm{norm}} </math>	<math>~=~</math>	<math>~\biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{(n+1)/(n-3)} \tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} </math>
	<math>~=~</math>	<math>~\biggl[ \frac{2\cdot 3^3}{\pi}\biggr]^{3} \tilde\xi^{12} \tilde\theta_n^{6}( - \tilde\theta' )^{6} </math>
<math>~\Rightarrow~~~ \biggl[ \frac{\pi}{2\cdot 3^3}\biggr]^{1/2}\biggl[\frac{P_\mathrm{e}}{P_\mathrm{norm}}\biggr]^{1/6}</math>	<math>~=~</math>	<math>~ \tilde\xi^{2} \tilde\theta_n( - \tilde\theta' ) </math>
	<math>~=~</math>	<math>~ 3\ell^2 (1+\ell^2)^{-1/2} \frac{\ell}{\sqrt{3}} (1+\ell^2)^{-3/2} </math>
	<math>~=~</math>	<math>~ \sqrt{3}\ell^3 (1+\ell^2)^{-2} </math>

We can therefore write,

<math>~(1+\ell^2)^{2}</math>	<math>~=~</math>	<math>~ p_0\ell^3 </math>
<math>~\Rightarrow~~~\ell^4 - p_0\ell^3 + 2\ell^2 + 1</math>	<math>~=~</math>	<math>~ 0 \, , </math>

where,

<math>p_0 \equiv \biggl[ \frac{2\cdot 3^4}{\pi}\biggr]^{1/2}\biggl[\frac{P_\mathrm{e}}{P_\mathrm{norm}}\biggr]^{-1/6}</math>

So, in essence, we seek two real roots of this quartic equation that are near <math>~P_\mathrm{max}</math>, that is, that are near <math>~\ell = \sqrt{3}</math> — where <math>~p_0 = (2^8/3^3)^{1/2}</math>.

Because we are hunting for equilibrium configurations near <math>~P_\mathrm{max}</math>, it makes sense to make the variable substitution,

<math>~\ell</math>

<math>~\rightarrow</math>

<math>~\sqrt{3}(1+\epsilon) \, ,</math>

and look for pairs of values, <math>~\epsilon_\pm</math> (both real, but one positive and the other negative).

<math>~0</math>	<math>~=~</math>	<math>~3^2(1+\epsilon)^4 - 3^{3/2}p_0(1+\epsilon)^3 + 6(1+\epsilon)^2 + 1</math>
	<math>~=~</math>	<math>~ 3^2\biggl[1 + 4\epsilon + 6\epsilon^2 + 4\epsilon^3 + \epsilon^4\biggr] - 3^{3/2}p_0\biggl[ 1+ 3\epsilon + 3\epsilon^2 + \epsilon^3 )\biggr] + 6\biggl[1 + 2\epsilon + \epsilon^2\biggr] + 1 </math>
	<math>~=~</math>	<math>~ \epsilon^4 \biggl[ 9 \biggr] +\epsilon^3 \biggl[ 36 - 3^{3/2}p_0 \biggr] +\epsilon^2 \biggl[ 54 - 3^{5/2}p_0 + 6 \biggr] +\epsilon \biggl[36 - 3^{5/2}p_0 + 12 \biggr] +(16- 3^{3/2}p_0)\, . </math>

And, because we will only be examining values of the external pressure that are less than <math>~P_\mathrm{max}</math>, and we know that at the point of maximum pressure, <math>~3^{3/2}p_0 = 16</math>, it makes sense to make the substitution,

<math>~3^{3/2}p_0 ~~~\rightarrow ~~~ (16+\delta) \, .</math>

Hence, for a fixed choice of <math>~\delta </math> (reasonably small, and positive), we seek two real roots (one positive and the other negative) of the quartic relation,

<math>~0</math>	<math>~=~</math>	<math>~ 9\epsilon^4 +\epsilon^3 \biggl[ 36 - (16+\delta ) \biggr] +\epsilon^2 \biggl[ 60 - 3(16+\delta ) \biggr] +\epsilon \biggl[48 - 3(16+\delta ) \biggr] -\delta </math>
	<math>~=~</math>	<math>~ 9\epsilon^4 +\epsilon^3 (20-\delta ) +\epsilon^2 ( 12 - 3\delta ) -\epsilon (3\delta ) -\delta \, . </math>

What are the reasonable limits on <math>~\delta</math>? Well, first note that,

<math>~p_0</math>	<math>~=</math>	<math>~\frac{(1+\ell^2)^2}{\ell^3}</math>
<math>~\Rightarrow ~~~ 16+\delta </math>	<math>~=</math>	<math>~3^{3/2}\biggl[\frac{(1+\ell^2)^2}{\ell^3}\biggr]</math>
<math>~\Rightarrow ~~~ \delta </math>	<math>~=</math>	<math>~3^{3/2}\biggl[\frac{(1+\ell^2)^2}{\ell^3}\biggr] - 2^4 \, .</math>

Now, according to our accompanying discussion, the relevant limits on <math>~\ell</math> are <math>~\sqrt{3}</math> (set by the maximum pressure turning point) and 2.223175 (set by the transition to dynamical instability). The corresponding values of <math>~\delta </math> are:   0 (by design) and 0.69938.

Quartic Solution

Here, we will draw from the Wikipedia discussion of the quartic function. The generic form is,

<math>~0</math>

<math>~=</math>

<math>~ax^4 + bx^3 + cx^2 + dx + e \,.</math>

Relating this to our specific quartic function, we should ultimately make the following assignments:

<math>~a</math>	<math>~=</math>	<math>~9</math>
<math>~b</math>	<math>~=</math>	<math>~20 - \delta</math>
<math>~c</math>	<math>~=</math>	<math>~12 - 3\delta = 3(4-\delta )</math>
<math>~d</math>	<math>~=</math>	<math>~-3 \delta</math>
<math>~e</math>	<math>~=</math>	<math>~-\delta</math>

We need to evaluate the following expressions:

<math>~p</math>	<math>~\equiv</math>	<math>~\frac{8ac-3b^2}{8a^2}</math>
	<math>~=</math>	<math>~\frac{2^3 \cdot 3^3(4-\delta )-3(20-\delta )^2}{2^3\cdot 3^4}</math>
<math>~q</math>	<math>~\equiv</math>	<math>~\frac{b^3 - 4abc + 8a^2d}{8a^3}</math>
	<math>~=</math>	<math>~\frac{(20 - \delta )^3 - 2^2\cdot 3^3(4-\delta ) (20 - \delta ) - 2^3\cdot 3^5\delta }{2^3 \cdot 3^6}</math>
<math>~\Delta_0</math>	<math>~\equiv</math>	<math>~c^2 - 3bd + 12ae</math>
	<math>~=</math>	<math>~3^2(4-\delta )^2 + 3^2\delta (20 - \delta ) - 2^2\cdot 3^3\delta</math>
	<math>~=</math>	<math>~144</math>
<math>~\Delta_1</math>	<math>~\equiv</math>	<math>~2c^3 - 9bcd + 27b^2e+27ad^2 - 72ace</math>
	<math>~=</math>	<math>~2\cdot 3^3(4-\delta)^3 + 3^4(20-\delta)(4-\delta)\delta - 3^3(20-\delta)^2 \delta+3^7\delta^2 + 2^3\cdot 3^5(4-\delta)\delta</math>
	<math>~=</math>	<math>~3^3(128 + 32\delta + \delta^2) \, .</math>
Note:   <math>~\Delta_1^2 - 4\Delta_0^3</math>	<math>~=</math>	<math>~3^6(2^{13}\delta + 2^8\cdot 5 \delta^2 + 2^6\delta^3 + \delta^4) \, .</math>

For a given value of <math>~\delta</math>, then, the pair of real roots is:

<math>~\epsilon_\pm</math>

<math>~=</math>

<math>~ -\frac{b}{4a} + S \pm \frac{1}{2}\biggl[ -4S^2 - 2p - \frac{q}{S} \biggr]^{1/2} \, , </math>

where,

<math>~S</math>	<math>~\equiv</math>	<math>~ \frac{1}{2}\biggl[- \frac{2p}{3} + \frac{1}{3a}\biggl(Q + \frac{\Delta_0}{Q}\biggr) \biggr]^{1/2} \, , </math>
<math>~Q</math>	<math>~\equiv</math>	<math>~ \biggl[ \frac{\Delta_1 + \sqrt{\Delta_1^2 - 4\Delta_0^3}}{2} \biggr]^{1/3} \, . </math>

We have used an Excel spreadsheet to evaluate these expressions. The following table identifies <math>~\epsilon_\pm</math> pairs (the middle two columns of numbers) for twenty different values of the external pressure; more specifically, for twenty values of <math>~0 \le \delta \le 0.69938</math>, equally spaced between the two limits. The corresponding pairs of <math>~\tilde\xi_\pm</math> are also listed (rightmost pair of columns).

Table 1

Sets of Paired Models from Quartic Solution P_e/P_norm delta eps_+ eps_- xi_+ xi_- 160.867 0.00000 0.00000 0.00000 3.00000 3.00000 158.664 0.03681 0.05747 -0.05338 3.17241 2.83986 156.497 0.07362 0.08253 -0.07435 3.24759 2.77695 154.363 0.11043 0.10227 -0.09000 3.30681 2.72999 152.264 0.14724 0.11927 -0.10291 3.35781 2.69127 150.198 0.18405 0.13452 -0.11407 3.40355 2.65780 148.164 0.22086 0.14852 -0.12398 3.44556 2.62805 146.163 0.25767 0.16159 -0.13296 3.48476 2.60111 144.193 0.29448 0.17391 -0.14120 3.52174 2.57640 142.254 0.33129 0.18563 -0.14883 3.55690 2.55351 140.345 0.36809 0.19685 -0.15596 3.59055 2.53212 138.466 0.40490 0.20764 -0.16266 3.62291 2.51203 136.617 0.44171 0.21805 -0.16898 3.65415 2.49305 134.796 0.47852 0.22814 -0.17498 3.68442 2.47505 133.003 0.51533 0.23794 -0.18070 3.71382 2.45791 131.239 0.55214 0.24748 -0.18615 3.74245 2.44154 129.501 0.58895 0.25680 -0.19138 3.77039 2.42586 127.790 0.62576 0.26590 -0.19640 3.79770 2.41081 126.106 0.66257 0.27481 -0.20122 3.82444 2.39634 124.447 0.69938 0.28355 -0.20587 3.85065 2.38238

Two Example Eigenfunctions

The following figure is fundamentally a reproduction of Figure 3 from an accompanying discussion. It presents the "Case M" equilibrium sequence from both an order-of-magnitude analysis (marked by light-blue squares) and a detailed force-balance analysis (light-green triangles). The dark green circular dot identifies the configuration at the pressure maximum of the sequence — <math>~P_\mathrm{max}/P_\mathrm{norm} = 160.867</math> — and the red circular dot identifies the location along the sequence where the transition from stable to dynamically unstable configurations occurs — <math>~P_e/P_\mathrm{norm} = 124.447</math>. (All pressures have been normalized to <math>~P_\mathrm{max}</math> in the figure.)

Figure 1

At any <math>~P_e</math> between these two limiting values, a pair of stable equilibrium configurations exist; approximately twenty example pairings are listed in Table 1. The horizontal, black dashed line in the figure has been drawn at <math>~P_e/P_\mathrm{norm} = 158.664</math>. The pair of equilibrium configurations associated with this pressure is identified graphically by the two points at which this dashed line intersects the detailed force-balance equilibrium sequence; as is detailed in the second row of Table 1, the configurations correspond to models having <math>~\tilde\xi = 2.83986</math> (right intersection) and <math>~\tilde\xi = 3.17241</math> (left intersection). The left-hand panel of Figure 2 shows how the Lagrangian radial coordinate varies with mass, <math>~r_\xi(m_\xi)</math>, throughout the interior of these two equilibrium configurations (the locus of green and orange dots, respectively); for reference, the profile of the configuration at <math>~P_\mathrm{max}</math> is presented as well (locus of black dots). The right-hand panel of Figure 2 shows the same paired configuration profiles, but relative to the profile of the configuration at <math>~P_\mathrm{max}</math>.

Figure 2

The horizontal, black dot-dash line in Figure 1 has been drawn at <math>~P_e/P_\mathrm{norm} = 124.447</math>. The pair of equilibrium configurations associated with this pressure is identified graphically by the two points at which this dot-dash line intersects the detailed force-balance equilibrium sequence; as is detailed in the last row of Table 1, the configurations correspond to models having <math>~\tilde\xi = 2.83986</math> (right intersection) and <math>~\tilde\xi = 3.17241</math> (left intersection), which is the configuration that marks the onset of a dynamical instability. The left-hand panel of Figure 3 shows how the Lagrangian radial coordinate varies with mass, <math>~r_\xi(m_\xi)</math>, throughout the interior of these two paired equilibrium configurations (the locus of green and orange dots, respectively); again, for reference, the profile of the configuration at <math>~P_\mathrm{max}</math> is presented as well (locus of black dots). The right-hand panel of Figure 3 shows the same paired configuration profiles, but relative to the profile of the configuration at <math>~P_\mathrm{max}</math>.

Figure 3

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation