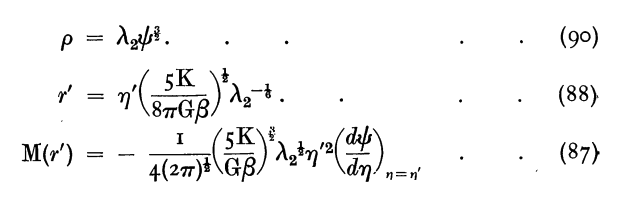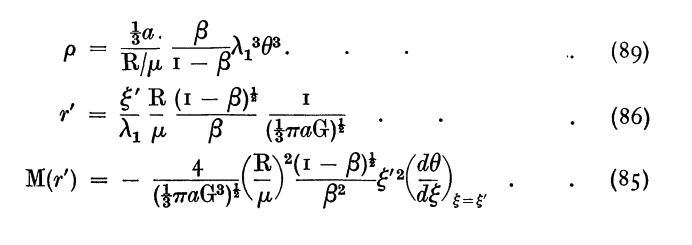User:Tohline/SSC/Structure/BiPolytropes/Analytic1.5 3
BiPolytrope with <math>n_c = \tfrac{3}{2}</math> and <math>n_e=3</math>

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Here we lay out the procedure for constructing a bipolytrope in which the core has an <math>~n_c=\tfrac{3}{2}</math> polytropic index and the envelope has an <math>~n_e=3</math> polytropic index. We will build our discussion around the work of E. A. Milne (1930, MNRAS, 91, 4) who, as we shall see, justified these two indexes on physical grounds. While this system cannot be described by closed-form, analytic expressions, it is of particular interest because — as far as we have been able to determine — its examination by Milne represents the first "composite polytrope" to be discussed in the astrophysics literature.
In deriving the properties of this model, we will follow the general solution steps for constructing a bipolytrope that are outlined in a separate chapter of this H_Book. That group of general solution steps was drawn largely from chapter IV, §28 of Chandrasekhar's book titled, "An Introduction to the Study of Stellar Structure" [C67]. At the end of that chapter (specifically, p. 182), Chandrasekhar acknowledges that "[Milne's] method is largely used in § 28." It seems fitting, therefore, that we highlight the features of the specific bipolytropic configuration that E. A. Milne (1930) chose to build.
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Milne's (1930) Choice of Equations of State
As has been detailed in our introductory discussion of analytically expressible equations of state and as is summarized in the following table, often the total gas pressure can be expressed as the sum of three separate components: a component of ideal gas pressure, a component of radiation pressure, and a component due to a degenerate electron gas. As a result, the total pressure is given by the expression,
|
<math>~P</math> |
<math>~=</math> |
<math>~P_\mathrm{gas} + P_\mathrm{deg} + P_\mathrm{rad} \, .</math> |
| Ideal Gas | Degenerate Electron Gas | Radiation | ||||||||||
|
|
|
||||||||||
With this construction in mind, Milne (1930) also introduced the parameter, <math>~\beta</math>, to define the ratio of gas pressure (meaning, ideal-gas plus degeneracy pressure) to total pressure, that is,
<math>\beta \equiv \frac{P_\mathrm{gas} + P_\mathrm{deg}}{P} \, ,</math>
in which case, also,
<math>\frac{P_\mathrm{rad}}{P} = 1-\beta </math> and <math>\frac{P_\mathrm{gas} + P_\mathrm{deg}}{P_\mathrm{rad}} = \frac{\beta}{1-\beta} \, .</math>
(We also have referenced this parameter, β, in the context of a broader discussion of equations of state and modeling time-dependent flows.)
Envelope
Now, inside the envelope of his composite polytrope, Milne (1930) considered that the effects of electron degeneracy pressure could be ignored and, accordingly, employed throughout the envelope the expression,
<math>\frac{P_\mathrm{gas}}{P_\mathrm{rad}} \biggr|_\mathrm{env} = \frac{\beta}{1-\beta} \, , </math>
or (see Milne's equation 24),
<math>\biggl( \frac{\mathfrak{\Re}}{\mu_e}\biggr) \rho = \frac{1}{3}a_\mathrm{rad}T^3 \biggl( \frac{\beta}{1-\beta} \biggr) \, .</math>
If the parameter, <math>~\beta</math>, is constant throughout the envelope — which Milne assumes — then this last expression can be interpreted as defining a <math>~T(\rho)</math> function throughout the envelope of the form,
<math>T = \biggl[ \biggl( \frac{\Re}{\mu_e}\biggr) \biggl(\frac{1-\beta}{\beta}\biggr) \frac{3}{a_\mathrm{rad}} \biggr]^{1/3} \rho^{1/3} \, .</math>
Now, returning to the definition of <math>~\beta</math> while ignoring the effects of degeneracy pressure, we recognize that the total pressure in the envelope can be written in the form of a modified ideal gas relation, namely,
<math>~\beta P = P_\mathrm{gas} + \cancelto{0}{P_\mathrm{deg}} = \biggl(\frac{\Re}{\mu_e}\biggr) \rho T \, ,</math>
with the specific <math>~T(\rho)</math> behavior just derived. This allows us to write the envelope's total pressure as,
|
<math>~P</math> |
<math>~=</math> |
<math>~\frac{1}{\beta}\biggl(\frac{\Re}{\mu_e}\biggr) \rho \biggl[ \biggl( \frac{\Re}{\mu_e}\biggr) \biggl(\frac{1-\beta}{\beta}\biggr) \frac{3}{a_\mathrm{rad}} \biggr]^{1/3} \rho^{1/3}</math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{\Re}{\mu_e}\biggr)^4 \biggl(\frac{1-\beta}{\beta^4}\biggr) \frac{3}{a_\mathrm{rad}} \biggr]^{1/3} \rho^{1 + 1/3} \, ,</math> |
which can be immediately associated with a polytropic relation of the form,
<math>~P = K_e \rho^{1 + 1/n_e} \, ,</math>
with,
|
<math>~n_e</math> |
<math>~=</math> |
<math>~3 \, ,</math> |
|
<math>~K_e</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{\Re}{\mu_e}\biggr)^4 \biggl(\frac{1-\beta}{\beta^4}\biggr) \frac{3}{a_\mathrm{rad}} \biggr]^{1/3} \, .</math> |
So, from the solution, <math>~\phi(\eta)</math>, to the Lane-Emden equation of index <math>~n=3</math>, we will be able to determine that,
|
<math>~\rho</math> |
<math>~=</math> |
<math>~\rho_e \phi^3 \, ,</math> |
and,
|
<math>~r</math> |
<math>~=</math> |
<math>~a_3 \eta \, ,</math> |
where — see our general introduction to the Lane-Emden equation —
|
<math>~a_3^2</math> |
<math>~=</math> |
<math>~\biggl( \frac{K_e}{\pi G}\biggr) \rho_e^{-2/3} \, .</math> |
This is the envelope structure that will be incorporated into our derivation of the bipolytrope's properties, below.
In contrast to this approach, Milne (1930) chose to relate the solution to the envelope's <math>~n=3</math> Lane-Emden equation directly to the temperature via the expression,
<math>T = \lambda \phi \, ,</math>
and deduced that the corresponding radial scale-factor is (see Milne's equation 27),
|
<math>~a^2_\mathrm{Milne}</math> |
<math>~=</math> |
<math>~\frac{1}{\lambda^2} \biggl(\frac{\Re}{\mu_e}\biggr)^{2} \frac{(1-\beta)}{\beta^2} \biggl(\frac{3}{\pi a_\mathrm{rad}G}\biggr)\, .</math> |
In order to demonstrate the relationship between our radial scale-factor <math>~(a_3)</math> and Milne's, we note that,
|
<math>~\phi^3</math> |
<math>~=</math> |
<math>~\biggl(\frac{T}{\lambda}\biggr)^3 = \frac{\rho}{\rho_e}</math> |
|
<math>~\Rightarrow~~~~~\lambda^3</math> |
<math>~=</math> |
<math>~\rho_e \biggl(\frac{T^3}{\rho}\biggr)</math> |
|
|
<math>~=</math> |
<math>~\rho_e \biggl[ \biggl( \frac{\Re}{\mu_e}\biggr) \biggl(\frac{1-\beta}{\beta}\biggr) \frac{3}{a_\mathrm{rad}} \biggr]</math> |
|
<math>~\Rightarrow~~~~~\lambda^{-2}</math> |
<math>~=</math> |
<math>~\rho_e^{-2/3} \biggl[ \biggl( \frac{\Re}{\mu_e}\biggr) \biggl(\frac{1-\beta}{\beta}\biggr) \frac{3}{a_\mathrm{rad}} \biggr]^{-2/3} \, .</math> |
Hence,
|
<math>~a^2_\mathrm{Milne}</math> |
<math>~=</math> |
<math>~\rho_e^{-2/3} \biggl[ \biggl( \frac{\Re}{\mu_e}\biggr) \biggl(\frac{1-\beta}{\beta}\biggr) \frac{3}{a_\mathrm{rad}} \biggr]^{-2/3}\biggl(\frac{\Re}{\mu_e}\biggr)^{2} \frac{(1-\beta)}{\beta^2} \biggl(\frac{3}{\pi a_\mathrm{rad}G}\biggr)</math> |
|
|
<math>~=</math> |
<math>~\rho_e^{-2/3} \biggl( \frac{1}{\pi G} \biggr) \biggl[ \biggl(\frac{\Re}{\mu_e}\biggr)^{4} \frac{(1-\beta)}{\beta^{4}} \biggl(\frac{3}{a_\mathrm{rad}}\biggr) \biggr]^{1/3}</math> |
|
|
<math>~=</math> |
<math>~\rho_e^{-2/3} \biggl( \frac{K_e}{\pi G} \biggr) \, .</math> |
It is clear, therefore, that the two radial scale-factors are the same. In preparation for our further discussion of the structure of this bipolytrope's envelope, below, it is useful to highlight the following two expressions that have been developed here in the process of showing the correspondence between our work and that of Milne:
| A Pair of Highlighted Relations | |||||||||
|
Core
In contrast to the envelope, Milne (1930) assumed that the (non-relativistic; "NR") electron degeneracy pressure dominates over the ideal-gas pressure in the core. That is, he assumed that, throughout the core of his composite polytropic configuration,
<math>~\beta P = \cancelto{0}{P_\mathrm{gas}} + P_\mathrm{deg}\biggr|_\mathrm{NR} \,.</math>
As we have demonstrated elsewhere, the non-relativistic expression for the degeneracy pressure is,
|
<math>~P_\mathrm{deg}\biggr|_\mathrm{NR}</math> |
<math>~=</math> |
<math>~\frac{1}{2^2 \cdot 5}\biggl( \frac{3}{\pi} \biggr)^{2/3} \biggl( \frac{h^2}{m_e} \biggr) \biggl[ \frac{\rho}{(\mu_{e^-}) m_p}\biggr]^{5/3} \, ,</math> |
which can be associated with a polytropic relation of the form,
<math>~P_\mathrm{deg}\biggr|_\mathrm{NR} = K_c \rho^{1 + 1/n_c} \, ,</math>
that is, a total pressure of the form,
<math>~\beta P = K_c \rho^{1 + 1/n_c} \, ,</math>
with,
|
<math>~n_c</math> |
<math>~=</math> |
<math>~\frac{3}{2} \, ,</math> |
|
<math>~K_c</math> |
<math>~=</math> |
<math>~\frac{1}{2^2 \cdot 5}\biggl( \frac{3}{\pi} \biggr)^{2/3} \biggl( \frac{h^2}{m_e} \biggr) \biggl[ \frac{1}{(\mu_{e^-}) m_p}\biggr]^{5/3} \, .</math> |
(Note that, here only, we have used the parameter, <math>~\mu_{e^-}</math>, to denote the molecular weight of electrons, instead of just <math>~\mu_e</math>, in order not to confuse it with the mean molecular weight assigned, below, to the envelope material.) So, from the solution, <math>~\theta(\xi)</math>, to the Lane-Emden equation of index <math>~n=\tfrac{3}{2}</math>, we will be able to determine that,
|
<math>~\rho</math> |
<math>~=</math> |
<math>~\rho_0 \theta^{3/2} \, ,</math> |
and,
|
<math>~r</math> |
<math>~=</math> |
<math>~a_{3/2} \xi \, ,</math> |
where — see our general introduction to the Lane-Emden equation —
|
<math>~(a_{3/2})^2</math> |
<math>~=</math> |
<math>~\biggl( \frac{5K_c}{2^3\pi G}\biggr) \rho_0^{-1/3} \, .</math> |
This is the core structure that will be incorporated into our derivation of the bipolytrope's properties, below.
This is precisely the approach taken by Milne (1930). Just before his equation (43), Milne states that, "the equation of state when the electrons alone are degenerate can be shown" to be,
|
<math>~p</math> |
<math>~=</math> |
<math>~\frac{1}{5}\biggl( \frac{3}{4\pi}\biggr)^{2/3} \frac{h^2}{(2m_H)^{5/3} m_e q_e^{2/3} }~ \rho^{5/3} \, ,</math> |
which, upon regrouping terms gives,
|
<math>~p</math> |
<math>~=</math> |
<math>~\frac{1}{5}\biggl( \frac{3}{\pi}\biggr)^{2/3}\biggl( \frac{1}{2^4 q_e^2 }\biggr)^{1/3} \frac{h^2}{m_e }\biggl( \frac{\rho}{2 m_H} \biggr)^{5/3} \, .</math> |
Recognizing that Milne set <math>~q_e = 2</math>, as "the statistical weight of an electron," and that he adopted a molecular weight of the electrons, <math>~\mu_{e^-}=2</math>, this expression for the equation of state exactly matches our expression for <math>~P_\mathrm{deg}|_\mathrm{NR}</math>. Our enlistment of an <math>~n_c = \tfrac{3}{2}</math> polytropic equation of state for the core is therefore also perfectly aligned with Milne's treatment of the core; in particular, according to Milne, at each radial location throughout the core the total pressure can be obtained from the expression,
<math>~P = \frac{K}{\beta} ~\rho^{5/3} \, ,</math>
with Milne's coefficient, <math>~K</math>, having the same definition as our coefficient, <math>~K_c</math>
Our Derivation
Steps 2 & 3
Throughout the core, the properties of this bipolytrope can be expressed in terms of the Lane-Emden function, <math>~\theta(\xi)</math>, which derives from a solution of the 2nd-order ODE,
<math> \frac{1}{\xi^2} \frac{d}{d\xi} \biggl[ \xi^2 \frac{d\theta}{d\xi}\biggr] = - \theta^{3/2} \, , </math>
subject to the boundary conditions,
<math>~\theta = 1</math> and <math>~\frac{d\theta}{d\xi} = 0</math> at <math>~\xi = 0</math>.
The first zero of the function <math>~\theta(\xi)</math> and, hence, the surface of the corresponding isolated <math>~n=\tfrac{3}{2}</math> polytrope is located at <math>~\xi_s = 3.65375</math> (see Table 4 in chapter IV on p. 96 of [C67]). Hence, the interface between the core and the envelope can be positioned anywhere within the range, <math>~0 < \xi_i < \xi_s = 3.65375</math>.
Step 4: Throughout the core <math>~(0 \le \xi \le \xi_i)</math>
|
Specify: <math>~K_c</math> and <math>~\rho_0 ~\Rightarrow</math> |
|
|||
|
<math>~\rho</math> |
<math>~=</math> |
<math>~\rho_0 \theta^{n_c}</math> |
<math>~=</math> |
<math>~\rho_0 \theta^{3/2}</math> |
|
<math>~P</math> |
<math>~=</math> |
<math>~K_c \rho_0^{1+1/n_c} \theta^{n_c + 1}</math> |
<math>~=</math> |
<math>~K_c \rho_0^{5/3} \theta^{5/2}</math> |
|
<math>~r</math> |
<math>~=</math> |
<math>~\biggl[ \frac{(n_c + 1)K_c}{4\pi G} \biggr]^{1/2} \rho_0^{(1-n_c)/(2n_c)} \xi</math> |
<math>~=</math> |
<math>~\biggl[ \frac{5K_c}{8\pi G} \biggr]^{1/2} \rho_0^{-1/6} \xi</math> |
|
<math>~M_r</math> |
<math>~=</math> |
<math>~4\pi \biggl[ \frac{(n_c + 1)K_c}{4\pi G} \biggr]^{3/2} \rho_0^{(3-n_c)/(2n_c)} \biggl(-\xi^2 \frac{d\theta}{d\xi} \biggr)</math> |
<math>~=</math> |
<math>~\frac{1}{2^2(2 \pi )^{1/2}} \biggl[ \frac{5K_c}{G} \biggr]^{3/2} \rho_0^{1/2} \biggl(-\xi^2 \frac{d\theta}{d\xi} \biggr)</math> |
By comparison, the expressions that Milne (1930) derived for the run of <math>~\rho</math>, <math>~r</math>, and <math>~M_r</math> throughout the core are presented in his paper as, respectively, equations (90), (88), and (87). In an effort to facilitate this comparison, Milne's expressions — which also specifically apply to the outer edge of the core, whose identity is associated with primed variable names in Milne's notation — are reprinted as extracted images in the following boxed-in table.
|
Equations extracted† from E. A. Milne (1930)
"The Analysis of Stellar Structure"
MNRAS, vol. 91, pp. 4 - 55 © Royal Astronomical Society |
|---|
| †Equations displayed here, as a single digital image, with presentation order & layout modified from the original publication. |
It is clear that the agreement between our derivation and Milne's is exact, once it is realized that Milne has used <math>~\psi(\eta)</math> to represent the Lane_Emden function for the <math>~n_c = \tfrac{3}{2}</math> core, whereas we have represented this function by <math>~\theta(\xi)</math>; and Milne has identified the configuration's central density as <math>~\lambda_2</math>, whereas we have used the notation, <math>~\rho_0</math>.
Step 5: Interface Conditions
|
|
Setting <math>~n_c=\tfrac{3}{2}</math>, <math>~n_e=3</math>, and <math>~\phi_i = 1 ~~~~\Rightarrow</math> |
|||
|
<math>\frac{\rho_e}{\rho_0}</math> |
<math>~=</math> |
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{n_c}_i \phi_i^{-n_e}</math> |
<math>~=</math> |
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{3/2}_i </math> |
|
<math>\biggl( \frac{K_e}{K_c} \biggr) </math> |
<math>~=</math> |
<math>\rho_0^{1/n_c - 1/n_e}\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-(1+1/n_e)} \theta^{1 - n_c/n_e}_i</math> |
<math>~=</math> |
<math>\rho_0^{1/3}\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-4/3} \theta^{1/2}_i</math> |
|
<math>\frac{\eta_i}{\xi_i}</math> |
<math>~=</math> |
<math>\biggl[ \frac{n_c + 1}{n_e+1} \biggr]^{1/2} \biggl( \frac{\mu_e}{\mu_c}\biggr) \theta_i^{(n_c-1)/2} \phi_i^{(1-n_e)/2}</math> |
<math>~=</math> |
<math>\biggl(\frac{5}{8}\biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c}\biggr) \theta_i^{1/4}</math> |
|
<math>\biggl( \frac{d\phi}{d\eta} \biggr)_i</math> |
<math>~=</math> |
<math>\biggl[ \frac{n_c + 1}{n_e + 1} \biggr]^{1/2} \theta_i^{- (n_c + 1)/2} \phi_i^{(n_e+1)/2} \biggl( \frac{d\theta}{d\xi} \biggr)_i</math> |
<math>~=</math> |
<math>\biggl(\frac{5}{8}\biggr)^{1/2} \theta_i^{- 5/4} \biggl( \frac{d\theta}{d\xi} \biggr)_i</math> |
Step 8: Throughout the envelope <math>~(\eta_i \le \eta \le \eta_s)</math>
|
|
Knowing: <math>~K_e/K_c</math> and <math>~\rho_e/\rho_0</math> from Step 5 <math>\Rightarrow</math> |
|||||
|
<math>~\rho</math> |
<math>~=</math> |
<math>~\rho_e \phi^{n_e}</math> |
<math>~=</math> |
<math>~\rho_0 \biggl(\frac{\rho_e}{\rho_0}\biggr) \phi^3</math> |
<math>~=</math> |
<math>~\rho_0 \biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{3/2}_i \phi^3</math> |
|
<math>~P</math> |
<math>~=</math> |
<math>~K_e \rho_e^{1+1/n_e} \phi^{n_e + 1}</math> |
<math>~=</math> |
<math>K_c \rho_0^{4/3} \biggl(\frac{K_e }{K_c}\biggr) \biggl(\frac{\rho_e}{\rho_0}\biggr)^{4/3} \phi^{4}</math> |
<math>=</math> |
<math>K_c \rho_0^{5/3} \theta^{5/2}_i \phi^{4}</math> |
|
<math>~r</math> |
<math>~=</math> |
<math>~\biggl[ \frac{(n_e + 1)K_e}{4\pi G} \biggr]^{1/2} \rho_e^{(1-n_e)/(2n_e)} \eta</math> |
<math>~=</math> |
<math>~\biggl[ \frac{K_c}{\pi G} \biggr]^{1/2} \rho_0^{-1/3} \biggl( \frac{K_e}{K_c}\biggr)^{1/2} \biggl( \frac{\rho_e}{\rho_0} \biggr)^{-1/3} \eta</math> |
<math>~=</math> |
<math>~\biggl[ \frac{K_c}{\pi G} \biggr]^{1/2} \rho_0^{-1/6} \biggl( \frac{\mu_e}{\mu_c}\biggr)^{-1} \theta_i^{-1/4} \eta</math> |
|
<math>~M_r</math> |
<math>~=</math> |
<math>~4\pi \biggl[ \frac{(n_e + 1)K_e}{4\pi G} \biggr]^{3/2} \rho_e^{(3-n_e)/(2n_e)} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math> |
<math>~=</math> |
<math>~4\pi \biggl[ \frac{K_c}{\pi G} \biggr]^{3/2} \biggl( \frac{K_e}{K_c}\biggr)^{3/2} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math> |
<math>~=</math> |
<math>~\biggl( \frac{2^4}{\pi} \biggr)^{1/2} \biggl[ \frac{K_c}{G} \biggr]^{3/2} \rho_0^{1/2} \biggl( \frac{\mu_e}{\mu_c}\biggr)^{-2} \theta_i^{3/4} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math> |
Instead of working completely across this table in order to relate the envelope's density, radial coordinate, and mass to properties of the core, it is worth pausing to insert into the leftmost set of relations the expressions for <math>~\rho_e</math> and <math>~K_e</math> that were derived above. In doing this, we obtain,
|
<math>~\rho</math> |
<math>~=</math> |
<math>~\rho_e \phi^{3}</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{\Re}{\mu_e}\biggr)^{-1} \frac{\beta}{(1-\beta)} \cdot \frac{1}{3} a_\mathrm{rad} \biggr] \lambda^3 \phi^3 \, ,</math> |
|
<math>~r</math> |
<math>~=</math> |
<math>~\biggl[ \frac{K_e}{\pi G} \biggr]^{1/2} \rho_e^{-1/3} \eta</math> |
<math>~=</math> |
<math>~\frac{1}{(\pi G)^{1/2}} \biggl[ \biggl( \frac{\Re}{\mu_e}\biggr)^4 \biggl(\frac{1-\beta}{\beta^4}\biggr) \frac{3}{a_\mathrm{rad}} \biggr]^{1/6} \biggl\{ \lambda^3 \biggl[ \biggl( \frac{\Re}{\mu_e}\biggr)^{-1} \frac{\beta}{(1-\beta)} \cdot \frac{1}{3} a_\mathrm{rad} \biggr] \biggr\}^{-1/3} \eta</math> |
|
|
|
|
<math>~=</math> |
<math>~\frac{1}{(\pi G)^{1/2}} \biggl[ \biggl( \frac{\Re}{\mu_e}\biggr)^4 \biggl(\frac{1-\beta}{\beta^4}\biggr) \frac{3}{a_\mathrm{rad}} \biggr]^{1/6} \biggl[ \biggl( \frac{\Re}{\mu_e}\biggr)^2\frac{(1-\beta)^2}{\beta^2} \biggl( \frac{3}{a_\mathrm{rad} }\biggr)^2 \biggr] ^{1/6} \frac{\eta}{\lambda} </math> |
|
|
|
|
<math>~=</math> |
<math>~\biggl(\frac{3}{\pi a_\mathrm{rad} G } \biggr)^{1/2} \biggl( \frac{\Re}{\mu_e}\biggr) \frac{(1-\beta)^{1/2}}{\beta} \cdot \frac{\eta}{\lambda} \, ,</math> |
|
<math>~M_r</math> |
<math>~=</math> |
<math>~4\pi \biggl[ \frac{K_e}{\pi G} \biggr]^{3/2} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math> |
<math>~=</math> |
<math>~\frac{4\pi }{(\pi G)^{3/2}} \biggl[ \biggl( \frac{\Re}{\mu_e}\biggr)^4 \biggl(\frac{1-\beta}{\beta^4}\biggr) \frac{3}{a_\mathrm{rad}} \biggr]^{1/2} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math> |
|
|
|
|
<math>~=</math> |
<math>~4 \biggl( \frac{3}{\pi a_\mathrm{rad}G^3} \biggr)^{1/2} \biggl(\frac{\Re}{\mu_e}\biggr)^2 \frac{(1-\beta)^{1/2}}{\beta^2} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr) \, .</math> |
By comparison, the expressions that Milne (1930) derived for the run of <math>~\rho</math>, <math>~r</math>, and <math>~M_r</math> throughout the envelope are presented in his paper as, respectively, equations (89), (86), and (85). In an effort to facilitate this comparison, Milne's expressions — which also specifically apply to the base of the envelope, whose identity is associated with primed variable names in Milne's notation — are reprinted as extracted images in the following boxed-in table.
|
Equations extracted† from E. A. Milne (1930)
"The Analysis of Stellar Structure"
MNRAS, vol. 91, pp. 4 - 55 © Royal Astronomical Society |
|---|
|
†Equations displayed here, as a single digital image, with presentation order & layout modified from the original publication. |
The agreement between our derivation and Milne's is exact, once it is realized that Milne has used <math>~\theta(\xi)</math> to represent the Lane_Emden function for the <math>~n_e = 3</math> envelope, whereas we have represented this function by <math>~\phi(\eta)</math>; and in place of Milne's coefficient, <math>~\lambda_1</math>, we have simply written, <math>~\lambda</math>.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |