User:Tohline/Apps/PapaloizouPringleTori

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Massless Polytropic Tori
(aka Papaloizou-Pringle Tori)
In a seminal paper that focused on an analysis of nonaxisymmetric instabilities in accretion disks, Papaloizou & Pringle (1984, MNRAS, 208, 721-750; hereafter, PP84) began by constructing equilibrium structures of axisymmetric, polytropic tori that reside in (orbit about) a Newtonian point-mass potential. The derived structures have analytic prescriptions. Although the tori constructed by PP84 were not self-gravitating — i.e., the tori were massless — it is nevertheless instructive for us to examine how these equilibrium structures were derived.
It is not widely appreciated that the equilibrium structure of Papaloizou-Pringle tori was first derived by Fishbone & Moncrief (1976), ApJ, 207, 962 in a paper whose primary aim was to analyze the properties of thick disks orbiting around Kerr black holes. In §IV of their paper, Fishbone & Moncrief show what thick-disk structures result in the Newtonian limit for homentropic systems with uniform specific angular momentum. These toroidal structures are identical to the ones whose stability was analyzed in PP84. After reviewing the PP84 derivation, we present the Fishbone & Moncrief (1976) description of these equilibrium systems.
Governing Relations
As has been derived elsewhere, for axisymmetric configurations that obey a barotropic equation of state, hydrostatic balance is governed by the following algebraic expression:
<math>~H + \Phi_\mathrm{eff} = C_\mathrm{B} ,</math>
where <math>~C_\mathrm{B}</math> is the Bernoulli constant,
<math>\Phi_\mathrm{eff} \equiv \Phi + \Psi ,</math>
and <math>~\Psi</math> is the relevant centrifugal potential. For self-gravitating configurations, this algebraic expression must be satisfied in concert with a self-consistent solution of the Poisson equation, but for the massless PP84 toroidal structures, <math>~\Phi</math> is just the Newtonian potential presented by a point-like object of mass <math>~M_\mathrm{pt}</math>, namely,
<math>\Phi = - \frac{GM_\mathrm{pt}}{(\varpi^2 + z^2)^{1/2}} .</math>
Hence, the enthalpy distribution <math>H(\varpi,z)</math> throughout the torus can be described analytically for any one of a number of different simple rotation profiles by plugging the appropriate expression for the associated centrifugal potential, <math>\Psi(\varpi)</math>, into the governing relation,
<math> H = -\Phi_\mathrm{eff} + C_\mathrm{B} = \frac{GM_\mathrm{pt}}{(\varpi^2 + z^2)^{1/2}} - \Psi + C_\mathrm{B} . </math>
Supplemental Relations
Following PP84, we supplement the above-specified set of governing equations with a polytropic equation of state, as defined in our overview of supplemental relations for time-independent problems. Specifically, we will assume that <math>~\rho</math> is related to <math>~H</math> through the relation,
<math>~H = (n+1)K_\mathrm{n} \rho^{1/n}</math> ,
or we can set,
<math> H = (n+1) \frac{P}{\rho} . </math>
Inverting the first of these two expressions allows us to immediately derive the density distribution <math>\rho(\varpi,z)</math> throughout the torus from the derived algebraic expression for <math>H(\varpi,z)</math>. Different density distributions will be obtained for different selected polytropic indexes and/or for different selected functional forms of the centrifugal potential.
Here, also following PP84, we impose a steady-state velocity flow-field that is described by a fluid with uniform specific angular momentum, <math>~j_0</math>. Drawing from our table of example simple rotation profiles, the centrifugal potential that describes this chosen flow-field is given by the expression,
<math> \Psi(\varpi) = \frac{j_0^2}{2\varpi^2} . </math>
Summary
Inserting the two supplemental relations into the governing algebraic expression for <math>H(\varpi,z)</math>, we conclude that the polytropic tori studied by PP84 must have structures that satisfy the equation,
<math> (n+1)\frac{P}{\rho} = \frac{GM_\mathrm{pt}}{(\varpi^2 + z^2)^{1/2}} - \frac{j_0^2}{2\varpi^2} + C_\mathrm{B} . </math>
This is identical to Eq. (2.8) of PP84.
Solution
As PP84 point out, for these toroidal structures it is convenient to normalize all lengths to the position in the equatorial plane, <math>~\varpi_0</math>, at which a fluid particle with specific angular momentum <math>~j_0</math> has an angular orbital frequency, <math>~\dot\varphi = j_0/\varpi^2</math>, that matches the Keplerian orbital frequency associated with the point-mass, <math>~M_\mathrm{pt}</math>,
<math> \omega_K \equiv \biggl[ \frac{GM_\mathrm{pt}}{\varpi^3} \biggr]^{1/2} . </math>
That is, it is convenient to define the dimensionless coordinates,
<math> \chi \equiv \frac{\varpi}{\varpi_0} ~~~~~\mathrm{and}~~~~~ \zeta \equiv \frac{z}{\varpi_0} , </math>
where,
<math> \varpi_0 \equiv \frac{j_0^2}{GM_\mathrm{pt}} . </math>
The algebraic relation defining the equilibrium structure then becomes,
<math> H = (n+1)\frac{P}{\rho} = \frac{GM_\mathrm{pt}}{\varpi_0} \biggl[ (\chi^2 + \zeta^2)^{-1/2} - \frac{1}{2}\chi^{-2} - C_\mathrm{B}^' \biggr] , </math>
where the normalized Bernoulli constant,
<math> C_\mathrm{B}^' \equiv - \frac{C_\mathrm{B} \varpi_0}{GM_\mathrm{pt}} . </math>
It is worth noting that, in terms of the dimensionless radial coordinate <math>~\chi</math>, the angular velocity and azimuthal velocity at any point inside the torus are, respectively,
<math> \dot\varphi = \chi^{-2} \omega_K |_0 \, , </math>
and,
<math> v_\varphi \equiv \varpi\dot\varphi = \chi^{-1} v_\varphi |_0 \, , </math>
where <math>\omega_K|_0 = (GM_\mathrm{pt} \varpi_0^{-3})^{1/2}</math> is the Keplerian frequency at <math>\varpi_0</math> and <math>v_\varphi|_0 = (GM_\mathrm{pt} \varpi_0^{-1})^{1/2}</math> is the azimuthal velocity at <math>\varpi_0</math>.
Pressure Maximum
It is instructive to examine at what location inside the torus the enthalpy (and density and gas pressure) assumes its maximum value. At any radial location, <math>~\chi_i</math>, <math>~H</math> has a vertical maximum where <math>~\partial H/\partial\zeta = 0.</math> That is, the maximum occurs where,
<math> \frac{\partial}{\partial\zeta} \biggl[ (\chi_i^2 + \zeta^2)^{-1/2} - \frac{1}{2}\chi_i^{-2} - C_\mathrm{B}^' \biggr] = -\zeta (\chi_i^2 + \zeta^2)^{-3/2} = 0 . </math>
For all values of <math>~\chi_i</math>, this relation will be satisfied only at <math>~\zeta = 0</math>. Hence, vertically, the enthalpy maximum will be located in the equatorial plane of the torus. Examining the radial enthalpy profile in the equatorial plane, we realize that the enthalpy maximum will occur where,
<math> \frac{\partial}{\partial\chi} \biggl[ \chi^{-1} - \frac{1}{2}\chi^{-2} - C_\mathrm{B}^' \biggr] = -\chi^{-2} + \chi^{-3} = 0 . </math>
This relation will be satisfied only at <math>~\chi = \varpi/\varpi_0 = 1</math>. Hence, <math>~\varpi_0</math> is not only the radial location (in the equatorial plane) where the angular frequency of the torus equals the Keplerian frequency, it is also the radial location of the pressure maximum.
Note that the enthalpy at the pressure maximum — that is, at the location <math>~(\chi,\zeta) = (1,0)</math> — is,
<math> H_0 = (n+1)\biggl[ \frac{P}{\rho} \biggr]_0 = \frac{GM_\mathrm{pt}}{\varpi_0} \biggl[ \frac{1}{2} - C_\mathrm{B}^' \biggr] = \frac{(v_\varphi |_0)^2}{2} [1 - 2C_\mathrm{B}^' ] \, . </math>
Boundary Conditions
In the equatorial plane, the locations of the inner and outer edges of the torus are obtained by setting both <math>~H</math> and <math>~\zeta</math> to zero, that is, they are obtained from the roots of the equation,
<math> ~\chi^{-2} - 2\chi^{-1} + 2C_\mathrm{B}^' = 0 , </math>
that is, the inner <math>~(\chi_-)</math> and outer <math>~(\chi_+)</math> edges are located at,
<math> ~\chi_\pm = \frac{1}{1 \mp \sqrt{1-2C_\mathrm{B}^'}} . </math>
Clearly, the relative cross-sectional size — or, as defined in PP84, the dimensionless distortion parameter <math>~\delta \equiv (\chi_+ + \chi_-)/2 = (2C_\mathrm{B}^')^{-1}</math> — is determined by the choice of the dimensionless Bernoulli constant, which must lie in the range, <math>~\tfrac{1}{2} \geq C_\mathrm{B}^' \geq 0</math>. For later reference, we will also note that the ratio of the inner edge to the outer edge is,
<math> ~\frac{\chi_{-}}{\chi_{+}} = \frac{ 1 - \sqrt{1-2C_\mathrm{B}^'} }{1 + \sqrt{1-2C_\mathrm{B}^'} } . </math>
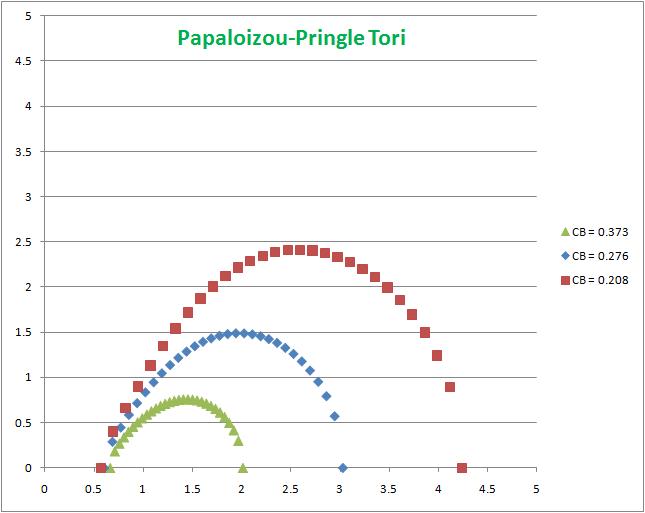
Indeed, more generally, at all vertical locations above and below the equatorial plane, the surface of the torus occurs where the enthalpy goes to zero. The meridional <math>~(\chi,\zeta)</math> cross-section through three such surfaces are displayed in the left panel of Figure 1. The displayed surfaces correspond to <math>~C_\mathrm{B}^' =</math> 0.208 (red curve), 0.276 (blue curve), and 0.373 (green curve). Carrying forward the above discussion, we note that in all three cases the pressure maximum is located at <math>(\chi,~\zeta) = (1,~0)</math>. Properties of these tori are described in more detail in an accompanying discussion entitled, Toroidal Configurations and Related Coordinate Systems.
We should perhaps emphasize that the shape of the surface of each torus, as shown in the left-hand panel of Figure 1, is independent of the chosen polytropic index.
| Figure 1: Papaloizou-Pringle Torus | |
|---|---|
| Left Panel — A meridional cross-section outlining the surface of three separate PP tori: <math>~C_\mathrm{B}^' =</math> 0.208 (red curve), 0.276 (blue curve), and 0.373 (green curve). | Right Panel — A three-dimensional, cutaway rendering illustrating the geometric structure of one PP torus having <math>~C_\mathrm{B}^' = 0.3239,~</math><math>~x_\mathrm{in} = \chi_{-}/\chi_{+} = 0.2551, ~</math> <math>~x_0 = 0.4065.</math> The separately colored contours illustrate four surfaces of constant enthalpy; the red contour identifies the toroidal surface. |
Model as Described by Kojima
From the above expression for <math>~\chi_\pm</math>, we see that,
<math> \sqrt{1-2C_\mathrm{B}^'} = \frac{1}{\chi_-} - 1 = 1 - \frac{1}{\chi_+} \, . </math>
Hence,
<math> \chi_+ = \biggl[ 2 - \frac{1}{\chi_-}\biggr]^{-1} = \frac{\chi_-}{2\chi_- - 1} \, . </math>
This agrees with the relation between <math>~\chi_+</math> (written as <math>~r_+</math>) and <math>~\chi_-</math> (written as <math>~r_-</math>) presented as equation (7) by Kojima (1986, Progress of Theoretical Physics, 75, 251-261), who also has examined the properties of Papaloizou-Pringle tori. In his equation (8), Kojima points out that the inner edge of the torus lies within the range, <math>~\tfrac{1}{2} < \chi_- < 1</math>, which is consistent with stating that the value of PB84's Bernoulli constant falls within the range, <math> ~\tfrac{1}{2} \geq C_\mathrm{B}^' \geq 0</math>.
Using the just-derived relationship between <math>~C_\mathrm{B}^'</math> and <math>~\chi_-</math>, we deduce that the enthalpy at the pressure maximum depends only on the choice of <math>~\chi_-</math> as follows:
<math> H_0 = (n+1)\biggl[ \frac{P}{\rho} \biggr]_0 = \frac{(v_\varphi |_0)^2}{2} \biggl[ \frac{1}{\chi_-} - 1 \biggr]^2 \, . </math>
Under adiabatic conditions, the sound speed of a gas is given by the algebraic relation,
<math> c_s^2 = \gamma \biggl[\frac{P}{\rho}\biggr] \, , </math>
where <math>~\gamma</math> is the specified adiabatic exponent. Hence, the expression just derived for <math>~H_0</math> also gives us the sound speed at the pressure maximum of the torus, namely,
<math> (c_s |_0)^2 = \frac{\gamma}{(n + 1)} \frac{(v_\varphi |_0)^2}{2} \biggl[ \frac{1}{\chi_-} - 1 \biggr]^2 \, , </math>
that is,
<math> \frac{c_s|_0}{v_\varphi |_0} = \biggl[ \frac{\gamma}{2(n + 1)} \biggr]^{1/2} \biggl[ \frac{1}{\chi_-} - 1 \biggr] \, . </math>
This matches Kojima's equation (11) with <math>~\chi_-</math> written in place of <math>~r_-</math>, namely,
<math> \biggl( \frac{c_s}{v_\varphi} \biggr)_0 = \frac{1}{\sqrt{6}} \biggl(\frac{1}{\chi_-} - 1 \biggr) \, , </math>
when one adopts Kojima's choice of <math>~\gamma = 4/3</math> and <math>~n = (\gamma - 1)^{-1} = 3</math>.
Hachisu Self-Consistent Field Technique
For the sake of contextual continuity, it is useful to relate the above result to the Hachisu self-consistent field (HSCF) technique, which we rely upon heavily to derive the equilibrium structure of self-gravitating systems. The HSCF technique begins by identifying the relevant algebraic expression for the enthalpy as derived above, namely,
<math> H = \frac{GM_\mathrm{pt}}{(\varpi^2 + z^2)^{1/2}} - \frac{j_0^2}{2\varpi^2} + C_\mathrm{B} . </math>
In the HSCF technique, it is customary to normalize all lengths to the distance <math>\varpi_{+}</math> from the origin to the point where the outer edge of the torus touches the equatorial plane. From this perspective, then, the relevant dimensionless coordinates are,
<math> x_\mathrm{HSCF} \equiv \frac{\varpi}{\varpi_{+}} ~~~~~\mathrm{and}~~~~~ z_\mathrm{HSCF} \equiv \frac{z}{\varpi_{+}} , </math>
and the equation for the dimensionless enthalpy becomes,
<math> H_\mathrm{HSCF} \equiv \frac{H}{(GM_\mathrm{pt}/\varpi_{+})} = (x_\mathrm{HSCF}^2 + z_\mathrm{HSCF}^2)^{-1/2} - \frac{1}{2} (j_\mathrm{HSCF}^2) x_\mathrm{HSCF}^{-2} - C_\mathrm{HSCF} , </math>
where the normalized Bernoulli constant,
<math> C_\mathrm{HSCF} \equiv - \frac{C_\mathrm{B} \varpi_{+}}{GM_\mathrm{pt}} , </math>
and the normalized specific angular momentum is,
<math> j_\mathrm{HSCF} \equiv \frac{j_0}{(GM_\mathrm{pt} \varpi_{+})^{1/2}} . </math>
This expression for the dimensionless enthalpy has two unknowns: <math>~j_\mathrm{HSCF}</math> and <math>~C_\mathrm{HSCF}</math>. Hence, two boundary points must be specified before a solution for <math>~H_\mathrm{HSCF}(\varpi,z)</math> can be obtained. In the HSCF technique, it is customary to specify the location of two points on the surface of the configuration, where by design <math>~H=0</math>. For toroidal configurations, it is furthermore customary for that specification to be where the inner and outer edges of the torus touch the equatorial plane. By design, the outer edge is at <math>~(x_\mathrm{HSCF}, ~z_\mathrm{HSCF}) = (1, ~0)</math>; the inner edge will be at <math>(x_\mathrm{HSCF}, ~z_\mathrm{HSCF}) = (x_{in}, ~0)</math>. Setting <math>~H_\mathrm{HSCF}=0</math> at both of these locations gives the following two algebraic relations,
<math> C_\mathrm{HSCF} = 1 - \frac{1}{2} (j_\mathrm{HSCF}^2) , </math>
and
<math> C_\mathrm{HSCF} = x_{in}^{-1} - \frac{1}{2} (j_\mathrm{HSCF}^2) x_{in}^{-2} , </math>
which can be used in combination to solve for the two unknowns. The result is,
<math> C_\mathrm{HSCF} = \frac{1}{1 + x_{in}} , </math>
and,
<math> j_\mathrm{HSCF} = \biggl[ \frac{2x_{in}}{1 + x_{in}} \biggr]^{1/2} . </math>
At what radial position in the equatorial plane, <math>~x_0</math>, is the pressure maximum located? The pressure maximum is also the enthalpy maximum, so the answer is given by looking in the equatorial plane <math>~(z_\mathrm{HSCF} = 0)</math> for the location where <math>~dH_\mathrm{HSCF}/dx_\mathrm{HSCF} = 0</math>. Since,
<math> \frac{dH_\mathrm{HSCF}}{dx_\mathrm{HSCF}} = - x_\mathrm{HSCF}^{-2} + (j_\mathrm{HSCF}^2) x_\mathrm{HSCF}^{-3} \, , </math>
the pressure maximum must be located at,
<math> x_\mathrm{HSCF} = x_0 = j_\mathrm{HSCF}^2 \, . </math>
Hence, in terms of <math>~x_{in}</math>,
<math> x_0 = \frac{2x_{in}}{1 + x_{in}} . </math>
Comparison
The solution derived by PP84 (presented above) is normalized such that the pressure maximum is always in the equatorial plane at radial coordinate <math>~\chi = 1</math>, and tori of different thicknesses are constructed by specifying different values of the dimensionless Bernoulli constant, <math>~C_\mathrm{B}^'</math>. Using the HSCF approach, the position of the outer edge of the torus is fixed and tori of different thicknesses are selected by moving the inner edge, <math>~x_{in}</math>, around. In order to examine whether or not the two solutions are, in fact, the same, we will re-write the expression given above for <math>~\chi_{-}/\chi_{+}</math> in terms of <math>~x_{in}</math>. In order to do this, we need to convert <math>~C_\mathrm{HSCF}</math> to <math>~C_\mathrm{B}^'</math>. Based on their definitions, the ratio
<math> \frac{C_\mathrm{B}^'}{C_\mathrm{HSCF} } = \frac{\varpi_0}{\varpi_{+}} = x_0 . </math>
Hence,
<math> C_\mathrm{B}^' = x_0~C_\mathrm{HSCF} = \biggl( \frac{2x_{in}}{1+x_{in}} \biggr) \biggl( \frac{1}{1+x_{in}} \biggr) = \frac{2x_{in}}{(1+x_{in})^2}. </math>
Therefore,
<math> 1 - 2C_\mathrm{B}^' = 1 - \frac{4x_{in}}{(1+x_{in})^2} = \frac{ (1+x_{in})^2 - 4x_{in} }{(1+x_{in})^2} = \frac{ (1-x_{in})^2 }{(1+x_{in})^2} \, , </math>
and,
<math> \frac{\chi_{-}}{\chi_{+}} = \frac{ 1 - \sqrt{1-2C_\mathrm{B}^'} }{1 + \sqrt{1-2C_\mathrm{B}^'} } = \frac{ 1 - \frac{1-x_{in}}{1+x_{in}} }{1 + \frac{1-x_{in}}{1+x_{in}}} = \frac{ (1+x_{in}) - (1-x_{in}) }{ (1+x_{in}) + (1-x_{in}) } = x_{in}. </math>
Hence, both the PP84 derivation and the HSCF derivation produce the same result.
Blaes (1985)
In a separate chapter, we review the analytic analysis of unstable nonaxisymmetric eigenmodes in geometrically thin PP tori that has been presented by Blaes (1985), MNRAS, 216, 553. Our review includes an explanation of how the equations derived here to describe the equilibrium structure of PP Tori are straightforwardly transformed into the equations and notation adopted by Blaes.
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Fishbone & Moncrief (1976)
Fishbone & Moncrief (1976), ApJ, 207, 962 derived the identical Papaloizou-Pringle torus structure using a spherical rather than cylindrical coordinate system.
Derived Equilibrium Structure
|
<math>~c^2 \frac{\partial w}{\partial r} \equiv \frac{1}{(nm)} \frac{\partial P}{\partial r}</math> |
<math>~=</math> |
<math>~\frac{\partial}{\partial r}\biggl(\frac{GM}{r}\biggr) + \omega^2 r^2 \sin^2\theta \, ,</math> |
|
<math>~c^2 \frac{\partial w}{\partial \theta} \equiv \frac{1}{(nm)} \frac{\partial P}{\partial \theta}</math> |
<math>~=</math> |
<math>~\frac{\partial}{\partial \theta}\biggl(\frac{GM}{r}\biggr) + \omega^2 r^2 \sin\theta \cos\theta \, .</math> |
As presented in their equation (4.4), imposing the condition of uniform specific angular momentum leads to an angular velocity profile of the form,
<math>~\omega = \frac{\ell}{r^2 \sin^2\theta} \, .</math>
Comparison
Key References
- Fishbone & Moncrief (1976), ApJ, 207, 962 — Relativistic fluid disks in orbit around Kerr black holes
- Papaloizou & Pringle (1984), MNRAS, 208, 721 — The dynamical stability of differentially rotating discs with constant specific angular momentum
- Papaloizou & Pringle (1985), MNRAS, 213, 799 — The dynamical stability of differentially rotating discs. II.
- Papaloizou & Pringle (1987), MNRAS, 225, 267 — The dynamical stability of differentially rotating discs. III.
- Goldreich & Narayan (1985), MNRAS, 213, 7 — Non-axisymmetric instability in thin discs
- Goldrich, Goodman & Narayan (1986), MNRAS, 221, 339 — The stability of accretion tori. I. -- Long-wavelength modes of slender tori
- Goodman, Narayan, & Goldreich (1987), MNRAS, 225, 695 — The stability of accretion tori. II -- Non-linear evolution to discrete planets
- Goodman & Narayan (1988), MNRAS, 231, 97 — The stability of accretion tori. III -- The effect of self-gravity
- Christodoulou & Narayan (1992), ApJ, 388, 451 — The stability of accretion tori. IV. Fission and fragmentation of slender, self-gravitating annuli
- Christodoulou (1993), ApJ, 412, 696 — The stability of accretion tori. V. Unstable modes and avoided crossings in extended, self-gravitating annuli
- Robertson & Frank (1986), MNRAS, 221, 279 — A numerical study of two-dimensional accretion flows
- Frank & Robertson (1988), MNRAS, 232, 1 — Numerical studies of the dynamical stability of differentially rotating tori
- Blaes (1985), MNRAS, 216, 553 — Oscillations of slender tori
- Kojima (1986), PThPh, 75, 251 — The Dynamical Stability of a Fat Disk with Constant Specific Angular Momentum
- Kojima (1989), MNRAS, 236, 589 — Non-axisymmetric unstable modes of a differentially rotating torus
- Hanawa (1986), MNRAS, 223, 859 — Dynamical instability of a homoentropic rotating torus and an upper limit on the growth rate
- Hawley (1987), MNRAS, 225, 677 — Non-linear evolution of a non-axisymmetric disc instability
- Blaes & Hawley (1988), ApJ, 326, 277 — Nonaxisymmetric disk instabilities -- A linear and nonlinear synthesis
- Hawley (1990), ApJ, 356, 580 — Nonaxisymmetric instabilities in a slender torus -- Two- and three-dimensional simulations
- Boss (1988), MNRAS, 231, 739 — Non-axisymmetric instability in three-dimensional accretion toroids
- Papaloizou & Lin (1989), ApJ, 344, 645 — Nonaxisymmetric instabilities in thin self-gravitating rings and disks
- Papaloizou & Savonije (1991), MNRAS, 248, 353 — Instabilities in self-gravitating gaseous discs
- Papaloizou & Lin (1995), Annual Reviews of Astronomy & Astrophysics, 33, 505 — Theory of Accretion Disks I: Angular Momentum Transport Processes
- Tohline & Hachisu (1990), ApJ, 361, 394 — The breakup of self-gravitating rings, tori, and thick accretion disks
- Woodward, Tohline & Hachisu (1994), ApJ, 420, 247 — The stability of thick, self-gravitating disks in protostellar systems
- Andalib, Tohline, & Christodoulou (1997), ApJS, 108, 471 — A Survey of the Principal Modes of Nonaxisymmetric Instability in Self-Gravitating Accretion Disk Models
- Hadley & Imamura (2011), Ap&SS, 334, 1 — Nonaxisymmetric instabilities of self-gravitating disks. I. Toroids
- Hadley, Fernandez, Imamura, Keever, Tumblin, & Dumas (2014), Ap&SS, 353, 191— Nonaxisymmetric instabilities in self-gravitating disks. II. Linear and quasi-linear analysis
- Hadley, Dumas, Imamura, Keever & Tumblin (2015), Ap&SS, 359, 10— Nonaxisymmetric instabilities in self-gravitating disks. III. Angular momentum transport
- Balbinski (1985), AA, 149, 487 — The character of the normal mode equationos for rotating perfect fluids
- P. J. Luyten (1990), MNRAS, 245, 614 — Non-Axisymmetric Dynamical Instability of Differentially Rotating Self-Gravitating Masses
- Bubrulle, Chomaz, Kumar, & Rieutord (1993), Geophysical and Astrophysical Fluid Dynamics, 70, 235 — Non linear stability of slender accretion disks by bifurcation method
- Liu & Wang (1995), ChA&A, 19, 507 — A numerical solution of the dynamical instability of a thin accretion torus
- Beyer (2002), RSPSA, 458, 359 — A framework for perturbations and stability of differentially rotating stars
- Watts, Andersson, & Williams (2004), MNRAS, 350, 927 — The oscillation and stability of differentially rotating spherical shells: the initial-value problem
- Passamonti & Andersson (2015), MNRAS, 446, 555 — The intimate relation between the low T/W instability and the corotation point
Related Wikipedia Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |