User:Tohline/Appendix/Ramblings/ToroidalCoordinates
Toroidal Configurations and Related Coordinate Systems
This rather long and rambling chapter reveals how my train of thought progressed as I effectively taught myself how to use a toroidal coordinate system to determine the gravitational potential of an axisymmetric configuration. A summary of the key results from this chapter can be found in a primary chapter of this H_Book titled, Using Toroidal Coordinates to Determine the Gravitational Potential.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Preamble
As I have studied the structure and analyzed the stability of (both self-gravitating and non-self-gravitating) toroidal configurations over the years, I have often wondered whether it might be useful to examine such systems mathematically using a toroidal — or at least a toroidal-like — coordinate system. Is it possible, for example, to build an equilibrium torus for which the density distribution is one-dimensional as viewed from a well-chosen toroidal-like system of coordinates?
I should begin by clarifying my terminology. In volume II (p. 666) of their treatise on Methods of Theoretical Physics, Morse & Feshbach (1953; hereafter MF53) define an orthogonal toroidal coordinate system in which the Laplacian is separable.1 (See details, below.) It is only this system that I will refer to as the toroidal coordinate system; all other functions that trace out toroidal surfaces but that don't conform precisely to Morse & Feshbach's coordinate system will be referred to as toroidal-like.
I became particularly interested in this idea while working with Howard Cohl (when he was an LSU graduate student). Howie's dissertation research uncovered a Compact Cylindrical Greens Function technique for evaluating Newtonian potentials of rotationally flattened (especially axisymmetric) configurations.2,3 The technique involves a multipole expansion in terms of half-integer-degree Legendre functions of the <math>2^\mathrm{nd}</math> kind — see NIST digital library discussion — where, if I recall correctly, the argument of this special function (or its inverse) seemed to resemble the radial coordinate of Morse & Feshbach's orthogonal toroidal coordinate system — see more on this, below.
Off-center Circle
In what follows, it will be useful to recall the algebraic expression that defines a circle whose center is not positioned at the origin of a Cartesian coordinate system. Specifically, consider a circle of radius, <math>~r_c</math>, whose center is located a distance <math>~x_0</math> along the plus-x axis and a distance <math>~y_0</math> along the plus-y axis. The equation for this circle is,
<math> ~(x-x_0)^2 + (y-y_0)^2 = r_c^2 . </math>
Toroidal Coordinates
Presentation by MF53
The orthogonal toroidal coordinate system <math>(\xi_1,\xi_2,\xi_3=\cos\varphi)</math> discussed by MF53 has the following properties:
|
<math> ~\frac{x}{a} </math> |
<math> ~= </math> |
<math> ~\biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr]\cos\varphi \, , </math> |
|
<math> ~\frac{y}{a} </math> |
<math> ~= </math> |
<math> ~\biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr]\sin\varphi \, , </math> |
|
<math> ~\frac{z}{a} </math> |
<math> ~= </math> |
<math> ~\frac{(1-\xi_2^2)^{1/2}}{\xi_1 - \xi_2} \, , </math> |
|
<math> ~\frac{\varpi}{a} \equiv \biggl[ \biggl(\frac{x}{a}\biggr)^2 + \biggl(\frac{y}{a}\biggr)^2 \biggr]^{1/2} </math> |
<math> ~= </math> |
<math> ~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \, , </math> |
|
<math> ~\frac{r}{a} \equiv \biggl[ \biggl(\frac{x}{a}\biggr)^2 + \biggl(\frac{y}{a}\biggr)^2 + \biggl(\frac{z}{a}\biggr)^2\biggr]^{1/2} </math> |
<math> ~= </math> |
<math> ~\biggl[ \frac{\xi_1 + \xi_2}{\xi_1 - \xi_2} \biggr]^{1/2} \, . </math> |
According to MF53, the associated scale factors of this orthogonal coordinate system are:
|
<math> ~\frac{h_1}{a} </math> |
<math> ~= </math> |
<math> ~\frac{1}{(\xi_1 - \xi_2)(\xi_1^2 - 1)^{1/2}} \, , </math> |
|
<math> ~\frac{h_2}{a} </math> |
<math> ~= </math> |
<math> ~\frac{1}{(\xi_1 - \xi_2)(1-\xi_2^2)^{1/2}} \, , </math> |
|
<math> ~\frac{h_3}{a} </math> |
<math> ~= </math> |
<math> ~\biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr]\frac{1}{\sin\varphi} \, . </math> |
That means that, in the meridional plane, an area element should be,
<math> ~d\sigma = (h_1 d\xi_1)(h_2 d\xi_2) = a^2 \biggl[ \frac{d\xi_1}{(\xi_1 - \xi_2)(\xi_1^2 - 1)^{1/2}} \biggr] \biggl[ \frac{d\xi_2}{(\xi_1 - \xi_2)(1-\xi_2^2)^{1/2}} \biggr] \, . </math>
Tohline's Ramblings
My inversion of these coordinate definitions has led to the following expressions:
|
<math> ~\xi_1 </math> |
<math> ~= </math> |
<math> \frac{r(r^2 + 1)} {[\chi^2(r^2-1)^2 + \zeta^2(r^2+1)^2]^{1/2}} \, , </math> |
|
<math> ~\xi_2 </math> |
<math> ~= </math> |
<math> \frac{r(r^2 - 1)}{[\chi^2(r^2-1)^2 + \zeta^2(r^2+1)^2]^{1/2}} \, , </math> |
where,
<math> \chi \equiv \frac{\varpi}{a} ~~~;~~~\zeta\equiv\frac{z}{a} ~~~\mathrm{and} ~~~ r=(\chi^2 + \zeta^2)^{1/2} . </math>
Apparently the allowed ranges of the two meridional-plane coordinates are:
<math> +1 \leq \xi_1 \leq \infty ~~~\mathrm{and} ~~~ -1 \leq \xi_2 \leq +1 . </math>
Example Toroidal Surfaces
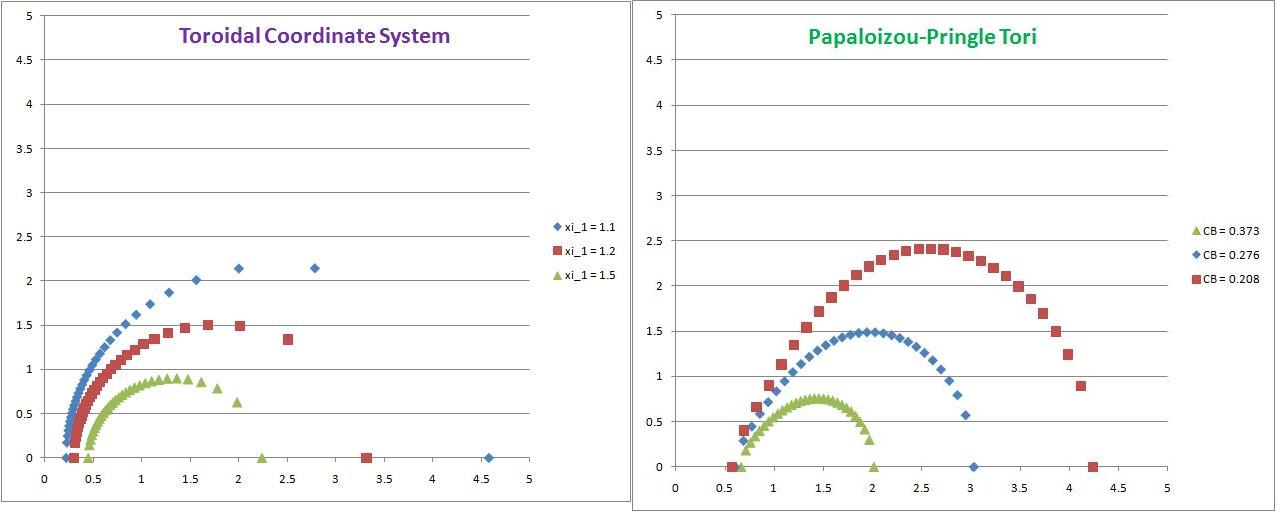
In the accompanying figure labeled "Toroidal Coordinate System," we've outlined three different <math>~\xi_1 = \mathrm{constant}</math> meridional contours for the MF53 toroidal coordinate system. The illustrated values are,
|
<math> ~\xi_1 </math> |
<math>~=</math> |
<math>~1.1</math> |
|
<math>~\mathrm{(blue)} \, ;</math> |
|
<math> ~\xi_1 </math> |
<math>~=</math> |
<math>~1.2</math> |
|
<math>~\mathrm{(red)} \, ;</math> |
|
<math> ~\xi_1 </math> |
<math>~=</math> |
<math>~1.5</math> |
|
<math>\mathrm{(gold)} \, .</math> |
The inner and outer edges of the toroidal surface in the equatorial plane should be determined by setting <math>~\xi_2 = -1</math> (inner) and <math>~\xi_2 = +1</math> (outer). Hence,
|
<math> ~\chi_\mathrm{inner} </math> |
<math>~=</math> |
<math> ~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 +1} = \biggl[\frac{(\xi_1 - 1)}{(\xi_1 + 1)} \biggr]^{1/2} </math> |
|
<math> ~\chi_\mathrm{outer} </math> |
<math>~=</math> |
<math> ~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - 1} = \biggl[\frac{(\xi_1 + 1)}{(\xi_1 - 1)} \biggr]^{1/2} </math> |
The equatorial-plane location of the "center" of each torus is,
<math> \chi_0 = \frac{1}{2} (\chi_\mathrm{outer} + \chi_\mathrm{inner}) = \frac{\xi_1}{(\xi_1^2 - 1)^{1/2}} , </math>
and the so-called distortion parameter,
<math> \delta \equiv \frac{\chi_\mathrm{outer}-\chi_\mathrm{inner}}{\chi_0}= \frac{2}{\xi_1} . </math>
|
Properties of <math>\xi_1 = \mathrm{constant}</math> Toroidal Surfaces |
|||||
|---|---|---|---|---|---|
|
Curve in |
<math>\xi_1</math> |
<math>\chi_\mathrm{inner}</math> |
<math>\chi_\mathrm{outer}</math> |
<math>\chi_0</math> |
<math>\delta</math> |
|
Blue |
1.1 |
0.218 |
4.583 |
2.400 |
1.818 |
|
Red |
1.2 |
0.302 |
3.317 |
1.809 |
1.667 |
|
Gold |
1.5 |
0.447 |
2.236 |
1.342 |
1.333 |
What function <math>~\zeta(\varpi)</math> coincides with these <math>~\xi_1 = \mathrm{constant}</math> surfaces? (To be answered!)
Off-center Circle
The curves drawn in the above figure labeled "Toroidal Coordinate System" resemble circles whose centers are positioned a distance <math>~\chi_0</math> away from the origin. Let's examine whether this is the case by drawing on the familiar expression for such a configuration, as presented above. If this is the case, then the circle as illustrated in the figure will have <math>~z_0 = 0</math> and a radius,
|
<math> ~\alpha_c \equiv \frac{r_c}{a} </math> |
<math> ~= </math> |
<math> ~\chi_\mathrm{outer} - \chi_0 </math> |
|
|
<math> ~= </math> |
<math> ~\biggl[\frac{(\xi_1 + 1)}{(\xi_1 - 1)} \biggr]^{1/2} - \frac{\xi_1}{(\xi_1^2 - 1)^{1/2}} </math> |
|
|
<math> ~= </math> |
<math> ~\frac{1}{(\xi_1^2 - 1)^{1/2}} \, , </math> |
and the algebraic expression describing the circle will take the form,
<math> ~(\chi - \chi_0)^2 + \zeta^2 = \alpha_c^2 = (\xi_1^2 - 1)^{-1} . </math>
Let's evaluate the left-hand-side of this expression to see if it indeed reduces to <math>(\xi_1^2 - 1)^{-1}</math>.
|
<math>~\mathrm{LHS}</math> |
<math>~=</math> |
<math> ~\biggl\{ \biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr] - \frac{\xi_1}{(\xi_1^2 - 1)^{1/2}} \biggr\}^2 + \biggl[ \frac{(1-\xi_2^2)^{1/2}}{\xi_1 - \xi_2} \biggr]^2
</math> |
|
|
<math>~=</math> |
<math> ~\frac{1}{(\xi_1 - \xi_2)^2 (\xi_1^2 - 1)} \biggl\{ (\xi_1^2 - 1) - \xi_1 (\xi_1-\xi_2) \biggr\}^2 + \frac{(1-\xi_2^2)}{(\xi_1 - \xi_2)^2} </math> |
|
|
<math>~=</math> |
<math> ~\frac{(\xi_1 \xi_2 - 1)^2}{(\xi_1 - \xi_2)^2 (\xi_1^2 - 1)} + \frac{(1-\xi_2^2)}{(\xi_1 - \xi_2)^2} </math> |
|
|
<math>~=</math> |
<math> ~\frac{1}{(\xi_1 - \xi_2)^2 (\xi_1^2 - 1)} \biggl[(\xi_1 \xi_2 - 1)^2 + (\xi_1^2 - 1)(1-\xi_2^2) \biggr] </math> |
|
|
<math>~=</math> |
<math> ~\frac{1}{(\xi_1 - \xi_2)^2 (\xi_1^2 - 1)} \biggl[ \xi_1^2 \xi_2^2 - 2\xi_1 \xi_2 + 1 ) + (\xi_1^2 - 1 -\xi_1^2 \xi_2^2 + \xi_2^2) \biggr] </math> |
|
|
<math>~=</math> |
<math> ~\frac{\xi_1^2 - 2\xi_1 \xi_2 + \xi_2^2}{(\xi_1 - \xi_2)^2 (\xi_1^2 - 1)} </math> |
|
|
<math>~=</math> |
<math> ~\frac{1}{(\xi_1^2 - 1)} \, . </math> |
Yes! So this means that the <math>~\xi_1 = \mathrm{constant}</math> toroidal contours can be described by the off-center circle expression,
<math> ~(\chi - \chi_0)^2 + \zeta^2 = (\chi_\mathrm{outer} - \chi_0)^2 \, , </math>
or,
<math> ~\biggl[ \chi - \frac{\xi_1}{(\xi_1^2 - 1)^{1/2}} \biggr]^2 + \zeta^2 = \frac{1}{(\xi_1^2 - 1)} \, . </math>
It also means that, while <math>~\xi_1</math> is the official radial coordinate of MF53's toroidal coordinate system, the actual dimensionless radius of the relevant cross-sectional circle is,
|
<math> ~\alpha_c </math> |
<math> ~= </math> |
<math> ~\frac{1}{(\xi_1^2 - 1)^{1/2}} . </math> |
Papaloizou-Pringle Tori
Summary of Structure
As derived elsewhere, the accretion tori constructed by Papaloizou & Pringle (1984; hereafter PP84) have the following surface properties. For a given choice of the dimensionless Bernoulli constant, <math>C_\mathrm{B}^'</math>,
|
<math> ~\chi_\mathrm{inner} </math> |
<math>~ =</math> |
<math>
~\frac{1}{1 + \sqrt{1-2C_\mathrm{B}^'}} \, ; </math> |
|
<math> ~\chi_\mathrm{outer} </math> |
<math>~=</math> |
<math>
~\frac{1}{1 - \sqrt{1-2C_\mathrm{B}^'}} \, ; </math> |
|
<math> ~\chi_0 </math> |
<math>~=</math> |
<math>
~\frac{1}{2} (\chi_\mathrm{outer} + \chi_\mathrm{inner}) = \frac{1}{2C_\mathrm{B}^'} \, ; </math> |
|
<math> ~\delta </math> |
<math>~\equiv</math> |
<math> ~\frac{\chi_\mathrm{outer} - \chi_\mathrm{inner}}{\chi_0} = 2\sqrt{1-2C_\mathrm{B}^'} \, . </math> |
So if I want to construct PP84 tori that are approximately the same size/shape as the MF53 tori illustrated above, I should choose values of the dimensionless Bernoulli constant as follows:
|
<math> ~{\chi_0}\biggr|_\mathrm{PP84} </math> |
<math>~=</math> |
<math>
~{\chi_0}\biggr|_\mathrm{MF53} </math> |
|
<math> \Rightarrow~~~~ \frac{1}{2C_\mathrm{B}^'} </math> |
<math>~=</math> |
<math>~\frac{\xi_1}{(\xi_1^2-1)^{1/2}} </math> |
|
<math> \Rightarrow~~~~ C_\mathrm{B}^' </math> |
<math>~=</math> |
<math>~\frac{(\xi_1^2-1)^{1/2}}{2\xi_1} \, . </math> |
In the accompanying figure labeled "Papaloizou-Pringle Tori," we've drawn three different <math>~C_\mathrm{B}^' = \mathrm{constant}</math> meridional contours for the PP84 tori where the values of the dimensionless Bernoulli constants have been chosen to produce values of <math>~\chi_0</math> that are identical to the values displayed by the three MF53 tori shown above. The following table details properties of these three PP84 tori that have been constructed in an effort to facilitate comparison with the table shown above for MF53 tori.
|
Properties of <math>C_\mathrm{B}^' = \mathrm{constant}</math> PP84 Toroidal Surfaces |
|||||
|---|---|---|---|---|---|
|
Curve in |
<math>C_\mathrm{B}^'</math> |
<math>\chi_\mathrm{inner}</math> |
<math>\chi_\mathrm{outer}</math> |
<math>\chi_0</math> |
<math>\delta</math> |
|
Red |
0.208 |
0.567 |
4.234 |
2.400 |
1.528 |
|
Blue |
0.276 |
0.599 |
3.019 |
1.809 |
1.338 |
|
Gold |
0.373 |
0.665 |
2.019 |
1.342 |
1.009 |
Advantageous Coordinate System
According to Kojima's (1986) review of the PP84 discussion — see his equation (14) — surfaces of constant density can be defined by the coordinate, <math>~\chi_{PP}</math>, where,
|
<math>~\tan\chi_{PP}</math> |
<math>~\equiv</math> |
<math>~ \frac{z}{ \frac{z^2}{\sqrt{\varpi^2 + z^2}} + \sqrt{\varpi^2 + z^2} - 1} </math> |
Indeed, equation (6.6) of PP84 defines the coordinate, <math>~\chi_{PP}</math>, via the expression,
|
<math>~\tan\chi_{PP}</math> |
<math>~\equiv</math> |
<math>~ \frac{\cos\theta}{ \cos^2\theta + 1 - \varpi_0/r} \, , </math> |
where,
|
<math>~z = r\cos\theta</math> |
and |
<math>~\varpi = r\sin\theta \, .</math> |
Let's see if these match. Starting from the Kojima expression, we have,
|
<math>~\tan\chi_{PP}</math> |
<math>~=</math> |
<math>~ \frac{r\cos\theta}{ \frac{r^2\cos^2\theta}{r} + r - 1} </math> |
|
|
<math>~=</math> |
<math>~ \frac{\cos\theta}{ \cos^2\theta + 1 - 1/r} \, . </math> |
Hence, they are the same, as long as we appreciate that Kojima assumes all length scales are normalized to <math>~\varpi_0</math>. Let's express this coordinate in terms of the <math>~(\xi_1, \xi_2)</math> toroidal coordinates as defined by MF53, namely,
|
<math> ~\frac{z}{a} </math> |
<math> ~= </math> |
<math> ~\frac{(1-\xi_2^2)^{1/2}}{\xi_1 - \xi_2} \, , </math> |
|
<math> ~\frac{\varpi}{a} \equiv \biggl[ \biggl(\frac{x}{a}\biggr)^2 + \biggl(\frac{y}{a}\biggr)^2 \biggr]^{1/2} </math> |
<math> ~= </math> |
<math> ~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \, , </math> |
|
<math> ~\frac{r}{a} \equiv \biggl[ \biggl(\frac{x}{a}\biggr)^2 + \biggl(\frac{y}{a}\biggr)^2 + \biggl(\frac{z}{a}\biggr)^2\biggr]^{1/2} </math> |
<math> ~= </math> |
<math> ~\biggl[ \frac{\xi_1 + \xi_2}{\xi_1 - \xi_2} \biggr]^{1/2} \, . </math> |
Kojima's expression becomes:
|
<math>~\tan\chi_{PP}</math> |
<math>~=</math> |
<math>~z \biggl[ \frac{z^2}{\sqrt{\varpi^2 + z^2}} + \sqrt{\varpi^2 + z^2} - 1 \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~\frac{(1-\xi_2^2)^{1/2}}{\xi_1 - \xi_2} \biggl\{ \biggl[\frac{(1-\xi_2^2)}{ (\xi_1 - \xi_2)^2} \biggr] \biggl[ \frac{\xi_1 - \xi_2}{\xi_1 + \xi_2} \biggr]^{1/2} + \biggl[ \frac{\xi_1 + \xi_2}{\xi_1 - \xi_2} \biggr]^{1/2} - 1 \biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~(1-\xi_2^2)^{1/2} \biggl\{ \frac{(1-\xi_2^2)}{ (\xi_1 - \xi_2)} \biggl[ \frac{\xi_1 - \xi_2}{\xi_1 + \xi_2} \biggr]^{1/2} + (\xi_1 + \xi_2)^{1/2} (\xi_1 - \xi_2)^{1/2} - ( \xi_1 - \xi_2 ) \biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~(1-\xi_2^2)^{1/2} \biggl\{ \frac{(1-\xi_2^2)}{ (\xi_1 - \xi_2)^{1/2} (\xi_1 + \xi_2)^{1/2}} + (\xi_1 + \xi_2)^{1/2} (\xi_1 - \xi_2)^{1/2} - ( \xi_1 - \xi_2 ) \biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~(1-\xi_2^2)^{1/2} (\xi_1 - \xi_2)^{1/2} (\xi_1 + \xi_2)^{1/2} \biggl\{ (1-\xi_2^2) + (\xi_1 - \xi_2)(\xi_1 + \xi_2) - ( \xi_1 - \xi_2 )(\xi_1 + \xi_2)^{1/2} (\xi_1 - \xi_2)^{1/2} \biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~(1-\xi_2^2)^{1/2} (\xi_1^2 - \xi_2^2)^{1/2} \biggl\{ (1-\xi_2^2) + (\xi_1^2 - \xi_2^2) - ( \xi_1 - \xi_2 )(\xi_1^2 - \xi_2^2)^{1/2} \biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{(1-\xi_2^2)}{ (\xi_1^2 - \xi_2^2) } \biggr]^{1/2} \biggl\{ \biggl[ \frac{(1-\xi_2^2)}{(\xi_1^2 - \xi_2^2)}\biggr] + 1 - \biggl[ \frac{ ( \xi_1 - \xi_2 )}{(\xi_1 + \xi_2)} \biggr]^{1/2}\biggr\}^{-1} \, . </math> |
This does not appear to be very useful or productive!
CCGF Expansion
Cohl & Tohline (1999; hereafter CT99) derive an expression for the Newtonian gravitational potential in terms of a Compact Cylindrical Green's Function expansion. They show, for example, that when expressed in terms of cylindrical coordinates, the axisymmetric potential is,
<math> \Phi(R,z) = - \frac{2G}{R^{1/2}} q_0 , </math>
where,
<math> q_0 = \int\int (R')^{1/2} \rho(R',z') Q_{-1/2}(\Chi) dR' dz', </math>
and the dimensionless argument (the modulus) of the special function, <math>~Q_{-1/2}</math>, is,
<math> \Chi \equiv \frac{R^2 + {R'}^2 + (z - z')^2}{2R R'} . </math>
Note: Here we are using <math>~\Chi</math> instead of <math>~\chi</math> (as used by CT99) to represent this dimensionless parameter in order to avoid confusion with our use of <math>~\chi</math>, above. Next, following the lead of CT99, we note that according to the Abramowitz & Stegun (1965),
<math>Q_{-1/2}(\Chi) = \mu K(\mu) \, ,</math>
where, the function <math>~K(\mu)</math> is the complete elliptical integral of the first kind and, for our particular problem,
|
<math>~\mu^2</math> |
<math>~\equiv</math> |
<math>~2(1+\Chi)^{-1}</math> |
|
|
<math>~=</math> |
<math>~ 2\biggl[ 1+\frac{R^2 + {R'}^2 + (z - z')^2}{2R R'} \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{4R R'}{(R + {R'})^2 + (z - z')^2} \biggr] \, . </math> |
Hence, we can write,
<math> q_0 = \int\int (R')^{1/2} \rho(R',z') \mu K(\mu) dR' dz' \, . </math>
Confirmation Provided by Trova, Huré and Hersant
In their study of the potential of self-gravitating, axisymmetric discs, A. Trova, J.-M. Huré and F. Hersant (2012; MNRAS, 424, 2635) write (see their equation 1),
|
<math>~\Phi(R,Z)</math> |
<math>~=</math> |
<math>~ -2G \int\int \sqrt{\frac{\varpi}{R}} \rho(\varpi, z) k K(k) d\varpi dz \, , </math> |
where, the modulus, <math>~k</math>, of the complete elliptical integral of the first kind is (see their equation 2),
|
<math>~k</math> |
<math>~=</math> |
<math>~ \frac{2\sqrt{\varpi R}}{\sqrt{(\varpi + R)^2 + (Z-z)^2}} \, , </math> |
and its relevant domain is, <math>~0 \leq k \leq 1</math>. After associating <math>~z \leftrightarrow Z</math>, <math>~z^' \leftrightarrow z</math>, and <math>~R^' \leftrightarrow \varpi</math>, we see that the modulus, <math>~k</math>, used by Trova et al. (2012), is precisely the same as the argument, <math>~\mu</math>, defined in CT99. Hence, the two expressions for the axisymmetric potential, <math>~\Phi(R,Z)</math>, are identical.
Recognition as Circle
If we scale all of the lengths in CT99's expression for <math>~\Chi</math>, to <math>~a</math> and, along the lines of what was done above, define,
<math> ~\chi \equiv \frac{R'}{a} ~~~~\mathrm{and}~~~~\zeta \equiv \frac{z-z'}{a} , </math>
we can rewrite the expression in the form,
|
<math>~ \biggl(\frac{R}{a}\biggr)^2 + \chi^2 + \zeta^2 </math> |
<math>~=</math> |
<math>~2 \Chi \biggl( \frac{R}{a}\biggr) \chi \, .</math> |
Now, because,
|
<math>~\biggl[ \chi - \Chi\biggl(\frac{R}{a}\biggr) \biggr]^2</math> |
<math>~=</math> |
<math>~\chi^2 - 2\Chi\biggl(\frac{R}{a}\biggr)\chi + \Chi^2 \biggl(\frac{R}{a}\biggr)^2</math> |
|
<math>~\Rightarrow ~~~~ 2\Chi\biggl(\frac{R}{a}\biggr)\chi </math> |
<math>~=</math> |
<math>~\chi^2 - \biggl[ \chi - \Chi\biggl(\frac{R}{a}\biggr) \biggr]^2 + \Chi^2 \biggl(\frac{R}{a}\biggr)^2 \, ,</math> |
we can further rewrite the expression as,
|
<math>~ \biggl(\frac{R}{a}\biggr)^2 + \chi^2 + \zeta^2 </math> |
<math>~=</math> |
<math>~\chi^2 - \biggl[ \chi - \Chi\biggl(\frac{R}{a}\biggr) \biggr]^2 + \Chi^2 \biggl(\frac{R}{a}\biggr)^2</math> |
|
<math>~\Rightarrow ~~~~ \biggl[ \chi - \Chi\biggl(\frac{R}{a}\biggr) \biggr]^2 + \zeta^2 </math> |
<math>~=</math> |
<math>~\biggl(\frac{R}{a}\biggr)^2(\Chi^2 -1) \, .</math> |
Finally, if we adopt the specific scale factor, <math>~a = R</math>, we have,
<math> ~(\chi - \Chi)^2 + \zeta^2 = (\Chi^2 - 1) . </math>
So, a curve of constant <math>~\Chi</math> produces an off-center circle whose center is located at <math>~\Chi</math> and whose radius is <math>~\sqrt{\Chi^2 - 1}</math>.
Relating CCGF Expansion to Toroidal Coordinates
We see that curves of constant <math>\Chi</math> (as defined in CT99) are in every respect identical to curves of constant <math>\xi_1</math> (as defined in MF53). The association is straightforward:
|
EUREKA! |
|---|
|
<math> \Chi^2 - 1 = \frac{1}{\xi_1^2 - 1} . </math> |
Do It Again
The question that I've had in the back of my mind for quite some time is, "For what astrophysically interesting problem might we effectively use the toroidal coordinate system in order to derive a much cleaner analytic description of an axisymmetric potential?" Originally, I thought that a suitable configuration might be a uniform-density torus that has a perfectly circular cross-section. After all, the surface of such a torus can be perfectly described as a <math>~\xi_1 = </math> constant configuration. In a subsection presented below, I began investigating this problem, setting up a toroidal coordinate system to appropriately conform to the surface of such a torus, then calling upon WolframAlpha's online integration tool to complete the integral over the orthogonal coordinate, <math>~\xi_2</math>, analytically. After giving the problem considerable more thought, however, I realized that, while I could legitimately move the mass-density outside of that first integral, it was not legitimate to move the <math>~\mu K(\mu)</math> factor outside of that integral. While it is true that CT99 showed that the <math>~\mu K(\mu)</math> factor only depends on the first coordinate in a toroidal coordinate system, it is a different toroidal coordinate system from the one that conveniently aligns with the physical torus! Let's set up the double integral again, but this time let's use the toroidal coordinate system that is defined within the CCGF discussion. We begin by describing geometric relationships between pairs of off-center circles and deriving algebraic expressions that define the conditions under which such circles overlap and/or simply intersect.
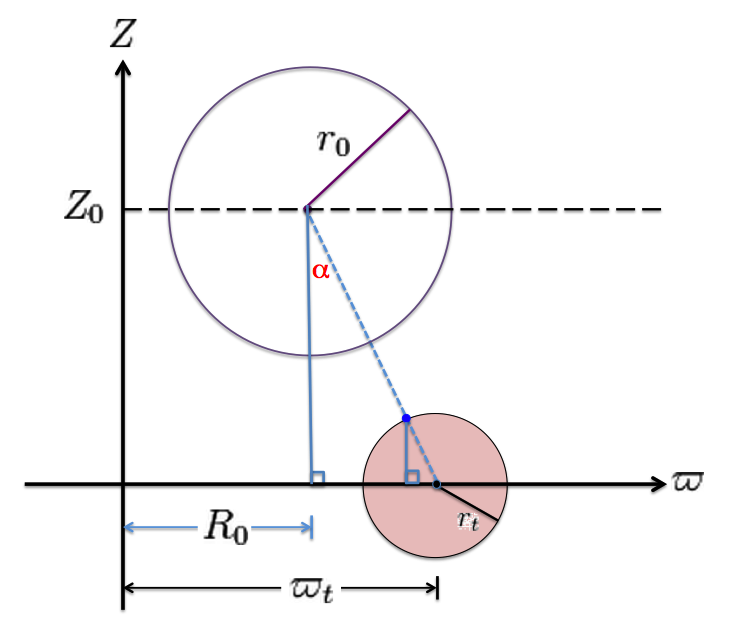
Overlap Between Two Off-Center Circles
Figure 2 displays two off-center circles. The solid pink circle represents a meridional cross-section through a uniform-density, axisymmetric torus whose center lies in the equatorial plane of a <math>~(\varpi, Z) </math>, cylindrical coordinate system; as depicted, <math>~\varpi_t</math> is the size of the major radius of this torus and its cross-sectional radius is <math>~r_t</math>. The other circle represents a single, <math>~\xi_1</math> = constant (toroidal) surface in toroidal coordinates; its major radius is, <math>~R_0</math>, and its cross-sectional radius is <math>~r_0</math>. The center of this <math>~\xi_1</math> = constant circle lies in the equatorial system of the associated toroidal coordinate system, which is parallel to but, as depicted, lies a distance, <math>~Z_0</math>, above the equatorial plane of the <math>~(\varpi, Z) </math>, cylindrical coordinate system.
As drawn, the figure does not identify the precise location of the origin of the toroidal coordinate system. But, in accordance with the properties of such coordinate systems, the origin must lie inside of the referenced circle and to the left of — that is, closer to the <math>~Z</math> (symmetry) axis than — the center of the circle, <math>~R_0</math>.
If the size of the <math>~\xi_1</math> = constant surface is varied while all the other key parameters <math>~(R_0, Z_0, \varpi_t, r_t)</math> are held fixed, what is the range of values of <math>~r_0</math> over which the two depicted circles overlap and/or simply intersect?
Initial Contact
Geometrically we appreciate that, as <math>~r_0</math> is increased, the two circles will first touch at a point that lies along the (blue-dashed) line-segment that connects the centers of both circles. More specifically, the initial interception will be at the point identified in Figure 2 by the solid blue dot lying on the surface of the pink torus. The distance between the two centers — which we will denote as <math>~h</math> — is also the hypotenuse of a right triangle whose other two sides are of length (opposite the angle, <math>~\alpha</math>) <math>~\varpi_t - R_0</math> and (adjacent to the angle, <math>~\alpha</math>) <math>~Z_0</math>. We see that the initial interception will occur when <math>~r_0 + r_t = h</math>, that is, when
|
<math>~r_0 = r_+</math> |
<math>~\equiv</math> |
<math>~h - r_t</math> |
|
|
<math>~=</math> |
<math>~[(\varpi_t - R_0)^2 + Z_0^2 ]^{1/2} - r_t </math> |
|
|
<math>~=</math> |
<math>~(\varpi_t - R_0)[1 + \Lambda^2 ]^{1/2} - r_t \, ,</math> |
where,
|
<math>~\Lambda</math> |
<math>~\equiv</math> |
<math>~\frac{Z_0}{\varpi_t - R_0} \, .</math> |
For later reference, we note that the cylindrical coordinates associated with this initial point of contact — i.e., the point identified in Figure 2 by the solid blue dot lying on the surface of the pink torus — are,
|
<math>~\varpi_+</math> |
<math>~=</math> |
<math>~\varpi_t - r_t \sin\alpha</math> |
|
|
<math>~=</math> |
<math>~\varpi_t - \frac{r_t (\varpi_t-R_0)}{[(\varpi_t - R_0)^2 + Z_0^2 ]^{1/2} }</math> |
|
|
<math>~=</math> |
<math>~\varpi_t - \frac{r_t }{[1+\Lambda^2 ]^{1/2} } \, ,</math> |
and,
|
<math>~Z_+</math> |
<math>~=</math> |
<math>~r_t \cos\alpha</math> |
|
|
<math>~=</math> |
<math>~\frac{r_t Z_0}{[(\varpi_t - R_0)^2 + Z_0^2 ]^{1/2} }</math> |
|
|
<math>~=</math> |
<math>~\frac{r_t \Lambda}{[1+\Lambda^2 ]^{1/2} } \, .</math> |
Final Contact
It is easy to see, geometrically, that if the (blue-dashed) line-of-centers and, in particular, if <math>~r_0</math> is increased beyond the "initial contact" length of <math>~r_+</math>, by exactly a length that equals the diameter of the pink torus, <math>~2r_t</math>, then the <math>~\xi_1</math> = constant circle will make its last contact with the circle that defines the surface of the equatorial-plane torus. Associating the subscript "-" with this point of last contact, we have,
|
<math>~r_-</math> |
<math>~\equiv</math> |
<math>~r_+ + 2r_t</math> |
|
|
<math>~=</math> |
<math>~(\varpi_t - R_0)[1 + \Lambda^2 ]^{1/2} + r_t \, ,</math> |
and the associated coordinate-location of this last point of contact,
|
<math>~\varpi_-</math> |
<math>~=</math> |
<math>~\varpi_t + \frac{r_t }{[1+\Lambda^2 ]^{1/2} } \, ,</math> |
and,
|
<math>~Z_-</math> |
<math>~=</math> |
<math>~-\frac{r_t \Lambda}{[1+\Lambda^2 ]^{1/2} } \, .</math> |
Region of Overlap
From the above discussion and derivations, we conclude that the <math>~\xi_1</math> = constant circle will overlap the pink torus and will, accordingly, intersect the surface of that torus in two places for all values of <math>~r_+ < r_0 < r_-</math>, that is, for,
|
<math>~(\varpi_t - R_0)[1 + \Lambda^2 ]^{1/2} - r_t </math> |
<math>~< r_0 < </math> |
<math>~(\varpi_t - R_0)[1 + \Lambda^2 ]^{1/2} + r_t \, .</math> |
Reality Check One
Let's see if these derived results make sense. As a first example, let's assign values of various Figure 2 parameters as follows:
| Example 1A | |||
|---|---|---|---|
| <math>~\varpi_t</math> | <math>~r_t</math> | <math>~Z_0</math> | <math>~\alpha</math> |
| <math>~\tfrac{3}{4}</math> | <math>~\tfrac{1}{4}</math> | <math>~1</math> | <math>~\tfrac{\pi}{6}</math> |
(Notice that the first pair of these parameter values aligns with the properties of the pink torus that was sketched in Figure 4 of Trova, Huré & Hersant (2012) — as reprinted immediately below — and that the chosen value of <math>~Z_0</math> aligns with the z-coordinate of their "Point B.")
|
Figure 4 extracted without modification from p. 2640 of Trova, Huré & Hersant (2012)
"The Potential of Discs from a 'Mean Green Function' "
Monthly Notices of the Royal Astronomical Society, vol. 424, pp. 2635-2645 © RAS |
|
<math>~\varpi_t = \tfrac{3}{4}\, ; ~ r_t = \tfrac{1}{4}</math>
Point A: <math>~(\varpi, Z) = (\tfrac{3}{4}, 0)</math>
Point B: <math>~(\varpi, Z) = (1, 1)</math>
Point C: <math>~(\varpi, Z) = (10, 10)</math> |
Taken together, this choice for the values of <math>~\alpha</math> and <math>~Z_0</math> implies: (1) That the hypotenuse of the blue right-triangle in our Figure 2 and, hence, the distance between the centers of the two circles, is
<math>~h = \frac{Z_0}{\cos\alpha} = \frac{2\sqrt{3}}{3} \, ;</math>
and, (2) that the side of the triangle that is opposite the angle, <math>~\alpha</math>, is,
|
<math>~\varpi_t - R_0</math> |
<math>~=</math> |
<math>~h \sin\alpha = \frac{\sqrt{3}}{3} \, ,</math> |
which, taken together with the choice of <math>~\varpi_t</math>, gives,
|
<math>~R_0</math> |
<math>~=</math> |
<math>~\frac{3}{4} - \frac{\sqrt{3}}{3} = \frac{9-4\sqrt{3}}{12} \approx 0.17265\, .</math> |
With this set of parameters held fixed, it is clear that, in order for the <math>~\xi_1</math> = constant circle to make first/final contact with the pink torus, it will need to have a radius,
<math>~r_\pm = h \mp r_t = \frac{2\sqrt{3}}{3} \mp \frac{1}{4} \, .</math>
Let's see if this expectation matches the result obtained via the expressions derived above. Specifically, we find,
|
<math>~\Lambda</math> |
<math>~\equiv</math> |
<math>~\frac{Z_0}{\varpi_t - R_0} = \sqrt{3} \, ;</math> |
hence,
|
<math>~r_\pm</math> |
<math>~=</math> |
<math>~(\varpi_t - R_0)[1 + \Lambda^2 ]^{1/2} \mp r_t </math> |
|
|
<math>~=</math> |
<math>~ \frac{\sqrt{3}}{3}\biggl[1 + (\sqrt{3})^2 \biggr]^{1/2} \mp \frac{1}{4} </math> |
|
|
<math>~=</math> |
<math>~ \frac{2\sqrt{3}}{3} \mp \frac{1}{4} \, .</math> |
This precisely matches our expectation.
Relate to Toroidal Coordinate System
Determine Overall Scale Length
In order to fully tie our "region of overlap" discussion back to MF53's system of toroidal coordinates, we must identify the specific location of the origin of that coordinate system in, for example, the Figure 2 diagram. As above, we will place the origin of the coordinate system an, as yet unspecified, distance, <math>~a</math>, from the symmetry axis while, as illustrated in Figure 2, displacing it a distance, <math>~Z_0</math>, above the (cylindrical coordinate system's) equatorial plane. Referring back to the properties of toroidal coordinate systems, as discussed above, we know that in the <math>~Z = Z_0</math> plane, the inner and outer edges of a <math>~\xi_1</math> = constant torus/circle have radial locations,
|
<math> ~\frac{\varpi_\mathrm{inner}}{a} = \chi_\mathrm{inner} </math> |
<math>~=</math> |
<math> ~\biggl[\frac{(\xi_1 - 1)}{(\xi_1 + 1)} \biggr]^{1/2} \, , </math> |
|
<math> ~\frac{\varpi_\mathrm{outer}}{a} = \chi_\mathrm{outer} </math> |
<math>~=</math> |
<math> ~\biggl[\frac{(\xi_1 + 1)}{(\xi_1 - 1)} \biggr]^{1/2} \, . </math> |
Hence, the major radius of the <math>~\xi_1</math> = constant toroidal surface is,
|
<math>~R_0</math> |
<math>~=</math> |
<math>~ \frac{1}{2} (\varpi_\mathrm{outer} + \varpi_\mathrm{inner})</math> |
|
|
<math>~=</math> |
<math>~ \frac{a}{2} \biggl\{ \biggl[\frac{(\xi_1 + 1)}{(\xi_1 - 1)} \biggr]^{1/2} + \biggl[\frac{(\xi_1 - 1)}{(\xi_1 + 1)} \biggr]^{1/2} \biggr\}</math> |
|
|
<math>~=</math> |
<math>~ \frac{a}{2} \biggl[\frac{(\xi_1 + 1) + (\xi_1-1)}{(\xi_1^2 - 1)^{1/2}} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{a\xi_1}{(\xi_1^2 - 1)^{1/2}} \, , </math> |
and its cross-sectional radius is,
|
<math>~r_0</math> |
<math>~=</math> |
<math>~ \frac{1}{2} (\varpi_\mathrm{outer} - \varpi_\mathrm{inner})</math> |
|
|
<math>~=</math> |
<math>~ \frac{a}{2} \biggl\{ \biggl[\frac{(\xi_1 + 1)}{(\xi_1 - 1)} \biggr]^{1/2} - \biggl[\frac{(\xi_1 - 1)}{(\xi_1 + 1)} \biggr]^{1/2} \biggr\}</math> |
|
|
<math>~=</math> |
<math>~ \frac{a}{2} \biggl[\frac{(\xi_1 + 1) - (\xi_1-1)}{(\xi_1^2 - 1)^{1/2}} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{a}{(\xi_1^2 - 1)^{1/2}} \, . </math> |
This also means that, if <math>~r_0</math> and <math>~R_0</math> are specified, the associated values of <math>~\xi_1</math> and the scale length, <math>~a</math>, are,
|
<math>~\xi_1</math> |
<math>~=</math> |
<math>~\frac{R_0}{r_0} \, ,</math> |
and,
|
<math>~a</math> |
<math>~=</math> |
<math>~r_0 \biggl[\biggl( \frac{R_0}{r_0} \biggr)^2 - 1 \biggr]^{1/2} \, .</math> |
Revise Overlap Discussion
Let's reassess the conclusions drawn in our overlap discussion, above. Rather than varying <math>~r_0</math> while holding <math>~R_0</math> fixed, let's consider varying <math>~\xi_1</math> while fixing the coordinate location of the origin of the toroidal coordinate system, <math>~(a, Z_0)</math>. This is the approach that is appropriately aligned with integration over the (pink) toroidal mass distribution.
Re-expressed, the pair of boundaries of the "region of overlap," <math>~r_\pm</math>, give:
|
<math>~(r_0 \pm r_t)^2 </math> |
<math>~=</math> |
<math>~(\varpi_t - R_0)^2 + Z_0^2</math> |
|
<math>~\Rightarrow ~~~~ \biggl[ \frac{a}{(\xi_1^2 - 1)^{1/2}} \pm r_t \biggr]^2 </math> |
<math>~=</math> |
<math>~\biggl[ \varpi_t - \frac{a\xi_1}{(\xi_1^2 - 1)^{1/2}} \biggr]^2 + Z_0^2</math> |
|
<math>~\Rightarrow ~~~~ \biggl[ a \pm r_t (\xi_1^2 - 1)^{1/2}\biggr]^2 </math> |
<math>~=</math> |
<math>~\biggl[ \varpi_t (\xi_1^2 - 1)^{1/2} - a\xi_1 \biggr]^2 + Z_0^2 (\xi_1^2 - 1)</math> |
|
<math>~\Rightarrow~~~~ a^2 \pm 2a r_t (\xi_1^2 - 1)^{1/2} + r_t^2 (\xi_1^2 - 1)</math> |
<math>~=</math> |
<math>~\varpi_t^2 (\xi_1^2 - 1) - 2a \varpi_t \xi_1 (\xi_1^2 - 1)^{1/2} + a^2\xi_1^2 + Z_0^2 (\xi_1^2 - 1)</math> |
|
<math> ~\Rightarrow~~~~(\xi_1^2 - 1)^{1/2}[2a \varpi_t \xi_1 \pm 2a r_t ] </math> |
<math>~=</math> |
<math>~[\varpi_t^2 +a^2 + Z_0^2](\xi_1^2 - 1) </math> |
|
<math> ~\Rightarrow~~~~(\xi_1^2 - 1)^{1/2} </math> |
<math>~=</math> |
<math>~\frac{2a(\varpi_t \xi_1 \pm r_t )}{(\varpi_t^2 +a^2 + Z_0^2)} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{\ell} \biggl[ \xi_1 \pm \frac{r_t}{\varpi_t} \biggr] \, ,</math> |
where,
<math>\ell \equiv \frac{1}{2}\biggl[ \frac{a^2 + \varpi_t^2 + Z_0^2}{a\varpi_t} \biggr] \, .</math>
After squaring both sides of this equation, we find that the values of <math>~\xi_1</math> corresponding to the limits of overlap can be obtained from the roots of the following quadratic equation:
|
<math> ~\ell^2 (\xi_1^2 - 1) </math> |
<math>~=</math> |
<math>~ \biggl[ \xi_1 \pm \frac{r_t}{\varpi_t} \biggr]^2</math> |
|
|
<math>~=</math> |
<math>~ \xi_1^2 \pm \xi_1\biggl(\frac{2r_t}{\varpi_t}\biggr) + \biggl(\frac{r_t}{\varpi_t}\biggr)^2 \, ,</math> |
that is,
|
<math>~0 </math> |
<math>~=</math> |
<math>~(1-\ell^2) \xi_1^2 \pm \xi_1\biggl(\frac{2r_t}{\varpi_t}\biggr) + \biggl[ \biggl(\frac{r_t}{\varpi_t}\biggr)^2 +\ell^2\biggr] \, .</math> |
After setting up this expression, it dawned on me that the "plus or minus" generalization is not appropriate in this situation. While either result — say, the "plus" result — can be shifted from a <math>~r_0 - R_0</math> specification to a <math>~a - \xi_1</math> specification, the pair of results generally will not share the same value of the scale length, <math>~a</math>. Hence the pair of solutions will be unrelated when viewed from the perspective of the toroidal coordinate system. Instead, let's determine the value of <math>~a</math> from the "first contact" solution — the superior sign in the expression — then figure out what the "final contact" solution will be if this scale length is held fixed. The solution to the quadratic equation is:
|
<math>~\xi_1</math> |
<math>~=</math> |
<math>~ \frac{1}{2(1-\ell^2)} \biggl\{ - \biggl(\frac{2r_t}{\varpi_t}\biggr) \pm \sqrt{\biggl(\frac{2r_t}{\varpi_t}\biggr)^2 -4(1-\ell^2) \biggl[ \biggl(\frac{r_t}{\varpi_t}\biggr)^2 +\ell^2\biggr]} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{r_t}{\varpi_t(1-\ell^2)} \biggl\{ - 1 \pm \sqrt{1 -(1-\ell^2) \biggl[ 1 +\biggl(\frac{\ell \varpi_t}{r_t}\biggr)^2\biggr]} \biggr\} \, . </math> |
Given that the allowed range of values for the "radial" toroidal coordinate is, <math>~1 \leq \xi_1 \leq \infty</math>, the relevant root is,
|
<math>~\xi_1\biggr|_\mathrm{first}</math> |
<math>~=</math> |
<math>~ \frac{r_t}{\varpi_t(1-\ell^2)} \biggl\{ \sqrt{1 -(1-\ell^2) \biggl[ 1 +\biggl(\frac{\ell \varpi_t}{r_t}\biggr)^2\biggr]} -1 \biggr\} \, . </math> |
Reality Check Two
Let's examine the behavior of these expressions, given the structural parameters provided in Example 1A, as defined above. Earlier, we deduced that "first contact" occurs when,
|
<math>~R_0</math> |
<math>~=</math> |
<math>~\frac{3}{4} - \frac{\sqrt{3}}{3} = \frac{9-4\sqrt{3}}{12} \, ,</math> |
and,
|
<math>~r_0 = r_+</math> |
<math>~=</math> |
<math>~ \frac{2\sqrt{3}}{3} - \frac{1}{4} = \frac{8\sqrt{3} - 3}{12} \, .</math> |
Hence, we should find that,
|
<math>~\xi_1\biggr|_\mathrm{first}</math> |
<math>~=</math> |
<math>~\frac{R_0}{r_0} = \frac{9-4\sqrt{3}}{8\sqrt{3} - 3} \approx 0.19084\, ,</math> |
and,
|
<math>~a</math> |
<math>~=</math> |
<math>~r_0 \biggl[\biggl( \frac{R_0}{r_0} \biggr)^2 - 1 \biggr]^{1/2} \, .</math> |
Other
Now, the surface of an equatorial-plane torus having major radius, <math>\varpi_t</math>, and cross-sectional radius, <math>~r_t</math>, is described by the expression,
So, as the vertical coordinate varies over the range, <math>-r_t \leq z \leq + r_t</math>, the horizontal coordinate varies over the range, <math>(\varpi_t - r_t ) \leq \varpi \leq (\varpi_t + r_t)</math>. But, more importantly, for a given value of <math>~\varpi</math>, the corresponding value of the vertical coordinate is,
<math> ~ z = \pm \biggl[ r_t^2 - (\varpi-\varpi_t)^2 \biggr]^{1/2}. </math>
Yet Again
Walk Through Step-By-Step
Keep the scale length of the toroidal coordinate system, <math>~a</math>, fixed while varying the value of <math>~\xi_1</math> and, hence, the radius,
<math>~r_0 = \frac{a}{(\xi_1^2 - 1)^{1/2}} \, ,</math>
of the <math>~\xi_1</math> = constant circle (hereafter, <math>\xi_1</math>-circle). The (cylindrical) coordinate location of the center of this circle will be, <math>~(R_0, Z_0)</math>, where,
<math>~R_0 = \frac{a\xi_1}{(\xi_1^2 - 1)^{1/2}} \, .</math>
For the time being, we will assume that <math>~Z_0 > 0</math>, as illustrated in our Figure 2. Our initial aim is to determine the range of values of <math>~\xi_1</math> for which the <math>\xi_1</math>-circle touches or overlaps the equatorial-plane torus, whose position and size are as defined in our Figure 2.
Lowest Point on Circle
We will identify the (cylindrical) coordinates of the lowest point on the <math>\xi_1</math>-circle as <math>~(R_0, Z_\mathrm{min})</math>, where,
<math>~Z_\mathrm{min} = Z_0 - r_0 = Z_0 - \frac{a}{(\xi_1^2 - 1)^{1/2}} \, .</math>
The <math>\xi_1</math>-circle cannot possibly touch the equatorial-plane torus until <math>~\xi_1</math> drops to a value such that <math>~Z_\mathrm{min}</math> is less than or equal to the radius of the torus, <math>~r_t</math>. This means that touching/overlap cannot occur unless,
<math>~\xi_1 \leq \xi_\mathrm{max} \equiv \biggl[1 + \biggl(\frac{a}{Z_0 - r_t} \biggr)^2\biggr]^{1/2} \, .</math>
A Critical Value of the Scale Length
Now, the two circles will come into contact at this limiting value, <math>~\xi_\mathrm{max}</math>, only if the corresponding "radial" coordinate location of the center of the <math>~\xi_1</math> circle exactly equals <math>~\varpi_t</math>, that is, only if
|
<math>~\frac{a\xi_\mathrm{max}}{(\xi_\mathrm{max}^2 - 1)^{1/2}}</math> |
<math>~=</math> |
<math>~\varpi_t</math> |
|
<math>~\Rightarrow~~~~ a^2\xi_\mathrm{max}^2 </math> |
<math>~=</math> |
<math>~\varpi_t^2(\xi_\mathrm{max}^2 - 1)</math> |
|
<math>~\Rightarrow~~~~ \xi_\mathrm{max}^2 </math> |
<math>~=</math> |
<math>~\frac{\varpi_t^2}{(\varpi_t^2 - a^2)}</math> |
|
<math>~\Rightarrow~~~~ 1 + \biggl(\frac{a}{Z_0 - r_t} \biggr)^2 </math> |
<math>~=</math> |
<math>~\frac{\varpi_t^2}{(\varpi_t^2 - a^2)}</math> |
|
<math>~\Rightarrow~~~~ (\varpi_t^2 - a^2)(Z_0 - r_t)^2 + a^2(\varpi_t^2 - a^2) </math> |
<math>~=</math> |
<math>~\varpi_t^2 (Z_0 - r_t)^2</math> |
|
<math>~\Rightarrow~~~~0</math> |
<math>~=</math> |
<math>~ a^2 (Z_0 - r_t)^2 - a^2(\varpi_t^2 - a^2) </math> |
|
|
<math>~=</math> |
<math>~ a^2 [(Z_0 - r_t)^2 - \varpi_t^2] + a^4 </math> |
|
<math>~\Rightarrow ~~~~ a = a_\mathrm{crit} </math> |
<math>~\equiv</math> |
<math>~ [\varpi_t^2 - (Z_0 - r_t)^2 ]^{1/2} \, . </math> |
Points of Intersection
In all meridional planes, the surface of the equatorial-plane torus is defined by the off-center circle expression,
|
<math>~(\varpi - \varpi_t)^2 + z^2</math> |
<math>~=</math> |
<math>~r_t^2</math> |
|
<math>~\Rightarrow~~~~z^2</math> |
<math>~=</math> |
<math>~r_t^2 - (\varpi - \varpi_t)^2 \, .</math> |
Independently, we know that the surface of the off-center, <math>\xi_1</math>-circle is defined by the expression,
|
<math>~(\varpi - R_0)^2 + (z- Z_0)^2</math> |
<math>~=</math> |
<math>~r_0^2</math> |
|
<math>~\Rightarrow~~~~[z- Z_0]^2</math> |
<math>~=</math> |
<math>~\frac{a^2}{(\xi_1^2 - 1)} - \biggl[ \varpi - \frac{a\xi_1}{(\xi_1^2 - 1)^{1/2}} \biggr]^2 </math> |
|
<math>~\Rightarrow~~~~z^2 - 2 z Z_0 + Z_0^2</math> |
<math>~=</math> |
<math>~\frac{a^2}{(\xi_1^2 - 1)} - \biggl[ \varpi^2 - \frac{2a \varpi \xi_1}{(\xi_1^2 - 1)^{1/2}} + \frac{a^2\xi_1^2}{(\xi_1^2 - 1)} \biggr] </math> |
|
|
<math>~=</math> |
<math>~-a^2 - \varpi^2 + \frac{2a \varpi \xi_1}{(\xi_1^2 - 1)^{1/2}} \, .</math> |
When the two circles intersect, the (cylindrical) coordinates of the point(s) at which the intersection occurs, <math>~(\varpi, z)=(\varpi_i, z_i)</math> must be shared by both circles. Eliminating <math>~z</math> between these two off-center circle expressions allows us to solve for the "radial" coordinate, <math>~\varpi_i</math>, of the intersection point(s). Specifically we find,
|
<math>~[ r_t^2 - (\varpi - \varpi_t)^2 ] - 2 [ r_t^2 - (\varpi - \varpi_t)^2 ]^{1/2} Z_0 + Z_0^2</math> |
<math>~=</math> |
<math>~-a^2 - \varpi^2 + \frac{2a \varpi \xi_1}{(\xi_1^2 - 1)^{1/2}} </math> |
|
<math>~\Rightarrow ~~~~2 [ r_t^2 - (\varpi - \varpi_t)^2 ]^{1/2} Z_0</math> |
<math>~=</math> |
<math>~Z_0^2 + a^2 + \varpi^2 + [ r_t^2 - (\varpi - \varpi_t)^2 ] - \frac{2a \varpi \xi_1}{(\xi_1^2 - 1)^{1/2}} </math> |
|
|
<math>~=</math> |
<math>~Z_0^2 + a^2 + \varpi^2 + r_t^2 - (\varpi^2 - 2 \varpi \varpi_t + \varpi_t^2) - \varpi\biggl[ \frac{2a \xi_1}{(\xi_1^2 - 1)^{1/2}}\biggr] </math> |
|
|
<math>~=</math> |
<math>~\Kappa + 2 \varpi \biggl[ \varpi_t - \frac{a \xi_1}{(\xi_1^2 - 1)^{1/2}} \biggr] \, ,</math> |
where,
<math>\Kappa \equiv Z_0^2 + a^2 - (\varpi_t^2 - r_t^2) \, .</math>
Squaring both sides of this expression gives,
|
<math>~4Z_0^2 [ r_t^2 - (\varpi^2 - 2\varpi \varpi_t + \varpi_t^2) ] </math> |
<math>~=</math> |
<math>~\Kappa^2 + 4 \varpi \Kappa\biggl[ \varpi_t - \frac{a \xi_1}{(\xi_1^2 - 1)^{1/2}} \biggr] + 4 \varpi^2 \biggl[ \varpi_t - \frac{a \xi_1}{(\xi_1^2 - 1)^{1/2}} \biggr]^2</math> |
|
<math>~\Rightarrow ~~~~ 0</math> |
<math>~=</math> |
<math>~[\Kappa^2 +4Z_0^2 (\varpi_t^2- r_t^2)] + \varpi [ 4\Kappa \beta - 8Z_0^2 \varpi_t ] + 4\varpi^2 [Z_0^2 + \beta^2 ] \, ,</math> |
where,
<math>\beta \equiv \varpi_t - \frac{a \xi_1}{(\xi_1^2 - 1)^{1/2}} \, .</math>
The roots of this quadratic equation provide the sought-after coordinate(s), <math>~\varpi_i</math>, of the point(s) of intersection. Specifically,
|
<math>~\varpi_i</math> |
<math>~=</math> |
<math>~ \frac{1}{8 [Z_0^2 + \beta^2 ]} \biggl\{ [ 8Z_0^2 \varpi_t- 4\Kappa \beta ] \pm \sqrt{[ 8Z_0^2 \varpi_t- 4\Kappa \beta ]^2 - 16[Z_0^2 + \beta^2 ] [\Kappa^2 +4Z_0^2 (\varpi_t^2- r_t^2)]} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{[ 8Z_0^2 \varpi_t- 4\Kappa \beta ]}{8 [Z_0^2 + \beta^2 ]} \biggl\{ 1 \pm \sqrt{1 - \frac{16[Z_0^2 + \beta^2 ] [\Kappa^2 +4Z_0^2 (\varpi_t^2- r_t^2)]}{[ 8Z_0^2 \varpi_t- 4\Kappa \beta ]^2 }} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{2Z_0^2 \varpi_t-\Kappa \beta }{2 (Z_0^2 + \beta^2 )} \biggl\{ 1 \pm \sqrt{1 - \ell } \biggr\}\, , </math> |
where,
<math>\ell \equiv \frac{(Z_0^2 + \beta^2 )[\Kappa^2 +4Z_0^2 (\varpi_t^2- r_t^2)]}{( 2Z_0^2 \varpi_t-\Kappa \beta )^2 } \, .</math>
Now, from the definition of Toroidal Coordinates, as provided above, we know that the cylindrical coordinate, <math>~\varpi</math>, is related to the pair of meridional-plane toroidal coordinates via the expression,
|
<math>~\frac{\varpi}{a}</math> |
<math>~=</math> |
<math>~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1-\xi_2} \, .</math> |
Therefore, once <math>~\varpi_i</math> has been determined for a given choice of <math>~\xi_1</math>, the corresponding value of <math>~\xi_2</math> at the intersection point is,
|
<math>~\xi_2</math> |
<math>~=</math> |
<math>~\xi_1 - \frac{(\xi_1^2 - 1)^{1/2}}{(\varpi_i/a)} \, .</math> |
Finally, given the pair of coordinate values, <math>~(\xi_1, \xi_2)_i</math>, the value of the (cylindrical) z-coordinate at the intersection point can be obtained via the relation,
|
<math>~\frac{Z_0}{a} - \frac{z}{a}</math> |
<math>~=</math> |
<math>~\frac{(1-\xi_2^2 )^{1/2}}{\xi_1-\xi_2} </math> |
|
<math>~\Rightarrow ~~~~z</math> |
<math>~=</math> |
<math>~Z_0 - \frac{a(1-\xi_2^2 )^{1/2}}{\xi_1-\xi_2} \, .</math> |
Limiting Values
All other parameters <math>~(a, Z_0, \varpi_t, r_t)</math> being held fixed, as the coordinate, <math>~\xi_1</math>, is varied, there will be a maximum value, <math>~\xi_1|_\mathrm{max}</math>, at which the <math>\xi_1</math>-circle will first make contact with the (pink) equatorial-plane torus, and there will be a minimum value, <math>~\xi_1|_\mathrm{min}</math>, at which it will have its final contact. At all values within the parameter range,
<math>~\xi_1|_\mathrm{max} > \xi_1 > ~\xi_1|_\mathrm{min} \, ,</math>
the <math>\xi_1</math>-circle will intersect the surface of the torus in two locations, defined by two different values of the associated angular coordinate, <math>~\xi_2</math> — see, for example, the coordinates listed in the table associated with example 2, below — but at the first and final points of contact, the two values of <math>~\xi_2</math> will be degenerate. Let's derive the mathematical relations that give the values of <math>~\xi_1|_\mathrm{max}</math> and <math>~\xi_1|_\mathrm{min}</math>.
The expression derived above for the "radial" coordinate of the points of intersection, <math>~\varpi_i</math>, gives two physically viable, real numbers as long as the composite parameter, <math>~1 > \ell \geq 0</math>. But only one real value is obtained when <math>~\ell = 1</math>, and that occurs when,
|
<math>~( 2Z_0^2 \varpi_t-\Kappa \beta )^2</math> |
<math>~=</math> |
<math>~(Z_0^2 + \beta^2 )[\Kappa^2 +4Z_0^2 (\varpi_t^2- r_t^2)] \, .</math> |
In this expression, <math>~\beta</math> is the only parameter that depends on <math>~\xi_1</math>. So, temporarily using the shorthand notation,
<math>~\Lambda \equiv [\Kappa^2 +4Z_0^2 (\varpi_t^2- r_t^2)] \, </math>
let's solve for the "critical" value(s), <math>~\beta_\mathrm{crit}</math>. We have,
|
<math>~4 Z_0^4 \varpi_t^2 - 4Z_0^2 \varpi_t \Kappa\beta + \Kappa^2\beta^2</math> |
<math>~=</math> |
<math>~Z_0^2\Lambda + \Lambda \beta^2 </math> |
|
<math>~\Rightarrow~~~~(\Kappa^2 - \Lambda)\beta^2 - (4Z_0^2 \varpi_t \Kappa)\beta + (4 Z_0^4 \varpi_t^2 -Z_0^2\Lambda)</math> |
<math>~=</math> |
<math>~0 \, .</math> |
The roots of this quadratic equation give,
|
<math>~\beta_\mathrm{crit}</math> |
<math>~=</math> |
<math>~\frac{ 2Z_0^2 \varpi_t \Kappa}{ (\Kappa^2 - \Lambda)} \biggl[1\mp \sqrt{1-\frac{(\Kappa^2 - \Lambda) (4 Z_0^4 \varpi_t^2 -Z_0^2\Lambda)}{4Z_0^4 \varpi_t^2 \Kappa^2 } } \biggr]</math> |
|
|
<math>~=</math> |
<math>~- \frac{ 2Z_0^2 \varpi_t \Kappa}{ 4Z_0^2 (\varpi_t^2- r_t^2)} \biggl[1\mp \sqrt{1+\frac{4Z_0^2 (\varpi_t^2- r_t^2)(4 Z_0^4 \varpi_t^2 -Z_0^2\Lambda)}{4Z_0^4 \varpi_t^2 \Kappa^2 } } \biggr]</math> |
|
|
<math>~=</math> |
<math>~- \frac{ \varpi_t \Kappa}{ 2 (\varpi_t^2- r_t^2)} \biggl[1\mp \sqrt{1+\frac{(\varpi_t^2- r_t^2)(4 Z_0^2 r_t^2 -\Kappa^2)}{\varpi_t^2 \Kappa^2 } } \biggr] \, .</math> |
Notice that a single critical value of <math>~\ell</math> — specifically, <math>~\ell = 1</math> — translates nicely into a pair of values of <math>~\beta_\mathrm{crit}</math>; these presumably relate directly to the pair of limiting coordinate values, <math>~\xi_1|_\mathrm{max}</math> and <math>~\xi_1|_\mathrm{min}</math>, that we are seeking. Via the definition of <math>~\beta</math>, we find,
|
<math>~\frac{\xi_1}{(\xi_1^2-1)^{1/2}}</math> |
<math>~=</math> |
<math>~\biggl(\frac{\varpi_t - \beta}{a} \biggr)</math> |
|
<math>~\Rightarrow~~~~\xi_1^2</math> |
<math>~=</math> |
<math>~\biggl(\frac{\varpi_t - \beta}{a} \biggr)^2(\xi_1^2-1)</math> |
|
<math>~\Rightarrow~~~~\xi_1^2\biggl[ \biggl(\frac{\varpi_t - \beta}{a} \biggr)^2-1\biggr]</math> |
<math>~=</math> |
<math>~\biggl(\frac{\varpi_t - \beta}{a} \biggr)^2</math> |
|
<math>~\Rightarrow~~~~\xi_1</math> |
<math>~=</math> |
<math>~\biggl[ \frac{(\varpi_t-\beta)^2}{(\varpi_t-\beta)^2-a^2}\biggr]^{1/2} \, .</math> |
Upon evaluation of this expression in conjunction with the pair of <math>~\beta_\mathrm{crit}</math> values, the table, below, provides numerical values for the limiting values of <math>~\xi_1|_\mathrm{max}</math> and <math>~\xi_1|_\mathrm{min}</math>, along with the respective values of their accompanying (degenerate) coordinate, <math>~\xi_2</math>.
Examples
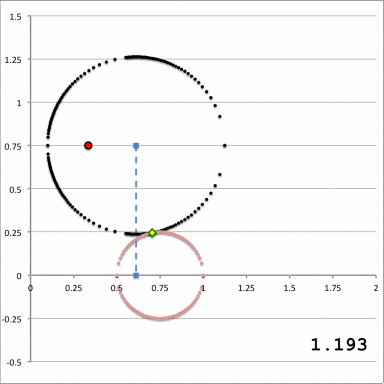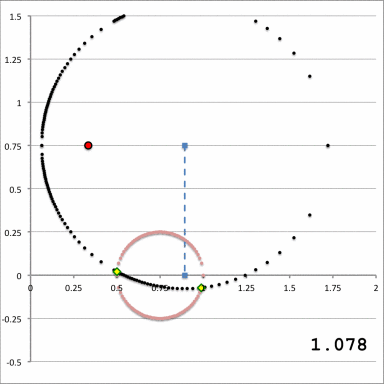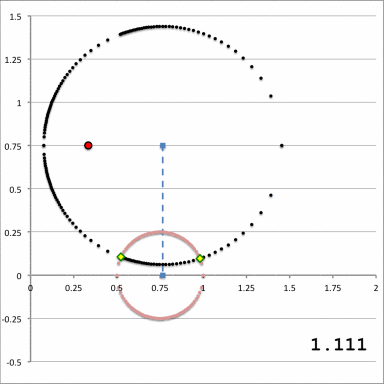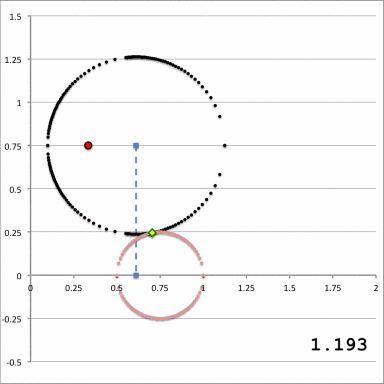
For reference purposes, Figure 2 has been displayed here, again, in the lefthand panel of Figure 4; the animation sequence presented in the righthand panel illustrates how the <math>\xi_1</math>-circle (depicted by the locus of small black dots) intersects the surface of the (pink) equatorial-plane torus as the value of <math>~\xi_1</math> is varied over the parameter range,
<math>~\xi_1|_\mathrm{max} \geq \xi_1 \geq ~\xi_1|_\mathrm{min} \, ,</math>
for a toroidal coordinate system whose origin (filled, red dot) remains fixed at the (cylindrical) coordinate location, <math>~(\varpi, z) = (a, Z_0) = (\tfrac{1}{3}, \tfrac{3}{4})</math>. For a toroidal coordinate system with this specified origin and an equatorial-plane torus having <math>~\varpi_t = \tfrac{3}{4}</math> and <math>~r_t = \tfrac{1}{4}</math> — as recorded in the top row of numbers in the Table, below — the <math>\xi_1</math>-circle makes first contact with the torus when <math>~\xi_1 = \xi_1|_\mathrm{max} = 1.1927843</math> and it makes final contact when <math>~\xi_1 = \xi_1|_\mathrm{min} = 1.0449467</math>. The animation sequence contains ten unique frames: The value of <math>~\xi_1</math> that is associated with the <math>\xi_1</math>-circle in each case appears near the bottom-right corner of the animation frame. These parameter values have also been recorded in the first column of ten separate rows in the following table, along with other relevant parameter values. For example, in each frame of the animation, the points of intersection between the surface of the torus and the <math>\xi_1</math>-circle are identified by filled, green diamonds; the (cylindrical) coordinates associated with these points of intersection, <math>~(\varpi_i, z_i)</math>, are listed in each table row, along with the corresponding value of the toroidal coordinate system's angular, <math>~\xi_2</math> coordinate.
| Example 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| <math>~\varpi_t</math> | <math>~r_t</math> | <math>~Z_0</math> | <math>~a</math> | <math>~\Kappa</math> | |||||
| <math>~\tfrac{3}{4}</math> | <math>~\tfrac{1}{4}</math> | <math>~\tfrac{3}{4}</math> | <math>~\tfrac{1}{3}</math> | <math>~(\tfrac{5}{12})^2</math> | |||||
| Torus Intersection Points | |||||||||
| <math>~\xi_1</math> | <math>~\beta</math> | <math>~\ell</math> | Intersection #1 (superior sign) | Intersection #2 (inferior sign) | |||||
| <math>~\xi_2</math> | <math>~\varpi_i</math> | <math>~z_i</math> | <math>~\xi_2</math> | <math>~\varpi_i</math> | <math>~z_i</math> | ||||
| <math>~1.1927843</math> | <math>~+0.138485</math> | <math>~1.000000</math> | <math>~0.885198</math> | <math>~0.704606</math> | <math>~0.245844</math> | Degenerate Coordinate Values | |||
| <math>~1.176</math> | <math>~+0.116568</math> | <math>~0.981258</math> | <math>~0.922142</math> | <math>~0.812595</math> | <math>~0.242037</math> | <math>~0.841611</math> | <math>~0.616896</math> | <math>~0.211621</math> | |
| <math>~1.160</math> | <math>~+0.092267</math> | <math>~0.962725</math> | <math>~0.933386</math> | <math>~0.864726</math> | <math>~0.222121</math> | <math>~0.824945</math> | <math>~0.584858</math> | <math>~0.187691</math> | |
| <math>~1.144</math> | <math>~+0.063705</math> | <math>~0.943871</math> | <math>~0.940238</math> | <math>~0.908969</math> | <math>~0.192948</math> | <math>~0.813713</math> | <math>~0.560766</math> | <math>~0.163372</math> | |
| <math>~1.127</math> | <math>~+0.027202</math> | <math>~0.924221</math> | <math>~0.944608</math> | <math>~0.949856</math> | <math>~0.150191</math> | <math>~0.806047</math> | <math>~0.539788</math> | <math>~0.135318</math> | |
| <math>~1.111</math> | <math>~-0.015045</math> | <math>~0.907444</math> | <math>~0.946487</math> | <math>~0.980806</math> | <math>~0.096065</math> | <math>~0.802617</math> | <math>~0.523232</math> | <math>~0.105244</math> | |
| <math>~1.094</math> | <math>~-0.071947</math> | <math>~0.894425</math> | <math>~0.945995</math> | <math>~0.999208</math> | <math>~0.019887</math> | <math>~0.803522</math> | <math>~0.509118</math> | <math>~0.066901</math> | |
| <math>~1.078</math> | <math>~-0.142539</math> | <math>~0.892548</math> | <math>~0.942353</math> | <math>~0.989322</math> | <math>~-0.072283</math> | <math>~0.810056</math> | <math>~0.500846</math> | <math>~0.020554</math> | |
| <math>~1.061</math> | <math>~-0.247448</math> | <math>~0.916366</math> | <math>~0.932024</math> | <math>~0.916375</math> | <math>~-0.186599</math> | <math>~0.827074</math> | <math>~0.505248</math> | <math>~-0.050956</math> | |
| <math>~1.0449467</math> | <math>~-0.398902</math> | <math>~1.000000</math> | <math>~0.885198</math> | <math>~0.632605</math> | <math>~-0.220722</math> | Degenerate Coordinate Values | |||
Notice in the animation that, while the origin of the selected toroidal coordinate system (the filled red dot) remains fixed, the center of the <math>\xi_1</math>-circle does not remain fixed. In order to highlight this behavior, the location of the center of the <math>\xi_1</math>-circle has been marked by a filled, light-blue square and, in keeping with the earlier Figure 2 sketch, a vertical, light-blue line connects this center to the equatorial plane.
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Confusing and Misleading Steps
But Not Every Circle Will Do
It is very important to appreciate that, although surfaces of constant <math>\Chi</math> (or, equivalently, surfaces of constant <math>\xi_1</math>) are always off-center circles, it is not the case that every off-center circle will prove to be a <math>\Chi= \mathrm{constant}</math> surface in the most relevant toroidal coordinate system. To be more specific, suppose we want to evaluate the potential at some location <math>(R,0)</math> inside or outside of a uniform-density torus whose meridional cross-section is a circle of radius <math>r_c</math> and whose center is located on the <math>x</math>-axis at position <math>x_0</math>. The equation describing the cross-sectional surface of this torus is,
<math> (R' - x_0)^2 - {z'}^2 = r_c^2 . </math>
Dividing through by the square of a (as yet unspecified) scale length, <math>a</math>, gives,
<math> \biggl[ \chi^2 - \frac{x_0}{a} \biggr]^2 - \zeta^2 = \frac{r_c^2}{a^2} . </math>
This dimensionless expression will only describe a <math>\Chi = \mathrm{constant}</math> surface in an MF53 toroidal coordinate system if, simultaneously,
<math> \Chi = \frac{x_0}{a} ~~~~~\mathrm{and}~~~~~ \Chi^2 - 1 = \frac{r_c^2}{a^2} . </math>
That is, only if,
<math> a = (x_0^2 - r_c^2)^{1/2} . </math>
But in the above discussion we were only able to associate the dimensionless argument of the special function in CT99's CCGF expansion with the "radial" coordinate of the MF53 toroidal coordinate system by setting <math>a = R</math>, that is, only by setting the scale length equal to the cylindrical coordinate value <math>R</math> at which the potential is to be evaluated. So the surface of our torus will only align with a <math>\xi_1 = \mathrm{constant}</math> surface in a toroidal coordinate system if,
<math> R = (x_0^2 - r_c^2)^{1/2} . </math>
This is a very tight constraint that usually will not be satisfied.
Multipole Moment in Toroidal Coordinates
While it might not be interesting or useful to impose this constraint in general, it will likely be instructive to evaluate the potential at the location where this constraint is satisfied. That is, we want to evaluate the potential inside a uniform density, circular-cross-section torus at the location,
<math> \Phi[(x_0^2 - r_c^2)^{1/2},0] = - \frac{2G}{(x_0^2 - r_c^2)^{1/4}} q_0 . </math>
Since in this case the argument of <math>~Q_{-1/2}</math> can be expressed in terms of the "radial" toroidal coordinate, it is reasonable to write the relevant moment of the mass distribution, <math>~q_0</math>, entirely in terms of toroidal coordinates. Specifically,
<math> ~q_0 = a^{5/2} \int\int \biggl[ \frac{({\xi_1'}^2 - 1)^{1/2}}{\xi_1' - \xi_2'} \biggr]^{1/2} \rho(\xi_1',\xi_2') Q_{-1/2}(\xi_1') \biggl[ \frac{d\xi_1'}{(\xi_1' - \xi_2')({\xi_1'}^2 - 1)^{1/2}} \biggr] \biggl[ \frac{d\xi_2'}{(\xi_1' - \xi_2')(1-{\xi_2'}^2)^{1/2}} \biggr] . </math>
Now suppose that the density distribution is only a function of the radial coordinate, that is, suppose that <math>~\rho = \rho(\xi_1')</math>. Then the integral can be written as,
<math> ~q_0 = a^{5/2} \int \rho(\xi_1') Q_{-1/2}(\xi_1')\biggl[ \frac{d\xi_1'}{({\xi_1'}^2 - 1)^{1/4}} \biggr] \int \biggl[ \frac{d\xi_2'}{(\xi_1' - \xi_2')^{5/2}(1-{\xi_2'}^2)^{1/2}} \biggr] . </math>
Presumably the integral over <math>~d\xi_2'</math> can be completed in closed form if the density distribution fills out the entire circular cross-section, that is, if the limits on integration are <math>~-1</math> to <math>~+1</math>. Alternatively, write <math>~\xi_2'</math> in terms of <math>~\sin\theta</math> and integrate from <math>~-\tfrac{\pi}{2}</math> to <math>~\tfrac{\pi}{2}</math>. Let's do this.
|
<math>~\frac{q_0}{a^{5/2}}</math> |
<math>~=</math> |
<math>~ \int\limits_0^{\xi_1^'} \rho(\xi_1') Q_{-1/2}(\xi_1')\biggl[ \frac{d\xi_1'}{({\xi_1'}^2 - 1)^{1/4}} \biggr] \int\limits_{-1}^{1} \biggl[ \frac{d\xi_2'}{(\xi_1' - \xi_2')^{5/2}(1-{\xi_2'}^2)^{1/2}} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \int\limits_0^{\xi_1^'} \rho(\xi_1') Q_{-1/2}(\xi_1')\biggl[ \frac{d\xi_1'}{({\xi_1'}^2 - 1)^{1/4}} \biggr] \int\limits_{-\pi/2}^{\pi/2} \biggl[ \frac{d\theta}{(\xi_1' - \sin\theta)^{5/2}} \biggr] \, . </math> |
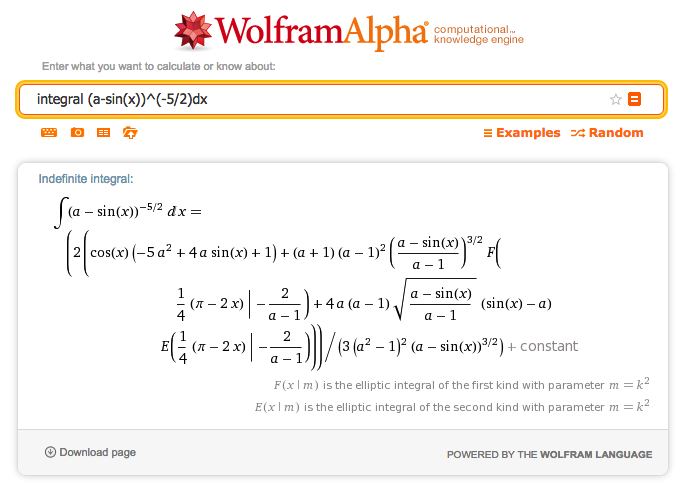
Now, using WolframAlpha's online integrator, we find …
Hence — continuing to substitute <math>~a</math> for <math>~\xi_1^'</math> — the definite integral gives,
|
<math>~\int\limits_{-\pi/2}^{\pi/2} \biggl[ \frac{d\theta}{(a - \sin\theta)^{5/2}} \biggr] </math> |
<math>~=</math> |
<math>~\biggl\{ \frac{2}{3(a^2-1)^2 (a-\sin\theta)^{3/2}} \biggl[ \cos\theta ( -5a^2 + 4a\sin\theta + 1) </math> |
|
|
|
<math>~ + (a+1)(a-1)^2 \biggl( \frac{a-\sin\theta}{a-1} \biggr)^{3/2} F\biggl(\frac{\pi - 2\theta}{4} \biggr| \frac{-2}{a-1} \biggr) </math> |
|
|
|
<math>~ + 4a(a-1)(\sin\theta-a) \biggl( \frac{a-\sin\theta}{a-1} \biggr)^{1/2} E\biggl(\frac{\pi - 2\theta}{4} \biggr| \frac{-2}{a-1} \biggr) \biggr] \biggr\}_{-\tfrac{\pi}{2}}^{\tfrac{\pi}{2}} </math> |
|
|
<math>~=</math> |
<math>~\biggl\{ \frac{2}{3(a^2-1)^2 (a-1)^{3/2}} \biggl[(a+1)(a-1)^2 \biggl( \frac{a-1}{a-1} \biggr)^{3/2} F\biggl(0\biggr| \frac{-2}{a-1} \biggr) </math> |
|
|
|
<math>~ + 4a(a-1)(1-a) \biggl( \frac{a-1}{a-1} \biggr)^{1/2} E\biggl(0 \biggr| \frac{-2}{a-1} \biggr) \biggr] \biggr\} </math> |
|
|
|
<math>~-\biggl\{ \frac{2}{3(a^2-1)^2 (a+1)^{3/2}} \biggl[(a+1)(a-1)^2 \biggl( \frac{a+1}{a-1} \biggr)^{3/2} F\biggl(\frac{\pi}{2}\biggr| \frac{-2}{a-1} \biggr) </math> |
|
|
|
<math>~ - 4a(a-1)(1+a) \biggl( \frac{a+1}{a-1} \biggr)^{1/2} E\biggl(\frac{\pi}{2} \biggr| \frac{-2}{a-1} \biggr) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl\{ \frac{2}{3(a-1)^2 (a+1)^2 (a-1)^{3/2}}\biggl[(a+1)(a-1)^2 F\biggl(0\biggr| \frac{2}{1-a} \biggr) + 4a(a-1)(1-a) E\biggl(0 \biggr| \frac{2}{1-a} \biggr) \biggr] \biggr\}</math> |
|
|
|
<math>~-\biggl\{ \frac{2}{3(a-1)^2 (a+1)^2 (a+1)^{3/2}} \biggl[(a+1)(a-1)^2 \biggl( \frac{a+1}{a-1} \biggr)^{3/2} F\biggl(\frac{\pi}{2}\biggr| \frac{2}{1-a} \biggr) </math> |
|
|
|
<math>~ - 4a(a-1)(1+a) \biggl( \frac{a+1}{a-1} \biggr)^{1/2} E\biggl(\frac{\pi}{2} \biggr| \frac{2}{1-a} \biggr) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{2}{3 (a+1) (a-1)^{3/2}} ~F\biggl(0\biggr| \frac{2}{1-a} \biggr) - \frac{8a }{3 (a+1)^2 (a-1)^{3/2}}~ E\biggl(0 \biggr| \frac{2}{1-a} \biggr) </math> |
|
|
|
<math>~-\frac{ 2 }{3 (a+1) (a-1)^{3/2}} ~ F\biggl(\frac{\pi}{2}\biggr| \frac{2}{1-a} \biggr) + \frac{8a }{3 (a+1)^{2} (a-1)^{3/2}} ~ E\biggl(\frac{\pi}{2} \biggr| \frac{2}{1-a} \biggr) </math> |
|
|
<math>~=</math> |
<math>~\frac{2}{3 (a+1) (a-1)^{3/2}} ~\biggl\{ \biggl[ F\biggl(0\biggr| \frac{2}{1-a} \biggr) - F\biggl(\frac{\pi}{2}\biggr| \frac{2}{1-a} \biggr) \biggr] - \frac{4a }{(a+1) }~ \biggl[ E\biggl(0 \biggr| \frac{2}{1-a} \biggr) - E\biggl(\frac{\pi}{2} \biggr| \frac{2}{1-a} \biggr) \biggr] \biggr\} \, . </math> |
Now, according to (for example) NIST's Digital Library of Mathematical Functions,
<math>~F(0,k) = 0</math> and <math>F(\tfrac{\pi}{2},k) = K(k) \, ,</math>
where, <math>~K(k)</math> is the complete elliptic integral of the first kind. Also, according to NIST's Digital Library of Mathematical Functions,
<math>~E(0,k) = 0</math> and <math>E(\tfrac{\pi}{2},k) = E(k) \, ,</math>
where, <math>~E(k)</math> is the complete elliptic integral of the second kind. Hence we deduce that,
|
<math>~\int\limits_{-\pi/2}^{\pi/2} \biggl[ \frac{d\theta}{(\xi_1' - \sin\theta)^{5/2}} \biggr] </math> |
<math>~=</math> |
<math>~\frac{2}{3 ({\xi_2'}^2-1) (\xi_1'-1)^{1/2}} ~\biggl[ \frac{4\xi_1' }{(\xi_1'+1) } \cdot E\biggl(\frac{2}{1-\xi_1'} \biggr) - K\biggl(\frac{2}{1-\xi_1'} \biggr) \biggr] \, , </math> |
which implies,
|
<math>~\frac{3q_0}{2a^{5/2}}</math> |
<math>~=</math> |
<math>~ \int\limits_0^{\xi_1^'} \rho(\xi_1') Q_{-1/2}(\xi_1')\biggl[ \frac{d\xi_1'}{({\xi_1'}^2 - 1)^{5/4} (\xi_1'-1)^{1/2}} \biggr] ~\biggl[ \frac{4\xi_1' }{(\xi_1'+1) } \cdot E\biggl(\frac{2}{1-\xi_1'} \biggr) - K\biggl(\frac{2}{1-\xi_1'} \biggr) \biggr] \, . </math> |
Next, we might as well also insert the NIST relation,
<math>Q_{-1/2}(\cos\theta) = K\biggl[\cos(\tfrac{1}{2}\theta)\biggr]\, .</math>
Older, Apparently Irrelevant Material
If we subtract "1" from both sides of this expression, the right-hand-side (RHS) takes on a familiar form:
|
<math> \chi_\mathrm{CT99}-1 </math> |
<math>=</math> |
<math> \frac{1}{2R R'} \biggl[ R^2 + {R'}^2 + (z - z')^2 - 2 R R' \biggr] </math> |
|
|
<math>=</math> |
<math> \frac{1}{2R R'} \biggl[ (R - R')^2 + (z - z')^2 \biggr] . </math> |
It appears as though the quantity, <math>[2R R'(\chi_\mathrm{CT99}-1)]^{1/2}</math>, is the radius <math>r_c</math> of a circle whose center is located at either <math>(R,z)</math> or <math>(R',z')</math>, that is, whose center is shifted off the origin of a cylindrical coordinate system. I'm not yet sure how/if we can benefit from recognizing this association.
Case A: Suppose we associate <math>R'</math> with the center of a toroidal cross-section and, at the same time, associate <math>R</math> with the inner edge of a particular toroidal cross-section that is associated with the toroidal coordinate <math>\xi_1</math>. We know that the scale-length <math>a</math> that is associated with the chosen toroidal coordinate system must be given by the ratio,
<math> a = \frac{R'}{\chi_0} . </math>
[NOTE: As I'm doing this, I'm realizing that it may be wiser to associate <math>a</math> directly with the coordinate location <math>R'</math>. But let's play this out first and see.]
Then it also will be true that,
<math> a = \frac{R}{\chi_\mathrm{inner}} = R \biggl[ \frac{\xi_1+1}{\xi_1 - 1} \biggr]^{1/2}. </math>
Hence, we conclude that,
<math>
\mathrm{Case~A:}~~~~~\frac{R}{R'} = \frac{\chi_\mathrm{inner}}{\chi_0} = \biggl[\frac{\xi_1 - 1}{\xi_1 + 1}\biggr]^{1/2} \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1} = \frac{(\xi_1 - 1)}{\xi_1}
</math>
<math> \Rightarrow~~~~~ \xi_1 = \biggl[1 - \frac{R}{R'} \biggr]^{-1} . </math>
What, then, is the expression for the scale-length <math>a</math> in terms of just <math>R</math> and <math>R'</math>? Well ...
<math> \xi_1 + 1 = \frac{1}{1-(R/R')} +1 = \frac{2 - R/R'}{1-(R/R')} , </math>
and
<math> \xi_1 - 1 = \frac{1}{1-(R/R')} -1 = \frac{R/R'}{1-(R/R')} . </math>
Hence,
<math> a = R \biggl[ \frac{2 - R/R'}{R/R'} \biggr]^{1/2} = ( 2RR' - R^2 )^{1/2}. </math>
Case B: On the other hand, if we associate <math>R'</math> directly with <math>a</math>, then we conclude,
<math>
\mathrm{Case~B:}~~~~~\frac{R}{R'} = \chi_\mathrm{inner} = \biggl[\frac{\xi_1 - 1}{\xi_1 + 1}\biggr]^{1/2} .
</math>
<math>
\Rightarrow~~~~~ (\xi_1 + 1)\biggl(\frac{R}{R'}\biggr)^2 = \xi_1 - 1 .
</math>
<math>
\Rightarrow~~~~~ \xi_1 \biggl[ 1 - \biggl(\frac{R}{R'}\biggr)^2 \biggr] = \biggl[1 + \biggl(\frac{R}{R'}\biggr)^2 \biggr].
</math>
<math> \Rightarrow~~~~~ \xi_1 = \biggl[1 + \biggl(\frac{R}{R'}\biggr)^2 \biggr]\biggl[ 1 - \biggl(\frac{R}{R'}\biggr)^2 \biggr] ^{-1}. </math>
References
- Morse, P.M. & Feshmach, H. 1953, Methods of Theoretical Physics — Volumes I and II
- Cohl, H.S. & Tohline, J.E. 1999, ApJ, 527, 86-101
- Cohl, H.S., Rau, A.R.P., Tohline, J.E., Browne, D.A., Cazes, J.E. & Barnes, E.I. 2001, Phys. Rev. A, 64, 052509

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |