Polytropic & Isothermal Tori

Overview

Here we will focus on the analysis of the structure self-gravitating tori that are composed of compressible — specifically, polytropic and isothermal — fluids as presented in a series of papers by Jeremiah P. Ostriker:

J. Ostriker (1964, ApJ, 140, 1056) — The Equilibrium of Polytropic and Isothermal Cylinders
J. Ostriker (1964, ApJ, 140, 1067) — The Equilibrium of Self-Gravitating Rings
J. Ostriker (1964, ApJ, 140, 1529) — On the Oscillations and the Stability of a Homogeneous Compressible Cylinder
J. Ostriker (1965, ApJ Supplements, 11, 167) — Cylindrical Emden and Associated Functions

I believe that much, if not all, of this material was drawn from Ostriker's doctoral dissertation research at the University of Chicago (and Yerkes Observatory) under the guidance of S. Chandrasekhar.

Coordinate System

Basics

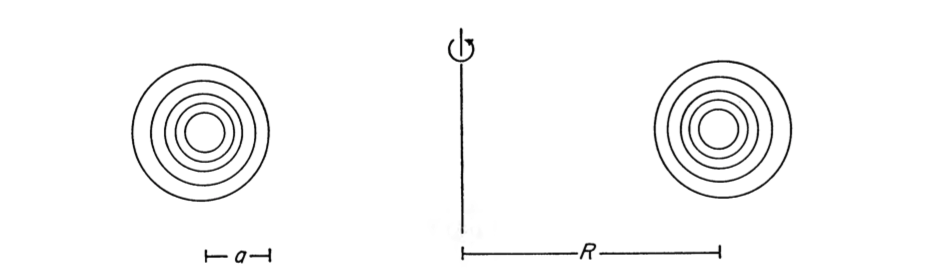
In §IIa of Paper II, Ostriker defines a set of orthogonal coordinates, <math>~(r,\phi,\theta)</math>, that is related to the traditional Cartesian coordinate system, <math>~(x,y,z)</math>, via the relations,

<math>~x</math>	<math>~=</math>	<math>~(R+r\cos\phi)\cos\theta \, ,</math>
<math>~y</math>	<math>~=</math>	<math>~(R+r\cos\phi)\sin\theta \, ,</math>
<math>~z</math>	<math>~=</math>	<math>~r\sin\phi \, .</math>

As Ostriker states, "The coordinate <math>~r</math> is the distance from a reference circle of radius <math>~R</math> (later chosen to be the major radius of the ring) …" The angle, <math>~\theta</math>, plays the role of the azimuthal angle, as is familiar in both cylindrical and spherical coordinates, while, here, <math>~\phi</math> is a meridional-plane polar angle measured counterclockwise from the equatorial plane. For axisymmetric systems, there will be no dependence on the azimuthal angle, so the pair of relevant coordinates in the meridional plane are,

<math>~\varpi \equiv (x^2+y^2)^{1 / 2}</math>

and,

Figure 1 extracted without modification from p. 1077 of J. P. Ostriker (1964; Paper II)

"The Equilibrium of Self-Gravitating Rings"

ApJ, vol. 140, pp. 1067-1087 © American Astronomical Society

For later reference, we note that (see eq. 3 of Paper II) the corresponding line element is,

<math>~\delta s^2</math>

<math>~ \delta r^2 + r^2 \delta\phi^2 + (R+r\cos\phi)^2\delta\theta^2 \, , </math>

which means that the relevant scale factors for the adopted coordinate system, <math>~(r,\phi,\theta)</math>, are

and the relevant differential volume element is,

<math>~h_1 h_2 h_3 dr d\phi d\theta = r(R+r\cos\phi) dr d\phi d\theta\, . </math>

Relationship to Toroidal Coordinate

Referring back to our separate discussion of the basic elements of a toroidal coordinate system, we know that, the meridional-plane toroidal coordinates <math>~(\eta,\theta)</math> are related to traditional meridional-plane cylindrical coordinate pair <math>~(\varpi,z)</math> via the expressions,

<math>~\frac{\varpi}{R}</math>

<math>~\frac{\sinh\eta}{\cosh\eta - \cos\theta} \, ,</math>

and,

<math>~\frac{\sin\theta}{\cosh\eta - \cos\theta} \, ,</math>

assuming that the cylindrical-coordinate location of the anchor ring is <math>~(\varpi,z) = (R,0)</math>. Let's determine how to transform between these two sets of coordinate pairs.

Independent Exploration

First, eliminating reference to Ostriker's "polar angle" <math>~\phi</math>, we see that,

<math>~\frac{r^2}{R^2} </math>	<math>~=</math>	<math>~\biggl(\frac{\varpi}{R} - 1 \biggr)^2 + \biggl(\frac{z}{R}\biggr)^2</math>
	<math>~=</math>	<math>~\biggl[ \frac{\sinh\eta}{\cosh\eta - \cos\theta} - 1 \biggr]^2 + \biggl[ \frac{\sin\theta}{\cosh\eta - \cos\theta} \biggr]^2</math>
	<math>~=</math>	<math>~\biggl[ \frac{(\sinh\eta - \cosh\eta + \cos\theta)^2 + \sin^2\theta}{(\cosh\eta - \cos\theta)^2} \biggr] \, .</math>

Then, eliminating reference to Ostriker's radial coordinate <math>~r</math>, we find,

<math>~\cot\phi</math>	<math>~=</math>	<math>~\frac{\varpi/R - 1}{z/R}</math>
	<math>~=</math>	<math>~\frac{\sinh\eta - \cosh\eta + \cos\theta}{\sin\theta}</math>
	<math>~=</math>	<math>~\cot\theta + \frac{\sinh\eta - \cosh\eta }{\sin\theta} \, .</math>

Now let's try to derive the alternate transformation. We'll start by eliminating the "polar angle" in toroidal coordinates.

<math>~\cosh\eta - \cos\theta</math>	<math>~=</math>	<math>~\frac{\sinh\eta}{\varpi/R}</math>
<math>~\Rightarrow ~~~ \cos\theta</math>	<math>~=</math>	<math>~\cosh\eta - \frac{\sinh\eta}{\varpi/R} \, .</math>

The same relation also implies that,

<math>~\frac{z}{R}</math>	<math>~=</math>	<math>~\biggl( \frac{\varpi}{R}\biggr) \frac{\sin\theta}{\sinh\eta}</math>
<math>~\Rightarrow ~~~ \sin\theta </math>	<math>~=</math>	<math>~\frac{z}{R}\biggl( \frac{\varpi}{R}\biggr)^{-1} \sinh\eta \, .</math>

Together, then, we have,

<math>~1 = \sin^2\theta + \cos^2\theta</math>	<math>~=</math>	<math>~ \biggl[ \frac{z}{R}\biggl( \frac{\varpi}{R}\biggr)^{-1} \sinh\eta \biggr]^2 + \biggl[ \cosh\eta - \frac{\sinh\eta}{\varpi/R} \biggr]^2 </math>
	<math>~=</math>	<math>~ \biggl( \frac{\varpi}{R}\biggr)^{-2} \biggl[ \frac{z}{R} \cdot \sinh\eta \biggr]^2 + \biggl(\frac{\varpi}{R}\biggr)^{-2} \biggl[ \frac{\varpi}{R}\cdot \cosh\eta - \sinh\eta \biggr]^2 </math>
<math>~\Rightarrow ~~~ \biggl( \frac{\varpi}{R}\biggr)^{2} </math>	<math>~=</math>	<math>~ \biggl[ \frac{z}{R} \cdot \sinh\eta \biggr]^2 + \biggl[ \frac{\varpi}{R}\cdot \cosh\eta - \sinh\eta \biggr]^2 \, . </math>

Alternatively, in an attempt to eliminate <math>~\eta</math>, we have,

<math>~\sinh\eta </math>	<math>~=</math>	<math>~\frac{\varpi}{R}\biggl( \frac{z}{R}\biggr)^{-1} \sin\theta </math>
<math>~\Rightarrow ~~~ \cosh\eta = \biggl[ 1 + \sinh^2\eta\biggr]^{1 / 2} </math>	<math>~=</math>	<math>~\biggl[ 1 + \biggl(\frac{\varpi}{R}\biggr)^2 \biggl( \frac{z}{R}\biggr)^{-2} \sin^2\theta \biggr]^{1 / 2} </math>
	<math>~=</math>	<math>~\biggl( \frac{z}{R}\biggr)^{-1} \biggl[ \biggl( \frac{z}{R}\biggr)^{2} + \biggl(\frac{\varpi}{R}\biggr)^2 \sin^2\theta \biggr]^{1 / 2} \, .</math>

But, also,

<math>~\cosh\eta</math>	<math>~=</math>	<math>~\biggl( \frac{z}{R} \biggr)^{-1} \sin\theta + \cos\theta</math>
<math>~\Rightarrow ~~~\biggl[ \biggl( \frac{z}{R}\biggr)^{2} + \biggl(\frac{\varpi}{R}\biggr)^2 \sin^2\theta \biggr]^{1 / 2}</math>	<math>~=</math>	<math>~\sin\theta + \biggl( \frac{z}{R}\biggr) \cos\theta</math>
<math>~\Rightarrow ~~~\biggl( \frac{z}{R}\biggr)^{2} + \biggl(\frac{\varpi}{R}\biggr)^2 \sin^2\theta </math>	<math>~=</math>	<math>~\sin^2\theta + 2\biggl( \frac{z}{R}\biggr)\sin\theta \cos\theta + \biggl( \frac{z}{R}\biggr)^2 \cos^2\theta</math>
<math>~\Rightarrow ~~~\biggl( \frac{z}{R}\biggr)^{2}\biggl[1-\cos^2\theta \biggr] </math>	<math>~=</math>	<math>~\sin^2\theta\biggl[1 - \biggl(\frac{\varpi}{R}\biggr)^2 \biggr] + 2\biggl( \frac{z}{R}\biggr)\sin\theta \cos\theta </math>
<math>~\Rightarrow ~~~0 </math>	<math>~=</math>	<math>~\sin^2\theta\biggl[1 - \biggl(\frac{\varpi}{R}\biggr)^2 - \biggl( \frac{z}{R}\biggr)^{2}\biggr] + 2\biggl( \frac{z}{R}\biggr)\sin\theta \cos\theta </math>
<math>~\Rightarrow ~~~\biggl[1 - \biggl(\frac{\varpi}{R}\biggr)^2 - \biggl( \frac{z}{R}\biggr)^{2}\biggr] </math>	<math>~=</math>	<math>~ - 2\biggl( \frac{z}{R}\biggr) \cot\theta </math>
<math>~\Rightarrow ~~~ \cot\theta </math>	<math>~=</math>	<math>~- \frac{1}{2}\biggl( \frac{z}{R}\biggr)^{-1} \biggl[1 - \biggl(\frac{\varpi}{R}\biggr)^2 - \biggl( \frac{z}{R}\biggr)^{2}\biggr] \, .</math>

Now that I think about it, this is all a bit silly because from the basic elements of a toroidal coordinate system we already know how to shift from cylindrical to toroidal coordinates.

Back to Basics

Mapping the other direction [see equations 2.13 - 2.15 of Wong (1973) ], we have,

<math>~\eta</math>	<math>~=</math>	<math>~\ln\biggl(\frac{r_1}{r_2} \biggr) \, ,</math>
<math>~\cos\theta</math>	<math>~=</math>	<math>~\frac{(r_1^2 + r_2^2 - 4R^2)}{2r_1 r_2} \, ,</math>

where,

<math>~\equiv</math>

<math>~[\varpi + R]^2 + z^2 \, ,</math>

and

<math>~\equiv</math>

<math>~[\varpi - R]^2 + z^2 \, ,</math>

and <math>~\theta</math> has the same sign as <math>~z</math>. Now, given that Ostriker's <math>~(r,\phi)</math> coordinates are related to cylindrical coordinates via the expressions,

<math>~\varpi </math>

and

we can write,

<math>~r_1^2</math>	<math>~=</math>	<math>~[2R + r\cos\phi]^2 + r^2\sin^2\phi </math>
	<math>~=</math>	<math>~4R^2 + 4Rr\cos\phi + r^2 \, ;</math>

and,

Hence,

<math>~\cos\theta</math>	<math>~=</math>	<math>~ \frac{1}{2r[4R^2 + 4Rr\cos\phi + r^2]^{1 / 2}} \biggl[ 4Rr\cos\phi + 2r^2 \biggr] </math>
	<math>~=</math>	<math>~ \frac{2R\cos\phi + r }{[4R^2 + 4Rr\cos\phi + r^2]^{1 / 2}} \, ; </math>
<math>~e^{2\eta}</math>	<math>~=</math>	<math>~ \frac{ 4R^2 + 4Rr\cos\phi + r^2 }{r^2} </math>
	<math>~=</math>	<math>~ 4\biggl( \frac{R}{r}\biggr)^2 + 4\biggl(\frac{R}{r}\biggr)\cos\phi + 1 \, . </math>

Summary

<math>~\frac{r^2}{R^2} </math>	<math>~=</math>	<math>~\biggl[ \frac{(\sinh\eta - \cosh\eta + \cos\theta)^2 + \sin^2\theta}{(\cosh\eta - \cos\theta)^2} \biggr] </math>
<math>~\cot\phi</math>	<math>~=</math>	<math>~\cot\theta + \frac{\sinh\eta - \cosh\eta }{\sin\theta} </math>

<math>~e^{2\eta}</math>	<math>~=</math>	<math>~ 4\biggl( \frac{R}{r}\biggr)^2 + 4\biggl(\frac{R}{r}\biggr)\cos\phi + 1 </math>
<math>~\cos\theta</math>	<math>~=</math>	<math>~ \frac{2R\cos\phi + r }{[4R^2 + 4Rr\cos\phi + r^2]^{1 / 2}} </math>

Second Attempt

Single Offset Circle

Now an off-center circle whose major and minor radii are, respectively, <math>~(\varpi_0,d)</math>, will be described by the expression,

<math>~ (\varpi - \varpi_0)^2 + z^2 \, . </math>

where both <math>~d</math> and <math>~\varpi_0</math> are held constant while mapping out the variation of <math>~z</math> with <math>~\varpi</math>. If we acknowledge that, in general, <math>~\varpi_0 \ne R_\mathrm{JPO}</math>, then we know how <math>~r</math> varies with <math>~\phi</math> via the relation,

<math>~d^2</math>	<math>~=</math>	<math>~ \biggl[ R_\mathrm{JPO} + r\cos\phi - \varpi_0\biggr]^2 + r^2\sin^2\phi </math>
	<math>~=</math>	<math>~ (R_\mathrm{JPO}-\varpi_0)^2 + 2\biggl[ (R_\mathrm{JPO}-\varpi_0) r\cos\phi \biggr] +r^2 </math>
<math>~\Rightarrow ~~~ 0 </math>	<math>~=</math>	<math>~ r^2 + 2r\biggl[ (R_\mathrm{JPO}-\varpi_0) \cos\phi \biggr] + \biggl[(R_\mathrm{JPO}-\varpi_0)^2 - d^2\biggr] </math>
<math>~\Rightarrow ~~~ r </math>	<math>~=</math>	<math>~ \frac{1}{2}\biggl\{ - 2\biggl[ (R_\mathrm{JPO}-\varpi_0) \cos\phi \biggr] \pm \sqrt{ 4\biggl[ (R_\mathrm{JPO}-\varpi_0) \cos\phi \biggr]^2 - 4\biggl[(R_\mathrm{JPO}-\varpi_0)^2 - d^2\biggr] } \biggr\} </math>
	<math>~=</math>	<math>~ \frac{1}{2}\biggl\{ 2\biggl[ (\varpi_0 - R_\mathrm{JPO}) \cos\phi \biggr] \pm \sqrt{ 4\biggl[ (\varpi_0 - R_\mathrm{JPO}) \cos\phi \biggr]^2 - 4\biggl[(\varpi_0 - R_\mathrm{JPO})^2 - d^2\biggr] } \biggr\} </math>
<math>~\Rightarrow~~~ \frac{r}{ (\varpi_0 - R_\mathrm{JPO}) }</math>	<math>~=</math>	<math>~ \cos\phi \pm \sqrt{ \cos^2\phi - 1 + d^2 (\varpi_0 - R_\mathrm{JPO})^{-2} } </math>
	<math>~=</math>	<math>~ \cos\phi \pm \sqrt{ d^2 (\varpi_0 - R_\mathrm{JPO})^{-2}-\sin^2\phi } </math>

In order to align this expression with the terminology (and variable labels) that we use in the context of a toroidal coordinate system, we associate the radius of the anchor ring as <math>~R_\mathrm{JPO}\leftrightarrow a</math>, and we associate the major radius of each circular torus as <math>~\varpi_0 \leftrightarrow R_0</math>. We therefore have,

<math>~\frac{r}{ (R_0-a) }</math>	<math>~=</math>	<math>~ \cos\phi \pm \sqrt{ d^2 (R_0-a)^{-2}-\sin^2\phi } </math>
<math>~\Rightarrow ~~~ \frac{r}{a}</math>	<math>~=</math>	<math>~\biggl(\frac{R_0}{a}-1 \biggr) \biggl[ \cos\phi \pm \sqrt{ \biggl(\frac{d}{a}\biggr)^2 \biggl(\frac{R_0}{a}-1 \biggr)^{-2}-\sin^2\phi } \biggr] </math>

and, the coordinates of points along the surface of the torus <math>~(\varpi,z)</math> are provided by the expressions,

<math>~\varpi</math>	<math>~=</math>	<math>~ a + (R_0 - a)\cos\phi \biggl[ \cos\phi \pm \sqrt{ d^2 (R_0 - a)^{-2}-\sin^2\phi } \biggr] </math>
<math>~z</math>	<math>~=</math>	<math>~ (R_0 - a)\sin\phi \biggl[ \cos\phi \pm \sqrt{ d^2 (R_0 - a)^{-2}-\sin^2\phi } \biggr] </math>

We have tested this pair of expressions using Excel and have successfully demonstrated that they do, indeed, trace out a circle of radius, <math>~d</math>, whose center is offset from the symmetry axis by a distance, <math>~R_0</math>.

Set of Circles Whose Offset Increases With Circle Diameter

A set of nested off-center circles will be described by allowing <math>~R_0 = R_0(d)</math>, that is, by having the off-set distance, <math>~R_0</math>, vary with the size of the circle, <math>~d</math>. The above prescription for the normalized "coordinate" <math>~r/a</math> will work for any prescribed <math>~R_0(d)</math> function.

But a particular <math>~R_0(d)</math> function is demanded if we want this derived prescription to represent the behavior of toroidal coordinates. In a toroidal coordinate system, a specification of the value of the "radial" coordinate, <math>~\eta</math>, automatically dictates the ratio <math>~R_0/d</math>; but we are not at liberty to separately define the value of the difference, <math>~(R_0 - d)</math>. Instead, we must enforce the toroidal-coordinate relation,

<math>~a^2</math>	<math>~=</math>	<math>~R_0^2 - d^2</math>
<math>~\Rightarrow~~~ \frac{R_0}{a}-1</math>	<math>~=</math>	<math>~\biggl[ 1 + \delta^2\biggr]^{1 / 2} -1 \, ,</math>

where we have adopted the shorthand notation, <math>~\delta\equiv d/a</math>. Hence,

<math>~[ \sqrt{1+\delta^2} -1 ] \{ \cos\phi \pm [\delta^2 ( \sqrt{1+\delta^2} -1 )^{-2}-\sin^2\phi ]^{1 / 2} \} </math>

Now, in a toroidal coordinate system, there is a similar "radial" coordinate, <math>~\eta</math>, whose value varies with distance from the anchor ring of radius, <math>~a</math>. Its value depends on both <math>~R_0</math> and <math>~d</math> via the relation,

This means that,

<math>~\cosh\eta</math>	<math>~=</math>	<math>~\frac{1}{\delta}\biggl(\frac{R_0}{a}\biggr) = \frac{\sqrt{1+\delta^2}}{\delta} </math>
<math>~\Rightarrow~~~ \delta^2 \cosh^2\eta</math>	<math>~=</math>	<math>~1 + \delta^2</math>
<math>~\Rightarrow~~~ \delta^2 </math>	<math>~=</math>	<math>~\frac{1}{\cosh^2\eta - 1} = \frac{1}{\sinh^2\eta} </math>
<math>~\Rightarrow~~~ \sqrt{1 + \delta^2} </math>	<math>~=</math>	<math>~\biggl[1 + \frac{1}{\sinh^2\eta} \biggr]^{1 / 2} = \coth\eta \, ,</math>

which also means that,

<math>~[ \coth\eta -1 ] \biggl\{ \cos\phi \pm \biggl[ ( \cosh\eta -\sinh\eta )^{-2} -\sin^2\phi \biggr]^{1 / 2} \biggr\} \, . </math>

Case of Small Offset

Another way to look at this issue is to go back to the expression,

<math>~d^2</math>	<math>~=</math>	<math>~ (R_\mathrm{JPO}-\varpi_0)^2 + 2\biggl[ (R_\mathrm{JPO}-\varpi_0) r\cos\phi \biggr] +r^2 </math>
<math>~\Rightarrow ~~~ \delta^2</math>	<math>~=</math>	<math>~\biggl(\frac{r}{a}\biggr)^2 + \frac{r}{a}\biggl[ 2\biggl(1 - \frac{R_0}{a}\biggr)\biggr] \cos\phi + \biggl(1 - \frac{R_0}{a}\biggr)^2 </math>

and assume that, while still dependent on the radial coordinate, the dimensionless offset is small. That is, assume that,

<math>~\Delta(\delta) \equiv 1 - \frac{R_0(\delta)}{a} \ll 1 \, .</math>

In this case, we can write,

<math>~ \delta^2</math>

<math>~\approx</math>

<math>~\biggl(\frac{r}{a}\biggr)^2 + 2\Delta(\delta) \biggl( \frac{r}{a} \biggr) \cos\phi +\cancelto{0}{\Delta^2(\delta)} \, . </math>

And differentiating both sides of the expression with respect to <math>~r/a</math> gives,

<math>~\approx</math>

<math>~2\biggl(\frac{r}{a}\biggr) + 2\Delta(\delta) \cos\phi</math>

COMMENT by Tohline (15 August 2018): I'm not sure that this is leading where I had hoped. I am gearing up to draw a comparison between these last expressions and eq. (74) in Ostriker's (1964) Paper II.

Gravitational Potential

Potential of a Thin Hoop

In §IIb of his Paper II, Ostriker (1964) derives an expression for the gravitational potential of a torus in the Thin Ring approximation, beginning specifically with the integral form of the Poisson equation that is widely referred to in the astrophysics community as an expression for the,

Scalar Gravitational Potential
<math>~ \Phi(\vec{x})</math>	<math>~\equiv</math>	<math>~ -G \iiint \frac{\rho(\vec{x}^{~'})}{\|\vec{x}^{~'} - \vec{x}\|} d^3x^' \, .</math>
[BT87], p. 31, Eq. (2-3) [EFE], §10, p. 17, Eq. (11) [T78], §4.2, p. 77, Eq. (12)

(Note: Consistent with the usage favored by his doctoral dissertation advisor in [EFE], throughout his collection of 1964 papers Ostriker adopts a different sign convention as well as a different variable name to represent the gravitational potential.) Employing Ostriker's adopted coordinate system, and recognizing that, "the distance between the point of integration <math>~(0,0,\theta^')</math> and the point of observation <math>~(r,\phi,0)</math>" is,

<math>~\|\vec{x}^{~'} - \vec{x}\|</math>	<math>~=</math>	<math>~[4R(R+r\cos\phi) \sin^2(\tfrac{1}{2}\theta^') + r^2]^{1 / 2} \, ,</math>
Ostriker's (1964) Paper II, p. 1070, Eq. (21)

this expression for the gravitational potential becomes,

<math>~ \Phi(r,\phi)</math>	<math>~=</math>	<math>~ -G \int \int \rho(r^',\phi^') r^' (R+r^'\cos\phi^') dr^' d\phi^' \int \frac{d\theta^'}{[4R(R+r\cos\phi) \sin^2(\tfrac{1}{2}\theta^') + r^2]^{1 / 2} } </math>
	<math>~=</math>	<math>~ -G (2\sigma R) \int_0^\pi \frac{d\theta^'}{[4R(R+r\cos\phi) \sin^2(\tfrac{1}{2}\theta^') + r^2]^{1 / 2} } </math>
	<math>~=</math>	<math>~ -\frac{4G \sigma R}{r} \int_0^\pi \frac{\tfrac{1}{2}d\theta^'}{[1 +n^2\sin^2(\tfrac{1}{2}\theta^')]^{1 / 2} } </math>
	<math>~=</math>	<math>~ -\frac{4G \sigma R}{r} \biggl[ \frac{K(k)}{\sqrt{n^2+1}} \biggr] \, ,</math>
Ostriker's (1964) Paper II, p. 1070, Eq. (22)

where,

<math>~n^2 \equiv \frac{4R(R+r\cos\phi)}{r^2}</math>	and	<math>~k \equiv \biggl[ \frac{n^2}{n^2+1} \biggr]^{1 / 2} \, .</math>
Ostriker's (1964) Paper II, p. 1070, Eq. (23)

Mapping back to cylindrical coordinates, for the moment, we recognize that,

<math>~r^2</math>	<math>~=</math>	<math>~(\varpi - R)^2 + z^2</math>
<math>~\Rightarrow ~~~ n^2</math>	<math>~=</math>	<math>~\frac{4R\varpi}{(\varpi - R)^2 + z^2}</math>
<math>~\Rightarrow ~~~ n^2 + 1</math>	<math>~=</math>	<math>~\frac{4R\varpi + (\varpi - R)^2 + z^2}{(\varpi - R)^2 + z^2} = \frac{(\varpi + R)^2 + z^2}{(\varpi - R)^2 + z^2} \, .</math>

Acknowledging as well that the mass of Ostriker's "thin hoop" is, <math>~M = 2\pi \sigma R</math>, his expression for the potential becomes,

<math>~\Phi(\varpi,z)</math>

<math>~ -\frac{2G M}{\pi} \biggl[ \frac{K(k)}{\sqrt{(\varpi + R)^2 + z^2}} \biggr] \, ,</math>

where,

<math>~\biggl[ \frac{4R\varpi}{(\varpi + R)^2 + z^2} \biggr]^{1 / 2} \, .</math>

After adopting the variable association, <math>~R \leftrightarrow a</math>, it is clear that Ostriker's derived expression is identical to the Key Equation that we have identified elsewhere as providing the,

Gravitational Potential in the Thin Ring (TR) Approximation

	<math>~\Phi_\mathrm{TR}(\varpi,z)</math>	<math>~=</math>	<math>~-\biggl[ \frac{2GM}{\pi } \biggr]\frac{K(k)}{\sqrt{(\varpi+a)^2 + z^2}}</math>
<math>\mathrm{where:}~~~k \equiv \{4\varpi a/[ (\varpi+a)^2 + z^2]\}^{1 / 2}</math>

Series Expansion

In the context of Ostriker's expression for the potential, we see that,

<math>~(k')^{-2} \equiv \biggl[ \frac{1}{1-k^2}\biggr]= n^2 + 1</math>	<math>~=</math>	<math>~ \frac{4R(R+r\cos\phi)}{r^2} + 1 </math>
	<math>~=</math>	<math>~\biggl( \frac{2R}{r}\biggr)^2 \biggl[ 1 + \frac{r}{R}\cos\phi + \biggl(\frac{r}{2R}\biggr)^2\biggr] \, . </math>

Hence, in the vicinity of the ring where <math>~r/R \ll 1</math> and <math>~k'</math> is a "small parameter," we can draw on the binomial theorem and write,

<math>~(k')^m</math>	<math>~=</math>	<math>~\frac{1}{2^m}\biggl( \frac{r}{R}\biggr)^{m} \biggl[ 1 + \frac{r}{R}\cos\phi + \biggl(\frac{r}{2R}\biggr)^2\biggr]^{-m / 2} </math>
	<math>~=</math>	<math>~\frac{1}{2^m}\biggl( \frac{r}{R}\biggr)^{m} \biggl\{ 1 -\frac{m}{2} \biggl[\frac{r}{R}\cos\phi + \biggl(\frac{r}{2R}\biggr)^2 \biggr] + \frac{1}{2}\biggl[ -\frac{m}{2}\biggl( -\frac{m}{2}-1\biggr) \biggr]\biggl[\frac{r}{R}\cos\phi + \biggl(\frac{r}{2R}\biggr)^2 \biggr]^2 + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr\} </math>
	<math>~=</math>	<math>~\frac{1}{2^m}\biggl( \frac{r}{R}\biggr)^{m} \biggl\{ 1 - \biggl(\frac{m}{2}\biggr) \frac{r}{R}\cos\phi - \biggl(\frac{m}{2^3}\biggr) \biggl(\frac{r}{R}\biggr)^2 + \frac{m}{4}\biggl( \frac{m}{2} + 1\biggr) \biggl[\frac{r}{R}\cos\phi \biggr]^2 + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr\} \, . </math>

Note, in particular, that,

<math>~\frac{1}{k'}</math>	<math>~=</math>	<math>~2\biggl( \frac{R}{r}\biggr) \biggl\{ 1 + \biggl(\frac{1}{2}\biggr) \frac{r}{R}\cos\phi + \biggl(\frac{1}{2^3}\biggr) \biggl(\frac{r}{R}\biggr)^2 - \frac{1}{2^3} \biggl[\frac{r}{R}\cos\phi \biggr]^2 + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr\} </math>
	<math>~=</math>	<math>~\frac{2R}{r} \biggl\{ 1 + \frac{1}{2} \biggl(\frac{r}{R}\biggr)\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 \sin^2\phi + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr\} \, ; </math>
<math>~k'</math>	<math>~=</math>	<math>~ \frac{r}{2R} \biggl[ 1 - \frac{r}{2R}\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 ( 3 \cos^2\phi -1 ) + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr] \, ; </math> and,
<math>~(k')^2</math>	<math>~=</math>	<math>~ \frac{1}{2^2}\biggl( \frac{r}{R}\biggr)^{2} \biggl[ 1 - \frac{r}{R}\cos\phi + \frac{1}{2^2} \biggl(\frac{r}{R}\biggr)^2 (4\cos^2\phi - 1 ) + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr] \, . </math>

Next we recognize that the following series expansion for the complete elliptic integral of the first kind — written in terms of the small parameter, <math>~k'</math> — appears, for example, as eq. (8.113.3) in the Fourth Edition of Gradshteyn & Ryzhik (1965):

<math>~K(k)</math>	<math>~=</math>	<math>~ \ln \frac{4}{k^'} + \frac{1}{2^2}\biggl( \ln\frac{4}{k^'} - \frac{2}{1\cdot 2} \biggr){k'}^2 + \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 \biggl( \ln\frac{4}{k^'} - \frac{2}{1\cdot 2} - \frac{2}{3\cdot 4} \biggr){k'}^4 </math>
		<math>~ + \biggl( \frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\biggr)^2 \biggl( \ln\frac{4}{k^'} - \frac{2}{1\cdot 2} - \frac{2}{3\cdot 4} - \frac{2}{5\cdot 6} \biggr){k'}^6 + \cdots </math>
	<math>~=</math>	<math>~ \ln \frac{4}{k^'} + \frac{1}{2^2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 + \frac{3^2}{2^6} \biggl( \ln\frac{4}{k^'} - \frac{7}{6} \biggr){k'}^4 + \frac{5^2}{2^8} \biggl( \ln\frac{4}{k^'} - \frac{37}{30} \biggr){k'}^6 + \cdots </math>

[This series expansion — up through the term <math>~\mathcal{O}(k'^4)</math> — appears as equation 24 in Ostriker's (1964) Paper II.] Put together, then, Ostriker's expression for the gravitational potential in the thin ring approximation becomes,

<math>~\Phi_\mathrm{TR}(r,\phi)\biggr\|_\mathrm{JPO}</math>	<math>~=</math>	<math>~ -\frac{2GM}{\pi r} k' K(k) </math>
	<math>~=</math>	<math>~ -\frac{2GM}{\pi r} \biggl[ k' \ln \frac{4}{k^'} + \frac{1}{2^2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^3 + \cdots \biggr] </math>
	<math>~=</math>	<math>~ -\frac{2GM}{\pi r} \biggl\{ \ln \frac{4}{k^'} \biggl[ k' + \frac{k'^3}{2^2} \biggr] - \frac{1}{4} k'^3 + \mathcal{O}\biggl( \frac{r^5}{R^5}\biggr) \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{2GM}{\pi r} \biggl\{ \ln \frac{4}{k^'} \biggl[ k' + \frac{k'^3}{2^2} \biggr] - \frac{1}{2^5}\biggl( \frac{r}{R}\biggr)^{3} \biggl[ 1 - \biggl(\frac{3}{2}\biggr) \frac{r}{R}\cos\phi - \biggl(\frac{3}{2^3}\biggr) \biggl(\frac{r}{R}\biggr)^2 + \frac{3}{4}\biggl( \frac{3}{2} + 1\biggr) \biggl(\frac{r}{R}\cos\phi \biggr)^2 + \mathcal{O}\biggl( \frac{r^3}{R^3}\biggr) \biggr] + \mathcal{O}\biggl( \frac{r^5}{R^5}\biggr) \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{2GM}{\pi R} \biggl\{ \ln \frac{4}{k^'} \biggl[ k' + \frac{k'^3}{2^2} \biggr] \frac{R}{r} - \frac{1}{2^5}\biggl( \frac{r}{R}\biggr)^{2} \biggl[ 1 - \biggl(\frac{3}{2}\biggr) \frac{r}{R}\cos\phi + \mathcal{O}\biggl( \frac{r^2}{R^2}\biggr) \biggr] + \mathcal{O}\biggl( \frac{r^5}{R^5}\biggr) \biggr\}\, , </math>

where, again, we have recognized that the mass of the thin hoop is, <math>~M = 2\pi\sigma R</math>. Now,

<math>~ k' \biggl[ 1 + \frac{k'^2}{2^2} \biggr] \frac{R}{r}</math>	<math>~=</math>	<math>~ \frac{1}{2}\biggl[ 1 - \frac{r}{2R}\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 ( 3 \cos^2\phi -1 ) + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr]\biggl\{1 + \frac{1}{2^4} \biggl[ \biggl( \frac{r}{R}\biggr)^{2} - \biggl(\frac{r}{R}\biggr)^3\cos\phi + \mathcal{O}\biggl(\frac{r^4}{R^4} \biggr) \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ \biggl[ 1 - \frac{r}{2R}\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 ( 3 \cos^2\phi -1 ) + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr]\biggl\{\frac{1}{2} + \frac{1}{2^5} \biggl( \frac{r}{R}\biggr)^{2} + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr\} </math>
	<math>~=</math>	<math>~ \frac{1}{2}\biggl[ 1 - \frac{r}{2R}\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 ( 3 \cos^2\phi -1 ) + \frac{1}{2^4} \biggl( \frac{r}{R}\biggr)^{2} + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr] \, ; </math>

and, given that,

<math>~ \ln a + x - \tfrac{1}{2}x^2 + \tfrac{1}{3}x^3 - \tfrac{1}{4}x^4 + \cdots </math>

we also have,

<math>~\ln \frac{4}{k'}</math>	<math>~=</math>	<math>~ \ln\biggl(\frac{8R}{r} \biggr) + \ln\biggl[ 1 + \frac{1}{2} \biggl(\frac{r}{R}\biggr)\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 \sin^2\phi + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr] </math>
	<math>~=</math>	<math>~ \ln\biggl(\frac{8R}{r} \biggr) + \biggl[\frac{1}{2} \biggl(\frac{r}{R}\biggr)\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 \sin^2\phi + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr] - \frac{1}{2} \biggl[\frac{1}{2} \biggl(\frac{r}{R}\biggr)\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 \sin^2\phi + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr]^2 </math>
		<math>~ + \frac{1}{3}\biggl[\frac{1}{2} \biggl(\frac{r}{R}\biggr)\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 \sin^2\phi + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr]^3 + \cdots </math>
	<math>~=</math>	<math>~ \ln\biggl(\frac{8R}{r} \biggr) + \biggl[\frac{1}{2} \biggl(\frac{r}{R}\biggr)\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 \sin^2\phi \biggr] - \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2\cos^2\phi + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) </math>
	<math>~=</math>	<math>~ \ln\biggl(\frac{8R}{r} \biggr) + \frac{1}{2} \biggl(\frac{r}{R}\biggr)\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 (1 - 2\cos^2\phi ) + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \, . </math>

So our series expansion for Ostriker's "thin ring" potential becomes,

<math>~\Phi_\mathrm{TR}(r,\phi)\biggr\|_\mathrm{JPO}</math>	<math>~=</math>	<math>~ -\frac{GM}{\pi R} \biggl\{ \ln \frac{4}{k^'} \biggl[ 1 - \frac{r}{2R}\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 ( 3 \cos^2\phi -1 ) + \frac{1}{2^4} \biggl( \frac{r}{R}\biggr)^{2} + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr] - \frac{1}{2^4}\biggl( \frac{r}{R}\biggr)^{2} + \mathcal{O}\biggl( \frac{r^3}{R^3}\biggr) \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{GM}{\pi R} \biggl\{ \ln \frac{8R}{r} \biggl[ 1 - \frac{r}{2R}\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 ( 3 \cos^2\phi -1 ) + \frac{1}{2^4} \biggl( \frac{r}{R}\biggr)^{2} + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr] </math>
		<math>~ + \biggl[ \frac{1}{2} \biggl(\frac{r}{R}\biggr)\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 (1 - 2\cos^2\phi ) + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr]\biggl[ 1 - \frac{r}{2R}\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 ( 3 \cos^2\phi -1 ) + \frac{1}{2^4} \biggl( \frac{r}{R}\biggr)^{2} + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr] </math>
		<math>~ - \frac{1}{2^4}\biggl( \frac{r}{R}\biggr)^{2} + \mathcal{O}\biggl( \frac{r^3}{R^3}\biggr) \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{GM}{\pi R} \biggl\{ \ln \frac{8R}{r} \biggl[ 1 - \frac{r}{2R}\cos\phi + \frac{1}{2^4} \biggl(\frac{r}{R}\biggr)^2 ( 6 \cos^2\phi - 1) + \mathcal{O}\biggl(\frac{r^3}{R^3} \biggr) \biggr] </math>
		<math>~ + \frac{1}{2} \biggl(\frac{r}{R}\biggr)\cos\phi + \frac{1}{2^3} \biggl(\frac{r}{R}\biggr)^2 (1 - 2\cos^2\phi ) - \frac{1}{2^2} \biggl(\frac{r}{R}\biggr)^2\cos^2\phi - \frac{1}{2^4}\biggl( \frac{r}{R}\biggr)^{2} + \mathcal{O}\biggl( \frac{r^3}{R^3}\biggr) \biggr\} \, . </math>

Finally, dropping the explicit mention of all terms <math>~\mathcal{O}(r^3/R^3)</math> and smaller gives the series expansion formulation presented by Ostriker, namely,

<math>~\Phi_\mathrm{TR}(r,\phi)\biggr\|_\mathrm{JPO}</math>	<math>~=</math>	<math>~ -\frac{GM}{\pi R} \biggl\{\ln \frac{8R}{r} - \frac{r}{2R}\biggl[ \ln \frac{8R}{r} - 1\biggr]\cos\phi ~+~ \frac{r^2}{2^4R^2} \biggl[ \ln \frac{8R}{r} ( 6 \cos^2\phi - 1) + (1 - 8\cos^2\phi ) \biggr] ~+ ~\cdots \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{GM}{\pi R} \biggl\{\ln \frac{8R}{r} - \frac{r}{2R}\biggl[ \ln \frac{8R}{r} - 1\biggr]\cos\phi ~+~ \frac{r^2}{2^4R^2} \biggl[ \biggl(2\ln\frac{8R}{r} - 3 \biggr) + \biggl( 3\ln\frac{8R}{r} - 4 \biggr)\cos 2\phi \biggr] ~+ ~\cdots \biggr\} \, . </math>
Ostriker's (1964) Paper II, p. 1071, Eq. (25)

The Dimensionless Radial Coordinate, ξ, and Smallness Parameter, β

As we have reviewed separately, when researchers in the astrophysics community discuss the structure of spherical polytropes, the

Lane-Emden Equation

<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H^n</math>

invariably arises, as it is the governing 2^nd-order ODE whose solution, <math>~\Theta_H(\xi)</math>, defines the internal structure of spherically symmetric equlibrium configurations. Traditionally, as well, the dimensionless radial coordinate,

<math>~\xi \equiv \frac{r}{a_n} \, ,</math>

is defined in terms of <math>~a_n</math>, which is a natural length scale of the (spherical) problem. Equation (42) of Ostriker's (1964) Paper II provides the traditional definition of <math>~a_n</math>. It is therefore not surprising that, even though Ostriker's set of 1964 papers deal largely with the equilibrium and stability of ring-like configurations, he adopts a similar definition for the dimensionless radial coordinate; specifically, eq. (5) of Paper II states that,

<math>~\alpha \xi \equiv r \, .</math>

But, of course, in the context of Ostriker's presentation, <math>~r</math> is not a spherical radial coordinate but is, rather, as defined above; and <math>~\alpha</math> is of the same order as the minor, cross-sectional radius of the torus.

In eq. (6) of Paper II, Ostriker also defines the dimensionless parameter,

<math>~\beta \equiv \frac{\alpha}{R} \, ,</math>

where <math>~R</math> is associated with the major radius of the ring. Then he states that, "… since <math>~\alpha \ll R</math> (by hypothesis), we may be sure that <math>~\beta \ll 1</math> …"

With the definitions of these two dimensionless parameters in hand — and, more specifically, after appreciating that,

<math>~\frac{R}{r} = \frac{1}{\beta\xi} ~~~\Rightarrow ~~~ \ln\frac{8R}{r} = \biggl[ \ln\frac{8}{\beta} - \ln\xi \biggr] </math>

— we can follow Ostriker's lead and rewrite his derived expression for <math>~\Phi_\mathrm{TR}</math> in the form,

<math>~\Phi_\mathrm{TR}(r,\phi)\biggr\|_\mathrm{JPO}</math>	<math>~=</math>	<math>~ -\frac{GM}{\pi R} \biggl\{ \ln\frac{8}{\beta} - \ln\xi + \frac{\beta\xi}{2}\biggl[ - \biggl( \ln\frac{8}{\beta} -1 \biggr) + \ln\xi \biggr]\cos\phi </math>
		<math>~ +~ \frac{\beta^2\xi^2}{2^4} \biggl[ \biggl(2 \ln\frac{8}{\beta} - 3 - 2\ln\xi \biggr) + \biggl( 3 \ln\frac{8}{\beta} - 4 - 3\ln\xi \biggr)\cos 2\phi \biggr] ~+ ~\cdots \biggr\} \, . </math>
Ostriker's (1964) Paper II, p. 1071, Eq. (26)

User:Tohline/Apps/Ostriker64

Contents

Polytropic & Isothermal Tori

Overview

Coordinate System

Basics

Relationship to Toroidal Coordinate

Independent Exploration

Back to Basics

Summary

Second Attempt

Single Offset Circle

Set of Circles Whose Offset Increases With Circle Diameter

Case of Small Offset

Gravitational Potential

Potential of a Thin Hoop

Series Expansion

The Dimensionless Radial Coordinate, ξ, and Smallness Parameter, β

See Also

Navigation menu

Search