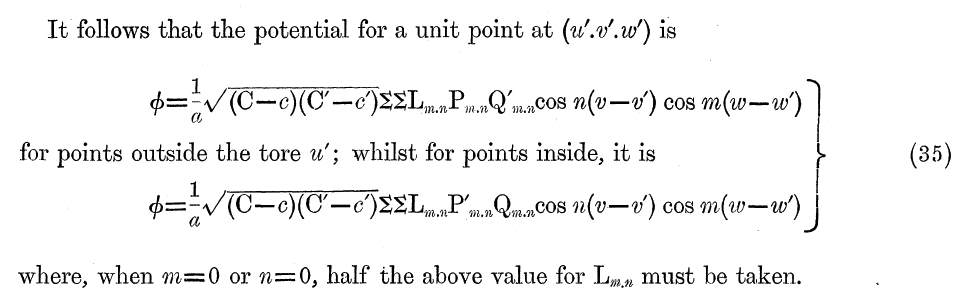User:Tohline/2DStructure/ToroidalGreenFunction
Using Toroidal Coordinates to Determine the Gravitational Potential
NOTE: An earlier version of this chapter has been shifted to our "Ramblings" Appendix.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Here we build upon our accompanying review of the types of numerical techniques that various astrophysics research groups have developed to solve for the Newtonian gravitational potential, <math>~\Phi(\vec{x})</math>, given a specified, three-dimensional mass distribution, <math>~\rho(\vec{x})</math>. Our focus is on the use of toroidal coordinates to solve the integral formulation of the Poisson equation, namely,
|
<math>~ \Phi(\vec{x})</math> |
<math>~=</math> |
<math>~ -G \iiint \frac{\rho(\vec{x}^{~'})}{|\vec{x}^{~'} - \vec{x}|} d^3x^' \, .</math> |
For the most part, we will adopt the notation used by C.-Y. Wong (1973, Annals of Physics, 77, 279); in an accompanying discussion, we review additional results from this insightful 1973 paper, as well as a paper of his that was published the following year in The Astrophysical Journal, namely, Wong (1974).
In order to accomplish this task, we first present the expressions that define how toroidal coordinates, <math>~(\eta,\theta,\psi)</math>, map to and from Cartesian coordinates <math>~(x, y, z)</math>, and present the toroidal-coordinate expression for the differential volume element, <math>~d^3 x</math>.
Basic Elements of a Toroidal Coordinate System
Given the meridional-plane coordinate location of a toroidal-coordinate system's axisymmetric anchor ring, <math>~(\varpi,z) = (a,Z_0)</math>, the relationship between toroidal coordinates <math>~(\eta,\theta,\psi) </math>and Cartesian coordinates <math>~(x, y, z)</math> is,
|
<math>~x</math> |
<math>~=</math> |
<math>~\frac{a \sinh\eta \cos\psi}{(\cosh\eta - \cos\theta)} \, ,</math> |
|
<math>~y</math> |
<math>~=</math> |
<math>~\frac{a \sinh\eta \sin\psi}{(\cosh\eta - \cos\theta)} \, ,</math> |
|
<math>~z - Z_0</math> |
<math>~=</math> |
<math>~\frac{a \sin\theta}{(\cosh\eta - \cos\theta)} \, .</math> |
This set of coordinate relations appears as equations 2.1 - 2.3 in Wong (1973). This set of relations may also be found, for example, on p. 1301 within eq. (10.3.75) of [MF53]; in §14.19 of NIST's Digital Library of Mathematical Functions; or even within Wikipedia. (In most cases the implicit assumption is that <math>~Z_0 = 0</math>.) It is clear, of course, that the cylindrical radial coordinate is,
|
<math>~\varpi = (x^2 + y^2)^{1 / 2}</math> |
<math>~=</math> |
<math>~\frac{a \sinh\eta}{(\cosh\eta - \cos\theta)} \, .</math> |
Mapping the other direction [see equations 2.13 - 2.15 of Wong (1973) ], we have,
|
<math>~\eta</math> |
<math>~=</math> |
<math>~\ln\biggl(\frac{r_1}{r_2} \biggr) \, ,</math> |
|
<math>~\cos\theta</math> |
<math>~=</math> |
<math>~\frac{(r_1^2 + r_2^2 - 4a^2)}{2r_1 r_2} \, ,</math> |
|
<math>~\tan\psi</math> |
<math>~=</math> |
<math>~\frac{y}{x} \, ,</math> |
where,
|
<math>~r_1^2 </math> |
<math>~\equiv</math> |
<math>~[(x^2 + y^2)^{1 / 2} + a]^2 + (z-Z_0)^2 \, ,</math> |
|
<math>~r_2^2 </math> |
<math>~\equiv</math> |
<math>~[(x^2 + y^2)^{1 / 2} - a]^2 + (z-Z_0)^2 \, ,</math> |
and <math>~\theta</math> has the same sign as <math>~(z-Z_0)</math>.
 |
||||||||||||
|
W. M. Hicks (1881) presents one of the first — if not the first — discussions of toroidal coordinates and associated toroidal functions. Equation (4) on p. 614 of his article provides the following definition of the pair of meridional-plane coordinates <math>~(u,v)</math>, written in terms of the traditional cylindrical-coordinate pair <math>~(\rho,z)</math> and the specified anchor ring radius, <math>~a</math>:
His equation (5) presents the reverse mapping, namely,
|
According to p. 1301, eq. (10.3.75) of [MF53] — or, for example, as found in Wikipedia — in toroidal coordinates the differential volume element is,
|
<math>~d^3x</math> |
<math>~=</math> |
<math>~h_\eta h_\theta h_\psi d\eta d\theta d\psi</math> |
<math>~=</math> |
<math>~\biggl[ \frac{a^3 \sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta~ d\psi \, .</math> |
Green's Function Expression
As presented by Wong (1973)
Referencing [MF53], Wong (1973) states that, in toroidal coordinates, the Green's function is,
|
<math>~\frac{1}{|~\vec{x} - {\vec{x}}^{~'} ~|} </math> |
<math>~=</math> |
<math>~ \frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } \sum\limits^\infty_{m,n=0} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} </math> |
|
|
|
<math>~ \times \cos[m(\psi - \psi^')]\cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, , </math> |
|
Wong (1973), p. 293, Eq. (2.53) |
||
where, <math>~P^m_{n-1 / 2}, Q^m_{n-1 / 2}</math> are Associated Legendre Functions of the first and second kind with degree <math>~n - \tfrac{1}{2}</math> and order <math>~m</math> (toroidal harmonics), and <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0 = 1</math> and <math>~\epsilon_m = 2</math> for all <math>~m \ge 1</math>. This Green's function expression can indeed be found as eq. (10.3.81) on p. 1304 of [MF53], but it should be noted that the MF53 expression differs from Wong's in two respects (see footnote 2 on p. 370 of Cohl et al. (2000) for a proposed explanation): First, the factor, <math>~(-1)^m</math>, appears as <math>~(-i)^m</math> in MF53; and, second, in the term that is composed of a ratio of gamma functions, the denominator appears in MF53 as <math>~\Gamma(n - m + \tfrac{1}{2})</math>, whereas it should be <math>~\Gamma(n + m + \tfrac{1}{2})</math>, as presented here.
As Presented by Hicks (1881)
Notably, more than 135 years ago, W. M. Hicks (1881) already had constructed a Green's function expression for the reciprocal distance between two points in toroidal coordinates. The following boxed-in table contains a snapshot image of equation (35) from Hicks (1881), along with its associated text; notice that he refers to <math>~\phi</math> as the "potential." Although notations are different — for example, <math>~C</math> is shorthand for <math>~\cosh u</math> and <math>~c</math> is shorthand for <math>~\cos v</math> — one can easily see factor-by-factor agreement when compared with the Green's function presented by Wong (1973).
 |
Rearranging Terms and Incorporating Special-Function Relations
Let's focus on the situation when <math>~\eta^' > \eta</math>, and begin rearranging or substituting terms.
|
<math>~\frac{1}{|~\vec{x} - {\vec{x}}^{~'} ~|} </math> |
<math>~=</math> |
<math>~ \frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } \sum\limits^\infty_{m=0} (-1)^m \epsilon_m \cos[m(\psi - \psi^')] </math> |
|
|
|
<math>~ \times \sum\limits^\infty_{n=0} \epsilon_n \cos[n(\theta - \theta^')] ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} ~P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') </math> |
|
|
<math>~=</math> |
<math>~ \frac{ [ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^')]^{1 /2 } }{\pi a \sqrt{\sinh\eta^'} \sqrt{\sinh\eta} } \sum\limits^\infty_{m=0} (-1)^m \epsilon_m \cos[m(\psi - \psi^')] </math> |
|
|
|
<math>~ \times \sum\limits^\infty_{n=0} \epsilon_n \cos[n(\theta - \theta^')] \biggl\{ ~ \sqrt{ \frac{\pi}{2} }~\Gamma(n-m+\tfrac{1}{2}) \sqrt{\sinh\eta}~P^m_{n-1 / 2}(\cosh\eta) \biggl\}\biggr\{ ~\sqrt{ \frac{2}{\pi} }~\frac{\sqrt{\sinh\eta^'}}{\Gamma(n + m + \tfrac{1}{2})} Q^m_{n-1 / 2}(\cosh\eta^') \biggr\} </math> |
The term contained within the first set of curly braces on the right-hand side of this expression can be replaced by the derived expression labeled ① in the Appendix, below, and simultaneously the term contained within the second set of curly braces can be replaced by the derived expression labeled ② in the same Appendix. After making these substitutions, we have,
|
<math>~\frac{1}{|~\vec{x} - {\vec{x}}^{~'} ~|} </math> |
<math>~=</math> |
<math>~ \frac{ [ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^')]^{1 /2 } }{\pi a \sqrt{\sinh\eta^'} \sqrt{\sinh\eta} } \sum\limits^\infty_{m=0} (-1)^m \epsilon_m \cos[m(\psi - \psi^')] </math> |
|
|
|
<math>~ \times \sum\limits^\infty_{n=0} \epsilon_n \cos[n(\theta - \theta^')] \biggl\{ ~ (-1)^{-n}Q^n_{m-1 / 2}(\coth\eta) \biggl\}\biggr\{ ~(-1)^{-m} P^{-n}_{m-1 / 2}(\coth\eta^') \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{ [ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^')]^{1 /2 } }{\pi a \sqrt{\sinh\eta^'} \sqrt{\sinh\eta} } \sum\limits^\infty_{m=0} \epsilon_m \cos[m(\psi - \psi^')] </math> |
|
|
|
<math>~ \times \sum\limits^\infty_{n=0} (-1)^{n} \epsilon_n \cos[n(\theta - \theta^')] Q^n_{m-1 / 2}(\coth\eta) P^{-n}_{m-1 / 2}(\coth\eta^') \, , </math> |
where, in writing this last expression we have acknowledged that, since <math>~n</math> is either zero or a positive integer, <math>~(-1)^{-n} = (-1)^n</math>. Next we draw upon the "Key Equation" relation,
|
<math>~ Q_\nu[t t^' - (t^2-1)^{1 / 2} (t^{'2} - 1)^{1 / 2} \cos\psi] </math> |
<math>~=</math> |
<math>~ Q_\nu(t) P_\nu(t^') + 2\sum_{n=1}^\infty (-1)^n Q^n_\nu(t) P^{-n}_\nu(t^') \cos(n\psi) </math> |
|
|
A. Erdélyi (1953): Volume I, §3.11, p. 169, eq. (4) |
|||
| Valid for: |
<math>~t, t^'</math> real |
|
<math>~1 < t^' < t</math> |
|
<math>~\nu \ne -1, -2, -3, </math> … |
|
<math>~\psi</math> real |
which, after making the substitutions, <math>~\nu \rightarrow (m - \tfrac{1}{2})</math> and <math>~\psi \rightarrow (\theta - \theta^')</math>, and incorporating the Neumann factor, <math>~\epsilon_n</math>, becomes,
|
<math>~ Q_{m - \frac{1}{2} }\ [t t^' - (t^2-1)^{1 / 2} (t^{'2} - 1)^{1 / 2} \cos(\theta- \theta^') ] </math> |
<math>~=</math> |
<math>~ \sum_{n=0}^\infty (-1)^n \epsilon_n Q^n_{m - \frac{1}{2} }(t) P^{-n}_{m - \frac{1}{2} }(t^') \cos[(n(\theta- \theta^')] \, . </math> |
Finally, after making the associations, <math>~t \rightarrow \coth\eta</math> and <math>~t^' \rightarrow \coth\eta^'</math>, this last expression allows us to rewrite Wong's (1973) Green's function in a significantly more compact form, namely,
|
<math>~\frac{1}{|~\vec{x} - {\vec{x}}^{~'} ~|} </math> |
<math>~=</math> |
<math>~ \frac{ [ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^')]^{1 /2 } }{\pi a \sqrt{\sinh\eta^'} \sqrt{\sinh\eta} } \sum\limits^\infty_{m=0} \epsilon_m \cos[m(\psi - \psi^')] Q_{m - \frac{1}{2}}(\Chi) \, , </math> |
where the argument, <math>~\Chi</math>, of the toroidal function, <math>~Q_{m - \frac{1}{2}}</math>, is,
|
<math>~\Chi</math> |
<math>~\equiv</math> |
<math>~ t t^' - (t^2-1)^{1 / 2} (t^{'2} - 1)^{1 / 2} \cos(\theta- \theta^') </math> |
|
|
<math>~=</math> |
<math>~ \coth\eta \coth\eta^' - (\coth^2\eta-1)^{1 / 2} (\coth^2\eta'- 1)^{1 / 2} \cos(\theta- \theta^') </math> |
|
|
<math>~=</math> |
<math>~ \frac{\cosh\eta \cosh\eta^'}{\sinh\eta \sinh\eta^'} - \biggl[ \frac{1}{\sinh^2\eta} \biggr]^{1 / 2} \biggl[ \frac{1}{\sinh^2\eta'}\biggr]^{1 / 2} \cos(\theta- \theta^') </math> |
|
|
<math>~=</math> |
<math>~ \frac{\cosh\eta \cosh\eta^' - \cos(\theta- \theta^') }{\sinh\eta \sinh\eta^'} \, . </math> |
As Presented in Cohl & Tohline (1999)
This last, compact Green's function expression — which we have derived, here, from Wong's (1973) published Green's function by drawing strategically upon a variety of special function relations — precisely matches the "compact cylindrical Green's function expression" that has been derived independently by Cohl & Tohline (1999) via a less tortuous route, namely,
|
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> |
<math>~=</math> |
<math>~ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\psi - \psi^')] Q_{m- 1 / 2}(\Chi) </math> |
|
Cohl & Tohline (1999), p. 88, Eq. (17) |
||
|
|
<math>~=</math> |
<math>~ \frac{1}{a\pi} \biggl[ \frac{(\cosh\eta^' - \cos\theta^')}{\sinh\eta^' } \frac{(\cosh\eta - \cos\theta)}{\sinh\eta } \biggr]^{1 / 2} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\psi - \psi^')] Q_{m- 1 / 2}(\Chi) \, , </math> |
where,
|
<math>~\Chi</math> |
<math>~\equiv</math> |
<math>~ \frac{(\varpi^')^2 + \varpi^2 + (z^' - z)^2}{2\varpi^' \varpi} </math> |
<math>~=</math> |
<math>~ \frac{\cosh\eta \cdot \cosh\eta^' - \cos(\theta^' - \theta) }{ \sinh\eta \cdot \sinh\eta^'} \, . </math> |
|
|
Cohl & Tohline (1999), p. 88, Eq. (16) |
|||
Note from J. E. Tohline (June, 2018): This is the first time that I have been able to formally demonstrate to myself that these two separately derived Green's function expressions are identical. See, however, the earlier identification of new addition theorems in association with equations (49) and (50) of Cohl et al. (2000).
Gravitational Potential
Quite generally, then, the gravitational potential can be obtained at any coordinate location, <math>~(\eta,\theta,\psi)</math> — both inside and outside of a specified mass distribution — by carrying out three nested spatial integrals over the product of: <math>~\rho(\vec{x}^{~'})</math>, the differential volume element, and the Green's function as specified either by Wong (1973) or by Cohl & Tohline (1999).
In what follows we will make an effort to elucidate the pros and cons of adopting one Green's function expression over the other. In each case we begin by writing the expression for the potential in such a way that variations in the azimuthal coordinate, <math>~\psi</math>, are described by Fourier components, <math>~\Phi_m^{(1)}(\eta,\theta)</math> and <math>~\Phi_m^{(2)}(\eta,\theta)</math>, of the potential, such that,
<math>~\Phi(\vec{x}) = \tfrac{1}{2}\Phi_0^{(1)}(\eta,\theta) + \sum_{m=1}^\infty \cos (m\psi) \Phi_m^{(1)}(\eta,\theta) + \sum_{m=1}^\infty \sin (m\psi) \Phi_m^{(2)}(\eta,\theta) \, .</math>
Each Fourier component of the potential depends explicitly on the corresponding Fourier component of the density distribution, defined such that,
<math>~\rho(\vec{x}) = \tfrac{1}{2}\rho_0^{(1)}(\eta,\theta) + \sum_{m=1}^\infty \cos (m\psi) \rho_m^{(1)}(\eta,\theta) + \sum_{m=1}^\infty \sin (m\psi) \rho_m^{(2)}(\eta,\theta) \, .</math>
|
LaTeX mathematical expressions cut-and-pasted directly from
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|
|
As an additional primary point of reference, note that according to §1.8(i) of NIST's Digital Library of Mathematical Functions, a Fourier Series is defined as follows:
|
Notice, therefore, that,
|
<math>~\rho_m^{(1)}(\eta,\theta)</math> |
<math>~=</math> |
<math>~\frac{1}{\pi}\int^{\pi}_{-\pi}\rho(\eta,\theta,\psi)\cos\bigl(m\psi\bigr)\mathrm{d}\psi,</math> |
and, |
<math>~\rho_m^{(2)}(\eta,\theta)</math> |
<math>~=</math> |
<math>~\frac{1}{\pi}\int^{\pi}_{-\pi}\rho(\eta,\theta,\psi)\sin\bigl(m\psi\bigr)\mathrm{d}\psi \, .</math> |
The CT99 Expression for the Potential
In Three-Dimensional Generality
Employing the Green's function expression derived by Cohl & Tohline (1999), the gravitational potential for any three-dimensional matter distribution is,
|
<math>~ \Phi(\eta,\theta,\psi)</math> |
<math>~=</math> |
<math>~ -G \iiint \rho(\eta^',\theta^',\psi^') \biggl\{ \frac{1}{|\vec{x}^{~'} - \vec{x}|} \biggr\} \biggl[ \frac{a^3 \sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^3} \biggr] d\eta^'~ d\theta^'~ d\psi^' </math> |
|
|
<math>~=</math> |
<math>~ -\frac{Ga^2}{\pi} \int d\eta^' \int d\theta^' \int d\psi^' \iiint \rho(\eta^',\theta^',\psi^') \biggl[ \frac{\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^3} \biggr] </math> |
|
|
|
<math>~ \times \biggl[ \frac{(\cosh\eta^' - \cos\theta^')}{\sinh\eta^' } \frac{(\cosh\eta - \cos\theta)}{\sinh\eta } \biggr]^{1 / 2} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\psi - \psi^')] Q_{m- 1 / 2}(\Chi) </math> |
|
|
<math>~=</math> |
<math>~ -\frac{Ga^2}{\pi} \biggl[ \frac{(\cosh\eta - \cos\theta)}{\sinh\eta } \biggr]^{1 / 2} \sum_{m=0}^{\infty} \epsilon_m \int d\eta^' \int d\theta^' \biggl[ \frac{\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^5} \biggr]^{1 / 2} Q_{m- 1 / 2}(\Chi) \int d\psi^' \rho(\eta^',\theta^',\psi^') </math> |
|
|
|
<math>~ \times [\cos(m\psi)\cos(m\psi^') + \sin(m\psi)\sin(m\psi^') ] </math> |
|
|
<math>~=</math> |
<math>~ -\frac{Ga^2}{\pi} \biggl[ \frac{(\cosh\eta - \cos\theta)}{\sinh\eta } \biggr]^{1 / 2} \biggl\{ \int d\eta^' \int d\theta^' \biggl[ \frac{\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^5} \biggr]^{1 / 2} Q_{- \frac{1}{2}}(\Chi) \int_{-\pi}^{\pi} d\psi^' \rho(\eta^',\theta^',\psi^') </math> |
|
|
|
<math>~ + \sum_{m=1}^{\infty} 2\cos(m\psi) \int d\eta^' \int d\theta^' \biggl[ \frac{\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^5} \biggr]^{1 / 2} Q_{m- 1 / 2}(\Chi) \int_{-\pi}^\pi d\psi^' \rho(\eta^',\theta^',\psi^') \cos(m\psi^') </math> |
|
|
|
<math>~ + \sum_{m=1}^{\infty} 2\sin(m\psi) \int d\eta^' \int d\theta^' \biggl[ \frac{\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^5} \biggr]^{1 / 2} Q_{m- 1 / 2}(\Chi) \int_{-\pi}^\pi d\psi^' \rho(\eta^',\theta^',\psi^') \sin(m\psi^') \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - Ga^2 \biggl[ \frac{(\cosh\eta - \cos\theta)}{\sinh\eta } \biggr]^{1 / 2} \biggl\{ \int d\eta^' \int d\theta^' \biggl[ \frac{\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^5} \biggr]^{1 / 2} Q_{- \frac{1}{2}}(\Chi) \rho_0^{(1)}(\eta^',\theta^') </math> |
|
|
|
<math>~ + \sum_{m=1}^{\infty} 2\cos(m\psi) \int d\eta^' \int d\theta^' \biggl[ \frac{\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^5} \biggr]^{1 / 2} Q_{m- 1 / 2}(\Chi) \rho_m^{(1)}(\eta^',\theta^') </math> |
|
|
|
<math>~ + \sum_{m=1}^{\infty} 2\sin(m\psi) \int d\eta^' \int d\theta^' \biggl[ \frac{\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^5} \biggr]^{1 / 2} Q_{m- 1 / 2}(\Chi) \rho_m^{(2)}(\eta^',\theta^') \biggr\} \, . </math> |
We conclude, therefore, that each one of the Fourier components of the gravitational potential is given by the expression,
|
<math>~\Phi_m^{(1),(2)}(\eta,\theta)</math> |
<math>~=</math> |
<math>~ - 2Ga^2 \biggl[ \frac{(\cosh\eta - \cos\theta)}{\sinh\eta } \biggr]^{1 / 2} \int d\eta^' \int d\theta^' \biggl[ \frac{\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^5} \biggr]^{1 / 2} Q_{m- 1 / 2}(\Chi) \rho_m^{(1),(2)}(\eta^',\theta^') \, , </math> |
|
Cohl & Tohline (1999), p. 88, Eq. (20) |
||
where, as above,
|
<math>~\Chi</math> |
<math>~\equiv</math> |
<math>~ \frac{\cosh\eta \cdot \cosh\eta^' - \cos(\theta^' - \theta) }{ \sinh\eta \cdot \sinh\eta^'} \, . </math> |
For Axisymmetric Systems
For axisymmetric systems, the density distribution has no dependence on the azimuthal coordinate, <math>~\psi</math>. Hence, for all <math>~m > 0</math>, the Fourier components of the density, <math>~\rho_m^{(1),(2)}</math>, are zero. The only nonzero component is, <math>~\rho_0^{(1)}(\eta,\theta) = 2\rho(\eta,\theta)</math>. For axisymmetric systems, then, the gravitational potential is,
|
<math>~\Phi(\eta,\theta)</math> |
<math>~=</math> |
<math>~\tfrac{1}{2}\Phi_0^{(1)}(\eta,\theta)</math> |
|
|
<math>~=</math> |
<math>~ - 2Ga^2 \biggl[ \frac{(\cosh\eta - \cos\theta)}{\sinh\eta } \biggr]^{1 / 2} \int d\eta^' \int d\theta^' \biggl[ \frac{\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^5} \biggr]^{1 / 2} Q_{- 1 / 2}(\Chi) \rho(\eta^',\theta^') \, . </math> |
|
Cohl & Tohline (1999), p. 88, Eqs. (31) & (32a) |
||
Wong's Expression for the Potential
Fully Three-Dimensional Case
Employing Wong's (1973) Green's function expression, the gravitational potential for any three-dimensional matter distribution is,
|
<math>~ \Phi(\vec{x})</math> |
<math>~=</math> |
<math>~ -G \iiint \rho(\eta^',\theta^',\psi^') \biggl\{ \frac{1}{|\vec{x}^{~'} - \vec{x}|} \biggr\} \biggl[ \frac{a^3 \sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^3} \biggr] d\eta^'~ d\theta^'~ d\psi^' </math> |
|
|
<math>~=</math> |
<math>~ - \frac{a^2G}{\pi} \int d\eta^' \int d\theta^' \int d\psi^' \biggl[ \frac{\rho(\eta^',\theta^',\psi^') ~\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^3} \biggr] \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } \sum\limits^\infty_{n=0} \sum\limits^\infty_{m=0}(-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} </math> |
|
|
|
<math>~ \times \cos[m(\psi - \psi^')]\cos[n(\theta - \theta^')] ~P^m_{n-1 / 2}(\cosh\eta_<) ~Q^m_{n-1 / 2}(\cosh\eta_>) </math> |
|
|
<math>~=</math> |
<math>~ - \frac{a^2G}{\pi} (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \sum\limits^\infty_{m=0}(-1)^m \epsilon_m ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} \int d\eta^' ~P^m_{n-1 / 2}(\cosh\eta_<) ~Q^m_{n-1 / 2}(\cosh\eta_>) </math> |
|
|
|
<math>~ \times~ \int d\theta^' \biggl[ \frac{ ~\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^{5/2}} \biggr]\cos[n(\theta - \theta^')] \int d\psi^' \rho(\eta^',\theta^',\psi^') [\cos(m\psi)\cos(m\psi^') + \sin(m\psi) \sin(m\psi^')] </math> |
|
|
<math>~=</math> |
<math>~ - \frac{a^2G}{\pi} (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \biggl\{ \int d\eta^' ~P_{n-1 / 2}(\cosh\eta_<) ~Q_{n-1 / 2}(\cosh\eta_>) \int d\theta^' \biggl[ \frac{ ~\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^{5/2}} \biggr]\cos[n(\theta - \theta^')] \int_{-\pi}^\pi d\psi^' \rho(\eta^',\theta^',\psi^') </math> |
|
|
|
<math>~ +~ \sum\limits^\infty_{m=1} 2\cos(m\psi)(-1)^m ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} \int d\eta^' ~P^m_{n-1 / 2}(\cosh\eta_<) ~Q^m_{n-1 / 2}(\cosh\eta_>) \int d\theta^' \biggl[ \frac{ ~\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^{5/2}} \biggr]\cos[n(\theta - \theta^')] \int_{-\pi}^\pi d\psi^' \rho(\eta^',\theta^',\psi^') \cos(m\psi^') </math> |
|
|
|
<math>~ +~ \sum\limits^\infty_{m=1} 2 \sin(m\psi)(-1)^m ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} \int d\eta^' ~P^m_{n-1 / 2}(\cosh\eta_<) ~Q^m_{n-1 / 2}(\cosh\eta_>) \int d\theta^' \biggl[ \frac{ ~\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^{5/2}} \biggr]\cos[n(\theta - \theta^')] \int_{-\pi}^\pi d\psi^' \rho(\eta^',\theta^',\psi^') \sin(m\psi^') \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - a^2G (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \biggl\{ \int d\eta^' ~P_{n-1 / 2}(\cosh\eta_<) ~Q_{n-1 / 2}(\cosh\eta_>) \int d\theta^' \biggl[ \frac{ ~\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^{5/2}} \biggr]\cos[n(\theta - \theta^')] \rho_0^{(1)}(\eta^',\theta^') </math> |
|
|
|
<math>~ +~ \sum\limits^\infty_{m=1} 2\cos(m\psi)(-1)^m ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} \int d\eta^' ~P^m_{n-1 / 2}(\cosh\eta_<) ~Q^m_{n-1 / 2}(\cosh\eta_>) \int d\theta^' \biggl[ \frac{ ~\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^{5/2}} \biggr]\cos[n(\theta - \theta^')] \rho_m^{(1)}(\eta^',\theta^') </math> |
|
|
|
<math>~ +~ \sum\limits^\infty_{m=1} 2 \sin(m\psi)(-1)^m ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} \int d\eta^' ~P^m_{n-1 / 2}(\cosh\eta_<) ~Q^m_{n-1 / 2}(\cosh\eta_>) \int d\theta^' \biggl[ \frac{ ~\sinh\eta^'}{(\cosh\eta^' - \cos\theta^')^{5/2}} \biggr]\cos[n(\theta - \theta^')] \rho_m^{(2)} (\eta^',\theta^') \biggr\} \, . </math> |
We conclude, therefore, that each one of the Fourier components of the gravitational potential is given by the expression,
|
<math>~\Phi_m^{(1),(2)} (\eta,\theta)</math> |
<math>~=</math> |
<math>~ - 2Ga^2 (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n (-1)^m ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} </math> |
|
|
|
<math>~\times \int d\eta^' ~\sinh\eta^' ~ P^m_{n-1 / 2}(\cosh\eta_<) ~ Q^m_{n-1 / 2}(\cosh\eta_>) \int d\theta^' \biggl\{ \frac{ \cos[n(\theta - \theta^')]}{(\cosh\eta^' - \cos\theta^')^{5/2}} \biggr\} \rho_m^{(1),(2)}(\eta^',\theta^') \, . </math> |
Axisymmetric Systems
For axisymmetric systems, the density distribution has no dependence on the azimuthal coordinate, <math>~\psi</math>. Hence, for all <math>~m > 0</math>, the Fourier components of the density, <math>~\rho_m^{(1),(2)}</math>, are zero. The only nonzero component is, <math>~\rho_0^{(1)}(\eta,\theta) = 2\rho(\eta,\theta)</math>. For axisymmetric systems, then, the gravitational potential is,
|
<math>~\Phi(\eta,\theta)</math> |
<math>~=</math> |
<math>~\tfrac{1}{2}\Phi_0^{(1)}(\eta,\theta)</math> |
|
|
<math>~=</math> |
<math>~ - 2Ga^2 (\cosh\eta - \cos\theta)^{1 / 2} \sum\limits^\infty_{n=0} \epsilon_n \int d\eta^' ~\sinh\eta^'~P^0_{n-1 / 2}(\cosh\eta_<) ~Q^0_{n-1 / 2}(\cosh\eta_>) \int d\theta^' \biggl\{ \frac{ ~\cos[n(\theta - \theta^')]}{(\cosh\eta^' - \cos\theta^')^{5/2}} \biggr\} \rho(\eta^',\theta^') \, . </math> |
|
Wong (1973), p. 293, Eq. (2.55) |
||
Uniform-Density Torus
In an accompanying discussion, we build upon the above technical foundation and detail how Wong (1973) was able to complete both integrals to derive an analytic expression for the potential (inside as well as outside) of axisymmetric, uniform-density tori having an arbitrarily specified ratio of the major to minor (cross-sectional) radii, <math>~R/d</math>. This is an outstanding accomplishment that has received little attention in the astrophysics literature and, therefore, has heretofore been underappreciated.
Appendix A: Selected Toroidal Function Relationships
Here, we draw from the set of toroidal function relationships that have been identified as "Key Equations" in our accompanying Equations appendix. Two related appendices — numbered A.3 and A.4 — may be found in an accompanying discussion.
A.1
|
Beginning with the identified "Key Equation",
we'll identify <math>~x</math> with <math>~\cosh\eta</math> — in which case we have <math>~\lambda = \coth\eta</math> — and switch the index notations, <math>~n \leftrightarrow m</math>. This gives,
Drawing upon the Euler reflection formula for gamma functions, namely,
where it is understood that <math>~m</math> and <math>~n</math> are each either zero or a positive integer, this toroidal-function relation becomes,
|
||||||||||||||||||||||||||||||||||||||||||||||
A.2
|
Again, beginning with the identified "Key Equation",
this time, without switching index notations, we'll identify <math>~x</math> with <math>~\coth\eta</math> — in which case we have <math>~\lambda = \cosh\eta</math>. This gives,
Drawing upon the same Euler reflection formula for gamma functions, as quoted above, this toroidal function relation can be rewritten as,
Finally, calling upon the "Key Equation" relation,
making the index notation substitution, <math>~\nu \rightarrow (m-\tfrac{1}{2})</math>, and associating <math>~z</math> with <math>~ \coth\eta</math> gives,
As a result, we can write,
|
||||||||||||||||||||||||||||||||||||||
A.3
|
Here, our objective is to evaluate the definite integral,
Notice that, since the limits of the integration are <math>~-\pi</math> to <math>~+\pi</math>: The second integral on the right-hand-side goes to zero because the numerator of its integrand — i.e., <math>~\sin(n\theta)</math> — is an odd function; and, with regard to the first integral on the right-hand-side, the lower integration limit can be set to zero and the result doubled because the numerator of its integrand — i.e., <math>~\cos(n\theta)</math> — is an even function. Drawing from Volume I of A. Erdélyi's (1953) Higher Transcendental Functions, we find the following "Key Equation":
Next we adopt the associations, <math>~z \rightarrow \cosh\eta</math>, <math>~t \rightarrow \theta</math>, <math>~\mu \rightarrow 2</math>, and, <math>~\nu \rightarrow n - \tfrac{1}{2}</math>, where <math>~n</math> is zero or a positive integer. In this case we have,
where the prefactor of the second term — that is, <math>~\cos[(n-\tfrac{1}{2})\pi] </math> — goes to zero for all allowable values of the integer, <math>~n</math>. Hence, we conclude that,
where we have set, <math>~ \Gamma(\tfrac{5}{2}) = \Gamma(\tfrac{1}{2} + 2) = \frac{ \sqrt{\pi} \cdot 4! }{4^2 \cdot 2!} = \frac{\sqrt{\pi} \cdot 2^3\cdot 3}{ 2^5 } = \frac{3 \sqrt{\pi}}{2^2} \, . </math> |
|||||||||||||||||||||||||||||
A.4
|
Beginning with the identified "Key Equation",
we will adopt the associations: <math>~z \rightarrow t</math>, <math>~\mu \rightarrow 2</math>, <math>~\nu \rightarrow (n - \tfrac{1}{2})</math>, <math>~\rho \rightarrow 0</math>, and <math>~\sigma \rightarrow ( n - \tfrac{1}{2})</math>. As a result, Erdélyi's (1953) expression becomes,
Drawing upon the recurrence "Key Equation,"
which means, after making the associations, <math>~z \rightarrow t</math>, <math>~\mu \rightarrow 0</math> and <math>~\nu \rightarrow (n-\tfrac{1}{2})</math>, that,
the integral can be rewritten as,
Returning to the same recurrence "Key Equation," but this time adopting the associations, <math>~z \rightarrow t</math>, <math>~\mu \rightarrow 2</math> and <math>~\nu \rightarrow (n-\tfrac{1}{2})</math>, we can write,
in which case the integral becomes,
|
||||||||||||||||||||||||||||||||||||||||
Appendix B: Elliptic Integrals
Summary Table
If the default argument of a complete elliptic integral function is the parameter, <math>~k</math>, then we should also appreciate that the following additional arguments may be useful:
| parameter | In terms of … | |||
| <math>~k</math> |
<math>~k_1</math> |
<math>~\frac{R}{R_1} = e^{-\eta}</math> | <math>~\eta \equiv \ln\biggl(\frac{R_1}{R}\biggr)</math> | |
| <math>~k</math> | <math>~k</math> | <math>~\frac{2\sqrt{k_1}}{1+k_1}</math> | <math>~\biggl[1 - \biggl( \frac{R}{R_1}\biggr)^2 \biggr]^{1 / 2}</math> | <math>~\biggl[ \frac{2}{\coth\eta + 1} \biggr]^{1 / 2}= \biggl[ 1 - e^{-2\eta} \biggr]^{1 / 2}</math> |
| <math>~k^{\prime}</math> | <math>~\sqrt{1 - k^2}</math> | <math>~\frac{1-k_1}{1+k_1}</math> | <math>~\frac{R}{R_1}</math> | <math>~\frac{1}{\cosh\eta + \sinh\eta} = e^{-\eta}</math> |
| <math>~k_1 = \frac{1-k^{\prime}}{1+k^{\prime}}</math> | <math>~\frac{1-\sqrt{1 - k^2}}{1+\sqrt{1 - k^2}}</math> | <math>~k_1</math> | <math>~\frac{R_1 - R}{R_1 +R}</math> | <math>~\tanh\biggl(\frac{\eta}{2}\biggr) = \frac{1 - e^{-\eta}}{1 + e^{-\eta}}</math> |
As published, for example, in §8.126 of Gradshteyn & Ryzhik (1965), the following mappings are valid:
|
Explicitly Published in §8.126 of G & R (1965) |
Additional Implications |
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|||||||||||||||
|
|
|||||||||||||||
One Set of Details
Following advice that we have received from Howard Cohl (private communication), we can demonstrate this most efficiently by employing the Descending Landen Transformation for the complete elliptic integral of the first kind, that is,
|
<math>~K(k)</math> |
<math>~=</math> |
<math>~ (1 + k_1)K(k_1) \, , </math> |
where, |
<math>~k_1</math> |
<math>~\equiv</math> |
<math>~ \frac{1-\sqrt{1-k^2}}{1+\sqrt{1-k^2}} \, . </math> |
Given our just-stated definition of the parameter, <math>~k</math>, we have,
|
<math>~\sqrt{1-k^2}</math> |
<math>~=</math> |
<math>~ \biggl[ 1 - \frac{2}{\coth\eta + 1} \biggr]^{1 / 2} = \biggl[ \frac{\coth\eta - 1 }{\coth\eta + 1} \biggr]^{1 / 2} </math> |
|
<math>~\Rightarrow ~~~ 1 \pm \sqrt{1-k^2}</math> |
<math>~=</math> |
<math>~ 1 \pm \biggl[ \frac{\coth\eta - 1 }{\coth\eta + 1} \biggr]^{1 / 2} = \frac{ [\coth\eta + 1]^{1 / 2} \pm [\coth\eta - 1]^{1 / 2} }{ [\coth\eta + 1]^{1 / 2} } </math> |
|
<math>~\Rightarrow ~~~k_1 \equiv \frac{1 - \sqrt{1-k^2}}{1 + \sqrt{1-k^2}}</math> |
<math>~=</math> |
<math>~ \frac{ [\coth\eta + 1]^{1 / 2} - [\coth\eta - 1]^{1 / 2} }{ [\coth\eta + 1]^{1 / 2} + [\coth\eta - 1]^{1 / 2} } </math> |
|
<math>~\Rightarrow ~~~k_1^2 </math> |
<math>~=</math> |
<math>~ \frac{ [\coth\eta + 1] -2[\coth\eta + 1]^{1 / 2}[\coth\eta - 1]^{1 / 2} + [\coth\eta - 1] }{ [\coth\eta + 1] + 2[\coth\eta + 1]^{1 / 2}[\coth\eta - 1]^{1 / 2} + [\coth\eta - 1] } </math> |
|
|
<math>~=</math> |
<math>~ \frac{ 2\coth\eta -2[\coth\eta + 1]^{1 / 2}[\coth\eta - 1]^{1 / 2} }{ 2\coth\eta + 2[\coth\eta + 1]^{1 / 2}[\coth\eta - 1]^{1 / 2} } </math> |
|
|
<math>~=</math> |
<math>~ \frac{ \coth\eta - [\coth^2\eta - 1]^{1 / 2} }{ \coth\eta + [\coth^2\eta - 1]^{1 / 2} } </math> |
|
|
<math>~=</math> |
<math>~ \frac{ \coth\eta/[\coth^2\eta - 1]^{1 / 2} - 1 }{ \coth\eta/[\coth^2\eta - 1]^{1 / 2} + 1 } </math> |
|
|
<math>~=</math> |
<math>~\frac{\cosh\eta - 1}{\cosh\eta + 1}</math> |
|
|
<math>~=</math> |
<math>~\tanh^2\biggl(\frac{\eta}{2}\biggr) \, .</math> |
Note as well that,
|
<math>~1 + k_1</math> |
<math>~=</math> |
<math>~1+ \frac{1 - \sqrt{1-k^2}}{1 + \sqrt{1-k^2}} = \frac{2}{1 + \sqrt{1-k^2}} \, .</math> |
Hence, the "second attempt" expression for <math>~P_{1 / 2}(z)</math> becomes,
|
<math>~P_{-1 / 2}(\cosh\eta)</math> |
<math>~=</math> |
<math>~ \frac{\sqrt{2}}{\pi}~ (\sinh\eta)^{-1 / 2} \biggl[ \frac{2k}{1 + \sqrt{1-k^2}} \biggr] K\biggl(\tanh \frac{\eta}{2} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{2^{2}}{\pi}~ (\sinh\eta)^{-1 / 2} \biggl[ \frac{1}{\coth\eta + 1}\biggr]^{1 / 2} \biggl\{ \frac{ [\coth\eta + 1]^{1 / 2} }{ [\coth\eta + 1]^{1 / 2} + [\coth\eta - 1]^{1 / 2} } \biggr\}K\biggl(\tanh \frac{\eta}{2} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{2^{2}}{\pi}~ \biggl[ ( \cosh\eta + \sinh\eta )^{1 / 2} + (\cosh\eta - \sinh\eta)^{1 / 2} \biggr]^{-1} K\biggl(\tanh \frac{\eta}{2} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{2^{2}}{\pi}~ \biggl[ e^{\eta/2} + e^{-\eta/2} \biggr]^{-1} K\biggl(\tanh \frac{\eta}{2} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{\pi}{2} \cdot \cosh\frac{\eta}{2} \biggr]^{-1} K\biggl(\tanh \frac{\eta}{2} \biggr) \, . </math> |
This is, indeed, identical to the "Attempt #1" expression for <math>~P_{-1 / 2}(z)</math> that was used by Wong.
Q.E.D.
Series Expansions
From our accompanying set of Key mathematical relations we find the following series expansions for complete elliptic integrals of, respectively, the first and second kind:
|
<math>~\frac{2K(k)}{\pi}</math> |
<math>~=</math> |
<math>~ 1 + \biggl( \frac{1}{2} \biggr)^2k^2 + \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k^4 + \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k^6 + \biggl( \frac{1\cdot 3\cdot 5 \cdot 7}{2^7 \cdot 3}\biggr)^2 k^8 + \cdots + \biggl[ \frac{(2n-1)!!}{2^n n!} \biggr]^2 k^{2n} + \cdots </math> |
|
|
Gradshteyn & Ryzhik (1965), §8.113.1 |
|||
|
<math>~\frac{2E(k)}{\pi}</math> |
<math>~=</math> |
<math>~ 1 - \frac{1}{2^2} ~k^2 - \frac{1^2\cdot 3}{2^2\cdot 4^2}~ k^4 - \biggl(\frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2~\frac{ k^6 }{5} - \biggl( \frac{1\cdot 3\cdot 5 \cdot 7}{2^7 \cdot 3}\biggr)^2 \frac{k^8}{7} ~-~ \cdots - \biggl[ \frac{(2n-1)!!}{2^n n!} \biggr]^2 \frac{k^{2n}}{2n-1}
~-~ \cdots </math> |
|
|
Gradshteyn & Ryzhik (1965), §8.114.1 |
|||
If you don't know how to handle a double factorial — also referred to as a semifactorial — see, for example, this wikipedia page.
See Also
- P. Lucht (2016), The Charged Bowl in Toroidal Coordinates — Note from Tohline: On 3 July 2018 I stumbled on this article by Phil Lucht, who lists his affiliation as Rimrock Digital Technology (rimrock at emission.com), Salt Lake City, Utah. As I have done over the past approximately half a year, Lucht appears to have spent quite a bit of time investigating how toroidal coordinates might be used to solve a few specific potential problems. He draws on many of the same, rich technical resource publications as I have done and, at one point, explicitly expresses amazement at the extensive amount of useful material that can be found in [MF53]. Anyone digging into this topic would be well-advised to read Lucht's Overview and Summary — especially including the subsection titled, Legendre Functions — and to recognize that his document contains a large number of technically detailed appendices.
To provide one point of comparison with [MF53], Lucht derived an analytic expression for the potential outside of a torus (with toroidal-coordinate radius, <math>~\eta_0</math>) whose surface is held at uniform potential, <math>~\Phi_0</math>. This is in contrast to Wong's (1973) derivation — which we have verified, above — of the potential outside (as well as inside) of a torus having uniform charge/mass. For his particular example problem, Lucht obtains,<math>~\Phi(\eta,\theta)</math>
<math>~=</math>
<math>~ \Phi_0 \frac{\sqrt{2}}{\pi} \sqrt{\cosh\eta - \cos\theta} \sum_{n=0}^\infty \epsilon_n P_{n-\frac{1}{2}}(\cosh\eta) \Biggl[ \frac{Q_{n-\frac{1}{2}}(\cosh\eta_0)}{P_{n-\frac{1}{2}}(\cosh\eta_0)} \Biggr] \cos(n\theta) \, , </math>
Lucht (2016), p. 68, Eq. (10.1.11)
then he points out that the associated expression for the potential, which appears as equation (10.3.80) on p. 1304 of [MF53], is missing the Neumann factor, <math>~\epsilon_n</math>.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |