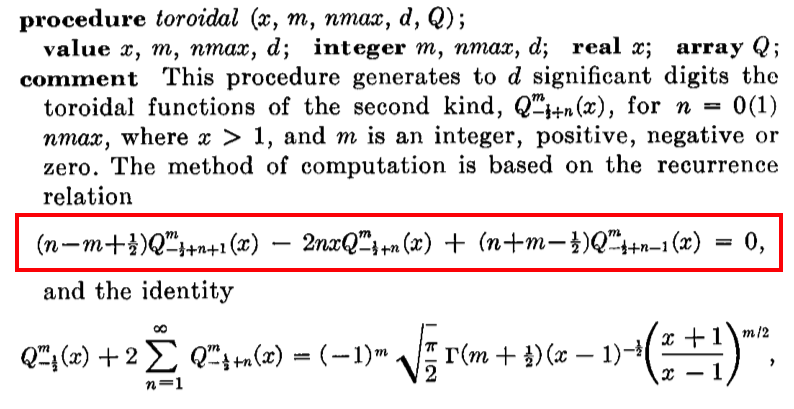Solving the (Multi-dimensional) Poisson Equation Numerically

Overview

The set of Principal Governing Equations that serves as the foundation of our study of the structure, stability, and dynamical evolution of self-gravitating fluids contains an equation of motion (the Euler equation) that includes an acceleration due to local gradients in the (Newtonian) gravitational potential, <math>~\Phi</math>. As has been pointed out in an accompanying chapter that discusses the origin of the Poisson equation, the mathematical definition of this acceleration is fundamentally drawn from Isaac Newton's inverse-square law of gravitation, but takes into account that our fluid systems are not ensembles of point-mass sources but, rather, are represented by a continuous distribution of mass via the function, <math>~\rho(\vec{x},t)</math>. As indicated, in our study, <math>~\rho</math> may depend on time as well as space. The acceleration felt at any point in space may be obtained by integrating over the accelerations exerted by each differential mass element. Alternatively — and more commonly — as has been explicitly demonstrated in, respectively, Step 1 and Step 3 of the same accompanying chapter, at any point in time the spatial variation of the gravitational potential, <math>~\Phi(\vec{x})</math>, is determined from <math>~\rho(\vec{x})</math> via either an integral or a differential equation as follows:

Table 1: Poisson Equation

Integral Representation

Differential Representation

<math>\nabla^2 \Phi = 4\pi G \rho</math>

While it is possible in some restricted situations to determine analytic expressions for the matched pair of functions, <math>~\Phi </math> and <math>~\rho</math>, that satisfy the Poisson equation, modeling the vast majority of interesting astrophysical problems requires the develop of a numerical scheme to solve the Poisson equation. In what follows, our aim is twofold: (a) To recount — in a reasonable amount of detail — the steps that we have taken over the past, approximately forty years to develop more and more accurate and efficient ways to solve the Poisson equation in full three-dimensional generality; and (b) to list/summarize alternative techniques that have been successfully employed by other research groups over the years.

Dimensionality …

2D or 3D

Computational Mesh Used for Differential Representation …

[Car]tesian [Cyl]indrical [Sph]erical Gridless ([Lag]rangian)

Green's Function for Integral Representation …

[Sph]erical [Tor]oidal Gridless ([Lag]rangian)

For each chosen problem, a research group must decide/specify, at a minimum: (1) The dimensionality of the problem; that is, whether the study will be restricted to 2D (e.g., axisymmetric) systems or whether the problem will be tackled in its full 3D complexity. (2) Whether the gravitational potential inside the mass distribution will be determined by solving the integral representation or the differential representation of the Poisson equation and, if the latter, in what coordinate frame (e.g., cylindrical or spherical) the differential operator and the computational mesh will be based. (Note that even when the interior solution is obtained by evaluating the differential representation of the Poisson equation, the integral representation will likely be employed to evaluate the potential on a boundary that lies outside the mass distribution.) (3) Which Green's function representation of the term, <math>~|\vec{x}^{~'} - \vec{x}|^{-1}</math>, will be used if/when the integral representation is evaluated. As the numerical techniques employed by each research group are introduced, below, a small red/green/yellow boxed icon has been interlaced with the text in an effort to highlight, up front, which choices the group has made.

Our Approach — Initially Heavily Influenced by Black & Bodenheimer (1975)

2D

Cyl

Sph

D. C. Black & P. Bodenheimer (1975, ApJ, 199, 619 - 632) published a detailed description of the numerical techniques that they implemented in an effort to model, in two dimensions, the dynamical collapse of axisymmetric interstellar gas clouds. Among the techniques was their method of solving, in cylindrical coordinates, the differential representation of the two-dimensional (2D) Poisson equation. Values of the potential along the outer boundaries of their cylindrical mesh were obtained by employing a spherical-harmonic expansion of the Green's function to evaluate the integral representation of the Poisson equation.

As is acknowledged in the last paragraph of their paper, Black & Bodenheimer were introduced "to the pitfalls of two-dimensional hydrodynamics" by Drs. J. LeBlanc and J. Wilson who, at the time, were both staff scientists at the Lawrence Livermore Laboratory. In 1976, having completed my formal graduate-level course work in the astronomy program at UC, Santa Cruz, Peter Bodenheimer (on the faculty of Lick Observatory and UC, Santa Cruz) asked me if I would be interested in working with him and David Black (a planetary scientist at NASA, Ames Research Center) on the development of a fully three-dimensional (3D) hydrodynamics code to study, not only the collapse, but also the fragmentation of self-gravitating gas clouds. I jumped at the opportunity. As a result, an effort to model the process of spontaneous cloud fragmentation became the focus of my doctoral dissertation research.

3D

Cyl

Sph

Borrowing from the Black & Bodenheimer (1975) work, I decided to solve the set of 3D principal governing equations on a cylindrical coordinate <math>~(\varpi, \phi, z)</math> mesh:

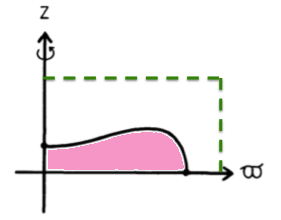
whose outermost radial and vertical boundaries were placed entirely outside of the mass distribution (by way of illustration, see the green-dashed lines in Figure 1);
that exhibited reflection symmetry through the <math>~(z = 0)</math> equatorial plane ;
that allowed for non-uniform (logarithmically stretched) grid spacing in both the radial and vertical directions; and,
(extending the Black & Bodenheimer work from 2D to 3D) with strictly uniform spacing in the azimuthal-coordinate direction.

Figure 1

Mesh Choice: In retrospect, I am still comfortable with the choice that was made, at the time, of a cylindrical coordinate mesh with uniform spacing in the azimuthal-coordinate direction. When expressed in terms of cylindrical coordinates — as opposed to cartesian coordinates, for example — the azimuthal component of the Euler equation offers a natural means by which the conservation of angular momentum can be monitored, if not enforced. And, by enabling the implementation of FFTs — hence, providing the ability to rapidly transform functions, like <math>~\Phi(\phi)</math> and <math>~\rho(\phi)</math>, back and forth between real space and Fourier space — a uniform descritization of the azimuthal grid facilitated the development of an efficient 3D Poisson solver as well as tools to straightforwardly analyze the behavior — e.g., the exponential growth — of individual nonaxisymmetric modes.

Also, following the lead of Black & Bodenheimer (1975), a hybrid scheme was developed to solve the Poisson equation. As defined in Table 1 above, its integral representation was evaluated at grid locations along the outermost radial and vertical boundaries — illustrated by the dashed green lines displayed in Figure 1 — by integrating over the "pink" mass distribution lying inside of these grid boundaries. Separately, the differential form of the Poisson equation was used to evaluate the potential at all interior grid locations; this differential expression was supplemented by the implementation of Neumann boundary conditions (reflection symmetry) along the equatorial plane, and by using the values of the potential just determined along the outermost grid boundaries to provide Dirichlet boundary conditions along those grid boundaries.

Determining Values of the Potential on the Mesh Boundary

Let's determine the potential, <math>~\Phi_B</math>, at all points along the boundary of the cylindrical coordinate mesh by evaluating Table 1's integral representation of the Poisson equation.

Using a Spherical Harmonic Expansion

Full Three-Dimensional Generality

Following the lead of Black & Bodenheimer (1975), we will insert into this integral relation the Green's function expression for <math>~|\vec{x}^{~'}- \vec{x} |^{-1} </math> as given in terms of Spherical Harmonics, <math>~Y_{\ell m}</math>, which in turn can be written in terms of Associated Legendre Functions. Table 2, below, provides the primary details.

Written in the context of a spherical coordinate system we have,

<math>~ \Phi_B(r,\theta,\phi)</math>	<math>~=</math>	<math>~ -G \int \frac{1}{\|\vec{x}^{~'} - \vec{x}\|} ~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~ -G \int \sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{+\ell} \frac{4\pi}{2\ell+1} \biggl[ \frac{r_<^\ell}{r_>^{\ell+1}} \biggr] Y_{\ell m}^*(\theta^', \phi^') Y_{\ell m}(\theta,\phi) ~\rho(r^', \theta^', \phi^') d^3x^' </math>
	<math>~=</math>	<math>~ -4\pi G \sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{+\ell} \frac{Y_{\ell m}(\theta,\phi)}{(2\ell+1)} \biggl[ \frac{1}{r^{\ell+1}}\int_0^r (r^')^\ell Y_{\ell m}^*(\theta^', \phi^') ~\rho(r^', \theta^', \phi^') d^3x^' </math>
		<math>~ + r^\ell \int_r^\infty (r^')^{-(\ell+1)} Y_{\ell m}^*(\theta^', \phi^') ~\rho(r^', \theta^', \phi^') d^3x^' \biggr] \, . </math>
[BT87], p. 66, Eq. (2-122)

If the distance from the origin, <math>~r</math>, of a boundary point (i.e., any point lying along the dashed green lines in Figure 1) is greater than the distance from the origin, <math>~r^'</math>, of all of the (pink) mass elements, the second integral can be completely ignored. We have, then, an expression that will henceforth be referred to as,

Form A of the Boundary Potential
<math>~ \Phi_B(r,\theta,\phi)</math>	<math>~=</math>	<math>~ -4\pi G \sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{+\ell} \frac{Y_{\ell m}(\theta,\phi)}{(2\ell+1)} \biggl[ \frac{1}{r^{\ell+1}}\int_0^r (r^')^\ell Y_{\ell m}^*(\theta^', \phi^') ~\rho(r^', \theta^', \phi^') d^3x^' \biggr] \, . </math>
Jackson (1975), p. 137, Eq. (4.2) [BLRY07], p. 238, Eqs. (7.53) - (7.54)

Rewriting this expression for <math>~\Phi_B</math> in terms of cylindrical coordinates — which aligns with our chosen grid coordinate system — and admitting that in practice our summation over the index, <math>~\ell</math>, cannot extend to infinity, we have,

<math>~ \Phi_B(\varpi, \phi, z)</math>

<math>~ -4\pi G \sum_{\ell=0}^{\ell_\mathrm{max}} \sum_{m=-\ell}^{+\ell} \frac{Y_{\ell m}}{(2\ell+1)} \biggl[ \varpi^2 + z^2 \biggr]^{-(\ell+1)/2} \int Y_{\ell m}^* \biggl[ (\varpi^')^2 + (z^')^2 \biggr]^{\ell/2} ~\rho(\varpi^', \phi^', z^') d^3x^' \, . </math>

Note that, as a consequence of assuming that our configurations have equatorial-plane symmetry, the weighted integral over the mass distribution necessarily goes to zero anytime the sum of the two indexes, <math>~(\ell + m)</math>, is an odd number. This is because, in each of these situations — again, see Table 2, below for details — the <math>~Y_{\ell m}</math> includes an overall factor of <math>~\cos\theta</math>, which necessarily switches signs between the two hemispheres. After setting <math>~\ell_\mathrm{max}=4</math> — and dropping all terms in the summation for which the index sum, <math>~(\ell + m)</math>, is odd — this expression becomes precisely the relation that was used to determine the boundary values of the gravitational potential in our earliest set of simulations; see, for example, Tohline (1978), Tohline (1980), and Bodenheimer, Tohline, & Black (1980).

Simplification for 2D, Axisymmetric Systems

It is easy to show that this last expression for <math>~\Phi_B</math> — which has been used in our 3D simulations — is a generalization of the expression for <math>~\Phi_B</math> that was employed by Black & Bodenheimer (1975) for 2D, axisymmetric simulations. In axisymmetric systems, by definition, physical variables exhibit no variation in the azimuthal coordinate direction. Hence, in the expression for <math>~\Phi_B</math>:

the azimuthal coordinate, <math>~\phi</math>, need not appear explicitly as an independent variable;
the index, <math>~m</math>, must be set to zero, so there is no summation over this index; and,
every surviving spherical harmonic can be written more simply in terms of a Legendre function, namely,

<math>~Y_{\ell m} \rightarrow Y_{\ell 0}</math>

where,

<math>~\chi \equiv \frac{z}{(\varpi^2 + z^2)^{1 / 2}} \, .</math>

Note that the argument, <math>~\chi</math>, is still the spherical-coordinate expression, <math>~\cos\theta</math>, but here it has been written in terms of cylindrical coordinates. We have, therefore,

<math>~ \Phi_B(\varpi, z)\biggr|_{2D}</math>

<math>~ - G \sum_{\ell=0}^{\ell_\mathrm{max}} P_\ell(\chi) \biggl[ \varpi^2 + z^2 \biggr]^{-(\ell+1)/2} \int P_\ell(\chi^') \biggl[ (\varpi^')^2 + (z^')^2 \biggr]^{\ell/2} ~\rho(\varpi^', z^') d^3x^' \, , </math>

where, <math>~d^3x^' = 2\pi \varpi^' d\varpi^' dz^'</math>. This is precisely the same as equation (5) from Black & Bodenheimer (1975); see also, equations (8) and (9) in Cohl & Tohline (1999).

Using Toroidal Functions

In 3D

3D

Cyl

Tor

NOTE: Throughout this chapter subsection, text that appears in a dark green font has been taken verbatim from H. S. Cohl & J. E. Tohline (1999).

As mentioned above, from the beginning of my research activities — following the lead of Black & Bodenheimer — it has seemed reasonable to me that numerical simulations of time-evolving, rotationally flattened fluid systems should be carried out on a cylindrical, rather than cartesian, coordinate mesh. When modeling rotationally flattened configurations, a cylindrical mesh has even seemed preferable to a spherical coordinate mesh because the "top" grid boundary (horizontal green-dashed line segment in Figure 1) can straightforwardly be dropped to a <math>~z</math>-coordinate location that is smaller than the <math>~\varpi</math>-coordinate location of the "side" grid boundary (vertical green-dashed line segment in Figure 1), thereby reducing the number of grid cells — and, correspondingly reducing the cost of modeling the less interesting, vacuum region — outside of the fluid system. [See, however, Boss (1980) for an alternate point of view.] At the same time, however, it has not seemed reasonable to determine the values of the potential along the (cylindrical-grid) boundary by adopting a Green's function that is expressed in terms spherical harmonics.

Over a period of approximately twenty years, off and on, my research group considered whether it might be advantageous in our numerical simulations to cast the Green's function in a cylindrical coordinate system. The "familiar" expression for the cylindrical Green's function expansion can be found in variety of references (see [MF53]; Jackson (1975)), and for convenience is repeated below. It is expressible in terms of an infinite sum over the azimuthal quantum number <math>~m</math> and an infinite integral over products of Bessel functions of various orders multiplied by an exponential function. Note that J. V. Villumsen (1985, ApJ, 290, 75 - 85) attempted to solve the potential problem in this manner; he presents a technique in which each infinite integral over products of Bessel functions is evaluated numerically using a Gauss-Legendre integrator … He then emphasizes the obvious problem that, because of the infinite integrals involved, a calculation of the potential via this straightforward application of the familiar cylindrical Green's function expansion is numerically much more difficult than a calculation of the potential using a spherical Green's function expansion.

Eureka! Via his dogged efforts and an extraordinarily in-depth investigation of this problem, in 1999 Howard S. Cohl discovered that, in cylindrical coordinates, the relevant Green's function can be written in a much more compact and much more practical form. Specifically, he realized that,

<math>~ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \, , </math>

where,

<math>~\chi \equiv \frac{\varpi^2 + (\varpi^')^2 + (z - z^')^2}{2\varpi \varpi^'} \, ,</math>

H. S. Cohl & J. E. Tohline (1999), p. 88, Eqs. (15) & (16)
See also: Selvaggi, Salon & Chari (2007) §II, eq. (5)
and the DLMF's definition of Toroidal Functions, <math>~Q_{m - 1 / 2}^{0}</math>

and, <math>~Q_{m - 1 / 2}</math> is the zero-order, half-(odd)integer degree, Llegendre function of the second kind — also referred to as a toroidal function of zeroth order; see additional details, below. Hence, anywhere along the boundary of our cylindrical-coordinate mesh, a valid expression for the gravitational potential is,

<math>~ \Phi_B(\varpi,\phi,z)</math>	<math>~=</math>	<math>~ -G \int \frac{1}{\|\vec{x}^{~'} - \vec{x}\|} ~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~ -G \int \biggl\{ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \biggr\}~ \rho(\varpi^',\phi^',z^') \varpi^' d\varpi^' d\phi^' dz^' </math>
	<math>~=</math>	<math>~ -\frac{G}{\pi \sqrt{\varpi}} \int \rho(\varpi^',\phi^',z^') \sqrt{\varpi^'} d\varpi^' d\phi^' dz^' \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, , </math>
H. S. Cohl & J. E. Tohline (1999), p. 88, Eq. (18)

where, <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0=1</math> and <math>~\epsilon_m = 2</math> for <math>~m\ge 1</math>. Following this discovery, most of my research group's 3D numerical modeling of self-gravitating fluids has been conducted using Toroidal functions instead of Spherical Harmonics to evaluate the boundary potential on our cylindrical-coordinate meshes; see, for example, P. M. Motl, J. E. Tohline & J. Frank (2002); C. D. Ott, S. Ou, J. E. Tohline & A. Burrows (2005); M. C. R. D'Souza, P. M. Motl, J. E. Tohline, & J. Frank (2006); and D. C. Marcello & J. E. Tohline (2012).

For Axisymmetric Systems

As was done, above, in the context of our discussion of a spherical-harmonics-based expression for the boundary potential, let's consider how this toroidal-function-based expression for the boundary potential can be simplified when examining 2D (axisymmetric) rather than fully 3D systems. In axisymmetric systems, by definition, physical variables exhibit no variation in the azimuthal coordinate direction. Hence, in the expression for <math>~\Phi_B</math>:

the azimuthal coordinate, <math>~\phi</math>, need not appear explicitly as an independent variable, so the integral over this angular coordinate immediately gives, <math>~2\pi</math>;
the index, <math>~m</math>, must be set to zero, so there is no summation over this index; and,
drawing from the additional details provided in Table 5, below the single surviving toroidal function is, <math>~Q_{-1 / 2}</math>, which can be rewritten in terms of the complete elliptic integral of the first kind.

As a result of these simplifications, anywhere along the boundary of our cylindrical-coordinate mesh, a valid expression for the axisymmetric gravitational potential is,

<math>~ \Phi_B(\varpi,z)\biggr\|_{2D}</math>	<math>~=</math>	<math>~ -\frac{2G}{\sqrt{\varpi}} \int\limits_{\varpi^'} \int\limits_{z^'} d\varpi^' dz^' \rho(\varpi^',z^') \sqrt{\varpi^'} Q_{- 1 / 2}(\chi) </math>
	<math>~=</math>	<math>~ -\frac{2G}{\sqrt{\varpi}} \int\limits_{\varpi^'} \int\limits_{z^'} d\varpi^' dz^' \rho(\varpi^',z^') \sqrt{\varpi^'} \mu K(\mu) \, , </math>
H. S. Cohl & J. E. Tohline (1999), p. 89, Eqs. (31) & (32)

where,

<math>~\equiv</math>

<math>~\biggl[ \frac{2}{1+\chi} \biggr]^{1 / 2} = \biggl[ \frac{4\varpi \varpi^'}{(\varpi + \varpi^')^2 + (z - z^')^2} \biggr]^{1 / 2} \, . </math>

Actually, this expression for the potential is not only valid along the outer boundaries of the computational mesh, but anywhere inside or outside of the mass distribution.

Extension from 2D to 3D

An extension from 2D to 3D was accomplished by using separate, finite Fourier series expansion to represent the azimuthal dependence of <math>~\rho</math> and <math>~\Phi</math>. This allowed us to decouple the differential expression for the Poisson equation into a finite number of independent Fourier modes, and to straightforwardly solve a finite set of 2D Helmholtz equations, instead of solving a single 2D Poisson equation.

Intermediate

Much of the material enclosed in this text box has been drawn from §3.1 of Jackson (1975).

In spherical coordinates, <math>~(r,\theta,\phi)</math>, the Poisson equation takes the form,

<math>~4\pi G \rho(r,\theta,\phi)</math>

<math>~ \frac{1}{r} \frac{\partial^2}{\partial r^2} (r\Phi) + \frac{1}{r^2 \sin\theta} \frac{\partial}{\partial\theta} \biggl( \sin\theta \frac{\partial\Phi}{\partial\theta}\biggr) + \frac{1}{r^2 \sin^2\theta} \frac{\partial^2\Phi}{\partial\phi^2} \, . </math>

As it turns out, the potential — which, generally, is a function of all three coordinates — can be written as the product of three functions, each of which is a function of only one coordinate. To demonstrate this, specifically suppose that,

<math>~\Phi(r,\theta,\phi)</math>

<math>~ \frac{U( r )}{r} P(\theta)Q(\phi) \, . </math>

Then the differential form of the Poisson equation can be rewritten as,

<math>~4\pi G \rho(r,\theta,\phi)</math>	<math>~=</math>	<math>~ \frac{PQ}{r} \frac{d^2U}{dr^2} + \frac{UQ}{r^3\sin\theta} \frac{d}{d\theta}\biggl(\sin\theta \frac{dP}{d\theta}\biggr) + \frac{UP}{r^3\sin^2\theta} \frac{d^2Q}{d\phi^2} </math>
<math>~\Rightarrow ~~~ \biggl[ \frac{r^3 \sin^2\theta}{ UPQ} \biggr] 4\pi G \rho(r,\theta,\phi)</math>	<math>~=</math>	<math>~\biggl[ \frac{r^3 \sin^2\theta}{ UPQ} \biggr] \biggl\{ \frac{PQ}{r} \frac{d^2U}{dr^2} + \frac{UQ}{r^3\sin\theta} \frac{d}{d\theta}\biggl(\sin\theta \frac{dP}{d\theta}\biggr) + \frac{UP}{r^3\sin^2\theta} \frac{d^2Q}{d\phi^2} \biggr\} </math>
	<math>~=</math>	<math>~ \biggl[ \frac{r^2\sin^2\theta}{U} \biggr] \frac{d^2U}{dr^2} + \frac{\sin\theta}{P} \frac{d}{d\theta}\biggl(\sin\theta \frac{dP}{d\theta}\biggr) + \frac{1}{Q} \frac{d^2Q}{d\phi^2} \, . </math>

Setting, <math>~Q = e^{\pm im\phi}</math>, gives,

<math>~ \biggl[ \frac{r^3 \sin^2\theta}{ UP e^{\pm i m\phi }} \biggr] 4\pi G \rho(r,\theta,\phi)</math>	<math>~=</math>	<math>~ \biggl[ \frac{r^2\sin^2\theta}{U} \biggr] \frac{d^2U}{dr^2} + \frac{\sin\theta}{P} \frac{d}{d\theta}\biggl(\sin\theta \frac{dP}{d\theta}\biggr) -m^2 </math>
<math>~\Rightarrow ~~~ \biggl[ \frac{r^3 }{ UP e^{\pm i m\phi}} \biggr] 4\pi G \rho(r,\theta,\phi)</math>	<math>~=</math>	<math>~ \biggl( \frac{r^2 }{U} \biggr) \frac{d^2U}{dr^2} + \biggl[ \frac{1}{P\sin\theta} \frac{d}{d\theta}\biggl(\sin\theta \frac{dP}{d\theta}\biggr) - \frac{m^2}{\sin^2\theta} \biggr] \, . </math>

Now, if for each selected pair of the integer indexes, <math>~(\ell, m)</math>, the function <math>~P</math> is identified as the associated Legendre function, <math>~P_\ell^m</math>, as defined above in Table 2, then the set of terms inside the square brackets on the right-hand-side of this last expression can be set equal to <math>~[-\ell(\ell + 1)]</math> because every associated Legendre function satisfies the differential equation,

<math>~ \frac{1}{P_\ell^m \sin\theta} \frac{d}{d\theta}\biggl(\sin\theta \frac{dP_\ell^m}{d\theta}\biggr) + \ell(\ell+1) - \frac{m^2}{\sin^2\theta}</math>

Rewriting our adopted separable expression for the potential as the sum over all possible <math>~(\ell,m)</math>-component solutions, that is,

<math>~\Phi(r,\theta,\phi) = \sum_{\ell=0}^\infty \sum_{m=-\ell}^\ell [\Phi(r,\theta,\phi)]_{\ell m}</math>

<math>~ \sum_{\ell=0}^\infty \sum_{m=-\ell}^\ell \frac{U_{\ell m}( r )}{r} P_\ell^m(\theta)Q_m(\phi) \, , </math>

a solution to the Poisson equation then imposes the requirement that, for each <math>~(\ell,m)</math> pair,

<math>~ \biggl( \frac{r^2 }{U_{\ell m}} \biggr) \frac{d^2U_{\ell m} }{dr^2} - \ell(\ell+1) </math>	<math>~=</math>	<math>~ \biggl[ \frac{r^3 }{ U_{\ell m} P_\ell^m e^{\pm i m\phi}} \biggr] 4\pi G [\rho(r,\theta\phi)]_{\ell m} </math>
<math>~\Rightarrow ~~~ \frac{1}{r} \frac{d^2U_{\ell m} }{dr^2} - \biggl[ \frac{\ell(\ell+1)}{r^2} \biggr]\frac{U_{\ell m} }{r} </math>	<math>~=</math>	<math>~ \biggl[ \frac{1}{ P_\ell^m e^{\pm i m\phi}} \biggr] 4\pi G [\rho(r,\theta\phi)]_{\ell m} \, .</math>

Other Approaches

Deupree (1974)

2D

Sph

Tor

"The fully nonlinear, nonradial, nonadiabatic calculation of stellar oscillations has not as yet been attempted by anyone, to the best of the author's knowledge. Only Deupree (1974b, 1975) so far seems to have taken some steps in this direction. He has carried out numerical calculations of the nonlinear axisymmetric oscillations in the adiabatic (Deupree 1974b) and nonadiabatic (Deupree 1975) approximations, with apparently encouraging results."

— Drawn from §3.5 of the review article by J. P. Cox (1976, ARAA, 14, 247 - 273)

Apparently, R. G. Deupree (1974, ApJ, 194, 393 - 402) was the first astronomer to employ self-gravitating, numerical hydrodynamic techniques to model nonlinear, nonradial stellar pulsations. He chose to carry out his simulations on a spherical coordinate mesh with his earliest simulations being restricted to the examination of 2D (axisymmetric) configurations. The outer boundary of his computational grid was identified as (see his §IIb) a spherical surface completely exterior to the star.

His Derived Expression for the Boundary Potential

In designing an algorithm to solve the Poisson equation, Deupree (1974) considered the major difficulty [to be] the evaluation of the potential boundary conditions. He decided to determine the boundary potential via an evaluation of the integral representation of the Poisson equation; once the boundary conditions [were] specified, the potential inside the star [was] evaluated by [employing] the Henyey method to solve the differential representation of the Poisson equation. The assumption of azimuthal symmetry meant that, for example, the density was specified at various meridional-plane locations, <math>~\rho(r,\theta)</math>, with each zone [being] considered as a uniform density circular ring. He argued that the potential of [each such] ring at any point on the spherical boundary [could] easily be evaluated by treating it as an infinitesimally thin ring of mass, <math>~\delta M = 2\pi a \rho ~\delta A</math> — where, <math>~\delta A</math> is the cross-sectional area of the [grid] zone, and <math>~a</math> is the radius of [that] ring — then drawing upon the analytic analysis described by Kellogg (1929) or, equivalently, by MacMillan (1958; originally 1930). Then, the total potential at the boundary is the sum of the potentials from all of the [meridional-plane] zones.

Note that, over the years, a number of other research groups have adopted this same approach to evaluate the gravitational potential of axisymmetric mass distributions — that is, summing up the potential contributions due to an ensemble of "infinitesimally thin rings." But none appear to have recognized Deupree's earlier, pioneering investigation. See, for example, the brief reviews that we have written regarding the related investigations by: Stahler (1983), Bannikova et al. (2011), and Fukushima (2016).

More specifically, equation (16) from Deupree (1974) states that the differential contribution to the boundary potential due to each infinitesimally thin ring is,

<math>~\delta\Phi_B</math>

<math>~ - \frac{2G(2\pi a\rho ~\delta A)}{\pi p} \int_0^{\pi/2} \frac{d\psi}{[\cos^2\psi + (q/p)^2\sin^2\psi]^{1 / 2}} \, , </math>

where, <math>~q</math> is the shortest distance between the ring and the boundary point, and <math>~p</math> is the longest distance. (Note that, in order to match our conventions, we have inserted the negative sign along with a leading factor of <math>~G</math>.) Referencing our accompanying detailed analysis of the potential due to a thin ring, and adopting the variable mappings, <math>~p \leftrightarrow \rho_1</math> and <math>~q \leftrightarrow \rho_2</math>, we see that Deupree's expression is indeed identical to the expression for the potential derived by MacMillan (1958). Recognizing, as did MacMillan, that the definite integral in this expression is related to the complete elliptic integral of the first kind, and introducing the ratio of lengths, <math>~c \equiv p/q</math>, Deupree's expression for the (differential contribution to the) potential can be rewritten as,

<math>~\delta\Phi_B</math>	<math>~=</math>	<math>~- \frac{2G (2\pi a\rho ~\delta A) c}{\pi p} \int_0^{\pi/2} \frac{d\psi}{ \sqrt{1 - k^2 \sin^2\psi }} </math>
	<math>~=</math>	<math>~- \biggl[ \frac{2G (2\pi a\rho ~\delta A) c}{\pi p} \biggr] K(k) \, ,</math>

where, <math>~K(k)</math> is the complete elliptic integral of the first kind for the modulus, <math>~k = \sqrt{1-c^2}</math>.

Comparison With Other Related Derivations

Now, given that Deupree chose to construct and evolve his models using a spherical coordinate system, he would have specified the relevant lengths, <math>~p</math> and <math>~q</math>, and each ring's differential cross-section, <math>~\delta A</math>, in terms of spherical coordinates. In an effort to more clearly illustrate the connection between Deupree's expression for the (differential contribution to the) boundary potential and the expression for the boundary potential that we have derived above for axisymmetric systems, we will insert expressions for these terms that apply, instead, to a cylindrical-coordinate mesh.

Following the same line of reasoning as has been presented in our accompanying discussion of MacMillan's work, if the meridional-plane locations of the infinitesimally thin ring and the desired point on the boundary are, respectively, <math>~(\varpi^',z^')</math> and <math>~(\varpi,z)</math>, we see that,

<math>~ \biggl[\frac{4\varpi \varpi^'}{(\varpi + \varpi^')^2 + (z - z^')^2 }\biggr]^{1 / 2} \, ,</math>

and,

<math>~\biggl[(\varpi + \varpi^')^2 + (z - z^')^2 \biggr]^{- 1 / 2} = \frac{k}{\sqrt{4\varpi \varpi^'}} \, .</math>

Hence — after acknowledging that, in cylindrical coordinates, the radius of each "infinitesimally thin ring" is, <math>~a = \varpi^'</math>, and the differential cross-section of each ring is, <math>~\delta A = \delta\varpi^' \delta z^'</math> — Deupree's expression for the (differential contribution to the) potential may be rewritten as,

<math>~\delta\Phi_B(\varpi,z)</math>	<math>~=</math>	<math>~- \frac{G (2\pi a \rho ~\delta A) }{\pi } \biggl[ \frac{k }{\sqrt{\varpi \varpi^'}} \biggr] K(k) </math>
	<math>~=</math>	<math>~- \frac{2G (\delta M) }{\pi } \cdot \frac{K(k) }{ \sqrt{(\varpi + a)^2 + (z - z^')^2 }} \, , </math>

or it may be rewritten as,

<math>~\delta\Phi_B(\varpi,z)</math>	<math>~=</math>	<math>~- \frac{G (2\pi a \rho ~\delta A) }{\pi } \biggl[ \frac{k }{\sqrt{\varpi \varpi^'}} \biggr] K(k) </math>
	<math>~=</math>	<math>~- \frac{2G }{\sqrt{\varpi}} \biggl[ \delta\varpi^' \delta z^' \rho(\varpi^', z^') \sqrt{\varpi^'} k K(k) \biggr] \, .</math>

Notice that the first of these two rewritten expressions aligns perfectly with our "key equation" that gives the gravitational potential of an axisymmetric torus in the thin ring (TR) approximation, namely,

	<math>~\Phi_\mathrm{TR}(\varpi,z)</math>	<math>~=</math>	<math>~-\biggl[ \frac{2GM}{\pi } \biggr]\frac{K(k)}{\sqrt{(\varpi+a)^2 + z^2}}</math>
<math>\mathrm{where:}~~~k \equiv \{4\varpi a/[ (\varpi+a)^2 + z^2]\}^{1 / 2}</math>

(See our accompanying discussion for more information on the meridional-plane contour plot that is displayed to the right of this equation.) Next, referring back to the expression that was derived above for axisymmetric systems from a toroidal-function-based Green's function, namely,

<math>~ \Phi_B(\varpi,z)\biggr\|_{2D}</math>	<math>~=</math>	<math>~ -\frac{2G}{\sqrt{\varpi}} \int\limits_{\varpi^'} \int\limits_{z^'} d\varpi^' dz^' \rho(\varpi^',z^') \sqrt{\varpi^'} \mu K(\mu) \, , </math>
H. S. Cohl & J. E. Tohline (1999), p. 89, Eqs. (31) & (32)

where,

<math>~ \biggl[ \frac{4\varpi \varpi^'}{(\varpi + \varpi^')^2 + (z - z^')^2} \biggr]^{1 / 2} \, , </math>

we see that the second of these rewritten expressions for Deupree's <math>~\delta\Phi_B</math> aligns perfectly with our derived expression for the differential contribution to the potential of any axisymmetric mass distribution. It is therefore fair to say that the expression that Deupree used to determine the gravitational potential along the boundary of his modeled configurations is derivable from a 3D Green's function that is written in terms of toroidal functions.

Cook (1977)

3D

Cyl

Key results from T. L. Cook's (1977) doctoral dissertation — titled, Three-Dimensional Dynamics of Protostellar Evolution — were published as T. L. Cook & F. H. Harlow (1978, ApJ, 225, 1005 - 1020). Cook's three-dimensional hydrodynamic simulations were conducted on a cylindrical-coordinate mesh. While few details of the technique used to solve the Poisson equation are provided in the ApJ article, §II.B of Cook's (1977) dissertation explains that values of the gravitational potential across the interior regions of the mesh were obtained by solving the differential representation of the Poisson equation, subject to the boundary conditions at each boundary point, calculated by "performing a numerical integration over all mass points" using the integral representation of the Poisson equation, namely,

<math>~ \Phi_B(\varpi,\phi,z)</math>

with,

<math>~\frac{1}{\|\vec{x}^{~'} - \vec{x}\|}</math>	<math>~=</math>	<math>~ \biggl[ \varpi^2 + (\varpi^')^2 - 2\varpi \varpi^' \cos\|\phi - \phi^'\| + (z - z^')^2 \biggr]^{- 1 / 2} \, . </math>
Cook (1977), p. 15, Eq. (II-16) See also: Selvaggi, Salon & Chari (2007) §II, eq. (2)

(Note that the leading factor of the gravitational constant, <math>~G</math>, does not appear explicitly in Cook's equation II-16, although it should.) Presumably the coordinate locations of the boundary cells, <math>~(\varpi,\phi,z)</math>, were in no case coincident with the coordinate locations of any of the interior grid cells, <math>~(\varpi^',\phi^',z^')</math>, so there was no danger that the integration would encounter a singularity as a consequence of the distance, <math>~|\vec{x}^{~'} - \vec{x}|</math>, being zero.

Norman and Wilson (1978)

3D

Cyl

Sph

Following the discussion presented in §4.1 of Jackson (1975), it is sometimes useful to rewrite Form A of the boundary potential as,

<math>~ \Phi_B(r,\theta,\phi)</math>

<math>~ -4\pi G \sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{+\ell} \frac{q_{\ell m}}{r^{\ell+1}} \frac{Y_{\ell m}(\theta,\phi)}{(2\ell+1)} \, , </math>

where we have introduced what is commonly referred to as the,

Multipole Moments of the Mass Distribution
<math>~q_{\ell m}</math>	<math>~\equiv</math>	<math>~ \int (r^')^\ell Y_{\ell m}^*(\theta^', \phi^') ~\rho(r^', \theta^', \phi^') d^3x^' \, . </math>
Jackson (1975), p. 137, Eq. (4.3)

When written explicitly in terms of cartesian coordinates — see Table 2, below, for each of the relevant <math>~Y_{\ell m}</math> expressions — the first few of these moments have the functional representations derived below. For the cases that correspond to positive values of the index, <math>~m</math>, the set of multipole moment expressions that have been included in our Table 3 summary exactly matches the set of expressions presented as equations (4.4), (4.5), and (4.6) in Jackson (1975). (Jackson's equation 4.7 explains how to map these expressions to the cases corresponding to negative values of the index, <math>~m</math>.)

Let's now look at various terms in the summed expression for the boundary potential with each term expressing the contribution for a separate value of the index, <math>~\ell</math>. Isolating the first three terms from all the rest, for example, we have,

<math>~ \Phi_B(r,\theta,\phi)</math>

<math>~ \Phi_B(r,\theta,\phi) \biggr|_{\ell=0} +~ \Phi_B(r,\theta,\phi)\biggr|_{\ell=1} + ~\Phi_B(r,\theta,\phi)\biggr|_{\ell=2} -~4\pi G \sum_{\ell=3}^{\infty} \sum_{m=-\ell}^{+\ell} \frac{q_{\ell m}}{r^{\ell+1}} \frac{Y_{\ell m}(\theta,\phi)}{(2\ell+1)} \, . </math>

We recognize, first, that as we consider boundary points that lie farther and farther away from the mass distribution, the magnitude of the first <math>(\ell = 0)</math> term drops off as <math>~r^{-1}</math> — the expected behavior of the potential outside of a point mass; the second <math>~(\ell=1)</math> term drops off as <math>~r^{-3}</math>; and the third <math>~(\ell=2)</math> term drops off as <math>~r^{-5}</math>. Below, we have evaluated in more detail the behavior of these first three terms. This evaluation gives us the,

Boundary Potential Written in Terms of Multipole Moments
<math>~ \Phi_B(r,\theta,\phi)</math>	<math>~=</math>	<math>~ ~-~~\frac{GM}{r} ~~- ~~\frac{GM}{r^3} \biggl[ \vec{x} \cdot \vec{x}_\mathrm{com} \biggr] ~~-~~\frac{G}{2r^5} \sum_{i=1}^3 \sum_{j=1}^3 Q_{i,j} \biggl[ x_i x_j \biggr] ~~-~~4\pi G \sum_{\ell=3}^{\infty} \sum_{m=-\ell}^{+\ell} \frac{q_{\ell m}}{r^{\ell+1}} \frac{Y_{\ell m}(\theta,\phi)}{(2\ell+1)} \, , </math>

where, as defined below, <math>~\vec{x}_\mathrm{com}</math> is the center-of-mass location, and <math>~Q_{i,j} </math> is the traceless quadrupole moment tensor.

If a modeled mass-density distribution, <math>~\rho( \vec{x}^{~'})</math>, has been configured such that the center-of-mass of the system coincides with the origin of the coordinate system — that is, if it has been configured such that <math>~\vec{x}_\mathrm{com} = 0</math> — then the second term in this series can be set to zero. If, in addition, all terms having <math>~\ell \ge 3</math> are ignored because their values drop off rapidly with distance — specifically, inverse distance to the <math>~(2\ell + 1)</math> power — then a reasonably good approximation for the potential on the boundary of the modeled system is given by the expression,

<math>~\approx</math>

<math>~ -\frac{GM}{r} ~-\frac{G}{2r^5} \sum_{i=1}^3 \sum_{j=1}^3 Q_{i,j} \biggl[ x_i x_j \biggr] \, . </math>

This is precisely the relation that was adopted by M. L. Norman & J. R. Wilson (1978, ApJ, 224, 497 - 511) when, in the context of star formation, they modeled the Fragmentation of Isothermal Rings — see specifically their equation (18).

Boss (1980)

3D

Sph

Building upon equations (5) and (7) from A. P. Boss (1980, ApJ, 236, 619 - 627) — see also Jackson's equation (3.58) — we can write,

<math>~\Phi(r,\theta,\phi)</math>

<math>~ \sum_{\ell=0}^\infty \sum_{m = -\ell}^{\ell} \Phi_{\ell m} ( r ) Y_{\ell m}(\theta,\phi) \, , </math>

and,

<math>~\rho(r,\theta,\phi)</math>

<math>~ \sum_{\ell=0}^\infty \sum_{m = -\ell}^{\ell} \rho_{\ell m} ( r ) Y_{\ell m}(\theta,\phi) \, , </math>

where the coefficients in the series expansion of <math>~\rho</math> can each be obtained from the known spatial density distribution via the integral expression,

<math>~ \int d\Omega Y_{\ell m}^*(\theta,\phi) \rho(r,\theta,\phi) \, , </math>

and the differential solid angle is,

<math>~d\Omega \equiv \sin\theta d\theta d\phi \, .</math>

Stahler (1983)

2D

Tor

Stahler (1983a) used a self-consistent-field technique to construct equilibrium sequences of rotationally flattened, isothermal gas clouds. At each iteration step, the method that he adopted to evaluate the gravitational potential along the outer boundary of his computational mesh was essentially the same as the method used by Deupree (1974) — see our above description — to model the time-dependent behavior of pulsating stars. It appears as though Stahler was unaware of Deupree's earlier development of this method to evaluate the boundary potential, as Deupree's (1974) paper is not among Stahler's list of references.

In describing Stahler's (1983a) method, we will first draw upon our "key equation" that gives the gravitational potential of an axisymmetric torus in the thin ring (TR) approximation, namely,

	<math>~\Phi_\mathrm{TR}(\varpi,z)</math>	<math>~=</math>	<math>~-\biggl[ \frac{2GM}{\pi } \biggr]\frac{K(k)}{\sqrt{(\varpi+a)^2 + z^2}}</math>
<math>\mathrm{where:}~~~k \equiv \{4\varpi a/[ (\varpi+a)^2 + z^2]\}^{1 / 2}</math>

(See our accompanying discussion for more information on the meridional-plane contour plot that is displayed to the right of this equation.) Stahler has argued that a reasonably good approximation to the gravitational potential due to any extended axisymmetric mass distribution can be obtained by adding up the contributions due to many thin rings — <math>~\delta M(\varpi^', z^')</math> being the appropriate differential mass contributed by each ring element — positioned at various meridional coordinate locations throughout the mass distribution. According to his independent derivation, the differential contribution to the potential, <math>~\delta\Phi_g(\varpi, z)</math>, due to each differential mass element is (see his equation 11 and the explanatory text that follows it):

<math>~\delta\Phi_g(\varpi,z)</math>	<math>~=</math>	<math>~ - \biggl[\frac{2G}{\pi \varpi^'}\biggr] \frac{\delta M}{[(\alpha + 1)^2 + \beta^2]^{1 / 2}} \times K\biggl\{ \biggl[ \frac{4\alpha}{(\alpha+1)^2 + \beta^2} \biggr]^{1 / 2} \biggr\} </math>
	<math>~=</math>	<math>~ - \biggl[\frac{2G}{\pi }\biggr] \frac{\delta M}{[(\varpi + \varpi^')^2 + (z^' - z)^2]^{1 / 2}} \times K\biggl\{ \biggl[ \frac{4\varpi^' \varpi}{(\varpi +\varpi^')^2 + (z^' - z)^2} \biggr]^{1 / 2} \biggr\} \, . </math>

Stahler's expression for each thin ring contribution is clearly the same as our "key equation" expression for <math>~\Phi_\mathrm{TR}</math> if the individual ring being considered cuts through the meridional plane at <math>~(\varpi^', z^') = (a, 0)</math>.

In the context of our above discussion of a Green's function expression written in terms of toroidal functions, we have shown that the exact integral expression for the gravitational potential due to any axisymmetric mass-density distribution, <math>~\rho(\varpi^', z^')</math>, is,

<math>~\Phi(\varpi, z)</math>

<math>~- \frac{2G}{\varpi^{1 / 2}} \int\int (\varpi^')^{1 / 2} \mu K(\mu) \rho(\varpi^', z^') d\varpi^' dz^' \, ,</math>

where,

<math>~ \biggl[\frac{4\varpi^' \varpi}{(\varpi + \varpi^')^2 + (z^' - z)^2} \biggr] \, . </math>

Recognizing that, for axisymmetric structures, the differential mass element is, <math>~dM^' = 2\pi \rho(\varpi^', z^') \varpi^' d\varpi^' dz^'</math>, this integral expression may be rewritten as,

<math>~\Phi(\varpi, z)</math>	<math>~=</math>	<math>~- \frac{2G}{\varpi^{1 / 2}} \int\int (\varpi^')^{1 / 2} \mu K(\mu) \biggl[ \frac{dM^'}{2\pi \varpi^'} \biggr] </math>
	<math>~=</math>	<math>~- \frac{G}{\pi} \int\int \biggl[ \frac{1}{\varpi^'\varpi}\biggr]^{1 / 2} \biggl[\frac{4\varpi^' \varpi}{(\varpi + \varpi^')^2 + (z^' - z)^2} \biggr]^{1 / 2} K(\mu) dM^' </math>
	<math>~=</math>	<math>~- \frac{2G}{\pi} \int\int \biggl[\frac{1}{(\varpi + \varpi^')^2 + (z^' - z)^2} \biggr]^{1 / 2} K(\mu) dM^' \, .</math>

We see that our expression for the differential contribution to the potential exactly matches Stahler's (1983a). It is therefore fair to say that Stahler's expression for the gravitational potential is derivable from a 3D Green's function that is written in terms of toroidal functions. We note that, in his study of axisymmetric systems, Stahler made the decision to evaluate the gravitational potential both inside as well as outside of the mass distribution using the same integral expression.

Constructing Two-Dimensional, Axisymmetric Structures

As has been explained in an accompanying discussion, our objective is to solve an algebraic expression for hydrostatic balance,

<math>~H + \Phi + \Psi = C_0</math> ,

in conjunction with the Poisson equation in a form that is appropriate for two-dimensional, axisymmetric systems, namely,

<math>~ \frac{1}{\varpi} \frac{\partial }{\partial\varpi} \biggl[ \varpi \frac{\partial \Phi}{\partial\varpi} \biggr] + \frac{\partial^2 \Phi}{\partial z^2} = 4\pi G \rho . </math>

Steps to Follow

Annotation of
Figure 1 from I. Hachisu (1986)

One quadrant of a meridional-plane cross-section (pink) through: (a) spheroidal structure; (b) toroidal structure. A green, dashed rectangular grid boundary is also illustrated.

Choose a particular barotropic equation of state. More specifically, functionally define the density-enthalpy relationship, <math>~\rho(H)</math>, and identify what value, <math>~H_\mathrm{surface}</math>, the enthalpy will have at the surface of your configuration. For example, if a polytropic equation of state is adopted, <math>~H_\mathrm{surface} = 0</math> is a physically reasonable prescription.
Choosing from, for example, a list of astrophysically relevant simple rotation profiles, specify the corresponding functional form of the centrifugal potential, <math>~\Psi(\varpi)</math>, that will define the radial distribution of specific angular momentum in your equilibrium configuration. If the choice is uniform rotation, then <math>~\Psi = - \varpi^2 \omega_0^2/2 \, ,</math> where <math>~\omega_0</math> is a constant to be determined.
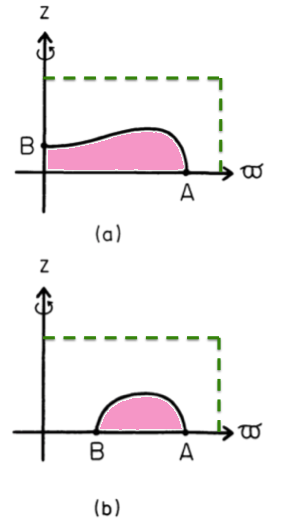
On your chosen computational lattice — for example, on a cylindrical-coordinate mesh — identify two boundary points, A and B, that will lie on the surface of your equilibrium configuration. These two points should remain fixed in space during the HSCF iteration cycle and ultimately will confine the volume and define the geometry of the derived equilibrium object. Note that, by definition, the enthalpy at these two points is, <math>~H_A = H_B = H_\mathrm{surface}</math>.
Throughout the volume of your computational lattice, guess a trial distribution of the mass density, <math>~\rho(\varpi,z)</math>, such that no material falls outside a volume defined by the two boundary points, A and B, that were identified in Step #3. Usually an initially uniform density distribution will suffice to start the SCF iteration.
Via some accurate numerical algorithm, solve the Poisson equation to determine the gravitational potential, <math>~\Phi(\varpi,z)</math>, throughout the computational lattice corresponding to the trial mass-density distribution that was specified in Step #4 (or in Step #9).
From the gravitational potential determined in Step #5, identify the values of <math>~\Phi_A</math> and <math>~\Phi_B</math> at the two boundary points that were selected in Step #3.
From the "known" values of the enthalpy (Step #3) and the gravitational potential (Step #6) at the two selected surface boundary points A and B, determine the values of the constants, <math>~C_0</math> and <math>~\omega_0</math>, that appear in the algebraic equation that defines hydrostatic equilibrium.
From the most recently determined values of the gravitational potential, <math>~\Phi(\varpi,z)</math> (Step #5), and the values of the two constants, <math>~C_0</math> and <math>~\omega_0</math> just determined (Step #7), determine the enthalpy distribution throughout the computational lattice.
From <math>~H(\varpi,z)</math> and the selected barotropic equation of state (Step #1), calculate an "improved guess" of the density distribution, <math>~\rho(\varpi,z)</math>, throughout the computational lattice.
Has the model converged to a satisfactory equilibrium solution? (Usually a satisfactory solution has been achieved when the derived model parameters — for example, the values of <math>~C_0</math> and <math>~\omega_0</math> — change very little between successive iterations and the viral error is sufficiently small.)
- If the answer is, "NO": Repeat steps 5 through 10.
- If the answer is, "YES": Stop iteration.

Special Functions & Other Broadly Used Representations

Spherical Harmonics and Associated Legendre Functions

Table 2:
Green's Function in Terms of Associated Legendre Functions, <math>~P_\ell^m(\cos\theta)</math>,
and the Spherical Harmonics, <math>~Y_{\ell m}(\theta,\phi)</math>

<math>~\sum_{\ell=0}^{\infty} \sum_{m=-\ell}^{+\ell} \frac{4\pi}{2\ell+1} \biggl[ \frac{r_<^\ell}{r_>^{\ell+1}} \biggr] Y_{\ell m}^*(\theta^', \phi^') Y_{\ell m}(\theta,\phi)</math>

J. D. Jackson (1975, 2^nd Edition), Eq. (3.70)
[BT87], p. 656, Eq. (1C-31)

Note:

<math>~Y_{\ell m}(\theta,\phi) = \biggl[ \frac{(2\ell + 1 )(\ell - m)!}{4\pi(\ell + m)!} \biggr]^{1 / 2} P_\ell^m(\cos\theta)e^{im\phi}</math>

Jackson (1975), Eq. (3.53)
DLMF §14.30i
[BT87], p. 655, Eq. (1C-27)

<math>~Y_{\ell,-m}(\theta,\phi) = (-1)^{m}Y_{\ell m}^*(\theta,\phi)</math>

Jackson (1975), Eq. (3.49)
DLMF §14.6i
[BT87], p. 655, Eq. (1C-20)
[T78], p. 481, Eq. (C.5)

Jackson (1975), Eq. (3.16)
[BT87], p. 655, Eq. (1C-21)

Leading Legendre Functions

P. Moon & D. E. Spencer (1971), p. 205
Jackson (1975), Eq. (3.15)
DLMF §18.5iv
[BT87], p. 655, Eq. (1C-25)

<math>~P_0(x)</math>	<math>~=</math>	<math>~1</math>
<math>~P_1(x)</math>	<math>~=</math>	<math>~x</math>
<math>~P_2(x)</math>	<math>~=</math>	<math>~\tfrac{1}{2}(3x^2 - 1)</math>
<math>~P_3(x)</math>	<math>~=</math>	<math>~\tfrac{1}{2}(5x^3 - 3x)</math>
<math>~P_4(x)</math>	<math>~=</math>	<math>~\tfrac{1}{8}(35x^4 - 30x^2 + 3)</math>
<math>~P_5(x)</math>	<math>~=</math>	<math>~\tfrac{1}{8}(63x^5 - 70x^3 + 15x)</math>
<math>~P_6(x)</math>	<math>~=</math>	<math>~\tfrac{1}{16}(231x^6 - 315x^4 + 105x^2 - 5)</math>

Leading Spherical Harmonics

Jackson (1975), §3.5
[BT87], p. 656, Eq. (1C-33)
[T78], p. 482, Eqs. (C.7) - (C.16)

<math>~Y_{00} </math>	<math>~=</math>	<math>~\frac{1}{\sqrt{4\pi}}</math>
<math>~Y_{1,\pm 1} </math>	<math>~=</math>	<math>~\mp \sqrt{\frac{3}{8\pi}} ~\sin\theta ~e^{\pm i\phi}</math>
<math>~Y_{10} </math>	<math>~=</math>	<math>~\sqrt{\frac{3}{4\pi}} ~\cos\theta </math>
<math>~Y_{2,\pm 2} </math>	<math>~=</math>	<math>~\frac{1}{4} \sqrt{\frac{15}{2\pi}} ~\sin^2\theta ~e^{\pm 2i\phi}</math>
<math>~Y_{2, \pm 1} </math>	<math>~=</math>	<math>~\mp \sqrt{\frac{15}{8\pi}} ~\sin\theta \cos\theta ~e^{\pm i\phi}</math>
<math>~Y_{20} </math>	<math>~=</math>	<math>~\sqrt{\frac{5}{4\pi}} ~(\tfrac{3}{2}\cos^2\theta - \tfrac{1}{2})</math>

<math>~Y_{3,\pm 3} </math>	<math>~=</math>	<math>~\mp \frac{1}{4} \sqrt{\frac{35}{4\pi}} ~\sin^3\theta ~e^{\pm 3i\phi}</math>
<math>~Y_{3, \pm 2} </math>	<math>~=</math>	<math>~\frac{1}{4}\sqrt{\frac{105}{2\pi}} ~\sin^2\theta \cos\theta ~e^{\pm 2i\phi}</math>
<math>~Y_{3, \pm 1} </math>	<math>~=</math>	<math>~\mp \frac{1}{4}\sqrt{\frac{21}{4\pi}} ~\sin\theta (5\cos^2\theta - 1) ~e^{\pm i\phi}</math>
<math>~Y_{30} </math>	<math>~=</math>	<math>~\sqrt{\frac{7}{4\pi}} ~(\tfrac{5}{2}\cos^3\theta - \tfrac{3}{2}\cos\theta) </math>

Note that, for all cases where <math>~m=0</math> :

<math>~Y_{\ell 0}(\theta,\phi) = \sqrt{\frac{(2\ell + 1 )}{4\pi} } ~P_\ell(\cos\theta)</math>

Jackson (1975), Eq. (3.57)

Multipole Expansions

Mass Multipole Moments

As an extension of the above discussion of

Multipole Moments of the Mass Distribution
<math>~q_{\ell m}</math>	<math>~\equiv</math>	<math>~ \int (r^')^\ell Y_{\ell m}^*(\theta^', \phi^') ~\rho(r^', \theta^', \phi^') d^3x^' \, , </math>
Jackson (1975), p. 137, Eq. (4.3)

here we evaluate a set of the leading order mass-multipole moments in terms of their cartesian-coordinate representations.

<math>~q_{00}</math>	<math>~=</math>	<math>~\frac{1}{\sqrt{4\pi}} \int \rho(\vec{x}^{~'}) d^3x^' \, ; </math>
<math>~q_{11}</math>	<math>~=</math>	<math>~ \int r^' \biggl[ Y_{11}^* \biggr]~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~ - ~\int r^' \biggl[ \sqrt{\frac{3}{8\pi}}\sin\theta ~\biggl(\cos\phi^' - i\sin\phi^' \biggr) \biggr]~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~ - \sqrt{\frac{3}{8\pi}}~\int r^' \biggl[ \frac{\sqrt{(x^')^2+(y^')^2}}{r^'} ~\biggl(\frac{x^'}{\sqrt{(x^')^2+(y^')^2}} - \frac{iy^'}{\sqrt{(x^')^2+(y^')^2}} \biggr)\biggr] ~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~ - \sqrt{\frac{3}{8\pi}}~\int (x^' - iy^') ~\rho(\vec{x}^{~'}) d^3x^' \, ; </math>
<math>~q_{1,- 1}</math>	<math>~=</math>	<math>~ + \sqrt{\frac{3}{8\pi}}~\int (x^' + iy^') ~\rho(\vec{x}^{~'}) d^3x^' \, ; </math>
<math>~q_{10}</math>	<math>~=</math>	<math>~ \int r^' \biggl[ Y_{10}^* \biggr]~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~ \int r^' \biggl[ \sqrt{\frac{3}{4\pi}}~\cos\theta^' \biggr]~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~ \sqrt{\frac{3}{4\pi}} \int z^' \rho(\vec{x}^{~'}) d^3x^' \, ; </math>
<math>~q_{22}</math>	<math>~=</math>	<math>~ \int (r^')^2 \biggl[ Y_{22}^*(\theta^', \phi^') \biggr]~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~ \int (r^')^2 \biggl\{ \frac{1}{4}\sqrt{\frac{15}{2\pi}} ~\sin^2\theta^' ~\biggl[\cos(2\phi^') - i\sin(2\phi^')\biggr] \biggr\}~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~\frac{1}{4}\sqrt{\frac{15}{2\pi}} \int (r^')^2 \biggl\{ \frac{(x^')^2+(y^')^2}{(r^')^2} ~\biggl[\frac{ (x^')^2 - (y^')^2 - 2i ( x^' y^' )}{(x^')^2+(y^')^2} \biggr] \biggr\}~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~\frac{1}{4}\sqrt{\frac{15}{2\pi}} \int (x^' -iy^')^2~\rho(\vec{x}^{~'}) d^3x^' \, ; </math>
<math>~q_{2,-2}</math>	<math>~=</math>	<math>~\frac{1}{4}\sqrt{\frac{15}{2\pi}} \int (x^' + iy^')^2~\rho(\vec{x}^{~'}) d^3x^' \, ; </math>
<math>~q_{21}</math>	<math>~=</math>	<math>~ \int (r^')^2 \biggl[ Y_{21}^*(\theta^', \phi^') \biggr]~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~ - \sqrt{\frac{15}{8\pi}} \int (r^')^2 \biggl[ \sin\theta^' \cos\theta^' (\cos\phi^' -i\sin\phi^') \biggr]~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~ - \sqrt{\frac{15}{8\pi}} \int (r^')^2 \biggl[ \frac{z^' \sqrt{(x^')^2+(y^')^2}}{(r^')^2} ~\biggl(\frac{x^'}{\sqrt{(x^')^2+(y^')^2}} - \frac{iy^'}{\sqrt{(x^')^2+(y^')^2}} \biggr)\biggr] ~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~ - \sqrt{\frac{15}{8\pi}} \int z^'(x^' - iy^') ~\rho(\vec{x}^{~'}) d^3x^' \, ; </math>
<math>~q_{2,-1}</math>	<math>~=</math>	<math>~ + \sqrt{\frac{15}{8\pi}} \int z^'(x^' + iy^') ~\rho(\vec{x}^{~'}) d^3x^' \, ; </math>
<math>~q_{20}</math>	<math>~=</math>	<math>~ \int (r^')^2 \biggl[ Y_{20}^*(\theta^', \phi^') \biggr]~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~ \int (r^')^2 \biggl[ \sqrt{\frac{5}{16\pi}} (3\cos^2\theta^' - 1) \biggr]~\rho(\vec{x}^{~'}) d^3x^' </math>
	<math>~=</math>	<math>~\sqrt{\frac{5}{16\pi}} \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \, . </math>

Table 3: Summary of Cartesian Expressions for Leading Mass-Multipole Moments

<math>~q_{0, 0}</math>	<math>~=</math>	<math>~\frac{1}{\sqrt{4\pi}} \int \rho(\vec{x}^{~'}) d^3x^' </math>
<math>~q_{1,\pm 1}</math>	<math>~=</math>	<math>~ \mp \sqrt{\frac{3}{8\pi}}~\int (x^' \mp iy^') ~\rho(\vec{x}^{~'}) d^3x^' </math>
<math>~q_{1,0}</math>	<math>~=</math>	<math>~ \sqrt{\frac{3}{4\pi}} \int z^' \rho(\vec{x}^{~'}) d^3x^' </math>
<math>~q_{2,\pm 2}</math>	<math>~=</math>	<math>~\frac{1}{4}\sqrt{\frac{15}{2\pi}} \int (x^' \mp iy^')^2~\rho(\vec{x}^{~'}) d^3x^' </math>
<math>~q_{2,\pm 1}</math>	<math>~=</math>	<math>~ \mp \sqrt{\frac{15}{8\pi}} \int z^'(x^' \mp iy^') ~\rho(\vec{x}^{~'}) d^3x^' </math>
<math>~q_{2,0}</math>	<math>~=</math>	<math>~\sqrt{\frac{5}{16\pi}} \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' </math>

Contributions to the Gravitational Potential in Terms of Multipole Moments

Expanding on the above discussion of the gravitational potential, written as a series expansion in terms of mass-multipole moments and spherical harmonics,

<math>~ \Phi_B(r,\theta,\phi)</math>

<math>~ \Phi_B(r,\theta,\phi) \biggr|_{\ell=0} +~ \Phi_B(r,\theta,\phi)\biggr|_{\ell=1} + ~\Phi_B(r,\theta,\phi)\biggr|_{\ell=2} -~4\pi G \sum_{\ell=3}^{\infty} \sum_{m=-\ell}^{+\ell} \frac{q_{\ell m}}{r^{\ell+1}} \frac{Y_{\ell m}(\theta,\phi)}{(2\ell+1)} \, , </math>

here we evaluate the first three, leading order terms.

First Term

First (term with <math>~\ell = 0</math>):

<math>~ \Phi_B(r,\theta,\phi)\biggr\|_{\ell = 0}</math>	<math>~=</math>	<math>~ -4\pi G \biggl[ q_{00} \biggr] \frac{ Y_{00}(\theta,\phi)}{r} </math>
	<math>~=</math>	<math>~ -4\pi G \biggl[ \frac{1}{\sqrt{4\pi}} \int \rho(\vec{x}^{~'}) d^3x^' \biggr] \frac{1}{\sqrt{4\pi}~r} </math>
	<math>~=</math>	<math>~ -\frac{GM}{r} \, . </math>

Second Term

Second (terms with <math>~\ell = 1</math>):

<math>~ \Phi_B(r,\theta,\phi)\biggr\|_{\ell = 1}</math>	<math>~=</math>	<math>~ -\frac{4\pi G}{3} \sum_{m=-1}^{+1} \biggl[ q_{1 m}\biggr] \frac{Y_{1 m}(\theta,\phi)}{r^2} </math>
	<math>~=</math>	<math>~ -\frac{4\pi G}{3r^2} \biggl\{ \biggl[ q_{1,- 1}\biggr] Y_{1, -1}(\theta,\phi) + \biggl[ q_{1 0}\biggr] Y_{1 0}(\theta,\phi) + \biggl[ q_{1 1}\biggr] Y_{1 1}(\theta,\phi) \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{4\pi G}{3r^2} \biggl\{ \biggl[ + \frac{3}{8\pi}~\int (x^' + iy^')~\rho(\vec{x}^{~'}) d^3x^' \biggr] \frac{(x - iy) }{r} </math>
		<math>~ + \biggl[ \frac{3}{4\pi} \int z^' \rho(\vec{x}^{~'}) d^3x^' \biggr] \frac{z}{r} + \biggl[ \frac{3}{8\pi}~\int (x^' - iy^')~\rho(\vec{x}^{~'}) d^3x^' \biggr] \frac{(x + iy) }{r} \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{G}{r^3} \biggl\{ \biggl[ \frac{1}{2}~\int (x^' + iy^')~\rho(\vec{x}^{~'}) d^3x^' \biggr] (x - iy) </math>
		<math>~ + \biggl[ \int z^' \rho(\vec{x}^{~'}) d^3x^' \biggr] z + \biggl[ \frac{1}{2}~\int (x^' - iy^')~\rho(\vec{x}^{~'}) d^3x^' \biggr] (x + iy) \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{G}{r^3} \biggl\{ \biggl[ \int (x^')~\rho(\vec{x}^{~'}) d^3x^' \biggr] (x ) + \biggl[ \int (y^')~\rho(\vec{x}^{~'}) d^3x^' \biggr] (y ) + \biggl[ \int z^' \rho(\vec{x}^{~'}) d^3x^' \biggr] z \biggr\} </math>
<math>~</math>	<math>~=</math>	<math>~- \frac{GM}{r^3} \biggl[ \vec{x} \cdot \vec{x}_\mathrm{com} \biggr]</math>
where:		<math>~ \vec{x}_\mathrm{com} \equiv \frac{1}{M} \int ~\vec{x}^{~'} \rho(\vec{x}^{~'}) d^3x^'\, . </math>

Third Term

Third (terms with <math>~\ell = 2</math>):

<math>~ \Phi_B(r,\theta,\phi)\biggr\|_{\ell = 2}</math>	<math>~=</math>	<math>~ -\frac{4\pi G}{5r^3} \biggl\{ \biggl[ q_{2, -2} \biggr] Y_{2,-2} + \biggl[ q_{2, 2} \biggr] Y_{2,2} + \biggl[ q_{2,-1} \biggr] Y_{2, -1} + \biggl[ q_{2,1} \biggr] Y_{2, 1} + \biggl[ q_{20} \biggr] Y_{20} \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{4\pi G}{5r^3} \biggl\{ \biggl[ \frac{1}{4}\sqrt{\frac{15}{2\pi}} \int (x^' + iy^')^2~\rho(\vec{x}^{~'}) d^3x^' \biggr] \frac{1}{4}\sqrt{\frac{15}{2\pi}} \sin^2\theta e^{-2i\phi} + \biggl[\frac{1}{4}\sqrt{\frac{15}{2\pi}} \int (x^' -iy^')^2~\rho(\vec{x}^{~'}) d^3x^' \biggr] \frac{1}{4}\sqrt{\frac{15}{2\pi}} \sin^2\theta e^{2i\phi} </math>
		<math>~ + \biggl[ \sqrt{\frac{15}{8\pi}} \int z^'(x^' + iy^') ~\rho(\vec{x}^{~'}) d^3x^' \biggr] \sqrt{\frac{15}{8\pi}} \sin\theta \cos\theta e^{-i\phi} + \biggl[ \sqrt{\frac{15}{8\pi}} \int z^'(x^' - iy^') ~\rho(\vec{x}^{~'}) d^3x^' \biggr] \sqrt{\frac{15}{8\pi}} \sin\theta \cos\theta e^{i\phi} </math>
		<math>~ + \biggl[ \sqrt{\frac{5}{16\pi}} \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \biggr] \sqrt{\frac{5}{16\pi}} (3\cos^2\theta - 1) \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{4\pi G}{5r^3} \biggl\{ \frac{3\cdot 5}{2^5 \pi} \biggl(\frac{\varpi}{r}\biggr)^2 \biggl[ \int (x^' + iy^')^2~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggl[ \cos(2\phi) - i\sin(2\phi) \biggr] + \frac{3\cdot 5}{2^5 \pi} \biggl(\frac{\varpi}{r}\biggr)^2 \biggl[\int (x^' -iy^')^2~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggl[ \cos(2\phi) + i\sin(2\phi) \biggr] </math>
		<math>~ + \frac{3\cdot 5}{2^3\pi} \biggl( \frac{\varpi z}{r^2} \biggr) \biggl[\int z^'(x^' + iy^') ~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggl[ \cos\phi - i\sin\phi \biggr] + \frac{3\cdot 5}{2^3\pi} \biggl( \frac{\varpi z}{r^2} \biggr) \biggl[ \int z^'(x^' - iy^') ~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggl[ \cos\phi + i\sin\phi \biggr] </math>
		<math>~ + \frac{5}{2^4\pi} \biggl[ \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggl( \frac{3z^2 - r^2}{r^2} \biggr) \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{4G}{r^5} \biggl\{ \frac{3}{2^5 } \biggl[ \int (x^' + iy^')^2~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggl[ x^2 - y^2 - 2i xy\biggr] + \frac{3}{2^5 } \biggl[\int (x^' -iy^')^2~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggl[ x^2 - y^2 + 2i xy \biggr] </math>
		<math>~ + \frac{3z}{2^3} \biggl[\int z^'(x^' + iy^') ~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggl[x - i y \biggr] + \frac{3z}{2^3} \biggl[ \int z^'(x^' - iy^') ~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggl[x + i y \biggr] </math>
		<math>~ + \biggl( \frac{3z^2 - r^2}{2^4} \biggr) \biggl[ \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{G}{2r^5} \biggl\{ \frac{3( x^2 - y^2 )}{2^2 } \biggl[ \int (x^' + iy^')^2~\rho(\vec{x}^{~'}) d^3x^' + \int (x^' -iy^')^2~\rho(\vec{x}^{~'}) d^3x^' \biggr] + \frac{3i xy}{2 } \biggl[\int (x^' -iy^')^2~\rho(\vec{x}^{~'}) d^3x^' - \int (x^' + iy^')^2~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ + 3xz \biggl[\int z^'(x^' + iy^') ~\rho(\vec{x}^{~'}) d^3x^' + \int z^'(x^' - iy^') ~\rho(\vec{x}^{~'}) d^3x^'\biggr] + 3i yz\biggl[ \int z^'(x^' - iy^') ~\rho(\vec{x}^{~'}) d^3x^' - \int z^'(x^' + iy^') ~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ + \biggl( \frac{3z^2 - r^2}{2} \biggr) \biggl[ \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{G}{2r^5} \biggl\{ \frac{3( x^2 - y^2 )}{2^2 } \biggl[ \int [2(x^')^2 - 2(y^')^2]~\rho(\vec{x}^{~'}) d^3x^' \biggr] + \frac{3i xy}{2 } \biggl[\int -4i x^' y^'~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ + 3xz \biggl[\int 2x^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 3i yz\biggl[ \int -2iy^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] + \biggl( \frac{3z^2 - r^2}{2} \biggr) \biggl[ \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{G}{2r^5} \biggl\{ \frac{3( x^2 - y^2 )}{2} \biggl[ \int [(x^')^2 - (y^')^2]~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 6 xy \biggl[\int x^' y^'~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ + 6xz \biggl[\int x^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 6yz\biggl[ \int y^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] + \biggl( \frac{3z^2 - r^2}{2} \biggr) \biggl[ \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggr\} \, . </math>

Rearranging terms, we have,

<math>~ \Phi_B(r,\theta,\phi)\biggr\|_{\ell = 2}</math>	<math>~=</math>	<math>~ -\frac{G}{2r^5} \biggl\{ 2 xy \biggl[\int 3x^' y^'~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 2xz \biggl[\int 3x^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 2yz\biggl[ \int 3y^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ +\frac{3( x^2 - y^2 )}{2} \biggl[ \int [(x^')^2 - (y^')^2]~\rho(\vec{x}^{~'}) d^3x^' \biggr] + \biggl( \frac{3z^2 - r^2}{2} \biggr) \biggl[ \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{G}{2r^5} \biggl\{ 2 xy \biggl[\int 3x^' y^'~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 2xz \biggl[\int 3x^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 2yz\biggl[ \int 3y^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ +\frac{3( x^2 )}{2} \biggl[ \int [(x^')^2 - (y^')^2]~\rho(\vec{x}^{~'}) d^3x^' \biggr] - \biggl( \frac{x^2}{2} \biggr) \biggl[ \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ -\frac{3( y^2 )}{2} \biggl[ \int [(x^')^2 - (y^')^2]~\rho(\vec{x}^{~'}) d^3x^' \biggr] - \biggl( \frac{y^2}{2} \biggr) \biggl[ \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ + z^2 \biggl[ \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{G}{2r^5} \biggl\{ 2 xy \biggl[\int 3x^' y^'~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 2xz \biggl[\int 3x^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 2yz\biggl[ \int 3y^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ + z^2 \biggl[ \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ +\frac{( x^2 )}{2} \biggl[ \int [3(x^')^2 - 3(y^')^2-3(z^')^2 + (r^')^2 ]~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ +\frac{( y^2 )}{2} \biggl[ \int [3(x^')^2 - 3(y^')^2 -3(z^')^2 + (r^')^2 ]~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{G}{2r^5} \biggl\{ 2 xy \biggl[\int 3x^' y^'~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 2xz \biggl[\int 3x^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 2yz\biggl[ \int 3y^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ + z^2 \biggl[ \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ +\frac{( x^2 )}{2} \biggl[ \int [3(x^')^2 - 3(y^')^2-3(z^')^2 + 3(r^')^2 - 3(r^')^2 + (r^')^2 ]~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ +\frac{( y^2 )}{2} \biggl[ \int [-3(x^')^2 + 3(y^')^2 -3(z^')^2 + 3(r^')^2 - 3(r^')^2 + (r^')^2 ]~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{G}{2r^5} \biggl\{ 2 xy \biggl[\int 3x^' y^'~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 2xz \biggl[\int 3x^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 2yz\biggl[ \int 3y^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ + z^2 \biggl[ \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \biggr] +\frac{( x^2 )}{2} \biggl[ \int [6(x^')^2 - 2(r^')^2 ]~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ +\frac{( y^2 )}{2} \biggl[ \int [6(y^')^2 - 2(r^')^2 ]~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{G}{2r^5} \biggl\{ 2 xy \biggl[\int 3x^' y^'~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 2xz \biggl[\int 3x^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] + 2yz\biggl[ \int 3y^' z^' ~\rho(\vec{x}^{~'}) d^3x^' \biggr] </math>
		<math>~ + x^2 \biggl[ \int [3(x^')^2 - (r^')^2 ]~\rho(\vec{x}^{~'}) d^3x^' \biggr] + y^2 \biggl[ \int [3(y^')^2 - 2(r^')^2 ]~\rho(\vec{x}^{~'}) d^3x^' \biggr] + z^2 \biggl[ \int \biggl[ 3(z^')^2 - (r^')^2 \biggr]~\rho(\vec{x}^{~'}) d^3x^' \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ -\frac{G}{2r^5} \sum_{i=1}^3 \sum_{j=1}^3 Q_{i,j} \biggl[ x_i x_j \biggr] \, , </math>

where, following Jackson (1975), we have introduced the,

Traceless Quadrupole Moment Tensor
<math>~Q_{i,j}</math>	<math>~\equiv</math>	<math>~ \int [ 3(x_i^') (x_j^') - (r^')^2 \delta_{ij} ] \rho(\vec{x}^{~'}) d^3x^' \, . </math>
Jackson (1975), p. 138, Eq. (4.9) M. L. Norman & J. R. Wilson (1978), p. 501, Eq. (19)

Familiar Expression for the Cylindrical Green's Function Expansion

Table 4: Cylindrical-Coordinate Green's Function Expansion

<math>~ \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')} \int_0^\infty dk ~J_m(k\varpi) ~J_m(k\varpi^') e^{-k(z_> - z_<)} </math>

where <math>~J_m</math> is an order <math>~m</math> Bessel function of the first kind.

Jackson (1975), exercise [3.14]
H. S. Cohl & J. E. Tohline (1999), p. 88, Eq. (3)

Toroidal Functions

Table 5: Green's Function in Terms of
Zero Order, Half-(Odd)Integer Degree, Associated Legendre Functions of the Second Kind, <math>~Q^0_{m-1 / 2}(\chi)</math>
(also referred to as Toroidal Functions)

<math>~ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) </math>

where:

<math>~\chi \equiv \frac{\varpi^2 + (\varpi^')^2 + (z - z^')^2}{2\varpi \varpi^'}</math>

H. S. Cohl & J. E. Tohline (1999), p. 88, Eqs. (15) & (16)
See also the DLMF's definition of Toroidal Functions, <math>~Q_{m - 1 / 2}^{0}</math>

Note that, according to, for example, equation (8.731.5) of Gradshteyn & Ryzhik (1994),

Hence, the Green's function can straightforwardly be rewritten in terms of a simpler summation over just non-negative values of the index, <math>~m</math>.

Referencing equations (8.13.3) and (8.13.7), respectively, of Abramowitz & Stegun (1965), we see that for the smallest two values of the non-negative index, <math>~m</math>, the function, <math>~Q_{m- 1 / 2}(\chi)</math>, can be rewritten in terms of, the more familiar, complete elliptic integrals of the first and second kind. Specifically,

for <math>~m = 0</math>,
<math>~Q_{m- 1 / 2}(\chi) ~\rightarrow~ Q_{-1 / 2}</math>	<math>~=</math>	<math>~ \mu K(\mu) \, , </math>
and, for <math>~m = 1</math>,
<math>~Q_{m- 1 / 2}(\chi) ~\rightarrow~ Q_{+ 1 / 2}</math>	<math>~=</math>	<math>~ \chi \mu K(\mu) - (1+\chi)\mu E(\mu) \, , </math>
where,
<math>~\mu \equiv \biggl[ \frac{2}{1+\chi} \biggr]^{1 / 2}</math>	<math>~=</math>	<math>~ \biggl[ \frac{4\varpi \varpi^'}{(\varpi + \varpi^')^2 + (z - z^')^2} \biggr]^{1 / 2} \, . </math>

Excerpt from p. 337 of M. Abramowitz & I. A. Stegun (1995)

Finally, equation (8.5.3) from Abramowitz & Stegun (1965) or equation (8.832.4) of Gradshteyn & Ryzhik (1994) — also see equation (2) of Gil, Segura & Temme (2000) — provide the recurrence relation for all other values of the index, <math>~m</math>. Specifically, for all <math>~m \ge 2</math>,

<math>~Q_{m - 1 / 2}(\chi) = 4\biggl[\frac{m-1}{2m-1}\biggr] \chi Q_{m- 3 / 2}(\chi) - \biggl[ \frac{2m-3}{2m-1}\biggr] Q_{m- 5 / 2}(\chi) \, .</math>

Excerpt from p. 490 of W. Guatschi (1965, Communications of the ACM, vol. 8, issue 8, 488 - 492)

Guatschi (1965, Communications of the ACM, 8, 488 - 492)

Related Discussions

Toroidal Functions

J. Selvaggi, S. Salon, & M. V. K. Chari (2007, American Journal of Physics, 75, 724 - 727) — An Application of Toroidal Functions in Electrostatics
A. Gil, J. Segura & N. M. Temme (2000, Journal of Computational Physics, 161, 204 - 217) — Computing Toroidal Functions for Wide Ranges of the Parameters
J. Segura & A. Gil (2000, Computer Physics Communications, 124, 104 - 122) — Evaluation of Toroidal Harmonics
J. W. Bates (1997, Journal of Mathematical Physics, vol. 38, issue 7, 3679-3691) — On Toroidal Green's Functions
W. Guatschi (1965, Communications of the ACM, 8, 488 - 492) — Algorithms (Algorithm 259): Legendre Functions for Arguments Larger than One

Note that, in this Guatschi (1965) article, a description of the "procedure toroidal" begins on p. 490, near the bottom of the right-hand column.

A. B. Basset (1893, American Journal of Mathematics, vol. 15, No. 4, pp. 287 - 302) — On Toroidal Functions
W. M. Hicks (1881, Philosophical Transactions of the Royal Society of London, vol. 172, pp. 609 - 652) — On Toroidal Functions

Reviews

P. A. Strittmatter (1969, Annual Review of Astronomy and Astrophysics, 7, 665 - 684) — Stellar Rotation
N. R. Lebovitz (1967, Annual Review of Astronomy and Astrophysics, 5, 465 - 480) — Rotating Fluid Masses

Solution Methods

Y. Eriguchi & E. Mueller (1985, A&A, 146, 260 - 268) — A General Computational Method for Obtaining Equilibria of Self-Gravitating and Rotating Gases
S. W. Stahler (1983, ApJ, 268, 155 - 184) — The Equilibria of Rotating, Isothermal Clouds. I. - Method of Solution
Y. Eriguchi (1978, PASJ, 30, 507 - 518) — Hydrostatic Equilibria of Rotating Polytropes
S. I. Blinnikov (1975, Soviet Astronomy, 19, 151 - 156) — Self-Consistent Field Method in the Theory of Rotating Stars
M. J. Clement (1974, ApJ, 194, 709 - 714) — On the Solution of Poisson's Equation for Rapidly Rotating Stars
S. Jackson (1970, ApJ, 161, 579 - 585) — Rapidly Rotating Stars. V. The Coupling of the Henyey and the Self-Consistent Methods
J. P. Ostriker & J. W.-K. Mark (1968, ApJ, 151, 1075 - 1088) — Rapidly Rotating Stars. I. The Self-Consistent-Field Method
R. A. James (1964, ApJ, 140, 552 - 582) — The Structure and Stability of Rotating Gas Masses

Early Eriguchi Applications

Y. Eriguchi & E. Mueller (1985, A&A, 147, 161 - 168) — Equilibrium Models of Differentially Rotating Polytropes and the Collapse of Rotating Stellar Cores
I. Hachisu & Y. Eriguchi (1984, PASJ, 36, 497 - 503) — Bifurcation Points on the Maclaurin Sequence
I. Hachisu & Y. Eriguchi (1984, PASJ, 36, 259 - 276) — Binary Fluid Star
I. Hachisu & Y. Eriguchi (1984, PASJ, 36, 239 - 257) — Fission of Dumbbell Equilibrium and Binary State of Rapidly Rotating Polytropes
I. Hachisu & Y. Eriguchi (1983, MNRAS, 204, 583 - 589) — Bifurcations and Phase Transitions of Self-Gravitating and Uniformly Rotating Fluid
I. Hachisu & Y. Eriguchi (1982, Prog. Theor. Phys., 68, 206 - 221) — Bifurcation and Fission of Three Dimensional, Rigidly Rotating and Self-Gravitating Polytropes
I. Hachisu, Y. Eriguchi, & D. Sugimoto (1982, Prog. Theor. Phys., 68, 191 - 205) — Rapidly Rotating Polytropes and Concave Hamburger Equilibrium
Y. Eriguchi & D. Sugimoto (1981, Prog. Theor. Phys., 65, 1870 - 1875) — Another Equilibrium Sequence of Self-Gravitating and Rotating Incompressible Fluid
T. Fukushima, Y. Eriguchi, D. Sugimoto, G. S. Bisnovatyi-Kogan (1980, Prog. Theor. Phys., 63, 1957 - 1970) — Concave Hamburger Equilibrium of Rotating Bodies

Other Example Applications

E. Mueller & Y. Eriguchi (1985, A&A, 152, 325 - 335) — Equilibrium Models of Differentially Rotating, Completely Catalyzed, Zero-Temperature Configurations With Central Densities Intermediate to White Dwarf and Neutron Star Densities
J. R. Ipser & R. A. Managan (1981, ApJ, 250, 362 - 372) — On the Existence and Structure of Inhomogeneous Analogs of the Dedekind and Jacobi Ellipsoids
C. T. Cunningham (1977, ApJ, 211, 568 - 578) — Rapidly Rotating Spheroids of Polytropic Index n = 1
R. H. Durisen (1975, ApJ, 199, 179 - 183) — Upper Mass Limits for Stable Rotating White Dwarfs
P. Bodenheimer & J. P. Ostriker (1973, ApJ, 180, 159 - 170) — Rapidly Rotating Stars. VIII. Zero-Viscosity Polytropic Sequences'
P. Bodenheimer (1971, ApJ, 167, 153 - 163) — Rapidly Rotating Stars. VII. Effects of Angular Momentum on Upper-Main-Sequence Models
P. Bodenheimer & J. P. Ostriker (1970, ApJ, 161, 1101 - 1113) — Rapidly Rotating Stars. VI. Pre-Main-Sequence Evolution of Massive Stars
R. Kippenhahn & H.-C. Thomas (1970) in Proceedings of the 4th IAU Colloquium, held at the Ohio State University, Columbus, Ohio, September 8 - 11, 1969, Dordrecht: Riedel Publishing Co., edited by A. Slettebak — Stellar Rotation ==> Purchase proceedings from Springer, from Australia, or from Google
- In the introductory section of his paper, S. Jackson (1970) references this article by Kippenhahn & Thomas in the context of uniformly rotating, and therefore only mildly distorted, structures.
J. P. Ostriker & J. L. Tassoul (1969, ApJ, 155, 987 - ) — On the Oscillations and Stability of Rotating Stellar Models. II. Rapidly Rotating White Dwarfs
M. J. Clement (1969, ApJ, 156, 1051 - 1068) — Differential Rotation in Stars on the Upper Main Sequence
J. W.-K. Mark (1968, ApJ, 154, 627 - ) — Rapidly Rotating Stars. III. Massive Main-Sequence Stars
J. P. Ostriker & P. Bodenheimer (1968, ApJ, 151, 1089 - ) — Rapidly Rotating Stars. II. Massive White Dwarfs
J. Faulkner, I. W. Roxburgh, & P. A. Strittmatter (1968, ApJ, 151, 203 - 216) — Uniformly Rotating Main-Sequence Stars
R. Stoeckly (1965, ApJ, 142, 208 - 228) — Polytropic Models with Fast, Non-Uniform Rotation
- In the introductory section of his paper, S. Jackson (1970) states that a differentially rotating polytropic structure with a rotationally induced extreme distortion was first illustrated in this article by Stoeckly.

Henyey Technique for Nonrotating Stars

L. G. Henyey, L. Wilets, K. H. Böhm, R. Lelevier, & R. D. Levee (1959, ApJ, 129, 628 - ) — A Method for Automatic Computation of Stellar Evolution
L. G. Henyey, J. E. Forbes, & N. L. Gould (1964, ApJ, 139, 306 - ) — A New Method of Automatic Computation of Stellar Evolution

User:Tohline/AxisymmetricConfigurations/PoissonEq

Solving the (Multi-dimensional) Poisson Equation Numerically

Overview

Our Approach — Initially Heavily Influenced by Black & Bodenheimer (1975)

Determining Values of the Potential on the Mesh Boundary

Using a Spherical Harmonic Expansion

Full Three-Dimensional Generality

Simplification for 2D, Axisymmetric Systems

Using Toroidal Functions

In 3D

For Axisymmetric Systems

Extension from 2D to 3D

Intermediate

Other Approaches

Deupree (1974)

His Derived Expression for the Boundary Potential

Comparison With Other Related Derivations

Cook (1977)

Norman and Wilson (1978)

Boss (1980)

Stahler (1983)

Constructing Two-Dimensional, Axisymmetric Structures

Steps to Follow

Special Functions & Other Broadly Used Representations

Spherical Harmonics and Associated Legendre Functions

Multipole Expansions

Mass Multipole Moments

Contributions to the Gravitational Potential in Terms of Multipole Moments

First Term

Second Term

Third Term

Familiar Expression for the Cylindrical Green's Function Expansion

Toroidal Functions

Related Discussions

Toroidal Functions

Reviews

Solution Methods

Early Eriguchi Applications

Other Example Applications

Henyey Technique for Nonrotating Stars

Navigation menu

Search