Riemann Type 1 Ellipsoids

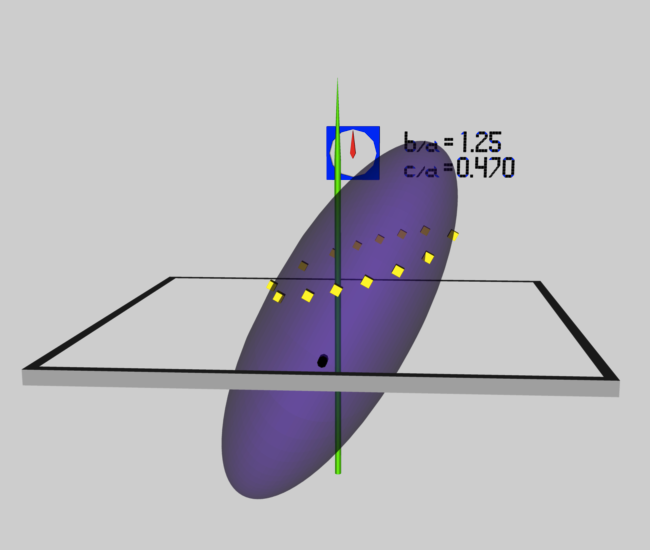
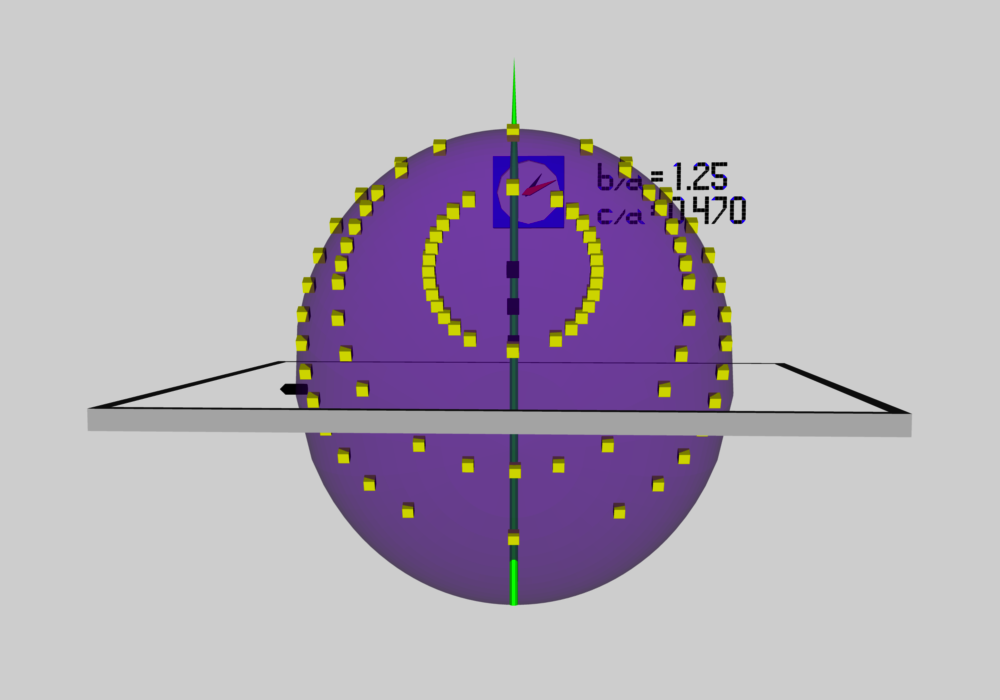
Example b1.25c0.470

Figure 2a	Figure 2b

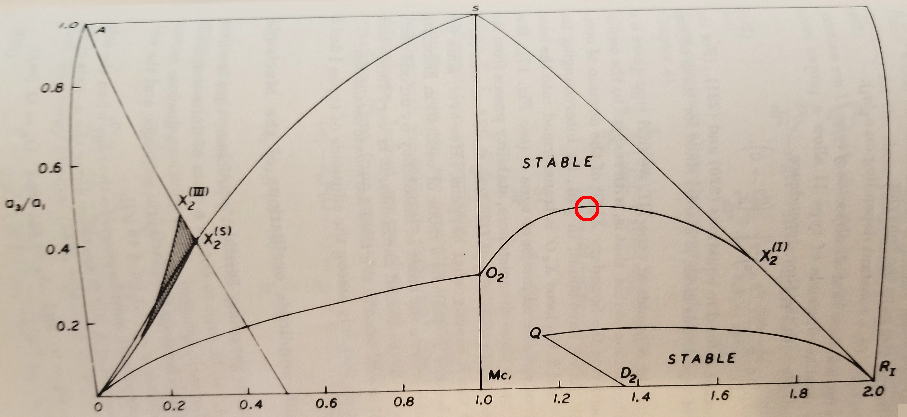
We have pulled the parameters for this example Type I Ellipsoid from Table XIII(a) on p. 170 of EFE; in addition, the superior values of β₊ and γ₊ have been obtained from eqs. (16) and (17), respectively, as found on p. 131 of Chapter 7, §47. This model sits along the locus O₂X₂^(I) shown in Figure 17 (p. 171) of EFE.

Example Type I Ellipsoid
<math>~\frac{b}{a} = \frac{a_2}{a_1}</math>	1.25
<math>~\frac{c}{a} = \frac{a_3}{a_1}</math>	0.4703
<math>~\Omega_2</math>	0.3639
<math>~\Omega_3</math>	0.6633
<math>~\tan^{-1} \biggl[ \frac{\Omega_3}{\Omega_2} \biggr]</math>	61.25°
<math>~\zeta_2</math>	-2.2794
<math>~\zeta_3</math>	-1.9637
<math>~\tan^{-1} \biggl[ \frac{\zeta_3}{\zeta_2} \biggr]</math>	40.74°
<math>~\beta_+</math>	1.13449 (1.13332)
<math>~\gamma_+</math>	1.8052

EFE Table XIII (p. 170)

EFE Figure 17 (p. 171)

In explaining the elements depicted in Figure 2 we will reference two separate cartesian frames: The (inertial) "lab" frame and a "body" frame affixed to the ellipsoid. The x-y plane of the inertial frame is identified by the square, grey/black frame and its z-axis is identified by a thin, green, pointed vertical stick. As depicted in both panels of Figure 2, the x-axis of the ellipsoid's body frame aligns with the x-axis of the inertial frame; in panel 2a, we're generally looking in the plus-x direction toward the clock, and in both panels a black arrow "tip" is affixed to the ellipsoid's negative x-axis. In this "Type I" ellipsoid — as opposed to the "S-Type" ellipsoids discussed earlier — the x-axis of the body frame aligns permanently with the intermediate axis of the (purple) ellipsoidal configuration; following EFE, we assign the value, a = 1, to this intermediate length. The body frame's y-axis is permanently aligned with the configurations's longest axis; in the particular model displayed in Figure 2, b/a = 1.25. And the body frame's z-axis is permanently aligned with the configuration's shortest axis; in this case, c/a = 0.470.

In S-Type ellipsoids (discussed previously), the ellipsoidal configuration spins about its shortest axis — this means that the ellipsoidal configuration's angular velocity vector has no component along either the x-axis or the y-axis (Ω₂ = Ω₁ = 0). But for the Type I ellipsoid shown in Figure 2, Ω₂ = 0.3639 while Ω₃ = 0.6633. This means that the configuration's spin axis — associated with the inertial frame's z-axis (the green pointed stick in both panels of Figure 2) — is not aligned with the z-axis of the (purple) ellipsoidal configuration. As is illustrated best in panel 2a, the ellipsoidal configuration is tipped about the x-axis (Ω₁ = 0) by an angle, 61.25° = tan^-1(Ω₃/Ω₂) to the spin axis. When this COLLADA-based 3D scene is animated, the purple ellipsoid spins about the z-axis (green pointed stick) of the inertial frame at a frequency, |Ω| = [Ω₂² + Ω₃²]^½ = 0.7566, in units of [π G ρ]^½.

In our COLLADA-based animation, we associate TIME=4 with one clock cycle. Given that <math>~|\Omega| = 0.7566 [\pi G \rho]^{1 / 2}</math> for this particular example Type I Riemann ellipsoid, we recognize that the number of clock cycles required to complete one spin about the green axis is <math>~1.0/0.7566 = 1.3217</math> cycles. Hence spinning through 360° is equivalent to TIME = 5.2868; or, TIME = 4 is equivalent to a spin angle of 272.38°.

Now … how do we determine the motion of Lagrangian fluid elements due to the nonzero internal vorticity of the ellipsoidal structure? Evidently the vorticity vector is tipped at an angle of 40.74° = tan^-1(ζ₃/ζ₂) to the inertial frame's z-axis. [The preceding sentence is incorrect! This is a misinterpretation of how the "tipping angle" is determined. The correct expression for this "tipping angle" is presented below.] This presumably means that, as viewed from the frame of reference of the spinning ellipsoidal figure, each Lagrangian fluid element moves along a closed (approximately elliptical?) path in a plane that is perpendicular to this vorticity vector. How we determine these various trajectories precisely?

First, we acknowledge that EFE provides an expression for the velocity vector of each fluid element, given its instantaneous body-coordinate position (x, y, z) = (x₁, x₂, x₃). Namely — see eq. 154 of Chapter 7, §51 (p. 156) —

<math>~u_1</math>	<math>~=</math>	<math>~- \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 y + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 z</math>	<math>~=</math>	<math>~+\biggl[ \frac{a^2}{ b^2} \biggr]\Omega_3 \gamma y - \biggl[ \frac{a^2}{c^2} \biggr] \Omega_2 \beta z \, ,</math>
<math>~u_2</math>	<math>~=</math>	<math>~+\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 x</math>	<math>~=</math>	<math>~- \Omega_3 \gamma x \, ,</math>
<math>~u_3</math>	<math>~=</math>	<math>~- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 x</math>	<math>~=</math>	<math>~-\Omega_2 \beta x \, .</math>

But we cannot immediately deduce, from these expressions alone, what the time-dependent behavior is of the three Lagrangian coordinates (x, y, z).

Second, we need to determine how to mathematically specify, then display, the coordinates of a plane that is tipped about the x-axis at an arbitrary angle to the equatorial plane of the (purple) ellipsoidal figure.

Regarding the second issue, let's identify the coordinates of a closed curve (an ellipse?) that identifies the the intersection between a "tipped" plane and the surface of the underlying ellipsoid. The surface of the ellipsoid is defined by the equation,

<math>~\biggl( \frac{x}{a} \biggr)^2 + \biggl( \frac{y}{b} \biggr)^2 + \biggl( \frac{z}{c} \biggr)^2 \, .</math>

And the "tipped" plane is defined such that, for any/all values of x,

This means,

<math>~1</math>	<math>~=</math>	<math>~\biggl( \frac{x}{a} \biggr)^2 + \frac{1}{b^2}\biggl( \frac{z-z_0}{m} \biggr)^2 + \biggl( \frac{z}{c} \biggr)^2 </math>
<math>~\Rightarrow ~~~\biggl( \frac{x}{a} \biggr)^2</math>	<math>~=</math>	<math>~1 - \biggl(\frac{z_0}{mb}\biggr)^2 \biggl( \frac{z}{z_0} - 1 \biggr)^2 - \biggl( \frac{z}{c} \biggr)^2 \, .</math>

If we specifically set m = 1 — that is, choose a slope of 45° — and set z₀ = c — that is, choose a plane that intersects the north pole of the (purple) ellipsoid — we then have,

<math>~\pm \biggl[ 1 - \biggl(\frac{c}{b}\biggr)^2 \biggl( \frac{z}{c} - 1 \biggr)^2 - \biggl( \frac{z}{c} \biggr)^2 \biggr]^{1 / 2} \, .</math>

[In retrospect, we acknowledge that this was a useful way to explore how to determine the shape of each Lagrangian-fluid-element orbit. It is important to emphasize, however, that our choice of a 45° tip angle was only meant to provide an example test calculation. Eventually (see below) we determined that, for this particular Type I example, the correct tipping angle is -19.02°.] Remembering that for the chosen ellipsoidal model (a, b, c) = (1.000, 1.250, 0.4703), the following table identifies the coordinates of a collection of points that simultaneously lie on the surface of the ellipsoid and within the chosen 45° "tipped" plane. These points are each represented by a small yellow cube in both panels of Figure 2.

m = 1 and z_0 = c
z	y	\|x\|
c	0	0
0.8c	-0.2c	0.5953
0.5c	-0.5c	0.8454
0.25c	-0.75c	0.9262
0	-c	0.9265
-0.25c	-1.25c	0.8464
-0.5c	-1.5c	0.6569
-0.75227c	-1.75227c	0

Here are a few thoughts/possible lines-of-attack to consider when addressing the first issue stated above.

It is likely that the angle at which the plane of motion is tilted about the x-axis of the "body" frame is directly related to the ratio, <math>~\zeta_3/\zeta_2</math>.
It is likely that the angle at which the plane of motion is tilted with respect to the z-axis of the "body" frame can be deduced by considering the ratio of the velocity components, v_y and v_z, when the x-component of the velocity vector is known to be zero; that is, when the fluid element is "crossing the x-axis."
Does the closed-orbit motion in the tipped plane always form a (off-center) ellipse?
Once you know the exact angle at which the orbital plane is tipped about the x-axis, an Euler-angle projection of every fluid particle's velocity vector should reduce to in-the-plane motion that has only two components. Once this transformation is made — especially if the resulting orbit is always a closed ellipse — we should be able to determine analytic expressions for the time-dependent behavior of each fluid element's x and y coordinate positions in the orbit plane and, subsequently, the (x, y, z) coordinate positions in the "body" frame.

Regarding thought "A"

For the example model depicted in Figure 2, we have,

<math>~\theta_\mathrm{tip} \equiv \tan^{-1}\biggl( \frac{\zeta_3}{\zeta_2} \biggr)</math>

<math>~\tan^{-1}\biggl( \frac{1.9637}{2.2794} \biggr) = 40.74^{\circ}</math>

Regarding thought "B"

When a fluid element crosses the x-axis we should expect z = 0. This needs to be rethought because the center of the closed elliptical trajectory of most fluid elements will be offset from the body's inherent z-axis.

Regarding thought "D"

<math>~v_x\biggr\|_\mathrm{tip}</math>	<math>~=</math>	<math>~v_x\biggr\|_\mathrm{body}</math>
<math>~v_y\biggr\|_\mathrm{tip}</math>	<math>~=</math>	<math>~v_y\|_\mathrm{body}\cdot \cos\theta + v_z\|_\mathrm{body}\cdot \sin\theta</math>
<math>~v_z\biggr\|_\mathrm{tip}</math>	<math>~=</math>	<math>~-v_y\|_\mathrm{body}\cdot \sin\theta + v_z\|_\mathrm{body}\cdot \cos\theta</math>

Setting <math>~v_z\biggr|_\mathrm{tip} = 0</math> implies,

<math>~v_y\|_\mathrm{body}\cdot \sin\theta </math>	<math>~=</math>	<math>~v_z\|_\mathrm{body}\cdot \cos\theta</math>
<math>~\Rightarrow ~~~ \tan\theta </math>	<math>~=</math>	<math>~\biggl(\frac{v_z}{v_y}\biggr)_\mathrm{body}</math>
	<math>~=</math>	<math>~- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 \cdot \biggl[ \frac{b^2}{a^2 + b^2} \biggr]^{-1} \zeta_3^{-1}</math>
	<math>~=</math>	<math>~- \frac{\zeta_2}{\zeta_3}\biggl[ \frac{(c/a)^2}{1 + (c/a)^2} \biggr] \biggl[ \frac{(b/a)^2}{1 + (b/a)^2} \biggr]^{-1} \, .</math>

For our particular example, then,

<math>~\tan\theta</math>	<math>~=</math>	<math>~- \frac{2.2794}{1.9637}\biggl[ \frac{(0.4703)^2}{1 + (0.4703)^2} \biggr] \biggl[ \frac{(1.25)^2}{1 + (1.25)^2} \biggr]^{-1} </math>
	<math>~=</math>	<math>~- \frac{2.2794}{1.9637}\biggl[ \frac{(0.4703)^2}{1 + (0.4703)^2} \biggr] \biggl[ \frac{(1.25)^2}{1 + (1.25)^2} \biggr]^{-1} = - 0.3448</math>
<math>~\Rightarrow ~~~ \theta</math>	<math>~=</math>	<math>~\tan^{-1}(-0.3448) = - 19.0^{\circ} \, . </math>

Now, given that,

<math>~x</math>	<math>~=</math>	<math>~x_t \, ,</math>
<math>~y</math>	<math>~=</math>	<math>~y_t \cos\theta - z_t \sin\theta \, ,</math>
<math>~z</math>	<math>~=</math>	<math>~z_t \cos\theta + y_t \sin\theta \, ,</math>

we can generate the following expressions for the fluid velocity components in the tipped plane:

<math>~v_z\biggr\|_\mathrm{tip}</math>	<math>~=</math>	<math>~0\, ,</math>
<math>~v_x\biggr\|_\mathrm{tip}</math>	<math>~=</math>	<math>~v_x\biggr\|_\mathrm{body}</math>
	<math>~=</math>	<math>~- \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 y + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 z</math>
	<math>~=</math>	<math>~- \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \biggl[ y_t \cos\theta - z_t \sin\theta \biggr] + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \biggl[ z_t \cos\theta + y_t \sin\theta \biggr]</math>
	<math>~=</math>	<math>~ y_t \biggl\{ \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta - \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta \biggr\} + z_t\biggl\{ \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \sin\theta + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \cos\theta \biggr\} \, , </math>
<math>~v_y\biggr\|_\mathrm{tip}</math>	<math>~=</math>	<math>~v_y\|_\mathrm{body}\cdot \cos\theta + v_z\|_\mathrm{body}\cdot \sin\theta</math>
	<math>~=</math>	<math>~\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 x \cdot \cos\theta - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 x \cdot \sin\theta</math>
	<math>~=</math>	<math>~x_t \biggl\{ \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 \cdot \cos\theta - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 \cdot \sin\theta \biggr\} \, .</math>

Now, following our earlier analysis for S-Type ellipsoids, let's assume that,

<math>~x_t = x_\mathrm{max}\cos(\varphi t)</math> and, <math>~y_t = y_0 - y_\mathrm{max}\sin(\varphi t) \, .</math>

(Insertion of the extra term, y₀, acknowledges that the center of the elliptical orbit in the "tipped" plane will be shifted off of the x-axis in the y_t-direction; the size of this shift should correlate with z_t, that is, with the vertical location of the tipped plane.) We have, then,

<math>~v_y\biggr\|_\mathrm{tip} = \frac{dy_t}{dt} = -y_\mathrm{max} \varphi \cos(\varphi t)</math>	<math>~=</math>	<math>~x_\mathrm{max} \cos(\varphi t) \biggl\{ \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 \cdot \cos\theta - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 \cdot \sin\theta \biggr\} \, ,</math>
<math>~v_x\biggr\|_\mathrm{tip} = \frac{dx_t}{dt} = -x_\mathrm{max}\varphi \sin(\varphi t)</math>	<math>~=</math>	<math>~ \biggl[ y_0 - y_\mathrm{max} \sin(\varphi t) \biggr]\biggl\{ \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta - \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta \biggr\} + z_t\biggl\{ \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \sin\theta + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \cos\theta \biggr\} \, . </math>
	<math>~=</math>	<math>~ - y_\mathrm{max} \sin(\varphi t) \biggl\{ \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta - \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta \biggr\} </math>
		<math>~ + y_0 \biggl\{ \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta - \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta \biggr\} + z_t\biggl\{ \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \sin\theta + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \cos\theta \biggr\} \, . </math>

So, in terms of the value of z_t, the offset in y_t must be,

<math>~ - y_0 \biggl\{ \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta - \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta \biggr\} </math>

<math>~ + z_t\biggl\{ \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \sin\theta + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \cos\theta \biggr\} \, ; </math>

in which case,

<math>~ -y_\mathrm{max} \varphi \cos(\varphi t)</math>	<math>~=</math>	<math>~x_\mathrm{max} \cos(\varphi t) \biggl\{ \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 \cdot \cos\theta - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 \cdot \sin\theta \biggr\} \, ,</math>
<math>~ \Rightarrow ~~~ \varphi </math>	<math>~=</math>	<math>~-\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \biggl\{ \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 \cdot \cos\theta - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 \cdot \sin\theta \biggr\} \, ,</math>

and,

<math>~-x_\mathrm{max}\varphi \sin(\varphi t)</math>	<math>~=</math>	<math>~ - y_\mathrm{max} \sin(\varphi t) \biggl\{ \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta - \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta \biggr\} </math>
<math>~\Rightarrow ~~~ \varphi </math>	<math>~=</math>	<math>~ \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]\biggl\{ \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta - \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta \biggr\} \, . </math>

In order for both of these expressions to be simultaneously true, we need,

<math>~\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \biggl\{ \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 \cdot \sin\theta - \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 \cdot \cos\theta \biggr\}</math>	<math>~=</math>	<math>~ \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]\biggl\{ \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta - \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta \biggr\} </math>
<math>~\Rightarrow ~~~ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 \cdot \sin\theta - \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 \cdot \cos\theta </math>	<math>~=</math>	<math>~ \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta </math>
<math>~\Rightarrow ~~~ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 \cdot \sin\theta - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta </math>	<math>~=</math>	<math>~ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 \cdot \cos\theta - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta </math>
<math>~\Rightarrow ~~~ \biggl\{ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] c^2 - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] a^2 \biggl\} \frac{\zeta_2 \sin\theta }{(a^2 + c^2)} </math>	<math>~=</math>	<math>~ \biggl\{ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] b^2 - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] a^2 \biggr\} \frac{\zeta_3 \cos\theta }{(a^2 + b^2)} \, . </math>

First Trial Value of θ

Now, from above, we determined that the "tip" angle must obey the expression,

<math>~\tan\theta </math>

<math>~- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 \cdot \biggl[ \frac{b^2}{a^2 + b^2} \biggr]^{-1} \zeta_3^{-1} \, .</math>

Hence, we require,

<math>~- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 \cdot \biggl[ \frac{b^2}{a^2 + b^2} \biggr]^{-1} \zeta_3^{-1} \biggl\{ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] c^2 - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] a^2 \biggl\} \frac{\zeta_2 }{(a^2 + c^2)} </math>	<math>~=</math>	<math>~ \biggl\{ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] b^2 - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] a^2 \biggr\} \frac{\zeta_3 }{(a^2 + b^2)} </math>
<math>~ \Rightarrow ~~~ \biggl\{ \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] a^2 - \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] c^2 \biggl\} \frac{c^2 \zeta_2^2 }{(a^2 + c^2)^2} </math>	<math>~=</math>	<math>~ \biggl\{ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] b^2 - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] a^2 \biggr\} \frac{b^2\zeta_3^2 }{(a^2 + b^2)^2} </math>
<math>~ \Rightarrow ~~~ \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2 c^2 \zeta_2^2 }{(a^2 + c^2)^2} - \frac{c^4 \zeta_2^2 }{(a^2 + c^2)^2} </math>	<math>~=</math>	<math>~ \frac{b^4 \zeta_3^2 }{(a^2 + b^2)^2} - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \frac{a^2 b^2\zeta_3^2 }{(a^2 + b^2)^2} \, . </math>

That is,

<math>~ \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 </math>	<math>~=</math>	<math>~ \biggl[ \frac{b^4 \zeta_3^2 }{(a^2 + b^2)^2} + \frac{c^4 \zeta_2^2 }{(a^2 + c^2)^2} \biggr] \biggl[ \frac{a^2 c^2 \zeta_2^2 }{(a^2 + c^2)^2} + \frac{a^2 b^2\zeta_3^2 }{(a^2 + b^2)^2} \biggr]^{-1} </math>
	<math>~=</math>	<math>~ \biggl[ b^4 \zeta_3^2 (a^2 + c^2)^2 + c^4 \zeta_2^2 (a^2 + b^2)^2 \biggr] \biggl[ a^2 c^2 \zeta_2^2 (a^2 + b^2)^2 + a^2 b^2\zeta_3^2 (a^2 + c^2)^2 \biggr]^{-1} \, . </math>

So for the example parameters provided above, we have,

<math>~ \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 </math>	<math>~=</math>	<math>~ \biggl[ 14.04 + 1.669 \biggr] \biggl[ 7.546 + 8.985 \biggr]^{-1} = 0.9502 </math>
<math>~ \Rightarrow~~~ \frac{y_\mathrm{max}}{x_\mathrm{max}} </math>	<math>~=</math>	<math>~ 0.9748 </math>

Second Trial Value of θ

Instead, what if we obtain the tip angle straight from the tabulated expression,

<math>~\tan\theta</math>

Then we have,

<math>~ \biggl\{ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] c^2 - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] a^2 \biggl\} \frac{1 }{(a^2 + c^2)} </math>	<math>~=</math>	<math>~ \biggl\{ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] b^2 - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] a^2 \biggr\} \frac{1 }{(a^2 + b^2)} </math>
<math>~\Rightarrow ~~~ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] c^2 (a^2 + b^2) - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] a^2 (a^2 + b^2) </math>	<math>~=</math>	<math>~ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] b^2 (a^2 + c^2) - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] a^2 (a^2 + c^2) </math>
<math>~\Rightarrow~~~ \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 </math>	<math>~=</math>	<math>~ \biggl[ c^2 (a^2 + b^2)- b^2 (a^2 + c^2) \biggr] \biggl[ a^2 (a^2 + b^2) - a^2 (a^2 + c^2) \biggr]^{-1} </math>
	<math>~=</math>	<math>~ [ c^2 - b^2 ] [ b^2 - c^2 ]^{-1} = -1 \, . </math>

And this is not physically acceptable. What if, instead, we set,

<math>~\tan\theta</math>

<math>~- \frac{\zeta_3}{\zeta_2} ~~~\Rightarrow ~~~ \theta = -40.74^\circ \, .</math>

Then we have,

<math>~ - \biggl\{ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] c^2 - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] a^2 \biggl\} \frac{1 }{(a^2 + c^2)} </math>	<math>~=</math>	<math>~ \biggl\{ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] b^2 - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] a^2 \biggr\} \frac{1 }{(a^2 + b^2)} </math>
<math>~\Rightarrow ~~~ - \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] c^2 (a^2 + b^2) + \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] a^2 (a^2 + b^2) </math>	<math>~=</math>	<math>~ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] b^2 (a^2 + c^2) - \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] a^2 (a^2 + c^2) </math>
<math>~\Rightarrow ~~~ \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] [ a^2 (a^2 + b^2) + a^2 (a^2 + c^2) ] </math>	<math>~=</math>	<math>~ \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] [ b^2 (a^2 + c^2) + c^2 (a^2 + b^2) ] </math>
<math>~\Rightarrow ~~~ \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 </math>	<math>~=</math>	<math>~ [ b^2 (a^2 + c^2) + c^2 (a^2 + b^2) ] [ a^2 (a^2 + b^2) + a^2 (a^2 + c^2) ]^{-1} \, . </math>

In our particular example, this means,

<math>~ \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 </math>	<math>~=</math>	<math>~ [ 2.4749 ] [ 3.7837 ]^{-1} = 0.6541 </math>
<math>~\Rightarrow ~~~ \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \bigg] </math>	<math>~=</math>	<math>~ 0.8088 \, . </math>

Try Again

Methodical Derivation of Orbital Parameters

Let the unprimed coordinates (x, y, z) represent the body frame of the ellipsoid, and the primed coordinates (x', y', z') represent a coordinate system in which the z'-axis is "tipped" — about the x' = x axis — away from the z-axis by an angle, θ. We assume that the motion of each Lagrangian fluid element will be restricted to an x'-y' equatorial plane — that is, we assume that <math>~\dot{z}' \equiv dz'/dt = 0</math> — but in general its velocity vector in the unprimed "body" frame will have the three nonzero components as specified in EFE and above. Here are some relevant transformations between these two coordinate systems.

<math>~x'</math>	<math>~=</math>	<math>~x \, ,</math>
<math>~y'</math>	<math>~=</math>	<math>~y \cos\theta + (z-z_0)\sin\theta \, ,</math>
<math>~z'</math>	<math>~=</math>	<math>~(z-z_0)\cos\theta - y\sin\theta \, .</math>

<math>~x</math>	<math>~=</math>	<math>~x' \, ,</math>
<math>~y</math>	<math>~=</math>	<math>~y' \cos\theta - z'\sin\theta \, ,</math>
<math>~z-z_0</math>	<math>~=</math>	<math>~z'\cos\theta + y'\sin\theta \, .</math>

<math>~\dot{x}'</math>	<math>~=</math>	<math>~\dot{x} \, ,</math>
<math>~\dot{y}'</math>	<math>~=</math>	<math>~\dot{y} \cos\theta + \dot{z}\sin\theta \, ,</math>
<math>~\cancelto{0}{\dot{z}'}</math>	<math>~=</math>	<math>~\dot{z} \cos\theta - \dot{y}\sin\theta \, .</math>

<math>~\dot{x}</math>	<math>~=</math>	<math>~\dot{x}' \, ,</math>
<math>~\dot{y}</math>	<math>~=</math>	<math>~\dot{y}' \cos\theta - \cancelto{0}{\dot{z}'}\sin\theta \, ,</math>
<math>~\dot{z}</math>	<math>~=</math>	<math>~\cancelto{0}{\dot{z}'}\cos\theta + \dot{y}'\sin\theta \, .</math>

NOTE: The center of each elliptical orbit is (x', y', z') = (0, y₀, 0). In "body" coordinates, then, (x, y, z) = (0, y₀ cosθ, z₀ + y₀ sinθ).

Focusing on the bottom-right quadrant of this equation-table, we note first that <math>~(\dot{x}, \dot{y}, \dot{z}) = (u_1, u_2, u_3)</math>, as provided above from EFE. Copying from the upper-right quadrant of this equation-table, let's rewrite these three velocity components in terms of the "tipped" plane coordinates, namely,

<math>~\dot{x} = u_1</math>	<math>~=</math>	<math>~ - \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \biggl[ y'\cos\theta - z'\sin\theta\biggr] + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \biggl[ z_0 + z'\cos\theta + y'\sin\theta \biggr] \, ,</math>
<math>~\dot{y} = u_2</math>	<math>~=</math>	<math>~+\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 x' \, ,</math>
<math>~\dot{z} = u_3</math>	<math>~=</math>	<math>~- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 x' \, .</math>

Now, if we assume that each Lagrangian particle executes a closed elliptical orbit in the plane of the tipped coordinate system (i.e., <math>~z' = \dot{z}' = 0</math> ), but whose orbit-center may be shifted by an amount, <math>~y_0</math>, away from the z'-axis, we expect …

<math>~x_\mathrm{max}\cos(\varphi t)</math>

and,

<math>~y_\mathrm{max}\sin(\varphi t) \, ,</math>

which implies,

<math>~- x_\mathrm{max}~ \varphi \cdot \sin(\varphi t)</math>

and,

<math>~y_\mathrm{max}~\varphi \cdot \cos(\varphi t) \, .</math>

The first of these equation pairs can be plugged directly into the expressions for u₁, u₂, and u₃ — further fleshing out the LHS of the equations in the bottom-right quadrant of the above equation-table — while the second pair can be used to re-express the RHS of the equations in the bottom-right quadrant of this equation table. We obtain,

<math>~ - \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \biggl\{ \biggl[ y_0 + y_\mathrm{max} \sin(\varphi t) \biggr] \cos\theta - \cancelto{0}{z'}\sin\theta \biggr\} + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \biggl\{ z_0 + \cancelto{0}{z'} \cos\theta + \biggl[ y_0 + y_\mathrm{max} \sin(\varphi t) \biggr]\sin\theta \biggr\} </math>	<math>~=</math>	<math>~-x_\mathrm{xmax} ~\varphi \cdot \sin(\varphi t) \, ,</math>
<math>~+\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 x_\mathrm{max}\cos(\varphi t) </math>	<math>~=</math>	<math>~y_\mathrm{max}~\varphi \cdot \cos(\varphi t) \cdot \cos\theta \, ,</math>
<math>~- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 x_\mathrm{max}\cos(\varphi t) </math>	<math>~=</math>	<math>~y_\mathrm{max}~\varphi \cdot \cos(\varphi t) \cdot \sin\theta \, .</math>

Combining the second and third of these conditions, we find first that,

<math>~\tan\theta </math>

<math>~- \frac{\zeta_2 }{ \zeta_3 } \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr]\frac{c^2}{b^2} \, ,</math>

which gives the "tipping" angle in terms of known parameter values; and second that …

<math>~\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 </math>	<math>~=</math>	<math>~\varphi \cdot \cos\theta \, ,</math>
<math>~\Rightarrow ~~~ \varphi \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] </math>	<math>~=</math>	<math>~ \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3}{\cos\theta} \, ,</math>

which gives the product of the two unknown quantities, <math>~\varphi</math> and the ratio <math>~y_\mathrm{max}/x_\mathrm{max}</math>, in terms of known parameter values. And from the first condition, we furthermore find that,

<math>~-x_\mathrm{max} ~\varphi \cdot \sin(\varphi t) </math>	<math>~=</math>	<math>~ - \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \biggl[ y_0 \cos\theta \biggr] - \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \biggl[ y_\mathrm{max} \sin(\varphi t) \biggr] \cos\theta + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \biggl[ z_0 + y_0 \sin\theta \biggr] + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \biggl[ y_\mathrm{max} \sin(\varphi t) \biggr]\sin\theta </math>
<math>~ \Rightarrow ~~~ x_\mathrm{max} ~\varphi \cdot \sin(\varphi t) + \biggl\{ \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta - \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta \biggr\} \biggl[ y_\mathrm{max} \sin(\varphi t) \biggr] </math>	<math>~=</math>	<math> \biggl\{ \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \biggl[ y_0 \cos\theta \biggr] - \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 z_0 - \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \biggl[ y_0 \sin\theta \biggr] \biggr\} \, . </math>

The LHS and the RHS must separately sum to zero, which means …

<math>~ \biggl\{ \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta - \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta \biggr\}y_0 </math>

<math> \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 z_0 \, , </math>

which gives the ratio, <math>~y_0/z_0</math> in terms of known parameter values; and,

<math>~ \biggl[ \frac{x_\mathrm{max}}{ y_\mathrm{max} } \biggr] ~\varphi </math>

<math>~ \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta - \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta \, , </math>

which in combination with the just-derived similar product relation can give expressions for both terms, namely,

<math>~ \biggl[ \frac{x_\mathrm{max}}{ y_\mathrm{max} } \biggr]^2 </math>

<math>~ \biggl\{ \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta - \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta \biggr\}\biggl[ \frac{a^2 + b^2}{b^2} \biggr] \frac{\cos\theta}{\zeta_3} \, , </math>

and,

<math>~ \varphi^2 </math>

<math>~ \biggl\{ \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 - \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \tan\theta \biggr\}\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 \, . </math>

Example Implementation

Drawing from the set of Case I parameters listed above, we will set a = 1, b = 1.25, c = 0.4703, ζ₂ = -2.2794, and ζ₃ = -1.9637. This means that,

<math>~\tan\theta </math>

<math>~- \frac{\zeta_2 }{ \zeta_3 } \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr]\frac{c^2}{b^2} = - 0.3448 ~~~\Rightarrow ~~~ \theta = -19.02^\circ \, .</math>

We deduce as well that,

<math>~ \frac{y_0}{z_0} </math>	<math>~=</math>	<math> \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \biggl\{ \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta - \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta \biggr\}^{-1} = -1.8666 \cdot \{-0.7245 - 0.6084 \}^{-1} = 1.4004 \, ; </math>
<math>~ \frac{x_\mathrm{max}}{ y_\mathrm{max} } </math>	<math>~=</math>	<math>~\biggl\{ \biggl[ \biggl( \frac{a^2}{a^2 + b^2} \biggr) \zeta_3 \cos\theta - \biggl( \frac{a^2}{a^2 + c^2} \biggr) \zeta_2 \sin\theta \biggr] \biggl[ \frac{a^2 + b^2}{b^2} \biggr] \frac{\cos\theta}{\zeta_3} \biggr\}^{1 / 2} = \{ [-1.3329] \cdot (-0.7895) \}^{1 / 2} = \sqrt{1.0524} = 1.0259 \, ; </math>
<math>~ \varphi </math>	<math>~=</math>	<math>~\biggl\{ \biggl[ \biggl( \frac{a^2}{a^2 + b^2} \biggr) \zeta_3 - \biggl( \frac{a^2}{a^2 + c^2} \biggr) \zeta_2 \tan\theta \biggr] \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 \biggr\}^{1 / 2} = 1.2993 \, . </math>

It is important to keep in mind that each Lagrangian fluid element will complete one full orbit in its "tipped" plane when <math>~\varphi t = 2\pi</math>, where <math>~t</math> is in units of <math>~[\pi G \rho]^{-1 / 2}</math> and <math>~\varphi</math> is in units of <math>~[\pi G \rho]^{+1 / 2}</math>. Note, as well, that in our COLLADA animations, we have adopted the convention that <math>~t = 1</math> when <math>~\mathrm{TIME} = 4</math>. Hence, one complete orbit will be completed when,

<math>~\frac{1}{4} \cdot \mathrm{TIME}</math>

<math>~\frac{2\pi}{\varphi} \, .</math>

That is to say, in the specific example being used here, on complete orbit is concluded when TIME = 19.343.

Referring back to our earlier geometric prescription of a "tipped plane" we insert this new slope having m = tanθ = -0.3448, and choose a particular plane by setting a value of z₀. Then we can map out a locus of points that show the intersection of the chosen plane with the surface of the ellipsoid by specifying various values of z, then calculating the corresponding values of y and x via the respective equations:

<math>~y </math>	<math>~=</math>	<math>~\frac{1}{\tan\theta} \biggl[ z - z_0 \biggr] \, ;</math>
<math>~\frac{x}{a} </math>	<math>~=</math>	<math>~\biggl[ 1 - \biggl(\frac{z_0}{b \tan\theta}\biggr)^2 \biggl( \frac{z}{z_0} - 1 \biggr)^2 - \biggl( \frac{z}{c} \biggr)^2 \biggr]^{1 / 2} \, .</math>

For each specified value of z₀, the relevant range of z values is given by the pair of values for which x/a = 0. For example, if we set z_0 = b tanθ = -0.4310, this pair is given by the roots of the quadratic expression,

<math>~1 </math>	<math>~=</math>	<math>~\biggl( \frac{z}{z_0} - 1 \biggr)^2 + \biggl( \frac{z}{c} \biggr)^2 </math>
<math>~\Rightarrow ~~~ 0 </math>	<math>~=</math>	<math>~z^2\biggl[ \frac{1}{z_0^2} + \frac{1}{c^2} \biggr] -\frac{2z}{z_0} </math>
	<math>~=</math>	<math>~z \biggl\{ z - \biggl[ \frac{2 z_0 c^2}{(c^2 + z_0^2)} \biggr] \biggr\} \biggl[ \frac{(c^2 + z_0^2)}{c^2 z_0^2} \biggr] \, .</math>

The roots are, then, <math>~z_\mathrm{max} = 0</math>, and

<math>~z_\mathrm{min}</math>

The middle three columns (table cells having bgcolor="lightblue") in the following table list values of |x| and y that correspond to various values of z that lie between this pair of limiting values.

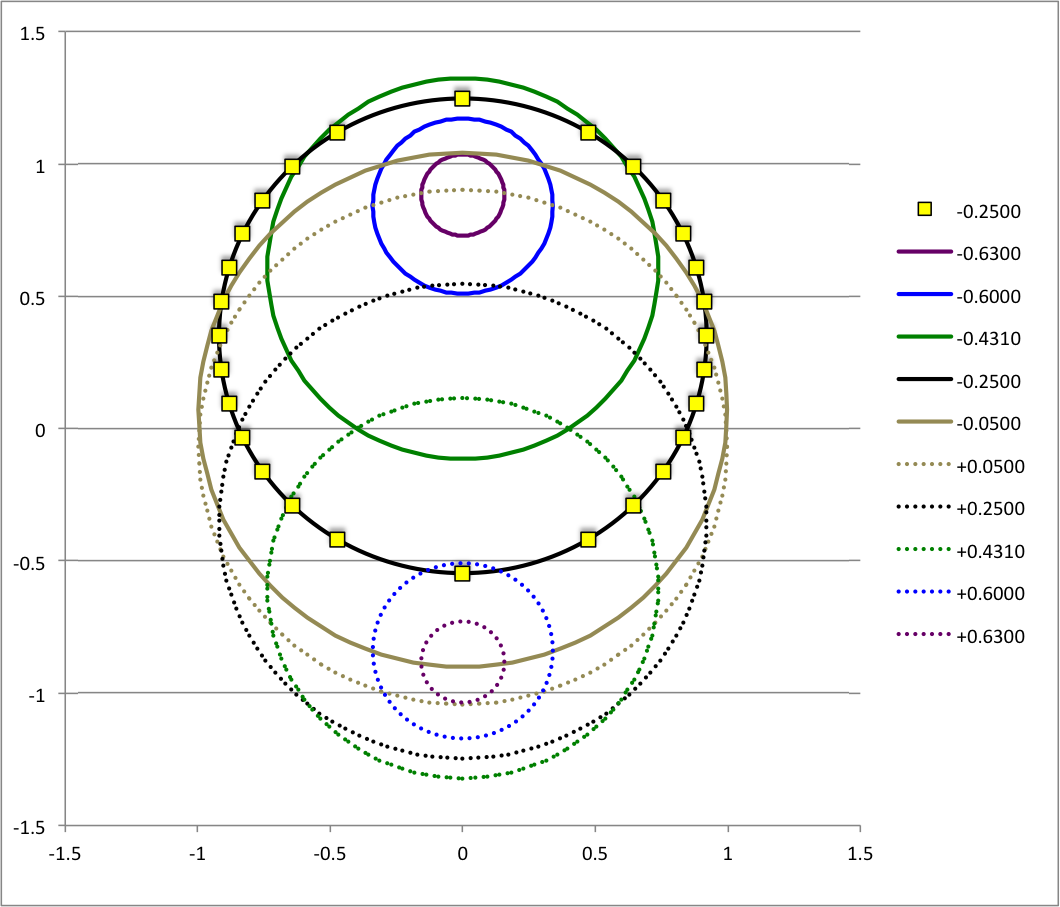
<math>~m = \tan\theta = -0.3448 ~~~ \Rightarrow ~~~ \theta = -19.02^\circ</math>
z_0 = -0.2500			z_0 = b tanθ = -0.4310			z_0 = -0.6000
z	y	\|x\|	z	y	\|x\|	z	y	\|x\|
0.1564	-1.1788	0.0000	0	-1.2500	0	-0.2182	-1.1073	0.0000
0.1147	-1.0577	0.4739	-0.02	- 1.1920	0.2981	-0.2336	-1.0626	0.1749
0.0729	-0.9366	0.6439	-0.05	-1.1050	0.4553	-0.2490	-1.0179	0.2377
0.0312	-0.8155	0.7550	-0.08	-1.0180	0.5548	-0.2645	-0.9732	0.2787
-0.0106	-0.6943	0.8312	-0.1	-0.9600	0.6042	-0.2799	-0.9285	0.3068
-0.0524	-0.5732	0.8817	-0.125	-0.8875	0.6521	-0.2953	-0.8838	0.3255
-0.0941	-0.4521	0.9106	-0.15	-0.8150	0.6879	-0.3107	-0.8390	0.3361
-0.1359	-0.3310	0.9200	-0.175	-0.7424	0.7133	-0.3261	-0.7943	0.3396
-0.1776	-0.2099	0.9106	-0.2	- 0.6699	0.7293	-0.3415	-0.7496	0.3361
-0.2194	-0.0887	0.8817	-0.25	- 0.5249	0.7356	-0.3570	-0.7049	0.3255
-0.2612	0.0324	0.8312	-0.30	- 0.3799	0.7076	-0.3724	-0.6602	0.3068
-0.3029	0.1535	0.7550	-0.35	- 0.2349	0.6410	-0.3878	-0.6155	0.2787
-0.3447	0.2746	0.6439	-0.4	- 0.0899	0.5210	-0.4032	-0.5708	0.2377
-0.3865	0.3957	0.4739	-0.43	- 0.0029	0.4050	-0.4186	-0.5261	0.1749
-0.4282	0.5169	0.0	-0.46	+0.0841	0.1950	-0.4340	-0.4814	0.0000
			-0.4685	+0.1088	0.0081

More generally, letting <math>~q \equiv z_0/(b\tan\theta)</math>, the pair of limiting values of z are given by the roots of the quadratic expression,

<math>~1 </math>	<math>~=</math>	<math>~q^2 \biggl( \frac{z}{z_0} - 1 \biggr)^2 + \biggl( \frac{z}{c} \biggr)^2 </math>
<math>~\Rightarrow ~~~0 </math>	<math>~=</math>	<math>~ z^2 \biggl[ \frac{ q^2c^2 + z_0^2)}{z_0^2 q^2 c^2} \biggr] - \frac{2z}{z_0} + \biggl[ 1 - \frac{1}{q^2} \biggr] \, .</math>

That is,

<math>~z </math>	<math>~=</math>	<math>~ \biggl[ \frac{z_0^2 q^2 c^2}{ 2(q^2 c^2 + z_0^2)} \biggr]\biggl\{ \frac{2}{z_0} \pm \biggl[\frac{4}{z_0^2} - \frac{ 4 (1 - q^{-2})(q^2 c^2 + z_0^2)}{z_0^2 q^2 c^2} \biggr]^{1 / 2} \biggr\} </math>
	<math>~=</math>	<math>~ \biggl[ \frac{z_0 q^2 c^2}{ (q^2 c^2 + z_0^2)} \biggr]\biggl\{ 1 \pm \biggl[1 - \frac{ (1 - q^{-2})(q^2 c^2 + z_0^2)}{ q^2 c^2} \biggr]^{1 / 2} \biggr\} \, .</math>

And we see that the constraint set on z₀ is given by the condition,

<math>~1</math>	<math>~\ge</math>	<math>~\frac{ (1 - q^{-2})(q^2c^2 + z_0^2)}{q^2c^2} </math>
<math>~\Rightarrow ~~~ q^2 c^2</math>	<math>~\ge</math>	<math>~(1 - q^{-2})(q^2c^2 + z_0^2) </math>
	<math>~\ge</math>	<math>~(q^2 - 1)(c^2 + b^2\tan^2\theta) </math>
<math>~\Rightarrow ~~~ 0</math>	<math>~\ge</math>	<math>~ (q^2 - 1)b^2\tan^2\theta - c^2</math>
	<math>~\ge</math>	<math>~ z_0^2 - c^2 - b^2\tan^2\theta</math>
<math>~\Rightarrow ~~~ z_0^2</math>	<math>~\le</math>	<math>~ c^2 + b^2\tan^2\theta \, .</math>

Therefore, for this example Type I ellipsoidal configuration, z₀ must lie within the range,

In the above table, we have detailed the loci of points along the surface trajectories that correspond to the values, z₀ = - 0.2500 (the leftmost three columns of the table) and z₀ = -0.6000 (the rightmost three columns of the table). The limiting values of z for these to choices of z₀ are, respectively, [z_min = -0.4283, z_max = +0.1564] and [z_min = -0.4340, z_max = -0.2182].

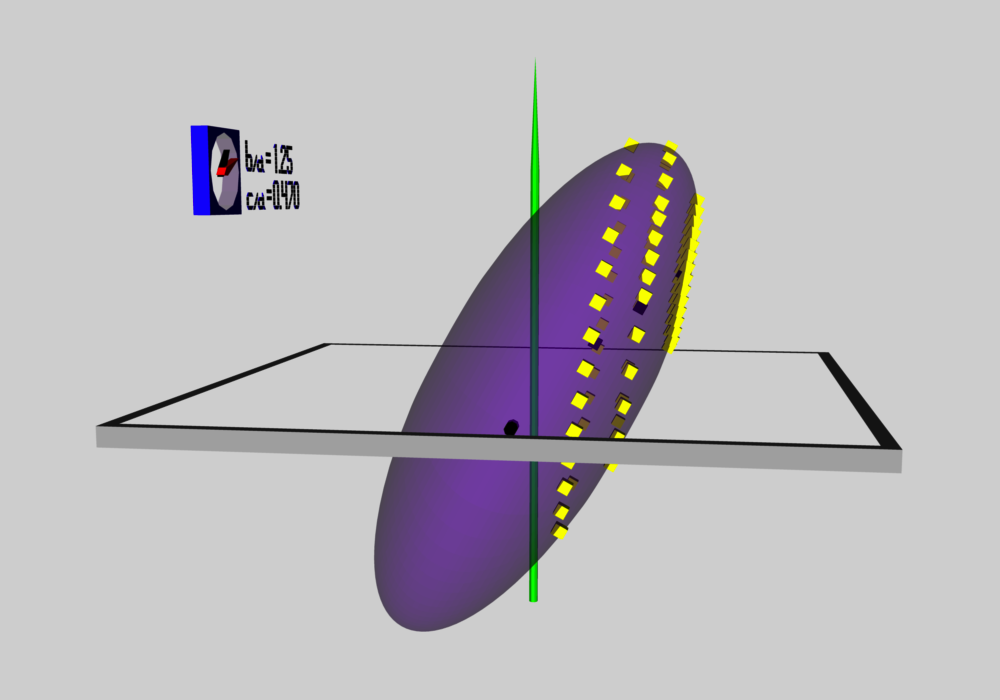
Using COLLADA, we have constructed an animated and interactive 3D scene that displays in purple the surface of our example Type I ellipsoid; panels a and b of Figure 3 show what this ellipsoid looks like when viewed from two different perspectives. (As a reminder — see the explanation accompanying Figure 2, above — the ellipsoid is tilted about the x-coordinate axis at an angle of 61.25° to the equilibrium spin axis, which is shown in green.) Yellow markers also have been placed in this 3D scene at each of the coordinate locations specified in the above table. From the perspective presented in Figure 3b, we can immediately identify three separate, nearly circular trajectories; the largest one corresponds to our choice of z₀ = -0.25, the smallest corresponds to our choice of z₀ = -0.60, and the one of intermediate size correspond to our choice of z₀ = -0.4310. When viewed from the perspective presented in Figure 3a, we see that these three trajectories define three separate planes; each plane is tipped at an angle of θ = -19.02° to the untilted equatorial, x-y plane of the purple ellipsoid.

Figure 3a	Figure 3b

Figure 3c

As we have created each orbit in the xml-based COLLADA file, we have first manually typed in the (TIME, x, y, z) coordinates of each orbit that has a negative value of z₀. Specifically, using the Figure 3c projection as a guide/reference, we typed in coordinates for the following orbits:

FLUID ELEMENT 1: <math>~z_0 = -0.6000</math>

nstep	TIME	x	y	z
1	0.000	0.000	-1.107	-0.218
26	4.836	-0.340	-0.794	-0.326
51	9.672	0.000	-0.481	-0.434
76	14.507	+0.340	-0.794	-0.326
101	19.343	0.000	-1.107	-0.218

FLUID ELEMENT 2: <math>~z_0 = -0.4300</math>

<math>~v_x\biggr\|_\mathrm{tip}</math>	<math>~=</math>	<math>~v_x\biggr\|_\mathrm{body}</math>
<math>~v_y\biggr\|_\mathrm{tip}</math>	<math>~=</math>	<math>~v_y\|_\mathrm{body}\cdot \cos\theta + v_z\|_\mathrm{body}\cdot \sin\theta</math>
<math>~v_z\biggr\|_\mathrm{tip}</math>	<math>~=</math>	<math>~-v_y\|_\mathrm{body}\cdot \sin\theta + v_z\|_\mathrm{body}\cdot \cos\theta</math>

User:Tohline/ThreeDimensionalConfigurations/RiemannTypeI

Contents

Riemann Type 1 Ellipsoids

Example b1.25c0.470

Regarding thought "A"

Regarding thought "B"

Regarding thought "D"

First Trial Value of θ

Second Trial Value of θ

Try Again

Methodical Derivation of Orbital Parameters

Example Implementation

See Also

Chandrasekhar's Detailed Analysis

Finite-Amplitude Oscillations

In the Context of Galaxy Disks

Other

Navigation menu

Search