User:Tohline/SphericallySymmetricConfigurations/Virial
Virial Equilibrium of Spherically Symmetric Configurations

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Free Energy Expression
Review
As has been introduced elsewhere in a more general context, associated with any isolated, self-gravitating, gaseous configuration we can identify a total Gibbs-like free energy, <math>\mathfrak{G}</math>, given by the sum of the relevant contributions to the total energy of the configuration,
<math> \mathfrak{G} = W_\mathrm{grav} + \mathfrak{S}_\mathrm{therm} + T_\mathrm{kin} + P_e V + \cdots </math>
Here, we have explicitly included the gravitational potential energy, <math>~W_\mathrm{grav}</math>, the ordered kinetic energy, <math>~T_\mathrm{kin}</math>, a term that accounts for surface effects if the configuration of volume <math>~V</math> is embedded in an external medium of pressure <math>~P_e,</math> and <math>~\mathfrak{S}_\mathrm{therm}</math>, the reservoir of thermodynamic energy that is available to perform work as the system expands or contracts. A mathematical expression encapsulating the physical definition of each of these energy terms, in full three-dimensional generality, can be found in our introductory discussion of the scalar virial theorem and the free-energy function.
Expressions for Various Energy Terms
We begin, here, by deriving an expression for each of the terms in the free-energy function as appropriate for spherically symmetric systems. In deriving each expression, we keep in mind two issues: First, for a given size system a determination of each term's total contribution to the free energy generally will involve integration through the entire volume of the configuration, effectively "summing up" the differential mass in each radial shell,
<math> dm = \rho(\vec{x}) d^3x = 4\pi \rho(r) r^2 dr \, , </math>
weighted by some specific energy expression. Second, each term must be formulated in such a way that it is clear how the energy contribution depends on the overall system size.
Volume Integrals
We note, first, that the mass enclosed within each interior radius, <math>~r</math>, is
|
<math>~M_r(r) = \int\limits_V dm</math> |
<math>~=</math> |
<math>~ \int_0^r 4\pi r^2 \rho dr \, .</math> |
Hence, if the volume of the configuration extends out to a radius denoted by <math>~R_\mathrm{limit}</math>, the configuration mass is,
|
<math>~M_\mathrm{limit}</math> |
<math>~=</math> |
<math>~ \int_0^{R_\mathrm{limit}} 4\pi r^2 \rho dr \, .</math> |
|
NOTE: The following considerations have led us to formally draw a distinction between <math>~M_\mathrm{limit}</math> and the "total" mass, <math>~M_\mathrm{tot}</math>, that we use (see below) for normalization. Isolated Polytropes: For isolated polytropes, the limit of integration, <math>~R_\mathrm{limit}</math>, will be the natural edge of the configuration, where the pressure and mass-density drop to zero. In this case, <math>~M_\mathrm{limit}</math> quite naturally corresponds to the total mass of the configuration. Pressure-Truncated Polytropes: But, a configuration embedded in an external medium of pressure, <math>~P_e</math>, will have a (pressure-truncated) surface whose radius, <math>~R_\mathrm{limit}</math>, corresponds to the radial location at which the configuration's internal pressure drops to a value that equals <math>~P_e</math>. In this case as well, one might choose to refer to <math>~M_\mathrm{limit}</math> as the total mass; on the other hand, it might be more useful to distinguish <math>~M_\mathrm{limit}</math> from <math>~M_\mathrm{tot}</math>, continuing to rely on <math>~M_\mathrm{tot}</math> to represent the mass of the corresponding isolated polytrope. BiPolytropes: When discussing bipolytropes, the limit of integration, <math>~R_\mathrm{limit}</math>, will naturally refer to the radial location that defines the outer edge of the configuration's "core" and, at the same time, identifies the radial "interface" between the bipolytrope's core and its envelope. In this case, <math>~M_\mathrm{limit}</math> corresponds to the mass of the core rather than to the total mass of the bipolytropic configuration. |
Confinement by External Pressure: For spherically symmetric configurations, the energy term due to confinement by an external pressure can be expressed, simply, in terms of the configuration's radius, <math>~R_\mathrm{limit}</math>, as,
|
<math>~P_e V</math> |
<math>~=</math> |
<math>~P_e \int_0^{R_\mathrm{limit}} 4\pi r^2 dr = \frac{4\pi}{3} P_e R_\mathrm{limit}^3 \, .</math> |
Gravitational Potential Energy: From our discussion of the scalar virial theorem — see, specifically, the reference to Equation (18), on p. 18 of [EFE] — the gravitational potential energy is given by the expression,
<math> W_\mathrm{grav} = - \int\limits_V \rho x_i \frac{\partial\Phi}{\partial x_i} d^3 x = - \int\limits_V \vec{r} \cdot \nabla\Phi dm = - \int_0^{R_\mathrm{limit}} \biggl( r \frac{d\Phi}{dr} \biggr) dm \, . </math>
For spherically symmetric systems, the
becomes,
|
<math>~\frac{1}{r^2} \frac{d}{dr} \biggl( r^2 \frac{d\Phi}{dr} \biggr) </math> |
<math>~=</math> |
<math>~4\pi G \rho(r) \, , </math> |
which implies,
|
<math>~r^2 \frac{d\Phi}{dr} </math> |
<math>~=</math> |
<math>~\int_0^r 4\pi G \rho(r) r^2 dr = GM_r(r) \, .</math> |
Hence — see, also, p. 64, Equation (12) of [C67] — the desired expression for the gravitational potential energy is,
|
<math>~W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~ - \int_0^{R_\mathrm{limit}} \biggl( \frac{GM_r}{r} \biggr) dm = - \int_0^{R_\mathrm{limit}} \frac{G}{r}\biggl[\int_0^r 4\pi r^2 \rho dr \biggr] 4\pi r^2 \rho dr \, .</math> |
|
Also, as pointed out by [C67] — see p. 64, Equation (16) — it may sometimes prove advantageous to recognize that, if a spherically symmetric system is in hydrostatic balance, an alternate expression for the total gravitational potential energy is,
|
Rotational Kinetic Energy: We will also consider a system that is rotating with a specified simple angular velocity profile, <math>~\dot\varphi(\varpi)</math>, in which case, from our discussion of the scalar virial theorem — see, specifically, the reference to Equation (8), on p. 16 of EFE — the (ordered) kinetic energy,
|
<math>~T_\mathrm{kin}</math> |
<math>~=</math> |
<math>~ \frac{1}{2} \int\limits_V \rho |\vec{v} |^2 d^3x = \frac{1}{2} \int\limits_V |\vec{v} |^2 dm \, ,</math> |
is entirely rotational kinetic energy, specifically,
|
<math>~T_\mathrm{kin} = T_\mathrm{rot}</math> |
<math>~=</math> |
<math>~ \frac{1}{2} \int\int\int \dot\varphi^2 \varpi^2 dm = \frac{1}{2} \int_0^{R_\mathrm{limit}} \dot\varphi^2 \varpi^2 \int_{-\sqrt{{R_\mathrm{limit}}^2 - \varpi^2}}^{\sqrt{{R_\mathrm{limit}}^2 - \varpi^2}} \rho(r(\varpi,z)) 2\pi \varpi d\varpi dz\, .</math> |
Reservoir of Thermodynamic Energy: As has been explained in our introductory discussion of the Gibbs-like free energy, formulation of an expression for the reservoir of thermodynamic energy, <math>~\mathfrak{S}_\mathrm{therm}</math>, depends on whether the system is expected to evolve adiabatically or isothermally. For isothermal systems,
<math> \mathfrak{S}_\mathrm{therm} ~~\rightarrow ~~\mathfrak{S}_I = + \int\limits_V c_s^2 \ln \biggl(\frac{\rho}{\rho_\mathrm{norm}}\biggr) dm = c_s^2 \int_0^{R_\mathrm{limit}} \ln \biggl(\frac{\rho}{\rho_\mathrm{norm}}\biggr) 4\pi r^2 \rho dr \, , </math>
where, <math>~c_s</math> is the isothermal sound speed and <math>~\rho_\mathrm{norm}</math> is a (as yet unspecified) reference mass density; while, for adiabatic systems,
<math> \mathfrak{S}_\mathrm{therm} ~~\rightarrow ~~ \mathfrak{S}_A = + \int\limits_V \frac{1}{({\gamma_g}-1)} \biggl( \frac{P}{\rho} \biggr) dm = \frac{1}{({\gamma_g}-1)} \int_0^{R_\mathrm{limit}} 4\pi r^2 P dr
\, ,</math>
where, <math>~P(r)</math> is the system's pressure distribution and <math>~\gamma_g</math> is the specified adiabatic index.
Normalizations
Our Choices
It is appropriate for us to define some characteristic scales against which various physical parameters can be normalized — and, hence, their relative significance can be specified or measured — as the free energy of various systems is examined. As the system size is varied in search of extrema in the free energy, we generally will hold constant the total system mass and the specific entropy of each fluid element. (When isothermal rather than adiabatic variations are considered, the sound speed rather than the specific entropy will be held constant.) Hence, following the lead of both Horedt (1970) and Whitworth (1981), we will express the various characteristic scales in terms of the constants, <math>~G, M_\mathrm{tot},</math> and the polytropic constant, <math>~K.</math> Specifically, we will normalize all length scales, pressures, energies, mass densities, and the square of the speed of sound by, respectively,
|
Adopted Normalizations | |||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Adiabatic Cases |
Isothermal Case <math>~(\gamma = 1; K = c_s^2)</math> |
||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
Note that, given the above definitions, the following relations hold: <math>~E_\mathrm{norm} = P_\mathrm{norm} R_\mathrm{norm}^3 = \frac{G M_\mathrm{tot}^2}{ R_\mathrm{norm}} = \biggl( \frac{3}{4\pi} \biggr) M_\mathrm{tot} c_\mathrm{norm}^2</math> | |||||||||||||||||||||||||||||||||||||
It should be emphasized that, as we discuss how a configuration's free energy varies with its size, the variable <math>~R_\mathrm{limit}</math> will be used to identify the configuration's size whether or not the system is in equilibrium, and the parameter,
<math>~\chi \equiv \frac{R_\mathrm{limit}}{R_\mathrm{norm}} \, ,</math>
will be used to identify the size as referenced to <math>~R_\mathrm{norm}</math>. When an equilibrium configuration is identified <math>~(R_\mathrm{limit} \rightarrow R_\mathrm{eq})</math>, we will affix the subscript "eq," specifically,
<math>~\chi_\mathrm{eq} \equiv \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \, .</math>
Choices Made by Other Researchers
As is detailed in a related discussion, our definitions of <math>~R_\mathrm{norm}</math> and <math>~P_\mathrm{norm}</math> are close, but not identical, to the scalings adopted by Horedt (1970) and by Whitworth (1981). The following relations can be used to switch from our normalizations to theirs:
|
|
|
||||||||||||||||||
It is also worth noting how the length-scale normalization that we are adopting here relates to the characteristic length scale,
<math>~a_n \equiv \biggl[ \frac{1}{4\pi G} \biggl( \frac{H_c}{\rho_c} \biggr) \biggr]^{1/2} \, ,</math>
that has classically been adopted in the context of the Lane-Emden equation, the solution of which provides a detailed description of the internal structure of spherical polytropes for a wide range of values of the polytropic index, <math>~n</math>. Recognizing that, via the polytropic equation of state, the pressure, density, and enthalpy of every element of fluid are related to one another via the expressions,
<math>~H\rho = (n+1)P</math> … and … <math>P = K\rho^{1+1/n} \, ,</math>
the specific enthalpy at the center of a polytropic sphere, <math>~H_c/\rho_c</math>, can be rewritten in terms of <math>~K</math> and <math>~\rho_c</math> to give,
<math>~a_n = \biggl[ \frac{(n+1)K}{4\pi G} \rho_c^{(1/n) -1} \biggr]^{1/2} \, ,</math>
which is the definition of this classical length scale introduced by [C67] (see, specifically, his equation 10 on p. 87). Switching from <math>~n</math> to the associated adiabatic exponent via the relation, <math>~\gamma = 1+1/n ~~~\Rightarrow~~~ n = 1/(\gamma-1)</math>, we see that,
|
<math>~\biggl( \frac{a_n}{R_\mathrm{norm}} \biggr)^2</math> |
<math>~=</math> |
<math>~\biggl( \frac{\gamma}{\gamma-1} \biggr) \frac{K \rho_c^{(\gamma-2)}}{4\pi G} \cdot \frac{1}{R_\mathrm{norm}^2}</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{4\pi}\biggl( \frac{\gamma}{\gamma-1} \biggr) \frac{K }{G} \biggl( \frac{\rho_c}{\bar\rho} \biggr)^{(\gamma-2)} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_\mathrm{eq}^3} \biggr)^{(\gamma-2)} \cdot \frac{1}{R_\mathrm{norm}^2} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{4\pi} \biggl( \frac{\gamma}{\gamma-1} \biggr) \biggl( \frac{3}{4\pi } \cdot \frac{\rho_c}{\bar\rho} \biggr)^{\gamma-2} \biggl[ \frac{K M_\mathrm{tot}^{\gamma-2} }{G} \biggr] \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{eq}} \biggr)^{3{(\gamma-2)}} \cdot \frac{1}{R_\mathrm{norm}^{3\gamma-4}} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{4\pi} \biggl( \frac{\gamma}{\gamma-1} \biggr) \biggl( \frac{3}{4\pi } \cdot \frac{\rho_c}{\bar\rho} \biggr)^{2-\gamma} \chi_\mathrm{eq}^{6-3\gamma} \biggl[ \frac{K M_\mathrm{tot}^{\gamma-2} }{G} \biggr] \cdot \biggl[ \biggl( \frac{G}{K} \biggr) M_\mathrm{tot}^{2-\gamma} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{4\pi} \biggl( \frac{\gamma}{\gamma-1} \biggr) \biggl( \frac{3}{4\pi } \cdot \frac{\rho_c}{\bar\rho} \biggr)^{2-\gamma} \chi_\mathrm{eq}^{6-3\gamma} \, . </math> |
Notice that, written in this manner, the scale length, <math>~a_n</math>, cannot actually be determined unless the normalized equilibrium radius, <math>~\chi_\mathrm{eq}</math>, is known. We will encounter analogous situations whenever the free energy function is used to identify the physical parameters that define equilibrium configurations — key attributes of a system that should be held fixed as the system size (or some other order parameter) is varied cannot actually be evaluated until an extremum in the free energy is identified and the corresponding value of <math>~\chi_\mathrm{eq}</math> is known. Because solutions of the Lane-Emden equation directly provide detailed force-balance models of polytropic spheres, [C67] did not encounter this issue. As we have discussed elsewhere, the equilibrium radius of a polytropic sphere is identified as the radial location,
<math>~\xi_1 = \frac{R_\mathrm{eq}}{a_n} \, ,</math>
at which the Lane-Emden function, <math>~\Theta_H(\xi)</math>, first goes to zero. Bypassing the free-energy analysis and using knowledge of <math>~\xi_1</math> to identify the equilibrium radius — specifically, setting,
|
<math>~\chi_\mathrm{eq}</math> |
<math>~=</math> |
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{norm}} = \xi_1 \biggl(\frac{a_n}{R_\mathrm{norm}} \biggr) \, ,</math> |
we can extend the above analysis to obtain,
|
<math>~\biggl( \frac{a_n}{R_\mathrm{norm}} \biggr)^2</math> |
<math>~=</math> |
<math>~\frac{1}{4\pi} \biggl( \frac{\gamma}{\gamma-1} \biggr) \biggl( \frac{4\pi }{3} \cdot \frac{\rho_c}{\bar\rho} \biggr)^{2-\gamma} \biggl[ \xi_1 \biggl(\frac{a_n}{R_\mathrm{norm}} \biggr) \biggr]^{6-3\gamma} </math> |
|
<math>\Rightarrow~~~~~\biggl( \frac{a_n}{R_\mathrm{norm}} \biggr)^{4-3\gamma}</math> |
<math>~=</math> |
<math>~4\pi \biggl( \frac{\gamma-1}{\gamma} \biggr) \biggl( \frac{4\pi }{3} \cdot \frac{\rho_c}{\bar\rho} \cdot \xi_1^3\biggr)^{\gamma-2} \, . </math> |
Implementation
Normalize
We will now judiciously introduce our adopted normalizations into the above-defined free-energy term expressions, using asterisks to denote dimensionless variables that have been accordingly normalized; for example,
<math> r^* \equiv \frac{r}{R_\mathrm{norm}} \, , ~~~~~~ P^* \equiv \frac{P}{P_\mathrm{norm}} \, , ~~~~~~ </math> and <math>\rho^* \equiv \frac{\rho}{\rho_\mathrm{norm}} \, . </math>
Normalized Mass:
|
<math>~M_r(r^*) </math> |
<math>~=</math> |
<math> R_\mathrm{norm}^3 \rho_\mathrm{norm} \int_0^{r^*} 4\pi (r^*)^2 \rho^* dr^* = M_\mathrm{tot} \int_0^{r^*} 3(r^*)^2 \rho^* dr^* \, . </math> |
Confinement by External Pressure (Normalized Volume):
|
<math>~P_e V</math> |
<math>~=</math> |
<math>~E_\mathrm{norm} \biggl[ \frac{4\pi}{3} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \biggl(\frac{R_\mathrm{limit}}{R_\mathrm{norm}}\biggr)^3 \biggr] \, .</math> |
Normalized Gravitational Potential Energy:
|
<math>~W_\mathrm{grav}</math> |
<math>~=</math> |
<math> - 4\pi GM_\mathrm{tot} R_\mathrm{norm}^2 \rho_\mathrm{norm} \int_0^{\chi=R_\mathrm{limit}^*} \biggl[\frac{M_r(r^*)}{M_\mathrm{tot}} \biggr] r^* \rho^* dr^* </math> |
|
|
<math>~=</math> |
<math> - E_\mathrm{norm} \int_0^{\chi = R_\mathrm{limit}^*} 3\biggl[\frac{M_r(r^*)}{M_\mathrm{tot}} \biggr] r^* \rho^* dr^* \, . </math> |
Normalized Reservoir of Thermodynamic Energy:
|
<math>~\mathfrak{S}_I</math> |
<math>~=</math> |
<math>~E_\mathrm{norm} \int_0^{\chi=R_\mathrm{limit}^*} 3 \ln (\rho^*) (r^*)^2 \rho^* dr^* \, ,</math> |
and,
|
<math>~\mathfrak{S}_A</math> |
<math>~=</math> |
<math>~\frac{E_\mathrm{norm}}{({\gamma_g}-1)} \int_0^{\chi=R_\mathrm{limit}^*} 4\pi (r^*)^2 P^* dr^* \, .</math> |
Normalized Rotational Kinetic Energy:
|
<math>~T_\mathrm{rot}</math> |
<math>~=</math> |
<math>~ \pi \dot\varphi_c^2 R_\mathrm{norm}^5 \rho_\mathrm{norm} \int_0^{\chi=R_\mathrm{limit}^*} \biggl[ \frac{\dot\varphi^2}{\dot\varphi_c^2} \biggr] (\varpi^*)^3 d\varpi^* \int_{-\sqrt{\chi^2 - (\varpi^*)^2}}^{\sqrt{\chi^2 - (\varpi^*)^2}} (\rho^*) dz^* </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{5^2\pi}{2^2} \biggr) \biggl[ \frac{J^2 R_\mathrm{norm} \rho_\mathrm{norm}}{M_\mathrm{tot}^2} \biggr] \chi_\mathrm{eq}^{-4} \int_0^{\chi=R_\mathrm{limit}^*} \biggl[ \frac{\dot\varphi^2}{\dot\varphi_c^2} \biggr] (\varpi^*)^3 d\varpi^* \int_{-\sqrt{\chi^2 - (\varpi^*)^2}}^{\sqrt{\chi^2 - (\varpi^*)^2}} (\rho^*) dz^* </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{3\cdot 5^2}{2^4} \biggr) \biggl[ \frac{J^2}{M_\mathrm{tot}} \biggl(\frac{E_\mathrm{norm} }{G M_\mathrm{tot}^2 }\biggr)^2 \biggr] \chi_\mathrm{eq}^{-4} \int_0^{\chi=R_\mathrm{limit}^*} \biggl[ \frac{\dot\varphi^2}{\dot\varphi_c^2} \biggr] (\varpi^*)^3 d\varpi^* \int_{-\sqrt{\chi^2 - (\varpi^*)^2}}^{\sqrt{\chi^2 - (\varpi^*)^2}} (\rho^*) dz^* </math> |
|
|
<math>~=</math> |
<math>~ E_\mathrm{norm} \biggl( \frac{3^2\cdot 5^2}{2^6 \pi} \biggr) \biggl[ \frac{J^2 c_\mathrm{norm}^2}{G^2 M_\mathrm{tot}^4} \biggr] \chi_\mathrm{eq}^{-4} \int_0^{\chi=R_\mathrm{limit}^*} \biggl[ \frac{\dot\varphi^2}{\dot\varphi_c^2} \biggr] (\varpi^*)^3 d\varpi^* \int_{-\sqrt{\chi^2 - (\varpi^*)^2}}^{\sqrt{\chi^2 - (\varpi^*)^2}} (\rho^*) dz^* \, , </math> |
where,
<math>\dot\varphi_c \equiv \frac{5J}{2M_\mathrm{tot} R_\mathrm{eq}^2} = \frac{5}{2} \biggl[ \frac{J}{M_\mathrm{tot} R_\mathrm{norm}^2} \biggr] \chi_\mathrm{eq}^{-2} \, ,</math>
is a characteristic rotation frequency in the equilibrium configuration whose value is set once the system's total angular momentum, <math>~J</math>, is specified.
Separate Time & Space
Our intent is to vary the size of the configuration <math>~(R_\mathrm{limit})</math> while holding the (properly normalized) internal structural profile fixed, so let's separate the spatial integral over the (fixed) structural profile from the time-varying configuration size. Making use of the dimensionless internal coordinates,
<math>~x \equiv \frac{r}{R_\mathrm{limit}} \, ,~~~~w \equiv \frac{\varpi}{R_\mathrm{limit}} \, , ~~~~\zeta \equiv \frac{z}{R_\mathrm{limit}} \, , </math>
that always run from zero to one, we have,
|
<math>~r^*</math> |
<math>~\rightarrow~</math> |
<math> ~x \biggl( \frac{R_\mathrm{limit}}{R_\mathrm{norm}} \biggr) = x \chi \, ; </math> and, likewise, <math> ~~~~\varpi^* ~\rightarrow~ w \chi \, ; ~~~~z^* ~\rightarrow~ \zeta \chi \, ; </math> |
|
<math>~\rho^*</math> |
<math>~\rightarrow~</math> |
<math> \biggl[ \frac{\rho(x)}{\bar\rho} \biggr] \biggl( \frac{\bar\rho}{\rho_\mathrm{norm}} \biggr) = \biggl[ \frac{\rho(x)}{\bar\rho} \biggr] \biggl( \frac{M_\mathrm{limit}/R_\mathrm{limit}^3}{M_\mathrm{tot}/R_\mathrm{norm}^3} \biggr) = \biggl[ \frac{\rho(x)}{\bar\rho} \biggr] \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \chi^{-3} = \frac{\rho_c}{\bar\rho} \biggl[ \frac{\rho(x)}{\rho_c} \biggr] \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \chi^{-3} \, ; </math> |
|
<math>~P^*</math> |
<math>~\rightarrow~</math> |
<math> \biggl[ \frac{P(x)}{P_c} \biggr] \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) = \biggl[ \frac{P(x)}{P_c} \biggr] \biggl( \frac{K\rho_c^\gamma}{P_\mathrm{norm}} \biggr) = \biggl[ \frac{P(x)}{P_c} \biggr] \biggl( \frac{\rho_c}{\bar\rho} \biggr)^\gamma \biggl[ \frac{(3M_\mathrm{limit}/4\pi R_\mathrm{limit}^3)^\gamma}{K^{-1}P_\mathrm{norm}} \biggr] </math> |
|
|
|
<math> = \biggl[ \frac{P(x)}{P_c} \biggr] \biggl[ \biggl(\frac{3}{4\pi} \biggr) \frac{\rho_c}{\bar\rho} \biggr]^\gamma \biggl[ \frac{K M_\mathrm{tot}^\gamma}{P_\mathrm{norm} R_\mathrm{norm}^{3\gamma}} \biggr] \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^\gamma \biggl( \frac{R_\mathrm{limit}}{R_\mathrm{norm}} \biggr)^{-3\gamma} = \biggl[ \frac{P(x)}{P_c} \biggr] \biggl[ \biggl(\frac{3}{4\pi} \biggr) \frac{\rho_c}{\bar\rho} \biggr]^\gamma \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^\gamma \chi^{-3\gamma} \, , </math> |
|
<math>~\frac{\dot\varphi}{\dot\varphi_c}</math> |
<math>~\rightarrow~</math> |
<math> \biggl[ \frac{\dot\varphi(w)}{\dot\varphi_\mathrm{limit}} \biggr] \biggl( \frac{\dot\varphi_\mathrm{limit}}{\dot\varphi_c}\biggr) = \biggl[ \frac{\dot\varphi(w)}{\dot\varphi_\mathrm{limit}} \biggr] \biggl( \frac{R_\mathrm{limit}}{R_\mathrm{eq}}\biggr)^{-2} = \biggl[ \frac{\dot\varphi(w)}{\dot\varphi_\mathrm{limit}} \biggr] \chi_\mathrm{eq}^{2} \chi^{-2} \, . </math> |
Summary of Normalized Expressions
Hence, our normalized expressions become,
|
Normalized Expressions | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||
|
[NOTE to self (21 September 2014): The expressions for <math>~\mathfrak{S}_I</math> and <math>~T_\mathrm{rot}</math> may not properly account for ratio of M_limit to M_tot.] |
It should be emphasized that the coefficient involving the density ratio, <math>~(\rho_c/\bar\rho)</math>, that lies outside of the integral in most of these expressions depends only on the internal structure, and not the overall size, of the configuration. It can therefore be evaluated at any time. We usually will choose to evaluate this coefficient in an equilibrium state, that is, when <math>~R_\mathrm{limit} \rightarrow R_\mathrm{eq}</math>. Accordingly, the subscript "eq" has been attached to this coefficient. The inverse of this density ratio can be obtained from the integral expression for <math>~M_r</math> by recognizing that <math>~M_r \rightarrow M_\mathrm{limit}</math> when the upper limit on the integral <math>~x \rightarrow 1</math>. Hence,
|
<math>~\biggl(\frac{\rho_c}{\bar\rho} \biggr)^{-1}_\mathrm{eq} </math> |
<math>~=</math> |
<math>~ \int_0^{1} 3x^2 \biggl[ \frac{\rho(x)}{\rho_c} \biggr]_\mathrm{eq} dx \, .</math> |
This coefficient also may be rewritten in terms of the central pressure in the equilibrium state; specifically, using a sequence of steps similar to the ones that were used, above, in rewriting <math>~P^*</math>, we can write,
|
<math> \biggl[ \biggl(\frac{3}{4\pi} \biggr) \frac{\rho_c}{\bar\rho} \biggr]_\mathrm{eq}^{\gamma} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^\gamma </math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) \chi^{3\gamma} \biggr]_\mathrm{eq} \, .</math> |
Looking Ahead to Bipolytropes
|
ASIDE: When we discuss the free energy of bipolytropic configurations, we will need to divide the expression for <math>~\mathfrak{S}_A/E_\mathrm{norm}</math> into two parts — one accounting for the reservoir of thermodynamic energy in the bipolytrope's "core" and one accounting for the reservoir of thermodynamic energy in the bipolytrope's "envelope." It is useful to develop this two-part expression here, while the definition of <math>~\mathfrak{S}_A</math> is fresh in our minds and to show how the two-part expression reduces to the simpler expression for <math>~\mathfrak{S}_A/E_\mathrm{norm}</math>, just derived, when there is no distinction drawn between the properties of the core and the envelope.
<math>~P_\mathrm{core}(x) = P_0 [1 - p_c(x)]</math> for <math>~0 \leq x \leq q \, ,</math> and that, for the envelope, the pressure drops monotonically from a value of <math>~P_{ie}</math> at the interface according to an expression of the form, <math>~P_\mathrm{env}(x) = P_{ie} [1 - p_e(x)]</math> for <math>~q \leq x \leq 1 \, ,</math> where <math>~p_c(x)</math> and <math>~p_e(x)</math> are both dimensionless functions that will depend on the equations of state that are chosen for the core and envelope, respectively. By prescription, the pressure in the envelope must drop to zero at the surface of the bipolytropic configuration, hence, we should expect that <math>~p_e(1) = 1</math>. Furthermore, by prescription, the pressure in the core will drop to a value, <math>~P_{ic}</math>, at the interface, so we can write, <math>~P_{ic} = P_0 [1 - p_c(q)] \, .</math> In equilibrium — that is, when <math>~R_\mathrm{edge} = R_\mathrm{eq}</math> — we will demand that the pressure at the interface be the same, whether it is referenced in the core or in the envelope, that is, we will demand that <math>~P_{ic} = P_{ie} \, .</math> It will therefore prove to be strategically advantageous to rewrite the expression for the run of pressure through the core in terms of the pressure at the interface rather than in terms of the central pressure; specifically, <math>~P_\mathrm{core}(x) = P_{ic} \biggl[\frac{1 - p_c(x)}{1-p_c(q)} \biggr] \, .</math> Referencing these prescriptions for <math>~P_\mathrm{core}(x)</math> and <math>~P_\mathrm{env}(x)</math>, the two-part expression for the reservoir of thermodynamic energy is,
As is implied by the subscripts on the adiabatic exponents that appear in the leading factor of each of the two terms, we are assuming that, as the bipolytropic system expands or contracts, the thermodynamic properties of the material in the envelope will vary as prescribed by an adiabat of index, <math>~\gamma_e</math>, while the thermodynamic properties of material in the core will vary as prescribed by a, generally different, adiabat of index, <math>~\gamma_c</math>. Therefore, as the radius of the bipolytropic configuration, <math>~R_\mathrm{edge}</math>, is varied, the density of each fluid element will vary and, in the core, the pressure of each fluid element will vary as <math>~P \propto \rho^{\gamma_c}</math> while, in the envelope, the pressure of each fluid element will vary as <math>~P \propto \rho^{\gamma_e}</math>. If we furthermore assume that the mass in the core and the mass in the envelope remain constant during a phase of contraction or expansion, the density of each fluid element will vary as <math>~R_\mathrm{edge}^{-3}</math>, whether the material is associated with the core or with the envelope. Therefore, using the subscript, "eq," to identify the value of thermodynamic quantities when the system is in an equilibrium state and, accordingly, <math>~R_\mathrm{edge} = R_\mathrm{eq}</math>, we can write,
and,
In particular, for any <math>~R_\mathrm{edge}</math>, material associated with the core that lies at the interface will have a pressure given by the relation,
while material associated with the envelope that lies at the interface will have a pressure given by the relation,
Hence,
We therefore obtain,
as desired. |
Idealized Configuration
(For simplicity throughout this subsection, we will assume that the mass enclosed within the configuration's limiting radius, <math>~M_\mathrm{limit}</math>, equals the normalization mass, <math>~M_\mathrm{tot}</math>.) In the idealized situation of a configuration that has uniform density, <math>~\rho(x) = \rho_c</math> — and, hence, the density ratio <math>~\rho_c/\bar\rho = 1</math> — the mass interior to each radius is,
|
<math>~\frac{M_r(x)}{M_\mathrm{tot} } </math> |
<math>~=</math> |
<math>~ \int_0^{x} 3x^2 dx = x^3 \, ,</math> |
and the normalized gravitational potential energy is,
|
<math>~\frac{W_\mathrm{grav}}{E_\mathrm{norm} }</math> |
<math>~=</math> |
<math> - \frac{3}{5} \chi^{-1} \int_0^{1} 5x \biggl\{ x^3\biggr\} dx = -\frac{3}{5} \chi^{-1} \, . </math> |
If, in addition, the configuration is uniformly rotating with angular velocity, <math>~\dot\varphi = \dot\varphi_\mathrm{edge}</math>, and has uniform pressure, <math>~P_c</math>, evaluation of the ordered kinetic energy and thermodynamic energy integrals yields,
|
<math>~\frac{T_\mathrm{rot}}{E_\mathrm{norm} }</math> |
<math>~=</math> |
<math>~ 2\chi^{-2} \biggl( \frac{3^2\cdot 5^2}{2^6\pi} \biggr) \biggl[ \frac{J^2 c_\mathrm{norm}^2}{G^2 M_\mathrm{tot}^4} \biggr] \int_0^{1} w^3 dw \int_{0}^{\sqrt{1 - w^2}} d\zeta </math> |
|
|
<math>~=</math> |
<math>~ \chi^{-2} \biggl( \frac{3^2\cdot 5^2}{2^5\pi} \biggr) \biggl[ \frac{J^2 c_\mathrm{norm}^2}{G^2 M_\mathrm{tot}^4} \biggr] \int_0^1 w^3 (1-w^2)^{1/2} dw </math> |
|
|
<math>~=</math> |
<math>~ \chi^{-2} \biggl( \frac{3^2\cdot 5^2}{2^5\pi} \biggr)\biggl[ \frac{J^2 c_\mathrm{norm}^2}{G^2 M_\mathrm{tot}^4} \biggr] \biggl[ -\frac{1}{15} (1-w^2)^{3/2} (3w^2 +2) \biggr]_0^1 </math> |
|
|
<math>~=</math> |
<math>~ \chi^{-2} \biggl( \frac{3\cdot 5}{2^4 \pi} \biggr) \biggl[ \frac{J^2 c_\mathrm{norm}^2}{G^2 M_\mathrm{tot}^4} \biggr] \, , </math> |
|
<math>~\frac{\mathfrak{S}_A}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\frac{4\pi }{3({\gamma_g}-1)} \cdot \chi^{3-3\gamma} \biggl\{ \biggl(\frac{3}{4\pi} \biggr)^{\gamma}\int_0^{1} 3x^2 dx \biggr\} = \frac{1}{({\gamma_g}-1)} \biggl(\frac{3}{4\pi} \biggr)^{\gamma-1} \chi^{3-3\gamma} \, ,</math> |
|
<math>~\frac{\mathfrak{S}_I}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~-3 \ln \chi + \mathrm{constant} \, , </math> |
where the various dimensionless integration variables are, <math>~x \equiv (r/R)</math>, <math>~\zeta \equiv (z/R)</math>, and <math>~w \equiv (\varpi/R)</math>.
Structural Form Factors
Keeping in mind the expressions that arise in the case of our just-defined, idealized configuration, in more realistic cases we generally will write each energy term as follows:
|
<math>~\frac{W_\mathrm{grav}}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math> - \frac{3}{5} \chi^{-1} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \, , </math> |
|
<math>~\frac{T_\mathrm{rot}}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{3\cdot 5}{2^4 \pi} \biggr)\chi^{-2} \biggl[ \frac{J^2 c_\mathrm{norm}^2}{G^2 M_\mathrm{tot}^4} \biggr] \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \cdot \frac{\mathfrak{f}_T}{\mathfrak{f}_M} \, , </math> |
|
<math>~\frac{\mathfrak{S}_A}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\frac{4\pi}{3({\gamma_g}-1)} \cdot \chi^{3-3\gamma} \biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \biggr]_\mathrm{eq}^{\gamma} \cdot \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma}} </math> |
|
|
<math>~=</math> |
<math>~\frac{4\pi}{3({\gamma_g}-1)} \cdot \chi^{3-3\gamma} \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} \cdot \mathfrak{f}_A \, ,</math> |
where the dimensionless form factors, <math>~\mathfrak{f}_i</math>, which are assumed to be independent of the overall configuration size and will each usually of order unity, are,
|
<math>~\mathfrak{f}_M </math> |
<math>~\equiv</math> |
<math>~ \int_0^1 3\biggl[ \frac{\rho(x)}{\rho_c}\biggr] x^2 dx = \biggl( \frac{\bar\rho}{\rho_c} \biggr)_\mathrm{eq} \, ,</math> |
|
<math>~\mathfrak{f}_W</math> |
<math>~\equiv</math> |
<math>~ 3\cdot 5 \int_0^1 \biggl\{ \int_0^x \biggl[ \frac{\rho(x)}{\rho_c}\biggr] x^2 dx \biggr\} \biggl[ \frac{\rho(x)}{\rho_c}\biggr] x dx\, ,</math> |
|
<math>~\mathfrak{f}_T</math> |
<math>~\equiv</math> |
<math>~ \frac{15}{2} \int_0^1 \biggl[ \frac{\dot\varphi(w)}{\dot\varphi_\mathrm{edge}} \biggr]^2 w^3 dw \int_0^{\sqrt{1 - w^2}} \biggl[ \frac{\rho(w,\zeta)}{\rho_c} \biggr] d\zeta\, ,</math> |
|
<math>~\mathfrak{f}_A</math> |
<math>~\equiv</math> |
<math>~ \int_0^1 3\biggl[ \frac{P(x)}{P_c}\biggr] x^2 dx \, .</math> |
In each case, the "idealized" energy expression is retrieved if/when the relevant form factor, <math>~\mathfrak{f}_i</math>, is set to unity.
Some Detailed Examples
In an accompanying discussion, we derive detailed expressions for a selected subset of the above structural form factors and corresponding energy terms in the case of spherically symmetric configurations that obey an <math>~n=5</math> or an <math>~n=1</math> polytropic equation of state. The hope is that this will illustrate, in a clear and helpful manner, how the task of calculating form factors is to be carried out, in practice; and, in particular, to provide one nontrivial example for which analytic expressions are derivable. This should help debug numerical algorithms that are designed to calculate structural form factors for more general cases that cannot be derived analytically. The limits of integration will be specified in a general enough fashion that the resulting expressions can be applied, not only to the structures of isolated polytropes, but to pressure-truncated polytropes that are embedded in a hot, tenuous external medium and to the cores of bipolytropes.
Gathering it all Together
Gathering all of the terms together we find that, to within an additive constant, the expression for the normalized free energy is,
<math> \mathfrak{G}^* \equiv \frac{\mathfrak{G}}{E_\mathrm{norm}} = -3A\chi^{-1} -~ \frac{(1-\delta_{1\gamma_g})}{(1-\gamma_g)} B \chi^{3-3\gamma_g} -~ \delta_{1\gamma_g} 3\ln \chi +~ C \chi^{-2} +~ D\chi^3 \, , </math>
where,
|
<math>~A</math> |
<math>~\equiv</math> |
<math>\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W \, ,</math> |
|
<math>~B</math> |
<math>~\equiv</math> |
<math> \frac{4\pi}{3} \biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]_\mathrm{eq}^{\gamma} \cdot \mathfrak{f}_A </math> |
|
|
<math>~=</math> |
<math> \frac{4\pi}{3} \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} \cdot \mathfrak{f}_A \, , </math> |
|
<math>~C</math> |
<math>~\equiv</math> |
<math> \frac{3\cdot 5}{2^4 \pi} \biggl[ \frac{J^2 c_\mathrm{norm}^2}{G^2 M_\mathrm{tot}^4} \biggr] \cdot \frac{\mathfrak{f}_T}{\mathfrak{f}_M} \, , </math> |
|
<math>~D</math> |
<math>~\equiv</math> |
<math> \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \, . </math> |
Once the pressure exerted by the external medium (<math>~P_e</math>), and the configuration's mass (<math>~M_\mathrm{tot}</math>), angular momentum (<math>~J</math>), and specific entropy (via <math>~K</math>) — or, in the isothermal case, sound speed (<math>~c_s</math>) — have been specified, the values of all of the coefficients are known and the above algebraic expression for <math>~\mathfrak{G}^*</math> describes how the free energy of the configuration will vary with the configuration's size (<math>~\chi</math>) for a given choice of <math>~\gamma_g</math>.
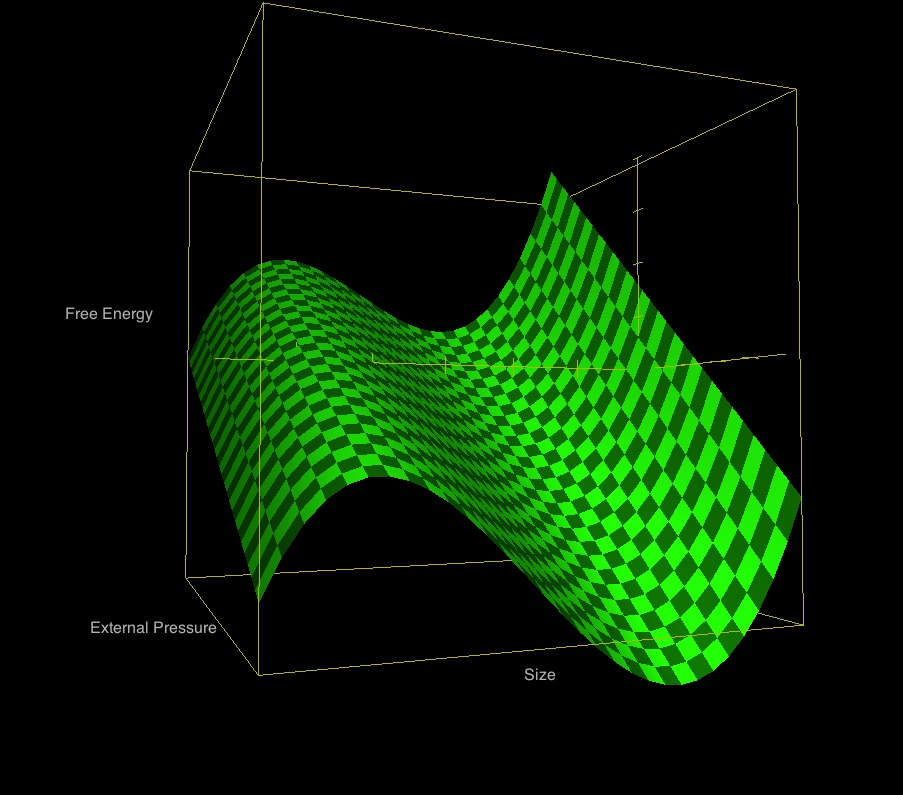
Visual Representation
|
Figure 1: Free Energy Surface |
|
|
This segment of the free energy "surface" shows how the free energy varies as the size of the configuration and the applied external pressure are varied, while all other relevant physical attributes are held fixed. The plotted function — derived from the above expression for <math>\mathfrak{G}^*</math>, with <math>~\gamma_\mathrm{g} = 1</math> and <math>~C=0</math> (see further discussion, below) — is, specifically, <math> \mathfrak{G}^* = 3000\biggl[ - \frac{1}{\chi} - \ln\chi + \frac{\Pi}{3}\chi^3 + 0.9558 \biggr] \, . </math> As shown, the size of the configuration <math>~(\chi)</math> increases to the right from <math>~1.2</math> to <math>~1.51</math>; the dimensionless external pressure <math>~(\Pi)</math> increases into the screen from <math>~0.103</math> to <math>~0.104</math>; and the dimensionless free energy, <math>~\mathfrak{G}^*</math>, increases upward. |
|
Energy Extrema
As is illustrated in Figure 1, the free energy surface generally will exhibit multiple local minima and local maxima, and may also possess one or more points of inflection. The locations along the energy surface where these special points arise identify equilibrium states, and the associated values of <math>~(R/R_0)_\mathrm{eq}</math> give the radii of the equilibrium configurations.
For a given choice of the set of physical parameters <math>~M</math>, <math>~K</math>, <math>~J</math>, <math>~P_e</math>, and <math>~\gamma_g</math>, extrema occur wherever,
<math> \frac{d\mathfrak{G^*}}{d\chi} = 0 \, . </math>
For the free energy function identified above,
<math> \frac{d\mathfrak{G^*}}{d\chi} = 3A\chi^{-2} -~ (1-\delta_{1\gamma_g})~3 B\chi^{2 -3\gamma_g} -~ \delta_{1\gamma_g} 3\chi^{-1} ~ -2C \chi^{-3} +~ 3D\chi^2 \, , </math>
so <math>\chi_\mathrm{eq} \equiv R_\mathrm{eq}/R_\mathrm{norm}</math> is obtained from the real root(s) of the equation,
<math> 2C \chi_\mathrm{eq}^{-2} + ~ (1-\delta_{1\gamma_g})~3 B\chi_\mathrm{eq}^{3 -3\gamma_g} +~ \delta_{1\gamma_g} 3 ~ -~3A\chi_\mathrm{eq}^{-1} -~ 3D\chi_\mathrm{eq}^3 = 0 \, . </math>
|
ASIDE: When we discuss the equilibrium of isothermal, rotating configurations that are immersed in an external medium, we will draw on the work of Weber (1976) — Oscillation and Collapse of Interstellar Clouds — and the work of Tohline (1985) — Star Formation: Phase Transition, not Jeans Instability — which, in turn draws upon Tohline (1981). In preparation for that discussion, we will go ahead and show how Tohline's (1985) statement of virial equilibrium — his equation (9) — is the same as the equation that defines free energy extrema that has been derived here; and we will show how Weber's (1976) "energy integral" — his equation (B3) — relates to our dimensionless free-energy function.
First, in order to match sign conventions, we need to multiply our "free energy extrema" equation through by minus one; second, we should set <math>~\delta_{1\gamma_g} = 1</math> because Tohline (1985) was only concerned with isothermal systems; then, because Tohline (1985) normalizes each energy term by <math>~E^* \equiv \biggl( \frac{2^2 \cdot 3^2}{5^3} \biggr) \frac{G^2 M_\mathrm{tot}^5}{J^2} \, ,</math> instead of by our <math>~E_\mathrm{norm}</math>, we need to multiply our equation through by the ratio, <math>~\frac{E_\mathrm{norm}}{E^*} = \biggl( \frac{5^3}{2^4 \cdot 3\pi} \biggr) \frac{J^2 c_\mathrm{norm}^2}{G^2 M_\mathrm{tot}^4} \, .</math> With these three modifications, our "free energy extrema" relation becomes,
Next, because Tohline (1985) considered only uniform-density configurations, all of the dimensionless filling factors can be set to unity in the definitions of the leading coefficients of all of our energy terms; but, following Tohline (1981), the leading coefficients of two of our energy terms should be modified to include a factor involving the configuration's eccentricity, <math>e \equiv \biggl( 1 - \frac{Z_\mathrm{eq}^2}{R_\mathrm{eq}^2} \biggr)^{1/2} \, ,</math> in order to account for rotational flattening. Properly adjusted, the four coefficients are,
Inserting these coefficient definitions, our "free energy extrema" relation becomes,
Next we need to appreciate that Tohline (1985) adopted the dimensionless parameter, <math>~\beta \equiv T_\mathrm{rot}/|W_\mathrm{grav}|</math>, instead of the normalized radius, <math>~\chi</math>, as the order parameter that is varied when searching for extrema in the free-energy function. So, in our equation that defines "free energy extrema" we need to replace <math>~\chi_\mathrm{eq}</math> with <math>~\beta_\mathrm{eq}</math>, using the relation,
Hence, our expression for the "free energy extrema" becomes,
Now,
which is the definition of the coefficient "<math>~k</math>" that is provided as equation (7) of Tohline (1985). Hence, dropping the factor of two out front, our expression for "free energy extrema" becomes,
Finally, realizing that the square of the sound speed is related to our <math>~c_\mathrm{norm}^2</math> via the relation [note that Tohline (1985) uses <math>~a^2</math> in place of <math>~c_s^2</math>], <math>~c_s^2 = \biggl( \frac{3}{4\pi} \biggr) c_\mathrm{norm}^2 \, ,</math> it is clear that this last form of our "free energy extrema" expression is identical to Tohline's (1985) virial equilibrium equation (9), which appears in print in a simpler but also more cryptic form as,
Plugging the same set of modified leading coefficients into our derived expression for the free energy becomes, <math> \mathfrak{G}^* = ~ \frac{3\cdot 5}{2^4 \pi} \biggl[ \frac{J^2 c_\mathrm{norm}^2}{G^2 M_\mathrm{tot}^4} \biggr] \chi^{-2} -~ 3 \ln \chi +~ \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} (1-e^2)^{1/2} \chi^3
- \frac{3}{5} \biggl( \frac{\sin^{-1}e}{e} \biggr) \chi^{-1}\, . </math> Now, recognize that,
where, for axisymmetric configurations (set <math>~\beta=\alpha</math> in Weber's (1976) equation 12), <math>J_\mathrm{Weber} \equiv \alpha^2 \Omega = \biggl( \frac{R}{R_0} \biggr)^2 (\dot\varphi_c t_0)^2 \, .</math> Hence, our expression for the free energy may be written as,
The right-hand-side of this expression exactly matches Weber's (1976) "energy integral" for oblate-spheroidal configurations — see his equation (B3) for the case, <math>~e > 0</math> — except that Weber's energy integral includes an additional pair of terms (<math>~{\dot\alpha}^2 + {\dot\gamma}^2/2</math>) to account for kinetic energy associated with the overall collapse or expansion of the configuration. [NOTE: The logarithmic term ultimately needs to be <math>~\ln \alpha^2\gamma</math> instead of <math>~\ln\chi^3</math> in order to reflect an oblate-spheroidal, rather than spherical, volume. This term also needs to be fixed in the above discussion of Tohline's work.]
|
Examples
- Polytropic Spheres
- Isothermal Spheres
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
BiPolytrope
[Following a discussion that Tohline had with Kundan Kadam on 3 July 2013, we have decided to carry out a virial equilibrium and stability analysis of nonrotating bipolytropes.]
We will adopt the following approach:
- Properties of the core <math>\cdots</math>
- Uniform density, <math>\rho_c</math>;
- Polytropic constant, <math>K_c</math>, and polytropic index, <math>n_c</math>;
- Surface of the core at <math>r_i</math>;
- Properties of the envelope <math>\cdots</math>
- Uniform density, <math>\rho_e</math>;
- Polytropic constant, <math>K_e</math>, and polytropic index, <math>n_e</math>;
- Base of the core at <math>r_i</math> and surface at <math>R</math>.
Use the dimensionless radius,
<math>\xi \equiv \frac{r}{r_i}</math>.
Then, <math>\xi_i = 1</math> and <math>\xi_s \equiv R/r_i</math>.
Expressions for Mass
Inside the core, the expression for the mass interior to any radius, <math>0 \le \xi \le 1</math>, is,
<math>M_\xi = \frac{4\pi}{3} \rho_c r_i^3 \xi^3</math> .
The expression for the mass interior to any position within the envelope, <math>1 \le \xi \le \xi_s</math>, is,
<math>M_\xi = \frac{4\pi}{3} r_i^3 \biggl[\rho_c + \rho_e(\xi^3 - 1) \biggr]</math> .
Hence, in terms of a reference mass, <math>~M_0 \equiv 4\pi \rho_0 R_0^3/3</math>, the mass of the core, the mass of the envelope, and the total mass are, respectively,
|
<math>~M_\mathrm{core}</math> |
<math>~=</math> |
<math> \frac{4\pi}{3} \rho_c r_i^3 = M_0 \biggl[ \frac{\rho_c}{\rho_0} \biggl( \frac{r_i}{R_0}\biggr)^3 \biggr] ~~~~~\Rightarrow~~~~~ \frac{\rho_c}{\rho_0} = \frac{M_\mathrm{core}}{M_0} \biggl( \frac{r_i}{R_0}\biggr)^{-3} \, ; </math> |
|
<math>~M_\mathrm{env}</math> |
<math>~=</math> |
<math> \frac{4\pi}{3} r_i^3 \biggl[\rho_e (\xi_s^3 - 1) \biggr] = M_0 (\xi_s^3 - 1) \biggl[ \frac{\rho_e}{\rho_0} \biggl( \frac{r_i}{R_0}\biggr)^3 \biggr] ~~~~~\Rightarrow~~~~~ \frac{\rho_e}{\rho_0} = \frac{M_\mathrm{env}}{M_0} \biggl( \frac{r_i}{R_0}\biggr)^{-3} (\xi_s^3 - 1)^{-1}\, ; </math> |
|
<math>~M_\mathrm{tot}</math> |
<math>~=</math> |
<math> \frac{4\pi}{3} r_i^3 \biggl[\rho_c + \rho_e(\xi_s^3 - 1) \biggr] = M_0 \biggl( \frac{\rho_c}{\rho_0} \biggr) \biggl( \frac{r_i}{R_0}\biggr)^3 \biggl[ 1 + \frac{\rho_e}{\rho_c} (\xi_s^3 - 1) \biggr] \, . </math> |
Following the work of Schönberg & Chandrasekhar (1942) — see our accompanying discussion — we will discuss bipolytropic equilibrium configurations in the context of a <math>~\nu - q</math> plane where,
|
<math>~\nu</math> |
<math>~\equiv</math> |
<math>~\frac{M_\mathrm{core}}{M_\mathrm{tot}} \, ,</math> |
|
<math>~q</math> |
<math>~\equiv</math> |
<math>~\frac{r_i}{R} = \frac{1}{\xi_s} \, .</math> |
With this in mind we can write,
<math>\frac{\rho_e}{\rho_c} = \frac{M_\mathrm{env}}{M_\mathrm{core}} (\xi_s^3 - 1)^{-1} = \frac{q^3 (1-\nu)}{\nu (1-q^3)} </math> ,
and,
<math>\nu \biggl(\frac{1-q^3}{q^3}\biggr) \biggl( \frac{\rho_e}{\rho_c} \biggr) = (1-\nu) ~~~~~\Rightarrow~~~~~ \nu = \biggl[ 1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1-q^3}{q^3}\biggr) \biggr]^{-1} \, .</math>
Energy Expressions
The gravitational potential energy of the bipolytropic configuration is obtained by integrating over the following differential energy contribution,
<math>dW_\mathrm{grav} = - \biggl( \frac{GM_r}{r} \biggr) dm</math> .
Hence,
|
<math>~W_\mathrm{grav} = W_\mathrm{core} + W_\mathrm{env}</math> |
<math> = - G \biggl\{ \int_0^{r_i} \biggl( \frac{M_r}{r} \biggr) 4\pi r^2 \rho_c dr + \int^R_{r_i} \biggl( \frac{M_r}{r} \biggr) 4\pi r^2 \rho_e dr \biggr\} </math> |
|
|
<math> = - G \biggl\{ \int_0^1 \biggl( \frac{4\pi }{3} \rho_c r_i^3 \xi^3 \biggr) 4\pi r_i^2 \rho_c \xi d\xi + \int_1^{\xi_s} \frac{4\pi}{3} \rho_c r_i^3 \biggl[ 1 + \frac{\rho_e}{\rho_c}(\xi^3 - 1) \biggr] 4\pi r_i^2 \rho_e \xi d\xi \biggr\} </math> |
|
|
<math> = - \frac{3GM^2_\mathrm{core}}{r_i} \biggl\{ \int_0^1 \xi^4 d\xi + \int_1^{\xi_s} \biggl[ 1 + \frac{\rho_e}{\rho_c}(\xi^3 - 1) \biggr] \biggl( \frac{\rho_e}{\rho_c} \biggr) \xi d\xi \biggr\} </math> |
|
|
<math> = - \frac{3GM^2_\mathrm{core}}{r_i} \biggl\{ \frac{1}{5} + \biggl( \frac{\rho_e}{\rho_c} \biggr) \int_1^{\xi_s} \xi d\xi + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \int_1^{\xi_s} (\xi^3 - 1) \xi d\xi \biggr\} </math> |
|
|
<math> = - \frac{3GM^2_\mathrm{tot}}{R} \biggl( \frac{M_\mathrm{core}}{M_\mathrm{tot}} \biggr)^2 \xi_s \biggl\{ \frac{1}{5} + \frac{1}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (\xi_s^2 - 1) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \frac{1}{5}(\xi_s^5 - 1) - \frac{1}{2}(\xi_s^2-1) \biggr] \biggr\} </math> |
I like the form of this expression. The leading term, which scales as <math>~R^{-1}</math>, encapsulates the behavior of the gravitational potential energy for a given choice of the internal structure, namely, a given choice of <math>~\xi_s</math>, <math>~\nu</math>, and density ratio <math>~(\rho_e/\rho_c)</math>. Actually, only two internal structural parameters need to be specified — <math>~\xi_s</math> and <math>~f_c</math>; from these two, the expressions shown above allow the determination of both <math>~(\rho_e/\rho_c)</math> and <math>~\nu</math>. Keeping in mind our desire to discuss the properties of bipolytropes in the context of the <math>~\nu - q</math> plane introduced by Schönberg & Chandrasekhar (1942), we will rewrite this expression for the gravitational potential energy as,
|
<math>~W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~- \frac{3}{5} \biggl( \frac{GM_\mathrm{tot}^2}{R} \biggr) \frac{\nu^2}{q} \cdot f\biggl(q, \frac{\rho_e}{\rho_c} \biggr) \, ,</math> |
where,
|
<math>~f\biggl(q, \frac{\rho_e}{\rho_c} \biggr)</math> |
<math>~\equiv</math> |
<math> 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2} - 1 \biggr) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \biggl( \frac{1}{q^5} - 1 \biggr) - \frac{5}{2}\biggl(\frac{1}{q^2} - 1 \biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math> 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (q^3- q^5 ) + \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl( \frac{2}{5} -q^3 + \frac{3}{5}q^5\biggr) \biggr] \, . </math> |
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |