Virial Equilibrium of Isothermal Spheres

Review

In an introductory discussion of the virial equilibrium structure of spherically symmetric configurations — see especially the section titled, Energy Extrema — we deduced that a system's equilibrium radius, <math>~R_\mathrm{eq}</math>, measured relative to a reference length scale, <math>~R_0</math>, i.e., the dimensionless equilibrium radius,

<math>~\chi_\mathrm{eq} \equiv \frac{R_\mathrm{eq}}{R_0} \, ,</math>

is given by the root(s) of the following equation:

<math> 2C \chi^{-2} + ~ (1-\delta_{1\gamma_g})~3 B\chi^{3 -3\gamma_g} +~ \delta_{1\gamma_g} 3B_I ~-~3A\chi^{-1} -~ 3D\chi^3 = 0 \, , </math>

where the definitions of the various coefficients are,

<math>~A</math>	<math>~\equiv</math>	<math>\frac{1}{5} \frac{GM_\mathrm{tot} ^2}{R_0} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \, ,</math>
<math>~B</math>	<math>~\equiv</math>	<math> K M_\mathrm{tot} \biggl( \frac{3M_\mathrm{tot} }{4\pi R_0^3} \biggr)^{\gamma_g - 1} \cdot \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} = \bar{c_s}^2 M_\mathrm{tot} \cdot \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} \, , </math>
<math>~B_I</math>	<math>~\equiv</math>	<math> c_s^2 M_\mathrm{tot} \, , </math>
<math>~C</math>	<math>~\equiv</math>	<math> \frac{5J^2}{4M_\mathrm{tot} R_0^2} \cdot \frac{\mathfrak{f}_M}{\mathfrak{f}_T} \, , </math>
<math>~D</math>	<math>~\equiv</math>	<math> \frac{4}{3} \pi R_0^3 P_e \, . </math>

Once the pressure exerted by the external medium (<math>~P_e</math>), and the configuration's mass (<math>~M_\mathrm{tot}</math>), angular momentum (<math>~J</math>), and specific entropy (via <math>~K</math>) — or, in the isothermal case, sound speed (<math>~c_s</math>) — have been specified, the values of all of the coefficients are known and <math>~\chi_\mathrm{eq}</math> can be determined.

Isolated, Nonrotating Configuration

For a nonrotating configuration <math>~(C=J=0)</math> that is not influenced by the effects of a bounding external medium <math>~(D=P_e = 0)</math>, the statement of virial equilibrium is,

<math>~ (1-\delta_{1\gamma_g})~3(\gamma_g-1) B\chi^{3 -3\gamma_g} +~ \delta_{1\gamma_g} B_I ~-~A\chi^{-1} = 0 \, . </math>

Isothermal Evolutions

For isothermal configurations <math>~(\delta_{1\gamma_g} = 1)</math>, one and only one equilibrium state arises where,

that is,

<math>~ R_\mathrm{eq} = R_0 \chi_\mathrm{eq} = \frac{A}{B_I}\cdot R_0 = \frac{GM}{5c_s^2} \, . </math>

Nonrotating Configuration Embedded in an External Medium

For a nonrotating configuration <math>(C=J=0)</math> that is embedded in, and is influenced by the pressure <math>P_e</math> of, an external medium, the statement of virial equilibrium is,

<math> (1-\delta_{1\gamma_g})~3 B\chi^{3 -3\gamma_g} +~ \delta_{1\gamma_g} 3B_I ~-~3A\chi^{-1} -~ 3D\chi^3 = 0 \, . </math>

Bounded Isothermal

For isothermal configurations <math>(\delta_{1\gamma_g} = 1)</math>, we deduce that equilibrium states exist at radii given by the roots of the equation,

Bonnor's (1956) Equivalent Relation

Inserting the expressions for the coefficients <math>~B_I</math>, <math>~A</math>, and <math>~D</math> gives,

<math>~ 3Mc_s^2 ~- \frac{3}{5} \frac{GM^2}{R} = 3 P_e \biggl( \frac{4\pi}{3} R^3\biggr) \, , </math>

or, because the volume <math>~V = (4\pi R^3/3)</math> for a spherical configuration, we can write,

<math> ~3P_e V = 3Mc_s^2 ~- \frac{3}{5} \biggl( \frac{4\pi}{3} \biggr)^{1/3} \frac{GM^2}{V^{1/3}} \, . </math>

It is instructive to compare this expression for a self-gravitating, isothermal equilibrium sphere to the one that was presented in 1956 by Bonnor (1956, MNRAS, 116, 351) as equation (1.2) in a paper titled, "Boyle's Law and Gravitational Instability":

Once we realize that, for an isothermal configuration, twice the thermal energy content, <math>~2S</math>, can be written as <math>~(3NkT)</math> just as well as via the product, <math>~(3Mc_s^2)</math>, we see that our expression is identical to Bonnor's if we set the prefactor on Bonnor's last term, <math>~\alpha = (4\pi/3)^{1/3}/5</math>. (Indeed, later on the first page of his paper, Bonnor points out that this is the appropriate value for <math>~\alpha</math> when considering a uniform density sphere.)

P-V Diagram

Returning to the dimensionless form of this expression and multiplying through by <math>~[-\chi/(3D)]</math>, we obtain,

Now, taking a cue from the solution presented above for an isolated isothermal configuration, we choose to set the previously unspecified scale factor, <math>~R_0</math>, to,

in which case <math>~B_I = A</math>, and the quartic equation governing the radii of equilibrium states becomes, simply,

where,

<math> \Pi \equiv \frac{D}{B_I} = \frac{4\pi R_0^3 P_e}{3Mc_s^2} = \frac{4\pi P_e G^3 M^2}{3\cdot 5^3 c_s^8} \, . </math>

For a given choice of <math>~P_e</math> and <math>~c_s</math>, <math>~\Pi^{1/2}</math> can represent a dimensionless mass, in which case,

<math> M = \Pi^{1/2} \biggl( \frac{3\cdot 5^3}{2^2\pi}\biggr)^{1/2} \biggl( \frac{c_s^8}{P_e G^3} \biggr)^{1/2} \, . </math>

Alternatively, for a given choice of configuration mass and sound speed, this parameter, <math>~\Pi</math>, can be viewed as a dimensionless external pressure; or, for a given choice of <math>~M</math> and <math>~P_e</math>, <math>~\Pi^{-1/8}</math> can represent a dimensionless sound speed. In most of what follows we will view <math>~\Pi</math> as a dimensionless external pressure.

The above quartic equation can be rearranged immediately to give the external pressure that is required to obtain a particular configuration radius, namely,

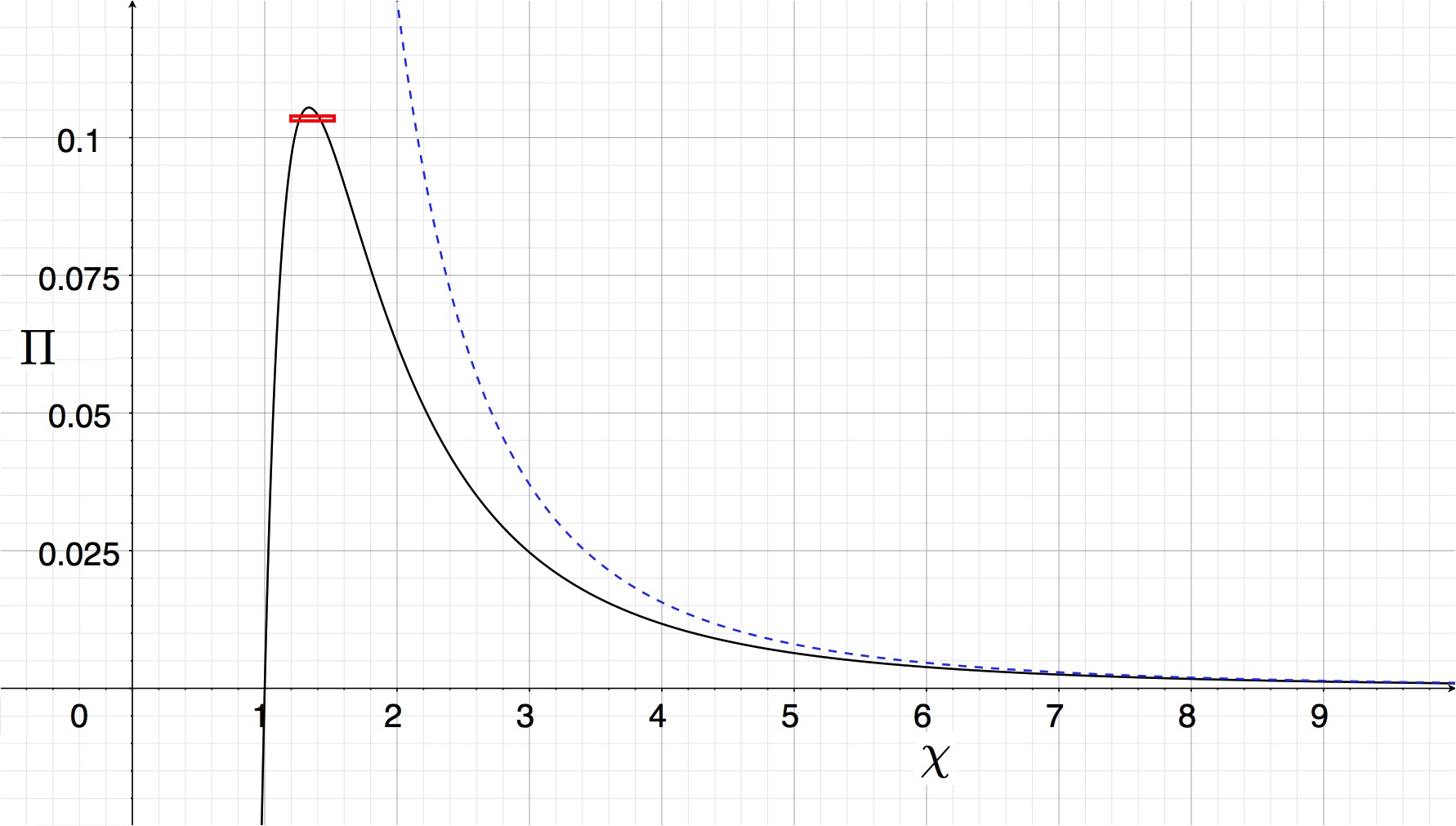
The resulting behavior is shown by the black curve in Figure 2.

Figure 2: Equilibrium Isothermal P-V Diagram

The black curve traces out the function,

and shows the dimensionless external pressure, <math>~\Pi</math>, that is required to construct a nonrotating, self-gravitating, isothermal sphere with an equilibrium radius <math>~\chi</math>. The pressure becomes negative at radii <math>~\chi < 1</math>, hence the solution in this regime is unphysical.

Figure 1 displays the free energy surface that "lies above" the two-dimensional parameter space <math>~(1.2 < \chi < 1.51</math>; <math>~0.103 < \Pi < 0.104)</math> that is identified here by the thin, red rectangle.

In the absence of self-gravity (i.e., <math>~A=0</math>), the product of the external pressure and the volume should be constant. The corresponding relation, <math>~\Pi = \chi^{-3}</math>, is shown by the blue dashed curve in the figure. As the figure illustrates, when gravity is included the P-V relationship pulls away from the PV = constant curve at sufficiently small volumes. Indeed, the curve turns over at a finite pressure, <math>~\Pi_\mathrm{max}</math>, and for every value of <math>~\Pi < \Pi_\mathrm{max}</math> a second, more compact equilibrium configuration appears. The location of <math>~\Pi_\mathrm{max}</math> along the curve is identified by setting <math>~\partial\Pi/\partial\chi = 0</math>, that is, it occurs where,

<math> \frac{\partial\Pi}{\partial\chi} = -4 \chi^{-5}(\chi - 1) + \chi^{-4} = 0 \, , </math>

<math> \Rightarrow ~~~~~ \chi = \frac{2^2}{3} \approx 1.333333 \, . </math>

Hence,

<math>~\Pi_\mathrm{max} = \biggl( \frac{2^2}{3} \biggr)^{-4} \biggl( \frac{2^2}{3}-1 \biggr) = \frac{3^3}{2^8} \approx 0.105469\, ;</math>

therefore, from above,

<math>~ M_\mathrm{max} = \biggl( \frac{3^4\cdot 5^3}{2^{10}\pi}\biggr)^{1/2} \biggl( \frac{c_s^8}{P_e G^3} \biggr)^{1/2} \approx 1.77408 \biggl( \frac{c_s^8}{P_e G^3} \biggr)^{1/2} \, . </math>

Quartic Solution

In the above <math>~P-V</math> diagram discussion, we rearranged the quartic equation governing equilibrium configurations to give <math>~\Pi</math> for any chosen value of <math>~\chi</math>. Alternatively, the four roots of the quartic equation — <math>~\chi_1</math>, <math>~\chi_2</math>, <math>~\chi_3</math> and <math>~\chi_4</math> in the presentation that follows — will identify the radii at which a spherical configuration will be in equilibrium for any choice of the external pressure, <math>~\Pi</math>, assuming the roots are real.

Roots of the quartic equation: <math>\chi^4 - \chi \Pi^{-1}+ \Pi^{-1} = 0 </math>

<math>~\chi_1</math>	<math>~=</math>	<math>~ +\frac{1}{2} y_r^{1/2} + \frac{1}{2} D_q \, ; </math>
<math>~\chi_2</math>	<math>~=</math>	<math>~ +\frac{1}{2} y_r^{1/2} - \frac{1}{2} D_q \, ; </math>
<math>~\chi_3</math>	<math>~=</math>	<math>~ -\frac{1}{2} y_r^{1/2} + \frac{1}{2} E_q \, ; </math>
<math>~\chi_4</math>	<math>~=</math>	<math>~ -\frac{1}{2} y_r^{1/2} - \frac{1}{2} E_q \, , </math>

where,

<math>~D_q</math>	<math>~\equiv</math>	<math>~ y_r^{1/2} \biggl[ \frac{2}{\Pi} y_r^{-3/2} - 1 \biggr]^{1/2} \, , </math>
<math>~E_q</math>	<math>~\equiv</math>	<math>~ y_r^{1/2} \biggl[ - \frac{2}{\Pi} y_r^{-3/2} - 1 \biggr]^{1/2} \, , </math>

and,

<math>~ y_r \equiv \biggl( \frac{1}{2\Pi^2} \biggr)^{1/3} \biggl\{ \biggl[ 1 + \sqrt{1-\frac{2^8}{3^3}\Pi} \biggr]^{1/3} + \biggl[ 1 - \sqrt{1-\frac{2^8}{3^3}\Pi} \biggr]^{1/3} \biggr\} \, , </math>

is the real root of the cubic equation,

Because <math>~\Pi</math> must be positive in physically realistic solutions, we conclude that the two roots involving <math>~E_q</math> — that is, <math>~\chi_3</math> and <math>~\chi_4</math> — are imaginary and, hence, unphysical. The other two roots — <math>~\chi_1</math> and <math>~\chi_2</math> — will be real only if the arguments inside the radicals in the expression for <math>~y_r</math> are positive. That is, <math>~\chi_1</math> and <math>~\chi_2</math> will be real only for values of the dimensionless external pressure,

<math>~\Pi \leq \Pi_\mathrm{max} \equiv \frac{3^3}{2^8} \, .</math>

This is the same upper limit on the external pressure that was derived above, via a different approach, and translates into a maximum mass for a pressure-bounded isothermal configuration of,

<math>~M_\mathrm{max} = \Pi_\mathrm{max}^{1/2} \biggl(\frac{3\cdot 5^3}{2^2\pi} \biggr)^{1/2} \biggl( \frac{c_s^8}{G^3 P_e} \biggr)^{1/2} = \biggl(\frac{3^4\cdot 5^3}{2^{10}\pi} \biggr)^{1/2} \biggl( \frac{c_s^8}{G^3 P_e} \biggr)^{1/2} \, .</math>

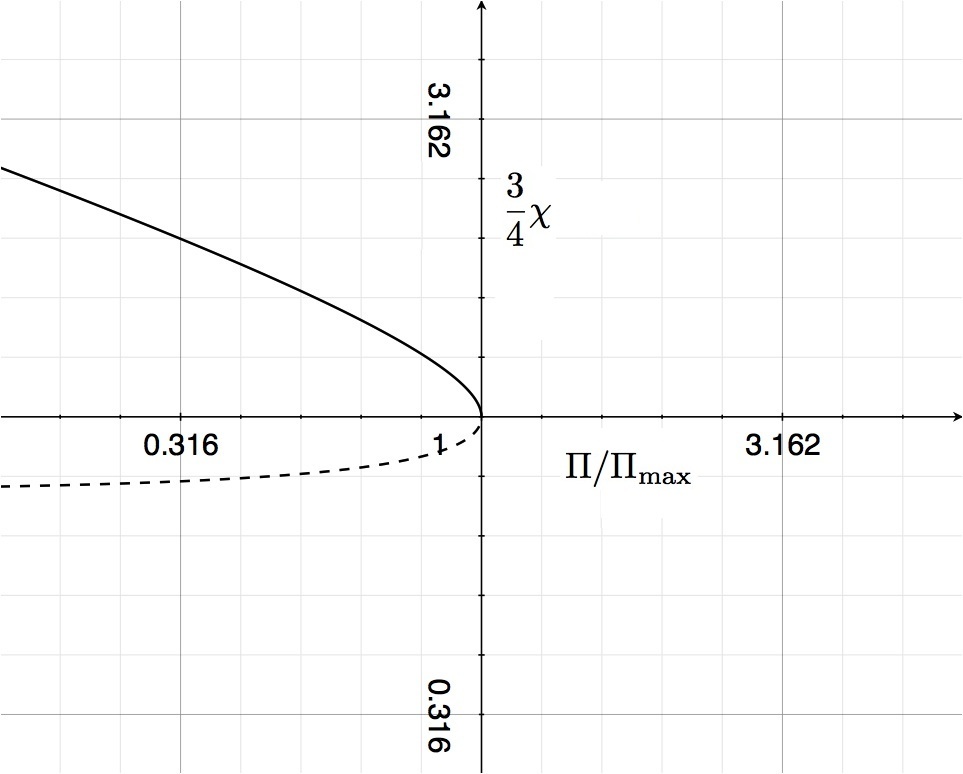
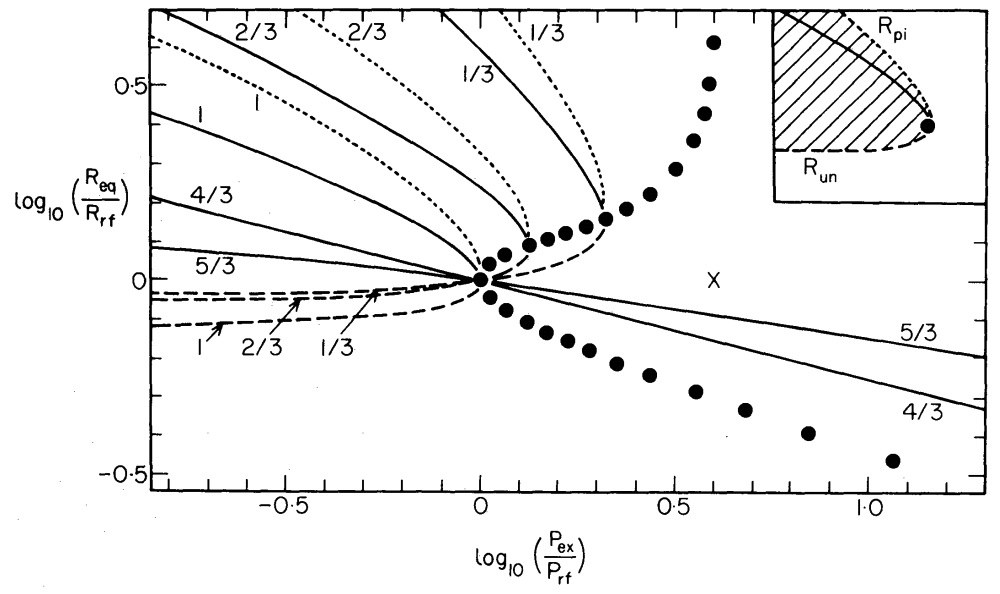
When combined, a plot of <math>~\chi_1</math> versus <math>~\Pi</math> and <math>~\chi_2</math> versus <math>~\Pi</math> will reproduce the solid black curve shown in Figure 2, but with the axes flipped. The top-right quadrant of Figure 3 presents such a plot, but in logarithmic units along both axes; also <math>~\Pi</math> is normalized to <math>~\Pi_\mathrm{max}</math> and <math>~\chi</math> is normalized to the equilibrium radius <math>~(4/3)</math> at that pressure. This is the manner in which Whitworth (1981, MNRAS, 195, 967) chose to present this result for uniform-density, spherical isothermal <math>~(\gamma_\mathrm{g}=1)</math> configurations. Our solid and dashed curve segments — identifying, respectively, the <math>~\chi_1(\Pi)</math> and <math>~\chi_2(\Pi)</math> solutions to the above quadratic equation — precisely match the solid and dashed curve segments labeled "1" in Whitworth's Figure 1a (replicated here in the bottom-right quadrant of Figure 3).

Figure 3: Equilibrium R-P Diagram

Top: The solid curve traces the function <math>~\chi_1(\Pi)</math> and the dashed curve traces the function <math>~\chi_2(\Pi)</math>, where <math>~\chi_1</math> and <math>~\chi_2</math> are the two real roots of the quartic equation,

Logarithmic units are used along both axes; <math>~\Pi</math> is normalized to <math>~\Pi_\mathrm{max}</math>; and <math>~\chi</math> is normalized to the equilibrium radius <math>~(4/3)</math> at <math>~\Pi_\mathrm{max}</math>.

Bottom: A reproduction of Figure 1a from Whitworth (1981, MNRAS, 195, 967). The solid and dashed segments of the curve labeled "1" identify the equilibrium radii, <math>~R_\mathrm{eq}</math>, that result from embedding a uniform-density, isothermal <math>~(\gamma_\mathrm{g} = 1)</math> gas cloud in an external medium of pressure <math>~P_\mathrm{ex}</math>.

Comparison: The curve shown above that traces out <math>~\chi_1(\Pi)</math> and <math>~\chi_2(\Pi)</math> should be identical to the "Whitworth" curve labeled "1".

User:Tohline/SSC/Virial/Isothermal

Contents