Difference between revisions of "User:Tohline/H BookTiledMenu"
| Line 443: | Line 443: | ||
* [https://ui.adsabs.harvard.edu/abs/1977ApJ...213..497H/abstract C. Hunter (1977)], ApJ, 213, 497: ''On Secular Stability, Secular Instability, and Points of Bifurcation of Rotating Gaseous Masses'' | * [https://ui.adsabs.harvard.edu/abs/1977ApJ...213..497H/abstract C. Hunter (1977)], ApJ, 213, 497: ''On Secular Stability, Secular Instability, and Points of Bifurcation of Rotating Gaseous Masses'' | ||
* [https://ui.adsabs.harvard.edu/abs/1985ApJ...294..474I/abstract J. N. Imamura, J. L. Friedman & R. H. Durisen (1985)], ApJ, 294, 474: ''Secular stability limits for rotating polytropic stars'' | * [https://ui.adsabs.harvard.edu/abs/1985ApJ...294..474I/abstract J. N. Imamura, J. L. Friedman & R. H. Durisen (1985)], ApJ, 294, 474: ''Secular stability limits for rotating polytropic stars'' | ||
<table border="0" align="center" width="100%" cellpadding="1"><tr> | |||
<td align="center" width="5%"> </td><td align="left"> | |||
<font color="green">The equilibrium models are calculated using the polytrope version (Bodenheimer & Ostriker 1973) of the Ostriker and Mark (1968) self-consistent field (SCF) code … the equilibrium models rotate on cylinders and are completely specified by <math>~n</math>, the total angular momentum, and the specific angular momentum distribution <math>~j(m_\varpi)</math>. Here <math>~m_\varpi</math> is the mass contained within a cylinder of radius <math>~\varpi</math> centered on the rotation axis. The angular momentum distribution is prescribed in several ways: (1) imposing strict uniform rotation; (2) using the same <math>~j(m_\varpi)</math> as that of a uniformly rotating spherical polybrope of index <math>~n^'</math> (see Bodenheimer and Ostriker 1973); and (3) using <math>~j(m_\varpi) \propto m_\varpi</math>, which we refer to as <math>~n^' = L</math>, <math>~L</math> for "linear."</font> | |||
</td></tr></table> | |||
* [https://ui.adsabs.harvard.edu/abs/1990ApJ...355..226I/abstract J. R. Ipser & L. Lindblom (1990)], ApJ, 355, 226: ''The Oscillations of Rapidly Rotating Newtonian Stellar Models'' | * [https://ui.adsabs.harvard.edu/abs/1990ApJ...355..226I/abstract J. R. Ipser & L. Lindblom (1990)], ApJ, 355, 226: ''The Oscillations of Rapidly Rotating Newtonian Stellar Models'' | ||
* [https://ui.adsabs.harvard.edu/abs/1991ApJ...373..213I/abstract J. R. Ipser & L. Lindblom (1991)], ApJ, 373, 213: ''The Oscillations of Rapidly Rotating Newtonian Stellar Models. II. Dissipative Effects'' | * [https://ui.adsabs.harvard.edu/abs/1991ApJ...373..213I/abstract J. R. Ipser & L. Lindblom (1991)], ApJ, 373, 213: ''The Oscillations of Rapidly Rotating Newtonian Stellar Models. II. Dissipative Effects'' | ||
Revision as of 03:18, 12 August 2019
Tiled Menu

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Context
| Global Energy Considerations |
|---|
| Principal Governing Equations (PGEs) |
Continuity | Euler | 1st Law of Thermodynamics |
Poisson |
|---|
| Equation of State (EOS) |
Ideal Gas | Total Pressure |
|---|
Spherically Symmetric Configurations
| (Initially) Spherically Symmetric Configurations |
|---|
|
Structural Form Factors |
Free-Energy of Spherical Systems |
|---|
| One-Dimensional PGEs |
|---|
Equilibrium Structures
| 1D STRUCTURE |
|---|

|
Scalar Virial Theorem |
|---|
| Hydrostatic Balance Equation |
Solution Strategies |
|---|
| Isothermal Sphere |
via Direct Numerical Integration |
|---|
| Isolated Polytropes |
Lane (1870) |
Known Analytic Solutions |
via Direct Numerical Integration |
via Self-Consistent Field (SCF) Technique |
|---|
| Zero-Temperature White Dwarf |
Chandrasekhar Limiting Mass (1935) |
|---|
| Virial Equilibrium of Pressure-Truncated Polytropes |
|---|
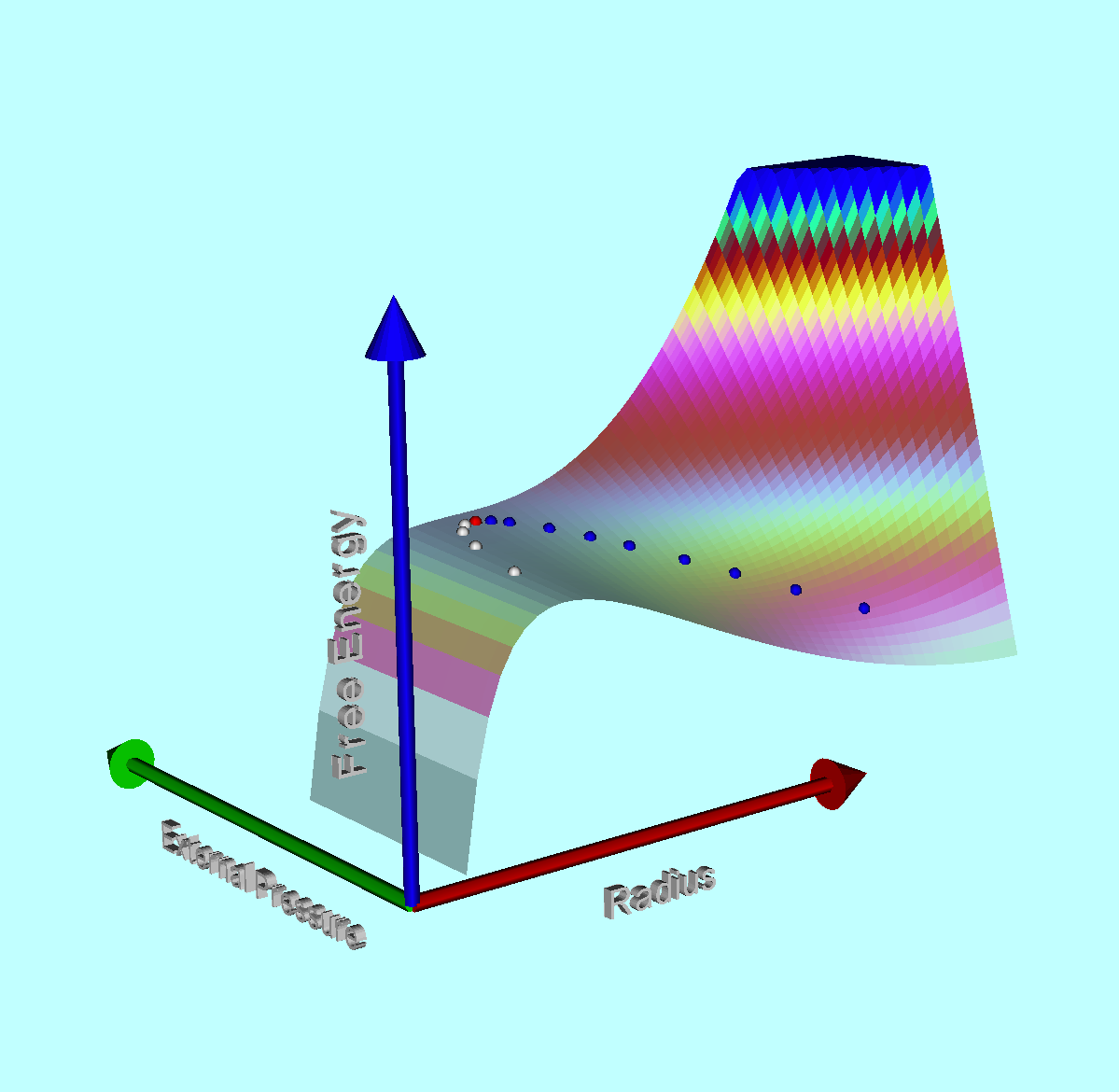
| Pressure-Truncated Configurations |
Bonnor-Ebert (Isothermal) Spheres (1955 - 56) |
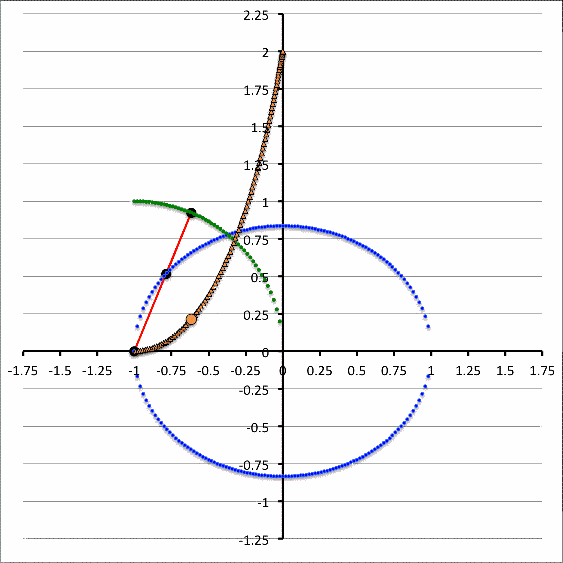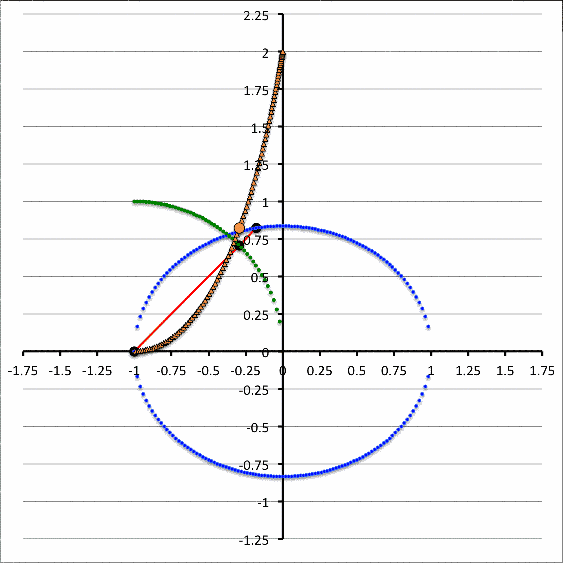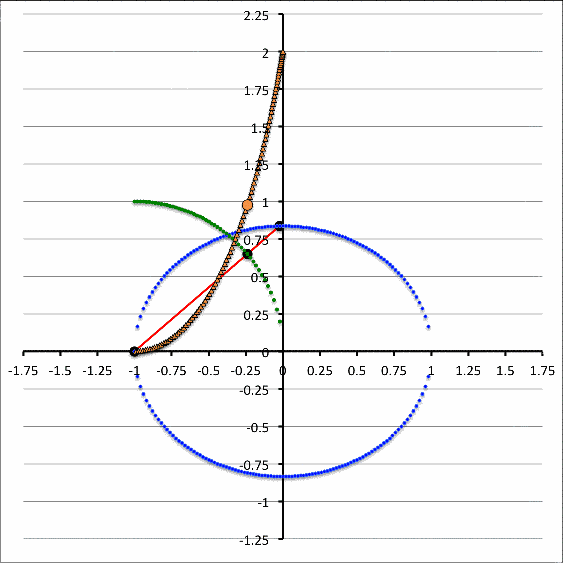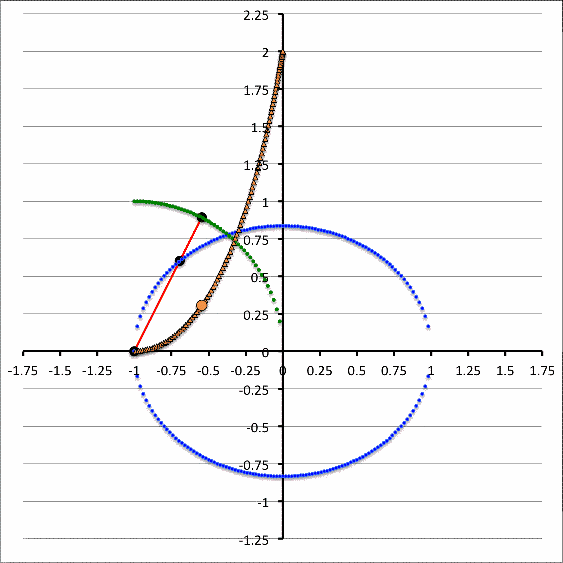
Polytropes | Equilibrium Sequence Turning-Points ♥ |
|
Turning-Points (Broader Context) |
|---|
| Free Energy of Bipolytropes (nc, ne) = (5, 1) |
|---|
| Composite Polytropes (Bipolytropes) |
Schönberg- Chandrasekhar Mass (1942) |
Analytic (nc, ne) = (5, 1) |
Analytic (nc, ne) = (1, 5) |
|---|
Stability Analysis
| 1D STABILITY |
|---|

|
Variational Principle |
|---|
| Radial Pulsation Equation |
Example Derivations & Statement of Eigenvalue Problem |
(poor attempt at) Reconciliation |
Relationship to Sound Waves |
|---|
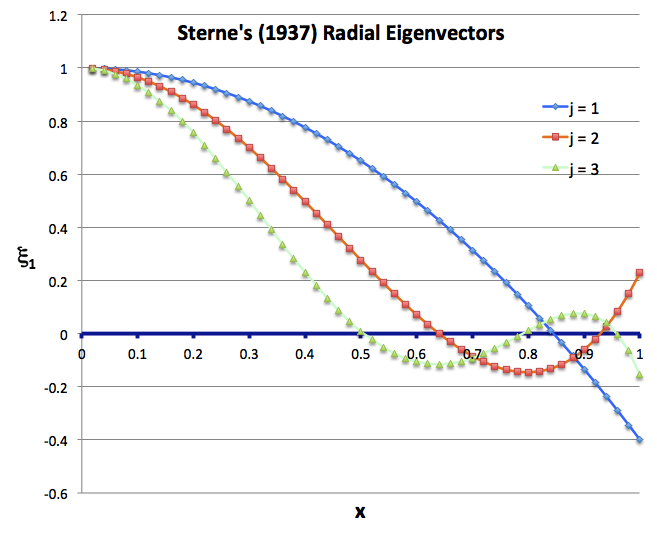
| Uniform-Density Configurations |
Sterne's Analytic Sol'n of Eigenvalue Problem (1937) |
|
|---|
| Pressure-Truncated Isothermal Spheres |
|
via Direct Numerical Integration |
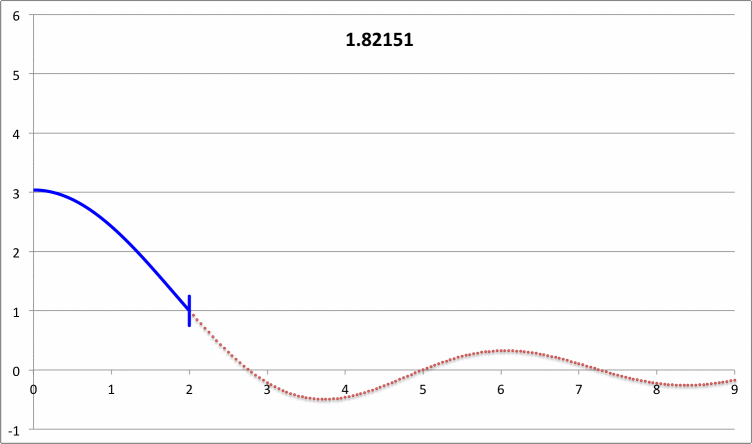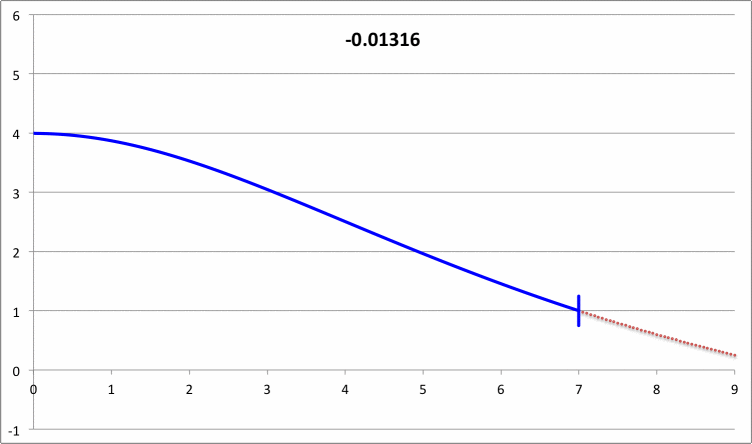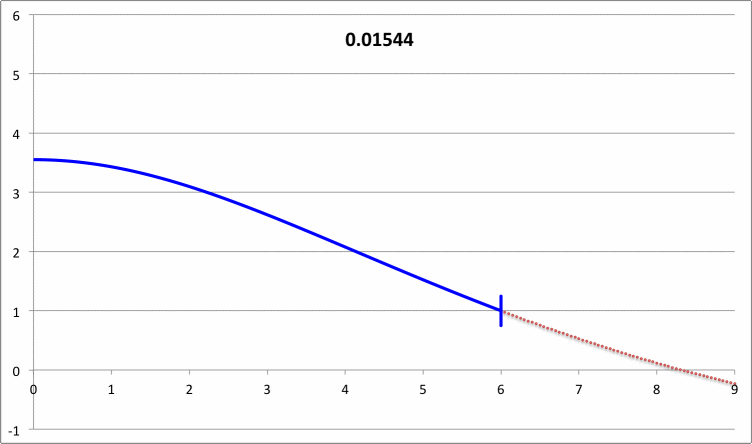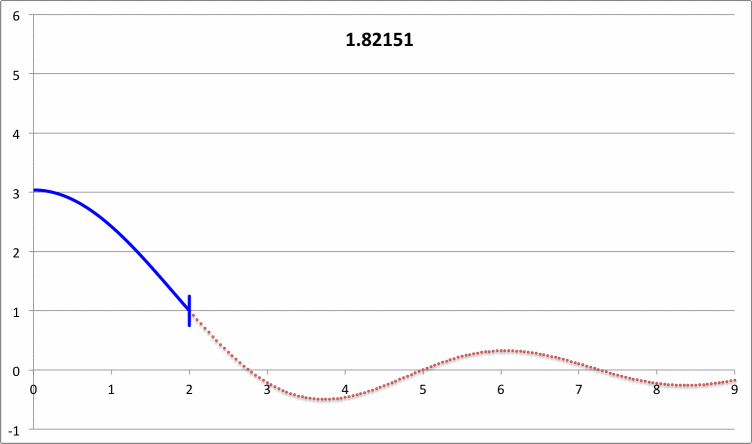
| |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Yabushita's Analytic Sol'n for Marginally Unstable Configurations (1974) |
|
|---|
| Polytropes |
|
Isolated n = 3 Polytrope |
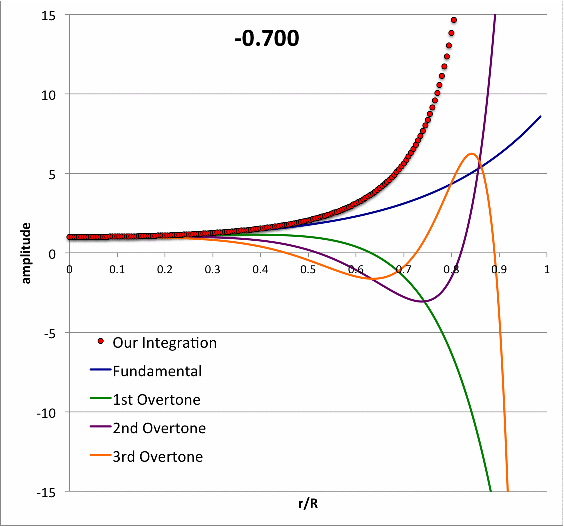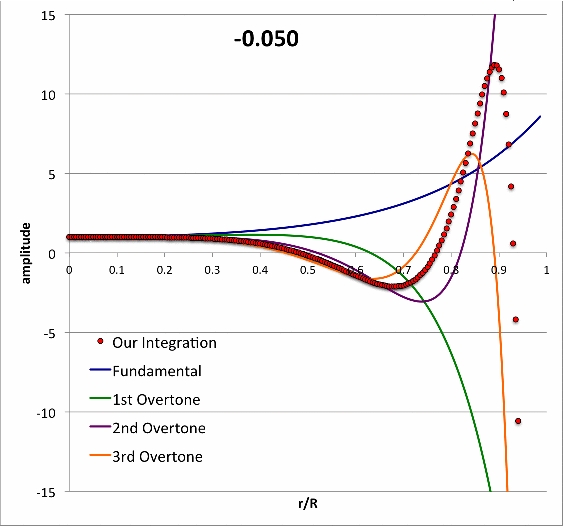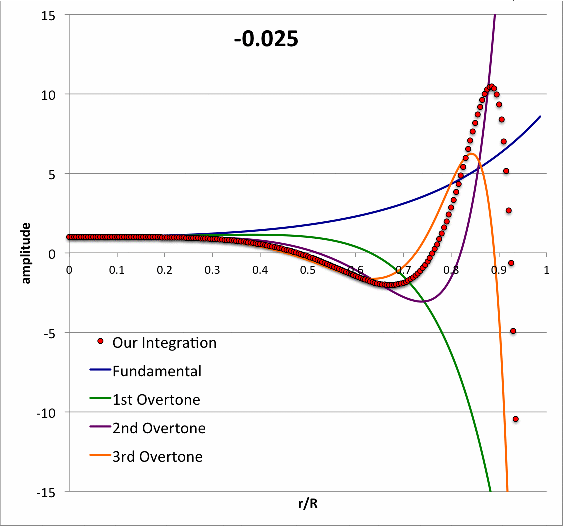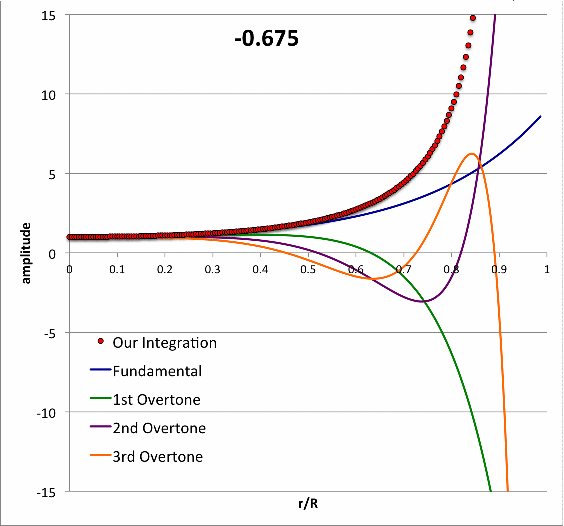
|
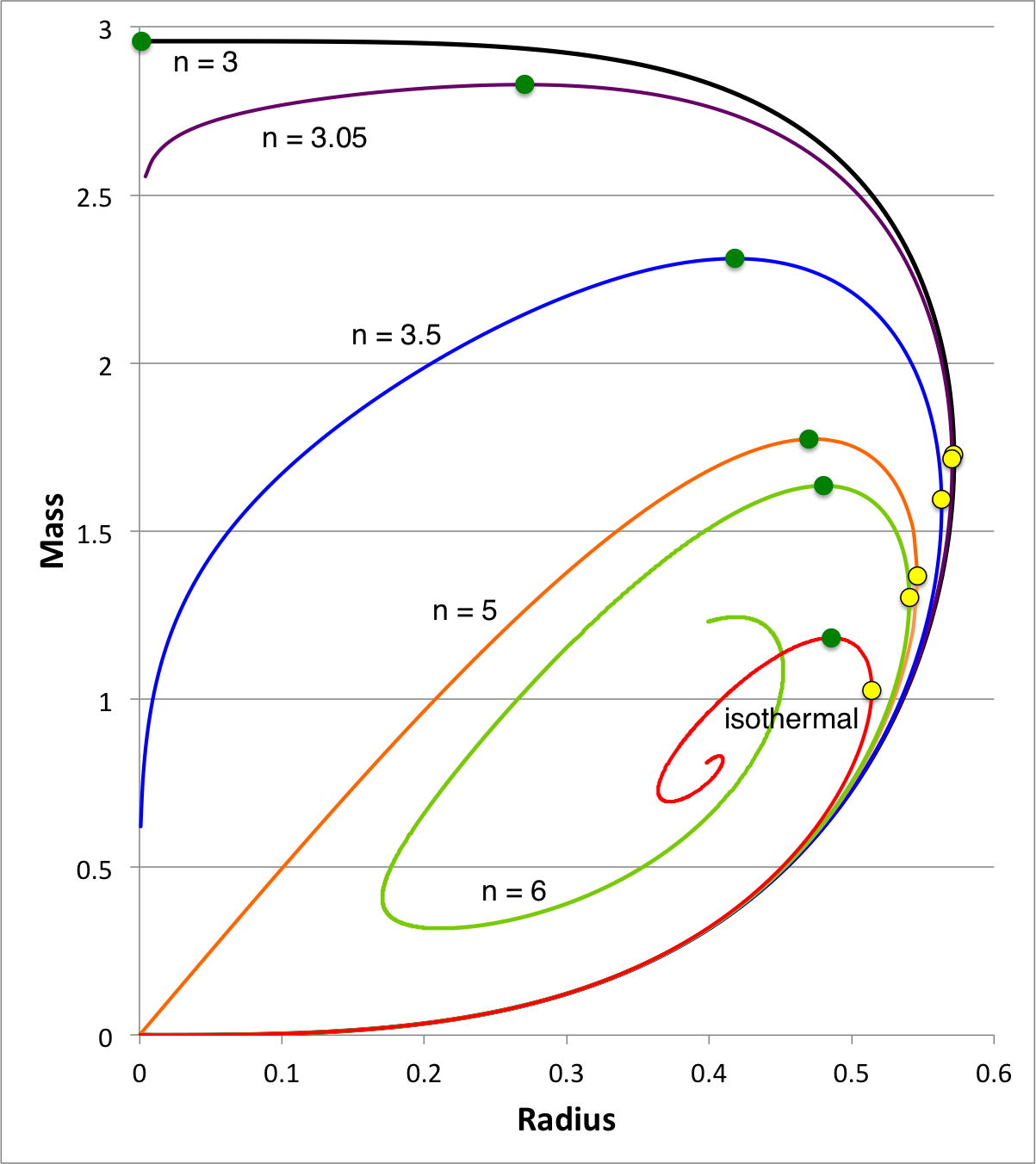
Pressure-Truncated n = 5 Configurations | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Exact Demonstration of B-KB74 Conjecture |
Exact Demonstration of Variational Principle |
Pressure-Truncated n = 5 Polytropes |
|---|
| Our Analytic Sol'n for Marginally Unstable Configurations (2017) ♥ |
|
|---|
| BiPolytropes | Murphy & Fiedler (1985b) (nc, ne) = (1,5) |
Our Broader Analysis |
|---|
Nonlinear Dynamical Evolution
| 1D DYNAMICS |
|---|
| Free-Fall Collapse |
|---|
| Collapse of Isothermal Spheres |
via Direct Numerical Integration |
Similarity Solution |
|---|
| Collapse of an Isolated n = 3 Polytrope |
|---|
Two-Dimensional Configurations (Axisymmetric)
| (Initially) Axisymmetric Configurations |
|---|
| Storyline |
|---|
| PGEs for Axisymmetric Systems |
|---|
Axisymmetric Equilibrium Structures
| 2D STRUCTURE |
|---|
| Constructing Steady-State Axisymmetric Configurations |
Axisymmetric Instabilities to Avoid |
Simple Rotation Profiles |
Hachisu Self-Consistent-Field [HSCF] Technique |
Solving the Poisson Equation |
|---|
| Using Toroidal Coordinates to Determine the Gravitational Potential |
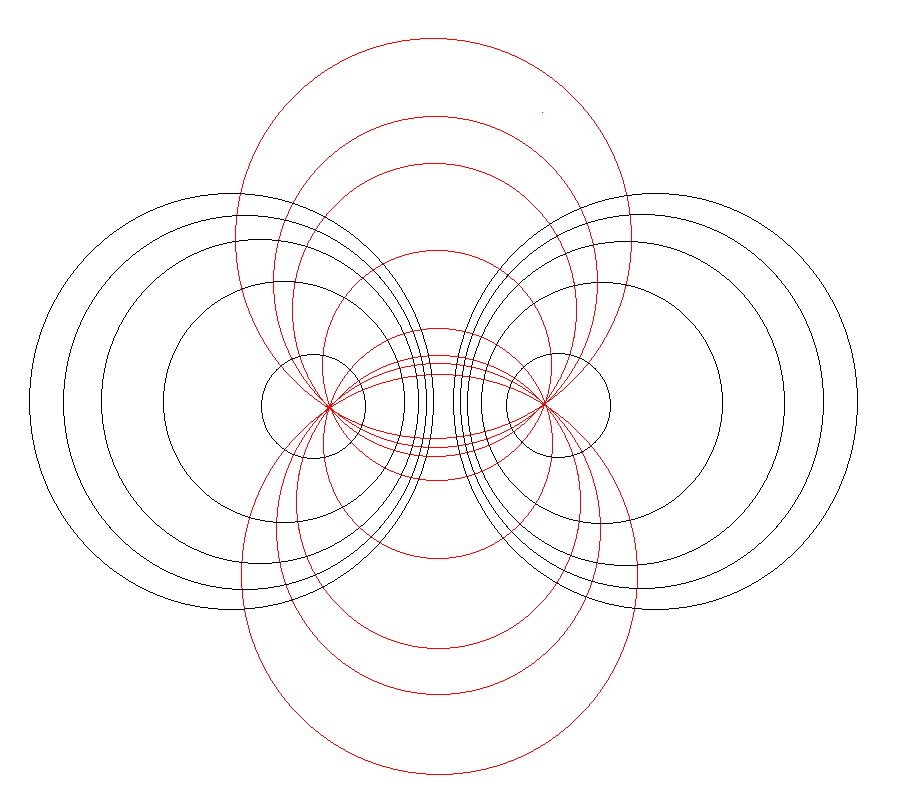
|
Attempt at Simplification ♥ |
Wong's Analytic Potential (1973) |
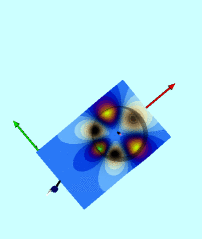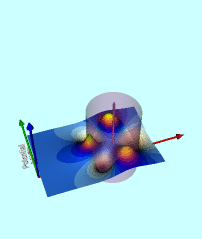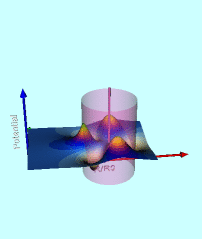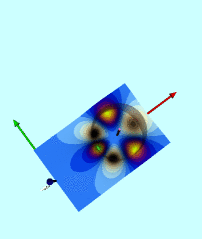
|
|---|
Spheroidal & Spheroidal-Like
| Uniform-Density (Maclaurin) Spheroids |
Maclaurin's Original Text & Analysis (1742) |
|---|
| Rotationally Flattened Isothermal Configurations |
Hayashi, Narita & Miyama's Analytic Sol'n (1982) |
Review of Stahler's (1983) Technique |
|---|
| Rotationally Flattened Polytropes |
Example Equilibria |
|---|
| Rotationally Flattened White Dwarfs |
Ostriker Bodenheimer & Lynden-Bell (1966) |
Example Equilibria |
|---|
Toroidal & Toroidal-Like
| Definition: anchor ring |
|---|
| Massless Polytropic Configurations |
Papaloizou-Pringle Tori (1984) |

|
|---|
| Self-Gravitating Incompressible Configurations |
Dyson (1893) |
Dyson-Wong Tori |
|---|
| Self-Gravitating Compressible Configurations |
Ostriker (1964) |
|---|
Stability Analysis
| 2D STABILITY |
|---|
Sheroidal & Spheroidal-Like
| Linear Analysis of Bar-Mode Instability |
Bifurcation from Maclaurin Sequence |
Traditional Analyses |
Time-Dependent Simulations |
|---|
- T. G. Cowling & R. A. Newing (1949), ApJ, 109, 149: The Oscillations of a Rotating Star
- M. J. Clement (1965), ApJ, 141, 210: The Radial and Non-Radial Oscillations of Slowly Rotating Gaseous Masses
- P. H. Roberts & K. Stewartson (1963), ApJ, 137, 777: On the Stability of a Maclaurin spheroid of small viscosity
- C. E. Rosenkilde (1967), ApJ, 148, 825: The tensor virial-theorem including viscous stress and the oscillations of a Maclaurin spheroid
- S. Chandrasekhar & N. R. Lebovitz (1968), ApJ, 152, 267: The Pulsations and the Dynamical Stability of Gaseous Masses in Uniform Rotation
- C. Hunter (1977), ApJ, 213, 497: On Secular Stability, Secular Instability, and Points of Bifurcation of Rotating Gaseous Masses
- J. N. Imamura, J. L. Friedman & R. H. Durisen (1985), ApJ, 294, 474: Secular stability limits for rotating polytropic stars
|
The equilibrium models are calculated using the polytrope version (Bodenheimer & Ostriker 1973) of the Ostriker and Mark (1968) self-consistent field (SCF) code … the equilibrium models rotate on cylinders and are completely specified by <math>~n</math>, the total angular momentum, and the specific angular momentum distribution <math>~j(m_\varpi)</math>. Here <math>~m_\varpi</math> is the mass contained within a cylinder of radius <math>~\varpi</math> centered on the rotation axis. The angular momentum distribution is prescribed in several ways: (1) imposing strict uniform rotation; (2) using the same <math>~j(m_\varpi)</math> as that of a uniformly rotating spherical polybrope of index <math>~n^'</math> (see Bodenheimer and Ostriker 1973); and (3) using <math>~j(m_\varpi) \propto m_\varpi</math>, which we refer to as <math>~n^' = L</math>, <math>~L</math> for "linear." |
- J. R. Ipser & L. Lindblom (1990), ApJ, 355, 226: The Oscillations of Rapidly Rotating Newtonian Stellar Models
- J. R. Ipser & L. Lindblom (1991), ApJ, 373, 213: The Oscillations of Rapidly Rotating Newtonian Stellar Models. II. Dissipative Effects
- J. N. Imamura, J. L. Friedman & R. H. Durisen (2000), ApJ, 528, 946: Nonaxisymmetric Dynamic Instabilities of Rotating Polytropes. II. Torques, Bars, and Mode Saturation with Applications to Protostars and Fizzlers
- G. P. Horedt (2019), ApJ, 877, 9: On the Instability of Polytropic Maclaurin and Roche ellipsoids
Toroidal & Toroidal-Like
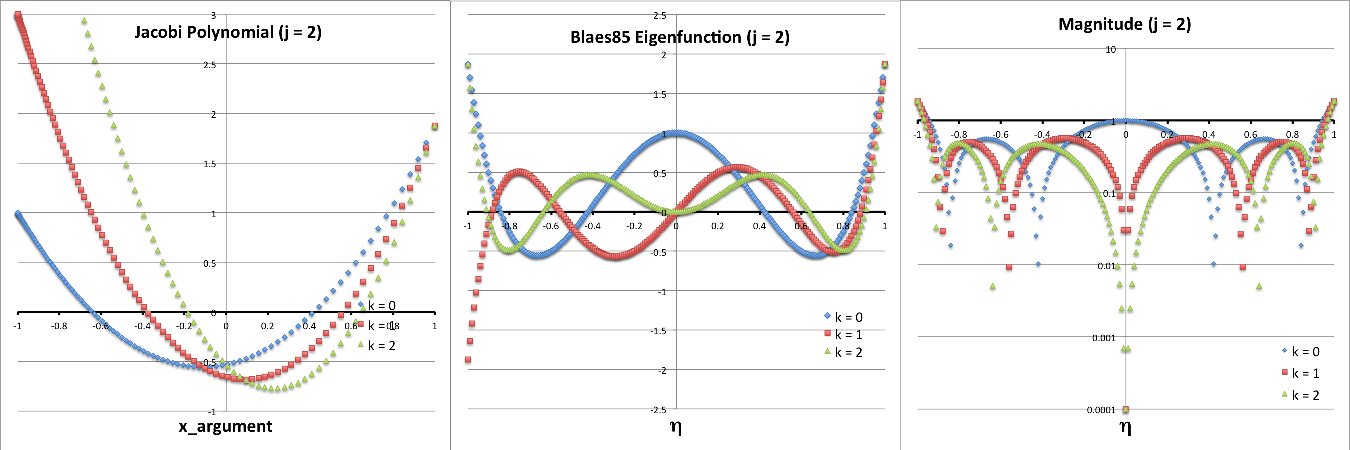
| Defining the Eigenvalue Problem |
|---|
| (Massless) Papaloizou-Pringle Tori |
Analytic Analysis by Blaes (1985) |
|---|
Nonlinear Dynamical Evolution
| 2D DYNAMICS |
|---|
| Free-Fall Collapse of an Homogeneous Spheroid |
|---|
Two-Dimensional Configurations (Nonaxisymmetric Disks)
| Infinitesimally Thin, Nonaxisymmetric Disks |
|---|
| 2D STRUCTURE |
|---|
| Constructing Infinitesimally Thin Nonaxisymmetric Disks |
|---|
Three-Dimensional Configurations
| (Initially) Three-Dimensional Configurations |
|---|
Equilibrium Structures
| 3D STRUCTURE |
|---|
|
"One interesting aspect of our models … is the pulsation characteristic of the final central triaxial figure … our interest in the pulsations stems from a general concern about the equilibrium structure of self-gravitating, triaxial objects. In the past, attempts to construct hydrostatic models of any equilibrium, triaxial structure having both a high <math>~T/|W|</math> value and a compressible equation of state have met with very limited success … they have been thwarted by a lack of understanding of how to represent complex internal motions in a physically realistic way… We suggest … that a natural attribute of [such] configurations may be pulsation and that, as a result, a search for simple circulation hydrostatic analogs of such systems may prove to a fruitless endeavor. |
|
— Drawn from §IVa of Williams & Tohline (1988), ApJ, 334, 449 |
|
Special numerical techniques must be developed "to build three-dimensional compressible equilibrium models with complicated flows." To date … "techniques have only been developed to build compressible equilibrium models of nonaxisymmetric configurations for a few systems with simplified rotational profiles, e.g., rigidly rotating systems (Hachisu & Eriguchi 1984; Hachisu 1986), irrotational systems (Uryū & Eriguchi 1998), and configurations that are stationary in the inertial frame (Uryū & Eriguchi 1996)." |
|
— Drawn from §1 of Ou (2006), ApJ, 639, 549 |
Ellipsoidal & Ellipsoidal-Like
| Constructing Ellipsoidal & Ellipsoidal-Like Configurations |
|---|
| Jacobi Ellipsoids |
|---|
- B. P. Kondrat'ev (1985), Astrophysics, 23, 654: Irrotational and zero angular momentum ellipsoids in the Dirichlet problem
- D. Lai, F. A. Rasio & S. L. Shapiro (1993), ApJS, 88, 205: Ellipsoidal Figures of Equilibrium: Compressible models
Binary Systems
- S. Chandrasekhar (1933), MNRAS, 93, 539: The equilibrium of distorted polytropes. IV. the rotational and the tidal distortions as functions of the density distribution
- S. Chandrasekhar (1963), ApJ, 138, 1182: The Equilibrium and the Stability of the Roche Ellipsoids
|
Roche's problem is concerned with the equilibrium and the stability of rotating homogeneous masses which are, further, distorted by the constant tidal action of an attendant rigid spherical mass. |
Stability Analysis
| 3D STABILITY |
|---|
Ellipsoidal & Ellipsoidal-Like
Binary Systems
- S. Chandrasekhar (1963), ApJ, 138, 1182: The Equilibrium and the Stability of the Roche Ellipsoids
- G. P. Horedt (2019), ApJ, 877, 9: On the Instability of Polytropic Maclaurin and Roche Ellipsoids
Nonlinear Evolution
| 3D DYNAMICS |
|---|
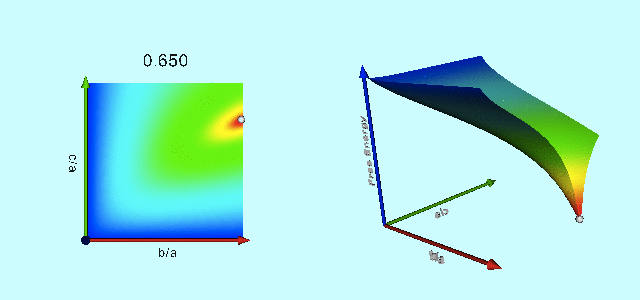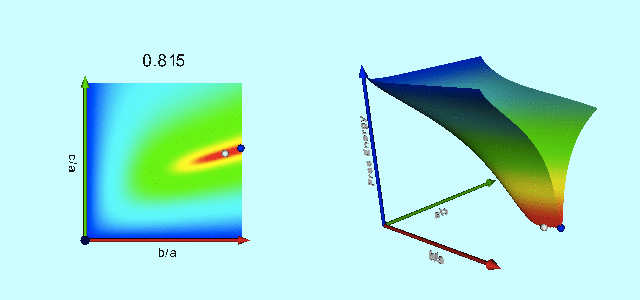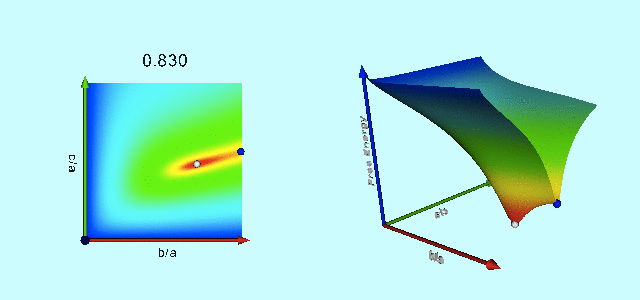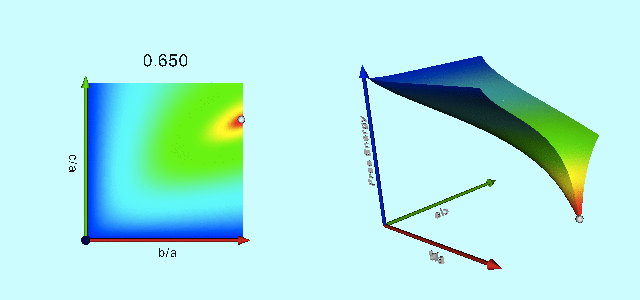
|
Free-Energy Evolution from the Maclaurin to the Jacobi Sequence |
|---|
| Fission Hypothesis |
|---|
Secular
- M. Fujimoto (1971), ApJ, 170, 143: Nonlinear Motions of Rotating Gaseous Ellipsoids
- W. H. Press & S. A. Teukolsky (1973), ApJ, 181, 513: On the Evolution of the Secularly Unstable, Viscous Maclaurin Spheroids
- S. L. Detweiler & L. Lindblom (1977), ApJ, 213, 193: On the evolution of the homogeneous ellipsoidal figures.
Dynamical
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |