Difference between revisions of "User:Tohline/SphericallySymmetricConfigurations/IntroductorySummary"
| Line 3: | Line 3: | ||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
=Applications= | =Applications= | ||
==Spherically Symmetric Configurations== | ==Spherically Symmetric Configurations== | ||
Revision as of 23:40, 1 March 2015

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Applications
Spherically Symmetric Configurations
Structure:
Here we show how the set of principal governing equations (PGEs) can be solved to determine the equilibrium structure of spherically symmetric fluid configurations — such as individual, nonrotating stars or protostellar gas clouds. After supplementing the PGEs by specifying an equation of state of the fluid, the system of equations is usually solved by employing one of three techniques to obtain a "detailed force-balanced" model that provides the radius, <math>~R_\mathrm{eq}</math>, of the equilibrium configuration — given its mass, <math>~M</math>, and central pressure, <math>~P_c</math>, for example — as well as details regarding the internal radial profiles of the fluid density and fluid pressure. As our various discussions illustrate, simply varying the power-law index, <math>~n</math>, in a polytropic equation of state,
|
<math>~P</math> |
<math>~=</math> |
<math>~K \rho^{(n+1)/n} \, ,</math> |
gives rise to equilibrium configurations that have a wide variety of internal structural profiles.
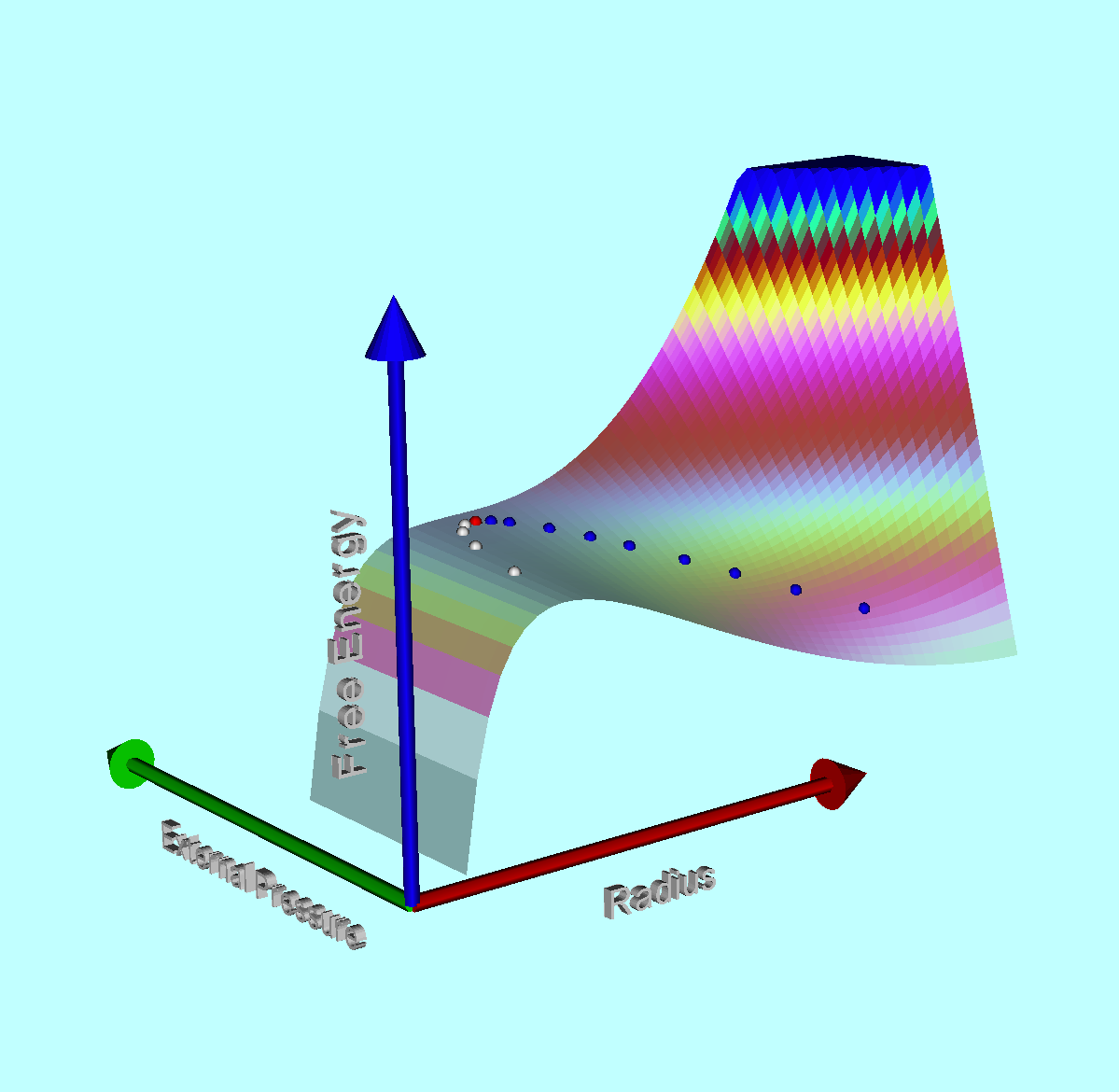
If one is not particularly concerned about details regarding the distribution of matter within the equilibrium configuration, a good estimate of the size of the equilibrium system can be determined by assuming a uniform-density structure then identifying local extrema in the system's global free energy. An illustrative, undulating free-energy surface is displayed here, on the right; blue dots identify equilibria associated with a "valley" of the free-energy surface while white dots identify equilibria that lie along a "ridge" in the free-energy surface.
In the astrophysics community, the mathematical relation that serves to define the properties of configurations that are associated with such free-energy extrema is often referred to as the scalar virial theorem. Specifically, for isolated systems in virial equilibrium, the following relation between configuration parameters holds:
|
<math>~\frac{GM^2}{P_c R_\mathrm{eq}^4}</math> |
<math>~=</math> |
<math>~\biggl(\frac{2^2\cdot 5 \pi}{3} \biggr) \frac{\mathfrak{f}_A \cdot \mathfrak{f}_M^2}{\mathfrak{f}_W} \, ,</math> |
where all three of the dimensionless structural form factors, <math>~\mathfrak{f}_M</math>, <math>~\mathfrak{f}_W</math>, and <math>~\mathfrak{f}_A</math>, are unity, under the assumption that the equilibrium configuration has uniform density and uniform pressure throughout, and are otherwise generically of order unity for detailed force-balanced models having a wide range of internal structures. Alternatively, if the specific entropy of fluid elements (set by the value of <math>~K</math>) throughout the system, rather than the central pressure, is held fixed while searching for extrema in the free-energy, the virial equilibrium relation for isolated polytropes is,
|
<math>~M^{(n-1)/n} R_\mathrm{eq}^{(3-n)/n} \biggl( \frac{G}{K} \biggr) </math> |
<math>~=</math> |
<math>~\frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} \biggl(\frac{3}{4\pi \mathfrak{f}_M}\biggr)^{1/n} \, . </math> |
If the physical system under consideration — such as a protostellar gas cloud — is not isolated but is, instead, embedded in a hot, tenuous medium that exerts on the system a confining external pressure, <math>~P_e</math>, the configuration's equilibrium parameters will be related via the expression,
|
<math>~\frac{GM^2}{P_c R_\mathrm{eq}^4}</math> |
<math>~=</math> |
<math>~\biggl(\frac{2^2\cdot 5 \pi}{3} \biggr) \frac{\mathfrak{f}_M^2}{\mathfrak{f}_W} \biggl[ \mathfrak{f}_A - \frac{P_e}{P_c} \biggr] \, ;</math> |
or, fixing <math>~K</math> instead of <math>~P_c</math>, the relevant virial equilibrium expression is,
|
<math>~P_e </math> |
<math>~=</math> |
<math>~K \mathfrak{f}_A \biggl( \frac{3M}{4\pi R_\mathrm{eq}^3} \cdot \frac{1}{\mathfrak{f}_M} \biggr)^{1 + 1/n} - \frac{\mathfrak{f}_W}{5} \biggl(\frac{3GM^2}{4\pi R_\mathrm{eq}^4} \cdot \frac{1}{\mathfrak{f}_M^2} \biggr) \, .</math> |
It is a virial expression specifically of this form <math>~(</math>with <math>n = \infty</math> and <math>\mathfrak{f}_M = \mathfrak{f}_W = \mathfrak{f}_A = 1)</math> that identifies extrema (e.g., valleys or ridges) in the rainbow-colored free-energy surface, <math>\mathfrak{G}^*(R_\mathrm{eq}, P_e)</math>, displayed above. As can be determined from this algebraic expression and as the figure illustrates, for any specified mass no equilibrium states exist if <math>~P_e</math> is greater than some limiting value, <math>~P_\mathrm{crit}</math>; the equilibrium configuration associated with the limiting condition, <math>~P_e = P_\mathrm{crit}</math>, is marked by a red dot on the displayed free-energy surface. The astrophysical significance of this critical state was first discussed in the mid 1950s in the context of star formation and, specifically, Bonnor-Ebert spheres.
After rearranging terms, for any specified values of the parameters <math>~P_e</math> and <math>~K</math>, this virial equilibrium expression can also be viewed as a mass-radius relation of the form,
|
<math>~a R_\mathrm{eq}^4 - b M^{(n+1)/n} R_\mathrm{eq}^{(n-3)/n} + c M^2</math> |
<math>~=</math> |
<math>~ 0\, ,</math> |
where,
|
<math>~a</math> |
<math>~\equiv</math> |
<math>~ \frac{4\pi}{3} \cdot P_e \, ,</math> |
|
<math>~b</math> |
<math>~\equiv</math> |
<math>~ \biggl( \frac{3}{4\pi} \biggr)^{1/n} \cdot K \mathfrak{f}_A \mathfrak{f}_M^{-(n+1)/n} \, ,</math> |
|
<math>~c</math> |
<math>~\equiv</math> |
<math>~ \frac{G\mathfrak{f}_W}{5\mathfrak{f}_M^2} \, .</math> |
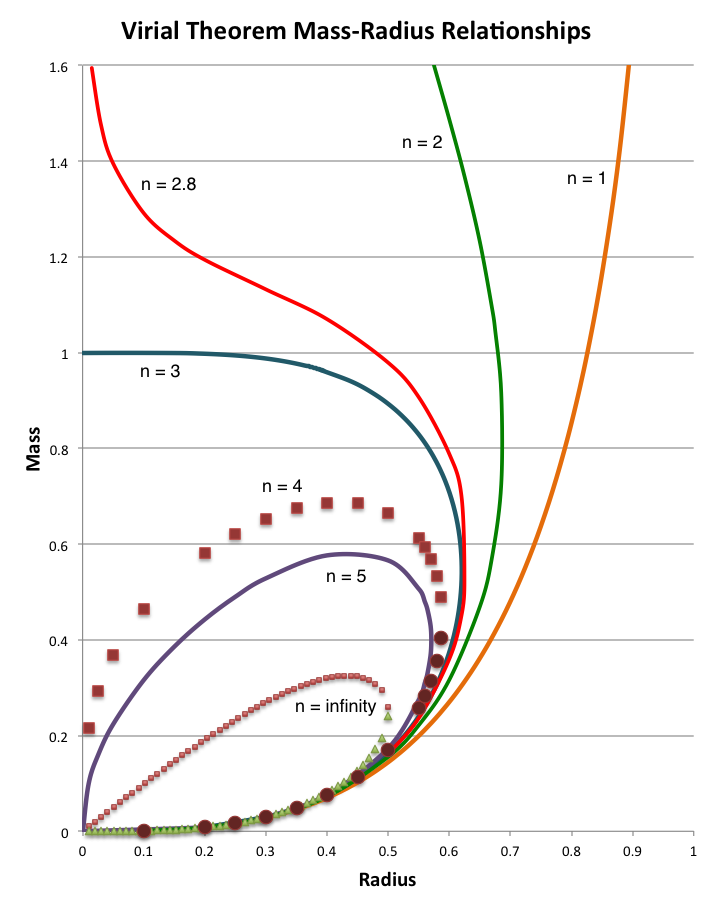
Using this virial equilibrium relation (and assuming a = b = c = 1), the curves drawn in the figure that is displayed here, on the right, show how the equilibrium radius of an embedded, pressure-truncated polytropic sphere varies with mass for seven different adopted polytropic indexes. In direct analogy with the critical pressure that is associated with Bonnor-Ebert spheres, for systems having <math>~n \ge 3</math>, there is a mass, <math>~M_\mathrm{max}</math>, above which equilibrium configurations do not exist; and, when <math>~n > 3</math>, two equilibrium configurations having different radii can be constructed for any system having a mass, <math>~M < M_\mathrm{max}</math>.
|
Solution Strategies: |
Detailed Force-Balance |
Virial Equilibrium |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |