User:Tohline/SSC/Structure/BiPolytropes/Analytic0 0
BiPolytrope with <math>n_c = 0</math> and <math>n_e=0</math>

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Here we construct a bipolytrope in which both the core and the envelope have uniform densities, that is, the structure of both the core and the envelope will be modeled using an <math>n = 0</math> polytropic index. It should be possible for the entire structure to be described by closed-form, analytic expressions. Generally, we will follow the general solution steps for constructing a bipolytrope that we have outlined elsewhere. [On 1 February 2014, J. E. Tohline wrote: This particular system became of interest to me during discussions with Kundan Kadam about the relative stability of bipolytropes.]
Step 4: Throughout the core (<math>0 \le \chi \le \chi_i</math>)
|
Specify: <math>~P_0</math> and <math>\rho_0 ~\Rightarrow</math> |
|
|||
|
<math>~\rho</math> |
<math>~=</math> |
<math>~\rho_0</math> |
|
|
|
<math>~P</math> |
<math>~=</math> |
<math>P_0 - \frac{2}{3} \pi G \rho_0^2 r^2</math> |
<math>~=</math> |
<math>P_0 \biggl( 1 - \frac{2\pi}{3}\chi^2 \biggr)</math> |
|
<math>~r</math> |
<math>~=</math> |
<math>\biggl[ \frac{P_0}{G \rho_0^2} \biggr]^{1/2} \chi</math> |
<math>~=</math> |
<math>\biggl[ \frac{P_0}{G \rho_0^2} \biggr]^{1/2} \chi</math> |
|
<math>~M_r</math> |
<math>~=</math> |
<math>\frac{4\pi}{3} \rho_0 r^3</math> |
<math>~=</math> |
<math>\frac{4\pi}{3} \rho_0 \biggl[ \frac{P_0}{G \rho_0^2} \biggr]^{3/2} \chi^3 = \frac{4\pi}{3} \biggl[ \frac{P_0^3}{G^3 \rho_0^4} \biggr]^{1/2} \chi^3</math> |
Step 5: Interface Conditions
|
Specify: <math>~\chi_i</math> and <math>~\rho_e/\rho_0</math>, and demand … |
|
|||
|
<math>~P_{ei}</math> |
<math>~=</math> |
<math>~P_{ci}</math> |
<math>~=</math> |
<math>P_0 \biggl( 1 - \frac{2\pi}{3}\chi_i^2 \biggr)</math> |
Step 6: Envelope Solution (<math>~\chi > \chi_i</math>)
|
<math>~\rho</math> |
<math>~=</math> |
<math>~\rho_e</math> |
|
<math>~P</math> |
<math>~=</math> |
<math>P_{ei} + \biggl(\frac{2}{3} \pi G \rho_e\biggr) \biggl[ 2(\rho_0 - \rho_e) r_i^3\biggl( \frac{1}{r} - \frac{1}{r_i}\biggr) - \rho_e(r^2 - r_i^2) \biggr]</math> |
|
|
<math>~=</math> |
<math>P_{ei} + \frac{2\pi}{3} \biggl(\frac{\rho_e}{\rho_0}\biggr) P_0 \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \chi_i^3\biggl( \frac{1}{\chi} - \frac{1}{\chi_i}\biggr) - \frac{\rho_e}{\rho_0} (\chi^2 - \chi_i^2) \biggr]</math> |
|
<math>~\frac{P}{P_0}</math> |
<math>~=</math> |
<math>1 - \frac{2\pi}{3}\chi_i^2 + \frac{2\pi}{3} \biggl(\frac{\rho_e}{\rho_0}\biggr) \chi_i^2 \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( \frac{1}{\xi} - 1\biggr) - \frac{\rho_e}{\rho_0} (\xi^2 - 1) \biggr]</math> |
|
<math>~M_r</math> |
<math>~=</math> |
<math>\frac{4\pi}{3} \biggl[ \rho_0 r_i^3 + \rho_e(r^3 - r_i^3) \biggr]</math> |
|
|
<math>~=</math> |
<math>\frac{4\pi}{3} \biggl[ \frac{P_0^3}{G^3 \rho_0^4} \biggr]^{1/2} \biggl[\chi_i^3 +\frac{\rho_e}{\rho_0} \biggl( \chi^3 - \chi_i^3 \biggr) \biggr]</math> |
|
|
<math>~=</math> |
<math>\frac{4\pi}{3} \biggl[ \frac{P_0^3}{G^3 \rho_0^4} \biggr]^{1/2} \chi_i^3\biggl[1 +\frac{\rho_e}{\rho_0} \biggl( \xi^3 - 1\biggr) \biggr]</math> |
Step 7: Surface Boundary Condition
At the surface (that is, at <math>r = R</math> and <math>M_r = M_\mathrm{tot}</math>), <math>P/P_0 = 0</math> and <math>\xi = \xi_s = R/r_i = 1/q</math>. Also, we can write,
<math> \chi_i = q\biggl[ \frac{G\rho_0^2 R^2}{P_0} \biggr]^{1/2} \, ; </math>
and, from earlier derivations,
<math> R^3 = \frac{3M_\mathrm{tot}}{4\pi \bar\rho} = \frac{3M_\mathrm{tot}}{4\pi \rho_0} \biggl( \frac{\nu}{q^3} \biggr) \, ; </math>
<math> \frac{\rho_e}{\rho_0} = \frac{q^3}{\nu} \biggl( \frac{1-\nu}{1-q^3}\biggr) \, . </math>
Therefore, setting the pressure to zero at the surface means,
|
<math>~\frac{3}{2\pi}\chi_i^{-2}</math> |
<math>~=</math> |
<math>1 - \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( q - 1\biggr) - \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr]</math> |
|
<math>\Rightarrow ~~~~~\biggl( \frac{3}{2\pi} \biggr) q^{-2} \biggl[ \frac{P_0}{G\rho_0^2 R^2} \biggr]</math> |
<math>~=</math> |
<math>1 + \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1- q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] </math> |
|
<math>\Rightarrow ~~~~~\biggl( \frac{3}{2\pi} \biggr) \biggl( \frac{4\pi}{3} \biggr)^{2/3} \nu^{-2/3} \biggl[ \frac{P_0^3}{G^3\rho_0^4 M_\mathrm{tot}^2} \biggr]^{1/3}</math> |
<math>~=</math> |
<math>1 + \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1- q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] </math> |
|
<math>\Rightarrow ~~~~~\biggl\{ \biggl( \frac{6}{\pi} \biggr) \frac{1}{\nu^{2} } \biggl[ \frac{P_0^3}{G^3\rho_0^4 M_\mathrm{tot}^2} \biggr] \biggr\}^{1/3}</math> |
<math>~=</math> |
<math>1 + \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1- q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] </math> |
It therefore seems prudent to define a function,
|
<math>~g(\nu,q)</math> |
<math>~\equiv</math> |
<math> \biggl\{ 1 + \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \biggr\}^{1/2} </math> |
|
<math> \Rightarrow ~~~~ q^2 g^2 </math> |
<math>~=</math> |
<math> q^2 + \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2q^2(1-q) + \biggl(\frac{\rho_e}{\rho_0}\biggr) (1-3q^2 + 2q^3) \biggr] \, , </math> |
in which case the expressions for the equilibrium radius and equilibrium total mass are, respectively,
|
<math> \biggl[ \frac{G\rho_0^2}{P_0} \biggr]^{1/2} R</math> |
<math>~=</math> |
<math>\biggl( \frac{3}{2\pi} \biggr)^{1/2} \frac{1}{q g} \, ;</math> |
|
<math> \biggl[ \frac{G^3\rho_0^4}{P_0^3} \biggr]^{1/2} M_\mathrm{tot}</math> |
<math>~=</math> |
<math>\biggl( \frac{6}{\pi} \biggr)^{1/2} \frac{1}{\nu g^3} \, .</math> |
Note that this means that,
<math> \chi_i^2 = \biggl( \frac{3}{2\pi}\biggr) \frac{1}{g^2} \, . </math>
We can also combine these two expressions and eliminate direct reference to the central density, <math>\rho_0</math>, obtaining,
|
<math> \biggl[ \frac{R^4}{GM_\mathrm{tot}^2} \biggr] P_0</math> |
<math>~=</math> |
<math>\biggl( \frac{3}{2^3\pi} \biggr) \frac{\nu^2 g^2}{q^4} </math> |
|
|
<math>~=~</math> |
<math> \biggl( \frac{3}{2^3\pi}\biggr) \frac{\nu^2}{q^6} \biggl[ q^2 + 2\biggl( \frac{\rho_e}{\rho_0} \biggr) q^2(1-q) + \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 ( 1 - 3q^2 + 2q^3) \biggr] \, .
</math> |
Thermal Energy Content
Knowing the pressure distribution throughout this bipolytropic configuration allows us to obtain an analytic expression for the configuration's total thermal content. Specifically, the differential contribution to the total thermal energy that is made by each spherical shell is,
<math>dS = \frac{3}{2} \biggl( \frac{P}{\rho} \biggr) dm = \frac{3}{2} \biggl( \frac{P}{\rho} \biggr) 4\pi \rho r^2 dr = 6\pi R^3 P(x) x^2 dx \, ,</math>
where,
<math>x \equiv \frac{r}{R} \, .</math>
(We are switching to a new normalization of the radial coordinate — using <math>~x</math> in preference to <math>~\chi</math> — because, at the interface between the core and the envelope, <math>~x=q</math>, while <math>~x=1 </math> at the surface of the bipolytropic configuration.) Hence, the thermal content of the core and of the envelope will be given by performing the following integrals, respectively:
|
<math>~S_\mathrm{core}</math> |
<math>~=~</math> |
<math>6\pi R^3 \int_0^q P_\mathrm{core}(x) x^2 dx \, ;</math> |
|
<math>~S_\mathrm{env}</math> |
<math>~=~</math> |
<math> 6\pi R^3 \int_q^1 P_\mathrm{env}(x) x^2 dx \, .</math> |
Drawing from the expressions obtained in step #4 and step #6, above, the relevant functions <math>~P(x)</math> are,
|
<math>~P_\mathrm{core}</math> |
<math>~=</math> |
<math>P_0 - \frac{2}{3} \pi G \rho_0^2 r^2 = P_i + \frac{2}{3} \pi G \rho_0^2(r_i^2 - r^2)</math> |
|
|
<math>~=</math> |
<math>P_i + \frac{2}{3} \pi G \rho_0^2 R^2 (q^2 - x^2) = P_i + \frac{3}{2^3 \pi} \biggl( \frac{GM_\mathrm{tot}^2}{R^4} \biggr) \biggl( \frac{\nu^2}{q^6} \biggr) (q^2 - x^2) \, ;</math> |
|
<math>~P_\mathrm{env}</math> |
<math>~=</math> |
<math>P_{i} - \biggl(\frac{2}{3} \pi G \rho_e\biggr) \biggl[ 2(\rho_0 - \rho_e) r_i^3\biggl( \frac{1}{r_i} - \frac{1}{r} \biggr) + \rho_e(r^2 - r_i^2) \biggr]</math> |
|
|
<math>~=</math> |
<math>P_{i} - \biggl(\frac{2}{3} \pi G \rho_0^2 R^2\biggr) \frac{\rho_e}{\rho_0} \biggl[ 2\biggl(1 - \frac{\rho_e}{\rho_0} \biggr) q^3\biggl( \frac{1}{q} - \frac{1}{x} \biggr) + \frac{\rho_e}{\rho_0} (x^2 - q^2) \biggr]</math> |
|
|
<math>~=</math> |
<math>P_{i} - \frac{3}{2^3 \pi} \biggl( \frac{GM_\mathrm{tot}^2}{R^4} \biggr) \biggl( \frac{\nu^2}{q^6} \biggr) \frac{\rho_e}{\rho_0} \biggl[ 2\biggl(1 - \frac{\rho_e}{\rho_0} \biggr) q^3\biggl( \frac{1}{q} - \frac{1}{x} \biggr) + \frac{\rho_e}{\rho_0} (x^2 - q^2) \biggr] \, .</math> |
|
Reminder: For a given choice of the parameter set <math>~(M_\mathrm{tot}, R, \nu, q)</math>, — and remembering that choosing the parameter pair <math>~(\nu,q)</math> sets the density ratio via the expression, <math>~\rho_e/\rho_0 = [q^3(1-\nu)]/[\nu(1-q^3)]</math> — the value of the pressure at the interface, <math>~P_i</math>, is determined by setting boundary conditions at the surface of the configuration, namely, by setting <math>~x=1</math> and <math>~P_\mathrm{env} = 0</math> in the second expression. Then, the central pressure <math>~(P_\mathrm{core} = P_0)</math> is determined by setting <math>~x=0</math> and inserting the determined value for <math>~P_i</math> in the first expression. |
Hence,
|
<math>~S_\mathrm{core}</math> |
<math>~=~</math> |
<math>6\pi R^3 \int_0^q \biggl\{ P_i + \Pi (q^2 - x^2) \biggr\} x^2 dx </math> |
|
|
<math>~=~</math> |
<math>6\pi R^3 \biggl\{ \biggl[ \biggl(P_i + q^2 \Pi \biggr)\frac{x^3}{3} \biggr]_0^q - \biggl[ \Pi \frac{x^5}{5} \biggr]_0^q \biggr\} </math> |
|
|
<math>~=~</math> |
<math>\biggl( \frac{4\pi}{5} \biggr) R^3 q^5 \biggl (\frac{5P_i}{2q^2} + \Pi \biggr) \, ,</math> |
|
<math>~S_\mathrm{env}</math> |
<math>~=~</math> |
<math> 6\pi R^3 \int_q^1 \biggl\{ P_i - \Pi \frac{\rho_e}{\rho_0} \biggl( a_e + \frac{b_e}{x} + c_e x^2\biggr) \biggr\} x^2 dx </math> |
|
|
<math>~=~</math> |
<math> 6\pi R^3 \biggl\{ \biggl[ P_i - a_e \Pi \biggl( \frac{\rho_e}{\rho_0} \biggr)\biggr] \frac{x^3}{3} \biggr|_q^1 - \biggl[ b_e \Pi \biggl( \frac{\rho_e}{\rho_0} \biggr) \frac{x^2}{2} \biggr]_q^1 - \biggl[ c_e \Pi \biggl( \frac{\rho_e}{\rho_0} \biggr) \frac{x^5}{5} \biggr]_q^1 \biggr\} </math> |
|
|
<math>~=~</math> |
<math> \frac{\pi R^3}{5} \biggl\{ 10 \biggl[ P_i - a_e \Pi \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggr] (1-q^3) - 15 \biggl[ b_e \Pi \biggl( \frac{\rho_e}{\rho_0} \biggr) (1-q^2) \biggr] - 6\biggl[ c_e \Pi \biggl( \frac{\rho_e}{\rho_0} \biggr) (1-q^5) \biggr] \biggr\} </math> |
|
|
<math>~=~</math> |
<math> \frac{\pi R^3}{5} \biggl\{ 10 P_i (1-q^3) - \Pi \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggl[ 10 a_e (1-q^3) + 15 b_e (1-q^2) + 6 c_e (1-q^5) \biggr] \biggr\} </math> |
|
|
<math>~=~</math> |
<math> \frac{\pi R^3}{5} \biggl\{ 10 P_i (1-q^3) </math> |
|
|
|
<math> +\Pi \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggl[ 30 \biggl( \frac{\rho_e}{\rho_0} - \frac{2}{3} \biggr) q^2 (1-q^3) + 30 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) q^3 (1-q^2) - 6 \frac{\rho_e}{\rho_0} (1-q^5) \biggr] \biggr\} </math> |
|
|
<math>~=~</math> |
<math> \frac{\pi R^3}{5} \biggl\{ 10 P_i (1-q^3) + 10 \Pi \biggl( \frac{\rho_e}{\rho_0} \biggr) q^2 \biggl[ 3 q (1-q^2) - 2 (1-q^3) \biggr] </math> |
|
|
|
<math> + 6 \Pi \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 \biggl[ 5 q^2 (1-q^3)- 5 q^3 (1-q^2) - (1-q^5) \biggr] \biggr\}
</math> |
|
|
<math>~=~</math> |
<math> \frac{\pi R^3}{5} \biggl\{ 10 P_i (1-q^3) + 10 \Pi \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggl[-2q^2 + 3q^3 - q^5 \biggr] + 6 \Pi \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 \biggl[ -1 + 5q^2 -5q^3 + q^5 \biggr] \biggr\} \, ,
</math> |
where,
<math> \Pi \equiv \frac{3}{2^3 \pi} \biggl( \frac{GM_\mathrm{tot}^2}{R^4} \biggr) \biggl( \frac{\nu^2}{q^6} \biggr) \, , </math>
and, in the expression for <math>~S_\mathrm{env}</math>, we temporarily used the shorthand notation,
|
<math>~a_e</math> |
<math>~\equiv~</math> |
<math>3 \biggl(\frac{2}{3} - \frac{\rho_e}{\rho_0} \biggr) q^2 \, ,</math> |
|
<math>~b_e</math> |
<math>~\equiv~</math> |
<math>- 2\biggl(1 - \frac{\rho_e}{\rho_0} \biggr) q^3 \, ,</math> |
|
<math>~c_e</math> |
<math>~\equiv~</math> |
<math>\frac{\rho_e}{\rho_0} \, .</math> |
The total thermal energy (per unit volume) may therefore be written as,
|
<math>\biggl( \frac{5}{\pi R^3} \biggr) S_\mathrm{tot}</math> |
<math>~=~</math> |
<math> 4 q^5 \biggl (\frac{5P_i}{2q^2} + \Pi \biggr) + 10 P_i (1-q^3) - \Pi \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggl[ 10 a_e (1-q^3) + 15 b_e (1-q^2) + 6 c_e (1-q^5) \biggr] </math> |
|
|
<math>~=~</math> |
<math> 10P_i + 2 \Pi \biggl[ 2q^5 - 5\biggl( \frac{\rho_e}{\rho_0} \biggr) (2q^2 - 3q^3 + q^5 ) - 3 \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 ( 1 - 5q^2 + 5q^3 - q^5 ) \biggr] \, ,
</math> |
or, because <math>~P_0 = P_i + \Pi q^2</math>, we can reference the central pressure instead of the pressure at the interface and write,
|
<math>\biggl( \frac{5}{\pi R^3} \biggr) S_\mathrm{tot}</math> |
<math>~=~</math> |
<math> 10P_0 - 2\Pi \biggl[5q^2 -2q^5 + 5\biggl( \frac{\rho_e}{\rho_0} \biggr) (2q^2 - 3q^3 + q^5 ) + 3 \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 ( 1 - 5q^2 + 5q^3 - q^5 ) \biggr] \, .
</math> |
Gravitational Potential Energy
In a separate discussion, we derived the following expression for the total gravitational potential energy of an <math>~(n_c, n_e) = (0, 0)</math> bipolytrope:
|
<math>~W</math> |
<math> ~= - \frac{3GM^2_\mathrm{tot}}{5R} \biggl( \frac{\nu^2}{q} \biggr) f(q, \rho_e/\rho_c) \, , </math> |
where,
<math> f(q, \rho_e/\rho_c) \equiv 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2} - 1 \biggr) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \biggl(\frac{1}{q^5} - 1 \biggr) - \frac{5}{2}\biggl(\frac{1}{q^2} - 1 \biggr) \biggr] \, . </math>
Adopting the parameters and normalizations used above in the context of the total thermal energy derivation, this can be rewritten as,
|
<math>~\biggl( \frac{5}{\pi R^3} \biggr) W</math> |
<math> ~= - 2^2 \Pi (2q^5 f) = - 2^2 \Pi \biggl\{ 2q^5 + 5q^3\biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^2) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ 2(1-q^5) - 5q^3(1-q^2) \biggr] \biggr\}\, . </math> |
Virial Equilibrium
In order for this system to be in virial equilibrium, we must have <math>(2S_\mathrm{tot} + W) = 0</math>, or,
|
<math>S_\mathrm{tot} = - \frac{W}{2} \, .</math> |
The central pressure that is required in order to establish this virial equilibrium condition is,
|
<math>~10P_0</math> |
<math>~=~</math> |
<math> 2\Pi \biggl[5q^2 -2q^5 + 5\biggl( \frac{\rho_e}{\rho_0} \biggr) (2q^2 - 3q^3 + q^5 ) + 3 \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 ( 1 - 5q^2 + 5q^3 - q^5 ) \biggr]
</math> |
|
|
|
<math> + 2\Pi \biggl\{ 2q^5 + 5q^3\biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^2) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ 2(1-q^5) - 5q^3(1-q^2) \biggr] \biggr\} </math> |
|
<math>\Rightarrow ~~~\frac{5P_0}{\Pi}</math> |
<math>~=~</math> |
<math> 5q^2 + 5\biggl( \frac{\rho_e}{\rho_0} \biggr) (2q^2 - 3q^3 + q^5 ) + 3 \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 ( 1 - 5q^2 + 5q^3 - q^5 )
</math> |
|
|
|
<math> + 5 \biggl( \frac{\rho_e}{\rho_c} \biggr) (q^3-q^5) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 ( 2 - 5q^3 + 3q^5 ) </math> |
|
<math>\Rightarrow ~~~\frac{P_0}{\Pi}</math> |
<math>~=~</math> |
<math> q^2 + 2\biggl( \frac{\rho_e}{\rho_0} \biggr) q^2(1-q) + \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 ( 1 - 3q^2 + 2q^3)
</math> |
|
<math>\Rightarrow ~~~\biggl[\frac{R^4}{GM_\mathrm{tot}^2}\biggr] P_0</math> |
<math>~=~</math> |
<math> \biggl( \frac{3}{2^3\pi}\biggr) \frac{\nu^2}{q^6} \biggl[ q^2 + 2\biggl( \frac{\rho_e}{\rho_0} \biggr) q^2(1-q) + \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 ( 1 - 3q^2 + 2q^3) \biggr] \, .
</math> |
Hooray! This precisely matches the expression for the central pressure, <math>~P_0</math>, that was obtained above at the end of step #7 of the detailed force balance derivation. It is very satisfying to see that the central pressure can be derived from demanding a balance of the thermal and gravitational potential energies via the virial equilibrium expression.
Note that, because <math>~P_0 = P_i + \Pi q^2</math>, we may alternatively write the solution in terms of the pressure at the interface, that is,
|
<math>\frac{P_i}{\Pi}</math> |
<math>~=~</math> |
<math> 2\biggl( \frac{\rho_e}{\rho_0} \biggr) q^2(1-q) + \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 ( 1 - 3q^2 + 2q^3) </math> |
|
|
<math>~=~</math> |
<math> q^2(g^2-1) \, . </math> |
Free Energy
Now, let's see if we can derive the virial equilibrium condition — and, hence the correct central pressure — from the free energy.
Expression for Free Energy
Rewrite the expressions for <math>~S_\mathrm{core}</math> and <math>~S_\mathrm{env}</math>, recognizing that, although we won't know its value until the equilibrium radius of the configuration has been determined, during a radial perturbation the dimensionless ratio,
<math>~\Lambda \equiv \frac{2 q^2\Pi}{5P_i} = \frac{3}{2^2\cdot 5 \pi} \biggl( \frac{GM_\mathrm{tot}^2}{R^4 P_i} \biggr) \biggl( \frac{\nu^2}{q^4} \biggr) = \biggl( \frac{2^2\pi}{3\cdot 5} \biggr) \frac{G\rho_0^2 r_i^2}{P_i} \, , </math>
will remain unchanged. Hence, we may write,
|
<math>~S_\mathrm{core}</math> |
<math>~=~</math> |
<math>2\pi q^3 R^3 P_{ic} \biggl (1 + \Lambda \biggr) \, ,</math> |
|
<math>~S_\mathrm{env}</math> |
<math>~=~</math> |
<math> \pi R^3 P_{ie} \biggl\{ 2 (1-q^3) + 5 \Lambda \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggl[-2 + 3q - q^3 \biggr] + \frac{3 \Lambda}{q^2} \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 \biggl[ -1 + 5q^2 -5q^3 + q^5 \biggr] \biggr\} \, .
</math> |
The free energy is, therefore,
|
<math>~\mathfrak{G}</math> |
<math>~=~</math> |
<math>~U_\mathrm{tot} + W</math> |
|
|
<math>~=~</math> |
<math>\biggl[ \frac{2}{3(\gamma_c -1)} \biggr] S_\mathrm{core} + \biggl[ \frac{2}{3(\gamma_e -1)} \biggr] S_\mathrm{env} + W</math> |
|
|
<math>~=~</math> |
<math>B_\mathrm{core}R^3 P_{ic} + B_\mathrm{env} R^3 P_{ie} - A_\mathrm{grav} R^{-1} \, , </math> |
where, for a given choice of the three parameters <math>~(M_\mathrm{tot}, \nu, q)</math>, the constant coefficients in this expression are,
|
<math>~A_\mathrm{grav}</math> |
<math>~\equiv~</math> |
<math> \frac{2^2 \pi}{5} \biggl[ \frac{3GM_\mathrm{tot}^2}{2^3\pi} \biggl(\frac{\nu^2}{q^6} \biggr) \biggr] \biggl\{ 2q^5 + 5q^3\biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^2) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ 2(1-q^5) - 5q^3(1-q^2) \biggr] \biggr\} \, , </math> |
|
<math>~B_\mathrm{core}</math> |
<math>~\equiv~</math> |
<math> \biggl[ \frac{4\pi q^3}{3(\gamma_c -1)} \biggr]\biggl(1 + \Lambda\biggr) \, ,
</math> |
|
<math>~B_\mathrm{env}</math> |
<math>~\equiv~</math> |
<math> \biggl[ \frac{2\pi}{3(\gamma_e -1)} \biggr] \biggl\{ 2 (1-q^3)
+ 5 \Lambda \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggl[-2 + 3q - q^3 \biggr] + \frac{3 \Lambda}{q^2} \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 \biggl[ -1 + 5q^2 -5q^3 + q^5 \biggr] \biggr\} \, .
</math> |
Notice that, in the expression for <math>~\mathfrak{G}</math>, we have been careful to maintain the separate identities of the interface pressure, depending on whether it is set by the core <math>~(P_{ic})</math> or by the envelope <math>~(P_{ie})</math>, because they scale differently — along two separate adiabats — with density and, hence, with radius. Specifically,
|
<math>~P_{ic}</math> |
<math>~=~</math> |
<math>K_c \rho_0^{\gamma_c} = K_c \biggl[ \frac{3M_\mathrm{tot} \nu}{4\pi q^3} \biggr]^{\gamma_c} R^{-3\gamma_c} \, ,</math> |
|
<math>~P_{ie}</math> |
<math>~=~</math> |
<math>K_e \rho_e^{\gamma_e} = K_e \biggl[ \frac{3M_\mathrm{tot} \nu}{4\pi q^3} \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggr]^{\gamma_e} R^{-3\gamma_e} \, .</math> |
With these pressure scalings in mind, the expression for the free energy becomes,
|
<math>~\mathfrak{G}</math> |
<math>~=~</math> |
<math> C_\mathrm{core} \biggl[ \frac{2}{3(\gamma_c - 1)} \biggr] R^{3-3\gamma_c} + C_\mathrm{env} \biggl[ \frac{2}{3(\gamma_e - 1)} \biggr] R^{3-3\gamma_e} -A_\mathrm{grav} R^{-1}\, , </math> |
where,
|
<math>~C_\mathrm{core}</math> |
<math>~\equiv~</math> |
<math> 2\pi q^3 K_c \biggl[ \frac{3M_\mathrm{tot} \nu}{4\pi q^3} \biggr]^{\gamma_c} \biggl(1 + \Lambda\biggr) \, , </math> |
|
<math>~C_\mathrm{env}</math> |
<math>~\equiv~</math> |
<math> \pi K_e \biggl[ \frac{3M_\mathrm{tot} \nu}{4\pi q^3} \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggr]^{\gamma_e} \biggl\{ 2 (1-q^3) + 5 \Lambda \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggl[-2 + 3q - q^3 \biggr] + \frac{3 \Lambda}{q^2} \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 \biggl[ -1 + 5q^2 -5q^3 + q^5 \biggr] \biggr\} \, .
</math> |
Equilibrium Condition
The equilibrium condition will be defined by determining at what radius, <math>~d\mathfrak{G}/dR = 0</math>. Let's do this!
|
<math>\frac{d\mathfrak{G}}{dR}</math> |
<math>~=~</math> |
<math> A_\mathrm{grav} R^{-2} - 2C_\mathrm{core} R^{2-3\gamma_c} - 2C_\mathrm{env} R^{2-3\gamma_e}</math> |
|
|
<math>~=~</math> |
<math>R^{-1} \biggl[ \frac{A_\mathrm{grav}}{R} - 2C_\mathrm{core} R^{3-3\gamma_c} - 2C_\mathrm{env} R^{3-3\gamma_e} \biggr] \, .</math> |
Setting this expression equal to zero means,
|
<math>\frac{A_\mathrm{grav}}{2R}</math> |
<math>~=~</math> |
<math>C_\mathrm{core} R^{3-3\gamma_c} + C_\mathrm{env} R^{3-3\gamma_e}</math> |
|
<math>\Rightarrow ~~~~ - \frac{W}{2}</math> |
<math>~=~</math> |
<math>C_\mathrm{core} R^{3-3\gamma_c} + C_\mathrm{env} R^{3-3\gamma_e}</math> |
|
|
<math>~=~</math> |
<math>2\pi q^3 R^3 P_{ic}\biggl(1 + \Lambda\biggr) + \pi R^3 P_{ie}\biggl\{ 2 (1-q^3) + 5 \Lambda \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggl[-2 + 3q - q^3 \biggr] + \frac{3 \Lambda}{q^2} \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 \biggl[ -1 + 5q^2 -5q^3 + q^5 \biggr] \biggr\} \, . </math>
|
If we now set the interface pressures equal to one another, that is,
|
<math>~P_{ie} = P_{ic}</math> |
<math>~=~</math> |
<math>P_i \, ,</math> |
we obtain,
|
<math>- \frac{W}{2}</math> |
<math>~=~</math> |
<math>2\pi q^3 R^3 \biggl(P_i + P_i \Lambda \biggr) + \pi R^3 P_i\biggl\{ 2 (1-q^3) + 5 \Lambda \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggl[-2 + 3q - q^3 \biggr] + \frac{3 \Lambda}{q^2} \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 \biggl[ -1 + 5q^2 -5q^3 + q^5 \biggr] \biggr\} </math>
|
|
|
<math>~=~</math> |
<math>2\pi q^3 R^3 P_i +2\pi R^3 P_i(1-q^3) + \pi R^3 P_i \Lambda \biggl\{ 2 q^3 + 5 \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggl[-2 + 3q - q^3 \biggr] + \frac{3 }{q^2} \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 \biggl[ -1 + 5q^2 -5q^3 + q^5 \biggr] \biggr\} </math>
|
|
|
<math>~=~</math> |
<math>2\pi R^3 P_i + 2\pi R^3 \biggl(\frac{q^2}{5}\biggr) \Pi \biggl\{ 2 q^3 + 5 \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggl[-2 + 3q - q^3 \biggr] + \frac{3}{q^2} \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 \biggl[ -1 + 5q^2 -5q^3 + q^5 \biggr] \biggr\} </math>
|
|
|
<math>~=~</math> |
<math>\biggl( \frac{\pi R^3}{5} \biggr) \biggl\{ 10 P_i + 2\Pi \biggl[ 2 q^5 + 5 \biggl( \frac{\rho_e}{\rho_0} \biggr) (-2q^2 + 3q^3 - q^5 ) + 3 \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 ( -1 + 5q^2 -5q^3 + q^5 ) \biggr] \biggr\} \, .</math>
|
Now, according to our earlier derivation of the total thermal energy content of this <math>~(n_c, n_e) = (0, 0)</math> bipolytrope, the right-hand side of this last expression is <math>~S_\mathrm{tot}</math>. Hence the equilibrium condition just derived from the first derivative of the free energy is precisely the virial equilibrium condition discussed above, namely,
|
<math>- \frac{W}{2}</math> |
<math>~=~</math> |
<math>S_\mathrm{tot} \, .</math> |
This, in turn, means that from the free energy expression we are able to deduce the equilibrium values of the dimensionless radius, mass, and central pressure that were derived earlier from the hydrostatic balance equation, namely,
|
<math> \biggl[ \frac{G\rho_0^2}{P_0} \biggr]^{1/2} R_\mathrm{eq}</math> |
<math>~=</math> |
<math>\biggl( \frac{3}{2\pi} \biggr)^{1/2} \frac{1}{q g} \, ;</math> |
|
<math> \biggl[ \frac{G^3\rho_0^4}{P_0^3} \biggr]^{1/2} M_\mathrm{tot}</math> |
<math>~=</math> |
<math>\biggl( \frac{6}{\pi} \biggr)^{1/2} \frac{1}{\nu g^3} \, ;</math> |
|
<math> \biggl[ \frac{R^4}{GM_\mathrm{tot}^2} \biggr] P_0</math> |
<math>~=</math> |
<math>\biggl( \frac{3}{2^3\pi} \biggr) \frac{\nu^2 g^2}{q^4} \, .</math> |
Also, because <math>~P_0 = P_i + q^2\Pi</math>, we conclude that,
|
<math> \biggl[ \frac{R^4}{GM_\mathrm{tot}^2} \biggr] P_i</math> |
<math>~=</math> |
<math>\biggl( \frac{3}{2^3\pi} \biggr) \frac{\nu^2}{q^4}(g^2-1) \, .</math> |
Hence, the dimensionless structural parameter that appears in our free energy expression takes on the value,
|
<math>~\frac{1}{\Lambda}</math> |
<math>~=</math> |
<math>\frac{5}{2}(g^2-1) = \frac{5}{2}\biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \, .</math> |
Stability Condition
Second Derivative of Free Energy
The relative stability of an equilibrium configuration can be determined by the sign of the second derivative of the free energy evaluated at the equilibrium radius; if the second derivative is negative, the system is dynamically unstable. The second derivative of the free energy is,
|
<math>\frac{d^2\mathfrak{G}}{dR^2} \biggr|_{R_\mathrm{eq}}</math> |
<math>~=~</math> |
<math>\biggl[ -2A_\mathrm{grav}R^{-3} - 2(2-3\gamma_c)C_\mathrm{core} R^{1-3\gamma_c} - 2(2-3\gamma_e)C_\mathrm{env} R^{1-3\gamma_e} \biggr]_\mathrm{eq} </math> |
|
|
<math>~=~</math> |
<math>2R^{-2}_\mathrm{eq} \biggl[ W - (2-3\gamma_c)C_\mathrm{core} R^{3-3\gamma_c} - (2-3\gamma_e)C_\mathrm{env} R^{3-3\gamma_e} \biggr]_\mathrm{eq} \, .</math> |
From the equilibrium condition derived above, we know that,
|
<math>- C_\mathrm{env} R^{3-3\gamma_e}</math> |
<math>~=~</math> |
<math>C_\mathrm{core} R^{3-3\gamma_c} + \frac{W}{2} \, .</math> |
Hence,
|
<math>\frac{1}{2} R^{2}_\mathrm{eq} \frac{d^2\mathfrak{G}}{dR^2} \biggr|_{R_\mathrm{eq}}</math> |
<math>~=~</math> |
<math>W_\mathrm{eq} - (2-3\gamma_c)C_\mathrm{core} R_\mathrm{eq}^{3-3\gamma_c} + (2-3\gamma_e) \biggl[ C_\mathrm{core} R^{3-3\gamma_c} + \frac{W}{2}\biggr]_\mathrm{eq} </math> |
|
|
<math>~=~</math> |
<math>\biggl( 2 - \frac{3}{2}\gamma_e \biggr) W_\mathrm{eq} + 3 (\gamma_c - \gamma_e)C_\mathrm{core} R_\mathrm{eq}^{3-3\gamma_c} \, .</math> |
But, from our above discussion, we can also write,
|
<math>~C_\mathrm{core}</math> |
<math>~=~</math> |
<math>2\pi q^3 P_i R_\mathrm{eq}^{3\gamma_c} (1+\Lambda) \, .</math> |
Hence,
|
<math>\biggl[ \frac{R^{2}_\mathrm{eq}}{2} \biggr] \frac{d^2\mathfrak{G}}{dR^2} \biggr|_{R_\mathrm{eq}}</math> |
<math>~=~</math> |
<math>6\pi (\gamma_c - \gamma_e)q^3 P_i R_\mathrm{eq}^{3} (1+\Lambda) + \biggl( 2 - \frac{3}{2}\gamma_e \biggr) W_\mathrm{eq} </math> |
|
<math>\Rightarrow ~~~~ \biggl[ \frac{1}{P_iR_\mathrm{eq}} \biggr] \frac{d^2\mathfrak{G}}{dR^2} \biggr|_{R_\mathrm{eq}}</math> |
<math>~=~</math> |
<math> 12\pi (\gamma_c - \gamma_e)q^3 (1+\Lambda) - \frac{1}{P_iR^3_\mathrm{eq}} ( 4 - 3\gamma_e) \biggl[ \frac{3GM_\mathrm{tot}^2}{5 R_\mathrm{eq}} \biggl(\frac{\nu^2}{q}\biggr) f \biggr] </math> |
|
|
<math>~=~</math> |
<math> ~12\pi (\gamma_c - \gamma_e)q^3 (1+\Lambda) - 4\pi ( 4 - 3\gamma_e) q^3 \Lambda f </math> |
|
<math>\Rightarrow ~~~~ \frac{d^2\mathfrak{G}}{dR^2} \biggr|_{R_\mathrm{eq}}</math> |
<math>~=~</math> |
<math> ~12\pi P_iR_\mathrm{eq}\biggl[ (\gamma_c - \gamma_e)q^3 (1+\Lambda) - \biggl( \frac{4}{3} - \gamma_e \biggr) q^3 \Lambda f \biggr] </math> |
|
|
<math>~=~</math> |
<math> ~12\pi P_iR_\mathrm{eq} (\gamma_e - \gamma_c) q^3 \Lambda \biggl[ \frac{( \gamma_e - \frac{4}{3})}{(\gamma_e - \gamma_c)} f - \biggl(1+\frac{1}{\Lambda} \biggr) \biggr] </math> |
|
|
<math>~=~</math> |
<math> ~12\pi P_iR_\mathrm{eq} (\gamma_e - \gamma_c) q^3 \Lambda \biggl[ \frac{( \gamma_e - \frac{4}{3})}{(\gamma_e - \gamma_c)} f -1 -\frac{5}{2} (g^2-1) \biggr] \, . </math> |
Associated Oscillation Frequency
When a stable configuration is displaced (by a radial perturbation) from its equilibrium state, it should radially oscillate back and forth through its equilibrium radius at a frequency, <math>~\omega_\mathfrak{G}</math>, such that,
|
<math>~\omega_\mathfrak{G}^2</math> |
<math>~=</math> |
<math>~\frac{1}{M_\mathrm{tot}} \cdot \frac{d^2\mathfrak{G}}{dR^2} \biggr|_{R_\mathrm{eq}} \, .</math> |
Recognizing, from above, that
|
<math>~P_i </math> |
<math>~=</math> |
<math>~P_c - q^2\Pi </math> |
|
|
<math>~=</math> |
<math>~\frac{3}{2^3\pi} \biggl(\frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}^4} \biggr) \frac{\nu^2}{q^4} (g^2-1) \, ,</math> |
and that,
|
<math>~\rho_c</math> |
<math>~=</math> |
<math>~\frac{3M_\mathrm{tot}}{4\pi G R_\mathrm{eq}^3} \cdot \frac{\nu}{q^3} \, ,</math> |
we can write,
|
<math>~\frac{P_i R_\mathrm{eq}}{M_\mathrm{tot}}</math> |
<math>~=</math> |
<math>~\biggl(\frac{G \rho_c}{2} \biggr) \frac{\nu}{q} (g^2-1) \, .</math> |
Hence, the characteristic oscillation frequency is,
|
<math>~\omega_\mathfrak{G}^2</math> |
<math>~=</math> |
<math>~ 6\pi G \rho_c \cdot \frac{\nu}{q} (g^2-1) ~(\gamma_e - \gamma_c) q^3 \Lambda \biggl[ \frac{( \gamma_e - \frac{4}{3})}{(\gamma_e - \gamma_c)} f -1 -\frac{5}{2} (g^2-1) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2\pi G \rho_c}{5}\biggr) \cdot q^2 \nu \biggl[ 2( 3\gamma_e - 4) f + 3(\gamma_e - \gamma_c)(3 - 5 g^2) \biggr] \, . </math> |
Summary
| |||||||||||||||||||||||||||||||||
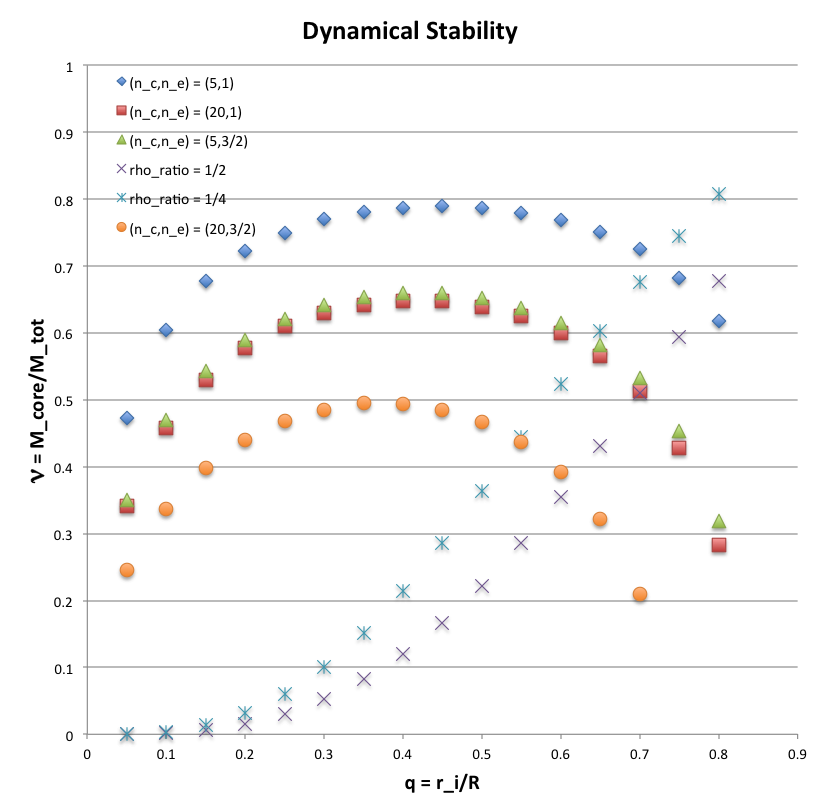
The "Dynamical Stability" figure below shows a large segment of the <math>~(q,\nu)</math> model parameter space. The figure displays stability boundaries for four different choices of the core/envelope adiabatic pairs <math>~(\gamma_c, \gamma_e)</math>, as detailed in the accompanying "Stability Boundaries" table. (The corresponding polytropic indexes are also listed, where, <math>~\gamma = 1+1/n</math>.) Two bipolytrope model sequences are also drawn: One shows how the core-to-total mass ratio, <math>~\nu</math>, varies with increasing <math>~q</math> when the density ratio at the core-envelope interface is <math>~\rho_e/\rho_c = 1/2</math> (purple crosses); the other shows the same information, but for <math>~\rho_e/\rho_c = 1/4</math> (purple asterisks). For a given choice of adiabatic indexes, equilibrium configurations that lie below the relevant stability boundary, along either sequence, are stable while configurations that lie above the relevant boundary are dynamically unstable.
|
|
|||||||||||||||||||||||||||||||
It is important to emphasize that the stability analysis presented above is an approximation in the following sense: The underlying equilibrium structure of each model is that of an <math>~(n_c, n_e) = (0, 0)</math> bipolytrope, that is, both the core and the envelope have uniform (but different) densities; the gravitational potential energy, <math>~W</math> and the thermal energy content of the component volumes, <math>~S_\mathrm{core}</math> and <math>~S_\mathrm{env}</math>, are determined exactly. However, the relative stability of a configuration is determined by assuming that, when the bipolytropic configuration is perturbed from its equilibriums state, its core and envelope heat up (or cool) by evolving along <math>~(\gamma_c, \gamma_e)</math> adiabats.
Bipolytrope Generalization
This subsection has been moved to another location because it more naturally stands on its own, that is, it should not be tied only to the discussion of the structure of <math>~(n_c, n_e) = (0, 0)</math> bipolytropes.
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Plotting Free-Energy Surfaces
Thus far, we have been able to determine what the equilibrium radius of the bipolytrope is for any specified set of parameters, <math>~(M_\mathrm{tot}, \nu, q)</math>. Now let's examine how the free energy varies across the two-dimensional plane defined by the parameters, <math>~(q, \nu)</math>. We begin by copying an informative segment from the above subsection where we developed an expression for the free energy.
The free energy is,
|
<math>~\mathfrak{G}</math> |
<math>~=~</math> |
<math>~U_\mathrm{tot} + W</math> |
|
|
<math>~=~</math> |
<math>\biggl[ \frac{2}{3(\gamma_c -1)} \biggr] S_\mathrm{core} + \biggl[ \frac{2}{3(\gamma_e -1)} \biggr] S_\mathrm{env} + W</math> |
|
|
<math>~=~</math> |
<math>B_\mathrm{core}R^3 P_{ic} + B_\mathrm{env} R^3 P_{ie} - A_\mathrm{grav} R^{-1} \, , </math> |
|
|
<math>~=~</math> |
<math>\frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}} \biggl[ (B_\mathrm{core}+B_\mathrm{env} ) \frac{R^4 P_i}{GM_\mathrm{tot}^2} - A^*_\mathrm{grav} \biggr] \, , </math> |
where, for a given choice of the three parameters <math>~(M_\mathrm{tot}, \nu, q)</math>, the constant coefficients in this expression are,
|
<math>~A^*_\mathrm{grav}</math> |
<math>~\equiv~</math> |
<math> \frac{3}{2\cdot 5} \biggl(\frac{\nu^2}{q^6} \biggr) \biggl\{ 2q^5 + 5q^3\biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^2) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ 2(1-q^5) - 5q^3(1-q^2) \biggr] \biggr\} \, , </math> |
|
<math>~B_\mathrm{core}</math> |
<math>~\equiv~</math> |
<math> \biggl[ \frac{4\pi n_c q^3}{3} \biggr]\biggl(1 + \Lambda\biggr) \, ,
</math> |
|
<math>~B_\mathrm{env}</math> |
<math>~\equiv~</math> |
<math> \biggl[ \frac{2\pi n_e}{3} \biggr] \biggl\{ 2 (1-q^3)
+ 5 \Lambda \biggl( \frac{\rho_e}{\rho_0} \biggr) \biggl[-2 + 3q - q^3 \biggr] + \frac{3 \Lambda}{q^2} \biggl( \frac{\rho_e}{\rho_0} \biggr)^2 \biggl[ -1 + 5q^2 -5q^3 + q^5 \biggr] \biggr\} \, .
</math> |
Now, the condition derived above for the equilibrium radius is,
<math> \biggl[ \frac{R^4}{GM_\mathrm{tot}^2} \biggr] P_i = \biggl( \frac{3}{2^3\pi} \biggr) \frac{\nu^2}{q^4} (g^2 -1) \, . </math>
Hence, the free energy expression becomes,
|
<math>~\mathfrak{G}</math> |
<math>~=~</math> |
<math>\frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}} \biggl[ (B_\mathrm{core}+B_\mathrm{env} ) \biggl( \frac{3}{2^3\pi} \biggr) \frac{\nu^2}{q^4} (g^2 -1) - A^*_\mathrm{grav} \biggr] \, . </math> |
Combining the same condition for the equilibrium radius with the expression for the pressure at the interface in the equilibrium configuration, namely,
|
<math>~P_i</math> |
<math>~=~</math> |
<math>K_c \biggl[ \frac{3M_\mathrm{tot} \nu}{4\pi q^3} \biggr]^{\gamma_c} R^{-3\gamma_c} \, ,</math> |
allows us to write the equilibrium radius in terms of <math>~M_\mathrm{tot}</math> and <math>~K_c</math>. Specifically, we obtain,
|
<math>R^{4-3\gamma_c} </math> |
<math>~~=~~</math> |
<math>\biggl[ \frac{GM_\mathrm{tot}^{2-\gamma_c}}{K_c } \biggr] \biggl( \frac{3\nu}{4\pi q^3} \biggr)^{1-\gamma_c} \biggl(\frac{\nu}{2q}\biggr) (g^2 -1) </math> |
|
<math>\Rightarrow ~~~~~ \frac{GM_\mathrm{tot}^2}{R}</math> |
<math>~~=~~</math> |
<math> \biggl[ \frac{G^{3\gamma_c - 3} M^{5\gamma_c -6}_\mathrm{tot}}{K_c} \biggr]^{1/(3\gamma_c - 4)} \biggl[ \biggl( \frac{4\pi q^3}{3\nu}\biggr)^{\gamma_c-1} \biggl(\frac{\nu}{2q}\biggr) (g^2 -1) \biggr]^{1/(3\gamma_c - 4)} \, .</math> |
Finally, then, recognizing that <math>~\gamma_c = 1 + 1/n_c</math> and, hence, <math>~1/(3\gamma_c - 4) = n_c/(3-n_c)</math>, we obtain,
|
<math>~\mathfrak{G}</math> |
<math>~=~</math> |
<math> \biggl[ \frac{K_c^{n_c}}{G^{3} M^{5-n_c}_\mathrm{tot}} \biggr]^{1/(n_c-3)} \biggl[ \biggl( \frac{4\pi q^3}{3\nu}\biggr)^{1/n_c} \biggl(\frac{\nu}{2q}\biggr) (g^2 -1) \biggr]^{-n_c/(n_c-3)} \biggl[ (B_\mathrm{core}+B_\mathrm{env} ) \biggl( \frac{3}{2^3\pi} \biggr) \frac{\nu^2}{q^4} (g^2 -1) - A^*_\mathrm{grav} \biggr] \, . </math> |
Related Discussions
- Analytic solution with <math>~n_c = 5</math> and <math>~n_e=1</math>.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |