User:Tohline/SSC/BipolytropeGeneralization
Bipolytrope Generalization

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
On 26 August 2014, Tohline finished rewriting the chapter titled "Bipolytrope Generalization" in a very concise manner (go here for this Version2 chapter) then set this chapter aside to provide a collection of older attempts at the derivations. While much of what follows is technically correct, it is overly detailed and cumbersome. Because it likely also contains some misguided steps, we label it in entirety as Work in Progress.
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Old Stuff
|
<math>~\mathfrak{G}</math> |
<math>~=</math> |
<math>~W_\mathrm{grav} + \mathfrak{S}_A\biggr|_\mathrm{core} + \mathfrak{S}_A\biggr|_\mathrm{env} </math> |
|
|
<math>~=</math> |
<math> ~W_\mathrm{grav} + \biggl[ \frac{2}{3(\gamma_c - 1)} \biggr] S_\mathrm{core} + \biggl[ \frac{2}{3(\gamma_e - 1)} \biggr] S_\mathrm{env} \, . </math> |
In addition to the gravitational potential energy, which is naturally written as,
|
<math>~W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~- \frac{3}{5} \biggl( \frac{GM_\mathrm{tot}^2}{R} \biggr) \cdot \mathfrak{f}_{WM} \, ,</math> |
it seems reasonable to write the separate thermal energy contributions as,
|
<math>~S_\mathrm{core}</math> |
<math>~=</math> |
<math> ~\frac{3}{2}\biggl[ M_\mathrm{core} \biggl( \frac{P_{ic}}{\rho_{ic}} \biggr) \biggr] s_\mathrm{core} = \frac{3}{2} \biggl[ \nu M_\mathrm{tot} P_{ic} \biggl( \frac{\rho_{ic}}{\bar\rho} \biggr)^{-1} \biggl( \frac{4\pi R^3}{3 M_\mathrm{tot}} \biggr) \biggr] s_\mathrm{core} = 2\pi R^3 P_{ic} \biggl[ q^3 s_\mathrm{core} \biggr] \, ,</math> |
|
<math>~S_\mathrm{env}</math> |
<math>~=</math> |
<math> ~\frac{3}{2}\biggl[ M_\mathrm{env} \biggl( \frac{P_{ie}}{\rho_{ie}} \biggr) \biggr] s_\mathrm{env} = \frac{3}{2} \biggl[ (1-\nu) M_\mathrm{tot} P_{ie} \biggl( \frac{\rho_{ie}}{\bar\rho} \biggr)^{-1} \biggl( \frac{4\pi R^3}{3 M_\mathrm{tot}} \biggr) \biggr] s_\mathrm{env} = 2\pi R^3 P_{ie} \biggl[ (1-q^3) s_\mathrm{env} \biggr] \, ,</math> |
where the subscript "<math>i</math>" means "at the interface," and <math>~\mathfrak{f}_{WM},</math> <math>~s_\mathrm{core},</math> and <math>~s_\mathrm{env}</math> are dimensionless functions of order unity (all three functions to be determined) akin to the structural form factors used in our examination of isolated polytropes.
While exploring how the free-energy function varies across parameter space, we choose to hold <math>~M_\mathrm{tot}</math> and <math>~K_c</math> fixed. By dimensional analysis, it is therefore reasonable to normalize all energies, length scales, densities and pressures by, respectively,
|
<math>~E_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{G^{3(\gamma_c-1)} M_\mathrm{tot}^{5\gamma_c-6}}{K_c} \biggr]^{1/(3\gamma_c -4)} \, ,</math> |
|
<math>~R_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \biggl( \frac{K_c}{G} \biggr) M_\mathrm{tot}^{\gamma_c-2} \biggr]^{1/(3\gamma_c -4)} \, ,</math> |
|
<math>~\rho_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\frac{3}{4\pi} \biggl[ \frac{G^3 M_\mathrm{tot}^2}{K_c^3} \biggr]^{1/(3\gamma_c -4)} \, ,</math> |
|
<math>~P_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{G^{3\gamma_c} M_\mathrm{tot}^{2\gamma_c}}{K_c^4} \biggr]^{1/(3\gamma_c -4)} \, .</math> |
As is detailed below — first, here, and via an independent derivation, here — quite generally the expression for the normalized free energy is,
|
<math>~\mathfrak{G}^* \equiv \frac{\mathfrak{G}}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math> - \frac{3}{5} \biggl( \frac{GM_\mathrm{tot}^2}{E_\mathrm{norm}} \biggr) \biggl( \frac{1}{R} \biggr) \cdot \mathfrak{f}_{WM} + \biggl[ \frac{4\pi q^3 s_\mathrm{core} }{3(\gamma_c - 1)} \biggr] \biggl[ \frac{ R^3 P_{ic} }{E_\mathrm{norm}} \biggr] + \biggl[ \frac{4\pi (1-q^3) s_\mathrm{env} }{3(\gamma_e - 1)} \biggr] \biggl[ \frac{ R^3 P_{ie} }{E_\mathrm{norm}} \biggr] </math> |
|
|
<math>~=</math> |
<math> - \frac{3\cdot \mathfrak{f}_{WM}}{5} \chi^{-1} + \biggl[ \frac{4\pi q^3 s_\mathrm{core} }{3(\gamma_c - 1)} \biggr] \biggl[ \frac{ R_\mathrm{norm}^4 P_\mathrm{norm} }{E_\mathrm{norm} R_\mathrm{norm}} \biggr] \biggl[ \biggl( \frac{P_{ic}}{P_\mathrm{norm}} \biggr) \chi^3 \biggr] </math> |
|
|
|
<math> + \biggl[ \frac{4\pi (1-q^3) s_\mathrm{env} }{3(\gamma_e - 1)} \biggr] \biggl[ \frac{ R_\mathrm{norm}^4 P_\mathrm{norm} }{E_\mathrm{norm} R_\mathrm{norm}} \biggr] \biggl[ \biggl( \frac{P_{ie}}{P_\mathrm{norm}} \biggr) \chi^3 \biggr] </math> |
|
|
<math>~=</math> |
<math> - \frac{3\cdot \mathfrak{f}_{WM}}{5} \chi^{-1} + \biggl[ \frac{4\pi q^3 s_\mathrm{core} }{3(\gamma_c - 1)} \biggr] \biggl[ \frac{P_{ic} \chi^{3\gamma_c}}{P_\mathrm{norm}} \biggr]_\mathrm{eq} \chi^{3 -3\gamma_c} + \biggl[ \frac{4\pi (1-q^3) s_\mathrm{env} }{3(\gamma_e - 1)} \biggr] \biggl[ \frac{P_{ie} \chi^{3\gamma_e}}{P_\mathrm{norm}} \biggr]_\mathrm{eq} \chi^{3 -3\gamma_e} </math> |
where we have introduced the parameter, <math>~\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math>. After defining the normalized (and dimensionless) configurarion radius, <math>~\chi \equiv R/R_\mathrm{norm}</math>, we can write the normalized free energy of a bipolytrope in the following compact form:
|
<math>~\mathfrak{G}^*</math> |
<math>~=</math> |
<math>~ -~ 3\mathcal{A} \chi^{-1} - \frac{\mathcal{B}}{(1-\gamma_c)} ~\chi^{3-3\gamma_c} - \frac{\mathcal{C}}{(1-\gamma_e)} ~\chi^{3-3\gamma_e} \, ,</math> |
where,
|
<math>~\mathcal{A}</math> |
<math>~\equiv</math> |
<math>~\frac{1}{5} \cdot \mathfrak{f}_{WM} \, ,</math> |
|
<math>~\mathcal{B}</math> |
<math>~\equiv</math> |
<math> \biggl( \frac{4\pi }{3} \biggr) q^3 s_\mathrm{core} \biggl[ \frac{P_{ic} \chi^{3\gamma_c}}{P_\mathrm{norm}} \biggr]_\mathrm{eq} \, , </math> |
|
<math>~\mathcal{C}</math> |
<math>~\equiv</math> |
<math>\biggl( \frac{4\pi }{3} \biggr) (1-q^3) s_\mathrm{env} \biggl[ \frac{P_{ie} \chi^{3\gamma_e}}{P_\mathrm{norm}} \biggr]_\mathrm{eq} \, .</math> |
As is further detailed below, the second expression for the coefficient, <math>~\mathcal{C}</math>, ensures that the pressure at the "surface" of the core matches the pressure at the "base" of the envelope; but it should only be employed after an equilibrium radius, <math>~\chi_\mathrm{eq}</math>, has been identified by locating an extremum in the free energy.
Simplest Bipolytrope
Familiar Setup
As has been shown in an accompanying presentation, for an <math>~(n_c, n_e) = (0, 0)</math> bipolytrope,
|
<math>~\mathfrak{f}_{WM}</math> |
<math>~\equiv</math> |
<math>~\frac{\nu^2}{q} \cdot f \, ,</math> |
|
<math>~s_\mathrm{core}</math> |
<math>~\equiv</math> |
<math> 1 + \Lambda_\mathrm{eq} \, , </math> |
|
<math>~(1-q^3) s_\mathrm{env}</math> |
<math>~\equiv</math> |
<math> (1-q^3) + \Lambda\biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \, ,</math> |
and where (see, for example, in the context of its original definition, or another, separate derivation),
|
<math>~\Lambda_\mathrm{eq} </math> |
<math>~=~</math> |
<math> \frac{1}{5} \biggl( \frac{\nu}{q} \biggr) \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{1-\gamma_c}
\chi_\mathrm{eq}^{3\gamma_c - 4} </math> |
|
|
<math>~=</math> |
<math>\frac{2}{5(g^2-1)} = \biggl\{ \frac{5}{2}\biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \biggr\}^{-1} \, ,</math> |
and where (see the associated discussion of relevant mass integrals),
<math> \frac{\rho_c}{\bar\rho} = \frac{\nu}{q^3} \, ; ~~~~~ \frac{\rho_e}{\bar\rho} = \frac{1-\nu}{1-q^3} \, ; ~~~~~ \frac{\rho_e}{\rho_c} = \frac{q^3(1-\nu)}{\nu (1-q^3)} ~~\Rightarrow ~~~ \frac{q^3}{\nu} = \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \, . </math>
Cleaner Virial Presentation
In an effort to show the similarity in structure among the several energy terms, we have also found it useful to write their expressions in the following forms:
|
<math>~W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~- \frac{3}{5} \biggl( \frac{GM_\mathrm{tot}^2}{R} \biggr) \frac{\nu^2}{q} \cdot f = - 4\pi P_i R^3 \biggl( \frac{3}{2^2\cdot 5\pi} \biggr) \frac{\nu^2}{q} \cdot \lambda_i f \, ,</math> |
|
<math>~S_\mathrm{core}</math> |
<math>~=</math> |
<math>~2\pi P_{ic} R^3 \biggl[ q^3 + \biggl( \frac{3}{2^2\cdot 5\pi} \biggr) \frac{\nu^2}{q} \cdot \lambda_{ic} \biggr] \, ,</math> |
|
<math>~S_\mathrm{env}</math> |
<math>~=</math> |
<math>~2\pi P_{ie} R^3 \biggl[ (1-q^3) + \biggl( \frac{3}{2^2\cdot 5\pi} \biggr) \frac{\nu^2}{q} \cdot \lambda_{ie} \mathfrak{F} \biggr] \, ,</math> |
where (see an associated discussion or the original derivation),
<math> f\biggl(q, \frac{\rho_e}{\rho_c}\biggr) = 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (q^3 - q^5 ) + \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl( \frac{2}{5} - q^3 + \frac{3}{5}q^5 \biggr) \biggr] \, , </math>
and where,
|
<math>~\lambda_i</math> |
<math>~\equiv</math> |
<math>~\frac{GM_\mathrm{tot}^2}{R^4 P_i} \, ,</math> |
|
<math>~\mathfrak{F} </math> |
<math>~\equiv</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (-2q^2 + 3q^3 - q^5) + \frac{3}{5} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\lambda_{ie}} \biggl( \frac{2^2 \cdot 5\pi}{3} \biggr) \frac{q(1-q^3)}{\nu^2} (s_\mathrm{env} -1) \, .</math> |
|
This also means that the three key terms used as shorthand notation in the above expressions for the three energy terms have the following definitions:
|
Hence, if all the interface pressures are equal — that is, if <math>~P_i = P_{ic} = P_{ie}</math> and, hence also, <math>~\lambda_{i} = \lambda_{ic} = \lambda_{ie}</math> — then the total thermal energy is,
|
<math>~S_\mathrm{tot} = S_\mathrm{core} + S_\mathrm{env}</math> |
<math>~=</math> |
<math> 2\pi P_{i} R^3 \biggl[ 1 + \biggl( \frac{3}{2^2\cdot 5\pi} \biggr) \frac{\nu^2}{q} \cdot \lambda_{i} (1+\mathfrak{F}) \biggr] \, ; </math> |
and the virial is,
|
<math>~2S_\mathrm{tot} + W_\mathrm{grav}</math> |
<math>~=</math> |
<math> 4\pi P_{i} R^3 \biggl[ 1 + \biggl( \frac{3}{2^2\cdot 5\pi} \biggr) \frac{\nu^2}{q} \cdot \lambda_{i} (1+\mathfrak{F} - f ) \biggr] \, . </math> |
The virial should sum to zero in equilibrium, which means,
|
<math>~\frac{1}{\lambda_i} \biggr|_\mathrm{eq}</math> |
<math>~=</math> |
<math> \biggl( \frac{3}{2^2\cdot 5\pi} \biggr) \frac{\nu^2}{q} \cdot (f - 1- \mathfrak{F} ) </math> |
|
<math>\Rightarrow ~~~~ \biggl[ \biggl( \frac{2^2\cdot 5\pi}{3} \biggr) \frac{q}{\nu^2} \biggr] \frac{R_\mathrm{eq}^4 P_i}{GM_\mathrm{tot}^2} </math> |
<math>~=</math> |
<math> f - 1- \mathfrak{F} </math> |
|
<math>\Rightarrow ~~~~ \biggl( \frac{\rho_e}{\rho_c} \biggr)^{-1} \biggl[ \biggl( \frac{2^3\pi}{3} \biggr) \frac{q^6}{\nu^2} \biggr] \frac{R_\mathrm{eq}^4 P_i}{GM_\mathrm{tot}^2} </math> |
<math>~=</math> |
<math> \biggl[ (q^3 - q^5 )+ \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl( \frac{2}{5} - q^3 + \frac{3}{5}q^5 \biggr) \biggr] - \biggl[ (-2q^2 + 3q^3 - q^5) + \biggl( \frac{\rho_e}{\rho_c}\biggr) (-\frac{3}{5} +3q^2 - 3q^3 + \frac{3}{5} q^5) \biggr] </math> |
|
|
<math>~=</math> |
<math> 2q^2(1-q) + \biggl( \frac{\rho_e}{\rho_c}\biggr) (1 -3q^2 + 2q^3 ) </math> |
|
|
<math>~=</math> |
<math> q^2 \biggl( \frac{\rho_e}{\rho_c} \biggr)^{-1} (g^2-1) </math> |
|
<math>\Rightarrow~~~~ \frac{1}{\lambda_i} \biggr|_\mathrm{eq}</math> |
<math>~=</math> |
<math> \frac{2\pi}{3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^2 q^2 (g^2-1) \, . </math> |
Shift to Central Pressure Normalization
Let's rework the definition of <math>~\lambda_i</math> in two ways: (1) Normalize <math>~R_\mathrm{eq}</math> to <math>~R_\mathrm{norm}</math> and normalize the pressure to <math>~P_\mathrm{norm}</math>; (2) shift the referenced pressure from the pressure at the interface <math>~(P_i)</math> to the central pressure <math>~(P_0)</math>, because it is <math>~P_0</math> that is directly related to <math>~K_c</math> and <math>~\rho_c</math>; specifically, <math>P_0 = K_c \rho_c^{\gamma_c}</math>. Appreciating that, in equilibrium,
|
<math>~P_i</math> |
<math>~=</math> |
<math>~P_0 - q^2 \Pi_\mathrm{eq} = K_c \rho_c^{\gamma_c} - \frac{3}{2^3 \pi} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}^4} \biggr) \biggl( \frac{\nu^2}{q^6} \biggr) q^2 \, ,</math> |
the left-hand-side of the last expression, above, can be rewritten as,
|
<math>~\frac{1}{\lambda_i} \biggr|_\mathrm{eq}</math> |
<math>~\equiv</math> |
<math>~\frac{R_\mathrm{eq}^4 P_i}{GM_\mathrm{tot}^2} </math> |
|
|
<math>~=</math> |
<math>~\frac{R_\mathrm{eq}^4}{GM_\mathrm{tot}^2} \biggl[ P_0 - \frac{3}{2^3 \pi} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}^4} \biggr) \biggl( \frac{\nu^2}{q^6} \biggr) q^2\biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{R_\mathrm{eq}^4 P_0}{GM_\mathrm{tot}^2} - \frac{2\pi}{3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^2 q^2 \, .</math> |
Hence, the virial equilibrium condition gives,
|
<math> \frac{R_\mathrm{eq}^4 P_0}{GM_\mathrm{tot}^2} - \frac{2\pi}{3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^2 q^2 </math> |
<math>~=</math> |
<math> \frac{2\pi}{3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^2 q^2 (g^2-1) </math> |
|
<math> \Rightarrow ~~~~ \frac{R_\mathrm{eq}^4 P_0}{GM_\mathrm{tot}^2} </math> |
<math>~=</math> |
<math> \frac{2\pi}{3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{2} q^2 g^2 \, . </math> |
This result precisely matches the result obtained via the detailed force-balanced conditions imposed through hydrostatic equilibrium.
Adopting our new variable normalizations and realizing, in particular, that,
|
<math>~R_\mathrm{norm}^4 P_\mathrm{norm}</math> |
<math>~=</math> |
<math>~GM_\mathrm{tot}^2 \, ,</math> |
the expression alternatively can be rewritten as,
|
<math>~\frac{1}{\lambda_i} \biggr|_\mathrm{eq}</math> |
<math>~\equiv</math> |
<math>~\frac{R_\mathrm{eq}^4 P_i}{GM_\mathrm{tot}^2} = \chi_\mathrm{eq}^4 \biggl( \frac{P_i}{P_\mathrm{norm}} \biggr) </math> |
|
|
<math>~=</math> |
<math> \chi_\mathrm{eq}^4 \biggl\{ \frac{K_c \rho_c^{\gamma_c}}{P_\mathrm{norm}} - \frac{2\pi}{3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3}\biggr]^2 q^2 \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}^4P_\mathrm{norm}} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math> \chi_\mathrm{eq}^4 \biggl\{ \frac{K_c }{P_\mathrm{norm}} \biggl[ \frac{\rho_c}{\bar\rho} \biggl( \frac{3M_\mathrm{tot}}{4\pi R_\mathrm{norm}^3} \biggr) \chi_\mathrm{eq}^{-3} \biggr]^{\gamma_c} - \frac{2\pi}{3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3}\biggr]^2 q^2 \chi_\mathrm{eq}^{-4} \biggr\} </math> |
|
|
<math>~=</math> |
<math> \chi_\mathrm{eq}^{4-3\gamma_c} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c} \frac{K_c }{P_\mathrm{norm}} \biggl( \frac{M_\mathrm{tot}^{\gamma_c}}{R_\mathrm{norm}^{3\gamma_c}} \biggr) - \frac{2\pi}{3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3}\biggr]^2 q^2 </math> |
|
|
<math>~=</math> |
<math> \chi_\mathrm{eq}^{4-3\gamma_c} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c} - \frac{2\pi}{3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3}\biggr]^2 q^2 \, . </math> |
Normalized in this manner, the virial equilibrium (as well as the hydrostatic balance) condition gives,
|
<math> \chi_\mathrm{eq}^{4-3\gamma_c} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c} - \frac{2\pi}{3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3}\biggr]^2 q^2 </math> |
<math>~=</math> |
<math> \frac{2\pi}{3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^2 q^2 (g^2-1) </math> |
|
<math> \Rightarrow ~~~~ \chi_\mathrm{eq}^{4-3\gamma_c} </math> |
<math>~=</math> |
<math> \frac{2\pi}{3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{2-\gamma_c} q^2 g^2 \, . </math> |
Free-Energy Coefficients
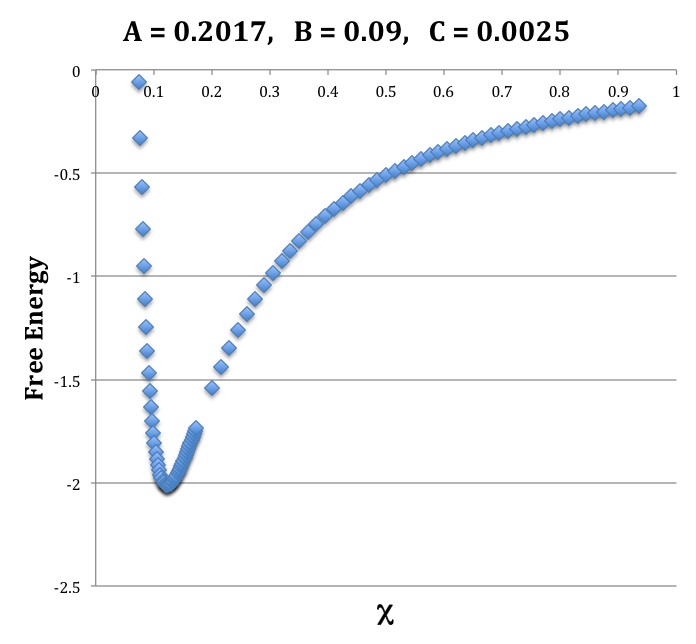
Therefore, for an <math>~(n_c, n_e) = (0, 0)</math> bipolytrope, the coefficients in the normalized free-energy function are,
|
<math>~\mathcal{A}</math> |
<math>~=</math> |
<math> ~\frac{\nu^2}{5q} \cdot f = \frac{1}{5} \biggl( \frac{\nu}{q^3} \biggr)^2 \biggl[ q^5 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) q^3 (1 - q^2 ) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl( 1 - \frac{5}{2} q^3 + \frac{3}{2}q^5 \biggr) \biggr] \, ,</math> |
|
<math>~\mathcal{B}</math> |
<math>~\equiv</math> |
<math> \biggl( \frac{4\pi }{3} \biggr) q^3 s_\mathrm{core} \biggl[ \frac{P_{ic} }{P_\mathrm{norm}} \biggr]_\mathrm{eq} \chi_\mathrm{eq}^{3\gamma_c} =\biggl( \frac{4\pi }{3} \biggr) q^3 s_\mathrm{core} \biggl[ \frac{1}{\lambda_{ic}} \biggr]_\mathrm{eq} \chi_\mathrm{eq}^{3\gamma_c-4} </math> |
|
|
<math>~=</math> |
<math> \biggl( \frac{4\pi }{3} \biggr) q^3 \biggl[ 1 + \biggl( \frac{3}{2^2\cdot 5\pi} \biggr) \frac{\nu^2}{q^4} \cdot \lambda_{ic} \biggr] \biggl[ \frac{1}{\lambda_{ic}} \biggr]_\mathrm{eq} \chi_\mathrm{eq}^{3\gamma_c-4} =\biggl( \frac{4\pi }{3} \biggr) q^3 \biggl[ \frac{1}{\lambda_{ic}} + \biggl( \frac{3}{2^2\cdot 5\pi} \biggr) \frac{\nu^2}{q^4} \biggr] \chi_\mathrm{eq}^{3\gamma_c-4} </math> |
|
|
<math>~=</math> |
<math> \biggl( \frac{4\pi }{3} \biggr) q^3 \biggl\{ \chi_\mathrm{eq}^{4-3\gamma_c} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c} - \frac{2\pi}{3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3}\biggr]^2 q^2 + \biggl( \frac{3}{2^2\cdot 5\pi} \biggr) \frac{\nu^2}{q^4} \biggr\} \chi_\mathrm{eq}^{3\gamma_c-4} </math> |
|
|
<math>~=</math> |
<math> \biggl( \frac{4\pi }{3} \biggr) q^3 \biggl\{ \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c} + \chi_\mathrm{eq}^{3\gamma_c-4} \biggl[\frac{3}{2^2\cdot 5\pi} - \frac{3}{2^3\pi} \biggr]\frac{\nu^2}{q^4} \biggr\} </math> |
|
|
<math>~=</math> |
<math> \biggl\{ \nu \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c-1} - \chi_\mathrm{eq}^{3\gamma_c-4} \biggl( \frac{3^2}{2^3\cdot 5\pi} \biggr) \frac{\nu^2}{q^4} \biggl( \frac{4\pi }{3} \biggr) q^3 \biggr\} = \nu \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c-1} - \chi_\mathrm{eq}^{3\gamma_c-4} \biggl( \frac{3}{10} \biggr) \frac{\nu^2}{q} </math> |
|
<math>~\mathcal{C}</math> |
<math>~\equiv</math> |
<math>\biggl( \frac{4\pi }{3} \biggr) (1-q^3) s_\mathrm{env} \biggl[ \frac{P_{ie} \chi^{3\gamma_e}}{P_\mathrm{norm}} \biggr]_\mathrm{eq} \, .</math> |
Note that, because <math>~P_{ie} = P_{ic}</math> in equilibrium, the ratio of coefficients,
|
<math>~\frac{\mathcal{C}}{\mathcal{B}}</math> |
<math>~=</math> |
<math>~\chi_\mathrm{eq}^{3(\gamma_e - \gamma_c)}\biggl\{\frac{(1-q^3) s_\mathrm{env}}{q^3 s_\mathrm{core}} \biggr\}</math> |
|
<math>\Rightarrow ~~~~ \chi_\mathrm{eq}^{3(\gamma_c - \gamma_e)} \biggl( \frac{\mathcal{C}}{\mathcal{B}} \biggr)</math> |
<math>~=</math> |
<math> \frac{ 20\pi q(1-q^3) \lambda_i^{-1} + 3\nu^2 \mathfrak{F} }{ 20\pi q^4 \lambda_i^{-1} + 3\nu^2 } \, . </math> |
The equilibrium condition is,
<math>\frac{\mathcal{A}}{\mathcal{B} + \mathcal{C}^'} = \chi_\mathrm{eq}^{4-3\gamma_c} \, ,</math>
where,
<math> \mathcal{C}^' \equiv \mathcal{C} \chi_\mathrm{eq}^{3(\gamma_c-\gamma_e)} \, . </math>
More General Derivation of Free-Energy Coefficients B and C
Keep in mind that, generally,
|
<math>GM_\mathrm{tot}^2</math> |
<math>~=</math> |
<math>~R_\mathrm{norm}^4 P_\mathrm{norm} = E_\mathrm{norm} R_\mathrm{norm} \, ;</math> |
|
<math>~\frac{1}{\lambda_i}</math> |
<math>~\equiv</math> |
<math> \frac{R^4 P_i}{GM_\mathrm{tot}^2} = \biggl( \frac{P_i}{P_\mathrm{norm}} \biggr) \chi^4 </math> … and, note that … <math> \frac{1}{\Lambda} = \biggl( \frac{3\cdot 5}{2^2\pi} \biggr) \frac{1}{\lambda_i} \cdot \frac{1}{q^2 \sigma^2} \, ; </math> |
|
<math>~\frac{\Pi}{P_\mathrm{norm}}</math> |
<math>~=</math> |
<math> \frac{3}{2^3\pi} \biggl( \frac{GM_\mathrm{tot}^2}{P_\mathrm{norm} R^4} \biggr) \frac{\nu^2}{q^6} =\biggl( \frac{2\pi}{3} \biggr) \sigma^2 \chi^{-4} \, ; </math> |
|
<math>~\frac{K_c \rho_c^{\gamma_c} }{P_\mathrm{norm}}</math> |
<math>~=</math> |
<math> \frac{K_c}{P_\mathrm{norm}} \biggl( \frac{\rho_c}{\bar\rho} \biggr)^{\gamma_c} \biggl[ \frac{3M_\mathrm{tot}}{4\pi R^3} \biggr]^{\gamma_c} = \frac{K_c M_\mathrm{tot}^{\gamma_c} }{R_\mathrm{norm}^{3\gamma_c} P_\mathrm{norm}} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c} \chi^{-3\gamma_c} = \sigma^{\gamma_c} \chi^{-3\gamma_c} \, , </math> |
where we have introduced the notation,
<math> \sigma \equiv \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \, . </math>
So, the free-energy coefficient,
|
<math>~\mathcal{B}</math> |
<math>~=</math> |
<math> \biggl( \frac{4\pi }{3} \biggr) q^3 s_\mathrm{core} \biggl[ \frac{P_{ic} }{P_\mathrm{norm}} \biggr]_\mathrm{eq} \chi_\mathrm{eq}^{3\gamma_c} =\biggl( \frac{4\pi }{3} \biggr) q^3 s_\mathrm{core} \biggl[ \frac{1}{\lambda_{ic}} \biggr]_\mathrm{eq} \chi_\mathrm{eq}^{3\gamma_c-4} </math> |
|
|
<math>~=</math> |
<math> \biggl( \frac{4\pi }{3} \biggr) q^3 \biggl[ 1 + \biggl( \frac{3}{2^2\cdot 5\pi} \biggr) \frac{\nu^2}{q^4} \cdot \lambda_{ic} \biggr]_\mathrm{eq} \biggl[ \frac{1}{\lambda_{ic}} \biggr]_\mathrm{eq} \chi_\mathrm{eq}^{3\gamma_c-4} =\biggl( \frac{4\pi }{3} \biggr) q^3 \biggl[ \frac{1}{\lambda_{ic}} + \biggl( \frac{3}{2^2\cdot 5\pi} \biggr) \frac{\nu^2}{q^4} \biggr]_\mathrm{eq} \chi_\mathrm{eq}^{3\gamma_c-4} </math> |
|
|
<math>~=</math> |
<math> \biggl( \frac{4\pi }{3} \biggr) q^3 \biggl[ \chi_\mathrm{eq}^4 \biggl( \frac{P_{ic}}{P_\mathrm{norm}} \biggr)_\mathrm{eq} + \biggl( \frac{4\pi}{3\cdot 5} \biggr) q^2 \sigma^2 \biggr] \chi_\mathrm{eq}^{3\gamma_c-4} \, .
</math> |
And the free-energy coefficient,
|
<math>~\mathcal{C}</math> |
<math>~\equiv</math> |
<math> \biggl( \frac{4\pi }{3} \biggr) (1-q^3) s_\mathrm{env} \biggl[ \frac{P_{ie} \chi^{3\gamma_e}}{P_\mathrm{norm}} \biggr]_\mathrm{eq} = \biggl( \frac{4\pi }{3} \biggr) (1-q^3) s_\mathrm{env} \biggl[ \frac{1 }{\lambda_{ie}} \biggr]_\mathrm{eq} \chi_\mathrm{eq}^{3\gamma_e-4} </math> |
|
|
<math>~=</math> |
<math> \biggl( \frac{4\pi }{3} \biggr) (1-q^3) \biggl\{ \frac{1 }{\lambda_{ie}} + \biggl( \frac{3}{2^2\cdot 5\pi} \biggr) \frac{\nu^2}{q(1-q^3)} \cdot \mathfrak{F} \biggr\}_\mathrm{eq} \chi_\mathrm{eq}^{3\gamma_e-4} </math> |
|
|
<math>~=</math> |
<math> \biggl( \frac{4\pi }{3} \biggr) \biggl\{ (1-q^3) \chi_\mathrm{eq}^4 \biggl( \frac{P_{ie}}{P_\mathrm{norm}} \biggr)_\mathrm{eq}+ \biggl( \frac{2\pi}{3} \biggr) \sigma^2 \biggl[ \frac{2}{5} q^5 \mathfrak{F} \biggr] \biggr\}_\mathrm{eq} \chi_\mathrm{eq}^{3\gamma_e-4} \, . </math> |
|
OLD DERIVATION <math>P_{ic} = K_c \rho_c^{\gamma_c}</math> |
NEW DERIVATION <math>P_{ic} = P_0 - q^2\Pi = K_c \rho_c^{\gamma_c} - q^2\Pi</math> |
||||||||||||||||||
|
… therefore … |
|||||||||||||||||||
|
|
||||||||||||||||||
|
… and, enforcing in equilibrium <math>~P_{ie} = P_{ic}</math> … |
|||||||||||||||||||
|
|
||||||||||||||||||
|
… and, also … |
|||||||||||||||||||
|
|
||||||||||||||||||
Extrema
Extrema in the free energy occur when,
|
<math>~\mathcal{A}</math> |
<math>~=</math> |
<math>~\mathcal{B} \chi_\mathrm{eq}^{4-3\gamma_c} + \mathcal{C} \chi_\mathrm{eq}^{4-3\gamma_e} \, .</math> |
Also, as stated above, because <math>~P_{ie} = P_{ic}</math> in equilibrium, the ratio of coefficients,
|
<math>~\frac{\mathcal{C}}{\mathcal{B}}</math> |
<math>~=</math> |
<math>~\chi_\mathrm{eq}^{3(\gamma_e - \gamma_c)}\biggl[ \frac{(1-q^3) s_\mathrm{env}}{q^3 s_\mathrm{core}} \biggr] \, .</math> |
When put together, these two relations imply,
|
<math>~\mathcal{A}</math> |
<math>~=</math> |
<math>~\mathcal{B} \chi_\mathrm{eq}^{4-3\gamma_c} + \chi_\mathrm{eq}^{4-3\gamma_c} \mathcal{B} \biggl[ \frac{(1-q^3) s_\mathrm{env}}{q^3 s_\mathrm{core}} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\mathcal{B} \chi_\mathrm{eq}^{4-3\gamma_c} \biggl[ 1+ \frac{(1-q^3) s_\mathrm{env}}{q^3 s_\mathrm{core}} \biggr] \, .</math> |
But the definition of <math>~\mathcal{B}</math> gives,
|
<math>~\mathcal{B} \chi_\mathrm{eq}^{4-3\gamma_c}</math> |
<math>~=</math> |
<math> \biggl( \frac{4\pi }{3} \biggr) q^3 s_\mathrm{core} \biggl[ \frac{1}{\lambda_{ic}} \biggr]_\mathrm{eq} \, . </math> |
Hence, extrema occur when,
|
<math>~\mathcal{A}</math> |
<math>~=</math> |
<math>~\biggl( \frac{4\pi }{3} \biggr) q^3 s_\mathrm{core} \biggl[ \frac{1}{\lambda_{ic}} \biggr]_\mathrm{eq} \biggl[ 1+ \frac{(1-q^3) s_\mathrm{env}}{q^3 s_\mathrm{core}} \biggr] </math> |
|
<math>\Rightarrow ~~~~ \biggl( \frac{3}{2^2 \cdot 5\pi } \biggr) \frac{\nu^2}{q} \cdot f</math> |
<math>~=</math> |
<math> \biggl[ \frac{1}{\lambda_{ic}} \biggr]_\mathrm{eq} \biggl[ q^3 s_\mathrm{core} + (1-q^3) s_\mathrm{env} \biggr] </math> |
|
|
<math>~=</math> |
<math> \frac{q^3}{[\lambda_i]_\mathrm{eq}} + \biggl( \frac{3}{2^2\cdot 5\pi} \biggr) \frac{\nu^2}{q} + \frac{(1-q^3)}{[\lambda_i]_\mathrm{eq}} + \biggl( \frac{3}{2^2\cdot 5\pi} \biggr) \frac{\nu^2}{q} \cdot \mathfrak{F} </math> |
|
<math>\Rightarrow ~~~~\biggl[ \frac{1}{\lambda_{ic}} \biggr]_\mathrm{eq} </math> |
<math>~=</math> |
<math> \biggl( \frac{3}{2^2 \cdot 5\pi } \biggr) \frac{\nu^2}{q} \cdot (f - 1 - \mathfrak{F}) </math> |
|
|
<math>~=</math> |
<math> \biggl( \frac{2\pi}{3 } \biggr) \sigma^{2} q^2 (g^2 - 1 ) \, . </math> |
In what follows, keep in mind that,
|
<math>~\chi_\mathrm{eq}^{4-3\gamma_c}</math> |
<math>~=</math> |
<math> \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^{4-3\gamma_c} = R_\mathrm{eq}^{4-3\gamma_c} \biggl( \frac{K_c}{G} \biggr) M_\mathrm{tot}^{\gamma_c-2} \, ; </math> |
|
<math>~K_c \rho_c^{\gamma_c}</math> |
<math>~=</math> |
<math> K_c \biggl( \frac{\rho_c}{\bar\rho} \biggr)^{\gamma_c} \biggl[ \frac{3M_\mathrm{tot}}{4\pi R^3} \biggr]^{\gamma_c} = K_c \sigma^{\gamma_c} M_\mathrm{tot}^{\gamma_c} R^{-3\gamma_c} \, ; </math> |
|
<math>~\Pi</math> |
<math>~=</math> |
<math> \frac{3}{2^3 \pi} \biggl( \frac{GM_\mathrm{tot}^2}{R^4} \biggr) \frac{\nu^2}{q^6} = \frac{2\pi}{3} \biggl( \frac{GM_\mathrm{tot}^2}{R^4} \biggr) \sigma^2 \, . </math> |
|
OLD DERIVATION <math>P_{i} = K_c \rho_c^{\gamma_c}</math> <math>\Rightarrow ~~~~ K_c = P_{i} \sigma^{-\gamma_c} M_\mathrm{tot}^{-\gamma_c} R^{+3\gamma_c} </math> |
NEW DERIVATION <math>P_0 = K_c \rho_c^{\gamma_c} </math> <math>\Rightarrow ~~~~ K_c = P_0 \sigma^{-\gamma_c} M_\mathrm{tot}^{-\gamma_c} R^{+3\gamma_c} </math> |
|||||||||||||||||||||
|
… hence, as derived in the above table … |
||||||||||||||||||||||
|
|
|||||||||||||||||||||
|
… which, when combined with the condition that identifies extrema, gives … |
||||||||||||||||||||||
|
|
|||||||||||||||||||||
|
These are consistent results because they result in the detailed force-balance relation, <math>P_0 - P_i = q^2 \Pi_\mathrm{eq} \, .</math> |
||||||||||||||||||||||
Examples
|
Identification of Local Extrema in Free Energy |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
<math>~\nu</math> |
<math>~q</math> |
<math>~ \frac{\rho_e}{\rho_c} </math> |
<math>~f\biggl(q, \frac{\rho_e}{\rho_c} \biggr)</math> |
<math>~g^2\biggl(q, \frac{\rho_e}{\rho_c} \biggr)</math> |
<math>~\Lambda_\mathrm{eq}</math> |
<math>~\chi_\mathrm{eq}</math> |
<math>~\mathcal{A}</math> |
<math>~\mathcal{B}</math> |
<math>~\mathcal{C}</math> |
MIN/MAX |
|
<math>~0.2</math> |
<math>~9^{-1/3} = 0.48075</math> |
<math>~0.5</math> |
<math>~12.5644</math> |
<math>~2.091312</math> |
<math>~0.366531</math> |
<math>~0.037453</math> |
<math>~0.2090801</math> |
<math>~0.2308269</math> |
<math>~2.06252 \times 10^{-4}</math> |
MIN |
|
<math>~0.4</math> |
<math>~4^{-1/3} = 0.62996</math> |
<math>~0.5</math> |
<math>~4.21974</math> |
<math>~1.56498</math> |
<math>~0.707989</math> |
<math>~0.0220475</math> |
<math>~0.2143496</math> |
<math>~0.5635746</math> |
<math>~4.4626 \times 10^{-5}</math> |
MIN |
|
<math>~0.473473</math> |
<math>~0.681838</math> |
<math>~0.516107</math> |
|
|
<math>~0.462927</math> |
<math>~0.08255</math> |
" |
" |
" |
MAX |
|
<math>~0.5</math> |
<math>~3^{-1/3} = 0.693361</math> |
<math>~0.5</math> |
<math>~2.985115</math> |
<math>~1.42334</math> |
<math>~0.9448663</math> |
<math>~0.0152116</math> |
<math>~0.2152641</math> |
<math>~0.791882</math> |
<math>~1.5464 \times 10^{-5}</math> |
MIN |
|
<math>~0.559839</math> |
<math>~0.729581</math> |
<math>~0.499188</math> |
|
|
<math>~0.75089</math> |
<math>~0.032196</math> |
" |
" |
" |
MAX |
|
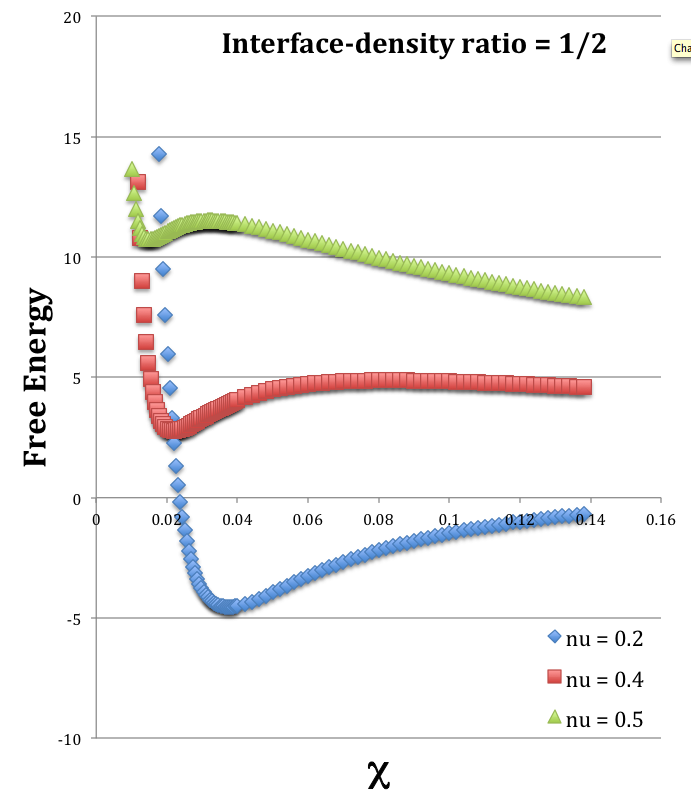
Free Energy Extrema when: <math>~~~~~\frac{\rho_e}{\rho_c} = \frac{1}{2} ~~~~\Rightarrow~~~~ q^3 = \frac{\nu}{2-\nu}</math> |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
<math>~\nu</math> |
<math>~q</math> |
<math>~ \frac{\rho_e}{\rho_c} </math> |
<math>~f\biggl(q, \frac{\rho_e}{\rho_c} \biggr)</math> |
<math>~g^2\biggl(q, \frac{\rho_e}{\rho_c} \biggr)</math> |
<math>~\frac{1}{\lambda_{i}}\biggr|_\mathrm{eq}</math> |
<math>~\chi_\mathrm{eq}</math> |
<math>~\mathcal{A}</math> |
<math>~\mathcal{B}_\mathrm{NEW}</math> |
<math>~\mathcal{C}_\mathrm{NEW}</math> |
<math>~G^*</math> |
Stability |
MIN/MAX |
|
<math>~0.5</math> |
<math>~\biggl( \frac{1}{3} \biggr)^{1/3}</math> |
<math>~0.5</math> |
<math>~2.985115</math> |
<math>~1.423340</math> |
<math>~0.05466039</math> |
<math>~0.3152983</math> |
<math>~0.21526406</math> |
<math>~0.23552725</math> |
<math>~6.643899 \times 10^{-3}</math> |
<math>~+ 0.5176146</math> |
<math>~+0.429245</math> |
MIN |
|
… |
… |
… |
|
|
|
<math>~0.6674</math> |
" |
" |
" |
<math>~+0.55572115</math> |
|
MAX |
|
<math>~0.6</math> |
<math>~\biggl( \frac{3}{7} \biggr)^{1/3}</math> |
<math>~0.5</math> |
<math>~2.2507129</math> |
<math>~1.31282895</math> |
<math>~0.04160318</math> |
<math>~0.3411545</math> |
<math>~0.21493717</math> |
<math>~0.26165939</math> |
<math>~5.208750 \times 10^{-3}</math> |
<math>~+ 0.73532249</math> |
<math>~+0.0935217</math> |
MIN |
|
… |
… |
… |
|
|
|
<math>~0.431745</math> |
" |
" |
" |
<math>~+0.7367797</math> |
|
MAX |
|
<math>~0.7</math> |
<math>~\biggl( \frac{7}{13} \biggr)^{1/3}</math> |
<math>~0.5</math> |
<math>~1.7707809</math> |
<math>~1.2209446</math> |
<math>~0.029500</math> |
<math>~0.3589388</math> |
<math>~0.21330744</math> |
<math>~0.28172532</math> |
<math>~3.389793 \times 10^{-3}</math> |
<math>~+ 0.8953395</math> |
<math>~- 0.0767108</math> |
MAX |
|
… |
… |
… |
|
|
|
<math>~0.270615</math> |
" |
" |
" |
<math>~+0.89227216</math> |
|
MIN |
|
System should be stable (with free energy minimum) if: <math>~~~~~\frac{( \gamma_e - \frac{4}{3})}{(\gamma_e - \gamma_c)} f - \biggl[1 + \frac{5}{2} (g^2-1) \biggr] ~>~ 0</math> |
||||||||||||
Solution Strategy
For a given set of free-energy coefficients, <math>~\mathcal{A}, \mathcal{B},</math> and <math>~\mathcal{C}</math>, along with a choice of the two adiabatic exponents <math>~(\gamma_c, \gamma_e)</math>, here's how to determine all of the physical parameters that are detailed in the above example table.
- Step 1: Guess a value of <math>~0 < q < 1</math>.
- Step 2: Given the pair of parameter values, <math>~(\mathcal{A}, q)</math>, determine the interface-density ratio, <math>~\rho_e/\rho_c</math>, by finding the appropriate root of the expression that defines the function, <math>~\mathcal{A}(q, \rho_e/\rho_c)</math>. This can be straightforwardly accomplished because, as demonstrated below, the relevant expression can be written as a quadratic function of <math>~(\rho_e/\rho_c)</math>.
- Step 3: Given the pair of parameter values, <math>~(q, \rho_e/\rho_c)</math>, determine the value of the core-to-total mass ratio, <math>~\nu</math>, from the expression that was obtained from an integration over the mass, namely,
|
<math>~\frac{1}{\nu}</math> |
<math>~=</math> |
<math>~1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl( \frac{1}{q^3} - 1 \biggr) \, .</math> |
- Step 4: Given the value of <math>~\mathcal{B}</math> along with the pair of parameter values, <math>~(q, \nu)</math>, the above expression that defines <math>~\mathcal{B}</math> can be solved to give the relevant value of the dimensionless parameter, <math>~\Lambda_\mathrm{eq}.</math>
- Step 5: The value of <math>~\mathcal{C}^'</math> — the coefficient that appears on the right-hand-side of the above expression that defines <math>~\mathcal{C}</math> — can be determined, given the values of parameter triplet, <math>~(q, \nu, \Lambda_\mathrm{eq})</math>.
- Step 6: Given the value of <math>~\mathcal{C}</math> and the just-determined value of the coefficient <math>~\mathcal{C}^'</math>, the normalized equilibrium radius, <math>~\chi_\mathrm{eq},</math> that corresponds to the value of <math>~q</math> that was guessed in Step #1 can be determined from the above definition of <math>~\mathcal{C}</math>, specifically,
|
<math>~\chi_\mathrm{eq}\biggr|_\mathrm{guess} </math> |
<math>~=</math> |
<math>~\biggl( \frac{\mathcal{C}}{\mathcal{C}^'} \biggr)^{1/(3\gamma_e - 3\gamma_c)} \, .</math> |
- Step 7: But, independent of this guessed value of <math>~\chi_\mathrm{eq},</math> the condition for virial equilibrium — which identifies extrema in the free-energy function — gives the following expression for the normalized equilibrium radius:
|
<math>~\chi_\mathrm{eq}\biggr|_\mathrm{virial} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{\mathcal{A}}{\mathcal{B} + \mathcal{C}^'} \biggr]^{1/(4 - 3\gamma_c)} \, .</math> |
- Step 8: If <math>~\chi_\mathrm{eq}|_\mathrm{guess} \ne \chi_\mathrm{eq}|_\mathrm{virial}</math>, return to Step #1 and guess a different value of <math>~q</math>. Repeat Steps #1 through #7 until the two independently derived values of the normalized radius match, to a desired level of precision.
- Keep in mind: (A) A graphical representation of the free-energy function, <math>~\mathfrak{G}(\chi)</math>, can also be used to identify the "correct" value of <math>~\chi_\mathrm{eq}</math> and, ultimately, the above-described iteration loop should converge on this value. (B) The free-energy function may exhibit more than one (or, actually, no) extrema, in which case more than one (or no) value of <math>~q</math> should lead to convergence of the above-described iteration loop.
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Detailed Derivations
Dividing the free-energy expression through by <math>~E_\mathrm{norm}</math> generates,
|
<math>~\mathfrak{G}^* \equiv \frac{\mathfrak{G}}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math> - \frac{3}{5} \biggl( \frac{GM_\mathrm{tot}^2}{E_\mathrm{norm}} \biggr) \biggl( \frac{1}{R} \biggr) \cdot \mathfrak{f}_{WM} + \biggl[ \frac{\nu s_\mathrm{core} }{(\gamma_c - 1)} \biggr] \biggl[ \frac{M_\mathrm{tot} K_c \rho_{ic}^{\gamma_c-1} }{E_\mathrm{norm}} \biggr] </math> |
|
|
|
<math> ~+ \biggl[ \frac{(1-\nu) s_\mathrm{env} }{(\gamma_e - 1)} \biggr] \biggl[ \frac{M_\mathrm{tot} K_e \rho_{ie}^{\gamma_e-1} }{E_\mathrm{norm}} \biggr] </math> |
|
|
<math>~=</math> |
<math> - \frac{3\cdot \mathfrak{f}_{WM}}{5} \biggl[ \frac{K_c G^{(3\gamma_c -4)}M_\mathrm{tot}^{2(3\gamma_c -4)}}{G^{3\gamma_c-3} M_\mathrm{tot}^{5\gamma_c-6}} \biggr]^{1/(3\gamma_c -4)} \biggl( \frac{1}{R} \biggr) </math> |
|
|
|
<math> + \biggl[ \frac{\nu s_\mathrm{core} }{(\gamma_c - 1)} \biggr] \biggl[ \frac{K_c M_\mathrm{tot}^{3\gamma_c -4} K_c^{3\gamma_c -4} }{G^{3\gamma_c-3} M_\mathrm{tot}^{5\gamma_c-6}} \biggr]^{1/(3\gamma_c -4)} \biggl( \frac{\rho_{ic}}{\bar\rho} \biggr)^{\gamma_c-1} \biggl[ \frac{3M_\mathrm{tot}}{4\pi R^3} \biggr]^{\gamma_c-1} </math> |
|
|
|
<math> ~+ \biggl[ \frac{(1-\nu) s_\mathrm{env} }{(\gamma_e - 1)} \biggr] \biggl[ \frac{K_c M_\mathrm{tot}^{3\gamma_c -4} K_e^{3\gamma_c -4} }{G^{3\gamma_c-3} M_\mathrm{tot}^{5\gamma_c-6}} \biggr]^{1/(3\gamma_c -4)} \biggl( \frac{\rho_{ie}}{\bar\rho} \biggr)^{\gamma_e-1} \biggl[ \frac{3M_\mathrm{tot}}{4\pi R^3} \biggr]^{\gamma_e-1} </math> |
|
|
<math>~=</math> |
<math> - \frac{3\cdot \mathfrak{f}_{WM}}{5} \biggl( \frac{R_\mathrm{norm}}{R} \biggr) </math> |
|
|
|
<math> + \biggl[ \frac{\nu s_\mathrm{core} }{(\gamma_c - 1)} \biggr] \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr)^{\gamma_c-1} \biggl[ \frac{ K_c^{3\gamma_c -3} }{G^{3\gamma_c-3} M_\mathrm{tot}^{2\gamma_c-2}} \biggr]^{1/(3\gamma_c -4)} \biggl[ \frac{R_\mathrm{norm}}{R} \biggr]^{3(\gamma_c-1)} \biggl[ \biggl( \frac{K_c}{G} \biggr) M_\mathrm{tot}^{\gamma_c-2} \biggr]^{-3(\gamma_c-1)/(3\gamma_c -4)} \biggl( \frac{\rho_{ic}}{\bar\rho} \biggr)^{\gamma_c-1} </math> |
|
|
|
<math> ~+ \biggl[ \frac{(1-\nu) s_\mathrm{env} }{(\gamma_e - 1)} \biggr] \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr)^{\gamma_e-1} \biggl[ \frac{K_c^{3\gamma_c - 3} (K_e/K_c)^{3\gamma_c -4} }{G^{3\gamma_c-3} M_\mathrm{tot}^{2\gamma_c-2}} \biggr]^{1/(3\gamma_c -4)} \biggl[ \frac{R_\mathrm{norm}}{R} \biggr]^{3(\gamma_e-1)} \biggl[ \biggl( \frac{K_c}{G} \biggr) M_\mathrm{tot}^{\gamma_c-2} \biggr]^{-3(\gamma_e-1)/(3\gamma_c -4)} \biggl( \frac{\rho_{ie}}{\bar\rho} \biggr)^{\gamma_e-1} </math> |
|
|
<math>~=</math> |
<math> - \frac{3\cdot \mathfrak{f}_{WM}}{5} \biggl( \frac{R_\mathrm{norm}}{R} \biggr) </math> |
|
|
|
<math> + \biggl[ \frac{\nu s_\mathrm{core} }{(\gamma_c - 1)} \biggr] \biggl( \frac{3}{4\pi} \biggr)^{\gamma_c-1} \biggl[ M_\mathrm{tot}^{3\gamma_c-4} \biggr]^{(\gamma_c-1)/(3\gamma_c-4)} \biggl[ M_\mathrm{tot}^{-2} \biggr]^{(\gamma_c-1)/(3\gamma_c -4)} \biggl[ M_\mathrm{tot}^{-3\gamma_c+6} \biggr]^{(\gamma_c-1)/(3\gamma_c -4)} \biggl[ \frac{R_\mathrm{norm}}{R} \biggr]^{3(\gamma_c-1)} \biggl( \frac{\rho_{ic}}{\bar\rho} \biggr)^{\gamma_c-1} </math> |
|
|
|
<math> ~+ \biggl[ \frac{(1-\nu) s_\mathrm{env} }{(\gamma_e - 1)} \biggr] \biggl( \frac{3}{4\pi} \biggr)^{\gamma_e-1} \biggl( \frac{K_e}{K_c} \biggr) \biggl[ M_\mathrm{tot}^{2(\gamma_e-1)-2(\gamma_c-1)}\biggr]^{1/(3\gamma_c-4)} \biggl[ \frac{R_\mathrm{norm}}{R} \biggr]^{3(\gamma_e-1)} \biggl[ \biggl( \frac{K_c}{G} \biggr)^{(\gamma_c-1)-(\gamma_e-1)} \biggr]^{3/(3\gamma_c -4)} \biggl( \frac{\rho_{ie}}{\bar\rho} \biggr)^{\gamma_e-1} </math> |
|
|
<math>~=</math> |
<math> - \frac{3\cdot \mathfrak{f}_{WM}}{5} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-1} + \frac{\nu s_\mathrm{core} }{(\gamma_c - 1)} \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c-1} \biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{-3(\gamma_c-1)} </math> |
|
|
|
<math> ~+ \frac{(1-\nu) s_\mathrm{env} }{(\gamma_e - 1)} \biggl( \frac{K_e}{K_c} \biggr) \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2} \biggr]^{(\gamma_c-\gamma_e)/(3\gamma_c -4)} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ie}}{\bar\rho} \biggr]^{\gamma_e-1} \biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{-3(\gamma_e-1)} \, . </math> |
We also want to ensure that envelope pressure matches the core pressure at the interface. This means,
|
<math>~K_e \rho_{ie}^{\gamma_e}</math> |
<math>~=</math> |
<math>~K_c \rho_{ic}^{\gamma_c}</math> |
|
<math>\Rightarrow ~~~~\frac{K_e}{K_c} </math> |
<math>~=</math> |
<math>~\rho_{ic}^{\gamma_c} \rho_{ie}^{-\gamma_e} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{\rho_{ic}}{\rho_\mathrm{norm}} \biggr]^{\gamma_c} \biggl[ \frac{\rho_{ie}}{\rho_\mathrm{norm}} \biggr]^{-\gamma_e} \rho_\mathrm{norm}^{\gamma_c - \gamma_e}</math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{\rho_{ic}}{\rho_\mathrm{norm}} \biggr]^{\gamma_c} \biggl[ \frac{\rho_{ie}}{\rho_\mathrm{norm}} \biggr]^{-\gamma_e} \biggl\{ \frac{3}{4\pi} \biggl[ \frac{G^3 M_\mathrm{tot}^2}{K_c^3} \biggr]^{1/(3\gamma_c -4)} \biggr\}^{\gamma_c - \gamma_e}</math> |
|
<math>\Rightarrow ~~~~\frac{K_e}{K_c} \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2} \biggr]^{(\gamma_c - \gamma_e)/(3\gamma_c -4)} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ie}}{\bar\rho} \biggr]^{\gamma_e-1}</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\rho_\mathrm{norm}} \biggr]^{\gamma_c} \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ie}}{\rho_\mathrm{norm}} \biggr]^{-\gamma_e} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ie}}{\bar\rho} \biggr]^{\gamma_e-1} </math> |
|
|
<math>~=</math> |
<math> \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c-1} \biggl( \frac{\rho_{ic}}{\rho_{ie}} \biggr) \biggl( \frac{\rho_\mathrm{norm}}{ \bar\rho } \biggr)^{\gamma_e - \gamma_c} </math> |
|
|
<math>~=</math> |
<math> \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c-1} \biggl( \frac{\rho_{ic}}{\rho_{ie}} \biggr) \biggl( \frac{ R}{R_\mathrm{norm}} \biggr)^{3(\gamma_e - \gamma_c)} </math> |
Hence, we can write the normalized (and dimensionless) free energy as,
|
<math>~\mathfrak{G}^*</math> |
<math>~=</math> |
<math> - \frac{3\cdot \mathfrak{f}_{WM}}{5} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-1} + \biggl\{ \frac{\nu s_\mathrm{core} }{(\gamma_c - 1)} + \frac{(1-\nu) s_\mathrm{env} }{(\gamma_e - 1)} \biggl( \frac{ \rho_{ic} }{ \rho_{ie} } \biggr)\biggr\} \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c-1} \biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{-3(\gamma_c-1)} \, . </math> |
Keep in mind that, if the envelope and core both have uniform (but different) densities, then <math>~\rho_{ic} = \rho_c</math>, <math>~\rho_{ie} = \rho_e</math>, and
<math> \frac{\rho_c}{\bar\rho} = \frac{\nu}{q^3} \, ; ~~~~~ \frac{\rho_e}{\bar\rho} = \frac{1-\nu}{1-q^3} \, ; ~~~~~ \frac{\rho_e}{\rho_c} = \frac{q^3(1-\nu)}{\nu (1-q^3)} \, . </math>
Free Energy and Its Derivatives
Now, the free energy can be written as,
|
<math>~\mathfrak{G}</math> |
<math>~=~</math> |
<math>~U_\mathrm{tot} + W</math> |
|
|
<math>~=~</math> |
<math>~\biggl[ \frac{2}{3(\gamma_c - 1)} \biggr] S_\mathrm{core} + \biggl[ \frac{2}{3(\gamma_e - 1)} \biggr] S_\mathrm{env} + W</math> |
|
|
<math>~=~</math> |
<math>~\biggl[ \frac{2}{3(\gamma_c - 1)} \biggr] C_\mathrm{core} R^{3-3\gamma_c} + \biggl[ \frac{2}{3(\gamma_e - 1)} \biggr] C_\mathrm{env} R^{3-3\gamma_e} - A R^{-1} \, .</math> |
The first derivative of the free energy with respect to radius is, then,
|
<math>~\frac{d\mathfrak{G}}{dR}</math> |
<math>~=~</math> |
<math>~ -2 C_\mathrm{core} R^{2-3\gamma_c} -2 C_\mathrm{env} R^{2-3\gamma_e} + A R^{-2} \, .</math> |
And the second derivative is,
|
<math>~\frac{d^2\mathfrak{G}}{dR^2}</math> |
<math>~=~</math> |
<math>~ -2 (2-3\gamma_c) C_\mathrm{core} R^{1-3\gamma_c} -2 (2-3\gamma_e) C_\mathrm{env} R^{1-3\gamma_e} - 2A R^{-3} \, .</math> |
|
|
<math>~=~</math> |
<math>~ \frac{2}{R^2} \biggl[(3\gamma_c-2) C_\mathrm{core} R^{3-3\gamma_c} + (3\gamma_e-2) C_\mathrm{env} R^{3-3\gamma_e} - A R^{-1} \biggr]</math> |
|
|
<math>~=~</math> |
<math>~ \frac{2}{R^2} \biggl[(3\gamma_c-2) S_\mathrm{core} + (3\gamma_e-2) S_\mathrm{env} +W \biggr] \, .</math> |
Equilibrium
The radius, <math>~R_\mathrm{eq}</math>, of the equilibrium configuration(s) is determined by setting the first derivative of the free energy to zero. Hence,
|
<math>~0 </math> |
<math>~=~</math> |
<math>~ 2 C_\mathrm{core} R_\mathrm{eq}^{2-3\gamma_c} + 2 C_\mathrm{env} R_\mathrm{eq}^{2-3\gamma_e} - A R_\mathrm{eq}^{-2} </math> |
|
|
<math>~=~</math> |
<math>~ R_\mathrm{eq}^{-1} \biggl[ 2 C_\mathrm{core} R_\mathrm{eq}^{3-3\gamma_c} + 2 C_\mathrm{env} R_\mathrm{eq}^{3-3\gamma_e} - A R_\mathrm{eq}^{-1} \biggr]</math> |
|
|
<math>~=~</math> |
<math>~ R_\mathrm{eq}^{-1} \biggl[ 2 S_\mathrm{core} + 2 S_\mathrm{env} +W \biggr]</math> |
|
<math>\Rightarrow ~~~~ 2 S_\mathrm{tot} + W </math> |
<math>~=~</math> |
<math>~0 \, .</math> |
This is the familiar statement of virial equilibrium. From it we should always be able to derive the radius of equilibrium configurations.
Stability
To assess the relative stability of an equilibrium configuration, we need to determine the sign of the second derivative of the free energy, evaluated at the equilibrium radius. If the sign of the second derivative is positive, the system is dynamically stable; if the sign is negative, he system is dynamically unstable. Using the above statement of virial equilibrium, that is, setting,
|
<math>~2 S_\mathrm{tot} + W</math> |
<math>~=~</math> |
<math>~0 \, ,</math> |
|
<math>\Rightarrow ~~~~ S_\mathrm{env} </math> |
<math>~=~</math> |
<math>~- S_\mathrm{core} - \frac{W}{2} \, ,</math> |
we obtain,
|
<math>~\frac{d^2\mathfrak{G}}{dR^2}\biggr|_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ \frac{2}{R_\mathrm{eq}^2} \biggl[ (3\gamma_c-2) S_\mathrm{core} +W - (3\gamma_e-2)\biggl( S_\mathrm{core} + \frac{W}{2}\biggr) \biggr]_\mathrm{eq} </math> |
|
|
<math>~=~</math> |
<math>~ \frac{2}{R_\mathrm{eq}^2} \biggl[ 3(\gamma_c-\gamma_e) S_\mathrm{core} + \biggl(2 - \frac{3}{2}\gamma_e\biggr)W \biggr]_\mathrm{eq} </math> |
|
|
<math>~=~</math> |
<math>~ \frac{6}{R_\mathrm{eq}^2} \biggl[ (\gamma_c-\gamma_e) S_\mathrm{core} + \frac{1}{2}\biggl(\frac{4}{3} - \gamma_e\biggr)W \biggr]_\mathrm{eq} </math> |
|
|
<math>~=~</math> |
<math>~ \frac{6}{R_\mathrm{eq}^2} \biggl[ -\frac{W}{2}\biggl( \gamma_e - \frac{4}{3}\biggr) - (\gamma_e-\gamma_c) S_\mathrm{core} \biggr]_\mathrm{eq} \, .</math> |
So, if when evaluated at the equilibrium state, the expression inside of the square brackets of this last expression is negative, the equilibrium configuration will be dynamically unstable. We have chosen to write the expression in this particular final form because we generally will be interested in bipolytropes for which the adiabatic exponent of the envelope is greater than <math>~4/3</math> and the adiabatic exponent of the core is less than or equal to <math>~4/3</math> — that is, <math>~\gamma_e > 4/3 \ge \gamma_c</math>. Hence, because the gravitational potential energy, <math>~W</math>, is intrinsically negative, the system will be dynamically unstable only if the second term (involving <math>~S_\mathrm{core}</math>) is greater in magnitude than the first term (involving <math>~W</math>).
It is worth noting that, instead of drawing upon <math>~S_\mathrm{core}</math> and <math>~W</math> to define the stability condition, we could have used an appropriate combination of <math>~S_\mathrm{env}</math> and <math>~W</math>, or the <math>~S_\mathrm{core}</math> and <math>~S_\mathrm{env}</math> pair. Also, for example, because the virial equilibrium condition is <math>~S_\mathrm{tot} = -W/2</math>, it is easy to see that the following inequality also equivalently defines stability:
|
<math>~ S_\mathrm{tot}\biggl( \gamma_e - \frac{4}{3}\biggr) - (\gamma_e-\gamma_c) S_\mathrm{core} </math> |
<math>~>~</math> |
<math>~ 0 \, .</math> |
Examples
(0, 0) Bipolytropes
Review
In an accompanying discussion we have derived analytic expressions describing the equilibrium structure and the stability of bipolytropes in which both the core and the envelope have uniform densities, that is, bipolytropes with <math>~(n_c, n_e) = (0, 0)</math>. From this work, we find that integrals over the mass and pressure distributions give:
|
<math>~ \frac{W}{R_\mathrm{eq}^3 P_i} = - \frac{A}{R_\mathrm{eq}^4 P_i} </math> |
<math>~=~</math> |
<math>- ~ \frac{3}{5} \biggl[ \frac{GM_\mathrm{tot}^2}{R^4P_i} \biggr] \biggl( \frac{\nu^2}{q} \biggr) f </math> |
|
|
<math>~=~</math> |
<math>- ~4\pi q^3 \Lambda f \, ,</math> |
|
<math>~\frac{S_\mathrm{core}}{R_\mathrm{eq}^3 P_i} = B_\mathrm{core}</math> |
<math>~=~</math> |
<math> ~2\pi q^3 (1 + \Lambda) \, ,</math> |
|
<math>~\frac{S_\mathrm{env}}{R_\mathrm{eq}^3 P_i} = B_\mathrm{env}</math> |
<math>~=~</math> |
<math> 2\pi \biggl[ (1-q^3) + \frac{5}{2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \, ,</math> |
where,
|
<math>~\Lambda</math> |
<math>~\equiv~</math> |
<math> \frac{3}{2^2 \cdot 5\pi} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}^4 P_i} \biggr) \frac{\nu^2}{q^4} \, ,</math>
|
|
<math>~f(q,\rho_e/\rho_c)</math> |
<math>~\equiv~</math> |
<math>1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2} - 1 \biggr) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \biggl(\frac{1}{q^5} - 1 \biggr) - \frac{5}{2}\biggl(\frac{1}{q^2} - 1 \biggr) \biggr] </math> |
|
|
<math>~=~</math> |
<math>1 + \frac{5}{2q^2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^2) + \frac{1}{2q^5} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 (2 - 5q^3 + 3q^5) \, ,</math> |
|
<math>~g^2(q,\rho_e/\rho_c)</math> |
<math>~\equiv~</math> |
<math>1 + \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] </math> |
|
|
<math>~\equiv~</math> |
<math>1 + \biggl[ 2\biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q) + \frac{1}{q^2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 (1 - 3q^2 + 2q^3 ) \biggr] \, , </math> |
Renormalize
Let's renormalize these energy terms in order to more readily relate them to the generalized expressions derived above.
|
<math>~R^3 P_i</math> |
<math>~=</math> |
<math> ~R^3 K_c \biggl(\frac{\rho_{ic}}{\bar\rho} \biggr)^{\gamma_c} \biggl[ \biggl( \frac{3}{4\pi}\biggr) \frac{M_\mathrm{tot}}{R^3} \biggr]^{\gamma_c} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{3-3\gamma_c} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c} K_c M_\mathrm{tot}^{\gamma_c} R_\mathrm{norm}^{3-3\gamma_c}</math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{3-3\gamma_c} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c} \biggl\{ K_c^{3\gamma_c -4} M_\mathrm{tot}^{\gamma_c(3\gamma_c -4)} \biggl[ \biggl( \frac{K_c}{G} \biggr) M_\mathrm{tot}^{\gamma_c-2} \biggr]^{3-3\gamma_c} \biggr\}^{1/(3\gamma_c -4)}</math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{3-3\gamma_c} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c} \biggl\{ \frac{G^{3\gamma_c-3} M_\mathrm{tot}^{5\gamma_c-6} }{K_c} \biggr\}^{1/(3\gamma_c -4)}</math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{3-3\gamma_c} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c} E_\mathrm{norm} \, .</math> |
Also,
|
<math>~\biggl[ \frac{GM_\mathrm{tot}^2}{R} \biggr]^{3\gamma_c -4}</math> |
<math>~=</math> |
<math> ~\biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-(3\gamma_c-4)} G^{3\gamma_c -4} M_\mathrm{tot}^{6\gamma_c -8} \biggl( \frac{G}{K_c} \biggr) M_\mathrm{tot}^{2-\gamma_c} </math> |
|
|
<math>~=</math> |
<math> ~\biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-(3\gamma_c-4)} \biggl[ \frac{ G^{3\gamma_c -3} M_\mathrm{tot}^{5\gamma_c -6} }{K_c} \biggr] </math> |
|
|
<math>~=</math> |
<math> ~\biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-(3\gamma_c-4)} E_\mathrm{norm}^{3\gamma_c-4} \, . </math> |
|
<math> \Rightarrow ~~~~\frac{GM_\mathrm{tot}^2}{R^4 P_i} </math> |
<math>~=</math> |
<math> ~\biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-1} \biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{3\gamma_c - 3} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{-\gamma_c} </math> |
|
|
<math>~=</math> |
<math> \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3\gamma_c - 4} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{-\gamma_c} \, . </math> |
Hence,
|
<math>~\Lambda</math> |
<math>~\equiv~</math> |
<math> \frac{3}{2^2 \cdot 5\pi} \frac{\nu^2}{q^4} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{-\gamma_c}
\biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3\gamma_c - 4} \, .</math> |
Given that <math>~\rho_{ic}/\bar\rho = \nu/q^3</math> for the <math>~(n_c, n_e) = (0, 0)</math> bipolytrope, we can finally write,
|
<math>~\frac{R^3 P_i}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3-3\gamma_c} \, ,</math> |
and,
|
<math>~\Lambda</math> |
<math>~\equiv~</math> |
<math> \frac{3}{2^2 \cdot 5\pi} \frac{\nu^2}{q^4} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{-\gamma_c} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3\gamma_c - 4} = \frac{1}{5} \frac{\nu}{q} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{1-\gamma_c} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3\gamma_c - 4} \, .</math> |
Hence the renormalized gravitational potential energy becomes,
|
<math> \frac{W_\mathrm{grav}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math> - \biggl( \frac{3}{5} \biggr) \frac{\nu^2}{q} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-1} \cdot f \, ;</math> |
and the two, renormalized contributions to the thermal energy become,
|
<math>~\frac{U_\mathrm{core}}{ E_\mathrm{norm} } = \frac{2}{3(\gamma_c-1)} \biggl[ \frac{S_\mathrm{core}}{ E_\mathrm{norm} } \biggr]</math> |
<math>~=~</math> |
<math> \frac{4\pi q^3 (1 + \Lambda) }{3(\gamma_c-1)} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3-3\gamma_c} \, ,</math> |
|
<math>~\frac{U_\mathrm{env}}{ E_\mathrm{norm} } = \frac{2}{3(\gamma_e-1)} \biggl[ \frac{S_\mathrm{env}}{ E_\mathrm{norm} } \biggr]</math> |
<math>~=~</math> |
<math> \frac{4\pi}{3(\gamma_e-1)} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e} \biggl( \frac{K_e}{K_c} \biggr) \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2} \biggr]^{(3\gamma_c-3\gamma_e)/(3\gamma_c-4)} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3-3\gamma_e} </math> |
|
|
|
<math> \times \biggl[ (1-q^3) + \frac{5}{2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \, ,</math> |
Finally, then, we can state that,
|
<math>~\mathfrak{f}_{WM}</math> |
<math>~\equiv</math> |
<math>~\frac{\nu^2}{q} \cdot f \, ,</math> |
|
<math>~s_\mathrm{core}</math> |
<math>~\equiv</math> |
<math> 1 + \Lambda \, , </math> |
|
<math>~(1-q^3) s_\mathrm{env}</math> |
<math>~\equiv</math> |
<math> (1-q^3) + \Lambda\biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_0}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_0}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \, .</math> |
Virial Equilibrium and Stability Evaluation
With these expressions in hand, we can deduce the equilibrium radius and relativity stability of <math>~(n_c, n_e) = (0, 0)</math> bipolytropes using the generalized expressions provided above. For example, from the statement of virial equilibrium <math>~(2S_\mathrm{tot} = - W )</math> we obtain,
|
<math>~q^3 (1 + \Lambda) + (1-q^3) + \frac{5}{2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) </math> |
<math>~=~</math> |
<math>~q^3 \Lambda \biggl[ 1 + \frac{5}{2q^2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^2) + \frac{1}{2q^5} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 (2 - 5q^3 + 3q^5) \biggr] </math> |
|
<math>\Rightarrow ~~~~ \frac{1}{\Lambda}</math> |
<math>~=~</math> |
<math>\frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (q-q^3) + \frac{1}{2q^2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 (2 - 5q^3 + 3q^5) - \biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_0}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_0}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
|
<math>~=~</math> |
<math>\frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (q-q^3 + 2 -3q +q^3) + \frac{1}{2q^2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 (2 - 5q^3 + 3q^5 +3 - 15q^2+15q^3 -3q^5) </math> |
|
|
<math>~=~</math> |
<math>\frac{5}{2}\biggl[ 2\biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q) + \frac{1}{q^2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 (1 - 3q^2 + 2q^3 ) \biggr] </math> |
|
|
<math>~=~</math> |
<math>\frac{5}{2}(g^2-1) </math> |
|
<math>\Rightarrow ~~~~ \biggl[ \frac{P_i}{GM_\mathrm{tot}^2} \biggr] R_\mathrm{eq}^4</math> |
<math>~=~</math> |
<math>\biggl( \frac{3}{2^3 \pi } \biggr) \frac{\nu^2}{q^4} (g^2-1) \, . </math> |
Or, given the above renormalization, this expression can be written as,
|
<math> \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{4-3\gamma_c } \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c} </math> |
<math>~=~</math> |
<math>\biggl( \frac{3}{2^3 \pi } \biggr) \frac{\nu^2}{q^4} (g^2-1) </math> |
|
<math> \Rightarrow ~~~~ \frac{R}{R_\mathrm{norm}} </math> |
<math>~=~</math> |
<math> \biggl\{ \biggl( \frac{3}{2^3 \pi } \biggr) \frac{\nu^2}{q^4} (g^2-1) \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c} \biggr\}^{1/(4-3\gamma_c)} \, . </math> |
And the condition for dynamical stability is,
|
<math>-\frac{W}{2}\biggl( \gamma_e - \frac{4}{3}\biggr) - (\gamma_e-\gamma_c) S_\mathrm{core} </math> |
<math>~>~</math> |
<math>~0 \, .</math> |
|
<math>\Rightarrow ~~~~ 2\pi q^3 \Lambda \biggl[ \biggl( \gamma_e - \frac{4}{3}\biggr) f - (\gamma_e-\gamma_c) \biggl( 1 + \frac{1}{\Lambda}\biggr) \biggr] </math> |
<math>~>~</math> |
<math>~0 \, .</math> |
|
<math>~\biggl( \gamma_e - \frac{4}{3} \biggr)f - (\gamma_e - \gamma_c) \biggl[1 + \frac{5}{2}(g^2-1) \biggr]</math> |
<math>~>~</math> |
<math>~0 \, .</math> |
(5, 1) Bipolytropes
In another accompanying discussion we have derived analytic expressions describing the equilibrium structure of bipolytropes with <math>~(n_c, n_e) = (5, 1)</math>. Can we perform a similar stability analysis of these configurations? Work in progress!
Best of the Best
One Derivation of Free Energy
|
<math>~\mathfrak{G}^*</math> |
<math>~=</math> |
<math> - \frac{3\cdot \mathfrak{f}_{WM}}{5} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-1} + \frac{\nu s_\mathrm{core} }{(\gamma_c - 1)} \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\nu}{q^3} \biggr]^{\gamma_c-1} \biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{-3(\gamma_c-1)} </math> |
|
|
|
<math> ~+ \frac{(1-\nu) s_\mathrm{env} }{(\gamma_e - 1)} \biggl( \frac{K_e}{K_c} \biggr) \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2} \biggr]^{(\gamma_c-\gamma_e)/(3\gamma_c -4)} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e-1} \biggl[ \frac{R}{R_\mathrm{norm}} \biggr]^{-3(\gamma_e-1)} \, . </math> |
Another Derivation of Free Energy
Hence the renormalized gravitational potential energy becomes,
|
<math> \frac{W_\mathrm{grav}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math> - \biggl( \frac{3}{5} \biggr) \frac{\nu^2}{q} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{-1} \cdot f \, ;</math> |
and the two, renormalized contributions to the thermal energy become,
|
<math>~\frac{U_\mathrm{core}}{ E_\mathrm{norm} } = \frac{2}{3(\gamma_c-1)} \biggl[ \frac{S_\mathrm{core}}{ E_\mathrm{norm} } \biggr]</math> |
<math>~=~</math> |
<math> \frac{4\pi q^3 (1 + \Lambda) }{3(\gamma_c-1)} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c} \biggl( \frac{R}{R_\mathrm{norm}} \biggr)^{3-3\gamma_c} </math> |
|
|
<math>~=~</math> |
<math> \frac{\nu (1 + \Lambda) }{(\gamma_c-1)} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{\gamma_c-1} \chi^{3-3\gamma_c} \, ,</math> |
|
<math>~\frac{U_\mathrm{env}}{ E_\mathrm{norm} } = \frac{2}{3(\gamma_e-1)} \biggl[ \frac{S_\mathrm{env}}{ E_\mathrm{norm} } \biggr]</math> |
<math>~=~</math> |
<math> \frac{2 (2\pi) }{3(\gamma_e-1)} \biggl[ \frac{R^3 P_{ie}}{ E_\mathrm{norm} } \biggr] \biggl[ (1-q^3) + \frac{5}{2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \Lambda \biggl( \frac{\rho_e}{\rho_0}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
|
<math>~=~</math> |
<math> \frac{2 (2\pi) }{3(\gamma_e-1)} \biggl[ \frac{\mathrm{BigTerm}}{E_\mathrm{norm}} \biggr] R^3 K_e \rho_{ie}^{\gamma_e} </math> |
|
|
<math>~=~</math> |
<math> \frac{2 (2\pi) }{3(\gamma_e-1)} \biggl[ \frac{\mathrm{BigTerm}}{E_\mathrm{norm}} \biggr] R^3 K_e \rho_\mathrm{norm}^{\gamma_e} \biggl( \frac{\rho_{ie}}{\bar\rho} \biggr)^{\gamma_e} \biggl( \frac{\bar\rho}{\rho_\mathrm{norm}} \biggr)^{\gamma_e} </math> |
|
|
<math>~=~</math> |
<math> \frac{2 (2\pi) }{3(\gamma_e-1)} \biggl[ \frac{\mathrm{BigTerm}}{E_\mathrm{norm}} \biggr] ( \rho_\mathrm{norm} R_\mathrm{norm}^3) K_e \rho_\mathrm{norm}^{\gamma_e-1} \biggl[ \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e} \chi^{3-3\gamma_e} </math> |
|
|
<math>~=~</math> |
<math> \frac{2 (2\pi) }{3(\gamma_e-1)} \biggl[ \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e} \chi^{3-3\gamma_e} \biggl[ \mathrm{BigTerm}\biggr] \biggl( \frac{3M_\mathrm{tot}}{4\pi} \biggr) \frac{K_e}{E_\mathrm{norm}} \biggl( \frac{3}{4\pi} \biggr)^{\gamma_e-1} \biggl[ \frac{G^3 M_\mathrm{tot}^2 }{K_c^3}\biggr]^{(\gamma_e-1)/(3\gamma_c-4)} </math> |
|
|
<math>~=~</math> |
<math> \frac{(1-\nu)}{ (1-q^3) (\gamma_e-1)} \biggl[ \frac{3}{4\pi} \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e-1} \biggl( \frac{K_e}{K_c} \biggr) \chi^{3-3\gamma_e} \biggl[ \mathrm{BigTerm}\biggr] \frac{K_c M_\mathrm{tot}}{E_\mathrm{norm}} \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2}\biggr]^{(1-\gamma_e)/(3\gamma_c-4)} </math> |
|
|
<math>~=~</math> |
<math> \frac{(1-\nu)}{ (1-q^3) (\gamma_e-1)} \biggl[ \frac{3}{4\pi} \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e-1} \biggl( \frac{K_e}{K_c} \biggr) \chi^{3-3\gamma_e} \biggl[ \mathrm{BigTerm}\biggr] \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2}\biggr]^{(1-\gamma_e)/(3\gamma_c-4)} \biggl[ \frac{K_c^{3\gamma_c-4} M_\mathrm{tot}^{3\gamma_c-4}}{ G^{3\gamma_c-3} M_\mathrm{tot}^{5\gamma_c-6} K_c^{-1}} \biggr]^{1/(3\gamma_c-4)} </math> |
|
|
<math>~=~</math> |
<math> \frac{(1-\nu)}{ (1-q^3) (\gamma_e-1)} \biggl[ \frac{3}{4\pi} \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e-1} \biggl( \frac{K_e}{K_c} \biggr) \chi^{3-3\gamma_e} \biggl[ \mathrm{BigTerm}\biggr] \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2}\biggr]^{(1-\gamma_e)/(3\gamma_c-4)} \biggl[ \frac{K_c^{3}}{G^{3} M_\mathrm{tot}^{2}} \biggr]^{(\gamma_c-1)/(3\gamma_c-4)} </math> |
|
|
<math>~=~</math> |
<math> \frac{(1-\nu)}{ (1-q^3) (\gamma_e-1)} \biggl[ \frac{3}{4\pi} \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e-1} \biggl( \frac{K_e}{K_c} \biggr) \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2}\biggr]^{(\gamma_c-\gamma_e)/(3\gamma_c-4)} \biggl[ \mathrm{BigTerm}\biggr] \chi^{3-3\gamma_e} </math> |
Finally, then, we can state that,
|
<math>~\mathfrak{f}_{WM}</math> |
<math>~\equiv</math> |
<math>~\frac{\nu^2}{q} \cdot f \, ,</math> |
|
<math>~s_\mathrm{core}</math> |
<math>~\equiv</math> |
<math> 1 + \Lambda \, , </math> |
|
<math>~(1-q^3) s_\mathrm{env}</math> |
<math>~\equiv</math> |
<math> (1-q^3) + \Lambda\biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_0}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_0}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \, .</math> |
Note,
|
<math>~\Lambda</math> |
<math>~\equiv~</math> |
<math> \frac{3}{2^2 \cdot 5\pi} \frac{\nu^2}{q^4} \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{-\gamma_c}
\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^{3\gamma_c - 4} = \frac{1}{5} \biggl( \frac{\nu}{q} \biggr) \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{1-\gamma_c} \chi_\mathrm{eq}^{3\gamma_c - 4} \, .</math> |
We also want to ensure that envelope pressure matches the core pressure at the interface. This means,
|
<math>~K_e \rho_{ie}^{\gamma_e}</math> |
<math>~=</math> |
<math>~K_c \rho_{ic}^{\gamma_c}</math> |
|
<math>\Rightarrow ~~~~\frac{K_e}{K_c} </math> |
<math>~=</math> |
<math>~\rho_{ic}^{\gamma_c} \rho_{ie}^{-\gamma_e} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{\rho_{ic}}{\rho_\mathrm{norm}} \biggr]^{\gamma_c} \biggl[ \frac{\rho_{ie}}{\rho_\mathrm{norm}} \biggr]^{-\gamma_e} \rho_\mathrm{norm}^{\gamma_c - \gamma_e}</math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{\rho_{ic}}{\rho_\mathrm{norm}} \biggr]^{\gamma_c} \biggl[ \frac{\rho_{ie}}{\rho_\mathrm{norm}} \biggr]^{-\gamma_e} \biggl\{ \frac{3}{4\pi} \biggl[ \frac{G^3 M_\mathrm{tot}^2}{K_c^3} \biggr]^{1/(3\gamma_c -4)} \biggr\}^{\gamma_c - \gamma_e}</math> |
|
<math>\Rightarrow ~~~~\frac{K_e}{K_c} \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2} \biggr]^{(\gamma_c - \gamma_e)/(3\gamma_c -4)} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ie}}{\bar\rho} \biggr]^{\gamma_e-1}</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\rho_\mathrm{norm}} \biggr]^{\gamma_c} \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ie}}{\rho_\mathrm{norm}} \biggr]^{-\gamma_e} \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{\rho_{ie}}{\bar\rho} \biggr]^{\gamma_e-1} </math> |
|
|
<math>~=</math> |
<math> \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c-1} \biggl( \frac{\rho_{ic}}{\rho_{ie}} \biggr) \biggl( \frac{\rho_\mathrm{norm}}{ \bar\rho } \biggr)^{\gamma_e - \gamma_c} </math> |
|
|
<math>~=</math> |
<math> \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\rho_{ic}}{\bar\rho} \biggr]^{\gamma_c-1} \biggl( \frac{\rho_{ic}}{\rho_{ie}} \biggr) \biggl( \frac{ R}{R_\mathrm{norm}} \biggr)^{3(\gamma_e - \gamma_c)} </math> |
Keep in mind that, if the envelope and core both have uniform (but different) densities, then <math>~\rho_{ic} = \rho_c</math>, <math>~\rho_{ie} = \rho_e</math>, and
<math> \frac{\rho_c}{\bar\rho} = \frac{\nu}{q^3} \, ; ~~~~~ \frac{\rho_e}{\bar\rho} = \frac{1-\nu}{1-q^3} \, ; ~~~~~ \frac{\rho_e}{\rho_c} = \frac{q^3(1-\nu)}{\nu (1-q^3)} \, . </math>
Summary
Understanding Free-Energy Behavior
Step 1: Pick values for the separate coefficients, <math>\mathcal{A}, \mathcal{B},</math> and <math>\mathcal{C},</math> of the three terms in the normalized free-energy expression,
|
<math>~\mathfrak{G}^*</math> |
<math>~=</math> |
<math>~ -~ 3\mathcal{A} \chi^{-1} - \frac{\mathcal{B}}{(1-\gamma_c)} ~\chi^{3-3\gamma_c} - \frac{\mathcal{C}}{(1-\gamma_e)} ~\chi^{3-3\gamma_e} </math> |
then plot the function, <math>\mathfrak{G}^*(\chi)</math>, and identify the value(s) of <math>~\chi_\mathrm{eq}</math> at which the function has an extremum (or multiple extrema).
Step 2: Note that,
|
<math>~\mathcal{A}</math> |
<math>~\equiv</math> |
<math>~\frac{\nu^2}{5q} \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2} - 1 \biggr) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \biggl(\frac{1}{q^5} - 1 \biggr) - \frac{5}{2}\biggl(\frac{1}{q^2} - 1 \biggr) \biggr] \biggr\}</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{5} \biggl( \frac{\nu}{q^3} \biggr)^2 \biggl[ q^5 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (1 - q^2 )q^3 + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl( 1 - \frac{5}{2}q^3 + \frac{3}{2}q^5\biggr) \biggr]</math> |
|
<math>~\mathcal{B}</math> |
<math>~\equiv</math> |
<math>~\nu \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\nu}{q^3} \biggr]^{\gamma_c-1} \biggl[ 1+\Lambda_\mathrm{eq} \biggr]</math> |
|
<math>~\mathcal{C}</math> |
<math>~\equiv</math> |
<math>~(1-\nu)\biggl( \frac{K_e}{K_c} \biggr)^* \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{(1-\nu)}{(1-q^3)} \biggr]^{\gamma_e-1} \biggl\{ 1 + \frac{\Lambda_\mathrm{eq}}{(1-q^3)}\biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \biggr\}</math> |
|
|
<math>~\equiv</math> |
<math>~ \nu \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\nu}{q^3} \biggr]^{\gamma_c-1} \biggl\{ \frac{(1-q^3)}{q^3} + \frac{\Lambda_\mathrm{eq}}{q^3} \biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \biggr\} \chi_\mathrm{eq}^{3(\gamma_e - \gamma_c)}</math> |
where (see, for example, in the context of its original definition),
|
<math>~\Lambda_\mathrm{eq} \equiv \frac{3}{2^2\pi \cdot 5} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}^4 P_i} \biggr) \frac{\nu^2}{q^4}
</math> |
<math>~=~</math> |
<math> \frac{1}{5} \biggl( \frac{\nu}{q} \biggr) \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{1-\gamma_c}
\chi_\mathrm{eq}^{3\gamma_c - 4} </math> |
and, where,
|
<math>\biggl( \frac{K_e}{K_c} \biggr)^* \equiv \frac{K_e}{K_c} \biggl[ \frac{K_c^3}{G^3 M_\mathrm{tot}^2} \biggr]^{(\gamma_c - \gamma_e)/(3\gamma_c -4)} </math> |
<math>~=</math> |
<math> \biggl[\biggl( \frac{3}{4\pi} \biggr) \frac{1-\nu}{1-q^3} \biggr]^{-\gamma_e} \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\nu}{q^3} \biggr]^{\gamma_c} \chi_\mathrm{eq}^{3(\gamma_e - \gamma_c)} \, . </math> |
Also, keep in mind that, if the envelope and core both have uniform (but different) densities, then <math>~\rho_{ic} = \rho_c</math>, <math>~\rho_{ie} = \rho_e</math>, and
<math> \frac{\rho_c}{\bar\rho} = \frac{\nu}{q^3} \, ; ~~~~~ \frac{\rho_e}{\bar\rho} = \frac{1-\nu}{1-q^3} \, ; ~~~~~ \frac{\rho_e}{\rho_c} = \frac{q^3(1-\nu)}{\nu (1-q^3)} ~~\Rightarrow ~~~ \frac{q^3}{\nu} = \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \, . </math>
Step 3: An analytic evaluation tells us that the following should happen. Using the numerically derived value for <math>~\chi_\mathrm{eq}</math>, define,
<math>~\mathcal{C}^' \equiv \mathcal{C} \chi_\mathrm{eq}^{3(\gamma_c - \gamma_e)} \, .</math>
We should then discover that,
<math>\frac{\mathcal{A}}{\mathcal{B} + \mathcal{C}^'} = \chi_\mathrm{eq}^{4-3\gamma_c} = \frac{1}{\Lambda_\mathrm{eq}} \cdot \frac{1}{5} \biggl( \frac{\nu}{q} \biggr) \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{1-\gamma_c} \, .</math>
Check It
|
<math>~\mathcal{B} + \mathcal{C}^'</math> |
<math>~=</math> |
<math>~ \nu \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\nu}{q^3} \biggr]^{\gamma_c-1} \biggl\{ \biggl[ 1+\Lambda_\mathrm{eq} \biggr] + \frac{(1-q^3)}{q^3} + \frac{\Lambda_\mathrm{eq}}{q^3} \biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] \biggr\} </math> |
|
<math>\Rightarrow~~~~\mathcal{A} \biggl[ \Lambda_\mathrm{eq} \cdot 5\biggl( \frac{q}{\nu^2} \biggr) \biggr]</math> |
<math>~=</math> |
<math>~ 1+\Lambda_\mathrm{eq} + \frac{(1-q^3)}{q^3} + \frac{\Lambda_\mathrm{eq}}{q^3} \biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
<math> \Rightarrow~~~~\Lambda_\mathrm{eq} \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2} - 1 \biggr) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \biggl(\frac{1}{q^5} - 1 \biggr) - \frac{5}{2}\biggl(\frac{1}{q^2} - 1 \biggr) \biggr] \biggr\} </math> |
<math>~=</math> |
<math>~ 1+\Lambda_\mathrm{eq} + \frac{(1-q^3)}{q^3} + \frac{\Lambda_\mathrm{eq}}{q^3} \biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
<math> \Rightarrow~~~~\Lambda_\mathrm{eq} \biggl\{ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2} - 1 \biggr) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \biggl(\frac{1}{q^5} - 1 \biggr) - \frac{5}{2}\biggl(\frac{1}{q^2} - 1 \biggr) \biggr] \biggr\} </math> |
<math>~=</math> |
<math>~ \frac{1}{q^3} + \frac{\Lambda_\mathrm{eq}}{q^3} \biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
<math>\Rightarrow~~~~ \frac{1}{\Lambda_\mathrm{eq}} </math> |
<math>~=</math> |
<math> q^3 \biggl\{ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2} - 1 \biggr) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \biggl(\frac{1}{q^5} - 1 \biggr) - \frac{5}{2}\biggl(\frac{1}{q^2} - 1 \biggr) \biggr] \biggr\} - \biggl[ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) + \frac{3}{2q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
<math>\Rightarrow~~~~ \frac{2}{\Lambda_\mathrm{eq}} </math> |
<math>~=</math> |
<math> 5\biggl( \frac{\rho_e}{\rho_c} \biggr) ( q - q^3 ) + \frac{2}{q^2}\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ (1 - q^5 ) - \frac{5}{2}( q^3 - q^5 ) \biggr] - 5 \biggl( \frac{\rho_e}{\rho_c}\biggr) (-2 + 3q - q^3) - \frac{3}{q^2} \biggl( \frac{\rho_e}{\rho_c}\biggr)^2 (-1 +5q^2 - 5q^3 + q^5) </math> |
|
|
<math>~=</math> |
<math> 5\biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl[ ( q - q^3 ) - (-2 + 3q - q^3) \biggr] + \frac{1}{q^2}\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ 2(1 - q^5 ) - 5( q^3 - q^5 ) - 3(-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
|
<math>~=</math> |
<math> 10\biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl[ 1-q \biggr] + \frac{5}{q^2}\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ 1 - 3q^2 + 2q^3 \biggr] </math> |
|
<math>\Rightarrow~~~~ \frac{1}{\Lambda_\mathrm{eq}} \biggl[ \frac{2q^2}{5} \biggl( \frac{\rho_e}{\rho_c} \biggr)^{-1} \biggr] </math> |
<math>~=</math> |
<math> 2q^2 (1-q )+ \biggl( \frac{\rho_e}{\rho_c} \biggr) ( 1 - 3q^2 + 2q^3 ) </math> |
Fortunately, this precisely matches our earlier derivation, which states that,
|
<math>~\frac{1}{\Lambda}</math> |
<math>~=</math> |
<math>\frac{5}{2}(g^2-1) = \frac{5}{2}\biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \, .</math> |
Playing With One Example
By setting,
|
<math>~\gamma_c = 6/5; ~~~ \gamma_e = 2</math> |
||
|
<math>~\mathcal{A}</math> |
<math>~\mathcal{B}</math> |
<math>~\mathcal{C}</math> |
|---|---|---|
|
2.5 |
1.0 |
2.0 |
a plot of <math>~\mathfrak{G}^*</math> versus <math>~\chi</math> exhibits the following, two extrema:
|
extremum |
<math>~\chi_\mathrm{eq}</math> |
<math>~\mathfrak{G}^*</math> |
|
<math>~\chi_\mathrm{eq}^{3(\gamma_c - \gamma_e)}</math> |
<math>~\mathcal{C}^'</math> |
<math>~\chi_\mathrm{eq}^{4-3\gamma_c}</math> |
<math>~\frac{\mathcal{A}}{\mathcal{B} +\mathcal{C}^'}</math> |
|
MIN |
<math>1.1824</math> |
<math>-0.611367</math> |
<math>~~~~\Rightarrow~~~~</math> |
<math>0.66891</math> |
<math>1.3378</math> |
<math>1.0693</math> |
<math>1.0694</math> |
|
MAX |
<math>9.6722</math> |
<math>+0.508104</math> |
<math>~\Rightarrow</math> |
<math>0.004313</math> |
<math>0.008625</math> |
<math>2.4786</math> |
<math>2.4786</math> |
The last two columns of this table confirm the internal consistency of the relationships presented in Step 3, above. But what does this mean in terms of the values of <math>~\nu</math>, <math>~q</math>, and the related ratio of densities at the interface, <math>~\rho_e/\rho_c</math>?
Let's assume that what we're trying to display and examine is the behavior of the free-energy surface for a fixed value of the ratio of densities at the interface. Once the value of <math>~\rho_e/\rho_c</math> has been specified, it is clear that the value of <math>~q</math> (and, hence, also <math>~\nu</math>) is set because <math>~\mathcal{A}</math> has also been specified. But our specification of <math>~\mathcal{B}</math> along with <math>~\rho_e/\rho_c</math> also forces a particular value of <math>~q</math>. It is unlikely that these two values of <math>~q</math> will be the same. In reality, once <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math> have both been specified, they force a particular <math>~(\nu, q)</math> pair. How do we (easily) figure out what this pair is?
Let's begin by rewriting the expressions for <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math> in terms of just <math>~q</math> and the ratio, <math>~\rho_e/\rho_c</math>, keeping in mind that, for the case of a uniform-density core (of density, <math>~\rho_c</math>) and a uniform-density envelope (of density, <math>~\rho_e</math>),
|
<math>~\frac{\rho_e}{\rho_c}</math> |
<math>~=</math> |
<math>~\frac{q^3(1-\nu)}{\nu(1-q^3)} \, ,</math> |
hence,
|
<math>~\nu</math> |
<math>~=</math> |
<math>~\biggl[ 1 + \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{(1-q^3)}{q^3} \biggr]^{-1}</math> |
and |
<math>~\frac{q^3}{\nu}</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \biggr] \, .</math> |
Putting the expression for <math>~\mathcal{A}</math> in the desired form is simple because <math>~\nu</math> only appears as a leading factor. Specifically, we have,
|
<math>~\mathcal{A}</math> |
<math>~=</math> |
<math>~\frac{\pi q^5}{5} \biggl[ \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \biggr]^{-2} \biggl\{ 1 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2} - 1 \biggr) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \biggl(\frac{1}{q^5} - 1 \biggr) - \frac{5}{2}\biggl(\frac{1}{q^2} - 1 \biggr) \biggr] \biggr\}</math> |
|
|
<math>~=</math> |
<math>~\frac{\pi }{5} \biggl[ \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \biggr]^{-2} \biggl\{ q^5 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (q^3 - q^5 ) + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[1-\frac{5}{2} q^3 + \frac{3}{2}q^5 \biggr] \biggr\} \, .</math> |
The expression for <math>~\mathcal{B}</math> can be written in the form,
|
<math>~\mathcal{B}</math> |
<math>~=</math> |
<math>~\nu \biggl[ \biggl( \frac{3}{4\pi} \biggr)\frac{\nu}{q^3} \biggr]^{\gamma_c-1} \biggl\{ 1+\frac{\pi}{5} \biggl( \frac{\nu}{q} \biggr) \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{1-\gamma_c} \chi_\mathrm{eq}^{3\gamma_c - 4} \biggr\}</math> |
|
|
<math>~=</math> |
<math>~\nu \biggl[ \biggl( \frac{4\pi}{3} \biggr)\frac{q^3}{\nu} \biggr]^{1-\gamma_c} +\frac{\pi q^5}{5} \biggl( \frac{\nu^2}{q^6} \biggr) \chi_\mathrm{eq}^{3\gamma_c - 4} </math> |
|
|
<math>~=</math> |
<math>~q^3 \biggl( \frac{4\pi}{3} \biggr)^{1-\gamma_c} \biggl[ \frac{q^3}{\nu} \biggr]^{-\gamma_c} +\frac{\pi q^5}{5} \biggl( \frac{q^3}{\nu} \biggr)^{-2} \chi_\mathrm{eq}^{3\gamma_c - 4} </math> |
|
|
<math>~=</math> |
<math>~q^3 \biggl( \frac{4\pi}{3} \biggr)^{1-\gamma_c} \biggl[ \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \biggr]^{-\gamma_c} +\frac{\pi q^5}{5} \biggl[ \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \biggr]^{-2} \chi_\mathrm{eq}^{3\gamma_c - 4} \, . </math> |
Generally speaking, the equilibrium radius, <math>~\chi_\mathrm{eq}</math>, which appears in the expression for <math>~\mathcal{B}</math>, is not known ahead of time. Indeed, as is illustrated in our simple example immediately above, the normal path is to pick values for the coefficients, <math>~\mathcal{A}</math>, <math>~\mathcal{B}</math>, and <math>~\mathcal{C}</math>, and determine the equilibrium radius by looking for extrema in the free-energy function. And because <math>~\chi_\mathrm{eq}</math> is not known ahead of time, it isn't clear how to (easily) figure out what pair of physical parameter values, <math>~(\nu, q)</math>, give self-consistent values for the coefficient pair, <math>~(\mathcal{A}, \mathcal{B})</math>.
Because we are using a uniform density core and uniform density envelope as our base model, however, we do know the analytic solution for <math>~\chi_\mathrm{eq}</math>. As stated above, it is,
|
<math>~\chi_\mathrm{eq}^{4-3\gamma_c}</math> |
<math>~=</math> |
<math>~\frac{1}{\Lambda_\mathrm{eq}} \cdot \frac{\pi}{5} \biggl( \frac{\nu}{q} \biggr) \biggl[ \biggl( \frac{3}{4\pi} \biggr) \frac{\nu}{q^3} \biggr]^{1-\gamma_c} </math> |
|
|
<math>~=</math> |
<math>~\frac{\pi q^2}{2} \biggl( \frac{3}{4\pi} \biggr)^{1-\gamma_c}\biggl( \frac{\nu}{q^3} \biggr) \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_c} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \cdot \biggl[ \frac{q^3}{\nu} \biggr]^{\gamma_c-1} </math> |
|
|
<math>~=</math> |
<math>~\frac{\pi}{2} \biggl( \frac{3}{4\pi} \biggr)^{1-\gamma_c} \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) ( q^2-q^3 ) + \frac{\rho_e}{\rho_c} (1 - q^2) \biggr] \cdot \biggl[ \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3\biggr]^{\gamma_c-2} </math> |
Combining this expression with the one for <math>~\mathcal{B}</math> gives us the desired result — although, strictly speaking, it is cheating! We can now methodically choose <math>~(\nu, q)</math> pairs and map them into the corresponding values of <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>. And, via an analogous "cheat," the choice of <math>~(\nu, q)</math> also gives us the self-consistent value of <math>~\mathcal{C}</math>. In this manner, we should be able to map out the free-energy surface for any desired set of physical parameters.
Second Example
Explain Logic
The figure presented here, on the right, shows a plot of the free energy, as a function of the dimensionless radius, <math>~\mathfrak{G}^*(\chi)</math>, where,
|
<math>~\mathfrak{G}^*</math> |
<math>~=</math> |
<math>~ -~ 3\mathcal{A} \chi^{-1} - \frac{\mathcal{B}}{(1-\gamma_c)} ~\chi^{3-3\gamma_c} - \frac{\mathcal{C}}{(1-\gamma_e)} ~\chi^{3-3\gamma_e} \, ,</math> |
and, where we have used the parameter values,
|
<math>~\gamma_c = 6/5; ~~~ \gamma_e = 2</math> |
||
|
<math>~\mathcal{A}</math> |
<math>~\mathcal{B}</math> |
<math>~\mathcal{C}</math> |
|---|---|---|
|
0.201707 |
0.0896 |
0.002484 |
Directly from this plot we deduce that this free-energy function exhibits a minimum at <math>~\chi_\mathrm{eq} = 0.1235</math> and that, at this equilibrium radius, the configuration has a free-energy value, <math>~\mathfrak{G}^*(\chi_\mathrm{eq} ) = -2.0097</math>. Via the steps described below, we demonstrate that this identified equilibrium radius is appropriate for an <math>~(n_c, n_e) = (0, 0)</math> bipolytrope (with the just-specified core and envelope adiabatic indexes) that has the following physical properties:
- Fractional core mass, <math>~\nu = 0.1</math>;
- Core-envelope interface located at <math>~r_i/R = q = 0.435</math>;
- Density jump at the core-envelope interface, <math>~\rho_e/\rho_c = 0.8</math>.
Step 1: Because the ratio, <math>~q^3/\nu</math>, is a linear function of the density ratio, <math>~\rho_e/\rho_c</math>, the full definition of the free-energy coefficient, <math>~\mathcal{A}</math>, can be restructured into a quadratic equation that gives the density ratio for any choice of the parameter pair, <math>~(q, \mathcal{A})</math>. Specifically,
|
<math>~5 \biggl( \frac{q^3}{\nu} \biggr)^2 \mathcal{A}</math> |
<math>~=</math> |
<math> q^5 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (1 - q^2 )q^3 + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl( 1 - \frac{5}{2}q^3 + \frac{3}{2}q^5\biggr) </math> |
|
<math>~\Rightarrow ~~~~ 5\mathcal{A} \biggl[ \biggl( \frac{\rho_e}{\rho_c} \biggr) (1-q^3) + q^3 \biggr]^2 </math> |
<math>~=</math> |
<math> q^5 + \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) (1 - q^2 )q^3 + \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl( 1 - \frac{5}{2}q^3 + \frac{3}{2}q^5\biggr) \, , </math> |
and this can be written in the form,
|
<math> \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 a + \biggl( \frac{\rho_e}{\rho_c} \biggr) b + c</math> |
<math>~=</math> |
<math> 0 \, , </math> |
where,
|
<math>~a</math> |
<math>~\equiv</math> |
<math>~5\mathcal{A} (1-q^3)^2 - 1 + \frac{5}{2}q^3 - \frac{3}{2}q^5 \, ,</math> |
|
<math>~b</math> |
<math>~\equiv</math> |
<math>~10\mathcal{A} q^3(1-q^3) - \frac{5}{2}q^3 (1-q^2) \, ,</math> |
|
<math>~c</math> |
<math>~\equiv</math> |
<math>~5\mathcal{A} q^6 - q^5 \, .</math> |
Hence,
|
<math>~\frac{\rho_e}{\rho_c}</math> |
<math>~=</math> |
<math>~\frac{1}{2a} \biggl[\pm ( b^2 - 4ac)^{1/2} - b \biggr] \, .</math> |
(For our physical problem it appears as though only the positive root is relevant.) For the purposes of this example, we set <math>~\mathcal{A} = 0.2017</math> and examined a range of values of <math>~q</math> to find a physically interesting value for the density ratio. We picked:
|
<math>~\mathcal{A}</math> |
<math>~q</math> |
|
<math>~a</math> |
<math>~b</math> |
<math>~c</math> |
|
<math>~\frac{\rho_e}{\rho_c}</math> |
|
<math>~\nu</math> |
|
<math>~0.2017</math> |
<math>~0.435</math> |
<math>\Rightarrow</math> |
<math>~0.03173</math> |
<math>~-0.01448</math> |
<math>~-0.008743</math> |
<math>\Rightarrow</math> |
<math>~0.80068</math> |
<math>\Rightarrow</math> |
<math>~0.10074</math> |
Step 2: Next, we chose the parameter pair,
<math> ~\biggl(q, \frac{\rho_e}{\rho_c} \biggr) = (0.43500, 0.80000) </math>
and determined the following parameter values from the known analytic solution:
|
<math>~\nu</math> |
<math>~f\biggl(q, \frac{\rho_e}{\rho_c} \biggr)</math> |
<math>~g^2\biggl(q, \frac{\rho_e}{\rho_c} \biggr)</math> |
<math>~\Lambda_\mathrm{eq}</math> |
<math>~\chi_\mathrm{eq}</math> |
<math>~\mathcal{A}</math> |
<math>~\mathcal{B}</math> |
<math>~\mathcal{C}</math> |
|
<math>~0.100816</math> |
<math>~43.16365</math> |
<math>~3.923017</math> |
<math>~0.13684</math> |
<math>~0.12349</math> |
<math>~0.201707</math> |
<math>~0.089625</math> |
<math>~0.002484</math> |
Construction Multiple Curves to Define a Free-Energy Surface
Okay. Now that we have the hang of this, let's construct a sequence of curves that represent physical evolution at a fixed interface-density ratio, <math>~\rho_e/\rho_c</math>, but for steadily increasing core-to-total mass ratio, <math>~\nu</math>. Specifically, we choose,
<math> ~\frac{\rho_e}{\rho_c} = \frac{1}{2} \, . </math>
From the known analytic solution, here are parameters defining several different equilibrium models:
|
Identification of Local Minimum in Free Energy |
||||||||
|---|---|---|---|---|---|---|---|---|
|
<math>~\nu</math> |
<math>~q</math> |
<math>~f\biggl(q, \frac{\rho_e}{\rho_c} \biggr)</math> |
<math>~g^2\biggl(q, \frac{\rho_e}{\rho_c} \biggr)</math> |
<math>~\Lambda_\mathrm{eq}</math> |
<math>~\chi_\mathrm{eq}</math> |
<math>~\mathcal{A}</math> |
<math>~\mathcal{B}</math> |
<math>~\mathcal{C}</math> |
|
<math>~0.2</math> |
<math>~9^{-1/3} = 0.48075</math> |
<math>~12.5644</math> |
<math>~2.091312</math> |
<math>~0.366531</math> |
<math>~0.037453</math> |
<math>~0.2090801</math> |
<math>~0.2308269</math> |
<math>~2.06252 \times 10^{-4}</math> |
|
<math>~0.4</math> |
<math>~4^{-1/3} = 0.62996</math> |
<math>~4.21974</math> |
<math>~1.56498</math> |
<math>~0.707989</math> |
<math>~0.0220475</math> |
<math>~0.2143496</math> |
<math>~0.5635746</math> |
<math>~4.4626 \times 10^{-5}</math> |
|
<math>~0.5</math> |
<math>~3^{-1/3} = 0.693361</math> |
<math>~2.985115</math> |
<math>~1.42334</math> |
<math>~0.9448663</math> |
<math>~0.0152116</math> |
<math>~0.2152641</math> |
<math>~0.791882</math> |
<math>~1.5464 \times 10^{-5}</math> |
|
Here we are examining the behavior of the free-energy function for bipolytropic models having <math>~(n_c, n_e) = (0, 0)</math>, <math>~(\gamma_c, \gamma_e) = (6/5, 2)</math>, and a density ratio at the core-envelope interface of <math>~\rho_e/\rho_c = 1/2</math>. The figure shown here, on the right, displays the three separate free-energy curves, <math>~\mathfrak{G}^*(\chi)</math> — where, <math>~\chi \equiv R/R_\mathrm{norm}</math> is the normalized configuration radius — that correspond to the three values of <math>~\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math> given in the first column of the above table. Along each curve, the local free-energy minimum corresponds to the the equilibrium radius, <math>~\chi_\mathrm{eq}</math>, recorded in column 6 of the above table. |
||||||||
Each of the free-energy curves shown above has been entirely defined by our specification of the three coefficients in the free-energy function, <math>~\mathcal{A}, \mathcal{B}</math>, and <math>~\mathcal{C}</math>. In each case, the values of these three coefficients was judiciously chosen to produce a curve with a local minimum at the correct value of <math>~\chi_\mathrm{eq}</math> corresponding to an equilibrium configuration having the desired <math>~(\nu, \rho_e/\rho_c)</math> model parameters. Upon plotting these three curves, we noticed that two of the curves — curves for <math>~\nu = 0.4</math> and <math>~\nu = 0.5</math> — also display a local maximum. Presumably, these maxima also identify equilibrium configurations, albeit unstable ones. From a careful inspection of the plotted curves, we have identified the value of <math>~\chi_\mathrm{eq}</math> that corresponds to the two newly discovered (unstable) equilibrium models; these values are recorded in the table that immediately follows this paragraph. By construction, we also know what values of <math>~\mathcal{A}, \mathcal{B}</math>, and <math>~\mathcal{C}</math> are associated with these two identified equilibria; these values also have been recorded in the table. But it is not immediately obvious what the values are of the <math>~(\nu, \rho_e/\rho_c)</math> model parameters that correspond to these two equilibrium models.
|
Subsequently Identified Local Energy Maxima |
||||||||
|
<math>~\chi_\mathrm{eq}</math> |
<math>~\mathfrak{G}^*</math> |
<math>~\chi_\mathrm{eq}^{4-3\gamma_c}</math> |
<math>~\therefore</math> |
<math>~\mathcal{A}</math> |
<math>~\mathcal{B}</math> |
<math>~\mathcal{C}</math> |
<math>~\mathcal{C}^' = \mathcal{A} \chi_\mathrm{eq}^{3\gamma_c-4} - \mathcal{B}</math> |
<math>~\biggl( \frac{\mathcal{C}}{\mathcal{C}^'} \biggr)^{1/(3\gamma_e - 3\gamma_c)}</math> |
|
<math>~0.08255</math> |
<math>~+ 4.87562</math> |
<math>~0.368715</math> |
<math>~0</math> |
<math>~0.2143496</math> |
<math>~0.5635746</math> |
<math>~4.4626 \times 10^{-5}</math> |
<math>~1.7768 \times 10^{-2}</math> |
<math>~0.08254</math> |
|
<math>~0.032196</math> |
<math>~+11.5187</math> |
<math>~0.25300</math> |
<math>~0</math> |
<math>~0.2152641</math> |
<math>~0.791882</math> |
<math>~1.5464 \times 10^{-5}</math> |
<math>~5.8964 \times 10^{-2}</math> |
<math>~0.032196</math> |
Related Discussions
- Newer, Version2 of Bipolytrope Generalization derivations.
- Analytic solution with <math>~n_c = 0</math> and <math>~n_e=0</math>.
- Analytic solution with <math>~n_c = 5</math> and <math>~n_e=1</math>.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |