Difference between revisions of "User:Tohline/SSC/FreeEnergy/PolytropesEmbedded"
(→From Detailed Force-Balance Models: Reformat w_grav expression) |
(→Summary: Finished proving that all four expressions are correct for case of n=5 as well!) |
||
| (149 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
__FORCETOC__ | __FORCETOC__ | ||
=Free-Energy | =Free-Energy Synopsis= | ||
{{LSU_HBook_header}} | {{LSU_HBook_header}} | ||
All of the self-gravitating configurations considered below have an associated Gibbs-like free-energy that can be expressed analytically as a power-law function of the dimensionless configuration radius, <math>~x</math>. Specifically, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 10: | Line 9: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathfrak{G}</math> | <math>~\mathfrak{G}^*_\mathrm{type}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 16: | Line 15: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~-ax^{-1} + b x^{-3/n} + c x^{-3/j} + \mathfrak{G}_0 \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
< | </table> | ||
</div> | |||
==Equilibrium Radii and Critical Radii== | |||
The first and second (partial) derivatives with respect to <math>~x</math> are, respectively, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{\partial\mathfrak{G}^*_\mathrm{type}}{\partial x}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 28: | Line 34: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ax^{-2} - \biggl(\frac{ 3b}{n}\biggr) x^{-3/n -1} -\biggl(\frac{3 c}{j}\biggr) x^{-3/j-1} </math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| Line 44: | Line 46: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{1}{x^2} \biggl[ a - \biggl(\frac{ 3b}{n}\biggr) x^{(n-3)/n } -\biggl(\frac{3 c}{j}\biggr) x^{(j-3)/j} \biggr] \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\frac{\partial^2 \mathfrak{G}^*_\mathrm{type}}{\partial x^2}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>\ | <math>~-2ax^{-3} + \biggl(\frac{ 3b}{n}\biggr) \biggl( \frac{n+3}{n}\biggr) x^{-3/n -2} + \biggl(\frac{3 c}{j}\biggr)\biggl( \frac{j+3}{j}\biggr) x^{-3/j-2} </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 89: | Line 70: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ \biggl( - \frac{3\ | <math>~ | ||
\frac{1}{x^3} \biggl\{ \biggl(\frac{ 3b}{n}\biggr) \biggl( \frac{n+3}{n}\biggr) x^{(n-3)/n} | |||
+ \biggl(\frac{3 c}{j}\biggr)\biggl( \frac{j+3}{j}\biggr) x^{(j-3)/j} -2a\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Equilibrium configurations are identified by setting the first derivative to zero. This gives, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~a - \biggl(\frac{ 3b}{n}\biggr) x^{(n-3)/n }_\mathrm{eq} -\biggl(\frac{3 c}{j}\biggr) x^{(j-3)/j}_\mathrm{eq} </math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 95: | Line 98: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>\ | <math>~\Rightarrow ~~~x^{(n-3)/n }_\mathrm{eq}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math>\frac{ | <math>~\biggl(\frac{n}{ 3b}\biggr) \biggl[a -\biggl(\frac{3 c}{j}\biggr) x^{(j-3)/j}_\mathrm{eq} \biggr] \, .</math> | ||
\biggl[\ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 109: | Line 110: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Rightarrow ~~~\frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} + \frac{1}{j}\cdot x^{(j-3)/j}_\mathrm{eq} </math> | ||
\ | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 117: | Line 116: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ 0 \, .</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | |||
We conclude, as well, that ''at'' this equilibrium radius, the second (partial) derivative assumes the value, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 134: | Line 128: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathfrak{ | <math>~\biggl[ \frac{\partial^2 \mathfrak{G}^*_\mathrm{type}}{\partial x^2} \biggr]_\mathrm{eq}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 140: | Line 134: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
( | \frac{1}{x^3_\mathrm{eq} } \biggl\{ \biggl(\frac{ 3b}{n}\biggr) \biggl( \frac{n+3}{n}\biggr) x^{(n-3)/n} | ||
+ \biggl(\frac{3 c}{j}\biggr)\biggl( \frac{j+3}{j}\biggr) x^{(j-3)/j} -2a\biggr\}_\mathrm{eq} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 148: | Line 143: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 154: | Line 149: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \frac{1}{x^3_\mathrm{eq} } \biggl\{ \biggl( \frac{n+3}{n}\biggr) \biggl[a -\biggl(\frac{3 c}{j}\biggr) x^{(j-3)/j}_\mathrm{eq} \biggr] | ||
\biggl[ | + \biggl(\frac{3 c}{j}\biggr)\biggl( \frac{j+3}{j}\biggr) x^{(j-3)/j}_\mathrm{eq} -2a\biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 163: | Line 158: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 170: | Line 165: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \frac{1}{x^3_\mathrm{eq} } \biggl\{ \biggl(\frac{3 c}{j}\biggr) \biggl[ \biggl( \frac{j+3}{j}\biggr) | ||
-\biggl( \frac{n+3}{n}\biggr) \biggl] x^{(j-3)/j}_\mathrm{eq} | |||
+ \biggl( \frac{3-n}{n}\biggr) a\biggr\} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 176: | Line 173: | ||
</table> | </table> | ||
</div> | </div> | ||
Hence, equilibrium configurations for which the ''second'' (as well as first) derivative of the free energy is zero are found at "critical" radii given by the expression, | |||
<div align="center"> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~0</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 195: | Line 186: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
\biggl(\frac{3 c}{j}\biggr) \biggl[ \biggl( \frac{j+3}{j}\biggr) | |||
-\biggl( \frac{n+3}{n}\biggr) \biggl] [x_\mathrm{eq}^{(j-3)/j}]_\mathrm{crit} | |||
+ \biggl( \frac{3-n}{n}\biggr) a | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Rightarrow ~~~[x_\mathrm{eq}^{(j-3)/j}]_\mathrm{crit} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl[ | <math>~\biggl[ \frac{j^2 a(n-3)}{3 c}\biggr] [ n(j+3) - j(n+3) ]^{-1} | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 224: | Line 209: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{a}{3^2c}\biggl[ \frac{j^2(n-3)}{n-j} \biggr] | |||
\, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
==Examples== | |||
===Pressure-Truncated Polytropes=== | |||
For pressure-truncated polytropes of index <math>~n</math>, we set, <math>~j = -1</math>, in which case, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding=" | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} - x^{4}_\mathrm{eq}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~0 \, ;</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
< | <tr> | ||
< | <td align="right"> | ||
<math>~\biggl[ \biggl(\frac{3}{4\pi}\biggr) \frac{ M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr]^{(n+1)/n} x^{(n-3)/n }_\mathrm{eq} | |||
- \frac{3}{20\pi} \biggl( \frac{n+1}{n}\biggr)\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr)^{2} - x^{4}_\mathrm{eq}</math> | |||
</td> | |||
<math> | <td align="center"> | ||
\ | <math>~=</math> | ||
</td> | |||
<td align="left"> | |||
</math> | <math>~0 \, ;</math> | ||
</ | </td> | ||
</tr> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~x^{(n-3)/n }_\mathrm{eq}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl( \frac{n | <math>~\biggl(\frac{n}{ 3b}\biggr) \biggl[a + 3cx^{4}_\mathrm{eq} \biggr] \, ;</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 290: | Line 270: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
and | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
| |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~[x_\mathrm{eq}]_\mathrm{crit} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 316: | Line 288: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{a(n-3)}{3^2 c (n+1)} \biggr]^{1/4} \, . | ||
\biggl | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 323: | Line 295: | ||
</div> | </div> | ||
====Case M==== | |||
<!-- Next segment supports PowerPoint presentation | |||
<div align="center"> | |||
<math>( {\tilde{\mathfrak{f}}}_M, {\tilde{\mathfrak{f}}}_W, {\tilde{\mathfrak{f}}}_A)</math> | |||
</div> | |||
<div align="center"> | <div align="center"> | ||
< | <math>~\frac{d}{dx_\mathrm{eq}}\biggl(\frac{P_e}{P_\mathrm{norm}}\biggr)= 0</math> | ||
</div> | |||
--> | |||
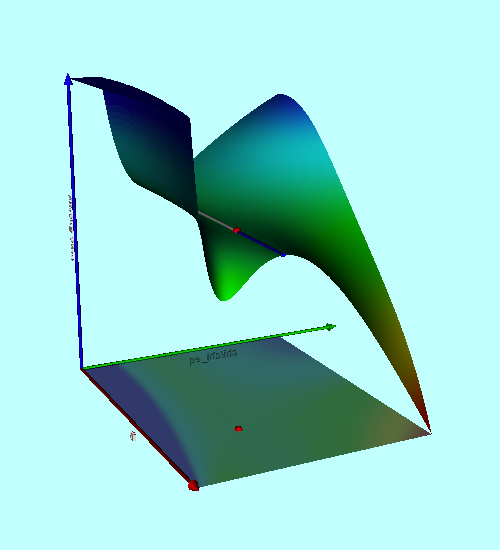
<tr> | More specifically, the expression that describes the [[#Case_M_Free-Energy_Surface|"Case M" free-energy surface]] is, | ||
<td align="right"> | <div align="center"> | ||
<math>~\mathfrak{G}_{K, | <table border="1" cellpadding="5" align="center"> | ||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}_{K,M}^* \equiv \frac{\mathfrak{G}_{K,M}}{E_\mathrm{norm}} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | -3\mathcal{A} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^{-1} +~ n\mathcal{B} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^{-3/n} | ||
+~ \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^3 | |||
\, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</td></tr> | |||
</table> | |||
</div> | |||
Hence, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~a</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~\equiv</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~3\mathcal{A} = \frac{3}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}\, , | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 361: | Line 353: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~b</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~n\mathcal{B} = n\biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, , | ||
\biggl( \frac{ | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~c</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~\equiv</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{4\pi}{3}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, , | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
where the structural form factors for pressure-truncated polytropes are precisely defined [[User:Tohline/SSC/Virial/FormFactors#PTtable|here]]. Therefore, the statement of virial equilibrium is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~0 </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 398: | Line 391: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} - x^{4}_\mathrm{eq}</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 406: | Line 397: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ \biggl(\frac{3}{4\pi}\biggr)c x_\mathrm{eq}^4 </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl(\frac{3}{4\pi}\biggr) \biggl[ \frac{ b}{n}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3} \biggr]</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 420: | Line 409: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ \biggl(\frac{P_e}{P_\mathrm{norm}}\biggr) x_\mathrm{eq}^4 </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl(\frac{3}{4\pi}\biggr) \biggl[ \biggl(\frac{3}{4\pi} \biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \cdot x^{(n-3)/n }_\mathrm{eq} | ||
- \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr]</math> | |||
\ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| Line 438: | Line 424: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \cdot x^{(n-3)/n }_\mathrm{eq} | ||
- \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \, .</math> | |||
\ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<!-- NEXT STEP IS FOR POWERPOINT PRESENTATION ... | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl(\frac{P_e}{P_\mathrm{norm}}\biggr) x_\mathrm{eq}^4 </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 456: | Line 441: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{3}{20\pi} \biggl[ 5\biggl(\frac{3}{4\pi} \biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \cdot x^{(n-3)/n }_\mathrm{eq} | ||
\biggl( \frac{ | - \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr] </math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
--> | |||
</table> | |||
</div> | |||
And we conclude that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~3c[x_\mathrm{eq}]^4_\mathrm{crit} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{(n-3)}{5(n+1)} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 479: | Line 468: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) [x_\mathrm{eq}]^4_\mathrm{crit}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{1}{20\pi} \biggl( \frac{n-3}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> | ||
\biggl(\frac{ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 495: | Line 480: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ \biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \cdot [ x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} | |||
- \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{1}{20\pi} \biggl( \frac{n-3}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> | ||
</td> | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathfrak{ | <math>~\Rightarrow ~~~ \biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \cdot [ x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 522: | Line 500: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{1}{20\pi} \biggl( \frac{n-3}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} | ||
\biggl( \frac{n}{n+1} \biggr)^{3 | + \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 533: | Line 510: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{1}{20\pi} \biggl( \frac{4n}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} | ||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 546: | Line 520: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ [ x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{1}{20\pi} \biggl(\frac{4\pi}{3} \biggr)^{(n+1)/n} \biggl( \frac{4n}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_A \tilde{\mathfrak{f}}_M^{(n-1)/n} } | ||
\biggl(\frac{ | |||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 563: | Line 534: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ [ x_\mathrm{eq} ]_\mathrm{crit} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ \biggl[\frac{4n}{15(n+1)} \biggl(\frac{4\pi}{3} \biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_A \tilde{\mathfrak{f}}_M^{(n-1)/n} } \biggr]^{n/(n-3)} \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="1" cellpadding="8" width="90%"><tr><td align="left"> | |||
<font color="red"><b>ASIDE:</b></font> Let's see what this requires for the case of <math>~n=5</math>, where everything is specifiable analytically. We have gathered together: | |||
* Form factors from [[User:Tohline/SSC/Virial/FormFactors#Summary_.28n.3D5.29|here]]. | |||
* Hoerdt's equilibrium expressions from [[User:Tohline/SSC/Structure/PolytropesEmbedded#Tabular_Summary_.28n.3D5.29|here]]. | |||
* Conversion from Horedt's units to ours as specified [[User:Tohline/SphericallySymmetricConfigurations/Virial#Choices_Made_by_Other_Researchers|here]]. | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~{\tilde\mathfrak{f}}_M</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 584: | Line 565: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
( 1 + \ell^2 )^{-3/2} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 592: | Line 573: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~{\tilde\mathfrak{f}}_W</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{5}{2^4} \cdot \ell^{-5} \biggl[ \ell \biggl( \ell^4 - \frac{8}{3}\ell^2 - 1 \biggr)(1 + \ell^2)^{-3} + \tan^{-1}(\ell ) \biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 607: | Line 587: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~{\tilde\mathfrak{f}}_A</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{3}{2^3} \ell^{-3} [ \tan^{-1}(\ell ) + \ell (\ell^2-1) (1+\ell^2)^{-2} ] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 623: | Line 601: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{norm}} = \frac{R_\mathrm{eq}}{R_\mathrm{Horedt}} \biggl[ \frac{4\pi}{(n+1)^n} \biggr]^{1/(n-3)}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl\{ 3 \biggl[ \frac{(\xi_e^2/3)^5}{(1+\xi_e^2/3)^{6}} \biggr] \biggr\}^{-1/2}\biggl[ \frac{4\pi}{(n+1)^n} \biggr]^{1/(n-3)}</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 644: | Line 619: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{(1+\ell^2)^{3}}{\ell^{5}} \biggr] \biggl[ \frac{\pi}{2^3\cdot 3^6} \biggr]^{1/2}</math> | ||
\biggl[\frac{ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 653: | Line 625: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{P_e}{P_\mathrm{norm}} = \frac{P_e}{P_\mathrm{Horedt}} \biggl[ \frac{(n+1)^3}{4\pi} \biggr]^{(n+1)/(n-3)}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~3^3 \biggl[ \frac{(\xi_e^2/3)^3}{(1+\xi_e^2/3)^{4}} \biggr]^3 \biggl[ \frac{(n+1)^3}{4\pi} \biggr]^{(n+1)/(n-3)}</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 675: | Line 643: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{\ell^{18}}{(1+\ell^2)^{12}} \biggr] \biggl[ \frac{2 \cdot 3^4}{\pi} \biggr]^{3}</math> | ||
\biggl[\frac{ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
So, the radius of the critical equilibrium state should be, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl[\frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr]^4_\mathrm{crit} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{(n-3)}{3\cdot 5(n+1)} \biggl(\frac{3}{2^2\pi}\biggr) \biggl(\frac{P_e}{P_\mathrm{norm}}\biggr)^{-1}\cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} | ||
\biggl(\frac{ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 705: | Line 671: | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{1}{2^2\cdot 3\cdot 5 \pi} | ||
\biggl\{\frac{(1+\ell^2)^{12}}{\ell^{18}} \biggl[ \frac{\pi}{2 \cdot 3^4} \biggr]^{3}\biggr\} (1+\ell^2)^3 | |||
+ \ | \cdot \biggl\{ \frac{5}{2^4} \cdot \ell^{-5} \biggl[ \ell \biggl( \ell^4 - \frac{8}{3}\ell^2 - 1 \biggr)(1 + \ell^2)^{-3} + \tan^{-1}(\ell ) \biggr] \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 733: | Line 687: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{\pi^2}{2^9\cdot 3^{13}} | ||
\biggl | \biggl\{\frac{(1+\ell^2)^{12}}{\ell^{23}} \biggr\} | ||
\cdot \biggl\{ \biggl[ \ell \biggl( \ell^4 - \frac{8}{3}\ell^2 - 1 \biggr) + (1 + \ell^2)^{3}\tan^{-1}(\ell ) \biggr] \biggr\} \, ; | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
whereas, each equilibrium configuration has, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\biggl[\frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr]^4 </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 761: | Line 705: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~\frac{\pi^2}{2^6\cdot 3^{12}} \biggl[ \frac{(1+\ell^2)^{12}}{\ell^{20}} \biggr] \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
So the equilibrium state that marks the critical configuration must have a value of <math>~\ell</math> that satisfies the relation, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{\pi^2}{2^6\cdot 3^{12}} \biggl[ \frac{(1+\ell^2)^{12}}{\ell^{20}} \biggr] </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{\pi^2}{2^9\cdot 3^{13}} | ||
\biggl\{\frac{(1+\ell^2)^{12}}{\ell^{23}} \biggr\} | |||
\cdot \biggl\{ \biggl[ \ell \biggl( \ell^4 - \frac{8}{3}\ell^2 - 1 \biggr) + (1 + \ell^2)^{3}\tan^{-1}(\ell ) \biggr] \biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 787: | Line 729: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Rightarrow ~~~2^3\cdot 3 \ell^3</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ell ( \ell^4 - \frac{8}{3}\ell^2 - 1 ) + (1 + \ell^2)^{3}\tan^{-1}(\ell ) | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 800: | Line 743: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~\biggl[ \frac{(1 + \ell^2)^{3}}{\ell} \biggr] \tan^{-1}(\ell ) </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~1 + \frac{80}{3}\cdot \ell^2 -\ell^4 \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
The solution is: <math>~\ell_\mathrm{crit} \approx 2.223175 \, .</math> | |||
</td></tr></table> | |||
</div> | |||
In addition, we know from [[User:Tohline/SSC/Virial/PolytropesEmbedded/SecondEffortAgain#Virial_Equilibrium_of_Adiabatic_Spheres_.28Summary.29|our dissection of Hoerdt's work on detailed force-balance models]] that, in the equilibrium state, | |||
<div align="center"> | |||
<table border="0" cellpadding="5"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl(\frac{P_e}{P_\mathrm{norm}}\biggr) \biggl(\frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 820: | Line 773: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\biggl[ \frac{\tilde\theta^{n+1} }{(4\pi)(n+1)( -\tilde\theta' )^{2}} \biggr] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 827: | Line 781: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~ 3c x_\mathrm{eq}^4</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\biggl[ \frac{\tilde\theta^{n+1} }{(n+1)( -\tilde\theta' )^{2}} \biggr] | |||
\, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
This means that, for any chosen polytropic index, the critical equilibrium state is the equilibrium configuration for which (needs to be checked), | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~2(9-2n){\tilde\theta}^{n+1}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 848: | Line 809: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | 3(n-3)\biggl[ (- {\tilde\theta}^')^2 - \frac{\tilde\theta(-{\tilde\theta}^')}{\tilde\xi}\biggr] \, . | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 854: | Line 815: | ||
</table> | </table> | ||
</div> | </div> | ||
We note, as well, that by combining the Horedt expression for <math>~x_\mathrm{eq}</math> with our virial equilibrium expression, we find (needs to be checked), | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 860: | Line 822: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~x_\mathrm{eq}^{n-3}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{4\pi}{3}\biggl[ \frac{3}{(n+1)\tilde\xi^2} + \frac{{\tilde\mathfrak{f}}_{W} - {\tilde\mathfrak{f}}_{M}}{5\tilde\mathfrak{f}_A} \biggr]^{n} {\tilde\mathfrak{f}}_{M}^{1-n} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
====Case P==== | |||
=====First Pass===== | |||
Alternatively, let's examine the [[#Case_P_Free-Energy_Surface|"Case P" free-energy surface]]. Drawing on [[User:Tohline/SSC/Structure/PolytropesEmbedded#Stahler.27s_Presentation|Stahler's presentation]], we adopt the following radius and mass normalizations: | |||
<div align="center"> | |||
<math>M_\mathrm{SWS} = | |||
\biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \, ,</math> | |||
</div> | |||
<div align="center"> | |||
<math> | |||
R_\mathrm{SWS} = \biggl( \frac{n+1}{n} \biggr)^{1/2} G^{-1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \, . | |||
</math> | |||
</div> | |||
In terms of these new normalizations, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~R_\mathrm{norm} \equiv \biggl[\biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{(n-1)} \biggr]^{1/(n-3)}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{G}{K} \biggr)^{n/(n-3)} M_\mathrm{tot}^{(n-1)/(n-3)} | |||
R_\mathrm{SWS} \biggl( \frac{n+1}{n} \biggr)^{-1/2} G^{1/2} K_n^{-n/(n+1)} P_\mathrm{e}^{-(1-n)/[2(n+1)]} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 884: | Line 868: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl[ \frac{ | <math>~+ | ||
M_\mathrm{SWS}^{-(n-1)/(n-3)} \biggl[ \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \biggr]^{(n-1)/(n-3)} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
< | <tr> | ||
< | <td align="right"> | ||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~R_\mathrm{SWS} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} | |||
\biggl( \frac{n+1}{n} \biggr)^{[3(n-1)-(n-3)]/[2(n-3)]} | |||
G^{[2n+(n-3)-3(n-1)]/[2(n-3)]} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~+ K_n^{n[2(n-1) - (n+1) - (n-3)]/[(n+1)(n-3)]} P_\mathrm{e}^{-(n-1)(3-n)/[2(n+1)(n-3)]} | ||
P_\mathrm{e}^{(n-1)(3-n)/[2(n+1)(n-3)]} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 923: | Line 917: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~R_\mathrm{SWS} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \, . | ||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 932: | Line 924: | ||
</div> | </div> | ||
and, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 938: | Line 930: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~P_\mathrm{norm} \equiv \biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)} } \biggr]^{1/(n-3)}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ \frac{K^{4n}}{G^{3(n+1)} } \biggr]^{1/(n-3)} | |||
- | \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{-2(n+1)/(n-3)} | ||
\biggl\{ \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]}\biggr\}^{-2(n+1)/(n-3)} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 957: | Line 949: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{-2(n+1)/(n-3)} | |||
\biggl( \frac{n+1}{n} \biggr)^{-3(n+1)/(n-3)} | |||
K^{4n/(n-3)} G^{-3(n+1)/(n-3)} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 972: | Line 965: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\times~ | ||
- | G^{3(n+1)/(n-3)} K_n^{-4n/(n-3)} | ||
\biggl\{ P_\mathrm{e}^{-(n-3)/[2(n+1)]}\biggr\}^{-2(n+1)/(n-3)} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 984: | Line 977: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 990: | Line 983: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~P_e | ||
\biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{-2(n+1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{-3(n+1)/(n-3)} \, . | |||
</math> | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
<span id="FirstPassFreeEnergy">Rewriting the expression for the free energy gives,</span> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathfrak{G}_{K,M}^* \equiv \frac{\mathfrak{G}_{K,M}}{E_\mathrm{norm}} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,006: | Line 1,004: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- | -3\mathcal{A} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} \biggl(\frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr) | ||
+ \mathcal{B} | +~ n\mathcal{B} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} \biggl(\frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr)^{3/n} | ||
+~ \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \biggl(\frac{R_\mathrm{norm}}{R_\mathrm{SWS}}\biggr)^{-3} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl | <math>~ | ||
-3\mathcal{A} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} \biggl[ \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)}\biggr] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,032: | Line 1,027: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl( \frac{ | <math>~ | ||
+~ n\mathcal{B} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} \biggl[ \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)}\biggr]^{3/n} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | +~ \biggl( \frac{4\pi}{3} \biggr) \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{2(n+1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{3(n+1)/(n-3)} | ||
\biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \biggl[ \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)}\biggr]^{-3} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
< | <td align="right"> | ||
< | | ||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-3\mathcal{A} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} | |||
+~ n\mathcal{B} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} | |||
\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl(\frac{ | <math>~ | ||
+~ \biggl( \frac{4\pi}{3} \biggr) \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} | |||
\biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(5-n)/(n-3)} | |||
\biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \, . | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,088: | Line 1,088: | ||
</div> | </div> | ||
Therefore, in this case, we have, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 1,095: | Line 1,095: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~a</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,101: | Line 1,101: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{3}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \, , | ||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,109: | Line 1,108: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~b</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,115: | Line 1,114: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl(\frac{ | <math>~ | ||
n\biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} | |||
\biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} | |||
\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~c</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{4\pi}{3} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(5-n)/(n-3)} \, , | ||
\frac{ | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
where the structural form factors for pressure-truncated polytropes are precisely defined [[User:Tohline/SSC/Virial/FormFactors#PTtable|here]]. The statement of virial equilibrium is, therefore, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~x^{4}_\mathrm{eq} + \alpha </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,151: | Line 1,150: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
\beta x^{(n-3)/n }_\mathrm{eq} \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\alpha \equiv \frac{a}{3c}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{1}{ | <math>~ | ||
\frac{ | \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} | ||
\biggl\{ \frac{3}{4\pi} \biggl( \frac{n+1}{n} \biggr)^{-3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(n-5)/(n-3)} \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,174: | Line 1,178: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{\ | <math>~ | ||
\frac{ | \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr) \mathfrak{m}^{2} \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,211: | Line 1,206: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\beta \equiv \frac{b}{nc}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,217: | Line 1,212: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~- | <math>~ | ||
\biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} | |||
\biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} | |||
\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} | |||
\biggl\{ \frac{3}{4\pi} \biggl( \frac{n+1}{n} \biggr)^{-3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(n-5)/(n-3)} \biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,223: | Line 1,223: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,235: | Line 1,237: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathfrak{m}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl(\frac{3}{4\pi}\biggr) \frac{1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr) \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
From a previous derivation, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~0 </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} - x^{4}_\mathrm{eq} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,267: | Line 1,277: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{3}{4\pi} \biggl( \frac{n+1}{n} \biggr)^{-3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(n-5)/(n-3)} \biggl\{ | ||
\biggl | \biggl(\frac{3}{4\pi} \biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} | ||
\biggl(\frac{ | \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} | ||
\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \biggr\} \cdot x^{(n-3)/n }_\mathrm{eq} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,276: | Line 1,287: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- \frac{3}{4\pi} \biggl( \frac{n+1}{n} \biggr)^{-3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(n-5)/(n-3)} \biggl\{ | |||
\biggl | \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggr\} | ||
- x^{4}_\mathrm{eq} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,291: | Line 1,303: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~0</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,297: | Line 1,309: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl | <math>~ | ||
\mathfrak{ | \biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} | ||
\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} x^{(n-3)/n }_\mathrm{eq} | |||
\biggl(\frac{ | - \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} - x^{4}_\mathrm{eq} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,322: | Line 1,325: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl( \frac{ | <math>~ \tilde{\mathfrak{f}}_A \biggl[ \biggl(\frac{3}{4\pi} \biggr) \frac{1}{\tilde{\mathfrak{f}}_M} | ||
\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)\biggr]^{(n+1)/n} x^{(n-3)/n }_\mathrm{eq} | |||
- \frac{1}{5} \biggl(\frac{4\pi}{3}\biggr) \cdot \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr)\biggl[ \biggl(\frac{3}{4\pi} \biggr) \frac{1}{\tilde{\mathfrak{f}}_M} | |||
\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)\biggr]^{2} - x^{4}_\mathrm{eq} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,329: | Line 1,335: | ||
</div> | </div> | ||
which, thankfully, matches! We conclude as well that the transition from stable to dynamically unstable configurations occurs at, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 1,335: | Line 1,341: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~[x_\mathrm{eq}]_\mathrm{crit}^4</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,341: | Line 1,347: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{(n-3)}{3 (n+1)} \biggr] \alpha \, . | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<!-- FOR POWERPOINT SYNOPSIS | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~[x_\mathrm{eq}]_\mathrm{crit}^4</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,363: | Line 1,361: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{(n-3)}{3 (n+1)} \biggr] \frac{a}{3c} | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,377: | Line 1,375: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \frac{(n-3)}{20\pi n} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~ [x_\mathrm{eq}]_\mathrm{crit}^{2(n+1)}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,395: | Line 1,388: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{n}{n-3} \biggr)^{(1-n)} | |||
\biggl( \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W} \biggr)^{(n+1)} | |||
\biggl(\frac{\tilde{\mathfrak{f}}_A}{4} \biggr)^{2n} \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
--> | |||
</table> | </table> | ||
</div> | </div> | ||
When combined with the statement of virial equilibrium ''at'' this critical point, we find, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 1,407: | Line 1,406: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~ | ||
\biggl\{ \biggl[ \frac{(n-3)}{3 (n+1)} \biggr] + 1\biggr\}\frac{ \alpha }{\beta} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
[x_\mathrm{eq}]^{(n-3)/n }_\mathrm{crit} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,419: | Line 1,422: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
\biggl\{ \biggl[ \frac{(n-3)}{3 (n+1)} \biggr] \alpha \biggr\}^{(n-3)/(4n) } | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl[ | <math>~\Rightarrow~~~ | ||
\biggl[ \frac{4n}{3 (n+1)} \biggr]^{4n} \biggl( \frac{ \alpha }{\beta} \biggr)^{4n} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ \frac{(n-3)}{3 (n+1)} \biggr]^{(n-3)} \alpha^{(n-3)} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,453: | Line 1,452: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ | <math>~\Rightarrow~~~ | ||
\biggl[ \frac{3 n}{(n-3)} \biggl( \frac{n+1}{n}\biggr) \biggr]^{(3-n)} \biggl[ \frac{3 }{4} \biggl( \frac{n+1}{n}\biggr) \biggr]^{4n} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \alpha^{3(n+1)} \beta^{-4n} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,472: | Line 1,471: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{ | \biggl\{ \biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr) \mathfrak{m}^{2} \biggr\}^{3(n+1)} | ||
\biggl | \biggl\{ \tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} \biggr\}^{-4n} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\tilde{\mathfrak{f}}_A^{-4n} | ||
\biggl( \frac{ | \biggl[ \biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr)\biggr]^{3(n+1)} \mathfrak{m}^{2(n+1)} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,505: | Line 1,497: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ | |||
\mathfrak{m}^{2(n+1)} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ \biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr)\biggr]^{-3(n+1)} | |||
\biggl( \frac{ | \biggl[ \frac{3 n}{(n-3)} \biggl( \frac{n+1}{n}\biggr) \biggr]^{(3-n)} \biggl[ \frac{3\tilde{\mathfrak{f}}_A }{4} \biggl( \frac{n+1}{n}\biggr) \biggr]^{4n} | ||
\biggl[ \mathfrak{ | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{3}{ | \biggl[ \biggl( \frac{3\cdot 5}{4\pi}\biggr) \frac{1}{\tilde{\mathfrak{f}}_W} \biggr]^{3(n+1)} | ||
\biggl[ | \biggl[ \frac{3 n}{(n-3)} \biggr]^{(3-n)} \biggl[ \frac{3\tilde{\mathfrak{f}}_A }{4} \biggr]^{4n} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ \frac{1}{ | <math>~ | ||
\biggl[ \frac{3^2 \cdot 5 n}{ 4\pi(n-3)} \cdot \frac{1}{\tilde{\mathfrak{f}}_W} \biggr]^{(3-n)} | |||
\biggl[ \biggl( \frac{3^2\cdot 5}{2^4\pi}\biggr) \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_W} \biggr]^{4n} \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
This also means that the critical radius is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~[x_\mathrm{eq}]_\mathrm{crit}^4</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{(n-3)}{3 (n+1)} \biggr] \biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr) \mathfrak{m}^{2} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,580: | Line 1,566: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ \frac{ | <math>~ \biggl[ \frac{3^2\cdot 5 n}{4\pi(n-3)} \cdot \frac{1}{\tilde{\mathfrak{f}}_W}\biggr]^{-1} \mathfrak{m}^{2} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~ [x_\mathrm{eq}]_\mathrm{crit}^{4(n+1)}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{3^2\cdot 5 n}{4\pi(n-3)} \cdot \frac{1}{\tilde{\mathfrak{f}}_W} \biggr]^{-(n+1)} | ||
\biggl | \biggl[ \frac{3^2 \cdot 5 n}{ 4\pi(n-3)} \cdot \frac{1}{\tilde{\mathfrak{f}}_W} \biggr]^{(3-n)} | ||
\biggl(\frac{ | \biggl[ \biggl( \frac{3^2\cdot 5}{2^4\pi}\biggr) \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_W} \biggr]^{4n} | ||
\ | </math> | ||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{4\pi(n-3)}{3^2\cdot 5 n} \cdot \tilde{\mathfrak{f}}_W \biggr]^{2(n-1)} | |||
\biggl[ \biggl( \frac{3^2\cdot 5}{2^4\pi}\biggr) \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_W} \biggr]^{4n} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Rightarrow ~~~ [x_\mathrm{eq}]_\mathrm{crit}^{2(n+1)}</math> | ||
\ | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ \frac{ | <math>~ | ||
\ | \biggl[ \frac{n}{(n-3)} \biggl( \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W} \biggr) \biggr]^{(1-n)} | ||
\biggl[ \biggl( \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W}\biggr) \frac{\tilde{\mathfrak{f}}_A}{4} \biggr]^{2n} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,641: | Line 1,620: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~ | ||
\biggl | \biggl( \frac{n}{n-3} \biggr)^{(1-n)} | ||
\biggl( \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W} \biggr)^{(n+1)} | |||
\biggl(\frac{\tilde{\mathfrak{f}}_A}{4} \biggr)^{2n} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
<!-- THERE IS A MISTAKE IN THIS OMITTED SUBSECTION | |||
From an earlier derivation, we obtained, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding=" | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\biggl[\frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]^4_\mathrm{crit} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~\biggl[ \frac{(n-3)}{3^2 (n+1)} \biggr] \frac{a}{c} | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,679: | Line 1,660: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\pi \ | <math>~\biggl[ \frac{(n-3)}{3^2 (n+1)} \biggr] | ||
\biggl[ \frac{3}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggr] | |||
\biggl[ \frac{3}{4\pi} \biggl( \frac{n+1}{n} \biggr)^{-3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(n-5)/(n-3)} \biggr] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,691: | Line 1,675: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~[x_\mathrm{eq}]_\mathrm{crit}^4</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{\pi}{2} | <math>~ | ||
\frac{(n-3)}{20\pi n} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} | |||
= \tilde{\mathfrak{f}}_W \cdot \frac{(n-3)}{15 n} \biggl(\frac{4\pi}{3}\biggr) \biggl[\biggl(\frac{3}{4\pi}\biggr)\frac{1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)\biggr]^{2} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ \ | <math>~\Rightarrow ~~~\biggl[\biggl(\frac{3}{4\pi}\biggr)\frac{1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)\biggr] | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
\biggl[ \frac{1}{\tilde{\mathfrak{f}}_W} \cdot \frac{15 n}{(n-3)} \biggl(\frac{3}{4\pi}\biggr)\biggr]^{1/2} [x_\mathrm{eq}]_\mathrm{crit}^2</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
which, when combined with the statement of virial equilibrium ''at'' this critical point, implies, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding=" | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl[\frac{ | <math>~\tilde{\mathfrak{f}}_A \biggl\{ \biggl[ \frac{1}{\tilde{\mathfrak{f}}_W} \cdot \frac{15 n}{(n-3)} \biggl(\frac{3}{4\pi}\biggr)\biggr]^{1/2} [x_\mathrm{eq}]_\mathrm{crit}^2\biggr\}^{(n+1)/n} [x_\mathrm{eq}]_\mathrm{crit}^{(n-3)/n }</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl\{ \biggl[ | [x_\mathrm{eq}]_\mathrm{crit}^4 | ||
+ \frac{1}{5} \biggl(\frac{4\pi}{3}\biggr) \cdot \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr) \biggl\{ \biggl[ \frac{1}{\tilde{\mathfrak{f}}_W} \cdot \frac{15 n}{(n-3)} \biggl(\frac{3}{4\pi}\biggr)\biggr]^{1/2} [x_\mathrm{eq}]_\mathrm{crit}^2\biggr\}^{2} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,738: | Line 1,724: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow~~~ \tilde{\mathfrak{f}}_A \biggl[ \frac{1}{\tilde{\mathfrak{f}}_W} \cdot \frac{15 n}{(n-3)} \biggl(\frac{3}{4\pi}\biggr)\biggr]^{(n+1)/(2n)} | |||
[x_\mathrm{eq}]_\mathrm{crit}^{(3n-1)/n }</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
[x_\mathrm{eq}]_\mathrm{crit}^4 \biggl\{ 1 | |||
+ \frac{1}{5} \biggl(\frac{4\pi}{3}\biggr) \cdot \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr) \biggl[ \frac{1}{\tilde{\mathfrak{f}}_W} \cdot \frac{15 n}{(n-3)} \biggl(\frac{3}{4\pi}\biggr)\biggr]^{2} \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,751: | Line 1,740: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow~~~ [x_\mathrm{eq}]_\mathrm{crit}^{(n+1)/n} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ -\biggl( \frac{ | <math>~ | ||
\biggl\{ | \tilde{\mathfrak{f}}_A \biggl[ \frac{1}{\tilde{\mathfrak{f}}_W} \cdot \frac{15 n}{(n-3)} \biggl(\frac{3}{4\pi}\biggr)\biggr]^{(n+1)/(2n)} | ||
\biggl\{ 1+ \frac{1}{5} \biggl(\frac{4\pi}{3}\biggr) \cdot \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr) \biggl[ \frac{1}{\tilde{\mathfrak{f}}_W} \cdot \frac{15 n}{(n-3)} \biggl(\frac{3}{4\pi}\biggr)\biggr]^{2} \biggr\}^{-1} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
END OMITTED SUBSECTION --> | |||
The following parallel derivation was done independently. [<font color="red">Note that a factor of 2n/(n-1) appears to correct a mistake made during the original derivation.</font>] Beginning with the virial expression, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\beta x^{(n-3)/n }_\mathrm{eq} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\alpha + x^{4}_\mathrm{eq} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | |||
\biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} | |||
\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} [x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} | ||
+ \frac{(n-3)}{20\pi n} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{(n-1)}{10\pi n} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl[ \frac{2n}{(n-1)}\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,815: | Line 1,815: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow~~~ | |||
[x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ \frac{ | <math>~ | ||
\ | \frac{2(n-1)}{15 n} \biggl(\frac{4\pi}{3} \biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_A\tilde{\mathfrak{f}}_M^{(n-1)/n}} \cdot | ||
\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/n} \biggl[ \frac{2n}{(n-1)}\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,830: | Line 1,832: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow~~~ | |||
[x_\mathrm{eq} ]^{(n-3) }_\mathrm{crit} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ \frac{ | <math>~ | ||
\ | \biggl[\frac{2(n-1)}{15 n} \biggr]^n \biggl(\frac{4\pi}{3} \biggr) \frac{\tilde{\mathfrak{f}}_W^n}{\tilde{\mathfrak{f}}_A^n \tilde{\mathfrak{f}}_M^{(n-1)}} | ||
\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)} \biggl[ \frac{2n}{(n-1)}\biggr]^n | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-\ | \biggl[\frac{2(n-1)}{15 n} \biggr]^n \biggl(\frac{4\pi}{3} \biggr) \frac{\tilde{\mathfrak{f}}_W^n}{\tilde{\mathfrak{f}}_A^n \tilde{\mathfrak{f}}_M^{(n-1)}} | ||
\biggl[ | \biggl\{ \biggl[ \frac{20\pi n}{(n-3)} \biggr]^{(n-1)/2} \biggl( \frac{\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W} \biggr)^{(n-1)/2} [x_\mathrm{eq} ]^{2(n-1) }_\mathrm{crit} \biggr\}\biggl[ \frac{2n}{(n-1)}\biggr]^n | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \biggl[\frac{2(n-1)}{15 n} \biggr]^n \biggl(\frac{4\pi}{3} \biggr) \frac{\tilde{\mathfrak{f}}_W^{(n+1)/2}}{\tilde{\mathfrak{f}}_A^n } | ||
\biggl\{ \biggl[ \frac{20\pi n}{(n-3)} \biggr]^{(n-1)/2} [x_\mathrm{eq} ]^{2(n-1) }_\mathrm{crit} \biggr\}\biggl[ \frac{2n}{(n-1)}\biggr]^n | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow~~~ | ||
[x_\mathrm{eq} ]^{(n+1) }_\mathrm{crit} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ \biggl(\frac{3}{4\pi} \biggr) | ||
\ | \biggl[\frac{15 n}{2(n-1)} \biggr]^n | ||
\biggl[ \frac{(n-3)}{20\pi n} \biggr]^{(n-1)/2} \frac{\tilde{\mathfrak{f}}_A^n }{\tilde{\mathfrak{f}}_W^{(n+1)/2}} \biggl[ \frac{(n-1)}{2n} \biggr]^n | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,907: | Line 1,896: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow~~~ | |||
[x_\mathrm{eq} ]^{(n+1) }_\mathrm{crit} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ \biggl(\frac{3}{4\pi} \biggr) | ||
\ | \biggl[\frac{15 }{2^2} \biggr]^n | ||
\biggl[ \frac{(n-3)}{20\pi n} \biggr]^{(n-1)/2} \frac{\tilde{\mathfrak{f}}_A^n }{\tilde{\mathfrak{f}}_W^{(n+1)/2}} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Also from [[User:Tohline/SSC/Structure/PolytropesEmbedded#Stahler.27s_Presentation|Stahler's work]] we know that the equilibrium mass and radius are, | |||
<div align="center"> | |||
<table border="0" cellpadding="3"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | |||
~\frac{M_\mathrm{tot}}{M_\mathrm{SWS}} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,926: | Line 1,929: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\biggl( \frac{n^3}{4\pi} \biggr)^{1/2} \biggl[ {\tilde\theta}_n^{(n-3)/2} {\tilde\xi}^2 (-{\tilde\theta}^') | |||
\biggr] \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,933: | Line 1,938: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math> | |||
~\frac{R_\mathrm{eq}}{R_\mathrm{SWS}} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,939: | Line 1,946: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\biggl( \frac{n}{4\pi} \biggr)^{1/2} \biggl[ \tilde\xi {\tilde\theta}_n^{(n-1)/2} \biggr] \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,946: | Line 1,954: | ||
</div> | </div> | ||
Additional details in support of an associated PowerPoint presentation can be found [[User:Tohline/SSC/FreeEnergy/PowerPoint|here]]. | |||
====Reconcile==== | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding=" | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\biggl[\frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]^4_\mathrm{crit} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\biggl[ \frac{(n-3)}{20\pi (n+1)} \biggr] \biggl(\frac{n+1}{n}\biggr) | ||
\biggl | \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} | ||
\frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4_\mathrm{crit}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\frac{1}{20\pi} \biggl( \frac{n-3}{n+1} \biggr) \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Taking the ratio, the RHS is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~P_e M_\mathrm{tot}^2 \biggl[ \frac{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)} }{K^{4n}} \biggr]^{1/(n-3)} | ||
\biggl\ | \biggl[ \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \biggr]^{-2} | ||
</math> | \biggl( \frac{n+1}{n}\biggr)</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl( \frac{n+1}{n} \biggr)^{-2}P_e M_\mathrm{tot}^2 \biggl[ G^{3} M_\mathrm{tot}^{2} \biggr]^{(n+1)/(n-3)} K_n^{-4n/(n-3)} | ||
\biggl[ G^{3} K_n^{-4n/(n+1)} P_\mathrm{e}^{(n-3)/(n+1)} \biggr]</math> | |||
\biggl[ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,034: | Line 2,034: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl( \frac{n+1}{n} \biggr)^{-2} \biggl[ G^{3} M_\mathrm{tot}^{2} \biggr]^{[(n-3)+(n+1)]/(n-3)} | ||
</math> | \biggl[ K_n^{[(n+1)+(n-3)]/[(n+1)(n-3)] } \biggr]^{-4n} P_\mathrm{e}^{[(n+1)+ (n-3)]/(n+1)} </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,047: | Line 2,047: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl( \frac{n+1}{n} \biggr)^{-2} M_\mathrm{tot}^{4(n-1)/(n-3)} G^{[6(n-1)]/(n-3)} | ||
K_n^{-8(n-1)/[(n+1)(n-3)] } P_\mathrm{e}^{2(n-1)/(n+1)} \, ;</math> | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
while the LHS is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr)^{4}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,061: | Line 2,067: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl | \biggl[\biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{(n-1)} \biggr]^{4/(n-3)} | ||
\biggl\{\biggl( \frac{n+1}{n} \biggr)^{1/2} G^{-1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]}\biggr\}^{-4} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,091: | Line 2,079: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl( \frac{n+1}{n} \biggr)^{-2} | ||
\ | M_\mathrm{tot}^{4(n-1)/(n-3)} | ||
G^{[6(n-1)]/(n-3)} | |||
K^{-8n(n-1)/[(n-3)(n+1)] } P_\mathrm{e}^{2(n-1)/(n+1)} \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
Q.E.D. | |||
Now, given that, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 2,111: | Line 2,100: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~M_\mathrm{SWS}^{-4(n-1)/(n-3)}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,117: | Line 2,106: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[\biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]}\biggr]^{-4(n-1)/(n-3)} </math> | ||
+ | |||
+ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,141: | Line 2,118: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl( \frac{n+1}{n} \biggr)^{-6(n-1)/(n-3)} G^{6(n-1)/(n-3)} K_n^{-8n(n-1)/[(n+1)(n-3)]} P_\mathrm{e}^{2(n-1)/(n+1)} </math> | ||
- | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
we have, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 2,157: | Line 2,130: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl | <math>~\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr)^{4}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,163: | Line 2,136: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl( \frac{n+1}{n} \biggr)^{-2} | ||
\biggl(\frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{4(n-1)/(n-3)} | |||
\biggl( \frac{n+1}{n} \biggr)^{6(n-1)/(n-3)} | |||
</math> | |||
+ | </td> | ||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,189: | Line 2,151: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \biggl(\frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{4(n-1)/(n-3)} | ||
\biggl( \frac{n+1}{n} \biggr)^{4n/(n-3)} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,199: | Line 2,160: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr)^{n-3}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,205: | Line 2,166: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl(\frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{n-1} | |||
\biggl( \frac{ | \biggl( \frac{n+1}{n} \biggr)^{n} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
By inspection, in the specific case of <math>~n=5</math> (see above), this critical configuration appears to coincide with one of the [[User:Tohline/SSC/Structure/PolytropesEmbedded#Other_Limits|"turning points" identified by Kimura]]. Specifically, it appears to coincide with the "extremal in r<sub>1</sub>" along an M<sub>1</sub> sequence, which satisfies the condition, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl[ \frac{n-3}{n-1} \biggr]_{n=5}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{\tilde\xi \tilde\theta^{n}}{(-\tilde\theta^')}\biggr]_{n=5}</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,236: | Line 2,194: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~\frac{1}{2} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,242: | Line 2,200: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~3^{1/2}\ell \biggl[ (1 + \ell^2)^{-1/2} \biggr]^5 \biggl[ \frac{\ell}{3^{1/2}} (1+\ell^2 )^{-3/2} \biggr]^{-1}</math> | ||
</td> | |||
</tr> | |||
\biggl[ \ | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
</math> | <td align="center"> | ||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~3(1 + \ell^2)^{-1} </math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,256: | Line 2,218: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow~~~ \ell </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~5^{1/2} \, .</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,272: | Line 2,230: | ||
</div> | </div> | ||
Hence, according to Kimura, the turning point associated with the configuration with the largest equilibrium radius, corresponds to the equilibrium configuration having, | |||
<div align="center"> | <div align="center"> | ||
<math>\ | <math>~\ell |_\mathrm{R_{max}} = \sqrt{5} \approx 2.2360680 \, .</math> | ||
</div> | </div> | ||
This is, indeed, very close to — but decidedly different from — the value of <math>~\ell_\mathrm{crit}</math> determined, above! | |||
====Streamlined==== | |||
Let's copy the expression for the [[#FirstPassFreeEnergy|"Case P" free energy derived above]], then factor out a common term: | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding=" | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{\mathfrak{G}_{K,M}}{E_\mathrm{norm}} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ - \biggl( \frac{ | <math>~ | ||
\biggl | -3\mathcal{A} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} | ||
+~ n\mathcal{B} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} | |||
\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,298: | Line 2,265: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl | +~ \biggl( \frac{4\pi}{3} \biggr) \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} | ||
\biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(5-n)/(n-3)} | |||
\biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \, . | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,309: | Line 2,278: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(5-n)/(n-3)} \biggl(\frac{n+1}{n}\biggr)^{3/(n-3)} \biggl\{ | ||
\biggl\{ | -3\mathcal{A} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} | ||
+~ n\mathcal{B} | |||
\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} | |||
+\frac{4\pi}{3} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Defining a new normalization energy, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~E_\mathrm{SWS}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~E_\mathrm{norm} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(5-n)/(n-3)} \biggl(\frac{n+1}{n}\biggr)^{3/(n-3)} </math> | |||
</td> | |||
</tr> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| Line 2,325: | Line 2,316: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl(\frac{n+1}{n}\biggr)^{3/2} K^{3n/(n+1)} G^{-3/2} P_e^{(5-n)/[2(n+1)]} \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
we can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\mathfrak{G}_{K,M}^* \equiv \frac{\mathfrak{G}_{K,M}}{E_\mathrm{SWS}} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ \frac{1}{ | <math>~ | ||
-3\mathcal{A} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} | |||
+~ n\mathcal{B} | |||
\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} | |||
+\frac{4\pi}{3} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
in which case the coefficients of the generic free-energy expression are, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~a</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ \frac{1}{ | <math>~ | ||
\frac{3}{5} \cdot \frac{ \tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl(\frac{n+1}{n}\biggr)\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^2 | |||
= \frac{3}{5} \cdot \biggl( \frac{4\pi }{3}\biggr)^2 \biggl(\frac{n+1}{n}\biggr)\tilde{\mathfrak{f}}_W \mathfrak{m}^{2}</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,360: | Line 2,368: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~b</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ n\biggl(\frac{3}{4\pi}\biggr)^{1/n} | ||
\frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} | |||
= \biggl( \frac{4\pi n}{3}\biggr) \tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,373: | Line 2,383: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~c</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~= | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~ \frac{4\pi}{3} \, , | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,385: | Line 2,395: | ||
</table> | </table> | ||
</div> | </div> | ||
where, as above, | |||
<div align="center"> | |||
<div | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\mathfrak{m}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl( \frac{3}{4\pi} \biggr) \frac{ 1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr) \, .</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
Now, if we define the pair of parameters, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 2,425: | Line 2,419: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\alpha</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,431: | Line 2,425: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~\frac{a}{3c}</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,437: | Line 2,431: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\beta</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,443: | Line 2,437: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~\frac{b}{nc} \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
then the statement of virial equilibrium is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~x_\mathrm{eq}^4 + \alpha</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~\beta x_\mathrm{eq}^{(n-3)/n} \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
and the boundary between dynamical stability and instability occurs at, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~[x_\mathrm{eq}]_\mathrm{crit}^4</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,467: | Line 2,471: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \frac{n-3}{3(n+1)} \biggr]\alpha \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
Combining these last two expressions means that the boundary between dynamical stability and instability is associated with the parameter condition, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 2,479: | Line 2,482: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~[x_\mathrm{eq}]^{(n-3)/n}_\mathrm{crit} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,485: | Line 2,488: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~\biggl[ \frac{n-3}{3(n+1)} + 1\biggr] \frac{\alpha}{\beta} </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,492: | Line 2,494: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~ | ||
\biggl\{ \biggl[ \frac{n-3}{3(n+1)} \biggr]\alpha \biggr\}^{(n-3)/(4n)} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,499: | Line 2,503: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \biggl[ \frac{ 4n }{3(n+1)}\biggr] \frac{\alpha}{\beta} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~ | ||
\beta \alpha^{-3(n+1)/(4n)} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,518: | Line 2,518: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl | <math>~ | ||
\biggl[ \frac{ 4n }{3(n+1)}\biggr] \biggl[ \frac{n-3}{n} \cdot \frac{n}{3(n+1)} \biggr]^{(3-n)/(4n)} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
4 \biggl[ \frac{ n }{3(n+1)}\biggr]^{3(n+1)/(4n)} \biggl[ \frac{n-3}{n} \biggr]^{(3-n)/(4n)} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Rightarrow ~~~ | ||
\frac{ | \biggl( \frac{\beta}{4}\biggr)^{4n} \alpha^{-3(n+1)} | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,564: | Line 2,548: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl | <math>~ | ||
\biggl[ \frac{ n }{3(n+1)}\biggr]^{3(n+1)} \biggl[ \frac{n-3}{n} \biggr]^{(3-n)} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Rightarrow ~~~ | ||
\biggl( \frac{\beta}{4}\biggr)^{4n} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math> | <math>~ | ||
\biggl[ \frac{ n\alpha }{3(n+1)}\biggr]^{3(n+1)} \biggl[ \frac{n}{n-3} \biggr]^{n-3} \, . | |||
\biggr | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
======Case M====== | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~a</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,599: | Line 2,584: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~3\mathcal{A} = \frac{3}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}\, , | ||
\frac{ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,608: | Line 2,591: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~b</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~n\mathcal{B} = n\biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, , | ||
\frac{ | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~c</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{4\pi}{3}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Hence, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\alpha</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,651: | Line 2,627: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl( \frac{ | <math>~\biggl(\frac{4\pi }{15} \biggr) \tilde{\mathfrak{f}}_W \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^2 \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1}</math> | ||
\biggl | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,659: | Line 2,633: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\beta</math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,666: | Line 2,639: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\tilde{\mathfrak{f}}_A \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{(n+1)/n} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \, .</math> | ||
</td> | |||
\biggl( \frac{ | </tr> | ||
</table> | |||
</math> | </div> | ||
</td> | |||
</tr> | So the dynamical stability conditions are: | ||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)\biggl( \frac{n}{n-3} \biggr) [x_\mathrm{eq}]_\mathrm{crit}^4</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,682: | Line 2,657: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr] \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^2 \, ;</math> | ||
\frac{ | |||
\biggl( \frac{ | |||
\ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,692: | Line 2,663: | ||
</div> | </div> | ||
and, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 2,698: | Line 2,669: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~ | ||
\biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{4n} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{4(n+1)} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-4n} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,705: | Line 2,678: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{1}{ | \biggl[ \frac{ n}{3(n+1)}\biggr]^{3(n+1)} \biggl[ \frac{n}{n-3} \biggr]^{n-3} | ||
\biggl( \frac{\ | \biggl(\frac{4\pi \tilde{\mathfrak{f}}_W}{15} \biggr)^{3(n+1)} | ||
\biggl | \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{6(n+1)} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-3(n+1)} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{ | <math>~\Rightarrow~~~ | ||
\biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{4n} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math> | <math>~ | ||
\biggl[\biggl(\frac{ n}{n+1}\biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{3(n+1)} | |||
\biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{2(n+1)} \biggl[ \frac{n}{n-3} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)\biggr]^{n-3} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,736: | Line 2,704: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow~~~\biggl[ \frac{n}{n-3} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)\biggr]^{n-3} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math> | <math>~ | ||
\biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{4n} | |||
\biggl( \frac{ | \biggl[\biggl(\frac{ n}{n+1}\biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{-3(n+1)} | ||
\ | \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{-2(n+1)} \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Together, then, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~[x_\mathrm{eq}]_\mathrm{crit}^{4(n-3)}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math> | <math>~\biggl[ \biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{n-3} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{2(n-3)} | ||
\biggl[ \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \frac{n}{n-3} \biggr]^{-(n-3)} </math> | |||
\biggl( \frac{\ | |||
\biggl[ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,773: | Line 2,745: | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math> | <math>~\biggl[ \biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{n-3} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{2(n-3)} | ||
\biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{-4n} | |||
\ | \biggl[\biggl(\frac{ n}{n+1}\biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{3(n+1)} | ||
\biggl( \frac{\ | \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{2(n+1)} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,799: | Line 2,762: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl[\biggl(\frac{ | <math>~\biggl[ \biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{4n} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{4(n-1)} | ||
\biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{-4n} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,805: | Line 2,770: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~[x_\mathrm{eq}]_\mathrm{crit}^{(n-3)}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,811: | Line 2,776: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl\{\biggl(\frac{ | <math>~\biggl[ \frac{4}{\tilde{\mathfrak{f}}_A}\biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^n \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{(n-1)} \, . | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
======Case P====== | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 2,823: | Line 2,789: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~a</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,829: | Line 2,795: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~1 | <math>~ | ||
\frac{3}{5} \cdot \biggl( \frac{4\pi }{3}\biggr)^2 \biggl(\frac{n+1}{n}\biggr)\tilde{\mathfrak{f}}_W \mathfrak{m}^{2}</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,835: | Line 2,802: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~b</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,841: | Line 2,808: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl\{\ | <math>~\biggl( \frac{4\pi n}{3}\biggr) \tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,847: | Line 2,815: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~c</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,853: | Line 2,821: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ \frac{4\pi}{3} \, , | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
where, as above, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 2,865: | Line 2,833: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\mathfrak{m}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\biggl( \frac{3}{4\pi} \biggr) \frac{ 1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr) \, .</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Hence, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\alpha</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,887: | Line 2,856: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~ | ||
\frac{1 }{ | \frac{1}{5} \cdot \biggl( \frac{4\pi }{3}\biggr) \biggl(\frac{n+1}{n}\biggr)\tilde{\mathfrak{f}}_W \mathfrak{m}^{2} | ||
\biggl( \frac{ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 2,897: | Line 2,864: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\beta</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,903: | Line 2,870: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~ | ||
\ | \tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} \, . | ||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
So the dynamical stability conditions are: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~[x_\mathrm{eq}]_\mathrm{crit}^4</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,920: | Line 2,889: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\biggl[ \frac{n}{3(n+1)} \biggr]\biggl[ \frac{n-3}{n} \biggr]\frac{1}{5} \cdot \biggl( \frac{4\pi }{3}\biggr) \biggl(\frac{n+1}{n}\biggr)\tilde{\mathfrak{f}}_W \mathfrak{m}^{2} </math> | ||
\biggl | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 2,938: | Line 2,901: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\biggl[ \frac{n-3}{n} \biggr]\biggl( \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5}\biggr) \mathfrak{m}^{2} </math> | ||
\frac{ | |||
\ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
and, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | |||
\biggl( \frac{\tilde{\mathfrak{f}}_A }{4}\biggr)^{4n} \mathfrak{m}^{4(n+1)} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,955: | Line 2,920: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~ | ||
\biggl[ \biggl( \frac{4\pi }{3^2\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \mathfrak{m}^{2}\biggr]^{3(n+1)} \biggl[ \frac{n}{n-3} \biggr]^{n-3} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~ \Rightarrow~~~ | ||
\mathfrak{m}^{2(n+1)} | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,981: | Line 2,937: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl(\frac{3}{ | \biggl[ \biggl( \frac{4\pi }{3^2\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggr]^{-3(n+1)} \biggl[ \frac{n}{n-3} \biggr]^{-(n-3)} \biggl( \frac{\tilde{\mathfrak{f}}_A }{4}\biggr)^{4n} \, . | ||
\biggl | |||
\biggl\{\ | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
Together, then, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~[x_\mathrm{eq}]_\mathrm{crit}^{4(n+1)}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,997: | Line 2,957: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl | \biggl[ \frac{n-3}{n} \biggr]^{(n+1)} \biggl( \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5}\biggr)^{(n+1)} | ||
\biggl( \frac{\ | \biggl( \frac{4\pi \tilde{\mathfrak{f}}_W }{3^2\cdot 5}\biggr)^{-3(n+1)} \biggl[ \frac{n-3}{n} \biggr]^{(n-3)} \biggl( \frac{\tilde{\mathfrak{f}}_A }{4}\biggr)^{4n} | ||
\biggl\{\ | |||
\biggl | |||
\biggl | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 3,015: | Line 2,972: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl | \biggl[ \frac{n-3}{n} \biggr]^{2(n-1)} | ||
\biggl( \frac{\ | \biggl( \frac{4\pi \tilde{\mathfrak{f}}_W }{3^2\cdot 5}\biggr)^{-2(n+1)} \biggl( \frac{\tilde{\mathfrak{f}}_A }{4}\biggr)^{4n} \, . | ||
\biggl\{\ | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
======Compare====== | |||
Let's see if the two cases, in fact, provide the same answer. | |||
<!-- | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{SWS}}\biggr)^{n-3} = \biggl[ \frac{x_\mathrm{P}}{x_\mathrm{M}} \biggr]_\mathrm{crit}^{n-3}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 3,032: | Line 2,996: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl | \biggl\{ \biggl[ \frac{n-3}{n} \biggr]^{2(n-1)} | ||
\biggl( \frac{\ | \biggl( \frac{4\pi \tilde{\mathfrak{f}}_W }{3^2\cdot 5}\biggr)^{-2(n+1)} \biggl( \frac{\tilde{\mathfrak{f}}_A }{4}\biggr)^{4n} | ||
\biggl\{\frac{ | \biggr\}^{(n-3)/[4(n+1)]} \biggl\{ \biggl[ \frac{4}{\tilde{\mathfrak{f}}_A}\biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^n \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{(n-1)} \biggr\}^{-1} | ||
\biggl | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 3,048: | Line 3,011: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl(\frac{n-3}{n}\biggr)^{2(n-1)(n-3)/[4(n+1)]} \biggl( \frac{4\pi \tilde{\mathfrak{f}}_W }{3^2\cdot 5}\biggr)^{-n -(n-3)/2} | ||
\biggl[ \biggl(\frac{ | \biggl( \frac{\tilde{\mathfrak{f}}_A }{4}\biggr)^{n+n(n-3)/(n+1)} | ||
\biggl( \frac{n+1}{n} \biggr)^{n} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{1-n} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 3,056: | Line 3,019: | ||
</table> | </table> | ||
</div> | </div> | ||
--> | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 3,063: | Line 3,025: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl( \frac{\ | <math>~\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{SWS}}\biggr)^{n-3} = \biggl[ \frac{x_\mathrm{P}}{x_\mathrm{M}} \biggr]_\mathrm{crit}^{n-3}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 3,069: | Line 3,031: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~ | ||
\biggl\{ \biggl[ \frac{n-3}{n} \biggr]\biggl( \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5}\biggr) \mathfrak{m}^{2} \biggr\}^{(n-3)/4} | |||
\biggl( \frac{ | \biggl\{ \biggl[ \frac{4}{\tilde{\mathfrak{f}}_A}\biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^n \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{(n-1)} \biggr\}^{-1} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 3,085: | Line 3,046: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~ | ||
\biggl\{ \biggl[ \frac{n-3}{n} \biggr]\biggl( \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5}\biggr) \mathfrak{m}^{2} \biggr\}^{(n-3)/4} | |||
\biggl | \biggl\{ \biggl[ \frac{4}{\tilde{\mathfrak{f}}_A}\biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^n \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{(n-1)} \biggr\}^{-1} | ||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
===Five-One Bipolytropes=== | |||
For analytically prescribed, "five-one" bipolytropes, <math>~n = 5</math> and <math>~j =1</math>, in which case, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~x^{2/5 }_\mathrm{eq}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 3,102: | Line 3,069: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\biggl(\frac{5}{ 3b}\biggr) \biggl[a -3 c x^{-2}_\mathrm{eq} \biggr] \, ;</math> | ||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
| |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~[x_\mathrm{eq}]_\mathrm{crit} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{18 c}{a }\biggr]^{1/2} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
More specifically, [[#BiPolytrope51|the expression that describes the free-energy surface]] is, | |||
<div align="center" id="FreeEnergy51"> | |||
<table border="1" cellpadding="5" align="center"> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}^*_{51} \equiv 2^4\biggl( \frac{q}{\nu^2}\biggr) \chi_\mathrm{eq} \biggl[\frac{\mathfrak{G}_{51}}{E_\mathrm{norm}} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{1}{\ell_i^2} \biggl[ | |||
\Chi^{-3/5} (5 \mathfrak{L}_i) | |||
+\Chi^{-3} (4\mathfrak{K}_i) | |||
-\Chi^{-1} (3\mathfrak{L}_i +12\mathfrak{K}_i ) \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | </table> | ||
</div> | </div> | ||
Hence, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~a</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ 3\chi_\mathrm{eq}(\mathfrak{L}_i + 4\mathfrak{K}_i) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~b</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ 5 \mathfrak{L}_i \chi_\mathrm{eq}^{3/5} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~c</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ 4 \mathfrak{K}_i \chi_\mathrm{eq}^{3} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and conclude that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~[\chi_\mathrm{eq}]_\mathrm{crit}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{18 (4 \mathfrak{K}_i \chi_\mathrm{eq}^{3} )}{ 3\chi_\mathrm{eq}(\mathfrak{L}_i + 4\mathfrak{K}_i)} \biggr]^{1/2}_\mathrm{crit} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~[\chi_\mathrm{eq}]_\mathrm{crit}\biggl[ \frac{24 \mathfrak{K}_i }{ (\mathfrak{L}_i + 4\mathfrak{K}_i)} \biggr]^{1/2} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~\biggl[ \frac{24 \mathfrak{K}_i }{ (\mathfrak{L}_i + 4\mathfrak{K}_i)} \biggr]_\mathrm{crit}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~\biggl[ \frac{\mathfrak{L}_i }{ \mathfrak{K}_i } \biggr]_\mathrm{crit}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~20 \, . </math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<span id="FiveOneRadius">Also, from our [[#Summary51|detailed force balance derivations]], we know that,</span> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{eq} \equiv \frac{ R_\mathrm{eq}}{R_\mathrm{norm}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
===Zero-Zero Bipolytropes=== | |||
====General Form==== | |||
In this case, we retain full generality making the substitutions, <math>~n \rightarrow n_c</math> and <math>~j \rightarrow n_e</math>, to obtain, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x^{(n_c-3)/n_c }_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{n_c}{ 3b} \biggl[a -\biggl(\frac{3 c}{n_e}\biggr) x^{(n_e-3)/n_e}_\mathrm{eq} \biggr] \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
| |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~[x_\mathrm{eq}^{(n_e-3)/n_e}]_\mathrm{crit} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{\frac{n_e^2(n_c-3)}{3[ n_c (n_e+3) - n_e(n_c+3) ]}\biggr\} \frac{a}{c} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[\frac{n_e^2(n_c-3)}{3^2(n_c - n_e)}\biggr] \frac{a}{c} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
And here, [[#BiPolytrope00|the expression that describes the free-energy surface]] is, | |||
<div align="center" id="FreeEnergy00"> | |||
<table border="1" cellpadding="5" align="center"> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}^*_{00} \equiv 5 \biggl(\frac{q}{\nu^2}\biggr) \chi_\mathrm{eq} | |||
\biggl[\frac{\mathfrak{G}_{00}}{E_\mathrm{norm}} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{5}{2q^3} \biggl[ | |||
n_c A_2\Chi^{-3/n_c} + n_e B_2\Chi^{-3/n_e} - 3C_2\Chi^{-1} \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
</div> | |||
Hence, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~a \equiv 3\chi_\mathrm{eq} \biggl(\frac{5}{2q^3} \biggr) C_2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
3f \chi_\mathrm{eq} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~b \equiv n_c \chi_\mathrm{eq}^{3/n_c} \biggl(\frac{5}{2q^3} \biggr) A_2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
n_c \chi_\mathrm{eq}^{3/n_c} \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~c \equiv n_e \chi_\mathrm{eq}^{3/n_e} \biggl(\frac{5}{2q^3} \biggr) B_2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ n_e \chi_\mathrm{eq}^{3/n_e} \biggl(\frac{5}{2q^3} \biggr) | |||
\biggl[\frac{2}{5} q^3 f - A_2\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
n_e \chi_\mathrm{eq}^{3/n_e} \biggl\{ f - \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \biggr\} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where the definitions of <math>~f</math> and <math>~\mathfrak{F}</math> are [[#BiPolytrope00|given below]]. We immediately deduce that the ''critical'' equilibrium state is identified by, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~[x_\mathrm{eq}^{(n_e-3)/n_e}]_\mathrm{crit} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{\frac{fn_e(n_c-3)}{3(n_c - n_e)}\biggr\} [\chi_\mathrm{eq}^{(n_e-3)/n_e}]_\mathrm{crit} \biggl\{ f - \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \biggr\}^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~\frac{1}{f}\biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ 1 - \biggl[ \frac{n_e(n_c-3)}{3(n_c-n_e)} \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{n_c(3-n_e)}{3(n_c-n_e)} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
From our [[#Equilibrium_Radius_2|associated detailed-force-balance derivation]], we know that the associated equilibrium radius is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ \biggl(\frac{\pi}{3}\biggr) 2^{2-n_c} \nu^{n_c-1} q^{3-n_c} | |||
\biggl[1 + \frac{2}{5} q^3(f-1-\mathfrak{F})\biggr]^{n_c} \biggr\}^{1/(n_c-3)} | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<!-- Coefficient mistake, I think! | |||
We have deduced that the system is unstable if, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{n_e}{3}\biggl[ \frac{3-n_e}{n_c-n_e} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~< </math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{A_2}{C_2} | |||
= \frac{1}{f} \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
--> | |||
====Compare with Five-One==== | |||
It is worthwhile to set <math>~n_c = 5</math> and <math>~n_e = 1</math> in this expression and compare the result to the [[#FiveOneRadius|comparable expression shown above for the "Five-One" Bipolytrope]]. Here we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[\chi_\mathrm{eq}\biggr]_{51}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ \biggl(\frac{\pi}{3}\biggr) 2^{-3} \nu^{4} q^{-2} | |||
\biggl[1 + \frac{2}{5} q^3(f-1-\mathfrak{F})\biggr]^{5} \biggr\}^{1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot | |||
\frac{1}{\sqrt{3}} \biggl[1 + \frac{2}{5} q^3(f-1-\mathfrak{F})\biggr]^{5/2} \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
whereas, rewriting the [[#FiveOneRadius|above relation]] gives, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{eq}\biggr|_{51}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{1}{\sqrt{3}} \biggl[\frac{(1+\ell_i^2)^{6/5}}{3\ell_i^2}\biggr]^{5/2} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
And, here, we should conclude that the ''critical'' equilibrium configuration is associated with, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{f}\biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{5}{6} \, .</math> | |||
</td> | |||
</tr> | |||
<!-- | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~q^3 (f - 1-\mathfrak{F} )</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{5}{6} \cdot f - 1</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~\biggl[1 + \frac{2}{5} q^3(f-1-\mathfrak{F})\biggr]_\mathrm{crit} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ 1 + \frac{2}{5}\biggl(\frac{5}{6} \cdot f - 1\biggr)</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{f}{3} + \frac{3}{5}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ [\chi_\mathrm{eq}]_\mathrm{crit}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot | |||
\frac{1}{\sqrt{3}} \biggl[\frac{f}{3} + \frac{3}{5}\biggr]^{5/2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
--> | |||
</table> | |||
</div> | |||
=Free-Energy of Truncated Polytropes= | |||
<!-- Equation for PowerPoint slide presentation | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial\mathfrak{G}|_{K,M,P_e}}{\partial R} = 0</math> | |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{\partial^2\mathfrak{G}|_{K,M,P_e}}{\partial R^2} \biggr]_\mathrm{eq} = 0</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
--> | |||
In this case, the Gibbs-like free energy is given by the sum of three separate energies, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~W_\mathrm{grav} + \mathfrak{S}_\mathrm{therm} + P_eV</math> | |||
</td> | |||
</tr> | |||
<!-- HIDE INTERMEDIATE EXPRESSION ... | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \biggl[\frac{3}{5}\cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr] \frac{GM^2}{R} | |||
+ \biggl[\biggl(\frac{3}{4\pi}\biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{\mathfrak{f}}}_M^{(n+1)/n}} \biggr] \frac{nKM^{(n+1)/n}}{R^{3/n}} | |||
+ \frac{4\pi}{3} \cdot P_e R^3 | |||
</math> | |||
</td> | |||
</tr> | |||
END EXPRESSION HIDING --> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 3\mathcal{A} \biggl[\frac{GM^2}{R} \biggr] + n\mathcal{B} \biggl[ \frac{KM^{(n+1)/n}}{R^{3/n}} \biggr] + \frac{4\pi}{3} \cdot P_e R^3 \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where the constants, | |||
<div align="center"> | |||
<table border="0" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A} \equiv \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}</math> | |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
<math>\mathcal{B} \equiv \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and, as [[User:Tohline/SSC/Virial/FormFactors#PTtable|derived elsewhere]], | |||
<div align="center" id="PTtable"> | |||
<table border="1" align="center" cellpadding="5"> | |||
<tr> | |||
<th align="center" colspan="1"> | |||
Structural Form Factors for <font color="red">Pressure-Truncated</font> Polytropes <math>~(n \ne 5)</math> | |||
</th> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tilde\mathfrak{f}_M</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl( - \frac{3\tilde\theta^'}{\tilde\xi} \biggr) </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>\tilde\mathfrak{f}_W</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>\frac{3\cdot 5}{(5-n)\tilde\xi^2} | |||
\biggl[\tilde\theta^{n+1} + 3 (\tilde\theta^')^2 - \tilde\mathfrak{f}_M \tilde\theta \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\tilde\mathfrak{f}_A | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{(5-n)} \biggl\{ 6\tilde\theta^{n+1} + (n+1) | |||
\biggl[3 (\tilde\theta^')^2 - \tilde\mathfrak{f}_M \tilde\theta \biggr] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left" colspan="1"> | |||
As [[User:Tohline/SSC/Virial/FormFactors#Summary_.28n.3D5.29|we have shown separately]], for the singular case of <math>~n = 5</math>, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{f}_M</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
( 1 + \ell^2 )^{-3/2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{f}_W</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{5}{2^4} \cdot \ell^{-5} | |||
\biggl[ \ell \biggl( \ell^4 - \frac{8}{3}\ell^2 - 1 \biggr)(1 + \ell^2)^{-3} + \tan^{-1}(\ell ) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{f}_A</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{3}{2^3} \ell^{-3} [ \tan^{-1}(\ell ) + \ell (\ell^2-1) (1+\ell^2)^{-2} ] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, <math>~\ell \equiv \tilde\xi/\sqrt{3} </math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
In general, then, the warped free-energy surface drapes across a four-dimensional parameter "plane" such that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathfrak{G}(R, K, M, P_e) \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
In order to effectively visualize the structure of this free-energy surface, we will reduce the parameter space from four to two, in two separate ways: First, we will hold constant the parameter pair, <math>~(K,M)</math>; giving a nod to [http://adsabs.harvard.edu/abs/1981PASJ...33..299K Kimura's (1981b)] nomenclature, we will refer to the resulting function, <math>~\mathfrak{G}_{K,M}(R,P_e)</math>, as a "Case M" free-energy surface because the mass is being held constant. Second, we will hold constant the parameter pair, <math>~(K,P_e)</math>, and examine the resulting "Case P" free-energy surface, <math>~\mathfrak{G}_{K,P_e}(R,M)</math>. | |||
==Virial Equilibrium and Dynamical Stability== | |||
The first (partial) derivative of <math>~\mathfrak{G}</math> with respect to <math>~R</math> is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial \mathfrak{G}}{\partial R}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{R} \biggl[ | |||
3\mathcal{A} GM^2 R^{-1} - 3\mathcal{B}KM^{(n+1)/n} R^{-3/n} + 4\pi P_e R^3 | |||
\biggr] \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and the second (partial) derivative is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial^2 \mathfrak{G}}{\partial R^2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{R^2} \biggl[ | |||
-6\mathcal{A} GM^2 R^{-1} + \biggl(\frac{n+3}{n}\biggr) 3\mathcal{B}KM^{(n+1)/n} R^{-3/n} + 8\pi P_e R^3 | |||
\biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
The virial equilibrium radius is identified by setting the first derivative to zero. This means that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~3\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
3\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + 4\pi P_e R_\mathrm{eq}^3 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This expression can be usefully rewritten in the following forms: | |||
<div align="center"> | |||
<table border="1" cellpadding="5" align="center"> | |||
<tr> | |||
<td colspan="2" align="center">Virial Equilibrium Condition</td> | |||
</tr> | |||
<tr> | |||
<td align="center">Case 1:</td> | |||
<td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~3(n+3)\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
3(n+3)\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + 4\pi (n+3) P_e R_\mathrm{eq}^3 | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center">Case 2:</td> | |||
<td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
-6n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ 8\pi nP_e R_\mathrm{eq}^3 - 6n\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} </math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center">Case 3:</td> | |||
<td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
8\pi nP_e R_\mathrm{eq}^3 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~6n\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} - 6n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} </math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Dynamical stability is determined by the sign of the second derivative expression ''evaluated at the equilibrium radius''; setting the second derivative to zero identifies the transition from stable to unstable configurations. The criterion is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ | |||
-6n\mathcal{A} GM^2 R^{-1} + 3(n+3) \mathcal{B}KM^{(n+1)/n} R^{-3/n} + 8\pi nP_e R^3\biggr]_{R_\mathrm{eq}} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
===Case 1 Stability Criterion=== | |||
Using the "Case 1" virial expression to define the equilibrium radius means that the stability criterion is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-6n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + 3(n+3)\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + 4\pi (n+3) P_e R_\mathrm{eq}^3 + 8\pi nP_e R_\mathrm{eq}^3 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mathcal{A} GM^2 R_\mathrm{eq}^{-1} [3(n+3)- 6n ] + 4\pi P_e R_\mathrm{eq}^3 [(n+3) + 2n] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ | |||
4\pi P_e R_\mathrm{eq}^3 [3(n+1) ] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mathcal{A} GM^2 R_\mathrm{eq}^{-1} [3(n-3)] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ | |||
4\pi P_e R_\mathrm{eq}^4 (n+1) | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mathcal{A} GM^2 (n-3) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
===Case 2 Stability Criterion=== | |||
Using the "Case 2" virial expression to define the equilibrium radius means that the stability criterion is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
8\pi nP_e R_\mathrm{eq}^3 - 6n\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} + 3(n+3) \mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} + 8\pi nP_e R_\mathrm{eq}^3 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
16\pi nP_e R_\mathrm{eq}^3 - [3(n-3)]\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
16\pi nP_e R_\mathrm{eq}^3 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[3(n-3)]\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
16\pi nP_e R_\mathrm{eq}^{3(n+1)/n} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
[3(n-3)]\mathcal{B}KM^{(n+1)/n} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
===Case 3 Stability Criterion=== | |||
Using the "Case 3" virial expression to define the equilibrium radius means that the stability criterion is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-6n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + 3(n+3) \mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} + 6n\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} - 6n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-12n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} | |||
+ [6n +3(n+3)] \mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
9(n+1) \mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
12n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
R_\mathrm{eq}^{n-3} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{4n\mathcal{A}}{3(n+1) \mathcal{B}} \biggr]^n \biggl(\frac{G}{K}\biggr)^n M^{n-1} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
===Case M=== | |||
Now, in our discussion of "Case M" sequence analyses, the configuration's radius is normalized to, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~R_\mathrm{norm}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~[ G^n K^{-n} M^{n-1} ]^{1/(n-3)} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Our "Case 3" stability criterion directly relates. We conclude that the transition from stability to dynamical instability occurs when, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\biggl[\frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr]_\mathrm{crit}^{n-3} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{4n\mathcal{A}}{3(n+1) \mathcal{B}} \biggr]^n | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
\biggl[\frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr]_\mathrm{crit}^{(n-3)/n} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{4n}{15(n+1) } \biggl(\frac{4\pi}{3}\biggr)^{1/n}\cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_A \tilde{\mathfrak{f}}_M^{(n-1)/n}} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Also in the "Case M" discussions, the external pressure is normalized to, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~P_\mathrm{norm}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~[ G^{-3(n+1)} K^{4n} M^{-2(n+1)} ]^{1/(n-3)} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
If we raise the "Case 1" stability criterion expression to the <math>~(n-3)</math> power, then divide it by the "Case 3" stability criterion expression raised to the fourth power, we find, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ | |||
[P_e]_\mathrm{crit}^{n-3} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{\mathcal{A} GM^2 (n-3)}{4\pi (n+1)}\biggr]^{n-3}\biggl\{ \biggl[\frac{4n\mathcal{A}}{3(n+1) \mathcal{B}} \biggr]^n \biggl(\frac{G}{K}\biggr)^n M^{n-1} \biggr\}^{-4} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{\mathcal{A} (n-3)}{4\pi (n+1)}\biggr]^{n-3} G^{n-3} M^{2(n-3)} \biggl[\frac{3(n+1) \mathcal{B}}{4n\mathcal{A}} \biggr]^{4n} \biggl(\frac{K}{G}\biggr)^{4n} M^{4(1-n)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} K^{4n} M^{-2(n+1)} G^{-3(n+1)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ | |||
\biggl[\frac{P_e}{P_\mathrm{norm}} \biggr]_\mathrm{crit}^{n-3} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \biggl[ \frac{ 5\tilde{\mathfrak{f}}_M^2 }{ \tilde{\mathfrak{f}}_W } \biggr]^{3(n+1)} | |||
\biggl( \frac{3}{4\pi}\biggr)^4 \biggl[ \frac{ \tilde{\mathfrak{f}}_A }{ \tilde{\mathfrak{f}}_M^{(n+1)/n} } \biggr]^{4n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{3}{4\pi}\biggr)^4 \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} | |||
\biggl[ \frac{ 5 }{ \tilde{\mathfrak{f}}_W } \biggr]^{3(n+1)} \tilde{\mathfrak{f}}_M^{2(n+1)} \tilde{\mathfrak{f}}_A^{4n} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
===Case P=== | |||
Flipping around this expression for <math>~[P_e]_\mathrm{crit}</math>, we also can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
[M]_\mathrm{crit}^{2(n+1)} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} K^{4n} G^{-3(n+1)} P_e^{3-n} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Now, in our "Case P" discussions we normalized the mass to | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~M_\mathrm{SWS}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{n+1}{n}\biggr)^{3/2} G^{-3/2} K^{2n/(n+1)} P_e^{(3-n)/[2(n+1)]} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[\frac{M}{M_\mathrm{SWS}} \biggr]_\mathrm{crit}^{2(n+1)} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} \biggl(\frac{n+1}{n}\biggr)^{-3(n+1)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl(\frac{3 }{4} \biggr)^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where the constants, | |||
<div align="center"> | |||
<table border="0" cellpadding="5"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A} \equiv \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}</math> | |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
<math>\mathcal{B} \equiv \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
So we can furthermore conclude that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[\frac{M}{M_\mathrm{SWS}} \biggr]_\mathrm{crit}^{2(n+1)} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl(\frac{3 }{4} \biggr)^{4n} \biggl\{ \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr\}^{-3(n+1)} | |||
\biggl\{ \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggr\}^{4n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl(\frac{3}{4\pi} \biggr)^{4} | |||
\biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl(\frac{3\tilde{\mathfrak{f}}_A }{4} \biggr)^{4n} \biggl[ \frac{5^3\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W^3} \biggr]^{(n+1)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Our expression for <math>~[M]_\mathrm{crit}^{2(n+1)}</math> can also be combined with the "Case 2 stability criterion" to eliminate the mass entirely, giving, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\biggl\{ 16\pi nP_e R_\mathrm{eq}^{3(n+1)/n} \biggr\}^{2n} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ [3(n-3)]\mathcal{B}K\biggr\}^{2n} | |||
\biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} K^{4n} G^{-3(n+1)} P_e^{3-n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
R_\mathrm{eq}^{6(n+1)} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{ 3(n-3)}{16\pi n} \biggr]^{2n} | |||
\biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{6n} K^{6n} G^{-3(n+1)} P_e^{3(1-n)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
R_\mathrm{eq}^{2(n+1)} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ \biggl[ \frac{ (n-3)}{4\pi n} \biggr]^{2n} \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl[\frac{(n+1) }{n} \biggr]^{4n+(3-n)} \biggl(\frac{3 }{4} \biggr)^{6n} \biggr\}^{1/3} | |||
\mathcal{A}^{-(n+1)} \mathcal{B}^{2n} K^{2n} G^{-(n+1)} P_e^{(1-n)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{ (n-3)}{4\pi n} \biggr]^{(n-1)} \biggl[\frac{(n+1) }{n} \biggr]^{(n+1)} \biggl(\frac{3 }{4} \biggr)^{2n} | |||
\mathcal{A}^{-(n+1)} \mathcal{B}^{2n} K^{2n} G^{-(n+1)} P_e^{(1-n)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Finally, recognizing that in our "Case P" discussions we normalized the radius to | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~R_\mathrm{SWS}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{n+1}{n}\biggr)^{1/2} G^{-1/2} K^{n/(n+1)} P_e^{(1-n)/[2(n+1)]} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
[R_\mathrm{eq}]_\mathrm{crit}^{2(n+1)} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{ (n-3)}{4\pi n} \biggr]^{(n-1)} \biggl(\frac{n+1 }{n} \biggr)^{(n+1)} \biggl(\frac{3 }{4} \biggr)^{2n} | |||
\mathcal{A}^{-(n+1)} \mathcal{B}^{2n} \biggl\{ R_\mathrm{SWS}\biggl(\frac{n+1 }{n} \biggr)^{-1/2} \biggr\}^{2(n+1)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
\biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]_\mathrm{crit}^{2(n+1)} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{ (n-3)}{4\pi n} \biggr]^{(n-1)} \biggl(\frac{3 }{4} \biggr)^{2n} | |||
\mathcal{A}^{-(n+1)} \mathcal{B}^{2n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{n}{n-3} \biggr]^{(1-n)} (4\pi)^{1-n}\biggl(\frac{3 }{4} \biggr)^{2n} | |||
\biggl[ \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr]^{-(n+1)} | |||
\biggl[ \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggr]^{2n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{n}{n-3} \biggr]^{(1-n)} (4\pi)^{1-n -2} 3^{2n+2} 4^{-2n} | |||
\biggl[ \frac{5\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W}\biggr]^{(n+1)} | |||
\biggl[ \frac{\tilde{\mathfrak{f}}_A^{2n}}{\tilde{\mathfrak{f}}_M^{2(n+1)}} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{n}{n-3} \biggr]^{(1-n)} | |||
\biggl[ \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W}\biggr]^{(n+1)} | |||
\biggl[\frac{ \tilde{\mathfrak{f}}_A}{4} \biggr]^{2n} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
==Case M Free-Energy Surface== | |||
It is useful to rewrite the free-energy function in terms of dimensionless parameters. Here we need to pick normalizations for energy, radius, and pressure that are expressed in terms of the gravitational constant, <math>~G</math>, and the two fixed parameters, <math>~K</math> and <math>~M</math>. We have chosen to use, | |||
<!-- Equation for use in PowerPoint presentation | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{R}{R_0}</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
--> | |||
<div align="center"> | |||
<table border="0" cellpadding="3"> | |||
<tr> | |||
<td align="right"> | |||
<math>~R_\mathrm{norm}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} \biggr]^{1/(n-3)} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~P_\mathrm{norm}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}} \biggr]^{1/(n-3)} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
which, as is detailed in an [[User:Tohline/SphericallySymmetricConfigurations/Virial#Choices_Made_by_Other_Researchers|accompanying discussion]], are similar but not identical to the normalizations used by [http://adsabs.harvard.edu/abs/1970MNRAS.151...81H Horedt (1970)] and by [http://adsabs.harvard.edu/abs/1981MNRAS.195..967W Whitworth (1981)]. The self-consistent energy normalization is, | |||
<div align="center"> | |||
<table border="0" cellpadding="3"> | |||
<tr> | |||
<td align="right"> | |||
<math>~E_\mathrm{norm}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~P_\mathrm{norm} R^3_\mathrm{norm} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
As we have [[User:Tohline/SphericallySymmetricConfigurations/Virial#Gathering_it_all_Together|demonstrated elsewhere]], after implementing these normalizations, the expression that describes the "Case M" free-energy surface is, | |||
<div align="center"> | |||
<math> | |||
\mathfrak{G}_{K,M}^* \equiv \frac{\mathfrak{G}_{K,M}}{E_\mathrm{norm}} = | |||
-3\mathcal{A} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^{-1} +~ n\mathcal{B} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^{-3/n} | |||
+~ \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^3 \, , | |||
</math> | |||
</div> | |||
Given the polytropic index, <math>~n</math>, we expect to obtain a different "Case M" free-energy surface for each choice of the dimensionless truncation radius, <math>~\tilde\xi</math>; this choice will imply corresponding values for <math>~\tilde\theta</math> and <math>~\tilde\theta^'</math> and, hence also, corresponding (constant) values of the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>. | |||
<!-- Supports PowerPoint summary | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{P_e}{P_\mathrm{norm}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{20\pi x_\mathrm{eq}^4} \biggl[ 15\biggl(\frac{3}{4\pi}\biggr)^{1/n} x_\mathrm{eq}^{(n-3)/n} - 3\biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~[x_\mathrm{eq}]_\mathrm{crit}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{4n}{15(n+1)} \biggl( \frac{4\pi}{3} \biggr)^{1/n} \biggr]^{n/(n-3)}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~[x_\mathrm{eq}]_\mathrm{turn}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{4n}{15(n+1)} \biggl( \frac{4\pi}{3} \biggr)^{1/n} \biggr]^{n/(n-3)}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{P_\mathrm{max}}{P_\mathrm{norm}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{20\pi} \biggl( \frac{n-3}{n+1} \biggr) \biggl[ \frac{15(n+1)}{4n}\biggl(\frac{3}{4\pi}\biggr)^{1/n} \biggr]^{4n/(n-3)}</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
--> | |||
==Case P Free-Energy Surface== | |||
Again, it is useful to rewrite the free-energy function in terms of dimensionless parameters. But here we need to pick normalizations for energy, radius, and mass that are expressed in terms of the gravitational constant, <math>~G</math>, and the two fixed parameters, <math>~K</math> and <math>~P_e</math>. As is [[User:Tohline/SSC/Structure/PolytropesEmbedded#Stahler.27s_Presentation|detailed in an accompanying discussion]], we have chosen to use the normalizations defined by [http://adsabs.harvard.edu/abs/1983ApJ...268..165S Stahler (1983)], namely, | |||
<div align="center"> | |||
<table border="0" cellpadding="3"> | |||
<tr> | |||
<td align="right"> | |||
<math>~R_\mathrm{SWS}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{n+1}{nG} \biggr)^{1/2} K^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~M_\mathrm{SWS}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{n+1}{nG} \biggr)^{3/2} K^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
The self-consistent energy normalization is, | |||
<div align="center"> | |||
<table border="0" cellpadding="3"> | |||
<tr> | |||
<td align="right"> | |||
<math>~E_\mathrm{SWS} \equiv \biggl( \frac{n}{n+1} \biggr) \frac{GM_\mathrm{SWS}^2}{R_\mathrm{SWS}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2}K^{3n/(n+1)} P_\mathrm{e}^{(5-n)/[2(n+1)]} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
After implementing these normalizations — see our [[User:Tohline/SSC/Virial/PolytropesEmbeddedOutline#Our_Case_M_Analysis|accompanying analysis]] for details — the expression that describes the "Case P" free-energy surface is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}_{K,P_e}^* \equiv \frac{\mathfrak{G}_{K,P_e}}{E_\mathrm{SWS}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<!-- HIDE LONG RE-DERIVATION ... | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{\biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2}K^{3n/(n+1)} P_\mathrm{e}^{(5-n)/[2(n+1)]} \biggr\}^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \biggl\{- \biggl[\frac{3}{5}\cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr] \frac{GM^2}{R} | |||
+ \biggl[\biggl(\frac{3}{4\pi}\biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{\mathfrak{f}}}_M^{(n+1)/n}} \biggr] \frac{nKM^{(n+1)/n}}{R^{3/n}} | |||
+ \frac{4\pi}{3} \cdot P_e R^3 | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- | |||
\biggl( \frac{n}{n+1} \biggr)^{3/2} G^{3/2}K^{-3n/(n+1)} P_\mathrm{e}^{(n-5)/[2(n+1)]} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \biggl\{\biggl[\frac{3}{5}\cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr] \frac{GM^2}{R} | |||
- \biggl[\biggl(\frac{3}{4\pi}\biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{\mathfrak{f}}}_M^{(n+1)/n}} \biggr] \frac{nKM^{(n+1)/n}}{R^{3/n}} | |||
- \frac{4\pi}{3} \cdot P_e R^3 | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- | |||
\biggl( \frac{n}{n+1} \biggr)^{3/2} G^{3/2}K^{-3n/(n+1)} P_\mathrm{e}^{(n-5)/[2(n+1)]} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \biggl\{\biggl[\frac{3}{5}\cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr] \biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 \frac{R_\mathrm{SWS}}{R} \biggl[G M_\mathrm{SWS}^2 R_\mathrm{SWS}^{-1} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \biggl[n\biggl(\frac{3}{4\pi}\biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{\mathfrak{f}}}_M^{(n+1)/n}} \biggr] \biggl(\frac{M}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R_\mathrm{SWS}}{R}\biggr)^{3/n} | |||
\biggl[K M_\mathrm{SWS}^{(n+1)/n} R_\mathrm{SWS}^{-3/n} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{4\pi}{3} \cdot \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^3 \biggl[ P_e R_\mathrm{SWS}^3 \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- | |||
\biggl( \frac{n}{n+1} \biggr)^{3/2} G^{3/2}K^{-3n/(n+1)} P_\mathrm{e}^{(n-5)/[2(n+1)]} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \biggl\{\biggl[\frac{3}{5}\cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr] \biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 | |||
\biggl(\frac{R_\mathrm{SWS}}{R}\biggr) G \biggl[\biggl( \frac{n+1}{nG} \biggr)^{3/2} K^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \biggr]^2 \biggl[\biggl( \frac{n+1}{nG} \biggr)^{1/2} K^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \biggr]^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \biggl[n\biggl(\frac{3}{4\pi}\biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{\mathfrak{f}}}_M^{(n+1)/n}} \biggr] | |||
\biggl(\frac{M}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R_\mathrm{SWS}}{R}\biggr)^{3/n} | |||
K \biggl[ \biggl( \frac{n+1}{nG} \biggr)^{3/2} K^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \biggr]^{(n+1)/n} \biggl[ \biggl( \frac{n+1}{nG} \biggr)^{1/2} K^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \biggr]^{-3/n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{4\pi}{3} \cdot \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^3 P_e \biggl[ \biggl( \frac{n+1}{nG} \biggr)^{1/2} K^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \biggr]^3 | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}_{K,P_e}^*</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- | |||
\biggl( \frac{n}{n+1} \biggr)^{3/2} G^{3/2}K^{-3n/(n+1)} P_\mathrm{e}^{(n-5)/[2(n+1)]} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \biggl\{\biggl[\frac{3}{5}\cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr] \biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 | |||
\biggl(\frac{R_\mathrm{SWS}}{R}\biggr) G \biggl[\biggl( \frac{n+1}{nG} \biggr)^{3} K^{4n/(n+1)} P_\mathrm{e}^{(3-n)/[(n+1)]} \biggr] | |||
\biggl[\biggl( \frac{n+1}{nG} \biggr)^{-1/2} K^{-n/(n+1)} P_\mathrm{e}^{(n-1)/[2(n+1)]} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \biggl[n\biggl(\frac{3}{4\pi}\biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{\mathfrak{f}}}_M^{(n+1)/n}} \biggr] | |||
\biggl(\frac{M}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R_\mathrm{SWS}}{R}\biggr)^{3/n} | |||
K \biggl[ \biggl( \frac{n+1}{nG} \biggr)^{3(n+1)/(2n)} K^{2} P_\mathrm{e}^{(3-n)/(2n)} \biggr] | |||
\biggl[ \biggl( \frac{n+1}{nG} \biggr)^{-3/2n} K^{-3/(n+1)} P_\mathrm{e}^{3(n-1)/[2n(n+1)]} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{4\pi}{3} \cdot \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^3 P_e \biggl[ \biggl( \frac{n+1}{nG} \biggr)^{3/2} K^{3n/(n+1)} P_\mathrm{e}^{3(1-n)/[2(n+1)]} \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- | |||
\biggl( \frac{n}{n+1} \biggr)^{3/2} G^{3/2}K^{-3n/(n+1)} P_\mathrm{e}^{(n-5)/[2(n+1)]} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\times \biggl\{\biggl[\frac{3}{5}\cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr] \biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 | |||
\biggl(\frac{R_\mathrm{SWS}}{R}\biggr) \biggl[\biggl( \frac{n+1}{n} \biggr)^{5/2} G^{-3/2} K^{3n/(n+1)} P_\mathrm{e}^{(5-n)/[2(n+1)]} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \biggl[n\biggl(\frac{3}{4\pi}\biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{\mathfrak{f}}}_M^{(n+1)/n}} \biggr] | |||
\biggl(\frac{M}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R_\mathrm{SWS}}{R}\biggr)^{3/n} | |||
\biggl[ \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K^{3n/(n+1)} P_\mathrm{e}^{(5-n)/[2(n+1)]} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{4\pi}{3} \cdot \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^3 \biggl[ \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2}K^{3n/(n+1)} P_\mathrm{e}^{(5-n)/[2(n+1)]} \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- | |||
\biggl[\frac{3}{5}\cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr] \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 | |||
\biggl(\frac{R_\mathrm{SWS}}{R}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \biggl[n\biggl(\frac{3}{4\pi}\biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{\mathfrak{f}}}_M^{(n+1)/n}} \biggr] | |||
\biggl(\frac{M}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R_\mathrm{SWS}}{R}\biggr)^{3/n} | |||
+ \frac{4\pi}{3} \cdot \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^3 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- | |||
\biggl[\frac{3}{5}\cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)\biggr] \biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 | |||
\biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \biggl[n\biggl(\frac{3}{4\pi}\biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{\mathfrak{f}}}_M^{(n+1)/n}} \biggr] | |||
\biggl(\frac{M}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} | |||
+ \frac{4\pi}{3} \cdot \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^3 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
END SUPPRESSION OF LONG DERIVATION --> | |||
<td align="left"> | |||
<math>~- 3 \mathcal{A} \biggl( \frac{n+1}{n} \biggr)\biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} | |||
+ n\mathcal{B} \biggl(\frac{M}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} | |||
+ \frac{4\pi}{3} \cdot \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^3 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Given the polytropic index, <math>~n</math>, we expect to obtain a different "Case P" free-energy surface for each choice of the dimensionless truncation radius, <math>~\tilde\xi</math>; this choice will imply corresponding values for <math>~\tilde\theta</math> and <math>~\tilde\theta^'</math> and, hence also, corresponding (constant) values of the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>. | |||
==Summary== | |||
<div align="center"> | |||
<table border="1" align="center" cellpadding="5"> | |||
<tr> | |||
<th align="center"> </th> | |||
<th align="center">DFB Equilibrium</th> | |||
<th align="center">Onset of Dynamical Instability</th> | |||
</tr> | |||
<tr> | |||
<th align="center" rowspan="2"><font size="+1">Case M:</font></th> | |||
<td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr]^{n-3}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{4\pi}{(n+1)^n} \biggr] {\tilde\xi}^{(n-3)} (-{\tilde\xi}^2 \tilde{\theta^'})^{(1-n)} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
<td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr]_\mathrm{crit}^{n-3}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{4n}{15(n+1) }\biggr]^n \biggl(\frac{4\pi}{3}\biggr) \frac{\tilde{\mathfrak{f}}_W^n}{\tilde{\mathfrak{f}}_A^n \tilde{\mathfrak{f}}_M^{(n-1)}} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{P_\mathrm{e}}{P_\mathrm{norm}}\biggr]^{n-3}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{(n+1)^3}{4\pi} \biggr]^{(n+1)} {\tilde\theta}^{(n+1)(n-3)} (-{\tilde\xi}^2 \tilde{\theta^'})^{2(n+1)} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
<td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{P_\mathrm{e}}{P_\mathrm{norm}}\biggr]_\mathrm{crit}^{n-3}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{3}{4\pi}\biggr)^4 \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl(\frac{n+1}{n} \biggr)^{3(n+1)} | |||
\biggl[ \frac{ 5^3 \tilde{\mathfrak{f}}_M^2}{ \tilde{\mathfrak{f}}_W^3 } \biggr]^{n+1} \biggl( \frac{3\tilde{\mathfrak{f}}_A}{4}\biggr)^{4n} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
<tr> | |||
<th align="center" rowspan="2"><font size="+1">Case P:</font></th> | |||
<td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{n}{4\pi}\biggr) {\tilde\xi}^2 {\tilde\theta}^{n-1} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
<td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]_\mathrm{crit}^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W}\biggr] | |||
\biggl[ \frac{n-3}{n} \biggr]^{(n-1)/(n+1)} | |||
\biggl[\frac{ \tilde{\mathfrak{f}}_A}{4} \biggr]^{2n/(n+1)} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr]^{2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{n^3}{4\pi}\biggr) {\tilde\theta}^{n-3} (-{\tilde\xi}^2 {\tilde{\theta^'}})^2 | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
<td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr]_\mathrm{crit}^{2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{5^3\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W^3} \biggr]\biggl(\frac{3}{4\pi} \biggr)^{4/(n+1)} | |||
\biggl[\frac{ (n-3)}{4\pi n}\biggr]^{(n-3)/(n+1)} \biggl(\frac{3\tilde{\mathfrak{f}}_A }{4} \biggr)^{4n/(n+1)} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left" colspan="3"> | |||
In all four cases, the expression on right intersects (is equal to) the expression on the left when the following condition applies: | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="left"> | |||
For <math>~n \ne 5</math>: | |||
</td> | |||
<td align="right"> | |||
<math>~ | |||
2(9-2n){\tilde\theta}^{n+1} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
3(n-3) \biggl[ (-{\tilde\theta}^')^2 - \biggl( -\frac{\tilde\theta {\tilde\theta}^'}{\tilde\xi} \biggr)\biggr] \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
For <math>~n = 5</math>: | |||
</td> | |||
<td align="right"> | |||
<math>~ | |||
\biggl[\frac{2^4\cdot 5}{3}\biggr] \ell^3 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
(1+\ell^2)^3 \tan^{-1}\ell + \ell(\ell^4-1) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
If (for <math>n\ne 5</math>) we adopt the shorthand notation, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Upsilon</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~[3 (-{\tilde\theta}^')^2 - {\tilde\mathfrak{f}}_M \tilde\theta] = | |||
3\biggl[ (-{\tilde\theta}^')^2 - \biggl( -\frac{\tilde\theta {\tilde\theta}^'}{\tilde\xi} \biggr)\biggr] \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="3"> | |||
and | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tau</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~{\tilde\theta}^{n+1} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
then the critical condition becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(n-3)\Upsilon</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2(9-2n)\tau \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and ''at'' the critical state, the expressions for the structural form-factors become, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~{\tilde\mathfrak{f}}_A</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{(5-n)} \biggl[6\tau + (n+1)\Upsilon \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{(5-n)} \biggl\{ 6 + (n+1)\biggl[ \frac{2(9-2n)}{n-3} \biggr] \biggr\}\tau </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{(5-n)} \biggl[ \frac{6(n-3) + 2(9-2n)(n+1)}{n-3} \biggr] \tau </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{(5-n)} \biggl[ \frac{4n(5-n)}{n-3} \biggr] \tau </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{4n\tau}{(n-3)} \, ;</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~{\tilde\mathfrak{f}}_W</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3\cdot 5}{(5-n) {\tilde\xi}^2} \biggl[\tau + \Upsilon \biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3\cdot 5}{(5-n) {\tilde\xi}^2} \biggl\{1 + \biggl[ \frac{2(9-2n)}{n-3} \biggr] \biggr\}\tau</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3\cdot 5}{(5-n) {\tilde\xi}^2} \biggl[ \frac{3(5-n)}{n-3} \biggr] \tau</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3^2\cdot 5 \tau}{(n-3) {\tilde\xi}^2} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
\frac{5^3\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W^3} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{(n-3) {\tilde\xi}^2}{3^2\tau} \biggr]^{3} \biggl(-\frac{3 {\tilde\theta}^'}{\tilde\xi} \biggr)^2 | |||
= 3^2\biggl[\frac{(n-3) {\tilde\xi}^2}{3^2\tau} \biggr]^{3} \biggl(-\frac{{\tilde\xi}^2 {\tilde\theta}^'}{ {\tilde\xi}^3 } \biggr)^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{(n-3)^3}{3^4\tau^3} \biggr] (-{\tilde\xi}^2 {\tilde\theta}^' )^2 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence (1), | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr]_\mathrm{crit}^{n-3}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{4\pi}{(n+1)^n }\biggr] | |||
\biggl[ \frac{4n}{15}\biggr]^n \biggl(\frac{1}{3}\biggr) | |||
\biggl[ \frac{3^2\cdot 5 }{4n {\tilde\xi}^2} \biggr]^n | |||
\tilde{\mathfrak{f}}_M^{1-n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{4\pi}{(n+1)^n }\biggr] | |||
\biggl[ \frac{1}{ {\tilde\xi}^{2n}} \biggr] | |||
\biggl( \frac{-{\tilde\xi}^2{\tilde\theta}^'}{{\tilde\xi}^3} \biggr)^{1-n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{4\pi}{(n+1)^n }\biggr] | |||
{\tilde\xi}^{n-3} | |||
(-{\tilde\xi}^2{\tilde\theta}^')^{1-n} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Q.E.D. | |||
And (2), | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{P_\mathrm{e}}{P_\mathrm{norm}}\biggr]_\mathrm{crit}^{n-3}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{3}{4\pi}\biggr)^4 \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl(\frac{n+1}{n} \biggr)^{3(n+1)} | |||
\biggl[ \frac{ 5^3 \tilde{\mathfrak{f}}_M^2}{ \tilde{\mathfrak{f}}_W^3 } \biggr]^{n+1} \biggl( \frac{3\tilde{\mathfrak{f}}_A}{4}\biggr)^{4n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~3^{4} (4\pi)^{-(n+1)} | |||
\biggl(\frac{ n-3}{n}\biggr)^{n-3} \biggl(\frac{n+1}{n} \biggr)^{3(n+1)} | |||
\biggl[ \frac{(n-3)^3}{3^4\tau^3} \biggr]^{n+1} (-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} | |||
\biggl[ \frac{3n\tau}{n-3} \biggr]^{4n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~3^{4} (4\pi)^{-(n+1)} | |||
\biggl(\frac{ n-3}{n}\biggr)^{n-3} \biggl(\frac{n+1}{n} \biggr)^{3(n+1)} n^{3(n+1)} | |||
\biggl[ \frac{n-3}{n} \biggr]^{3(n+1)} (-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} | |||
\biggl[ \frac{n}{n-3} \biggr]^{4n} \tau^{4n-3(n+1)} 3^{4n-4(n+1)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{n+1} | |||
(-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} | |||
\tau^{n-3} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~\biggl[ \frac{P_\mathrm{e}}{P_\mathrm{norm}}\biggr]_\mathrm{crit}^{n-3}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{n+1} | |||
(-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} {\tilde\theta}^{(n+1)(n-3)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Q.E.D. | |||
And (3), | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]^{2(n+1)}_\mathrm{crit}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W}\biggr]^{n+1} | |||
\biggl[ \frac{n-3}{n} \biggr]^{(n-1) } | |||
\biggl[\frac{ \tilde{\mathfrak{f}}_A}{4} \biggr]^{2n } | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{3^2\cdot 5}{4\pi }\biggr]^{n+1} | |||
\biggl[ \frac{n-3}{n} \biggr]^{(n-1) } | |||
\biggl[ \frac{ n\tau}{n-3} \biggr]^{2n } \biggl[ \frac{(n-3){\tilde\xi}^2}{3^2\cdot 5 \tau} \biggr]^{n+1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{1}{4\pi }\biggr]^{n+1} | |||
\biggl[ \frac{ n}{n-3} \biggr]^{n+1 } \biggl[ (n-3){\tilde\xi}^2\biggr]^{n+1} \tau^{n-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]^{2}_\mathrm{crit}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{n}{4\pi }\biggr) {\tilde\xi}^2 {\tilde\theta}^{n-1} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Q.E.D. | |||
And (4), | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr]_\mathrm{crit}^{2(n+1)}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{5^3\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W^3} \biggr]^{n+1} \biggl(\frac{3}{4\pi} \biggr)^{4} | |||
\biggl[\frac{ (n-3)}{4\pi n}\biggr]^{(n-3)} \biggl(\frac{3\tilde{\mathfrak{f}}_A }{4} \biggr)^{4n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{ \biggl[ \frac{(n-3)^3}{3^4\tau^3} \biggr] (-{\tilde\xi}^2 {\tilde\theta}^' )^2 \biggr\}^{n+1} 3^4(4\pi)^{-(n+1)} | |||
\biggl(\frac{ n-3}{n}\biggr)^{(n-3)} | |||
\biggl[\frac{3n\tau }{n-3} \biggr]^{4n} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ \frac{n^3}{4\pi}\biggr]^{n+1}(-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} | |||
\tau^{n-3} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
\biggl[ \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr]_\mathrm{crit}^{2} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ \frac{n^3}{4\pi}\biggr](-{\tilde\xi}^2 {\tilde\theta}^' )^{2} | |||
{\tilde\theta}^{n-3} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Q.E.D. | |||
=Free-Energy of Bipolytropes= | |||
In this case, the Gibbs-like free energy is given by the sum of four separate energies, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[W_\mathrm{grav} + \mathfrak{S}_\mathrm{therm}\biggr]_\mathrm{core} + \biggl[W_\mathrm{grav} + \mathfrak{S}_\mathrm{therm}\biggr]_\mathrm{env} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
In addition to specifying (generally) separate polytropic indexes for the core, <math>~n_c</math>, and envelope, <math>~n_e</math>, and an envelope-to-core mean molecular weight ratio, <math>~\mu_e/\mu_c</math>, we will assume that the system is fully defined via specification of the following five physical parameters: | |||
* Total mass, <math>~M_\mathrm{tot}</math>; | |||
* Total radius, <math>~R</math>; | |||
* Interface radius, <math>~R_i</math>, and associated dimensionless interface marker, <math>~q \equiv R_i/R</math>; | |||
* Core mass, <math>~M_c</math>, and associated dimensionless mass fraction, <math>~\nu \equiv M_c/M_\mathrm{tot}</math>; | |||
* Polytropic constant in the core, <math>~K_c</math>. | |||
In general, the warped free-energy surface drapes across a five-dimensional parameter "plane" such that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathfrak{G}(R, K_c, M_\mathrm{tot}, q, \nu) \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
==Order of Magnitude Derivation== | |||
Let's begin by providing very rough, approximate expressions for each of these four terms, assuming that <math>~n_c = 5</math> and <math>~n_e = 1</math>. | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~W_\mathrm{grav}\biggr|_\mathrm{core}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \mathfrak{a}_c \biggl[ \frac{GM_\mathrm{tot} M_c}{(R_i/2)} \biggr] | |||
= - 2\mathfrak{a}_c \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggl(\frac{\nu}{q}\biggr) \biggr] \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~W_\mathrm{grav}\biggr|_\mathrm{env}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \mathfrak{a}_e \biggl[ \frac{GM_\mathrm{tot} M_e}{(R_i+R)/2} \biggr] | |||
= - 2\mathfrak{a}_e \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{S}_\mathrm{therm}\biggr|_\mathrm{core} = U_\mathrm{int}\biggr|_\mathrm{core} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathfrak{b}_c \cdot n_cK_c M_c ({\bar\rho}_c)^{1/n_c} | |||
= 5\mathfrak{b}_c \cdot K_c M_\mathrm{tot}\nu \biggl[ \frac{3M_c}{4\pi R_i^3} \biggr]^{1/5} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} K_c (M_\mathrm{tot}\nu)^{6/5} (Rq)^{-3/5} | |||
\, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{S}_\mathrm{therm}\biggr|_\mathrm{env} = U_\mathrm{int}\biggr|_\mathrm{env} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathfrak{b}_e \cdot n_eK_e M_\mathrm{env} ({\bar\rho}_e)^{1/n_e} | |||
= \mathfrak{b}_e \cdot K_e M_\mathrm{tot}(1-\nu) \biggl[ \frac{3M_\mathrm{env}}{4\pi (R^3-R_i^3)} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr) K_e [M_\mathrm{tot}(1-\nu)]^2 [R^3(1-q^3)]^{-1} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
In writing this last expression, it has been necessary to (temporarily) introduce a sixth physical parameter, namely, the polytropic constant that characterizes the envelope material, <math>~K_e</math>. But this constant can be expressed in terms of <math>~K_c</math> via a relation that ensures continuity of pressure across the interface while taking into account the drop in mean molecular weight across the interface, that is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~K_e ({\bar\rho}_e)^{(n_e+1)/n_e}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~K_c ({\bar\rho}_c)^{(n_c+1)/n_c}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~~ K_e \biggl[\biggl( \frac{\mu_e}{\mu_c} \biggr) {\bar\rho}_c\biggr]^{2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~K_c ({\bar\rho}_c)^{6/5}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~~ \frac{K_e}{K_c} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \frac{3M_\mathrm{tot}\nu}{4\pi (Rq)^3} \biggr]^{-4/5} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence, the fourth energy term may be rewritten in the form, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{S}_\mathrm{therm}\biggr|_\mathrm{env} = U_\mathrm{int}\biggr|_\mathrm{env} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr) \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} | |||
K_c\biggl[ \frac{3M_\mathrm{tot}\nu}{4\pi (Rq)^3} \biggr]^{-4/5} [M_\mathrm{tot}(1-\nu)]^2 [R^3(1-q^3)]^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr)^{1/5} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} | |||
K_c M_\mathrm{tot}^{6/5}R^{-3/5}\biggl[ \frac{q^3}{\nu} \biggr]^{4/5} \frac{(1-\nu)^2}{(1-q^3)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Putting all the terms together gives, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 2\mathfrak{a}_c \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggl(\frac{\nu}{q}\biggr) \biggr] | |||
- 2\mathfrak{a}_e \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] | |||
+ \mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} K_c (M_\mathrm{tot}\nu)^{6/5} (Rq)^{-3/5} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr)^{1/5} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} | |||
K_c M_\mathrm{tot}^{6/5}R^{-3/5}\biggl[ \frac{q^3}{\nu} \biggr]^{4/5} \frac{(1-\nu)^2}{(1-q^3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 2 \mathcal{A}_\mathrm{biP} \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggr] | |||
+ \mathcal{B}_\mathrm{biP} K_c \biggl[\frac{(\nu M_\mathrm{tot})^{2}}{ qR} \biggr]^{3/5} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~~ \frac{\mathfrak{G}}{E_\mathrm{norm}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 2 \mathcal{A}_\mathrm{biP} \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggr] \biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} | |||
+ \mathcal{B}_\mathrm{biP} \biggl(\frac{\nu^2}{q}\biggr)^{3/5} K_c \biggl[\frac{M_\mathrm{tot}^{2}}{ R} \biggr]^{3/5}\biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- 2 \mathcal{A}_\mathrm{biP} \biggl[ \frac{R_\mathrm{norm}}{R} \biggr] | |||
+ \mathcal{B}_\mathrm{biP} \biggl(\frac{\nu^2}{q}\biggr)^{3/5} \biggl[\frac{R_\mathrm{norm}}{ R} \biggr]^{3/5} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{A}_\mathrm{biP}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ \mathfrak{a}_c\biggl(\frac{\nu}{q}\biggr) + \mathfrak{a}_e \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathcal{B}_\mathrm{biP}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{3}{2^2\pi} \biggr)^{1/5} \biggl[5\mathfrak{b}_c | |||
+ \mathfrak{b}_e \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \frac{q^3(1-\nu)^2}{\nu^2(1-q^3)} \biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
==Equilibrium Radius== | |||
===Order of Magnitude Estimate=== | |||
This means that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial\mathfrak{G}}{\partial R}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 2 \mathcal{A}_\mathrm{biP}\biggl[ \frac{GM_\mathrm{tot}^2 }{R^2} \biggr] | |||
- \frac{3}{5} \mathcal{B}_\mathrm{biP} K_c \biggl[\frac{\nu^{2}}{ q} \biggr]^{3/5} M_\mathrm{tot}^{6/5} R^{-8/5} | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence, because equilibrium radii are identified by setting <math>~\partial\mathfrak{G}/\partial R = 0</math>, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{norm}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl(\frac{2\cdot 5}{3}\biggr)^{5/2} \biggl[\frac{\mathcal{A}_\mathrm{biP} }{\mathcal{B}_\mathrm{biP}}\biggr]^{5/2} \biggl(\frac{ q} {\nu^{2}}\biggr)^{3/2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
===Reconcile With Known Analytic Expression=== | |||
From our [[User:Tohline/SSC/Structure/BiPolytropes/FreeEnergy5_1#The_Core_2|earlier derivations]], it appears as though, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{eq} \equiv \frac{R_\mathrm{eq}}{R_\mathrm{norm}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{3^8}{2^5\pi} \biggr)^{-1/2} | |||
\biggl(\frac{3}{2^4}\biggr) \biggl( \frac{q}{\ell_i}\biggr)^{5}\biggl(\frac{\nu}{q^3} \biggr)^2 \biggl( 1 + \ell_i^2 \biggr)^{3} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl(\frac{2\cdot 5}{3}\biggr)^{5/2} \biggl(\frac{q}{\nu^2} \biggr)^{3/2} | |||
\biggl[\biggl( \frac{\pi}{2^8 \cdot 3 \cdot 5^5} \biggr)^{1/2} \biggl(\frac{\nu^2}{q} \biggr)^{5/2} | |||
\frac{(1 + \ell_i^2)^3}{\ell_i^5} \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This implies that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\mathcal{A}_\mathrm{biP} }{\mathcal{B}_\mathrm{biP}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\biggl( \frac{\pi}{2^8 \cdot 3 \cdot 5^5} \biggr)^{1/2} \biggl(\frac{\nu^2}{q} \biggr)^{5/2} | |||
\frac{(1 + \ell_i^2)^3}{\ell_i^5} \biggr]^{2/5} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl(\frac{\nu^2}{q} \biggr) | |||
\biggl( \frac{\pi}{2^8 \cdot 3 \cdot 5^5} \biggr)^{1/5} \frac{(1 + \ell_i^2)^{6/5}}{\ell_i^2} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~~ \biggl[ \mathfrak{a}_c\biggl(\frac{\nu}{q}\biggr) + \mathfrak{a}_e \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{2^2\cdot 5}\biggl(\frac{\nu^2}{q} \biggr) | |||
\frac{(1 + \ell_i^2)^{6/5}}{\ell_i^2} \biggl[5\mathfrak{b}_c | |||
+ \mathfrak{b}_e \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \frac{q^3(1-\nu)^2}{\nu^2(1-q^3)} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~~ \biggl[ \mathfrak{a}_c + \mathfrak{a}_e \cdot \frac{q(1-\nu)}{\nu(1+q)} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\nu}{2^2\cdot 5} | |||
\frac{(1 + \ell_i^2)^{6/5}}{\ell_i^2} \biggl[5\mathfrak{b}_c | |||
+ \mathfrak{b}_e \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \frac{q^3(1-\nu)^2}{\nu^2(1-q^3)} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
==Focus on Five-One Free-Energy Expression== | |||
===Approximate Expressions=== | |||
Let's plug this equilibrium radius back into each term of the free-energy expression. | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{W_\mathrm{grav}}{E_\mathrm{norm}}\biggr|_\mathrm{core}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- 2\mathfrak{a}_c \biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} \biggl[ \frac{GM_\mathrm{tot}^2 }{R_\mathrm{eq}} \biggl(\frac{\nu}{q}\biggr) \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- 2\mathfrak{a}_c \biggl(\frac{\nu}{q}\biggr) \biggl[ \frac{R_\mathrm{norm} }{R_\mathrm{eq}} \biggr] \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{W_\mathrm{grav}}{E_\mathrm{norm}}\biggr|_\mathrm{env}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- 2\mathfrak{a}_e \biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} \biggl[ \frac{GM_\mathrm{tot}^2 }{R_\mathrm{eq}} \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- 2\mathfrak{a}_e \biggl(\frac{1-\nu}{1+q}\biggr) \biggl[ \frac{R_\mathrm{norm} }{R_\mathrm{eq}} \biggr] \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{S_\mathrm{core}}{E_\mathrm{norm}} = \biggl[\frac{3(\gamma_c-1)}{2}\biggr] \frac{U_\mathrm{int}}{E_\mathrm{norm}}\biggr|_\mathrm{core} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[\frac{3}{2\cdot 5}\biggr]\mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} \biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} | |||
K_c (M_\mathrm{tot}\nu)^{6/5} (R_\mathrm{eq}q)^{-3/5} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[\frac{3}{2\cdot 5}\biggr]\mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} | |||
\biggl(\frac{\nu^2}{q}\biggr)^{3/5} \biggl(\frac{R_\mathrm{norm}}{R_\mathrm{eq}}\biggr)^{3/5} | |||
\, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{S_\mathrm{env}}{E_\mathrm{norm}} = \biggl[\frac{3(\gamma_e-1)}{2}\biggr] \frac{U_\mathrm{int}}{E_\mathrm{norm}}\biggr|_\mathrm{env} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[\frac{3}{2}\biggr] | |||
\mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr)^{1/5} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} | |||
\biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} K_c M_\mathrm{tot}^{6/5}R_\mathrm{eq}^{-3/5}\biggl[ \frac{q^3}{\nu} \biggr]^{4/5} \frac{(1-\nu)^2}{(1-q^3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[\frac{3}{2}\biggr] | |||
\mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr)^{1/5} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} | |||
\biggl[ \frac{q^3}{\nu} \biggr]^{4/5} \frac{(1-\nu)^2}{(1-q^3)} | |||
\biggl(\frac{R_\mathrm{norm}}{R_\mathrm{eq}}\biggr)^{3/5} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
===From Detailed Force-Balance Models=== | |||
In the following derivations, we will use the expression, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{eq} \equiv \frac{ R_\mathrm{eq}}{R_\mathrm{norm}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{\mu_e}{\mu_c} \biggr)^3 \biggl( \frac{\pi}{2^3} \biggr)^{1/2} \frac{1}{A^2\eta_s} | |||
= \biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Keep in mind, as well — as derived in an [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Background|accompanying discussion]] — that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\nu \equiv \frac{M_\mathrm{core}}{M_\mathrm{tot}} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ (m_3^2 \ell_i^3) (1 + \ell_i^2)^{-1/2} [1 + (1-m_3)^2 \ell_i^2]^{-1/2} \biggl[ m_3\ell_i + (1+\ell_i^2) \biggl(\frac{\pi}{2} + \tan^{-1} \Lambda_i \biggr) \biggr]^{-1} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<math>m_3 \equiv 3 \biggl( \frac{\mu_e}{\mu_c} \biggr) \, .</math> | |||
</div> | |||
From the [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Parameter_Values|accompanying Table 1 parameter values]], we also can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~q</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\eta_i}{\eta_s} | |||
= \eta_i \biggl\{\frac{\pi}{2} + \eta_i + \tan^{-1}\biggl[ \frac{1}{\eta_i} - \ell_i \biggr] \biggr\}^{-1}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\eta_i \biggl\{\eta_i + \cot^{-1}\biggl[ \ell_i - \frac{1}{\eta_i} \biggr] \biggr\}^{-1} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\eta_i</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~m_3 \biggl[\frac{\ell_i }{(1+\ell_i^2)}\biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Let's also define the following shorthand notation: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{L}_i</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{(\ell_i^4-1)}{\ell_i^2} + \frac{(1+\ell_i^2)^3}{\ell_i^3} \cdot \tan^{-1}\ell_i \, ;</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{K}_i</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] + \frac{\Lambda_i}{\eta_i} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
====Gravitational Potential Energy of the Core==== | |||
Pulling from [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Expression_for_Free_Energy|our detailed derivations]], | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - \biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} | |||
\biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) (1 + \ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] \, .</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~~ -\chi_\mathrm{eq} \biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} | |||
\biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) (1 + \ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] | |||
\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{3}{2^4} \biggr) \frac{\nu^2}{q} \cdot \frac{1}{\ell_i^5} | |||
\biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) + (1 + \ell_i^2)^{3}\tan^{-1}(\ell_i) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Out of equilibrium, then, we should expect, | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{W_\mathrm{core}}{E_\mathrm{norm}} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - \chi^{-1} | |||
\biggl( \frac{3}{2^4} \biggr) \frac{\nu^2}{q} \cdot \frac{1}{\ell_i^5} | |||
\biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) + (1 + \ell_i^2)^{3}\tan^{-1}(\ell_i) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \chi^{-1} | |||
\biggl( \frac{3}{2^4} \biggr) \frac{\nu^2}{q} \cdot \frac{1}{\ell_i^2} | |||
\biggl[ \mathfrak{L}_i - \frac{8}{3} \biggr] | |||
\, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
which, in comparison with our above approximate expression, implies, | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{a}_c </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{3}{2^5} \biggr) \frac{\nu}{\ell_i^5} | |||
\biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) + (1 + \ell_i^2)^{3}\tan^{-1}(\ell_i) \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
====Thermal Energy of the Core==== | |||
Again, pulling from [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Expression_for_Free_Energy|our detailed derivations]], | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{1}{2} \biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~~ \chi_\mathrm{eq}^{3} \biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]^5_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2^5} \biggl( \frac{3^8}{2^5\pi} \biggr)^{5/2} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr]^5 | |||
\biggl[\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5}\biggr]^{3} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{1}{\pi}\biggl(\frac{3}{2^{2}}\biggr)^{11} | |||
\biggl(\frac{\nu^2}{q}\biggr)^{3} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr]^5 | |||
\biggl[\frac{(1+\ell_i^2)^9}{\ell_i^{15}}\biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Out of equilibrium, we should then expect, | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{S_\mathrm{core}}{E_\mathrm{norm}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{3}{2^2\pi} \biggr)^{1/5}\biggl[ \chi^{-1} | |||
\biggl(\frac{\nu^2}{q}\biggr) \frac{1}{(1+\ell_i^2)^{2}} \biggr]^{3/5} \biggl(\frac{3}{2^{2}}\biggr)^{2}\mathfrak{L}_i | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
In comparison with our above approximate expression, we therefore have, | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\biggl[ \biggl(\frac{3}{2\cdot 5}\biggr)\mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} | |||
\biggl(\frac{\nu^2}{q}\biggr)^{3/5} \biggr]^5</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{1}{\pi}\biggl(\frac{3}{2^{2}}\biggr)^{11} | |||
\biggl(\frac{\nu^2}{q}\biggr)^{3} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr]^5 | |||
\biggl[\frac{(1+\ell_i^2)^9}{\ell_i^{15}}\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~~ | |||
\mathfrak{b}_c | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{ 3 }{2^3\ell_i^{3}(1+\ell_i^2)^{6/5}} | |||
\biggl[ \ell_i (\ell_i^4 - 1 ) + (1+\ell_i^2)^{3}\tan^{-1}(\ell_i) \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
====Gravitational Potential Energy of the Envelope==== | |||
Again, pulling from [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Expression_for_Free_Energy|our detailed derivations]] and appreciating, in particular, that (see, for example, [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Equilibrium_Condition|our notes on equilibrium conditions]]), | |||
<div align="center"> | |||
<table border="0" cellpadding="3"> | |||
<tr> | |||
<td align="right"> | |||
<math>~A</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\eta_i}{\sin(\eta_i - B)} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~(\eta_s - B)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\pi \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\eta_i - B</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\pi}{2} - \tan^{-1}(\Lambda_i)\, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \sin(\eta_i -B) = (1+\Lambda_i^2)^{-1/2}</math> | |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
<math>~\sin[2(\eta_i-B)] = 2\Lambda_i(1 + \Lambda_i^2)^{-1} \ ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ -\biggl( \frac{1}{2^3\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} A^2 | |||
\biggl\{ \biggl[6(\eta_s-B) - 3\sin[2(\eta_s - B)] -4\eta_s\sin^2(\eta_s-B) + 4B\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ - \biggl[6(\eta_i-B) - 3\sin[2(\eta_i - B)] -4\eta_i\sin^2(\eta_i-B) + 4B \biggr]\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ -\biggl( \frac{1}{2^3\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \biggl[\frac{\eta_i}{\sin(\eta_i - B)} \biggr]^2 | |||
\biggl\{ 6\pi - \biggl[6(\eta_i-B) - 3\sin[2(\eta_i - B)] -4\eta_i\sin^2(\eta_i-B) \biggr]\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ -\biggl( \frac{1}{2^3\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2(1+\Lambda_i^2) | |||
\biggl\{ 6\pi - 6\biggl[\frac{\pi}{2} - \tan^{-1}(\Lambda_i)\biggr] + 6\biggl[ \frac{\Lambda_i}{(1 + \Lambda_i^2)} \biggr] | |||
+ 4\eta_i \biggl[ \frac{1}{(1+\Lambda_i^2)} \biggr] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ -\biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 | |||
\biggl\{ (1+\Lambda_i^2)\biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \Lambda_i + \frac{2}{3} \cdot \eta_i \biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
So, in equilibrium we can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~-\chi_\mathrm{eq}\biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 | |||
\biggl\{ (1+\Lambda_i^2)\biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \Lambda_i + \frac{2}{3} \cdot \eta_i \biggr\} | |||
\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{3}{2^2} \biggl(\frac{\eta_i}{m_3}\biggr)^3 | |||
\biggl\{ \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \frac{\Lambda_i}{\eta_i} + \frac{2}{3} \biggr\} | |||
\frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{\ell_i^5} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{3}{2^2} \biggl(\frac{\nu^2}{q} \biggr) \frac{1}{\ell_i^2} | |||
\biggl\{ \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \frac{\Lambda_i}{\eta_i} + \frac{2}{3} \biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
And out of equilibrium, | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{W_\mathrm{env}}{E_\mathrm{norm}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\chi^{-1}\cdot \frac{3}{2^2} \biggl(\frac{\nu^2}{q} \biggr) \frac{1}{\ell_i^2} | |||
\biggl[\mathfrak{K}_i+ \frac{2}{3} \biggr] | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This, in turn, implies that both in and out of equilibrium, | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{a}_e </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{3}{2^3} \biggl[\frac{\nu^2(1+q)}{q(1-\nu)} \biggr] \frac{1}{\ell_i^2} | |||
\biggl\{ \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \frac{\Lambda_i}{\eta_i} + \frac{2}{3} \biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
====Thermal Energy of the Envelope==== | |||
Again, pulling from [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Expression_for_Free_Energy|our detailed derivations]], | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ ~ \biggl( \frac{1}{2^5\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} A^2 | |||
\biggl\{ \biggl[6(\eta_s - B) - 3\sin[2(\eta_s-B)] \biggr] - \biggl[6(\eta_i - B) - 3\sin[2(\eta_i-B)] \biggr] \biggr\}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ ~ \biggl( \frac{1}{2^5\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \biggl[\frac{\eta_i}{\sin(\eta_i - B)} \biggr]^2 | |||
\biggl\{ 6\pi - 6(\eta_i - B) + 3\sin[2(\eta_i-B)] \biggr\}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ ~ \biggl( \frac{1}{2^5\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 (1 + \Lambda_i^2) | |||
\biggl\{ 6\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + 6\biggl[\Lambda_i(1 + \Lambda_i^2)^{-1} \biggr] \biggr\}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ ~\frac{1}{2} \biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 | |||
\biggl\{ (1 + \Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \Lambda_i \biggr\} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
So, in equilibrium we can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{eq}^{3}\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ ~\frac{1}{2} \biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 | |||
\biggl\{ (1 + \Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \Lambda_i \biggr\} | |||
\biggl[\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5}\biggr]^{3} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ ~\biggl(\frac{\nu^2}{q} \biggr)^3 \biggl( \frac{3^2\pi^2}{2^{12}} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^3 | |||
\biggl\{ \frac{(1 + \Lambda_i^2)}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \frac{\Lambda_i}{\eta_i} \biggr\} | |||
\biggl[\frac{(1+\ell_i^2)^9}{3^9\ell_i^{15}}\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ ~\biggl(\frac{\nu^2}{q} \biggr)^3 \biggl( \frac{\pi}{2^{6}\cdot 3^5} \biggr) \biggl[\frac{(1+\ell_i^2)^6}{\ell_i^{12}}\biggr] | |||
\biggl\{ \frac{(1 + \Lambda_i^2)}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \frac{\Lambda_i}{\eta_i} \biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
And, out of equilibrium, | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ ~ | |||
\chi^{-3}\biggl(\frac{\nu^2}{q} \biggr)^3 \biggl( \frac{\pi}{2^{6}\cdot 3^5} \biggr) | |||
\biggl[\frac{(1+\ell_i^2)^6}{\ell_i^{12}}\biggr]\mathfrak{K} | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
====Combined in Equilibrium==== | |||
Notice that, in combination, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[\frac{2S_\mathrm{env} + W_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - \frac{2}{3}\biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^3 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - \frac{2}{3}\biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} | |||
\biggl[3 \biggl( \frac{\mu_e}{\mu_c} \biggr) \ell_i \biggl( 1 + \ell_i^2 \biggr)^{-1}\biggr]^3 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - \biggl( \frac{2\cdot 3^6}{\pi} \biggr)^{1/2} | |||
\biggl[\frac{\ell_i^3}{( 1 + \ell_i^2)^3}\biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Also, from above, | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{2S_\mathrm{core}+W_\mathrm{core}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - \biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} | |||
\biggl[ \ell_i \biggl(- \frac{8}{3} \ell_i^2 \biggr) (1 + \ell_i^2)^{-3} \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ + \biggl( \frac{2\cdot 3^6}{\pi } \biggr)^{1/2} | |||
\biggl[ \frac{\ell_i^3}{(1 + \ell_i^2)^{3}} \biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
So, in equilibrium, these terms from the core and envelope sum to zero, as they should. | |||
====Out of Equilibrium==== | |||
And now, in combination ''out'' of equilibrium, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\mathfrak{G}}{E_\mathrm{norm}} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-1} \biggl\{ \biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} | |||
+ \biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}\biggr\} | |||
+\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-3/5} \biggl(\frac{2n_c}{3}\biggr) \biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} | |||
+\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-3} \biggl(\frac{2n_e}{3}\biggr)\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence, quite generally ''out'' of equilibrium, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial}{\partial \chi} \biggl[ \frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\chi^{-1}\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-1} \biggl\{ \biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} | |||
+ \biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}\biggr\} | |||
-\frac{3}{5}\chi^{-1}\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-3/5} \biggl(\frac{10}{3}\biggr) \biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} | |||
-3\chi^{-1}\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-3} \biggl(\frac{2}{3}\biggr)\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Let's see what the value of this derivative is if the dimensionless radius, <math>~\chi</math>, is set to the value that has been determined, via a detailed force-balanced analysis, to be the equilibrium radius, namely, <math>~\chi = \chi_\mathrm{eq}</math>. In this case, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl\{\frac{\partial}{\partial \chi} \biggl[ \frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr] \biggr\}_\mathrm{\chi \rightarrow \chi_\mathrm{eq}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ -\chi_\mathrm{eq}^{-1}\biggl\{ | |||
\biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} | |||
+ \biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} | |||
+2\biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} | |||
+2\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} \biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
But, according to the virial theorem — and, as we have just demonstrated — the four terms inside the curly braces sum to zero. So this demonstrates that the derivative of our out-of-equilibrium free-energy expression does go to zero at the equilibrium radius, as it should! | |||
===Summary51=== | |||
In summary, the desired ''out'' of equilibrium free-energy expression is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\mathfrak{G}}{E_\mathrm{norm}} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{W_\mathrm{core}}{E_\mathrm{norm}} + \frac{W_\mathrm{env}}{E_\mathrm{norm}} | |||
+\biggl(\frac{2n_c}{3}\biggr)\frac{S_\mathrm{core}}{E_\mathrm{norm}} | |||
+\biggl(\frac{2n_e}{3}\biggr)\frac{S_\mathrm{env}}{E_\mathrm{norm}} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \chi^{-1} | |||
\biggl( \frac{3}{2^4} \biggr) \frac{\nu^2}{q} \cdot \frac{1}{\ell_i^2} | |||
\biggl[ \mathfrak{L}_i - \frac{8}{3} \biggr] | |||
-\chi^{-1}\cdot \frac{3}{2^2} \biggl(\frac{\nu^2}{q} \biggr) \frac{1}{\ell_i^2} | |||
\biggl[\mathfrak{K}_i+ \frac{2}{3} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ | |||
\biggl(\frac{2\cdot 5}{3}\biggr) \biggl(\frac{3}{2^2\pi} \biggr)^{1/5}\biggl[ \chi^{-1} | |||
\biggl(\frac{\nu^2}{q}\biggr) \frac{1}{(1+\ell_i^2)^{2}} \biggr]^{3/5} \biggl(\frac{3}{2^{2}}\biggr)^{2}\mathfrak{L}_i | |||
+\biggl(\frac{2}{3}\biggr) | |||
\chi^{-3}\biggl(\frac{\nu^2}{q} \biggr)^3 \biggl( \frac{\pi}{2^{6}\cdot 3^5} \biggr) | |||
\biggl[\frac{(1+\ell_i^2)^6}{\ell_i^{12}}\biggr]\mathfrak{K} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- | |||
\biggl( \frac{3}{2^4} \biggr) \biggl[\chi^{-1}\frac{\nu^2}{q} \cdot \frac{1}{\ell_i^2}\biggr] | |||
\biggl[ \mathfrak{L}_i + 4\mathfrak{K}_i \biggr] | |||
+ | |||
\biggl(\frac{3}{2^2\pi} \biggr)^{1/5}\biggl(\frac{3\cdot 5}{2^3}\biggr) \biggl[ \chi^{-1} | |||
\biggl(\frac{\nu^2}{q}\biggr) \frac{1}{(1+\ell_i^2)^{2}} \biggr]^{3/5} | |||
\mathfrak{L}_i | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \biggl( \frac{\pi}{2^{5}\cdot 3^6} \biggr) | |||
\biggl[\chi^{-1}\biggl(\frac{\nu^2}{q} \biggr) | |||
\frac{(1+\ell_i^2)^2}{\ell_i^{4}}\biggr]^3\mathfrak{K} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Or, in terms of the ratio, | |||
<div align="center"> | |||
<math>\Chi \equiv \frac{\chi}{\chi_\mathrm{eq}} \, ,</math> | |||
</div> | |||
and pulling from the above expressions, | |||
<div align="center"> | |||
<table border="0" cellpadding="4"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - \biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} | |||
\biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) (1 + \ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - \biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} \biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]^{3} | |||
\biggl[ \mathfrak{L}_i - \frac{8}{3}\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ -\biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 | |||
\biggl\{ (1+\Lambda_i^2)\biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \Lambda_i + \frac{2}{3} \cdot \eta_i \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ -\biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]^{3} | |||
\biggl[4\mathfrak{K}_i + \frac{8}{3} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{1}{2} \biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{1}{2} \biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]^{3}\mathfrak{L}_i </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ ~\frac{1}{2} \biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 | |||
\biggl\{ (1 + \Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \Lambda_i \biggr\} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ ~\frac{1}{2} \biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]^{3} (4\mathfrak{K}_i) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
we have the streamlined, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{2^5\pi}{3^6} \biggr)^{1/2} \biggl[ \frac{(1+\ell_i^2)}{\ell_i} \biggr]^{3} \biggl[\frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+\Chi^{-3/5} (5 \mathfrak{L}_i) | |||
+\Chi^{-3} (4\mathfrak{K}_i) | |||
-\Chi^{-1} (3\mathfrak{L}_i +12\mathfrak{K}_i ) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
or, better yet, | |||
<div align="center" id="BiPolytropeFreeEnergy"> | |||
<table border="1" cellpadding="5" align="center"> | |||
<tr> | |||
<th align="center"> | |||
<font size="+1">Out-of-Equilibrium, Free-Energy Expression for BiPolytropes with</font> <math>~(n_c, n_e) = (5, 1)</math> | |||
</th> | |||
</tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~2^4\biggl( \frac{q\ell_i^2}{\nu^2}\biggr) \chi_\mathrm{eq} \biggl[\frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\Chi^{-3/5} (5 \mathfrak{L}_i) | |||
+\Chi^{-3} (4\mathfrak{K}_i) | |||
-\Chi^{-1} (3\mathfrak{L}_i +12\mathfrak{K}_i ) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{L}_i</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{(\ell_i^4-1)}{\ell_i^2} + \frac{(1+\ell_i^2)^3}{\ell_i^3} \cdot \tan^{-1}\ell_i \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{K}_i</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\Lambda_i}{\eta_i} + \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Lambda_i</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{\eta_i} - \ell_i \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\eta_i</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~3 \biggl( \frac{\mu_e}{\mu_c} \biggr) \biggl[\frac{\ell_i }{(1+\ell_i^2)}\biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
From the [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Parameter_Values|accompanying Table 1 parameter values]], we also can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{q}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\eta_s}{\eta_i} | |||
= 1 + \frac{1}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\nu</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\ell_i q}{(1+\Lambda_i^2)^{1/2}} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="1" cellpadding="5" align="center"> | |||
<tr><td align="center">Radial Derivatives</td></tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial \mathfrak{G}^*}{\partial \Chi}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-\Chi^{-8/5} (3 \mathfrak{L}_i) | |||
-\Chi^{-4} (12\mathfrak{K}_i) | |||
+\Chi^{-2} (3\mathfrak{L}_i +12\mathfrak{K}_i ) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial^2 \mathfrak{G}^*}{\partial \Chi^2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3}{5}\biggl[ | |||
\Chi^{-13/5} (8\mathfrak{L}_i) | |||
+\Chi^{-5} (80\mathfrak{K}_i) | |||
-\Chi^{-1} (10\mathfrak{L}_i +40\mathfrak{K}_i )\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
</div> | |||
Consistent with our [[User:Tohline/SSC/BipolytropeGeneralization#Free_Energy_and_Its_Derivatives|generic discussion of the stability of bipolytropes]] and the ''specific'' discussion of [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Stability_Condition|the stability of bipolytropes having]] <math>~(n_c, n_e) = (5, 1)</math>, it can straightforwardly be shown that <math>~\partial \mathfrak{G}/\partial \chi = 0</math> is satisfied by setting <math>~\Chi = 1</math>; that is, the equilibrium condition is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi = \chi_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Furthermore, the equilibrium configuration is unstable whenever <math>~\partial^2 \mathfrak{G}/\partial \chi^2 < 0</math>, that is, it is unstable whenever, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{ \mathfrak{L}_i}{\mathfrak{K}_i}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~></math> | |||
</td> | |||
<td align="left"> | |||
<math>~20 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
[[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Stability_Condition|Table 1 of an accompanying chapter]] — and the red-dashed curve in the figure adjacent to that table — identifies some key properties of the model that marks the transition from stable to unstable configurations along equilibrium sequences that have various values of the mean-molecular weight ratio, <math>~\mu_e/\mu_c</math>. | |||
==Focus on Zero-Zero Free-Energy Expression== | |||
Here, we will draw heavily from the following accompanying chapters: | |||
* [[User:Tohline/SSC/Structure/BiPolytropes/Analytic0_0#Step_7:__Surface_Boundary_Condition|Analytic Detailed Force Balance Models]] | |||
* [[User:Tohline/SSC/Structure/BiPolytropes/FreeEnergy0_0#Free_Energy_of_BiPolytrope_with|Free-Energy Analysis]] | |||
===From Detailed Force-Balance Models=== | |||
====Equilibrium Radius==== | |||
=====First View===== | |||
In an [[User:Tohline/SSC/Structure/BiPolytropes/FreeEnergy0_0#Virial_Theorem|accompanying chapter]] we find, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\frac{P_0 R_\mathrm{eq}^4}{G M_\mathrm{tot}^2 } </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{3}{2^3 \pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^2 | |||
\biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~f</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
1+ | |||
\frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2}-1 \biggr) +\biggl( \frac{\rho_e}{\rho_c} | |||
\biggr)^2 \biggl[ \frac{1}{q^5}-1 + \frac{5}{2} \biggl( 1-\frac{1}{q^2}\biggr)\biggr] \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{F} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (-2q^2 + 3q^3 - q^5) + | |||
\frac{3}{5} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-1 +5q^2 - 5q^3 + q^5) \biggr] \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\rho_e}{\rho_c} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{q^3(1-\nu)}{\nu(1-q^3)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Here, we prefer to normalize the equilibrium radius to <math>~R_\mathrm{norm}</math>. So, let's replace the central pressure with its expression in terms of <math>~K_c</math>. Specifically, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~P_0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
K_c \rho_c^{\gamma_c} = K_c \biggl[ \frac{3M_\mathrm{core}}{4\pi R_i^3} \biggr]^{\gamma_c} | |||
= K_c \biggl[ \frac{3\nu M_\mathrm{tot}}{4\pi q^3 R_\mathrm{eq}^3} \biggr]^{(n_c+1)/n_c} | |||
~~~\Rightarrow~~~ \frac{P_0}{P_\mathrm{norm}} = \biggl[ \frac{3}{4\pi}\biggl(\frac{\nu}{q^3}\biggr) \frac{1}{\chi_\mathrm{eq}^3}\biggr]^{(n_c+1)/n_c} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~K_c \biggl[ \frac{3\nu M_\mathrm{tot}}{4\pi q^3 R_\mathrm{eq}^3} \biggr]^{(n_c+1)/n_c} | |||
\frac{R_\mathrm{eq}^4}{G M_\mathrm{tot}^2 } </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{3}{2^3 \pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^2 | |||
\biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~R_\mathrm{eq}^{(n_c-3)/n_c} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{G}{K_c}\biggr) M_\mathrm{tot}^{(n_c-1)/n_c} \biggl[ \frac{3\nu }{4\pi q^3 } \biggr]^{-(n_c+1)/n_c} | |||
\biggl( \frac{3}{2^3 \pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^2 | |||
\biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~\chi_\mathrm{eq}^{(n_c-3)/n_c} \equiv \biggl[\frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr]^{(n_c-3)/n_c}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2}\biggl(\frac{4\pi}{3} \biggr)^{1/n_c} | |||
\biggl( \frac{\nu}{q^3}\biggr)^{(n_c-1)/n_c} | |||
\biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Or, in terms of <math>~\gamma_c</math>, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{eq}^{4-3\gamma_c} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2}\biggl(\frac{3}{4\pi} \biggr)^{1-\gamma_c} | |||
\biggl( \frac{\nu}{q^3}\biggr)^{2-\gamma_c} | |||
\biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=====Second View===== | |||
Alternatively, from our derivation and discussion of [[User:Tohline/SSC/Structure/BiPolytropes/Analytic0_0#CentralPressure|analytic detailed force-balance models]], | |||
<div align="center"> | |||
<table border="0"> | |||
<tr> | |||
<td align="right"> | |||
<math> | |||
\biggl[ \frac{R^4}{GM_\mathrm{tot}^2} \biggr] P_0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>\biggl( \frac{3}{2^3\pi} \biggr) \frac{\nu^2 g^2}{q^4} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~[g(\nu,q)]^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
1 + \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1-q \biggr) + | |||
\frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
In order to show that this expression is the same as the other one, [[#First_View_2|above]], we need to show that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="left"> | |||
<math>~\biggl( \frac{3}{2^3 \pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^2 | |||
\biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>\biggl( \frac{3}{2^3\pi} \biggr) \frac{\nu^2 g^2}{q^4} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ | |||
f - 1-\mathfrak{F} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{5}{2q^3} \biggl[g^2-1\biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{5}{2q^3} \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1-q \biggr) + | |||
\frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{5}{2q^5} \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl\{ 2 ( q^2 - q^3 ) | |||
+ \frac{\rho_e}{\rho_0}\biggl[ 1 - 3q^2+ 2q^3 \biggr] \biggr\} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Let's see … | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
f - 1-\mathfrak{F} | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2}-1 \biggr) +\biggl( \frac{\rho_e}{\rho_c} | |||
\biggr)^2 \biggl[ \frac{1}{q^5}-1 + \frac{5}{2} \biggl( 1-\frac{1}{q^2}\biggr)\biggr] - | |||
\frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (-2q^2 + 3q^3 - q^5) + | |||
\frac{3}{5} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-1 +5q^2 - 5q^3 + q^5) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2}-1 \biggr) | |||
- \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (-2q^2 + 3q^3 - q^5) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
- \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ \frac{3}{5} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-1 +5q^2 - 5q^3 + q^5) \biggr] | |||
+\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \frac{1}{q^5}-1 + \frac{5}{2} \biggl( 1-\frac{1}{q^2}\biggr)\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl\{ (q^3- q^5 ) | |||
+ (2q^2 - 3q^3 + q^5) \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \frac{1}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \frac{1}{q^5} \biggl[ 3 (1 -5q^2 + 5q^3 - q^5) \biggr] | |||
+\frac{1}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \frac{1}{q^5} \biggl[ 2 - 2q^5 + 5\biggl( q^5-q^3\biggr)\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (q^3- q^5 ) + (2q^2 - 3q^3 + q^5) \biggr] | |||
+ \frac{1}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \frac{1}{q^5} \biggl[ 3 (1 -5q^2 + 5q^3 - q^5)+2 - 2q^5 + 5( q^5-q^3) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ 2q^2 - 2q^3 \biggr] | |||
+ \frac{5}{2q^5} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ 1 - 3q^2 + 2q^3 \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Q.E.D. | |||
Hence, the equilibrium radius can also be written as, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{eq}^{4-3\gamma_c} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2}\biggl(\frac{3}{4\pi} \biggr)^{1-\gamma_c} | |||
\biggl( \frac{\nu}{q^3}\biggr)^{2-\gamma_c} q^2 g^2 \, ; | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
or, in terms of the polytropic index, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{eq}^{n_c-3} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) | |||
\biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
====Gravitational Potential Energy==== | |||
Also from our [[User:Tohline/SSC/Structure/BiPolytropes/FreeEnergy0_0#Gravitational_Potential_Energy|accompanying discussion]], we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{W_\mathrm{grav}}{E_\mathrm{norm}} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
- \Chi^{-1} \biggl( \frac{3}{5}\biggr) \biggl(\frac{\nu}{q^3} \biggr)^2 q^5 | |||
\biggl[ \frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c} \biggr]^{-1/(n_c-3)} f(\nu,q) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
- \Chi^{-1} \biggl( \frac{6}{5}\biggr) q^5 f | |||
\biggl[ 2^{n_c-(n_c-3)} \biggl(\frac{3}{4\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{(1-n_c)+2(n_c-3)} b_\xi^{n_c} \biggr]^{1/(n_c-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
- \Chi^{-1} \biggl( \frac{6}{5}\biggr) q^5 f | |||
\biggl[ \biggl(\frac{6}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} b_\xi^{n_c} \biggr]^{1/(n_c-3)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
====Internal Energy Components==== | |||
=====First View===== | |||
Before writing out the expressions for the internal energy of the core and of the envelope, we [[User:Tohline/SSC/Structure/BiPolytropes/FreeEnergy0_0#Virial_Theorem|note from our separate detailed derivation]] that, in either case, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[\frac{P_i \chi^{3\gamma}}{P_\mathrm{norm}} \biggr]_\mathrm{eq} \chi^{3-3\gamma}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[\biggl(\frac{P_i }{P_0} \biggr) \biggl(\frac{P_0 }{P_\mathrm{norm}} \biggr)\chi^{3}\biggr]_\mathrm{eq} \biggl[\frac{\chi}{\chi_\mathrm{eq}}\biggr]^{3-3\gamma}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{\biggl(\frac{P_i }{P_0} \biggr) \biggl[ \frac{3}{4\pi } \biggl( \frac{\nu}{q^3} \biggr)\biggr]^{\gamma_c}\chi^{3-3\gamma_c}\biggr\}_\mathrm{eq} \Chi^{3-3\gamma} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, in equilibrium, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl(\frac{P_i }{P_0} \biggr)_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 - b_\xi q^2</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~b_\xi q^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{\frac{2}{5}q^3 f + \biggl[1 - \frac{2}{5} q^3( 1+\mathfrak{F} ) \biggr]\biggr\}^{-1} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[1 + \frac{2}{5}q^3 (f - 1-\mathfrak{F} ) \biggr]^{-1} </math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
So, copying from our [[User:Tohline/SSC/Structure/BiPolytropes/FreeEnergy0_0#InternalEnergies|accompanying detailed derivation]], we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{core}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{4\pi/3 }{({\gamma_c}-1)} | |||
\biggl\{\biggl(\frac{P_i }{P_0} \biggr) \biggl[ \frac{3}{4\pi } \biggl( \frac{\nu}{q^3} \biggr)\biggr]^{\gamma_c}\chi^{3-3\gamma_c}\biggr\}_\mathrm{eq} \Chi^{3-3\gamma_c} | |||
\biggl\{ \biggl( \frac{P_0}{P_{ic}} \biggr) \biggl[ q^3 - \biggl( \frac{3b_\xi}{5} \biggr) q^5 \biggr] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{1 }{({\gamma_c}-1)} \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} | |||
\biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] \Chi^{3-3\gamma_c} | |||
q^3\biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{env}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{4\pi/3 }{({\gamma_e}-1)} | |||
\biggl\{\biggl(\frac{P_i }{P_0} \biggr) \biggl[ \frac{3}{4\pi } \biggl( \frac{\nu}{q^3} \biggr)\biggr]^{\gamma_c}\chi^{3-3\gamma_c}\biggr\}_\mathrm{eq} \Chi^{3-3\gamma_e} | |||
\biggl\{ (1-q^3) + b_\xi \biggl(\frac{P_0}{P_{ie} } \biggr) \biggl[\frac{2}{5} q^5 \mathfrak{F} | |||
\biggr] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{1}{({\gamma_e}-1)} \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} | |||
\biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] | |||
\Chi^{3-3\gamma_e} \biggl(\frac{P_i }{P_0} \biggr) | |||
\biggl\{ (1-q^3) + b_\xi \biggl(\frac{P_0}{P_{ie} } \biggr) \biggl[\frac{2}{5} q^5 \mathfrak{F} | |||
\biggr] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{1}{({\gamma_e}-1)} \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} | |||
\biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] | |||
\Chi^{3-3\gamma_e} | |||
\biggl\{ (1-b_\xi q^2)(1-q^3) + b_\xi \biggl[\frac{2}{5} q^5 \mathfrak{F} \biggr] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{1}{({\gamma_e}-1)} \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} | |||
\biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] | |||
\Chi^{3-3\gamma_e} (1-q^3) | |||
\biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Furthermore, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} | |||
\biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{3}{4\pi}\biggr)^{\gamma_c - 1} | |||
\biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c} | |||
\biggl\{\chi_\mathrm{eq}^{4-3\gamma_c}\biggr\}^{(3-3\gamma_c)/(4-3\gamma_c)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{3}{4\pi}\biggr)^{\gamma_c - 1} | |||
\biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c} | |||
\biggl\{\frac{1}{2}\biggl(\frac{3}{4\pi} \biggr)^{1-\gamma_c} | |||
\biggl( \frac{\nu}{q^3}\biggr)^{2-\gamma_c} | |||
\biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] \biggr\}^{(3-3\gamma_c)/(4-3\gamma_c)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{3}{4\pi}\biggr)^{(\gamma_c - 1)/(4-3\gamma_c)} | |||
\biggl( \frac{\nu}{q^3} \biggr)^{(6-5\gamma_c)(4-3\gamma_c)} | |||
\biggl\{\frac{q^2}{2} | |||
\biggl[ 1 + \frac{2}{5} q^3( f - 1-\mathfrak{F} )\biggr] \biggr\}^{(3-3\gamma_c)/(4-3\gamma_c)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{3}{4\pi}\biggr)^{1/(n_c-3)} | |||
\biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)(n_c-3)} | |||
\biggl\{\frac{q^2}{2} | |||
\biggl[ 1 + \frac{2}{5} q^3( f - 1-\mathfrak{F} )\biggr] \biggr\}^{-3/(n_c-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^3\biggr]^{1/(n_c-3)} | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Hence, we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{core}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
n_c \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} | |||
\biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] \Chi^{-3/n_c} | |||
q^3\biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
n_c | |||
\biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^3\biggr]^{1/(n_c-3)} | |||
\Chi^{-3/n_c} | |||
q^3\biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{env}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
n_e | |||
\biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^3\biggr]^{1/(n_c-3)} | |||
\Chi^{-3/n_e} (1-q^3) | |||
\biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=====Second View===== | |||
In our [[User:Tohline/SSC/Structure/BiPolytropes/Analytic0_0#PiDefinition|accompanying discussion of energies associated with detailed force balance models]], we used the notation, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Pi</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{3}{2^3\pi}\biggr) \frac{GM_\mathrm{tot}^2}{R^4} \biggl(\frac{\nu}{q^3}\biggr)^2 | |||
= P_\mathrm{norm} \chi^{-4}\biggl(\frac{3}{2^3\pi}\biggr) \biggl(\frac{\nu}{q^3}\biggr)^2 \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
which allows us to rewrite the [[#Second_View|above quoted relationship]] between the central pressure and the radius of the bipolytrope as, | |||
<div align="center"> | |||
<math>~P_0 = \Pi (qg)^2 \, .</math> | |||
</div> | |||
We [[User:Tohline/SSC/Structure/BiPolytropes/Analytic0_0#Virial_Equilibrium|also showed]] that, in equilibrium, the relationship between the central pressure and the interface pressure is, | |||
<div align="center"> | |||
<math>~P_0 =P_i + \Pi_\mathrm{eq} q^2 \, .</math> | |||
</div> | |||
This means that, in equilibrium, the ratio of the interface pressure to the central pressure is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl(\frac{P_i}{P_0}\biggr)_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 - \frac{\Pi_\mathrm{eq} q^2}{P_0} | |||
= 1- \frac{1}{g^2} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
or given that (see [[#Second_View|above]]), | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
\frac{5}{2q^3} \biggl[g^2-1\biggr] | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
f - 1-\mathfrak{F} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~~ | |||
g^2 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ 1+\frac{2}{5} q^3 ( f - 1-\mathfrak{F} ) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl(\frac{P_i}{P_0}\biggr)_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 - \frac{\Pi_\mathrm{eq} q^2}{P_0} | |||
= 1- \biggl[ 1+\frac{2}{5} q^3 ( f - 1-\mathfrak{F} ) \biggr]^{-1} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
This is exactly the pressure-ratio expression presented in our "first view" and unveils the notation association, | |||
<div align="center"> | |||
<table border="0"> | |||
<tr> | |||
<td align="right"> | |||
<math>~b_\xi q^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\leftrightarrow~</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{1}{g^2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
From [[User:Tohline/SSC/Structure/BiPolytropes/Analytic0_0#Thermal_Energy_Content|our separate derivation]], we have, in equilibrium, | |||
<div align="center"> | |||
<table border="0"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}_\mathrm{core} = \biggl(\frac{2n_c}{3}\biggr) S_\mathrm{core}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>\biggl(\frac{2n_c}{3}\biggr) \biggl( \frac{4\pi}{5} \biggr) R_\mathrm{eq}^3 q^5 \biggl (\frac{5P_i}{2q^2} + \Pi \biggr)_\mathrm{eq} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>\biggl( \frac{ q^5n_c}{5} \biggr) R_\mathrm{eq}^3 \biggl( \frac{2^3\pi}{3} \biggr) \Pi_\mathrm{eq} \biggl[\frac{5}{2q^2} \biggl( \frac{P_i}{\Pi} \biggr)_\mathrm{eq} + 1 \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>\biggl( \frac{ n_c}{5} \biggr) \biggl[ R_\mathrm{norm}^3 | |||
P_\mathrm{norm} \biggr] \chi_\mathrm{eq}^{-1} \biggl(\frac{\nu^2}{q}\biggr) | |||
\biggl[\frac{5}{2q^2} \biggl( \frac{P_i}{P_0} \biggr)_\mathrm{eq}\biggl( \frac{P_0}{\Pi} \biggr)_\mathrm{eq} + 1 \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~\biggl[ \frac{\mathfrak{G}_\mathrm{core} }{E_\mathrm{norm}}\biggr]_\mathrm{eq} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{ n_c}{5} \biggr) \biggl(\frac{\nu^2}{q}\biggr) | |||
\biggl[\frac{5}{2q^2} \biggl( 1-\frac{1}{g^2} \biggr)\biggl( q^2g^2\biggr) + 1 \biggr] \chi_\mathrm{eq}^{-1} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{ n_c}{2} \biggr) \biggl(\frac{\nu^2}{q}\biggr) | |||
\biggl[ g^2-\frac{3}{5} \biggr] | |||
\biggl\{\frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) | |||
\biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c} | |||
\biggr\}^{-1/(n_c-3)}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~n_c \biggl[ 1- \biggl(\frac{3}{5}\biggr) \frac{1}{g^2} \biggr] | |||
\biggl( \frac{ 1}{2} \biggr) \biggl(\frac{\nu^2}{q}\biggr) g^2 | |||
\biggl\{2^{n_c}\biggl(\frac{3}{4\pi} \biggr) | |||
\biggl( \frac{\nu}{q^3}\biggr)^{1-n_c} (q g)^{-2n_c} | |||
\biggr\}^{1/(n_c-3)}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~n_c \biggl[ 1- \biggl(\frac{3}{5}\biggr) \frac{1}{g^2} \biggr] | |||
\biggl\{2^{n_c}\cdot 2^{(3-n_c)}\biggl(\frac{3}{4\pi} \biggr) | |||
\biggl( \frac{\nu}{q^3}\biggr)^{1-n_c} \biggl(\frac{\nu}{q^3}\biggr)^{2(n_c-3)} q^{5(n_c-3)} q^{-2n_c} g^{-2n_c} g^{2(n_c-3)} | |||
\biggr\}^{1/(n_c-3)}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~n_c \biggl[ 1- \biggl(\frac{3}{5}\biggr) \frac{1}{g^2} \biggr] | |||
\biggl\{\biggl(\frac{2\cdot 3}{\pi} \biggr) | |||
\biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{3n_c-15} g^{-6} | |||
\biggr\}^{1/(n_c-3)} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Finally, switching from the <math>~g</math> notation to the <math>~b_\xi</math> notation gives, | |||
<div align="center"> | |||
<table border="0"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{\mathfrak{G}_\mathrm{core} }{E_\mathrm{norm}}\biggr]_\mathrm{eq} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~n_c \biggl[ 1- \biggl(\frac{3}{5}\biggr) b_\xi q^2 \biggr] | |||
\biggl\{\biggl(\frac{2\cdot 3}{\pi} \biggr) | |||
\biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{3n_c-15} b_\xi^3 q^{6} | |||
\biggr\}^{1/(n_c-3)} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~n_c q^3 \biggl[ 1- \biggl(\frac{3}{5}\biggr) b_\xi q^2 \biggr] | |||
\biggl\{\biggl(\frac{2\cdot 3}{\pi} \biggr) | |||
\biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} b_\xi^3 \biggr\}^{1/(n_c-3)} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
which, after setting <math>~\Chi = 1</math>, precisely matches the above, "first view" expression. Also from our [[User:Tohline/SSC/Structure/BiPolytropes/Analytic0_0#Thermal_Energy_Content|previous derivation]], we can write, | |||
<div align="center"> | |||
<table border="0"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}_\mathrm{env} = \biggl(\frac{2n_e}{3}\biggr) S_\mathrm{env}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ 2\pi\biggl(\frac{2n_e}{3}\biggr) | |||
R_\mathrm{eq}^3 \Pi_\mathrm{eq} \biggl\{ (1-q^3) \biggl(\frac{P_i }{\Pi}\biggr)_\mathrm{eq} | |||
+ \biggl( \frac{\rho_e}{\rho_0} \biggr)\biggl[ (-2q^2 + 3q^3 - q^5 ) | |||
+ \frac{3}{5} \biggl( \frac{\rho_e}{\rho_0} \biggr) ( -1 + 5q^2 -5q^3 + q^5 )\biggr]\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ 2\pi\biggl(\frac{2n_e}{3}\biggr) | |||
R_\mathrm{eq}^3 \biggl[ P_\mathrm{norm} \chi^{-4}\biggl(\frac{3}{2^3\pi}\biggr) \biggl(\frac{\nu}{q^3}\biggr)^2\biggr]_\mathrm{eq} | |||
\biggl\{ (1-q^3) q^2(g^2-1) + \biggl(\frac{2}{5}\biggr) q^5 \mathfrak{F} \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ P_\mathrm{norm} R_\mathrm{norm}^3 \biggr] \frac{n_e}{2} | |||
\biggl(\frac{\nu^2}{q^4}\biggr)(1-q^3) | |||
\biggl\{ (g^2-1) + \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr\} | |||
\chi^{-1}_\mathrm{eq} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~\biggl[ \frac{\mathfrak{G}_\mathrm{env} }{E_\mathrm{norm}}\biggr]_\mathrm{eq} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ n_e (1-q^3) | |||
\biggl\{ (g^2-1) + \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr\} \frac{q^2}{2}\biggl(\frac{\nu}{q^3}\biggr)^2 | |||
\biggl[\frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) | |||
\biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c}\biggr]^{-1/(n_c-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ n_e (1-q^3) | |||
\biggl\{ (g^2-1) + \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr\} | |||
\biggl[2^{[n_c-(n_c-3)]} \biggl(\frac{3}{4\pi} \biggr) | |||
\biggl( \frac{\nu}{q^3}\biggr)^{(1-n_c)+2(n_c-3)} q^{2(n_c-3)-2n_c} g^{-2n_c} \biggr]^{1/(n_c-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ n_e (1-q^3) | |||
\biggl\{ (g^2-1) + \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr\} | |||
\biggl[\biggl(\frac{2\cdot 3}{\pi} \biggr) | |||
\biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{-6} g^{-2n_c} \biggr]^{1/(n_c-3)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
And, finally, switching from the <math>~g</math> notation to the <math>~b_\xi</math> notation gives, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl[ \frac{\mathfrak{G}_\mathrm{env} }{E_\mathrm{norm}}\biggr]_\mathrm{eq} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ n_e (1-q^3) (b_\xi q^2)^{-1} | |||
\biggl\{ 1 - \biggl[1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr]b_\xi q^2\biggr\} | |||
\biggl[\biggl(\frac{2\cdot 3}{\pi} \biggr) | |||
\biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{-6} (b_\xi q^2)^{n_c} \biggr]^{1/(n_c-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ n_e (1-q^3) | |||
\biggl\{ 1 - \biggl[1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr]b_\xi q^2\biggr\} | |||
\biggl[\biggl(\frac{2\cdot 3}{\pi} \biggr) | |||
\biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{-6-2(n_c-3)+2n_c} b_\xi^{3-n_c+n_c} \biggr]^{1/(n_c-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=~</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ n_e\biggl[\biggl(\frac{2\cdot 3}{\pi} \biggr)\biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} b_\xi^{3} \biggr]^{1/(n_c-3)} (1-q^3) | |||
\biggl\{ 1 - \biggl[1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr]b_\xi q^2\biggr\} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
which, after setting <math>~\Chi = 1</math>, precisely matches the above, "first view" expression. | |||
====Summary00==== | |||
In summary, the desired ''out'' of equilibrium free-energy expression is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\mathfrak{G}}{E_\mathrm{norm}} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
A_0\Chi^{-3/n_c} + B_0\Chi^{-3/n_e} - C_0\Chi^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~A_0 \equiv \biggl( \frac{\mathfrak{S}_\mathrm{core}}{E_\mathrm{norm}} \biggr)_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{n_c}{b_\xi} | |||
\biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^{n_c}\biggr]^{1/(n_c-3)} | |||
q^3\biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~B_0 \equiv \biggl( \frac{\mathfrak{S}_\mathrm{env}}{E_\mathrm{norm}} \biggr)_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{n_e}{b_\xi} | |||
\biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^{n_c} \biggr]^{1/(n_c-3)} (1-q^3) | |||
\biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~C_0 \equiv \biggl( \frac{W_\mathrm{grav}}{E_\mathrm{norm}} \biggr)_\mathrm{eq} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl( \frac{6}{5}\biggr) q^5 f | |||
\biggl[ \biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} b_\xi^{n_c} \biggr]^{1/(n_c-3)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Or, in a more compact form, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}^* \equiv \biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^{n_c}\biggr]^{-1/(n_c-3)} | |||
\biggl[\frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
n_c A_1\Chi^{-3/n_c} + n_e B_1\Chi^{-3/n_e} - 3C_1\Chi^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~A_1 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{1}{b_\xi} (q^3) \biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~B_1 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{1}{b_\xi} (1-q^3)\biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~C_1 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl( \frac{2}{5}\biggr) q^5 f \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Let's examine the behavior of the first radial derivative. | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\partial \mathfrak{G}^*}{\partial \Chi}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3}{\Chi} \biggl[ - A_1\Chi^{-3/n_c} - B_1\Chi^{-3/n_e} + C_1\Chi^{-1} \biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Let's see whether the sum of terms inside the square brackets is zero at the derived equilibrium radius, that is, when <math>~\Chi = 1</math> and, hence, when | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi = \chi_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c} \biggr]^{1/(n_c-3)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ \frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} b_\xi^{-n_c} \biggr]^{1/(n_c-3)} | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ | |||
C_1 - A_1 - B_1 | |||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{2}{5}\biggr) q^5 f | |||
- \frac{1}{b_\xi} (q^3) \biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] | |||
- \frac{1}{b_\xi} (1-q^3)\biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{2}{5}\biggr) q^5 f | |||
- \frac{1}{b_\xi} \biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} | |||
+ \frac{q^3}{b_\xi} \biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} | |||
- \frac{q^3}{b_\xi} \biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{2}{5}\biggr) q^5 f - \frac{1}{b_\xi} | |||
+ \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]q^2 | |||
+ \frac{q^3}{b_\xi} | |||
- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]q^5 | |||
- \frac{q^3}{b_\xi} + \biggl( \frac{3}{5} \biggr) q^5 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~q^2\biggl\{ | |||
\biggl( \frac{2}{5}\biggr) q^3 f - \frac{1}{b_\xi q^2} | |||
+ \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr] (1-q^3) | |||
+ \biggl( \frac{3}{5} \biggr) q^3 | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~q^2\biggl\{ | |||
\biggl( \frac{2}{5}\biggr) q^3 f - \biggl[ 1+\frac{2}{5} q^3(f-1-\mathfrak{F}) \biggr] | |||
+ \biggl[ (1-q^3) - \frac{2}{5} q^3 \mathfrak{F} \biggr] | |||
+ \biggl( \frac{3}{5} \biggr) q^3 | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~q^2\biggl\{0\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Q.E.D. | |||
Even slightly better: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{q^2}\biggl[ \biggl(\frac{\pi}{2\cdot 3}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(5-n_c)} b_\xi^{-n_c}\biggr]^{1/(n_c-3)} | |||
\biggl[\frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
n_c A_2\Chi^{-3/n_c} + n_e B_2\Chi^{-3/n_e} - 3C_2\Chi^{-1} \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
or, better yet, | |||
<div align="center" id="BiPolytropeFreeEnergy"> | |||
<table border="1" cellpadding="5" align="center"> | |||
<tr> | |||
<th align="center"> | |||
<font size="+1">Out-of-Equilibrium, Free-Energy Expression for BiPolytropes with ''Structural'' </font> <math>~(n_c, n_e) = (0, 0)</math> | |||
</th> | |||
</tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~2\biggl(\frac{q^2}{\nu}\biggr)^2 \chi_\mathrm{eq} | |||
\biggl[\frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
n_c A_2\Chi^{-3/n_c} + n_e B_2\Chi^{-3/n_e} - 3C_2\Chi^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
</div> | |||
where, keeping in mind that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{(b_\xi q^2)}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[1 + \frac{2}{5}q^3 (f - 1-\mathfrak{F} ) \biggr] \, , </math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~A_2 \equiv \frac{A_1}{q^2} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{q^3}{(b_\xi q^2)} \biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
q^3 \biggl\{ \biggl[1 + \frac{2}{5}q^3 (f - 1-\mathfrak{F} ) \biggr] - \biggl( \frac{3}{5} \biggr) \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{2}{5}q^3 \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~B_2 \equiv \frac{B_1}{q^2} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{1}{(b_\xi q^2)} (1-q^3)\biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
(1-q^3)\biggl\{ \frac{1}{(b_\xi q^2)} -1 + \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
(1-q^3)\biggl\{ \biggl[1 + \frac{2}{5}q^3 (f - 1-\mathfrak{F} ) \biggr] - 1 + \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{2}{5} q^3 \biggl\{ (1-q^3) (f - 1-\mathfrak{F} ) + \mathfrak{F} \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{2}{5} q^3 \biggl\{ f - \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr]\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{2}{5} q^3 f - A_2 \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~C_2 \equiv \frac{C_1}{q^2} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{2}{5} q^3 f \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
As before, the equilibrium system is dynamically unstable if <math>~\partial^2 \mathfrak{G}/\partial \Chi^2 < 0</math>. We have deduced that the system is unstable if, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{n_e}{3}\biggl[ \frac{3-n_e}{n_c-n_e} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~< </math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{A_2}{C_2} | |||
= \frac{1}{f} \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
==Overview== | |||
===BiPolytrope51=== | |||
====Key Analytic Expressions==== | |||
<div align="center" id="FreeEnergy51"> | |||
<table border="1" cellpadding="5" align="center"> | |||
<tr> | |||
<th align="center"> | |||
<font size="+1">Out-of-Equilibrium, Free-Energy Expression for BiPolytropes with</font> <math>~(n_c, n_e) = (5, 1)</math> | |||
</th> | |||
</tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}^*_{51} \equiv 2^4\biggl( \frac{q}{\nu^2}\biggr) \chi_\mathrm{eq} \biggl[\frac{\mathfrak{G}_{51}}{E_\mathrm{norm}} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{1}{\ell_i^2} \biggl[ | |||
\Chi^{-3/5} (5 \mathfrak{L}_i) | |||
+\Chi^{-3} (4\mathfrak{K}_i) | |||
-\Chi^{-1} (3\mathfrak{L}_i +12\mathfrak{K}_i ) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{L}_i</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{(\ell_i^4-1)}{\ell_i^2} + \frac{(1+\ell_i^2)^3}{\ell_i^3} \cdot \tan^{-1}\ell_i \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{K}_i</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\Lambda_i}{\eta_i} + \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Lambda_i</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{\eta_i} - \ell_i \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\eta_i</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~3 \biggl( \frac{\mu_e}{\mu_c} \biggr) \biggl[\frac{\ell_i }{(1+\ell_i^2)}\biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
From the [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Parameter_Values|accompanying Table 1 parameter values]], we also can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{q}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\eta_s}{\eta_i} | |||
= 1 + \frac{1}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\nu</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\ell_i q}{(1+\Lambda_i^2)^{1/2}} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Consistent with our [[User:Tohline/SSC/BipolytropeGeneralization#Free_Energy_and_Its_Derivatives|generic discussion of the stability of bipolytropes]] and the ''specific'' discussion of [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Stability_Condition|the stability of bipolytropes having]] <math>~(n_c, n_e) = (5, 1)</math>, it can straightforwardly be shown that <math>~\partial \mathfrak{G}^*_{51}/\partial \chi = 0</math> is satisfied by setting <math>~\Chi = 1</math>; that is, the equilibrium condition is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi = \chi_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{ \biggl(\frac{\pi}{3}\biggr) 2^{2-n_c} \nu^{n_c-1} q^{3-n_c} \biggl[\frac{(1+\ell_i^2)^{6/5}}{(3\ell_i^2)} \biggr]^{n_c} \biggr\}^{1/(n_c-3)} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where the last expression has been cast into a form that more clearly highlights overlap with the expression, below, for the equilibrium radius for zero-zero bipolytropes. Furthermore, the equilibrium configuration is unstable whenever, | |||
<div align="center"> | |||
<math>~\biggl[ \frac{\partial^2 \mathfrak{G}^*_{51}}{\partial \chi^2}\biggr]_{\Chi=1} < 0 \, ,</math> | |||
</div> | |||
that is, it is unstable whenever, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{ \mathfrak{L}_i}{\mathfrak{K}_i}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~></math> | |||
</td> | |||
<td align="left"> | |||
<math>~20 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
[[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Stability_Condition|Table 1 of an accompanying chapter]] — and the red-dashed curve in the figure adjacent to that table — identifies some key properties of the model that marks the transition from stable to unstable configurations along equilibrium sequences that have various values of the mean-molecular weight ratio, <math>~\mu_e/\mu_c</math>. | |||
====Behavior of Equilibrium Sequence==== | |||
Here we reprint Figure 1 from an [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Model_Sequences|accompanying chapter wherein the structure of five-one bipolytropes has been derived]]. It displays detailed force-balance sequences in the <math>~q - \nu</math> plane for a variety of choices of the ratio of mean-molecular-weights, <math>~\mu_e/\mu_c</math>, as labeled. | |||
[[File:PlotSequencesBest02.png|450px|center|Five-One Bipolytropic Equilibrium Sequences for Various ratios of the mean molecular weight]] | |||
=====Limiting Values===== | |||
Each sequence begins <math>~(\ell_i = 0)</math> at the origin, that is, at <math>~(q,\nu) = (0,0)</math>. As <math>~\ell_i \rightarrow \infty</math>, however, the sequences terminate at different coordinate locations, depending on the value of <math>~m_3 \equiv 3(\mu_e/\mu_c)</math>. In deriving the various limits, it will be useful to note that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{\eta_i}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{(1 + \ell_i^2)}{m_3 \ell_i} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Lambda_i</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{(1+\ell_i^2)}{m_3\ell_i}-\ell_i</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{m_3\ell_i} + \biggl[\frac{(1 -m_3)}{m_3} \biggr]\ell_i </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{m_3\ell_i} \biggl[ 1 - (m_3-1) \ell_i^2\biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \frac{ (m_3-1) \ell_i}{m_3} \biggl[ 1 - \frac{1}{(m_3-1) \ell_i^2}\biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~1 + \Lambda_i^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 + \frac{1}{m_3^2\ell_i^2}\biggl[1 + (1 -m_3) \ell_i^2 \biggr]^2</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{m_3^2\ell_i^2}\biggl\{ m_3^2\ell_i^2 + \biggl[1 + (1 -m_3) \ell_i^2 \biggr]^2\biggr\}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{m_3^2\ell_i^2}\biggl\{ 1 + (2 -2m_3 + m_3^2) \ell_i^2 + (1 -m_3)^2 \ell_i^4 \biggr\}</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Examining the three relevant parameter regimes, we see that: | |||
* For <math>~\mu_e/\mu_c < \tfrac{1}{3}</math>, that is, <math>~m_3 < 1</math> … | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tan^{-1} \Lambda_i \biggr|_{\ell_i \rightarrow \infty}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx </math> | |||
</td> | |||
<td align="left"> | |||
<math>~\tan^{-1} \biggl[\frac{(1 -m_3)}{m_3} \biggr]\ell_i</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx </math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\pi}{2} - \biggl[\frac{m_3}{(1 -m_3)\ell_i} \biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \frac{1}{q}\biggr|_{\ell_i \rightarrow \infty}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \frac{(1 + \ell_i^2)}{m_3 \ell_i}\biggl[\pi - \frac{m_3}{(1 -m_3)\ell_i} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{m_3 + \pi \ell_i}{m_3} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ q\biggr|_{\ell_i \rightarrow \infty}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{1 + (\pi \ell_i/m_3)} \rightarrow 0 \, . | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
| |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl(\frac{\nu}{q}\biggr)^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\ell_i^2}{1 + \Lambda_i^2}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~m_3^2\ell_i^4 \biggl\{ 1 + (2 -2m_3 + m_3^2) \ell_i^2 + (1 -m_3)^2 \ell_i^4 \biggr\}^{-1}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~m_3^2\biggl\{ \ell_i^{-4} + (2 -2m_3 + m_3^2) \ell_i^{-2} + (1 -m_3)^2 \biggr\}^{-1}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \frac{\nu}{q}\biggr|_{\ell_i\rightarrow \infty}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{m_3}{1-m_3} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \nu \biggr|_{\ell_i\rightarrow \infty}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[\frac{m_3}{1-m_3}\biggr]\frac{1}{1 + (\pi \ell_i/m_3)} \rightarrow 0 \, . </math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
* For <math>~\mu_e/\mu_c = \tfrac{1}{3}</math>, that is, <math>~m_3 = 1</math> … | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tan^{-1} \Lambda_i </math> | |||
</td> | |||
<td align="center"> | |||
<math>~= </math> | |||
</td> | |||
<td align="left"> | |||
<math>~\tan^{-1} \biggl(\frac{1}{\ell_i}\biggr)</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \tan^{-1} \Lambda_i \biggr|_{\ell_i \rightarrow \infty}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx </math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{\ell_i}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \frac{1}{q}\biggr|_{\ell_i \rightarrow \infty}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \frac{(1 + \ell_i^2)}{\ell_i}\biggl[\frac{\pi}{2} + \frac{1}{\ell_i }\biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{\pi}{2}\biggr)\ell_i</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ q\biggr|_{\ell_i \rightarrow \infty}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2}{\pi \ell_i} \rightarrow 0</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
| |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl(\frac{\nu}{q}\biggr)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\ell_i}{(1 + 1/\ell_i^2)^{1/2}}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \nu \biggr|_{\ell_i \rightarrow \infty}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\ell_i \biggl(\frac{2}{\pi \ell_i} \biggr) = \frac{2}{\pi} \approx 0.63662</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
* For <math>~\mu_e/\mu_c > \tfrac{1}{3}</math>, that is, <math>~m_3 > 1</math> … | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\tan^{-1} \Lambda_i \biggr|_{\ell_i \rightarrow \infty}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx </math> | |||
</td> | |||
<td align="left"> | |||
<math>~\tan^{-1} \biggl[-\biggl(\frac{m_3-1}{m_3} \biggr)\ell_i\biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx </math> | |||
</td> | |||
<td align="left"> | |||
<math>~-\frac{\pi}{2} + \biggl[\frac{m_3}{(m_3-1)\ell_i} \biggr]</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \frac{1}{q}\biggr|_{\ell_i \rightarrow \infty}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \frac{(1 + \ell_i^2)}{m_3 \ell_i}\biggl[ \frac{m_3}{(m_3-1)\ell_i} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \frac{(1 + 1/\ell_i^2)}{(m_3-1) } | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \frac{1}{(m_3-1) } = \frac{m_3}{(m_3-1)} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ q\biggr|_{\ell_i \rightarrow \infty}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{(m_3-1)}{m_3} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
| |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl(\frac{\nu}{q}\biggr)^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\ell_i^2}{1 + \Lambda_i^2}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~m_3^2\ell_i^4 \biggl\{ 1 + (2 -2m_3 + m_3^2) \ell_i^2 + (m_3-1)^2 \ell_i^4 \biggr\}^{-1}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~m_3^2\biggl\{ \ell_i^{-4} + (2 -2m_3 + m_3^2) \ell_i^{-2} + (m_3-1)^2 \biggr\}^{-1}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \frac{\nu}{q}\biggr|_{\ell_i\rightarrow \infty}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{m_3}{m_3-1} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \nu \biggr|_{\ell_i\rightarrow \infty}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{m_3}{m_3-1} \biggl[\frac{m_3 - 1}{m_3}\biggr] \rightarrow 1 \, . </math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Summarizing: | |||
* For <math>~\mu_e/\mu_c < \tfrac{1}{3}</math>, that is, <math>~m_3 < 1</math> … <math>~(q,\nu)_{\ell_i \rightarrow \infty} = (0, 0) \, .</math> | |||
* For <math>~\mu_e/\mu_c = \tfrac{1}{3}</math>, that is, <math>~m_3 = 1</math> … <math>~(q,\nu)_{\ell_i \rightarrow \infty} = (0, \tfrac{2}{\pi}) \, .</math> | |||
* For <math>~\mu_e/\mu_c > \tfrac{1}{3}</math>, that is, <math>~m_3 > 1</math> … <math>~(q,\nu)_{\ell_i \rightarrow \infty} = [(m_3-1)/m_3, 1] \, .</math> | |||
=====Turning Points===== | |||
Let's identify the location of two turning points along the <math>~\nu(q)</math> sequence — one defines <math>~q_\mathrm{max}</math> and the other identifies <math>~\nu_\mathrm{max}</math>. They occur, respectively, where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{d\ln q}{d\ln \ell_i} = 0</math> | |||
</td> | |||
<td align="center"> | |||
and | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{d\ln \nu}{d\ln \ell_i} = 0 \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
In deriving these expressions, we will use the relations, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{d\eta_i}{d\ell_i}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{m_3 (1-\ell_i^2)}{(1+\ell_i^2)^2} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{d\Lambda_i}{d\ell_i}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \frac{1}{m_3\ell_i^2} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<math>~m_3 \equiv 3\biggl(\frac{\mu_e}{\mu_c}\biggr) \, .</math> | |||
</div> | |||
Given that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~q </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl\{ 1 + \frac{1}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] \biggr\}^{-1} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
we find, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{d\ln q}{d\ln \ell_i}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\ell_i}{q} \cdot ( -q^2) \frac{d}{d\ell_i} \biggl\{ | |||
\frac{1}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~-q\ell_i \biggl\{-\frac{1}{\eta_i^2}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr]\frac{d\eta_i}{d\ell_i} | |||
+ \frac{1}{\eta_i(1+\Lambda_i^2)} \frac{d\Lambda_i}{d\ell_i} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~q\ell_i \biggl\{\frac{(1-\ell_i^2)}{m_3 \ell_i^2}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] | |||
+ \frac{(1+\ell_i^2)}{m_3^2 \ell_i^3(1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{q}{m_3^2}{\ell_i^2}\biggl\{m_3 \ell_i (1-\ell_i^2) \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] | |||
+ \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
And, given that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\nu </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{\ell_i q}{(1+\Lambda_i^2)^{1/2}} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
we find, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{d\ln \nu}{d\ln \ell_i}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\ell_i}{\nu} \biggl\{ | |||
\frac{q}{(1+\Lambda_i^2)^{1/2}} + \frac{q}{(1+\Lambda_i^2)^{1/2}} \frac{d\ln q}{d\ln \ell_i} | |||
- \frac{\ell_i q \Lambda_i }{(1+\Lambda_i^2)^{3/2}} \frac{d\Lambda_i}{d\ell_i} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{q \ell_i}{ \nu(1+\Lambda_i^2)^{1/2}}\biggl\{ | |||
1 + \frac{d\ln q}{d\ln \ell_i} | |||
+ \frac{\Lambda_i }{m_3 \ell_i (1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
In summary, then, the <math>~q_\mathrm{max}</math> turning point occurs where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<!-- | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ m_3 \ell_i (1-\ell_i^2) \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] | |||
+ \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] | |||
\, ; | |||
</math> | |||
</td> | |||
</tr> | |||
--> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ (1+\Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] | |||
+ \frac{(1+\ell_i^2)}{m_3 \ell_i (1-\ell_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] | |||
\, ; | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and the <math>~\nu_\mathrm{max}</math> turning point occurs where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 + \frac{\Lambda_i }{m_3 \ell_i (1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] | |||
+ \frac{q \ell_i^3 (1-\ell_i^2)}{m_3} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] | |||
+ \frac{q\ell_i^2}{m_3^2}\cdot \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 | |||
+ \frac{q \ell_i^3 (1-\ell_i^2)}{m_3} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] | |||
+ \biggl[ \frac{\Lambda_i }{m_3 \ell_i (1+\Lambda_i^2)} | |||
+ \frac{q\ell_i^2}{m_3^2}\cdot \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggr] \cdot \biggl[ 1 - \ell_i^2(1-m_3) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 | |||
+ \frac{q \ell_i^3 (1-\ell_i^2)}{m_3} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] | |||
+ \frac{1}{m_3 \ell_i} \biggl[ \frac{\Lambda_i }{(1+\Lambda_i^2)} | |||
+ \frac{q\ell_i^3}{m_3}\cdot \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggr] \cdot \biggl[ 1 - \ell_i^2(1-m_3) \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<table border="0" width="80%" cellpadding="5" align="center"><tr><td align="left"> | |||
<font color="red"><b>NOTE:</b></font> As we show [[#Limiting_Values|above]], for the special case of <math>~m_3 = 1</math> — that is, when <math>~\mu_e/\mu_c = \tfrac{1}{3}</math>, precisely — the equilibrium sequence (as <math>~\ell_i \rightarrow \infty</math>) intersects the <math>~q = 0</math> axis at precisely the value, <math>~\nu = 2/\pi</math>. As is illustrated graphically in [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Model_Sequences|Figure 1 of an accompanying chapter]], no <math>~\nu_\mathrm{max}</math> turning point exists for values of <math>~m_3 > 1</math>. | |||
</td></tr> | |||
</table> | |||
For the record, we repeat, as well, that the transition from stable to dynamically unstable configurations occurs along the sequence when, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{(\ell_i^4-1)}{\ell_i^2} + \frac{(1+\ell_i^2)^3}{\ell_i^3} \cdot \tan^{-1}\ell_i </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~20 \biggl\{ \frac{\Lambda_i}{\eta_i} + \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \biggr\} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{20(1+\Lambda_i^2)(1+\ell_i^2)}{m_3\ell_i} \biggl\{ \frac{\Lambda_i}{(1+\Lambda_i^2)} + \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \biggr\} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ m_3 \ell_i (\ell_i^4-1) + m_3(1+\ell_i^2)^3\cdot \tan^{-1}\ell_i </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~20\ell_i^2 (1+\Lambda_i^2)(1+\ell_i^2) \biggl\{ \frac{\Lambda_i}{(1+\Lambda_i^2)} + \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \biggr\} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \frac{m_3 \ell_i (\ell_i^4-1) + m_3(1+\ell_i^2)^3\cdot \tan^{-1}\ell_i }{ 20\ell_i^2 (1+\ell_i^2)}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\Lambda_i + (1+\Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
In order to clarify what equilibrium sequences do not have any turning points, let's examine how the <math>~q_\mathrm{max}</math> turning-point expression behaves as <math>~\ell_i \rightarrow \infty</math>. | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ m_3 \ell_i (\ell_i^2-1) \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \Rightarrow ~~~ \frac{(1+\ell_i^2)}{ m_3 \ell_i (\ell_i^2-1) } \biggl[ 1 + \ell_i^2(m_3-1) \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl\{ 1 + \frac{1}{m_3^2\ell_i^2}\biggl[ (m_3-1) \ell_i^2-1 \biggr]^2 \biggr\} \biggl\{ \frac{\pi}{2} | |||
+ \biggl[ -\frac{\pi}{2} - \frac{1}{\Lambda_i} + \frac{1 }{3\Lambda_i^3} + \mathcal{O}(\Lambda_i^{-5} )\biggr] \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \Rightarrow ~~~ \frac{(1+\ell_i^2) \ell_i^2(m_3-1)}{ m_3 \ell_i (\ell_i^2-1) } \biggl[ 1 + \frac{1}{\ell_i^2(m_3-1)} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl\{ 1 + \frac{(m_3-1)^2 \ell_i^2}{m_3^2}\biggl[ 1 - \frac{1}{ (m_3-1) \ell_i^2 } \biggr]^2 \biggr\} \cdot | |||
\frac{1}{(-\Lambda_i)} \biggl[ 1 - \frac{1 }{3\Lambda_i^2} + \cancelto{0}{\mathcal{O}(\Lambda_i^{-4} )}\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \Rightarrow ~~~ \frac{(1+\ell_i^2)}{ \ell_i (\ell_i^2-1) } \cdot \frac{m_3}{(m_3-1)} \biggl[ 1 + \frac{1}{\ell_i^2(m_3-1)} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ 1 - \frac{2}{ (m_3-1) \ell_i^2 } + \frac{m_3^2}{(m_3-1)^2 \ell_i^2} + \frac{1}{ (m_3-1)^2 \ell_i^4 } \biggr] \cdot \frac{m_3}{(m_3-1)\ell_i} \biggl[1 - \frac{1}{(m_3-1)\ell_i^2}\biggr]^{-1} | |||
\biggl\{ 1 - \frac{m_3^2}{3(m_3-1)^2\ell_i^2} \biggl[1 - \frac{1}{(m_3-1)\ell_i^2}\biggr]^{-2} \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \Rightarrow ~~~\biggl(1 + \frac{1}{\ell_i^2} \biggr) \biggl[ 1 + \frac{1}{\ell_i^2(m_3-1)} \biggr]\biggl[1 - \frac{1}{(m_3-1)\ell_i^2}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl(1 - \frac{1}{\ell_i^2} \biggr) \biggl[ 1 - \frac{2}{ (m_3-1) \ell_i^2 } + \frac{m_3^2}{(m_3-1)^2 \ell_i^2} + \frac{1}{ (m_3-1)^2 \ell_i^4 } \biggr] | |||
\biggl\{ 1 - \frac{m_3^2}{3(m_3-1)^2\ell_i^2} \biggl[1 - \frac{1}{(m_3-1)\ell_i^2}\biggr]^{-2} \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
The leading-order term is unity on both sides of this expression, so they cancel; let's see what results from keeping terms <math>~\propto \ell_i^{-2}</math>. | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \frac{1}{\ell_i^2} \biggl[ 1 + \frac{1}{(m_3-1)} - \frac{1}{(m_3-1)}\biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{1}{\ell_i^2} \biggl[- 1 - \frac{2}{ (m_3-1) } + \frac{m_3^2}{(m_3-1)^2 } - \frac{m_3^2}{3(m_3-1)^2} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ 2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - \frac{2}{ (m_3-1) } + \frac{2m_3^2}{3(m_3-1)^2 } | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ 6(m_3-1)^2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - 6(m_3-1) + 2m_3^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ 6m_3^2-12m_3 + 6 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ - 6m_3+6 + 2m_3^2 | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow~~~ m_3</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{3}{2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
We therefore conclude that the <math>~q_\mathrm{max}</math> turning point does not appear along any sequence for which, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~m_3</math> | |||
</td> | |||
<td align="center"> | |||
<math>~></math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3}{2}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \frac{\mu_e}{\mu_c}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~></math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{2}\, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
<!-- | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~ \frac{1}{\ell_i^2} \biggl[ 2 + \frac{1}{\alpha m_3} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{1}{\ell_i^2}\biggl[ | |||
\frac{1}{\alpha^2 } - \frac{2}{ m_3 \alpha } -\frac{1}{3\alpha^2 } \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \biggl[ 2\alpha^2 m_3 + \alpha \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ | |||
\frac{2m_3}{3} - 2\alpha \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ 2\alpha^2 m_3 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2m_3}{3} - 3\alpha | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
--> | |||
<div align="center"> | |||
<table border="1" align="center" cellpadding="5"> | |||
<tr> | |||
<td align="center" colspan="2">Five-One Bipolytrope Equilibrium Sequences in <math>~q - \nu</math> Plane</td> | |||
</tr> | |||
<tr> | |||
<td align="center" width="50%"> | |||
Full Sequences for Various <math>~\frac{\mu_e}{\mu_c}</math> | |||
</td> | |||
<td align="center" width="50%"> | |||
Magnified View with Turning Points and Stability Transition-Points Identified | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="center" colspan="2"> | |||
[[File:Qvsnu51combined.png|750 px|Five-One Sequences]] | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
====Graphical Depiction of Free-Energy Surface==== | |||
<div align="center"> | |||
<table border="0" cellpadding="8" width="880px"> | |||
<tr><td align="center"><font size="+1"><b> | |||
Figure 1: Free-Energy Surface for <math>~(n_c,n_e) = (5,1)</math> and <math>~\frac{\mu_e}{\mu_c} = 1</math></b></font></td></tr> | |||
<tr><td align="center"> | |||
<table border="1" cellpadding="5"> | |||
<tr> | |||
<td align="center" bgcolor="#CCFFFF"> | |||
[[File:FreeEnergy51Surface2.png|center|300px|Free-Energy surface for 5_1 bipolytrope]] | |||
</td> | |||
<td align="center" bgcolor="#CCFFFF"> | |||
<!-- [[File:Bipolytrope51Muratio1.gif|center|439px|Free-Energy surface for 5_1 bipolytrope]] --> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left" colspan="2"> | |||
''Left Panel:'' The free energy (vertical, blue axis) is plotted as a function of the radial interface location, <math>~\xi_i</math> (red axis), and the normalized configuration radius, <math>~\Chi \equiv \chi/\chi_\mathrm{eq}</math> (green axis). ''Right Panel:'' Same as the left panel, but animated in order to highlight undulations of the surface. The value of the free energy is indicated by color as well as by the height of the warped surface — red identifies the lowest depicted energies while blue identifies the highest depicted energies; these same colors have been projected down onto the <math>~z = 0</math> plane to present a two-dimensional, color-contour plot. A multi-colored line segment drawn parallel to the <math>~\xi_i</math> axis at the value, <math>~\Chi = 1</math>, identifies the configuration's ''equilibrium'' radius for each value of the interface location. Equilibrium configurations marked in white lie at the bottom of the principal free-energy "valley" and are stable, while configurations marked in blue lie at the top of a free-energy "hill," indicating that they are unstable; the red dot identifies the location along this equilibrium sequence where the transition from stable to unstable configurations occurs. | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
</div> | |||
For purposes of reproducibility, it is incumbent upon us to clarify how the values of the free energy were normalized in order to produce the free-energy surface displayed in Figure 1. The normalization steps are explicitly detailed within the [[#Fortran_Code|fortran program, below]], that generated the data for plotting purposes; here we provide a brief summary. We evaluated the normalized free energy, <math>~\mathfrak{G}^*_{51}</math>, across a <math>~200 \times 200</math> zone grid of uniform spacing, covering the following <math>~(x,y) = (\ell_i,\Chi)</math> domain: | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{1}{\sqrt{3}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\le \ell_i \le</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{3}{\sqrt{3}}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~0.469230769</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\le \Chi\le</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2.0</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
(With this specific definition of the ''y''-coordinate grid, <math>~\Chi = 1</math> is associated with zone 70.) After this evaluation, a constant, <math>~E_\mathrm{fudge} = -10</math>, was added to <math>~\mathfrak{G}^*</math> in order to ensure that the free energy was negative across the entire domain. Then (inorm = 1), for each specified interface location, <math>~x = \ell_i</math>, employing the ''equilibrium'' value of the free energy, | |||
<div align="center"> | |||
<math>~E_0 = \mathfrak{G}^*_{51}(\ell_i, \Chi = 1) + E_\mathrm{fudge} \, ,</math> | |||
</div> | |||
the free energy was normalized across all values of <math>~y = \Chi</math> via the expression, | |||
<div align="center"> | |||
<math>~\mathrm{fe} = \frac{(\mathfrak{G}^*_{51} + E_\mathrm{fudge}) - (E_0)_i}{|E_0|_i} \, .</math> | |||
</div> | |||
Finally, for plotting purposes, at each grid cell vertex ("vertex") — as well as at each grid cell center ("cell") — the value of the free energy, <math>~\mathrm{fe}</math>, was renormalized as follows, | |||
<div align="center"> | |||
<math>~\mathrm{vertex} = \frac{\mathrm{fe} - \mathrm{min}(\mathrm{fe})}{ \mathrm{max}(\mathrm{fe}) - \mathrm{min}(\mathrm{fe})} \, .</math> | |||
</div> | |||
Via this last step, the minimum "vertex" energy across the entire domain was 0.0 while the maximum "vertex" energy was 1.0. | |||
<div align="center"> | |||
<table border="1" cellpadding="8" align="center"> | |||
<tr> | |||
<th align="center" colspan="3">FORTRAN Program Documentation</th> | |||
<th align="center" colspan="3">Example Evaluations<p></p>(See also [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Stability_Condition|associated Table 1]])</th> | |||
</tr> | |||
<tr> | |||
<th align="center" colspan="1">Coord. Axis</th> | |||
<th align="center" colspan="1">Coord. Name</th> | |||
<th align="left">Associated Physical Quantity</th> | |||
<td align="center"><math>~\frac{\mu_e}{\mu_c} = 1</math></td> | |||
<td align="center" colspan="2"><math>~\frac{\mu_e}{\mu_c} = 0.305</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center">x-axis</td> | |||
<td align="center">bsize</td> | |||
<td align="left"><math>~\ell_i \equiv \frac{\xi_i}{\sqrt{3}}</math></td> | |||
<td align="center"><math>~\frac{2.416}{\sqrt{3}} = 1.395</math></td> | |||
<td align="center"><math>~\frac{8.1938}{\sqrt{3}} = 4.7307</math></td> | |||
<td align="center"><math>~\frac{14.389}{\sqrt{3}} = 8.3076</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center">y-axis</td> | |||
<td align="center">csize</td> | |||
<td align="left"><math>~\Chi \equiv \frac{\chi}{\chi_\mathrm{eq}}</math></td> | |||
<td align="center"><math>~1</math></td> | |||
<td align="center"><math>~1</math></td> | |||
<td align="center"><math>~1</math></td> | |||
</tr> | |||
<tr> | |||
<th align="center" colspan="3">Relevant Lines of Code</th> | |||
<td colspan="3" rowspan="3"> </td> | |||
</tr> | |||
<tr> | |||
<td align="left" colspan="3"> | |||
<pre> | |||
eta = 3.0d0*muratio*bsize/(1.0d0+bsize**2) | |||
Gami = 1.0d0/eta-bsize | |||
frakL = (bsize**4-1.0d0)/bsize**2 + & | |||
& DATAN(bsize)*((1.0d0+bsize**2)/bsize)**3 | |||
frakK = Gami/eta + ((1.0d0+Gami**2)/eta)*(pii/2.0d0+DATAN(Gami)) | |||
E0 = ((5.0d0*frakL) + (4.0d0*frakK)& | |||
& - (3.0d0*frakL+12.0d0*frakK))/bsize**2+Efudge | |||
fescalar(j,k) = (csize**(-0.6d0)*(5.0d0*frakL)& | |||
& + csize**(-3.0d0)*(4.0d0*frakK)& | |||
& - (3.0d0*frakL+12.0d0*frakK)/csize)/bsize**2 + Efudge | |||
if(inorm.eq.1)fescalar(j,k)=fescalar(j,k)/DABS(E0) & | |||
& - E0/DABS(E0) | |||
</pre> | |||
</td> | |||
</tr> | |||
<tr> | |||
<th align="center" colspan="1">Variable</th> | |||
<th align="center" colspan="1">Represents</th> | |||
<th align="left">Value calculated via the expression …</th> | |||
</tr> | |||
<tr> | |||
<td align="center">eta</td> | |||
<td align="center"><math>~\eta_i</math></td> | |||
<td align="left"> | |||
<math>~3 \biggl(\frac{\mu_e}{\mu_c}\biggr)\biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]</math> | |||
</td> | |||
<td align="center"><math>~1.421</math></td> | |||
<td align="center"><math>~0.1851</math></td> | |||
<td align="center"><math>~0.1086</math></td> | |||
<tr> | |||
<td align="center">Gami</td> | |||
<td align="center"><math>~\Lambda_i</math></td> | |||
<td align="left"><math>~\frac{1}{\eta_i} - \ell_i</math></td> | |||
<td align="center"><math>~-0.691</math></td> | |||
<td align="center"><math>~0.6705</math></td> | |||
<td align="center"><math>~0.9033</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center">frakL</td> | |||
<td align="center"><math>~\mathfrak{L}_i</math></td> | |||
<td align="left"><math>~ | |||
\frac{(\ell_i^4 - 1)}{\ell_i^2} + \biggl[ \frac{1+\ell_i^2}{\ell_i} \biggr]^3 \tan^{-1}\ell_i | |||
</math></td> | |||
<td align="center"><math>~10.37</math></td> | |||
<td align="center"><math>~186.80</math></td> | |||
<td align="center"><math>~937.64</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center">frakK</td> | |||
<td align="center"><math>~\mathfrak{K}_i</math></td> | |||
<td align="left"><math>~ | |||
\frac{\Lambda_i}{\eta_i} + \frac{(1 + \Lambda_i^2)}{\eta_i} \biggl[ \frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] | |||
</math></td> | |||
<td align="center"><math>~0.518</math></td> | |||
<td align="center"><math>~20.544</math></td> | |||
<td align="center"><math>~46.882</math></td> | |||
</tr> | |||
<tr> | |||
<td align="center"> </td> | |||
<td align="center"><math>~\frac{\mathfrak{L}_i}{\mathfrak{K}_i}</math></td> | |||
<td align="left"> </td> | |||
<td align="center"><math>~20</math></td> | |||
<td align="center"><math>~9.093</math></td> | |||
<td align="center"><math>~20</math></td> | |||
</tr> | |||
<!-- OMIT | |||
<tr> | |||
<td align="center">fescalar(x,y) - Efudge</td> | |||
<td align="center"><math>~\mathfrak{G}^*_{51}(\ell_i,\Chi)</math></td> | |||
<td align="left"> | |||
<math>~ \frac{1}{\ell_i^2} \biggl[ | |||
\Chi^{-3/5} (5 \mathfrak{L}_i) | |||
+\Chi^{-3} (4\mathfrak{K}_i) | |||
-\Chi^{-1} (3\mathfrak{L}_i +12\mathfrak{K}_i ) \biggr] | |||
</math> | |||
</td> | |||
<td align="center"><math>~8.525</math></td> | |||
<td align="center">…</td> | |||
<td align="center">…</td> | |||
</tr> | |||
END OMIT--> | |||
<tr> | |||
<td align="center">E0 - Efudge</td> | |||
<td align="center"><math>~\mathfrak{G}^*_{51}(\ell_i,\Chi=1)</math></td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{\ell_i^2} \biggl[ 5 \mathfrak{L}_i + 4\mathfrak{K}_i - (3\mathfrak{L}_i +12\mathfrak{K}_i ) \biggr] | |||
= \frac{2(\mathfrak{L}_i - 4\mathfrak{K}_i)}{\ell_i^2} | |||
</math> | |||
</td> | |||
<td align="center"><math>~8.525</math></td> | |||
<td align="center"><math>~9.3496</math></td> | |||
<td align="center"><math>~21.737</math></td> | |||
</tr> | |||
</table> | |||
</div> | |||
<div align="center"> | |||
<table border="0" cellpadding="8" width="880px"> | |||
<tr><td align="center"><font size="+1"><b> | |||
Figure 2: Free-Energy Surface for <math>~(n_c,n_e) = (5,1)</math> and <math>~\frac{\mu_e}{\mu_c} = 0.305</math></b></font></td></tr> | |||
<tr><td align="center"> | |||
<table border="1" cellpadding="5"> | |||
<tr> | |||
<td align="center" bgcolor="#CCFFFF"> | |||
[[File:FEsurface01.png|center|400px|Free-Energy surface for 5_1 bipolytrope]] | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left" colspan="1"> | |||
''Left Panel:'' The free energy (vertical, blue axis) is plotted as a function of the radial interface location, <math>~\xi_i</math> (red axis), and the normalized configuration radius, <math>~\Chi \equiv \chi/\chi_\mathrm{eq}</math> (green axis). ''Right Panel:'' Same as the left panel, but animated in order to highlight undulations of the surface. The value of the free energy is indicated by color as well as by the height of the warped surface — red identifies the lowest depicted energies while blue identifies the highest depicted energies; these same colors have been projected down onto the <math>~z = 0</math> plane to present a two-dimensional, color-contour plot. A multi-colored line segment drawn parallel to the <math>~\xi_i</math> axis at the value, <math>~\Chi = 1</math>, identifies the configuration's ''equilibrium'' radius for each value of the interface location. Equilibrium configurations marked in white lie at the bottom of the principal free-energy "valley" and are stable, while configurations marked in blue lie at the top of a free-energy "hill," indicating that they are unstable; the red dot identifies the location along this equilibrium sequence where the transition from stable to unstable configurations occurs. | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
</div> | |||
===BiPolytrope00=== | |||
<div align="center" id="FreeEnergy00"> | |||
<table border="1" cellpadding="5" align="center"> | |||
<tr> | |||
<th align="center"> | |||
<font size="+1">Out-of-Equilibrium, Free-Energy Expression for BiPolytropes with ''Structural'' </font> <math>~(n_c, n_e) = (0, 0)</math> | |||
</th> | |||
</tr> | |||
<tr><td align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}^*_{00} \equiv 5 \biggl(\frac{q}{\nu^2}\biggr) \chi_\mathrm{eq} | |||
\biggl[\frac{\mathfrak{G}_{00}}{E_\mathrm{norm}} \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \frac{5}{2q^3} \biggl[ | |||
n_c A_2\Chi^{-3/n_c} + n_e B_2\Chi^{-3/n_e} - 3C_2\Chi^{-1} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
</div> | |||
where, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~A_2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{2}{5}q^3 \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~B_2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{2}{5} q^3 f - A_2 \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~C_2 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\frac{2}{5} q^3 f \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~f</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
1+ | |||
\frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2}-1 \biggr) +\biggl( \frac{\rho_e}{\rho_c} | |||
\biggr)^2 \biggl[ \frac{1}{q^5}-1 + \frac{5}{2} \biggl( 1-\frac{1}{q^2}\biggr)\biggr] \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{F} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (-2q^2 + 3q^3 - q^5) + | |||
\frac{3}{5} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-1 +5q^2 - 5q^3 + q^5) \biggr] \, , | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\rho_e}{\rho_c} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{q^3(1-\nu)}{\nu(1-q^3)} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
The associated equilibrium radius is, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\chi_\mathrm{eq}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ \biggl(\frac{\pi}{3}\biggr) 2^{2-n_c} \nu^{n_c-1} q^{3-n_c} | |||
\biggl[1 + \frac{2}{5} q^3(f-1-\mathfrak{F})\biggr]^{n_c} \biggr\}^{1/(n_c-3)} | |||
\, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
We have deduced that the system is unstable if, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{n_e}{3}\biggl[ \frac{3-n_e}{n_c-n_e} \biggr] </math> | |||
</td> | |||
<td align="center"> | |||
<math>~< </math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{A_2}{C_2} | |||
= \frac{1}{f} \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
==Fortran Code== | |||
This is the program that generated the free-energy data for the "five-one" bipolytrope that is displayed in the above, Figure 1 image/animation. | |||
<pre> | |||
PROGRAM BiPolytrope | |||
real*8 pii | |||
real*8 bmin,bmax,cmin,cmax,db,dc | |||
real*8 c(200),b(200),chalf(199),bhalf(199) | |||
real*8 bsize,csize,emin,emax | |||
real*8 fepoint(200,200),fescalar(199,199) | |||
real*8 ell(200),ellhalf(199) | |||
real*8 muratio,eta,Gami,frakK,frakL | |||
real*8 eshift,ediff | |||
real xx(200),yy(200),cell(199,199),vertex(200,200) | |||
real valuemin,minlog,valufudge | |||
real*8 q,nu,chiEq,Enorm,E0,Efudge | |||
integer j,k,n,nmax,inorm | |||
101 format(4x,'bsize',7x,'csize',8x,'xi',10x,'A',12x,'B',12x,& | |||
&'fM',13x,'fW',11x,'fA',/) | |||
! 102 format(1p8d12.4) | |||
103 format(2i5,1p3d14.6) | |||
201 format(5x,'valuemin = ',1pe15.5,//) | |||
205 format(5x,'For Cell-center ... emin, emax = ',1p2d14.6,/) | |||
206 format(5x,'For Cell-vertex ... emin, emax = ',1p2d14.6,/) | |||
701 format(5x,1p10d10.2) | |||
700 format(8x,'xi',9x,'ell',8x,'eta',8x,'Lambda',5x,'frakK',& | |||
& 5x,'frakL',8x,'q',5x,'nu',5x,'chiEq',8x,'E0',/) | |||
!!!!!!!! | |||
!!!!!!!! | |||
inorm=1 | |||
pii = 4.0d0*datan(1.0d0) | |||
muratio = 1.0d0 | |||
bsize = 0.0d0 | |||
csize = 0.0d0 | |||
Efudge = -10.0d0 | |||
write(*,101) | |||
! write(*,102)bsize,csize,xival,coefA,coefB,fM,fW,fA | |||
!!!!!!!!!!! | |||
! | |||
! In this free-energy routine, c = X = chi/chi_eq and b = xi_i | |||
! | |||
!!!!!!!!!!! | |||
nmax = 200 | |||
bmin = 1.0d0 | |||
bmax = 3.0d0 | |||
db = (bmax-bmin)/dfloat(nmax-1) | |||
b(1) = bmin | |||
ell(1) = b(1)/dsqrt(3.0d0) | |||
! These values of cmin and cmax ensure that X=1 occurs at zone 70 | |||
cmin = 0.469230769d0 | |||
cmax = 2.00d0 | |||
dc = (cmax-cmin)/dfloat(nmax-1) | |||
c(1) = cmin | |||
do n=2,nmax | |||
b(n) = b(n-1)+db | |||
c(n) = c(n-1)+dc | |||
ell(n) = b(n)/dsqrt(3.0d0) | |||
enddo | |||
do n=1,nmax-1 | |||
bhalf(n) = 0.5d0*(b(n)+b(n+1)) | |||
chalf(n) = 0.5d0*(c(n)+c(n+1)) | |||
ellhalf(n) = bhalf(n)/dsqrt(3.0d0) | |||
enddo | |||
! | |||
! BEGIN LOOP to evaluate free energy (cell center) | |||
! | |||
emin = 0.0d0 | |||
emax = 0.0d0 | |||
write(*,700) | |||
do j=1,nmax-1 | |||
bsize = ellhalf(j) | |||
eta = 3.0d0*muratio*bsize/(1.0d0+bsize**2) | |||
Gami = 1.0d0/eta-bsize | |||
frakL = (bsize**4-1.0d0)/bsize**2 + & | |||
& DATAN(bsize)*((1.0d0+bsize**2)/bsize)**3 | |||
frakK = Gami/eta + ((1.0d0+Gami**2)/eta)*(pii/2.0d0+DATAN(Gami)) | |||
q = 1.0d0/(1.0d0 + (0.5d0*pii+DATAN(Gami))/eta) | |||
nu = bsize*q/dsqrt(1.0d0+Gami**2) | |||
chiEq = dsqrt(pii/8.0d0)*(nu**2/(q*bsize**2))& | |||
& *((1.0d0+bsize**2)/(3.0d0*bsize))**3 | |||
Enorm = 16.0d0*(q/nu**2)*chiEq | |||
E0 = ((5.0d0*frakL) + (4.0d0*frakK)& | |||
& - (3.0d0*frakL+12.0d0*frakK))/bsize**2+Efudge | |||
write(*,701)b(j),bsize,eta,Gami,frakK,frakL,q,nu,chiEq,E0 | |||
do k=1,nmax-1 | |||
csize=chalf(k) | |||
fescalar(j,k) = (csize**(-0.6d0)*(5.0d0*frakL)& | |||
& + csize**(-3.0d0)*(4.0d0*frakK)& | |||
& - (3.0d0*frakL+12.0d0*frakK)/csize)/bsize**2 + Efudge | |||
if(inorm.eq.1)fescalar(j,k)=fescalar(j,k)/DABS(E0) & | |||
& - E0/DABS(E0) | |||
if(fescalar(j,k).gt.0.5d0)fescalar(j,k)=0.5d0 | |||
if(fescalar(j,k).lt.emin)emin=fescalar(j,k) | |||
if(fescalar(j,k).gt.emax)emax=fescalar(j,k) | |||
! write(*,103)j,k,bsize,csize,fescalar(j,k) | |||
enddo | |||
enddo | |||
write(*,205)emin,emax | |||
! | |||
! BEGIN LOOP to evaluate free energy (cell vertex) | |||
! | |||
emin = 0.0d0 | |||
emax = 0.0d0 | |||
do j=1,nmax | |||
bsize = ell(j) | |||
eta = 3.0d0*muratio*bsize/(1.0d0+bsize**2) | |||
Gami = 1.0d0/eta-bsize | |||
frakL = (bsize**4-1.0d0)/bsize**2 + & | |||
& DATAN(bsize)*((1.0d0+bsize**2)/bsize)**3 | |||
frakK = Gami/eta + ((1.0d0+Gami**2)/eta)*(pii/2.0d0+DATAN(Gami)) | |||
q = 1.0d0/(1.0d0 + (0.5d0*pii+DATAN(Gami))/eta) | |||
nu = bsize*q/dsqrt(1.0d0+Gami**2) | |||
chiEq = dsqrt(pii/8.0d0)*(nu**2/(q*bsize**2))& | |||
& *((1.0d0+bsize**2)/(3.0d0*bsize))**3 | |||
Enorm = 16.0d0*(q/nu**2)*chiEq | |||
E0 = ((5.0d0*frakL) + (4.0d0*frakK)& | |||
& - (3.0d0*frakL+12.0d0*frakK))/bsize**2 + Efudge | |||
do k=1,nmax | |||
csize=c(k) | |||
fepoint(j,k) = (csize**(-0.6d0)*(5.0d0*frakL)& | |||
& + csize**(-3.0d0)*(4.0d0*frakK)& | |||
& - (3.0d0*frakL+12.0d0*frakK)/csize)/bsize**2 + Efudge | |||
if(inorm.eq.1)fepoint(j,k)=fepoint(j,k)/DABS(E0) & | |||
& - E0/DABS(E0) | |||
if(fepoint(j,k).gt.0.5d0)fepoint(j,k)=0.5d0 | |||
if(fepoint(j,k).lt.emin)emin=fepoint(j,k) | |||
if(fepoint(j,k).gt.emax)emax=fepoint(j,k) | |||
! write(*,103)j,k,bsize,csize,fepoint(j,k) | |||
enddo | |||
enddo | |||
write(*,206)emin,emax | |||
! | |||
! Now fill single-precision arrays for plotting. | |||
! | |||
do n=1,nmax | |||
! xx(n)=b(n)/b(nmax) | |||
! yy(n)=c(n)/c(nmax) | |||
xx(n)=b(n)-bmin | |||
yy(n)=c(n)-cmin | |||
! xx(n)=b(n) | |||
! yy(n)=c(n) | |||
enddo | |||
valuemin= -emin | |||
valufudge = 1.0d0/(emax-emin) | |||
do k=1,nmax | |||
do j=1,nmax | |||
vertex(j,k)=fepoint(j,k)+valuemin | |||
vertex(j,k)=vertex(j,k)*valufudge | |||
enddo | |||
enddo | |||
do k=1,nmax-1 | |||
do j=1,nmax-1 | |||
cell(j,k)=fescalar(j,k)+valuemin | |||
cell(j,k)=cell(j,k)*valufudge | |||
enddo | |||
enddo | |||
call XMLwriter01(nmax,xx,yy,cell,vertex) | |||
stop | |||
END PROGRAM BiPolytrope | |||
Subroutine XMLwriter01(imax,x,y,cell_scalar,point_scalar) | |||
real x(200),y(200),z(1) | |||
real cell_scalar(199,199),point_scalar(200,200) | |||
integer imax | |||
integer extentX,extentY,extentZ | |||
integer ix0,iy0,iz0 | |||
integer norm(200,3) | |||
! imax=200 | |||
ix0=0 | |||
iy0=0 | |||
iz0=0 | |||
extentX=imax-1 | |||
extentY=imax-1 | |||
extentZ=0 | |||
z(1) = 0.0 | |||
! Set normal vector 1D array | |||
do i=1,imax | |||
norm(i,1)=0 | |||
norm(i,2)=0 | |||
norm(i,3)=1 | |||
enddo | |||
201 format('<?xml version="1.0"?>') | |||
202 format('<VTKFile type="RectilinearGrid" version="0.1" byte_order="LittleEndian">') | |||
302 format('</VTKFile>') | |||
203 format(2x,'<RectilinearGrid WholeExtent="',6I4,'">') | |||
303 format(2x,'</RectilinearGrid>') | |||
204 format(4x,'<Piece Extent="',6I4,'">') | |||
304 format(4x,'</Piece>') | |||
205 format(6x,'<CellData Scalars="cell_scalars" Normals="magnify">') | |||
305 format(6x,'</CellData>') | |||
206 format(8x,'<DataArray type="Float32" Name="magnify" NumberOfComponents="3" format="ascii">') | |||
207 format(8x,'<DataArray type="Float32" Name="cell_scalars" format="ascii">') | |||
399 format(8x,'</DataArray>') | |||
208 format(6x,'<PointData Scalars="colorful" Normals="direction">') | |||
308 format(6x,'</PointData>') | |||
209 format(8x,'<DataArray type="Float32" Name="colorful" format="ascii">') | |||
210 format(6x,'<Coordinates>') | |||
310 format(6x,'</Coordinates>') | |||
211 format(8x,'<DataArray type="Float32" format="ascii" RangeMin="0" RangeMax="5">') | |||
212 format(8x,'<DataArray type="Float32" format="ascii">') | |||
213 format(8x,'<DataArray type="Float32" Name="direction" NumberOfComponents="3" format="ascii">') | |||
501 format(10f9.5) | |||
502 format(10f9.5) | |||
503 format(5x,9(1x,3I2)) | |||
504 format(10f9.5) | |||
505 format(5x,10(1x,3I2)) | |||
!!!!! | |||
! | |||
! Begin writing out XML tags. | |||
! | |||
!!!!! | |||
write(*,201) !<?xml | |||
write(*,202) !VTKFile | |||
write(*,203)ix0,extentX,iy0,extentY,iz0,extentZ ! RectilinearGrid | |||
write(*,204)ix0,extentX,iy0,extentY,iz0,extentZ ! Piece | |||
write(*,205) ! CellData | |||
write(*,207) ! DataArray(cell_scalars) | |||
do j=1,imax-1 | |||
write(*,501)(cell_scalar(i,j),i=1,imax-1) | |||
enddo | |||
write(*,399) ! /DataArray | |||
write(*,206) ! DataArray(cell_scalars) | |||
do j=1,imax-1 | |||
write(*,503)(norm(i,1),norm(i,2),norm(i,3),i=1,imax-1) | |||
enddo | |||
write(*,399) ! /DataArray | |||
write(*,305) ! /CellData | |||
write(*,208) ! PointData | |||
write(*,209) ! DataArray(points) | |||
write(*,502)((point_scalar(i,j),i=1,imax),j=1,imax) | |||
write(*,399) ! /DataArray | |||
write(*,213) ! DataArray(cell_scalars) | |||
do j=1,imax | |||
write(*,505)(norm(i,1),norm(i,2),norm(i,3),i=1,imax) | |||
enddo | |||
write(*,399) ! /DataArray | |||
write(*,308) ! /PointData | |||
write(*,210) ! Coordinates | |||
write(*,212) ! DataArray(x-direction) | |||
write(*,504)(x(i),i=1,imax) | |||
write(*,399) ! /DataArray | |||
write(*,212) ! DataArray(y-direction) | |||
write(*,504)(y(i),i=1,imax) | |||
write(*,399) ! /DataArray | |||
write(*,212) ! DataArray(z-direction) | |||
write(*,504)z(1) | |||
write(*,399) ! /DataArray | |||
write(*,310) ! /Coordinates | |||
write(*,304) ! /Piece | |||
write(*,303) ! /RectilinearGrid | |||
write(*,302) !/VTKFile | |||
return | |||
end | |||
</pre> | |||
=Nonstandard Examination= | |||
In our introductory remarks, [[#Free-Energy_of_Bipolytropes|above]], we said the warped free-energy surface drapes across a five-dimensional parameter "plane" such that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}_{51}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathfrak{G}(R, K_c, M_\mathrm{tot}, q, \nu) \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
From a more pragmatic point of view, we should have said that the "five-one" free-energy surface drapes across a five-dimensional parameter "plane" such that, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\mathfrak{G}_{51}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\mathfrak{G}(R, K_c, M_\mathrm{tot}, \ell_i, \tfrac{\mu_e}{\mu_c}) \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
In our initial, standard examination of the structure of this warped free-energy surface, we held three parameters fixed — namely, <math>~K_c, M_\mathrm{tot}, \tfrac{\mu_e}{\mu_c}</math> — and plotted <math>~\mathfrak{G}_{51}(\ell_i, \Chi\equiv R/R_\mathrm{eq})</math>. Now, let's fix <math>~\Chi = 1</math> and plot <math>~\mathfrak{G}_{51}(\ell_i, \tfrac{\mu_e}{\mu_c})</math>. The following plot shows how a portion of the <math>~(\ell_i, \mu_e/\mu_c)</math> grid maps onto the traditional <math>~(q, \nu)</math> plane. The numerical labels identify lines of constant <math>~\xi_i = \sqrt{3}\ell_i</math> — 7 (light green), 9 (pink), and 12 (orange) — and lines of constant <math>~\mu_e/\mu_c</math> — 0.330 (purple), 0.315 (dark green), and 0.305 (white/blue). | |||
[[File:GridOnNuQplot.png|center|500px|xi-ell grid drawn on q-nu grid]] | |||
=See Also= | =See Also= | ||
Latest revision as of 20:43, 23 September 2016
Free-Energy Synopsis

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
All of the self-gravitating configurations considered below have an associated Gibbs-like free-energy that can be expressed analytically as a power-law function of the dimensionless configuration radius, <math>~x</math>. Specifically,
|
<math>~\mathfrak{G}^*_\mathrm{type}</math> |
<math>~=</math> |
<math>~-ax^{-1} + b x^{-3/n} + c x^{-3/j} + \mathfrak{G}_0 \, .</math> |
Equilibrium Radii and Critical Radii
The first and second (partial) derivatives with respect to <math>~x</math> are, respectively,
|
<math>~\frac{\partial\mathfrak{G}^*_\mathrm{type}}{\partial x}</math> |
<math>~=</math> |
<math>~ax^{-2} - \biggl(\frac{ 3b}{n}\biggr) x^{-3/n -1} -\biggl(\frac{3 c}{j}\biggr) x^{-3/j-1} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{x^2} \biggl[ a - \biggl(\frac{ 3b}{n}\biggr) x^{(n-3)/n } -\biggl(\frac{3 c}{j}\biggr) x^{(j-3)/j} \biggr] \, ,</math> |
|
<math>~\frac{\partial^2 \mathfrak{G}^*_\mathrm{type}}{\partial x^2}</math> |
<math>~=</math> |
<math>~-2ax^{-3} + \biggl(\frac{ 3b}{n}\biggr) \biggl( \frac{n+3}{n}\biggr) x^{-3/n -2} + \biggl(\frac{3 c}{j}\biggr)\biggl( \frac{j+3}{j}\biggr) x^{-3/j-2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{x^3} \biggl\{ \biggl(\frac{ 3b}{n}\biggr) \biggl( \frac{n+3}{n}\biggr) x^{(n-3)/n} + \biggl(\frac{3 c}{j}\biggr)\biggl( \frac{j+3}{j}\biggr) x^{(j-3)/j} -2a\biggr\} \, . </math> |
Equilibrium configurations are identified by setting the first derivative to zero. This gives,
|
<math>~0</math> |
<math>~=</math> |
<math>~a - \biggl(\frac{ 3b}{n}\biggr) x^{(n-3)/n }_\mathrm{eq} -\biggl(\frac{3 c}{j}\biggr) x^{(j-3)/j}_\mathrm{eq} </math> |
|
<math>~\Rightarrow ~~~x^{(n-3)/n }_\mathrm{eq}</math> |
<math>~=</math> |
<math>~\biggl(\frac{n}{ 3b}\biggr) \biggl[a -\biggl(\frac{3 c}{j}\biggr) x^{(j-3)/j}_\mathrm{eq} \biggr] \, .</math> |
|
<math>~\Rightarrow ~~~\frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} + \frac{1}{j}\cdot x^{(j-3)/j}_\mathrm{eq} </math> |
<math>~=</math> |
<math>~ 0 \, .</math> |
We conclude, as well, that at this equilibrium radius, the second (partial) derivative assumes the value,
|
<math>~\biggl[ \frac{\partial^2 \mathfrak{G}^*_\mathrm{type}}{\partial x^2} \biggr]_\mathrm{eq}</math> |
<math>~=</math> |
<math>~ \frac{1}{x^3_\mathrm{eq} } \biggl\{ \biggl(\frac{ 3b}{n}\biggr) \biggl( \frac{n+3}{n}\biggr) x^{(n-3)/n} + \biggl(\frac{3 c}{j}\biggr)\biggl( \frac{j+3}{j}\biggr) x^{(j-3)/j} -2a\biggr\}_\mathrm{eq} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{x^3_\mathrm{eq} } \biggl\{ \biggl( \frac{n+3}{n}\biggr) \biggl[a -\biggl(\frac{3 c}{j}\biggr) x^{(j-3)/j}_\mathrm{eq} \biggr] + \biggl(\frac{3 c}{j}\biggr)\biggl( \frac{j+3}{j}\biggr) x^{(j-3)/j}_\mathrm{eq} -2a\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{x^3_\mathrm{eq} } \biggl\{ \biggl(\frac{3 c}{j}\biggr) \biggl[ \biggl( \frac{j+3}{j}\biggr) -\biggl( \frac{n+3}{n}\biggr) \biggl] x^{(j-3)/j}_\mathrm{eq} + \biggl( \frac{3-n}{n}\biggr) a\biggr\} \, . </math> |
Hence, equilibrium configurations for which the second (as well as first) derivative of the free energy is zero are found at "critical" radii given by the expression,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \biggl(\frac{3 c}{j}\biggr) \biggl[ \biggl( \frac{j+3}{j}\biggr) -\biggl( \frac{n+3}{n}\biggr) \biggl] [x_\mathrm{eq}^{(j-3)/j}]_\mathrm{crit} + \biggl( \frac{3-n}{n}\biggr) a </math> |
|
<math>~\Rightarrow ~~~[x_\mathrm{eq}^{(j-3)/j}]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{j^2 a(n-3)}{3 c}\biggr] [ n(j+3) - j(n+3) ]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \frac{a}{3^2c}\biggl[ \frac{j^2(n-3)}{n-j} \biggr] \, . </math> |
Examples
Pressure-Truncated Polytropes
For pressure-truncated polytropes of index <math>~n</math>, we set, <math>~j = -1</math>, in which case,
|
<math>~\frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} - x^{4}_\mathrm{eq}</math> |
<math>~=</math> |
<math>~0 \, ;</math> |
|
<math>~\biggl[ \biggl(\frac{3}{4\pi}\biggr) \frac{ M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr]^{(n+1)/n} x^{(n-3)/n }_\mathrm{eq} - \frac{3}{20\pi} \biggl( \frac{n+1}{n}\biggr)\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr)^{2} - x^{4}_\mathrm{eq}</math> |
<math>~=</math> |
<math>~0 \, ;</math> |
|
<math>~x^{(n-3)/n }_\mathrm{eq}</math> |
<math>~=</math> |
<math>~\biggl(\frac{n}{ 3b}\biggr) \biggl[a + 3cx^{4}_\mathrm{eq} \biggr] \, ;</math> |
|
|
and |
|
|
<math>~[x_\mathrm{eq}]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{a(n-3)}{3^2 c (n+1)} \biggr]^{1/4} \, . </math> |
Case M
More specifically, the expression that describes the "Case M" free-energy surface is,
|
Hence, we have,
|
<math>~a</math> |
<math>~\equiv</math> |
<math>~3\mathcal{A} = \frac{3}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}\, , </math> |
|
<math>~b</math> |
<math>~\equiv</math> |
<math>~n\mathcal{B} = n\biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, , </math> |
|
<math>~c</math> |
<math>~\equiv</math> |
<math>~\frac{4\pi}{3}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, , </math> |
where the structural form factors for pressure-truncated polytropes are precisely defined here. Therefore, the statement of virial equilibrium is,
|
<math>~0 </math> |
<math>~=</math> |
<math>~\frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} - x^{4}_\mathrm{eq}</math> |
|
<math>~\Rightarrow ~~~ \biggl(\frac{3}{4\pi}\biggr)c x_\mathrm{eq}^4 </math> |
<math>~=</math> |
<math>~\biggl(\frac{3}{4\pi}\biggr) \biggl[ \frac{ b}{n}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3} \biggr]</math> |
|
<math>~\Rightarrow ~~~ \biggl(\frac{P_e}{P_\mathrm{norm}}\biggr) x_\mathrm{eq}^4 </math> |
<math>~=</math> |
<math>~\biggl(\frac{3}{4\pi}\biggr) \biggl[ \biggl(\frac{3}{4\pi} \biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \cdot x^{(n-3)/n }_\mathrm{eq} - \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr]</math> |
|
|
<math>~=</math> |
<math>~\biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \cdot x^{(n-3)/n }_\mathrm{eq} - \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \, .</math> |
And we conclude that,
|
<math>~3c[x_\mathrm{eq}]^4_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\frac{(n-3)}{5(n+1)} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) [x_\mathrm{eq}]^4_\mathrm{crit}</math> |
<math>~=</math> |
<math>~\frac{1}{20\pi} \biggl( \frac{n-3}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
|
<math>~\Rightarrow ~~~ \biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \cdot [ x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} - \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
<math>~=</math> |
<math>~\frac{1}{20\pi} \biggl( \frac{n-3}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
|
<math>~\Rightarrow ~~~ \biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \cdot [ x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\frac{1}{20\pi} \biggl( \frac{n-3}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} + \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{20\pi} \biggl( \frac{4n}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
|
<math>~\Rightarrow ~~~ [ x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\frac{1}{20\pi} \biggl(\frac{4\pi}{3} \biggr)^{(n+1)/n} \biggl( \frac{4n}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_A \tilde{\mathfrak{f}}_M^{(n-1)/n} } </math> |
|
<math>~\Rightarrow ~~~ [ x_\mathrm{eq} ]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{4n}{15(n+1)} \biggl(\frac{4\pi}{3} \biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_A \tilde{\mathfrak{f}}_M^{(n-1)/n} } \biggr]^{n/(n-3)} \, . </math> |
|
ASIDE: Let's see what this requires for the case of <math>~n=5</math>, where everything is specifiable analytically. We have gathered together:
So, the radius of the critical equilibrium state should be,
whereas, each equilibrium configuration has,
So the equilibrium state that marks the critical configuration must have a value of <math>~\ell</math> that satisfies the relation,
The solution is: <math>~\ell_\mathrm{crit} \approx 2.223175 \, .</math> |
In addition, we know from our dissection of Hoerdt's work on detailed force-balance models that, in the equilibrium state,
|
<math>~\biggl(\frac{P_e}{P_\mathrm{norm}}\biggr) \biggl(\frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4</math> |
<math>~=</math> |
<math> \biggl[ \frac{\tilde\theta^{n+1} }{(4\pi)(n+1)( -\tilde\theta' )^{2}} \biggr] </math> |
|
<math>~\Rightarrow ~~~ 3c x_\mathrm{eq}^4</math> |
<math>~=</math> |
<math> \biggl[ \frac{\tilde\theta^{n+1} }{(n+1)( -\tilde\theta' )^{2}} \biggr] \, . </math> |
This means that, for any chosen polytropic index, the critical equilibrium state is the equilibrium configuration for which (needs to be checked),
|
<math>~2(9-2n){\tilde\theta}^{n+1}</math> |
<math>~=</math> |
<math>~ 3(n-3)\biggl[ (- {\tilde\theta}^')^2 - \frac{\tilde\theta(-{\tilde\theta}^')}{\tilde\xi}\biggr] \, . </math> |
We note, as well, that by combining the Horedt expression for <math>~x_\mathrm{eq}</math> with our virial equilibrium expression, we find (needs to be checked),
|
<math>~x_\mathrm{eq}^{n-3}</math> |
<math>~=</math> |
<math>~\frac{4\pi}{3}\biggl[ \frac{3}{(n+1)\tilde\xi^2} + \frac{{\tilde\mathfrak{f}}_{W} - {\tilde\mathfrak{f}}_{M}}{5\tilde\mathfrak{f}_A} \biggr]^{n} {\tilde\mathfrak{f}}_{M}^{1-n} \, .</math> |
Case P
First Pass
Alternatively, let's examine the "Case P" free-energy surface. Drawing on Stahler's presentation, we adopt the following radius and mass normalizations:
<math>M_\mathrm{SWS} = \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \, ,</math>
<math> R_\mathrm{SWS} = \biggl( \frac{n+1}{n} \biggr)^{1/2} G^{-1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \, . </math>
In terms of these new normalizations, we have,
|
<math>~R_\mathrm{norm} \equiv \biggl[\biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{(n-1)} \biggr]^{1/(n-3)}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{G}{K} \biggr)^{n/(n-3)} M_\mathrm{tot}^{(n-1)/(n-3)} R_\mathrm{SWS} \biggl( \frac{n+1}{n} \biggr)^{-1/2} G^{1/2} K_n^{-n/(n+1)} P_\mathrm{e}^{-(1-n)/[2(n+1)]} </math> |
|
|
|
<math>~+ M_\mathrm{SWS}^{-(n-1)/(n-3)} \biggl[ \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \biggr]^{(n-1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~R_\mathrm{SWS} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{[3(n-1)-(n-3)]/[2(n-3)]} G^{[2n+(n-3)-3(n-1)]/[2(n-3)]} </math> |
|
|
|
<math>~+ K_n^{n[2(n-1) - (n+1) - (n-3)]/[(n+1)(n-3)]} P_\mathrm{e}^{-(n-1)(3-n)/[2(n+1)(n-3)]} P_\mathrm{e}^{(n-1)(3-n)/[2(n+1)(n-3)]} </math> |
|
|
<math>~=</math> |
<math>~R_\mathrm{SWS} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \, . </math> |
and,
|
<math>~P_\mathrm{norm} \equiv \biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)} } \biggr]^{1/(n-3)}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{K^{4n}}{G^{3(n+1)} } \biggr]^{1/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{-2(n+1)/(n-3)} \biggl\{ \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]}\biggr\}^{-2(n+1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{-2(n+1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{-3(n+1)/(n-3)} K^{4n/(n-3)} G^{-3(n+1)/(n-3)} </math> |
|
|
|
<math>~\times~ G^{3(n+1)/(n-3)} K_n^{-4n/(n-3)} \biggl\{ P_\mathrm{e}^{-(n-3)/[2(n+1)]}\biggr\}^{-2(n+1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~P_e \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{-2(n+1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{-3(n+1)/(n-3)} \, . </math> |
Rewriting the expression for the free energy gives,
|
<math>~\mathfrak{G}_{K,M}^* \equiv \frac{\mathfrak{G}_{K,M}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~ -3\mathcal{A} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} \biggl(\frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr) +~ n\mathcal{B} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} \biggl(\frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr)^{3/n} +~ \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \biggl(\frac{R_\mathrm{norm}}{R_\mathrm{SWS}}\biggr)^{-3} </math> |
|
|
<math>~=</math> |
<math>~ -3\mathcal{A} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} \biggl[ \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)}\biggr] </math> |
|
|
|
<math>~ +~ n\mathcal{B} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} \biggl[ \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)}\biggr]^{3/n} </math> |
|
|
|
<math>~ +~ \biggl( \frac{4\pi}{3} \biggr) \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{2(n+1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{3(n+1)/(n-3)} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \biggl[ \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)}\biggr]^{-3} </math> |
|
|
<math>~=</math> |
<math>~ -3\mathcal{A} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} +~ n\mathcal{B} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} </math> |
|
|
|
<math>~ +~ \biggl( \frac{4\pi}{3} \biggr) \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(5-n)/(n-3)} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \, . </math> |
Therefore, in this case, we have,
|
<math>~a</math> |
<math>~=</math> |
<math>~\frac{3}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \, , </math> |
|
<math>~b</math> |
<math>~=</math> |
<math>~ n\biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \, , </math> |
|
<math>~c</math> |
<math>~=</math> |
<math>~\frac{4\pi}{3} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(5-n)/(n-3)} \, , </math> |
where the structural form factors for pressure-truncated polytropes are precisely defined here. The statement of virial equilibrium is, therefore,
|
<math>~x^{4}_\mathrm{eq} + \alpha </math> |
<math>~=</math> |
<math>~ \beta x^{(n-3)/n }_\mathrm{eq} \, , </math> |
where,
|
<math>~\alpha \equiv \frac{a}{3c}</math> |
<math>~=</math> |
<math>~ \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl\{ \frac{3}{4\pi} \biggl( \frac{n+1}{n} \biggr)^{-3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(n-5)/(n-3)} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr) \mathfrak{m}^{2} \, , </math> |
|
<math>~\beta \equiv \frac{b}{nc}</math> |
<math>~=</math> |
<math>~ \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \biggl\{ \frac{3}{4\pi} \biggl( \frac{n+1}{n} \biggr)^{-3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(n-5)/(n-3)} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} \, , </math> |
|
<math>~\mathfrak{m}</math> |
<math>~\equiv</math> |
<math>~ \biggl(\frac{3}{4\pi}\biggr) \frac{1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr) \, . </math> |
From a previous derivation, we have,
|
<math>~0 </math> |
<math>~=</math> |
<math>~ \frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} - x^{4}_\mathrm{eq} </math> |
|
|
<math>~=</math> |
<math>~\frac{3}{4\pi} \biggl( \frac{n+1}{n} \biggr)^{-3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(n-5)/(n-3)} \biggl\{ \biggl(\frac{3}{4\pi} \biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \biggr\} \cdot x^{(n-3)/n }_\mathrm{eq} </math> |
|
|
|
<math>~ - \frac{3}{4\pi} \biggl( \frac{n+1}{n} \biggr)^{-3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(n-5)/(n-3)} \biggl\{ \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggr\} - x^{4}_\mathrm{eq} </math> |
|
<math>~0</math> |
<math>~=</math> |
<math>~ \biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} x^{(n-3)/n }_\mathrm{eq} - \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} - x^{4}_\mathrm{eq} </math> |
|
|
<math>~=</math> |
<math>~ \tilde{\mathfrak{f}}_A \biggl[ \biggl(\frac{3}{4\pi} \biggr) \frac{1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)\biggr]^{(n+1)/n} x^{(n-3)/n }_\mathrm{eq} - \frac{1}{5} \biggl(\frac{4\pi}{3}\biggr) \cdot \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr)\biggl[ \biggl(\frac{3}{4\pi} \biggr) \frac{1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)\biggr]^{2} - x^{4}_\mathrm{eq} </math> |
which, thankfully, matches! We conclude as well that the transition from stable to dynamically unstable configurations occurs at,
|
<math>~[x_\mathrm{eq}]_\mathrm{crit}^4</math> |
<math>~=</math> |
<math>~\biggl[ \frac{(n-3)}{3 (n+1)} \biggr] \alpha \, . </math> |
When combined with the statement of virial equilibrium at this critical point, we find,
|
<math>~ \biggl\{ \biggl[ \frac{(n-3)}{3 (n+1)} \biggr] + 1\biggr\}\frac{ \alpha }{\beta} </math> |
<math>~=</math> |
<math>~ [x_\mathrm{eq}]^{(n-3)/n }_\mathrm{crit} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \biggl[ \frac{(n-3)}{3 (n+1)} \biggr] \alpha \biggr\}^{(n-3)/(4n) } </math> |
|
<math>~\Rightarrow~~~ \biggl[ \frac{4n}{3 (n+1)} \biggr]^{4n} \biggl( \frac{ \alpha }{\beta} \biggr)^{4n} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{(n-3)}{3 (n+1)} \biggr]^{(n-3)} \alpha^{(n-3)} </math> |
|
<math>~\Rightarrow~~~ \biggl[ \frac{3 n}{(n-3)} \biggl( \frac{n+1}{n}\biggr) \biggr]^{(3-n)} \biggl[ \frac{3 }{4} \biggl( \frac{n+1}{n}\biggr) \biggr]^{4n} </math> |
<math>~=</math> |
<math>~ \alpha^{3(n+1)} \beta^{-4n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr) \mathfrak{m}^{2} \biggr\}^{3(n+1)} \biggl\{ \tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} \biggr\}^{-4n} </math> |
|
|
<math>~=</math> |
<math>~\tilde{\mathfrak{f}}_A^{-4n} \biggl[ \biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr)\biggr]^{3(n+1)} \mathfrak{m}^{2(n+1)} </math> |
|
<math>~\Rightarrow ~~~ \mathfrak{m}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr)\biggr]^{-3(n+1)} \biggl[ \frac{3 n}{(n-3)} \biggl( \frac{n+1}{n}\biggr) \biggr]^{(3-n)} \biggl[ \frac{3\tilde{\mathfrak{f}}_A }{4} \biggl( \frac{n+1}{n}\biggr) \biggr]^{4n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{3\cdot 5}{4\pi}\biggr) \frac{1}{\tilde{\mathfrak{f}}_W} \biggr]^{3(n+1)} \biggl[ \frac{3 n}{(n-3)} \biggr]^{(3-n)} \biggl[ \frac{3\tilde{\mathfrak{f}}_A }{4} \biggr]^{4n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{3^2 \cdot 5 n}{ 4\pi(n-3)} \cdot \frac{1}{\tilde{\mathfrak{f}}_W} \biggr]^{(3-n)} \biggl[ \biggl( \frac{3^2\cdot 5}{2^4\pi}\biggr) \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_W} \biggr]^{4n} \, . </math> |
This also means that the critical radius is,
|
<math>~[x_\mathrm{eq}]_\mathrm{crit}^4</math> |
<math>~=</math> |
<math>~\biggl[ \frac{(n-3)}{3 (n+1)} \biggr] \biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr) \mathfrak{m}^{2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{3^2\cdot 5 n}{4\pi(n-3)} \cdot \frac{1}{\tilde{\mathfrak{f}}_W}\biggr]^{-1} \mathfrak{m}^{2} </math> |
|
<math>~\Rightarrow ~~~ [x_\mathrm{eq}]_\mathrm{crit}^{4(n+1)}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{3^2\cdot 5 n}{4\pi(n-3)} \cdot \frac{1}{\tilde{\mathfrak{f}}_W} \biggr]^{-(n+1)} \biggl[ \frac{3^2 \cdot 5 n}{ 4\pi(n-3)} \cdot \frac{1}{\tilde{\mathfrak{f}}_W} \biggr]^{(3-n)} \biggl[ \biggl( \frac{3^2\cdot 5}{2^4\pi}\biggr) \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_W} \biggr]^{4n} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{4\pi(n-3)}{3^2\cdot 5 n} \cdot \tilde{\mathfrak{f}}_W \biggr]^{2(n-1)} \biggl[ \biggl( \frac{3^2\cdot 5}{2^4\pi}\biggr) \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_W} \biggr]^{4n} </math> |
|
<math>~\Rightarrow ~~~ [x_\mathrm{eq}]_\mathrm{crit}^{2(n+1)}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{n}{(n-3)} \biggl( \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W} \biggr) \biggr]^{(1-n)} \biggl[ \biggl( \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W}\biggr) \frac{\tilde{\mathfrak{f}}_A}{4} \biggr]^{2n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{n}{n-3} \biggr)^{(1-n)} \biggl( \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W} \biggr)^{(n+1)} \biggl(\frac{\tilde{\mathfrak{f}}_A}{4} \biggr)^{2n} \, . </math> |
The following parallel derivation was done independently. [Note that a factor of 2n/(n-1) appears to correct a mistake made during the original derivation.] Beginning with the virial expression,
|
<math>~\beta x^{(n-3)/n }_\mathrm{eq} </math> |
<math>~=</math> |
<math>~ \alpha + x^{4}_\mathrm{eq} </math> |
|
<math>~ \biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} [x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} + \frac{(n-3)}{20\pi n} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{(n-1)}{10\pi n} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl[ \frac{2n}{(n-1)}\biggr] </math> |
|
<math>~\Rightarrow~~~ [x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \frac{2(n-1)}{15 n} \biggl(\frac{4\pi}{3} \biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_A\tilde{\mathfrak{f}}_M^{(n-1)/n}} \cdot \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/n} \biggl[ \frac{2n}{(n-1)}\biggr] </math> |
|
<math>~\Rightarrow~~~ [x_\mathrm{eq} ]^{(n-3) }_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{2(n-1)}{15 n} \biggr]^n \biggl(\frac{4\pi}{3} \biggr) \frac{\tilde{\mathfrak{f}}_W^n}{\tilde{\mathfrak{f}}_A^n \tilde{\mathfrak{f}}_M^{(n-1)}} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)} \biggl[ \frac{2n}{(n-1)}\biggr]^n </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{2(n-1)}{15 n} \biggr]^n \biggl(\frac{4\pi}{3} \biggr) \frac{\tilde{\mathfrak{f}}_W^n}{\tilde{\mathfrak{f}}_A^n \tilde{\mathfrak{f}}_M^{(n-1)}} \biggl\{ \biggl[ \frac{20\pi n}{(n-3)} \biggr]^{(n-1)/2} \biggl( \frac{\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W} \biggr)^{(n-1)/2} [x_\mathrm{eq} ]^{2(n-1) }_\mathrm{crit} \biggr\}\biggl[ \frac{2n}{(n-1)}\biggr]^n </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{2(n-1)}{15 n} \biggr]^n \biggl(\frac{4\pi}{3} \biggr) \frac{\tilde{\mathfrak{f}}_W^{(n+1)/2}}{\tilde{\mathfrak{f}}_A^n } \biggl\{ \biggl[ \frac{20\pi n}{(n-3)} \biggr]^{(n-1)/2} [x_\mathrm{eq} ]^{2(n-1) }_\mathrm{crit} \biggr\}\biggl[ \frac{2n}{(n-1)}\biggr]^n </math> |
|
<math>~\Rightarrow~~~ [x_\mathrm{eq} ]^{(n+1) }_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \biggl(\frac{3}{4\pi} \biggr) \biggl[\frac{15 n}{2(n-1)} \biggr]^n \biggl[ \frac{(n-3)}{20\pi n} \biggr]^{(n-1)/2} \frac{\tilde{\mathfrak{f}}_A^n }{\tilde{\mathfrak{f}}_W^{(n+1)/2}} \biggl[ \frac{(n-1)}{2n} \biggr]^n </math> |
|
<math>~\Rightarrow~~~ [x_\mathrm{eq} ]^{(n+1) }_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \biggl(\frac{3}{4\pi} \biggr) \biggl[\frac{15 }{2^2} \biggr]^n \biggl[ \frac{(n-3)}{20\pi n} \biggr]^{(n-1)/2} \frac{\tilde{\mathfrak{f}}_A^n }{\tilde{\mathfrak{f}}_W^{(n+1)/2}} </math> |
Also from Stahler's work we know that the equilibrium mass and radius are,
|
<math> ~\frac{M_\mathrm{tot}}{M_\mathrm{SWS}} </math> |
<math>~=~</math> |
<math> \biggl( \frac{n^3}{4\pi} \biggr)^{1/2} \biggl[ {\tilde\theta}_n^{(n-3)/2} {\tilde\xi}^2 (-{\tilde\theta}^') \biggr] \, , </math> |
|
<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{SWS}} </math> |
<math>~=~</math> |
<math> \biggl( \frac{n}{4\pi} \biggr)^{1/2} \biggl[ \tilde\xi {\tilde\theta}_n^{(n-1)/2} \biggr] \, . </math> |
Additional details in support of an associated PowerPoint presentation can be found here.
Reconcile
|
<math>~\biggl[\frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]^4_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{(n-3)}{20\pi (n+1)} \biggr] \biggl(\frac{n+1}{n}\biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
|
<math>~\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4_\mathrm{crit}</math> |
<math>~=</math> |
<math>~\frac{1}{20\pi} \biggl( \frac{n-3}{n+1} \biggr) \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
Taking the ratio, the RHS is,
|
<math>~\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)</math> |
<math>~=</math> |
<math>~P_e M_\mathrm{tot}^2 \biggl[ \frac{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)} }{K^{4n}} \biggr]^{1/(n-3)} \biggl[ \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \biggr]^{-2} \biggl( \frac{n+1}{n}\biggr)</math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{n+1}{n} \biggr)^{-2}P_e M_\mathrm{tot}^2 \biggl[ G^{3} M_\mathrm{tot}^{2} \biggr]^{(n+1)/(n-3)} K_n^{-4n/(n-3)} \biggl[ G^{3} K_n^{-4n/(n+1)} P_\mathrm{e}^{(n-3)/(n+1)} \biggr]</math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{n+1}{n} \biggr)^{-2} \biggl[ G^{3} M_\mathrm{tot}^{2} \biggr]^{[(n-3)+(n+1)]/(n-3)} \biggl[ K_n^{[(n+1)+(n-3)]/[(n+1)(n-3)] } \biggr]^{-4n} P_\mathrm{e}^{[(n+1)+ (n-3)]/(n+1)} </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{n+1}{n} \biggr)^{-2} M_\mathrm{tot}^{4(n-1)/(n-3)} G^{[6(n-1)]/(n-3)} K_n^{-8(n-1)/[(n+1)(n-3)] } P_\mathrm{e}^{2(n-1)/(n+1)} \, ;</math> |
while the LHS is,
|
<math>~\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr)^{4}</math> |
<math>~=</math> |
<math>~ \biggl[\biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{(n-1)} \biggr]^{4/(n-3)} \biggl\{\biggl( \frac{n+1}{n} \biggr)^{1/2} G^{-1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]}\biggr\}^{-4} </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{n+1}{n} \biggr)^{-2} M_\mathrm{tot}^{4(n-1)/(n-3)} G^{[6(n-1)]/(n-3)} K^{-8n(n-1)/[(n-3)(n+1)] } P_\mathrm{e}^{2(n-1)/(n+1)} \, . </math> |
Q.E.D.
Now, given that,
|
<math>~M_\mathrm{SWS}^{-4(n-1)/(n-3)}</math> |
<math>~=</math> |
<math>~\biggl[\biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]}\biggr]^{-4(n-1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{n+1}{n} \biggr)^{-6(n-1)/(n-3)} G^{6(n-1)/(n-3)} K_n^{-8n(n-1)/[(n+1)(n-3)]} P_\mathrm{e}^{2(n-1)/(n+1)} </math> |
we have,
|
<math>~\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr)^{4}</math> |
<math>~=</math> |
<math>~\biggl( \frac{n+1}{n} \biggr)^{-2} \biggl(\frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{4(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{6(n-1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{4(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{4n/(n-3)} </math> |
|
<math>~\Rightarrow ~~~\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr)^{n-3}</math> |
<math>~=</math> |
<math>~ \biggl(\frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{n-1} \biggl( \frac{n+1}{n} \biggr)^{n} </math> |
By inspection, in the specific case of <math>~n=5</math> (see above), this critical configuration appears to coincide with one of the "turning points" identified by Kimura. Specifically, it appears to coincide with the "extremal in r1" along an M1 sequence, which satisfies the condition,
|
<math>~\biggl[ \frac{n-3}{n-1} \biggr]_{n=5}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{\tilde\xi \tilde\theta^{n}}{(-\tilde\theta^')}\biggr]_{n=5}</math> |
|
<math>~\Rightarrow ~~~\frac{1}{2} </math> |
<math>~=</math> |
<math>~3^{1/2}\ell \biggl[ (1 + \ell^2)^{-1/2} \biggr]^5 \biggl[ \frac{\ell}{3^{1/2}} (1+\ell^2 )^{-3/2} \biggr]^{-1}</math> |
|
|
<math>~=</math> |
<math>~3(1 + \ell^2)^{-1} </math> |
|
<math>~\Rightarrow~~~ \ell </math> |
<math>~=</math> |
<math>~5^{1/2} \, .</math> |
Hence, according to Kimura, the turning point associated with the configuration with the largest equilibrium radius, corresponds to the equilibrium configuration having,
<math>~\ell |_\mathrm{R_{max}} = \sqrt{5} \approx 2.2360680 \, .</math>
This is, indeed, very close to — but decidedly different from — the value of <math>~\ell_\mathrm{crit}</math> determined, above!
Streamlined
Let's copy the expression for the "Case P" free energy derived above, then factor out a common term:
|
<math>~\frac{\mathfrak{G}_{K,M}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~ -3\mathcal{A} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} +~ n\mathcal{B} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} </math> |
|
|
|
<math>~ +~ \biggl( \frac{4\pi}{3} \biggr) \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(5-n)/(n-3)} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \, . </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(5-n)/(n-3)} \biggl(\frac{n+1}{n}\biggr)^{3/(n-3)} \biggl\{ -3\mathcal{A} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} +~ n\mathcal{B} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} +\frac{4\pi}{3} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \biggr\} </math> |
Defining a new normalization energy,
|
<math>~E_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~E_\mathrm{norm} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(5-n)/(n-3)} \biggl(\frac{n+1}{n}\biggr)^{3/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{n+1}{n}\biggr)^{3/2} K^{3n/(n+1)} G^{-3/2} P_e^{(5-n)/[2(n+1)]} \, , </math> |
we can write,
|
<math>~\mathfrak{G}_{K,M}^* \equiv \frac{\mathfrak{G}_{K,M}}{E_\mathrm{SWS}} </math> |
<math>~=</math> |
<math>~ -3\mathcal{A} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} +~ n\mathcal{B} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} +\frac{4\pi}{3} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \, , </math> |
in which case the coefficients of the generic free-energy expression are,
|
<math>~a</math> |
<math>~=</math> |
<math>~ \frac{3}{5} \cdot \frac{ \tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl(\frac{n+1}{n}\biggr)\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^2 = \frac{3}{5} \cdot \biggl( \frac{4\pi }{3}\biggr)^2 \biggl(\frac{n+1}{n}\biggr)\tilde{\mathfrak{f}}_W \mathfrak{m}^{2}</math> |
|
<math>~b</math> |
<math>~=</math> |
<math>~ n\biggl(\frac{3}{4\pi}\biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} = \biggl( \frac{4\pi n}{3}\biggr) \tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} </math> |
|
<math>~c</math> |
<math>~=</math> |
<math>~ \frac{4\pi}{3} \, , </math> |
where, as above,
|
<math>~\mathfrak{m}</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{3}{4\pi} \biggr) \frac{ 1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr) \, .</math> |
Now, if we define the pair of parameters,
|
<math>~\alpha</math> |
<math>~\equiv</math> |
<math>~\frac{a}{3c}</math> |
|
<math>~\beta</math> |
<math>~\equiv</math> |
<math>~\frac{b}{nc} \, ,</math> |
then the statement of virial equilibrium is,
|
<math>~x_\mathrm{eq}^4 + \alpha</math> |
<math>~=</math> |
<math>~\beta x_\mathrm{eq}^{(n-3)/n} \, ,</math> |
and the boundary between dynamical stability and instability occurs at,
|
<math>~[x_\mathrm{eq}]_\mathrm{crit}^4</math> |
<math>~=</math> |
<math>~\biggl[ \frac{n-3}{3(n+1)} \biggr]\alpha \, .</math> |
Combining these last two expressions means that the boundary between dynamical stability and instability is associated with the parameter condition,
|
<math>~[x_\mathrm{eq}]^{(n-3)/n}_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{n-3}{3(n+1)} + 1\biggr] \frac{\alpha}{\beta} </math> |
|
<math>~\Rightarrow ~~~ \biggl\{ \biggl[ \frac{n-3}{3(n+1)} \biggr]\alpha \biggr\}^{(n-3)/(4n)} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ 4n }{3(n+1)}\biggr] \frac{\alpha}{\beta} </math> |
|
<math>~\Rightarrow ~~~ \beta \alpha^{-3(n+1)/(4n)} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ 4n }{3(n+1)}\biggr] \biggl[ \frac{n-3}{n} \cdot \frac{n}{3(n+1)} \biggr]^{(3-n)/(4n)} </math> |
|
|
<math>~=</math> |
<math>~ 4 \biggl[ \frac{ n }{3(n+1)}\biggr]^{3(n+1)/(4n)} \biggl[ \frac{n-3}{n} \biggr]^{(3-n)/(4n)} </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{\beta}{4}\biggr)^{4n} \alpha^{-3(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ n }{3(n+1)}\biggr]^{3(n+1)} \biggl[ \frac{n-3}{n} \biggr]^{(3-n)} </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{\beta}{4}\biggr)^{4n} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ n\alpha }{3(n+1)}\biggr]^{3(n+1)} \biggl[ \frac{n}{n-3} \biggr]^{n-3} \, . </math> |
Case M
|
<math>~a</math> |
<math>~\equiv</math> |
<math>~3\mathcal{A} = \frac{3}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}\, , </math> |
|
<math>~b</math> |
<math>~\equiv</math> |
<math>~n\mathcal{B} = n\biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, , </math> |
|
<math>~c</math> |
<math>~\equiv</math> |
<math>~\frac{4\pi}{3}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, . </math> |
Hence,
|
<math>~\alpha</math> |
<math>~=</math> |
<math>~\biggl(\frac{4\pi }{15} \biggr) \tilde{\mathfrak{f}}_W \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^2 \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1}</math> |
|
<math>~\beta</math> |
<math>~=</math> |
<math>~\tilde{\mathfrak{f}}_A \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{(n+1)/n} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \, .</math> |
So the dynamical stability conditions are:
|
<math>~\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)\biggl( \frac{n}{n-3} \biggr) [x_\mathrm{eq}]_\mathrm{crit}^4</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr] \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^2 \, ;</math> |
and,
|
<math>~ \biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{4n} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{4(n+1)} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-4n} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ n}{3(n+1)}\biggr]^{3(n+1)} \biggl[ \frac{n}{n-3} \biggr]^{n-3} \biggl(\frac{4\pi \tilde{\mathfrak{f}}_W}{15} \biggr)^{3(n+1)} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{6(n+1)} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-3(n+1)} </math> |
|
<math>~\Rightarrow~~~ \biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{4n} </math> |
<math>~=</math> |
<math>~ \biggl[\biggl(\frac{ n}{n+1}\biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{3(n+1)} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{2(n+1)} \biggl[ \frac{n}{n-3} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)\biggr]^{n-3} </math> |
|
<math>~\Rightarrow~~~\biggl[ \frac{n}{n-3} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)\biggr]^{n-3} </math> |
<math>~=</math> |
<math>~ \biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{4n} \biggl[\biggl(\frac{ n}{n+1}\biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{-3(n+1)} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{-2(n+1)} \, . </math> |
Together, then,
|
<math>~[x_\mathrm{eq}]_\mathrm{crit}^{4(n-3)}</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{n-3} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{2(n-3)} \biggl[ \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \frac{n}{n-3} \biggr]^{-(n-3)} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{n-3} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{2(n-3)} \biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{-4n} \biggl[\biggl(\frac{ n}{n+1}\biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{3(n+1)} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{2(n+1)} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{4n} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{4(n-1)} \biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{-4n} </math> |
|
<math>~\Rightarrow ~~~[x_\mathrm{eq}]_\mathrm{crit}^{(n-3)}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{4}{\tilde{\mathfrak{f}}_A}\biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^n \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{(n-1)} \, . </math> |
Case P
|
<math>~a</math> |
<math>~=</math> |
<math>~ \frac{3}{5} \cdot \biggl( \frac{4\pi }{3}\biggr)^2 \biggl(\frac{n+1}{n}\biggr)\tilde{\mathfrak{f}}_W \mathfrak{m}^{2}</math> |
|
<math>~b</math> |
<math>~=</math> |
<math>~\biggl( \frac{4\pi n}{3}\biggr) \tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} </math> |
|
<math>~c</math> |
<math>~=</math> |
<math>~ \frac{4\pi}{3} \, , </math> |
where, as above,
|
<math>~\mathfrak{m}</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{3}{4\pi} \biggr) \frac{ 1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr) \, .</math> |
Hence,
|
<math>~\alpha</math> |
<math>~=</math> |
<math>~ \frac{1}{5} \cdot \biggl( \frac{4\pi }{3}\biggr) \biggl(\frac{n+1}{n}\biggr)\tilde{\mathfrak{f}}_W \mathfrak{m}^{2} </math> |
|
<math>~\beta</math> |
<math>~=</math> |
<math>~ \tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} \, . </math> |
So the dynamical stability conditions are:
|
<math>~[x_\mathrm{eq}]_\mathrm{crit}^4</math> |
<math>~=</math> |
<math>~\biggl[ \frac{n}{3(n+1)} \biggr]\biggl[ \frac{n-3}{n} \biggr]\frac{1}{5} \cdot \biggl( \frac{4\pi }{3}\biggr) \biggl(\frac{n+1}{n}\biggr)\tilde{\mathfrak{f}}_W \mathfrak{m}^{2} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{n-3}{n} \biggr]\biggl( \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5}\biggr) \mathfrak{m}^{2} </math> |
and,
|
<math>~ \biggl( \frac{\tilde{\mathfrak{f}}_A }{4}\biggr)^{4n} \mathfrak{m}^{4(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{4\pi }{3^2\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \mathfrak{m}^{2}\biggr]^{3(n+1)} \biggl[ \frac{n}{n-3} \biggr]^{n-3} </math> |
|
<math>~ \Rightarrow~~~ \mathfrak{m}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{4\pi }{3^2\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggr]^{-3(n+1)} \biggl[ \frac{n}{n-3} \biggr]^{-(n-3)} \biggl( \frac{\tilde{\mathfrak{f}}_A }{4}\biggr)^{4n} \, . </math> |
Together, then,
|
<math>~[x_\mathrm{eq}]_\mathrm{crit}^{4(n+1)}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{n-3}{n} \biggr]^{(n+1)} \biggl( \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5}\biggr)^{(n+1)} \biggl( \frac{4\pi \tilde{\mathfrak{f}}_W }{3^2\cdot 5}\biggr)^{-3(n+1)} \biggl[ \frac{n-3}{n} \biggr]^{(n-3)} \biggl( \frac{\tilde{\mathfrak{f}}_A }{4}\biggr)^{4n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{n-3}{n} \biggr]^{2(n-1)} \biggl( \frac{4\pi \tilde{\mathfrak{f}}_W }{3^2\cdot 5}\biggr)^{-2(n+1)} \biggl( \frac{\tilde{\mathfrak{f}}_A }{4}\biggr)^{4n} \, . </math> |
Compare
Let's see if the two cases, in fact, provide the same answer.
|
<math>~\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{SWS}}\biggr)^{n-3} = \biggl[ \frac{x_\mathrm{P}}{x_\mathrm{M}} \biggr]_\mathrm{crit}^{n-3}</math> |
<math>~=</math> |
<math>~ \biggl\{ \biggl[ \frac{n-3}{n} \biggr]\biggl( \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5}\biggr) \mathfrak{m}^{2} \biggr\}^{(n-3)/4} \biggl\{ \biggl[ \frac{4}{\tilde{\mathfrak{f}}_A}\biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^n \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{(n-1)} \biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \biggl[ \frac{n-3}{n} \biggr]\biggl( \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5}\biggr) \mathfrak{m}^{2} \biggr\}^{(n-3)/4} \biggl\{ \biggl[ \frac{4}{\tilde{\mathfrak{f}}_A}\biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^n \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{(n-1)} \biggr\}^{-1} </math> |
Five-One Bipolytropes
For analytically prescribed, "five-one" bipolytropes, <math>~n = 5</math> and <math>~j =1</math>, in which case,
|
<math>~x^{2/5 }_\mathrm{eq}</math> |
<math>~=</math> |
<math>~\biggl(\frac{5}{ 3b}\biggr) \biggl[a -3 c x^{-2}_\mathrm{eq} \biggr] \, ;</math> |
|
|
and |
|
|
<math>~[x_\mathrm{eq}]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{18 c}{a }\biggr]^{1/2} \, . </math> |
More specifically, the expression that describes the free-energy surface is,
|
Hence, we have,
|
<math>~a</math> |
<math>~\equiv</math> |
<math>~ 3\chi_\mathrm{eq}(\mathfrak{L}_i + 4\mathfrak{K}_i) \, , </math> |
|
<math>~b</math> |
<math>~\equiv</math> |
<math>~ 5 \mathfrak{L}_i \chi_\mathrm{eq}^{3/5} \, , </math> |
|
<math>~c</math> |
<math>~\equiv</math> |
<math>~ 4 \mathfrak{K}_i \chi_\mathrm{eq}^{3} \, , </math> |
and conclude that,
|
<math>~[\chi_\mathrm{eq}]_\mathrm{crit}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{18 (4 \mathfrak{K}_i \chi_\mathrm{eq}^{3} )}{ 3\chi_\mathrm{eq}(\mathfrak{L}_i + 4\mathfrak{K}_i)} \biggr]^{1/2}_\mathrm{crit} </math> |
|
|
<math>~=</math> |
<math>~[\chi_\mathrm{eq}]_\mathrm{crit}\biggl[ \frac{24 \mathfrak{K}_i }{ (\mathfrak{L}_i + 4\mathfrak{K}_i)} \biggr]^{1/2} </math> |
|
<math>~\Rightarrow~~~\biggl[ \frac{24 \mathfrak{K}_i }{ (\mathfrak{L}_i + 4\mathfrak{K}_i)} \biggr]_\mathrm{crit}</math> |
<math>~=</math> |
<math>~1 </math> |
|
<math>~\Rightarrow~~~\biggl[ \frac{\mathfrak{L}_i }{ \mathfrak{K}_i } \biggr]_\mathrm{crit}</math> |
<math>~=</math> |
<math>~20 \, . </math> |
Also, from our detailed force balance derivations, we know that,
|
<math>~\chi_\mathrm{eq} \equiv \frac{ R_\mathrm{eq}}{R_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} \, .</math> |
Zero-Zero Bipolytropes
General Form
In this case, we retain full generality making the substitutions, <math>~n \rightarrow n_c</math> and <math>~j \rightarrow n_e</math>, to obtain,
|
<math>~x^{(n_c-3)/n_c }_\mathrm{eq}</math> |
<math>~=</math> |
<math>~\frac{n_c}{ 3b} \biggl[a -\biggl(\frac{3 c}{n_e}\biggr) x^{(n_e-3)/n_e}_\mathrm{eq} \biggr] \, ;</math> |
|
|
and |
|
|
<math>~[x_\mathrm{eq}^{(n_e-3)/n_e}]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl\{\frac{n_e^2(n_c-3)}{3[ n_c (n_e+3) - n_e(n_c+3) ]}\biggr\} \frac{a}{c} </math> |
|
|
<math>~=</math> |
<math>~\biggl[\frac{n_e^2(n_c-3)}{3^2(n_c - n_e)}\biggr] \frac{a}{c} \, . </math> |
And here, the expression that describes the free-energy surface is,
|
Hence, we have,
|
<math>~a \equiv 3\chi_\mathrm{eq} \biggl(\frac{5}{2q^3} \biggr) C_2 </math> |
<math>~=</math> |
<math> 3f \chi_\mathrm{eq} \, , </math> |
|
<math>~b \equiv n_c \chi_\mathrm{eq}^{3/n_c} \biggl(\frac{5}{2q^3} \biggr) A_2 </math> |
<math>~\equiv</math> |
<math> n_c \chi_\mathrm{eq}^{3/n_c} \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, , </math> |
|
<math>~c \equiv n_e \chi_\mathrm{eq}^{3/n_e} \biggl(\frac{5}{2q^3} \biggr) B_2 </math> |
<math>~\equiv</math> |
<math>~ n_e \chi_\mathrm{eq}^{3/n_e} \biggl(\frac{5}{2q^3} \biggr) \biggl[\frac{2}{5} q^3 f - A_2\biggr] </math> |
|
|
<math>~=</math> |
<math>~ n_e \chi_\mathrm{eq}^{3/n_e} \biggl\{ f - \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \biggr\} \, , </math> |
where the definitions of <math>~f</math> and <math>~\mathfrak{F}</math> are given below. We immediately deduce that the critical equilibrium state is identified by,
|
<math>~[x_\mathrm{eq}^{(n_e-3)/n_e}]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl\{\frac{fn_e(n_c-3)}{3(n_c - n_e)}\biggr\} [\chi_\mathrm{eq}^{(n_e-3)/n_e}]_\mathrm{crit} \biggl\{ f - \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \biggr\}^{-1} </math> |
|
<math>~\Rightarrow ~~~\frac{1}{f}\biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr]</math> |
<math>~=</math> |
<math>~ 1 - \biggl[ \frac{n_e(n_c-3)}{3(n_c-n_e)} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{n_c(3-n_e)}{3(n_c-n_e)} \, .</math> |
From our associated detailed-force-balance derivation, we know that the associated equilibrium radius is,
|
<math>~\chi_\mathrm{eq}</math> |
<math>~=</math> |
<math>~ \biggl\{ \biggl(\frac{\pi}{3}\biggr) 2^{2-n_c} \nu^{n_c-1} q^{3-n_c} \biggl[1 + \frac{2}{5} q^3(f-1-\mathfrak{F})\biggr]^{n_c} \biggr\}^{1/(n_c-3)} \, . </math> |
Compare with Five-One
It is worthwhile to set <math>~n_c = 5</math> and <math>~n_e = 1</math> in this expression and compare the result to the comparable expression shown above for the "Five-One" Bipolytrope. Here we have,
|
<math>~\biggl[\chi_\mathrm{eq}\biggr]_{51}</math> |
<math>~=</math> |
<math>~ \biggl\{ \biggl(\frac{\pi}{3}\biggr) 2^{-3} \nu^{4} q^{-2} \biggl[1 + \frac{2}{5} q^3(f-1-\mathfrak{F})\biggr]^{5} \biggr\}^{1/2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{1}{\sqrt{3}} \biggl[1 + \frac{2}{5} q^3(f-1-\mathfrak{F})\biggr]^{5/2} \, ; </math> |
whereas, rewriting the above relation gives,
|
<math>~\chi_\mathrm{eq}\biggr|_{51}</math> |
<math>~=</math> |
<math>~\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{1}{\sqrt{3}} \biggl[\frac{(1+\ell_i^2)^{6/5}}{3\ell_i^2}\biggr]^{5/2} \, .</math> |
And, here, we should conclude that the critical equilibrium configuration is associated with,
|
<math>~\frac{1}{f}\biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr]</math> |
<math>~=</math> |
<math>~ \frac{5}{6} \, .</math> |
Free-Energy of Truncated Polytropes
In this case, the Gibbs-like free energy is given by the sum of three separate energies,
|
<math>~\mathfrak{G}</math> |
<math>~=</math> |
<math>~W_\mathrm{grav} + \mathfrak{S}_\mathrm{therm} + P_eV</math> |
|
|
<math>~=</math> |
<math>~ - 3\mathcal{A} \biggl[\frac{GM^2}{R} \biggr] + n\mathcal{B} \biggl[ \frac{KM^{(n+1)/n}}{R^{3/n}} \biggr] + \frac{4\pi}{3} \cdot P_e R^3 \, ,</math> |
where the constants,
|
<math>~\mathcal{A} \equiv \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}</math> |
and |
<math>\mathcal{B} \equiv \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, ,</math> |
and, as derived elsewhere,
|
Structural Form Factors for Pressure-Truncated Polytropes <math>~(n \ne 5)</math> |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|||||||||
|
As we have shown separately, for the singular case of <math>~n = 5</math>,
where, <math>~\ell \equiv \tilde\xi/\sqrt{3} </math> |
In general, then, the warped free-energy surface drapes across a four-dimensional parameter "plane" such that,
|
<math>~\mathfrak{G}</math> |
<math>~=</math> |
<math>~\mathfrak{G}(R, K, M, P_e) \, .</math> |
In order to effectively visualize the structure of this free-energy surface, we will reduce the parameter space from four to two, in two separate ways: First, we will hold constant the parameter pair, <math>~(K,M)</math>; giving a nod to Kimura's (1981b) nomenclature, we will refer to the resulting function, <math>~\mathfrak{G}_{K,M}(R,P_e)</math>, as a "Case M" free-energy surface because the mass is being held constant. Second, we will hold constant the parameter pair, <math>~(K,P_e)</math>, and examine the resulting "Case P" free-energy surface, <math>~\mathfrak{G}_{K,P_e}(R,M)</math>.
Virial Equilibrium and Dynamical Stability
The first (partial) derivative of <math>~\mathfrak{G}</math> with respect to <math>~R</math> is,
|
<math>~\frac{\partial \mathfrak{G}}{\partial R}</math> |
<math>~=</math> |
<math>~ \frac{1}{R} \biggl[ 3\mathcal{A} GM^2 R^{-1} - 3\mathcal{B}KM^{(n+1)/n} R^{-3/n} + 4\pi P_e R^3 \biggr] \, ; </math> |
and the second (partial) derivative is,
|
<math>~\frac{\partial^2 \mathfrak{G}}{\partial R^2}</math> |
<math>~=</math> |
<math>~ \frac{1}{R^2} \biggl[ -6\mathcal{A} GM^2 R^{-1} + \biggl(\frac{n+3}{n}\biggr) 3\mathcal{B}KM^{(n+1)/n} R^{-3/n} + 8\pi P_e R^3 \biggr] \, . </math> |
The virial equilibrium radius is identified by setting the first derivative to zero. This means that,
|
<math>~3\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n}</math> |
<math>~=</math> |
<math>~ 3\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + 4\pi P_e R_\mathrm{eq}^3 \, . </math> |
This expression can be usefully rewritten in the following forms:
| Virial Equilibrium Condition | ||||
| Case 1: |
|
|||
| Case 2: |
|
|||
| Case 3: |
|
|||
Dynamical stability is determined by the sign of the second derivative expression evaluated at the equilibrium radius; setting the second derivative to zero identifies the transition from stable to unstable configurations. The criterion is,
|
<math>~0</math> |
<math>~=</math> |
<math>~\biggl[ -6n\mathcal{A} GM^2 R^{-1} + 3(n+3) \mathcal{B}KM^{(n+1)/n} R^{-3/n} + 8\pi nP_e R^3\biggr]_{R_\mathrm{eq}} </math> |
Case 1 Stability Criterion
Using the "Case 1" virial expression to define the equilibrium radius means that the stability criterion is,
|
<math>~0</math> |
<math>~=</math> |
<math>~ -6n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + 3(n+3)\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + 4\pi (n+3) P_e R_\mathrm{eq}^3 + 8\pi nP_e R_\mathrm{eq}^3 </math> |
|
|
<math>~=</math> |
<math>~ \mathcal{A} GM^2 R_\mathrm{eq}^{-1} [3(n+3)- 6n ] + 4\pi P_e R_\mathrm{eq}^3 [(n+3) + 2n] </math> |
|
<math>~\Rightarrow ~~~ 4\pi P_e R_\mathrm{eq}^3 [3(n+1) ] </math> |
<math>~=</math> |
<math>~ \mathcal{A} GM^2 R_\mathrm{eq}^{-1} [3(n-3)] </math> |
|
<math>~\Rightarrow ~~~ 4\pi P_e R_\mathrm{eq}^4 (n+1) </math> |
<math>~=</math> |
<math>~ \mathcal{A} GM^2 (n-3) </math> |
Case 2 Stability Criterion
Using the "Case 2" virial expression to define the equilibrium radius means that the stability criterion is,
|
<math>~0</math> |
<math>~=</math> |
<math>~ 8\pi nP_e R_\mathrm{eq}^3 - 6n\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} + 3(n+3) \mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} + 8\pi nP_e R_\mathrm{eq}^3
</math> |
|
|
<math>~=</math> |
<math>~ 16\pi nP_e R_\mathrm{eq}^3 - [3(n-3)]\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} </math> |
|
<math>~\Rightarrow~~~ 16\pi nP_e R_\mathrm{eq}^3 </math> |
<math>~=</math> |
<math>~ [3(n-3)]\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} </math> |
|
<math>~\Rightarrow~~~ 16\pi nP_e R_\mathrm{eq}^{3(n+1)/n} </math> |
<math>~=</math> |
<math>~ [3(n-3)]\mathcal{B}KM^{(n+1)/n} </math> |
Case 3 Stability Criterion
Using the "Case 3" virial expression to define the equilibrium radius means that the stability criterion is,
|
<math>~0</math> |
<math>~=</math> |
<math>~ -6n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + 3(n+3) \mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} + 6n\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} - 6n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} </math> |
|
|
<math>~=</math> |
<math>~ -12n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + [6n +3(n+3)] \mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} </math> |
|
<math>~\Rightarrow~~~ 9(n+1) \mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} </math> |
<math>~=</math> |
<math>~ 12n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} </math> |
|
<math>~\Rightarrow~~~ R_\mathrm{eq}^{n-3} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{4n\mathcal{A}}{3(n+1) \mathcal{B}} \biggr]^n \biggl(\frac{G}{K}\biggr)^n M^{n-1} </math> |
Case M
Now, in our discussion of "Case M" sequence analyses, the configuration's radius is normalized to,
|
<math>~R_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~[ G^n K^{-n} M^{n-1} ]^{1/(n-3)} \, .</math> |
Our "Case 3" stability criterion directly relates. We conclude that the transition from stability to dynamical instability occurs when,
|
<math>~ \biggl[\frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr]_\mathrm{crit}^{n-3} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{4n\mathcal{A}}{3(n+1) \mathcal{B}} \biggr]^n </math> |
|
<math>~\Rightarrow~~~ \biggl[\frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr]_\mathrm{crit}^{(n-3)/n} </math> |
<math>~=</math> |
<math>~ \frac{4n}{15(n+1) } \biggl(\frac{4\pi}{3}\biggr)^{1/n}\cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_A \tilde{\mathfrak{f}}_M^{(n-1)/n}} </math> |
Also in the "Case M" discussions, the external pressure is normalized to,
|
<math>~P_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~[ G^{-3(n+1)} K^{4n} M^{-2(n+1)} ]^{1/(n-3)} \, .</math> |
If we raise the "Case 1" stability criterion expression to the <math>~(n-3)</math> power, then divide it by the "Case 3" stability criterion expression raised to the fourth power, we find,
|
<math>~\Rightarrow ~~~ [P_e]_\mathrm{crit}^{n-3} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{\mathcal{A} GM^2 (n-3)}{4\pi (n+1)}\biggr]^{n-3}\biggl\{ \biggl[\frac{4n\mathcal{A}}{3(n+1) \mathcal{B}} \biggr]^n \biggl(\frac{G}{K}\biggr)^n M^{n-1} \biggr\}^{-4} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{\mathcal{A} (n-3)}{4\pi (n+1)}\biggr]^{n-3} G^{n-3} M^{2(n-3)} \biggl[\frac{3(n+1) \mathcal{B}}{4n\mathcal{A}} \biggr]^{4n} \biggl(\frac{K}{G}\biggr)^{4n} M^{4(1-n)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} K^{4n} M^{-2(n+1)} G^{-3(n+1)} </math> |
|
<math>~\Rightarrow ~~~ \biggl[\frac{P_e}{P_\mathrm{norm}} \biggr]_\mathrm{crit}^{n-3} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \biggl[ \frac{ 5\tilde{\mathfrak{f}}_M^2 }{ \tilde{\mathfrak{f}}_W } \biggr]^{3(n+1)} \biggl( \frac{3}{4\pi}\biggr)^4 \biggl[ \frac{ \tilde{\mathfrak{f}}_A }{ \tilde{\mathfrak{f}}_M^{(n+1)/n} } \biggr]^{4n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{3}{4\pi}\biggr)^4 \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \biggl[ \frac{ 5 }{ \tilde{\mathfrak{f}}_W } \biggr]^{3(n+1)} \tilde{\mathfrak{f}}_M^{2(n+1)} \tilde{\mathfrak{f}}_A^{4n} </math> |
Case P
Flipping around this expression for <math>~[P_e]_\mathrm{crit}</math>, we also can write,
|
<math>~ [M]_\mathrm{crit}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} K^{4n} G^{-3(n+1)} P_e^{3-n} \, . </math> |
Now, in our "Case P" discussions we normalized the mass to
|
<math>~M_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~ \biggl(\frac{n+1}{n}\biggr)^{3/2} G^{-3/2} K^{2n/(n+1)} P_e^{(3-n)/[2(n+1)]} \, . </math> |
Hence, we have,
|
<math>~\biggl[\frac{M}{M_\mathrm{SWS}} \biggr]_\mathrm{crit}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} \biggl(\frac{n+1}{n}\biggr)^{-3(n+1)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl(\frac{3 }{4} \biggr)^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} \, , </math> |
where the constants,
|
<math>~\mathcal{A} \equiv \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}</math> |
and |
<math>\mathcal{B} \equiv \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, .</math> |
So we can furthermore conclude that,
|
<math>~\biggl[\frac{M}{M_\mathrm{SWS}} \biggr]_\mathrm{crit}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl(\frac{3 }{4} \biggr)^{4n} \biggl\{ \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr\}^{-3(n+1)} \biggl\{ \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggr\}^{4n} </math> |
|
|
<math>~=</math> |
<math>~\biggl(\frac{3}{4\pi} \biggr)^{4} \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl(\frac{3\tilde{\mathfrak{f}}_A }{4} \biggr)^{4n} \biggl[ \frac{5^3\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W^3} \biggr]^{(n+1)} \, . </math> |
Our expression for <math>~[M]_\mathrm{crit}^{2(n+1)}</math> can also be combined with the "Case 2 stability criterion" to eliminate the mass entirely, giving,
|
<math>~ \biggl\{ 16\pi nP_e R_\mathrm{eq}^{3(n+1)/n} \biggr\}^{2n} </math> |
<math>~=</math> |
<math>~ \biggl\{ [3(n-3)]\mathcal{B}K\biggr\}^{2n} \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} K^{4n} G^{-3(n+1)} P_e^{3-n} </math> |
|
<math>~\Rightarrow~~~ R_\mathrm{eq}^{6(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ 3(n-3)}{16\pi n} \biggr]^{2n} \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{6n} K^{6n} G^{-3(n+1)} P_e^{3(1-n)} </math> |
|
<math>~\Rightarrow~~~ R_\mathrm{eq}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl\{ \biggl[ \frac{ (n-3)}{4\pi n} \biggr]^{2n} \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl[\frac{(n+1) }{n} \biggr]^{4n+(3-n)} \biggl(\frac{3 }{4} \biggr)^{6n} \biggr\}^{1/3} \mathcal{A}^{-(n+1)} \mathcal{B}^{2n} K^{2n} G^{-(n+1)} P_e^{(1-n)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{ (n-3)}{4\pi n} \biggr]^{(n-1)} \biggl[\frac{(n+1) }{n} \biggr]^{(n+1)} \biggl(\frac{3 }{4} \biggr)^{2n} \mathcal{A}^{-(n+1)} \mathcal{B}^{2n} K^{2n} G^{-(n+1)} P_e^{(1-n)} \, . </math> |
Finally, recognizing that in our "Case P" discussions we normalized the radius to
|
<math>~R_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~ \biggl(\frac{n+1}{n}\biggr)^{1/2} G^{-1/2} K^{n/(n+1)} P_e^{(1-n)/[2(n+1)]} \, , </math> |
we have,
|
<math>~ [R_\mathrm{eq}]_\mathrm{crit}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ (n-3)}{4\pi n} \biggr]^{(n-1)} \biggl(\frac{n+1 }{n} \biggr)^{(n+1)} \biggl(\frac{3 }{4} \biggr)^{2n} \mathcal{A}^{-(n+1)} \mathcal{B}^{2n} \biggl\{ R_\mathrm{SWS}\biggl(\frac{n+1 }{n} \biggr)^{-1/2} \biggr\}^{2(n+1)} </math> |
|
<math>~\Rightarrow~~~ \biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]_\mathrm{crit}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ (n-3)}{4\pi n} \biggr]^{(n-1)} \biggl(\frac{3 }{4} \biggr)^{2n} \mathcal{A}^{-(n+1)} \mathcal{B}^{2n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{n}{n-3} \biggr]^{(1-n)} (4\pi)^{1-n}\biggl(\frac{3 }{4} \biggr)^{2n} \biggl[ \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr]^{-(n+1)} \biggl[ \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggr]^{2n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{n}{n-3} \biggr]^{(1-n)} (4\pi)^{1-n -2} 3^{2n+2} 4^{-2n} \biggl[ \frac{5\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W}\biggr]^{(n+1)} \biggl[ \frac{\tilde{\mathfrak{f}}_A^{2n}}{\tilde{\mathfrak{f}}_M^{2(n+1)}} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{n}{n-3} \biggr]^{(1-n)} \biggl[ \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W}\biggr]^{(n+1)} \biggl[\frac{ \tilde{\mathfrak{f}}_A}{4} \biggr]^{2n} \, . </math> |
Case M Free-Energy Surface
It is useful to rewrite the free-energy function in terms of dimensionless parameters. Here we need to pick normalizations for energy, radius, and pressure that are expressed in terms of the gravitational constant, <math>~G</math>, and the two fixed parameters, <math>~K</math> and <math>~M</math>. We have chosen to use,
|
<math>~R_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} \biggr]^{1/(n-3)} \, ,</math> |
|
<math>~P_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}} \biggr]^{1/(n-3)} \, ,</math> |
which, as is detailed in an accompanying discussion, are similar but not identical to the normalizations used by Horedt (1970) and by Whitworth (1981). The self-consistent energy normalization is,
|
<math>~E_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~P_\mathrm{norm} R^3_\mathrm{norm} \, .</math> |
As we have demonstrated elsewhere, after implementing these normalizations, the expression that describes the "Case M" free-energy surface is,
<math> \mathfrak{G}_{K,M}^* \equiv \frac{\mathfrak{G}_{K,M}}{E_\mathrm{norm}} = -3\mathcal{A} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^{-1} +~ n\mathcal{B} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^{-3/n} +~ \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^3 \, , </math>
Given the polytropic index, <math>~n</math>, we expect to obtain a different "Case M" free-energy surface for each choice of the dimensionless truncation radius, <math>~\tilde\xi</math>; this choice will imply corresponding values for <math>~\tilde\theta</math> and <math>~\tilde\theta^'</math> and, hence also, corresponding (constant) values of the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>.
Case P Free-Energy Surface
Again, it is useful to rewrite the free-energy function in terms of dimensionless parameters. But here we need to pick normalizations for energy, radius, and mass that are expressed in terms of the gravitational constant, <math>~G</math>, and the two fixed parameters, <math>~K</math> and <math>~P_e</math>. As is detailed in an accompanying discussion, we have chosen to use the normalizations defined by Stahler (1983), namely,
|
<math>~R_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{n+1}{nG} \biggr)^{1/2} K^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \, ,</math> |
|
<math>~M_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{n+1}{nG} \biggr)^{3/2} K^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \, .</math> |
The self-consistent energy normalization is,
|
<math>~E_\mathrm{SWS} \equiv \biggl( \frac{n}{n+1} \biggr) \frac{GM_\mathrm{SWS}^2}{R_\mathrm{SWS}}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2}K^{3n/(n+1)} P_\mathrm{e}^{(5-n)/[2(n+1)]} \, .</math> |
After implementing these normalizations — see our accompanying analysis for details — the expression that describes the "Case P" free-energy surface is,
|
<math>~\mathfrak{G}_{K,P_e}^* \equiv \frac{\mathfrak{G}_{K,P_e}}{E_\mathrm{SWS}}</math> |
<math>~=</math> |
<math>~- 3 \mathcal{A} \biggl( \frac{n+1}{n} \biggr)\biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} + n\mathcal{B} \biggl(\frac{M}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} + \frac{4\pi}{3} \cdot \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^3 \, . </math> |
Given the polytropic index, <math>~n</math>, we expect to obtain a different "Case P" free-energy surface for each choice of the dimensionless truncation radius, <math>~\tilde\xi</math>; this choice will imply corresponding values for <math>~\tilde\theta</math> and <math>~\tilde\theta^'</math> and, hence also, corresponding (constant) values of the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>.
Summary
| DFB Equilibrium | Onset of Dynamical Instability | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Case M: |
|
|
||||||||
|
|
|||||||||
| Case P: |
|
|
||||||||
|
|
|||||||||
|
In all four cases, the expression on right intersects (is equal to) the expression on the left when the following condition applies:
|
||||||||||
If (for <math>n\ne 5</math>) we adopt the shorthand notation,
|
<math>~\Upsilon</math> |
<math>~\equiv</math> |
<math>~[3 (-{\tilde\theta}^')^2 - {\tilde\mathfrak{f}}_M \tilde\theta] = 3\biggl[ (-{\tilde\theta}^')^2 - \biggl( -\frac{\tilde\theta {\tilde\theta}^'}{\tilde\xi} \biggr)\biggr] \, , </math> |
|
and |
||
|
<math>~\tau</math> |
<math>~\equiv</math> |
<math>~{\tilde\theta}^{n+1} \, , </math> |
then the critical condition becomes,
|
<math>~(n-3)\Upsilon</math> |
<math>~=</math> |
<math>~2(9-2n)\tau \, ,</math> |
and at the critical state, the expressions for the structural form-factors become,
|
<math>~{\tilde\mathfrak{f}}_A</math> |
<math>~=</math> |
<math>~\frac{1}{(5-n)} \biggl[6\tau + (n+1)\Upsilon \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{(5-n)} \biggl\{ 6 + (n+1)\biggl[ \frac{2(9-2n)}{n-3} \biggr] \biggr\}\tau </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{(5-n)} \biggl[ \frac{6(n-3) + 2(9-2n)(n+1)}{n-3} \biggr] \tau </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{(5-n)} \biggl[ \frac{4n(5-n)}{n-3} \biggr] \tau </math> |
|
|
<math>~=</math> |
<math>~\frac{4n\tau}{(n-3)} \, ;</math> |
|
<math>~{\tilde\mathfrak{f}}_W</math> |
<math>~=</math> |
<math>~\frac{3\cdot 5}{(5-n) {\tilde\xi}^2} \biggl[\tau + \Upsilon \biggr]</math> |
|
|
<math>~=</math> |
<math>~\frac{3\cdot 5}{(5-n) {\tilde\xi}^2} \biggl\{1 + \biggl[ \frac{2(9-2n)}{n-3} \biggr] \biggr\}\tau</math> |
|
|
<math>~=</math> |
<math>~\frac{3\cdot 5}{(5-n) {\tilde\xi}^2} \biggl[ \frac{3(5-n)}{n-3} \biggr] \tau</math> |
|
|
<math>~=</math> |
<math>~\frac{3^2\cdot 5 \tau}{(n-3) {\tilde\xi}^2} </math> |
|
<math>~\Rightarrow~~~ \frac{5^3\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W^3} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{(n-3) {\tilde\xi}^2}{3^2\tau} \biggr]^{3} \biggl(-\frac{3 {\tilde\theta}^'}{\tilde\xi} \biggr)^2 = 3^2\biggl[\frac{(n-3) {\tilde\xi}^2}{3^2\tau} \biggr]^{3} \biggl(-\frac{{\tilde\xi}^2 {\tilde\theta}^'}{ {\tilde\xi}^3 } \biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(n-3)^3}{3^4\tau^3} \biggr] (-{\tilde\xi}^2 {\tilde\theta}^' )^2 \, . </math> |
Hence (1),
|
<math>~\biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr]_\mathrm{crit}^{n-3}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{4\pi}{(n+1)^n }\biggr] \biggl[ \frac{4n}{15}\biggr]^n \biggl(\frac{1}{3}\biggr) \biggl[ \frac{3^2\cdot 5 }{4n {\tilde\xi}^2} \biggr]^n \tilde{\mathfrak{f}}_M^{1-n} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{4\pi}{(n+1)^n }\biggr] \biggl[ \frac{1}{ {\tilde\xi}^{2n}} \biggr] \biggl( \frac{-{\tilde\xi}^2{\tilde\theta}^'}{{\tilde\xi}^3} \biggr)^{1-n} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{4\pi}{(n+1)^n }\biggr] {\tilde\xi}^{n-3} (-{\tilde\xi}^2{\tilde\theta}^')^{1-n} </math> |
Q.E.D.
And (2),
|
<math>~\biggl[ \frac{P_\mathrm{e}}{P_\mathrm{norm}}\biggr]_\mathrm{crit}^{n-3}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{3}{4\pi}\biggr)^4 \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl(\frac{n+1}{n} \biggr)^{3(n+1)} \biggl[ \frac{ 5^3 \tilde{\mathfrak{f}}_M^2}{ \tilde{\mathfrak{f}}_W^3 } \biggr]^{n+1} \biggl( \frac{3\tilde{\mathfrak{f}}_A}{4}\biggr)^{4n} </math> |
|
|
<math>~=</math> |
<math>~3^{4} (4\pi)^{-(n+1)} \biggl(\frac{ n-3}{n}\biggr)^{n-3} \biggl(\frac{n+1}{n} \biggr)^{3(n+1)} \biggl[ \frac{(n-3)^3}{3^4\tau^3} \biggr]^{n+1} (-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} \biggl[ \frac{3n\tau}{n-3} \biggr]^{4n} </math> |
|
|
<math>~=</math> |
<math>~3^{4} (4\pi)^{-(n+1)} \biggl(\frac{ n-3}{n}\biggr)^{n-3} \biggl(\frac{n+1}{n} \biggr)^{3(n+1)} n^{3(n+1)} \biggl[ \frac{n-3}{n} \biggr]^{3(n+1)} (-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} \biggl[ \frac{n}{n-3} \biggr]^{4n} \tau^{4n-3(n+1)} 3^{4n-4(n+1)} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{n+1} (-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} \tau^{n-3} </math> |
|
<math>~\Rightarrow ~~~\biggl[ \frac{P_\mathrm{e}}{P_\mathrm{norm}}\biggr]_\mathrm{crit}^{n-3}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{n+1} (-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} {\tilde\theta}^{(n+1)(n-3)} \, . </math> |
Q.E.D.
And (3),
|
<math>~\biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]^{2(n+1)}_\mathrm{crit}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W}\biggr]^{n+1} \biggl[ \frac{n-3}{n} \biggr]^{(n-1) } \biggl[\frac{ \tilde{\mathfrak{f}}_A}{4} \biggr]^{2n } </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{3^2\cdot 5}{4\pi }\biggr]^{n+1} \biggl[ \frac{n-3}{n} \biggr]^{(n-1) } \biggl[ \frac{ n\tau}{n-3} \biggr]^{2n } \biggl[ \frac{(n-3){\tilde\xi}^2}{3^2\cdot 5 \tau} \biggr]^{n+1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{1}{4\pi }\biggr]^{n+1} \biggl[ \frac{ n}{n-3} \biggr]^{n+1 } \biggl[ (n-3){\tilde\xi}^2\biggr]^{n+1} \tau^{n-1} </math> |
|
<math>~\Rightarrow ~~~ \biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]^{2}_\mathrm{crit}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{n}{4\pi }\biggr) {\tilde\xi}^2 {\tilde\theta}^{n-1} </math> |
Q.E.D.
And (4),
|
<math>~\biggl[ \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr]_\mathrm{crit}^{2(n+1)}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{5^3\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W^3} \biggr]^{n+1} \biggl(\frac{3}{4\pi} \biggr)^{4} \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{(n-3)} \biggl(\frac{3\tilde{\mathfrak{f}}_A }{4} \biggr)^{4n} </math> |
|
|
<math>~=</math> |
<math>~\biggl\{ \biggl[ \frac{(n-3)^3}{3^4\tau^3} \biggr] (-{\tilde\xi}^2 {\tilde\theta}^' )^2 \biggr\}^{n+1} 3^4(4\pi)^{-(n+1)} \biggl(\frac{ n-3}{n}\biggr)^{(n-3)} \biggl[\frac{3n\tau }{n-3} \biggr]^{4n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{n^3}{4\pi}\biggr]^{n+1}(-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} \tau^{n-3} </math> |
|
<math>~\Rightarrow~~~ \biggl[ \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr]_\mathrm{crit}^{2} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{n^3}{4\pi}\biggr](-{\tilde\xi}^2 {\tilde\theta}^' )^{2} {\tilde\theta}^{n-3} </math> |
Q.E.D.
Free-Energy of Bipolytropes
In this case, the Gibbs-like free energy is given by the sum of four separate energies,
|
<math>~\mathfrak{G}</math> |
<math>~=</math> |
<math>~ \biggl[W_\mathrm{grav} + \mathfrak{S}_\mathrm{therm}\biggr]_\mathrm{core} + \biggl[W_\mathrm{grav} + \mathfrak{S}_\mathrm{therm}\biggr]_\mathrm{env} \, . </math> |
In addition to specifying (generally) separate polytropic indexes for the core, <math>~n_c</math>, and envelope, <math>~n_e</math>, and an envelope-to-core mean molecular weight ratio, <math>~\mu_e/\mu_c</math>, we will assume that the system is fully defined via specification of the following five physical parameters:
- Total mass, <math>~M_\mathrm{tot}</math>;
- Total radius, <math>~R</math>;
- Interface radius, <math>~R_i</math>, and associated dimensionless interface marker, <math>~q \equiv R_i/R</math>;
- Core mass, <math>~M_c</math>, and associated dimensionless mass fraction, <math>~\nu \equiv M_c/M_\mathrm{tot}</math>;
- Polytropic constant in the core, <math>~K_c</math>.
In general, the warped free-energy surface drapes across a five-dimensional parameter "plane" such that,
|
<math>~\mathfrak{G}</math> |
<math>~=</math> |
<math>~\mathfrak{G}(R, K_c, M_\mathrm{tot}, q, \nu) \, .</math> |
Order of Magnitude Derivation
Let's begin by providing very rough, approximate expressions for each of these four terms, assuming that <math>~n_c = 5</math> and <math>~n_e = 1</math>.
|
<math>~W_\mathrm{grav}\biggr|_\mathrm{core}</math> |
<math>~\approx</math> |
<math>~- \mathfrak{a}_c \biggl[ \frac{GM_\mathrm{tot} M_c}{(R_i/2)} \biggr] = - 2\mathfrak{a}_c \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggl(\frac{\nu}{q}\biggr) \biggr] \, ;</math> |
|
<math>~W_\mathrm{grav}\biggr|_\mathrm{env}</math> |
<math>~\approx</math> |
<math>~- \mathfrak{a}_e \biggl[ \frac{GM_\mathrm{tot} M_e}{(R_i+R)/2} \biggr] = - 2\mathfrak{a}_e \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] \, ;</math> |
|
<math>~\mathfrak{S}_\mathrm{therm}\biggr|_\mathrm{core} = U_\mathrm{int}\biggr|_\mathrm{core} </math> |
<math>~\approx</math> |
<math>~\mathfrak{b}_c \cdot n_cK_c M_c ({\bar\rho}_c)^{1/n_c} = 5\mathfrak{b}_c \cdot K_c M_\mathrm{tot}\nu \biggl[ \frac{3M_c}{4\pi R_i^3} \biggr]^{1/5} </math> |
|
|
<math>~=</math> |
<math>~\mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} K_c (M_\mathrm{tot}\nu)^{6/5} (Rq)^{-3/5} \, ;</math> |
|
<math>~\mathfrak{S}_\mathrm{therm}\biggr|_\mathrm{env} = U_\mathrm{int}\biggr|_\mathrm{env} </math> |
<math>~\approx</math> |
<math>~\mathfrak{b}_e \cdot n_eK_e M_\mathrm{env} ({\bar\rho}_e)^{1/n_e} = \mathfrak{b}_e \cdot K_e M_\mathrm{tot}(1-\nu) \biggl[ \frac{3M_\mathrm{env}}{4\pi (R^3-R_i^3)} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr) K_e [M_\mathrm{tot}(1-\nu)]^2 [R^3(1-q^3)]^{-1} \, . </math> |
In writing this last expression, it has been necessary to (temporarily) introduce a sixth physical parameter, namely, the polytropic constant that characterizes the envelope material, <math>~K_e</math>. But this constant can be expressed in terms of <math>~K_c</math> via a relation that ensures continuity of pressure across the interface while taking into account the drop in mean molecular weight across the interface, that is,
|
<math>~K_e ({\bar\rho}_e)^{(n_e+1)/n_e}</math> |
<math>~\approx</math> |
<math>~K_c ({\bar\rho}_c)^{(n_c+1)/n_c}</math> |
|
<math>~\Rightarrow ~~~~ K_e \biggl[\biggl( \frac{\mu_e}{\mu_c} \biggr) {\bar\rho}_c\biggr]^{2}</math> |
<math>~\approx</math> |
<math>~K_c ({\bar\rho}_c)^{6/5}</math> |
|
<math>~\Rightarrow ~~~~ \frac{K_e}{K_c} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{2}</math> |
<math>~\approx</math> |
<math>~\biggl[ \frac{3M_\mathrm{tot}\nu}{4\pi (Rq)^3} \biggr]^{-4/5} \, .</math> |
Hence, the fourth energy term may be rewritten in the form,
|
<math>~\mathfrak{S}_\mathrm{therm}\biggr|_\mathrm{env} = U_\mathrm{int}\biggr|_\mathrm{env} </math> |
<math>~\approx</math> |
<math>~ \mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr) \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} K_c\biggl[ \frac{3M_\mathrm{tot}\nu}{4\pi (Rq)^3} \biggr]^{-4/5} [M_\mathrm{tot}(1-\nu)]^2 [R^3(1-q^3)]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr)^{1/5} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} K_c M_\mathrm{tot}^{6/5}R^{-3/5}\biggl[ \frac{q^3}{\nu} \biggr]^{4/5} \frac{(1-\nu)^2}{(1-q^3)} \, . </math> |
Putting all the terms together gives,
|
<math>~\mathfrak{G}</math> |
<math>~\approx</math> |
<math>~ - 2\mathfrak{a}_c \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggl(\frac{\nu}{q}\biggr) \biggr] - 2\mathfrak{a}_e \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] + \mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} K_c (M_\mathrm{tot}\nu)^{6/5} (Rq)^{-3/5} </math> |
|
|
|
<math>~ + \mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr)^{1/5} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} K_c M_\mathrm{tot}^{6/5}R^{-3/5}\biggl[ \frac{q^3}{\nu} \biggr]^{4/5} \frac{(1-\nu)^2}{(1-q^3)} </math> |
|
|
<math>~=</math> |
<math>~ - 2 \mathcal{A}_\mathrm{biP} \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggr] + \mathcal{B}_\mathrm{biP} K_c \biggl[\frac{(\nu M_\mathrm{tot})^{2}}{ qR} \biggr]^{3/5} </math> |
|
<math>~\Rightarrow ~~~~ \frac{\mathfrak{G}}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~ - 2 \mathcal{A}_\mathrm{biP} \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggr] \biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} + \mathcal{B}_\mathrm{biP} \biggl(\frac{\nu^2}{q}\biggr)^{3/5} K_c \biggl[\frac{M_\mathrm{tot}^{2}}{ R} \biggr]^{3/5}\biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} </math> |
|
|
<math>~=</math> |
<math>~ - 2 \mathcal{A}_\mathrm{biP} \biggl[ \frac{R_\mathrm{norm}}{R} \biggr] + \mathcal{B}_\mathrm{biP} \biggl(\frac{\nu^2}{q}\biggr)^{3/5} \biggl[\frac{R_\mathrm{norm}}{ R} \biggr]^{3/5} \, , </math> |
where,
|
<math>~\mathcal{A}_\mathrm{biP}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \mathfrak{a}_c\biggl(\frac{\nu}{q}\biggr) + \mathfrak{a}_e \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] \, ,</math> |
|
<math>~\mathcal{B}_\mathrm{biP}</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{3}{2^2\pi} \biggr)^{1/5} \biggl[5\mathfrak{b}_c + \mathfrak{b}_e \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \frac{q^3(1-\nu)^2}{\nu^2(1-q^3)} \biggr] \, .</math> |
Equilibrium Radius
Order of Magnitude Estimate
This means that,
|
<math>~\frac{\partial\mathfrak{G}}{\partial R}</math> |
<math>~=</math> |
<math>~ + 2 \mathcal{A}_\mathrm{biP}\biggl[ \frac{GM_\mathrm{tot}^2 }{R^2} \biggr] - \frac{3}{5} \mathcal{B}_\mathrm{biP} K_c \biggl[\frac{\nu^{2}}{ q} \biggr]^{3/5} M_\mathrm{tot}^{6/5} R^{-8/5} \, . </math> |
Hence, because equilibrium radii are identified by setting <math>~\partial\mathfrak{G}/\partial R = 0</math>, we have,
|
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl(\frac{2\cdot 5}{3}\biggr)^{5/2} \biggl[\frac{\mathcal{A}_\mathrm{biP} }{\mathcal{B}_\mathrm{biP}}\biggr]^{5/2} \biggl(\frac{ q} {\nu^{2}}\biggr)^{3/2} \, . </math> |
Reconcile With Known Analytic Expression
From our earlier derivations, it appears as though,
|
<math>~\chi_\mathrm{eq} \equiv \frac{R_\mathrm{eq}}{R_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl( \frac{3^8}{2^5\pi} \biggr)^{-1/2} \biggl(\frac{3}{2^4}\biggr) \biggl( \frac{q}{\ell_i}\biggr)^{5}\biggl(\frac{\nu}{q^3} \biggr)^2 \biggl( 1 + \ell_i^2 \biggr)^{3} </math> |
|
|
<math>~=</math> |
<math>~\biggl(\frac{2\cdot 5}{3}\biggr)^{5/2} \biggl(\frac{q}{\nu^2} \biggr)^{3/2} \biggl[\biggl( \frac{\pi}{2^8 \cdot 3 \cdot 5^5} \biggr)^{1/2} \biggl(\frac{\nu^2}{q} \biggr)^{5/2} \frac{(1 + \ell_i^2)^3}{\ell_i^5} \biggr] \, . </math> |
This implies that,
|
<math>~\frac{\mathcal{A}_\mathrm{biP} }{\mathcal{B}_\mathrm{biP}}</math> |
<math>~\approx</math> |
<math>~ \biggl[\biggl( \frac{\pi}{2^8 \cdot 3 \cdot 5^5} \biggr)^{1/2} \biggl(\frac{\nu^2}{q} \biggr)^{5/2} \frac{(1 + \ell_i^2)^3}{\ell_i^5} \biggr]^{2/5} </math> |
|
|
<math>~=</math> |
<math>~\biggl(\frac{\nu^2}{q} \biggr) \biggl( \frac{\pi}{2^8 \cdot 3 \cdot 5^5} \biggr)^{1/5} \frac{(1 + \ell_i^2)^{6/5}}{\ell_i^2} </math> |
|
<math>~\Rightarrow ~~~~ \biggl[ \mathfrak{a}_c\biggl(\frac{\nu}{q}\biggr) + \mathfrak{a}_e \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] </math> |
<math>~\approx</math> |
<math>~\frac{1}{2^2\cdot 5}\biggl(\frac{\nu^2}{q} \biggr) \frac{(1 + \ell_i^2)^{6/5}}{\ell_i^2} \biggl[5\mathfrak{b}_c + \mathfrak{b}_e \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \frac{q^3(1-\nu)^2}{\nu^2(1-q^3)} \biggr] </math> |
|
<math>~\Rightarrow ~~~~ \biggl[ \mathfrak{a}_c + \mathfrak{a}_e \cdot \frac{q(1-\nu)}{\nu(1+q)} \biggr] </math> |
<math>~\approx</math> |
<math>~\frac{\nu}{2^2\cdot 5} \frac{(1 + \ell_i^2)^{6/5}}{\ell_i^2} \biggl[5\mathfrak{b}_c + \mathfrak{b}_e \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \frac{q^3(1-\nu)^2}{\nu^2(1-q^3)} \biggr] </math> |
Focus on Five-One Free-Energy Expression
Approximate Expressions
Let's plug this equilibrium radius back into each term of the free-energy expression.
|
<math>~\frac{W_\mathrm{grav}}{E_\mathrm{norm}}\biggr|_\mathrm{core}</math> |
<math>~\approx</math> |
<math>~- 2\mathfrak{a}_c \biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} \biggl[ \frac{GM_\mathrm{tot}^2 }{R_\mathrm{eq}} \biggl(\frac{\nu}{q}\biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~- 2\mathfrak{a}_c \biggl(\frac{\nu}{q}\biggr) \biggl[ \frac{R_\mathrm{norm} }{R_\mathrm{eq}} \biggr] \, ;</math> |
|
<math>~\frac{W_\mathrm{grav}}{E_\mathrm{norm}}\biggr|_\mathrm{env}</math> |
<math>~\approx</math> |
<math>~- 2\mathfrak{a}_e \biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} \biggl[ \frac{GM_\mathrm{tot}^2 }{R_\mathrm{eq}} \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~- 2\mathfrak{a}_e \biggl(\frac{1-\nu}{1+q}\biggr) \biggl[ \frac{R_\mathrm{norm} }{R_\mathrm{eq}} \biggr] \, ;</math> |
|
<math>~\frac{S_\mathrm{core}}{E_\mathrm{norm}} = \biggl[\frac{3(\gamma_c-1)}{2}\biggr] \frac{U_\mathrm{int}}{E_\mathrm{norm}}\biggr|_\mathrm{core} </math> |
<math>~\approx</math> |
<math>~\biggl[\frac{3}{2\cdot 5}\biggr]\mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} \biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} K_c (M_\mathrm{tot}\nu)^{6/5} (R_\mathrm{eq}q)^{-3/5} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{3}{2\cdot 5}\biggr]\mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} \biggl(\frac{\nu^2}{q}\biggr)^{3/5} \biggl(\frac{R_\mathrm{norm}}{R_\mathrm{eq}}\biggr)^{3/5} \, ;</math> |
|
<math>~\frac{S_\mathrm{env}}{E_\mathrm{norm}} = \biggl[\frac{3(\gamma_e-1)}{2}\biggr] \frac{U_\mathrm{int}}{E_\mathrm{norm}}\biggr|_\mathrm{env} </math> |
<math>~\approx</math> |
<math>~\biggl[\frac{3}{2}\biggr] \mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr)^{1/5} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} K_c M_\mathrm{tot}^{6/5}R_\mathrm{eq}^{-3/5}\biggl[ \frac{q^3}{\nu} \biggr]^{4/5} \frac{(1-\nu)^2}{(1-q^3)} </math> |
|
|
<math>~=</math> |
<math>~\biggl[\frac{3}{2}\biggr] \mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr)^{1/5} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \biggl[ \frac{q^3}{\nu} \biggr]^{4/5} \frac{(1-\nu)^2}{(1-q^3)} \biggl(\frac{R_\mathrm{norm}}{R_\mathrm{eq}}\biggr)^{3/5} \, . </math> |
From Detailed Force-Balance Models
In the following derivations, we will use the expression,
|
<math>~\chi_\mathrm{eq} \equiv \frac{ R_\mathrm{eq}}{R_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl( \frac{\mu_e}{\mu_c} \biggr)^3 \biggl( \frac{\pi}{2^3} \biggr)^{1/2} \frac{1}{A^2\eta_s} = \biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} \, .</math> |
Keep in mind, as well — as derived in an accompanying discussion — that,
|
<math>~\nu \equiv \frac{M_\mathrm{core}}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~ (m_3^2 \ell_i^3) (1 + \ell_i^2)^{-1/2} [1 + (1-m_3)^2 \ell_i^2]^{-1/2} \biggl[ m_3\ell_i + (1+\ell_i^2) \biggl(\frac{\pi}{2} + \tan^{-1} \Lambda_i \biggr) \biggr]^{-1} \, ,</math> |
where,
<math>m_3 \equiv 3 \biggl( \frac{\mu_e}{\mu_c} \biggr) \, .</math>
From the accompanying Table 1 parameter values, we also can write,
|
<math>~q</math> |
<math>~=</math> |
<math>~\frac{\eta_i}{\eta_s} = \eta_i \biggl\{\frac{\pi}{2} + \eta_i + \tan^{-1}\biggl[ \frac{1}{\eta_i} - \ell_i \biggr] \biggr\}^{-1}</math> |
|
|
<math>~=</math> |
<math>~ \eta_i \biggl\{\eta_i + \cot^{-1}\biggl[ \ell_i - \frac{1}{\eta_i} \biggr] \biggr\}^{-1} \, , </math> |
where,
|
<math>~\eta_i</math> |
<math>~=</math> |
<math>~m_3 \biggl[\frac{\ell_i }{(1+\ell_i^2)}\biggr] \, .</math> |
Let's also define the following shorthand notation:
|
<math>~\mathfrak{L}_i</math> |
<math>~\equiv</math> |
<math>~\frac{(\ell_i^4-1)}{\ell_i^2} + \frac{(1+\ell_i^2)^3}{\ell_i^3} \cdot \tan^{-1}\ell_i \, ;</math> |
|
<math>~\mathfrak{K}_i</math> |
<math>~\equiv</math> |
<math>~\frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] + \frac{\Lambda_i}{\eta_i} \, .</math> |
Gravitational Potential Energy of the Core
Pulling from our detailed derivations,
|
<math>~\biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ - \biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} \biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) (1 + \ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] \, .</math> |
|
<math>~\Rightarrow ~~~~ -\chi_\mathrm{eq} \biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ \biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} \biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) (1 + \ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] \biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} </math> |
|
|
<math>~=~</math> |
<math>~ \biggl( \frac{3}{2^4} \biggr) \frac{\nu^2}{q} \cdot \frac{1}{\ell_i^5} \biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) + (1 + \ell_i^2)^{3}\tan^{-1}(\ell_i) \biggr] </math> |
Out of equilibrium, then, we should expect,
|
<math>~\frac{W_\mathrm{core}}{E_\mathrm{norm}} </math> |
<math>~=~</math> |
<math>~ - \chi^{-1} \biggl( \frac{3}{2^4} \biggr) \frac{\nu^2}{q} \cdot \frac{1}{\ell_i^5} \biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) + (1 + \ell_i^2)^{3}\tan^{-1}(\ell_i) \biggr] </math> |
|
|
<math>~=~</math> |
<math>~ - \chi^{-1} \biggl( \frac{3}{2^4} \biggr) \frac{\nu^2}{q} \cdot \frac{1}{\ell_i^2} \biggl[ \mathfrak{L}_i - \frac{8}{3} \biggr] \, , </math> |
which, in comparison with our above approximate expression, implies,
|
<math>~\mathfrak{a}_c </math> |
<math>~=~</math> |
<math>~ \biggl( \frac{3}{2^5} \biggr) \frac{\nu}{\ell_i^5} \biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) + (1 + \ell_i^2)^{3}\tan^{-1}(\ell_i) \biggr] \, . </math> |
Thermal Energy of the Core
Again, pulling from our detailed derivations,
|
<math>~\biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ \frac{1}{2} \biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] </math> |
|
<math>~\Rightarrow ~~~~ \chi_\mathrm{eq}^{3} \biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]^5_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ \frac{1}{2^5} \biggl( \frac{3^8}{2^5\pi} \biggr)^{5/2} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr]^5 \biggl[\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5}\biggr]^{3} </math> |
|
|
<math>~=~</math> |
<math>~ \frac{1}{\pi}\biggl(\frac{3}{2^{2}}\biggr)^{11} \biggl(\frac{\nu^2}{q}\biggr)^{3} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr]^5 \biggl[\frac{(1+\ell_i^2)^9}{\ell_i^{15}}\biggr] \, . </math> |
Out of equilibrium, we should then expect,
|
<math>~\frac{S_\mathrm{core}}{E_\mathrm{norm}}</math> |
<math>~=~</math> |
<math>~ \biggl(\frac{3}{2^2\pi} \biggr)^{1/5}\biggl[ \chi^{-1} \biggl(\frac{\nu^2}{q}\biggr) \frac{1}{(1+\ell_i^2)^{2}} \biggr]^{3/5} \biggl(\frac{3}{2^{2}}\biggr)^{2}\mathfrak{L}_i \, . </math> |
In comparison with our above approximate expression, we therefore have,
|
<math>~ \biggl[ \biggl(\frac{3}{2\cdot 5}\biggr)\mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} \biggl(\frac{\nu^2}{q}\biggr)^{3/5} \biggr]^5</math> |
<math>~=~</math> |
<math>~ \frac{1}{\pi}\biggl(\frac{3}{2^{2}}\biggr)^{11} \biggl(\frac{\nu^2}{q}\biggr)^{3} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr]^5 \biggl[\frac{(1+\ell_i^2)^9}{\ell_i^{15}}\biggr] </math> |
|
<math>~\Rightarrow~~~~ \mathfrak{b}_c </math> |
<math>~=~</math> |
<math>~\frac{ 3 }{2^3\ell_i^{3}(1+\ell_i^2)^{6/5}} \biggl[ \ell_i (\ell_i^4 - 1 ) + (1+\ell_i^2)^{3}\tan^{-1}(\ell_i) \biggr] \, . </math> |
Gravitational Potential Energy of the Envelope
Again, pulling from our detailed derivations and appreciating, in particular, that (see, for example, our notes on equilibrium conditions),
|
<math>~A</math> |
<math>~=~</math> |
<math>~\frac{\eta_i}{\sin(\eta_i - B)} \, ,</math> |
|
<math>~(\eta_s - B)</math> |
<math>~=~</math> |
<math>~\pi \, ,</math> |
|
<math>~\eta_i - B</math> |
<math>~=~</math> |
<math>~\frac{\pi}{2} - \tan^{-1}(\Lambda_i)\, ,</math> |
|
<math>~\Rightarrow ~~~ \sin(\eta_i -B) = (1+\Lambda_i^2)^{-1/2}</math> |
and |
<math>~\sin[2(\eta_i-B)] = 2\Lambda_i(1 + \Lambda_i^2)^{-1} \ ,</math> |
we have,
|
<math>~\biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ -\biggl( \frac{1}{2^3\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} A^2 \biggl\{ \biggl[6(\eta_s-B) - 3\sin[2(\eta_s - B)] -4\eta_s\sin^2(\eta_s-B) + 4B\biggr] </math> |
|
|
|
<math>~ - \biggl[6(\eta_i-B) - 3\sin[2(\eta_i - B)] -4\eta_i\sin^2(\eta_i-B) + 4B \biggr]\biggr\} </math> |
|
|
<math>~=~</math> |
<math>~ -\biggl( \frac{1}{2^3\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \biggl[\frac{\eta_i}{\sin(\eta_i - B)} \biggr]^2 \biggl\{ 6\pi - \biggl[6(\eta_i-B) - 3\sin[2(\eta_i - B)] -4\eta_i\sin^2(\eta_i-B) \biggr]\biggr\} </math> |
|
|
<math>~=~</math> |
<math>~ -\biggl( \frac{1}{2^3\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2(1+\Lambda_i^2) \biggl\{ 6\pi - 6\biggl[\frac{\pi}{2} - \tan^{-1}(\Lambda_i)\biggr] + 6\biggl[ \frac{\Lambda_i}{(1 + \Lambda_i^2)} \biggr] + 4\eta_i \biggl[ \frac{1}{(1+\Lambda_i^2)} \biggr] \biggr\} </math> |
|
|
<math>~=~</math> |
<math>~ -\biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 \biggl\{ (1+\Lambda_i^2)\biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \Lambda_i + \frac{2}{3} \cdot \eta_i \biggr\} \, . </math> |
So, in equilibrium we can write,
|
<math>~-\chi_\mathrm{eq}\biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ \biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 \biggl\{ (1+\Lambda_i^2)\biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \Lambda_i + \frac{2}{3} \cdot \eta_i \biggr\} \biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} </math> |
|
|
<math>~=~</math> |
<math>~ \frac{3}{2^2} \biggl(\frac{\eta_i}{m_3}\biggr)^3 \biggl\{ \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \frac{\Lambda_i}{\eta_i} + \frac{2}{3} \biggr\} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{\ell_i^5} </math> |
|
|
<math>~=~</math> |
<math>~ \frac{3}{2^2} \biggl(\frac{\nu^2}{q} \biggr) \frac{1}{\ell_i^2} \biggl\{ \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \frac{\Lambda_i}{\eta_i} + \frac{2}{3} \biggr\} \, . </math> |
And out of equilibrium,
|
<math>~\frac{W_\mathrm{env}}{E_\mathrm{norm}}</math> |
<math>~=~</math> |
<math>~ -\chi^{-1}\cdot \frac{3}{2^2} \biggl(\frac{\nu^2}{q} \biggr) \frac{1}{\ell_i^2} \biggl[\mathfrak{K}_i+ \frac{2}{3} \biggr] \, . </math> |
This, in turn, implies that both in and out of equilibrium,
|
<math>~\mathfrak{a}_e </math> |
<math>~=~</math> |
<math>~ \frac{3}{2^3} \biggl[\frac{\nu^2(1+q)}{q(1-\nu)} \biggr] \frac{1}{\ell_i^2} \biggl\{ \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \frac{\Lambda_i}{\eta_i} + \frac{2}{3} \biggr\} \, . </math> |
Thermal Energy of the Envelope
Again, pulling from our detailed derivations,
|
<math>~\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ ~ \biggl( \frac{1}{2^5\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} A^2 \biggl\{ \biggl[6(\eta_s - B) - 3\sin[2(\eta_s-B)] \biggr] - \biggl[6(\eta_i - B) - 3\sin[2(\eta_i-B)] \biggr] \biggr\}</math> |
|
|
<math>~=~</math> |
<math>~ ~ \biggl( \frac{1}{2^5\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \biggl[\frac{\eta_i}{\sin(\eta_i - B)} \biggr]^2 \biggl\{ 6\pi - 6(\eta_i - B) + 3\sin[2(\eta_i-B)] \biggr\}</math> |
|
|
<math>~=~</math> |
<math>~ ~ \biggl( \frac{1}{2^5\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 (1 + \Lambda_i^2) \biggl\{ 6\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + 6\biggl[\Lambda_i(1 + \Lambda_i^2)^{-1} \biggr] \biggr\}</math> |
|
|
<math>~=~</math> |
<math>~ ~\frac{1}{2} \biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 \biggl\{ (1 + \Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \Lambda_i \biggr\} \, .</math> |
So, in equilibrium we can write,
|
<math>~\chi_\mathrm{eq}^{3}\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ ~\frac{1}{2} \biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 \biggl\{ (1 + \Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \Lambda_i \biggr\} \biggl[\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5}\biggr]^{3} </math> |
|
|
<math>~=~</math> |
<math>~ ~\biggl(\frac{\nu^2}{q} \biggr)^3 \biggl( \frac{3^2\pi^2}{2^{12}} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^3 \biggl\{ \frac{(1 + \Lambda_i^2)}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \frac{\Lambda_i}{\eta_i} \biggr\} \biggl[\frac{(1+\ell_i^2)^9}{3^9\ell_i^{15}}\biggr] </math> |
|
|
<math>~=~</math> |
<math>~ ~\biggl(\frac{\nu^2}{q} \biggr)^3 \biggl( \frac{\pi}{2^{6}\cdot 3^5} \biggr) \biggl[\frac{(1+\ell_i^2)^6}{\ell_i^{12}}\biggr] \biggl\{ \frac{(1 + \Lambda_i^2)}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \frac{\Lambda_i}{\eta_i} \biggr\} \, . </math> |
And, out of equilibrium,
|
<math>~\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ ~ \chi^{-3}\biggl(\frac{\nu^2}{q} \biggr)^3 \biggl( \frac{\pi}{2^{6}\cdot 3^5} \biggr) \biggl[\frac{(1+\ell_i^2)^6}{\ell_i^{12}}\biggr]\mathfrak{K} \, . </math> |
Combined in Equilibrium
Notice that, in combination,
|
<math>~\biggl[\frac{2S_\mathrm{env} + W_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=</math> |
<math>~ - \frac{2}{3}\biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^3 </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2}{3}\biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \biggl[3 \biggl( \frac{\mu_e}{\mu_c} \biggr) \ell_i \biggl( 1 + \ell_i^2 \biggr)^{-1}\biggr]^3 </math> |
|
|
<math>~=</math> |
<math>~ - \biggl( \frac{2\cdot 3^6}{\pi} \biggr)^{1/2} \biggl[\frac{\ell_i^3}{( 1 + \ell_i^2)^3}\biggr] \, . </math> |
Also, from above,
|
<math>~\biggl[ \frac{2S_\mathrm{core}+W_\mathrm{core}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ - \biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} \biggl[ \ell_i \biggl(- \frac{8}{3} \ell_i^2 \biggr) (1 + \ell_i^2)^{-3} \biggr] </math> |
|
|
<math>~=~</math> |
<math>~ + \biggl( \frac{2\cdot 3^6}{\pi } \biggr)^{1/2} \biggl[ \frac{\ell_i^3}{(1 + \ell_i^2)^{3}} \biggr] \, .</math> |
So, in equilibrium, these terms from the core and envelope sum to zero, as they should.
Out of Equilibrium
And now, in combination out of equilibrium,
|
<math>~\frac{\mathfrak{G}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~ \biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-1} \biggl\{ \biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} + \biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}\biggr\} +\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-3/5} \biggl(\frac{2n_c}{3}\biggr) \biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} +\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-3} \biggl(\frac{2n_e}{3}\biggr)\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} \, . </math> |
Hence, quite generally out of equilibrium,
|
<math>~\frac{\partial}{\partial \chi} \biggl[ \frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr] </math> |
<math>~=</math> |
<math>~ -\chi^{-1}\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-1} \biggl\{ \biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} + \biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}\biggr\} -\frac{3}{5}\chi^{-1}\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-3/5} \biggl(\frac{10}{3}\biggr) \biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} -3\chi^{-1}\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-3} \biggl(\frac{2}{3}\biggr)\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} \, . </math> |
Let's see what the value of this derivative is if the dimensionless radius, <math>~\chi</math>, is set to the value that has been determined, via a detailed force-balanced analysis, to be the equilibrium radius, namely, <math>~\chi = \chi_\mathrm{eq}</math>. In this case, we have,
|
<math>~\biggl\{\frac{\partial}{\partial \chi} \biggl[ \frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr] \biggr\}_\mathrm{\chi \rightarrow \chi_\mathrm{eq}}</math> |
<math>~=</math> |
<math>~ -\chi_\mathrm{eq}^{-1}\biggl\{ \biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} + \biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} +2\biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} +2\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} \biggr\} \, . </math> |
But, according to the virial theorem — and, as we have just demonstrated — the four terms inside the curly braces sum to zero. So this demonstrates that the derivative of our out-of-equilibrium free-energy expression does go to zero at the equilibrium radius, as it should!
Summary51
In summary, the desired out of equilibrium free-energy expression is,
|
<math>~\frac{\mathfrak{G}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~ \frac{W_\mathrm{core}}{E_\mathrm{norm}} + \frac{W_\mathrm{env}}{E_\mathrm{norm}} +\biggl(\frac{2n_c}{3}\biggr)\frac{S_\mathrm{core}}{E_\mathrm{norm}} +\biggl(\frac{2n_e}{3}\biggr)\frac{S_\mathrm{env}}{E_\mathrm{norm}} </math> |
|
|
<math>~=</math> |
<math>~ - \chi^{-1} \biggl( \frac{3}{2^4} \biggr) \frac{\nu^2}{q} \cdot \frac{1}{\ell_i^2} \biggl[ \mathfrak{L}_i - \frac{8}{3} \biggr] -\chi^{-1}\cdot \frac{3}{2^2} \biggl(\frac{\nu^2}{q} \biggr) \frac{1}{\ell_i^2} \biggl[\mathfrak{K}_i+ \frac{2}{3} \biggr] </math> |
|
|
|
<math>~ + \biggl(\frac{2\cdot 5}{3}\biggr) \biggl(\frac{3}{2^2\pi} \biggr)^{1/5}\biggl[ \chi^{-1} \biggl(\frac{\nu^2}{q}\biggr) \frac{1}{(1+\ell_i^2)^{2}} \biggr]^{3/5} \biggl(\frac{3}{2^{2}}\biggr)^{2}\mathfrak{L}_i +\biggl(\frac{2}{3}\biggr) \chi^{-3}\biggl(\frac{\nu^2}{q} \biggr)^3 \biggl( \frac{\pi}{2^{6}\cdot 3^5} \biggr) \biggl[\frac{(1+\ell_i^2)^6}{\ell_i^{12}}\biggr]\mathfrak{K} </math> |
|
|
<math>~=</math> |
<math>~ - \biggl( \frac{3}{2^4} \biggr) \biggl[\chi^{-1}\frac{\nu^2}{q} \cdot \frac{1}{\ell_i^2}\biggr] \biggl[ \mathfrak{L}_i + 4\mathfrak{K}_i \biggr] + \biggl(\frac{3}{2^2\pi} \biggr)^{1/5}\biggl(\frac{3\cdot 5}{2^3}\biggr) \biggl[ \chi^{-1} \biggl(\frac{\nu^2}{q}\biggr) \frac{1}{(1+\ell_i^2)^{2}} \biggr]^{3/5} \mathfrak{L}_i </math> |
|
|
|
<math>~ + \biggl( \frac{\pi}{2^{5}\cdot 3^6} \biggr) \biggl[\chi^{-1}\biggl(\frac{\nu^2}{q} \biggr) \frac{(1+\ell_i^2)^2}{\ell_i^{4}}\biggr]^3\mathfrak{K} \, . </math> |
Or, in terms of the ratio,
<math>\Chi \equiv \frac{\chi}{\chi_\mathrm{eq}} \, ,</math>
and pulling from the above expressions,
|
<math>~\biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ - \biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} \biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) (1 + \ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] </math> |
|
|
<math>~=~</math> |
<math>~ - \biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} \biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]^{3} \biggl[ \mathfrak{L}_i - \frac{8}{3}\biggr] </math> |
|
<math>~\biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ -\biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 \biggl\{ (1+\Lambda_i^2)\biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \Lambda_i + \frac{2}{3} \cdot \eta_i \biggr\} </math> |
|
|
<math>~=~</math> |
<math>~ -\biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]^{3} \biggl[4\mathfrak{K}_i + \frac{8}{3} \biggr] </math> |
|
<math>~\biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ \frac{1}{2} \biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] </math> |
|
|
<math>~=~</math> |
<math>~ \frac{1}{2} \biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]^{3}\mathfrak{L}_i </math> |
|
<math>~\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ ~\frac{1}{2} \biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 \biggl\{ (1 + \Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \Lambda_i \biggr\} </math> |
|
|
<math>~=~</math> |
<math>~ ~\frac{1}{2} \biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]^{3} (4\mathfrak{K}_i) \, , </math> |
we have the streamlined,
|
<math>~\biggl( \frac{2^5\pi}{3^6} \biggr)^{1/2} \biggl[ \frac{(1+\ell_i^2)}{\ell_i} \biggr]^{3} \biggl[\frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr]</math> |
<math>~=</math> |
<math>~ +\Chi^{-3/5} (5 \mathfrak{L}_i) +\Chi^{-3} (4\mathfrak{K}_i) -\Chi^{-1} (3\mathfrak{L}_i +12\mathfrak{K}_i ) </math> |
or, better yet,
|
Out-of-Equilibrium, Free-Energy Expression for BiPolytropes with <math>~(n_c, n_e) = (5, 1)</math> |
|||
|---|---|---|---|
|
where,
|
<math>~\mathfrak{L}_i</math> |
<math>~\equiv</math> |
<math>~\frac{(\ell_i^4-1)}{\ell_i^2} + \frac{(1+\ell_i^2)^3}{\ell_i^3} \cdot \tan^{-1}\ell_i \, ,</math> |
|
<math>~\mathfrak{K}_i</math> |
<math>~\equiv</math> |
<math>~\frac{\Lambda_i}{\eta_i} + \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \, ,</math> |
|
<math>~\Lambda_i</math> |
<math>~\equiv</math> |
<math>~\frac{1}{\eta_i} - \ell_i \, ,</math> |
|
<math>~\eta_i</math> |
<math>~=</math> |
<math>~3 \biggl( \frac{\mu_e}{\mu_c} \biggr) \biggl[\frac{\ell_i }{(1+\ell_i^2)}\biggr] \, .</math> |
From the accompanying Table 1 parameter values, we also can write,
|
<math>~\frac{1}{q}</math> |
<math>~=</math> |
<math>~\frac{\eta_s}{\eta_i} = 1 + \frac{1}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] \, ,</math> |
|
<math>~\nu</math> |
<math>~=</math> |
<math>~ \frac{\ell_i q}{(1+\Lambda_i^2)^{1/2}} \, . </math> |
| Radial Derivatives | ||||||
|
Consistent with our generic discussion of the stability of bipolytropes and the specific discussion of the stability of bipolytropes having <math>~(n_c, n_e) = (5, 1)</math>, it can straightforwardly be shown that <math>~\partial \mathfrak{G}/\partial \chi = 0</math> is satisfied by setting <math>~\Chi = 1</math>; that is, the equilibrium condition is,
|
<math>~\chi = \chi_\mathrm{eq}</math> |
<math>~=</math> |
<math>~\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} \, .</math> |
Furthermore, the equilibrium configuration is unstable whenever <math>~\partial^2 \mathfrak{G}/\partial \chi^2 < 0</math>, that is, it is unstable whenever,
|
<math>~\frac{ \mathfrak{L}_i}{\mathfrak{K}_i}</math> |
<math>~></math> |
<math>~20 \, .</math> |
Table 1 of an accompanying chapter — and the red-dashed curve in the figure adjacent to that table — identifies some key properties of the model that marks the transition from stable to unstable configurations along equilibrium sequences that have various values of the mean-molecular weight ratio, <math>~\mu_e/\mu_c</math>.
Focus on Zero-Zero Free-Energy Expression
Here, we will draw heavily from the following accompanying chapters:
From Detailed Force-Balance Models
Equilibrium Radius
First View
In an accompanying chapter we find,
|
<math>~ \frac{P_0 R_\mathrm{eq}^4}{G M_\mathrm{tot}^2 } </math> |
<math>~=</math> |
<math>~\biggl( \frac{3}{2^3 \pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^2 \biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] </math> |
where,
|
<math>~f</math> |
<math>~\equiv</math> |
<math> 1+ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2}-1 \biggr) +\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \frac{1}{q^5}-1 + \frac{5}{2} \biggl( 1-\frac{1}{q^2}\biggr)\biggr] \, , </math> |
|
<math>~\mathfrak{F} </math> |
<math>~\equiv</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (-2q^2 + 3q^3 - q^5) + \frac{3}{5} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-1 +5q^2 - 5q^3 + q^5) \biggr] \, , </math> |
|
<math>~\frac{\rho_e}{\rho_c} </math> |
<math>~=</math> |
<math>~ \frac{q^3(1-\nu)}{\nu(1-q^3)} \, . </math> |
Here, we prefer to normalize the equilibrium radius to <math>~R_\mathrm{norm}</math>. So, let's replace the central pressure with its expression in terms of <math>~K_c</math>. Specifically,
|
<math>~P_0</math> |
<math>~=</math> |
<math>~ K_c \rho_c^{\gamma_c} = K_c \biggl[ \frac{3M_\mathrm{core}}{4\pi R_i^3} \biggr]^{\gamma_c} = K_c \biggl[ \frac{3\nu M_\mathrm{tot}}{4\pi q^3 R_\mathrm{eq}^3} \biggr]^{(n_c+1)/n_c} ~~~\Rightarrow~~~ \frac{P_0}{P_\mathrm{norm}} = \biggl[ \frac{3}{4\pi}\biggl(\frac{\nu}{q^3}\biggr) \frac{1}{\chi_\mathrm{eq}^3}\biggr]^{(n_c+1)/n_c} </math> |
|
<math>~\Rightarrow~~~K_c \biggl[ \frac{3\nu M_\mathrm{tot}}{4\pi q^3 R_\mathrm{eq}^3} \biggr]^{(n_c+1)/n_c} \frac{R_\mathrm{eq}^4}{G M_\mathrm{tot}^2 } </math> |
<math>~=</math> |
<math>~\biggl( \frac{3}{2^3 \pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^2 \biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] </math> |
|
<math>~\Rightarrow~~~R_\mathrm{eq}^{(n_c-3)/n_c} </math> |
<math>~=</math> |
<math>~ \biggl(\frac{G}{K_c}\biggr) M_\mathrm{tot}^{(n_c-1)/n_c} \biggl[ \frac{3\nu }{4\pi q^3 } \biggr]^{-(n_c+1)/n_c} \biggl( \frac{3}{2^3 \pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^2 \biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] </math> |
|
<math>~\Rightarrow~~~\chi_\mathrm{eq}^{(n_c-3)/n_c} \equiv \biggl[\frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr]^{(n_c-3)/n_c}</math> |
<math>~=</math> |
<math>~ \frac{1}{2}\biggl(\frac{4\pi}{3} \biggr)^{1/n_c} \biggl( \frac{\nu}{q^3}\biggr)^{(n_c-1)/n_c} \biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] \, . </math> |
Or, in terms of <math>~\gamma_c</math>,
|
<math>~\chi_\mathrm{eq}^{4-3\gamma_c} </math> |
<math>~=</math> |
<math>~ \frac{1}{2}\biggl(\frac{3}{4\pi} \biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3}\biggr)^{2-\gamma_c} \biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] \, . </math> |
Second View
Alternatively, from our derivation and discussion of analytic detailed force-balance models,
|
<math> \biggl[ \frac{R^4}{GM_\mathrm{tot}^2} \biggr] P_0</math> |
<math>~=</math> |
<math>\biggl( \frac{3}{2^3\pi} \biggr) \frac{\nu^2 g^2}{q^4} \, ,</math> |
where,
|
<math>~[g(\nu,q)]^2</math> |
<math>~\equiv</math> |
<math> 1 + \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \, . </math> |
In order to show that this expression is the same as the other one, above, we need to show that,
|
<math>~\biggl( \frac{3}{2^3 \pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^2 \biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] </math> |
<math>~=</math> |
<math>\biggl( \frac{3}{2^3\pi} \biggr) \frac{\nu^2 g^2}{q^4} </math> |
|
<math>~\Rightarrow~~~ f - 1-\mathfrak{F}
</math> |
<math>~=</math> |
<math>~\frac{5}{2q^3} \biggl[g^2-1\biggr]</math> |
|
|
<math>~=</math> |
<math>~\frac{5}{2q^3} \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{5}{2q^5} \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl\{ 2 ( q^2 - q^3 ) + \frac{\rho_e}{\rho_0}\biggl[ 1 - 3q^2+ 2q^3 \biggr] \biggr\} \, .</math> |
Let's see …
|
<math>~ f - 1-\mathfrak{F}
</math> |
<math>~=</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2}-1 \biggr) +\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \frac{1}{q^5}-1 + \frac{5}{2} \biggl( 1-\frac{1}{q^2}\biggr)\biggr] - \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (-2q^2 + 3q^3 - q^5) + \frac{3}{5} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2}-1 \biggr) - \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (-2q^2 + 3q^3 - q^5) \biggr] </math> |
|
|
|
<math>~ - \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ \frac{3}{5} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-1 +5q^2 - 5q^3 + q^5) \biggr] +\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \frac{1}{q^5}-1 + \frac{5}{2} \biggl( 1-\frac{1}{q^2}\biggr)\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl\{ (q^3- q^5 ) + (2q^2 - 3q^3 + q^5) \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \frac{1}{q^5} \biggl[ 3 (1 -5q^2 + 5q^3 - q^5) \biggr] +\frac{1}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \frac{1}{q^5} \biggl[ 2 - 2q^5 + 5\biggl( q^5-q^3\biggr)\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (q^3- q^5 ) + (2q^2 - 3q^3 + q^5) \biggr] + \frac{1}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \frac{1}{q^5} \biggl[ 3 (1 -5q^2 + 5q^3 - q^5)+2 - 2q^5 + 5( q^5-q^3) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ 2q^2 - 2q^3 \biggr] + \frac{5}{2q^5} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ 1 - 3q^2 + 2q^3 \biggr] \, . </math> |
Q.E.D.
Hence, the equilibrium radius can also be written as,
|
<math>~\chi_\mathrm{eq}^{4-3\gamma_c} </math> |
<math>~=</math> |
<math>~ \frac{1}{2}\biggl(\frac{3}{4\pi} \biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3}\biggr)^{2-\gamma_c} q^2 g^2 \, ; </math> |
or, in terms of the polytropic index,
|
<math>~\chi_\mathrm{eq}^{n_c-3} </math> |
<math>~=</math> |
<math>~ \frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c} \, . </math> |
Gravitational Potential Energy
Also from our accompanying discussion, we have,
|
<math>~\frac{W_\mathrm{grav}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math> - \Chi^{-1} \biggl( \frac{3}{5}\biggr) \biggl(\frac{\nu}{q^3} \biggr)^2 q^5 \biggl[ \frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c} \biggr]^{-1/(n_c-3)} f(\nu,q) </math> |
|
|
<math>~=</math> |
<math> - \Chi^{-1} \biggl( \frac{6}{5}\biggr) q^5 f \biggl[ 2^{n_c-(n_c-3)} \biggl(\frac{3}{4\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{(1-n_c)+2(n_c-3)} b_\xi^{n_c} \biggr]^{1/(n_c-3)} </math> |
|
|
<math>~=</math> |
<math> - \Chi^{-1} \biggl( \frac{6}{5}\biggr) q^5 f \biggl[ \biggl(\frac{6}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} b_\xi^{n_c} \biggr]^{1/(n_c-3)} \, . </math> |
Internal Energy Components
First View
Before writing out the expressions for the internal energy of the core and of the envelope, we note from our separate detailed derivation that, in either case,
|
<math>~\biggl[\frac{P_i \chi^{3\gamma}}{P_\mathrm{norm}} \biggr]_\mathrm{eq} \chi^{3-3\gamma}</math> |
<math>~=</math> |
<math>~\biggl[\biggl(\frac{P_i }{P_0} \biggr) \biggl(\frac{P_0 }{P_\mathrm{norm}} \biggr)\chi^{3}\biggr]_\mathrm{eq} \biggl[\frac{\chi}{\chi_\mathrm{eq}}\biggr]^{3-3\gamma}</math> |
|
|
<math>~=</math> |
<math>~\biggl\{\biggl(\frac{P_i }{P_0} \biggr) \biggl[ \frac{3}{4\pi } \biggl( \frac{\nu}{q^3} \biggr)\biggr]^{\gamma_c}\chi^{3-3\gamma_c}\biggr\}_\mathrm{eq} \Chi^{3-3\gamma} \, ,</math> |
where, in equilibrium,
|
<math>~\biggl(\frac{P_i }{P_0} \biggr)_\mathrm{eq}</math> |
<math>~=</math> |
<math>~1 - b_\xi q^2</math> |
|
<math>~b_\xi q^2</math> |
<math>~=</math> |
<math>~\biggl\{\frac{2}{5}q^3 f + \biggl[1 - \frac{2}{5} q^3( 1+\mathfrak{F} ) \biggr]\biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~\biggl[1 + \frac{2}{5}q^3 (f - 1-\mathfrak{F} ) \biggr]^{-1} </math> |
So, copying from our accompanying detailed derivation, we have,
|
<math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{core}</math> |
<math>~=</math> |
<math> \frac{4\pi/3 }{({\gamma_c}-1)} \biggl\{\biggl(\frac{P_i }{P_0} \biggr) \biggl[ \frac{3}{4\pi } \biggl( \frac{\nu}{q^3} \biggr)\biggr]^{\gamma_c}\chi^{3-3\gamma_c}\biggr\}_\mathrm{eq} \Chi^{3-3\gamma_c} \biggl\{ \biggl( \frac{P_0}{P_{ic}} \biggr) \biggl[ q^3 - \biggl( \frac{3b_\xi}{5} \biggr) q^5 \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{1 }{({\gamma_c}-1)} \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] \Chi^{3-3\gamma_c} q^3\biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] \, , </math> |
|
<math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{env}</math> |
<math>~=</math> |
<math> \frac{4\pi/3 }{({\gamma_e}-1)} \biggl\{\biggl(\frac{P_i }{P_0} \biggr) \biggl[ \frac{3}{4\pi } \biggl( \frac{\nu}{q^3} \biggr)\biggr]^{\gamma_c}\chi^{3-3\gamma_c}\biggr\}_\mathrm{eq} \Chi^{3-3\gamma_e} \biggl\{ (1-q^3) + b_\xi \biggl(\frac{P_0}{P_{ie} } \biggr) \biggl[\frac{2}{5} q^5 \mathfrak{F} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{1}{({\gamma_e}-1)} \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] \Chi^{3-3\gamma_e} \biggl(\frac{P_i }{P_0} \biggr) \biggl\{ (1-q^3) + b_\xi \biggl(\frac{P_0}{P_{ie} } \biggr) \biggl[\frac{2}{5} q^5 \mathfrak{F} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{1}{({\gamma_e}-1)} \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] \Chi^{3-3\gamma_e} \biggl\{ (1-b_\xi q^2)(1-q^3) + b_\xi \biggl[\frac{2}{5} q^5 \mathfrak{F} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{1}{({\gamma_e}-1)} \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] \Chi^{3-3\gamma_e} (1-q^3) \biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} \, . </math> |
Furthermore,
|
<math>~\biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr]</math> |
<math>~=</math> |
<math>~ \biggl(\frac{3}{4\pi}\biggr)^{\gamma_c - 1} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c} \biggl\{\chi_\mathrm{eq}^{4-3\gamma_c}\biggr\}^{(3-3\gamma_c)/(4-3\gamma_c)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{3}{4\pi}\biggr)^{\gamma_c - 1} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c} \biggl\{\frac{1}{2}\biggl(\frac{3}{4\pi} \biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3}\biggr)^{2-\gamma_c} \biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] \biggr\}^{(3-3\gamma_c)/(4-3\gamma_c)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{3}{4\pi}\biggr)^{(\gamma_c - 1)/(4-3\gamma_c)} \biggl( \frac{\nu}{q^3} \biggr)^{(6-5\gamma_c)(4-3\gamma_c)} \biggl\{\frac{q^2}{2} \biggl[ 1 + \frac{2}{5} q^3( f - 1-\mathfrak{F} )\biggr] \biggr\}^{(3-3\gamma_c)/(4-3\gamma_c)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{3}{4\pi}\biggr)^{1/(n_c-3)} \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)(n_c-3)} \biggl\{\frac{q^2}{2} \biggl[ 1 + \frac{2}{5} q^3( f - 1-\mathfrak{F} )\biggr] \biggr\}^{-3/(n_c-3)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^3\biggr]^{1/(n_c-3)} \, . </math> |
Hence, we have,
|
<math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{core}</math> |
<math>~=</math> |
<math> n_c \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] \Chi^{-3/n_c} q^3\biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] </math> |
|
|
<math>~=</math> |
<math> n_c \biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^3\biggr]^{1/(n_c-3)} \Chi^{-3/n_c} q^3\biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] \, , </math> |
|
<math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{env}</math> |
<math>~=</math> |
<math> n_e \biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^3\biggr]^{1/(n_c-3)} \Chi^{-3/n_e} (1-q^3) \biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} \, . </math> |
Second View
In our accompanying discussion of energies associated with detailed force balance models, we used the notation,
|
<math>~\Pi</math> |
<math>~\equiv</math> |
<math>~ \biggl(\frac{3}{2^3\pi}\biggr) \frac{GM_\mathrm{tot}^2}{R^4} \biggl(\frac{\nu}{q^3}\biggr)^2 = P_\mathrm{norm} \chi^{-4}\biggl(\frac{3}{2^3\pi}\biggr) \biggl(\frac{\nu}{q^3}\biggr)^2 \, , </math> |
which allows us to rewrite the above quoted relationship between the central pressure and the radius of the bipolytrope as,
<math>~P_0 = \Pi (qg)^2 \, .</math>
We also showed that, in equilibrium, the relationship between the central pressure and the interface pressure is,
<math>~P_0 =P_i + \Pi_\mathrm{eq} q^2 \, .</math>
This means that, in equilibrium, the ratio of the interface pressure to the central pressure is,
|
<math>~\biggl(\frac{P_i}{P_0}\biggr)_\mathrm{eq}</math> |
<math>~=</math> |
<math>~1 - \frac{\Pi_\mathrm{eq} q^2}{P_0} = 1- \frac{1}{g^2} \, , </math> |
or given that (see above),
|
<math>~ \frac{5}{2q^3} \biggl[g^2-1\biggr]
</math> |
<math>~=</math> |
<math>~ f - 1-\mathfrak{F} </math> |
|
<math>~\Rightarrow~~~~ g^2 </math> |
<math>~=</math> |
<math>~ 1+\frac{2}{5} q^3 ( f - 1-\mathfrak{F} ) \, , </math> |
we have,
|
<math>~\biggl(\frac{P_i}{P_0}\biggr)_\mathrm{eq}</math> |
<math>~=</math> |
<math>~1 - \frac{\Pi_\mathrm{eq} q^2}{P_0} = 1- \biggl[ 1+\frac{2}{5} q^3 ( f - 1-\mathfrak{F} ) \biggr]^{-1} \, . </math> |
This is exactly the pressure-ratio expression presented in our "first view" and unveils the notation association,
|
<math>~b_\xi q^2</math> |
<math>~\leftrightarrow~</math> |
<math> \frac{1}{g^2} \, . </math> |
From our separate derivation, we have, in equilibrium,
|
<math>~\mathfrak{G}_\mathrm{core} = \biggl(\frac{2n_c}{3}\biggr) S_\mathrm{core}</math> |
<math>~=~</math> |
<math>\biggl(\frac{2n_c}{3}\biggr) \biggl( \frac{4\pi}{5} \biggr) R_\mathrm{eq}^3 q^5 \biggl (\frac{5P_i}{2q^2} + \Pi \biggr)_\mathrm{eq} </math> |
|
|
<math>~=~</math> |
<math>\biggl( \frac{ q^5n_c}{5} \biggr) R_\mathrm{eq}^3 \biggl( \frac{2^3\pi}{3} \biggr) \Pi_\mathrm{eq} \biggl[\frac{5}{2q^2} \biggl( \frac{P_i}{\Pi} \biggr)_\mathrm{eq} + 1 \biggr] </math> |
|
|
<math>~=~</math> |
<math>\biggl( \frac{ n_c}{5} \biggr) \biggl[ R_\mathrm{norm}^3 P_\mathrm{norm} \biggr] \chi_\mathrm{eq}^{-1} \biggl(\frac{\nu^2}{q}\biggr) \biggl[\frac{5}{2q^2} \biggl( \frac{P_i}{P_0} \biggr)_\mathrm{eq}\biggl( \frac{P_0}{\Pi} \biggr)_\mathrm{eq} + 1 \biggr] </math> |
|
<math>~\Rightarrow ~~~\biggl[ \frac{\mathfrak{G}_\mathrm{core} }{E_\mathrm{norm}}\biggr]_\mathrm{eq} </math> |
<math>~=~</math> |
<math>~\biggl( \frac{ n_c}{5} \biggr) \biggl(\frac{\nu^2}{q}\biggr) \biggl[\frac{5}{2q^2} \biggl( 1-\frac{1}{g^2} \biggr)\biggl( q^2g^2\biggr) + 1 \biggr] \chi_\mathrm{eq}^{-1} </math> |
|
|
<math>~=~</math> |
<math>~\biggl( \frac{ n_c}{2} \biggr) \biggl(\frac{\nu^2}{q}\biggr) \biggl[ g^2-\frac{3}{5} \biggr] \biggl\{\frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c} \biggr\}^{-1/(n_c-3)}</math> |
|
|
<math>~=~</math> |
<math>~n_c \biggl[ 1- \biggl(\frac{3}{5}\biggr) \frac{1}{g^2} \biggr] \biggl( \frac{ 1}{2} \biggr) \biggl(\frac{\nu^2}{q}\biggr) g^2 \biggl\{2^{n_c}\biggl(\frac{3}{4\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{1-n_c} (q g)^{-2n_c} \biggr\}^{1/(n_c-3)}</math> |
|
|
<math>~=~</math> |
<math>~n_c \biggl[ 1- \biggl(\frac{3}{5}\biggr) \frac{1}{g^2} \biggr] \biggl\{2^{n_c}\cdot 2^{(3-n_c)}\biggl(\frac{3}{4\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{1-n_c} \biggl(\frac{\nu}{q^3}\biggr)^{2(n_c-3)} q^{5(n_c-3)} q^{-2n_c} g^{-2n_c} g^{2(n_c-3)} \biggr\}^{1/(n_c-3)}</math> |
|
|
<math>~=~</math> |
<math>~n_c \biggl[ 1- \biggl(\frac{3}{5}\biggr) \frac{1}{g^2} \biggr] \biggl\{\biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{3n_c-15} g^{-6} \biggr\}^{1/(n_c-3)} \, .</math> |
Finally, switching from the <math>~g</math> notation to the <math>~b_\xi</math> notation gives,
|
<math>~\biggl[ \frac{\mathfrak{G}_\mathrm{core} }{E_\mathrm{norm}}\biggr]_\mathrm{eq} </math> |
<math>~=~</math> |
<math>~n_c \biggl[ 1- \biggl(\frac{3}{5}\biggr) b_\xi q^2 \biggr] \biggl\{\biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{3n_c-15} b_\xi^3 q^{6} \biggr\}^{1/(n_c-3)} </math> |
|
|
<math>~=~</math> |
<math>~n_c q^3 \biggl[ 1- \biggl(\frac{3}{5}\biggr) b_\xi q^2 \biggr] \biggl\{\biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} b_\xi^3 \biggr\}^{1/(n_c-3)} \, ,</math> |
which, after setting <math>~\Chi = 1</math>, precisely matches the above, "first view" expression. Also from our previous derivation, we can write,
|
<math>~\mathfrak{G}_\mathrm{env} = \biggl(\frac{2n_e}{3}\biggr) S_\mathrm{env}</math> |
<math>~=~</math> |
<math>~ 2\pi\biggl(\frac{2n_e}{3}\biggr) R_\mathrm{eq}^3 \Pi_\mathrm{eq} \biggl\{ (1-q^3) \biggl(\frac{P_i }{\Pi}\biggr)_\mathrm{eq} + \biggl( \frac{\rho_e}{\rho_0} \biggr)\biggl[ (-2q^2 + 3q^3 - q^5 ) + \frac{3}{5} \biggl( \frac{\rho_e}{\rho_0} \biggr) ( -1 + 5q^2 -5q^3 + q^5 )\biggr]\biggr\}
</math> |
|
|
<math>~=~</math> |
<math>~ 2\pi\biggl(\frac{2n_e}{3}\biggr) R_\mathrm{eq}^3 \biggl[ P_\mathrm{norm} \chi^{-4}\biggl(\frac{3}{2^3\pi}\biggr) \biggl(\frac{\nu}{q^3}\biggr)^2\biggr]_\mathrm{eq} \biggl\{ (1-q^3) q^2(g^2-1) + \biggl(\frac{2}{5}\biggr) q^5 \mathfrak{F} \biggr\} </math> |
|
|
<math>~=~</math> |
<math>~ \biggl[ P_\mathrm{norm} R_\mathrm{norm}^3 \biggr] \frac{n_e}{2} \biggl(\frac{\nu^2}{q^4}\biggr)(1-q^3) \biggl\{ (g^2-1) + \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr\} \chi^{-1}_\mathrm{eq} </math> |
|
<math>~\Rightarrow~~~\biggl[ \frac{\mathfrak{G}_\mathrm{env} }{E_\mathrm{norm}}\biggr]_\mathrm{eq} </math> |
<math>~=~</math> |
<math>~ n_e (1-q^3) \biggl\{ (g^2-1) + \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr\} \frac{q^2}{2}\biggl(\frac{\nu}{q^3}\biggr)^2 \biggl[\frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c}\biggr]^{-1/(n_c-3)} </math> |
|
|
<math>~=~</math> |
<math>~ n_e (1-q^3) \biggl\{ (g^2-1) + \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr\} \biggl[2^{[n_c-(n_c-3)]} \biggl(\frac{3}{4\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{(1-n_c)+2(n_c-3)} q^{2(n_c-3)-2n_c} g^{-2n_c} \biggr]^{1/(n_c-3)} </math> |
|
|
<math>~=~</math> |
<math>~ n_e (1-q^3) \biggl\{ (g^2-1) + \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr\} \biggl[\biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{-6} g^{-2n_c} \biggr]^{1/(n_c-3)} \, . </math> |
And, finally, switching from the <math>~g</math> notation to the <math>~b_\xi</math> notation gives,
|
<math>~\biggl[ \frac{\mathfrak{G}_\mathrm{env} }{E_\mathrm{norm}}\biggr]_\mathrm{eq} </math> |
<math>~=~</math> |
<math>~ n_e (1-q^3) (b_\xi q^2)^{-1} \biggl\{ 1 - \biggl[1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr]b_\xi q^2\biggr\} \biggl[\biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{-6} (b_\xi q^2)^{n_c} \biggr]^{1/(n_c-3)} </math> |
|
|
<math>~=~</math> |
<math>~ n_e (1-q^3) \biggl\{ 1 - \biggl[1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr]b_\xi q^2\biggr\} \biggl[\biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{-6-2(n_c-3)+2n_c} b_\xi^{3-n_c+n_c} \biggr]^{1/(n_c-3)} </math> |
|
|
<math>~=~</math> |
<math>~ n_e\biggl[\biggl(\frac{2\cdot 3}{\pi} \biggr)\biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} b_\xi^{3} \biggr]^{1/(n_c-3)} (1-q^3) \biggl\{ 1 - \biggl[1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr]b_\xi q^2\biggr\} \, , </math> |
which, after setting <math>~\Chi = 1</math>, precisely matches the above, "first view" expression.
Summary00
In summary, the desired out of equilibrium free-energy expression is,
|
<math>~\frac{\mathfrak{G}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~ A_0\Chi^{-3/n_c} + B_0\Chi^{-3/n_e} - C_0\Chi^{-1} </math> |
where,
|
<math>~A_0 \equiv \biggl( \frac{\mathfrak{S}_\mathrm{core}}{E_\mathrm{norm}} \biggr)_\mathrm{eq}</math> |
<math>~=</math> |
<math> \frac{n_c}{b_\xi} \biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^{n_c}\biggr]^{1/(n_c-3)} q^3\biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] \, , </math> |
|
<math>~B_0 \equiv \biggl( \frac{\mathfrak{S}_\mathrm{env}}{E_\mathrm{norm}} \biggr)_\mathrm{eq}</math> |
<math>~=</math> |
<math> \frac{n_e}{b_\xi} \biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^{n_c} \biggr]^{1/(n_c-3)} (1-q^3) \biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} \, , </math> |
|
<math>~C_0 \equiv \biggl( \frac{W_\mathrm{grav}}{E_\mathrm{norm}} \biggr)_\mathrm{eq} </math> |
<math>~=</math> |
<math> \biggl( \frac{6}{5}\biggr) q^5 f \biggl[ \biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} b_\xi^{n_c} \biggr]^{1/(n_c-3)} \, . </math> |
Or, in a more compact form,
|
<math>~\mathfrak{G}^* \equiv \biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^{n_c}\biggr]^{-1/(n_c-3)} \biggl[\frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr]</math> |
<math>~=</math> |
<math>~ n_c A_1\Chi^{-3/n_c} + n_e B_1\Chi^{-3/n_e} - 3C_1\Chi^{-1} </math> |
where,
|
<math>~A_1 </math> |
<math>~\equiv</math> |
<math> \frac{1}{b_\xi} (q^3) \biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] \, , </math> |
|
<math>~B_1 </math> |
<math>~\equiv</math> |
<math> \frac{1}{b_\xi} (1-q^3)\biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} \, , </math> |
|
<math>~C_1 </math> |
<math>~\equiv</math> |
<math> \biggl( \frac{2}{5}\biggr) q^5 f \, . </math> |
Let's examine the behavior of the first radial derivative.
|
<math>~\frac{\partial \mathfrak{G}^*}{\partial \Chi}</math> |
<math>~=</math> |
<math>~\frac{3}{\Chi} \biggl[ - A_1\Chi^{-3/n_c} - B_1\Chi^{-3/n_e} + C_1\Chi^{-1} \biggr] \, .</math> |
Let's see whether the sum of terms inside the square brackets is zero at the derived equilibrium radius, that is, when <math>~\Chi = 1</math> and, hence, when
|
<math>~\chi = \chi_\mathrm{eq}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c} \biggr]^{1/(n_c-3)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} b_\xi^{-n_c} \biggr]^{1/(n_c-3)} \, . </math> |
|
<math>~ C_1 - A_1 - B_1 </math> |
<math>~=</math> |
<math>~ \biggl( \frac{2}{5}\biggr) q^5 f - \frac{1}{b_\xi} (q^3) \biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] - \frac{1}{b_\xi} (1-q^3)\biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2}{5}\biggr) q^5 f - \frac{1}{b_\xi} \biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} + \frac{q^3}{b_\xi} \biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} - \frac{q^3}{b_\xi} \biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2}{5}\biggr) q^5 f - \frac{1}{b_\xi} + \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]q^2 + \frac{q^3}{b_\xi} - \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]q^5 - \frac{q^3}{b_\xi} + \biggl( \frac{3}{5} \biggr) q^5 </math> |
|
|
<math>~=</math> |
<math>~q^2\biggl\{ \biggl( \frac{2}{5}\biggr) q^3 f - \frac{1}{b_\xi q^2} + \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr] (1-q^3) + \biggl( \frac{3}{5} \biggr) q^3 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~q^2\biggl\{ \biggl( \frac{2}{5}\biggr) q^3 f - \biggl[ 1+\frac{2}{5} q^3(f-1-\mathfrak{F}) \biggr] + \biggl[ (1-q^3) - \frac{2}{5} q^3 \mathfrak{F} \biggr] + \biggl( \frac{3}{5} \biggr) q^3 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~q^2\biggl\{0\biggr\} \, . </math> |
Q.E.D.
Even slightly better:
|
<math>~\frac{1}{q^2}\biggl[ \biggl(\frac{\pi}{2\cdot 3}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(5-n_c)} b_\xi^{-n_c}\biggr]^{1/(n_c-3)} \biggl[\frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr]</math> |
<math>~=</math> |
<math>~ n_c A_2\Chi^{-3/n_c} + n_e B_2\Chi^{-3/n_e} - 3C_2\Chi^{-1} \, , </math> |
or, better yet,
|
Out-of-Equilibrium, Free-Energy Expression for BiPolytropes with Structural <math>~(n_c, n_e) = (0, 0)</math> |
|||
|---|---|---|---|
|
where, keeping in mind that,
|
<math>~\frac{1}{(b_\xi q^2)}</math> |
<math>~=</math> |
<math>~\biggl[1 + \frac{2}{5}q^3 (f - 1-\mathfrak{F} ) \biggr] \, , </math> |
we have,
|
<math>~A_2 \equiv \frac{A_1}{q^2} </math> |
<math>~\equiv</math> |
<math> \frac{q^3}{(b_\xi q^2)} \biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] </math> |
|
|
<math>~=</math> |
<math> q^3 \biggl\{ \biggl[1 + \frac{2}{5}q^3 (f - 1-\mathfrak{F} ) \biggr] - \biggl( \frac{3}{5} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{2}{5}q^3 \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, , </math> |
|
<math>~B_2 \equiv \frac{B_1}{q^2} </math> |
<math>~\equiv</math> |
<math> \frac{1}{(b_\xi q^2)} (1-q^3)\biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math> (1-q^3)\biggl\{ \frac{1}{(b_\xi q^2)} -1 + \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr\} </math> |
|
|
<math>~=</math> |
<math> (1-q^3)\biggl\{ \biggl[1 + \frac{2}{5}q^3 (f - 1-\mathfrak{F} ) \biggr] - 1 + \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{2}{5} q^3 \biggl\{ (1-q^3) (f - 1-\mathfrak{F} ) + \mathfrak{F} \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{2}{5} q^3 \biggl\{ f - \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr]\biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{2}{5} q^3 f - A_2 \, , </math> |
|
<math>~C_2 \equiv \frac{C_1}{q^2} </math> |
<math>~\equiv</math> |
<math> \frac{2}{5} q^3 f \, . </math> |
As before, the equilibrium system is dynamically unstable if <math>~\partial^2 \mathfrak{G}/\partial \Chi^2 < 0</math>. We have deduced that the system is unstable if,
|
<math>~\frac{n_e}{3}\biggl[ \frac{3-n_e}{n_c-n_e} \biggr] </math> |
<math>~< </math> |
<math>~ \frac{A_2}{C_2} = \frac{1}{f} \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, . </math> |
Overview
BiPolytrope51
Key Analytic Expressions
|
Out-of-Equilibrium, Free-Energy Expression for BiPolytropes with <math>~(n_c, n_e) = (5, 1)</math> |
|||
|---|---|---|---|
|
where,
|
<math>~\mathfrak{L}_i</math> |
<math>~\equiv</math> |
<math>~\frac{(\ell_i^4-1)}{\ell_i^2} + \frac{(1+\ell_i^2)^3}{\ell_i^3} \cdot \tan^{-1}\ell_i \, ,</math> |
|
<math>~\mathfrak{K}_i</math> |
<math>~\equiv</math> |
<math>~\frac{\Lambda_i}{\eta_i} + \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \, ,</math> |
|
<math>~\Lambda_i</math> |
<math>~\equiv</math> |
<math>~\frac{1}{\eta_i} - \ell_i \, ,</math> |
|
<math>~\eta_i</math> |
<math>~=</math> |
<math>~3 \biggl( \frac{\mu_e}{\mu_c} \biggr) \biggl[\frac{\ell_i }{(1+\ell_i^2)}\biggr] \, .</math> |
From the accompanying Table 1 parameter values, we also can write,
|
<math>~\frac{1}{q}</math> |
<math>~=</math> |
<math>~\frac{\eta_s}{\eta_i} = 1 + \frac{1}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] \, ,</math> |
|
<math>~\nu</math> |
<math>~=</math> |
<math>~ \frac{\ell_i q}{(1+\Lambda_i^2)^{1/2}} \, . </math> |
Consistent with our generic discussion of the stability of bipolytropes and the specific discussion of the stability of bipolytropes having <math>~(n_c, n_e) = (5, 1)</math>, it can straightforwardly be shown that <math>~\partial \mathfrak{G}^*_{51}/\partial \chi = 0</math> is satisfied by setting <math>~\Chi = 1</math>; that is, the equilibrium condition is,
|
<math>~\chi = \chi_\mathrm{eq}</math> |
<math>~=</math> |
<math>~\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} </math> |
|
|
<math>~=</math> |
<math>~\biggl\{ \biggl(\frac{\pi}{3}\biggr) 2^{2-n_c} \nu^{n_c-1} q^{3-n_c} \biggl[\frac{(1+\ell_i^2)^{6/5}}{(3\ell_i^2)} \biggr]^{n_c} \biggr\}^{1/(n_c-3)} \, ,</math> |
where the last expression has been cast into a form that more clearly highlights overlap with the expression, below, for the equilibrium radius for zero-zero bipolytropes. Furthermore, the equilibrium configuration is unstable whenever,
<math>~\biggl[ \frac{\partial^2 \mathfrak{G}^*_{51}}{\partial \chi^2}\biggr]_{\Chi=1} < 0 \, ,</math>
that is, it is unstable whenever,
|
<math>~\frac{ \mathfrak{L}_i}{\mathfrak{K}_i}</math> |
<math>~></math> |
<math>~20 \, .</math> |
Table 1 of an accompanying chapter — and the red-dashed curve in the figure adjacent to that table — identifies some key properties of the model that marks the transition from stable to unstable configurations along equilibrium sequences that have various values of the mean-molecular weight ratio, <math>~\mu_e/\mu_c</math>.
Behavior of Equilibrium Sequence
Here we reprint Figure 1 from an accompanying chapter wherein the structure of five-one bipolytropes has been derived. It displays detailed force-balance sequences in the <math>~q - \nu</math> plane for a variety of choices of the ratio of mean-molecular-weights, <math>~\mu_e/\mu_c</math>, as labeled.
Limiting Values
Each sequence begins <math>~(\ell_i = 0)</math> at the origin, that is, at <math>~(q,\nu) = (0,0)</math>. As <math>~\ell_i \rightarrow \infty</math>, however, the sequences terminate at different coordinate locations, depending on the value of <math>~m_3 \equiv 3(\mu_e/\mu_c)</math>. In deriving the various limits, it will be useful to note that,
|
<math>~\frac{1}{\eta_i}</math> |
<math>~=</math> |
<math>~\frac{(1 + \ell_i^2)}{m_3 \ell_i} \, ,</math> |
|
<math>~\Lambda_i</math> |
<math>~=</math> |
<math>~\frac{(1+\ell_i^2)}{m_3\ell_i}-\ell_i</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{m_3\ell_i} + \biggl[\frac{(1 -m_3)}{m_3} \biggr]\ell_i </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{m_3\ell_i} \biggl[ 1 - (m_3-1) \ell_i^2\biggr] </math> |
|
|
<math>~=</math> |
<math>~- \frac{ (m_3-1) \ell_i}{m_3} \biggl[ 1 - \frac{1}{(m_3-1) \ell_i^2}\biggr] \, ,</math> |
|
<math>~1 + \Lambda_i^2</math> |
<math>~=</math> |
<math>~1 + \frac{1}{m_3^2\ell_i^2}\biggl[1 + (1 -m_3) \ell_i^2 \biggr]^2</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{m_3^2\ell_i^2}\biggl\{ m_3^2\ell_i^2 + \biggl[1 + (1 -m_3) \ell_i^2 \biggr]^2\biggr\}</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{m_3^2\ell_i^2}\biggl\{ 1 + (2 -2m_3 + m_3^2) \ell_i^2 + (1 -m_3)^2 \ell_i^4 \biggr\}</math> |
Examining the three relevant parameter regimes, we see that:
- For <math>~\mu_e/\mu_c < \tfrac{1}{3}</math>, that is, <math>~m_3 < 1</math> …
|
<math>~\tan^{-1} \Lambda_i \biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx </math> |
<math>~\tan^{-1} \biggl[\frac{(1 -m_3)}{m_3} \biggr]\ell_i</math> |
|
|
<math>~\approx </math> |
<math>~\frac{\pi}{2} - \biggl[\frac{m_3}{(1 -m_3)\ell_i} \biggr]</math> |
|
<math>~\Rightarrow ~~~ \frac{1}{q}\biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~ 1 + \frac{(1 + \ell_i^2)}{m_3 \ell_i}\biggl[\pi - \frac{m_3}{(1 -m_3)\ell_i} \biggr] </math> |
|
|
<math>~\approx</math> |
<math>~ \frac{m_3 + \pi \ell_i}{m_3} </math> |
|
<math>~\Rightarrow ~~~ q\biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~ \frac{1}{1 + (\pi \ell_i/m_3)} \rightarrow 0 \, . </math> |
|
|
and |
|
|
<math>~\biggl(\frac{\nu}{q}\biggr)^2</math> |
<math>~=</math> |
<math>~\frac{\ell_i^2}{1 + \Lambda_i^2}</math> |
|
|
<math>~=</math> |
<math>~m_3^2\ell_i^4 \biggl\{ 1 + (2 -2m_3 + m_3^2) \ell_i^2 + (1 -m_3)^2 \ell_i^4 \biggr\}^{-1}</math> |
|
|
<math>~=</math> |
<math>~m_3^2\biggl\{ \ell_i^{-4} + (2 -2m_3 + m_3^2) \ell_i^{-2} + (1 -m_3)^2 \biggr\}^{-1}</math> |
|
<math>~\Rightarrow ~~~ \frac{\nu}{q}\biggr|_{\ell_i\rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~\frac{m_3}{1-m_3} </math> |
|
<math>~\Rightarrow ~~~ \nu \biggr|_{\ell_i\rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~\biggl[\frac{m_3}{1-m_3}\biggr]\frac{1}{1 + (\pi \ell_i/m_3)} \rightarrow 0 \, . </math> |
- For <math>~\mu_e/\mu_c = \tfrac{1}{3}</math>, that is, <math>~m_3 = 1</math> …
|
<math>~\tan^{-1} \Lambda_i </math> |
<math>~= </math> |
<math>~\tan^{-1} \biggl(\frac{1}{\ell_i}\biggr)</math> |
|
<math>~\Rightarrow ~~~ \tan^{-1} \Lambda_i \biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx </math> |
<math>~\frac{1}{\ell_i}</math> |
|
<math>~\Rightarrow ~~~ \frac{1}{q}\biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~ 1 + \frac{(1 + \ell_i^2)}{\ell_i}\biggl[\frac{\pi}{2} + \frac{1}{\ell_i }\biggr] </math> |
|
|
<math>~\approx</math> |
<math>~ \biggl(\frac{\pi}{2}\biggr)\ell_i</math> |
|
<math>~\Rightarrow ~~~ q\biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~ \frac{2}{\pi \ell_i} \rightarrow 0</math> |
|
|
and |
|
|
<math>~\biggl(\frac{\nu}{q}\biggr)</math> |
<math>~=</math> |
<math>~\frac{\ell_i}{(1 + 1/\ell_i^2)^{1/2}}</math> |
|
<math>~\Rightarrow ~~~ \nu \biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~\ell_i \biggl(\frac{2}{\pi \ell_i} \biggr) = \frac{2}{\pi} \approx 0.63662</math> |
- For <math>~\mu_e/\mu_c > \tfrac{1}{3}</math>, that is, <math>~m_3 > 1</math> …
|
<math>~\tan^{-1} \Lambda_i \biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx </math> |
<math>~\tan^{-1} \biggl[-\biggl(\frac{m_3-1}{m_3} \biggr)\ell_i\biggr]</math> |
|
|
<math>~\approx </math> |
<math>~-\frac{\pi}{2} + \biggl[\frac{m_3}{(m_3-1)\ell_i} \biggr]</math> |
|
<math>~\Rightarrow ~~~ \frac{1}{q}\biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~ 1 + \frac{(1 + \ell_i^2)}{m_3 \ell_i}\biggl[ \frac{m_3}{(m_3-1)\ell_i} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 1 + \frac{(1 + 1/\ell_i^2)}{(m_3-1) } </math> |
|
|
<math>~\approx</math> |
<math>~ 1 + \frac{1}{(m_3-1) } = \frac{m_3}{(m_3-1)} </math> |
|
<math>~\Rightarrow ~~~ q\biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~=</math> |
<math>~ \frac{(m_3-1)}{m_3} </math> |
|
|
and |
|
|
<math>~\biggl(\frac{\nu}{q}\biggr)^2</math> |
<math>~=</math> |
<math>~\frac{\ell_i^2}{1 + \Lambda_i^2}</math> |
|
|
<math>~=</math> |
<math>~m_3^2\ell_i^4 \biggl\{ 1 + (2 -2m_3 + m_3^2) \ell_i^2 + (m_3-1)^2 \ell_i^4 \biggr\}^{-1}</math> |
|
|
<math>~=</math> |
<math>~m_3^2\biggl\{ \ell_i^{-4} + (2 -2m_3 + m_3^2) \ell_i^{-2} + (m_3-1)^2 \biggr\}^{-1}</math> |
|
<math>~\Rightarrow ~~~ \frac{\nu}{q}\biggr|_{\ell_i\rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~\frac{m_3}{m_3-1} </math> |
|
<math>~\Rightarrow ~~~ \nu \biggr|_{\ell_i\rightarrow \infty}</math> |
<math>~=</math> |
<math>~\frac{m_3}{m_3-1} \biggl[\frac{m_3 - 1}{m_3}\biggr] \rightarrow 1 \, . </math> |
Summarizing:
- For <math>~\mu_e/\mu_c < \tfrac{1}{3}</math>, that is, <math>~m_3 < 1</math> … <math>~(q,\nu)_{\ell_i \rightarrow \infty} = (0, 0) \, .</math>
- For <math>~\mu_e/\mu_c = \tfrac{1}{3}</math>, that is, <math>~m_3 = 1</math> … <math>~(q,\nu)_{\ell_i \rightarrow \infty} = (0, \tfrac{2}{\pi}) \, .</math>
- For <math>~\mu_e/\mu_c > \tfrac{1}{3}</math>, that is, <math>~m_3 > 1</math> … <math>~(q,\nu)_{\ell_i \rightarrow \infty} = [(m_3-1)/m_3, 1] \, .</math>
Turning Points
Let's identify the location of two turning points along the <math>~\nu(q)</math> sequence — one defines <math>~q_\mathrm{max}</math> and the other identifies <math>~\nu_\mathrm{max}</math>. They occur, respectively, where,
|
<math>~\frac{d\ln q}{d\ln \ell_i} = 0</math> |
and |
<math>~\frac{d\ln \nu}{d\ln \ell_i} = 0 \, .</math> |
In deriving these expressions, we will use the relations,
|
<math>~\frac{d\eta_i}{d\ell_i}</math> |
<math>~=</math> |
<math>~\frac{m_3 (1-\ell_i^2)}{(1+\ell_i^2)^2} \, ,</math> |
|
<math>~\frac{d\Lambda_i}{d\ell_i}</math> |
<math>~=</math> |
<math>~- \frac{1}{m_3\ell_i^2} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] \, ,</math> |
where,
<math>~m_3 \equiv 3\biggl(\frac{\mu_e}{\mu_c}\biggr) \, .</math>
Given that,
|
<math>~q </math> |
<math>~=</math> |
<math>~\biggl\{ 1 + \frac{1}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] \biggr\}^{-1} \, ,</math> |
we find,
|
<math>~\frac{d\ln q}{d\ln \ell_i}</math> |
<math>~=</math> |
<math>~\frac{\ell_i}{q} \cdot ( -q^2) \frac{d}{d\ell_i} \biggl\{ \frac{1}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~-q\ell_i \biggl\{-\frac{1}{\eta_i^2}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr]\frac{d\eta_i}{d\ell_i} + \frac{1}{\eta_i(1+\Lambda_i^2)} \frac{d\Lambda_i}{d\ell_i} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~q\ell_i \biggl\{\frac{(1-\ell_i^2)}{m_3 \ell_i^2}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] + \frac{(1+\ell_i^2)}{m_3^2 \ell_i^3(1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{q}{m_3^2}{\ell_i^2}\biggl\{m_3 \ell_i (1-\ell_i^2) \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] + \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] \biggr\} \, . </math> |
And, given that,
|
<math>~\nu </math> |
<math>~=</math> |
<math>~ \frac{\ell_i q}{(1+\Lambda_i^2)^{1/2}} \, . </math> |
we find,
|
<math>~\frac{d\ln \nu}{d\ln \ell_i}</math> |
<math>~=</math> |
<math>~\frac{\ell_i}{\nu} \biggl\{ \frac{q}{(1+\Lambda_i^2)^{1/2}} + \frac{q}{(1+\Lambda_i^2)^{1/2}} \frac{d\ln q}{d\ln \ell_i} - \frac{\ell_i q \Lambda_i }{(1+\Lambda_i^2)^{3/2}} \frac{d\Lambda_i}{d\ell_i} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{q \ell_i}{ \nu(1+\Lambda_i^2)^{1/2}}\biggl\{ 1 + \frac{d\ln q}{d\ln \ell_i} + \frac{\Lambda_i }{m_3 \ell_i (1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] \biggr\} </math> |
In summary, then, the <math>~q_\mathrm{max}</math> turning point occurs where,
|
<math>~0</math> |
<math>~=</math> |
<math>~ (1+\Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] + \frac{(1+\ell_i^2)}{m_3 \ell_i (1-\ell_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] \, ; </math> |
and the <math>~\nu_\mathrm{max}</math> turning point occurs where,
|
<math>~0</math> |
<math>~=</math> |
<math>~ 1 + \frac{\Lambda_i }{m_3 \ell_i (1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] + \frac{q \ell_i^3 (1-\ell_i^2)}{m_3} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] + \frac{q\ell_i^2}{m_3^2}\cdot \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 1 + \frac{q \ell_i^3 (1-\ell_i^2)}{m_3} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] + \biggl[ \frac{\Lambda_i }{m_3 \ell_i (1+\Lambda_i^2)} + \frac{q\ell_i^2}{m_3^2}\cdot \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggr] \cdot \biggl[ 1 - \ell_i^2(1-m_3) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 1 + \frac{q \ell_i^3 (1-\ell_i^2)}{m_3} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] + \frac{1}{m_3 \ell_i} \biggl[ \frac{\Lambda_i }{(1+\Lambda_i^2)} + \frac{q\ell_i^3}{m_3}\cdot \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggr] \cdot \biggl[ 1 - \ell_i^2(1-m_3) \biggr] \, . </math> |
|
NOTE: As we show above, for the special case of <math>~m_3 = 1</math> — that is, when <math>~\mu_e/\mu_c = \tfrac{1}{3}</math>, precisely — the equilibrium sequence (as <math>~\ell_i \rightarrow \infty</math>) intersects the <math>~q = 0</math> axis at precisely the value, <math>~\nu = 2/\pi</math>. As is illustrated graphically in Figure 1 of an accompanying chapter, no <math>~\nu_\mathrm{max}</math> turning point exists for values of <math>~m_3 > 1</math>. |
For the record, we repeat, as well, that the transition from stable to dynamically unstable configurations occurs along the sequence when,
|
<math>~\frac{(\ell_i^4-1)}{\ell_i^2} + \frac{(1+\ell_i^2)^3}{\ell_i^3} \cdot \tan^{-1}\ell_i </math> |
<math>~=</math> |
<math>~20 \biggl\{ \frac{\Lambda_i}{\eta_i} + \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{20(1+\Lambda_i^2)(1+\ell_i^2)}{m_3\ell_i} \biggl\{ \frac{\Lambda_i}{(1+\Lambda_i^2)} + \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \biggr\} </math> |
|
<math>~\Rightarrow ~~~ m_3 \ell_i (\ell_i^4-1) + m_3(1+\ell_i^2)^3\cdot \tan^{-1}\ell_i </math> |
<math>~=</math> |
<math>~20\ell_i^2 (1+\Lambda_i^2)(1+\ell_i^2) \biggl\{ \frac{\Lambda_i}{(1+\Lambda_i^2)} + \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \biggr\} </math> |
|
<math>~\Rightarrow ~~~ \frac{m_3 \ell_i (\ell_i^4-1) + m_3(1+\ell_i^2)^3\cdot \tan^{-1}\ell_i }{ 20\ell_i^2 (1+\ell_i^2)}</math> |
<math>~=</math> |
<math>~\Lambda_i + (1+\Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \, .</math> |
In order to clarify what equilibrium sequences do not have any turning points, let's examine how the <math>~q_\mathrm{max}</math> turning-point expression behaves as <math>~\ell_i \rightarrow \infty</math>.
|
<math>~ \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr]</math> |
<math>~=</math> |
<math>~ m_3 \ell_i (\ell_i^2-1) \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] </math> |
|
<math>~ \Rightarrow ~~~ \frac{(1+\ell_i^2)}{ m_3 \ell_i (\ell_i^2-1) } \biggl[ 1 + \ell_i^2(m_3-1) \biggr]</math> |
<math>~=</math> |
<math>~ \biggl\{ 1 + \frac{1}{m_3^2\ell_i^2}\biggl[ (m_3-1) \ell_i^2-1 \biggr]^2 \biggr\} \biggl\{ \frac{\pi}{2} + \biggl[ -\frac{\pi}{2} - \frac{1}{\Lambda_i} + \frac{1 }{3\Lambda_i^3} + \mathcal{O}(\Lambda_i^{-5} )\biggr] \biggr\} </math> |
|
<math>~ \Rightarrow ~~~ \frac{(1+\ell_i^2) \ell_i^2(m_3-1)}{ m_3 \ell_i (\ell_i^2-1) } \biggl[ 1 + \frac{1}{\ell_i^2(m_3-1)} \biggr]</math> |
<math>~=</math> |
<math>~ \biggl\{ 1 + \frac{(m_3-1)^2 \ell_i^2}{m_3^2}\biggl[ 1 - \frac{1}{ (m_3-1) \ell_i^2 } \biggr]^2 \biggr\} \cdot \frac{1}{(-\Lambda_i)} \biggl[ 1 - \frac{1 }{3\Lambda_i^2} + \cancelto{0}{\mathcal{O}(\Lambda_i^{-4} )}\biggr] </math> |
|
<math>~ \Rightarrow ~~~ \frac{(1+\ell_i^2)}{ \ell_i (\ell_i^2-1) } \cdot \frac{m_3}{(m_3-1)} \biggl[ 1 + \frac{1}{\ell_i^2(m_3-1)} \biggr]</math> |
<math>~=</math> |
<math>~ \biggl[ 1 - \frac{2}{ (m_3-1) \ell_i^2 } + \frac{m_3^2}{(m_3-1)^2 \ell_i^2} + \frac{1}{ (m_3-1)^2 \ell_i^4 } \biggr] \cdot \frac{m_3}{(m_3-1)\ell_i} \biggl[1 - \frac{1}{(m_3-1)\ell_i^2}\biggr]^{-1} \biggl\{ 1 - \frac{m_3^2}{3(m_3-1)^2\ell_i^2} \biggl[1 - \frac{1}{(m_3-1)\ell_i^2}\biggr]^{-2} \biggr\} </math> |
|
<math>~ \Rightarrow ~~~\biggl(1 + \frac{1}{\ell_i^2} \biggr) \biggl[ 1 + \frac{1}{\ell_i^2(m_3-1)} \biggr]\biggl[1 - \frac{1}{(m_3-1)\ell_i^2}\biggr]</math> |
<math>~=</math> |
<math>~\biggl(1 - \frac{1}{\ell_i^2} \biggr) \biggl[ 1 - \frac{2}{ (m_3-1) \ell_i^2 } + \frac{m_3^2}{(m_3-1)^2 \ell_i^2} + \frac{1}{ (m_3-1)^2 \ell_i^4 } \biggr] \biggl\{ 1 - \frac{m_3^2}{3(m_3-1)^2\ell_i^2} \biggl[1 - \frac{1}{(m_3-1)\ell_i^2}\biggr]^{-2} \biggr\} </math> |
The leading-order term is unity on both sides of this expression, so they cancel; let's see what results from keeping terms <math>~\propto \ell_i^{-2}</math>.
|
<math>~ \frac{1}{\ell_i^2} \biggl[ 1 + \frac{1}{(m_3-1)} - \frac{1}{(m_3-1)}\biggr]</math> |
<math>~=</math> |
<math>~ \frac{1}{\ell_i^2} \biggl[- 1 - \frac{2}{ (m_3-1) } + \frac{m_3^2}{(m_3-1)^2 } - \frac{m_3^2}{3(m_3-1)^2} \biggr] </math> |
|
<math>~\Rightarrow~~~ 2 </math> |
<math>~=</math> |
<math>~ - \frac{2}{ (m_3-1) } + \frac{2m_3^2}{3(m_3-1)^2 } </math> |
|
<math>~\Rightarrow~~~ 6(m_3-1)^2 </math> |
<math>~=</math> |
<math>~ - 6(m_3-1) + 2m_3^2 </math> |
|
<math>~\Rightarrow~~~ 6m_3^2-12m_3 + 6 </math> |
<math>~=</math> |
<math>~ - 6m_3+6 + 2m_3^2 </math> |
|
<math>~\Rightarrow~~~ m_3</math> |
<math>~=</math> |
<math>~ \frac{3}{2} \, . </math> |
We therefore conclude that the <math>~q_\mathrm{max}</math> turning point does not appear along any sequence for which,
|
<math>~m_3</math> |
<math>~></math> |
<math>~\frac{3}{2}</math> |
|
<math>~\Rightarrow ~~~ \frac{\mu_e}{\mu_c}</math> |
<math>~></math> |
<math>~\frac{1}{2}\, .</math> |
| Five-One Bipolytrope Equilibrium Sequences in <math>~q - \nu</math> Plane | |
|
Full Sequences for Various <math>~\frac{\mu_e}{\mu_c}</math> |
Magnified View with Turning Points and Stability Transition-Points Identified |
Graphical Depiction of Free-Energy Surface
| Figure 1: Free-Energy Surface for <math>~(n_c,n_e) = (5,1)</math> and <math>~\frac{\mu_e}{\mu_c} = 1</math> | ||||
| ||||
For purposes of reproducibility, it is incumbent upon us to clarify how the values of the free energy were normalized in order to produce the free-energy surface displayed in Figure 1. The normalization steps are explicitly detailed within the fortran program, below, that generated the data for plotting purposes; here we provide a brief summary. We evaluated the normalized free energy, <math>~\mathfrak{G}^*_{51}</math>, across a <math>~200 \times 200</math> zone grid of uniform spacing, covering the following <math>~(x,y) = (\ell_i,\Chi)</math> domain:
|
<math>~\frac{1}{\sqrt{3}}</math> |
<math>~\le \ell_i \le</math> |
<math>~\frac{3}{\sqrt{3}}</math> |
|
<math>~0.469230769</math> |
<math>~\le \Chi\le</math> |
<math>~2.0</math> |
(With this specific definition of the y-coordinate grid, <math>~\Chi = 1</math> is associated with zone 70.) After this evaluation, a constant, <math>~E_\mathrm{fudge} = -10</math>, was added to <math>~\mathfrak{G}^*</math> in order to ensure that the free energy was negative across the entire domain. Then (inorm = 1), for each specified interface location, <math>~x = \ell_i</math>, employing the equilibrium value of the free energy,
<math>~E_0 = \mathfrak{G}^*_{51}(\ell_i, \Chi = 1) + E_\mathrm{fudge} \, ,</math>
the free energy was normalized across all values of <math>~y = \Chi</math> via the expression,
<math>~\mathrm{fe} = \frac{(\mathfrak{G}^*_{51} + E_\mathrm{fudge}) - (E_0)_i}{|E_0|_i} \, .</math>
Finally, for plotting purposes, at each grid cell vertex ("vertex") — as well as at each grid cell center ("cell") — the value of the free energy, <math>~\mathrm{fe}</math>, was renormalized as follows,
<math>~\mathrm{vertex} = \frac{\mathrm{fe} - \mathrm{min}(\mathrm{fe})}{ \mathrm{max}(\mathrm{fe}) - \mathrm{min}(\mathrm{fe})} \, .</math>
Via this last step, the minimum "vertex" energy across the entire domain was 0.0 while the maximum "vertex" energy was 1.0.
| FORTRAN Program Documentation | Example Evaluations(See also associated Table 1) | ||||
|---|---|---|---|---|---|
| Coord. Axis | Coord. Name | Associated Physical Quantity | <math>~\frac{\mu_e}{\mu_c} = 1</math> | <math>~\frac{\mu_e}{\mu_c} = 0.305</math> | |
| x-axis | bsize | <math>~\ell_i \equiv \frac{\xi_i}{\sqrt{3}}</math> | <math>~\frac{2.416}{\sqrt{3}} = 1.395</math> | <math>~\frac{8.1938}{\sqrt{3}} = 4.7307</math> | <math>~\frac{14.389}{\sqrt{3}} = 8.3076</math> |
| y-axis | csize | <math>~\Chi \equiv \frac{\chi}{\chi_\mathrm{eq}}</math> | <math>~1</math> | <math>~1</math> | <math>~1</math> |
| Relevant Lines of Code | |||||
eta = 3.0d0*muratio*bsize/(1.0d0+bsize**2)
Gami = 1.0d0/eta-bsize
frakL = (bsize**4-1.0d0)/bsize**2 + &
& DATAN(bsize)*((1.0d0+bsize**2)/bsize)**3
frakK = Gami/eta + ((1.0d0+Gami**2)/eta)*(pii/2.0d0+DATAN(Gami))
E0 = ((5.0d0*frakL) + (4.0d0*frakK)&
& - (3.0d0*frakL+12.0d0*frakK))/bsize**2+Efudge
fescalar(j,k) = (csize**(-0.6d0)*(5.0d0*frakL)&
& + csize**(-3.0d0)*(4.0d0*frakK)&
& - (3.0d0*frakL+12.0d0*frakK)/csize)/bsize**2 + Efudge
if(inorm.eq.1)fescalar(j,k)=fescalar(j,k)/DABS(E0) &
& - E0/DABS(E0)
|
|||||
| Variable | Represents | Value calculated via the expression … | |||
| eta | <math>~\eta_i</math> |
<math>~3 \biggl(\frac{\mu_e}{\mu_c}\biggr)\biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]</math> |
<math>~1.421</math> | <math>~0.1851</math> | <math>~0.1086</math> |
| Gami | <math>~\Lambda_i</math> | <math>~\frac{1}{\eta_i} - \ell_i</math> | <math>~-0.691</math> | <math>~0.6705</math> | <math>~0.9033</math> |
| frakL | <math>~\mathfrak{L}_i</math> | <math>~
\frac{(\ell_i^4 - 1)}{\ell_i^2} + \biggl[ \frac{1+\ell_i^2}{\ell_i} \biggr]^3 \tan^{-1}\ell_i </math> |
<math>~10.37</math> | <math>~186.80</math> | <math>~937.64</math> |
| frakK | <math>~\mathfrak{K}_i</math> | <math>~
\frac{\Lambda_i}{\eta_i} + \frac{(1 + \Lambda_i^2)}{\eta_i} \biggl[ \frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] </math> |
<math>~0.518</math> | <math>~20.544</math> | <math>~46.882</math> |
| <math>~\frac{\mathfrak{L}_i}{\mathfrak{K}_i}</math> | <math>~20</math> | <math>~9.093</math> | <math>~20</math> | ||
| E0 - Efudge | <math>~\mathfrak{G}^*_{51}(\ell_i,\Chi=1)</math> |
<math>~ \frac{1}{\ell_i^2} \biggl[ 5 \mathfrak{L}_i + 4\mathfrak{K}_i - (3\mathfrak{L}_i +12\mathfrak{K}_i ) \biggr] = \frac{2(\mathfrak{L}_i - 4\mathfrak{K}_i)}{\ell_i^2} </math> |
<math>~8.525</math> | <math>~9.3496</math> | <math>~21.737</math> |
| Figure 2: Free-Energy Surface for <math>~(n_c,n_e) = (5,1)</math> and <math>~\frac{\mu_e}{\mu_c} = 0.305</math> | ||
|
BiPolytrope00
|
Out-of-Equilibrium, Free-Energy Expression for BiPolytropes with Structural <math>~(n_c, n_e) = (0, 0)</math> |
|||
|---|---|---|---|
|
where,
|
<math>~A_2 </math> |
<math>~\equiv</math> |
<math> \frac{2}{5}q^3 \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, , </math> |
|
<math>~B_2 </math> |
<math>~\equiv</math> |
<math> \frac{2}{5} q^3 f - A_2 \, , </math> |
|
<math>~C_2 </math> |
<math>~\equiv</math> |
<math> \frac{2}{5} q^3 f \, , </math> |
|
<math>~f</math> |
<math>~\equiv</math> |
<math> 1+ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2}-1 \biggr) +\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \frac{1}{q^5}-1 + \frac{5}{2} \biggl( 1-\frac{1}{q^2}\biggr)\biggr] \, , </math> |
|
<math>~\mathfrak{F} </math> |
<math>~\equiv</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (-2q^2 + 3q^3 - q^5) + \frac{3}{5} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-1 +5q^2 - 5q^3 + q^5) \biggr] \, , </math> |
|
<math>~\frac{\rho_e}{\rho_c} </math> |
<math>~=</math> |
<math>~ \frac{q^3(1-\nu)}{\nu(1-q^3)} \, . </math> |
The associated equilibrium radius is,
|
<math>~\chi_\mathrm{eq}</math> |
<math>~=</math> |
<math>~ \biggl\{ \biggl(\frac{\pi}{3}\biggr) 2^{2-n_c} \nu^{n_c-1} q^{3-n_c} \biggl[1 + \frac{2}{5} q^3(f-1-\mathfrak{F})\biggr]^{n_c} \biggr\}^{1/(n_c-3)} \, . </math> |
We have deduced that the system is unstable if,
|
<math>~\frac{n_e}{3}\biggl[ \frac{3-n_e}{n_c-n_e} \biggr] </math> |
<math>~< </math> |
<math>~ \frac{A_2}{C_2} = \frac{1}{f} \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, . </math> |
Fortran Code
This is the program that generated the free-energy data for the "five-one" bipolytrope that is displayed in the above, Figure 1 image/animation.
PROGRAM BiPolytrope
real*8 pii
real*8 bmin,bmax,cmin,cmax,db,dc
real*8 c(200),b(200),chalf(199),bhalf(199)
real*8 bsize,csize,emin,emax
real*8 fepoint(200,200),fescalar(199,199)
real*8 ell(200),ellhalf(199)
real*8 muratio,eta,Gami,frakK,frakL
real*8 eshift,ediff
real xx(200),yy(200),cell(199,199),vertex(200,200)
real valuemin,minlog,valufudge
real*8 q,nu,chiEq,Enorm,E0,Efudge
integer j,k,n,nmax,inorm
101 format(4x,'bsize',7x,'csize',8x,'xi',10x,'A',12x,'B',12x,&
&'fM',13x,'fW',11x,'fA',/)
! 102 format(1p8d12.4)
103 format(2i5,1p3d14.6)
201 format(5x,'valuemin = ',1pe15.5,//)
205 format(5x,'For Cell-center ... emin, emax = ',1p2d14.6,/)
206 format(5x,'For Cell-vertex ... emin, emax = ',1p2d14.6,/)
701 format(5x,1p10d10.2)
700 format(8x,'xi',9x,'ell',8x,'eta',8x,'Lambda',5x,'frakK',&
& 5x,'frakL',8x,'q',5x,'nu',5x,'chiEq',8x,'E0',/)
!!!!!!!!
!!!!!!!!
inorm=1
pii = 4.0d0*datan(1.0d0)
muratio = 1.0d0
bsize = 0.0d0
csize = 0.0d0
Efudge = -10.0d0
write(*,101)
! write(*,102)bsize,csize,xival,coefA,coefB,fM,fW,fA
!!!!!!!!!!!
!
! In this free-energy routine, c = X = chi/chi_eq and b = xi_i
!
!!!!!!!!!!!
nmax = 200
bmin = 1.0d0
bmax = 3.0d0
db = (bmax-bmin)/dfloat(nmax-1)
b(1) = bmin
ell(1) = b(1)/dsqrt(3.0d0)
! These values of cmin and cmax ensure that X=1 occurs at zone 70
cmin = 0.469230769d0
cmax = 2.00d0
dc = (cmax-cmin)/dfloat(nmax-1)
c(1) = cmin
do n=2,nmax
b(n) = b(n-1)+db
c(n) = c(n-1)+dc
ell(n) = b(n)/dsqrt(3.0d0)
enddo
do n=1,nmax-1
bhalf(n) = 0.5d0*(b(n)+b(n+1))
chalf(n) = 0.5d0*(c(n)+c(n+1))
ellhalf(n) = bhalf(n)/dsqrt(3.0d0)
enddo
!
! BEGIN LOOP to evaluate free energy (cell center)
!
emin = 0.0d0
emax = 0.0d0
write(*,700)
do j=1,nmax-1
bsize = ellhalf(j)
eta = 3.0d0*muratio*bsize/(1.0d0+bsize**2)
Gami = 1.0d0/eta-bsize
frakL = (bsize**4-1.0d0)/bsize**2 + &
& DATAN(bsize)*((1.0d0+bsize**2)/bsize)**3
frakK = Gami/eta + ((1.0d0+Gami**2)/eta)*(pii/2.0d0+DATAN(Gami))
q = 1.0d0/(1.0d0 + (0.5d0*pii+DATAN(Gami))/eta)
nu = bsize*q/dsqrt(1.0d0+Gami**2)
chiEq = dsqrt(pii/8.0d0)*(nu**2/(q*bsize**2))&
& *((1.0d0+bsize**2)/(3.0d0*bsize))**3
Enorm = 16.0d0*(q/nu**2)*chiEq
E0 = ((5.0d0*frakL) + (4.0d0*frakK)&
& - (3.0d0*frakL+12.0d0*frakK))/bsize**2+Efudge
write(*,701)b(j),bsize,eta,Gami,frakK,frakL,q,nu,chiEq,E0
do k=1,nmax-1
csize=chalf(k)
fescalar(j,k) = (csize**(-0.6d0)*(5.0d0*frakL)&
& + csize**(-3.0d0)*(4.0d0*frakK)&
& - (3.0d0*frakL+12.0d0*frakK)/csize)/bsize**2 + Efudge
if(inorm.eq.1)fescalar(j,k)=fescalar(j,k)/DABS(E0) &
& - E0/DABS(E0)
if(fescalar(j,k).gt.0.5d0)fescalar(j,k)=0.5d0
if(fescalar(j,k).lt.emin)emin=fescalar(j,k)
if(fescalar(j,k).gt.emax)emax=fescalar(j,k)
! write(*,103)j,k,bsize,csize,fescalar(j,k)
enddo
enddo
write(*,205)emin,emax
!
! BEGIN LOOP to evaluate free energy (cell vertex)
!
emin = 0.0d0
emax = 0.0d0
do j=1,nmax
bsize = ell(j)
eta = 3.0d0*muratio*bsize/(1.0d0+bsize**2)
Gami = 1.0d0/eta-bsize
frakL = (bsize**4-1.0d0)/bsize**2 + &
& DATAN(bsize)*((1.0d0+bsize**2)/bsize)**3
frakK = Gami/eta + ((1.0d0+Gami**2)/eta)*(pii/2.0d0+DATAN(Gami))
q = 1.0d0/(1.0d0 + (0.5d0*pii+DATAN(Gami))/eta)
nu = bsize*q/dsqrt(1.0d0+Gami**2)
chiEq = dsqrt(pii/8.0d0)*(nu**2/(q*bsize**2))&
& *((1.0d0+bsize**2)/(3.0d0*bsize))**3
Enorm = 16.0d0*(q/nu**2)*chiEq
E0 = ((5.0d0*frakL) + (4.0d0*frakK)&
& - (3.0d0*frakL+12.0d0*frakK))/bsize**2 + Efudge
do k=1,nmax
csize=c(k)
fepoint(j,k) = (csize**(-0.6d0)*(5.0d0*frakL)&
& + csize**(-3.0d0)*(4.0d0*frakK)&
& - (3.0d0*frakL+12.0d0*frakK)/csize)/bsize**2 + Efudge
if(inorm.eq.1)fepoint(j,k)=fepoint(j,k)/DABS(E0) &
& - E0/DABS(E0)
if(fepoint(j,k).gt.0.5d0)fepoint(j,k)=0.5d0
if(fepoint(j,k).lt.emin)emin=fepoint(j,k)
if(fepoint(j,k).gt.emax)emax=fepoint(j,k)
! write(*,103)j,k,bsize,csize,fepoint(j,k)
enddo
enddo
write(*,206)emin,emax
!
! Now fill single-precision arrays for plotting.
!
do n=1,nmax
! xx(n)=b(n)/b(nmax)
! yy(n)=c(n)/c(nmax)
xx(n)=b(n)-bmin
yy(n)=c(n)-cmin
! xx(n)=b(n)
! yy(n)=c(n)
enddo
valuemin= -emin
valufudge = 1.0d0/(emax-emin)
do k=1,nmax
do j=1,nmax
vertex(j,k)=fepoint(j,k)+valuemin
vertex(j,k)=vertex(j,k)*valufudge
enddo
enddo
do k=1,nmax-1
do j=1,nmax-1
cell(j,k)=fescalar(j,k)+valuemin
cell(j,k)=cell(j,k)*valufudge
enddo
enddo
call XMLwriter01(nmax,xx,yy,cell,vertex)
stop
END PROGRAM BiPolytrope
Subroutine XMLwriter01(imax,x,y,cell_scalar,point_scalar)
real x(200),y(200),z(1)
real cell_scalar(199,199),point_scalar(200,200)
integer imax
integer extentX,extentY,extentZ
integer ix0,iy0,iz0
integer norm(200,3)
! imax=200
ix0=0
iy0=0
iz0=0
extentX=imax-1
extentY=imax-1
extentZ=0
z(1) = 0.0
! Set normal vector 1D array
do i=1,imax
norm(i,1)=0
norm(i,2)=0
norm(i,3)=1
enddo
201 format('<?xml version="1.0"?>')
202 format('<VTKFile type="RectilinearGrid" version="0.1" byte_order="LittleEndian">')
302 format('</VTKFile>')
203 format(2x,'<RectilinearGrid WholeExtent="',6I4,'">')
303 format(2x,'</RectilinearGrid>')
204 format(4x,'<Piece Extent="',6I4,'">')
304 format(4x,'</Piece>')
205 format(6x,'<CellData Scalars="cell_scalars" Normals="magnify">')
305 format(6x,'</CellData>')
206 format(8x,'<DataArray type="Float32" Name="magnify" NumberOfComponents="3" format="ascii">')
207 format(8x,'<DataArray type="Float32" Name="cell_scalars" format="ascii">')
399 format(8x,'</DataArray>')
208 format(6x,'<PointData Scalars="colorful" Normals="direction">')
308 format(6x,'</PointData>')
209 format(8x,'<DataArray type="Float32" Name="colorful" format="ascii">')
210 format(6x,'<Coordinates>')
310 format(6x,'</Coordinates>')
211 format(8x,'<DataArray type="Float32" format="ascii" RangeMin="0" RangeMax="5">')
212 format(8x,'<DataArray type="Float32" format="ascii">')
213 format(8x,'<DataArray type="Float32" Name="direction" NumberOfComponents="3" format="ascii">')
501 format(10f9.5)
502 format(10f9.5)
503 format(5x,9(1x,3I2))
504 format(10f9.5)
505 format(5x,10(1x,3I2))
!!!!!
!
! Begin writing out XML tags.
!
!!!!!
write(*,201) !<?xml
write(*,202) !VTKFile
write(*,203)ix0,extentX,iy0,extentY,iz0,extentZ ! RectilinearGrid
write(*,204)ix0,extentX,iy0,extentY,iz0,extentZ ! Piece
write(*,205) ! CellData
write(*,207) ! DataArray(cell_scalars)
do j=1,imax-1
write(*,501)(cell_scalar(i,j),i=1,imax-1)
enddo
write(*,399) ! /DataArray
write(*,206) ! DataArray(cell_scalars)
do j=1,imax-1
write(*,503)(norm(i,1),norm(i,2),norm(i,3),i=1,imax-1)
enddo
write(*,399) ! /DataArray
write(*,305) ! /CellData
write(*,208) ! PointData
write(*,209) ! DataArray(points)
write(*,502)((point_scalar(i,j),i=1,imax),j=1,imax)
write(*,399) ! /DataArray
write(*,213) ! DataArray(cell_scalars)
do j=1,imax
write(*,505)(norm(i,1),norm(i,2),norm(i,3),i=1,imax)
enddo
write(*,399) ! /DataArray
write(*,308) ! /PointData
write(*,210) ! Coordinates
write(*,212) ! DataArray(x-direction)
write(*,504)(x(i),i=1,imax)
write(*,399) ! /DataArray
write(*,212) ! DataArray(y-direction)
write(*,504)(y(i),i=1,imax)
write(*,399) ! /DataArray
write(*,212) ! DataArray(z-direction)
write(*,504)z(1)
write(*,399) ! /DataArray
write(*,310) ! /Coordinates
write(*,304) ! /Piece
write(*,303) ! /RectilinearGrid
write(*,302) !/VTKFile
return
end
Nonstandard Examination
In our introductory remarks, above, we said the warped free-energy surface drapes across a five-dimensional parameter "plane" such that,
|
<math>~\mathfrak{G}_{51}</math> |
<math>~=</math> |
<math>~\mathfrak{G}(R, K_c, M_\mathrm{tot}, q, \nu) \, .</math> |
From a more pragmatic point of view, we should have said that the "five-one" free-energy surface drapes across a five-dimensional parameter "plane" such that,
|
<math>~\mathfrak{G}_{51}</math> |
<math>~=</math> |
<math>~\mathfrak{G}(R, K_c, M_\mathrm{tot}, \ell_i, \tfrac{\mu_e}{\mu_c}) \, .</math> |
In our initial, standard examination of the structure of this warped free-energy surface, we held three parameters fixed — namely, <math>~K_c, M_\mathrm{tot}, \tfrac{\mu_e}{\mu_c}</math> — and plotted <math>~\mathfrak{G}_{51}(\ell_i, \Chi\equiv R/R_\mathrm{eq})</math>. Now, let's fix <math>~\Chi = 1</math> and plot <math>~\mathfrak{G}_{51}(\ell_i, \tfrac{\mu_e}{\mu_c})</math>. The following plot shows how a portion of the <math>~(\ell_i, \mu_e/\mu_c)</math> grid maps onto the traditional <math>~(q, \nu)</math> plane. The numerical labels identify lines of constant <math>~\xi_i = \sqrt{3}\ell_i</math> — 7 (light green), 9 (pink), and 12 (orange) — and lines of constant <math>~\mu_e/\mu_c</math> — 0.330 (purple), 0.315 (dark green), and 0.305 (white/blue).
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |