User:Tohline/SSC/FreeEnergy/PolytropesEmbedded
Free-Energy Synopsis

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
All of the self-gravitating configurations considered below have an associated Gibbs-like free-energy that can be expressed analytically as a power-law function of the dimensionless configuration radius, <math>~x</math>. Specifically,
|
<math>~\mathfrak{G}^*_\mathrm{type}</math> |
<math>~=</math> |
<math>~-ax^{-1} + b x^{-3/n} + c x^{-3/j} + \mathfrak{G}_0 \, .</math> |
Equilibrium Radii and Critical Radii
The first and second (partial) derivatives with respect to <math>~x</math> are, respectively,
|
<math>~\frac{\partial\mathfrak{G}^*_\mathrm{type}}{\partial x}</math> |
<math>~=</math> |
<math>~ax^{-2} - \biggl(\frac{ 3b}{n}\biggr) x^{-3/n -1} -\biggl(\frac{3 c}{j}\biggr) x^{-3/j-1} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{x^2} \biggl[ a - \biggl(\frac{ 3b}{n}\biggr) x^{(n-3)/n } -\biggl(\frac{3 c}{j}\biggr) x^{(j-3)/j} \biggr] \, ,</math> |
|
<math>~\frac{\partial^2 \mathfrak{G}^*_\mathrm{type}}{\partial x^2}</math> |
<math>~=</math> |
<math>~-2ax^{-3} + \biggl(\frac{ 3b}{n}\biggr) \biggl( \frac{n+3}{n}\biggr) x^{-3/n -2} + \biggl(\frac{3 c}{j}\biggr)\biggl( \frac{j+3}{j}\biggr) x^{-3/j-2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{x^3} \biggl\{ \biggl(\frac{ 3b}{n}\biggr) \biggl( \frac{n+3}{n}\biggr) x^{(n-3)/n} + \biggl(\frac{3 c}{j}\biggr)\biggl( \frac{j+3}{j}\biggr) x^{(j-3)/j} -2a\biggr\} \, . </math> |
Equilibrium configurations are identified by setting the first derivative to zero. This gives,
|
<math>~0</math> |
<math>~=</math> |
<math>~a - \biggl(\frac{ 3b}{n}\biggr) x^{(n-3)/n }_\mathrm{eq} -\biggl(\frac{3 c}{j}\biggr) x^{(j-3)/j}_\mathrm{eq} </math> |
|
<math>~\Rightarrow ~~~x^{(n-3)/n }_\mathrm{eq}</math> |
<math>~=</math> |
<math>~\biggl(\frac{n}{ 3b}\biggr) \biggl[a -\biggl(\frac{3 c}{j}\biggr) x^{(j-3)/j}_\mathrm{eq} \biggr] \, .</math> |
|
<math>~\Rightarrow ~~~\frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} + \frac{1}{j}\cdot x^{(j-3)/j}_\mathrm{eq} </math> |
<math>~=</math> |
<math>~ 0 \, .</math> |
We conclude, as well, that at this equilibrium radius, the second (partial) derivative assumes the value,
|
<math>~\biggl[ \frac{\partial^2 \mathfrak{G}^*_\mathrm{type}}{\partial x^2} \biggr]_\mathrm{eq}</math> |
<math>~=</math> |
<math>~ \frac{1}{x^3_\mathrm{eq} } \biggl\{ \biggl(\frac{ 3b}{n}\biggr) \biggl( \frac{n+3}{n}\biggr) x^{(n-3)/n} + \biggl(\frac{3 c}{j}\biggr)\biggl( \frac{j+3}{j}\biggr) x^{(j-3)/j} -2a\biggr\}_\mathrm{eq} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{x^3_\mathrm{eq} } \biggl\{ \biggl( \frac{n+3}{n}\biggr) \biggl[a -\biggl(\frac{3 c}{j}\biggr) x^{(j-3)/j}_\mathrm{eq} \biggr] + \biggl(\frac{3 c}{j}\biggr)\biggl( \frac{j+3}{j}\biggr) x^{(j-3)/j}_\mathrm{eq} -2a\biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{x^3_\mathrm{eq} } \biggl\{ \biggl(\frac{3 c}{j}\biggr) \biggl[ \biggl( \frac{j+3}{j}\biggr) -\biggl( \frac{n+3}{n}\biggr) \biggl] x^{(j-3)/j}_\mathrm{eq} + \biggl( \frac{3-n}{n}\biggr) a\biggr\} \, . </math> |
Hence, equilibrium configurations for which the second (as well as first) derivative of the free energy is zero are found at "critical" radii given by the expression,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \biggl(\frac{3 c}{j}\biggr) \biggl[ \biggl( \frac{j+3}{j}\biggr) -\biggl( \frac{n+3}{n}\biggr) \biggl] [x_\mathrm{eq}^{(j-3)/j}]_\mathrm{crit} + \biggl( \frac{3-n}{n}\biggr) a </math> |
|
<math>~\Rightarrow ~~~[x_\mathrm{eq}^{(j-3)/j}]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{j^2 a(n-3)}{3 c}\biggr] [ n(j+3) - j(n+3) ]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \frac{a}{3^2c}\biggl[ \frac{j^2(n-3)}{n-j} \biggr] \, . </math> |
Examples
Pressure-Truncated Polytropes
For pressure-truncated polytropes of index <math>~n</math>, we set, <math>~j = -1</math>, in which case,
|
<math>~\frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} - x^{4}_\mathrm{eq}</math> |
<math>~=</math> |
<math>~0 \, ;</math> |
|
<math>~\biggl[ \biggl(\frac{3}{4\pi}\biggr) \frac{ M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr]^{(n+1)/n} x^{(n-3)/n }_\mathrm{eq} - \frac{3}{20\pi} \biggl( \frac{n+1}{n}\biggr)\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}} \biggr)^{2} - x^{4}_\mathrm{eq}</math> |
<math>~=</math> |
<math>~0 \, ;</math> |
|
<math>~x^{(n-3)/n }_\mathrm{eq}</math> |
<math>~=</math> |
<math>~\biggl(\frac{n}{ 3b}\biggr) \biggl[a + 3cx^{4}_\mathrm{eq} \biggr] \, ;</math> |
|
|
and |
|
|
<math>~[x_\mathrm{eq}]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{a(n-3)}{3^2 c (n+1)} \biggr]^{1/4} \, . </math> |
Case M
More specifically, the expression that describes the "Case M" free-energy surface is,
|
Hence, we have,
|
<math>~a</math> |
<math>~\equiv</math> |
<math>~3\mathcal{A} = \frac{3}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}\, , </math> |
|
<math>~b</math> |
<math>~\equiv</math> |
<math>~n\mathcal{B} = n\biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, , </math> |
|
<math>~c</math> |
<math>~\equiv</math> |
<math>~\frac{4\pi}{3}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, , </math> |
where the structural form factors for pressure-truncated polytropes are precisely defined here. Therefore, the statement of virial equilibrium is,
|
<math>~0 </math> |
<math>~=</math> |
<math>~\frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} - x^{4}_\mathrm{eq}</math> |
|
<math>~\Rightarrow ~~~ \biggl(\frac{3}{4\pi}\biggr)c x_\mathrm{eq}^4 </math> |
<math>~=</math> |
<math>~\biggl(\frac{3}{4\pi}\biggr) \biggl[ \frac{ b}{n}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3} \biggr]</math> |
|
<math>~\Rightarrow ~~~ \biggl(\frac{P_e}{P_\mathrm{norm}}\biggr) x_\mathrm{eq}^4 </math> |
<math>~=</math> |
<math>~\biggl(\frac{3}{4\pi}\biggr) \biggl[ \biggl(\frac{3}{4\pi} \biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \cdot x^{(n-3)/n }_\mathrm{eq} - \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr]</math> |
|
|
<math>~=</math> |
<math>~\biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \cdot x^{(n-3)/n }_\mathrm{eq} - \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \, .</math> |
And we conclude that,
|
<math>~3c[x_\mathrm{eq}]^4_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\frac{(n-3)}{5(n+1)} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) [x_\mathrm{eq}]^4_\mathrm{crit}</math> |
<math>~=</math> |
<math>~\frac{1}{20\pi} \biggl( \frac{n-3}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
|
<math>~\Rightarrow ~~~ \biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \cdot [ x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} - \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
<math>~=</math> |
<math>~\frac{1}{20\pi} \biggl( \frac{n-3}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
|
<math>~\Rightarrow ~~~ \biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \cdot [ x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\frac{1}{20\pi} \biggl( \frac{n-3}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} + \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{20\pi} \biggl( \frac{4n}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
|
<math>~\Rightarrow ~~~ [ x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\frac{1}{20\pi} \biggl(\frac{4\pi}{3} \biggr)^{(n+1)/n} \biggl( \frac{4n}{n+1} \biggr) \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_A \tilde{\mathfrak{f}}_M^{(n-1)/n} } </math> |
|
<math>~\Rightarrow ~~~ [ x_\mathrm{eq} ]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{4n}{15(n+1)} \biggl(\frac{4\pi}{3} \biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_A \tilde{\mathfrak{f}}_M^{(n-1)/n} } \biggr]^{n/(n-3)} \, . </math> |
|
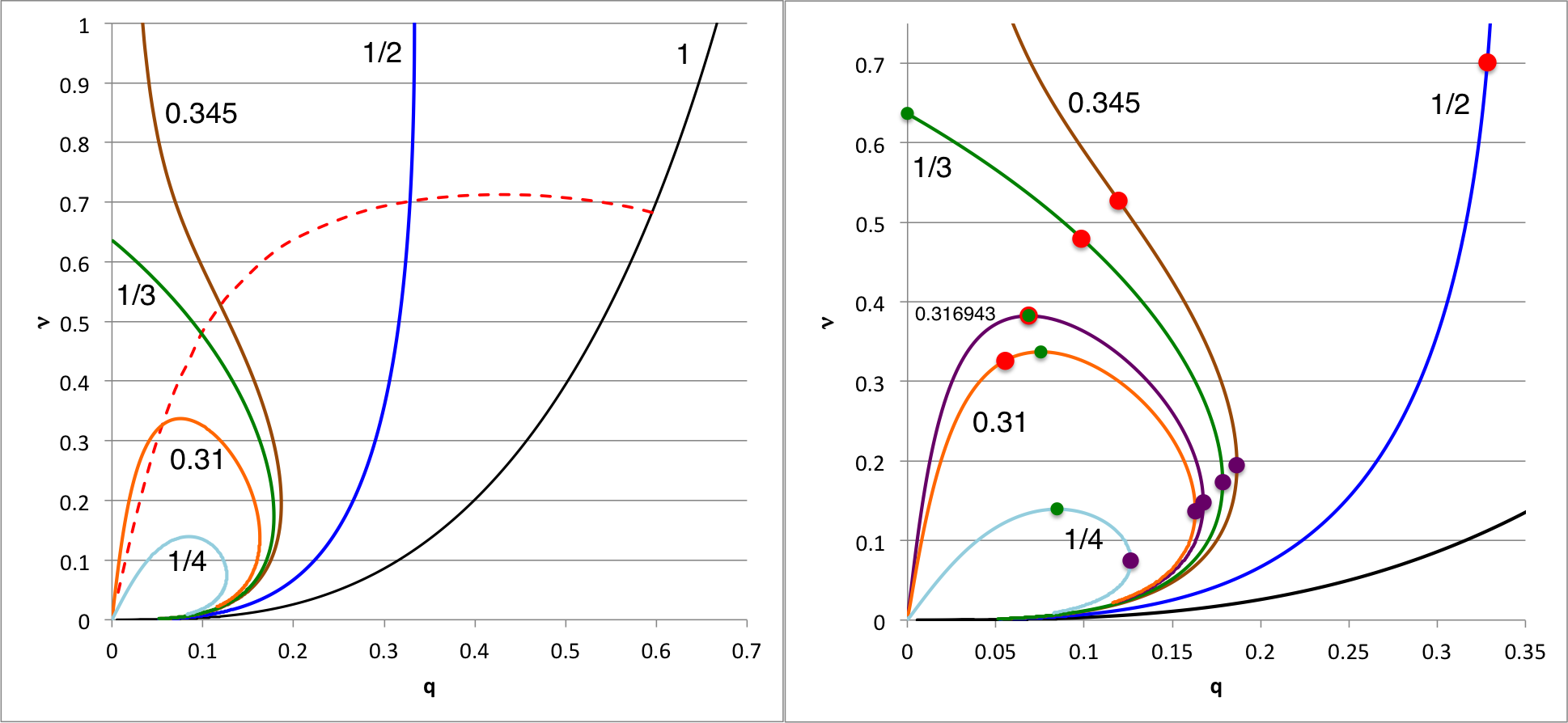
ASIDE: Let's see what this requires for the case of <math>~n=5</math>, where everything is specifiable analytically. We have gathered together:
So, the radius of the critical equilibrium state should be,
whereas, each equilibrium configuration has,
So the equilibrium state that marks the critical configuration must have a value of <math>~\ell</math> that satisfies the relation,
The solution is: <math>~\ell_\mathrm{crit} \approx 2.223175 \, .</math> |
In addition, we know from our dissection of Hoerdt's work on detailed force-balance models that, in the equilibrium state,
|
<math>~\biggl(\frac{P_e}{P_\mathrm{norm}}\biggr) \biggl(\frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4</math> |
<math>~=</math> |
<math> \biggl[ \frac{\tilde\theta^{n+1} }{(4\pi)(n+1)( -\tilde\theta' )^{2}} \biggr] </math> |
|
<math>~\Rightarrow ~~~ 3c x_\mathrm{eq}^4</math> |
<math>~=</math> |
<math> \biggl[ \frac{\tilde\theta^{n+1} }{(n+1)( -\tilde\theta' )^{2}} \biggr] \, . </math> |
This means that, for any chosen polytropic index, the critical equilibrium state is the equilibrium configuration for which (needs to be checked),
|
<math>~2(9-2n){\tilde\theta}^{n+1}</math> |
<math>~=</math> |
<math>~ 3(n-3)\biggl[ (- {\tilde\theta}^')^2 - \frac{\tilde\theta(-{\tilde\theta}^')}{\tilde\xi}\biggr] \, . </math> |
We note, as well, that by combining the Horedt expression for <math>~x_\mathrm{eq}</math> with our virial equilibrium expression, we find (needs to be checked),
|
<math>~x_\mathrm{eq}^{n-3}</math> |
<math>~=</math> |
<math>~\frac{4\pi}{3}\biggl[ \frac{3}{(n+1)\tilde\xi^2} + \frac{{\tilde\mathfrak{f}}_{W} - {\tilde\mathfrak{f}}_{M}}{5\tilde\mathfrak{f}_A} \biggr]^{n} {\tilde\mathfrak{f}}_{M}^{1-n} \, .</math> |
Case P
First Pass
Alternatively, let's examine the "Case P" free-energy surface. Drawing on Stahler's presentation, we adopt the following radius and mass normalizations:
<math>M_\mathrm{SWS} = \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \, ,</math>
<math> R_\mathrm{SWS} = \biggl( \frac{n+1}{n} \biggr)^{1/2} G^{-1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \, . </math>
In terms of these new normalizations, we have,
|
<math>~R_\mathrm{norm} \equiv \biggl[\biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{(n-1)} \biggr]^{1/(n-3)}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{G}{K} \biggr)^{n/(n-3)} M_\mathrm{tot}^{(n-1)/(n-3)} R_\mathrm{SWS} \biggl( \frac{n+1}{n} \biggr)^{-1/2} G^{1/2} K_n^{-n/(n+1)} P_\mathrm{e}^{-(1-n)/[2(n+1)]} </math> |
|
|
|
<math>~+ M_\mathrm{SWS}^{-(n-1)/(n-3)} \biggl[ \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \biggr]^{(n-1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~R_\mathrm{SWS} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{[3(n-1)-(n-3)]/[2(n-3)]} G^{[2n+(n-3)-3(n-1)]/[2(n-3)]} </math> |
|
|
|
<math>~+ K_n^{n[2(n-1) - (n+1) - (n-3)]/[(n+1)(n-3)]} P_\mathrm{e}^{-(n-1)(3-n)/[2(n+1)(n-3)]} P_\mathrm{e}^{(n-1)(3-n)/[2(n+1)(n-3)]} </math> |
|
|
<math>~=</math> |
<math>~R_\mathrm{SWS} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \, . </math> |
and,
|
<math>~P_\mathrm{norm} \equiv \biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)} } \biggr]^{1/(n-3)}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{K^{4n}}{G^{3(n+1)} } \biggr]^{1/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{-2(n+1)/(n-3)} \biggl\{ \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]}\biggr\}^{-2(n+1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{-2(n+1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{-3(n+1)/(n-3)} K^{4n/(n-3)} G^{-3(n+1)/(n-3)} </math> |
|
|
|
<math>~\times~ G^{3(n+1)/(n-3)} K_n^{-4n/(n-3)} \biggl\{ P_\mathrm{e}^{-(n-3)/[2(n+1)]}\biggr\}^{-2(n+1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~P_e \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{-2(n+1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{-3(n+1)/(n-3)} \, . </math> |
Rewriting the expression for the free energy gives,
|
<math>~\mathfrak{G}_{K,M}^* \equiv \frac{\mathfrak{G}_{K,M}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~ -3\mathcal{A} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} \biggl(\frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr) +~ n\mathcal{B} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} \biggl(\frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr)^{3/n} +~ \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \biggl(\frac{R_\mathrm{norm}}{R_\mathrm{SWS}}\biggr)^{-3} </math> |
|
|
<math>~=</math> |
<math>~ -3\mathcal{A} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} \biggl[ \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)}\biggr] </math> |
|
|
|
<math>~ +~ n\mathcal{B} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} \biggl[ \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)}\biggr]^{3/n} </math> |
|
|
|
<math>~ +~ \biggl( \frac{4\pi}{3} \biggr) \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{2(n+1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{3(n+1)/(n-3)} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \biggl[ \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)}\biggr]^{-3} </math> |
|
|
<math>~=</math> |
<math>~ -3\mathcal{A} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} +~ n\mathcal{B} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} </math> |
|
|
|
<math>~ +~ \biggl( \frac{4\pi}{3} \biggr) \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(5-n)/(n-3)} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \, . </math> |
Therefore, in this case, we have,
|
<math>~a</math> |
<math>~=</math> |
<math>~\frac{3}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \, , </math> |
|
<math>~b</math> |
<math>~=</math> |
<math>~ n\biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \, , </math> |
|
<math>~c</math> |
<math>~=</math> |
<math>~\frac{4\pi}{3} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(5-n)/(n-3)} \, , </math> |
where the structural form factors for pressure-truncated polytropes are precisely defined here. The statement of virial equilibrium is, therefore,
|
<math>~x^{4}_\mathrm{eq} + \alpha </math> |
<math>~=</math> |
<math>~ \beta x^{(n-3)/n }_\mathrm{eq} \, , </math> |
where,
|
<math>~\alpha \equiv \frac{a}{3c}</math> |
<math>~=</math> |
<math>~ \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl\{ \frac{3}{4\pi} \biggl( \frac{n+1}{n} \biggr)^{-3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(n-5)/(n-3)} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr) \mathfrak{m}^{2} \, , </math> |
|
<math>~\beta \equiv \frac{b}{nc}</math> |
<math>~=</math> |
<math>~ \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \biggl\{ \frac{3}{4\pi} \biggl( \frac{n+1}{n} \biggr)^{-3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(n-5)/(n-3)} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} \, , </math> |
|
<math>~\mathfrak{m}</math> |
<math>~\equiv</math> |
<math>~ \biggl(\frac{3}{4\pi}\biggr) \frac{1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr) \, . </math> |
From a previous derivation, we have,
|
<math>~0 </math> |
<math>~=</math> |
<math>~ \frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} - x^{4}_\mathrm{eq} </math> |
|
|
<math>~=</math> |
<math>~\frac{3}{4\pi} \biggl( \frac{n+1}{n} \biggr)^{-3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(n-5)/(n-3)} \biggl\{ \biggl(\frac{3}{4\pi} \biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \biggr\} \cdot x^{(n-3)/n }_\mathrm{eq} </math> |
|
|
|
<math>~ - \frac{3}{4\pi} \biggl( \frac{n+1}{n} \biggr)^{-3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(n-5)/(n-3)} \biggl\{ \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggr\} - x^{4}_\mathrm{eq} </math> |
|
<math>~0</math> |
<math>~=</math> |
<math>~ \biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} x^{(n-3)/n }_\mathrm{eq} - \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} - x^{4}_\mathrm{eq} </math> |
|
|
<math>~=</math> |
<math>~ \tilde{\mathfrak{f}}_A \biggl[ \biggl(\frac{3}{4\pi} \biggr) \frac{1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)\biggr]^{(n+1)/n} x^{(n-3)/n }_\mathrm{eq} - \frac{1}{5} \biggl(\frac{4\pi}{3}\biggr) \cdot \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr)\biggl[ \biggl(\frac{3}{4\pi} \biggr) \frac{1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)\biggr]^{2} - x^{4}_\mathrm{eq} </math> |
which, thankfully, matches! We conclude as well that the transition from stable to dynamically unstable configurations occurs at,
|
<math>~[x_\mathrm{eq}]_\mathrm{crit}^4</math> |
<math>~=</math> |
<math>~\biggl[ \frac{(n-3)}{3 (n+1)} \biggr] \alpha \, . </math> |
When combined with the statement of virial equilibrium at this critical point, we find,
|
<math>~ \biggl\{ \biggl[ \frac{(n-3)}{3 (n+1)} \biggr] + 1\biggr\}\frac{ \alpha }{\beta} </math> |
<math>~=</math> |
<math>~ [x_\mathrm{eq}]^{(n-3)/n }_\mathrm{crit} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \biggl[ \frac{(n-3)}{3 (n+1)} \biggr] \alpha \biggr\}^{(n-3)/(4n) } </math> |
|
<math>~\Rightarrow~~~ \biggl[ \frac{4n}{3 (n+1)} \biggr]^{4n} \biggl( \frac{ \alpha }{\beta} \biggr)^{4n} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{(n-3)}{3 (n+1)} \biggr]^{(n-3)} \alpha^{(n-3)} </math> |
|
<math>~\Rightarrow~~~ \biggl[ \frac{3 n}{(n-3)} \biggl( \frac{n+1}{n}\biggr) \biggr]^{(3-n)} \biggl[ \frac{3 }{4} \biggl( \frac{n+1}{n}\biggr) \biggr]^{4n} </math> |
<math>~=</math> |
<math>~ \alpha^{3(n+1)} \beta^{-4n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr) \mathfrak{m}^{2} \biggr\}^{3(n+1)} \biggl\{ \tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} \biggr\}^{-4n} </math> |
|
|
<math>~=</math> |
<math>~\tilde{\mathfrak{f}}_A^{-4n} \biggl[ \biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr)\biggr]^{3(n+1)} \mathfrak{m}^{2(n+1)} </math> |
|
<math>~\Rightarrow ~~~ \mathfrak{m}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr)\biggr]^{-3(n+1)} \biggl[ \frac{3 n}{(n-3)} \biggl( \frac{n+1}{n}\biggr) \biggr]^{(3-n)} \biggl[ \frac{3\tilde{\mathfrak{f}}_A }{4} \biggl( \frac{n+1}{n}\biggr) \biggr]^{4n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{3\cdot 5}{4\pi}\biggr) \frac{1}{\tilde{\mathfrak{f}}_W} \biggr]^{3(n+1)} \biggl[ \frac{3 n}{(n-3)} \biggr]^{(3-n)} \biggl[ \frac{3\tilde{\mathfrak{f}}_A }{4} \biggr]^{4n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{3^2 \cdot 5 n}{ 4\pi(n-3)} \cdot \frac{1}{\tilde{\mathfrak{f}}_W} \biggr]^{(3-n)} \biggl[ \biggl( \frac{3^2\cdot 5}{2^4\pi}\biggr) \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_W} \biggr]^{4n} \, . </math> |
This also means that the critical radius is,
|
<math>~[x_\mathrm{eq}]_\mathrm{crit}^4</math> |
<math>~=</math> |
<math>~\biggl[ \frac{(n-3)}{3 (n+1)} \biggr] \biggl( \frac{4\pi}{3\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggl( \frac{n+1}{n} \biggr) \mathfrak{m}^{2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{3^2\cdot 5 n}{4\pi(n-3)} \cdot \frac{1}{\tilde{\mathfrak{f}}_W}\biggr]^{-1} \mathfrak{m}^{2} </math> |
|
<math>~\Rightarrow ~~~ [x_\mathrm{eq}]_\mathrm{crit}^{4(n+1)}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{3^2\cdot 5 n}{4\pi(n-3)} \cdot \frac{1}{\tilde{\mathfrak{f}}_W} \biggr]^{-(n+1)} \biggl[ \frac{3^2 \cdot 5 n}{ 4\pi(n-3)} \cdot \frac{1}{\tilde{\mathfrak{f}}_W} \biggr]^{(3-n)} \biggl[ \biggl( \frac{3^2\cdot 5}{2^4\pi}\biggr) \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_W} \biggr]^{4n} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{4\pi(n-3)}{3^2\cdot 5 n} \cdot \tilde{\mathfrak{f}}_W \biggr]^{2(n-1)} \biggl[ \biggl( \frac{3^2\cdot 5}{2^4\pi}\biggr) \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_W} \biggr]^{4n} </math> |
|
<math>~\Rightarrow ~~~ [x_\mathrm{eq}]_\mathrm{crit}^{2(n+1)}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{n}{(n-3)} \biggl( \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W} \biggr) \biggr]^{(1-n)} \biggl[ \biggl( \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W}\biggr) \frac{\tilde{\mathfrak{f}}_A}{4} \biggr]^{2n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{n}{n-3} \biggr)^{(1-n)} \biggl( \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W} \biggr)^{(n+1)} \biggl(\frac{\tilde{\mathfrak{f}}_A}{4} \biggr)^{2n} \, . </math> |
The following parallel derivation was done independently. [Note that a factor of 2n/(n-1) appears to correct a mistake made during the original derivation.] Beginning with the virial expression,
|
<math>~\beta x^{(n-3)/n }_\mathrm{eq} </math> |
<math>~=</math> |
<math>~ \alpha + x^{4}_\mathrm{eq} </math> |
|
<math>~ \biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} [x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \frac{3}{20\pi} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} + \frac{(n-3)}{20\pi n} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{(n-1)}{10\pi n} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl[ \frac{2n}{(n-1)}\biggr] </math> |
|
<math>~\Rightarrow~~~ [x_\mathrm{eq} ]^{(n-3)/n }_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \frac{2(n-1)}{15 n} \biggl(\frac{4\pi}{3} \biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_A\tilde{\mathfrak{f}}_M^{(n-1)/n}} \cdot \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/n} \biggl[ \frac{2n}{(n-1)}\biggr] </math> |
|
<math>~\Rightarrow~~~ [x_\mathrm{eq} ]^{(n-3) }_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{2(n-1)}{15 n} \biggr]^n \biggl(\frac{4\pi}{3} \biggr) \frac{\tilde{\mathfrak{f}}_W^n}{\tilde{\mathfrak{f}}_A^n \tilde{\mathfrak{f}}_M^{(n-1)}} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)} \biggl[ \frac{2n}{(n-1)}\biggr]^n </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{2(n-1)}{15 n} \biggr]^n \biggl(\frac{4\pi}{3} \biggr) \frac{\tilde{\mathfrak{f}}_W^n}{\tilde{\mathfrak{f}}_A^n \tilde{\mathfrak{f}}_M^{(n-1)}} \biggl\{ \biggl[ \frac{20\pi n}{(n-3)} \biggr]^{(n-1)/2} \biggl( \frac{\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W} \biggr)^{(n-1)/2} [x_\mathrm{eq} ]^{2(n-1) }_\mathrm{crit} \biggr\}\biggl[ \frac{2n}{(n-1)}\biggr]^n </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{2(n-1)}{15 n} \biggr]^n \biggl(\frac{4\pi}{3} \biggr) \frac{\tilde{\mathfrak{f}}_W^{(n+1)/2}}{\tilde{\mathfrak{f}}_A^n } \biggl\{ \biggl[ \frac{20\pi n}{(n-3)} \biggr]^{(n-1)/2} [x_\mathrm{eq} ]^{2(n-1) }_\mathrm{crit} \biggr\}\biggl[ \frac{2n}{(n-1)}\biggr]^n </math> |
|
<math>~\Rightarrow~~~ [x_\mathrm{eq} ]^{(n+1) }_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \biggl(\frac{3}{4\pi} \biggr) \biggl[\frac{15 n}{2(n-1)} \biggr]^n \biggl[ \frac{(n-3)}{20\pi n} \biggr]^{(n-1)/2} \frac{\tilde{\mathfrak{f}}_A^n }{\tilde{\mathfrak{f}}_W^{(n+1)/2}} \biggl[ \frac{(n-1)}{2n} \biggr]^n </math> |
|
<math>~\Rightarrow~~~ [x_\mathrm{eq} ]^{(n+1) }_\mathrm{crit} </math> |
<math>~=</math> |
<math>~ \biggl(\frac{3}{4\pi} \biggr) \biggl[\frac{15 }{2^2} \biggr]^n \biggl[ \frac{(n-3)}{20\pi n} \biggr]^{(n-1)/2} \frac{\tilde{\mathfrak{f}}_A^n }{\tilde{\mathfrak{f}}_W^{(n+1)/2}} </math> |
Also from Stahler's work we know that the equilibrium mass and radius are,
|
<math> ~\frac{M_\mathrm{tot}}{M_\mathrm{SWS}} </math> |
<math>~=~</math> |
<math> \biggl( \frac{n^3}{4\pi} \biggr)^{1/2} \biggl[ {\tilde\theta}_n^{(n-3)/2} {\tilde\xi}^2 (-{\tilde\theta}^') \biggr] \, , </math> |
|
<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{SWS}} </math> |
<math>~=~</math> |
<math> \biggl( \frac{n}{4\pi} \biggr)^{1/2} \biggl[ \tilde\xi {\tilde\theta}_n^{(n-1)/2} \biggr] \, . </math> |
Additional details in support of an associated PowerPoint presentation can be found here.
Reconcile
|
<math>~\biggl[\frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]^4_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{(n-3)}{20\pi (n+1)} \biggr] \biggl(\frac{n+1}{n}\biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
|
<math>~\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4_\mathrm{crit}</math> |
<math>~=</math> |
<math>~\frac{1}{20\pi} \biggl( \frac{n-3}{n+1} \biggr) \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} </math> |
Taking the ratio, the RHS is,
|
<math>~\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)</math> |
<math>~=</math> |
<math>~P_e M_\mathrm{tot}^2 \biggl[ \frac{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)} }{K^{4n}} \biggr]^{1/(n-3)} \biggl[ \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \biggr]^{-2} \biggl( \frac{n+1}{n}\biggr)</math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{n+1}{n} \biggr)^{-2}P_e M_\mathrm{tot}^2 \biggl[ G^{3} M_\mathrm{tot}^{2} \biggr]^{(n+1)/(n-3)} K_n^{-4n/(n-3)} \biggl[ G^{3} K_n^{-4n/(n+1)} P_\mathrm{e}^{(n-3)/(n+1)} \biggr]</math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{n+1}{n} \biggr)^{-2} \biggl[ G^{3} M_\mathrm{tot}^{2} \biggr]^{[(n-3)+(n+1)]/(n-3)} \biggl[ K_n^{[(n+1)+(n-3)]/[(n+1)(n-3)] } \biggr]^{-4n} P_\mathrm{e}^{[(n+1)+ (n-3)]/(n+1)} </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{n+1}{n} \biggr)^{-2} M_\mathrm{tot}^{4(n-1)/(n-3)} G^{[6(n-1)]/(n-3)} K_n^{-8(n-1)/[(n+1)(n-3)] } P_\mathrm{e}^{2(n-1)/(n+1)} \, ;</math> |
while the LHS is,
|
<math>~\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr)^{4}</math> |
<math>~=</math> |
<math>~ \biggl[\biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{(n-1)} \biggr]^{4/(n-3)} \biggl\{\biggl( \frac{n+1}{n} \biggr)^{1/2} G^{-1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]}\biggr\}^{-4} </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{n+1}{n} \biggr)^{-2} M_\mathrm{tot}^{4(n-1)/(n-3)} G^{[6(n-1)]/(n-3)} K^{-8n(n-1)/[(n-3)(n+1)] } P_\mathrm{e}^{2(n-1)/(n+1)} \, . </math> |
Q.E.D.
Now, given that,
|
<math>~M_\mathrm{SWS}^{-4(n-1)/(n-3)}</math> |
<math>~=</math> |
<math>~\biggl[\biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]}\biggr]^{-4(n-1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{n+1}{n} \biggr)^{-6(n-1)/(n-3)} G^{6(n-1)/(n-3)} K_n^{-8n(n-1)/[(n+1)(n-3)]} P_\mathrm{e}^{2(n-1)/(n+1)} </math> |
we have,
|
<math>~\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr)^{4}</math> |
<math>~=</math> |
<math>~\biggl( \frac{n+1}{n} \biggr)^{-2} \biggl(\frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{4(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{6(n-1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{4(n-1)/(n-3)} \biggl( \frac{n+1}{n} \biggr)^{4n/(n-3)} </math> |
|
<math>~\Rightarrow ~~~\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{SWS}} \biggr)^{n-3}</math> |
<math>~=</math> |
<math>~ \biggl(\frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{n-1} \biggl( \frac{n+1}{n} \biggr)^{n} </math> |
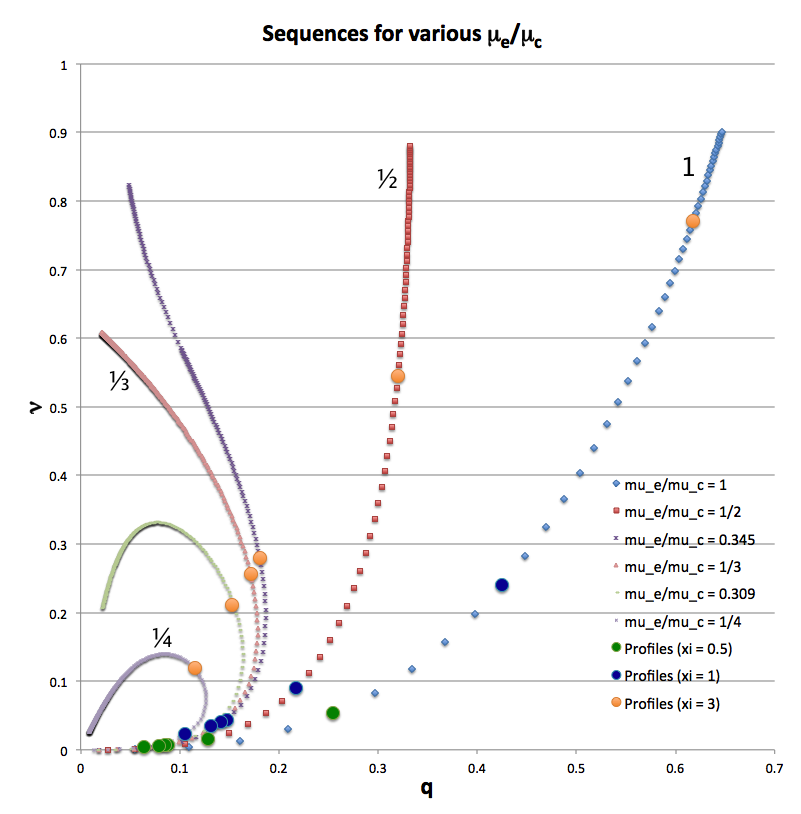
By inspection, in the specific case of <math>~n=5</math> (see above), this critical configuration appears to coincide with one of the "turning points" identified by Kimura. Specifically, it appears to coincide with the "extremal in r1" along an M1 sequence, which satisfies the condition,
|
<math>~\biggl[ \frac{n-3}{n-1} \biggr]_{n=5}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{\tilde\xi \tilde\theta^{n}}{(-\tilde\theta^')}\biggr]_{n=5}</math> |
|
<math>~\Rightarrow ~~~\frac{1}{2} </math> |
<math>~=</math> |
<math>~3^{1/2}\ell \biggl[ (1 + \ell^2)^{-1/2} \biggr]^5 \biggl[ \frac{\ell}{3^{1/2}} (1+\ell^2 )^{-3/2} \biggr]^{-1}</math> |
|
|
<math>~=</math> |
<math>~3(1 + \ell^2)^{-1} </math> |
|
<math>~\Rightarrow~~~ \ell </math> |
<math>~=</math> |
<math>~5^{1/2} \, .</math> |
Hence, according to Kimura, the turning point associated with the configuration with the largest equilibrium radius, corresponds to the equilibrium configuration having,
<math>~\ell |_\mathrm{R_{max}} = \sqrt{5} \approx 2.2360680 \, .</math>
This is, indeed, very close to — but decidedly different from — the value of <math>~\ell_\mathrm{crit}</math> determined, above!
Streamlined
Let's copy the expression for the "Case P" free energy derived above, then factor out a common term:
|
<math>~\frac{\mathfrak{G}_{K,M}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~ -3\mathcal{A} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} +~ n\mathcal{B} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} </math> |
|
|
|
<math>~ +~ \biggl( \frac{4\pi}{3} \biggr) \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(5-n)/(n-3)} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \, . </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(5-n)/(n-3)} \biggl(\frac{n+1}{n}\biggr)^{3/(n-3)} \biggl\{ -3\mathcal{A} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} +~ n\mathcal{B} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} +\frac{4\pi}{3} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \biggr\} </math> |
Defining a new normalization energy,
|
<math>~E_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~E_\mathrm{norm} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(5-n)/(n-3)} \biggl(\frac{n+1}{n}\biggr)^{3/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{n+1}{n}\biggr)^{3/2} K^{3n/(n+1)} G^{-3/2} P_e^{(5-n)/[2(n+1)]} \, , </math> |
we can write,
|
<math>~\mathfrak{G}_{K,M}^* \equiv \frac{\mathfrak{G}_{K,M}}{E_\mathrm{SWS}} </math> |
<math>~=</math> |
<math>~ -3\mathcal{A} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} +~ n\mathcal{B} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} +\frac{4\pi}{3} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^3 \, , </math> |
in which case the coefficients of the generic free-energy expression are,
|
<math>~a</math> |
<math>~=</math> |
<math>~ \frac{3}{5} \cdot \frac{ \tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl(\frac{n+1}{n}\biggr)\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^2 = \frac{3}{5} \cdot \biggl( \frac{4\pi }{3}\biggr)^2 \biggl(\frac{n+1}{n}\biggr)\tilde{\mathfrak{f}}_W \mathfrak{m}^{2}</math> |
|
<math>~b</math> |
<math>~=</math> |
<math>~ n\biggl(\frac{3}{4\pi}\biggr)^{1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} = \biggl( \frac{4\pi n}{3}\biggr) \tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} </math> |
|
<math>~c</math> |
<math>~=</math> |
<math>~ \frac{4\pi}{3} \, , </math> |
where, as above,
|
<math>~\mathfrak{m}</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{3}{4\pi} \biggr) \frac{ 1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr) \, .</math> |
Now, if we define the pair of parameters,
|
<math>~\alpha</math> |
<math>~\equiv</math> |
<math>~\frac{a}{3c}</math> |
|
<math>~\beta</math> |
<math>~\equiv</math> |
<math>~\frac{b}{nc} \, ,</math> |
then the statement of virial equilibrium is,
|
<math>~x_\mathrm{eq}^4 + \alpha</math> |
<math>~=</math> |
<math>~\beta x_\mathrm{eq}^{(n-3)/n} \, ,</math> |
and the boundary between dynamical stability and instability occurs at,
|
<math>~[x_\mathrm{eq}]_\mathrm{crit}^4</math> |
<math>~=</math> |
<math>~\biggl[ \frac{n-3}{3(n+1)} \biggr]\alpha \, .</math> |
Combining these last two expressions means that the boundary between dynamical stability and instability is associated with the parameter condition,
|
<math>~[x_\mathrm{eq}]^{(n-3)/n}_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{n-3}{3(n+1)} + 1\biggr] \frac{\alpha}{\beta} </math> |
|
<math>~\Rightarrow ~~~ \biggl\{ \biggl[ \frac{n-3}{3(n+1)} \biggr]\alpha \biggr\}^{(n-3)/(4n)} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ 4n }{3(n+1)}\biggr] \frac{\alpha}{\beta} </math> |
|
<math>~\Rightarrow ~~~ \beta \alpha^{-3(n+1)/(4n)} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ 4n }{3(n+1)}\biggr] \biggl[ \frac{n-3}{n} \cdot \frac{n}{3(n+1)} \biggr]^{(3-n)/(4n)} </math> |
|
|
<math>~=</math> |
<math>~ 4 \biggl[ \frac{ n }{3(n+1)}\biggr]^{3(n+1)/(4n)} \biggl[ \frac{n-3}{n} \biggr]^{(3-n)/(4n)} </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{\beta}{4}\biggr)^{4n} \alpha^{-3(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ n }{3(n+1)}\biggr]^{3(n+1)} \biggl[ \frac{n-3}{n} \biggr]^{(3-n)} </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{\beta}{4}\biggr)^{4n} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ n\alpha }{3(n+1)}\biggr]^{3(n+1)} \biggl[ \frac{n}{n-3} \biggr]^{n-3} \, . </math> |
Case M
|
<math>~a</math> |
<math>~\equiv</math> |
<math>~3\mathcal{A} = \frac{3}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}\, , </math> |
|
<math>~b</math> |
<math>~\equiv</math> |
<math>~n\mathcal{B} = n\biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, , </math> |
|
<math>~c</math> |
<math>~\equiv</math> |
<math>~\frac{4\pi}{3}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, . </math> |
Hence,
|
<math>~\alpha</math> |
<math>~=</math> |
<math>~\biggl(\frac{4\pi }{15} \biggr) \tilde{\mathfrak{f}}_W \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^2 \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1}</math> |
|
<math>~\beta</math> |
<math>~=</math> |
<math>~\tilde{\mathfrak{f}}_A \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{(n+1)/n} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \, .</math> |
So the dynamical stability conditions are:
|
<math>~\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)\biggl( \frac{n}{n-3} \biggr) [x_\mathrm{eq}]_\mathrm{crit}^4</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr] \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^2 \, ;</math> |
and,
|
<math>~ \biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{4n} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{4(n+1)} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-4n} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ n}{3(n+1)}\biggr]^{3(n+1)} \biggl[ \frac{n}{n-3} \biggr]^{n-3} \biggl(\frac{4\pi \tilde{\mathfrak{f}}_W}{15} \biggr)^{3(n+1)} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{6(n+1)} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-3(n+1)} </math> |
|
<math>~\Rightarrow~~~ \biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{4n} </math> |
<math>~=</math> |
<math>~ \biggl[\biggl(\frac{ n}{n+1}\biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{3(n+1)} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{2(n+1)} \biggl[ \frac{n}{n-3} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)\biggr]^{n-3} </math> |
|
<math>~\Rightarrow~~~\biggl[ \frac{n}{n-3} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)\biggr]^{n-3} </math> |
<math>~=</math> |
<math>~ \biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{4n} \biggl[\biggl(\frac{ n}{n+1}\biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{-3(n+1)} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{-2(n+1)} \, . </math> |
Together, then,
|
<math>~[x_\mathrm{eq}]_\mathrm{crit}^{4(n-3)}</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{n-3} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{2(n-3)} \biggl[ \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \frac{n}{n-3} \biggr]^{-(n-3)} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{n-3} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{2(n-3)} \biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{-4n} \biggl[\biggl(\frac{ n}{n+1}\biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{3(n+1)} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{2(n+1)} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^{4n} \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{4(n-1)} \biggl(\frac{\tilde{\mathfrak{f}}_A}{4}\biggr)^{-4n} </math> |
|
<math>~\Rightarrow ~~~[x_\mathrm{eq}]_\mathrm{crit}^{(n-3)}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{4}{\tilde{\mathfrak{f}}_A}\biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^n \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{(n-1)} \, . </math> |
Case P
|
<math>~a</math> |
<math>~=</math> |
<math>~ \frac{3}{5} \cdot \biggl( \frac{4\pi }{3}\biggr)^2 \biggl(\frac{n+1}{n}\biggr)\tilde{\mathfrak{f}}_W \mathfrak{m}^{2}</math> |
|
<math>~b</math> |
<math>~=</math> |
<math>~\biggl( \frac{4\pi n}{3}\biggr) \tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} </math> |
|
<math>~c</math> |
<math>~=</math> |
<math>~ \frac{4\pi}{3} \, , </math> |
where, as above,
|
<math>~\mathfrak{m}</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{3}{4\pi} \biggr) \frac{ 1}{\tilde{\mathfrak{f}}_M} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr) \, .</math> |
Hence,
|
<math>~\alpha</math> |
<math>~=</math> |
<math>~ \frac{1}{5} \cdot \biggl( \frac{4\pi }{3}\biggr) \biggl(\frac{n+1}{n}\biggr)\tilde{\mathfrak{f}}_W \mathfrak{m}^{2} </math> |
|
<math>~\beta</math> |
<math>~=</math> |
<math>~ \tilde{\mathfrak{f}}_A \mathfrak{m}^{(n+1)/n} \, . </math> |
So the dynamical stability conditions are:
|
<math>~[x_\mathrm{eq}]_\mathrm{crit}^4</math> |
<math>~=</math> |
<math>~\biggl[ \frac{n}{3(n+1)} \biggr]\biggl[ \frac{n-3}{n} \biggr]\frac{1}{5} \cdot \biggl( \frac{4\pi }{3}\biggr) \biggl(\frac{n+1}{n}\biggr)\tilde{\mathfrak{f}}_W \mathfrak{m}^{2} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{n-3}{n} \biggr]\biggl( \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5}\biggr) \mathfrak{m}^{2} </math> |
and,
|
<math>~ \biggl( \frac{\tilde{\mathfrak{f}}_A }{4}\biggr)^{4n} \mathfrak{m}^{4(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{4\pi }{3^2\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \mathfrak{m}^{2}\biggr]^{3(n+1)} \biggl[ \frac{n}{n-3} \biggr]^{n-3} </math> |
|
<math>~ \Rightarrow~~~ \mathfrak{m}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{4\pi }{3^2\cdot 5}\biggr) \tilde{\mathfrak{f}}_W \biggr]^{-3(n+1)} \biggl[ \frac{n}{n-3} \biggr]^{-(n-3)} \biggl( \frac{\tilde{\mathfrak{f}}_A }{4}\biggr)^{4n} \, . </math> |
Together, then,
|
<math>~[x_\mathrm{eq}]_\mathrm{crit}^{4(n+1)}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{n-3}{n} \biggr]^{(n+1)} \biggl( \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5}\biggr)^{(n+1)} \biggl( \frac{4\pi \tilde{\mathfrak{f}}_W }{3^2\cdot 5}\biggr)^{-3(n+1)} \biggl[ \frac{n-3}{n} \biggr]^{(n-3)} \biggl( \frac{\tilde{\mathfrak{f}}_A }{4}\biggr)^{4n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{n-3}{n} \biggr]^{2(n-1)} \biggl( \frac{4\pi \tilde{\mathfrak{f}}_W }{3^2\cdot 5}\biggr)^{-2(n+1)} \biggl( \frac{\tilde{\mathfrak{f}}_A }{4}\biggr)^{4n} \, . </math> |
Compare
Let's see if the two cases, in fact, provide the same answer.
|
<math>~\biggl( \frac{R_\mathrm{norm}}{R_\mathrm{SWS}}\biggr)^{n-3} = \biggl[ \frac{x_\mathrm{P}}{x_\mathrm{M}} \biggr]_\mathrm{crit}^{n-3}</math> |
<math>~=</math> |
<math>~ \biggl\{ \biggl[ \frac{n-3}{n} \biggr]\biggl( \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5}\biggr) \mathfrak{m}^{2} \biggr\}^{(n-3)/4} \biggl\{ \biggl[ \frac{4}{\tilde{\mathfrak{f}}_A}\biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^n \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{(n-1)} \biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ \biggl[ \frac{n-3}{n} \biggr]\biggl( \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5}\biggr) \mathfrak{m}^{2} \biggr\}^{(n-3)/4} \biggl\{ \biggl[ \frac{4}{\tilde{\mathfrak{f}}_A}\biggl( \frac{n}{n+1} \biggr) \frac{4\pi \tilde{\mathfrak{f}}_W}{3^2\cdot 5} \biggr]^n \biggl(\frac{3}{4\pi \tilde{\mathfrak{f}}_M}\biggr)^{(n-1)} \biggr\}^{-1} </math> |
Five-One Bipolytropes
For analytically prescribed, "five-one" bipolytropes, <math>~n = 5</math> and <math>~j =1</math>, in which case,
|
<math>~x^{2/5 }_\mathrm{eq}</math> |
<math>~=</math> |
<math>~\biggl(\frac{5}{ 3b}\biggr) \biggl[a -3 c x^{-2}_\mathrm{eq} \biggr] \, ;</math> |
|
|
and |
|
|
<math>~[x_\mathrm{eq}]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl[ \frac{18 c}{a }\biggr]^{1/2} \, . </math> |
More specifically, the expression that describes the free-energy surface is,
|
Hence, we have,
|
<math>~a</math> |
<math>~\equiv</math> |
<math>~ 3\chi_\mathrm{eq}(\mathfrak{L}_i + 4\mathfrak{K}_i) \, , </math> |
|
<math>~b</math> |
<math>~\equiv</math> |
<math>~ 5 \mathfrak{L}_i \chi_\mathrm{eq}^{3/5} \, , </math> |
|
<math>~c</math> |
<math>~\equiv</math> |
<math>~ 4 \mathfrak{K}_i \chi_\mathrm{eq}^{3} \, , </math> |
and conclude that,
|
<math>~[\chi_\mathrm{eq}]_\mathrm{crit}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{18 (4 \mathfrak{K}_i \chi_\mathrm{eq}^{3} )}{ 3\chi_\mathrm{eq}(\mathfrak{L}_i + 4\mathfrak{K}_i)} \biggr]^{1/2}_\mathrm{crit} </math> |
|
|
<math>~=</math> |
<math>~[\chi_\mathrm{eq}]_\mathrm{crit}\biggl[ \frac{24 \mathfrak{K}_i }{ (\mathfrak{L}_i + 4\mathfrak{K}_i)} \biggr]^{1/2} </math> |
|
<math>~\Rightarrow~~~\biggl[ \frac{24 \mathfrak{K}_i }{ (\mathfrak{L}_i + 4\mathfrak{K}_i)} \biggr]_\mathrm{crit}</math> |
<math>~=</math> |
<math>~1 </math> |
|
<math>~\Rightarrow~~~\biggl[ \frac{\mathfrak{L}_i }{ \mathfrak{K}_i } \biggr]_\mathrm{crit}</math> |
<math>~=</math> |
<math>~20 \, . </math> |
Also, from our detailed force balance derivations, we know that,
|
<math>~\chi_\mathrm{eq} \equiv \frac{ R_\mathrm{eq}}{R_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} \, .</math> |
Zero-Zero Bipolytropes
General Form
In this case, we retain full generality making the substitutions, <math>~n \rightarrow n_c</math> and <math>~j \rightarrow n_e</math>, to obtain,
|
<math>~x^{(n_c-3)/n_c }_\mathrm{eq}</math> |
<math>~=</math> |
<math>~\frac{n_c}{ 3b} \biggl[a -\biggl(\frac{3 c}{n_e}\biggr) x^{(n_e-3)/n_e}_\mathrm{eq} \biggr] \, ;</math> |
|
|
and |
|
|
<math>~[x_\mathrm{eq}^{(n_e-3)/n_e}]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl\{\frac{n_e^2(n_c-3)}{3[ n_c (n_e+3) - n_e(n_c+3) ]}\biggr\} \frac{a}{c} </math> |
|
|
<math>~=</math> |
<math>~\biggl[\frac{n_e^2(n_c-3)}{3^2(n_c - n_e)}\biggr] \frac{a}{c} \, . </math> |
And here, the expression that describes the free-energy surface is,
|
Hence, we have,
|
<math>~a \equiv 3\chi_\mathrm{eq} \biggl(\frac{5}{2q^3} \biggr) C_2 </math> |
<math>~=</math> |
<math> 3f \chi_\mathrm{eq} \, , </math> |
|
<math>~b \equiv n_c \chi_\mathrm{eq}^{3/n_c} \biggl(\frac{5}{2q^3} \biggr) A_2 </math> |
<math>~\equiv</math> |
<math> n_c \chi_\mathrm{eq}^{3/n_c} \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, , </math> |
|
<math>~c \equiv n_e \chi_\mathrm{eq}^{3/n_e} \biggl(\frac{5}{2q^3} \biggr) B_2 </math> |
<math>~\equiv</math> |
<math>~ n_e \chi_\mathrm{eq}^{3/n_e} \biggl(\frac{5}{2q^3} \biggr) \biggl[\frac{2}{5} q^3 f - A_2\biggr] </math> |
|
|
<math>~=</math> |
<math>~ n_e \chi_\mathrm{eq}^{3/n_e} \biggl\{ f - \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \biggr\} \, , </math> |
where the definitions of <math>~f</math> and <math>~\mathfrak{F}</math> are given below. We immediately deduce that the critical equilibrium state is identified by,
|
<math>~[x_\mathrm{eq}^{(n_e-3)/n_e}]_\mathrm{crit} </math> |
<math>~=</math> |
<math>~\biggl\{\frac{fn_e(n_c-3)}{3(n_c - n_e)}\biggr\} [\chi_\mathrm{eq}^{(n_e-3)/n_e}]_\mathrm{crit} \biggl\{ f - \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \biggr\}^{-1} </math> |
|
<math>~\Rightarrow ~~~\frac{1}{f}\biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr]</math> |
<math>~=</math> |
<math>~ 1 - \biggl[ \frac{n_e(n_c-3)}{3(n_c-n_e)} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{n_c(3-n_e)}{3(n_c-n_e)} \, .</math> |
From our associated detailed-force-balance derivation, we know that the associated equilibrium radius is,
|
<math>~\chi_\mathrm{eq}</math> |
<math>~=</math> |
<math>~ \biggl\{ \biggl(\frac{\pi}{3}\biggr) 2^{2-n_c} \nu^{n_c-1} q^{3-n_c} \biggl[1 + \frac{2}{5} q^3(f-1-\mathfrak{F})\biggr]^{n_c} \biggr\}^{1/(n_c-3)} \, . </math> |
Compare with Five-One
It is worthwhile to set <math>~n_c = 5</math> and <math>~n_e = 1</math> in this expression and compare the result to the comparable expression shown above for the "Five-One" Bipolytrope. Here we have,
|
<math>~\biggl[\chi_\mathrm{eq}\biggr]_{51}</math> |
<math>~=</math> |
<math>~ \biggl\{ \biggl(\frac{\pi}{3}\biggr) 2^{-3} \nu^{4} q^{-2} \biggl[1 + \frac{2}{5} q^3(f-1-\mathfrak{F})\biggr]^{5} \biggr\}^{1/2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{1}{\sqrt{3}} \biggl[1 + \frac{2}{5} q^3(f-1-\mathfrak{F})\biggr]^{5/2} \, ; </math> |
whereas, rewriting the above relation gives,
|
<math>~\chi_\mathrm{eq}\biggr|_{51}</math> |
<math>~=</math> |
<math>~\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{1}{\sqrt{3}} \biggl[\frac{(1+\ell_i^2)^{6/5}}{3\ell_i^2}\biggr]^{5/2} \, .</math> |
And, here, we should conclude that the critical equilibrium configuration is associated with,
|
<math>~\frac{1}{f}\biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr]</math> |
<math>~=</math> |
<math>~ \frac{5}{6} \, .</math> |
Free-Energy of Truncated Polytropes
In this case, the Gibbs-like free energy is given by the sum of three separate energies,
|
<math>~\mathfrak{G}</math> |
<math>~=</math> |
<math>~W_\mathrm{grav} + \mathfrak{S}_\mathrm{therm} + P_eV</math> |
|
|
<math>~=</math> |
<math>~ - 3\mathcal{A} \biggl[\frac{GM^2}{R} \biggr] + n\mathcal{B} \biggl[ \frac{KM^{(n+1)/n}}{R^{3/n}} \biggr] + \frac{4\pi}{3} \cdot P_e R^3 \, ,</math> |
where the constants,
|
<math>~\mathcal{A} \equiv \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}</math> |
and |
<math>\mathcal{B} \equiv \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, ,</math> |
and, as derived elsewhere,
|
Structural Form Factors for Pressure-Truncated Polytropes <math>~(n \ne 5)</math> |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|||||||||
|
As we have shown separately, for the singular case of <math>~n = 5</math>,
where, <math>~\ell \equiv \tilde\xi/\sqrt{3} </math> |
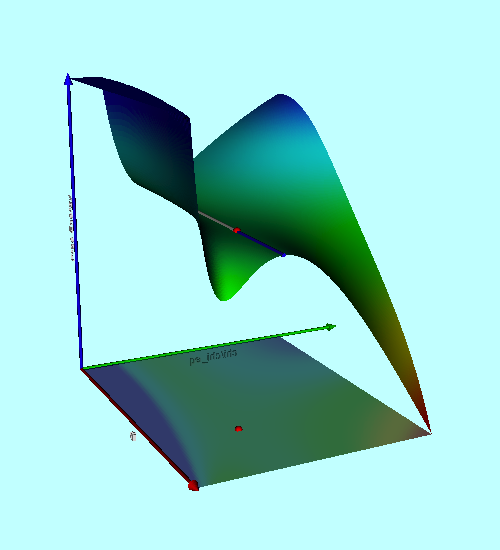
In general, then, the warped free-energy surface drapes across a four-dimensional parameter "plane" such that,
|
<math>~\mathfrak{G}</math> |
<math>~=</math> |
<math>~\mathfrak{G}(R, K, M, P_e) \, .</math> |
In order to effectively visualize the structure of this free-energy surface, we will reduce the parameter space from four to two, in two separate ways: First, we will hold constant the parameter pair, <math>~(K,M)</math>; giving a nod to Kimura's (1981b) nomenclature, we will refer to the resulting function, <math>~\mathfrak{G}_{K,M}(R,P_e)</math>, as a "Case M" free-energy surface because the mass is being held constant. Second, we will hold constant the parameter pair, <math>~(K,P_e)</math>, and examine the resulting "Case P" free-energy surface, <math>~\mathfrak{G}_{K,P_e}(R,M)</math>.
Virial Equilibrium and Dynamical Stability
The first (partial) derivative of <math>~\mathfrak{G}</math> with respect to <math>~R</math> is,
|
<math>~\frac{\partial \mathfrak{G}}{\partial R}</math> |
<math>~=</math> |
<math>~ \frac{1}{R} \biggl[ 3\mathcal{A} GM^2 R^{-1} - 3\mathcal{B}KM^{(n+1)/n} R^{-3/n} + 4\pi P_e R^3 \biggr] \, ; </math> |
and the second (partial) derivative is,
|
<math>~\frac{\partial^2 \mathfrak{G}}{\partial R^2}</math> |
<math>~=</math> |
<math>~ \frac{1}{R^2} \biggl[ -6\mathcal{A} GM^2 R^{-1} + \biggl(\frac{n+3}{n}\biggr) 3\mathcal{B}KM^{(n+1)/n} R^{-3/n} + 8\pi P_e R^3 \biggr] \, . </math> |
The virial equilibrium radius is identified by setting the first derivative to zero. This means that,
|
<math>~3\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n}</math> |
<math>~=</math> |
<math>~ 3\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + 4\pi P_e R_\mathrm{eq}^3 \, . </math> |
This expression can be usefully rewritten in the following forms:
| Virial Equilibrium Condition | ||||
| Case 1: |
|
|||
| Case 2: |
|
|||
| Case 3: |
|
|||
Dynamical stability is determined by the sign of the second derivative expression evaluated at the equilibrium radius; setting the second derivative to zero identifies the transition from stable to unstable configurations. The criterion is,
|
<math>~0</math> |
<math>~=</math> |
<math>~\biggl[ -6n\mathcal{A} GM^2 R^{-1} + 3(n+3) \mathcal{B}KM^{(n+1)/n} R^{-3/n} + 8\pi nP_e R^3\biggr]_{R_\mathrm{eq}} </math> |
Case 1 Stability Criterion
Using the "Case 1" virial expression to define the equilibrium radius means that the stability criterion is,
|
<math>~0</math> |
<math>~=</math> |
<math>~ -6n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + 3(n+3)\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + 4\pi (n+3) P_e R_\mathrm{eq}^3 + 8\pi nP_e R_\mathrm{eq}^3 </math> |
|
|
<math>~=</math> |
<math>~ \mathcal{A} GM^2 R_\mathrm{eq}^{-1} [3(n+3)- 6n ] + 4\pi P_e R_\mathrm{eq}^3 [(n+3) + 2n] </math> |
|
<math>~\Rightarrow ~~~ 4\pi P_e R_\mathrm{eq}^3 [3(n+1) ] </math> |
<math>~=</math> |
<math>~ \mathcal{A} GM^2 R_\mathrm{eq}^{-1} [3(n-3)] </math> |
|
<math>~\Rightarrow ~~~ 4\pi P_e R_\mathrm{eq}^4 (n+1) </math> |
<math>~=</math> |
<math>~ \mathcal{A} GM^2 (n-3) </math> |
Case 2 Stability Criterion
Using the "Case 2" virial expression to define the equilibrium radius means that the stability criterion is,
|
<math>~0</math> |
<math>~=</math> |
<math>~ 8\pi nP_e R_\mathrm{eq}^3 - 6n\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} + 3(n+3) \mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} + 8\pi nP_e R_\mathrm{eq}^3
</math> |
|
|
<math>~=</math> |
<math>~ 16\pi nP_e R_\mathrm{eq}^3 - [3(n-3)]\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} </math> |
|
<math>~\Rightarrow~~~ 16\pi nP_e R_\mathrm{eq}^3 </math> |
<math>~=</math> |
<math>~ [3(n-3)]\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} </math> |
|
<math>~\Rightarrow~~~ 16\pi nP_e R_\mathrm{eq}^{3(n+1)/n} </math> |
<math>~=</math> |
<math>~ [3(n-3)]\mathcal{B}KM^{(n+1)/n} </math> |
Case 3 Stability Criterion
Using the "Case 3" virial expression to define the equilibrium radius means that the stability criterion is,
|
<math>~0</math> |
<math>~=</math> |
<math>~ -6n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + 3(n+3) \mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} + 6n\mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} - 6n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} </math> |
|
|
<math>~=</math> |
<math>~ -12n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} + [6n +3(n+3)] \mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} </math> |
|
<math>~\Rightarrow~~~ 9(n+1) \mathcal{B}KM^{(n+1)/n} R_\mathrm{eq}^{-3/n} </math> |
<math>~=</math> |
<math>~ 12n\mathcal{A} GM^2 R_\mathrm{eq}^{-1} </math> |
|
<math>~\Rightarrow~~~ R_\mathrm{eq}^{n-3} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{4n\mathcal{A}}{3(n+1) \mathcal{B}} \biggr]^n \biggl(\frac{G}{K}\biggr)^n M^{n-1} </math> |
Case M
Now, in our discussion of "Case M" sequence analyses, the configuration's radius is normalized to,
|
<math>~R_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~[ G^n K^{-n} M^{n-1} ]^{1/(n-3)} \, .</math> |
Our "Case 3" stability criterion directly relates. We conclude that the transition from stability to dynamical instability occurs when,
|
<math>~ \biggl[\frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr]_\mathrm{crit}^{n-3} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{4n\mathcal{A}}{3(n+1) \mathcal{B}} \biggr]^n </math> |
|
<math>~\Rightarrow~~~ \biggl[\frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr]_\mathrm{crit}^{(n-3)/n} </math> |
<math>~=</math> |
<math>~ \frac{4n}{15(n+1) } \biggl(\frac{4\pi}{3}\biggr)^{1/n}\cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_A \tilde{\mathfrak{f}}_M^{(n-1)/n}} </math> |
Also in the "Case M" discussions, the external pressure is normalized to,
|
<math>~P_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~[ G^{-3(n+1)} K^{4n} M^{-2(n+1)} ]^{1/(n-3)} \, .</math> |
If we raise the "Case 1" stability criterion expression to the <math>~(n-3)</math> power, then divide it by the "Case 3" stability criterion expression raised to the fourth power, we find,
|
<math>~\Rightarrow ~~~ [P_e]_\mathrm{crit}^{n-3} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{\mathcal{A} GM^2 (n-3)}{4\pi (n+1)}\biggr]^{n-3}\biggl\{ \biggl[\frac{4n\mathcal{A}}{3(n+1) \mathcal{B}} \biggr]^n \biggl(\frac{G}{K}\biggr)^n M^{n-1} \biggr\}^{-4} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{\mathcal{A} (n-3)}{4\pi (n+1)}\biggr]^{n-3} G^{n-3} M^{2(n-3)} \biggl[\frac{3(n+1) \mathcal{B}}{4n\mathcal{A}} \biggr]^{4n} \biggl(\frac{K}{G}\biggr)^{4n} M^{4(1-n)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} K^{4n} M^{-2(n+1)} G^{-3(n+1)} </math> |
|
<math>~\Rightarrow ~~~ \biggl[\frac{P_e}{P_\mathrm{norm}} \biggr]_\mathrm{crit}^{n-3} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \biggl[ \frac{ 5\tilde{\mathfrak{f}}_M^2 }{ \tilde{\mathfrak{f}}_W } \biggr]^{3(n+1)} \biggl( \frac{3}{4\pi}\biggr)^4 \biggl[ \frac{ \tilde{\mathfrak{f}}_A }{ \tilde{\mathfrak{f}}_M^{(n+1)/n} } \biggr]^{4n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{3}{4\pi}\biggr)^4 \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \biggl[ \frac{ 5 }{ \tilde{\mathfrak{f}}_W } \biggr]^{3(n+1)} \tilde{\mathfrak{f}}_M^{2(n+1)} \tilde{\mathfrak{f}}_A^{4n} </math> |
Case P
Flipping around this expression for <math>~[P_e]_\mathrm{crit}</math>, we also can write,
|
<math>~ [M]_\mathrm{crit}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} K^{4n} G^{-3(n+1)} P_e^{3-n} \, . </math> |
Now, in our "Case P" discussions we normalized the mass to
|
<math>~M_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~ \biggl(\frac{n+1}{n}\biggr)^{3/2} G^{-3/2} K^{2n/(n+1)} P_e^{(3-n)/[2(n+1)]} \, . </math> |
Hence, we have,
|
<math>~\biggl[\frac{M}{M_\mathrm{SWS}} \biggr]_\mathrm{crit}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} \biggl(\frac{n+1}{n}\biggr)^{-3(n+1)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl(\frac{3 }{4} \biggr)^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} \, , </math> |
where the constants,
|
<math>~\mathcal{A} \equiv \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}</math> |
and |
<math>\mathcal{B} \equiv \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, .</math> |
So we can furthermore conclude that,
|
<math>~\biggl[\frac{M}{M_\mathrm{SWS}} \biggr]_\mathrm{crit}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl(\frac{3 }{4} \biggr)^{4n} \biggl\{ \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr\}^{-3(n+1)} \biggl\{ \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggr\}^{4n} </math> |
|
|
<math>~=</math> |
<math>~\biggl(\frac{3}{4\pi} \biggr)^{4} \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl(\frac{3\tilde{\mathfrak{f}}_A }{4} \biggr)^{4n} \biggl[ \frac{5^3\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W^3} \biggr]^{(n+1)} \, . </math> |
Our expression for <math>~[M]_\mathrm{crit}^{2(n+1)}</math> can also be combined with the "Case 2 stability criterion" to eliminate the mass entirely, giving,
|
<math>~ \biggl\{ 16\pi nP_e R_\mathrm{eq}^{3(n+1)/n} \biggr\}^{2n} </math> |
<math>~=</math> |
<math>~ \biggl\{ [3(n-3)]\mathcal{B}K\biggr\}^{2n} \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{4n} K^{4n} G^{-3(n+1)} P_e^{3-n} </math> |
|
<math>~\Rightarrow~~~ R_\mathrm{eq}^{6(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ 3(n-3)}{16\pi n} \biggr]^{2n} \biggl[\frac{ (n-3)}{4\pi (n+1)}\biggr]^{n-3} \biggl[\frac{3(n+1) }{4n} \biggr]^{4n} \mathcal{A}^{-3(n+1)} \mathcal{B}^{6n} K^{6n} G^{-3(n+1)} P_e^{3(1-n)} </math> |
|
<math>~\Rightarrow~~~ R_\mathrm{eq}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl\{ \biggl[ \frac{ (n-3)}{4\pi n} \biggr]^{2n} \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl[\frac{(n+1) }{n} \biggr]^{4n+(3-n)} \biggl(\frac{3 }{4} \biggr)^{6n} \biggr\}^{1/3} \mathcal{A}^{-(n+1)} \mathcal{B}^{2n} K^{2n} G^{-(n+1)} P_e^{(1-n)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{ (n-3)}{4\pi n} \biggr]^{(n-1)} \biggl[\frac{(n+1) }{n} \biggr]^{(n+1)} \biggl(\frac{3 }{4} \biggr)^{2n} \mathcal{A}^{-(n+1)} \mathcal{B}^{2n} K^{2n} G^{-(n+1)} P_e^{(1-n)} \, . </math> |
Finally, recognizing that in our "Case P" discussions we normalized the radius to
|
<math>~R_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~ \biggl(\frac{n+1}{n}\biggr)^{1/2} G^{-1/2} K^{n/(n+1)} P_e^{(1-n)/[2(n+1)]} \, , </math> |
we have,
|
<math>~ [R_\mathrm{eq}]_\mathrm{crit}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ (n-3)}{4\pi n} \biggr]^{(n-1)} \biggl(\frac{n+1 }{n} \biggr)^{(n+1)} \biggl(\frac{3 }{4} \biggr)^{2n} \mathcal{A}^{-(n+1)} \mathcal{B}^{2n} \biggl\{ R_\mathrm{SWS}\biggl(\frac{n+1 }{n} \biggr)^{-1/2} \biggr\}^{2(n+1)} </math> |
|
<math>~\Rightarrow~~~ \biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]_\mathrm{crit}^{2(n+1)} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{ (n-3)}{4\pi n} \biggr]^{(n-1)} \biggl(\frac{3 }{4} \biggr)^{2n} \mathcal{A}^{-(n+1)} \mathcal{B}^{2n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{n}{n-3} \biggr]^{(1-n)} (4\pi)^{1-n}\biggl(\frac{3 }{4} \biggr)^{2n} \biggl[ \frac{1}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggr]^{-(n+1)} \biggl[ \biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggr]^{2n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{n}{n-3} \biggr]^{(1-n)} (4\pi)^{1-n -2} 3^{2n+2} 4^{-2n} \biggl[ \frac{5\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W}\biggr]^{(n+1)} \biggl[ \frac{\tilde{\mathfrak{f}}_A^{2n}}{\tilde{\mathfrak{f}}_M^{2(n+1)}} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{n}{n-3} \biggr]^{(1-n)} \biggl[ \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W}\biggr]^{(n+1)} \biggl[\frac{ \tilde{\mathfrak{f}}_A}{4} \biggr]^{2n} \, . </math> |
Case M Free-Energy Surface
It is useful to rewrite the free-energy function in terms of dimensionless parameters. Here we need to pick normalizations for energy, radius, and pressure that are expressed in terms of the gravitational constant, <math>~G</math>, and the two fixed parameters, <math>~K</math> and <math>~M</math>. We have chosen to use,
|
<math>~R_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} \biggr]^{1/(n-3)} \, ,</math> |
|
<math>~P_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}} \biggr]^{1/(n-3)} \, ,</math> |
which, as is detailed in an accompanying discussion, are similar but not identical to the normalizations used by Horedt (1970) and by Whitworth (1981). The self-consistent energy normalization is,
|
<math>~E_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~P_\mathrm{norm} R^3_\mathrm{norm} \, .</math> |
As we have demonstrated elsewhere, after implementing these normalizations, the expression that describes the "Case M" free-energy surface is,
<math> \mathfrak{G}_{K,M}^* \equiv \frac{\mathfrak{G}_{K,M}}{E_\mathrm{norm}} = -3\mathcal{A} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^{-1} +~ n\mathcal{B} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^{-3/n} +~ \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \biggl(\frac{R}{R_\mathrm{norm}}\biggr)^3 \, , </math>
Given the polytropic index, <math>~n</math>, we expect to obtain a different "Case M" free-energy surface for each choice of the dimensionless truncation radius, <math>~\tilde\xi</math>; this choice will imply corresponding values for <math>~\tilde\theta</math> and <math>~\tilde\theta^'</math> and, hence also, corresponding (constant) values of the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>.
Case P Free-Energy Surface
Again, it is useful to rewrite the free-energy function in terms of dimensionless parameters. But here we need to pick normalizations for energy, radius, and mass that are expressed in terms of the gravitational constant, <math>~G</math>, and the two fixed parameters, <math>~K</math> and <math>~P_e</math>. As is detailed in an accompanying discussion, we have chosen to use the normalizations defined by Stahler (1983), namely,
|
<math>~R_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{n+1}{nG} \biggr)^{1/2} K^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \, ,</math> |
|
<math>~M_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{n+1}{nG} \biggr)^{3/2} K^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \, .</math> |
The self-consistent energy normalization is,
|
<math>~E_\mathrm{SWS} \equiv \biggl( \frac{n}{n+1} \biggr) \frac{GM_\mathrm{SWS}^2}{R_\mathrm{SWS}}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2}K^{3n/(n+1)} P_\mathrm{e}^{(5-n)/[2(n+1)]} \, .</math> |
After implementing these normalizations — see our accompanying analysis for details — the expression that describes the "Case P" free-energy surface is,
|
<math>~\mathfrak{G}_{K,P_e}^* \equiv \frac{\mathfrak{G}_{K,P_e}}{E_\mathrm{SWS}}</math> |
<math>~=</math> |
<math>~- 3 \mathcal{A} \biggl( \frac{n+1}{n} \biggr)\biggl( \frac{M}{M_\mathrm{SWS}}\biggr)^2 \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} + n\mathcal{B} \biggl(\frac{M}{M_\mathrm{SWS}}\biggr)^{(n+1)/n} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} + \frac{4\pi}{3} \cdot \biggl( \frac{R}{R_\mathrm{SWS}}\biggr)^3 \, . </math> |
Given the polytropic index, <math>~n</math>, we expect to obtain a different "Case P" free-energy surface for each choice of the dimensionless truncation radius, <math>~\tilde\xi</math>; this choice will imply corresponding values for <math>~\tilde\theta</math> and <math>~\tilde\theta^'</math> and, hence also, corresponding (constant) values of the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>.
Summary
| DFB Equilibrium | Onset of Dynamical Instability | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Case M: |
|
|
||||||||
|
|
|||||||||
| Case P: |
|
|
||||||||
|
|
|||||||||
|
In all four cases, the expression on right intersects (is equal to) the expression on the left when the following condition applies:
|
||||||||||
If (for <math>n\ne 5</math>) we adopt the shorthand notation,
|
<math>~\Upsilon</math> |
<math>~\equiv</math> |
<math>~[3 (-{\tilde\theta}^')^2 - {\tilde\mathfrak{f}}_M \tilde\theta] = 3\biggl[ (-{\tilde\theta}^')^2 - \biggl( -\frac{\tilde\theta {\tilde\theta}^'}{\tilde\xi} \biggr)\biggr] \, , </math> |
|
and |
||
|
<math>~\tau</math> |
<math>~\equiv</math> |
<math>~{\tilde\theta}^{n+1} \, , </math> |
then the critical condition becomes,
|
<math>~(n-3)\Upsilon</math> |
<math>~=</math> |
<math>~2(9-2n)\tau \, ,</math> |
and at the critical state, the expressions for the structural form-factors become,
|
<math>~{\tilde\mathfrak{f}}_A</math> |
<math>~=</math> |
<math>~\frac{1}{(5-n)} \biggl[6\tau + (n+1)\Upsilon \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{(5-n)} \biggl\{ 6 + (n+1)\biggl[ \frac{2(9-2n)}{n-3} \biggr] \biggr\}\tau </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{(5-n)} \biggl[ \frac{6(n-3) + 2(9-2n)(n+1)}{n-3} \biggr] \tau </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{(5-n)} \biggl[ \frac{4n(5-n)}{n-3} \biggr] \tau </math> |
|
|
<math>~=</math> |
<math>~\frac{4n\tau}{(n-3)} \, ;</math> |
|
<math>~{\tilde\mathfrak{f}}_W</math> |
<math>~=</math> |
<math>~\frac{3\cdot 5}{(5-n) {\tilde\xi}^2} \biggl[\tau + \Upsilon \biggr]</math> |
|
|
<math>~=</math> |
<math>~\frac{3\cdot 5}{(5-n) {\tilde\xi}^2} \biggl\{1 + \biggl[ \frac{2(9-2n)}{n-3} \biggr] \biggr\}\tau</math> |
|
|
<math>~=</math> |
<math>~\frac{3\cdot 5}{(5-n) {\tilde\xi}^2} \biggl[ \frac{3(5-n)}{n-3} \biggr] \tau</math> |
|
|
<math>~=</math> |
<math>~\frac{3^2\cdot 5 \tau}{(n-3) {\tilde\xi}^2} </math> |
|
<math>~\Rightarrow~~~ \frac{5^3\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W^3} </math> |
<math>~=</math> |
<math>~ \biggl[\frac{(n-3) {\tilde\xi}^2}{3^2\tau} \biggr]^{3} \biggl(-\frac{3 {\tilde\theta}^'}{\tilde\xi} \biggr)^2 = 3^2\biggl[\frac{(n-3) {\tilde\xi}^2}{3^2\tau} \biggr]^{3} \biggl(-\frac{{\tilde\xi}^2 {\tilde\theta}^'}{ {\tilde\xi}^3 } \biggr)^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(n-3)^3}{3^4\tau^3} \biggr] (-{\tilde\xi}^2 {\tilde\theta}^' )^2 \, . </math> |
Hence (1),
|
<math>~\biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr]_\mathrm{crit}^{n-3}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{4\pi}{(n+1)^n }\biggr] \biggl[ \frac{4n}{15}\biggr]^n \biggl(\frac{1}{3}\biggr) \biggl[ \frac{3^2\cdot 5 }{4n {\tilde\xi}^2} \biggr]^n \tilde{\mathfrak{f}}_M^{1-n} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{4\pi}{(n+1)^n }\biggr] \biggl[ \frac{1}{ {\tilde\xi}^{2n}} \biggr] \biggl( \frac{-{\tilde\xi}^2{\tilde\theta}^'}{{\tilde\xi}^3} \biggr)^{1-n} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{4\pi}{(n+1)^n }\biggr] {\tilde\xi}^{n-3} (-{\tilde\xi}^2{\tilde\theta}^')^{1-n} </math> |
Q.E.D.
And (2),
|
<math>~\biggl[ \frac{P_\mathrm{e}}{P_\mathrm{norm}}\biggr]_\mathrm{crit}^{n-3}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{3}{4\pi}\biggr)^4 \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{n-3} \biggl(\frac{n+1}{n} \biggr)^{3(n+1)} \biggl[ \frac{ 5^3 \tilde{\mathfrak{f}}_M^2}{ \tilde{\mathfrak{f}}_W^3 } \biggr]^{n+1} \biggl( \frac{3\tilde{\mathfrak{f}}_A}{4}\biggr)^{4n} </math> |
|
|
<math>~=</math> |
<math>~3^{4} (4\pi)^{-(n+1)} \biggl(\frac{ n-3}{n}\biggr)^{n-3} \biggl(\frac{n+1}{n} \biggr)^{3(n+1)} \biggl[ \frac{(n-3)^3}{3^4\tau^3} \biggr]^{n+1} (-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} \biggl[ \frac{3n\tau}{n-3} \biggr]^{4n} </math> |
|
|
<math>~=</math> |
<math>~3^{4} (4\pi)^{-(n+1)} \biggl(\frac{ n-3}{n}\biggr)^{n-3} \biggl(\frac{n+1}{n} \biggr)^{3(n+1)} n^{3(n+1)} \biggl[ \frac{n-3}{n} \biggr]^{3(n+1)} (-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} \biggl[ \frac{n}{n-3} \biggr]^{4n} \tau^{4n-3(n+1)} 3^{4n-4(n+1)} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{n+1} (-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} \tau^{n-3} </math> |
|
<math>~\Rightarrow ~~~\biggl[ \frac{P_\mathrm{e}}{P_\mathrm{norm}}\biggr]_\mathrm{crit}^{n-3}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{n+1} (-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} {\tilde\theta}^{(n+1)(n-3)} \, . </math> |
Q.E.D.
And (3),
|
<math>~\biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]^{2(n+1)}_\mathrm{crit}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{3^2\cdot 5}{4\pi \tilde{\mathfrak{f}}_W}\biggr]^{n+1} \biggl[ \frac{n-3}{n} \biggr]^{(n-1) } \biggl[\frac{ \tilde{\mathfrak{f}}_A}{4} \biggr]^{2n } </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{3^2\cdot 5}{4\pi }\biggr]^{n+1} \biggl[ \frac{n-3}{n} \biggr]^{(n-1) } \biggl[ \frac{ n\tau}{n-3} \biggr]^{2n } \biggl[ \frac{(n-3){\tilde\xi}^2}{3^2\cdot 5 \tau} \biggr]^{n+1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{1}{4\pi }\biggr]^{n+1} \biggl[ \frac{ n}{n-3} \biggr]^{n+1 } \biggl[ (n-3){\tilde\xi}^2\biggr]^{n+1} \tau^{n-1} </math> |
|
<math>~\Rightarrow ~~~ \biggl[ \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr]^{2}_\mathrm{crit}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{n}{4\pi }\biggr) {\tilde\xi}^2 {\tilde\theta}^{n-1} </math> |
Q.E.D.
And (4),
|
<math>~\biggl[ \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr]_\mathrm{crit}^{2(n+1)}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{5^3\tilde{\mathfrak{f}}_M^2}{\tilde{\mathfrak{f}}_W^3} \biggr]^{n+1} \biggl(\frac{3}{4\pi} \biggr)^{4} \biggl[\frac{ (n-3)}{4\pi n}\biggr]^{(n-3)} \biggl(\frac{3\tilde{\mathfrak{f}}_A }{4} \biggr)^{4n} </math> |
|
|
<math>~=</math> |
<math>~\biggl\{ \biggl[ \frac{(n-3)^3}{3^4\tau^3} \biggr] (-{\tilde\xi}^2 {\tilde\theta}^' )^2 \biggr\}^{n+1} 3^4(4\pi)^{-(n+1)} \biggl(\frac{ n-3}{n}\biggr)^{(n-3)} \biggl[\frac{3n\tau }{n-3} \biggr]^{4n} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{n^3}{4\pi}\biggr]^{n+1}(-{\tilde\xi}^2 {\tilde\theta}^' )^{2(n+1)} \tau^{n-3} </math> |
|
<math>~\Rightarrow~~~ \biggl[ \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr]_\mathrm{crit}^{2} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{n^3}{4\pi}\biggr](-{\tilde\xi}^2 {\tilde\theta}^' )^{2} {\tilde\theta}^{n-3} </math> |
Q.E.D.
Free-Energy of Bipolytropes
In this case, the Gibbs-like free energy is given by the sum of four separate energies,
|
<math>~\mathfrak{G}</math> |
<math>~=</math> |
<math>~ \biggl[W_\mathrm{grav} + \mathfrak{S}_\mathrm{therm}\biggr]_\mathrm{core} + \biggl[W_\mathrm{grav} + \mathfrak{S}_\mathrm{therm}\biggr]_\mathrm{env} \, . </math> |
In addition to specifying (generally) separate polytropic indexes for the core, <math>~n_c</math>, and envelope, <math>~n_e</math>, and an envelope-to-core mean molecular weight ratio, <math>~\mu_e/\mu_c</math>, we will assume that the system is fully defined via specification of the following five physical parameters:
- Total mass, <math>~M_\mathrm{tot}</math>;
- Total radius, <math>~R</math>;
- Interface radius, <math>~R_i</math>, and associated dimensionless interface marker, <math>~q \equiv R_i/R</math>;
- Core mass, <math>~M_c</math>, and associated dimensionless mass fraction, <math>~\nu \equiv M_c/M_\mathrm{tot}</math>;
- Polytropic constant in the core, <math>~K_c</math>.
In general, the warped free-energy surface drapes across a five-dimensional parameter "plane" such that,
|
<math>~\mathfrak{G}</math> |
<math>~=</math> |
<math>~\mathfrak{G}(R, K_c, M_\mathrm{tot}, q, \nu) \, .</math> |
Order of Magnitude Derivation
Let's begin by providing very rough, approximate expressions for each of these four terms, assuming that <math>~n_c = 5</math> and <math>~n_e = 1</math>.
|
<math>~W_\mathrm{grav}\biggr|_\mathrm{core}</math> |
<math>~\approx</math> |
<math>~- \mathfrak{a}_c \biggl[ \frac{GM_\mathrm{tot} M_c}{(R_i/2)} \biggr] = - 2\mathfrak{a}_c \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggl(\frac{\nu}{q}\biggr) \biggr] \, ;</math> |
|
<math>~W_\mathrm{grav}\biggr|_\mathrm{env}</math> |
<math>~\approx</math> |
<math>~- \mathfrak{a}_e \biggl[ \frac{GM_\mathrm{tot} M_e}{(R_i+R)/2} \biggr] = - 2\mathfrak{a}_e \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] \, ;</math> |
|
<math>~\mathfrak{S}_\mathrm{therm}\biggr|_\mathrm{core} = U_\mathrm{int}\biggr|_\mathrm{core} </math> |
<math>~\approx</math> |
<math>~\mathfrak{b}_c \cdot n_cK_c M_c ({\bar\rho}_c)^{1/n_c} = 5\mathfrak{b}_c \cdot K_c M_\mathrm{tot}\nu \biggl[ \frac{3M_c}{4\pi R_i^3} \biggr]^{1/5} </math> |
|
|
<math>~=</math> |
<math>~\mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} K_c (M_\mathrm{tot}\nu)^{6/5} (Rq)^{-3/5} \, ;</math> |
|
<math>~\mathfrak{S}_\mathrm{therm}\biggr|_\mathrm{env} = U_\mathrm{int}\biggr|_\mathrm{env} </math> |
<math>~\approx</math> |
<math>~\mathfrak{b}_e \cdot n_eK_e M_\mathrm{env} ({\bar\rho}_e)^{1/n_e} = \mathfrak{b}_e \cdot K_e M_\mathrm{tot}(1-\nu) \biggl[ \frac{3M_\mathrm{env}}{4\pi (R^3-R_i^3)} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr) K_e [M_\mathrm{tot}(1-\nu)]^2 [R^3(1-q^3)]^{-1} \, . </math> |
In writing this last expression, it has been necessary to (temporarily) introduce a sixth physical parameter, namely, the polytropic constant that characterizes the envelope material, <math>~K_e</math>. But this constant can be expressed in terms of <math>~K_c</math> via a relation that ensures continuity of pressure across the interface while taking into account the drop in mean molecular weight across the interface, that is,
|
<math>~K_e ({\bar\rho}_e)^{(n_e+1)/n_e}</math> |
<math>~\approx</math> |
<math>~K_c ({\bar\rho}_c)^{(n_c+1)/n_c}</math> |
|
<math>~\Rightarrow ~~~~ K_e \biggl[\biggl( \frac{\mu_e}{\mu_c} \biggr) {\bar\rho}_c\biggr]^{2}</math> |
<math>~\approx</math> |
<math>~K_c ({\bar\rho}_c)^{6/5}</math> |
|
<math>~\Rightarrow ~~~~ \frac{K_e}{K_c} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{2}</math> |
<math>~\approx</math> |
<math>~\biggl[ \frac{3M_\mathrm{tot}\nu}{4\pi (Rq)^3} \biggr]^{-4/5} \, .</math> |
Hence, the fourth energy term may be rewritten in the form,
|
<math>~\mathfrak{S}_\mathrm{therm}\biggr|_\mathrm{env} = U_\mathrm{int}\biggr|_\mathrm{env} </math> |
<math>~\approx</math> |
<math>~ \mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr) \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} K_c\biggl[ \frac{3M_\mathrm{tot}\nu}{4\pi (Rq)^3} \biggr]^{-4/5} [M_\mathrm{tot}(1-\nu)]^2 [R^3(1-q^3)]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr)^{1/5} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} K_c M_\mathrm{tot}^{6/5}R^{-3/5}\biggl[ \frac{q^3}{\nu} \biggr]^{4/5} \frac{(1-\nu)^2}{(1-q^3)} \, . </math> |
Putting all the terms together gives,
|
<math>~\mathfrak{G}</math> |
<math>~\approx</math> |
<math>~ - 2\mathfrak{a}_c \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggl(\frac{\nu}{q}\biggr) \biggr] - 2\mathfrak{a}_e \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] + \mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} K_c (M_\mathrm{tot}\nu)^{6/5} (Rq)^{-3/5} </math> |
|
|
|
<math>~ + \mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr)^{1/5} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} K_c M_\mathrm{tot}^{6/5}R^{-3/5}\biggl[ \frac{q^3}{\nu} \biggr]^{4/5} \frac{(1-\nu)^2}{(1-q^3)} </math> |
|
|
<math>~=</math> |
<math>~ - 2 \mathcal{A}_\mathrm{biP} \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggr] + \mathcal{B}_\mathrm{biP} K_c \biggl[\frac{(\nu M_\mathrm{tot})^{2}}{ qR} \biggr]^{3/5} </math> |
|
<math>~\Rightarrow ~~~~ \frac{\mathfrak{G}}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~ - 2 \mathcal{A}_\mathrm{biP} \biggl[ \frac{GM_\mathrm{tot}^2 }{R} \biggr] \biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} + \mathcal{B}_\mathrm{biP} \biggl(\frac{\nu^2}{q}\biggr)^{3/5} K_c \biggl[\frac{M_\mathrm{tot}^{2}}{ R} \biggr]^{3/5}\biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} </math> |
|
|
<math>~=</math> |
<math>~ - 2 \mathcal{A}_\mathrm{biP} \biggl[ \frac{R_\mathrm{norm}}{R} \biggr] + \mathcal{B}_\mathrm{biP} \biggl(\frac{\nu^2}{q}\biggr)^{3/5} \biggl[\frac{R_\mathrm{norm}}{ R} \biggr]^{3/5} \, , </math> |
where,
|
<math>~\mathcal{A}_\mathrm{biP}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \mathfrak{a}_c\biggl(\frac{\nu}{q}\biggr) + \mathfrak{a}_e \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] \, ,</math> |
|
<math>~\mathcal{B}_\mathrm{biP}</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{3}{2^2\pi} \biggr)^{1/5} \biggl[5\mathfrak{b}_c + \mathfrak{b}_e \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \frac{q^3(1-\nu)^2}{\nu^2(1-q^3)} \biggr] \, .</math> |
Equilibrium Radius
Order of Magnitude Estimate
This means that,
|
<math>~\frac{\partial\mathfrak{G}}{\partial R}</math> |
<math>~=</math> |
<math>~ + 2 \mathcal{A}_\mathrm{biP}\biggl[ \frac{GM_\mathrm{tot}^2 }{R^2} \biggr] - \frac{3}{5} \mathcal{B}_\mathrm{biP} K_c \biggl[\frac{\nu^{2}}{ q} \biggr]^{3/5} M_\mathrm{tot}^{6/5} R^{-8/5} \, . </math> |
Hence, because equilibrium radii are identified by setting <math>~\partial\mathfrak{G}/\partial R = 0</math>, we have,
|
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl(\frac{2\cdot 5}{3}\biggr)^{5/2} \biggl[\frac{\mathcal{A}_\mathrm{biP} }{\mathcal{B}_\mathrm{biP}}\biggr]^{5/2} \biggl(\frac{ q} {\nu^{2}}\biggr)^{3/2} \, . </math> |
Reconcile With Known Analytic Expression
From our earlier derivations, it appears as though,
|
<math>~\chi_\mathrm{eq} \equiv \frac{R_\mathrm{eq}}{R_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl( \frac{3^8}{2^5\pi} \biggr)^{-1/2} \biggl(\frac{3}{2^4}\biggr) \biggl( \frac{q}{\ell_i}\biggr)^{5}\biggl(\frac{\nu}{q^3} \biggr)^2 \biggl( 1 + \ell_i^2 \biggr)^{3} </math> |
|
|
<math>~=</math> |
<math>~\biggl(\frac{2\cdot 5}{3}\biggr)^{5/2} \biggl(\frac{q}{\nu^2} \biggr)^{3/2} \biggl[\biggl( \frac{\pi}{2^8 \cdot 3 \cdot 5^5} \biggr)^{1/2} \biggl(\frac{\nu^2}{q} \biggr)^{5/2} \frac{(1 + \ell_i^2)^3}{\ell_i^5} \biggr] \, . </math> |
This implies that,
|
<math>~\frac{\mathcal{A}_\mathrm{biP} }{\mathcal{B}_\mathrm{biP}}</math> |
<math>~\approx</math> |
<math>~ \biggl[\biggl( \frac{\pi}{2^8 \cdot 3 \cdot 5^5} \biggr)^{1/2} \biggl(\frac{\nu^2}{q} \biggr)^{5/2} \frac{(1 + \ell_i^2)^3}{\ell_i^5} \biggr]^{2/5} </math> |
|
|
<math>~=</math> |
<math>~\biggl(\frac{\nu^2}{q} \biggr) \biggl( \frac{\pi}{2^8 \cdot 3 \cdot 5^5} \biggr)^{1/5} \frac{(1 + \ell_i^2)^{6/5}}{\ell_i^2} </math> |
|
<math>~\Rightarrow ~~~~ \biggl[ \mathfrak{a}_c\biggl(\frac{\nu}{q}\biggr) + \mathfrak{a}_e \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] </math> |
<math>~\approx</math> |
<math>~\frac{1}{2^2\cdot 5}\biggl(\frac{\nu^2}{q} \biggr) \frac{(1 + \ell_i^2)^{6/5}}{\ell_i^2} \biggl[5\mathfrak{b}_c + \mathfrak{b}_e \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \frac{q^3(1-\nu)^2}{\nu^2(1-q^3)} \biggr] </math> |
|
<math>~\Rightarrow ~~~~ \biggl[ \mathfrak{a}_c + \mathfrak{a}_e \cdot \frac{q(1-\nu)}{\nu(1+q)} \biggr] </math> |
<math>~\approx</math> |
<math>~\frac{\nu}{2^2\cdot 5} \frac{(1 + \ell_i^2)^{6/5}}{\ell_i^2} \biggl[5\mathfrak{b}_c + \mathfrak{b}_e \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \frac{q^3(1-\nu)^2}{\nu^2(1-q^3)} \biggr] </math> |
Focus on Five-One Free-Energy Expression
Approximate Expressions
Let's plug this equilibrium radius back into each term of the free-energy expression.
|
<math>~\frac{W_\mathrm{grav}}{E_\mathrm{norm}}\biggr|_\mathrm{core}</math> |
<math>~\approx</math> |
<math>~- 2\mathfrak{a}_c \biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} \biggl[ \frac{GM_\mathrm{tot}^2 }{R_\mathrm{eq}} \biggl(\frac{\nu}{q}\biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~- 2\mathfrak{a}_c \biggl(\frac{\nu}{q}\biggr) \biggl[ \frac{R_\mathrm{norm} }{R_\mathrm{eq}} \biggr] \, ;</math> |
|
<math>~\frac{W_\mathrm{grav}}{E_\mathrm{norm}}\biggr|_\mathrm{env}</math> |
<math>~\approx</math> |
<math>~- 2\mathfrak{a}_e \biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} \biggl[ \frac{GM_\mathrm{tot}^2 }{R_\mathrm{eq}} \biggl(\frac{1-\nu}{1+q}\biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~- 2\mathfrak{a}_e \biggl(\frac{1-\nu}{1+q}\biggr) \biggl[ \frac{R_\mathrm{norm} }{R_\mathrm{eq}} \biggr] \, ;</math> |
|
<math>~\frac{S_\mathrm{core}}{E_\mathrm{norm}} = \biggl[\frac{3(\gamma_c-1)}{2}\biggr] \frac{U_\mathrm{int}}{E_\mathrm{norm}}\biggr|_\mathrm{core} </math> |
<math>~\approx</math> |
<math>~\biggl[\frac{3}{2\cdot 5}\biggr]\mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} \biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} K_c (M_\mathrm{tot}\nu)^{6/5} (R_\mathrm{eq}q)^{-3/5} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{3}{2\cdot 5}\biggr]\mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} \biggl(\frac{\nu^2}{q}\biggr)^{3/5} \biggl(\frac{R_\mathrm{norm}}{R_\mathrm{eq}}\biggr)^{3/5} \, ;</math> |
|
<math>~\frac{S_\mathrm{env}}{E_\mathrm{norm}} = \biggl[\frac{3(\gamma_e-1)}{2}\biggr] \frac{U_\mathrm{int}}{E_\mathrm{norm}}\biggr|_\mathrm{env} </math> |
<math>~\approx</math> |
<math>~\biggl[\frac{3}{2}\biggr] \mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr)^{1/5} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \biggl(\frac{G^3}{K_c^5}\biggr)^{1/2} K_c M_\mathrm{tot}^{6/5}R_\mathrm{eq}^{-3/5}\biggl[ \frac{q^3}{\nu} \biggr]^{4/5} \frac{(1-\nu)^2}{(1-q^3)} </math> |
|
|
<math>~=</math> |
<math>~\biggl[\frac{3}{2}\biggr] \mathfrak{b}_e \biggl( \frac{3}{2^2\pi } \biggr)^{1/5} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \biggl[ \frac{q^3}{\nu} \biggr]^{4/5} \frac{(1-\nu)^2}{(1-q^3)} \biggl(\frac{R_\mathrm{norm}}{R_\mathrm{eq}}\biggr)^{3/5} \, . </math> |
From Detailed Force-Balance Models
In the following derivations, we will use the expression,
|
<math>~\chi_\mathrm{eq} \equiv \frac{ R_\mathrm{eq}}{R_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl( \frac{\mu_e}{\mu_c} \biggr)^3 \biggl( \frac{\pi}{2^3} \biggr)^{1/2} \frac{1}{A^2\eta_s} = \biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} \, .</math> |
Keep in mind, as well — as derived in an accompanying discussion — that,
|
<math>~\nu \equiv \frac{M_\mathrm{core}}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~ (m_3^2 \ell_i^3) (1 + \ell_i^2)^{-1/2} [1 + (1-m_3)^2 \ell_i^2]^{-1/2} \biggl[ m_3\ell_i + (1+\ell_i^2) \biggl(\frac{\pi}{2} + \tan^{-1} \Lambda_i \biggr) \biggr]^{-1} \, ,</math> |
where,
<math>m_3 \equiv 3 \biggl( \frac{\mu_e}{\mu_c} \biggr) \, .</math>
From the accompanying Table 1 parameter values, we also can write,
|
<math>~q</math> |
<math>~=</math> |
<math>~\frac{\eta_i}{\eta_s} = \eta_i \biggl\{\frac{\pi}{2} + \eta_i + \tan^{-1}\biggl[ \frac{1}{\eta_i} - \ell_i \biggr] \biggr\}^{-1}</math> |
|
|
<math>~=</math> |
<math>~ \eta_i \biggl\{\eta_i + \cot^{-1}\biggl[ \ell_i - \frac{1}{\eta_i} \biggr] \biggr\}^{-1} \, , </math> |
where,
|
<math>~\eta_i</math> |
<math>~=</math> |
<math>~m_3 \biggl[\frac{\ell_i }{(1+\ell_i^2)}\biggr] \, .</math> |
Let's also define the following shorthand notation:
|
<math>~\mathfrak{L}_i</math> |
<math>~\equiv</math> |
<math>~\frac{(\ell_i^4-1)}{\ell_i^2} + \frac{(1+\ell_i^2)^3}{\ell_i^3} \cdot \tan^{-1}\ell_i \, ;</math> |
|
<math>~\mathfrak{K}_i</math> |
<math>~\equiv</math> |
<math>~\frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] + \frac{\Lambda_i}{\eta_i} \, .</math> |
Gravitational Potential Energy of the Core
Pulling from our detailed derivations,
|
<math>~\biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ - \biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} \biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) (1 + \ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] \, .</math> |
|
<math>~\Rightarrow ~~~~ -\chi_\mathrm{eq} \biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ \biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} \biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) (1 + \ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] \biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} </math> |
|
|
<math>~=~</math> |
<math>~ \biggl( \frac{3}{2^4} \biggr) \frac{\nu^2}{q} \cdot \frac{1}{\ell_i^5} \biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) + (1 + \ell_i^2)^{3}\tan^{-1}(\ell_i) \biggr] </math> |
Out of equilibrium, then, we should expect,
|
<math>~\frac{W_\mathrm{core}}{E_\mathrm{norm}} </math> |
<math>~=~</math> |
<math>~ - \chi^{-1} \biggl( \frac{3}{2^4} \biggr) \frac{\nu^2}{q} \cdot \frac{1}{\ell_i^5} \biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) + (1 + \ell_i^2)^{3}\tan^{-1}(\ell_i) \biggr] </math> |
|
|
<math>~=~</math> |
<math>~ - \chi^{-1} \biggl( \frac{3}{2^4} \biggr) \frac{\nu^2}{q} \cdot \frac{1}{\ell_i^2} \biggl[ \mathfrak{L}_i - \frac{8}{3} \biggr] \, , </math> |
which, in comparison with our above approximate expression, implies,
|
<math>~\mathfrak{a}_c </math> |
<math>~=~</math> |
<math>~ \biggl( \frac{3}{2^5} \biggr) \frac{\nu}{\ell_i^5} \biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) + (1 + \ell_i^2)^{3}\tan^{-1}(\ell_i) \biggr] \, . </math> |
Thermal Energy of the Core
Again, pulling from our detailed derivations,
|
<math>~\biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ \frac{1}{2} \biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] </math> |
|
<math>~\Rightarrow ~~~~ \chi_\mathrm{eq}^{3} \biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]^5_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ \frac{1}{2^5} \biggl( \frac{3^8}{2^5\pi} \biggr)^{5/2} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr]^5 \biggl[\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5}\biggr]^{3} </math> |
|
|
<math>~=~</math> |
<math>~ \frac{1}{\pi}\biggl(\frac{3}{2^{2}}\biggr)^{11} \biggl(\frac{\nu^2}{q}\biggr)^{3} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr]^5 \biggl[\frac{(1+\ell_i^2)^9}{\ell_i^{15}}\biggr] \, . </math> |
Out of equilibrium, we should then expect,
|
<math>~\frac{S_\mathrm{core}}{E_\mathrm{norm}}</math> |
<math>~=~</math> |
<math>~ \biggl(\frac{3}{2^2\pi} \biggr)^{1/5}\biggl[ \chi^{-1} \biggl(\frac{\nu^2}{q}\biggr) \frac{1}{(1+\ell_i^2)^{2}} \biggr]^{3/5} \biggl(\frac{3}{2^{2}}\biggr)^{2}\mathfrak{L}_i \, . </math> |
In comparison with our above approximate expression, we therefore have,
|
<math>~ \biggl[ \biggl(\frac{3}{2\cdot 5}\biggr)\mathfrak{b}_c \biggl( \frac{3\cdot 5^5}{2^2\pi} \biggr)^{1/5} \biggl(\frac{\nu^2}{q}\biggr)^{3/5} \biggr]^5</math> |
<math>~=~</math> |
<math>~ \frac{1}{\pi}\biggl(\frac{3}{2^{2}}\biggr)^{11} \biggl(\frac{\nu^2}{q}\biggr)^{3} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr]^5 \biggl[\frac{(1+\ell_i^2)^9}{\ell_i^{15}}\biggr] </math> |
|
<math>~\Rightarrow~~~~ \mathfrak{b}_c </math> |
<math>~=~</math> |
<math>~\frac{ 3 }{2^3\ell_i^{3}(1+\ell_i^2)^{6/5}} \biggl[ \ell_i (\ell_i^4 - 1 ) + (1+\ell_i^2)^{3}\tan^{-1}(\ell_i) \biggr] \, . </math> |
Gravitational Potential Energy of the Envelope
Again, pulling from our detailed derivations and appreciating, in particular, that (see, for example, our notes on equilibrium conditions),
|
<math>~A</math> |
<math>~=~</math> |
<math>~\frac{\eta_i}{\sin(\eta_i - B)} \, ,</math> |
|
<math>~(\eta_s - B)</math> |
<math>~=~</math> |
<math>~\pi \, ,</math> |
|
<math>~\eta_i - B</math> |
<math>~=~</math> |
<math>~\frac{\pi}{2} - \tan^{-1}(\Lambda_i)\, ,</math> |
|
<math>~\Rightarrow ~~~ \sin(\eta_i -B) = (1+\Lambda_i^2)^{-1/2}</math> |
and |
<math>~\sin[2(\eta_i-B)] = 2\Lambda_i(1 + \Lambda_i^2)^{-1} \ ,</math> |
we have,
|
<math>~\biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ -\biggl( \frac{1}{2^3\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} A^2 \biggl\{ \biggl[6(\eta_s-B) - 3\sin[2(\eta_s - B)] -4\eta_s\sin^2(\eta_s-B) + 4B\biggr] </math> |
|
|
|
<math>~ - \biggl[6(\eta_i-B) - 3\sin[2(\eta_i - B)] -4\eta_i\sin^2(\eta_i-B) + 4B \biggr]\biggr\} </math> |
|
|
<math>~=~</math> |
<math>~ -\biggl( \frac{1}{2^3\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \biggl[\frac{\eta_i}{\sin(\eta_i - B)} \biggr]^2 \biggl\{ 6\pi - \biggl[6(\eta_i-B) - 3\sin[2(\eta_i - B)] -4\eta_i\sin^2(\eta_i-B) \biggr]\biggr\} </math> |
|
|
<math>~=~</math> |
<math>~ -\biggl( \frac{1}{2^3\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2(1+\Lambda_i^2) \biggl\{ 6\pi - 6\biggl[\frac{\pi}{2} - \tan^{-1}(\Lambda_i)\biggr] + 6\biggl[ \frac{\Lambda_i}{(1 + \Lambda_i^2)} \biggr] + 4\eta_i \biggl[ \frac{1}{(1+\Lambda_i^2)} \biggr] \biggr\} </math> |
|
|
<math>~=~</math> |
<math>~ -\biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 \biggl\{ (1+\Lambda_i^2)\biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \Lambda_i + \frac{2}{3} \cdot \eta_i \biggr\} \, . </math> |
So, in equilibrium we can write,
|
<math>~-\chi_\mathrm{eq}\biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ \biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 \biggl\{ (1+\Lambda_i^2)\biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \Lambda_i + \frac{2}{3} \cdot \eta_i \biggr\} \biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} </math> |
|
|
<math>~=~</math> |
<math>~ \frac{3}{2^2} \biggl(\frac{\eta_i}{m_3}\biggr)^3 \biggl\{ \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \frac{\Lambda_i}{\eta_i} + \frac{2}{3} \biggr\} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{\ell_i^5} </math> |
|
|
<math>~=~</math> |
<math>~ \frac{3}{2^2} \biggl(\frac{\nu^2}{q} \biggr) \frac{1}{\ell_i^2} \biggl\{ \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \frac{\Lambda_i}{\eta_i} + \frac{2}{3} \biggr\} \, . </math> |
And out of equilibrium,
|
<math>~\frac{W_\mathrm{env}}{E_\mathrm{norm}}</math> |
<math>~=~</math> |
<math>~ -\chi^{-1}\cdot \frac{3}{2^2} \biggl(\frac{\nu^2}{q} \biggr) \frac{1}{\ell_i^2} \biggl[\mathfrak{K}_i+ \frac{2}{3} \biggr] \, . </math> |
This, in turn, implies that both in and out of equilibrium,
|
<math>~\mathfrak{a}_e </math> |
<math>~=~</math> |
<math>~ \frac{3}{2^3} \biggl[\frac{\nu^2(1+q)}{q(1-\nu)} \biggr] \frac{1}{\ell_i^2} \biggl\{ \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \frac{\Lambda_i}{\eta_i} + \frac{2}{3} \biggr\} \, . </math> |
Thermal Energy of the Envelope
Again, pulling from our detailed derivations,
|
<math>~\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ ~ \biggl( \frac{1}{2^5\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} A^2 \biggl\{ \biggl[6(\eta_s - B) - 3\sin[2(\eta_s-B)] \biggr] - \biggl[6(\eta_i - B) - 3\sin[2(\eta_i-B)] \biggr] \biggr\}</math> |
|
|
<math>~=~</math> |
<math>~ ~ \biggl( \frac{1}{2^5\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \biggl[\frac{\eta_i}{\sin(\eta_i - B)} \biggr]^2 \biggl\{ 6\pi - 6(\eta_i - B) + 3\sin[2(\eta_i-B)] \biggr\}</math> |
|
|
<math>~=~</math> |
<math>~ ~ \biggl( \frac{1}{2^5\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 (1 + \Lambda_i^2) \biggl\{ 6\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + 6\biggl[\Lambda_i(1 + \Lambda_i^2)^{-1} \biggr] \biggr\}</math> |
|
|
<math>~=~</math> |
<math>~ ~\frac{1}{2} \biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 \biggl\{ (1 + \Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \Lambda_i \biggr\} \, .</math> |
So, in equilibrium we can write,
|
<math>~\chi_\mathrm{eq}^{3}\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ ~\frac{1}{2} \biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 \biggl\{ (1 + \Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \Lambda_i \biggr\} \biggl[\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5}\biggr]^{3} </math> |
|
|
<math>~=~</math> |
<math>~ ~\biggl(\frac{\nu^2}{q} \biggr)^3 \biggl( \frac{3^2\pi^2}{2^{12}} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^3 \biggl\{ \frac{(1 + \Lambda_i^2)}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \frac{\Lambda_i}{\eta_i} \biggr\} \biggl[\frac{(1+\ell_i^2)^9}{3^9\ell_i^{15}}\biggr] </math> |
|
|
<math>~=~</math> |
<math>~ ~\biggl(\frac{\nu^2}{q} \biggr)^3 \biggl( \frac{\pi}{2^{6}\cdot 3^5} \biggr) \biggl[\frac{(1+\ell_i^2)^6}{\ell_i^{12}}\biggr] \biggl\{ \frac{(1 + \Lambda_i^2)}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \frac{\Lambda_i}{\eta_i} \biggr\} \, . </math> |
And, out of equilibrium,
|
<math>~\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ ~ \chi^{-3}\biggl(\frac{\nu^2}{q} \biggr)^3 \biggl( \frac{\pi}{2^{6}\cdot 3^5} \biggr) \biggl[\frac{(1+\ell_i^2)^6}{\ell_i^{12}}\biggr]\mathfrak{K} \, . </math> |
Combined in Equilibrium
Notice that, in combination,
|
<math>~\biggl[\frac{2S_\mathrm{env} + W_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=</math> |
<math>~ - \frac{2}{3}\biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^3 </math> |
|
|
<math>~=</math> |
<math>~ - \frac{2}{3}\biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \biggl[3 \biggl( \frac{\mu_e}{\mu_c} \biggr) \ell_i \biggl( 1 + \ell_i^2 \biggr)^{-1}\biggr]^3 </math> |
|
|
<math>~=</math> |
<math>~ - \biggl( \frac{2\cdot 3^6}{\pi} \biggr)^{1/2} \biggl[\frac{\ell_i^3}{( 1 + \ell_i^2)^3}\biggr] \, . </math> |
Also, from above,
|
<math>~\biggl[ \frac{2S_\mathrm{core}+W_\mathrm{core}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ - \biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} \biggl[ \ell_i \biggl(- \frac{8}{3} \ell_i^2 \biggr) (1 + \ell_i^2)^{-3} \biggr] </math> |
|
|
<math>~=~</math> |
<math>~ + \biggl( \frac{2\cdot 3^6}{\pi } \biggr)^{1/2} \biggl[ \frac{\ell_i^3}{(1 + \ell_i^2)^{3}} \biggr] \, .</math> |
So, in equilibrium, these terms from the core and envelope sum to zero, as they should.
Out of Equilibrium
And now, in combination out of equilibrium,
|
<math>~\frac{\mathfrak{G}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~ \biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-1} \biggl\{ \biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} + \biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}\biggr\} +\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-3/5} \biggl(\frac{2n_c}{3}\biggr) \biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} +\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-3} \biggl(\frac{2n_e}{3}\biggr)\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} \, . </math> |
Hence, quite generally out of equilibrium,
|
<math>~\frac{\partial}{\partial \chi} \biggl[ \frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr] </math> |
<math>~=</math> |
<math>~ -\chi^{-1}\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-1} \biggl\{ \biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} + \biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}\biggr\} -\frac{3}{5}\chi^{-1}\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-3/5} \biggl(\frac{10}{3}\biggr) \biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} -3\chi^{-1}\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{-3} \biggl(\frac{2}{3}\biggr)\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} \, . </math> |
Let's see what the value of this derivative is if the dimensionless radius, <math>~\chi</math>, is set to the value that has been determined, via a detailed force-balanced analysis, to be the equilibrium radius, namely, <math>~\chi = \chi_\mathrm{eq}</math>. In this case, we have,
|
<math>~\biggl\{\frac{\partial}{\partial \chi} \biggl[ \frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr] \biggr\}_\mathrm{\chi \rightarrow \chi_\mathrm{eq}}</math> |
<math>~=</math> |
<math>~ -\chi_\mathrm{eq}^{-1}\biggl\{ \biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} + \biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} +2\biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} +2\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq} \biggr\} \, . </math> |
But, according to the virial theorem — and, as we have just demonstrated — the four terms inside the curly braces sum to zero. So this demonstrates that the derivative of our out-of-equilibrium free-energy expression does go to zero at the equilibrium radius, as it should!
Summary51
In summary, the desired out of equilibrium free-energy expression is,
|
<math>~\frac{\mathfrak{G}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~ \frac{W_\mathrm{core}}{E_\mathrm{norm}} + \frac{W_\mathrm{env}}{E_\mathrm{norm}} +\biggl(\frac{2n_c}{3}\biggr)\frac{S_\mathrm{core}}{E_\mathrm{norm}} +\biggl(\frac{2n_e}{3}\biggr)\frac{S_\mathrm{env}}{E_\mathrm{norm}} </math> |
|
|
<math>~=</math> |
<math>~ - \chi^{-1} \biggl( \frac{3}{2^4} \biggr) \frac{\nu^2}{q} \cdot \frac{1}{\ell_i^2} \biggl[ \mathfrak{L}_i - \frac{8}{3} \biggr] -\chi^{-1}\cdot \frac{3}{2^2} \biggl(\frac{\nu^2}{q} \biggr) \frac{1}{\ell_i^2} \biggl[\mathfrak{K}_i+ \frac{2}{3} \biggr] </math> |
|
|
|
<math>~ + \biggl(\frac{2\cdot 5}{3}\biggr) \biggl(\frac{3}{2^2\pi} \biggr)^{1/5}\biggl[ \chi^{-1} \biggl(\frac{\nu^2}{q}\biggr) \frac{1}{(1+\ell_i^2)^{2}} \biggr]^{3/5} \biggl(\frac{3}{2^{2}}\biggr)^{2}\mathfrak{L}_i +\biggl(\frac{2}{3}\biggr) \chi^{-3}\biggl(\frac{\nu^2}{q} \biggr)^3 \biggl( \frac{\pi}{2^{6}\cdot 3^5} \biggr) \biggl[\frac{(1+\ell_i^2)^6}{\ell_i^{12}}\biggr]\mathfrak{K} </math> |
|
|
<math>~=</math> |
<math>~ - \biggl( \frac{3}{2^4} \biggr) \biggl[\chi^{-1}\frac{\nu^2}{q} \cdot \frac{1}{\ell_i^2}\biggr] \biggl[ \mathfrak{L}_i + 4\mathfrak{K}_i \biggr] + \biggl(\frac{3}{2^2\pi} \biggr)^{1/5}\biggl(\frac{3\cdot 5}{2^3}\biggr) \biggl[ \chi^{-1} \biggl(\frac{\nu^2}{q}\biggr) \frac{1}{(1+\ell_i^2)^{2}} \biggr]^{3/5} \mathfrak{L}_i </math> |
|
|
|
<math>~ + \biggl( \frac{\pi}{2^{5}\cdot 3^6} \biggr) \biggl[\chi^{-1}\biggl(\frac{\nu^2}{q} \biggr) \frac{(1+\ell_i^2)^2}{\ell_i^{4}}\biggr]^3\mathfrak{K} \, . </math> |
Or, in terms of the ratio,
<math>\Chi \equiv \frac{\chi}{\chi_\mathrm{eq}} \, ,</math>
and pulling from the above expressions,
|
<math>~\biggl[ \frac{W_\mathrm{core}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ - \biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} \biggl[ \ell_i \biggl(\ell_i^4 - \frac{8}{3} \ell_i^2 -1 \biggr) (1 + \ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] </math> |
|
|
<math>~=~</math> |
<math>~ - \biggl( \frac{3^8}{2^5\pi } \biggr)^{1/2} \biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]^{3} \biggl[ \mathfrak{L}_i - \frac{8}{3}\biggr] </math> |
|
<math>~\biggl[\frac{W_\mathrm{env}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ -\biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 \biggl\{ (1+\Lambda_i^2)\biggl[\frac{\pi}{2}+\tan^{-1}(\Lambda_i)\biggr] + \Lambda_i + \frac{2}{3} \cdot \eta_i \biggr\} </math> |
|
|
<math>~=~</math> |
<math>~ -\biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]^{3} \biggl[4\mathfrak{K}_i + \frac{8}{3} \biggr] </math> |
|
<math>~\biggl[ \frac{S_\mathrm{core}}{E_\mathrm{norm}}\biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ \frac{1}{2} \biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \ell_i (\ell_i^4 - 1 )(1+\ell_i^2)^{-3} + \tan^{-1}(\ell_i) \biggr] </math> |
|
|
<math>~=~</math> |
<math>~ \frac{1}{2} \biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]^{3}\mathfrak{L}_i </math> |
|
<math>~\biggl[\frac{S_\mathrm{env}}{E_\mathrm{norm}} \biggr]_\mathrm{eq}</math> |
<math>~=~</math> |
<math>~ ~\frac{1}{2} \biggl( \frac{3^2}{2\pi} \biggr)^{1/2} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \eta_i^2 \biggl\{ (1 + \Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}(\Lambda_i) \biggr] + \Lambda_i \biggr\} </math> |
|
|
<math>~=~</math> |
<math>~ ~\frac{1}{2} \biggl( \frac{3^8}{2^5\pi} \biggr)^{1/2} \biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]^{3} (4\mathfrak{K}_i) \, , </math> |
we have the streamlined,
|
<math>~\biggl( \frac{2^5\pi}{3^6} \biggr)^{1/2} \biggl[ \frac{(1+\ell_i^2)}{\ell_i} \biggr]^{3} \biggl[\frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr]</math> |
<math>~=</math> |
<math>~ +\Chi^{-3/5} (5 \mathfrak{L}_i) +\Chi^{-3} (4\mathfrak{K}_i) -\Chi^{-1} (3\mathfrak{L}_i +12\mathfrak{K}_i ) </math> |
or, better yet,
|
Out-of-Equilibrium, Free-Energy Expression for BiPolytropes with <math>~(n_c, n_e) = (5, 1)</math> |
|||
|---|---|---|---|
|
where,
|
<math>~\mathfrak{L}_i</math> |
<math>~\equiv</math> |
<math>~\frac{(\ell_i^4-1)}{\ell_i^2} + \frac{(1+\ell_i^2)^3}{\ell_i^3} \cdot \tan^{-1}\ell_i \, ,</math> |
|
<math>~\mathfrak{K}_i</math> |
<math>~\equiv</math> |
<math>~\frac{\Lambda_i}{\eta_i} + \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \, ,</math> |
|
<math>~\Lambda_i</math> |
<math>~\equiv</math> |
<math>~\frac{1}{\eta_i} - \ell_i \, ,</math> |
|
<math>~\eta_i</math> |
<math>~=</math> |
<math>~3 \biggl( \frac{\mu_e}{\mu_c} \biggr) \biggl[\frac{\ell_i }{(1+\ell_i^2)}\biggr] \, .</math> |
From the accompanying Table 1 parameter values, we also can write,
|
<math>~\frac{1}{q}</math> |
<math>~=</math> |
<math>~\frac{\eta_s}{\eta_i} = 1 + \frac{1}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] \, ,</math> |
|
<math>~\nu</math> |
<math>~=</math> |
<math>~ \frac{\ell_i q}{(1+\Lambda_i^2)^{1/2}} \, . </math> |
| Radial Derivatives | ||||||
|
Consistent with our generic discussion of the stability of bipolytropes and the specific discussion of the stability of bipolytropes having <math>~(n_c, n_e) = (5, 1)</math>, it can straightforwardly be shown that <math>~\partial \mathfrak{G}/\partial \chi = 0</math> is satisfied by setting <math>~\Chi = 1</math>; that is, the equilibrium condition is,
|
<math>~\chi = \chi_\mathrm{eq}</math> |
<math>~=</math> |
<math>~\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} \, .</math> |
Furthermore, the equilibrium configuration is unstable whenever <math>~\partial^2 \mathfrak{G}/\partial \chi^2 < 0</math>, that is, it is unstable whenever,
|
<math>~\frac{ \mathfrak{L}_i}{\mathfrak{K}_i}</math> |
<math>~></math> |
<math>~20 \, .</math> |
Table 1 of an accompanying chapter — and the red-dashed curve in the figure adjacent to that table — identifies some key properties of the model that marks the transition from stable to unstable configurations along equilibrium sequences that have various values of the mean-molecular weight ratio, <math>~\mu_e/\mu_c</math>.
Focus on Zero-Zero Free-Energy Expression
Here, we will draw heavily from the following accompanying chapters:
From Detailed Force-Balance Models
Equilibrium Radius
First View
In an accompanying chapter we find,
|
<math>~ \frac{P_0 R_\mathrm{eq}^4}{G M_\mathrm{tot}^2 } </math> |
<math>~=</math> |
<math>~\biggl( \frac{3}{2^3 \pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^2 \biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] </math> |
where,
|
<math>~f</math> |
<math>~\equiv</math> |
<math> 1+ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2}-1 \biggr) +\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \frac{1}{q^5}-1 + \frac{5}{2} \biggl( 1-\frac{1}{q^2}\biggr)\biggr] \, , </math> |
|
<math>~\mathfrak{F} </math> |
<math>~\equiv</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (-2q^2 + 3q^3 - q^5) + \frac{3}{5} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-1 +5q^2 - 5q^3 + q^5) \biggr] \, , </math> |
|
<math>~\frac{\rho_e}{\rho_c} </math> |
<math>~=</math> |
<math>~ \frac{q^3(1-\nu)}{\nu(1-q^3)} \, . </math> |
Here, we prefer to normalize the equilibrium radius to <math>~R_\mathrm{norm}</math>. So, let's replace the central pressure with its expression in terms of <math>~K_c</math>. Specifically,
|
<math>~P_0</math> |
<math>~=</math> |
<math>~ K_c \rho_c^{\gamma_c} = K_c \biggl[ \frac{3M_\mathrm{core}}{4\pi R_i^3} \biggr]^{\gamma_c} = K_c \biggl[ \frac{3\nu M_\mathrm{tot}}{4\pi q^3 R_\mathrm{eq}^3} \biggr]^{(n_c+1)/n_c} ~~~\Rightarrow~~~ \frac{P_0}{P_\mathrm{norm}} = \biggl[ \frac{3}{4\pi}\biggl(\frac{\nu}{q^3}\biggr) \frac{1}{\chi_\mathrm{eq}^3}\biggr]^{(n_c+1)/n_c} </math> |
|
<math>~\Rightarrow~~~K_c \biggl[ \frac{3\nu M_\mathrm{tot}}{4\pi q^3 R_\mathrm{eq}^3} \biggr]^{(n_c+1)/n_c} \frac{R_\mathrm{eq}^4}{G M_\mathrm{tot}^2 } </math> |
<math>~=</math> |
<math>~\biggl( \frac{3}{2^3 \pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^2 \biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] </math> |
|
<math>~\Rightarrow~~~R_\mathrm{eq}^{(n_c-3)/n_c} </math> |
<math>~=</math> |
<math>~ \biggl(\frac{G}{K_c}\biggr) M_\mathrm{tot}^{(n_c-1)/n_c} \biggl[ \frac{3\nu }{4\pi q^3 } \biggr]^{-(n_c+1)/n_c} \biggl( \frac{3}{2^3 \pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^2 \biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] </math> |
|
<math>~\Rightarrow~~~\chi_\mathrm{eq}^{(n_c-3)/n_c} \equiv \biggl[\frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr]^{(n_c-3)/n_c}</math> |
<math>~=</math> |
<math>~ \frac{1}{2}\biggl(\frac{4\pi}{3} \biggr)^{1/n_c} \biggl( \frac{\nu}{q^3}\biggr)^{(n_c-1)/n_c} \biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] \, . </math> |
Or, in terms of <math>~\gamma_c</math>,
|
<math>~\chi_\mathrm{eq}^{4-3\gamma_c} </math> |
<math>~=</math> |
<math>~ \frac{1}{2}\biggl(\frac{3}{4\pi} \biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3}\biggr)^{2-\gamma_c} \biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] \, . </math> |
Second View
Alternatively, from our derivation and discussion of analytic detailed force-balance models,
|
<math> \biggl[ \frac{R^4}{GM_\mathrm{tot}^2} \biggr] P_0</math> |
<math>~=</math> |
<math>\biggl( \frac{3}{2^3\pi} \biggr) \frac{\nu^2 g^2}{q^4} \, ,</math> |
where,
|
<math>~[g(\nu,q)]^2</math> |
<math>~\equiv</math> |
<math> 1 + \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \, . </math> |
In order to show that this expression is the same as the other one, above, we need to show that,
|
<math>~\biggl( \frac{3}{2^3 \pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^2 \biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] </math> |
<math>~=</math> |
<math>\biggl( \frac{3}{2^3\pi} \biggr) \frac{\nu^2 g^2}{q^4} </math> |
|
<math>~\Rightarrow~~~ f - 1-\mathfrak{F}
</math> |
<math>~=</math> |
<math>~\frac{5}{2q^3} \biggl[g^2-1\biggr]</math> |
|
|
<math>~=</math> |
<math>~\frac{5}{2q^3} \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{5}{2q^5} \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl\{ 2 ( q^2 - q^3 ) + \frac{\rho_e}{\rho_0}\biggl[ 1 - 3q^2+ 2q^3 \biggr] \biggr\} \, .</math> |
Let's see …
|
<math>~ f - 1-\mathfrak{F}
</math> |
<math>~=</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2}-1 \biggr) +\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \frac{1}{q^5}-1 + \frac{5}{2} \biggl( 1-\frac{1}{q^2}\biggr)\biggr] - \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (-2q^2 + 3q^3 - q^5) + \frac{3}{5} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-1 +5q^2 - 5q^3 + q^5) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2}-1 \biggr) - \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (-2q^2 + 3q^3 - q^5) \biggr] </math> |
|
|
|
<math>~ - \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ \frac{3}{5} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-1 +5q^2 - 5q^3 + q^5) \biggr] +\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \frac{1}{q^5}-1 + \frac{5}{2} \biggl( 1-\frac{1}{q^2}\biggr)\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl\{ (q^3- q^5 ) + (2q^2 - 3q^3 + q^5) \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \frac{1}{q^5} \biggl[ 3 (1 -5q^2 + 5q^3 - q^5) \biggr] +\frac{1}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \frac{1}{q^5} \biggl[ 2 - 2q^5 + 5\biggl( q^5-q^3\biggr)\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (q^3- q^5 ) + (2q^2 - 3q^3 + q^5) \biggr] + \frac{1}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \frac{1}{q^5} \biggl[ 3 (1 -5q^2 + 5q^3 - q^5)+2 - 2q^5 + 5( q^5-q^3) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ 2q^2 - 2q^3 \biggr] + \frac{5}{2q^5} \biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ 1 - 3q^2 + 2q^3 \biggr] \, . </math> |
Q.E.D.
Hence, the equilibrium radius can also be written as,
|
<math>~\chi_\mathrm{eq}^{4-3\gamma_c} </math> |
<math>~=</math> |
<math>~ \frac{1}{2}\biggl(\frac{3}{4\pi} \biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3}\biggr)^{2-\gamma_c} q^2 g^2 \, ; </math> |
or, in terms of the polytropic index,
|
<math>~\chi_\mathrm{eq}^{n_c-3} </math> |
<math>~=</math> |
<math>~ \frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c} \, . </math> |
Gravitational Potential Energy
Also from our accompanying discussion, we have,
|
<math>~\frac{W_\mathrm{grav}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math> - \Chi^{-1} \biggl( \frac{3}{5}\biggr) \biggl(\frac{\nu}{q^3} \biggr)^2 q^5 \biggl[ \frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c} \biggr]^{-1/(n_c-3)} f(\nu,q) </math> |
|
|
<math>~=</math> |
<math> - \Chi^{-1} \biggl( \frac{6}{5}\biggr) q^5 f \biggl[ 2^{n_c-(n_c-3)} \biggl(\frac{3}{4\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{(1-n_c)+2(n_c-3)} b_\xi^{n_c} \biggr]^{1/(n_c-3)} </math> |
|
|
<math>~=</math> |
<math> - \Chi^{-1} \biggl( \frac{6}{5}\biggr) q^5 f \biggl[ \biggl(\frac{6}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} b_\xi^{n_c} \biggr]^{1/(n_c-3)} \, . </math> |
Internal Energy Components
First View
Before writing out the expressions for the internal energy of the core and of the envelope, we note from our separate detailed derivation that, in either case,
|
<math>~\biggl[\frac{P_i \chi^{3\gamma}}{P_\mathrm{norm}} \biggr]_\mathrm{eq} \chi^{3-3\gamma}</math> |
<math>~=</math> |
<math>~\biggl[\biggl(\frac{P_i }{P_0} \biggr) \biggl(\frac{P_0 }{P_\mathrm{norm}} \biggr)\chi^{3}\biggr]_\mathrm{eq} \biggl[\frac{\chi}{\chi_\mathrm{eq}}\biggr]^{3-3\gamma}</math> |
|
|
<math>~=</math> |
<math>~\biggl\{\biggl(\frac{P_i }{P_0} \biggr) \biggl[ \frac{3}{4\pi } \biggl( \frac{\nu}{q^3} \biggr)\biggr]^{\gamma_c}\chi^{3-3\gamma_c}\biggr\}_\mathrm{eq} \Chi^{3-3\gamma} \, ,</math> |
where, in equilibrium,
|
<math>~\biggl(\frac{P_i }{P_0} \biggr)_\mathrm{eq}</math> |
<math>~=</math> |
<math>~1 - b_\xi q^2</math> |
|
<math>~b_\xi q^2</math> |
<math>~=</math> |
<math>~\biggl\{\frac{2}{5}q^3 f + \biggl[1 - \frac{2}{5} q^3( 1+\mathfrak{F} ) \biggr]\biggr\}^{-1} </math> |
|
|
<math>~=</math> |
<math>~\biggl[1 + \frac{2}{5}q^3 (f - 1-\mathfrak{F} ) \biggr]^{-1} </math> |
So, copying from our accompanying detailed derivation, we have,
|
<math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{core}</math> |
<math>~=</math> |
<math> \frac{4\pi/3 }{({\gamma_c}-1)} \biggl\{\biggl(\frac{P_i }{P_0} \biggr) \biggl[ \frac{3}{4\pi } \biggl( \frac{\nu}{q^3} \biggr)\biggr]^{\gamma_c}\chi^{3-3\gamma_c}\biggr\}_\mathrm{eq} \Chi^{3-3\gamma_c} \biggl\{ \biggl( \frac{P_0}{P_{ic}} \biggr) \biggl[ q^3 - \biggl( \frac{3b_\xi}{5} \biggr) q^5 \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{1 }{({\gamma_c}-1)} \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] \Chi^{3-3\gamma_c} q^3\biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] \, , </math> |
|
<math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{env}</math> |
<math>~=</math> |
<math> \frac{4\pi/3 }{({\gamma_e}-1)} \biggl\{\biggl(\frac{P_i }{P_0} \biggr) \biggl[ \frac{3}{4\pi } \biggl( \frac{\nu}{q^3} \biggr)\biggr]^{\gamma_c}\chi^{3-3\gamma_c}\biggr\}_\mathrm{eq} \Chi^{3-3\gamma_e} \biggl\{ (1-q^3) + b_\xi \biggl(\frac{P_0}{P_{ie} } \biggr) \biggl[\frac{2}{5} q^5 \mathfrak{F} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{1}{({\gamma_e}-1)} \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] \Chi^{3-3\gamma_e} \biggl(\frac{P_i }{P_0} \biggr) \biggl\{ (1-q^3) + b_\xi \biggl(\frac{P_0}{P_{ie} } \biggr) \biggl[\frac{2}{5} q^5 \mathfrak{F} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{1}{({\gamma_e}-1)} \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] \Chi^{3-3\gamma_e} \biggl\{ (1-b_\xi q^2)(1-q^3) + b_\xi \biggl[\frac{2}{5} q^5 \mathfrak{F} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{1}{({\gamma_e}-1)} \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] \Chi^{3-3\gamma_e} (1-q^3) \biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} \, . </math> |
Furthermore,
|
<math>~\biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr]</math> |
<math>~=</math> |
<math>~ \biggl(\frac{3}{4\pi}\biggr)^{\gamma_c - 1} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c} \biggl\{\chi_\mathrm{eq}^{4-3\gamma_c}\biggr\}^{(3-3\gamma_c)/(4-3\gamma_c)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{3}{4\pi}\biggr)^{\gamma_c - 1} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c} \biggl\{\frac{1}{2}\biggl(\frac{3}{4\pi} \biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3}\biggr)^{2-\gamma_c} \biggl[ q^2 + \frac{2}{5} q^5( f - 1-\mathfrak{F} )\biggr] \biggr\}^{(3-3\gamma_c)/(4-3\gamma_c)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{3}{4\pi}\biggr)^{(\gamma_c - 1)/(4-3\gamma_c)} \biggl( \frac{\nu}{q^3} \biggr)^{(6-5\gamma_c)(4-3\gamma_c)} \biggl\{\frac{q^2}{2} \biggl[ 1 + \frac{2}{5} q^3( f - 1-\mathfrak{F} )\biggr] \biggr\}^{(3-3\gamma_c)/(4-3\gamma_c)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{3}{4\pi}\biggr)^{1/(n_c-3)} \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)(n_c-3)} \biggl\{\frac{q^2}{2} \biggl[ 1 + \frac{2}{5} q^3( f - 1-\mathfrak{F} )\biggr] \biggr\}^{-3/(n_c-3)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^3\biggr]^{1/(n_c-3)} \, . </math> |
Hence, we have,
|
<math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{core}</math> |
<math>~=</math> |
<math> n_c \biggl[\biggl(\frac{4\pi}{3}\biggr)^{1-\gamma_c} \biggl( \frac{\nu}{q^3} \biggr)^{\gamma_c}\chi_\mathrm{eq}^{3-3\gamma_c}\biggr] \Chi^{-3/n_c} q^3\biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] </math> |
|
|
<math>~=</math> |
<math> n_c \biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^3\biggr]^{1/(n_c-3)} \Chi^{-3/n_c} q^3\biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] \, , </math> |
|
<math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{env}</math> |
<math>~=</math> |
<math> n_e \biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^3\biggr]^{1/(n_c-3)} \Chi^{-3/n_e} (1-q^3) \biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} \, . </math> |
Second View
In our accompanying discussion of energies associated with detailed force balance models, we used the notation,
|
<math>~\Pi</math> |
<math>~\equiv</math> |
<math>~ \biggl(\frac{3}{2^3\pi}\biggr) \frac{GM_\mathrm{tot}^2}{R^4} \biggl(\frac{\nu}{q^3}\biggr)^2 = P_\mathrm{norm} \chi^{-4}\biggl(\frac{3}{2^3\pi}\biggr) \biggl(\frac{\nu}{q^3}\biggr)^2 \, , </math> |
which allows us to rewrite the above quoted relationship between the central pressure and the radius of the bipolytrope as,
<math>~P_0 = \Pi (qg)^2 \, .</math>
We also showed that, in equilibrium, the relationship between the central pressure and the interface pressure is,
<math>~P_0 =P_i + \Pi_\mathrm{eq} q^2 \, .</math>
This means that, in equilibrium, the ratio of the interface pressure to the central pressure is,
|
<math>~\biggl(\frac{P_i}{P_0}\biggr)_\mathrm{eq}</math> |
<math>~=</math> |
<math>~1 - \frac{\Pi_\mathrm{eq} q^2}{P_0} = 1- \frac{1}{g^2} \, , </math> |
or given that (see above),
|
<math>~ \frac{5}{2q^3} \biggl[g^2-1\biggr]
</math> |
<math>~=</math> |
<math>~ f - 1-\mathfrak{F} </math> |
|
<math>~\Rightarrow~~~~ g^2 </math> |
<math>~=</math> |
<math>~ 1+\frac{2}{5} q^3 ( f - 1-\mathfrak{F} ) \, , </math> |
we have,
|
<math>~\biggl(\frac{P_i}{P_0}\biggr)_\mathrm{eq}</math> |
<math>~=</math> |
<math>~1 - \frac{\Pi_\mathrm{eq} q^2}{P_0} = 1- \biggl[ 1+\frac{2}{5} q^3 ( f - 1-\mathfrak{F} ) \biggr]^{-1} \, . </math> |
This is exactly the pressure-ratio expression presented in our "first view" and unveils the notation association,
|
<math>~b_\xi q^2</math> |
<math>~\leftrightarrow~</math> |
<math> \frac{1}{g^2} \, . </math> |
From our separate derivation, we have, in equilibrium,
|
<math>~\mathfrak{G}_\mathrm{core} = \biggl(\frac{2n_c}{3}\biggr) S_\mathrm{core}</math> |
<math>~=~</math> |
<math>\biggl(\frac{2n_c}{3}\biggr) \biggl( \frac{4\pi}{5} \biggr) R_\mathrm{eq}^3 q^5 \biggl (\frac{5P_i}{2q^2} + \Pi \biggr)_\mathrm{eq} </math> |
|
|
<math>~=~</math> |
<math>\biggl( \frac{ q^5n_c}{5} \biggr) R_\mathrm{eq}^3 \biggl( \frac{2^3\pi}{3} \biggr) \Pi_\mathrm{eq} \biggl[\frac{5}{2q^2} \biggl( \frac{P_i}{\Pi} \biggr)_\mathrm{eq} + 1 \biggr] </math> |
|
|
<math>~=~</math> |
<math>\biggl( \frac{ n_c}{5} \biggr) \biggl[ R_\mathrm{norm}^3 P_\mathrm{norm} \biggr] \chi_\mathrm{eq}^{-1} \biggl(\frac{\nu^2}{q}\biggr) \biggl[\frac{5}{2q^2} \biggl( \frac{P_i}{P_0} \biggr)_\mathrm{eq}\biggl( \frac{P_0}{\Pi} \biggr)_\mathrm{eq} + 1 \biggr] </math> |
|
<math>~\Rightarrow ~~~\biggl[ \frac{\mathfrak{G}_\mathrm{core} }{E_\mathrm{norm}}\biggr]_\mathrm{eq} </math> |
<math>~=~</math> |
<math>~\biggl( \frac{ n_c}{5} \biggr) \biggl(\frac{\nu^2}{q}\biggr) \biggl[\frac{5}{2q^2} \biggl( 1-\frac{1}{g^2} \biggr)\biggl( q^2g^2\biggr) + 1 \biggr] \chi_\mathrm{eq}^{-1} </math> |
|
|
<math>~=~</math> |
<math>~\biggl( \frac{ n_c}{2} \biggr) \biggl(\frac{\nu^2}{q}\biggr) \biggl[ g^2-\frac{3}{5} \biggr] \biggl\{\frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c} \biggr\}^{-1/(n_c-3)}</math> |
|
|
<math>~=~</math> |
<math>~n_c \biggl[ 1- \biggl(\frac{3}{5}\biggr) \frac{1}{g^2} \biggr] \biggl( \frac{ 1}{2} \biggr) \biggl(\frac{\nu^2}{q}\biggr) g^2 \biggl\{2^{n_c}\biggl(\frac{3}{4\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{1-n_c} (q g)^{-2n_c} \biggr\}^{1/(n_c-3)}</math> |
|
|
<math>~=~</math> |
<math>~n_c \biggl[ 1- \biggl(\frac{3}{5}\biggr) \frac{1}{g^2} \biggr] \biggl\{2^{n_c}\cdot 2^{(3-n_c)}\biggl(\frac{3}{4\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{1-n_c} \biggl(\frac{\nu}{q^3}\biggr)^{2(n_c-3)} q^{5(n_c-3)} q^{-2n_c} g^{-2n_c} g^{2(n_c-3)} \biggr\}^{1/(n_c-3)}</math> |
|
|
<math>~=~</math> |
<math>~n_c \biggl[ 1- \biggl(\frac{3}{5}\biggr) \frac{1}{g^2} \biggr] \biggl\{\biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{3n_c-15} g^{-6} \biggr\}^{1/(n_c-3)} \, .</math> |
Finally, switching from the <math>~g</math> notation to the <math>~b_\xi</math> notation gives,
|
<math>~\biggl[ \frac{\mathfrak{G}_\mathrm{core} }{E_\mathrm{norm}}\biggr]_\mathrm{eq} </math> |
<math>~=~</math> |
<math>~n_c \biggl[ 1- \biggl(\frac{3}{5}\biggr) b_\xi q^2 \biggr] \biggl\{\biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{3n_c-15} b_\xi^3 q^{6} \biggr\}^{1/(n_c-3)} </math> |
|
|
<math>~=~</math> |
<math>~n_c q^3 \biggl[ 1- \biggl(\frac{3}{5}\biggr) b_\xi q^2 \biggr] \biggl\{\biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} b_\xi^3 \biggr\}^{1/(n_c-3)} \, ,</math> |
which, after setting <math>~\Chi = 1</math>, precisely matches the above, "first view" expression. Also from our previous derivation, we can write,
|
<math>~\mathfrak{G}_\mathrm{env} = \biggl(\frac{2n_e}{3}\biggr) S_\mathrm{env}</math> |
<math>~=~</math> |
<math>~ 2\pi\biggl(\frac{2n_e}{3}\biggr) R_\mathrm{eq}^3 \Pi_\mathrm{eq} \biggl\{ (1-q^3) \biggl(\frac{P_i }{\Pi}\biggr)_\mathrm{eq} + \biggl( \frac{\rho_e}{\rho_0} \biggr)\biggl[ (-2q^2 + 3q^3 - q^5 ) + \frac{3}{5} \biggl( \frac{\rho_e}{\rho_0} \biggr) ( -1 + 5q^2 -5q^3 + q^5 )\biggr]\biggr\}
</math> |
|
|
<math>~=~</math> |
<math>~ 2\pi\biggl(\frac{2n_e}{3}\biggr) R_\mathrm{eq}^3 \biggl[ P_\mathrm{norm} \chi^{-4}\biggl(\frac{3}{2^3\pi}\biggr) \biggl(\frac{\nu}{q^3}\biggr)^2\biggr]_\mathrm{eq} \biggl\{ (1-q^3) q^2(g^2-1) + \biggl(\frac{2}{5}\biggr) q^5 \mathfrak{F} \biggr\} </math> |
|
|
<math>~=~</math> |
<math>~ \biggl[ P_\mathrm{norm} R_\mathrm{norm}^3 \biggr] \frac{n_e}{2} \biggl(\frac{\nu^2}{q^4}\biggr)(1-q^3) \biggl\{ (g^2-1) + \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr\} \chi^{-1}_\mathrm{eq} </math> |
|
<math>~\Rightarrow~~~\biggl[ \frac{\mathfrak{G}_\mathrm{env} }{E_\mathrm{norm}}\biggr]_\mathrm{eq} </math> |
<math>~=~</math> |
<math>~ n_e (1-q^3) \biggl\{ (g^2-1) + \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr\} \frac{q^2}{2}\biggl(\frac{\nu}{q^3}\biggr)^2 \biggl[\frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c}\biggr]^{-1/(n_c-3)} </math> |
|
|
<math>~=~</math> |
<math>~ n_e (1-q^3) \biggl\{ (g^2-1) + \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr\} \biggl[2^{[n_c-(n_c-3)]} \biggl(\frac{3}{4\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{(1-n_c)+2(n_c-3)} q^{2(n_c-3)-2n_c} g^{-2n_c} \biggr]^{1/(n_c-3)} </math> |
|
|
<math>~=~</math> |
<math>~ n_e (1-q^3) \biggl\{ (g^2-1) + \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr\} \biggl[\biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{-6} g^{-2n_c} \biggr]^{1/(n_c-3)} \, . </math> |
And, finally, switching from the <math>~g</math> notation to the <math>~b_\xi</math> notation gives,
|
<math>~\biggl[ \frac{\mathfrak{G}_\mathrm{env} }{E_\mathrm{norm}}\biggr]_\mathrm{eq} </math> |
<math>~=~</math> |
<math>~ n_e (1-q^3) (b_\xi q^2)^{-1} \biggl\{ 1 - \biggl[1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr]b_\xi q^2\biggr\} \biggl[\biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{-6} (b_\xi q^2)^{n_c} \biggr]^{1/(n_c-3)} </math> |
|
|
<math>~=~</math> |
<math>~ n_e (1-q^3) \biggl\{ 1 - \biggl[1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr]b_\xi q^2\biggr\} \biggl[\biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} q^{-6-2(n_c-3)+2n_c} b_\xi^{3-n_c+n_c} \biggr]^{1/(n_c-3)} </math> |
|
|
<math>~=~</math> |
<math>~ n_e\biggl[\biggl(\frac{2\cdot 3}{\pi} \biggr)\biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} b_\xi^{3} \biggr]^{1/(n_c-3)} (1-q^3) \biggl\{ 1 - \biggl[1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3} \biggr)\mathfrak{F} \biggr]b_\xi q^2\biggr\} \, , </math> |
which, after setting <math>~\Chi = 1</math>, precisely matches the above, "first view" expression.
Summary00
In summary, the desired out of equilibrium free-energy expression is,
|
<math>~\frac{\mathfrak{G}}{E_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~ A_0\Chi^{-3/n_c} + B_0\Chi^{-3/n_e} - C_0\Chi^{-1} </math> |
where,
|
<math>~A_0 \equiv \biggl( \frac{\mathfrak{S}_\mathrm{core}}{E_\mathrm{norm}} \biggr)_\mathrm{eq}</math> |
<math>~=</math> |
<math> \frac{n_c}{b_\xi} \biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^{n_c}\biggr]^{1/(n_c-3)} q^3\biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] \, , </math> |
|
<math>~B_0 \equiv \biggl( \frac{\mathfrak{S}_\mathrm{env}}{E_\mathrm{norm}} \biggr)_\mathrm{eq}</math> |
<math>~=</math> |
<math> \frac{n_e}{b_\xi} \biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^{n_c} \biggr]^{1/(n_c-3)} (1-q^3) \biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} \, , </math> |
|
<math>~C_0 \equiv \biggl( \frac{W_\mathrm{grav}}{E_\mathrm{norm}} \biggr)_\mathrm{eq} </math> |
<math>~=</math> |
<math> \biggl( \frac{6}{5}\biggr) q^5 f \biggl[ \biggl(\frac{2\cdot 3}{\pi} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-5} b_\xi^{n_c} \biggr]^{1/(n_c-3)} \, . </math> |
Or, in a more compact form,
|
<math>~\mathfrak{G}^* \equiv \biggl[ \biggl(\frac{2\cdot 3}{\pi}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(n_c-5)} b_\xi^{n_c}\biggr]^{-1/(n_c-3)} \biggl[\frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr]</math> |
<math>~=</math> |
<math>~ n_c A_1\Chi^{-3/n_c} + n_e B_1\Chi^{-3/n_e} - 3C_1\Chi^{-1} </math> |
where,
|
<math>~A_1 </math> |
<math>~\equiv</math> |
<math> \frac{1}{b_\xi} (q^3) \biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] \, , </math> |
|
<math>~B_1 </math> |
<math>~\equiv</math> |
<math> \frac{1}{b_\xi} (1-q^3)\biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} \, , </math> |
|
<math>~C_1 </math> |
<math>~\equiv</math> |
<math> \biggl( \frac{2}{5}\biggr) q^5 f \, . </math> |
Let's examine the behavior of the first radial derivative.
|
<math>~\frac{\partial \mathfrak{G}^*}{\partial \Chi}</math> |
<math>~=</math> |
<math>~\frac{3}{\Chi} \biggl[ - A_1\Chi^{-3/n_c} - B_1\Chi^{-3/n_e} + C_1\Chi^{-1} \biggr] \, .</math> |
Let's see whether the sum of terms inside the square brackets is zero at the derived equilibrium radius, that is, when <math>~\Chi = 1</math> and, hence, when
|
<math>~\chi = \chi_\mathrm{eq}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} (q g)^{2n_c} \biggr]^{1/(n_c-3)} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{1}{2^{n_c}}\biggl(\frac{4\pi}{3} \biggr) \biggl( \frac{\nu}{q^3}\biggr)^{n_c-1} b_\xi^{-n_c} \biggr]^{1/(n_c-3)} \, . </math> |
|
<math>~ C_1 - A_1 - B_1 </math> |
<math>~=</math> |
<math>~ \biggl( \frac{2}{5}\biggr) q^5 f - \frac{1}{b_\xi} (q^3) \biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] - \frac{1}{b_\xi} (1-q^3)\biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2}{5}\biggr) q^5 f - \frac{1}{b_\xi} \biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} + \frac{q^3}{b_\xi} \biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} - \frac{q^3}{b_\xi} \biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2}{5}\biggr) q^5 f - \frac{1}{b_\xi} + \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]q^2 + \frac{q^3}{b_\xi} - \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]q^5 - \frac{q^3}{b_\xi} + \biggl( \frac{3}{5} \biggr) q^5 </math> |
|
|
<math>~=</math> |
<math>~q^2\biggl\{ \biggl( \frac{2}{5}\biggr) q^3 f - \frac{1}{b_\xi q^2} + \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr] (1-q^3) + \biggl( \frac{3}{5} \biggr) q^3 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~q^2\biggl\{ \biggl( \frac{2}{5}\biggr) q^3 f - \biggl[ 1+\frac{2}{5} q^3(f-1-\mathfrak{F}) \biggr] + \biggl[ (1-q^3) - \frac{2}{5} q^3 \mathfrak{F} \biggr] + \biggl( \frac{3}{5} \biggr) q^3 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~q^2\biggl\{0\biggr\} \, . </math> |
Q.E.D.
Even slightly better:
|
<math>~\frac{1}{q^2}\biggl[ \biggl(\frac{\pi}{2\cdot 3}\biggr) \biggl( \frac{\nu}{q^3} \biggr)^{(5-n_c)} b_\xi^{-n_c}\biggr]^{1/(n_c-3)} \biggl[\frac{\mathfrak{G}}{E_\mathrm{norm}} \biggr]</math> |
<math>~=</math> |
<math>~ n_c A_2\Chi^{-3/n_c} + n_e B_2\Chi^{-3/n_e} - 3C_2\Chi^{-1} \, , </math> |
or, better yet,
|
Out-of-Equilibrium, Free-Energy Expression for BiPolytropes with Structural <math>~(n_c, n_e) = (0, 0)</math> |
|||
|---|---|---|---|
|
where, keeping in mind that,
|
<math>~\frac{1}{(b_\xi q^2)}</math> |
<math>~=</math> |
<math>~\biggl[1 + \frac{2}{5}q^3 (f - 1-\mathfrak{F} ) \biggr] \, , </math> |
we have,
|
<math>~A_2 \equiv \frac{A_1}{q^2} </math> |
<math>~\equiv</math> |
<math> \frac{q^3}{(b_\xi q^2)} \biggl[ 1 - \biggl( \frac{3}{5} \biggr) b_\xi q^2 \biggr] </math> |
|
|
<math>~=</math> |
<math> q^3 \biggl\{ \biggl[1 + \frac{2}{5}q^3 (f - 1-\mathfrak{F} ) \biggr] - \biggl( \frac{3}{5} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{2}{5}q^3 \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, , </math> |
|
<math>~B_2 \equiv \frac{B_1}{q^2} </math> |
<math>~\equiv</math> |
<math> \frac{1}{(b_\xi q^2)} (1-q^3)\biggl\{ 1- \biggl[ 1 - \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr]b_\xi q^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math> (1-q^3)\biggl\{ \frac{1}{(b_\xi q^2)} -1 + \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr\} </math> |
|
|
<math>~=</math> |
<math> (1-q^3)\biggl\{ \biggl[1 + \frac{2}{5}q^3 (f - 1-\mathfrak{F} ) \biggr] - 1 + \frac{2}{5} \biggl(\frac{q^3}{1-q^3}\biggr) \mathfrak{F} \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{2}{5} q^3 \biggl\{ (1-q^3) (f - 1-\mathfrak{F} ) + \mathfrak{F} \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{2}{5} q^3 \biggl\{ f - \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr]\biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{2}{5} q^3 f - A_2 \, , </math> |
|
<math>~C_2 \equiv \frac{C_1}{q^2} </math> |
<math>~\equiv</math> |
<math> \frac{2}{5} q^3 f \, . </math> |
As before, the equilibrium system is dynamically unstable if <math>~\partial^2 \mathfrak{G}/\partial \Chi^2 < 0</math>. We have deduced that the system is unstable if,
|
<math>~\frac{n_e}{3}\biggl[ \frac{3-n_e}{n_c-n_e} \biggr] </math> |
<math>~< </math> |
<math>~ \frac{A_2}{C_2} = \frac{1}{f} \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, . </math> |
Overview
BiPolytrope51
Key Analytic Expressions
|
Out-of-Equilibrium, Free-Energy Expression for BiPolytropes with <math>~(n_c, n_e) = (5, 1)</math> |
|||
|---|---|---|---|
|
where,
|
<math>~\mathfrak{L}_i</math> |
<math>~\equiv</math> |
<math>~\frac{(\ell_i^4-1)}{\ell_i^2} + \frac{(1+\ell_i^2)^3}{\ell_i^3} \cdot \tan^{-1}\ell_i \, ,</math> |
|
<math>~\mathfrak{K}_i</math> |
<math>~\equiv</math> |
<math>~\frac{\Lambda_i}{\eta_i} + \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \, ,</math> |
|
<math>~\Lambda_i</math> |
<math>~\equiv</math> |
<math>~\frac{1}{\eta_i} - \ell_i \, ,</math> |
|
<math>~\eta_i</math> |
<math>~=</math> |
<math>~3 \biggl( \frac{\mu_e}{\mu_c} \biggr) \biggl[\frac{\ell_i }{(1+\ell_i^2)}\biggr] \, .</math> |
From the accompanying Table 1 parameter values, we also can write,
|
<math>~\frac{1}{q}</math> |
<math>~=</math> |
<math>~\frac{\eta_s}{\eta_i} = 1 + \frac{1}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] \, ,</math> |
|
<math>~\nu</math> |
<math>~=</math> |
<math>~ \frac{\ell_i q}{(1+\Lambda_i^2)^{1/2}} \, . </math> |
Consistent with our generic discussion of the stability of bipolytropes and the specific discussion of the stability of bipolytropes having <math>~(n_c, n_e) = (5, 1)</math>, it can straightforwardly be shown that <math>~\partial \mathfrak{G}^*_{51}/\partial \chi = 0</math> is satisfied by setting <math>~\Chi = 1</math>; that is, the equilibrium condition is,
|
<math>~\chi = \chi_\mathrm{eq}</math> |
<math>~=</math> |
<math>~\biggl(\frac{\pi}{2^3}\biggr)^{1/2} \frac{\nu^2}{q} \cdot \frac{(1+\ell_i^2)^3}{3^3\ell_i^5} </math> |
|
|
<math>~=</math> |
<math>~\biggl\{ \biggl(\frac{\pi}{3}\biggr) 2^{2-n_c} \nu^{n_c-1} q^{3-n_c} \biggl[\frac{(1+\ell_i^2)^{6/5}}{(3\ell_i^2)} \biggr]^{n_c} \biggr\}^{1/(n_c-3)} \, ,</math> |
where the last expression has been cast into a form that more clearly highlights overlap with the expression, below, for the equilibrium radius for zero-zero bipolytropes. Furthermore, the equilibrium configuration is unstable whenever,
<math>~\biggl[ \frac{\partial^2 \mathfrak{G}^*_{51}}{\partial \chi^2}\biggr]_{\Chi=1} < 0 \, ,</math>
that is, it is unstable whenever,
|
<math>~\frac{ \mathfrak{L}_i}{\mathfrak{K}_i}</math> |
<math>~></math> |
<math>~20 \, .</math> |
Table 1 of an accompanying chapter — and the red-dashed curve in the figure adjacent to that table — identifies some key properties of the model that marks the transition from stable to unstable configurations along equilibrium sequences that have various values of the mean-molecular weight ratio, <math>~\mu_e/\mu_c</math>.
Behavior of Equilibrium Sequence
Here we reprint Figure 1 from an accompanying chapter wherein the structure of five-one bipolytropes has been derived. It displays detailed force-balance sequences in the <math>~q - \nu</math> plane for a variety of choices of the ratio of mean-molecular-weights, <math>~\mu_e/\mu_c</math>, as labeled.
Limiting Values
Each sequence begins <math>~(\ell_i = 0)</math> at the origin, that is, at <math>~(q,\nu) = (0,0)</math>. As <math>~\ell_i \rightarrow \infty</math>, however, the sequences terminate at different coordinate locations, depending on the value of <math>~m_3 \equiv 3(\mu_e/\mu_c)</math>. In deriving the various limits, it will be useful to note that,
|
<math>~\frac{1}{\eta_i}</math> |
<math>~=</math> |
<math>~\frac{(1 + \ell_i^2)}{m_3 \ell_i} \, ,</math> |
|
<math>~\Lambda_i</math> |
<math>~=</math> |
<math>~\frac{(1+\ell_i^2)}{m_3\ell_i}-\ell_i</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{m_3\ell_i} + \biggl[\frac{(1 -m_3)}{m_3} \biggr]\ell_i </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{m_3\ell_i} \biggl[ 1 - (m_3-1) \ell_i^2\biggr] </math> |
|
|
<math>~=</math> |
<math>~- \frac{ (m_3-1) \ell_i}{m_3} \biggl[ 1 - \frac{1}{(m_3-1) \ell_i^2}\biggr] \, ,</math> |
|
<math>~1 + \Lambda_i^2</math> |
<math>~=</math> |
<math>~1 + \frac{1}{m_3^2\ell_i^2}\biggl[1 + (1 -m_3) \ell_i^2 \biggr]^2</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{m_3^2\ell_i^2}\biggl\{ m_3^2\ell_i^2 + \biggl[1 + (1 -m_3) \ell_i^2 \biggr]^2\biggr\}</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{m_3^2\ell_i^2}\biggl\{ 1 + (2 -2m_3 + m_3^2) \ell_i^2 + (1 -m_3)^2 \ell_i^4 \biggr\}</math> |
Examining the three relevant parameter regimes, we see that:
- For <math>~\mu_e/\mu_c < \tfrac{1}{3}</math>, that is, <math>~m_3 < 1</math> …
|
<math>~\tan^{-1} \Lambda_i \biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx </math> |
<math>~\tan^{-1} \biggl[\frac{(1 -m_3)}{m_3} \biggr]\ell_i</math> |
|
|
<math>~\approx </math> |
<math>~\frac{\pi}{2} - \biggl[\frac{m_3}{(1 -m_3)\ell_i} \biggr]</math> |
|
<math>~\Rightarrow ~~~ \frac{1}{q}\biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~ 1 + \frac{(1 + \ell_i^2)}{m_3 \ell_i}\biggl[\pi - \frac{m_3}{(1 -m_3)\ell_i} \biggr] </math> |
|
|
<math>~\approx</math> |
<math>~ \frac{m_3 + \pi \ell_i}{m_3} </math> |
|
<math>~\Rightarrow ~~~ q\biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~ \frac{1}{1 + (\pi \ell_i/m_3)} \rightarrow 0 \, . </math> |
|
|
and |
|
|
<math>~\biggl(\frac{\nu}{q}\biggr)^2</math> |
<math>~=</math> |
<math>~\frac{\ell_i^2}{1 + \Lambda_i^2}</math> |
|
|
<math>~=</math> |
<math>~m_3^2\ell_i^4 \biggl\{ 1 + (2 -2m_3 + m_3^2) \ell_i^2 + (1 -m_3)^2 \ell_i^4 \biggr\}^{-1}</math> |
|
|
<math>~=</math> |
<math>~m_3^2\biggl\{ \ell_i^{-4} + (2 -2m_3 + m_3^2) \ell_i^{-2} + (1 -m_3)^2 \biggr\}^{-1}</math> |
|
<math>~\Rightarrow ~~~ \frac{\nu}{q}\biggr|_{\ell_i\rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~\frac{m_3}{1-m_3} </math> |
|
<math>~\Rightarrow ~~~ \nu \biggr|_{\ell_i\rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~\biggl[\frac{m_3}{1-m_3}\biggr]\frac{1}{1 + (\pi \ell_i/m_3)} \rightarrow 0 \, . </math> |
- For <math>~\mu_e/\mu_c = \tfrac{1}{3}</math>, that is, <math>~m_3 = 1</math> …
|
<math>~\tan^{-1} \Lambda_i </math> |
<math>~= </math> |
<math>~\tan^{-1} \biggl(\frac{1}{\ell_i}\biggr)</math> |
|
<math>~\Rightarrow ~~~ \tan^{-1} \Lambda_i \biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx </math> |
<math>~\frac{1}{\ell_i}</math> |
|
<math>~\Rightarrow ~~~ \frac{1}{q}\biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~ 1 + \frac{(1 + \ell_i^2)}{\ell_i}\biggl[\frac{\pi}{2} + \frac{1}{\ell_i }\biggr] </math> |
|
|
<math>~\approx</math> |
<math>~ \biggl(\frac{\pi}{2}\biggr)\ell_i</math> |
|
<math>~\Rightarrow ~~~ q\biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~ \frac{2}{\pi \ell_i} \rightarrow 0</math> |
|
|
and |
|
|
<math>~\biggl(\frac{\nu}{q}\biggr)</math> |
<math>~=</math> |
<math>~\frac{\ell_i}{(1 + 1/\ell_i^2)^{1/2}}</math> |
|
<math>~\Rightarrow ~~~ \nu \biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~\ell_i \biggl(\frac{2}{\pi \ell_i} \biggr) = \frac{2}{\pi} \approx 0.63662</math> |
- For <math>~\mu_e/\mu_c > \tfrac{1}{3}</math>, that is, <math>~m_3 > 1</math> …
|
<math>~\tan^{-1} \Lambda_i \biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx </math> |
<math>~\tan^{-1} \biggl[-\biggl(\frac{m_3-1}{m_3} \biggr)\ell_i\biggr]</math> |
|
|
<math>~\approx </math> |
<math>~-\frac{\pi}{2} + \biggl[\frac{m_3}{(m_3-1)\ell_i} \biggr]</math> |
|
<math>~\Rightarrow ~~~ \frac{1}{q}\biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~ 1 + \frac{(1 + \ell_i^2)}{m_3 \ell_i}\biggl[ \frac{m_3}{(m_3-1)\ell_i} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 1 + \frac{(1 + 1/\ell_i^2)}{(m_3-1) } </math> |
|
|
<math>~\approx</math> |
<math>~ 1 + \frac{1}{(m_3-1) } = \frac{m_3}{(m_3-1)} </math> |
|
<math>~\Rightarrow ~~~ q\biggr|_{\ell_i \rightarrow \infty}</math> |
<math>~=</math> |
<math>~ \frac{(m_3-1)}{m_3} </math> |
|
|
and |
|
|
<math>~\biggl(\frac{\nu}{q}\biggr)^2</math> |
<math>~=</math> |
<math>~\frac{\ell_i^2}{1 + \Lambda_i^2}</math> |
|
|
<math>~=</math> |
<math>~m_3^2\ell_i^4 \biggl\{ 1 + (2 -2m_3 + m_3^2) \ell_i^2 + (m_3-1)^2 \ell_i^4 \biggr\}^{-1}</math> |
|
|
<math>~=</math> |
<math>~m_3^2\biggl\{ \ell_i^{-4} + (2 -2m_3 + m_3^2) \ell_i^{-2} + (m_3-1)^2 \biggr\}^{-1}</math> |
|
<math>~\Rightarrow ~~~ \frac{\nu}{q}\biggr|_{\ell_i\rightarrow \infty}</math> |
<math>~\approx</math> |
<math>~\frac{m_3}{m_3-1} </math> |
|
<math>~\Rightarrow ~~~ \nu \biggr|_{\ell_i\rightarrow \infty}</math> |
<math>~=</math> |
<math>~\frac{m_3}{m_3-1} \biggl[\frac{m_3 - 1}{m_3}\biggr] \rightarrow 1 \, . </math> |
Summarizing:
- For <math>~\mu_e/\mu_c < \tfrac{1}{3}</math>, that is, <math>~m_3 < 1</math> … <math>~(q,\nu)_{\ell_i \rightarrow \infty} = (0, 0) \, .</math>
- For <math>~\mu_e/\mu_c = \tfrac{1}{3}</math>, that is, <math>~m_3 = 1</math> … <math>~(q,\nu)_{\ell_i \rightarrow \infty} = (0, \tfrac{2}{\pi}) \, .</math>
- For <math>~\mu_e/\mu_c > \tfrac{1}{3}</math>, that is, <math>~m_3 > 1</math> … <math>~(q,\nu)_{\ell_i \rightarrow \infty} = [(m_3-1)/m_3, 1] \, .</math>
Turning Points
Let's identify the location of two turning points along the <math>~\nu(q)</math> sequence — one defines <math>~q_\mathrm{max}</math> and the other identifies <math>~\nu_\mathrm{max}</math>. They occur, respectively, where,
|
<math>~\frac{d\ln q}{d\ln \ell_i} = 0</math> |
and |
<math>~\frac{d\ln \nu}{d\ln \ell_i} = 0 \, .</math> |
In deriving these expressions, we will use the relations,
|
<math>~\frac{d\eta_i}{d\ell_i}</math> |
<math>~=</math> |
<math>~\frac{m_3 (1-\ell_i^2)}{(1+\ell_i^2)^2} \, ,</math> |
|
<math>~\frac{d\Lambda_i}{d\ell_i}</math> |
<math>~=</math> |
<math>~- \frac{1}{m_3\ell_i^2} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] \, ,</math> |
where,
<math>~m_3 \equiv 3\biggl(\frac{\mu_e}{\mu_c}\biggr) \, .</math>
Given that,
|
<math>~q </math> |
<math>~=</math> |
<math>~\biggl\{ 1 + \frac{1}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] \biggr\}^{-1} \, ,</math> |
we find,
|
<math>~\frac{d\ln q}{d\ln \ell_i}</math> |
<math>~=</math> |
<math>~\frac{\ell_i}{q} \cdot ( -q^2) \frac{d}{d\ell_i} \biggl\{ \frac{1}{\eta_i}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~-q\ell_i \biggl\{-\frac{1}{\eta_i^2}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr]\frac{d\eta_i}{d\ell_i} + \frac{1}{\eta_i(1+\Lambda_i^2)} \frac{d\Lambda_i}{d\ell_i} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~q\ell_i \biggl\{\frac{(1-\ell_i^2)}{m_3 \ell_i^2}\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] + \frac{(1+\ell_i^2)}{m_3^2 \ell_i^3(1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{q}{m_3^2}{\ell_i^2}\biggl\{m_3 \ell_i (1-\ell_i^2) \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] + \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] \biggr\} \, . </math> |
And, given that,
|
<math>~\nu </math> |
<math>~=</math> |
<math>~ \frac{\ell_i q}{(1+\Lambda_i^2)^{1/2}} \, . </math> |
we find,
|
<math>~\frac{d\ln \nu}{d\ln \ell_i}</math> |
<math>~=</math> |
<math>~\frac{\ell_i}{\nu} \biggl\{ \frac{q}{(1+\Lambda_i^2)^{1/2}} + \frac{q}{(1+\Lambda_i^2)^{1/2}} \frac{d\ln q}{d\ln \ell_i} - \frac{\ell_i q \Lambda_i }{(1+\Lambda_i^2)^{3/2}} \frac{d\Lambda_i}{d\ell_i} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{q \ell_i}{ \nu(1+\Lambda_i^2)^{1/2}}\biggl\{ 1 + \frac{d\ln q}{d\ln \ell_i} + \frac{\Lambda_i }{m_3 \ell_i (1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] \biggr\} </math> |
In summary, then, the <math>~q_\mathrm{max}</math> turning point occurs where,
|
<math>~0</math> |
<math>~=</math> |
<math>~ (1+\Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] + \frac{(1+\ell_i^2)}{m_3 \ell_i (1-\ell_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] \, ; </math> |
and the <math>~\nu_\mathrm{max}</math> turning point occurs where,
|
<math>~0</math> |
<math>~=</math> |
<math>~ 1 + \frac{\Lambda_i }{m_3 \ell_i (1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] + \frac{q \ell_i^3 (1-\ell_i^2)}{m_3} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] + \frac{q\ell_i^2}{m_3^2}\cdot \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 1 + \frac{q \ell_i^3 (1-\ell_i^2)}{m_3} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] + \biggl[ \frac{\Lambda_i }{m_3 \ell_i (1+\Lambda_i^2)} + \frac{q\ell_i^2}{m_3^2}\cdot \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggr] \cdot \biggl[ 1 - \ell_i^2(1-m_3) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 1 + \frac{q \ell_i^3 (1-\ell_i^2)}{m_3} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] + \frac{1}{m_3 \ell_i} \biggl[ \frac{\Lambda_i }{(1+\Lambda_i^2)} + \frac{q\ell_i^3}{m_3}\cdot \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggr] \cdot \biggl[ 1 - \ell_i^2(1-m_3) \biggr] \, . </math> |
|
NOTE: As we show above, for the special case of <math>~m_3 = 1</math> — that is, when <math>~\mu_e/\mu_c = \tfrac{1}{3}</math>, precisely — the equilibrium sequence (as <math>~\ell_i \rightarrow \infty</math>) intersects the <math>~q = 0</math> axis at precisely the value, <math>~\nu = 2/\pi</math>. As is illustrated graphically in Figure 1 of an accompanying chapter, no <math>~\nu_\mathrm{max}</math> turning point exists for values of <math>~m_3 > 1</math>. |
For the record, we repeat, as well, that the transition from stable to dynamically unstable configurations occurs along the sequence when,
|
<math>~\frac{(\ell_i^4-1)}{\ell_i^2} + \frac{(1+\ell_i^2)^3}{\ell_i^3} \cdot \tan^{-1}\ell_i </math> |
<math>~=</math> |
<math>~20 \biggl\{ \frac{\Lambda_i}{\eta_i} + \frac{(1+\Lambda_i^2)}{\eta_i} \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{20(1+\Lambda_i^2)(1+\ell_i^2)}{m_3\ell_i} \biggl\{ \frac{\Lambda_i}{(1+\Lambda_i^2)} + \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \biggr\} </math> |
|
<math>~\Rightarrow ~~~ m_3 \ell_i (\ell_i^4-1) + m_3(1+\ell_i^2)^3\cdot \tan^{-1}\ell_i </math> |
<math>~=</math> |
<math>~20\ell_i^2 (1+\Lambda_i^2)(1+\ell_i^2) \biggl\{ \frac{\Lambda_i}{(1+\Lambda_i^2)} + \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \biggr\} </math> |
|
<math>~\Rightarrow ~~~ \frac{m_3 \ell_i (\ell_i^4-1) + m_3(1+\ell_i^2)^3\cdot \tan^{-1}\ell_i }{ 20\ell_i^2 (1+\ell_i^2)}</math> |
<math>~=</math> |
<math>~\Lambda_i + (1+\Lambda_i^2)\biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i\biggr] \, .</math> |
In order to clarify what equilibrium sequences do not have any turning points, let's examine how the <math>~q_\mathrm{max}</math> turning-point expression behaves as <math>~\ell_i \rightarrow \infty</math>.
|
<math>~ \frac{(1+\ell_i^2)}{(1+\Lambda_i^2)} \biggl[ 1 - \ell_i^2(1-m_3) \biggr]</math> |
<math>~=</math> |
<math>~ m_3 \ell_i (\ell_i^2-1) \biggl[\frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] </math> |
|
<math>~ \Rightarrow ~~~ \frac{(1+\ell_i^2)}{ m_3 \ell_i (\ell_i^2-1) } \biggl[ 1 + \ell_i^2(m_3-1) \biggr]</math> |
<math>~=</math> |
<math>~ \biggl\{ 1 + \frac{1}{m_3^2\ell_i^2}\biggl[ (m_3-1) \ell_i^2-1 \biggr]^2 \biggr\} \biggl\{ \frac{\pi}{2} + \biggl[ -\frac{\pi}{2} - \frac{1}{\Lambda_i} + \frac{1 }{3\Lambda_i^3} + \mathcal{O}(\Lambda_i^{-5} )\biggr] \biggr\} </math> |
|
<math>~ \Rightarrow ~~~ \frac{(1+\ell_i^2) \ell_i^2(m_3-1)}{ m_3 \ell_i (\ell_i^2-1) } \biggl[ 1 + \frac{1}{\ell_i^2(m_3-1)} \biggr]</math> |
<math>~=</math> |
<math>~ \biggl\{ 1 + \frac{(m_3-1)^2 \ell_i^2}{m_3^2}\biggl[ 1 - \frac{1}{ (m_3-1) \ell_i^2 } \biggr]^2 \biggr\} \cdot \frac{1}{(-\Lambda_i)} \biggl[ 1 - \frac{1 }{3\Lambda_i^2} + \cancelto{0}{\mathcal{O}(\Lambda_i^{-4} )}\biggr] </math> |
|
<math>~ \Rightarrow ~~~ \frac{(1+\ell_i^2)}{ \ell_i (\ell_i^2-1) } \cdot \frac{m_3}{(m_3-1)} \biggl[ 1 + \frac{1}{\ell_i^2(m_3-1)} \biggr]</math> |
<math>~=</math> |
<math>~ \biggl[ 1 - \frac{2}{ (m_3-1) \ell_i^2 } + \frac{m_3^2}{(m_3-1)^2 \ell_i^2} + \frac{1}{ (m_3-1)^2 \ell_i^4 } \biggr] \cdot \frac{m_3}{(m_3-1)\ell_i} \biggl[1 - \frac{1}{(m_3-1)\ell_i^2}\biggr]^{-1} \biggl\{ 1 - \frac{m_3^2}{3(m_3-1)^2\ell_i^2} \biggl[1 - \frac{1}{(m_3-1)\ell_i^2}\biggr]^{-2} \biggr\} </math> |
|
<math>~ \Rightarrow ~~~\biggl(1 + \frac{1}{\ell_i^2} \biggr) \biggl[ 1 + \frac{1}{\ell_i^2(m_3-1)} \biggr]\biggl[1 - \frac{1}{(m_3-1)\ell_i^2}\biggr]</math> |
<math>~=</math> |
<math>~\biggl(1 - \frac{1}{\ell_i^2} \biggr) \biggl[ 1 - \frac{2}{ (m_3-1) \ell_i^2 } + \frac{m_3^2}{(m_3-1)^2 \ell_i^2} + \frac{1}{ (m_3-1)^2 \ell_i^4 } \biggr] \biggl\{ 1 - \frac{m_3^2}{3(m_3-1)^2\ell_i^2} \biggl[1 - \frac{1}{(m_3-1)\ell_i^2}\biggr]^{-2} \biggr\} </math> |
The leading-order term is unity on both sides of this expression, so they cancel; let's see what results from keeping terms <math>~\propto \ell_i^{-2}</math>.
|
<math>~ \frac{1}{\ell_i^2} \biggl[ 1 + \frac{1}{(m_3-1)} - \frac{1}{(m_3-1)}\biggr]</math> |
<math>~=</math> |
<math>~ \frac{1}{\ell_i^2} \biggl[- 1 - \frac{2}{ (m_3-1) } + \frac{m_3^2}{(m_3-1)^2 } - \frac{m_3^2}{3(m_3-1)^2} \biggr] </math> |
|
<math>~\Rightarrow~~~ 2 </math> |
<math>~=</math> |
<math>~ - \frac{2}{ (m_3-1) } + \frac{2m_3^2}{3(m_3-1)^2 } </math> |
|
<math>~\Rightarrow~~~ 6(m_3-1)^2 </math> |
<math>~=</math> |
<math>~ - 6(m_3-1) + 2m_3^2 </math> |
|
<math>~\Rightarrow~~~ 6m_3^2-12m_3 + 6 </math> |
<math>~=</math> |
<math>~ - 6m_3+6 + 2m_3^2 </math> |
|
<math>~\Rightarrow~~~ m_3</math> |
<math>~=</math> |
<math>~ \frac{3}{2} \, . </math> |
We therefore conclude that the <math>~q_\mathrm{max}</math> turning point does not appear along any sequence for which,
|
<math>~m_3</math> |
<math>~></math> |
<math>~\frac{3}{2}</math> |
|
<math>~\Rightarrow ~~~ \frac{\mu_e}{\mu_c}</math> |
<math>~></math> |
<math>~\frac{1}{2}\, .</math> |
| Five-One Bipolytrope Equilibrium Sequences in <math>~q - \nu</math> Plane | |
|
Full Sequences for Various <math>~\frac{\mu_e}{\mu_c}</math> |
Magnified View with Turning Points and Stability Transition-Points Identified |
Graphical Depiction of Free-Energy Surface
| Figure 1: Free-Energy Surface for <math>~(n_c,n_e) = (5,1)</math> and <math>~\frac{\mu_e}{\mu_c} = 1</math> | ||||
| ||||
For purposes of reproducibility, it is incumbent upon us to clarify how the values of the free energy were normalized in order to produce the free-energy surface displayed in Figure 1. The normalization steps are explicitly detailed within the fortran program, below, that generated the data for plotting purposes; here we provide a brief summary. We evaluated the normalized free energy, <math>~\mathfrak{G}^*_{51}</math>, across a <math>~200 \times 200</math> zone grid of uniform spacing, covering the following <math>~(x,y) = (\ell_i,\Chi)</math> domain:
|
<math>~\frac{1}{\sqrt{3}}</math> |
<math>~\le \ell_i \le</math> |
<math>~\frac{3}{\sqrt{3}}</math> |
|
<math>~0.469230769</math> |
<math>~\le \Chi\le</math> |
<math>~2.0</math> |
(With this specific definition of the y-coordinate grid, <math>~\Chi = 1</math> is associated with zone 70.) After this evaluation, a constant, <math>~E_\mathrm{fudge} = -10</math>, was added to <math>~\mathfrak{G}^*</math> in order to ensure that the free energy was negative across the entire domain. Then (inorm = 1), for each specified interface location, <math>~x = \ell_i</math>, employing the equilibrium value of the free energy,
<math>~E_0 = \mathfrak{G}^*_{51}(\ell_i, \Chi = 1) + E_\mathrm{fudge} \, ,</math>
the free energy was normalized across all values of <math>~y = \Chi</math> via the expression,
<math>~\mathrm{fe} = \frac{(\mathfrak{G}^*_{51} + E_\mathrm{fudge}) - (E_0)_i}{|E_0|_i} \, .</math>
Finally, for plotting purposes, at each grid cell vertex ("vertex") — as well as at each grid cell center ("cell") — the value of the free energy, <math>~\mathrm{fe}</math>, was renormalized as follows,
<math>~\mathrm{vertex} = \frac{\mathrm{fe} - \mathrm{min}(\mathrm{fe})}{ \mathrm{max}(\mathrm{fe}) - \mathrm{min}(\mathrm{fe})} \, .</math>
Via this last step, the minimum "vertex" energy across the entire domain was 0.0 while the maximum "vertex" energy was 1.0.
| FORTRAN Program Documentation | Example Evaluations(See also associated Table 1) | ||||
|---|---|---|---|---|---|
| Coord. Axis | Coord. Name | Associated Physical Quantity | <math>~\frac{\mu_e}{\mu_c} = 1</math> | <math>~\frac{\mu_e}{\mu_c} = 0.305</math> | |
| x-axis | bsize | <math>~\ell_i \equiv \frac{\xi_i}{\sqrt{3}}</math> | <math>~\frac{2.416}{\sqrt{3}} = 1.395</math> | <math>~\frac{8.1938}{\sqrt{3}} = 4.7307</math> | <math>~\frac{14.389}{\sqrt{3}} = 8.3076</math> |
| y-axis | csize | <math>~\Chi \equiv \frac{\chi}{\chi_\mathrm{eq}}</math> | <math>~1</math> | <math>~1</math> | <math>~1</math> |
| Relevant Lines of Code | |||||
eta = 3.0d0*muratio*bsize/(1.0d0+bsize**2)
Gami = 1.0d0/eta-bsize
frakL = (bsize**4-1.0d0)/bsize**2 + &
& DATAN(bsize)*((1.0d0+bsize**2)/bsize)**3
frakK = Gami/eta + ((1.0d0+Gami**2)/eta)*(pii/2.0d0+DATAN(Gami))
E0 = ((5.0d0*frakL) + (4.0d0*frakK)&
& - (3.0d0*frakL+12.0d0*frakK))/bsize**2+Efudge
fescalar(j,k) = (csize**(-0.6d0)*(5.0d0*frakL)&
& + csize**(-3.0d0)*(4.0d0*frakK)&
& - (3.0d0*frakL+12.0d0*frakK)/csize)/bsize**2 + Efudge
if(inorm.eq.1)fescalar(j,k)=fescalar(j,k)/DABS(E0) &
& - E0/DABS(E0)
|
|||||
| Variable | Represents | Value calculated via the expression … | |||
| eta | <math>~\eta_i</math> |
<math>~3 \biggl(\frac{\mu_e}{\mu_c}\biggr)\biggl[ \frac{\ell_i}{(1+\ell_i^2)} \biggr]</math> |
<math>~1.421</math> | <math>~0.1851</math> | <math>~0.1086</math> |
| Gami | <math>~\Lambda_i</math> | <math>~\frac{1}{\eta_i} - \ell_i</math> | <math>~-0.691</math> | <math>~0.6705</math> | <math>~0.9033</math> |
| frakL | <math>~\mathfrak{L}_i</math> | <math>~
\frac{(\ell_i^4 - 1)}{\ell_i^2} + \biggl[ \frac{1+\ell_i^2}{\ell_i} \biggr]^3 \tan^{-1}\ell_i </math> |
<math>~10.37</math> | <math>~186.80</math> | <math>~937.64</math> |
| frakK | <math>~\mathfrak{K}_i</math> | <math>~
\frac{\Lambda_i}{\eta_i} + \frac{(1 + \Lambda_i^2)}{\eta_i} \biggl[ \frac{\pi}{2} + \tan^{-1}\Lambda_i \biggr] </math> |
<math>~0.518</math> | <math>~20.544</math> | <math>~46.882</math> |
| <math>~\frac{\mathfrak{L}_i}{\mathfrak{K}_i}</math> | <math>~20</math> | <math>~9.093</math> | <math>~20</math> | ||
| E0 - Efudge | <math>~\mathfrak{G}^*_{51}(\ell_i,\Chi=1)</math> |
<math>~ \frac{1}{\ell_i^2} \biggl[ 5 \mathfrak{L}_i + 4\mathfrak{K}_i - (3\mathfrak{L}_i +12\mathfrak{K}_i ) \biggr] = \frac{2(\mathfrak{L}_i - 4\mathfrak{K}_i)}{\ell_i^2} </math> |
<math>~8.525</math> | <math>~9.3496</math> | <math>~21.737</math> |
| Figure 2: Free-Energy Surface for <math>~(n_c,n_e) = (5,1)</math> and <math>~\frac{\mu_e}{\mu_c} = 0.305</math> | ||
|
BiPolytrope00
|
Out-of-Equilibrium, Free-Energy Expression for BiPolytropes with Structural <math>~(n_c, n_e) = (0, 0)</math> |
|||
|---|---|---|---|
|
where,
|
<math>~A_2 </math> |
<math>~\equiv</math> |
<math> \frac{2}{5}q^3 \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, , </math> |
|
<math>~B_2 </math> |
<math>~\equiv</math> |
<math> \frac{2}{5} q^3 f - A_2 \, , </math> |
|
<math>~C_2 </math> |
<math>~\equiv</math> |
<math> \frac{2}{5} q^3 f \, , </math> |
|
<math>~f</math> |
<math>~\equiv</math> |
<math> 1+ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \biggl(\frac{1}{q^2}-1 \biggr) +\biggl( \frac{\rho_e}{\rho_c} \biggr)^2 \biggl[ \frac{1}{q^5}-1 + \frac{5}{2} \biggl( 1-\frac{1}{q^2}\biggr)\biggr] \, , </math> |
|
<math>~\mathfrak{F} </math> |
<math>~\equiv</math> |
<math>~ \frac{5}{2} \biggl( \frac{\rho_e}{\rho_c} \biggr) \frac{1}{q^5} \biggl[ (-2q^2 + 3q^3 - q^5) + \frac{3}{5} \biggl( \frac{\rho_e}{\rho_c}\biggr) (-1 +5q^2 - 5q^3 + q^5) \biggr] \, , </math> |
|
<math>~\frac{\rho_e}{\rho_c} </math> |
<math>~=</math> |
<math>~ \frac{q^3(1-\nu)}{\nu(1-q^3)} \, . </math> |
The associated equilibrium radius is,
|
<math>~\chi_\mathrm{eq}</math> |
<math>~=</math> |
<math>~ \biggl\{ \biggl(\frac{\pi}{3}\biggr) 2^{2-n_c} \nu^{n_c-1} q^{3-n_c} \biggl[1 + \frac{2}{5} q^3(f-1-\mathfrak{F})\biggr]^{n_c} \biggr\}^{1/(n_c-3)} \, . </math> |
We have deduced that the system is unstable if,
|
<math>~\frac{n_e}{3}\biggl[ \frac{3-n_e}{n_c-n_e} \biggr] </math> |
<math>~< </math> |
<math>~ \frac{A_2}{C_2} = \frac{1}{f} \biggl[1 + q^3 (f - 1-\mathfrak{F} ) \biggr] \, . </math> |
Fortran Code
This is the program that generated the free-energy data for the "five-one" bipolytrope that is displayed in the above, Figure 1 image/animation.
PROGRAM BiPolytrope
real*8 pii
real*8 bmin,bmax,cmin,cmax,db,dc
real*8 c(200),b(200),chalf(199),bhalf(199)
real*8 bsize,csize,emin,emax
real*8 fepoint(200,200),fescalar(199,199)
real*8 ell(200),ellhalf(199)
real*8 muratio,eta,Gami,frakK,frakL
real*8 eshift,ediff
real xx(200),yy(200),cell(199,199),vertex(200,200)
real valuemin,minlog,valufudge
real*8 q,nu,chiEq,Enorm,E0,Efudge
integer j,k,n,nmax,inorm
101 format(4x,'bsize',7x,'csize',8x,'xi',10x,'A',12x,'B',12x,&
&'fM',13x,'fW',11x,'fA',/)
! 102 format(1p8d12.4)
103 format(2i5,1p3d14.6)
201 format(5x,'valuemin = ',1pe15.5,//)
205 format(5x,'For Cell-center ... emin, emax = ',1p2d14.6,/)
206 format(5x,'For Cell-vertex ... emin, emax = ',1p2d14.6,/)
701 format(5x,1p10d10.2)
700 format(8x,'xi',9x,'ell',8x,'eta',8x,'Lambda',5x,'frakK',&
& 5x,'frakL',8x,'q',5x,'nu',5x,'chiEq',8x,'E0',/)
!!!!!!!!
!!!!!!!!
inorm=1
pii = 4.0d0*datan(1.0d0)
muratio = 1.0d0
bsize = 0.0d0
csize = 0.0d0
Efudge = -10.0d0
write(*,101)
! write(*,102)bsize,csize,xival,coefA,coefB,fM,fW,fA
!!!!!!!!!!!
!
! In this free-energy routine, c = X = chi/chi_eq and b = xi_i
!
!!!!!!!!!!!
nmax = 200
bmin = 1.0d0
bmax = 3.0d0
db = (bmax-bmin)/dfloat(nmax-1)
b(1) = bmin
ell(1) = b(1)/dsqrt(3.0d0)
! These values of cmin and cmax ensure that X=1 occurs at zone 70
cmin = 0.469230769d0
cmax = 2.00d0
dc = (cmax-cmin)/dfloat(nmax-1)
c(1) = cmin
do n=2,nmax
b(n) = b(n-1)+db
c(n) = c(n-1)+dc
ell(n) = b(n)/dsqrt(3.0d0)
enddo
do n=1,nmax-1
bhalf(n) = 0.5d0*(b(n)+b(n+1))
chalf(n) = 0.5d0*(c(n)+c(n+1))
ellhalf(n) = bhalf(n)/dsqrt(3.0d0)
enddo
!
! BEGIN LOOP to evaluate free energy (cell center)
!
emin = 0.0d0
emax = 0.0d0
write(*,700)
do j=1,nmax-1
bsize = ellhalf(j)
eta = 3.0d0*muratio*bsize/(1.0d0+bsize**2)
Gami = 1.0d0/eta-bsize
frakL = (bsize**4-1.0d0)/bsize**2 + &
& DATAN(bsize)*((1.0d0+bsize**2)/bsize)**3
frakK = Gami/eta + ((1.0d0+Gami**2)/eta)*(pii/2.0d0+DATAN(Gami))
q = 1.0d0/(1.0d0 + (0.5d0*pii+DATAN(Gami))/eta)
nu = bsize*q/dsqrt(1.0d0+Gami**2)
chiEq = dsqrt(pii/8.0d0)*(nu**2/(q*bsize**2))&
& *((1.0d0+bsize**2)/(3.0d0*bsize))**3
Enorm = 16.0d0*(q/nu**2)*chiEq
E0 = ((5.0d0*frakL) + (4.0d0*frakK)&
& - (3.0d0*frakL+12.0d0*frakK))/bsize**2+Efudge
write(*,701)b(j),bsize,eta,Gami,frakK,frakL,q,nu,chiEq,E0
do k=1,nmax-1
csize=chalf(k)
fescalar(j,k) = (csize**(-0.6d0)*(5.0d0*frakL)&
& + csize**(-3.0d0)*(4.0d0*frakK)&
& - (3.0d0*frakL+12.0d0*frakK)/csize)/bsize**2 + Efudge
if(inorm.eq.1)fescalar(j,k)=fescalar(j,k)/DABS(E0) &
& - E0/DABS(E0)
if(fescalar(j,k).gt.0.5d0)fescalar(j,k)=0.5d0
if(fescalar(j,k).lt.emin)emin=fescalar(j,k)
if(fescalar(j,k).gt.emax)emax=fescalar(j,k)
! write(*,103)j,k,bsize,csize,fescalar(j,k)
enddo
enddo
write(*,205)emin,emax
!
! BEGIN LOOP to evaluate free energy (cell vertex)
!
emin = 0.0d0
emax = 0.0d0
do j=1,nmax
bsize = ell(j)
eta = 3.0d0*muratio*bsize/(1.0d0+bsize**2)
Gami = 1.0d0/eta-bsize
frakL = (bsize**4-1.0d0)/bsize**2 + &
& DATAN(bsize)*((1.0d0+bsize**2)/bsize)**3
frakK = Gami/eta + ((1.0d0+Gami**2)/eta)*(pii/2.0d0+DATAN(Gami))
q = 1.0d0/(1.0d0 + (0.5d0*pii+DATAN(Gami))/eta)
nu = bsize*q/dsqrt(1.0d0+Gami**2)
chiEq = dsqrt(pii/8.0d0)*(nu**2/(q*bsize**2))&
& *((1.0d0+bsize**2)/(3.0d0*bsize))**3
Enorm = 16.0d0*(q/nu**2)*chiEq
E0 = ((5.0d0*frakL) + (4.0d0*frakK)&
& - (3.0d0*frakL+12.0d0*frakK))/bsize**2 + Efudge
do k=1,nmax
csize=c(k)
fepoint(j,k) = (csize**(-0.6d0)*(5.0d0*frakL)&
& + csize**(-3.0d0)*(4.0d0*frakK)&
& - (3.0d0*frakL+12.0d0*frakK)/csize)/bsize**2 + Efudge
if(inorm.eq.1)fepoint(j,k)=fepoint(j,k)/DABS(E0) &
& - E0/DABS(E0)
if(fepoint(j,k).gt.0.5d0)fepoint(j,k)=0.5d0
if(fepoint(j,k).lt.emin)emin=fepoint(j,k)
if(fepoint(j,k).gt.emax)emax=fepoint(j,k)
! write(*,103)j,k,bsize,csize,fepoint(j,k)
enddo
enddo
write(*,206)emin,emax
!
! Now fill single-precision arrays for plotting.
!
do n=1,nmax
! xx(n)=b(n)/b(nmax)
! yy(n)=c(n)/c(nmax)
xx(n)=b(n)-bmin
yy(n)=c(n)-cmin
! xx(n)=b(n)
! yy(n)=c(n)
enddo
valuemin= -emin
valufudge = 1.0d0/(emax-emin)
do k=1,nmax
do j=1,nmax
vertex(j,k)=fepoint(j,k)+valuemin
vertex(j,k)=vertex(j,k)*valufudge
enddo
enddo
do k=1,nmax-1
do j=1,nmax-1
cell(j,k)=fescalar(j,k)+valuemin
cell(j,k)=cell(j,k)*valufudge
enddo
enddo
call XMLwriter01(nmax,xx,yy,cell,vertex)
stop
END PROGRAM BiPolytrope
Subroutine XMLwriter01(imax,x,y,cell_scalar,point_scalar)
real x(200),y(200),z(1)
real cell_scalar(199,199),point_scalar(200,200)
integer imax
integer extentX,extentY,extentZ
integer ix0,iy0,iz0
integer norm(200,3)
! imax=200
ix0=0
iy0=0
iz0=0
extentX=imax-1
extentY=imax-1
extentZ=0
z(1) = 0.0
! Set normal vector 1D array
do i=1,imax
norm(i,1)=0
norm(i,2)=0
norm(i,3)=1
enddo
201 format('<?xml version="1.0"?>')
202 format('<VTKFile type="RectilinearGrid" version="0.1" byte_order="LittleEndian">')
302 format('</VTKFile>')
203 format(2x,'<RectilinearGrid WholeExtent="',6I4,'">')
303 format(2x,'</RectilinearGrid>')
204 format(4x,'<Piece Extent="',6I4,'">')
304 format(4x,'</Piece>')
205 format(6x,'<CellData Scalars="cell_scalars" Normals="magnify">')
305 format(6x,'</CellData>')
206 format(8x,'<DataArray type="Float32" Name="magnify" NumberOfComponents="3" format="ascii">')
207 format(8x,'<DataArray type="Float32" Name="cell_scalars" format="ascii">')
399 format(8x,'</DataArray>')
208 format(6x,'<PointData Scalars="colorful" Normals="direction">')
308 format(6x,'</PointData>')
209 format(8x,'<DataArray type="Float32" Name="colorful" format="ascii">')
210 format(6x,'<Coordinates>')
310 format(6x,'</Coordinates>')
211 format(8x,'<DataArray type="Float32" format="ascii" RangeMin="0" RangeMax="5">')
212 format(8x,'<DataArray type="Float32" format="ascii">')
213 format(8x,'<DataArray type="Float32" Name="direction" NumberOfComponents="3" format="ascii">')
501 format(10f9.5)
502 format(10f9.5)
503 format(5x,9(1x,3I2))
504 format(10f9.5)
505 format(5x,10(1x,3I2))
!!!!!
!
! Begin writing out XML tags.
!
!!!!!
write(*,201) !<?xml
write(*,202) !VTKFile
write(*,203)ix0,extentX,iy0,extentY,iz0,extentZ ! RectilinearGrid
write(*,204)ix0,extentX,iy0,extentY,iz0,extentZ ! Piece
write(*,205) ! CellData
write(*,207) ! DataArray(cell_scalars)
do j=1,imax-1
write(*,501)(cell_scalar(i,j),i=1,imax-1)
enddo
write(*,399) ! /DataArray
write(*,206) ! DataArray(cell_scalars)
do j=1,imax-1
write(*,503)(norm(i,1),norm(i,2),norm(i,3),i=1,imax-1)
enddo
write(*,399) ! /DataArray
write(*,305) ! /CellData
write(*,208) ! PointData
write(*,209) ! DataArray(points)
write(*,502)((point_scalar(i,j),i=1,imax),j=1,imax)
write(*,399) ! /DataArray
write(*,213) ! DataArray(cell_scalars)
do j=1,imax
write(*,505)(norm(i,1),norm(i,2),norm(i,3),i=1,imax)
enddo
write(*,399) ! /DataArray
write(*,308) ! /PointData
write(*,210) ! Coordinates
write(*,212) ! DataArray(x-direction)
write(*,504)(x(i),i=1,imax)
write(*,399) ! /DataArray
write(*,212) ! DataArray(y-direction)
write(*,504)(y(i),i=1,imax)
write(*,399) ! /DataArray
write(*,212) ! DataArray(z-direction)
write(*,504)z(1)
write(*,399) ! /DataArray
write(*,310) ! /Coordinates
write(*,304) ! /Piece
write(*,303) ! /RectilinearGrid
write(*,302) !/VTKFile
return
end
Nonstandard Examination
In our introductory remarks, above, we said the warped free-energy surface drapes across a five-dimensional parameter "plane" such that,
|
<math>~\mathfrak{G}_{51}</math> |
<math>~=</math> |
<math>~\mathfrak{G}(R, K_c, M_\mathrm{tot}, q, \nu) \, .</math> |
From a more pragmatic point of view, we should have said that the "five-one" free-energy surface drapes across a five-dimensional parameter "plane" such that,
|
<math>~\mathfrak{G}_{51}</math> |
<math>~=</math> |
<math>~\mathfrak{G}(R, K_c, M_\mathrm{tot}, \ell_i, \tfrac{\mu_e}{\mu_c}) \, .</math> |
In our initial, standard examination of the structure of this warped free-energy surface, we held three parameters fixed — namely, <math>~K_c, M_\mathrm{tot}, \tfrac{\mu_e}{\mu_c}</math> — and plotted <math>~\mathfrak{G}_{51}(\ell_i, \Chi\equiv R/R_\mathrm{eq})</math>. Now, let's fix <math>~\Chi = 1</math> and plot <math>~\mathfrak{G}_{51}(\ell_i, \tfrac{\mu_e}{\mu_c})</math>. The following plot shows how a portion of the <math>~(\ell_i, \mu_e/\mu_c)</math> grid maps onto the traditional <math>~(q, \nu)</math> plane. The numerical labels identify lines of constant <math>~\xi_i = \sqrt{3}\ell_i</math> — 7 (light green), 9 (pink), and 12 (orange) — and lines of constant <math>~\mu_e/\mu_c</math> — 0.330 (purple), 0.315 (dark green), and 0.305 (white/blue).
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |