Difference between revisions of "User:Tohline/SSC/Virial/PolytropesEmbedded/FirstEffortAgain"
| Line 2,768: | Line 2,768: | ||
====P-V Diagram==== | ====P-V Diagram==== | ||
For an arbitrary value of the adiabatic exponent, <math>~\gamma_g</math>, it isn't possible to invert this virial relation to obtain an analytic expression for <math>~\chi_\mathrm{ad}</math> as a function of <math>~\Pi_\mathrm{ad}</math>. But, as written, the virial relation dictates the behavior of <math>~\Pi_\mathrm{ad}</math> as a function of <math>~\ | For an arbitrary value of the adiabatic exponent, <math>~\gamma_g</math>, it isn't possible to invert this virial relation to obtain an analytic expression for <math>~\chi_\mathrm{ad}</math> as a function of <math>~\Pi_\mathrm{ad}</math>. But, as written, the virial relation dictates the behavior of <math>~\Pi_\mathrm{ad}</math> as a function of <math>~\Chi_\mathrm{ad}</math>. Figure 4 displays this <math>~\Pi_\mathrm{ad}(\chi_\mathrm{ad})</math> behavior for a number of different values of <math>~\gamma_g</math>. | ||
<div align="center"> | <div align="center"> | ||
| Line 2,782: | Line 2,782: | ||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
~\Pi_\mathrm{ad} = (\ | ~\Pi_\mathrm{ad} = (\Chi_\mathrm{ad}^{4-3\gamma_g} - 1)/\Chi_\mathrm{ad}^4 \, , | ||
</math> | </math> | ||
</div> | </div> | ||
for six different values of <math>~\gamma_g</math> — specifically, for <math>2, ~5/3, ~7/5, ~6/5, ~1, ~2/3</math>, as labeled — and show the dimensionless external pressure, <math>~\Pi_\mathrm{ad}</math>, that is required to construct a nonrotating, self-gravitating, pressure-truncated adiabatic sphere with an equilibrium radius <math>~\ | for six different values of <math>~\gamma_g</math> — specifically, for <math>2, ~5/3, ~7/5, ~6/5, ~1, ~2/3</math>, as labeled — and show the dimensionless external pressure, <math>~\Pi_\mathrm{ad}</math>, that is required to construct a nonrotating, self-gravitating, pressure-truncated adiabatic sphere with an equilibrium radius <math>~\Chi_\mathrm{ad}</math>. The solid red curve identifies the behavior of an isothermal <math>~(\gamma_g=1)</math> system. The mathematical solution becomes unphysical wherever the pressure becomes negative. | ||
</td> | </td> | ||
<td align="center" bgcolor="white"> | <td align="center" bgcolor="white"> | ||
| Line 2,795: | Line 2,795: | ||
For physically relevant solutions, both <math>~\ | For physically relevant solutions, both <math>~\Chi_\mathrm{ad}</math> and <math>~\Pi_\mathrm{ad}</math> must be nonnegative. Hence, as is illustrated by the curves in Figure 4, the physically allowable range of equilibrium radii is, | ||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
1 \le \ | 1 \le \Chi_\mathrm{ad} \le \infty \, ~~~~~\mathrm{for}~ \gamma_g < 4/3 \, ; | ||
</math> | </math> | ||
<math> | <math> | ||
0 < \ | 0 < \Chi_\mathrm{ad} \le 1 \, ~~~~~~\mathrm{for}~ \gamma_g > 4/3 \, . | ||
</math> | </math> | ||
</div> | </div> | ||
Each of the <math>~\Pi_\mathrm{ad}(\ | Each of the <math>~\Pi_\mathrm{ad}(\Chi_\mathrm{ad})</math> curves drawn in Figure 4 exhibits an extremum. In each case this extremum occurs at a configuration radius, <math>~\Chi_\mathrm{extreme}</math>, given by, | ||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
\frac{\partial\Pi_\mathrm{ad}}{\partial\ | \frac{\partial\Pi_\mathrm{ad}}{\partial\Chi_\mathrm{ad}} = 0 \, , | ||
</math> | </math> | ||
</div> | </div> | ||
| Line 2,815: | Line 2,815: | ||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
4 - 3\gamma_g \ | 4 - 3\gamma_g \Chi_\mathrm{ad}^{4-3\gamma_g} = 0 ~~~~\Rightarrow ~~~~~ \Chi_\mathrm{extreme} = \biggl[ \frac{4}{3\gamma_g} \biggr]^{1/(4-3\gamma_g)} \, . | ||
</math> | </math> | ||
</div> | </div> | ||
For each value of <math>\gamma_g</math>, the corresponding dimensionless pressure is, | For each value of <math>~\gamma_g</math>, the corresponding dimensionless pressure is, | ||
<div align="center"> | <div align="center"> | ||
<math> | <math> | ||
| Line 2,829: | Line 2,829: | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center"> | ||
<math>~\ | <math>~\Chi_\mathrm{extreme} = \biggl[ \frac{4n}{3(n+1)} \biggr]^{n/(n-3)}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,840: | Line 2,840: | ||
</table> | </table> | ||
</div> | </div> | ||
(In a [[User:Tohline/SSC/Virial/PolytropesEmbedded/SecondEffortAgain#Stability|separate, related discussion of the free-energy function]], we demonstrate that this "extremum" also serves as a dividing line between dynamically stable and unstable models along a given curve.) | |||
In examining the group of plotted curves, notice that, for <math>~\gamma_g > 4/3</math>, an equilibrium configuration with a positive radius can be constructed for all physically realistic — that is, for all positive — values of <math>~\Pi_\mathrm{ad}</math>. Also, consistent with the behavior of the curves shown in Figure 4, the extremum arises in the regime of physically relevant — ''i.e.,'' positive — pressures only for values of <math>~\gamma_g < 4/3</math>; and in each case it represents a ''maximum'' limiting pressure. | |||
Latest revision as of 19:18, 21 January 2015
Virial Equilibrium of Adiabatic Spheres
Highlights of the rather detailed discussion presented below have been summarized in an accompanying chapter of this H_Book.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Review
Adopted Normalizations
In an introductory discussion of the virial equilibrium structure of spherically symmetric configurations, we adopted the following physical parameter normalizations for adiabatic systems.
|
Adopted Normalizations for Adiabatic Systems | |||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
In Terms of <math>~\gamma_g</math> |
In Terms of <math>~n</math> | ||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
Virial Equilibrium
Also in our introductory discussion — see especially the section titled, Energy Extrema — we deduced that an adiabatic system's dimensionless equilibrium radius,
<math>~\chi_\mathrm{eq} \equiv \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \, ,</math>
is given by the root(s) of the following equation:
<math> 2\mathcal{C} \chi_\mathrm{eq}^{-2} + ~3 \mathcal{B}\chi_\mathrm{eq}^{3 -3\gamma_g} -~3\mathcal{A}\chi_\mathrm{eq}^{-1} -~ 3\mathcal{D} \chi_\mathrm{eq}^3 = 0 \, , </math>
where the definitions of the various coefficients are,
|
<math>~\mathcal{A}</math> |
<math>~\equiv</math> |
<math>\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W \, ,</math> |
|
<math>~\mathcal{B}</math> |
<math>~\equiv</math> |
<math> \frac{4\pi}{3} \biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]_\mathrm{eq}^{\gamma} \cdot \mathfrak{f}_A </math> |
|
|
<math>~=</math> |
<math> \frac{4\pi}{3} \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} \cdot \mathfrak{f}_A \, , </math> |
|
<math>~\mathcal{C}</math> |
<math>~\equiv</math> |
<math> \frac{3\cdot 5}{2^4 \pi} \biggl[ \frac{J^2 c_\mathrm{norm}^2}{G^2 M_\mathrm{tot}^4} \biggr] \cdot \frac{\mathfrak{f}_T}{\mathfrak{f}_M} \, , </math> |
|
<math>~\mathcal{D}</math> |
<math>~\equiv</math> |
<math> \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \, . </math> |
(The dimensionless structural form factors, <math>~\mathfrak{f}_i,</math> that appear in these expressions are defined for isolated polytropes in our accompanying introductory discussion and are discussed further, below.) Once the pressure exerted by the external medium (<math>~P_e</math>), and the configuration's mass (<math>~M_\mathrm{tot}</math>), angular momentum (<math>~J</math>), and specific entropy (via <math>~K</math>) have been specified, the values of all of the coefficients are known and <math>~\chi_\mathrm{eq}</math> can be determined.
|
For later use, we note that after making the substitution, <math>~\gamma_g \rightarrow (n+1)/n</math>,
and,
|
Isolated Nonrotating Adiabatic Configuration
For a nonrotating configuration <math>~(C=J=0)</math> that is not influenced by the effects of a bounding external medium <math>~(D=P_e = 0)</math>, the statement of virial equilibrium is,
<math> 3 B\chi_\mathrm{eq}^{3 -3\gamma_g} -~3A\chi_\mathrm{eq}^{-1} = 0 \, . </math>
Hence, one equilibrium state exists for each value of <math>~\gamma_g</math> and it occurs where,
|
<math>~\chi_\mathrm{eq}^{4-3\gamma_g} = \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^{4-3\gamma_g} </math> |
<math>~=</math> |
<math> \frac{A}{B} \, . </math> |
|
Two Points of View |
||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
In terms of <math>~K</math> and <math>~M_\mathrm{limit} ~(= M_\mathrm{tot})</math> |
In terms of <math>~P_c</math> and <math>~M_\mathrm{limit} ~(= M_\mathrm{tot})</math> |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
According to the solution shown in the left-hand column, for fluid with a given specify entropy content, the equilibrium mass-radius relationship for adiabatic configurations is,
<math> M_\mathrm{tot}^{(\gamma_g - 2)} \propto R_\mathrm{eq}^{(3\gamma_g -4)} \, . </math>
We see that, for <math>~\gamma_g=2</math>, the equilibrium radius depends only on the specific entropy of the gas and is independent of the configuration's mass. Conversely, for <math>~\gamma_g = 4/3</math>, the mass of the configuration is independent of the radius. For <math>~\gamma_g > 2</math> or <math>~\gamma_g < 4/3</math>, configurations with larger mass (but the same specific entropy) have larger equilibrium radii. However, for <math>~\gamma_g</math> in the range, <math>~2 > \gamma_g > 4/3</math>, configurations with larger mass have smaller equilibrium radii. (Note that the related result for isothermal configurations can be obtained by setting <math>~\gamma_g = 1</math> in this adiabatic solution, because <math>~K = c_s^2</math> when <math>~\gamma_g = 1</math>.)
Role of Structural Form Factors
When employing a virial analysis to determine the radius of an equilibrium configuration, it is customary to set the structural form factors, <math>~\mathfrak{f}_M</math>, <math>~\mathfrak{f}_W</math> and <math>~\mathfrak{f}_A</math>, to unity and accept that the expression derived for <math>~R_\mathrm{eq}</math> is an estimate of the configuration's radius that is good to within a factor of order unity. As has been demonstrated in our related discussion of the equilibrium of uniform-density spheres, these form factors can be evaluated if/when the internal structural profile of an equilibrium configuration is known from a complementary detailed force-balance analysis. In the case being discussed here of isolated, spherical polytropes, solutions to the,
Lane-Emden Equation
|
<math>~\frac{1}{\xi^2} \frac{d}{d\xi}\biggl( \xi^2 \frac{d\Theta_H}{d\xi} \biggr) = - \Theta_H^n</math> |
can provide the desired internal structural information. Here we draw on Chandrasekhar's [C67] discussion of the structure of spherical polytropes to show precisely how our structural form factors can be expressed in terms of the Lane-Emden function, <math>~\Theta_H</math>, dimensionless radial coordinate, <math>~\xi</math>, and the function derivative, <math>~\Theta^' = d\Theta_H/d\xi</math>.
Mass
We note, first, that Chandrasekhar [C67] — see his Equation (78) on p. 99 — presents the following expression for the mean-to-central density ratio:
|
<math>~\frac{\bar\rho}{\rho_c}</math> |
<math>~=</math> |
<math>~ \biggl[ - \frac{3\Theta^'}{\xi} \biggr]_{\xi_1} \, ,</math> |
where the notation at the bottom of the closing square bracket means that everything inside the square brackets should be, "evaluated at the surface of the configuration," that is, at the radial location, <math>~\xi_1</math>, where the Lane-Emden function, <math>~\Theta_H(\xi)</math>, first goes to zero. But, as we pointed out when defining the structural form factors, the form factor associated with the configuration mass, <math>~\mathfrak{f}_M</math>, is equivalent to the mean-to-central density ratio. We conclude, therefore, that,
|
<math>~\mathfrak{f}_M</math> |
<math>~=</math> |
<math>~ \biggl[ - \frac{3\Theta^'}{\xi} \biggr]_{\xi_1} \, .</math> |
Gravitational Potential Energy
Second, we note that Chandrasekhar's [C67] expression for the gravitational potential energy — see his Equation (90), p. 101 — is,
|
<math>~-W</math> |
<math>~=</math> |
<math>~\frac{3}{5-n} \biggl( \frac{GM^2}{R} \biggr) \, ,</math> |
whereas our analogous expression is,
|
<math>~-W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~\frac{3}{5} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}} \biggr) \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \, .</math> |
We conclude, therefore, that,
|
<math>~\frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} </math> |
<math>~=</math> |
<math>~\frac{5}{5-n} </math> |
|
<math>\Rightarrow ~~~~\mathfrak{f}_W </math> |
<math>~=</math> |
<math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\Theta^'}{\xi} \biggr]^2_{\xi_1} \, .</math> |
Mass-Radius Relationship
Third, Chandrasekhar [C67] shows — see his Equation (72), p. 98 — that the general mass-radius relationship for isolated spherical polytropes is,
|
<math>~GM^{(n-1)/n} R^{(3-n)/n}</math> |
<math>~=</math> |
<math> ~\frac{(n+1)K}{(4\pi)^{1/n}} \biggl[ - \xi^{(n+1)/(n-1)} \frac{d\Theta_H}{d\xi} \biggr]^{(n-1)/n}_{\xi=\xi_1} \, , </math> |
which we choose to rewrite as,
|
<math>~4\pi \biggl( \frac{G}{K}\biggr)^n M^{(n-1)} R^{(3-n)}</math> |
<math>~=</math> |
<math> ~(n+1)^n\biggl[ \xi^{(n+1)} (-\Theta^')^{(n-1)}\biggr]_{\xi=\xi_1} </math> |
|
|
<math>~=</math> |
<math> - \biggl( \frac{\xi}{\Theta^'} \biggr)_{\xi=\xi_1} \biggl[ (n+1) \xi ~(-\Theta^') \biggr]^n_{\xi=\xi_1} \, . </math> |
By comparison, the expression for the equilibrium radius that has been derived, above, from an analysis of extrema in the free energy function — specifically, see the last expression in the left-hand column of the table titled "Two Points of View" — we obtain,
|
<math>~4\pi \biggl( \frac{G}{K}\biggr)^n M^{(n-1)} R_\mathrm{eq}^{(3-n)}</math> |
<math>~=</math> |
<math> ~\frac{3}{\mathfrak{f}_M} \biggl( \frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} \biggr)^n \, . </math> |
Hence, it appears as though, quite generally,
|
<math>~ \frac{1}{\mathfrak{f}_M} \biggl( \frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} \biggr)^n </math> |
<math>~=</math> |
<math> - \biggl( \frac{\xi}{3\Theta^'} \biggr)_{\xi=\xi_1} \biggl[ (n+1) \xi ~(-\Theta^') \biggr]^n_{\xi=\xi_1} \, . </math> |
Or, taking into account the expressions for <math>~\mathfrak{f}_M</math> and <math>~\mathfrak{f}_W</math> that have just been uncovered, we conclude that,
|
<math>~ \frac{5\mathfrak{f}_A \mathfrak{f}_M}{\mathfrak{f}_W} </math> |
<math>~=</math> |
<math> \biggl[ (n+1) \xi ~(-\Theta^') \biggr]_{\xi=\xi_1} </math> |
|
<math>\Rightarrow ~~~~ \frac{\mathfrak{f}_A}{\mathfrak{f}_W} </math> |
<math>~=</math> |
<math> \frac{(n+1) }{3\cdot 5} ~\xi_1^2 \, . </math> |
|
<math>\Rightarrow ~~~~ \mathfrak{f}_A </math> |
<math>~=</math> |
<math> \frac{(n+1) }{3\cdot 5} ~\xi_1^2 \biggl\{ \frac{3^2\cdot 5}{5-n} \biggl[ \frac{\Theta^'}{\xi} \biggr]^2_{\xi_1} \biggr\}\, . </math> |
|
|
<math>~=</math> |
<math> \frac{3(n+1) }{(5-n)} ~\biggl[ \Theta^' \biggr]^2_{\xi_1} \, . </math> |
Central and Mean Pressure
It is also worth pointing out that Chandrasekhar [C67] — see his Equations (80) & (81), p. 99 — introduces a dimensionless structural form factor, <math>~W_n</math>, for the central pressure via the expression,
|
<math>~P_c</math> |
<math>~=</math> |
<math>~W_n \biggl( \frac{GM^2}{R^4} \biggr) \, ,</math> |
and demonstrates that,
|
<math>~\frac{1}{W_n}</math> |
<math>~\equiv</math> |
<math>~4\pi (n+1) \biggl[ \Theta^' \biggr]^2_{\xi_1} \, .</math> |
It is therefore clear that a spherical polytrope's central pressure is expressible in terms of our structural form factor, <math>~\mathfrak{f}_A</math>, as,
|
<math>~P_c</math> |
<math>~=</math> |
<math>~\frac{3}{4\pi (5-n)} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}^4} \biggr) \frac{1}{\mathfrak{f}_A} \, .</math> |
Looking back at our original definition of the structural form factors, we note that,
<math>\mathfrak{f}_A = \biggl( \frac{\bar{P}}{P_c} \biggr)_\mathrm{eq} \, .</math>
Hence, this last equilibrium relation can be rewritten as,
<math> \frac{\bar{P} R_\mathrm{eq}^4}{GM_\mathrm{tot}^2} = \frac{3}{4\pi (5-n)} \, .</math>
Alternate Derivation of Gravitational Potential Energy
As has been discussed elsewhere, we have learned from Chandrasekhar's discussion of polytropic spheres [C67] — see his Equation (16), p. 64 — that if a spherically symmetric system is in hydrostatic balance, the total gravitational potential energy can be obtained from the following integral:
|
<math>~W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~ + \frac{1}{2} \int_0^R \Phi(r) dm \, .</math> |
Using "technique #3" to solve the differential equation that governs the statement of hydrostatic balance, we know that in any polytropic sphere, <math>~\Phi(r)</math> is related to the configuration's radial enthalpy profile, <math>~H(r)</math>, via the algebraic expression,
|
<math>~\Phi(r) + H(r)</math> |
<math>~=</math> |
<math>~C_B \, ,</math> |
where, <math>~C_B</math>, is an integration constant. At the surface of the equilibrium configuration, <math>~H = 0</math> and <math>~\Phi = - GM_\mathrm{tot}/R_\mathrm{eq}</math>, so the integration constant is,
|
<math>~C_B</math> |
<math>~=</math> |
<math>~- \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \, ,</math> |
which implies,
|
<math>~\Phi(r) </math> |
<math>~=</math> |
<math>~ - H(r) - \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \, .</math> |
Now, from our general discussion of barotropic relations, we can write,
|
<math>~H(r)</math> |
<math>~=</math> |
<math>~(n+1) \frac{P(r)}{\rho(r)} \, .</math> |
Hence,
|
<math>~-\Phi(r)</math> |
<math>~=</math> |
<math>~(n+1) \frac{P(r)}{\rho(r)} + \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \, ,</math> |
and,
|
<math>~W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~ - \frac{1}{2} \int_0^R \biggl[ (n+1) \frac{P(r)}{\rho(r)} + \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \biggr] 4\pi \rho(r) r^2 dr </math> |
|
|
<math>~=</math> |
<math>~ - 2\pi \biggl\{ (n+1) \int_0^R P(r) r^2 dr + \frac{GM_\mathrm{tot}}{R_\mathrm{eq}} \int_0^R \rho(r) r^2 dr \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - 2\pi \biggl\{ \frac{1}{3} (n+1)P_c R_\mathrm{eq}^3 \int_0^1 3\biggl[ \frac{P(x)}{P_c} \biggr] x^2 dx + \frac{GM_\mathrm{tot}}{3R_\mathrm{eq}} \biggl( \rho_c R_\mathrm{eq}^3 \biggr) \int_0^1 3 \biggl[ \frac{\rho(x)}{\rho_c} \biggr] x^2 dx \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - 2\pi \biggl\{ \frac{1}{3} (n+1)P_c R_\mathrm{eq}^3 \mathfrak{f}_A + \frac{GM_\mathrm{tot}}{3R_\mathrm{eq}} \biggl( \rho_c R_\mathrm{eq}^3 \biggr) \mathfrak{f}_M \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}} \biggl\{ \frac{2\pi}{3} (n+1) \biggl[ \frac{P_c R_\mathrm{eq}^4}{GM_\mathrm{tot}^2} \biggr] \mathfrak{f}_A + \frac{1}{2} \biggl[ \frac{4\pi \rho_c R_\mathrm{eq}^3}{3M_\mathrm{tot}} \biggr] \mathfrak{f}_M \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - \frac{1}{2} \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}} \biggl\{ \frac{4\pi}{3} (n+1) \biggl[ \frac{P_c R_\mathrm{eq}^4}{GM_\mathrm{tot}^2} \biggr] \mathfrak{f}_A + 1 \biggr\} \, .</math> |
We now recall two earlier expressions that show the role that our structural form factors play in the evaluation of <math>~W</math> and <math>~P_c</math>, namely,
|
<math>~W_\mathrm{grav}</math> |
<math>~=</math> |
<math>~ - \frac{3}{5} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}} \biggr) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> |
and,
|
<math>~P_c</math> |
<math>~=</math> |
<math>~ \frac{3 }{20\pi }\biggl( \frac{G M_\mathrm{tot}^2}{R_\mathrm{eq}^4} \biggr) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_A \mathfrak{f}_M^2} \, .</math> |
Plugging these into our newly derived expression for the gravitational potential energy gives,
|
<math>~- \frac{3}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> |
<math>~=</math> |
<math>~ - \frac{1}{2} \biggl\{ \frac{4\pi}{3} (n+1) \biggl[ \frac{3 }{20\pi }\cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_A \mathfrak{f}_M^2} \biggr] \mathfrak{f}_A + 1 \biggr\} </math> |
|
<math>\Rightarrow ~~~~ (2\cdot 3) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> |
<math>~=</math> |
<math>~ (n+1) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} + 5 </math> |
|
<math>\Rightarrow ~~~~ (5 - n) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> |
<math>~=</math> |
<math>~ 5 </math> |
|
<math>\Rightarrow ~~~~ \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2}</math> |
<math>~=</math> |
<math>~ \frac{5}{5-n} \, . </math> |
As it should, this agrees with the expression for the ratio, <math>\mathfrak{f}_W/\mathfrak{f}_M^2</math>, that was derived in our above discussion of the gravitational potential energy.
Summary
In summary, expressions for the three structural form factors associated with isolated, spherically symmetric polytropes are as follows:
|
Structural Form Factors for Isolated Polytropes | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
Nonrotating Adiabatic Configuration Embedded in an External Medium
For a nonrotating configuration <math>~(C=J=0)</math> that is embedded in, and is influenced by the pressure <math>~P_e</math> of, an external medium, the statement of virial equilibrium is,
<math> 3 B\chi_\mathrm{eq}^{3 -3\gamma_g} -~3A\chi_\mathrm{eq}^{-1} -~ 3D\chi_\mathrm{eq}^3 = 0 \, . </math>
Solution Expressed in Terms of K and M (Whitworth's 1981 Relation)
This is precisely the same condition that derives from setting equation (3) to zero in Whitworth's (1981, MNRAS, 195, 967) discussion of the Global Gravitational Stability for One-dimensional Polytropes. The overlap with Whitworth's narative is clearer after introducing the algebraic expressions for the coefficients <math>~A</math>, <math>~B</math>, and <math>~D</math>, to obtain,
|
<math>~4\pi \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \chi_\mathrm{eq}^3 </math> |
<math>~=</math> |
<math>~3 \biggl( \frac{4\pi}{3} \biggr)^{1-\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} \cdot \chi_\mathrm{eq}^{3 -3\gamma_g} ~-~\frac{3}{5} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \cdot \chi_\mathrm{eq}^{-1} \, ;</math> |
dividing the equation through by <math>~(4\pi \chi_\mathrm{eq}^3/P_\mathrm{norm})</math>,
|
<math>~P_e </math> |
<math>~=</math> |
<math>~P_\mathrm{norm} \biggl[ \biggl( \frac{3}{4\pi} \biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} \cdot \chi_\mathrm{eq}^{-3\gamma_g} ~- \biggl(\frac{3}{20\pi} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \cdot \chi_\mathrm{eq}^{-4} \biggr] </math> |
|
|
<math>~=</math> |
<math>~P_\mathrm{norm} R_\mathrm{norm}^4\biggl[ \biggl( \frac{3}{4\pi R_\mathrm{eq}^3} \biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} \cdot R_\mathrm{norm}^{3\gamma_g-4} - \biggl(\frac{3}{20\pi R_\mathrm{eq}^4} \biggr)\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \biggr] \, ;</math> |
and inserting expressions for the parameter normalizations as defined in our accompanying introductory discussion to obtain,
|
<math>~P_e </math> |
<math>~=</math> |
<math>~GM_\mathrm{tot}^2\biggl[ \biggl( \frac{3}{4\pi R_\mathrm{eq}^3} \biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} \cdot \frac{K M_\mathrm{tot}^{\gamma_g-2}}{G} - \biggl(\frac{3}{20\pi R_\mathrm{eq}^4} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \biggr] </math> |
|
|
<math>~=</math> |
<math>~K \biggl( \frac{3M_\mathrm{limit}}{4\pi R_\mathrm{eq}^3} \biggr)^{\gamma_g} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{\gamma_g}} - \biggl(\frac{3GM_\mathrm{limit}^2}{20\pi R_\mathrm{eq}^4} \biggr) \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \, .</math> |
If the structural form factors are set equal to unity, this exactly matches equation (5) of Whitworth, which reads:
Notice that, when <math>~P_e \rightarrow 0</math>, this expression reduces to the solution we obtained for an isolated polytrope, expressed in terms of <math>~K</math> and <math>~M_\mathrm{limit}</math> (see the left-hand column of our table titled "Two Points of View").
Solution Expressed in Terms of M and Central Pressure
Beginning again with the relevant statement of virial equilibirum, namely,
<math> A = B\chi_\mathrm{eq}^{4 -3\gamma_g} -~ D\chi_\mathrm{eq}^4 \, , </math>
but adopting the alternate expression for the coefficient, <math>~B</math>, given above, that is,
<math> B = \frac{4\pi}{3} \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} \cdot \mathfrak{f}_A \, , </math>
we can write,
|
<math>~\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W</math> |
<math>~=</math> |
<math>~ \frac{4\pi}{3} \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3\gamma} \biggr]_\mathrm{eq} \mathfrak{f}_A \cdot \chi_\mathrm{eq}^{4 -3\gamma_g} -~ \biggl( \frac{4\pi}{3} \biggr) \frac{P_e}{P_\mathrm{norm}} \chi_\mathrm{eq}^4 </math> |
|
<math>~\Rightarrow~~~\frac{3}{20\pi} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\mathfrak{f}_M} \biggr]^2 \cdot \mathfrak{f}_W</math> |
<math>~=</math> |
<math>~ \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr) \mathfrak{f}_A -~ \frac{P_e}{P_\mathrm{norm}} \biggr] \chi_\mathrm{eq}^4 </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \mathfrak{f}_A P_c -~ P_e\biggr] \frac{R_\mathrm{eq}^4}{G M_\mathrm{tot}^2} </math> |
|
<math>\Rightarrow ~~~ \frac{3}{20\pi} \biggl( \frac{G M_\mathrm{limit}^2}{R_\mathrm{eq}^4}\biggr) \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} </math> |
<math>~=</math> |
<math>~ \mathfrak{f}_A P_c -~ P_e \, . </math> |
Again notice that, when <math>~P_e \rightarrow 0</math>, this expression reduces to the solution we obtained for an isolated polytrope, but this time expressed in terms of <math>~P_c</math> and <math>~M_\mathrm{limit}</math> (see the right-hand column of our table titled "Two Points of View").
Contrast with Detailed Force-Balanced Solution
As has just been demonstrated, the virial theorem provides a mathematical expression that allows us to relate the equilibrium radius of a configuration to the applied external pressure, once the configuration's mass and either its specific entropy or central pressure are specified. In contrast to this, as has been discussed in detail in another chapter, Horedt (1970), Whitworth (1981) and Stahler (1983) have each derived separate analytic expressions for <math>~R_\mathrm{eq}</math> and <math>~P_e</math> — given in terms of the Lane-Emden function, <math>~\Theta</math>, and its radial derivative — without demonstrating how the equilibrium radius and external pressure directly relate to one another. That is to say, solution of the detailed force-balanced equations provides a pair of equilibrium expressions that are parametrically related to one another through the Lane-Emden function. For example — see our related discussion for more details — Horedt derives the following set of parametric equations relating the configuration's dimensionless radius, <math>~r_a</math>, to a specified dimensionless bounding pressure, <math>~p_a</math>:
|
<math> ~r_a \equiv \frac{R_\mathrm{eq}}{R_\mathrm{Horedt}} </math> |
<math>~=~</math> |
<math> \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} \, , </math> |
|
<math> ~p_a \equiv \frac{P_\mathrm{e}}{P_\mathrm{Horedt}} </math> |
<math>~=~</math> |
<math> \tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \, , </math> |
where,
|
<math> ~R_\mathrm{Horedt} </math> |
<math>~=</math> |
<math> \biggl[ \frac{4\pi}{(n+1)^n}\biggl( \frac{G}{K} \biggr)^n M_\mathrm{limit}^{n-1} \biggr]^{1/(n-3)} \, , </math> |
|
<math> ~P_\mathrm{Horedt} </math> |
<math>~=</math> |
<math> K^{4n/(n-3)}\biggl[ \frac{(n+1)^3}{4\pi G^3 M_\mathrm{limit}^2} \biggr]^{(n+1)/(n-3)} \, . </math> |
It is important to appreciate that, in the expressions for <math>~r_a</math> and <math>~p_a</math>, the tilde indicates that the Lane-Emden function and its derivative are to be evaluated, not at the radial coordinate, <math>~\xi_1</math>, that is traditionally associated with the "first zero" of the Lane-Emden function and therefore with the surface of the isolated polytrope, but at the radial coordinate, <math>~\tilde\xi</math>, where the internal pressure of the isolated polytrope equals <math>~P_e</math> and at which the embedded polytrope is to be truncated. The coordinate, <math>~\tilde\xi</math>, therefore identifies the surface of the embedded — or, pressure-truncated — polytrope. We also have taken the liberty of attaching the subscript "limit" to <math>~M</math> in both defining relations because it is clear that Hoerdt intended for the normalization mass to be the mass of the pressure-truncated object, not the mass of the associated isolated (and untruncated) polytrope. In anticipation of further derivations, below, we note here the ratio of Hoerdt's normalization parameters to ours, assuming <math>~\gamma = (n+1)/n</math>:
|
<math>~\biggl( \frac{R_\mathrm{Hoerdt}}{R_\mathrm{norm}} \biggr)^{n-3}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{4\pi}{(n+1)^n}\biggl( \frac{G}{K} \biggr)^n M_\mathrm{limit}^{n-1} \biggr] \biggl[ \biggl( \frac{K}{G}\biggr)^n M_\mathrm{tot}^{1-n}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{4\pi}{(n+1)^n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{n-1} \, , </math> |
|
<math>~\biggl( \frac{P_\mathrm{Hoerdt}}{P_\mathrm{norm}} \biggr)^{n-3}</math> |
<math>~=</math> |
<math>~ K^{4n}\biggl[ \frac{(n+1)^3}{4\pi G^3 M_\mathrm{limit}^2} \biggr]^{n+1} \biggl[ \frac{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}}{K^{4n}} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(n+1)^3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2}\biggr]^{n+1} \, . </math> |
Next, we demonstrate that this pair of parametric relations satisfies the virial theorem and, in so doing, demonstrate how <math>~r_a</math> and <math>~p_a</math> may be directly related to each other. Given that Hoerdt's chosen normalization radius and normalization pressure are defined in terms of <math>~K</math> and <math>~M_\mathrm{limit}</math>, we begin with the virial theorem derived above in terms of <math>~K</math> and <math>~M_\mathrm{limit}</math>, setting <math>~\gamma_g = (n+1)/n</math>.
|
<math>~P_e </math> |
<math>~=</math> |
<math>~K \biggl( \frac{3M_\mathrm{limit}}{4\pi R_\mathrm{eq}^3} \biggr)^{(n+1)/n} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{(n+1)/n}} - \biggl(\frac{3GM_\mathrm{limit}^2}{20\pi R_\mathrm{eq}^4} \biggr) \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \, .</math> |
After setting <math>~R_\mathrm{eq} = r_a R_\mathrm{Horedt} </math>, a bit of algebraic manipulation shows that the first term on the right-hand side of the virial equilibrium expression becomes,
|
<math>~ K \biggl( \frac{3M_\mathrm{limit}}{4\pi R_\mathrm{eq}^3} \biggr)^{(n+1)/n} \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{(n+1)/n}} </math> |
<math>~=</math> |
<math>~ r_a^{-3(n+1)/n} \mathfrak{f}_A \biggl[ \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{n-3} \frac{(n+1)^{3n}}{(4\pi)^n}\biggr]^{(n+1)/[n(n-3)]} [K^{4n} G^{-3(n+1)} M_\mathrm{limit}^{-2(n+1)} ]^{1/(n-3)} \, , </math> |
while the second term on the right-hand side becomes,
|
<math>~ \biggl(\frac{3GM_\mathrm{limit}^2}{20\pi R_\mathrm{eq}^4} \biggr) \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} </math> |
<math>~=</math> |
<math>~ \frac{3}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \cdot r_a^{-4} (4\pi)^{-(n+1)/(n-3)} (n+1)^{4n/(n-3)}~ [K^{4n} G^{-3(n+1)} M_\mathrm{limit}^{-2(n+1)} ]^{1/(n-3)} \, . </math> |
But, using Horedt's expression for <math>~P_e</math>, the left-hand side of the virial equilibrium equation becomes,
|
<math>~P_e = p_a P_\mathrm{Hoerdt}</math> |
<math>~=</math> |
<math>~ p_a~(4\pi)^{-(n+1)/(n-3)} ~(n+1)^{3(n+1)/(n-3)} [K^{4n} G^{-3(n+1)} M_\mathrm{limit}^{-2(n+1)} ]^{1/(n-3)} \, . </math> |
Hence, the statement of virial equilibrium is,
|
<math>~ p_a~ </math> |
<math>~=</math> |
<math>~ \biggr\{ r_a^{-3(n+1)/n} \mathfrak{f}_A \biggl[ \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{n-3} \frac{(n+1)^{3n}}{(4\pi)^n}\biggr]^{(n+1)/[n(n-3)]} </math> |
|
|
|
<math>~~ - \frac{3}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \cdot r_a^{-4} (4\pi)^{-(n+1)/(n-3)} (n+1)^{4n/(n-3)} \biggr\}(4\pi)^{(n+1)/(n-3)} ~(n+1)^{-3(n+1)/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ \mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M \cdot r_a^3} \biggr)^{(n+1)/n} - \frac{3(n+1)}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} \cdot r_a^{-4} \, ; </math> |
or, multiplying through by <math>~r_a^4</math> and rearranging terms,
|
Now, Hoerdt has given analytic expressions for <math>~r_a</math> and <math>~p_a</math> in terms of the Lane-Emden function and its first derivative. The question is, what should the expressions for our structural form factors be in order for this virial expression to hold true for all pressure-truncated polytropic structures? As has been summarized above, in the case of an isolated polytrope, whose surface is located at <math>~\xi_1</math> and whose global properties are defined by evaluation of the Lane-Emden function at <math>~\xi_1</math>, we know that (see the above summary),
|
Structural Form Factors for Isolated Polytropes | |||||||||
|---|---|---|---|---|---|---|---|---|---|
|
These same expressions may or may not work for pressure-truncated polytropes, even if the evaluation radius is shifted from <math>~\xi_1</math> to <math>~\tilde\xi</math>. Let's see …
Inserting Hoerdt's expressions for <math>~r_a</math> and <math>~p_a</math> into the viral equilibrium expression, we have,
|
<math>~ \frac{3(n+1)}{5} \cdot \frac{\mathfrak{f}_W}{\mathfrak{f}_M^2} </math> |
<math>~=</math> |
<math>~ \mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{(n+1)/n} [ \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} ]^{(n-3)/n} ~-~ \tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} [ \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} ]^{4} </math> |
|
|
<math>~=</math> |
<math>~ \mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{(n+1)/n} [ \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} ]^{(n-3)/n} ~-~ \tilde\theta_n^{n+1} \tilde\xi^4 [( -\tilde\xi^2 \tilde\theta' )^{2(n+1)+4(1-n)} ]^{1/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ \mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{(n+1)/n} [ \tilde\xi^{(n-3)} ( -\tilde\xi^2 \tilde\theta' )^{(1-n)} ]^{1/n} ~-~ \tilde\theta_n^{n+1} \tilde\xi^4 [( -\tilde\xi^2 \tilde\theta' )^{-2} ] </math> |
|
|
<math>~=</math> |
<math>~ \mathfrak{f}_A \biggl( \frac{3}{\mathfrak{f}_M} \biggr)^{(n+1)/n} \tilde\xi^{-(n+1)/n} ( -\tilde\theta' )^{(1-n)/n} ~-~ \frac{\tilde\theta_n^{n+1} }{( -\tilde\theta' )^{2} } \, . </math> |
Assuming that the structural form factor, <math>~\mathfrak{f}_M</math>, has the same functional expression as in the case of isolated polytropes (but evaluated at <math>~\tilde\xi</math> instead of at <math>~\xi_1</math>), the virial relation further reduces to the form,
|
<math>~ \frac{\tilde\theta_n^{n+1} }{( -\tilde\theta' )^{2} } </math> |
<math>~=</math> |
<math>~ \mathfrak{f}_A \biggl( \frac{\tilde\xi}{- \tilde\theta'} \biggr)^{(n+1)/n} \tilde\xi^{-(n+1)/n} ( -\tilde\theta' )^{(1-n)/n} - \biggl[ \frac{(n+1)}{3\cdot 5} \biggr] \frac{\tilde\xi^2}{(-\tilde\theta^')^2} \cdot \mathfrak{f}_W </math> |
|
|
<math>~=</math> |
<math>~ \frac{\mathfrak{f}_A}{(- \tilde\theta' )^2} - \biggl[ \frac{(n+1)}{3\cdot 5} \biggr] \frac{\tilde\xi^2}{(-\tilde\theta^')^2} \cdot \mathfrak{f}_W </math> |
|
<math>~ \Rightarrow~~~\tilde\theta^{n+1} </math> |
<math>~=</math> |
<math>~ \mathfrak{f}_A - \biggl[ \frac{(n+1)}{3\cdot 5} \biggr] \tilde\xi^2 \cdot \mathfrak{f}_W </math> |
|
<math>~ \Rightarrow~~~\frac{\mathfrak{f}_A - \tilde\theta^{n+1} }{\mathfrak{f}_W} </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{(n+1)}{3\cdot 5} \biggr] \tilde\xi^2 \, . </math> |
While this does not give us individual expressions for the form factors, <math>~\mathfrak{f}_W</math> and <math>~\mathfrak{f}_W</math>, the expression derived for the ratio of the form factors makes sense because the term that has been subtracted from <math>~\mathfrak{f}_A</math> in the numerator on the lefthand side, that is, <math>\tilde\theta^{n+1}</math>, naturally goes to zero in the limit of <math>~\tilde\xi \rightarrow \xi_1</math>, producing the correct expression for the ratio, <math>\mathfrak{f}_A/\mathfrak{f}_W</math>, in isolated polytropes. In summary, then, we have,
|
Structural Form Factors for Pressure-Truncated Polytropes | ||||||
|---|---|---|---|---|---|---|
|
Notice that, in an effort to differentiate them from their counterparts developed earlier for "isolated" polytropes, we have affixed a tilde to each of these three form-factors, <math>~\mathfrak{f}_i</math>.
Renormalization
Grunt Work
Returning to the dimensionless form of the virial expression and multiplying through by <math>~[-\chi_\mathrm{eq}/(3D)]</math>, we obtain,
<math> \chi_\mathrm{eq}^4 = \frac{B}{D} \chi_\mathrm{eq}^{4-3\gamma_g} - \frac{A}{D} \, , </math>
or, after plugging in definitions of the coefficients, <math>~A</math>, <math>~B</math>, and <math>~D</math>, and rewriting <math>~\chi_\mathrm{eq}</math> explicitly as <math>~R_\mathrm{eq}/R_\mathrm{norm}</math>,
|
<math>~\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4 </math> |
<math>~=</math> |
<math> \biggl(\frac{3}{4\pi}\biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{\gamma_g}} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^{4-3\gamma_g} - \frac{3}{20\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \, .</math> |
This relation can be written in a more physically concise form, as follows. First, normalize <math>~P_e</math> to a new pressure scale — call it <math>~P_\mathrm{ad}</math> — and multiply through by <math>~(R_\mathrm{norm}/R_\mathrm{ad})^4</math> in order to normalizing <math>~R_\mathrm{eq}</math> to a new length scale,<math>~R_\mathrm{ad}</math>:
|
<math>~\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{ad}} \biggr)^4 </math> |
<math>~=</math> |
<math> \biggl(\frac{3}{4\pi}\biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{P_e}{P_\mathrm{ad}} \biggr)^{-1} \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{\gamma_g}} \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{3\gamma_g}\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{ad}} \biggr)^{4-3\gamma_g} </math> |
|
|
|
<math> ~- \frac{3}{20\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} \biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggl( \frac{P_e}{P_\mathrm{ad}} \biggr)^{-1} \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{4} \, , </math> |
or,
|
<math>~\Chi_\mathrm{ad}^4 </math> |
<math>~=</math> |
<math> \biggl(\frac{3}{4\pi}\biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{3\gamma_g} \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{\gamma_g}}\cdot \frac{\Chi_\mathrm{ad}^{4-3\gamma_g} }{\Pi_\mathrm{ad}} - \frac{3}{20\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} \biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{4} \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \cdot \frac{1}{\Pi_\mathrm{ad}} \, ,</math> |
where,
|
<math>~\Chi_\mathrm{ad}</math> |
<math>~\equiv</math> |
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{ad}} \, ,</math> |
|
<math>~\Pi_\mathrm{ad}</math> |
<math>~\equiv</math> |
<math>~\frac{P_\mathrm{e}}{P_\mathrm{ad}} \, .</math> |
By demanding that the leading coefficients of both terms on the right-hand-side of the expression are simultaneously unity — that is, by demanding that,
|
<math>~\biggl(\frac{3}{4\pi}\biggr)^{\gamma_g} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{\gamma_g} \biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{3\gamma_g} \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{\gamma_g}}</math> |
<math>~=</math> |
<math>~1 \, ,</math> |
and,
|
<math>~\frac{3}{20\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2} \biggl( \frac{P_\mathrm{norm}}{P_\mathrm{ad}} \biggr) \biggl( \frac{R_\mathrm{norm}}{R_\mathrm{ad}} \biggr)^{4} \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} </math> |
<math>~=</math> |
<math>~1 \, ,</math> |
we obtain the expressions for <math>~R_\mathrm{ad}/R_\mathrm{norm}</math> and <math>~P_\mathrm{ad}/P_\mathrm{norm}</math> as shown in the following table.
|
Renormalization for Adiabatic (ad) Systems | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Using these new normalizations, we arrive at the desired, concise virial equilibrium relation, namely,
|
<math>~\Pi_\mathrm{ad} = \Chi_\mathrm{ad}^{-3\gamma_g} - \Chi_\mathrm{ad}^{-4}</math> |
<math>\Leftrightarrow</math> |
<math>~ \Pi_\mathrm{ad} = \Chi_\mathrm{ad}^{-3(n+1)/n} - \Chi_\mathrm{ad}^{-4}</math> |
or,
|
<math>~~\Chi_\mathrm{ad}^{4-3\gamma_g} - \Pi_\mathrm{ad} \Chi_\mathrm{ad}^4 = 1</math> |
<math>\Leftrightarrow</math> |
<math>~\Chi_\mathrm{ad}^{(n-3)/n} - \Pi_\mathrm{ad} \Chi_\mathrm{ad}^4 = 1 \, .</math> |
In Terms of Free-Energy Coefficients
Referring back to relations between our free-energy coefficients, as presented earlier, we note that,
|
<math>~\frac{R_\mathrm{ad}}{R_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl( \frac{\mathcal{A}}{\mathcal{B}}\biggr)^{n/(n-3)} \, ,</math> |
|
<math>~\frac{P_\mathrm{ad}}{P_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\frac{3}{4\pi} \biggl[ \frac{\mathcal{B}^{4n}}{\mathcal{A}^{3(n+1)}} \biggr]^{1/(n-3)} \, .</math> |
Hence, we can write,
|
<math>~\Chi_\mathrm{ad}</math> |
<math>~=</math> |
<math>~\chi_\mathrm{eq} ~\biggl( \frac{\mathcal{B}}{\mathcal{A}}\biggr)^{n/(n-3)} \, ,</math> |
|
<math>~\Pi_\mathrm{ad}</math> |
<math>~=</math> |
<math>~\mathcal{D} ~\biggl[ \frac{\mathcal{A}^{3(n+1)}}{\mathcal{B}^{4n}} \biggr]^{1/(n-3)} \, .</math> |
In Terms of Horedt's Equilibrium Parameters
For later use it is also worth developing expressions for both <math>~\Chi_\mathrm{ad}</math> and <math>~\Pi_\mathrm{ad}</math> that are in terms of our structural form factors and Horedt's two dimensionless functions, <math>~r_a</math> and <math>~p_a</math>. (Adopting a unified notation, we will set <math>~\gamma_g \rightarrow (n+1)/n</math>.)
|
<math>~\Chi_\mathrm{ad} \equiv \frac{R_\mathrm{eq}}{R_\mathrm{ad}}</math> |
<math>~=</math> |
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{Hoerdt}} \cdot \frac{R_\mathrm{Hoerdt}}{R_\mathrm{norm}} \cdot \frac{R_\mathrm{norm}}{R_\mathrm{ad}}</math> |
|
|
<math>~=</math> |
<math>~ r_a \cdot \biggl[ \frac{4\pi}{(n+1)^n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{n-1} \biggr]^{1/(n-3)} \cdot \biggl[ 5^n \biggl( \frac{3}{4\pi} \biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{1-n} \frac{\tilde\mathfrak{f}_A^n}{\tilde\mathfrak{f}_W^n \cdot \tilde\mathfrak{f}_M^{1-n}} \biggr]^{1/(n-3)} </math> |
|
<math>~\Rightarrow~~~\Chi_\mathrm{ad}^{n-3} </math> |
<math>~=</math> |
<math>~ 3 r_a^{n-3} \cdot \biggl[ \frac{5}{(n+1)} \cdot \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_W} \biggr]^n \tilde\mathfrak{f}_M^{n-1} \, . </math> |
And,
|
<math>~\Pi_\mathrm{ad} \equiv \frac{P_e}{P_\mathrm{ad}}</math> |
<math>~=</math> |
<math>~\frac{P_e}{P_\mathrm{Hoerdt}} \cdot \frac{P_\mathrm{Hoerdt}}{P_\mathrm{norm}} \cdot \frac{P_\mathrm{norm}}{P_\mathrm{ad}}</math> |
|
|
<math>~=</math> |
<math>~ p_a \cdot \biggl[ \frac{(n+1)^3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2}\biggr]^{(n+1)/(n-3)} \cdot \biggl[ \tilde\mathfrak{f}_A^{-4n} \cdot \biggl( \frac{4\pi}{3\cdot 5^3} \cdot \frac{\tilde\mathfrak{f}_W^3}{\tilde\mathfrak{f}_M^2} \biggr)^{(n+1)} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{2(n+1)} \biggr]^{1/(n-3)} </math> |
|
<math>~\Rightarrow~~~\Pi_\mathrm{ad}^{n-3} </math> |
<math>~=</math> |
<math>~ p_a^{n-3}~ \tilde\mathfrak{f}_A^{-4n} \cdot \biggl[ \frac{(n+1)^3}{3\cdot 5^3} \biggl( \frac{\tilde\mathfrak{f}_W^3}{\tilde\mathfrak{f}_M^2} \biggr) \biggr]^{n+1} \, . </math> |
Plugging in the expressions for <math>~r_a</math> and <math>~p_a</math>, as reprinted, for example, above, along with our deduced expressions for <math>~\mathfrak{f}_M</math> and <math>~\mathfrak{f}_A</math> (in terms of <math>~\mathfrak{f}_W</math>), these two relations become:
|
<math>~\Chi_\mathrm{ad}^{n-3} </math> |
<math>~=</math> |
<math>~ 3 \biggl[ \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} \biggr]^{n-3} \cdot \biggl[ \frac{5}{(n+1)} \cdot \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_W} \biggr]^n \biggl[- \frac{3\tilde\theta^'}{\tilde\xi} \biggr]^{n-1} </math> |
|
|
<math>~=</math> |
<math>~ \tilde\xi^{[(n-3)+2(1-n)-(n-1)]} \cdot \biggl[ \frac{3\cdot 5}{(n+1)} \cdot \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_W} \biggr]^n </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{3\cdot 5}{(n+1)\tilde\xi^2} \cdot \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_W} \biggr]^n \, ; </math> |
and,
|
<math>~\Pi_\mathrm{ad}^{n-3} </math> |
<math>~=</math> |
<math>~ \biggl[ \tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \biggr]^{n-3}~ \tilde\mathfrak{f}_A^{-4n} \cdot \biggl[ \frac{(n+1)}{3\cdot 5} \cdot \tilde\mathfrak{f}_W \biggr]^{3(n+1)} \biggl( \frac{3}{\tilde\mathfrak{f}_M}\biggr)^{2(n+1)} </math> |
|
|
<math>~=</math> |
<math>~ \tilde\theta_n^{(n+1)(n-3)}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)} ~ \tilde\mathfrak{f}_A^{-4n} \cdot \tilde\xi^{-6(n+1)} \biggl[ \frac{(n+1)\tilde\xi^2}{3\cdot 5} \cdot \tilde\mathfrak{f}_W \biggr]^{3(n+1)} \tilde\xi^{2(n+1)} (-\tilde\theta^')^{-2(n+1)} </math> |
|
|
<math>~=</math> |
<math>~ \tilde\theta_n^{(n+1)(n-3)}~ \tilde\mathfrak{f}_A^{-4n} \cdot \biggl[ \frac{(n+1)\tilde\xi^2}{3\cdot 5} \cdot \tilde\mathfrak{f}_W \biggr]^{3(n+1)} \, . </math> |
Summary
If we define,
|
<math>~a_\mathrm{ad}</math> |
<math>~\equiv</math> |
<math>~\frac{(n+1)\tilde\xi^2 }{3\cdot 5} \cdot \mathfrak{f}_W \, ,</math> and, |
|
<math>~b_\mathrm{ad}</math> |
<math>~\equiv</math> |
<math>~\tilde\theta^{n+1} \, ,</math> |
in which case the relationship between <math>~\mathfrak{f}_A</math> and <math>~\mathfrak{f}_A</math> for pressure-truncated polytropes can be rewritten as,
|
<math>~\mathfrak{f}_A </math> |
<math>~=</math> |
<math>~a_\mathrm{ad} + b_\mathrm{ad} \, .</math> |
In addition, the expressions for the dimensionless equilibrium radius and the dimensionless external pressure, as just derived, may be written as, respectively,
|
<math>~\Chi_\mathrm{ad}</math> |
<math>~=</math> |
<math>~ \biggl[ 1 + \frac{b_\mathrm{ad}}{a_\mathrm{ad}} \biggr]^{n/(n-3)} \, , </math> and, |
|
<math>~\Pi_\mathrm{ad} </math> |
<math>~=</math> |
<math>~ b_\mathrm{ad} \biggl[ \frac{a_\mathrm{ad}^{3(n+1)} }{( a_\mathrm{ad} + b_\mathrm{ad} )^{4n} } \biggr]^{1/(n-3)} = \frac{b_\mathrm{ad}}{a_\mathrm{ad}} \biggl[ 1 + \frac{b_\mathrm{ad}}{a_\mathrm{ad}} \biggr]^{-4n/(n-3)} \, . </math> |
Using these expressions, it is easy to demonstrate that the virial equilibrium relation is satisfied, namely,
|
<math>~\Pi_\mathrm{ad} </math> |
<math>~=</math> |
<math>~\Chi_\mathrm{ad}^{-3(n+1)/n} - \Chi_\mathrm{ad}^{-4} \, .</math> |
P-V Diagram
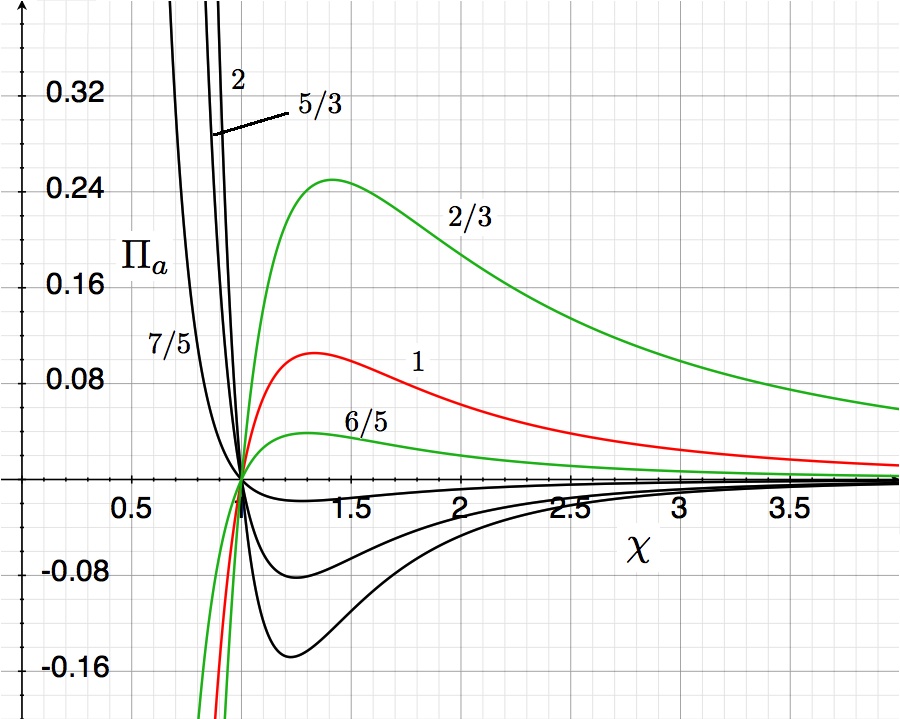
For an arbitrary value of the adiabatic exponent, <math>~\gamma_g</math>, it isn't possible to invert this virial relation to obtain an analytic expression for <math>~\chi_\mathrm{ad}</math> as a function of <math>~\Pi_\mathrm{ad}</math>. But, as written, the virial relation dictates the behavior of <math>~\Pi_\mathrm{ad}</math> as a function of <math>~\Chi_\mathrm{ad}</math>. Figure 4 displays this <math>~\Pi_\mathrm{ad}(\chi_\mathrm{ad})</math> behavior for a number of different values of <math>~\gamma_g</math>.
|
Figure 4: Equilibrium Adiabatic P-V Diagram |
|
|
The curves shown here, on the right, trace out the function, <math> ~\Pi_\mathrm{ad} = (\Chi_\mathrm{ad}^{4-3\gamma_g} - 1)/\Chi_\mathrm{ad}^4 \, , </math> for six different values of <math>~\gamma_g</math> — specifically, for <math>2, ~5/3, ~7/5, ~6/5, ~1, ~2/3</math>, as labeled — and show the dimensionless external pressure, <math>~\Pi_\mathrm{ad}</math>, that is required to construct a nonrotating, self-gravitating, pressure-truncated adiabatic sphere with an equilibrium radius <math>~\Chi_\mathrm{ad}</math>. The solid red curve identifies the behavior of an isothermal <math>~(\gamma_g=1)</math> system. The mathematical solution becomes unphysical wherever the pressure becomes negative. |
|
For physically relevant solutions, both <math>~\Chi_\mathrm{ad}</math> and <math>~\Pi_\mathrm{ad}</math> must be nonnegative. Hence, as is illustrated by the curves in Figure 4, the physically allowable range of equilibrium radii is,
<math> 1 \le \Chi_\mathrm{ad} \le \infty \, ~~~~~\mathrm{for}~ \gamma_g < 4/3 \, ; </math>
<math> 0 < \Chi_\mathrm{ad} \le 1 \, ~~~~~~\mathrm{for}~ \gamma_g > 4/3 \, . </math>
Each of the <math>~\Pi_\mathrm{ad}(\Chi_\mathrm{ad})</math> curves drawn in Figure 4 exhibits an extremum. In each case this extremum occurs at a configuration radius, <math>~\Chi_\mathrm{extreme}</math>, given by,
<math> \frac{\partial\Pi_\mathrm{ad}}{\partial\Chi_\mathrm{ad}} = 0 \, , </math>
that is, where,
<math> 4 - 3\gamma_g \Chi_\mathrm{ad}^{4-3\gamma_g} = 0 ~~~~\Rightarrow ~~~~~ \Chi_\mathrm{extreme} = \biggl[ \frac{4}{3\gamma_g} \biggr]^{1/(4-3\gamma_g)} \, . </math>
For each value of <math>~\gamma_g</math>, the corresponding dimensionless pressure is,
<math> ~\Pi_\mathrm{extreme} = \biggl(\frac{4}{3\gamma} - 1 \biggr) \biggl[ \frac{3\gamma_g}{4} \biggr]^{4/(4-3\gamma_g)} \, . </math>
In terms of the polytropic index, the equivalent limiting expressions are,
|
<math>~\Chi_\mathrm{extreme} = \biggl[ \frac{4n}{3(n+1)} \biggr]^{n/(n-3)}</math> |
and |
<math>~\Pi_\mathrm{extreme}^{(n-3)} = (4n)^{-4n} (n-3)^{n-3} [3(n+1)]^{3(n+1)} \, .</math> |
(In a separate, related discussion of the free-energy function, we demonstrate that this "extremum" also serves as a dividing line between dynamically stable and unstable models along a given curve.)
In examining the group of plotted curves, notice that, for <math>~\gamma_g > 4/3</math>, an equilibrium configuration with a positive radius can be constructed for all physically realistic — that is, for all positive — values of <math>~\Pi_\mathrm{ad}</math>. Also, consistent with the behavior of the curves shown in Figure 4, the extremum arises in the regime of physically relevant — i.e., positive — pressures only for values of <math>~\gamma_g < 4/3</math>; and in each case it represents a maximum limiting pressure.
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Maximum Mass
<math>n=5</math> Polytropic
When <math>~\gamma_a = 6/5</math> — which corresponds to an <math>~n=5</math> polytropic configuration — we obtain,
<math> ~\Pi_\mathrm{max} = \Pi_\mathrm{ad}\biggr|_\mathrm{extreme}^{(\gamma_g = 6/5)} = \biggl( \frac{3^{18}}{2^{10}\cdot 5^{10}} \biggr) \, , </math>
which corresponds to a maximum mass for pressure-bounded <math>~n=5</math> polytropic configurations of,
<math>~M_\mathrm{max} = \Pi_\mathrm{max}^{1/2} \biggl(\frac{3\cdot 5^3}{2^2\pi} \biggr)^{1/2} \biggl( \frac{\bar{c_s}^8}{G^3 P_e} \biggr)^{1/2} = \biggl(\frac{3^{19}}{2^{12}\cdot 5^{7}\pi} \biggr)^{1/2} \biggl( \frac{\bar{c_s}^8}{G^3 P_e} \biggr)^{1/2} \, .</math>
This result can be compared to other determinations of the Bonnor-Ebert mass limit.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |