Difference between revisions of "User:Tohline/SSC/Stability/BiPolytropes"
| Line 76: | Line 76: | ||
** Solve the relevant eigenvalue problem for this specific model, initially for <math>~(\gamma_c, \gamma_e) = (6/5, 2)</math> and initially for the fundamental mode of oscillation. | ** Solve the relevant eigenvalue problem for this specific model, initially for <math>~(\gamma_c, \gamma_e) = (6/5, 2)</math> and initially for the fundamental mode of oscillation. | ||
= | =Virial Analysis= | ||
==Various Energy Expressions== | |||
Drawing from an [[User:Tohline/SSC/Structure/BiPolytropes/FreeEnergy5_1#Free_Energy_of_BiPolytrope_with|accompanying detailed discussion]], we have, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\mathfrak{G}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 93: | Line 90: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~W_\mathrm{grav}\biggr|_\mathrm{core} + \mathfrak{S}_A\biggr|_\mathrm{core} + W_\mathrm{grav}\biggr|_\mathrm{env} + \mathfrak{S}_A\biggr|_\mathrm{env} </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 110: | Line 102: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math> | ||
~W_\mathrm{grav}\biggr|_\mathrm{core} + \biggl[ \frac{2}{3(\gamma_c - 1)} \biggr] S_\mathrm{core} + W_\mathrm{grav}\biggr|_\mathrm{env} + \biggl[ \frac{2}{3(\gamma_e - 1)} \biggr] S_\mathrm{env} \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | |||
Recognizing that, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~q</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 128: | Line 121: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{r_i}{R} = \frac{\eta_i}{\eta_s} \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 136: | Line 127: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\nu</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{M_\mathrm{core}}{M_\mathrm{tot}} \, ,</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 154: | Line 139: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ell</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{\xi}{\sqrt{3}} \, ,</math> | ||
\frac{ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\chi_\mathrm{eq} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{3\ | <math>~\biggl( \frac{\pi}{2^3 \cdot 3^6}\biggr)^{1 / 2} | ||
\biggl( \frac{\nu}{q^3} \biggr)^{2} \biggl( 1 + \ell_i^2 \biggr)^{3} \biggl( \frac{q}{\ell_i}\biggr)^{5 } \, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~- \chi \biggl[ \frac{W_\mathrm{grav}}{E_\mathrm{norm}} \biggr]_\mathrm{core}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math> | <math> | ||
\biggl( \frac{ | \biggl[\biggl(\frac{3}{2^4}\biggr) \biggl( \frac{q}{\ell_i}\biggr)^{5}\biggl(\frac{\nu}{q^3} \biggr)^2 \biggl( 1 + \ell_i^2 \biggr)^{3} \biggr]_\mathrm{eq} | ||
\biggl[ | |||
\frac{ | \ell_i (\ell_i^4 - \frac{8}{3}\ell_i^2 - 1) (\ell_i^2 +1)^{-3} + \tan^{-1}\ell_i | ||
\biggr] | |||
\frac{ | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ \frac{ | <math>~\Rightarrow ~~~ \biggl[ \frac{W_\mathrm{grav}}{E_\mathrm{norm}} \biggr]_\mathrm{core}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math> | <math>- \frac{\chi_\mathrm{eq}}{\chi} | ||
\biggl( \frac{3^8}{2^5 \pi}\biggr)^{1 / 2} | |||
\biggl[ | |||
\ell_i (\ell_i^4 - \frac{8}{3}\ell_i^2 - 1) (\ell_i^2 +1)^{-3} + \tan^{-1}\ell_i | |||
\biggr] \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Next, given that, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 231: | Line 207: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~b_\eta = \eta_s</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
and | |||
| |||
</td> | |||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~b_\eta q = \eta_i = 3\biggl( \frac{\mu_e}{\mu_c} \biggr) \ell_i (1 + \ell_i^2)^{-1} \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
we have, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\biggl[ \frac{W_\mathrm{grav}}{E_\mathrm{norm}} \biggr]_\mathrm{env}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math> | <math> | ||
- \frac{\chi_\mathrm{eq}}{\chi} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \biggl( \frac{1}{2^3\pi} \biggr)^{1/2} A^2 | |||
\biggl[6 b_\eta x - 3\sin[2(b_\eta x-B)] - 4b_\eta x \sin^2(b_\eta x - B) \biggr]_q^1 | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 266: | Line 245: | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math> | <math> | ||
- \frac{\chi_\mathrm{eq}}{\chi} | |||
\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \biggl( \frac{1}{2^3\pi} \biggr)^{1/2} A^2 | |||
\biggl\{ | |||
\biggl[ 6 \eta_s - 3\sin[2(\eta_s -B)] - 4\eta_s \sin^2(\eta_s - B) \biggr] | |||
- | |||
\biggl[ 6 \eta_i - 3\sin[2(\eta_i -B)] - 4\eta_i \sin^2(\eta_i - B) \biggr] | |||
\biggr\} \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Also, given that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~q a_\xi^{1 / 2}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 279: | Line 270: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{\xi_i}{\sqrt{3}} \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{core}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{\ | <math> | ||
\frac{2}{3({\gamma_c}-1)} \biggl( \frac{\chi}{\chi_\mathrm{eq}} \biggr)^{3-3\gamma_c} | |||
\biggl\{\biggl( \frac{3^8}{2^7\pi} \biggr)^{1/2} \biggl[ | |||
\tan^{-1}[a_\xi^{1/2}q] - a_\xi^{1/2}q ~\frac{(1 - a_\xi q^2)}{(1 + a_\xi q^2)^2} \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\frac{2}{3({\gamma_c}-1)} \biggl( \frac{\chi}{\chi_\mathrm{eq}} \biggr)^{3-3\gamma_c} | |||
\biggl\{\biggl( \frac{3^8}{2^7\pi} \biggr)^{1/2} \biggl[ | |||
\tan^{-1}\biggl( \frac{\xi_i}{\sqrt{3}}\biggr) - \biggl( \frac{\xi_i}{\sqrt{3}}\biggr)\frac{(1 - \xi_i^2/3)}{(1 + \xi_i^2/3)^2} \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Finally, then, we can write, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{env}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <td align="left"> | ||
<math> | |||
\frac{2}{3({\gamma_e}-1)} \biggl( \frac{\chi}{\chi_\mathrm{eq}} \biggr)^{3-3\gamma_e} \biggl\{ | |||
\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} A^2 \biggl( \frac{3^2}{2^5\pi} \biggr)^{1/2} \biggl[ 2b_\eta x -\sin[2(b_\eta x - B)] \biggr]_q^1 \biggr\} | |||
</math> | |||
</td> | </td> | ||
</tr> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <td align="left"> | ||
<math> | |||
\frac{2}{3({\gamma_e}-1)} \biggl( \frac{\chi}{\chi_\mathrm{eq}} \biggr)^{3-3\gamma_e} | |||
\bigg( \frac{\mu_e}{\mu_c} \biggr)^{-3} A^2 \biggl( \frac{3^2}{2^5\pi} \biggr)^{1/2} \biggl\{ | |||
\biggl[ 2\eta_s -\sin[2(\eta_s - B)] \biggr] | |||
- | |||
\biggl[ 2\eta_i -\sin[2(\eta_i - B)] \biggr] | |||
\biggr\} \ . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
We | ==Free Energy and Its Derivatives== | ||
We can now rewrite the free-energy expression in the form, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\mathfrak{g} \equiv \frac{\mathfrak{G}}{E_\mathrm{norm}}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 363: | Line 370: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math> | ||
~-\biggl(\frac{\chi_\mathrm{eq}}{\chi}\biggr)\mathfrak{w} | |||
+ \biggl[ \frac{2}{3(\gamma_c - 1)} \biggr] \biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{3 - 3\gamma_c}\mathfrak{s}_\mathrm{core} | |||
+ \biggl[ \frac{2}{3(\gamma_e - 1)} \biggr] \biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{3 - 3\gamma_e}\mathfrak{s}_\mathrm{env} | |||
\, , | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
where, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathfrak{s}_\mathrm{core}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{3^8}{2^7\pi} \biggr)^{1/2} \biggl[ | |||
\tan^{-1}\biggl( \frac{\xi_i}{\sqrt{3}}\biggr) - \biggl( \frac{\xi_i}{\sqrt{3}}\biggr)\frac{(1 - \xi_i^2/3)}{(1 + \xi_i^2/3)^2} \biggr]\, , | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 383: | Line 400: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\mathfrak{s}_\mathrm{env}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \bigg( \frac{\mu_e}{\mu_c} \biggr)^{-3} A^2 \biggl( \frac{3^2}{2^5\pi} \biggr)^{1/2} \biggl\{ | ||
\biggl[ 2\eta_s -\sin[2(\eta_s - B)] \biggr] | |||
- | |||
\biggl[ 2\eta_i -\sin[2(\eta_i - B)] \biggr] | |||
\biggr\} \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\mathfrak{w}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \biggl( \frac{3^8}{2^5 \pi}\biggr)^{1 / 2} | ||
\biggl[ | |||
\ell_i (\ell_i^4 - \frac{8}{3}\ell_i^2 - 1) (\ell_i^2 +1)^{-3} + \tan^{-1}\ell_i | |||
\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+~ | |||
\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \biggl( \frac{1}{2^3\pi} \biggr)^{1/2} A^2 | |||
\biggl\{ | |||
\biggl[ 6 \eta_s - 3\sin[2(\eta_s -B)] - 4\eta_s \sin^2(\eta_s - B) \biggr] | |||
- | |||
\biggl[ 6 \eta_i - 3\sin[2(\eta_i -B)] - 4\eta_i \sin^2(\eta_i - B) \biggr] | |||
\biggr\} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
The first derivative is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{d\mathfrak{g}}{d\chi} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 443: | Line 465: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
+~\biggl(\frac{\chi_\mathrm{eq}}{\chi^2}\biggr)\mathfrak{w} | |||
~+~ | ~-~\frac{2}{\chi_\mathrm{eq}} \biggl[\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{2 - 3\gamma_c}\mathfrak{s}_\mathrm{core} | ||
~+~\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{2 - 3\gamma_e}\mathfrak{s}_\mathrm{env} \biggr] \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
And the second derivative is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{d^2\mathfrak{g}}{d\chi^2} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 459: | Line 484: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math> | ||
\frac{ | -~2\biggl(\frac{\chi_\mathrm{eq}}{\chi^3}\biggr)\mathfrak{w} | ||
~+~ | ~-~\frac{2}{\chi_\mathrm{eq}^2} \biggl[(2 - 3\gamma_c) \biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{1 - 3\gamma_c}\mathfrak{s}_\mathrm{core} | ||
~+~(2 - 3\gamma_e)\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{1 - 3\gamma_e}\mathfrak{s}_\mathrm{env} \biggr] \ . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
==What to Expect for Equilibrium Configurations== | |||
In equilibrium we should set <math>~d\mathfrak{g}/d\chi = 0</math> and <math>~\chi = \chi_\mathrm{eq}</math>. In which case we should expect to find that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~0 </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 475: | Line 505: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\frac{ | \frac{1}{\chi_\mathrm{eq}}\biggl[\mathfrak{w} | ||
~-~2(\mathfrak{s}_\mathrm{core} | |||
~+~\mathfrak{s}_\mathrm{env}) \biggr] \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
In addition, an evaluation of the second derivative should give, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{\chi_\mathrm{eq}^2}{2} \cdot \frac{d^2\mathfrak{g}}{d\chi^2} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 490: | Line 524: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math> | ||
\ | -~\mathfrak{w} | ||
+ | ~-~ \biggl[(2 - 3\gamma_c) \mathfrak{s}_\mathrm{core} | ||
~+~(2 - 3\gamma_e)\mathfrak{s}_\mathrm{env} \biggr] \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Then, the transition from stable to unstable configurations occurs when <math>~d^2\mathfrak{g}/d\chi^2 = 0</math>, that is, when, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~\mathfrak{w} </math> | |||
</td> | </td> | ||
<td align="center | <td align="center"> | ||
<math>~=</math> | |||
<math>~ | |||
</td> | </td> | ||
<td align=" | <td align="left"> | ||
<math> | |||
~-~ \biggl[(2 - 3\gamma_c) \mathfrak{s}_\mathrm{core} | |||
~+~(2 - 3\gamma_e)\mathfrak{s}_\mathrm{env} \biggr] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~0</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align=" | <td align="left"> | ||
<math>~\ | <math> | ||
~(4 - 3\gamma_c) \mathfrak{s}_\mathrm{core} | |||
~+~(4 - 3\gamma_e)\mathfrak{s}_\mathrm{env} | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~ | <math>~\Rightarrow ~~~\frac{\mathfrak{s}_\mathrm{core} }{\mathfrak{s}_\mathrm{env}} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math> | <math>~=</math> | ||
</td> | </td> | ||
<td align=" | <td align="left"> | ||
<math> | <math> | ||
~-~\frac{(4 - 3\gamma_e) }{(4 - 3\gamma_c) } \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | |||
</table> | |||
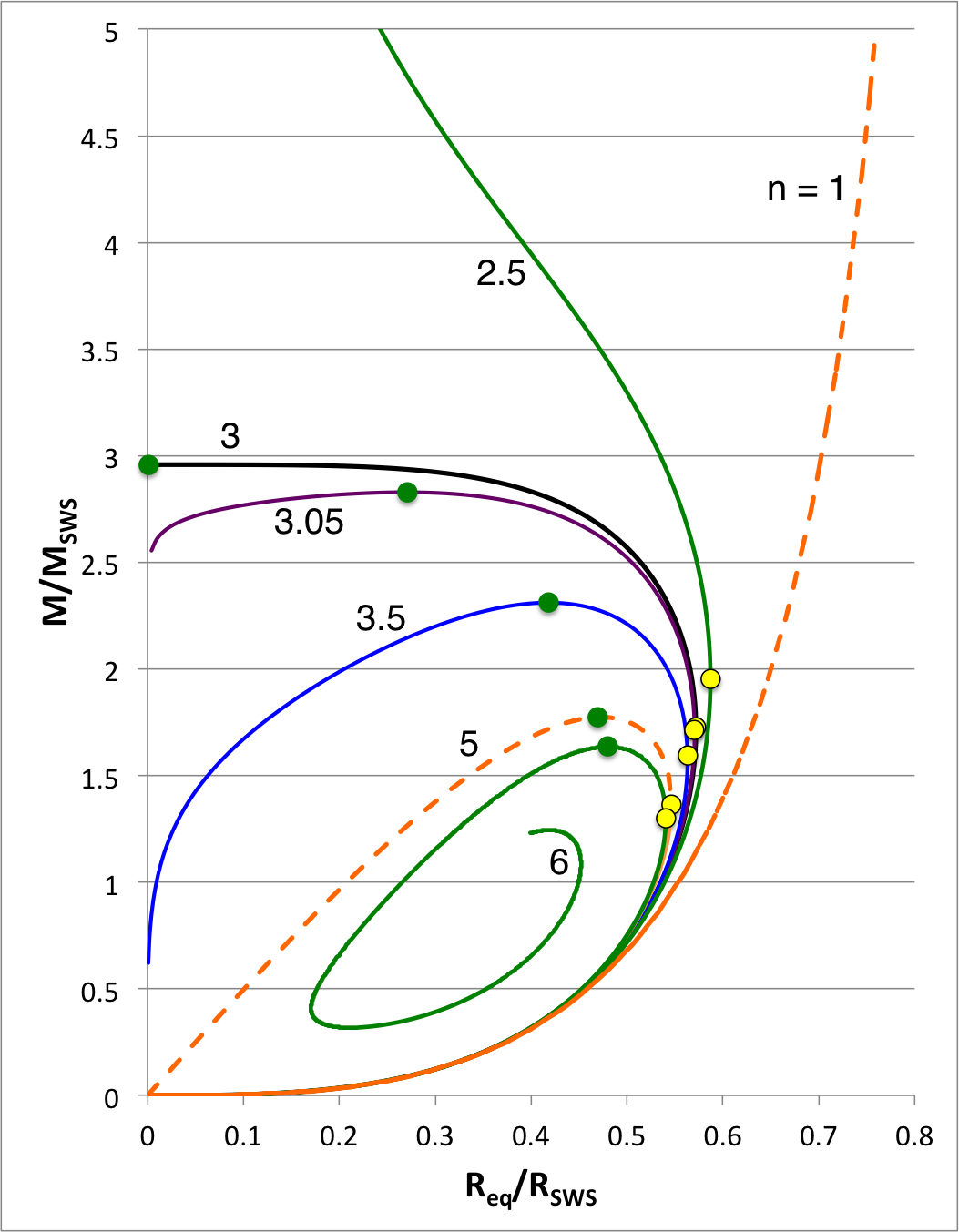
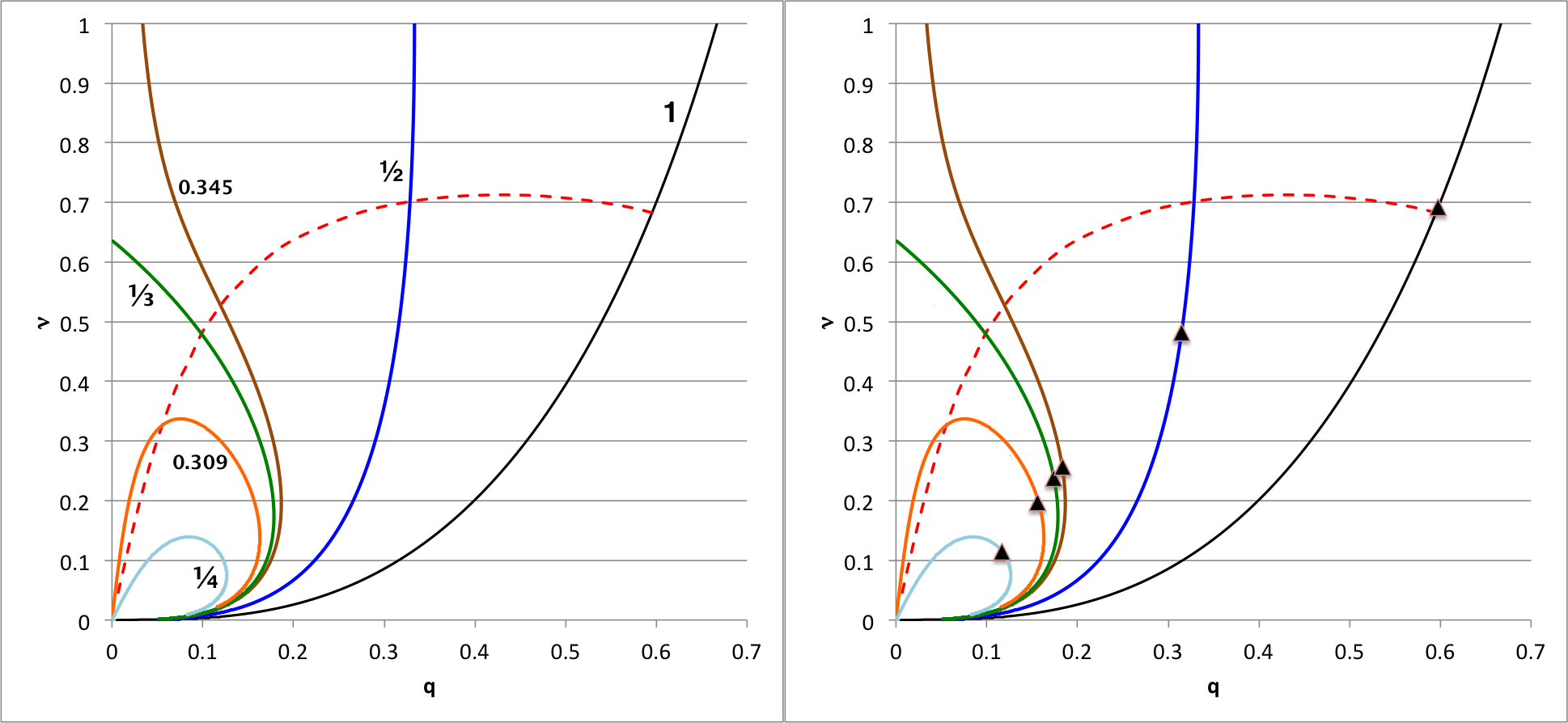
For example, if we set <math>~\gamma_c = 6/5</math> and <math>~\gamma_e = 2</math>, this implies, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~\ | <math>~\frac{\mathfrak{s}_\mathrm{core} }{\mathfrak{s}_\mathrm{env}} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math> | <math>~=</math> | ||
</td> | </td> | ||
<td align=" | <td align="left"> | ||
<math> | <math> | ||
~\frac{2 }{(4 - 18/5) } = 5 \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | |||
</table> | |||
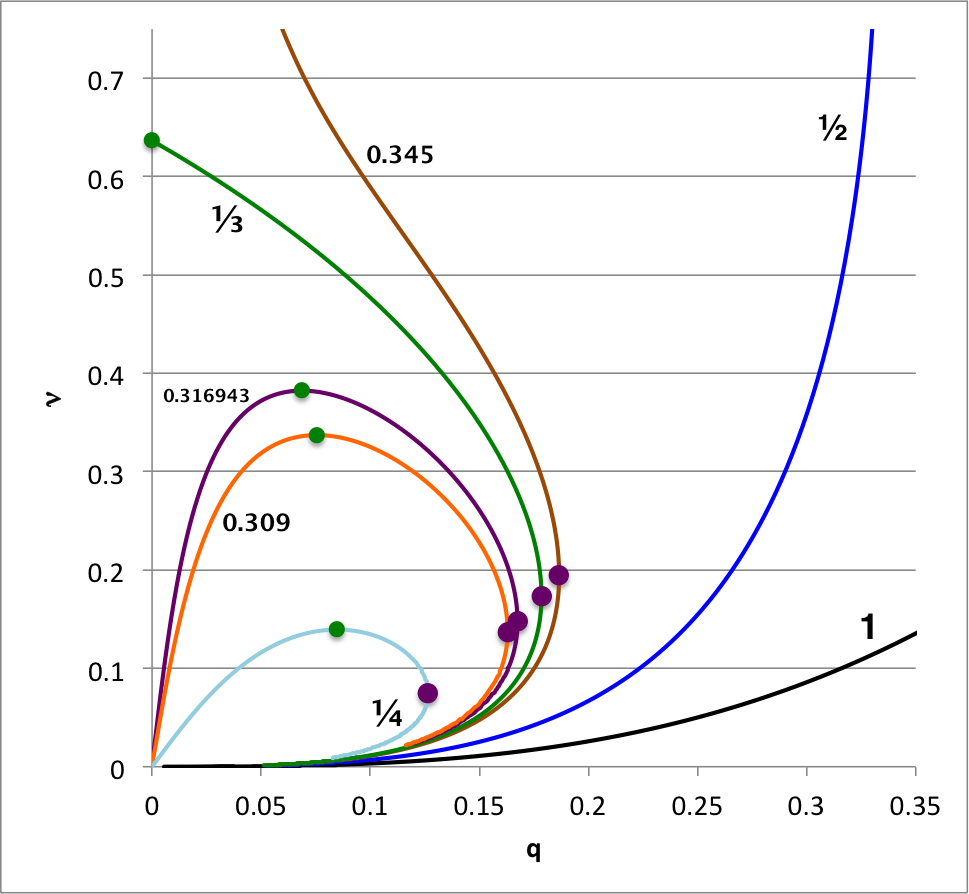
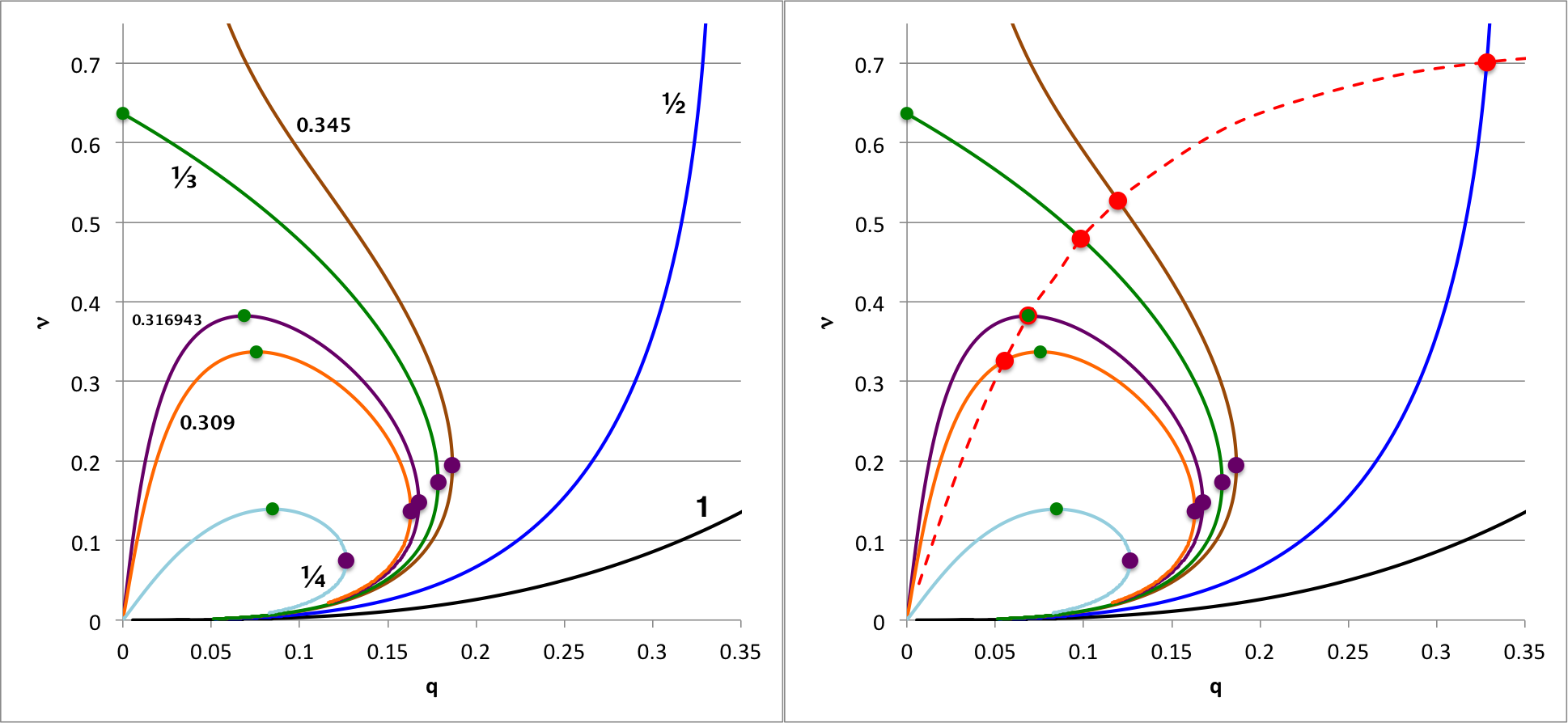
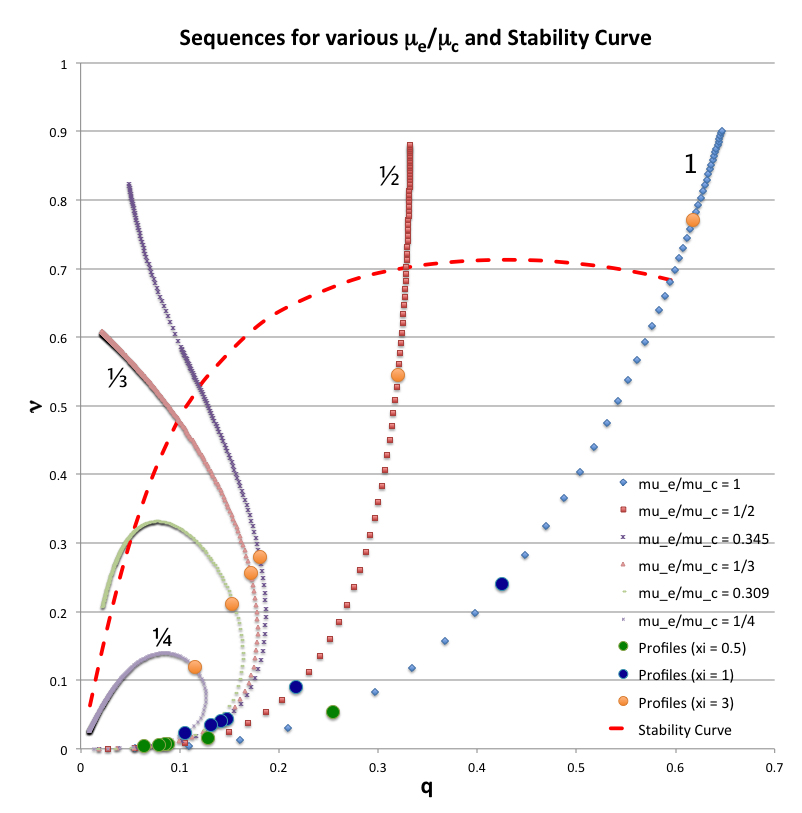
<table border="0" align="center" cellpadding="8"> | |||
<tr> | |||
<td align="center"> | <td align="center"> | ||
[[File:CompositeAlabeled.png|700px|dynamical stability in qNu plane]] | |||
</td> | </td> | ||
<td align=" | </tr> | ||
</table> | |||
=Review of the Analysis by Murphy & Fiedler (1985b)= | |||
As we have [[User:Tohline/SSC/Stability/Polytropes#Boundary_Conditions|detailed separately]], the boundary condition at the center of a polytropic configuration is, | |||
<div align="center"> | |||
<math>~\frac{dx}{d\xi} \biggr|_{\xi=0} = 0 \, ;</math> | |||
</div> | |||
and the boundary condition at the surface of an isolated polytropic configuration is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{d\ln x}{d\ln\xi}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \alpha + \frac{\omega^2}{\gamma_g } \biggl( \frac{1}{4\pi G \rho_c } \biggr) \frac{\xi}{(-\theta^')} </math> | |||
at <math>~\xi = \xi_s \, .</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
But this surface condition is not applicable to bipolytropes. Instead, let's return to the [[User:Tohline/SSC/Perturbations#Ensure_Finite-Amplitude_Fluctuations|original, more general expression of the surface boundary condition]]: | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~ | <math>~ \frac{d\ln x}{d\ln\xi}\biggr|_s</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math> | <math>~=</math> | ||
</td> | </td> | ||
<td align=" | <td align="left"> | ||
<math>\ | <math>~- \alpha + \frac{\omega^2 R^3}{\gamma_g GM_\mathrm{tot}} \, .</math> | ||
</td> | </td> | ||
</tr> | |||
</table> | |||
<table border="1" align="center" width="85%" cellpadding="10"><tr><td align="left"> | |||
Utilizing an [[User:Tohline/SSC/Stability/Polytropes#Groundwork|accompanying discussion]], let's examine the frequency normalization used by [http://adsabs.harvard.edu/abs/1985PASAu...6..222M Murphy & Fiedler (1985b)] (see the top of the left-hand column on p. 223): | |||
<table border="0" cellpadding="5" align="center"> | |||
<td align=" | <tr> | ||
< | <td align="right"> | ||
<math>~\Omega^2</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~\equiv</math> | |||
</td> | </td> | ||
<td align=" | <td align="left"> | ||
[ | <math>~ | ||
\omega^2 \biggl[ \frac{R^3}{GM_\mathrm{tot}} \biggr] | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math> | <math>~=</math> | ||
</td> | </td> | ||
<td align=" | <td align="left"> | ||
<math>\biggl | <math>~ | ||
\omega^2 \biggl[ \frac{3}{4\pi G \bar\rho} \biggr] | |||
= | |||
\omega^2 \biggl[ \frac{3}{4\pi G \rho_c} \biggr] \frac{\rho_c}{\bar\rho} | |||
= | |||
\frac{3\omega^2}{(n_c+1)} \biggl[ \frac{(n_c+1)}{4\pi G \rho_c} \biggr] \frac{\rho_c}{\bar\rho} | |||
</math> | |||
</td> | </td> | ||
</tr> | |||
<td align=" | <tr> | ||
<td align="right"> | |||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align=" | <td align="left"> | ||
<math>~ | |||
\frac{3\omega^2}{(n_c+1)} \biggl[ \frac{a_n^2\rho_c}{P_c} \cdot \theta_c \biggr] \frac{\rho_c}{\bar\rho} | |||
= | |||
\frac{3\gamma}{(n_c+1)} \frac{\rho_c}{\bar\rho} \biggl[ \frac{a_n^2\rho_c}{P_c} \cdot \frac{\omega^2 \theta_c}{\gamma} \biggr] \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
For a given radial quantum number, <math>~k</math>, the factor inside the square brackets in this last expression is what [http://adsabs.harvard.edu/abs/1985PASAu...6..222M Murphy & Fiedler (1985b)] refer to as <math>~\omega^2_k \theta_c</math>. Keep in mind, as well, that, in the notation we are using, | |||
<table border="0" cellpadding="5" align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\sigma_c^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{3\omega^2}{2\pi G \rho_c}</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 647: | Line 718: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~ \sigma_c^2</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 654: | Line 725: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{2\ | \biggl( \frac{2\bar\rho}{\rho_c}\biggr) \Omega^2 | ||
= | |||
\, | \frac{6\gamma}{(n_c+1)} \biggl[ \frac{a_n^2\rho_c}{P_c} \cdot \frac{\omega^2 \theta_c}{\gamma} \biggr] | ||
= | |||
\frac{6\gamma}{(n_c+1)} \biggl[ \omega_k^2 \theta_c \biggr] \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
This also means that the surface boundary condition may be rewritten as, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{\ | <math>~ \frac{d\ln x}{d\ln\xi}\biggr|_s</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 673: | Line 746: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{\Omega^2}{\gamma_g } - \alpha \, .</math> | ||
\, | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</td></tr></table> | |||
<tr> | |||
Let's apply these relations to the core and envelope, separately. | |||
==Interface Conditions== | |||
Here, we will simply copy the discussion already provided in the context of our attempt to analyze the stability of <math>~(n_c, n_e) = (0, 0)</math> bipolytropes; specifically, we will draw from [[User:Tohline/SSC/Stability/BiPolytrope0_0#Piecing_Together|<font color="red">'''STEP 4:'''</font> in the ''Piecing Together'' subsection]]. Following the discussion in §§57 & 58 of [http://adsabs.harvard.edu/abs/1958HDP....51..353L P. Ledoux & Th. Walraven (1958)], the proper treatment is to ensure that fractional perturbation in the gas pressure (see their equation 57.31), | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
<math>~\frac{ | <math>~\frac{\delta P}{P}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 688: | Line 769: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~- \gamma x \biggl( 3 + \frac{d\ln x}{d\ln \xi} \biggr) \, ,</math> | ||
\, | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | |||
is continuous across the interface. That is to say, at the interface <math>~(\xi = \xi_i)</math>, we need to enforce the relation, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 713: | Line 787: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl[ \gamma_c x_\mathrm{core} \biggl( 3 + \frac{d\ln x_\mathrm{core}}{d\ln \xi} \biggr) - \gamma_e x_\mathrm{env} \biggl( 3 + \frac{d\ln x_\mathrm{env}}{d\ln \xi} \biggr)\biggr]_{\xi=\xi_i}</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 730: | Line 799: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~\gamma_e \biggl[ \frac{\gamma_c}{\gamma_e} \biggl( 3 + \frac{d\ln x_\mathrm{core}}{d\ln \xi} \biggr) - \biggl( 3 + \frac{d\ln x_\mathrm{env}}{d\ln \xi} \biggr)\biggr]_{\xi=\xi_i}</math> | ||
</td> | </td> | ||
< | </tr> | ||
<tr> | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\Rightarrow~~~ \frac{d\ln x_\mathrm{env}}{d\ln \xi} \biggr|_{\xi=\xi_i}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 740: | Line 811: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{d | <math>~3\biggl(\frac{\gamma_c}{\gamma_e} -1\biggr) + \frac{\gamma_c}{\gamma_e} \biggl( \frac{d\ln x_\mathrm{core}}{d\ln \xi} \biggr)_{\xi=\xi_i} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | |||
< | In the context of this interface-matching constraint (see their equation 62.1), [http://adsabs.harvard.edu/abs/1958HDP....51..353L P. Ledoux & Th. Walraven (1958)] state the following: <font color="darkgreen"><b>In the static</b></font> (''i.e.,'' unperturbed equilibrium) <font color="darkgreen"><b>model</b></font> … <font color="darkgreen"><b>discontinuities in <math>~\rho</math> or in <math>~\gamma</math> might occur at some [radius]</b></font>. <font color="darkgreen"><b>In the first case</b></font> — that is, a discontinuity only in density, while <math>~\gamma_e = \gamma_c</math> — the interface conditions <font color="darkgreen"><b>imply the continuity of <math>~\tfrac{1}{x} \cdot \tfrac{dx}{d\xi}</math> at that [radius]. In the second case</b></font> — that is, a discontinuity in the adiabatic exponent — <font color="darkgreen"><b>the dynamical condition may be written</b></font> as above. <font color="darkgreen"><b>This implies a discontinuity of the first derivative at any discontinuity of <math>~\gamma</math></b></font>. | ||
The algorithm that [http://adsabs.harvard.edu/abs/1985PASAu...6..222M Murphy & Fiedler (1985b)] used to "<font color="#007700">… [integrate] through each zone …</font>" was designed "<font color="#007700">… with continuity in <math>~x</math> and <math>~dx/d\xi</math> being imposed at the interface …</font>" Given that they set <math>~\gamma_c = \gamma_e = 5/3</math>, their interface matching condition is consistent with the one prescribed by [http://adsabs.harvard.edu/abs/1958HDP....51..353L P. Ledoux & Th. Walraven (1958)]. | |||
=Radial Oscillations of (n<sub>c</sub>, n<sub>e</sub>) = (5, 1) Models= | |||
==Foundation== | |||
In an [[User:Tohline/SSC/Perturbations#2ndOrderODE|accompanying discussion]], we derived the so-called, | |||
<tr> | <div align="center" id="2ndOrderODE"> | ||
<td align="right"> | <font color="#770000">'''Adiabatic Wave''' (or ''Radial Pulsation'') '''Equation'''</font><br /> | ||
<math>~ | |||
</td> | {{User:Tohline/Math/EQ_RadialPulsation01}} | ||
<td align="center"> | </div> | ||
<math>~\ | |||
whose solution gives eigenfunctions that describe various radial modes of oscillation in spherically symmetric, self-gravitating fluid configurations. Assuming that the underlying equilibrium structure is that of a bipolytrope having <math>~(n_c, n_e) = (5, 1)</math>, it makes sense to adopt the normalizations used when defining the equilibrium structure, namely, | |||
<div align="center"> | |||
<table border="0" cellpadding="3"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\rho^*</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{\rho_0}{\rho_c}</math> | ||
\frac{ | |||
</math> | |||
</td> | </td> | ||
<td align="center"> | |||
<td align="center">; </td> | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~r^*</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~\ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{r_0}{[K_c^{1/2}/(G^{1/2}\rho_c^{2/5})]}</math> | ||
\frac{ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~P^*</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\frac{P_0}{K_c\rho_c^{6/5}}</math> | ||
</math> | |||
</td> | </td> | ||
< | <td align="center">; </td> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~M_r^*</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~\frac{M_r}{[K_c^{3/2}/(G^{3/2}\rho_c^{1/5})]}</math> | ||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</div> | |||
We note as well that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~g_0</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 813: | Line 895: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{GM(r_0)}{r_0^2}</math> | ||
\ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl\{ | G \biggl[ M_r^* \rho_c^{-1 / 5} \biggl( \frac{K_c}{G}\biggr)^{3 / 2} \biggr] \biggl[ r^* \rho_c^{-2 / 5}\biggl( \frac{K_c}{G}\biggr)^{1 / 2} \biggr]^{-2} | ||
</math> | </math> | ||
</td> | </td> | ||
< | </tr> | ||
<tr> | |||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{2\ | \frac{G M_r^*}{(r^*)^2} \biggl[ \rho_c^{3 / 5} \biggl( \frac{K_c}{G}\biggr)^{1 / 2} \biggr] \, . | ||
</math> | </math> | ||
</td> | </td> | ||
< | </tr> | ||
<td align="right"> | </table> | ||
<math>~ | |||
Hence, multiplying the LAWE through by <math>~(K_c/G)\rho_c^{-4 / 5}</math> gives, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl(\frac{\ | \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} | ||
+ \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 867: | Line 948: | ||
</table> | </table> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~0</math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 883: | Line 961: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{d^2x}{dr*^2} + \biggl[\frac{4}{r^*} ~-~ \rho_c^{-2 / 5} \biggl( \frac{K_c}{G} \biggr)^{1 / 2}\biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr*} | |||
~+~ \rho_c^{-4 / 5}\biggl( \frac{K_c}{G} \biggr)\biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 ~+~ (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \frac{d^2x}{dr*^2} ~+~ \biggl\{\frac{4}{r^*} ~-~ \rho_c^{-2 / 5} \biggl( \frac{K_c}{G} \biggr)^{1 / 2} \frac{G M_r^*}{(r^*)^2} \biggl[ \rho_c^{3 / 5} \biggl( \frac{K_c}{G}\biggr)^{1 / 2} \biggr] \biggl[ \frac{\rho_c \rho^*}{P^* K_c \rho_c^{6/5}}\biggr] \biggr\} \frac{dx}{dr*} | ||
~+~ \rho_c^{-4 / 5}\biggl( \frac{K_c}{G} \biggr)\biggl[ \frac{\rho_c \rho^*}{\gamma_\mathrm{g}P^* K_c \rho_c^{6/5}}\biggr] | |||
\biggr\} | \biggl\{\omega^2 ~+~ (4 - 3\gamma_\mathrm{g}) \frac{G M_r^*}{(r^*)^2} \biggl[ \rho_c^{3 / 5} \biggl( \frac{K_c}{G}\biggr)^{1 / 2} \biggr] \frac{\rho_c^{2 / 5}}{r^*}\biggl( \frac{G}{K_c}\biggr)^{1 / 2} \biggr\} x | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 923: | Line 992: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{d^2x}{dr*^2} ~+~ \biggl\{\frac{4}{r^*} ~-~ \frac{M_r^*}{(r^*)^2} \biggl[ \frac{\rho^*}{P^* }\biggr] \biggr\} \frac{dx}{dr*} | |||
~+~ \biggl( \frac{1}{G\rho_c} \biggr)\biggl[ \frac{ \rho^*}{\gamma_\mathrm{g}P^* }\biggr] | |||
\frac{ | \biggl\{\omega^2 ~+~ (4 - 3\gamma_\mathrm{g}) \frac{G\rho_c M_r^*}{(r^*)^3} \biggr\} x | ||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 941: | Line 1,008: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \frac{d^2x}{dr*^2} + \biggl\{ \frac{4}{r^*} -\biggl(\frac{\rho^*}{P^*}\biggr)\frac{ M_r^*}{(r^*)^2}\biggr\} \frac{dx}{dr*} | ||
\ | + \biggl(\frac{\rho^*}{ P^* } \biggr)\biggl\{ \frac{\omega^2}{\gamma_\mathrm{g} G\rho_c} + \biggl(\frac{4}{\gamma_\mathrm{g}} - 3\biggr)\frac{ M_r^*}{(r^*)^3}\biggr\} x | ||
\ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 957: | Line 1,023: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \frac{d^2x}{dr*^2} + \biggl\{ 4 -\biggl(\frac{\rho^*}{P^*}\biggr)\frac{ M_r^*}{(r^*)}\biggr\}\frac{1}{r^*} \frac{dx}{dr*} | ||
\biggl | + \biggl(\frac{\rho^*}{ P^* } \biggr)\biggl\{ \frac{2\pi \sigma_c^2}{3\gamma_\mathrm{g}} ~-~\frac{\alpha_\mathrm{g} M_r^*}{(r^*)^3}\biggr\} x \, . | ||
\biggr\}\ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 965: | Line 1,030: | ||
</table> | </table> | ||
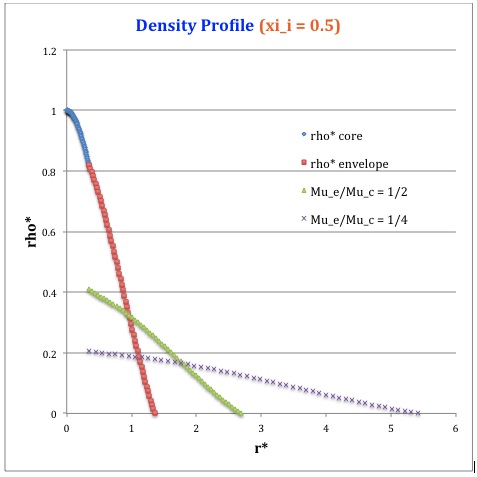
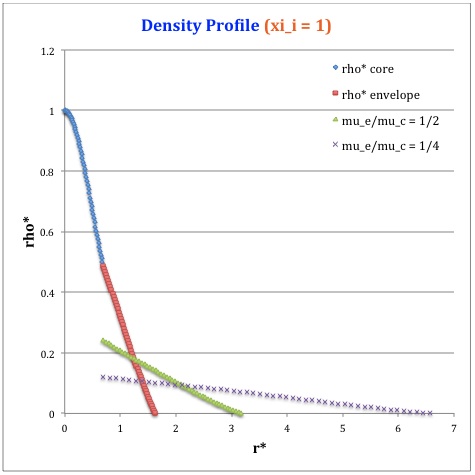
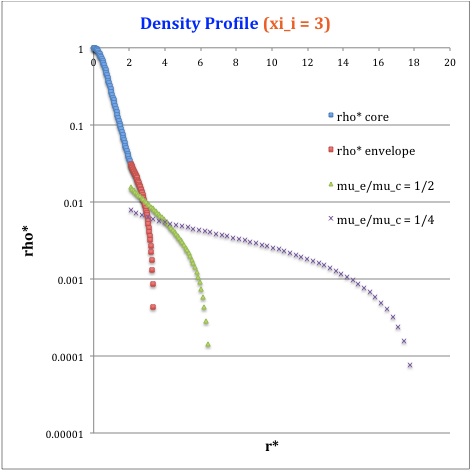
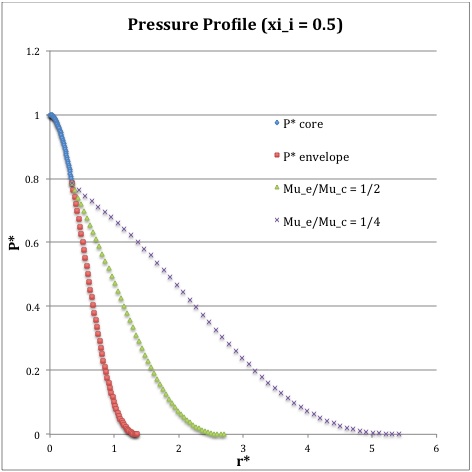
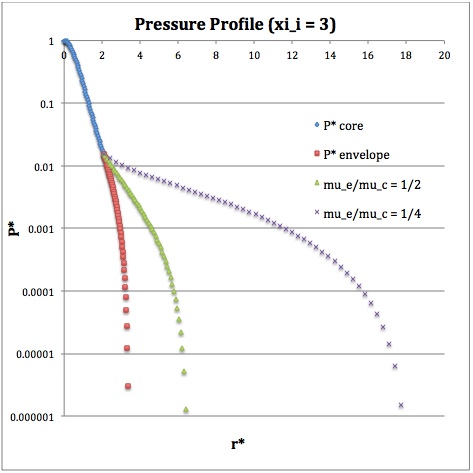
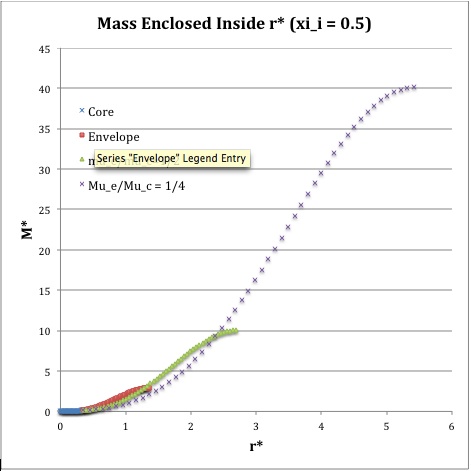
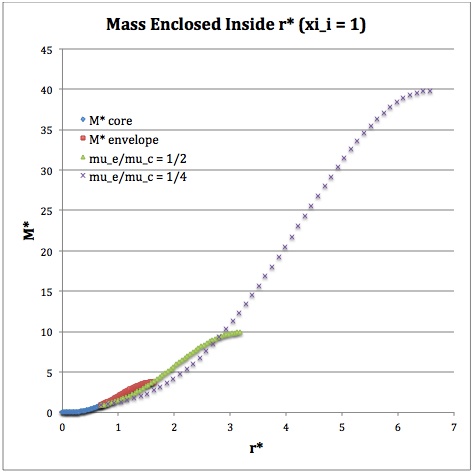
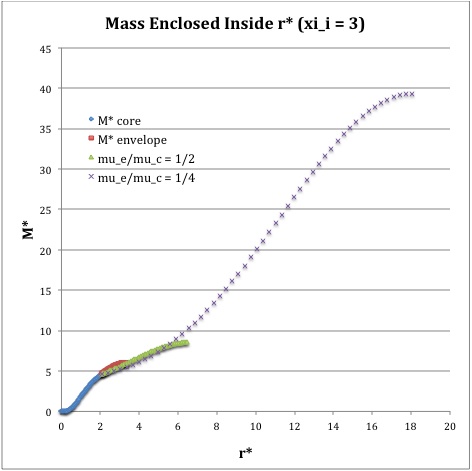
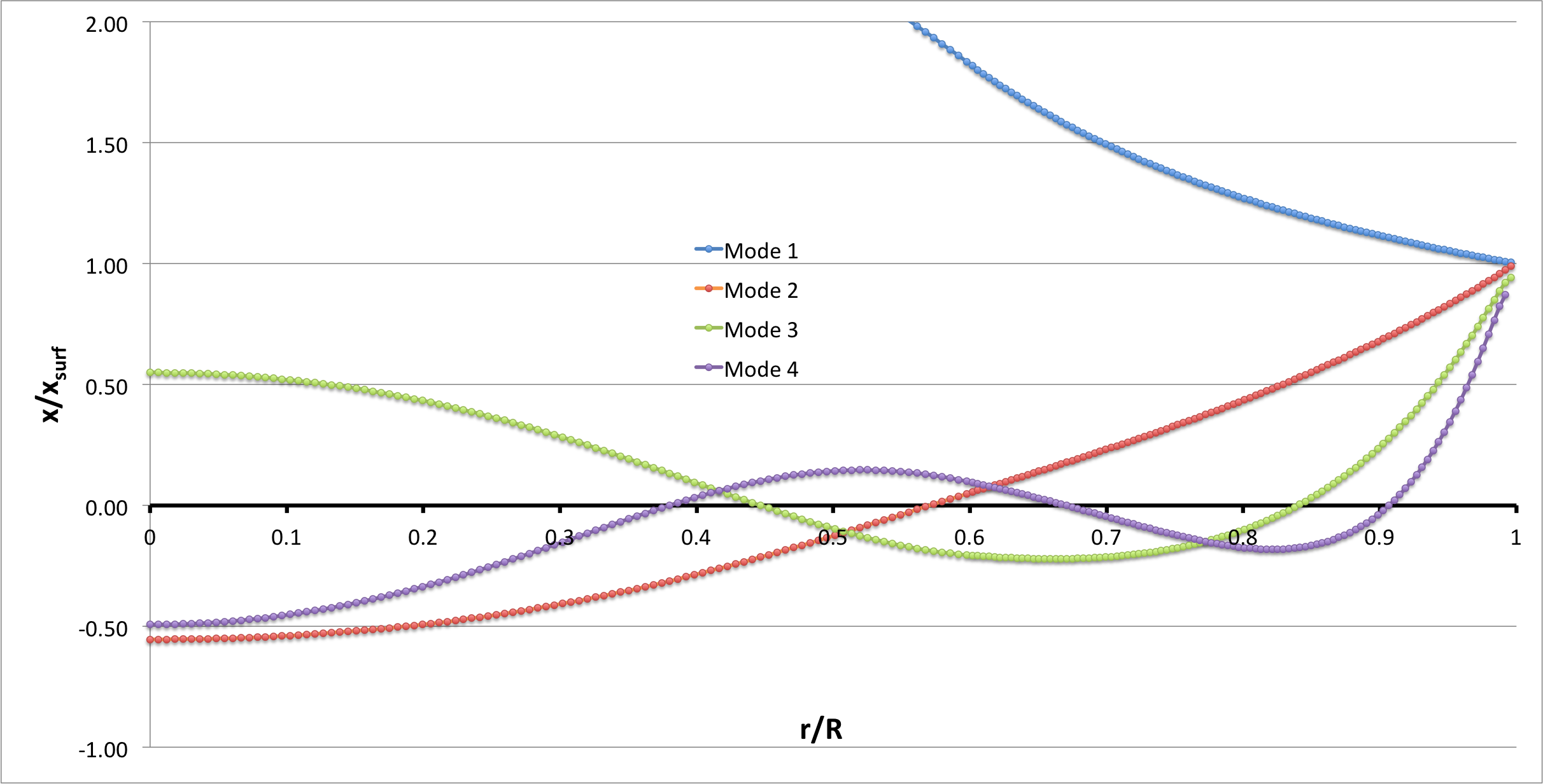
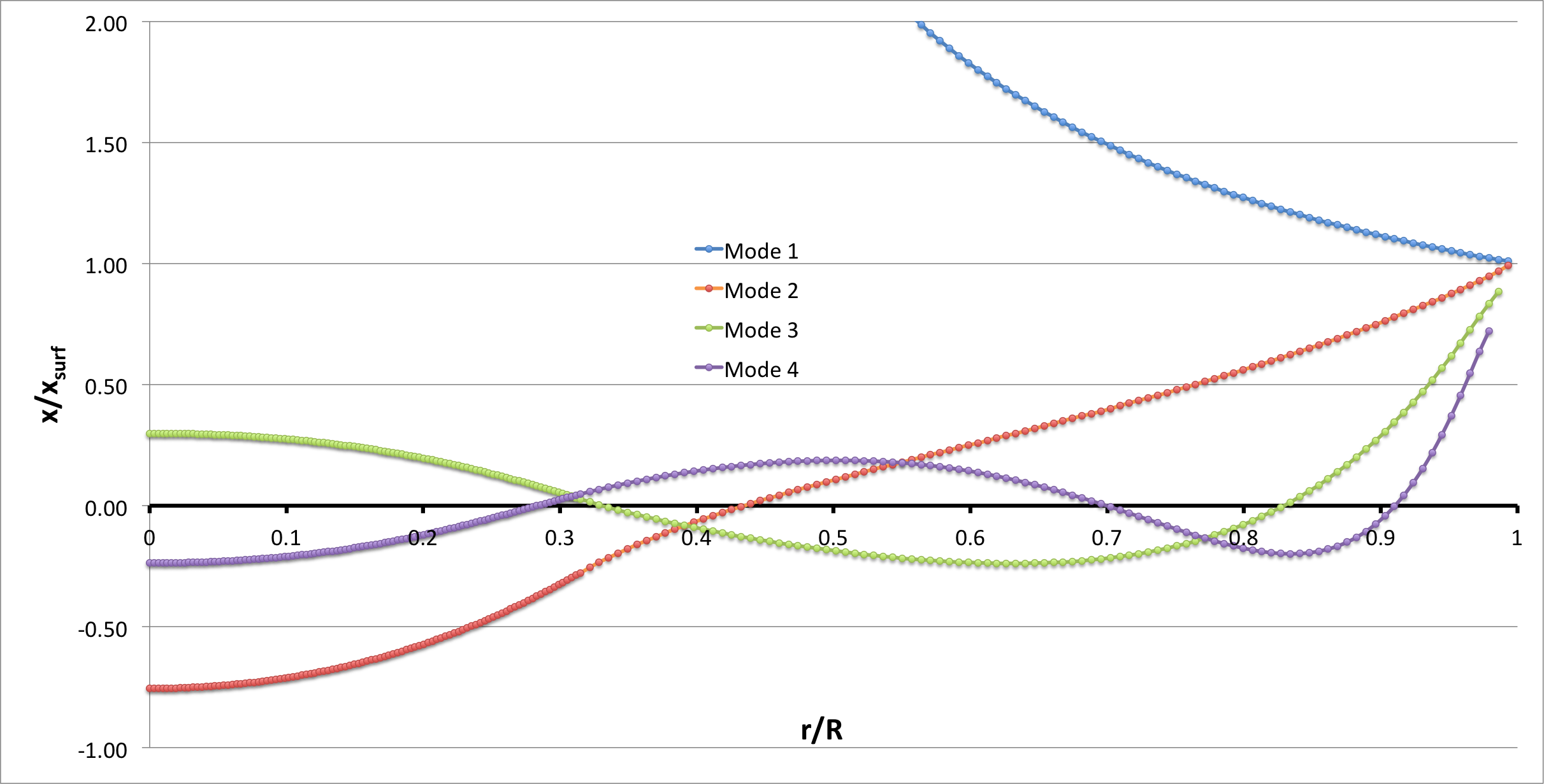
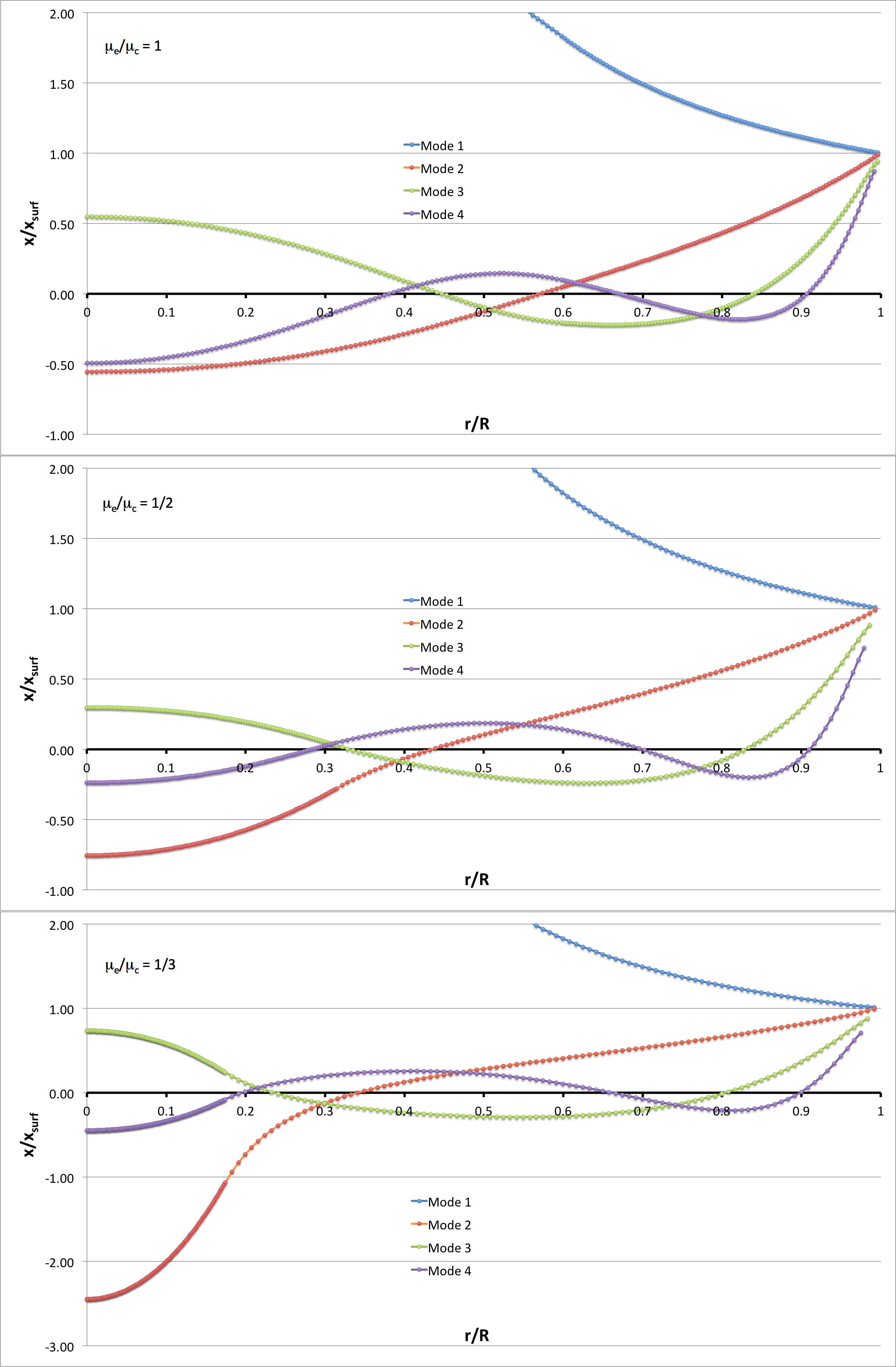
==Profile== | |||
Now, referencing the [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Profile|derived bipolytropic model profile]], we should incorporate the following relations: | |||
<div align="center"> | |||
<b>Table 2: Radial Profile of Various Physical Variables</b> | |||
<table border="1" cellpadding="6"> | |||
<tr> | <tr> | ||
<td align=" | <td align="center" rowspan="2"> | ||
<math>~ | Variable | ||
</td> | |||
<td align="center" rowspan="2"> | |||
Throughout the Core<br> | |||
<math>~0 \le \xi \le \xi_i</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center" rowspan="2"> | ||
<math>~\ | Throughout the Envelope<sup>†</sup><br> | ||
<math>~\eta_i \le \eta \le \eta_s</math> | |||
</td> | </td> | ||
<td align=" | |||
<td align="center" colspan="3"> | |||
Plotted Profiles | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center"> | ||
<math>~\ | <math>~\xi_i = 0.5</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~\xi_i = 1.0</math> | ||
</td> | </td> | ||
<td align=" | <td align="center"> | ||
<math>~ | <math>~\xi_i = 3.0</math> | ||
\ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center"> | ||
<math>~ | <math>~r^*</math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math> | <math>\biggl( \frac{3}{2\pi} \biggr)^{1/2} \xi</math> | ||
</td> | </td> | ||
<td align=" | <td align="center"> | ||
<math> | <math>\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1} \theta^{-2}_i (2\pi)^{-1/2}\eta</math> | ||
2\ | |||
</math> | |||
</td> | </td> | ||
<td align="center" colspan="3"> | |||
| |||
<td align="center" | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center"> | ||
<math>~ | <math>~\rho^*</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math> | <math>\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-5/2}</math> | ||
</td> | </td> | ||
<td align=" | <td align="center"> | ||
<math> | <math>\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{5}_i \phi(\eta)</math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | |||
<!-- [[File:PlotDensity_xi_0.5.jpg|thumb|75px]] --> | |||
[[Image:DenXi05.jpg|thumb|75px]] | |||
<td align=" | |||
< | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
[[Image:DenXi10.jpg|thumb|75px]] | |||
</td> | </td> | ||
<td align=" | <td align="center"> | ||
[[Image:DenXi30.jpg|thumb|75px]] | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center"> | ||
<math>~ | <math>~P^*</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math> | <math>\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3}</math> | ||
</td> | </td> | ||
<td align=" | <td align="center"> | ||
<math> | <math>\theta^{6}_i [\phi(\eta)]^{2}</math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | |||
<td align=" | <!-- [[File:PlotPressure_xi_0.5.jpg|thumb|75px]] --> | ||
< | [[Image:PresXi05.jpg|thumb|75px]] | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
[[Image:PresXi10.jpg|thumb|75px]] | |||
</td> | </td> | ||
<td align=" | <td align="center"> | ||
[[Image:PresXi30.jpg|thumb|75px]] | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center"> | ||
<math>~ | <math>~M_r^*</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math> | <math>\biggl( \frac{2\cdot 3}{\pi } \biggr)^{1/2} \biggl[ \xi^3 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3/2} \biggr]</math> | ||
</td> | </td> | ||
<td align=" | <td align="center"> | ||
<math> | <math>\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \theta^{-1}_i \biggl( \frac{2}{\pi} \biggr)^{1/2} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math> | ||
\frac{ | </td> | ||
<td align="center"> | |||
</math> | <!-- [[File:PlotPressure_xi_0.5.jpg|thumb|75px]] --> | ||
[[Image:MassXi05.jpg|thumb|75px]] | |||
</td> | |||
<td align="center"> | |||
[[Image:MassXi10.jpg|thumb|75px]] | |||
</td> | |||
<td align="center"> | |||
[[Image:MassXi30.jpg|thumb|75px]] | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="left" colspan="6"> | |||
<sup>†</sup>In order to obtain the various envelope profiles, it is necessary to evaluate <math>\phi(\eta)</math> and its first derivative using the information presented in Step 6, above. | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | |||
Therefore, throughout the core we have, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{\rho^*}{P^*}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,143: | Line 1,173: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{1 / 2} \, ;</math> | ||
+ \frac{1}{ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{ | <math>~\frac{M_r^*}{r^*}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,163: | Line 1,186: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{2\cdot 3}{\pi } \biggr)^{1/2} \biggl[ \xi^3 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3/2} \biggr]\biggl( \frac{2\pi}{3}\biggr)^{1 / 2} \frac{1}{\xi} | |||
= 2 \xi^2 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3/2} | |||
\, ; | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
and, throughout the envelope we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\frac{\rho^*}{P^*}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,177: | Line 1,206: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{-1}_i \phi(\eta)^{-1} | |||
\, ; | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,184: | Line 1,214: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{M_r^*}{r^*}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,191: | Line 1,221: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl | \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \theta^{-1}_i \biggl( \frac{2}{\pi} \biggr)^{1/2} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr) | ||
\biggl[ \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1} \theta^{-2}_i (2\pi)^{-1/2}\eta \biggr]^{-1} | |||
= | |||
2 \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1} \theta_i \eta \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr) | |||
\, . | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 1,197: | Line 1,231: | ||
</table> | </table> | ||
==Numerical Integration== | |||
===General Approach=== | |||
Here, we begin by recognizing that the 2<sup>nd</sup>-order ODE that must be integrated to obtain the desired eigenvectors has the generic form, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~0</math> | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,210: | Line 1,246: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
x'' + \frac{\mathcal{H}}{r^*} x' + \mathcal{K}x \, , | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
where, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~x'</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,232: | Line 1,262: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~\frac{dx}{dr^*}</math> | ||
</td> | </td> | ||
< | <td align="center"> and </td> | ||
< | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~x''</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,244: | Line 1,272: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{d^2x}{d(r^*)^2} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Adopting the same approach [[User:Tohline/SSC/Stability/Polytropes#Numerical_Integration_from_the_Center.2C_Outward|as before when we integrated the LAWE for pressure-truncated polytropes]], we will enlist the finite-difference approximations, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~x'</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\approx</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{x_+ - x_-}{2\delta r^*} | |||
</math> | |||
</td> | </td> | ||
< | <td align="center"> and </td> | ||
< | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~x''</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\approx</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{ | <math>~ | ||
\frac{x_+ -2x_j + x_-}{(\delta r^*)^2} \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
The finite-difference representation of the LAWE is, therefore, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\frac{x_+ -2x_j + x_-}{(\delta r^*)^2}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,288: | Line 1,317: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-~ \frac{\mathcal{H}}{r^*} \biggl[ \frac{x_+ - x_-}{2\delta r^*} \biggr] ~-~ \mathcal{K}x_j | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,294: | Line 1,325: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~ x_+ -2x_j + x_-</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,300: | Line 1,331: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-~ \frac{\delta r^*}{2r^*} \biggl[ x_+ - x_- \biggr]\mathcal{H} ~-~ (\delta r^*)^2\mathcal{K}x_j | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 1,306: | Line 1,339: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{\ | <math>~\Rightarrow ~~~ x_{j+1} \biggl[1 + \biggl( \frac{\delta r^*}{2r^*}\biggr) \mathcal{H} \biggr]</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,312: | Line 1,345: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ 2 - (\delta r^*)^2\mathcal{K}\biggr] x_j ~-~\biggl[ 1 - \biggl( \frac{\delta r^*}{2r^*} \biggr) \mathcal{H} \biggr]x_{j-1} \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
In what follows we will also find it useful to rewrite <math>~\mathcal{K}</math> in the form, | |||
<div align="center"> | |||
<math>~\mathcal{K} ~\rightarrow ~\biggl(\frac{\sigma_c^2}{\gamma_\mathrm{g}}\biggr) \mathcal{K}_1 - \alpha_\mathrm{g} \mathcal{K}_2 \, .</math> | |||
</div> | |||
The relevant coefficient expressions for ''all'' regions of the configuration are, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\mathcal{H}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\equiv</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl\{ 4 -\biggl(\frac{\rho^*}{P^*}\biggr)\frac{ M_r^*}{(r^*)}\biggr\} | |||
</math> | |||
</td> | |||
<td align="center"> , </td> | |||
<td align="right"> | |||
<math>~\mathcal{K}_1</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{2\pi }{3}\biggl(\frac{\rho^*}{ P^* } \biggr) | |||
</math> | |||
</td> | |||
<td align="center"> and </td> | |||
<td align="right"> | |||
<math>~\mathcal{K}_2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl(\frac{\rho^*}{ P^* } \biggr)\frac{M_r^*}{(r^*)^3} \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
<table border=" | ===Special Handling at the Center=== | ||
In order to kick-start the integration, we set the displacement function value to <math>~x_1 = 1</math> at the center of the configuration <math>~(\xi_1 = 0)</math>, then draw on the [[User:Tohline/Appendix/Ramblings/PowerSeriesExpressions#PolytropicDisplacement|derived power-series expression]] to determine the value of the displacement function at the first radial grid line, <math>~\xi_2 = \delta\xi</math>, away from the center. Specifically, we set, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="center" | <td align="right"> | ||
<math>~ | |||
</td> | x_2 | ||
</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
x_1 \biggl[ 1 - \frac{(n+1) \mathfrak{F} (\delta\xi)^2}{60} \biggr]_{n=5} | |||
= | |||
x_1 \biggl[ 1 - \frac{\mathfrak{F} (\delta\xi)^2}{10} \biggr] | |||
\, .</math> | |||
</td> | |||
</tr> | </tr> | ||
</table> | |||
</div> | |||
===Special Handling at the Interface=== | |||
Integrating outward from the center, the ''general approach'' will work up through the determination of <math>~x_{j+1}</math> when "j+1" refers to the interface location. In order to properly transition from the core to the envelope, we need to determine the value of the slope at this interface location. Let's do this by setting j = i, then projecting forward to what <math>~x_+</math> ''would be'' — that is, to what the amplitude just beyond the interface ''would be'' — if the core were to be extended one more zone. Then, the slope at the interface (as viewed from the perspective of the core) will be, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~x'_i\biggr|_\mathrm{core}</math> | |||
</td> | |||
<td align="center"><math>~\ | <td align="center"> | ||
<math>~\approx</math> | |||
<td align=" | </td> | ||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2\delta r^*} \biggl\{ | |||
x_+ - x_{i-1} | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | |||
<td align="right" | | ||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
<td align=" | </td> | ||
<td align="left"> | |||
<math>~ | |||
<td align=" | -\frac{x_{i-1}}{2\delta r^*} | ||
+ | |||
\frac{1}{2\delta r^*} \biggl\{ | |||
\biggl[ 2 - (\delta r^*)^2\mathcal{K}\biggr] x_i ~-~\biggl[ 1 - \biggl( \frac{\delta r^*}{2r^*} \biggr) \mathcal{H} \biggr]x_{i-1} | |||
\biggr\}\biggl[1 + \biggl( \frac{\delta r^*}{2r^*}\biggr) \mathcal{H} \biggr]^{-1} | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | |||
<td align="right" | | ||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
<td align=" | </td> | ||
<td align="left"> | |||
<math>~ | |||
<td align=" | \frac{1}{2\delta r^*} \biggl\{ | ||
\biggl[ 2 - (\delta r^*)^2\mathcal{K}\biggr] x_i ~-~\biggl[ 1 - \biggl( \frac{\delta r^*}{2r^*} \biggr) \mathcal{H} \biggr]x_{i-1} ~-~\biggl[1 + \biggl( \frac{\delta r^*}{2r^*}\biggr) \mathcal{H} \biggr]x_{i-1} | |||
\biggr\}\biggl[1 + \biggl( \frac{\delta r^*}{2r^*}\biggr) \mathcal{H} \biggr]^{-1} | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | |||
<td align="right" | | ||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
<td align=" | </td> | ||
<td align="left"> | |||
<math>~ | |||
<td align=" | \frac{1}{2\delta r^*} \biggl\{ | ||
\biggl[ 2 - (\delta r^*)^2\mathcal{K}\biggr] x_i ~-~2x_{i-1} | |||
\biggr\}\biggl[1 + \biggl( \frac{\delta r^*}{2r^*}\biggr) \mathcal{H} \biggr]^{-1} | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
</table> | |||
Conversely, as viewed from the ''envelope'', if we assume that we know <math>~x_i</math> and <math>~x'_i</math>, we can determine the amplitude, <math>~x_{i+1}</math>, at the first zone beyond the interface as follows: | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | |||
<td align="right" | <math>~x_-</math> | ||
</td> | |||
<td align="center"> | |||
<td align=" | <math>~\approx</math> | ||
</td> | |||
<td align="left"> | |||
<td align=" | <math>~ | ||
x_{i+1} - 2\delta r^*\cdot x'_i\biggr|_\mathrm{env} | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~\Rightarrow ~~~ x_{i+1} \biggl[1 + \biggl( \frac{\delta r^*}{2r^*}\biggr) \mathcal{H} \biggr]</math> | |||
</td> | |||
<td align=" | <td align="center"> | ||
<math>~=</math> | |||
</td> | |||
<td align=" | <td align="left"> | ||
<math>~ | |||
\biggl[ 2 - (\delta r^*)^2\mathcal{K}\biggr] x_i ~-~\biggl[ 1 - \biggl( \frac{\delta r^*}{2r^*} \biggr) \mathcal{H} \biggr] | |||
\biggl[ x_{i+1} - 2\delta r^*\cdot x'_i\biggr|_\mathrm{env} | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~\Rightarrow ~~~ x_{i+1} \biggl[1 + \biggl( \frac{\delta r^*}{2r^*}\biggr) \mathcal{H} \biggr] | |||
~+~ | |||
<td align=" | \biggl[ 1 - \biggl( \frac{\delta r^*}{2r^*} \biggr) \mathcal{H} \biggr] | ||
x_{i+1} | |||
</math> | |||
<td align=" | </td> | ||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ 2 - (\delta r^*)^2\mathcal{K}\biggr] x_i | |||
~+~ | |||
\biggl[ 1 - \biggl( \frac{\delta r^*}{2r^*} \biggr) \mathcal{H} \biggr] | |||
2\delta r^*\cdot x'_i\biggr|_\mathrm{env} | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | |||
<td align="right" | <math>~\Rightarrow ~~~ x_{i+1} | ||
</math> | |||
</td> | |||
<td align="center"> | |||
<td align=" | <math>~=</math> | ||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ 1 - \tfrac{1}{2}(\delta r^*)^2\mathcal{K}\biggr] x_i | |||
~+~ | |||
\biggl[ 1 - \biggl( \frac{\delta r^*}{2r^*} \biggr) \mathcal{H} \biggr] | |||
\delta r^*\cdot x'_i\biggr|_\mathrm{env} | |||
</math> | |||
<td align="left | |||
<math>~\ | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
== | ==Splitting Analysis Into Separate Core and Envelope Components== | ||
===Core:=== | |||
Given that, <math>~\sqrt{2\pi/3}~r^* = \xi</math>, lets multiply the LAWE through by <math>~3/(2\pi)</math>. This gives, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~0</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{d^2x}{d\xi^2} + \biggl\{ 4 -\biggl(\frac{\rho^*}{P^*}\biggr)\frac{ M_r^*}{(r^*)}\biggr\}\frac{1}{\xi} \cdot \frac{dx}{d\xi} | |||
+ \frac{3}{2\pi}\biggl(\frac{\rho^*}{ P^* } \biggr)\biggl\{ \frac{2\pi \sigma_c^2}{3\gamma_\mathrm{g}} ~-~\frac{\alpha_\mathrm{g} M_r^*}{(r^*)^3}\biggr\} x \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Specifically for the core, therefore, the finite-difference representation of the LAWE is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
< | <td align="right"> | ||
<math>~\frac{x_+ -2x_j + x_-}{(\delta \xi)^2}</math> | |||
</ | </td> | ||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~ \frac{\mathcal{H}}{\xi} \biggl[ \frac{x_+ - x_-}{2\delta \xi} \biggr] ~-~ \biggl[ \frac{3\mathcal{K}}{2\pi} \biggr]x_j | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<td align="center"><math>~ | <math>~\Rightarrow ~~~ x_+ -2x_j + x_-</math> | ||
<td align=" | </td> | ||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
-~ \frac{\delta \xi}{2\xi} \biggl[ x_+ - x_- \biggr]\mathcal{H} ~-~ (\delta \xi)^2 \biggl[ \frac{3\mathcal{K}}{2\pi} \biggr] x_j | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~\Rightarrow ~~~ x_{j+1} \biggl[1 + \biggl( \frac{\delta \xi}{2\xi}\biggr) \mathcal{H} \biggr]</math> | |||
</td> | |||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | |||
<td align=" | <td align="left"> | ||
<math>~ | |||
\biggl[ 2 - (\delta \xi)^2\biggl( \frac{3\mathcal{K}}{2\pi} \biggr) \biggr] x_j ~-~\biggl[ 1 - \biggl( \frac{\delta \xi}{2\xi} \biggr) \mathcal{H} \biggr]x_{j-1} \, . | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
</table> | |||
This also means that, as viewed from the perspective of the core, the slope at the interface is | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~\biggl[ \frac{dx}{d\xi}\biggr]_\mathrm{interface}</math> | |||
<td align="center"> | </td> | ||
<td align="center"> | |||
<math>~=</math> | |||
<td align=" | </td> | ||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2\delta \xi} \biggl\{ | |||
\biggl[ 2 - (\delta \xi)^2 \biggl( \frac{3\mathcal{K}}{2\pi} \biggr)\biggr] x_i ~-~2x_{i-1} | |||
\biggr\}\biggl[1 + \biggl( \frac{\delta \xi}{2\xi}\biggr) \mathcal{H} \biggr]^{-1} \, . | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
</table> | |||
===Envelope:=== | |||
Given that, | |||
<div align="center"> | |||
<math>~\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta_i^2 (2\pi)^{1 / 2}~r^* = \eta \, ,</math> | |||
</div> | |||
let's multiply the LAWE through by <math>~(2\pi)^{-1} \theta_i^{-4}( \mu_e/\mu_c)^{-2} </math>. This gives, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~0</math> | |||
<td align="center"> | </td> | ||
<td align="center"> | |||
<math>~=</math> | |||
<td align=" | </td> | ||
<td align="left"> | |||
<math>~ | |||
\frac{d^2x}{d\eta^2} + \biggl\{ 4 -\biggl(\frac{\rho^*}{P^*}\biggr)\frac{ M_r^*}{(r^*)}\biggr\}\frac{1}{\eta} \cdot \frac{dx}{d\eta} | |||
+ \frac{1}{2\pi \theta_i^4} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \biggl(\frac{\rho^*}{ P^* } \biggr)\biggl\{ \frac{2\pi \sigma_c^2}{3\gamma_\mathrm{g}} ~-~\frac{\alpha_\mathrm{g} M_r^*}{(r^*)^3}\biggr\} x \, . | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
</table> | |||
Specifically for the envelope, therefore, the finite-difference representation of the LAWE is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~\frac{x_+ -2x_j + x_-}{(\delta \eta)^2}</math> | |||
<td align="center" | </td> | ||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align=" | <td align="left"> | ||
<math>~ | |||
-~ \frac{\mathcal{H}}{\eta} \biggl[ \frac{x_+ - x_-}{2\delta \eta} \biggr] ~-~ \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2}\biggl[ \frac{\mathcal{K}}{2\pi \theta_i^4} \biggr]x_j | |||
</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~ x_+ -2x_j + x_-</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,557: | Line 1,708: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{\ | <math>~ | ||
-~ \frac{\delta \eta}{2\eta} \biggl[ x_+ - x_- \biggr]\mathcal{H} ~-~ (\delta \eta)^2 \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2}\biggl[ \frac{\mathcal{K}}{2\pi \theta_i^4} \biggr] x_j | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{ | <math>~\Rightarrow ~~~ x_{j+1} \biggl[1 + \biggl( \frac{\delta \eta}{2\eta}\biggr) \mathcal{H} \biggr]</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,573: | Line 1,722: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ 2 - (\delta \eta)^2 \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \biggl( \frac{\mathcal{K}}{2\pi \theta_i^4} \biggr) \biggr] x_j ~-~\biggl[ 1 - \biggl( \frac{\delta \eta}{2\eta} \biggr) \mathcal{H} \biggr]x_{j-1} \, . | |||
</math> | |||
</td> | </td> | ||
< | </tr> | ||
</table> | |||
This also means that, once we know the slope at the interface (see immediately below), the amplitude at the first zone outside of the interface will be given by the expression, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~x_{i+1} | ||
</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,583: | Line 1,741: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[ 1 - \tfrac{1}{2}(\delta \eta)^2 \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \biggl( \frac{\mathcal{K}}{2\pi \theta_i^4} \biggr)\biggr] x_i | |||
~+~ | |||
\biggl[ 1 - \biggl( \frac{\delta \eta}{2\eta} \biggr) \mathcal{H} \biggr] | |||
\delta \eta \cdot \biggl[ \frac{dx}{d\eta} \biggr]_\mathrm{interface} \, . | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
<table border=" | ===Interface=== | ||
If we consider only cases where <math>~\gamma_e = \gamma_c</math>, then at the interface we expect, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~\frac{d\ln x}{d\ln r^*}</math> | |||
<math>~ | </td> | ||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{d\ln x}{d\ln \xi} = \frac{d\ln x}{d\ln \eta}</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~\Rightarrow ~~~ r^*\frac{dx}{d r^*}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="center | <td align="left"> | ||
<math>~\xi \frac{dx}{d \xi} = \eta \frac{d x}{d \eta}</math> | |||
<td align=" | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center"> | <td align="right"> | ||
<td align=" | <math>~\Rightarrow ~~~ \frac{dx}{dr^*}</math> | ||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl(\frac{2\pi}{3} \biggr)^{1 / 2}\frac{dx}{d\xi} = \biggl(\frac{\mu_e}{\mu_c}\biggr) \theta_i^2 (2\pi)^{1 / 2} \frac{dx}{d\eta} \, .</math> | |||
</td> | |||
</tr> | </tr> | ||
</table> | |||
Switching at the interface from <math>~\xi</math> to <math>~\eta</math> therefore means that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | |||
<math>~ \biggl[ \frac{dx}{d\eta}\biggr]_\mathrm{interface}</math> | |||
<td align="right" | </td> | ||
<td align="center"> | |||
<math>~=</math> | |||
<td align=" | </td> | ||
<td align="left"> | |||
<math>~\frac{1}{\sqrt{3}} \biggl(\frac{\mu_e}{\mu_c}\biggr)^{-1} \theta_i^{-2} \biggl[ \frac{dx}{d\xi}\biggr]_\mathrm{interface} \, .</math> | |||
</td> | |||
<td align=" | |||
</tr> | </tr> | ||
</table> | |||
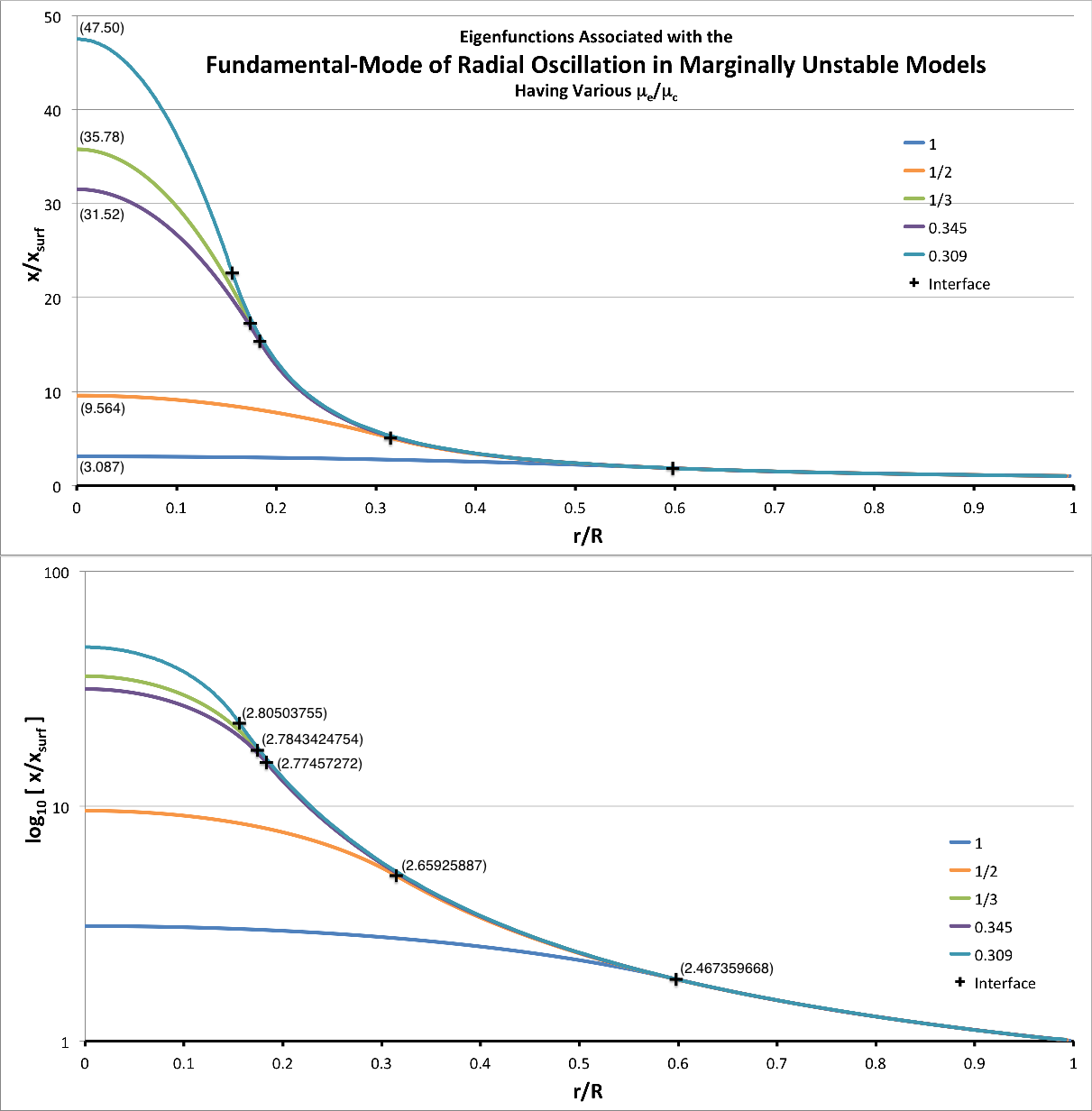
==Model 10== | |||
As we have [[User:Tohline/SSC/Structure/BiPolytropes/Analytic1_5#Murphy_and_Fiedler_.281985.29|reviewed in an accompanying discussion]], equilibrium Model 10 from [http://adsabs.harvard.edu/abs/1985PASAu...6..219M Murphy & Fiedler (1985, Proc. Astr. Soc. of Australia, 6, 219)] is defined by setting <math>~(\xi_i, m) = (2.5646, 1)</math>. Drawing directly from [[User:Tohline/SSC/Structure/BiPolytropes/Analytic1_5#Murphy_and_Fiedler_.281985.29|our reproduction of their Table 1]], we see that a few relevant structural parameters of Model 10 are, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | |||
<math>~\xi_s</math> | |||
<td align="right" | </td> | ||
<td align="center"> | |||
<math>~=</math> | |||
<td align=" | </td> | ||
<td align="left"> | |||
<math>~6.5252876</math> | |||
</td> | |||
<td align=" | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~\frac{r_i}{R} = \frac{\xi_i}{\xi_s}</math> | |||
</td> | |||
<td align="center"> | |||
<td align=" | <math>~=</math> | ||
</td> | |||
<td align="left"> | |||
<math>~0.39302482</math> | |||
<td align=" | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | |||
<math>~\frac{\rho_c}{\bar\rho} </math> | |||
</td> | |||
<td align="right" | <td align="center"> | ||
<math>~=</math> | |||
</td> | |||
<td align=" | <td align="left"> | ||
<math>~34.346</math> | |||
</td> | |||
<td align=" | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{ | <math>~\frac{M_\mathrm{env}}{M_\mathrm{tot}} </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,687: | Line 1,856: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~5.89 \times 10^{-4}</math> | ||
</td> | </td> | ||
</tr> | |||
</table> | |||
Here we list a few other model parameter values that will aid in our attempt to correctly integrate the LAWE to find various radial oscillation eigenvectors. | |||
<table border="1" cellpadding="5" align="center"> | |||
</tr> | |||
</table> | |||
<table border="1" | |||
<tr> | <tr> | ||
<td align="center" colspan="12"> | <td align="center" colspan="12"> | ||
''' | '''A Sampling of Model 10's Equilibrium Parameter Values'''<sup>†</sup> | ||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center" | <td align="center">Grid<br />Line</td> | ||
<td align="center | <td align="center"><math>~\frac{r}{R}</math></td> | ||
<td align="center | <td align="center"><math>~\xi</math></td> | ||
<td align="center | <td align="center"><math>~\eta</math></td> | ||
<td align="center | <td align="center"><math>~\Delta</math></td> | ||
<td align="center | <td align="center"><math>~\phi</math></td> | ||
<td align="center | <td align="center"><math>~- \frac{d\phi}{d\eta}</math></td> | ||
<td align="center | <td align="center"><math>~r^*</math></td> | ||
<td align="center | <td align="center"><math>~\rho^*</math></td> | ||
<td align="center" | <td align="center"><math>~P^*</math></td> | ||
<td align="center | <td align="center"><math>~M_r^*</math></td> | ||
<td align="center"><math>~g_0^*\equiv \frac{M_r^*}{(r^*)^2}</math></td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center" bgcolor="yellow">25</td> | ||
<td align=" | <td align="right">0.12093071</td> | ||
<td align="right">0.789108</td> | |||
<td align="right"> </td> | |||
<td align="right"> </td> | |||
<td align="right"> </td> | |||
<td align="right"> </td> | |||
<td align="right">0.31480842</td> | |||
<td align="right">0.89940188</td> | |||
<td align="right">0.80892374</td> | |||
<td align="right">0.122726799</td> | |||
<td align="right">1.23835945</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center" | <td align="center" bgcolor="yellow">40</td> | ||
<td align=" | <td align="right"> 0.19651241</td> | ||
<td align=" | <td align="right">1.2823</td> | ||
<td align="right"> | <td align="right"> </td> | ||
<td align="right"> | <td align="right"> </td> | ||
<td align="right"> | <td align="right"> </td> | ||
<td align=" | <td align="right"> </td> | ||
<td align=" | <td align="right"> 0.51156369</td> | ||
<td align=" | <td align="right"> 0.74761972</td> | ||
<td align=" | <td align="right"> 0.55893525</td> | ||
<td align=" | <td align="right"> 0.473819194</td> | ||
<td align=" | <td align="right"> 1.81056130</td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center" bgcolor="yellow">79</td> | ||
<td align=" | <td align="right"> 0.393025</td> | ||
<td align=" | <td align="right">2.5646</td> | ||
<td align="right"> | <td align="right"> </td> | ||
<td align="right"> | <td align="right"> </td> | ||
<td align="right"> | <td align="right"> </td> | ||
<td align="right"> | <td align="right"> </td> | ||
<td align="right"> | <td align="right"> 1.02312737</td> | ||
<td align=" | <td align="right"> 0.21270605</td> | ||
<td align=" | <td align="right"> 0.04524386</td> | ||
<td align=" | <td align="right"> 2.150231108</td> | ||
<td align=" | <td align="right"> 2.05411964</td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center" bgcolor="lightgreen">79</td> | ||
<td align=" | <td align="right"> 0.393025</td> | ||
<td align=" | <td align="right"> </td> | ||
<td align="right"> | <td align="right">1.4806725</td> | ||
<td align="right"> | <td align="right">2.6746514</td> | ||
<td align="right"> | <td align="right">1.000000</td> | ||
<td align="right"> | <td align="right">1.112155</td> | ||
<td align="right"> | <td align="right"> 1.02312737</td> | ||
<td align="right">0. | <td align="right"> 0.21270605</td> | ||
<td align="right">0. | <td align="right"> 0.04524386</td> | ||
<td align=" | <td align="right"> 2.15023111</td> | ||
<td align=" | <td align="right"> 2.0541196</td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center" bgcolor="lightgreen">100</td> | ||
<td align=" | <td align="right"> 0.49883919</td> | ||
<td align=" | <td align="right"> </td> | ||
<td align="right"> | <td align="right">1.8793151</td> | ||
<td align="right"> | <td align="right">2.7938569</td> | ||
<td align="right"> | <td align="right">0.6505914</td> | ||
<td align="right">0. | <td align="right">0.69070815</td> | ||
<td align="right"> | <td align="right"> 1.2985847</td> | ||
<td align="right">0. | <td align="right"> 0.0247926</td> | ||
<td align="right">0. | <td align="right"> 0.0034309</td> | ||
<td align=" | <td align="right"> 2.15127319</td> | ||
<td align=" | <td align="right"> 1.2757189</td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center" | <td align="center" bgcolor="lightgreen">150</td> | ||
</ | <td align="right"> 0.7507782</td> | ||
</ | <td align="right"> </td> | ||
<td align="right">2.8284641</td> | |||
<td align="right">2.9982701</td> | |||
< | <td align="right">0.2149684</td> | ||
< | <td align="right">0.30495637</td> | ||
<td align=" | <td align="right"> 1.95443562</td> | ||
<td align="right"> 9.7646E-05</td> | |||
<td align="right"> 4.4649E-06</td> | |||
</td> | <td align="right"> 2.15149752</td> | ||
<td align="right">0.563246</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center" bgcolor="lightgreen">199</td> | ||
<td align=" | <td align="right"> 0.9976784</td> | ||
<td align=" | <td align="right"> </td> | ||
<td align=" | <td align="right">3.7586302</td> | ||
<td align=" | <td align="right">3.1404305</td> | ||
<td align=" | <td align="right">0.00150695</td> | ||
<td align=" | <td align="right">0.17269514</td> | ||
<td align="right">2.59716948</td> | |||
<td align="right"> 1.653E-15</td> | |||
<td align="right"> 5.2984E-19</td> | |||
<td align="right"> 2.15149876</td> | |||
<td align="right">0.31896316</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="left" colspan="12"> | ||
<sup>†</sup>Our chosen (uniform) grid spacing is, | |||
<div align="center"> | |||
<math>~\frac{\delta r}{R} = \frac{1}{78}\biggl( \frac{r_i}{R} \biggr) \approx 0.00503878 \, ;</math> | |||
</div> | |||
as a result, the center is at zone 1, the interface is at grid line 79, and the surface is just beyond grid line 199. | |||
</td> | |||
</tr> | </tr> | ||
</table> | |||
==Eigenvectors== | |||
We now have the tools in hand to identify the eigenvectors — that is, various radial eigenfunctions and the corresponding eigenfrequency for each — associated with various modes of oscillation in <math>~(n_c, n_e) = (5,1)</math> bipolytropes. Which models should we examine? | |||
In our [[User:Tohline/SSC/Stability/MurphyFiedler85#Review_of_the_BiPolytrope_Stability_Analysis_by_Murphy_.26_Fiedler_.281985b.29|accompanying review of the bipolytrope stability analysis presented by Murphy & Fiedler (1983b)]], our primary objective was to show that we were able to match their results quantitatively. We therefore set <math>~\mu_e/\mu_c</math> = 1 — the only <math>~\mu</math>-ratio that they considered — and picked values of the core-envelope interface radius, <math>~\xi_i</math>, that were listed among their set of chosen models. For a fixed value of <math>~\xi_i</math>, we integrated the relevant LAWE from the center toward the surface for many different eigenfrequency <math>~(\sigma_c^2)</math> ''guesses'' until an eigenfunction was found whose behavior at the surface matched with high precision the physically justified surface boundary condition. | |||
Here we have chosen to focus on models that reside along five of the analytically defined equilibrium sequences depicted above in Figure 2 — specifically, the sequences for which <math>~\mu_e/\mu_c</math> = 1, ½, 0.345, ⅓, and 0.309 — and to examine, first, whether any model along each sequence marks a transition from dynamically stable to dynamically unstable configurations. We accomplished this by setting <math>~\sigma_c^2</math> = 0, then integrating the relevant LAWE from the center toward the surface for many different ''guesses'' of the core-envelope interface radius until an eigenfunction with no radial nodes — ''i.e.,'' an eigenfunction associated with the fundamental mode of radial oscillation — was found whose behavior at the surface matched with high precision the physically desired surface boundary condition. We were successful in this endeavor. A marginally unstable model was identified on each of the five separate equilibrium sequences. | |||
The following table summarizes some of the equilibrium properties of these five models. For example, the second column of the table gives the value of the core-envelope interface radius, <math>~\xi_i</math>, associated with each marginally unstable model. The table also lists: the value of <math>~q</math>, <math>~\nu</math>, and the central-to-mean density associated with each model; and in each case the dimensionless thermal energy <math>~(S^*)</math> and dimensionless gravitational potential energy <math>~(W^*)</math> associated, separately, with the core and the envelope. Note that, once the pair of parameters, <math>~(\mu_e/\mu_c, \xi_i)</math>, has been specified, we can legitimately assign high-precision values to all of the other model parameters because they are [[User:Tohline/SSC/Structure/BiPolytropes/Analytic5_1#Parameter_Values|analytically prescribed]]. | |||
<table border="1" cellpadding="8" align="center"> | |||
<tr> | <tr> | ||
< | <th align="center" colspan="9"> | ||
Properties of Marginally Unstable Bipolytropes Having<br /><br /><math>~(n_c, n_e) = (5, 1)</math> and <math>~(\gamma_c, \gamma_e) = (\tfrac{6}{5}, 2)</math><br /><br />Determined from Integration of the LAWE | |||
</th> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center" | <td align="center"><math>~\frac{\mu_e}{\mu_c}</math></td> | ||
<td align="center" | <td align="center"><math>~\xi_i</math></td> | ||
<td align=" | <td align="center"><math>~q \equiv \frac{r_\mathrm{core}}{R_\mathrm{surf}}</math></td> | ||
<td align=" | <td align="center"><math>~\nu \equiv \frac{M_\mathrm{core}}{M_\mathrm{tot}}</math></td> | ||
<td align=" | <td align="center"><math>~\frac{\rho_c}{\bar\rho}</math></td> | ||
<td align=" | <td align="center"><math>~S^*_\mathrm{env}</math></td> | ||
<td align=" | <td align="center"><math>~W^*_\mathrm{env}</math></td> | ||
<td align="center"><math>~S^*_\mathrm{core}</math></td> | |||
<td align="center"><math>~W^*_\mathrm{core}</math></td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center">1</td> | ||
<td align="left">0. | <td align="left">2.467359668</td> | ||
<td align=" | <td align="center">0.597684036</td> | ||
<td align=" | <td align="center">0.692367564</td> | ||
<td align=" | <td align="center">17.09749847</td> | ||
<td align=" | <td align="center">4.518031091</td> | ||
<td align="center">-6.79580606</td> | |||
<td align="center">0.857904827</td> | |||
<td align="center">-3.956065776</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center"><math>~\tfrac{1}{2}</math></td> | ||
<td align="left">2.65925887</td> | |||
</td> | <td align="center">0.314759926</td> | ||
<td align="center">0.481811565</td> | |||
<td align="center">95.04044773</td> | |||
<td align="center">4.759771212</td> | |||
<td align="center">-7.459080087</td> | |||
<td align="center">3.20977926</td> | |||
<td align="center">-8.480020858</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="center"> | <td align="center">0.345</td> | ||
<td align="left">2.77457272408</td> | |||
</td> | <td align="center">0.183201946</td> | ||
</ | <td align="center">0.25725514</td> | ||
</ | <td align="center">281.7482802</td> | ||
<td align="center">4.887554727</td> | |||
<td align="center">-7.822410223</td> | |||
<td align="center">10.22665208</td> | |||
< | <td align="center">-22.40600339</td> | ||
</tr> | |||
<tr> | <tr> | ||
<td align="center"> | <td align="center"><math>~\tfrac{1}{3}</math></td> | ||
<td align="left">2.7843424754</td> | |||
</td> | <td align="center">0.17412463</td> | ||
<td align="center"> | <td align="center">0.237677946</td> | ||
<td align="center">305.4881577</td> | |||
</td> | <td align="center">4.897826446</td> | ||
<td align="center">-7.852004624</td> | |||
<td align="center">11.6114224</td> | |||
<td align="center">-25.16649306</td> | |||
</tr> | </tr> | ||
</ | <tr> | ||
<td align="center">0.309</td> | |||
= | <td align="left">2.8050375512</td> | ||
== | <td align="center">0.156021514</td> | ||
<td align="center">0.197918988</td> | |||
< | <td align="center">359.3276918</td> | ||
<table border="0" cellpadding="5" align="center"> | <td align="center">4.91930991</td> | ||
<td align="center">-7.914090174</td> | |||
<td align="center">15.49005222</td> | |||
<td align="center">-32.90463409</td> | |||
</tr> | |||
</table> | |||
<!-- | |||
Keep in mind that, for all models, we ''expect'' that, at the surface, the logarithmic derivative of each proper eigenfunction will be, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\frac{d\ln x}{d\ln r^*}\biggr|_\mathrm{surf}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,883: | Line 2,089: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~\frac{\Omega^2}{\gamma} - \alpha \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Also, keep in mind that, for Model 10 <math>~(\xi_i = 2.5646)</math>: | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{r_i}{R}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 1,895: | Line 2,105: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math> | <math>~0.39302482</math> | ||
~ | |||
</math> | |||
</td> | </td> | ||
< | <td align="center"> , </td> | ||
< | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{\rho_c}{\bar\rho}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~34.3460405</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
--> | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr> | <tr> | ||
<td align=" | <td align="center" colspan="12"> | ||
'''Our Determinations for Marginally Unstable Model Having <math>~\mu_e/\mu_c = 1</math>'''<br /> <br /> | |||
<math>~[ ~\xi_i = 2.467359668 ~]</math> | |||
<math>~\ | |||
<math>~\ | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center" rowspan="2">Mode</td> | ||
<math>~\ | <td align="center" rowspan="2"><math>~\sigma_c^2</math></td> | ||
</td> | <td align="center" rowspan="2"><math>~\Omega^2 \equiv \frac{\sigma_c^2}{2} \biggl( \frac{\rho_c}{\bar\rho}\biggr)</math></td> | ||
<td align="center"> | <td align="center" rowspan="2"><math>~x_\mathrm{surf}</math></td> | ||
<math>~\ | <td align="center" colspan="2"><math>~\frac{d\ln x}{d\ln r^*}\biggr|_\mathrm{surf}</math></td> | ||
</td> | <td align="center" rowspan="2"><math>~\frac{r}{R}\biggr|_1</math></td> | ||
<td align=" | <td align="center" rowspan="2"><math>~1 - \frac{M_r}{M_\mathrm{tot}}\biggr|_1</math></td> | ||
<math>~\frac{\ | <td align="center" rowspan="2"><math>~\frac{r}{R}\biggr|_2</math></td> | ||
</td> | <td align="center" rowspan="2"><math>~1 - \frac{M_r}{M_\mathrm{tot}}\biggr|_2</math></td> | ||
<td align="center" rowspan="2"><math>~\frac{r}{R}\biggr|_3</math></td> | |||
<td align="center" rowspan="2"><math>~1 - \frac{M_r}{M_\mathrm{tot}}\biggr|_3</math></td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center">''expected''</td> | ||
<td align="center">measured</td> | |||
<td align="center"> | |||
</tr> | </tr> | ||
< | <tr> | ||
<td align="center">1<br /><font size="-1">(Fundamental)</font></td> | |||
<td align="right">0.00</td> | |||
< | <td align="right">0.00</td> | ||
<td align="right">+0.32394</td> | |||
< | <td align="right">-1</td> | ||
<td align="right"> | <td align="right">-0.999999371</td> | ||
< | <td align="center">n/a</td> | ||
</td> | <td align="center">n/a</td> | ||
<td align="center"> | <td align="center">n/a</td> | ||
< | <td align="center">n/a</td> | ||
</td> | <td align="center">n/a</td> | ||
<td align="center">n/a</td> | |||
< | |||
</ | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="center">2</td> | ||
< | <td align="right">1.09165937</td> | ||
</td> | <td align="right">9.33232221</td> | ||
<td align=" | <td align="right">- 1.8067</td> | ||
< | <td align="right">3.666161103</td> | ||
</td> | <td align="right">3.66616128</td> | ||
<td align="right">0.5724</td> | |||
< | <td align="right">0.340</td> | ||
<td align="center">n/a</td> | |||
<td align="center">n/a</td> | |||
<td align="center">n/a</td> | |||
<td align="center">n/a</td> | |||
</ | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="center">3</td> | ||
< | <td align="right">2.8214727</td> | ||
</td> | <td align="right">24.12006</td> | ||
<td align=" | <td align="right">+1.8212</td> | ||
<td align="right">11.060031</td> | |||
<td align="right">11.060042</td> | |||
<td align="right">0.447</td> | |||
<td align="right">0.539</td> | |||
<td align=" | <td align="right">0.842</td> | ||
< | <td align="right">0.0619</td> | ||
</td> | <td align="center">n/a</td> | ||
<td align="center">n/a</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="center">4</td> | ||
< | <td align="right">4.87854411</td> | ||
</td> | <td align="right">41.7054502</td> | ||
<td align=" | <td align="right">-2.032</td> | ||
< | <td align="right">19.8527251</td> | ||
</td> | <td align="right">19.8527251</td> | ||
<td align="right">0.3803</td> | |||
< | <td align="right">0.6174</td> | ||
<td align="right">0.671</td> | |||
<td align="right">0.2246</td> | |||
</ | <td align="center">0.907</td> | ||
</td> | <td align="center">0.0227</td> | ||
</tr> | |||
<tr> | |||
<td align="center" colspan="12">[[File:Mu100Eigenfunctions.png|1000px|Our determination of multiple eigenvectors for mu_ratio = 1]]</td> | |||
</tr> | </tr> | ||
</table> | |||
<!-- | |||
For Model 17 <math>~(\xi_i = 3.0713)</math>: | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{r_i}{R}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math> | <math>~0.93276717</math> | ||
</math> | |||
</td> | </td> | ||
< | <td align="center"> , </td> | ||
< | |||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~\frac{\rho_c}{\bar\rho}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 2,063: | Line 2,229: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~3.79693903</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
--> | |||
<table border="1" align="center" cellpadding="8"> | |||
<tr> | <tr> | ||
<td align=" | <td align="center" colspan="12"> | ||
<math>~\ | '''Our Determinations for Marginally Unstable Model Having <math>~\mu_e/\mu_c = \tfrac{1}{2}</math>'''<br /> <br /> | ||
<math>~[ ~\xi_i = 2.65925887 ~]</math> | |||
<math>~ | |||
\ | |||
</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center" rowspan="2">Mode</td> | ||
<td align="center" rowspan="2"><math>~\sigma_c^2</math></td> | |||
<td align="center" rowspan="2"><math>~\Omega^2 \equiv \frac{\sigma_c^2}{2} \biggl( \frac{\rho_c}{\bar\rho}\biggr)</math></td> | |||
<td align="center"> | <td align="center" rowspan="2"><math>~x_\mathrm{surf}</math></td> | ||
<math>~ | <td align="center" colspan="2"><math>~\frac{d\ln x}{d\ln r^*}\biggr|_\mathrm{surf}</math></td> | ||
<td align="center" rowspan="2"><math>~\frac{r}{R}\biggr|_1</math></td> | |||
<td align=" | <td align="center" rowspan="2"><math>~1 - \frac{M_r}{M_\mathrm{tot}}\biggr|_1</math></td> | ||
<math> | <td align="center" rowspan="2"><math>~\frac{r}{R}\biggr|_2</math></td> | ||
\frac{2}{ | <td align="center" rowspan="2"><math>~1 - \frac{M_r}{M_\mathrm{tot}}\biggr|_2</math></td> | ||
\ | <td align="center" rowspan="2"><math>~\frac{r}{R}\biggr|_3</math></td> | ||
<td align="center" rowspan="2"><math>~1 - \frac{M_r}{M_\mathrm{tot}}\biggr|_3</math></td> | |||
</tr> | |||
</ | <tr> | ||
</td> | <td align="center">''expected''</td> | ||
<td align="center">measured</td> | |||
</tr> | |||
<tr> | |||
<td align="center">1<br /><font size="-1">(Fundamental)</font></td> | |||
<td align="left">0.00</td> | |||
<td align="left">0.00</td> | |||
<td align="right">+0.1046</td> | |||
<td align="right">-1</td> | |||
<td align="right">-1.000026</td> | |||
<td align="center">n/a</td> | |||
<td align="center">n/a</td> | |||
<td align="center">n/a</td> | |||
<td align="center">n/a</td> | |||
<td align="center">n/a</td> | |||
<td align="center">n/a</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center">2</td> | ||
< | <td align="left">0.157237193</td> | ||
</td> | <td align="left">7.47194659</td> | ||
<td align=" | <td align="right">- 1.325</td> | ||
< | <td align="right">2.73597330</td> | ||
</td> | <td align="right">2.73597332</td> | ||
<td align=" | <td align="right">0.4324</td> | ||
<td align=" | <td align="right">0.4248</td> | ||
< | <td align="center">n/a</td> | ||
<td align="center">n/a</td> | |||
<td align="center">n/a</td> | |||
</ | <td align="center">n/a</td> | ||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center">3</td> | ||
<td align="left">0.485458532</td> | |||
</td> | <td align="left">23.0690981</td> | ||
<td align=" | <td align="right">+3.345</td> | ||
< | <td align="right">10.53454906</td> | ||
</td> | <td align="right">10.53454907</td> | ||
<td align=" | <td align="right">0.3314</td> | ||
<td align=" | <td align="right">0.5065</td> | ||
< | <td align="right">0.8291</td> | ||
<td align="right">0.0608</td> | |||
<td align="center">n/a</td> | |||
<td align="center">n/a</td> | |||
</ | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center">4</td> | ||
< | <td align="left">1.015635277</td> | ||
</td> | <td align="left">48.2632157</td> | ||
<td align=" | <td align="right">-4.224</td> | ||
< | <td align="right">23.13160787</td> | ||
</td> | <td align="right">23.13160788</td> | ||
<td align=" | <td align="right">0.2830</td> | ||
< | <td align="right">0.5651</td> | ||
<td align="right">0.6995</td> | |||
<td align="right">0.1657</td> | |||
<td align="center">0.9100</td> | |||
<td align="center">0.0182</td> | |||
< | </tr> | ||
</td> | <tr> | ||
<td align="center" colspan="12">[[File:Mu050Eigenfunctions.png|1000px|Our determination of multiple eigenvectors for mu_ratio = 1/2]]</td> | |||
</tr> | </tr> | ||
</table> | </table> | ||
<table border="1" align="center" cellpadding="8" > | |||
<tr> | <tr> | ||
<td align=" | <td align="center" colspan="7"> | ||
'''Numerical Values for Some Selected <math>~(n_c, n_e) = (1, 5)</math> Bipolytropes'''<br /> | |||
[to be compared with Table 1 of [http://adsabs.harvard.edu/abs/1985PASAu...6..219M Murphy & Fiedler (1985)]] | |||
<math>~ | |||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center">MODEL</td> | ||
<math>~\ | <td align="center">Source</td> | ||
</td> | <td align="center"><math>~\frac{r_i}{R}</math></td> | ||
<td align="center"> | <td align="center"><math>~\Omega_0^2</math></td> | ||
<math>~\ | <td align="center"><math>~\Omega_1^2</math></td> | ||
<td align="center"><math>~\frac{r}{R}\biggr|_1</math></td> | |||
<td align=" | <td align="center"><math>~1-\frac{M_r}{M_\mathrm{tot}}\biggr|_1</math></td> | ||
<math>~ | </tr> | ||
<tr> | |||
<td align="center" rowspan="2">10</td> | |||
<td align="center" bgcolor="pink">MF85</td> | |||
<td align="left">0.393</td> | |||
<td align="left">15.9298</td> | |||
</ | <td align="left">21.2310</td> | ||
</td> | <td align="left">0.573</td> | ||
<td align="left">1.00E-03</td> | |||
</tr> | |||
<tr> | |||
<td align="center">Here</td> | |||
<td align="right">0.39302</td> | |||
<td align="right">15.93881161</td> | |||
<td align="right">21.24571822</td> | |||
<td align="right">0.5724</td> | |||
<td align="left">3.05E-05</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align=" | <td align="center" rowspan="2">17</td> | ||
< | <td align="center" bgcolor="pink">MF85</td> | ||
</td> | <td align="left">0.933</td> | ||
<td align=" | <td align="left">2.1827</td> | ||
< | <td align="left">13.9351</td> | ||
</td> | <td align="left">0.722</td> | ||
<td align="left"> | <td align="left">0.232</td> | ||
< | </tr> | ||
<tr> | |||
<td align="center">Here</td> | |||
<td align="left">0.93277</td> | |||
<td align="left">2.182932207</td> | |||
</ | <td align="left">13.93880866</td> | ||
</td> | <td align="left">0.7215</td> | ||
<td align="left">0.24006</td> | |||
</tr> | </tr> | ||
</table> | |||
==Summary== | |||
<table border="0" align="center" cellpadding="8"> | |||
<tr> | <tr> | ||
<td align=" | <td align="center"> | ||
[[File:CompositeAlabeled.png|700px|dynamical stability in qNu plane]] | |||
</td> | </td> | ||
</tr> | |||
<tr> | |||
<td align="center"> | <td align="center"> | ||
[[File:CompositeBlabeled.png|700px|dynamical stability in qNu plane]] | |||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
<table border="0" align="center" cellpadding="8"> | |||
<tr> | <tr> | ||
<td align=" | <td align="center"> | ||
[[File:Mode0EigenfunctionsCombinedLabel.png|600px|Eigenfunctions for Marginally Unstable Models]] | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
[[File:CompositeEigenfunctions.png|400px|Eigenfunctioins for multiple modes in three separate models]] | |||
</td> | </td> | ||
</tr> | </tr> | ||
Revision as of 21:55, 19 December 2018
Marginally Unstable (nc,ne) = (5,1) Bipolytropes

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Overview
| Figure 1: Equilibrium Sequences of Pressure-Truncated Polytropes |
|---|
We expect the content of this chapter — which examines the relative stability of bipolytropes — to parallel in many ways the content of an accompanying chapter in which we have successfully analyzed the relative stability of pressure-truncated polytopes. Figure 1, shown here on the right, has been copied from a closely related discussion. The curves show the mass-radius relationship for pressure-truncated model sequences having a variety of polytropic indexes, as labeled, over the range <math>1 \le n \le 6</math>. (Another version of this figure includes the isothermal sequence.) On each sequence for which <math>~n \ge 3</math>, the green filled circle identifies the model with the largest mass. We have shown analytically that the oscillation frequency of the fundamental-mode of radial oscillation is precisely zero† for each one of these maximum-mass models. As a consequence, we know that each green circular marker identifies the point along its associated sequence that separates dynamically stable (larger radii) from dynamically unstable (smaller radii) models.
†In each case, the fundamental-mode oscillation frequency is precisely zero if, and only if, the adiabatic index governing expansions/contractions is related to the underlying structural polytropic index via the relation, <math>~\gamma_g = (n + 1)/n</math>, and if a constant surface-pressure boundary condition is imposed.
In another accompanying chapter, we have used purely analytic techniques to construct equilibrium sequences of spherically symmetric bipolytropes that have, <math>~(n_c,n_e) = (5,1)</math>. For a given choice of <math>~\mu_e/\mu_c</math> — the ratio of the mean-molecular weight of envelope material to the mean-molecular weight of material in the core — a physically relevant sequence of models can be constructed by steadily increasing the value of the dimensionless radius at the core/envelope interface, <math>~\xi_i</math>, from zero to infinity. Figure 2, whose content is essentially the same as Figure 1 of this separate chapter, shows how the fractional core mass, <math>\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math>, varies with the fractional core radius, <math>q \equiv r_\mathrm{core}/R</math>, along sequences having seven different values of <math>~\mu_e/\mu_c</math>, as labeled: 1 (black), ½ (dark blue), 0.345 (brown), ⅓ (dark green), 0.316943 (purple), 0.309 (orange), and ¼ (light blue).
When modeling bipolytropes, the default expectation is that an increase in <math>~\xi_i</math> along a given sequence will correspond to an increase in the relative size — both the radius and the mass — of the core. This expectation is realized along the Figure 2 sequences that have the largest mean-molecular weight ratios: <math>~\mu_e/\mu_c</math> = 1 and ½. But the behavior is different along the other five illustrated sequences. For sufficiently large <math>~\xi_i</math>, the relative radius of the core begins to decrease; along each sequence, a solid purple circular marker identifies the location of this turning point in radius. Furthermore, along sequences for which <math>~\mu_e/\mu_c < \tfrac{1}{3}</math>, eventually the fractional mass of the core reaches a maximum and, thereafter, decreases even as the value of <math>~\xi_i</math> continues to increase; a solid green circular marker identifies the location of this maximum mass turning point along each of these sequences. (Additional properties of these equilibrium sequences are discussed in yet another accompanying chapter.)
The principal question is: Along bipolytropic sequences, are maximum-mass models associated with the onset of dynamical instabilities?
Planned Approach
| Figure 2: Equilibrium Sequences of Bipolytropes with <math>~(n_c,n_e) = (5,1)</math> and Various <math>~\mu_e/\mu_c</math> |
|
|---|---|
Ideally we would like to answer the just-stated "principal question" using purely analytic techniques. But, to date, we have been unable to fully address the relevant issues analytically, even in what would be expected to be the simplest case: bipolytropic models that have <math>~(n_c,n_e) = (0, 0)</math>. Instead, we will streamline the investigation a bit and proceed — at least initially — using a blend of techniques. We will investigate the relative stability of bipolytropic models having <math>~(n_c,n_e) = (5,1) </math> whose equilibrium structures are completely defined analytically; then the eigenvectors describing radial modes of oscillation will be determined, one at a time, by solving the relevant LAWE(s) numerically. We are optimistic that this can be successfully accomplished because we have had experience numerically integrating the LAWE that governs the oscillation of:
- Isolated n = 3 polytropes — including a quantitative comparison against Schwarzschild's (1941) published work;
- Pressure-truncated isothermal spheres — including a quantitative comparison against the published analysis of Taff & Van Horn (1974); and
- Pressure-truncated n = 5 polytropes.
A key reference throughout this investigation will be the paper by J. O. Murphy & R. Fiedler (1985b, Proc. Astr. Soc. of Australia, 6, 222). They studied Radial Pulsations and Vibrational Stability of a Sequence of Two Zone Polytropic Stellar Models. Specifically, their underlying equilibrium models were bipolytropes that have <math>~(n_c,n_e) = (1, 5)</math>. In an accompanying chapter, we describe in detail how Murphy & Fiedler obtained these equilibrium bipolytropic structures and detail some of their equilibrium properties.
Here are the steps we initially plan to take:
- Governing LAWEs:
- Identify the relevant LAWEs that govern the behavior of radial oscillations in the <math>~n_c = 5</math> core and, separately, in the <math>~n_e = 1</math> envelope. Check these LAWE specifications against the published work of Murphy & Fiedler (1985b).
- Determine the matching conditions that must be satisfied across the core/envelope interface. Be sure to take into account the critical interface jump conditions spelled out by P. Ledoux & Th. Walraven (1958), as we have already discussed in the context of an analysis of radial oscillations in zero-zero bipolytropes.
- Determine what surface boundary condition should be imposed on physically relevant LAWE solutions, i.e., on the physically relevant radial-oscillation eigenvectors.
- Initial Analysis:
- Choose a maximum-mass model along the bipolytropic sequence that has, for example, <math>~\mu_e/\mu_c = 1/4</math>. Hopefully, we will be able to identify precisely (analytically) where this maximum-mass model lies along the sequence. Yes! Our earlier analysis does provide an analytic prescription of the model that sits at the maximum-mass location along the chosen sequence.
- Solve the relevant eigenvalue problem for this specific model, initially for <math>~(\gamma_c, \gamma_e) = (6/5, 2)</math> and initially for the fundamental mode of oscillation.
Virial Analysis
Various Energy Expressions
Drawing from an accompanying detailed discussion, we have,
|
<math>~\mathfrak{G}</math> |
<math>~=</math> |
<math>~W_\mathrm{grav}\biggr|_\mathrm{core} + \mathfrak{S}_A\biggr|_\mathrm{core} + W_\mathrm{grav}\biggr|_\mathrm{env} + \mathfrak{S}_A\biggr|_\mathrm{env} </math> |
|
|
<math>~=</math> |
<math> ~W_\mathrm{grav}\biggr|_\mathrm{core} + \biggl[ \frac{2}{3(\gamma_c - 1)} \biggr] S_\mathrm{core} + W_\mathrm{grav}\biggr|_\mathrm{env} + \biggl[ \frac{2}{3(\gamma_e - 1)} \biggr] S_\mathrm{env} \, . </math> |
Recognizing that,
|
<math>~q</math> |
<math>~\equiv</math> |
<math>~\frac{r_i}{R} = \frac{\eta_i}{\eta_s} \, ,</math> |
|
<math>~\nu</math> |
<math>~\equiv</math> |
<math>~\frac{M_\mathrm{core}}{M_\mathrm{tot}} \, ,</math> |
|
<math>~\ell</math> |
<math>~\equiv</math> |
<math>~\frac{\xi}{\sqrt{3}} \, ,</math> |
|
<math>~\chi_\mathrm{eq} </math> |
<math>~=</math> |
<math>~\biggl( \frac{\pi}{2^3 \cdot 3^6}\biggr)^{1 / 2} \biggl( \frac{\nu}{q^3} \biggr)^{2} \biggl( 1 + \ell_i^2 \biggr)^{3} \biggl( \frac{q}{\ell_i}\biggr)^{5 } \, , </math> |
we have,
|
<math>~- \chi \biggl[ \frac{W_\mathrm{grav}}{E_\mathrm{norm}} \biggr]_\mathrm{core}</math> |
<math>~=</math> |
<math> \biggl[\biggl(\frac{3}{2^4}\biggr) \biggl( \frac{q}{\ell_i}\biggr)^{5}\biggl(\frac{\nu}{q^3} \biggr)^2 \biggl( 1 + \ell_i^2 \biggr)^{3} \biggr]_\mathrm{eq} \biggl[ \ell_i (\ell_i^4 - \frac{8}{3}\ell_i^2 - 1) (\ell_i^2 +1)^{-3} + \tan^{-1}\ell_i \biggr] </math> |
|
<math>~\Rightarrow ~~~ \biggl[ \frac{W_\mathrm{grav}}{E_\mathrm{norm}} \biggr]_\mathrm{core}</math> |
<math>~=</math> |
<math>- \frac{\chi_\mathrm{eq}}{\chi} \biggl( \frac{3^8}{2^5 \pi}\biggr)^{1 / 2} \biggl[ \ell_i (\ell_i^4 - \frac{8}{3}\ell_i^2 - 1) (\ell_i^2 +1)^{-3} + \tan^{-1}\ell_i \biggr] \, . </math> |
Next, given that,
|
<math>~b_\eta = \eta_s</math> |
and |
<math>~b_\eta q = \eta_i = 3\biggl( \frac{\mu_e}{\mu_c} \biggr) \ell_i (1 + \ell_i^2)^{-1} \, ,</math> |
we have,
|
<math>~\biggl[ \frac{W_\mathrm{grav}}{E_\mathrm{norm}} \biggr]_\mathrm{env}</math> |
<math>~=</math> |
<math> - \frac{\chi_\mathrm{eq}}{\chi} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \biggl( \frac{1}{2^3\pi} \biggr)^{1/2} A^2 \biggl[6 b_\eta x - 3\sin[2(b_\eta x-B)] - 4b_\eta x \sin^2(b_\eta x - B) \biggr]_q^1 </math> |
|
|
<math>~=</math> |
<math> - \frac{\chi_\mathrm{eq}}{\chi} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \biggl( \frac{1}{2^3\pi} \biggr)^{1/2} A^2 \biggl\{ \biggl[ 6 \eta_s - 3\sin[2(\eta_s -B)] - 4\eta_s \sin^2(\eta_s - B) \biggr] - \biggl[ 6 \eta_i - 3\sin[2(\eta_i -B)] - 4\eta_i \sin^2(\eta_i - B) \biggr] \biggr\} \, . </math> |
Also, given that,
|
<math>~q a_\xi^{1 / 2}</math> |
<math>~=</math> |
<math>~\frac{\xi_i}{\sqrt{3}} \, ,</math> |
we have,
|
<math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{core}</math> |
<math>~=</math> |
<math> \frac{2}{3({\gamma_c}-1)} \biggl( \frac{\chi}{\chi_\mathrm{eq}} \biggr)^{3-3\gamma_c} \biggl\{\biggl( \frac{3^8}{2^7\pi} \biggr)^{1/2} \biggl[ \tan^{-1}[a_\xi^{1/2}q] - a_\xi^{1/2}q ~\frac{(1 - a_\xi q^2)}{(1 + a_\xi q^2)^2} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math> \frac{2}{3({\gamma_c}-1)} \biggl( \frac{\chi}{\chi_\mathrm{eq}} \biggr)^{3-3\gamma_c} \biggl\{\biggl( \frac{3^8}{2^7\pi} \biggr)^{1/2} \biggl[ \tan^{-1}\biggl( \frac{\xi_i}{\sqrt{3}}\biggr) - \biggl( \frac{\xi_i}{\sqrt{3}}\biggr)\frac{(1 - \xi_i^2/3)}{(1 + \xi_i^2/3)^2} \biggr] \biggr\} </math> |
Finally, then, we can write,
|
<math>~\biggl( \frac{\mathfrak{S}_A}{E_\mathrm{norm}} \biggr)_\mathrm{env}</math> |
<math>~=</math> |
<math> \frac{2}{3({\gamma_e}-1)} \biggl( \frac{\chi}{\chi_\mathrm{eq}} \biggr)^{3-3\gamma_e} \biggl\{ \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} A^2 \biggl( \frac{3^2}{2^5\pi} \biggr)^{1/2} \biggl[ 2b_\eta x -\sin[2(b_\eta x - B)] \biggr]_q^1 \biggr\} </math> |
|
|
|
<math>~=</math> |
<math> \frac{2}{3({\gamma_e}-1)} \biggl( \frac{\chi}{\chi_\mathrm{eq}} \biggr)^{3-3\gamma_e} \bigg( \frac{\mu_e}{\mu_c} \biggr)^{-3} A^2 \biggl( \frac{3^2}{2^5\pi} \biggr)^{1/2} \biggl\{ \biggl[ 2\eta_s -\sin[2(\eta_s - B)] \biggr] - \biggl[ 2\eta_i -\sin[2(\eta_i - B)] \biggr] \biggr\} \ . </math> |
Free Energy and Its Derivatives
We can now rewrite the free-energy expression in the form,
|
<math>~\mathfrak{g} \equiv \frac{\mathfrak{G}}{E_\mathrm{norm}}</math> |
<math>~=</math> |
<math> ~-\biggl(\frac{\chi_\mathrm{eq}}{\chi}\biggr)\mathfrak{w} + \biggl[ \frac{2}{3(\gamma_c - 1)} \biggr] \biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{3 - 3\gamma_c}\mathfrak{s}_\mathrm{core} + \biggl[ \frac{2}{3(\gamma_e - 1)} \biggr] \biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{3 - 3\gamma_e}\mathfrak{s}_\mathrm{env} \, , </math> |
where,
|
<math>~\mathfrak{s}_\mathrm{core}</math> |
<math>~\equiv</math> |
<math>~ \biggl( \frac{3^8}{2^7\pi} \biggr)^{1/2} \biggl[ \tan^{-1}\biggl( \frac{\xi_i}{\sqrt{3}}\biggr) - \biggl( \frac{\xi_i}{\sqrt{3}}\biggr)\frac{(1 - \xi_i^2/3)}{(1 + \xi_i^2/3)^2} \biggr]\, , </math> |
|
<math>~\mathfrak{s}_\mathrm{env}</math> |
<math>~\equiv</math> |
<math>~ \bigg( \frac{\mu_e}{\mu_c} \biggr)^{-3} A^2 \biggl( \frac{3^2}{2^5\pi} \biggr)^{1/2} \biggl\{ \biggl[ 2\eta_s -\sin[2(\eta_s - B)] \biggr] - \biggl[ 2\eta_i -\sin[2(\eta_i - B)] \biggr] \biggr\} \, , </math> |
|
<math>~\mathfrak{w}</math> |
<math>~\equiv</math> |
<math>~ \biggl( \frac{3^8}{2^5 \pi}\biggr)^{1 / 2} \biggl[ \ell_i (\ell_i^4 - \frac{8}{3}\ell_i^2 - 1) (\ell_i^2 +1)^{-3} + \tan^{-1}\ell_i \biggr] </math> |
|
|
|
<math>~ +~ \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-3} \biggl( \frac{1}{2^3\pi} \biggr)^{1/2} A^2 \biggl\{ \biggl[ 6 \eta_s - 3\sin[2(\eta_s -B)] - 4\eta_s \sin^2(\eta_s - B) \biggr] - \biggl[ 6 \eta_i - 3\sin[2(\eta_i -B)] - 4\eta_i \sin^2(\eta_i - B) \biggr] \biggr\} \, . </math> |
The first derivative is,
|
<math>~\frac{d\mathfrak{g}}{d\chi} </math> |
<math>~=</math> |
<math> +~\biggl(\frac{\chi_\mathrm{eq}}{\chi^2}\biggr)\mathfrak{w} ~-~\frac{2}{\chi_\mathrm{eq}} \biggl[\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{2 - 3\gamma_c}\mathfrak{s}_\mathrm{core} ~+~\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{2 - 3\gamma_e}\mathfrak{s}_\mathrm{env} \biggr] \, . </math> |
And the second derivative is,
|
<math>~\frac{d^2\mathfrak{g}}{d\chi^2} </math> |
<math>~=</math> |
<math> -~2\biggl(\frac{\chi_\mathrm{eq}}{\chi^3}\biggr)\mathfrak{w} ~-~\frac{2}{\chi_\mathrm{eq}^2} \biggl[(2 - 3\gamma_c) \biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{1 - 3\gamma_c}\mathfrak{s}_\mathrm{core} ~+~(2 - 3\gamma_e)\biggl(\frac{\chi}{\chi_\mathrm{eq}}\biggr)^{1 - 3\gamma_e}\mathfrak{s}_\mathrm{env} \biggr] \ . </math> |
What to Expect for Equilibrium Configurations
In equilibrium we should set <math>~d\mathfrak{g}/d\chi = 0</math> and <math>~\chi = \chi_\mathrm{eq}</math>. In which case we should expect to find that,
|
<math>~0 </math> |
<math>~=</math> |
<math> \frac{1}{\chi_\mathrm{eq}}\biggl[\mathfrak{w} ~-~2(\mathfrak{s}_\mathrm{core} ~+~\mathfrak{s}_\mathrm{env}) \biggr] \, . </math> |
In addition, an evaluation of the second derivative should give,
|
<math>~\frac{\chi_\mathrm{eq}^2}{2} \cdot \frac{d^2\mathfrak{g}}{d\chi^2} </math> |
<math>~=</math> |
<math> -~\mathfrak{w} ~-~ \biggl[(2 - 3\gamma_c) \mathfrak{s}_\mathrm{core} ~+~(2 - 3\gamma_e)\mathfrak{s}_\mathrm{env} \biggr] \, . </math> |
Then, the transition from stable to unstable configurations occurs when <math>~d^2\mathfrak{g}/d\chi^2 = 0</math>, that is, when,
|
<math>~\mathfrak{w} </math> |
<math>~=</math> |
<math> ~-~ \biggl[(2 - 3\gamma_c) \mathfrak{s}_\mathrm{core} ~+~(2 - 3\gamma_e)\mathfrak{s}_\mathrm{env} \biggr] </math> |
|
<math>~\Rightarrow ~~~0</math> |
<math>~=</math> |
<math> ~(4 - 3\gamma_c) \mathfrak{s}_\mathrm{core} ~+~(4 - 3\gamma_e)\mathfrak{s}_\mathrm{env} </math> |
|
<math>~\Rightarrow ~~~\frac{\mathfrak{s}_\mathrm{core} }{\mathfrak{s}_\mathrm{env}} </math> |
<math>~=</math> |
<math> ~-~\frac{(4 - 3\gamma_e) }{(4 - 3\gamma_c) } \, . </math> |
For example, if we set <math>~\gamma_c = 6/5</math> and <math>~\gamma_e = 2</math>, this implies,
|
<math>~\frac{\mathfrak{s}_\mathrm{core} }{\mathfrak{s}_\mathrm{env}} </math> |
<math>~=</math> |
<math> ~\frac{2 }{(4 - 18/5) } = 5 \, . </math> |
Review of the Analysis by Murphy & Fiedler (1985b)
As we have detailed separately, the boundary condition at the center of a polytropic configuration is,
<math>~\frac{dx}{d\xi} \biggr|_{\xi=0} = 0 \, ;</math>
and the boundary condition at the surface of an isolated polytropic configuration is,
|
<math>~\frac{d\ln x}{d\ln\xi}</math> |
<math>~=</math> |
<math>~- \alpha + \frac{\omega^2}{\gamma_g } \biggl( \frac{1}{4\pi G \rho_c } \biggr) \frac{\xi}{(-\theta^')} </math> at <math>~\xi = \xi_s \, .</math> |
But this surface condition is not applicable to bipolytropes. Instead, let's return to the original, more general expression of the surface boundary condition:
|
<math>~ \frac{d\ln x}{d\ln\xi}\biggr|_s</math> |
<math>~=</math> |
<math>~- \alpha + \frac{\omega^2 R^3}{\gamma_g GM_\mathrm{tot}} \, .</math> |
|
Utilizing an accompanying discussion, let's examine the frequency normalization used by Murphy & Fiedler (1985b) (see the top of the left-hand column on p. 223):
For a given radial quantum number, <math>~k</math>, the factor inside the square brackets in this last expression is what Murphy & Fiedler (1985b) refer to as <math>~\omega^2_k \theta_c</math>. Keep in mind, as well, that, in the notation we are using,
This also means that the surface boundary condition may be rewritten as,
|
Let's apply these relations to the core and envelope, separately.
Interface Conditions
Here, we will simply copy the discussion already provided in the context of our attempt to analyze the stability of <math>~(n_c, n_e) = (0, 0)</math> bipolytropes; specifically, we will draw from STEP 4: in the Piecing Together subsection. Following the discussion in §§57 & 58 of P. Ledoux & Th. Walraven (1958), the proper treatment is to ensure that fractional perturbation in the gas pressure (see their equation 57.31),
|
<math>~\frac{\delta P}{P}</math> |
<math>~=</math> |
<math>~- \gamma x \biggl( 3 + \frac{d\ln x}{d\ln \xi} \biggr) \, ,</math> |
is continuous across the interface. That is to say, at the interface <math>~(\xi = \xi_i)</math>, we need to enforce the relation,
|
<math>~0</math> |
<math>~=</math> |
<math>~\biggl[ \gamma_c x_\mathrm{core} \biggl( 3 + \frac{d\ln x_\mathrm{core}}{d\ln \xi} \biggr) - \gamma_e x_\mathrm{env} \biggl( 3 + \frac{d\ln x_\mathrm{env}}{d\ln \xi} \biggr)\biggr]_{\xi=\xi_i}</math> |
|
|
<math>~=</math> |
<math>~\gamma_e \biggl[ \frac{\gamma_c}{\gamma_e} \biggl( 3 + \frac{d\ln x_\mathrm{core}}{d\ln \xi} \biggr) - \biggl( 3 + \frac{d\ln x_\mathrm{env}}{d\ln \xi} \biggr)\biggr]_{\xi=\xi_i}</math> |
|
<math>~\Rightarrow~~~ \frac{d\ln x_\mathrm{env}}{d\ln \xi} \biggr|_{\xi=\xi_i}</math> |
<math>~=</math> |
<math>~3\biggl(\frac{\gamma_c}{\gamma_e} -1\biggr) + \frac{\gamma_c}{\gamma_e} \biggl( \frac{d\ln x_\mathrm{core}}{d\ln \xi} \biggr)_{\xi=\xi_i} \, .</math> |
In the context of this interface-matching constraint (see their equation 62.1), P. Ledoux & Th. Walraven (1958) state the following: In the static (i.e., unperturbed equilibrium) model … discontinuities in <math>~\rho</math> or in <math>~\gamma</math> might occur at some [radius]. In the first case — that is, a discontinuity only in density, while <math>~\gamma_e = \gamma_c</math> — the interface conditions imply the continuity of <math>~\tfrac{1}{x} \cdot \tfrac{dx}{d\xi}</math> at that [radius]. In the second case — that is, a discontinuity in the adiabatic exponent — the dynamical condition may be written as above. This implies a discontinuity of the first derivative at any discontinuity of <math>~\gamma</math>.
The algorithm that Murphy & Fiedler (1985b) used to "… [integrate] through each zone …" was designed "… with continuity in <math>~x</math> and <math>~dx/d\xi</math> being imposed at the interface …" Given that they set <math>~\gamma_c = \gamma_e = 5/3</math>, their interface matching condition is consistent with the one prescribed by P. Ledoux & Th. Walraven (1958).
Radial Oscillations of (nc, ne) = (5, 1) Models
Foundation
In an accompanying discussion, we derived the so-called,
Adiabatic Wave (or Radial Pulsation) Equation
|
<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 </math> |
whose solution gives eigenfunctions that describe various radial modes of oscillation in spherically symmetric, self-gravitating fluid configurations. Assuming that the underlying equilibrium structure is that of a bipolytrope having <math>~(n_c, n_e) = (5, 1)</math>, it makes sense to adopt the normalizations used when defining the equilibrium structure, namely,
|
<math>~\rho^*</math> |
<math>~\equiv</math> |
<math>~\frac{\rho_0}{\rho_c}</math> |
; |
<math>~r^*</math> |
<math>~\equiv</math> |
<math>~\frac{r_0}{[K_c^{1/2}/(G^{1/2}\rho_c^{2/5})]}</math> |
|
<math>~P^*</math> |
<math>~\equiv</math> |
<math>~\frac{P_0}{K_c\rho_c^{6/5}}</math> |
; |
<math>~M_r^*</math> |
<math>~\equiv</math> |
<math>~\frac{M_r}{[K_c^{3/2}/(G^{3/2}\rho_c^{1/5})]}</math> |
We note as well that,
|
<math>~g_0</math> |
<math>~=</math> |
<math>~\frac{GM(r_0)}{r_0^2}</math> |
|
|
<math>~=</math> |
<math>~ G \biggl[ M_r^* \rho_c^{-1 / 5} \biggl( \frac{K_c}{G}\biggr)^{3 / 2} \biggr] \biggl[ r^* \rho_c^{-2 / 5}\biggl( \frac{K_c}{G}\biggr)^{1 / 2} \biggr]^{-2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{G M_r^*}{(r^*)^2} \biggl[ \rho_c^{3 / 5} \biggl( \frac{K_c}{G}\biggr)^{1 / 2} \biggr] \, . </math> |
Hence, multiplying the LAWE through by <math>~(K_c/G)\rho_c^{-4 / 5}</math> gives,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x </math> |
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{d^2x}{dr*^2} + \biggl[\frac{4}{r^*} ~-~ \rho_c^{-2 / 5} \biggl( \frac{K_c}{G} \biggr)^{1 / 2}\biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr*} ~+~ \rho_c^{-4 / 5}\biggl( \frac{K_c}{G} \biggr)\biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 ~+~ (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x </math> |
|
|
<math>~=</math> |
<math>~ \frac{d^2x}{dr*^2} ~+~ \biggl\{\frac{4}{r^*} ~-~ \rho_c^{-2 / 5} \biggl( \frac{K_c}{G} \biggr)^{1 / 2} \frac{G M_r^*}{(r^*)^2} \biggl[ \rho_c^{3 / 5} \biggl( \frac{K_c}{G}\biggr)^{1 / 2} \biggr] \biggl[ \frac{\rho_c \rho^*}{P^* K_c \rho_c^{6/5}}\biggr] \biggr\} \frac{dx}{dr*} ~+~ \rho_c^{-4 / 5}\biggl( \frac{K_c}{G} \biggr)\biggl[ \frac{\rho_c \rho^*}{\gamma_\mathrm{g}P^* K_c \rho_c^{6/5}}\biggr] \biggl\{\omega^2 ~+~ (4 - 3\gamma_\mathrm{g}) \frac{G M_r^*}{(r^*)^2} \biggl[ \rho_c^{3 / 5} \biggl( \frac{K_c}{G}\biggr)^{1 / 2} \biggr] \frac{\rho_c^{2 / 5}}{r^*}\biggl( \frac{G}{K_c}\biggr)^{1 / 2} \biggr\} x
</math> |
|
|
<math>~=</math> |
<math>~ \frac{d^2x}{dr*^2} ~+~ \biggl\{\frac{4}{r^*} ~-~ \frac{M_r^*}{(r^*)^2} \biggl[ \frac{\rho^*}{P^* }\biggr] \biggr\} \frac{dx}{dr*} ~+~ \biggl( \frac{1}{G\rho_c} \biggr)\biggl[ \frac{ \rho^*}{\gamma_\mathrm{g}P^* }\biggr] \biggl\{\omega^2 ~+~ (4 - 3\gamma_\mathrm{g}) \frac{G\rho_c M_r^*}{(r^*)^3} \biggr\} x
</math> |
|
|
<math>~=</math> |
<math>~ \frac{d^2x}{dr*^2} + \biggl\{ \frac{4}{r^*} -\biggl(\frac{\rho^*}{P^*}\biggr)\frac{ M_r^*}{(r^*)^2}\biggr\} \frac{dx}{dr*} + \biggl(\frac{\rho^*}{ P^* } \biggr)\biggl\{ \frac{\omega^2}{\gamma_\mathrm{g} G\rho_c} + \biggl(\frac{4}{\gamma_\mathrm{g}} - 3\biggr)\frac{ M_r^*}{(r^*)^3}\biggr\} x </math> |
|
|
<math>~=</math> |
<math>~ \frac{d^2x}{dr*^2} + \biggl\{ 4 -\biggl(\frac{\rho^*}{P^*}\biggr)\frac{ M_r^*}{(r^*)}\biggr\}\frac{1}{r^*} \frac{dx}{dr*} + \biggl(\frac{\rho^*}{ P^* } \biggr)\biggl\{ \frac{2\pi \sigma_c^2}{3\gamma_\mathrm{g}} ~-~\frac{\alpha_\mathrm{g} M_r^*}{(r^*)^3}\biggr\} x \, . </math> |
Profile
Now, referencing the derived bipolytropic model profile, we should incorporate the following relations:
Table 2: Radial Profile of Various Physical Variables
|
Variable |
Throughout the Core |
Throughout the Envelope† |
Plotted Profiles |
||
|
<math>~\xi_i = 0.5</math> |
<math>~\xi_i = 1.0</math> |
<math>~\xi_i = 3.0</math> |
|||
|
<math>~r^*</math> |
<math>\biggl( \frac{3}{2\pi} \biggr)^{1/2} \xi</math> |
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1} \theta^{-2}_i (2\pi)^{-1/2}\eta</math> |
|
||
|
<math>~\rho^*</math> |
<math>\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-5/2}</math> |
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{5}_i \phi(\eta)</math> |
|||
|
<math>~P^*</math> |
<math>\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3}</math> |
<math>\theta^{6}_i [\phi(\eta)]^{2}</math> |
|||
|
<math>~M_r^*</math> |
<math>\biggl( \frac{2\cdot 3}{\pi } \biggr)^{1/2} \biggl[ \xi^3 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3/2} \biggr]</math> |
<math>\biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \theta^{-1}_i \biggl( \frac{2}{\pi} \biggr)^{1/2} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr)</math> |
|||
|
†In order to obtain the various envelope profiles, it is necessary to evaluate <math>\phi(\eta)</math> and its first derivative using the information presented in Step 6, above. |
|||||
Therefore, throughout the core we have,
|
<math>~\frac{\rho^*}{P^*}</math> |
<math>~=</math> |
<math>~\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{1 / 2} \, ;</math> |
|
<math>~\frac{M_r^*}{r^*}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{2\cdot 3}{\pi } \biggr)^{1/2} \biggl[ \xi^3 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3/2} \biggr]\biggl( \frac{2\pi}{3}\biggr)^{1 / 2} \frac{1}{\xi} = 2 \xi^2 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3/2} \, ; </math> |
and, throughout the envelope we have,
|
<math>~\frac{\rho^*}{P^*}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\mu_e}{\mu_c} \biggr) \theta^{-1}_i \phi(\eta)^{-1} \, ; </math> |
|
<math>~\frac{M_r^*}{r^*}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \theta^{-1}_i \biggl( \frac{2}{\pi} \biggr)^{1/2} \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr) \biggl[ \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1} \theta^{-2}_i (2\pi)^{-1/2}\eta \biggr]^{-1} = 2 \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-1} \theta_i \eta \biggl(-\eta^2 \frac{d\phi}{d\eta} \biggr) \, . </math> |
Numerical Integration
General Approach
Here, we begin by recognizing that the 2nd-order ODE that must be integrated to obtain the desired eigenvectors has the generic form,
|
<math>~0</math> |
<math>~=</math> |
<math>~ x + \frac{\mathcal{H}}{r^*} x' + \mathcal{K}x \, , </math> |
where,
|
<math>~x'</math> |
<math>~=</math> |
<math>~\frac{dx}{dr^*}</math> |
and |
<math>~x</math> |
<math>~=</math> |
<math>~\frac{d^2x}{d(r^*)^2} \, .</math> |
Adopting the same approach as before when we integrated the LAWE for pressure-truncated polytropes, we will enlist the finite-difference approximations,
|
<math>~x'</math> |
<math>~\approx</math> |
<math>~ \frac{x_+ - x_-}{2\delta r^*} </math> |
and |
<math>~x</math> |
<math>~\approx</math> |
<math>~ \frac{x_+ -2x_j + x_-}{(\delta r^*)^2} \, . </math> |
The finite-difference representation of the LAWE is, therefore,
|
<math>~\frac{x_+ -2x_j + x_-}{(\delta r^*)^2}</math> |
<math>~=</math> |
<math>~ -~ \frac{\mathcal{H}}{r^*} \biggl[ \frac{x_+ - x_-}{2\delta r^*} \biggr] ~-~ \mathcal{K}x_j </math> |
|
<math>~\Rightarrow ~~~ x_+ -2x_j + x_-</math> |
<math>~=</math> |
<math>~ -~ \frac{\delta r^*}{2r^*} \biggl[ x_+ - x_- \biggr]\mathcal{H} ~-~ (\delta r^*)^2\mathcal{K}x_j </math> |
|
<math>~\Rightarrow ~~~ x_{j+1} \biggl[1 + \biggl( \frac{\delta r^*}{2r^*}\biggr) \mathcal{H} \biggr]</math> |
<math>~=</math> |
<math>~ \biggl[ 2 - (\delta r^*)^2\mathcal{K}\biggr] x_j ~-~\biggl[ 1 - \biggl( \frac{\delta r^*}{2r^*} \biggr) \mathcal{H} \biggr]x_{j-1} \, . </math> |
In what follows we will also find it useful to rewrite <math>~\mathcal{K}</math> in the form,
<math>~\mathcal{K} ~\rightarrow ~\biggl(\frac{\sigma_c^2}{\gamma_\mathrm{g}}\biggr) \mathcal{K}_1 - \alpha_\mathrm{g} \mathcal{K}_2 \, .</math>
The relevant coefficient expressions for all regions of the configuration are,
|
<math>~\mathcal{H}</math> |
<math>~\equiv</math> |
<math>~ \biggl\{ 4 -\biggl(\frac{\rho^*}{P^*}\biggr)\frac{ M_r^*}{(r^*)}\biggr\} </math> |
, |
<math>~\mathcal{K}_1</math> |
<math>~\equiv</math> |
<math>~ \frac{2\pi }{3}\biggl(\frac{\rho^*}{ P^* } \biggr) </math> |
and |
<math>~\mathcal{K}_2</math> |
<math>~\equiv</math> |
<math>~ \biggl(\frac{\rho^*}{ P^* } \biggr)\frac{M_r^*}{(r^*)^3} \, . </math> |
Special Handling at the Center
In order to kick-start the integration, we set the displacement function value to <math>~x_1 = 1</math> at the center of the configuration <math>~(\xi_1 = 0)</math>, then draw on the derived power-series expression to determine the value of the displacement function at the first radial grid line, <math>~\xi_2 = \delta\xi</math>, away from the center. Specifically, we set,
|
<math>~ x_2 </math> |
<math>~=</math> |
<math>~ x_1 \biggl[ 1 - \frac{(n+1) \mathfrak{F} (\delta\xi)^2}{60} \biggr]_{n=5} = x_1 \biggl[ 1 - \frac{\mathfrak{F} (\delta\xi)^2}{10} \biggr] \, .</math> |
Special Handling at the Interface
Integrating outward from the center, the general approach will work up through the determination of <math>~x_{j+1}</math> when "j+1" refers to the interface location. In order to properly transition from the core to the envelope, we need to determine the value of the slope at this interface location. Let's do this by setting j = i, then projecting forward to what <math>~x_+</math> would be — that is, to what the amplitude just beyond the interface would be — if the core were to be extended one more zone. Then, the slope at the interface (as viewed from the perspective of the core) will be,
|
<math>~x'_i\biggr|_\mathrm{core}</math> |
<math>~\approx</math> |
<math>~ \frac{1}{2\delta r^*} \biggl\{ x_+ - x_{i-1} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -\frac{x_{i-1}}{2\delta r^*} + \frac{1}{2\delta r^*} \biggl\{ \biggl[ 2 - (\delta r^*)^2\mathcal{K}\biggr] x_i ~-~\biggl[ 1 - \biggl( \frac{\delta r^*}{2r^*} \biggr) \mathcal{H} \biggr]x_{i-1} \biggr\}\biggl[1 + \biggl( \frac{\delta r^*}{2r^*}\biggr) \mathcal{H} \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2\delta r^*} \biggl\{ \biggl[ 2 - (\delta r^*)^2\mathcal{K}\biggr] x_i ~-~\biggl[ 1 - \biggl( \frac{\delta r^*}{2r^*} \biggr) \mathcal{H} \biggr]x_{i-1} ~-~\biggl[1 + \biggl( \frac{\delta r^*}{2r^*}\biggr) \mathcal{H} \biggr]x_{i-1} \biggr\}\biggl[1 + \biggl( \frac{\delta r^*}{2r^*}\biggr) \mathcal{H} \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2\delta r^*} \biggl\{ \biggl[ 2 - (\delta r^*)^2\mathcal{K}\biggr] x_i ~-~2x_{i-1} \biggr\}\biggl[1 + \biggl( \frac{\delta r^*}{2r^*}\biggr) \mathcal{H} \biggr]^{-1} </math> |
Conversely, as viewed from the envelope, if we assume that we know <math>~x_i</math> and <math>~x'_i</math>, we can determine the amplitude, <math>~x_{i+1}</math>, at the first zone beyond the interface as follows:
|
<math>~x_-</math> |
<math>~\approx</math> |
<math>~ x_{i+1} - 2\delta r^*\cdot x'_i\biggr|_\mathrm{env} </math> |
|
<math>~\Rightarrow ~~~ x_{i+1} \biggl[1 + \biggl( \frac{\delta r^*}{2r^*}\biggr) \mathcal{H} \biggr]</math> |
<math>~=</math> |
<math>~ \biggl[ 2 - (\delta r^*)^2\mathcal{K}\biggr] x_i ~-~\biggl[ 1 - \biggl( \frac{\delta r^*}{2r^*} \biggr) \mathcal{H} \biggr] \biggl[ x_{i+1} - 2\delta r^*\cdot x'_i\biggr|_\mathrm{env} \biggr] </math> |
|
<math>~\Rightarrow ~~~ x_{i+1} \biggl[1 + \biggl( \frac{\delta r^*}{2r^*}\biggr) \mathcal{H} \biggr] ~+~ \biggl[ 1 - \biggl( \frac{\delta r^*}{2r^*} \biggr) \mathcal{H} \biggr] x_{i+1} </math> |
<math>~=</math> |
<math>~ \biggl[ 2 - (\delta r^*)^2\mathcal{K}\biggr] x_i ~+~ \biggl[ 1 - \biggl( \frac{\delta r^*}{2r^*} \biggr) \mathcal{H} \biggr] 2\delta r^*\cdot x'_i\biggr|_\mathrm{env} </math> |
|
<math>~\Rightarrow ~~~ x_{i+1} </math> |
<math>~=</math> |
<math>~ \biggl[ 1 - \tfrac{1}{2}(\delta r^*)^2\mathcal{K}\biggr] x_i ~+~ \biggl[ 1 - \biggl( \frac{\delta r^*}{2r^*} \biggr) \mathcal{H} \biggr] \delta r^*\cdot x'_i\biggr|_\mathrm{env} </math> |
Splitting Analysis Into Separate Core and Envelope Components
Core:
Given that, <math>~\sqrt{2\pi/3}~r^* = \xi</math>, lets multiply the LAWE through by <math>~3/(2\pi)</math>. This gives,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{d^2x}{d\xi^2} + \biggl\{ 4 -\biggl(\frac{\rho^*}{P^*}\biggr)\frac{ M_r^*}{(r^*)}\biggr\}\frac{1}{\xi} \cdot \frac{dx}{d\xi} + \frac{3}{2\pi}\biggl(\frac{\rho^*}{ P^* } \biggr)\biggl\{ \frac{2\pi \sigma_c^2}{3\gamma_\mathrm{g}} ~-~\frac{\alpha_\mathrm{g} M_r^*}{(r^*)^3}\biggr\} x \, . </math> |
Specifically for the core, therefore, the finite-difference representation of the LAWE is,
|
<math>~\frac{x_+ -2x_j + x_-}{(\delta \xi)^2}</math> |
<math>~=</math> |
<math>~ -~ \frac{\mathcal{H}}{\xi} \biggl[ \frac{x_+ - x_-}{2\delta \xi} \biggr] ~-~ \biggl[ \frac{3\mathcal{K}}{2\pi} \biggr]x_j </math> |
|
<math>~\Rightarrow ~~~ x_+ -2x_j + x_-</math> |
<math>~=</math> |
<math>~ -~ \frac{\delta \xi}{2\xi} \biggl[ x_+ - x_- \biggr]\mathcal{H} ~-~ (\delta \xi)^2 \biggl[ \frac{3\mathcal{K}}{2\pi} \biggr] x_j </math> |
|
<math>~\Rightarrow ~~~ x_{j+1} \biggl[1 + \biggl( \frac{\delta \xi}{2\xi}\biggr) \mathcal{H} \biggr]</math> |
<math>~=</math> |
<math>~ \biggl[ 2 - (\delta \xi)^2\biggl( \frac{3\mathcal{K}}{2\pi} \biggr) \biggr] x_j ~-~\biggl[ 1 - \biggl( \frac{\delta \xi}{2\xi} \biggr) \mathcal{H} \biggr]x_{j-1} \, . </math> |
This also means that, as viewed from the perspective of the core, the slope at the interface is
|
<math>~\biggl[ \frac{dx}{d\xi}\biggr]_\mathrm{interface}</math> |
<math>~=</math> |
<math>~ \frac{1}{2\delta \xi} \biggl\{ \biggl[ 2 - (\delta \xi)^2 \biggl( \frac{3\mathcal{K}}{2\pi} \biggr)\biggr] x_i ~-~2x_{i-1} \biggr\}\biggl[1 + \biggl( \frac{\delta \xi}{2\xi}\biggr) \mathcal{H} \biggr]^{-1} \, . </math> |
Envelope:
Given that,
<math>~\biggl( \frac{\mu_e}{\mu_c} \biggr) \theta_i^2 (2\pi)^{1 / 2}~r^* = \eta \, ,</math>
let's multiply the LAWE through by <math>~(2\pi)^{-1} \theta_i^{-4}( \mu_e/\mu_c)^{-2} </math>. This gives,
|
<math>~0</math> |
<math>~=</math> |
<math>~ \frac{d^2x}{d\eta^2} + \biggl\{ 4 -\biggl(\frac{\rho^*}{P^*}\biggr)\frac{ M_r^*}{(r^*)}\biggr\}\frac{1}{\eta} \cdot \frac{dx}{d\eta} + \frac{1}{2\pi \theta_i^4} \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \biggl(\frac{\rho^*}{ P^* } \biggr)\biggl\{ \frac{2\pi \sigma_c^2}{3\gamma_\mathrm{g}} ~-~\frac{\alpha_\mathrm{g} M_r^*}{(r^*)^3}\biggr\} x \, . </math> |
Specifically for the envelope, therefore, the finite-difference representation of the LAWE is,
|
<math>~\frac{x_+ -2x_j + x_-}{(\delta \eta)^2}</math> |
<math>~=</math> |
<math>~ -~ \frac{\mathcal{H}}{\eta} \biggl[ \frac{x_+ - x_-}{2\delta \eta} \biggr] ~-~ \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2}\biggl[ \frac{\mathcal{K}}{2\pi \theta_i^4} \biggr]x_j </math> |
|
<math>~\Rightarrow ~~~ x_+ -2x_j + x_-</math> |
<math>~=</math> |
<math>~ -~ \frac{\delta \eta}{2\eta} \biggl[ x_+ - x_- \biggr]\mathcal{H} ~-~ (\delta \eta)^2 \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2}\biggl[ \frac{\mathcal{K}}{2\pi \theta_i^4} \biggr] x_j </math> |
|
<math>~\Rightarrow ~~~ x_{j+1} \biggl[1 + \biggl( \frac{\delta \eta}{2\eta}\biggr) \mathcal{H} \biggr]</math> |
<math>~=</math> |
<math>~ \biggl[ 2 - (\delta \eta)^2 \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \biggl( \frac{\mathcal{K}}{2\pi \theta_i^4} \biggr) \biggr] x_j ~-~\biggl[ 1 - \biggl( \frac{\delta \eta}{2\eta} \biggr) \mathcal{H} \biggr]x_{j-1} \, . </math> |
This also means that, once we know the slope at the interface (see immediately below), the amplitude at the first zone outside of the interface will be given by the expression,
|
<math>~x_{i+1} </math> |
<math>~=</math> |
<math>~ \biggl[ 1 - \tfrac{1}{2}(\delta \eta)^2 \biggl( \frac{\mu_e}{\mu_c} \biggr)^{-2} \biggl( \frac{\mathcal{K}}{2\pi \theta_i^4} \biggr)\biggr] x_i ~+~ \biggl[ 1 - \biggl( \frac{\delta \eta}{2\eta} \biggr) \mathcal{H} \biggr] \delta \eta \cdot \biggl[ \frac{dx}{d\eta} \biggr]_\mathrm{interface} \, . </math> |
Interface
If we consider only cases where <math>~\gamma_e = \gamma_c</math>, then at the interface we expect,
|
<math>~\frac{d\ln x}{d\ln r^*}</math> |
<math>~=</math> |
<math>~\frac{d\ln x}{d\ln \xi} = \frac{d\ln x}{d\ln \eta}</math> |
|
<math>~\Rightarrow ~~~ r^*\frac{dx}{d r^*}</math> |
<math>~=</math> |
<math>~\xi \frac{dx}{d \xi} = \eta \frac{d x}{d \eta}</math> |
|
<math>~\Rightarrow ~~~ \frac{dx}{dr^*}</math> |
<math>~=</math> |
<math>~\biggl(\frac{2\pi}{3} \biggr)^{1 / 2}\frac{dx}{d\xi} = \biggl(\frac{\mu_e}{\mu_c}\biggr) \theta_i^2 (2\pi)^{1 / 2} \frac{dx}{d\eta} \, .</math> |
Switching at the interface from <math>~\xi</math> to <math>~\eta</math> therefore means that,
|
<math>~ \biggl[ \frac{dx}{d\eta}\biggr]_\mathrm{interface}</math> |
<math>~=</math> |
<math>~\frac{1}{\sqrt{3}} \biggl(\frac{\mu_e}{\mu_c}\biggr)^{-1} \theta_i^{-2} \biggl[ \frac{dx}{d\xi}\biggr]_\mathrm{interface} \, .</math> |
Model 10
As we have reviewed in an accompanying discussion, equilibrium Model 10 from Murphy & Fiedler (1985, Proc. Astr. Soc. of Australia, 6, 219) is defined by setting <math>~(\xi_i, m) = (2.5646, 1)</math>. Drawing directly from our reproduction of their Table 1, we see that a few relevant structural parameters of Model 10 are,
|
<math>~\xi_s</math> |
<math>~=</math> |
<math>~6.5252876</math> |
|
<math>~\frac{r_i}{R} = \frac{\xi_i}{\xi_s}</math> |
<math>~=</math> |
<math>~0.39302482</math> |
|
<math>~\frac{\rho_c}{\bar\rho} </math> |
<math>~=</math> |
<math>~34.346</math> |
|
<math>~\frac{M_\mathrm{env}}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~5.89 \times 10^{-4}</math> |
Here we list a few other model parameter values that will aid in our attempt to correctly integrate the LAWE to find various radial oscillation eigenvectors.
|
A Sampling of Model 10's Equilibrium Parameter Values† |
|||||||||||
| Grid Line |
<math>~\frac{r}{R}</math> | <math>~\xi</math> | <math>~\eta</math> | <math>~\Delta</math> | <math>~\phi</math> | <math>~- \frac{d\phi}{d\eta}</math> | <math>~r^*</math> | <math>~\rho^*</math> | <math>~P^*</math> | <math>~M_r^*</math> | <math>~g_0^*\equiv \frac{M_r^*}{(r^*)^2}</math> |
| 25 | 0.12093071 | 0.789108 | 0.31480842 | 0.89940188 | 0.80892374 | 0.122726799 | 1.23835945 | ||||
| 40 | 0.19651241 | 1.2823 | 0.51156369 | 0.74761972 | 0.55893525 | 0.473819194 | 1.81056130 | ||||
| 79 | 0.393025 | 2.5646 | 1.02312737 | 0.21270605 | 0.04524386 | 2.150231108 | 2.05411964 | ||||
| 79 | 0.393025 | 1.4806725 | 2.6746514 | 1.000000 | 1.112155 | 1.02312737 | 0.21270605 | 0.04524386 | 2.15023111 | 2.0541196 | |
| 100 | 0.49883919 | 1.8793151 | 2.7938569 | 0.6505914 | 0.69070815 | 1.2985847 | 0.0247926 | 0.0034309 | 2.15127319 | 1.2757189 | |
| 150 | 0.7507782 | 2.8284641 | 2.9982701 | 0.2149684 | 0.30495637 | 1.95443562 | 9.7646E-05 | 4.4649E-06 | 2.15149752 | 0.563246 | |
| 199 | 0.9976784 | 3.7586302 | 3.1404305 | 0.00150695 | 0.17269514 | 2.59716948 | 1.653E-15 | 5.2984E-19 | 2.15149876 | 0.31896316 | |
|
†Our chosen (uniform) grid spacing is, <math>~\frac{\delta r}{R} = \frac{1}{78}\biggl( \frac{r_i}{R} \biggr) \approx 0.00503878 \, ;</math> as a result, the center is at zone 1, the interface is at grid line 79, and the surface is just beyond grid line 199. |
|||||||||||
Eigenvectors
We now have the tools in hand to identify the eigenvectors — that is, various radial eigenfunctions and the corresponding eigenfrequency for each — associated with various modes of oscillation in <math>~(n_c, n_e) = (5,1)</math> bipolytropes. Which models should we examine?
In our accompanying review of the bipolytrope stability analysis presented by Murphy & Fiedler (1983b), our primary objective was to show that we were able to match their results quantitatively. We therefore set <math>~\mu_e/\mu_c</math> = 1 — the only <math>~\mu</math>-ratio that they considered — and picked values of the core-envelope interface radius, <math>~\xi_i</math>, that were listed among their set of chosen models. For a fixed value of <math>~\xi_i</math>, we integrated the relevant LAWE from the center toward the surface for many different eigenfrequency <math>~(\sigma_c^2)</math> guesses until an eigenfunction was found whose behavior at the surface matched with high precision the physically justified surface boundary condition.
Here we have chosen to focus on models that reside along five of the analytically defined equilibrium sequences depicted above in Figure 2 — specifically, the sequences for which <math>~\mu_e/\mu_c</math> = 1, ½, 0.345, ⅓, and 0.309 — and to examine, first, whether any model along each sequence marks a transition from dynamically stable to dynamically unstable configurations. We accomplished this by setting <math>~\sigma_c^2</math> = 0, then integrating the relevant LAWE from the center toward the surface for many different guesses of the core-envelope interface radius until an eigenfunction with no radial nodes — i.e., an eigenfunction associated with the fundamental mode of radial oscillation — was found whose behavior at the surface matched with high precision the physically desired surface boundary condition. We were successful in this endeavor. A marginally unstable model was identified on each of the five separate equilibrium sequences.
The following table summarizes some of the equilibrium properties of these five models. For example, the second column of the table gives the value of the core-envelope interface radius, <math>~\xi_i</math>, associated with each marginally unstable model. The table also lists: the value of <math>~q</math>, <math>~\nu</math>, and the central-to-mean density associated with each model; and in each case the dimensionless thermal energy <math>~(S^*)</math> and dimensionless gravitational potential energy <math>~(W^*)</math> associated, separately, with the core and the envelope. Note that, once the pair of parameters, <math>~(\mu_e/\mu_c, \xi_i)</math>, has been specified, we can legitimately assign high-precision values to all of the other model parameters because they are analytically prescribed.
|
Properties of Marginally Unstable Bipolytropes Having |
||||||||
|---|---|---|---|---|---|---|---|---|
| <math>~\frac{\mu_e}{\mu_c}</math> | <math>~\xi_i</math> | <math>~q \equiv \frac{r_\mathrm{core}}{R_\mathrm{surf}}</math> | <math>~\nu \equiv \frac{M_\mathrm{core}}{M_\mathrm{tot}}</math> | <math>~\frac{\rho_c}{\bar\rho}</math> | <math>~S^*_\mathrm{env}</math> | <math>~W^*_\mathrm{env}</math> | <math>~S^*_\mathrm{core}</math> | <math>~W^*_\mathrm{core}</math> |
| 1 | 2.467359668 | 0.597684036 | 0.692367564 | 17.09749847 | 4.518031091 | -6.79580606 | 0.857904827 | -3.956065776 |
| <math>~\tfrac{1}{2}</math> | 2.65925887 | 0.314759926 | 0.481811565 | 95.04044773 | 4.759771212 | -7.459080087 | 3.20977926 | -8.480020858 |
| 0.345 | 2.77457272408 | 0.183201946 | 0.25725514 | 281.7482802 | 4.887554727 | -7.822410223 | 10.22665208 | -22.40600339 |
| <math>~\tfrac{1}{3}</math> | 2.7843424754 | 0.17412463 | 0.237677946 | 305.4881577 | 4.897826446 | -7.852004624 | 11.6114224 | -25.16649306 |
| 0.309 | 2.8050375512 | 0.156021514 | 0.197918988 | 359.3276918 | 4.91930991 | -7.914090174 | 15.49005222 | -32.90463409 |
|
Numerical Values for Some Selected <math>~(n_c, n_e) = (1, 5)</math> Bipolytropes |
||||||
| MODEL | Source | <math>~\frac{r_i}{R}</math> | <math>~\Omega_0^2</math> | <math>~\Omega_1^2</math> | <math>~\frac{r}{R}\biggr|_1</math> | <math>~1-\frac{M_r}{M_\mathrm{tot}}\biggr|_1</math> |
| 10 | MF85 | 0.393 | 15.9298 | 21.2310 | 0.573 | 1.00E-03 |
| Here | 0.39302 | 15.93881161 | 21.24571822 | 0.5724 | 3.05E-05 | |
| 17 | MF85 | 0.933 | 2.1827 | 13.9351 | 0.722 | 0.232 |
| Here | 0.93277 | 2.182932207 | 13.93880866 | 0.7215 | 0.24006 | |
Summary
Reconciliation
In an accompanying discussion of the viral stability of <math>~(n_c, n_e) = (5, 1)</math > bipolytropes — see also an associated discussion of the free-energy of these configurations — we find the following table of models. Let's start by finding a set of eigenvectors associated with each the subset of models highlighted in yellow.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Figure 3: Largely the same as Figure 1, above, but a red-dashed curve has been added that separates the <math>~q - \nu</math> domain into regions that contain stable models (lying below the curve) from dynamically unstable models (lying above the curve), as determined by the virial stability analysis presented here. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In the context of our present discussion, we find that when <math>~\mu_e/\mu_c = 1/3</math>:
- Our virial analysis shows that the model having marginal stability has the properties: <math>~\xi = 8.548</math>, <math>~q = 0.0990</math>, and <math>~\nu = 0.4790</math>.
- In contrast, our solution to the LAWE identifies the marginally stable configuration has the properties: <math>~\xi = 2.78434248</math>, <math>~q = 0.1741</math>, and <math>~\nu = 0.2377</math>.
See Also
- K. De et al. (12 October 2018, Science, Vol. 362, No. 6411, pp. 201 - 206), A Hot and Fast Ultra-stripped Supernova that likely formed a Compact Neutron Star Binary.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |