User:Tohline/Appendix/Mathematics/ToroidalFunctions
Relationships Between Toroidal Functions

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Wong Toroidal Coordinates
Wong's Expression for the Potential
This chapter has been put together in an effort to lay the groundwork for an evaluation of Wong's (1973) derived expression for the gravitational potential both inside and outside of a uniform-density, axisymmetric torus. After multiplying his expression by the negative of <math>~G</math>, then replacing his total charge, <math>~q</math>, with the total mass, <math>~M</math>, Wong's interior (i.e., <math>~\eta^' > \eta_0</math>) solution is,
|
<math>~U(\eta^',\theta^')\biggr|_{\mathrm{for}~\eta^' \ge \eta_0}</math> |
<math>~=</math> |
<math>~- \frac{2^{5 / 2} a^2 G}{3} \biggl[ \frac{1}{2\pi^2 a^2}\biggl(\frac{M}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggr] \biggl\{ - \frac{3\pi^2}{2^{5/ 2}} \biggl[ \frac{\sinh^2\eta^'}{(\cosh \eta^' - \cos \theta^')^2} \biggr] +~ (\cosh \eta^' - \cos \theta^')^{1 / 2} </math> |
|
|
|
<math>~ \times \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) \biggr\} \, , </math> |
|
Wong (1973), Eq. (2.65) |
||
where,
|
<math>~B_n(\cosh\eta_0)</math> |
<math>~\equiv</math> |
<math>~ (n+\tfrac{1}{2})P_{n+1/2} (\cosh\eta_0)Q^2_{n-1/2} (\cosh\eta_0) - (n-\tfrac{3}{2})P_{n-1/2} (\cosh\eta_0)Q^2_{n+1/2} (\cosh\eta_0) \, . </math> |
|
Wong (1973), Eq. (2.62) |
||
Summary of Toroidal Coordinates and Toroidal Functions
|
Summary |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Suppose you want to evaluate the potential of a uniform-density torus whose major radius is, <math>~R</math>, and minor cross-sectional radius is, <math>~d</math>. Evaluation of the potential can be relatively easily expressed in terms of a toroidal coordinate system, <math>~(\eta,\theta)</math>, whose "origin" is at a distance, <math>~a</math>, from the symmetry axis, where, <math>~a^2 \equiv R^2 - d^2 ~~~\Rightarrow ~~~ \frac{a^2}{d^2} = \frac{R^2}{d^2} - 1\, .</math>
The surface of the uniform-density torus is defined by the toroidal "radial" coordinate, <math>~\eta_0</math>, such that,
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
The volume of a torus is, <math>~V = 2\pi R(\pi d^2) \, .</math> When this is rewritten in terms of our toroidal coordinate system, we have,
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Expressions for the relevant toroidal functions are as follows:
where, <math>~K</math> and <math>~E</math> are complete elliptic integrals of the first and second kind, respectively. In equation (23) of Cohl & Tohline (1999), this last expression has been written in the more compact form,
where, <math>~\mu \equiv [2/(\chi + 1)]^{1 / 2}</math> and, for example, <math>~\chi = \cosh\eta</math>.
We also will employ the so-called recurrence relation,
After setting, <math>~\mu = 0</math>, and making the association, <math>~\nu \rightarrow (m - \tfrac{3}{2})</math>, for example, this gives,
which, for all <math>~m \ge 2</math> provides a means by which an expression for the associated toroidal function, <math>~Q_{m - \frac{1}{2}}</math>, can be generated from the foundation pair of expressions given above for <math>~Q_{- \frac{1}{2}}</math> and <math>~Q_{+ \frac{1}{2}}</math>. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Asymptotic Behavior
|
<math>~\lim_{\chi\rightarrow \infty} Q_{m-\frac{1}{2}}(\chi)</math> |
<math>~=</math> |
<math>~ \frac{\Gamma(m+\frac{1}{2}) \sqrt{\pi} }{ \Gamma(m+1) (2\chi)^{m+\frac{1}{2}} } </math> |
|
|
<math>~=</math> |
<math>~ \frac{\sqrt{\pi} }{ (2\chi)^{m+\frac{1}{2}} } \cdot \biggl[ \Gamma(m+\frac{1}{2}) \biggr] \biggl[ \Gamma(m+1) \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \frac{\sqrt{\pi} }{ (2\chi)^{m+\frac{1}{2}} } \cdot \biggl[\frac{\sqrt{\pi}}{2^m} \cdot (2m-1)!! \biggr] \biggl[ m (m-1)! \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \frac{\pi }{2^{2m+\frac{1}{2}} \chi^{m+\frac{1}{2}} } \cdot \biggl[ \frac{(2m-1)!! }{ m (m-1)! }\biggr] </math> |
|
Asymptotic behavior: | |
|---|---|
| <math>~m</math> |
<math>~\lim_{\chi\rightarrow \infty} Q_{m-\frac{1}{2}}(\chi)</math> |
| 0 |
<math>~ \frac{\Gamma(\frac{1}{2}) \sqrt{\pi} }{ \Gamma(1) (2\chi)^{\frac{1}{2}} } = \frac{\pi}{ (2\chi)^{1 / 2} } \, . </math> |
| 1 |
<math>~ \frac{\pi }{2^{5/2} \chi^{3/2} } </math> |
| 2 |
<math>~ \frac{\pi }{2^{\frac{9}{2}} \chi^{\frac{5}{2}} } \cdot \biggl[ \frac{(3)!! }{ 2 }\biggr] = \frac{360~\pi }{2^{9/2} \chi^{5/2} } = \frac{45~\pi }{2^{3/2} \chi^{5/2} } </math> |
Dimensionless Potential Expression
Given that the portion of the leading term in Wong's expression that sits inside the square brackets is equivalent to the density, <math>~\rho_0 = M/V</math>, of the torus material — that is, given that,
|
<math>~\frac{1}{2\pi^2 a^2}\biggl(\frac{M}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} </math> |
<math>~=</math> |
<math>~\frac{\rho_0 V}{2\pi^2 a^3} \biggl[ \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggr] </math> |
<math>~=</math> |
<math>~\rho_0\, ,</math> |
— a reasonable dimensionless version of Wong's expression could be obtained by dividing through by the quantity, <math>~(G\rho_0 a^2) </math>. We prefer, instead, to normalize Wong's expression to the quantity, <math>~GM/R</math> , in which case the dimensionless version of the expression becomes,
|
<math>~\frac{U(\eta^',\theta^')}{GM/R} \biggr|_{\mathrm{for}~\eta^' \ge \eta_0}</math> |
<math>~=</math> |
<math>~- \frac{2^{5 / 2} }{3} \biggl[ \frac{1}{2\pi^2}\biggl(\frac{R}{a}\biggr) \frac{\sinh^3 \eta_0}{\cosh\eta_0} \biggr] \biggl\{ - \frac{3\pi^2}{2^{5/ 2}} \biggl[ \frac{\sinh^2\eta^'}{(\cosh \eta^' - \cos \theta^')^2} \biggr] +~ (\cosh \eta^' - \cos \theta^')^{1 / 2} </math> |
|
|
|
<math>~ \times \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~- \frac{2^{3 / 2} \sinh^2\eta_0 }{3\pi^2}\biggl\{ - \frac{3\pi^2}{2^{5/ 2}} \biggl[ \frac{\sinh^2\eta^'}{(\cosh \eta^' - \cos \theta^')^2} \biggr] +~ (\cosh \eta^' - \cos \theta^')^{1 / 2} </math> |
|
|
|
<math>~ \times \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\sinh^2\eta_0 \biggl\{ \frac{\sinh^2\eta^'}{2 (\cosh \eta^' - \cos \theta^')^2} ~- ~\frac{2^{3 / 2} }{3\pi^2} (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_{n=0}^\infty \epsilon_n \cos(n\theta^') Q_{n-1 / 2}(\cosh\eta^') B_n(\cosh\eta_0) \biggr\} \, . </math> |
Prior to the Integration
The Green's function written in toroidal coordinates is,
|
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> |
<math>~=</math> |
<math>~ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \, , </math> |
where,
and, <math>~Q_{m - 1 / 2}</math> is the zero-order, half-(odd)integer degree, Llegendre function of the second kind — also referred to as a toroidal function of zeroth order. Hence, a valid expression for the gravitational potential is,
|
<math>~ \Phi_B(\varpi,\phi,z)</math> |
<math>~=</math> |
<math>~ -G \int \frac{1}{|\vec{x}^{~'} - \vec{x}|} ~\rho(\vec{x}^{~'}) d^3x^' </math> |
|
|
<math>~=</math> |
<math>~ -G \int \biggl\{ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \biggr\}~ \rho(\varpi^',\phi^',z^') \varpi^' d\varpi^' d\phi^' dz^' </math> |
|
|
<math>~=</math> |
<math>~ -\frac{G}{\pi \sqrt{\varpi}} \int \rho(\varpi^',\phi^',z^') \sqrt{\varpi^'} d\varpi^' d\phi^' dz^' \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, , </math> |
where, <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0=1</math> and <math>~\epsilon_m = 2</math> for <math>~m\ge 1</math>.
Wong (1973) states that in toroidal coordinates the Green's function is,
|
<math>~\frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} </math> |
<math>~=</math> |
<math>~ \frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } \sum\limits_{m,n} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} </math> |
|
|
|
<math>~ \times \cos[m(\psi - \psi^')][\cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, , </math> |
|
Wong (1973), Eq. (2.53) |
||
where, <math>~P^m_{n-1 / 2}, Q^m_{n-1 / 2}</math> are "Legendre functions of the first and second kind with order <math>~n - \tfrac{1}{2}</math> and degree <math>~m</math> (toroidal harmonics)," and <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0 = 1</math> and <math>~\epsilon_m = 2</math> for all <math>~m \ge 1</math>,
|
<math>~\eta</math> |
<math>~=</math> |
<math>~\ln\biggl(\frac{r_1}{r_2} \biggr) \, ,</math> |
|
<math>~\cos\theta</math> |
<math>~=</math> |
<math>~\frac{(r_1^2 + r_2^2 - 4a^2)}{2r_1 r_2} \, ,</math> |
|
<math>~\tan\psi</math> |
<math>~=</math> |
<math>~\frac{y}{x} \, ,</math> |
and,
|
<math>~r_1^2 </math> |
<math>~\equiv</math> |
<math>~[(x^2 + y^2)^{1 / 2} + a]^2 + z^2 \, ,</math> |
|
<math>~r_2^2 </math> |
<math>~\equiv</math> |
<math>~[(x^2 + y^2)^{1 / 2} - a]^2 + z^2 \, ,</math> |
and <math>~\theta</math> has the same sign as <math>~z</math>.
Hence, the potential, <math>~U({\vec{r}}~')</math>, at a point <math>~{\vec{r}}~'</math> due to an arbitrary mass distribution, <math>~\rho({\vec{r}})</math>, is,
|
<math>~U({\vec{r}}~')</math> |
<math>~=</math> |
<math>~-G \iiint \frac{\rho(\vec{r}) d^3r}{|~\vec{r} - {\vec{r}}^{~'} ~|} \, .</math> |
|
|
<math>~=</math> |
<math>~-G \rho_0 a^3 \iiint \frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} \biggl[ \frac{\Theta(\upsilon) \sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta~ d\psi~ \, .</math> |
|
|
<math>~=</math> |
<math>~-G \rho_0 a^3\iiint \biggl[ \frac{\Theta(\upsilon) \sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr]~d\eta~ d\theta~ d\psi~ </math> |
|
|
|
<math>~\times \frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } \sum\limits_{m,n} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} </math> |
|
|
|
<math>~ \times \cos[m(\psi - \psi^')][\cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases} \biggr\} </math> |
This should be compared with,
|
<math>~ \Phi_B(\varpi,\phi,z)</math> |
<math>~=</math> |
<math>~ -G \iiint \frac{1}{|\vec{x}^{~'} - \vec{x}|} ~\rho(\vec{x}^{~'}) d^3x^' </math> |
|
|
<math>~=</math> |
<math>~ -G \iiint \biggl\{ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \biggr\}~ \rho(\varpi^',\phi^',z^') \varpi^' d\varpi^' d\phi^' dz^' </math> |
|
|
<math>~=</math> |
<math>~ -\frac{G}{\pi \sqrt{\varpi}} \iiint\rho(\varpi^',\phi^',z^') \sqrt{\varpi^'} d\varpi^' d\phi^' dz^' \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, , </math> |
The above expression for the potential of a uniform-density torus has been obtained by Wong (1973) from the (double) integral expression,
|
<math>~U(\eta^',\theta^')</math> |
<math>~=</math> |
<math>~ 2\rho_0 a^2 (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \int_{\eta_0}^\infty d\eta \int_{-\pi}^{\pi} \biggl[\frac{\cos[n(\theta - \theta^')]}{(\cosh\eta - \cos\theta)^{5 / 2}} \biggr]d\theta </math> |
|
|
|
<math>~ \times \sinh\eta ~\begin{cases}P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P_{n-1 / 2}(\cosh\eta^') ~Q_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, </math> |
|
Wong (1973), Eq. (2.55) |
||
which is valid for any azimuthal angle, <math>~\psi^'</math>. Notice that the step function, <math>~\Theta(\upsilon)</math>, no longer explicitly appears in this expression for the Coulomb (or gravitational) potential; it has been used to establish the specific limits on the "radial" coordinate integration. Next, he completes the integration over the angle, <math>~\theta</math>, to obtain,
CT99 Coordinates
Eureka! Via his dogged efforts and an extraordinarily in-depth investigation of this problem, in 1999 Howard S. Cohl discovered that, in cylindrical coordinates, the relevant Green's function can be written in a much more compact and much more practical form. Specifically, he realized that,
|
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> |
<math>~=</math> |
<math>~ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \, , </math> |
where,
H. S. Cohl & J. E. Tohline (1999), p. 88, Eqs. (15) & (16)
See also: Selvaggi, Salon & Chari (2007) §II, eq. (5)
and the DLMF's definition of Toroidal Functions, <math>~Q_{m - 1 / 2}^{0}</math>
and, <math>~Q_{m - 1 / 2}</math> is the zero-order, half-(odd)integer degree, Llegendre function of the second kind — also referred to as a toroidal function of zeroth order; see additional details, below. Hence, anywhere along the boundary of our cylindrical-coordinate mesh, a valid expression for the gravitational potential is,
|
<math>~ \Phi_B(\varpi,\phi,z)</math> |
<math>~=</math> |
<math>~ -G \int \frac{1}{|\vec{x}^{~'} - \vec{x}|} ~\rho(\vec{x}^{~'}) d^3x^' </math> |
|
|
<math>~=</math> |
<math>~ -G \int \biggl\{ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \biggr\}~ \rho(\varpi^',\phi^',z^') \varpi^' d\varpi^' d\phi^' dz^' </math> |
|
|
<math>~=</math> |
<math>~ -\frac{G}{\pi \sqrt{\varpi}} \int \rho(\varpi^',\phi^',z^') \sqrt{\varpi^'} d\varpi^' d\phi^' dz^' \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, , </math> |
|
H. S. Cohl & J. E. Tohline (1999), p. 88, Eq. (18) |
||
where, <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0=1</math> and <math>~\epsilon_m = 2</math> for <math>~m\ge 1</math>. Following this discovery, most of my research group's 3D numerical modeling of self-gravitating fluids has been conducted using Toroidal functions instead of Spherical Harmonics to evaluate the boundary potential on our cylindrical-coordinate meshes.
In our accompanying statement of this problem, we have written,
|
<math>~\Phi(R_*,Z_*)</math> |
<math>~=</math> |
<math>~- \frac{2G}{R_*^{1 / 2}} \int\int \varpi^{1 / 2} \mu K(\mu) \rho(\varpi, Z) d\varpi dZ \, ,</math> |
where, <math>~K(\mu)</math> is the complete elliptic integral of the first kind, and,
|
<math>~\mu^2</math> |
<math>~=</math> |
<math>~ \biggl[\frac{4R_*\varpi}{(R_* + \varpi)^2 + (Z_* - Z)^2} \biggr] \, . </math> |
Observer Toroidal Coordinates
Our Mucking Around
Begins on p. 332 of M. Abramowitz & I. A. Stegun (1995)
Recurrence Relations
According to M. Abramowitz & I. A. Stegun (1995), both <math>~P_\nu^\mu</math> and <math>~Q_\nu^\mu</math> satisfy the same recurrence relations.
|
<math>~P_\nu^{\mu+1}(z)</math> |
<math>~=</math> |
<math>~ (z^2 - 1)^{- 1 / 2} \biggl[ (\nu - \mu)z P_\nu^\mu(z) - (\nu + \mu)P_{\nu - 1}^\mu(z) \biggr] \, ; </math> |
|
<math>~(z^2-1) \frac{dP_\nu^{\mu}(z)}{dz}</math> |
<math>~=</math> |
<math>~ (\nu + \mu)(\nu - \mu +1_(z^2-1)^{1 / 2} P_\nu^{\mu - 1}(z) - \mu zP_\nu^\mu(z) \, ; </math> |
|
<math>~(\nu - \mu + 1)P_{\nu + 1}^{\mu}(z)</math> |
<math>~=</math> |
<math>~ (2\nu+1)zP_\nu^\mu (z) -(\nu + \mu)P_{\nu-1}^\mu(z) \, ; </math> |
|
<math>~(z^2-1) \frac{dP_\nu^{\mu}(z)}{dz}</math> |
<math>~=</math> |
<math>~ \nu z P_\nu^{\mu }(z) - (\nu + \mu)P_{\nu-1}^\mu(z) \, . </math> |
|
According to equation (14) of A. B. Basset (1893, American Journal of Mathematics, vol. 15, No. 4, pp. 287 - 302),
After replacing, <math>~n</math>, with <math>~(n + \tfrac{1}{2})</math>,
The coefficients of this last expression precisely match the coefficients in the above expression provided by M. Abramowitz & I. A. Stegun (1995), but the subscript notation is off by <math>~\tfrac{1}{2}</math>. This inconsistency most likely should be blamed on the notation adopted by Basset (1893). At the top of his p. 289 — which is a couple of pages before his equation (14) — Basset says: A toroidal function is an associated function of degree <math>~n - \tfrac{1}{2}</math> and order <math>~m</math>; and the notation which ought in strictness to be adopted for the two kinds of toroidal functions is <math>~P_{n-1 / 2}^m</math> and <math>~Q_{n-1 / 2}^m</math>; but as these functions rarely if ever occur in an investigation which also involves associated functions of integral degree <math>~n</math>, it will be generally sufficient to employ the suffix <math>~n</math> instead of <math>~n - \tfrac{1}{2}</math>. Thus, we probably should have shifted the subscript notation in his equation (14) by "-½" before incorporating our additional replacement everywhere of <math>~n</math> by <math>~(n + \tfrac{1}{2})</math>.
Independently, from equation (56) of Basset's (1888, Cambridge: Beighton, Bell and Co.) A Treatise on Hydrodynamics, we have,
This matches the Abramowitz & Stegun expression if, as before, we employ the mapping, <math>~n \rightarrow n-\tfrac{1}{2}</math>, in the subscripts only; also, note that, due to what must have been a typesetting error, the coefficient, <math>~C</math>, in Basset's expression must be replaced by the independent variable, <math>~\nu</math>. From equations (57) - (60) of Basset's (1888) Hydrodynamics, we also obtain,
where,
|
Toroidal Functions
Relationship between one another, as per equation (8) in A. Gil, J. Segura, & N. M. Temme (2000, JCP, 161, 204 - 217):
|
<math>~Q_{n-1 / 2}^m (\lambda)</math> |
<math>~=</math> |
<math>~(-1)^n \frac{\pi^{3/2}}{\sqrt{2}~ \Gamma(n-m+1 / 2)} (x^2-1)^{1 / 4} P_{m-1 / 2}^n(x) \, , </math> |
|
|
Gil, Segura, & Temme (2000): eq. (8) |
|||
| where: |
<math>~\lambda \equiv x/\sqrt{x^2-1}</math> |
Note that the relationship between <math>~\lambda</math> and <math>~x</math> is the same as the relationship between <math>~\cosh\alpha</math> and <math>~\coth\alpha</math>, that is,
|
<math>~\coth\alpha</math> |
<math>~=</math> |
<math>~\frac{\pm \cosh\alpha}{ \sqrt{\cosh^2\alpha - 1}} \, ;</math> |
or |
<math>~\cosh\alpha</math> |
<math>~=</math> |
<math>~\frac{1}{\sqrt{1-\tanh^2\alpha}} </math> |
<math>~=</math> |
<math>~\frac{\pm \coth\alpha}{ \sqrt{\coth^2\alpha - 1 }} \, .</math> |
Relation to Elliptic Integrals
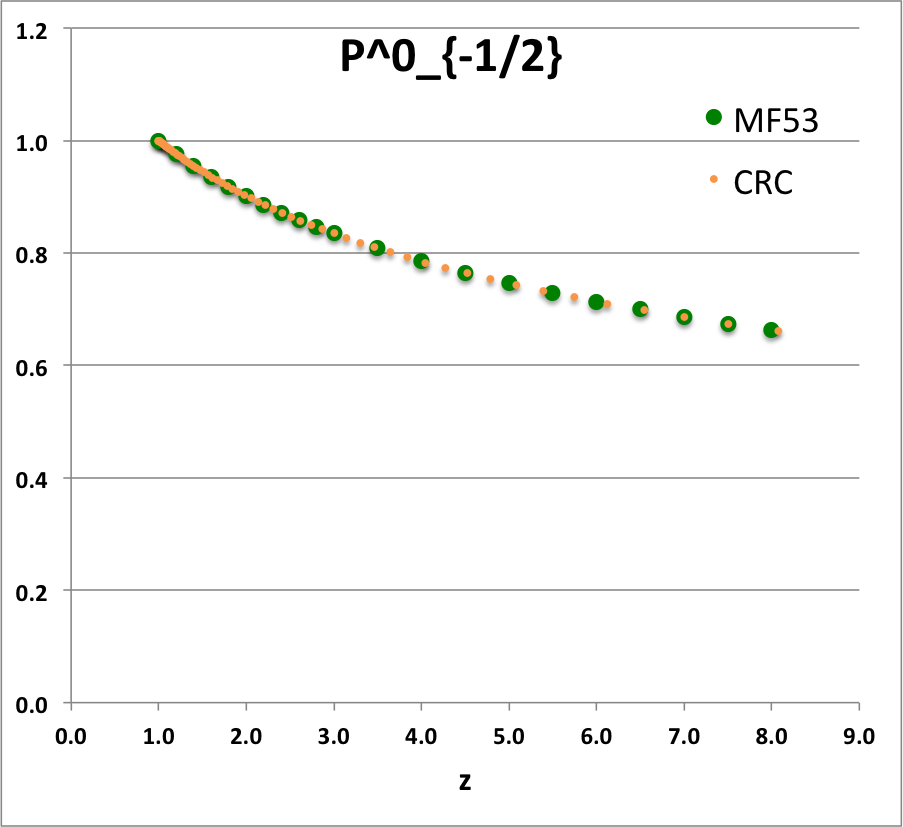
PminusHalf01
|
<math>~P_{-\frac{1}{2}}(z)</math> |
<math>~=</math> |
<math>~ \frac{2}{\pi} \biggl[\frac{2}{z+1}\biggr]^{1 / 2} ~K\biggl( \sqrt{ \frac{z-1}{z+1}} \biggr) </math> |
for example … |
<math>~P_{-\frac{1}{2}}(\cosh\eta)</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{\pi}{2} \cdot \cosh \frac{\eta}{2} \biggr]^{-1} K\biggl( \tanh \frac{\eta}{2} \biggr) </math> |
|
|
Abramowitz & Stegun (1995), p. 337, eq. (8.13.1) |
Abramowitz & Stegun (1995), p. 337, eq. (8.13.2) |
||||||
|
Proof that these are the same expressions: |
||||||||||||||
|
From standard relationships between hyperbolic functions, we know that,
So, if we let <math>~u \equiv \eta/2</math> and make the association,
Also,
Q.E.D. |
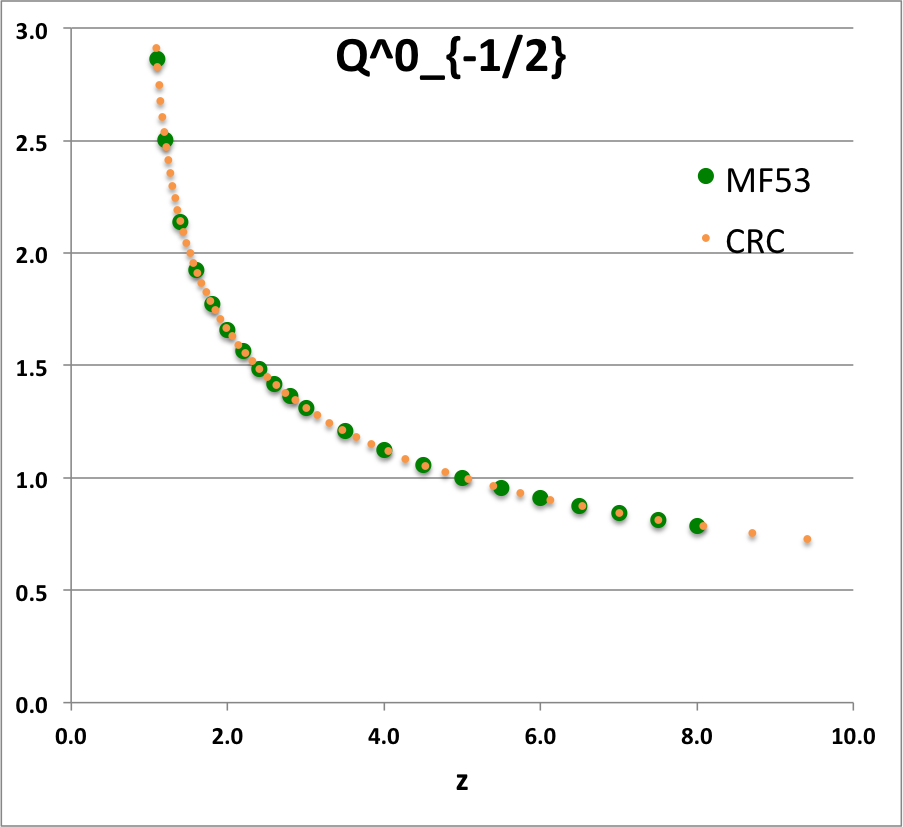
QminusHalf01
|
<math>~Q_{-\frac{1}{2}}(z)</math> |
<math>~=</math> |
<math>~ \sqrt{ \frac{2}{z+1} } ~K\biggl( \sqrt{ \frac{2}{z+1}} \biggr) </math> |
for example … |
<math>~Q_{-\frac{1}{2}}(\cosh\eta)</math> |
<math>~=</math> |
<math>~ 2 e^{-\eta/2} K(e^{-\eta}) </math> |
|
|
Abramowitz & Stegun (1995), p. 337, eq. (8.13.3) |
Abramowitz & Stegun (1995), p. 337, eq. (8.13.4) |
||||||
|
Proof that these are the same expressions: |
|||||||||||||||||||||||||||||||||
|
Copying the Whipple's formula from §14.19 of DLMF,
then setting <math>~m = n = 0</math>, we have,
Step #1: Associate … <math>z \leftrightarrow \cosh\xi</math>. Then,
Step #2: Now making the association … <math>\Lambda \leftrightarrow z/\sqrt{z^2-1}</math>, we can write,
Step #3: Again, making the association … <math>z \leftrightarrow \cosh\xi</math>, means,
which, apart from the leading factor of <math>~\pi^{-1 / 2}</math>, exactly matches the above expression. Note: From Howard Cohl's online overview — see, also, below — we find that the Whipple formula is slightly different from the one (quoted above) drawn from DLMF. According to Cohl the Whipple formula should be,
The DLMF expression needs to be multiplied by <math>~(-1)^m\Gamma (m + n + \tfrac{1}{2} )</math> in order to match the expression provided by Cohl; for the case being considered here of <math>~m=n=0</math>, this factor is precisely <math>~\Gamma(\tfrac{1}{2}) = \sqrt{\pi}</math> — see, for example, Wikipedia's discussion of the gamma function — which cancels this confusing factor of <math>~\pi^{-1 / 2}</math>. |
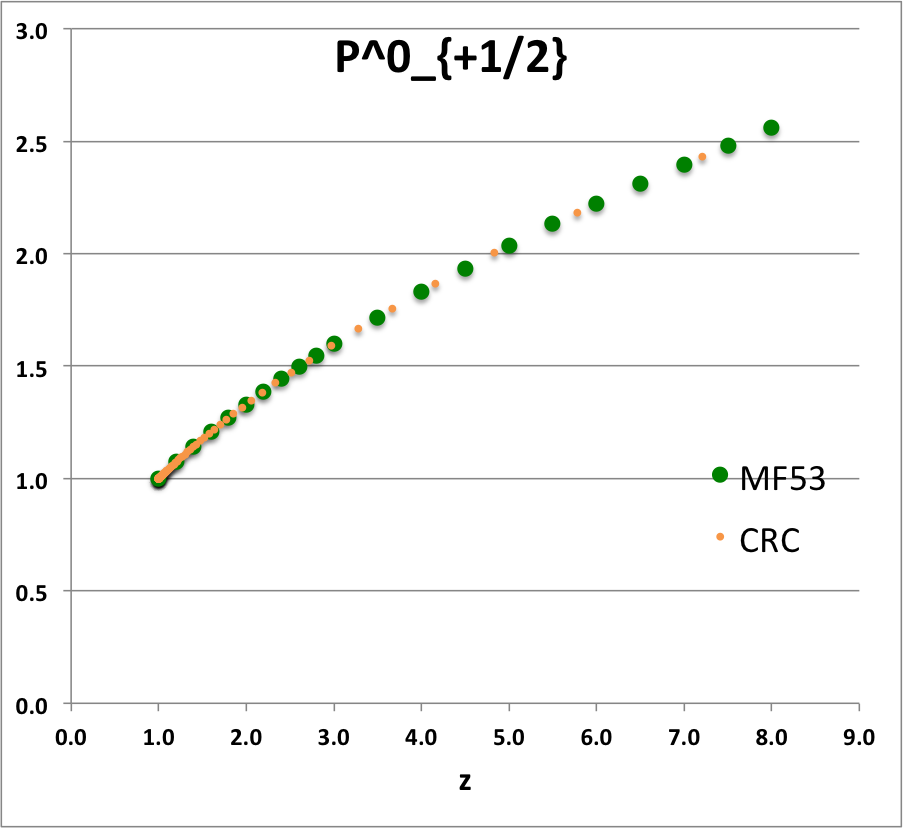
PplusHalf01
|
<math>~P_{+ \frac{1}{2}}(z)</math> |
<math>~=</math> |
<math>~ \frac{2}{\pi} \biggl[z + \sqrt{ z^2-1} \biggr]^{1 / 2} ~E\biggl( \sqrt{ \frac{2(z^2-1)^{1 / 2}}{z + (z^2-1)^{1 / 2}}} \biggr) </math> |
for example … |
<math>~P_{+ \frac{1}{2}}(\cosh\eta)</math> |
<math>~=</math> |
<math>~ \frac{2}{\pi}~e^{\eta/2}~ E( \sqrt{1-e^{-2\eta}} ) </math> |
|
|
Abramowitz & Stegun (1995), p. 337, eq. (8.13.5) |
Abramowitz & Stegun (1995), p. 337, eq. (8.13.6) |
||||||
|
Proof that these are the same expressions: |
|||||||||||||||||||||||||||
|
If we associate,
It also means that,
Q.E.D. |
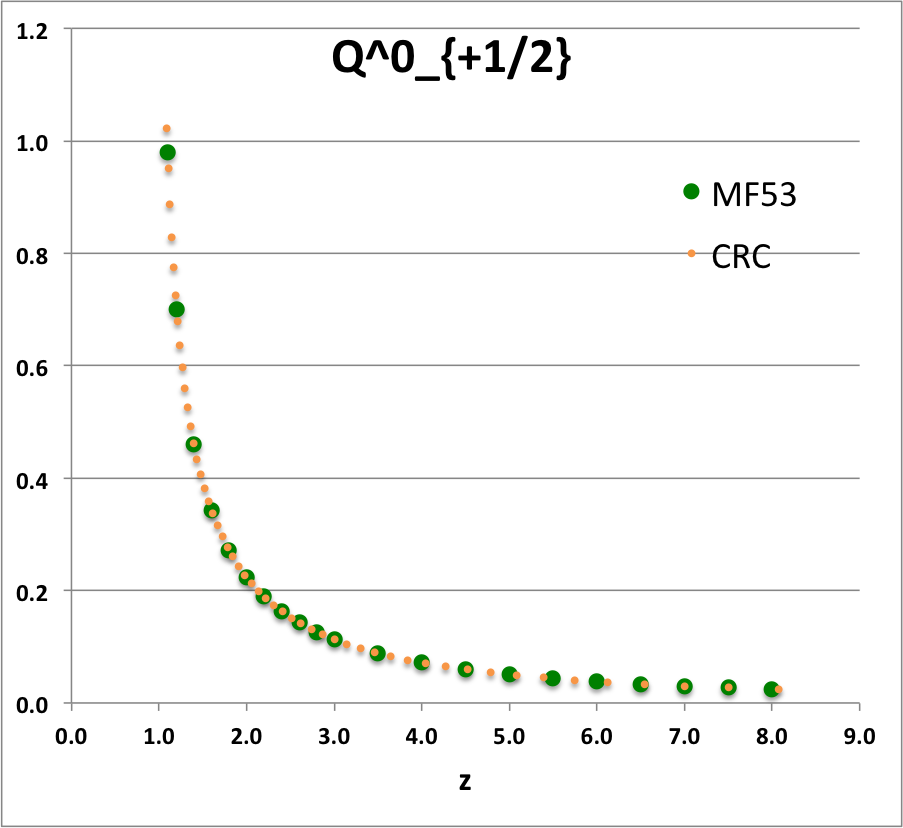
QplusHalf01
|
<math>~Q_{+\frac{1}{2}}(z)</math> |
<math>~=</math> |
<math>~ z \sqrt{ \frac{2}{z+1} }~K\biggl( \sqrt{ \frac{2}{z+1} } \biggr) ~-~ [2(z+1)]^{1 / 2} E\biggl( \sqrt{ \frac{2}{z+1} } \biggr) </math> |
|
|
Abramowitz & Stegun (1995), p. 337, eq. (8.13.7) |
|||
Other
When the argument, <math>~x</math>, lies in the range, <math>~-1 < x < 1</math>:
|
<math>~P_{-1 / 2}(x)</math> |
<math>~=</math> |
<math>~ \frac{2}{\pi} ~K\biggl( \sqrt{ \frac{1-x}{2} } \biggr) \, ; </math> |
|
<math>~P_{-1 / 2}(\cos\theta)</math> |
<math>~=</math> |
<math>~ \frac{2}{\pi} ~K\biggl( \sin \frac{\theta}{2}\biggr) \, ; </math> |
|
<math>~Q_{-1 / 2}(x)</math> |
<math>~=</math> |
<math>~ K\biggl( \sqrt{ \frac{1+x}{2} } \biggr) \, ; </math> |
|
<math>~P_{+1 / 2}(x)</math> |
<math>~=</math> |
<math>~ \frac{2}{\pi} \biggl[2E\biggl( \sqrt{ \frac{1-x}{2} } \biggr) - ~K\biggl( \sqrt{ \frac{1-x}{2} } \biggr) \biggr] \, ; </math> |
|
<math>~Q_{+ 1 / 2}(x)</math> |
<math>~=</math> |
<math>~ K\biggl( \sqrt{ \frac{1+x}{2} } \biggr) - 2E\biggl( \sqrt{ \frac{1+x}{2} } \biggr)\, ; </math> |
Piece Together
When <math>~\mu = 0</math>, and <math>~\nu = (m- 3/ 2)</math>, the recurrence relation should be …
|
<math>~(m - \tfrac{1}{2})P_{m-1 / 2}(z)</math> |
<math>~=</math> |
<math>~ [2m-2]zP_{m-3 / 2} (z) -(m - \tfrac{3}{2} )P_{m - 5 / 2} (z) </math> |
|
<math>~\Rightarrow ~~~(2m -1)P_{m - 1 / 2}(z)</math> |
<math>~=</math> |
<math>~ 4(m-1)zP_{m - 3 /2 } (z) - (2m -3)P_{m-5 / 2} (z) </math> |
|
<math>~\Rightarrow ~~~P_{m - 1 / 2}(z)</math> |
<math>~=</math> |
<math>~\biggl[ \frac{ 4(m-1)zP_{m - 3 /2 } (z) - (2m -3)P_{m-5 / 2} (z) }{(2m -1)} \biggr] \, , </math> |
for all <math>~m \ge 2</math>.
Overview by Howard Cohl
This subsection is drawn verbatim from Howard Cohl's online overview of toroidal functions.
… These last two expressions allow us to express toroidal functions of a certain kind (first or second, respectively) with argument hyperbolic cosine, as a direct proportionality in terms of the toroidal function of the other kind (second or first, respectively) with argument hyperbolic cotangent. The Whipple formulae may also be expressed as follows:
|
<math>~Q^n_{m- 1 / 2}(\cosh\alpha)</math> |
<math>~=</math> |
<math>~(-1)^n ~\Gamma(n-m + \tfrac{1}{2}) \biggl[ \frac{\pi}{2\sinh\alpha} \biggr]^{1 / 2} P^m_{n- 1 / 2}(\coth\alpha)\, , </math> |
| … and … | ||
|
<math>~Q^n_{m- 1 / 2}(\coth\alpha)</math> |
<math>~=</math> |
<math>~(-1)^m ~\frac{\pi}{\Gamma(m-n + \tfrac{1}{2})} \biggl[ \frac{\pi \sinh\alpha}{2} \biggr]^{1 / 2} P^m_{n- 1 / 2}(\cosh\alpha) \, . </math> |
These interesting formulae have the property that they can relate Legendre functions of the first and second kinds directly in terms of each other. The only hitch is that you need a different argument to relate them. The way it works is as such. The Legendre functions of the first kind generally are well-behaved near the origin and blow up at positive infinity. Consequently the Legendre functions of the second kind blow up at unity and exponentially converges towards zero for large values of the argument. The relevant domain for toroidal functions is from 1 to infinity. The standard hyperbolic argument for these functions are naturally chosen to be the hyperbolic cosine since it ranges from 1 to infinity. The Whipple formulae relate the Legendre functions with argument 1 to infinity, cosh, to a reversed range given by the hyperbolic cotangent function. the hyperbolic cotangent function ranges from infinity at unity to unity at infinity. At what point alpha does cosh alpha equal coth alpha? The point alpha is given by
|
<math>~\alpha</math> |
<math>~=</math> |
<math>~ \ln(1+\sqrt{2}) \cong 0.88137359 \, . </math> |
Therefore, <math>~e^\alpha</math> and <math>~e^{-\alpha}</math> are given, respectively, by
|
<math>~e^\alpha</math> |
<math>~=</math> |
<math>~ \sqrt{2} + 1 \cong 2.41421356 \, , </math> |
and |
<math>~e^{-\alpha}</math> |
<math>~=</math> |
<math>~ \sqrt{2} - 1 \cong 0.41421356 \, . </math> |
The value that <math>~\cosh \alpha</math> and <math>~\coth \alpha</math> obtain at <math>~\alpha</math> is given by
|
<math>~\cosh\alpha = \coth\alpha</math> |
<math>~=</math> |
<math>~ \sqrt{2} \cong 1.41421356 \, . </math> |
The value that <math>~1/\cosh\alpha</math> and <math>~\tanh \alpha</math> obtain at <math>~\alpha</math> is given by
|
<math>~\frac{1}{\cosh\alpha} = \tanh\alpha</math> |
<math>~=</math> |
<math>~ \frac{1}{\sqrt{2}} \cong 0.70710678 \, . </math> |
Finally, <math>~\sinh \alpha</math> and it's inverse are given respectively by unity,
|
<math>~\sinh\alpha = \frac{1}{\sinh\alpha} </math> |
<math>~=</math> |
<math>~ 1 \, . </math> |
We now see that the value at which the argument of the Legendre functions inversely maps the entire domain is given by cosh alpha = coth alpha ~ 1.4142356. By using the Whipple formulae for ring functions, we can inversely map the entire domain from 1 to infinity about this point cosh alpha, the square root of 2, and take full advantage of this new symmetry for Legendre functions. There being previously more definite and indefinite integrals tabulated for the Legendre function of the first kind than for the Legendre function of the second kind. In fact, this new transformation, when applied to toroidal functions yields distinct expressions which relate correspondingly the complete elliptic integrals of the first and second kind, which don't seem to be related to the linear and quadratic transformations of hypergeometric functions.
Note that, as shown above, Gil, et al. (2000) state:
|
<math>~Q_{n-1 / 2}^m (\lambda)</math> |
<math>~=</math> |
<math>~(-1)^n \frac{\pi^{3/2}}{\sqrt{2}~ \Gamma(n-m+1 / 2)} (x^2-1)^{1 / 4} P_{m-1 / 2}^n(x) \, , </math> |
|
|
Gil, Segura, & Temme (2000): eq. (8) |
|||
| where: |
<math>~\lambda \equiv x/\sqrt{x^2-1}</math> |
Hence, if we swap the indexes, <math>~m\leftrightarrow n</math>, and make the assignments, <math>~x \leftrightarrow \cosh\alpha</math> and <math>~\lambda \leftrightarrow \coth\alpha</math>, this last relation becomes,
|
<math>~Q_{m-1 / 2}^n (\coth\alpha)</math> |
<math>~=</math> |
<math>~(-1)^m \frac{\pi^{3/2}}{\sqrt{2} \Gamma(m-n+1 / 2)} (\cosh^2\alpha-1)^{1 / 4} P_{n-1 / 2}^m(\cosh\alpha) </math> |
|
|
<math>~=</math> |
<math>~(-1)^m \frac{\pi}{ \Gamma(m-n+1 / 2)} \biggl[ \frac{\pi\sinh\alpha }{2} \biggr]^{1 / 2} P_{n-1 / 2}^m(\cosh\alpha) </math> |
Alternatively, if we swap the indexes, <math>~m\leftrightarrow n</math>, and make the assignments, <math>~x \leftrightarrow \coth\alpha</math> and <math>~\lambda \leftrightarrow \cosh\alpha</math>, the Gil, et al. (2000) relation becomes,
|
<math>~Q_{m-1 / 2}^n (\cosh\alpha)</math> |
<math>~=</math> |
<math>~(-1)^m \frac{\pi^{3/2}}{\sqrt{2} \Gamma(m-n+1 / 2)} (\coth^2\alpha-1)^{1 / 4} P_{n-1 / 2}^m(\coth\alpha) </math> |
|
|
<math>~=</math> |
<math>~(-1)^m \frac{\pi}{ \Gamma(m-n+1 / 2)} \biggl[ \frac{ \pi}{2\sinh\alpha} \biggr]^{1 / 2} P_{n-1 / 2}^m(\coth\alpha) </math> |
However, in our situation the so-called "Euler reflection formula for gamma functions" gives the relation,
|
<math>~ \Gamma(z) ~\Gamma(1-z) </math> |
<math>~=</math> |
<math>~ \frac{\pi}{\sin(\pi z)} </math> |
<math>~\biggl|</math> |
for example, if
|
||||||||
| <math>~\biggl|</math> | ||||||||||||
| Valid for: |
<math>~z \ne0, \pm 1, \pm 2, </math> … |
<math>~\biggl|</math> | ||||||||||
that is,
|
<math>~\frac{\pi (-1)^{m}}{\Gamma(m-n+\frac{1}{2}) }</math> |
<math>~=</math> |
<math>~(-1)^{n}\Gamma(n-m+\tfrac{1}{2}) \, .</math> |
So,
|
<math>~Q_{m-1 / 2}^n (\cosh\alpha)</math> |
<math>~=</math> |
<math>~ (-1)^{n}\Gamma(n-m+\tfrac{1}{2})\biggl[ \frac{ \pi}{2\sinh\alpha} \biggr]^{1 / 2} P_{n-1 / 2}^m(\coth\alpha) </math> |
We see, then, that we are able to generate both of Cohl's relations from the Gil et al. relation. Yeah!
Drawn From Discussion of Solving the Poisson Equation
The following has been copied (May 2018) from an accompanying chapter that presents the integral representation of the Poisson equation in terms of toroidal functions.
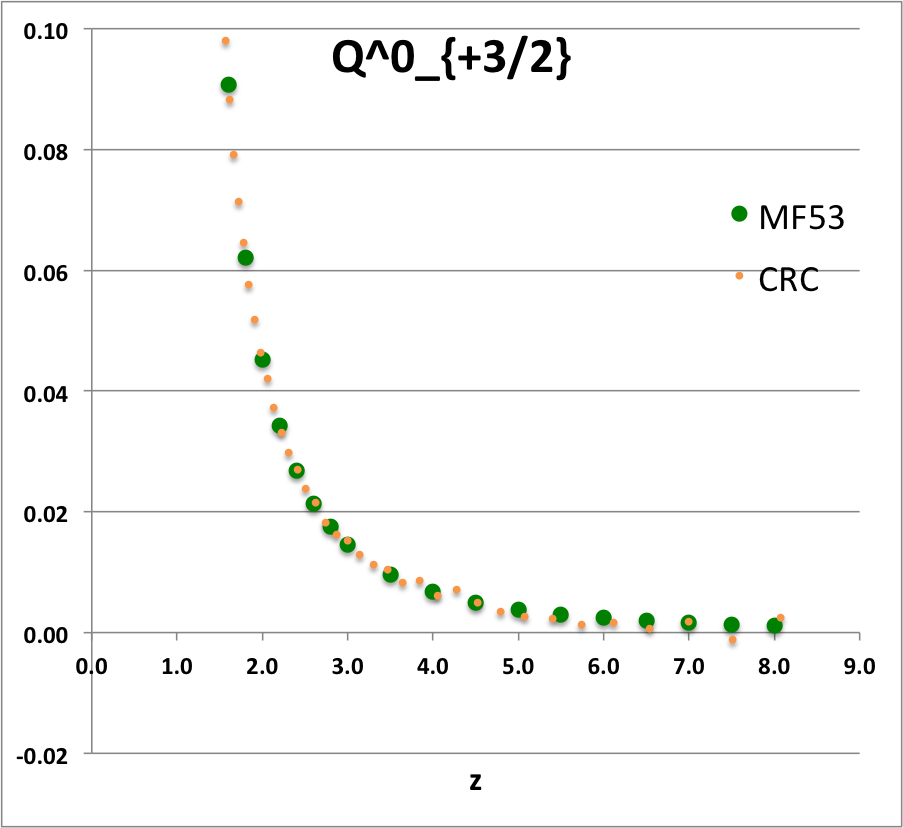
| Table 5: Green's Function in Terms of Zero Order, Half-(Odd)Integer Degree, Associated Legendre Functions of the Second Kind, <math>~Q^0_{m-1 / 2}(\chi)</math> (also referred to as Toroidal Functions) |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
where: <math>~\chi \equiv \frac{\varpi^2 + (\varpi^')^2 + (z - z^')^2}{2\varpi \varpi^'}</math>
H. S. Cohl & J. E. Tohline (1999), p. 88, Eqs. (15) & (16) |
||||||||||||||||||
|
Note that, according to, for example, equation (8.731.5) of Gradshteyn & Ryzhik (1994), <math>~Q^0_{-m - 1 / 2}(\chi) = Q^0_{m- 1 / 2}(\chi) \, .</math> Hence, the Green's function can straightforwardly be rewritten in terms of a simpler summation over just non-negative values of the index, <math>~m</math>. |
||||||||||||||||||
|
Referencing equations (8.13.3) and (8.13.7), respectively, of Abramowitz & Stegun (1965), we see that for the smallest two values of the non-negative index, <math>~m</math>, the function, <math>~Q_{m- 1 / 2}(\chi)</math>, can be rewritten in terms of, the more familiar, complete elliptic integrals of the first and second kind. Specifically,
Excerpt from p. 337 of M. Abramowitz & I. A. Stegun (1995) |
||||||||||||||||||
|
Finally, equation (8.5.3) from Abramowitz & Stegun (1965) or equation (8.832.4) of Gradshteyn & Ryzhik (1994) — also see equation (2) of Gil, Segura & Temme (2000) — provide the recurrence relation for all other values of the index, <math>~m</math>. Specifically, for all <math>~m \ge 2</math>, <math>~Q_{m - 1 / 2}(\chi) = 4\biggl[\frac{m-1}{2m-1}\biggr] \chi Q_{m- 3 / 2}(\chi) - \biggl[ \frac{2m-3}{2m-1}\biggr] Q_{m- 5 / 2}(\chi) \, .</math> Excerpt from p. 490 of W. Guatschi (1965, Communications of the ACM, 8, 488 - 492) |
||||||||||||||||||
Just Compare Green Functions
First Dabbling
According to CT99, the Green's function written in toroidal coordinates is,
|
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> |
<math>~=</math> |
<math>~ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=-\infty}^{\infty} e^{im(\phi - \phi^')}Q_{m- 1 / 2}(\chi) \, , </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, , </math> |
where,
and, <math>~Q_{m - 1 / 2}</math> is the zero-order, half-(odd)integer degree, Llegendre function of the second kind — also referred to as a toroidal function of zeroth order.
From the Dyson-Wong Toroid chapter,
|
<math>~\varpi</math> |
<math>~=</math> |
<math>~\frac{a \sinh\eta }{(\cosh\eta - \cos\theta)} \, ,</math> |
|
<math>~z</math> |
<math>~=</math> |
<math>~\frac{a \sin\theta}{(\cosh\eta - \cos\theta)} \, .</math> |
Hence, we can rewrite the Green's function as,
|
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> |
<math>~=</math> |
<math>~ \frac{1}{\pi} \biggl[ \frac{a \sinh\eta^' }{(\cosh\eta^' - \cos\theta^')} \frac{a \sinh\eta }{(\cosh\eta - \cos\theta)}\biggr]^{- 1 / 2} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\pi a} [\sinh\eta^' \sinh\eta]^{- 1 / 2} \biggl[ (\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta)\biggr]^{1 / 2} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) </math> |
Wong (1973) states that in toroidal coordinates the Green's function is,
|
<math>~\frac{1}{|~\vec{r} - {\vec{r}}^{~'} ~|} </math> |
<math>~=</math> |
<math>~ \frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } \sum\limits_{m,n} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} </math> |
|
|
|
<math>~ \times \cos[m(\psi - \psi^')][\cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, , </math> |
|
Wong (1973), Eq. (2.53) |
||
where, <math>~P^m_{n-1 / 2}, Q^m_{n-1 / 2}</math> are "Legendre functions of the first and second kind with order <math>~n - \tfrac{1}{2}</math> and degree <math>~m</math> (toroidal harmonics)," and <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0 = 1</math> and <math>~\epsilon_m = 2</math> for all <math>~m \ge 1</math>,
|
<math>~\eta</math> |
<math>~=</math> |
<math>~\ln\biggl(\frac{r_1}{r_2} \biggr) \, ,</math> |
|
<math>~\cos\theta</math> |
<math>~=</math> |
<math>~\frac{(r_1^2 + r_2^2 - 4a^2)}{2r_1 r_2} \, ,</math> |
|
<math>~\tan\psi</math> |
<math>~=</math> |
<math>~\frac{y}{x} \, ,</math> |
and,
|
<math>~r_1^2 </math> |
<math>~\equiv</math> |
<math>~[(x^2 + y^2)^{1 / 2} + a]^2 + z^2 \, ,</math> |
|
<math>~r_2^2 </math> |
<math>~\equiv</math> |
<math>~[(x^2 + y^2)^{1 / 2} - a]^2 + z^2 \, ,</math> |
and <math>~\theta</math> has the same sign as <math>~z</math>.
Note that:
|
<math>~\cosh\eta</math> |
<math>~=</math> |
<math>~\frac{1}{2}\biggl[ e^\eta + e^{-\eta} \biggr] = ~\frac{1}{2}\biggl[ \frac{r_1}{r_2} + \frac{r_2}{r_1}\biggr]</math> |
|
|
<math>~=</math> |
<math>~\frac{1}{2}\biggl[ \frac{\sqrt{[ \varpi + a]^2 + z^2}}{\sqrt{[ \varpi - a]^2 + z^2}} + \frac{\sqrt{[ \varpi - a]^2 + z^2}}{\sqrt{[ \varpi + a]^2 + z^2}}\biggr]</math> |
|
<math>~\Rightarrow ~~~ 4\cosh^2\eta</math> |
<math>~=</math> |
<math>~\biggl\{ \frac{ [( \varpi + a)^2 + z^2]^{1 / 2} }{ [( \varpi - a)^2 + z^2]^{1 / 2}} + \frac{[( \varpi - a)^2 + z^2]^{1 / 2}}{ [( \varpi + a)^2 + z^2]^{1 / 2} }\biggr\}^2</math> |
|
<math>~\Rightarrow ~~~ 4\cosh^2\eta~ [( \varpi + a)^2 + z^2] [( \varpi - a)^2 + z^2]</math> |
<math>~=</math> |
<math>~\biggl\{ [( \varpi + a)^2 + z^2] + [( \varpi - a)^2 + z^2] \biggr\}^2</math> |
|
<math>~\Rightarrow ~~~ 4\cosh^2\eta~ [ \varpi^2 + 2a\varpi + a^2 + z^2] [ \varpi^2 -2a\varpi + a^2 + z^2]</math> |
<math>~=</math> |
<math>~4 [ \varpi^2 + a^2 + z^2]^2</math> |
|
<math>~\Rightarrow ~~~ \frac{ [ \varpi^2 + a^2 + z^2]^2}{\cosh^2\eta} </math> |
<math>~=</math> |
<math>~ [ \varpi^4 -2a\varpi^3 + a^2\varpi^2 + \varpi^2 z^2 + 2a\varpi^3 - 4a^2\varpi^2 +2a^3\varpi + 2a\varpi z^2 + a^2\varpi^2 - 2a^3\varpi + a^4 + a^2z^2 + \varpi^2 z^2 -2a\varpi z^2 +a^2z^2 + z^4 ] </math> |
|
|
<math>~=</math> |
<math>~ [ \varpi^4 + 2\varpi^2 z^2 - 2a^2\varpi^2 + a^4 + 2a^2z^2 + z^4 ] </math> |
Second Dabbling
If <math>~\eta = \ln(r_1/r_2)</math>, as defined by Wong, then we can show that,
|
<math>~\coth\eta</math> |
<math>~=</math> |
<math>~ \frac{ \varpi^2 + a^2 + z^2 }{ 2a\varpi } \, . </math> |
This expression matches the expression for <math>~\Chi</math>, as defined in the CT99; see, for example, our accompanying discussion,
|
<math>~\Chi</math> |
<math>~=</math> |
<math>~ \frac{ \varpi^2 + R_*^2 + (Z_* -Z)^2 }{ 2R_*\varpi } \, . </math> |
It is the context of the CT99 derivation that we state,
<math>Q_{-1/2}(\Chi)= Q_{-1/2}(\coth\eta) = \mu K(\mu) \, ,</math>
where the argument of the elliptic integral is related to <math>~\Chi</math> via the relation,
|
<math>~\mu^2</math> |
<math>~\equiv</math> |
<math>~\frac{2}{1+\Chi}</math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{4R_*\varpi}{(R_* + \varpi)^2 + (Z_* - Z)^2} \biggr] \, . </math> |
|
In a separate discussion, we have derived expressions for the quantities, <math>~\Chi</math> and <math>~\mu^2</math>, in terms of Wong's toroidal coordinates. |
We note that, while the argument of the CT99 toroidal function is <math>~\coth\eta</math>, the argument of Wong's toroidal function is <math>~\cosh\eta</math>. It should be useful to keep in mind, therefore, that you can move back and forth between <math>~\coth\eta</math> and <math>~\cosh\eta</math> via the mapping (in either direction),
|
<math>~\lambda</math> |
<math>~=</math> |
<math>~\frac{ x }{ \sqrt{x^2-1} } \, .</math> |
Hence, for example, we have,
|
<math>~\cosh^2\eta</math> |
<math>~=</math> |
<math>~\coth^2\eta \biggl[ \coth^2\eta-1 \biggr]^{-1}</math> |
|
|
<math>~=</math> |
<math>~\biggl[\frac{ \varpi^2 + a^2 + z^2 }{ 2a\varpi } \biggr]^{2} \biggl\{ \biggl[\frac{ \varpi^2 + a^2 + z^2 }{ 2a\varpi } \biggr]^{2}-1 \biggr\}^{-1}</math> |
|
<math>~\Rightarrow ~~~ \biggl[ \frac{\varpi^2 + a^2 + z^2}{\cosh\eta} \biggr]^2</math> |
<math>~=</math> |
<math>~4a^2\varpi^2 \biggl\{ \biggl[\frac{ \varpi^2 + a^2 + z^2 }{ 2a\varpi } \biggr]^{2}-1 \biggr\}</math> |
|
|
<math>~=</math> |
<math>~ [ \varpi^2 + a^2 + z^2 ]^{2} - 4a^2\varpi^2 </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ ( \varpi^2 + a^2 + z^2 ) + 2a \varpi \biggr] \biggl[ ( \varpi^2 + a^2 + z^2 ) - 2a \varpi \biggr]</math> |
|
|
<math>~=</math> |
<math>~ [ (\varpi + a)^2 + z^2 ] [ (\varpi - a)^2 + z^2 ] </math> |
|
<math>~\Rightarrow ~~~\cosh\eta</math> |
<math>~=</math> |
<math>~ \biggl\{ \frac{ [ \varpi^2 + a^2 + z^2 ]^2 }{ [ (\varpi + a)^2 + z^2 ] [ (\varpi - a)^2 + z^2 ] } \biggr\}^{1 / 2} \, .</math> |
So, according to Wong, for <math>~\eta^' > \eta</math>, the axisymmetric potential is,
|
<math>~U(\eta^',\theta^')\biggr|_\mathrm{ axi }</math> |
<math>~=</math> |
<math>~ 2\rho_0 a^2 (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \int_{\eta_0}^\infty d\eta \int_{-\pi}^{\pi} \biggl[\frac{\cos[n(\theta - \theta^')]}{(\cosh\eta - \cos\theta)^{5 / 2}} \biggr]d\theta </math> |
|
|
|
<math>~ \times \sinh\eta ~\begin{cases}P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P_{n-1 / 2}(\cosh\eta^') ~Q_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, </math> |
|
Wong (1973), Eq. (2.55) |
||
|
<math>~U(\eta^',\theta^')\biggr|_\mathrm{ axi }</math> |
<math>~=</math> |
<math>~ 2\rho_0 a^2 (\cosh \eta^' - \cos \theta^')^{1 / 2} \sum\limits_n \epsilon_n \int_{\eta_0}^\infty \int_{-\pi}^{\pi} \biggl[\frac{\cos[n(\theta - \theta^')]}{(\cosh\eta - \cos\theta)^{5 / 2}} \biggr] \sinh\eta ~P_{n-1 / 2}(\cosh\eta) ~Q_{n-1 / 2}(\cosh\eta^') ~d\theta ~d\eta </math> |
Drawing from equations (2.7), (2.17) and (2.18) of Wong (1973), we see that the volume, <math>~V</math>, of a torus that is bounded by surface <math>~\eta_s</math> is,
|
<math>~\frac{V}{a^3} = \frac{1}{a^3} \iiint\limits_{\eta_s}d^3 r</math> |
<math>~=</math> |
<math>~\iiint\limits_{\eta_s} \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta~ d\psi~ = \frac{2\pi^2\cosh{\eta_s}}{\sinh^3\eta_s} \, .</math> |
This means that, in toroidal coordinates, just the integration over the azimuthal angle,
|
<math>~\frac{1}{a^3} \iiint\limits_{\eta_s}d^3 r</math> |
<math>~=</math> |
<math>~2\pi \iint\limits \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta \, .</math> |
To be compared with the same expression in cylindrical coordinates,
|
<math>~\frac{1}{a^3} \iiint\limits_{\eta_s}d^3 r</math> |
<math>~=</math> |
<math>~\frac{2\pi}{a^3} \iint\limits \varpi ~d\varpi ~dz \, .</math> |
This means that the coordinate mapping is,
|
<math>~\frac{\varpi ~d\varpi ~dz}{a^3} </math> |
<math>~\leftrightarrow</math> |
<math>~\biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta \, .</math> |
This means that the CT99 axisymmetric potential is,
|
<math>~\Phi(R_*,Z_*)\biggr|_\mathrm{ axi }</math> |
<math>~=</math> |
<math>~- 2G \iint \frac{Q_{-1/2}(\coth\eta)}{ (R_* \varpi)^{1 / 2}} \rho(\varpi, Z) ~\varpi~d\varpi dZ</math> |
|
|
<math>~=</math> |
<math>~- 2Ga^3 \iint \frac{Q_{-1/2}(\coth\eta)}{ (R_* \varpi)^{1 / 2}} \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] \rho~d\eta~ d\theta</math> |
Given that,
|
<math>~\frac{ 1 }{ \varpi }</math> |
<math>~=</math> |
<math>~\frac{(\cosh\eta - \cos\theta)}{a \sinh\eta} \, ,</math> |
we therefore have,
|
<math>~\Phi(R_*,Z_*)\biggr|_\mathrm{ axi }</math> |
<math>~=</math> |
<math>~- 2Ga^2\biggl( \frac{a}{R_*}\biggr)^{1 / 2} \iint Q_{-1/2}(\coth\eta) \biggl[ \frac{\sinh\eta}{(\cosh\eta - \cos\theta)^5} \biggr]^{1 / 2} \rho~d\eta~ d\theta</math> |
Third Dabbling
From our "First Dabbling" expression for the Green's Function, we have,
|
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> |
<math>~=</math> |
<math>~ \frac{1}{\pi a} [\sinh\eta^' \sinh\eta]^{- 1 / 2} \biggl[ (\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta)\biggr]^{1 / 2} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\phi - \phi^')] Q_{m- 1 / 2}(\chi) \, . </math> |
And from our examination of the summation expression, we have found that,
|
<math>~ \sum_{n=0}^{\infty} \epsilon_n Q_{n-\frac{1}{2}}\left(\cosh\xi\right) \cos\left(n \phi\right) </math> |
<math>~=</math> |
<math>~ \biggl[ \dfrac{ \pi/\sqrt{2} }{\left(\cosh\xi-\cos\phi\right)^{\frac{1}{2}} }\biggr] \, . </math> |
|
<math>~\Rightarrow ~~~ \sum_{m=0}^{\infty} \epsilon_m Q_{m-\frac{1}{2}} \left(\cosh\xi\right) \cos\left[m( \phi - \phi^')\right] </math> |
<math>~=</math> |
<math>~ \frac{\pi}{\sqrt{2}} \biggl\{ \cosh\xi-\cos\left[( \phi - \phi^')\right]\biggr\}^{ - \frac{1}{2}} \, . </math> |
How does this jive with our separate recognition that,
|
<math>~\chi</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{\cosh\eta \cdot \cosh\eta^' - \cos(\theta^' - \theta) }{ \sinh\eta \cdot \sinh\eta^' } \biggr] \, ; </math> |
Is it completely legitimate to make the association, <math>~\chi \leftrightarrow \cosh\xi</math> ? If so, then the Green's function becomes,
|
<math>~ \frac{1}{|\vec{x} - \vec{x}^{~'}|}</math> |
<math>~=</math> |
<math>~ \frac{1}{a \sqrt{2}} [\sinh\eta^' \sinh\eta]^{- 1 / 2} \biggl[ (\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta)\biggr]^{1 / 2} \biggl\{ \biggl[ \frac{\cosh\eta \cdot \cosh\eta^' - \cos(\theta^' - \theta) }{ \sinh\eta \cdot \sinh\eta^' } \biggr]-\cos\left[( \phi - \phi^')\right]\biggr\}^{ - \frac{1}{2}} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{a \sqrt{2}} \biggl[ \frac{ (\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta) }{ \sinh\eta^' \sinh\eta } \biggr]^{1 / 2} \biggl[ \frac{ \sinh\eta \cdot \sinh\eta^' }{\cosh\eta \cdot \cosh\eta^' - \sinh\eta \cdot \sinh\eta^'\cos ( \phi - \phi^') - \cos(\theta^' - \theta) } \biggr]^{ \frac{1}{2}} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{a \sqrt{2}} \biggl[ \frac{(\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta) }{\cosh\eta \cdot \cosh\eta^' - \sinh\eta \cdot \sinh\eta^'\cos ( \phi - \phi^') - \cos(\theta^' - \theta) } \biggr]^{ \frac{1}{2}} \, . </math> |
See Also
- R. S. Maier (2017) — Associated Legendre Functions and Spherical Harmonics of Fractional Degree and Order
- R. S. Maier (2016, Proceedings of the Royal Society A, Vol. 472, Issue 2188, id. 20160097) — Legendre Functions of Fractional Degree: Transformations and Evaluations

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |