Synopsis of Toroidal Coordinate Approach

Basics

Here we attempt to bring together — in as succinct a manner as possible — our approach and C.-Y. Wong's (1973) approach to determining the gravitational potential of an axisymmetric, uniform-density torus that has a major radius, <math>~R</math>, and a minor, cross-sectional radius, <math>~d</math>. The relevant toroidal coordinate system is one based on an anchor ring of major radius,

<math>~a^2 \equiv R^2 - d^2 \, .</math>

If the meridional-plane location of the anchor ring — as written in cylindrical coordinates — is, <math>~(\varpi, z) = (a,Z_0)</math>, then the preferred toroidal-coordinate system has meridional-plane coordinates, <math>~(\eta, \theta)</math>, defined such that,

<math>~\ln\biggl(\frac{r_1}{r_2} \biggr) \, ,</math>

and,

<math>~\cos\theta</math>

where,

<math>~\equiv</math>

<math>~(\varpi + a)^2 + (z-Z_0)^2 \, ,</math>

and,

<math>~\equiv</math>

<math>~(\varpi - a)^2 + (z-Z_0)^2 \, ,</math>

and <math>~\theta</math> has the same sign as <math>~(z-Z_0)</math>. Mapping the other direction, we have,

<math>~\varpi</math>

<math>~\frac{a \sinh\eta }{(\cosh\eta - \cos\theta)} \, ,</math>

and,

<math>~\frac{a \sin\theta}{(\cosh\eta - \cos\theta)} \, .</math>

The three-dimensional differential volume element is,

<math>\varpi d\varpi ~dz ~d\psi</math>

<math>~\biggl[ \frac{a^3\sinh\eta}{(\cosh\eta - \cos\theta)^3} \biggr] d\eta~ d\theta~ d\psi \, .</math>

Note that, if <math>~\eta_0</math> identifies the surface of the uniform-density torus, then,

and,

and when the integral over the volume element is completed — that is, over all <math>~\psi</math>, over all <math>~\theta</math>, and over the "radial" interval, <math>~\eta_0 \le \eta \le \infty</math> — the resulting volume is,

Also, given that,

<math>~\frac{1}{2}\biggl[ e^\eta + e^{-\eta} \biggr]</math>

and,

<math>~\frac{1}{2}\biggl[ e^\eta - e^{-\eta} \biggr] \, ,</math>

we have,

<math>~\coth\eta</math>	<math>~=</math>	<math>~\biggl[ e^\eta + e^{-\eta} \biggr]\biggl[ e^\eta - e^{-\eta} \biggr]^{-1}</math>	<math>~=</math>	<math>~\biggl[ \frac{r_1}{r_2} + \frac{r_2}{r_1} \biggr]\biggl[ \frac{r_1}{r_2} - \frac{r_2}{r_1} \biggr]^{-1}</math>
	<math>~=</math>	<math>~\biggl[ \frac{r_1^2 + r_2^2}{r_1 r_2} \biggr]\biggl[ \frac{r_1^2 - r_2^2}{r_1 r_2} \biggr]^{-1}</math>	<math>~=</math>	<math>~\biggl[ \frac{r_1^2 + r_2^2}{r_1^2 - r_2^2} \biggr]</math>
	<math>~=</math>	<math>~ \frac{ \varpi^2 + a^2 + (z - Z_0)^2 }{ 2a\varpi } \, . </math>

Arguments of Q and K

Want to explore argument of <math>~Q_{-1 / 2}(\Chi)</math>, namely,

<math> \Chi \equiv \frac{(\varpi^')^2 + \varpi^2 + (z^' - z)^2}{2\varpi^' \varpi} . </math>

Therefore,

<math>~2\varpi \biggl[ \varpi^' \Chi - a\coth\eta\biggr]</math>	<math>~=</math>	<math>~ (\varpi^')^2 + \varpi^2 + (z^' - z)^2 - [\varpi^2 + a^2 + (z - Z_0)^2 ] </math>
	<math>~=</math>	<math>~ (\varpi^')^2 - a^2 + [ (z^')^2 - 2z^' z + z^2]- [z^2 - 2zZ_0 + Z_0^2] </math>
	<math>~=</math>	<math>~ (\varpi^')^2 - a^2 + (z^')^2- Z_0^2 +2z(Z_0 - z^' ) </math>
<math>~\Rightarrow ~~~2a\biggl[ \frac{\sinh\eta }{(\cosh\eta - \cos\theta)} \biggr]\biggl[ \varpi^' \Chi - a\coth\eta\biggr]</math>	<math>~=</math>	<math>~ (\varpi^')^2 - a^2 + (z^')^2- Z_0^2 +2(Z_0 - z^' )\biggl[ Z_0 + \frac{a \sin\theta}{(\cosh\eta - \cos\theta)} \biggr] </math>
	<math>~=</math>	<math>~ 2aC_0 +2a(Z_0 - z^' )\biggl[ \frac{\sin\theta}{(\cosh\eta - \cos\theta)} \biggr] </math>
<math>~\Rightarrow ~~~ \sinh\eta \biggl[ \varpi^' \Chi - a\coth\eta\biggr]</math>	<math>~=</math>	<math>~ C_0 (\cosh\eta - \cos\theta) + (Z_0 - z^' ) \sin\theta </math>
<math>~\Rightarrow ~~~ \varpi^' \Chi </math>	<math>~=</math>	<math>~ \frac{1}{\sinh\eta} \biggl[ C_0 (\cosh\eta - \cos\theta) + (Z_0 - z^' ) \sin\theta + a\cosh\eta\biggr] </math>
<math>~\Rightarrow ~~~ \Chi </math>	<math>~=</math>	<math>~ \frac{1}{\varpi^' \sinh\eta} \biggl[ (C_0 + a)\cosh\eta + (Z_0 - z^' ) \sin\theta - C_0 \cos\theta \biggr] </math>

where,

<math>~ C_0 \equiv \frac{1}{2a}\biggl[ (\varpi^')^2 - a^2 + (z^')^2- Z_0^2 +2Z_0 (Z_0 - z^' ) \biggr] = \frac{1}{2a}\biggl[ (\varpi^')^2 - a^2 + (z^')^2 +Z_0^2 - 2Z_0 z^' \biggr] = \frac{1}{2a}\biggl[ (\varpi^')^2 - a^2 + (z^' - Z_0)^2 \biggr] \, . </math>

Now, notice that,

<math>~ ( \varpi^')^2 + a^2 + (z^' - Z_0)^2 </math>	<math>~=</math>	<math>~ 2a\varpi^'~\coth\eta^' </math>
<math>~\Rightarrow ~~~ ( \varpi^')^2 - a^2 + (z^' - Z_0)^2 </math>	<math>~=</math>	<math>~ 2a\varpi^'~\coth\eta^' - 2a^2 </math>
<math>~\Rightarrow ~~~ C_0 </math>	<math>~=</math>	<math>~ \varpi^'~\coth\eta^' - a </math>
	<math>~=</math>	<math>~ \biggl[ \frac{a \sinh\eta^' }{(\cosh\eta^' - \cos\theta^')} \biggr] ~\coth\eta^' - a </math>
	<math>~=</math>	<math>~ \biggl[ \frac{a \cosh\eta^' }{(\cosh\eta^' - \cos\theta^')} \biggr] - a \, . </math>

Hence,

<math>~ \Chi </math>	<math>~=</math>	<math>~ \frac{\cosh\eta}{\varpi^' \sinh\eta} \biggl[ \varpi^' \coth\eta^' \biggr] + \frac{1}{\sinh\eta} \biggl[ \frac{(\cosh\eta^' - \cos\theta^')}{a \sinh\eta^' } \biggr] \biggl[ (Z_0 - z^' ) \sin\theta - C_0 \cos\theta \biggr] </math>
	<math>~=</math>	<math>~ \coth\eta \cdot \coth\eta^' + \biggl[ \frac{(\cosh\eta^' - \cos\theta^')}{a \sinh\eta \cdot \sinh\eta^' } \biggr] \biggl[ (Z_0 - z^' ) \sin\theta - C_0 \cos\theta \biggr] </math>
	<math>~=</math>	<math>~ \coth\eta \cdot \coth\eta^' - \biggl[ \frac{(\cosh\eta^' - \cos\theta^')}{a \sinh\eta \cdot \sinh\eta^' } \biggr] \biggl\{ \biggl[ \frac{a \sin\theta^'}{(\cosh\eta^' - \cos\theta^')} \biggr] \sin\theta + \biggl[ \frac{a \cosh\eta^' }{(\cosh\eta^' - \cos\theta^')} \biggr] \cos\theta - a\cos\theta\biggr\} </math>
	<math>~=</math>	<math>~ \coth\eta \cdot \coth\eta^' - \biggl[ \frac{1 }{ \sinh\eta \cdot \sinh\eta^' } \biggr] \biggl\{ \sin\theta^' \sin\theta + \cosh\eta^' \cos\theta - (\cosh\eta^' - \cos\theta^')\cos\theta\biggr\} </math>
	<math>~=</math>	<math>~ \coth\eta \cdot \coth\eta^' - \biggl[ \frac{\sin\theta^' \sin\theta +\cos\theta^'\cos\theta }{ \sinh\eta \cdot \sinh\eta^' } \biggr] </math>
	<math>~=</math>	<math>~ \biggl[ \frac{\cosh\eta \cdot \cosh\eta^' - \cos(\theta^' - \theta) }{ \sinh\eta \cdot \sinh\eta^' } \biggr] \, . </math>

Also,

<math>~ \Chi +1 </math>	<math>~=</math>	<math>~ \biggl[ \frac{\sinh\eta \cdot \sinh\eta^' + \cosh\eta \cdot \cosh\eta^' - \cos(\theta^' - \theta) }{ \sinh\eta \cdot \sinh\eta^' } \biggr] </math>
	<math>~=</math>	<math>~ \biggl[ \frac{ \cosh(\eta^' + \eta) - \cos(\theta^' - \theta) }{ \sinh\eta \cdot \sinh\eta^' } \biggr] </math>
<math>~ \Rightarrow ~~~\mu^2 \equiv \frac{ 2 }{\Chi +1 }</math>	<math>~=</math>	<math>~ \biggl[ \frac{2 \sinh\eta \cdot \sinh\eta^' }{ \cosh(\eta^' + \eta) - \cos(\theta^' - \theta) } \biggr] \, . </math>

NOTE by Tohline: On 5 June 2018, I used Excel to test the validity of the toroidal-coordinate-based expressions that have been derived here, and summarized in the following table.

Summary Table

Quantity

Raw Expression in Cylindrical Coordinates

Expression in Terms of Toroidal Coordinates

<math>

\frac{(\varpi^')^2 + \varpi^2 + (z^' - z)^2}{2\varpi^'  \varpi}

</math>

<math>~ \frac{\cosh\eta \cdot \cosh\eta^' - \cos(\theta^' - \theta) }{ \sinh\eta \cdot \sinh\eta^' } </math>

<math>~\mu^2 \equiv \frac{2}{\Chi + 1}</math>

<math> \frac{4\varpi^' \varpi}{(\varpi^' + \varpi)^2 + (z^' - z)^2} </math>

<math>~ \frac{2 \sinh\eta \cdot \sinh\eta^' }{ \cosh(\eta^' + \eta) - \cos(\theta^' - \theta) } </math>

Potential

The potential, <math>~U({\vec{r}}~')</math>, at a point <math>~{\vec{r}}~'</math> due to an arbitrary mass distribution, <math>~\rho({\vec{r}})</math>, is,

<math>~-G \iiint \frac{\rho(\vec{r}) d^3r}{|~\vec{r} - {\vec{r}}^{~'} ~|} \, .</math>

Volume Element

See above.

Green's Function

Wong (1973) points out that in toroidal coordinates the Green's function is,

<math>~\frac{1}{\|~\vec{r} - {\vec{r}}^{~'} ~\|} </math>	<math>~=</math>	<math>~ \frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } \sum\limits_{m,n} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} </math>
		<math>~ \times \cos[m(\psi - \psi^')][\cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, , </math>
Wong (1973), Eq. (2.53)

where, <math>~P^m_{n-1 / 2}, Q^m_{n-1 / 2}</math> are "Legendre functions of the first and second kind with order <math>~n - \tfrac{1}{2}</math> and degree <math>~m</math> (toroidal harmonics)," and <math>~\epsilon_m</math> is the Neumann factor, that is, <math>~\epsilon_0 = 1</math> and <math>~\epsilon_m = 2</math> for all <math>~m \ge 1</math>. According to CT99, the Green's function written in toroidal coordinates is,

<math>~ \frac{1}{\|\vec{x} - \vec{x}^{~'}\|}</math>	<math>~=</math>	<math>~ \frac{1}{\pi \sqrt{\varpi \varpi^'}} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\psi - \psi^')] Q_{m- 1 / 2}(\Chi) </math>
	<math>~=</math>	<math>~ \frac{1}{a\pi} \biggl[ \frac{(\cosh\eta^' - \cos\theta^')}{\sinh\eta^' } \frac{(\cosh\eta - \cos\theta)}{\sinh\eta } \biggr]^{1 / 2} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\psi - \psi^')] Q_{m- 1 / 2}(\Chi) \, . </math>

Things to note:

The argument of <math>~Q_{m - 1 / 2}</math> in the CT99 expression is very different from the argument of <math>~Q^m_{n - 1 / 2}</math> (or <math>~P^m_{n - 1 / 2}</math>) in Wong's expression.

In both expressions, <math>~m</math> is the integer multiplying the azimuthal angle, <math>~\psi</math>, but in the CT99 expression this index serves as the subscript index of the function, <math>~Q</math>, whereas in Wong's expression it serves as the superscript index of both functions, <math>~Q</math> and <math>~P</math>. In this context, note that,

<math>~(-1)^m \sqrt{\frac{\pi}{2}} ~\Gamma(m-n+\tfrac{1}{2}) \biggl[ \frac{1}{ \sqrt{\sinh\eta}} \biggr] P^{n}_{m - \frac{1}{2}} (\coth\eta) \, . </math>

Wong's expression contains not only a summation over the index, <math>~m</math>, but also an explicit summation over the index, <math>~n</math>, which multiplies the "polar" angle, <math>~\theta</math>; no such additional summation appears in the CT99 expression, indicating that the summation over <math>~n</math> has implicitly already been completed. In this context, note that the summation expression gives,

<math>~ Q^{\mu}_{-\frac{1}{2}}\left(\cosh\xi\right) + 2\sum_{n=1}^{\infty} Q^{\mu}_{n-\frac{1}{2}}\left(\cosh\xi\right) \cos\left[ n (\theta - \theta^') \right] </math>

<math>~ e^{\mu\pi i} \Gamma\left(\mu+ \tfrac{1}{2} \right) \biggl[ \dfrac{\left(\frac{1}{2}\pi\right)^{1/2}\left(\sinh\xi\right)^{\mu }}{\left\{ \cosh\xi -\cos\left[ n (\theta - \theta^') \right] \right\}^{\mu+(1/2)}}\biggr] \, ; </math>

or, specifically for the case of <math>~\mu = 0</math>,

<math>~ \sum_{n=0}^{\infty} \epsilon_n Q_{n-\frac{1}{2}}\left(\cosh\xi\right) \cos\left[ n(\theta - \theta^') \right] </math>

<math>~ \dfrac{ \pi/\sqrt{2} }{\left[ \cosh\xi-\cos(\theta - \theta^') \right]^{\frac{1}{2}} } \, . </math>

Next thought …

New Insight

Identical Green's Function Expressions

Caltech's electronic version of A. Erdélyi's (1953) Higher Transcendental Functions; in particular, §3.11, p. 169 of Volume I gives,

	<math>~ Q_\nu[t t^' - (t^2-1)^{1 / 2} (t^{'2} - 1)^{1 / 2} \cos\psi] </math>	<math>~=</math>	<math>~ Q_\nu(t) P_\nu(t^') + 2\sum_{n=1}^\infty (-1)^n Q^n_\nu(t) P^{-n}_\nu(t^') \cos(n\psi) </math>
A. Erdélyi (1953): Volume I, §3.11, p. 169, eq. (4)

Valid for:

<math>~t, t^'</math> real

<math>~\nu \ne -1, -2, -3, </math> …

<math>~\psi</math> real

If we make the association, <math>~t \leftrightarrow \coth\eta</math>, then we also have,

in which case,

<math>~ \Chi </math>	<math>~=</math>	<math>~ \frac{\cosh\eta \cdot \cosh\eta^' - \cos(\theta^' - \theta) }{ \sinh\eta \cdot \sinh\eta^' } </math>
	<math>~=</math>	<math>~ t t^' - (t^2-1)^{1 / 2}(t^{'2}-1)^{1 / 2}\cos(\theta^' - \theta) \, . </math>

Put together, then, these expressions mean,

<math>~ Q_{m - 1 / 2}(\Chi) </math>	<math>~=</math>	<math>~ Q_{m-1 / 2}(\coth\eta) P_{m - 1 / 2}(\coth\eta^') + 2\sum_{n=1}^\infty (-1)^n Q^n_{m - 1 / 2}(\coth\eta) P^{-n}_{m - 1 / 2}(\coth\eta^') \cos[n(\theta^' - \theta)] </math>
	<math>~=</math>	<math>~ \sum_{n=0}^\infty \epsilon_n (-1)^n Q^n_{m - 1 / 2}(\coth\eta) P^{-n}_{m - 1 / 2}(\coth\eta^') \cos[n(\theta^' - \theta)] \, . </math>

Also, from our derived <math>~Q-P</math> relation,

<math>~Q^m_{n-\frac{1}{2}}(\cosh\eta)</math>	<math>~=</math>	<math>~ \sqrt{\frac{\pi}{2}} ~\Gamma(n+m + \tfrac{1}{2}) ~(-1)^m\biggl[ \frac{1}{ \sqrt{\sinh\eta}} \biggr] P^{-n}_{m - \frac{1}{2}} (\coth\eta) </math>
<math>~\Rightarrow ~~~ P^{-n}_{m - \frac{1}{2}} (\coth\eta)</math>	<math>~=</math>	<math>~ \sqrt{\frac{2}{\pi}} ~\frac{(-1)^m \sqrt{\sinh\eta} }{\Gamma(n+m + \tfrac{1}{2})} ~ Q^m_{n-\frac{1}{2}}(\cosh\eta) \, . </math>

we can write,

<math>~ \sum_{n=0}^\infty \epsilon_n (-1)^n Q^n_{m - 1 / 2}(\coth\eta) \biggl\{ \sqrt{\frac{2}{\pi}} ~\frac{(-1)^m \sqrt{\sinh\eta^'} }{\Gamma(n+m + \tfrac{1}{2})} ~ Q^m_{n-\frac{1}{2}}(\cosh\eta^') \biggr\} \cos[n(\theta^' - \theta)] </math>

Next, we pull from the accompanying discussion of the Gil et al. (2000) expression,

	<math>~Q_{n-1 / 2}^m (\lambda)</math>	<math>~=</math>	<math>~(-1)^n \frac{\pi^{3/2}}{\sqrt{2}~ \Gamma(n-m+1 / 2)} (x^2-1)^{1 / 4} P_{m-1 / 2}^n(x) \, , </math>
Gil, Segura, & Temme (2000): eq. (8)

where:

<math>~\lambda \equiv x/\sqrt{x^2-1}</math>

Identifying <math>~x</math> with <math>~\cosh\eta</math>, in which case we have <math>~\lambda = \coth\eta</math>, and, switching index notation, <math>~n \leftrightarrow m</math>, gives,

<math>~Q_{m-1 / 2}^n (\coth\eta)</math>	<math>~=</math>	<math>~(-1)^m \frac{\pi^{3/2}}{\sqrt{2} \Gamma(m-n+\frac{1}{2})} (\sinh\eta)^{1 / 2} P_{n-1 / 2}^m(\cosh\eta) </math>
	<math>~=</math>	<math>~ (-1)^n \sqrt{ \frac{\pi}{2} } ~\Gamma(n - m + \tfrac{1}{2} )(\sinh\eta)^{1 / 2} P_{n-1 / 2}^m(\cosh\eta) \, , </math>

where, this last step also incorporates the "Euler reflection formula for gamma functions", namely,

<math>~\frac{1}{\Gamma(m-n+\tfrac{1}{2})} </math>

<math>~\frac{\Gamma(n-m+\frac{1}{2}) }{\pi (-1)^{m+n}} \, .</math>

So we have,

<math>~ Q_{m - 1 / 2}(\Chi) </math>	<math>~=</math>	<math>~ \sum_{n=0}^\infty \epsilon_n (-1)^n \biggl\{(-1)^n \sqrt{ \frac{\pi}{2} } ~\Gamma(n - m + \tfrac{1}{2} )(\sinh\eta)^{1 / 2} P_{n-1 / 2}^m(\cosh\eta)\biggr\} \biggl\{ \sqrt{\frac{2}{\pi}} ~\frac{(-1)^m \sqrt{\sinh\eta^'} }{\Gamma(n+m + \tfrac{1}{2})} ~ Q^m_{n-\frac{1}{2}}(\cosh\eta^') \biggr\} \cos[n(\theta^' - \theta)] </math>
	<math>~=</math>	<math>~\sqrt{\sinh\eta^'} \sqrt{\sinh\eta} \sum_{n=0}^\infty \epsilon_n (-1)^m \frac{ \Gamma(n - m + \tfrac{1}{2})}{\Gamma(n+m + \tfrac{1}{2})} P_{n-1 / 2}^m(\cosh\eta) Q^m_{n-\frac{1}{2}}(\cosh\eta^') \cos[n(\theta^' - \theta)] \, . </math>

Hence, the CT99 Green's function may be rewritten as,

<math>~ \frac{1}{\|\vec{x} - \vec{x}^{~'}\|}</math>	<math>~=</math>	<math>~ \frac{1}{a\pi} [ (\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta)]^{1 / 2} \sum_{m=0}^{\infty} \epsilon_m \cos[m(\psi - \psi^')] \sum_{n=0}^\infty \epsilon_n (-1)^m \frac{ \Gamma(n - m + \tfrac{1}{2})}{\Gamma(n+m + \tfrac{1}{2})} P_{n-1 / 2}^m(\cosh\eta) Q^m_{n-\frac{1}{2}}(\cosh\eta^') \cos[n(\theta^' - \theta)] </math>
	<math>~=</math>	<math>~ \frac{1}{a\pi} [ (\cosh\eta^' - \cos\theta^') (\cosh\eta - \cos\theta)]^{1 / 2} \sum_{m=0}^{\infty} \sum_{n=0}^\infty \epsilon_m\epsilon_n (-1)^m \frac{ \Gamma(n - m + \tfrac{1}{2})}{\Gamma(n+m + \tfrac{1}{2})} \cos[m(\psi - \psi^')] \cos[n(\theta^' - \theta)] P_{n-1 / 2}^m(\cosh\eta) Q^m_{n-\frac{1}{2}}(\cosh\eta^') \, . </math>

Let's compare this with Wong's (1973) Green's function, namely,

<math>~\frac{1}{\|~\vec{r} - {\vec{r}}^{~'} ~\|} </math>	<math>~=</math>	<math>~ \frac{1}{\pi a} \biggl[ (\cosh\eta - \cos\theta)(\cosh \eta^' - \cos\theta^') \biggr]^{1 /2 } \sum\limits_{m,n} (-1)^m \epsilon_m \epsilon_n ~\frac{\Gamma(n-m+\tfrac{1}{2})}{\Gamma(n + m + \tfrac{1}{2})} </math>
		<math>~ \times \cos[m(\psi - \psi^')][\cos[n(\theta - \theta^')] ~\begin{cases}P^m_{n-1 / 2}(\cosh\eta) ~Q^m_{n-1 / 2}(\cosh\eta^') ~~~\eta^' > \eta \\P^m_{n-1 / 2}(\cosh\eta^') ~Q^m_{n-1 / 2}(\cosh\eta)~~~\eta^' < \eta \end{cases}\, . </math>
Wong (1973), Eq. (2.53)

[June 10, 2018] Amazing! The two expressions match precisely!

Integral Over Polar Angle

On p. 293 of his article, Wong (1973) references A. Erdélyi's (1953) Higher Transcendental Functions and states, "It can be shown that …"

<math>~ \int^\pi_{-\pi} d\theta (\cosh\eta - \cos\theta)^{-\tfrac{5}{2}} \cos[n(\theta - \theta^')] </math>	<math>~=</math>	<math>~ (8\sqrt{2}/3) Q^2_{n - \frac{1}{2}} (\cosh\eta) \cos (n\theta^')/\sinh^2\eta \, . </math>
Wong (1973), Eq. (2.56)

Let's see if we can replicate this integration result. (We tried using WolframAlpha's integration tool, but were unsuccessful.) We presume that Wong initially took the following steps to simplify the left-hand-side of this integral expression:

<math>~\int_{-\pi}^{\pi} \frac{\cos[n(\theta - \theta^')] d\theta}{(\cosh\eta - \cos\theta)^{5 / 2}} </math>	<math>~=</math>	<math>~ \cos(n\theta^') \int_{-\pi}^{\pi} \frac{ \cos(n\theta) ~ d\theta}{(\cosh\eta - \cos\theta)^{5 / 2}} + \sin(n\theta^') \cancelto{0}{ \int_{-\pi}^{\pi} \frac{ \sin(n\theta) d\theta}{(\cosh\eta - \cos\theta)^{5 / 2}} } </math>
	<math>~=</math>	<math>~ 2 \cos(n\theta^') \int_{0}^{\pi} \frac{ \cos(n\theta)~ d\theta}{(\cosh\eta - \cos\theta)^{5 / 2}} \, . </math>

That is to say, given that the limits of the integration are <math>~-\pi</math> to <math>~+\pi</math>: The second integral on the right-hand-side will go to zero because the numerator of its integrand — i.e., <math>~\sin(n\theta)</math> — is an odd function; and, with regard to the first integral on the right-hand-side, the lower integration limit can be set to zero and the result doubled because the numerator of its integrand — i.e., <math>~\cos(n\theta)</math> — is an even function.

Now, examining Wong's reference to A. Erdélyi's (1953) Higher Transcendental Functions, we find:

Equation (5) in §3.7, p. 155 of Volume I gives,

<math>~ e^{i \mu \pi} ~2^{-\nu - 1} \frac{\Gamma(\nu + \mu + 1) }{\Gamma(\nu + 1) } (z^2 - 1)^{-\mu/2} \int_0^\pi (z+\cos t)^{\mu - \nu - 1} (\sin t)^{2\nu + 1} dt \, . </math>

This is valid for,

<math>~\mathrm{Re} ~\nu > -1</math>

and

<math>~\mathrm{Re} (\nu + \mu + 1) > 0 \, .</math>

Equation (10) in §3.7, p. 156 of Volume I gives,

	<math>~Q_\nu^\mu(z)</math>	<math>~=</math>	<math>~ e^{i \mu \pi} ~ (2\pi)^{-\frac{1}{2}} (z^2-1)^{\mu/2} ~\Gamma(\mu + \tfrac{1}{2})~\biggl\{ \int_0^\pi (z - \cos t)^{-\mu - \frac{1}{2}} \cos[(\nu + \tfrac{1}{2})t] ~dt -\cos(\nu\pi) \int_0^\infty (z + \cosh t)^{-\mu - \frac{1}{2}} e^{-(\nu + \frac{1}{2})t} ~dt \biggr\} </math>
A. Erdélyi (1953): Volume I, §3.7, p. 156, eq. (10)

Valid for:

<math>~\mathrm{Re} ~\nu > -\tfrac{1}{2}</math>

and

<math>~\mathrm{Re} (\nu + \mu + 1) > 0 \, .</math>

Focusing in on this second integral definition of the Legendre function, <math>~Q^\mu_\nu</math>, let's set <math>~z = \cosh\eta</math>, <math>~t = \theta</math>, <math>~\mu = 2</math>, and, <math>~\nu = n - \tfrac{1}{2}</math>, where <math>~n</math> is zero or a positive integer. in this case we have,

<math>~ (2\pi)^{-\frac{1}{2}} (\cosh^2\eta-1) ~\Gamma(\tfrac{5}{2})~\biggl\{ \int_0^\pi (\cosh\eta - \cos \theta)^{-\frac{5}{2}} \cos(n\theta) ~d\theta - \cancelto{0}{\cos[(n-\tfrac{1}{2})\pi] }~~\int_0^\infty (\cosh\eta + \cosh \theta)^{- \frac{5}{2}} e^{-n\theta} ~d\theta \biggr\} \, , </math>

where the prefactor of the second term — that is, <math>~\cos[(n-\tfrac{1}{2})\pi] </math> — goes to zero for all allowable values of the integer, <math>~n</math>. Hence,

<math>~2\cos(n\theta^') \int_0^\pi \frac{ \cos(n\theta)~d\theta }{ (\cosh\eta - \cos \theta)^{\frac{5}{2}} } </math>	<math>~=</math>	<math>~\frac{ 2(2\pi)^{\frac{1}{2}} Q_{n - \frac{1}{2}}^2 (\cosh\eta) \cos(n\theta^')}{ (\cosh^2\eta-1) ~\Gamma(\tfrac{5}{2})~ } </math>
	<math>~=</math>	<math>~\biggl[ \frac{ 2^3 \sqrt{2} }{ 3 } \biggr] \frac{ Q_{n - \frac{1}{2}}^2(\cosh\eta) \cos(n\theta^')}{ \sinh^2\eta } \, . </math>

where we have set,

<math>~ \Gamma(\tfrac{5}{2}) = \Gamma(\tfrac{1}{2} + 2) = \frac{ \sqrt{\pi} \cdot 4! }{4^2 \cdot 2!} = \frac{\sqrt{\pi} \cdot 2^3\cdot 3}{ 2^5 } = \frac{3 \sqrt{\pi}}{2^2} \, . </math>

The right-hand-side of this last expression exactly matches the result published by Wong (1973) and rewritten inside the box, above.

Q.E.D.

Integral Over Radial Coordinate

On p. 294 of his article, Wong (1973) references A. Erdélyi's (1953) Higher Transcendental Functions and states that,

<math>~ \int^x dt \Biggl[ \frac{Q^2_{n - \frac{1}{2}}(t) X_{n-\frac{1}{2}}(t)}{t^2 - 1} \Biggr] </math>	<math>~=</math>	<math>~ \frac{1}{4} \biggl[ (n-\tfrac{3}{2}) X_{n-\frac{1}{2}}(x)~ Q^2_{n+\frac{1}{2}}(x) - (n+\tfrac{1}{2}) X_{n+\frac{1}{2}}(x) ~Q^2_{n-\frac{1}{2}}(x) \biggr] \, . </math>
Wong (1973), Eq. (2.58)

Let's see if we can replicate this integration result. Let's start with the "Key Equation",

	<math>~ \int_a^b\biggl[(\nu - \sigma)(\nu + \sigma + 1) + (\rho^2 - \mu^2)(1 - z^2)^{-1} \biggr] w_\nu^\mu ~w_\sigma^\rho ~dz </math>	<math>~=</math>	<math>~ \biggl[ z(\nu-\sigma) w_\nu^\mu ~w_\sigma^\rho + (\sigma+\rho) w_\nu^\mu ~ w_{\sigma-1}^\rho - (\nu + \mu) w_{\nu - 1}^\mu ~w_\sigma^\rho \biggr]_a^b </math>
A. Erdélyi (1953): Volume I, §3.12, p. 169, eq. (1)

where, <math>~w_\nu^\mu(z)</math> and <math>~w_\sigma^\rho(z)</math> denote any solutions of Legendre's differential equation

In order to match the left-hand side of Wong's expression, we should adopt the associations: <math>~z \rightarrow t</math>, <math>~\mu \rightarrow 2</math>, <math>~\nu \rightarrow (n - \tfrac{1}{2})</math>, <math>~\rho \rightarrow 0</math>, and <math>~\sigma \rightarrow ( n - \tfrac{1}{2})</math>. In which case, Erdélyi's (1953) expression becomes,

<math>~ \int_a^b\biggl[ -4(1 - t^2)^{-1} \biggr] Q_{n - \frac{1}{2}}^2(t) ~X_{n - \frac{1}{2}}(t) ~dt </math>

<math>~ \biggl[ (n - \tfrac{1}{2} ) Q_{n - \frac{1}{2}}^2(t) ~ X_{n - \frac{3}{2}}(t) - (n + \tfrac{3}{2}) Q_{n - \frac{3}{2}}^2(t) ~X_{n - \frac{1}{2}}(t) \biggr]_a^b \, . </math>

This is very similar to, but does not appear to match, Wong's expression.

Reconciliation Attempt #1: Keeping in mind that,

	<math>~(\nu - \mu + 1)P^\mu_{\nu + 1} (z)</math>	<math>~=</math>	<math>~ (2\nu + 1)z P_\nu^\mu(z) - (\nu + \mu)P^\mu_{\nu-1}(z) </math>
Abramowitz & Stegun (1995), p. 334, eq. (8.5.3)

NOTE: <math>~Q_\nu^\mu</math>, as well as <math>~P_\nu^\mu</math>, satisfies this same recurrence relation.

which means, after making the associations, <math>~z \rightarrow t</math>, <math>~\mu \rightarrow 0</math> and <math>~\nu \rightarrow (n-\tfrac{1}{2})</math>, that,

<math>~(n+\tfrac{1}{2})X_{n+\frac{1}{2}}(t)</math>	<math>~=</math>	<math>~2n t X_{n-\frac{1}{2}}(t) - (n-\tfrac{1}{2})X_{n - \frac{3}{2}}(t)</math>
<math>~\Rightarrow ~~~(n-\tfrac{1}{2})X_{n - \frac{3}{2}}(t) </math>	<math>~=</math>	<math>~2n t X_{n-\frac{1}{2}}(t) - (n+\tfrac{1}{2})X_{n+\frac{1}{2}}(t)</math>

the integral can be rewritten as,

<math>~ \int_a^b\biggl[ \frac{Q_{n - \frac{1}{2}}^2(t) ~X_{n - \frac{1}{2}}(t) }{(t^2-1)}\biggr]~dt </math>	<math>~=</math>	<math>~ \frac{1}{4} \biggl\{ \biggl[ 2n t X_{n-\frac{1}{2}}(t) - (n+\tfrac{1}{2})X_{n+\frac{1}{2}}(t) \biggr] Q_{n - \frac{1}{2}}^2(t) - (n + \tfrac{3}{2}) Q_{n - \frac{3}{2}}^2(t) ~X_{n - \frac{1}{2}}(t) \biggr\}_a^b </math>
	<math>~=</math>	<math>~ \frac{1}{4} \biggl\{ \biggl[ 2n t Q_{n - \frac{1}{2}}^2(t) - (n + \tfrac{3}{2}) Q_{n - \frac{3}{2}}^2(t) \biggr] X_{n - \frac{1}{2}}(t) - (n+\tfrac{1}{2})X_{n+\frac{1}{2}}(t) Q_{n - \frac{1}{2}}^2(t) \biggr\}_a^b </math>

Returning to the same recurrence "Key Equation," but this time adopting the associations, <math>~z \rightarrow t</math>, <math>~\mu \rightarrow 2</math> and <math>~\nu \rightarrow (n-\tfrac{1}{2})</math>, we can write,

<math>~(n - \tfrac{3}{2})Q^2_{n + \frac{1}{2}}(t)</math>

<math>~ 2n t Q^2_{n - \frac{1}{2}}(t) - (n + \tfrac{3}{2}) Q^2_{n - \frac{3}{2}} (t) \, , </math>

in which case the integral becomes,

<math>~ \int_a^b\biggl[ \frac{Q_{n - \frac{1}{2}}^2(t) ~X_{n - \frac{1}{2}}(t) }{(t^2-1)}\biggr]~dt </math>

<math>~ \frac{1}{4} \biggl\{ (n - \tfrac{3}{2})Q^2_{n + \frac{1}{2}}(t) ~ X_{n - \frac{1}{2}}(t) - (n+\tfrac{1}{2})X_{n+\frac{1}{2}}(t) Q_{n - \frac{1}{2}}^2(t) \biggr\}_a^b \, . </math>

Hooray! This does indeed match Wong's relation (2.58)!

Evaluating Q²_ν

How do we evaluate an "order 2" associated Legendre function, such as, <math>~Q_\nu^2</math> ?

Start by recognizing that, from our identified set of "Key Equations,"

	<math>~P_\nu^{\mu + 1}(z)</math>	<math>~=</math>	<math>~ (z^2-1)^{-\frac{1}{2}} \{ (\nu - \mu) z P^\mu_\nu(z) - (\nu + \mu)P^\mu_{\nu - 1}(z)\} </math>
Abramowitz & Stegun (1995), p. 333, eq. (8.5.1)

NOTE: <math>~Q_\nu^\mu</math>, as well as <math>~P_\nu^\mu</math>, satisfies this same recurrence relation.

Hence, after adopting the association, <math>~\nu \rightarrow (n - \tfrac{1}{2})</math>, we have, when <math>~\mu = 0</math>,

<math>~ (n-\tfrac{1}{2}) (z^2-1)^{-\frac{1}{2}} [z Q_{n - \frac{1}{2}}(z) - Q_{n - \frac{3}{2}}(z)] </math>

…

for <math>~n \ge 1 \, ,</math>

and, when <math>~\mu = 1</math>,

<math>~ (z^2-1)^{-\frac{1}{2}} \{ (n-\tfrac{3}{2}) z Q^1_{n - \frac{1}{2}}(z) - (n+\tfrac{1}{2})Q^1_{n - \frac{3}{2}}(z)\} </math>

…

for <math>~n \ge 1 \, .</math>

All we are missing, then, is expressions for the index, <math>~n=0</math>, that is, we need independent expressions for <math>~Q^1_{-\frac{1}{2}}</math> and for <math>~Q^2_{-\frac{1}{2}}</math>.

From DLMF §14.6.2, or from §3.6.1, eq. (7) (p. 149) of A. Erdélyi's (1953) Higher Transcendental Functions we find,

<math>~\mathsf{Q}^{m}_{\nu}\left(x\right)</math>

<math>~(-1)^{m}\left(1-x^{2}\right)^{m/2}\frac{{\mathrm{d}}^{m}\mathsf{Q}_{\nu}\left(x\right)}{{\mathrm{d}x}^{m}}</math>

or, from DLMF §14.6.4, and from §3.6.1, eq. (5) (p. 148) of A. Erdélyi's (1953) Higher Transcendental Functions we have,

<math>~Q^{m}_{\nu}\left(x\right)</math>

<math>~\left(x^{2}-1\right)^{m/2}\frac{{\mathrm{d}}^{m}Q_{\nu}\left(x\right)}{{\mathrm{d}x}^{m}}</math>

Leaning on the latter of the two possible expressions, we therefore have,

<math>~Q^1_{-\frac{1}{2}}(z)</math>	<math>~=</math>	<math>~ (z^2 - 1)^{1 / 2} \frac{d}{dz} \biggl[ Q_{-\frac{1}{2}}(z) \biggr] \, ; </math>
<math>~Q^2_{-\frac{1}{2}}(z)</math>	<math>~=</math>	<math>~ (z^2 - 1) \frac{d^2}{dz^2} \biggl[ Q_{-\frac{1}{2}}(z) \biggr] \, . </math>

Therefore, starting from the "Key Equation",

	<math>~Q_{-\frac{1}{2}}(z)</math>	<math>~=</math>	<math>~ \sqrt{ \frac{2}{z+1} } ~K\biggl( \sqrt{ \frac{2}{z+1}} \biggr) </math>	for example …	<math>~Q_{-\frac{1}{2}}(\cosh\eta)</math>	<math>~=</math>	<math>~ 2 e^{-\eta/2} K(e^{-\eta}) </math>
Abramowitz & Stegun (1995), p. 337, eq. (8.13.3)					Abramowitz & Stegun (1995), p. 337, eq. (8.13.4)

we associate <math>~k^2 \leftrightarrow 2/(z+1)</math>, which implies,

Hence, drawing on the DLMF's §19.4 expressions for the derivatives of complete elliptic integrals and appreciating that, <math>~(k')^2 \equiv (1-k^2)</math>, we find,

<math>~\frac{d}{dz} \biggl[ Q_{-\frac{1}{2}}(z) \biggr]</math>	<math>~=</math>	<math>~\frac{dk}{dz} \cdot \frac{d}{dk} \biggl[ k K(k) \biggr]</math>
	<math>~=</math>	<math>~\frac{dk}{dz} \cdot \biggl[ K(k) + \frac{E(k) - (k')^2 K(k) }{(k')^2} \biggr]</math>
	<math>~=</math>	<math>~ - \biggl[\frac{1}{2(z+1)^3} \biggr]^{1 / 2} \biggl[ \frac{E(k) }{(k')^2} \biggr]</math>
	<math>~=</math>	<math>~ - \biggl[\frac{1}{2(z+1)^3} \biggr]^{1 / 2} E(k) \biggl[ \frac{z+1}{z-1} \biggr] </math>
	<math>~=</math>	<math>~ - \biggl[\frac{1}{2(z+1)(z-1)^2} \biggr]^{1 / 2} E(k) \, .</math>

As a result,

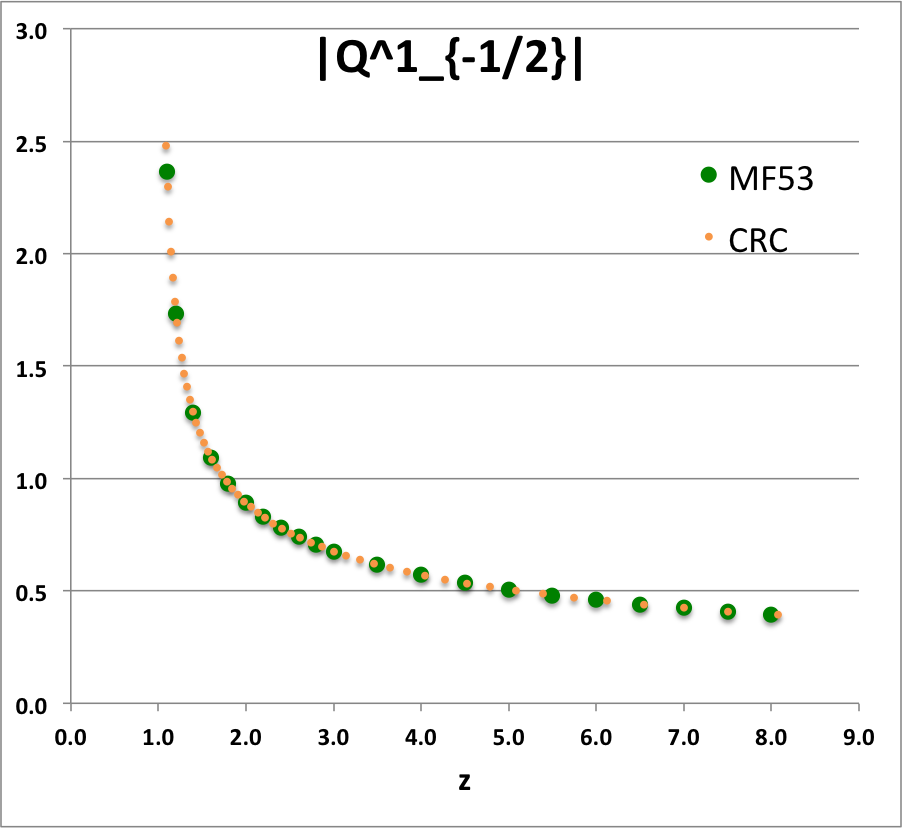
<math>~Q^1_{-\frac{1}{2}}(z)</math>	<math>~=</math>	<math>~ - (z^2 - 1)^{1 / 2} \biggl[\frac{1}{2(z^2-1)(z-1)} \biggr]^{1 / 2} E(k) </math>
	<math>~=</math>	<math>~ - \biggl[\frac{1}{2(z-1)} \biggr]^{1 / 2} E(k) </math>
	<math>~=</math>	<math>~ - \biggl[\frac{1}{2(z-1)} \biggr]^{1 / 2} E\biggl( \sqrt{ \frac{2}{z+1} } \biggr) \, . </math>

With the exception of the leading negative sign, this appears to match the tabulated values published in the bottom half of Table IX (p. 1923) of [MF53].

Now, let's evaluate the second derivative …

<math>~\frac{d}{dz} \biggl[ Q_{-\frac{1}{2}}(z) \biggr]</math>	<math>~=</math>	<math>~ - 2^{-\frac{1}{2}} (z+1)^{-\frac{1}{2}} (z-1)^{-1}E(k) </math>
<math>~\Rightarrow ~~~ \frac{d^2}{dz^2} \biggl[ Q_{-\frac{1}{2}}(z) \biggr]</math>	<math>~=</math>	<math>~ - 2^{-\frac{1}{2}} \biggl\{ -\frac{1}{2}(z+1)^{-\frac{3}{2}}(z-1)^{-1}E(k) - (z+1)^{-\frac{1}{2}}(z-1)^{-2}E(k) + (z+1)^{-\frac{1}{2}}(z-1)^{-1} \frac{dk}{dz} \cdot \frac{dE(k)}{dk} \biggr\}</math>
	<math>~=</math>	<math>~ 2^{-\frac{1}{2}} \biggl\{ \frac{1}{2}(z+1)^{-\frac{3}{2}}(z-1)^{-1}E(k) + (z+1)^{-\frac{1}{2}}(z-1)^{-2}E(k) + (z+1)^{-\frac{1}{2}}(z-1)^{-1} [2(z+1)^3]^{-1 / 2} \biggl[ \frac{E(k) - K(k)}{k} \biggr] \biggr\}</math>
	<math>~=</math>	<math>~ 2^{-\frac{1}{2}} (z+1)^{-\frac{3}{2}} (z-1)^{-2}\biggl\{ \frac{1}{2} (z-1) E(k) + (z+1) E(k) + (z+1)(z-1) [2(z+1)^3]^{-1 / 2} \biggl[ E(k) - K(k)\biggr]\biggl[ \frac{z+1}{2} \biggr]^{\frac{1}{2}} \biggr\}</math>
	<math>~=</math>	<math>~ 2^{-\frac{1}{2}} (z+1)^{-\frac{3}{2}} (z-1)^{-2}\biggl\{ \frac{1}{2} (z-1) E(k) + (z+1) E(k) + \frac{1}{2} (z-1) \biggl[ E(k) - K(k)\biggr] \biggr\}</math>
	<math>~=</math>	<math>~ 2^{-\frac{3}{2}} (z+1)^{-\frac{3}{2}} (z-1)^{-2}\biggl\{ 4 z E(k) - (z-1) K(k) \biggr\} \, .</math>

Hence, we have,

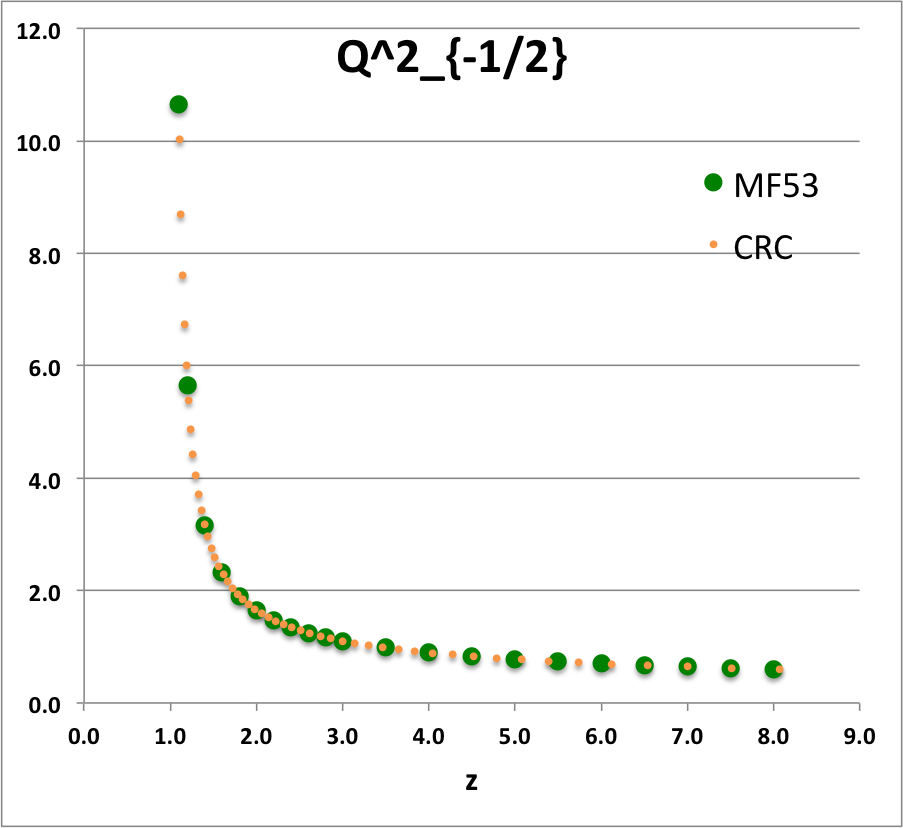
<math>~Q^2_{-\frac{1}{2}}(z)</math>	<math>~=</math>	<math>~ (z^2 - 1) \frac{d^2}{dz^2} \biggl[ Q_{-\frac{1}{2}}(z) \biggr] </math>
	<math>~=</math>	<math>~ 2^{-\frac{3}{2}} (z+1)^{-\frac{1}{2}} (z-1)^{-1}\biggl\{ 4 z E(k) - (z-1) K(k) \biggr\} </math>
	<math>~=</math>	<math>~ \frac{ 4 z E(k) - (z-1) K(k) }{ [2^{3} (z+1) (z-1)^{2} ]^{1 / 2}} \, . </math>

This also appears to match the tabulated values published in the bottom half of Table IX (p. 1923) of [MF53].

Summary

<math>~Q^1_{-\frac{1}{2}}(z)</math>	<math>~=</math>	<math>~ - \biggl[\frac{1}{2(z-1)} \biggr]^{1 / 2} E(k) </math>
<math>~Q^2_{-\frac{1}{2}}(z)</math>	<math>~=</math>	<math>~ \frac{ 4 z E(k) - (z-1) K(k) }{ [2^{3} (z+1) (z-1)^{2} ]^{1 / 2}} </math>
where: <math>~k = \sqrt{ \frac{2}{z+1}} \, .</math>

<math>~\| ~Q^1_{-\frac{1}{2}}(z) ~\|</math>	<math>~Q^2_{-\frac{1}{2}}(z)</math>

See relevant caption.

Let's push forward a bit more; specifically, let's find the expressions that are relevant when <math>~n = +1</math>. When <math>~\mu = 0</math>,

<math>~Q_{+ \frac{1}{2}}^{1}(z)</math>	<math>~=</math>	<math>~ \frac{1}{2} (z^2-1)^{-\frac{1}{2}} \biggl\{ z Q_{+\frac{1}{2}}(z) - Q_{ - \frac{1}{2}}(z) \biggr\} </math>
	<math>~=</math>	<math>~ \frac{1}{2} (z^2-1)^{-\frac{1}{2}} \biggl\{ z^2 k~K ( k ) ~-~ [2z^2(z+1)]^{1 / 2} E( k ) ~-~ k K(k)\biggr\} </math>
	<math>~=</math>	<math>~ \frac{1}{2} \biggl\{ (z^2 - 1)^{1 / 2} k~K ( k ) ~-~ \biggl[ \frac{2z^2(z+1)}{z^2-1} \biggr]^{1 / 2} E( k ) \biggr\} </math>
	<math>~=</math>	<math>~ \frac{1}{2} \biggl[ (z^2 - 1)^{1 / 2} k~K ( k ) ~-~ \biggl( \frac{2z^2}{z-1} \biggr)^{1 / 2} E( k ) \biggr] \, . </math>

And, when <math>~\mu = 1</math>,

<math>~Q_{+ \frac{1}{2}}^{2}(z)</math>	<math>~=</math>	<math>~ -~\frac{1}{2}(z^2-1)^{-\frac{1}{2}} \biggl\{ z Q^1_{+\frac{1}{2}}(z) ~+~3Q^1_{- \frac{1}{2}}(z) \biggr\} </math>
	<math>~=</math>	<math>~ -~\frac{1}{2}(z^2-1)^{-\frac{1}{2}} \biggl\{ \frac{z}{2} \biggl[ (z^2 - 1)^{1 / 2} k~K ( k ) ~-~ \biggl( \frac{2z^2}{z-1} \biggr)^{1 / 2} E( k ) \biggr] ~-~3 \biggl[\frac{1}{2(z-1)} \biggr]^{1 / 2} E(k)\biggr\} </math>
	<math>~=</math>	<math>~ -~\frac{1}{2^2}(z^2-1)^{-\frac{1}{2}} \biggl\{ z (z^2 - 1)^{1 / 2} k~K ( k ) ~-~(z^2+3) \biggl( \frac{2}{z-1} \biggr)^{1 / 2} E(k)\biggr\} </math>
	<math>~=</math>	<math>~ -~\frac{1}{2^2}\biggl\{ z k~K ( k ) ~-~(z^2+3) \biggl[ \frac{2}{(z-1)(z^2-1)} \biggr]^{1 / 2} E(k)\biggr\} \, . </math>

User:Tohline/Appendix/Mathematics/ToroidalSynopsis01

Contents

Synopsis of Toroidal Coordinate Approach

Basics

Arguments of Q and K