Difference between revisions of "User:Tohline/ThreeDimensionalConfigurations/EFE Energies"
(→Free Energy Surface(s): Begin describing Figure 1) |
(→Adopted Evolutionary Constraints: More discussion of Figure 1) |
||
| Line 508: | Line 508: | ||
===Conserve Only L=== | ===Conserve Only L=== | ||
Let's fix the total angular momentum, <math>~L</math>, of a triaxial configuration and examine how | Let's fix the total angular momentum, <math>~L</math>, of a triaxial configuration and examine how the configuration's free energy varies as we allow it to contort through different triaxial shapes — that is, as its pair of axis ratios varies, always maintaining <math>~\tfrac{b}{a} < 1</math> — and as we vary <math>~x</math>, which characterizes the fraction of angular momentum that is stored in internal spin versus overall figure rotation. The desired free-energy function, <math>~E(\tfrac{b}{a},\tfrac{c}{a}, x)|_L</math>, has just been defined, but visualizing its behavior is difficult because, in this situation, the free energy is a three-dimensional "surface" lying in the four-dimensional domain, <math>~(\tfrac{b}{a},\tfrac{c}{a}, x, E_L)</math>. | ||
But, acknowledging that we are primarily interested in identifying extrema of this free-energy function, the discussion presented in §3.2 of [http://adsabs.harvard.edu/abs/1995ApJ...446..472C Christodoulou et al. (1995)] shows us how to reduce the dimensionality of this problem by one. There, it is shown that, as long as <math>~\tfrac{b}{a} \ne 1</math>, extrema exist in the <math>~x</math>-coordinate direction — that is, <math>~\partial E_L/\partial x = 0</math> — only if <math>~x = 0.</math> For a given choice of <math>~L</math>, therefore, the relevant free-energy "surface" is defined by the expression, | |||
<div align="center"> | <div align="center"> | ||
| Line 515: | Line 518: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~E\biggl(\frac{b}{a}, \frac{c}{a}\biggr)\biggr|_L</math> | <math>~E\biggl(\frac{b}{a}, \frac{c}{a}, x=0\biggr)\biggr|_L</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 530: | Line 533: | ||
</div> | </div> | ||
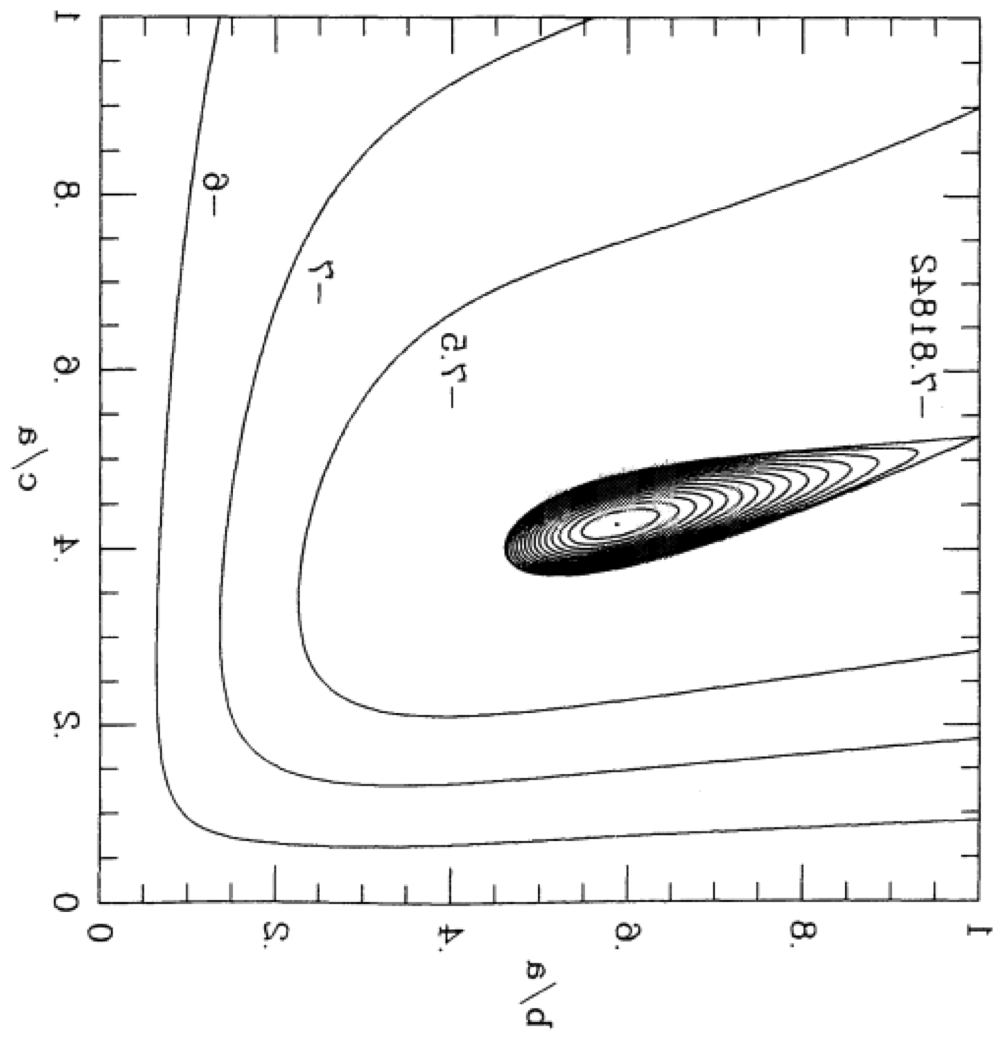
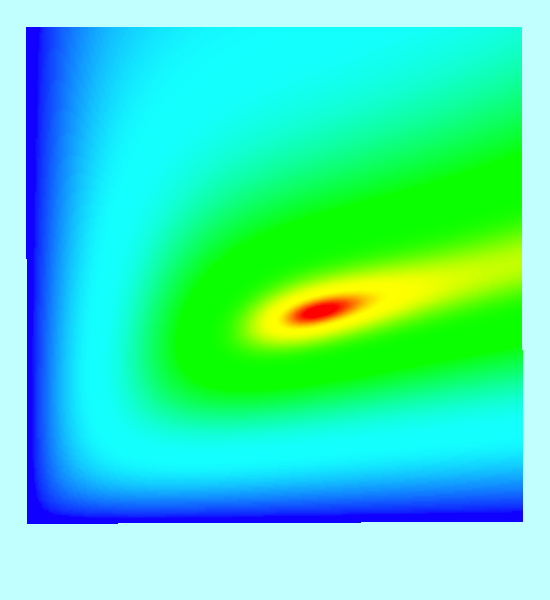
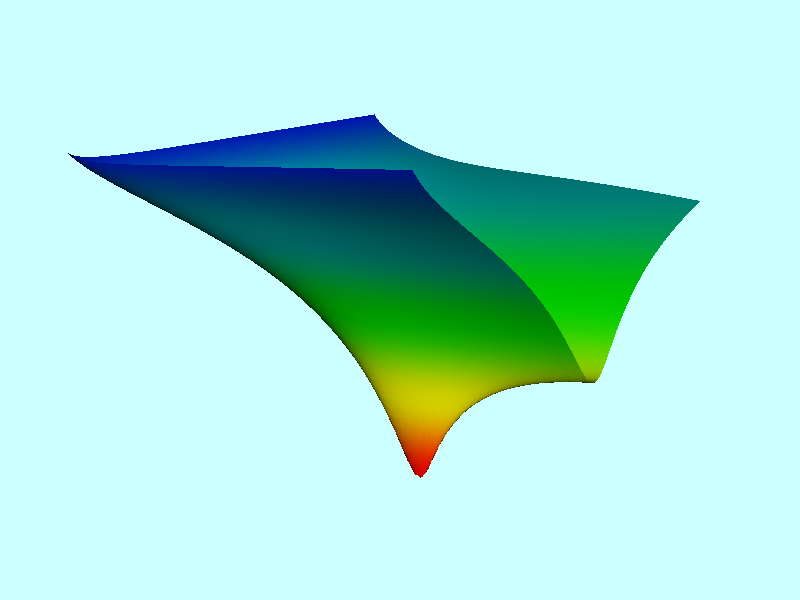
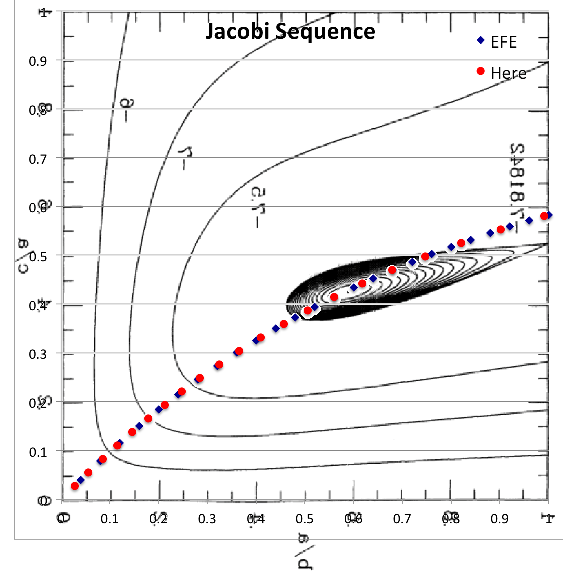
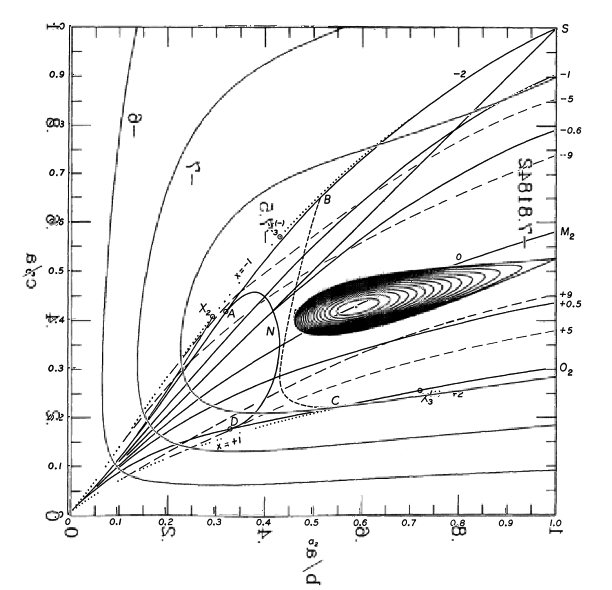
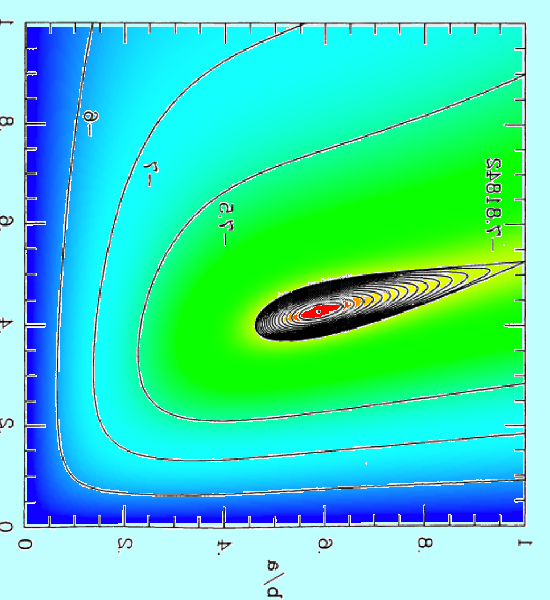
Figure 3 of [http://adsabs.harvard.edu/abs/1995ApJ...446..472C Christodoulou et al. (1995)] presents a contour plot of this <math>~E_L</math> function for the specific case of <math>~L = 4.71488</math>, which, for reference, is the total angular momentum of an equilibrium Maclaurin spheroid having an eccentricity, <math>~e = 0.85</math>. We have | Figure 3 of [http://adsabs.harvard.edu/abs/1995ApJ...446..472C Christodoulou et al. (1995)] presents a black-and-white contour plot of this <math>~E_L</math> function for the specific case of <math>~L = 4.71488</math>, which, for reference, is the total angular momentum of an equilibrium Maclaurin spheroid having an eccentricity, <math>~e = 0.85</math>. We have extracted this black-and-white contour plot from p. 477 of [http://adsabs.harvard.edu/abs/1995ApJ...446..472C Christodoulou et al. (1995)] and have reprinted it as the left panel in row (''i'') of our Figure 1 montage; note, however, that we have flipped the plot horizontally and rotated it by 90° so that the orientation of the axis pair, <math>~(\tfrac{b}{a},\tfrac{c}{a})</math>, conforms with the orientation used by [http://adsabs.harvard.edu/abs/1965ApJ...142..890C Chandrasekhar (1965)] — see also our [[User:Tohline/ThreeDimensionalConfigurations/JacobiEllipsoids#Sequence_Plots|accompanying discussion of equilibrium sequence plots]]. In row (''ii'') of our Figure 1 montage, we display this <math>~E_L</math> function as a free-energy surface, where color as well as depth is used to tag energy values. The colored contour plot presented as the right-hand segment of row (''i'') in our Figure 1 montage results from the projection of this free-energy surface onto the <math>~(\tfrac{b}{a},\tfrac{c}{a})</math> plane. It reproduces in quantitative detail the black-and-white contour plot that we have extracted from [http://adsabs.harvard.edu/abs/1995ApJ...446..472C Christodoulou et al. (1995)]. | ||
, [http://adsabs.harvard.edu/abs/1995ApJ...446..472C Christodoulou et al. (1995)] contour plot represents a projection of this surface onto the <math>~(\tfrac{b}{a},\tfrac{c}{a})</math> plane. | |||
Revision as of 22:21, 29 June 2016

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Properties of Homogeneous Ellipsoids (2)
In addition to pulling from §53 of Chandrasekhar's EFE, here, we lean heavily on the papers by M. D. Weinberg & S. Tremaine (1983, ApJ, 271, 586) (hereafter, WT83) and by D. M. Christodoulou, D. Kazanas, I. Shlosman, & J. E. Tohline (1995, ApJ, 446, 472) (hereafter, Paper I).
Sequence-Defining Dimensionless Parameters
A Riemann sequence of S-type ellipsoids is defined by the value of the dimensionless parameter,
|
<math>~f</math> |
<math>~\equiv</math> |
<math>~\frac{\zeta}{\Omega} = </math> constant, |
[ EFE, §48, Eq. (31) ]
[ WT83, Eq. (5) ]
[ Paper I, Eq. (2.1) ]
where, <math>~\zeta</math> is the system's vorticity as measured in a frame rotating with angular velocity, <math>~\Omega</math>. Alternatively, we can use the dimensionless parameter,
|
<math>~x</math> |
<math>~\equiv</math> |
<math>~\biggl[\frac{ab}{a^2 + b^2} \biggr]f \, ,</math> |
or,
|
<math>~\Lambda</math> |
<math>~\equiv</math> |
<math>~-\biggl[\frac{ab}{a^2 + b^2} \biggr] \Omega f = -\Omega x \, .</math> |
[ WT83, Eq. (4) ]
Conserved Quantities
Algebraic expressions for the conserved energy, <math>~E</math>, angular momentum, <math>~L</math>, and circulation, <math>~C</math>, are, respectively,
|
<math>~E</math> |
<math>~=</math> |
<math>~\frac{1}{2}v^2 + \frac{1}{2}(a^2 + b^2)(\Lambda^2 + \Omega^2) - 2ab\Lambda\Omega - 2I </math> |
|
|
<math>~\rightarrow</math> |
<math>~\cancelto{0}{\frac{1}{2}v^2} + \frac{1}{2} [(a+bx)^2 + (b+ax)^2]\Omega^2 - 2I \, ,</math> |
[ 1st expression — EFE, §53, Eq. (239) ]
[ 2nd expression — Paper I, Eq. (2.7) ]
where — see an accompanying discussion for the definitions of <math>~A_1</math>, <math>~A_2</math>, and <math>~A_3</math>,
|
<math>~I</math> |
<math>~=</math> |
<math>~A_1a^2 + A_2b^2 + A_3c^2 \, ;</math> |
[ 1st expression — EFE, §53, Eq. (239) ]
[ 2nd expression — Paper I, Eq. (2.8) ]
|
<math>~\frac{5L}{M}</math> |
<math>~=</math> |
<math>~(a^2 + b^2)\Omega - 2ab\Lambda</math> |
|
|
<math>~=</math> |
<math>~ (a^2 + b^2 + 2abx)\Omega \, ;</math> |
[ 1st expression — EFE, §53, Eq. (240) ]
[ 2nd expression — Paper I, Eq. (2.5) ]
|
<math>~\frac{5C}{M}</math> |
<math>~=</math> |
<math>~(a^2 + b^2)\Lambda - 2ab\Omega</math> |
|
|
<math>~=</math> |
<math>~- [2ab + (a^2 + b^2)x ]\Omega \, .</math> |
[ 1st expression — EFE, §53, Eq. (241) ]
[ 2nd expression — Paper I, Eq. (2.6) ]
If we rewrite the expression for the system's free energy in terms of <math>~L</math> (and x) instead of <math>~\Omega</math> (and x), we have,
|
<math>~E</math> |
<math>~=</math> |
<math>~\frac{1}{2} \biggl(\frac{5L}{M}\biggr)^2 \frac{(a+bx)^2 + (b+ax)^2}{(a^2 + b^2 + 2abx)^2} - 2I \, ,</math> |
[ Paper I, Eq. (3.4) ]
Note that, based on the units chosen in Paper I, <math>~M = 5</math>, and <math>~abc = 15/4</math>.
Aside: Chandra's Notation
According to equation (107) in §21 of EFE, it appears as though,
|
<math>~A_i - A_j</math> |
<math>~=</math> |
<math>~- (a_i^2 - a_j^2)A_{ij} \, .</math> |
And, according to equation (105) in §21 of EFE, it appears as though,
|
<math>~B_{ij}</math> |
<math>~=</math> |
<math>~A_j - a_i^2A_{ij} \, .</math> |
So, for example,
|
<math>~A_{12} </math> |
<math>~=</math> |
<math>~-\biggl[ \frac{A_1 - A_2}{a_1^2 - a_2^2} \biggr] \, ,</math> |
and,
|
<math>~B_{12} </math> |
<math>~=</math> |
<math>~A_2 + a_1^2\biggl[ \frac{A_1 - A_2}{a_1^2 - a_2^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{(a_1^2 - a_2^2)A_2 + a_1^2(A_1 - A_2)}{a_1^2 - a_2^2} </math> |
|
|
<math>~=</math> |
<math>~\frac{a_1^2A_1 - a_2^2A_2 }{a_1^2 - a_2^2} \, .</math> |
Free Energy Surface(s)
Scope
Consider a self-gravitating ellipsoid having the following properties:
- Semi-axis lengths, <math>~(x,y,z)_\mathrm{surface} = (a,b,c)</math>, and corresponding volume, <math>~4\pi/(3abc)</math> ; and consider only the situations <math>0 \le b/a \le 1</math> and <math>0 \le c/a \le 1</math> ;
- Total mass, <math>~M</math> ;
- Uniform density, <math>~\rho = (3 M)/(4\pi abc) </math> ;
- Figure is spinning about its c axis with angular velocity, <math>~\Omega</math> ;
- Internal, steady-state flow exhibiting the following characteristics:
- No vertical (z) motion;
- Elliptical (x-y plane) streamlines everywhere having an ellipticity that matches that of the overall figure, that is, <math>~e = (1-b^2/a^2)^{1/2}</math> ;
- The velocity components, <math>~v_x</math> and <math>~v_y</math>, are linear in the coordinate and, overall, characterized by the magnitude of the vorticity, <math>~\zeta</math> .
Such a configuration is uniquely specified by the choice of six key parameters: <math>~a</math>, <math>~b</math>, <math>~c</math>, <math>~M</math>, <math>~\Omega</math>, and <math>~\zeta</math> .
Free Energy of Incompressible, Constant Mass Systems
We are interested, here, in examining how the free energy of such a system will vary as it is allowed to "evolve" as an incompressible fluid — i.e., holding <math>~\rho</math> fixed — through different ellipsoidal shapes while conserving its total mass. Following Paper I, we choose to set <math>~M = 5</math> — which removes mass from the list of unspecified key parameters — and we choose to set <math>~\rho = \pi^{-1}</math>, which is then reflected in a specification of the semi-axis, <math>~a</math>, in terms of the pair of dimensionless axis ratios, <math>~b/a</math> and <math>~c/a</math>, namely,
|
<math>~a^3</math> |
<math>~=</math> |
<math>~\frac{3Ma^2}{4\pi(bc)\rho} = \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1}\, .</math> |
Moving forward, then, a unique ellipsoidal configuration is identified via the specification of four, rather than six, key parameters — <math>~b/a</math>, <math>~c/a</math>, <math>~\Omega</math>, and <math>~x</math> — and the free energy of that configuration is given by the expression,
|
<math>~E\biggl(\frac{b}{a}, \frac{c}{a}, \Omega, x\biggr)</math> |
<math>~=</math> |
<math>~\frac{a^2}{2} \biggl[\biggl(1+\frac{b}{a} \cdot x\biggr)^2 + \biggl(\frac{b}{a}+x\biggr)^2\biggr]\Omega^2 - 2I </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{2/3} \biggl\{\frac{1}{2} \biggl[\biggl(1+\frac{b}{a} \cdot x\biggr)^2 + \biggl(\frac{b}{a}+x\biggr)^2\biggr]\Omega^2 - \frac{2I}{a^2}\biggr\} \, ,</math> |
where,
|
<math>~x</math> |
<math>~\equiv</math> |
<math>~\biggl[\frac{(b/a)}{1 + (b/a)^2} \biggr]\frac{\zeta}{\Omega} \, ,</math> |
|
<math>~\frac{I}{a^2}</math> |
<math>~=</math> |
<math>~\biggl[A_1 + A_2\biggl(\frac{b}{a}\biggr)^2 + A_3\biggl(\frac{c}{a}\biggr)^2 \biggr] \, ,</math> |
and the functional behavior of the coefficients, <math>~A_1</math>, <math>~A_2</math>, and <math>~A_3</math>, are given by the expressions provided in an accompanying discussion.
Alternatively, replacing <math>~\Omega</math> in favor of <math>~L</math>, we have,
|
<math>~E\biggl(\frac{b}{a}, \frac{c}{a}, L, x\biggr)</math> |
<math>~=</math> |
<math>~\frac{L^2}{2a^2} \biggl[ \biggl(1+\frac{b}{a}\cdot x \biggr)^2 + \biggl(\frac{b}{a}+x \biggr)^2 \biggr] \biggl[ 1 + \biggl(\frac{b}{a}\biggr)^2 + 2\biggl(\frac{b}{a}\biggr)x \biggr]^{-2} - 2I </math> |
|
|
<math>~=</math> |
<math>~\frac{L^2}{2} \biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{-2/3} \biggl[ \biggl(1+\frac{b}{a}\cdot x \biggr)^2 + \biggl(\frac{b}{a}+x \biggr)^2 \biggr] \biggl[ 1 + \biggl(\frac{b}{a}\biggr)^2 + 2\biggl(\frac{b}{a}\biggr)x \biggr]^{-2} </math> |
|
|
|
<math>~- 2\biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{2/3} \biggl[A_1 + A_2\biggl(\frac{b}{a}\biggr)^2 + A_3\biggl(\frac{c}{a}\biggr)^2 \biggr]\, .</math> |
Adopted Evolutionary Constraints
Conserve Only L
Let's fix the total angular momentum, <math>~L</math>, of a triaxial configuration and examine how the configuration's free energy varies as we allow it to contort through different triaxial shapes — that is, as its pair of axis ratios varies, always maintaining <math>~\tfrac{b}{a} < 1</math> — and as we vary <math>~x</math>, which characterizes the fraction of angular momentum that is stored in internal spin versus overall figure rotation. The desired free-energy function, <math>~E(\tfrac{b}{a},\tfrac{c}{a}, x)|_L</math>, has just been defined, but visualizing its behavior is difficult because, in this situation, the free energy is a three-dimensional "surface" lying in the four-dimensional domain, <math>~(\tfrac{b}{a},\tfrac{c}{a}, x, E_L)</math>.
But, acknowledging that we are primarily interested in identifying extrema of this free-energy function, the discussion presented in §3.2 of Christodoulou et al. (1995) shows us how to reduce the dimensionality of this problem by one. There, it is shown that, as long as <math>~\tfrac{b}{a} \ne 1</math>, extrema exist in the <math>~x</math>-coordinate direction — that is, <math>~\partial E_L/\partial x = 0</math> — only if <math>~x = 0.</math> For a given choice of <math>~L</math>, therefore, the relevant free-energy "surface" is defined by the expression,
|
<math>~E\biggl(\frac{b}{a}, \frac{c}{a}, x=0\biggr)\biggr|_L</math> |
<math>~=</math> |
<math>~\frac{L^2}{2} \biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{-2/3} \biggl[ 1 + \biggl(\frac{b}{a}\biggr)^2\biggr]^{-1} - 2\biggl[ \frac{15}{4}\biggl(\frac{b}{a}\biggr)^{-1} \biggl(\frac{c}{a}\biggr)^{-1} \biggr]^{2/3} \biggl[A_1 + A_2\biggl(\frac{b}{a}\biggr)^2 + A_3\biggl(\frac{c}{a}\biggr)^2 \biggr]\, .</math> |
Figure 3 of Christodoulou et al. (1995) presents a black-and-white contour plot of this <math>~E_L</math> function for the specific case of <math>~L = 4.71488</math>, which, for reference, is the total angular momentum of an equilibrium Maclaurin spheroid having an eccentricity, <math>~e = 0.85</math>. We have extracted this black-and-white contour plot from p. 477 of Christodoulou et al. (1995) and have reprinted it as the left panel in row (i) of our Figure 1 montage; note, however, that we have flipped the plot horizontally and rotated it by 90° so that the orientation of the axis pair, <math>~(\tfrac{b}{a},\tfrac{c}{a})</math>, conforms with the orientation used by Chandrasekhar (1965) — see also our accompanying discussion of equilibrium sequence plots. In row (ii) of our Figure 1 montage, we display this <math>~E_L</math> function as a free-energy surface, where color as well as depth is used to tag energy values. The colored contour plot presented as the right-hand segment of row (i) in our Figure 1 montage results from the projection of this free-energy surface onto the <math>~(\tfrac{b}{a},\tfrac{c}{a})</math> plane. It reproduces in quantitative detail the black-and-white contour plot that we have extracted from Christodoulou et al. (1995).
, Christodoulou et al. (1995) contour plot represents a projection of this surface onto the <math>~(\tfrac{b}{a},\tfrac{c}{a})</math> plane.
| Figure 1: 3D Free-Energy Surface & Its Projection onto the <math>~(\tfrac{b}{a},\tfrac{c}{a})</math> Plane | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |