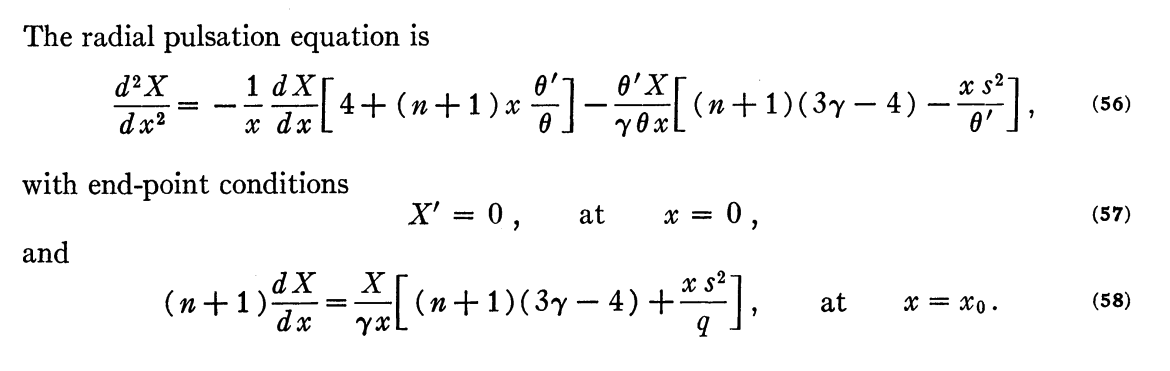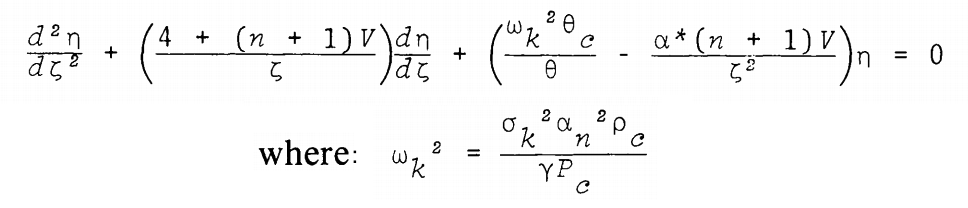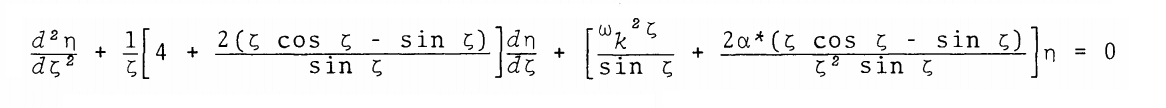User:Tohline/SSC/Stability/Polytropes
Radial Oscillations of Polytropic Spheres

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Groundwork
In an accompanying discussion, we derived the so-called,
Adiabatic Wave Equation
<math> \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 \, , </math>
whose solution gives eigenfunctions that describe various radial modes of oscillation in spherically symmetric, self-gravitating fluid configurations. If the initial, unperturbed equilibrium configuration is a polytropic sphere whose internal structure is defined by the function, <math>~\theta(\xi)</math>, then
|
<math>~r_0</math> |
<math>~=</math> |
<math>~a_n \xi \, ,</math> |
|
<math>~\rho_0</math> |
<math>~=</math> |
<math>~\rho_c \theta^{n} \, ,</math> |
|
<math>~P_0</math> |
<math>~=</math> |
<math>~K\rho_0^{(n+1)/n} = K\rho_c^{(n+1)/n} \theta^{n+1} \, ,</math> |
|
<math>~g_0</math> |
<math>~=</math> |
<math>~\frac{GM(r_0)}{r_0^2} = \frac{G}{r_0^2} \biggl[ 4\pi a_n^3 \rho_c \biggl(-\xi^2 \frac{d\theta}{d\xi}\biggr) \biggr] \, ,</math> |
where,
|
<math>~a_n</math> |
<math>~=</math> |
<math>~\biggl[\frac{(n+1)K}{4\pi G} \cdot \rho_c^{(1-n)/n} \biggr]^{1/2} \, .</math> |
Hence, after multiplying through by <math>~a_n^2</math>, the above adiabatic wave equation can be rewritten in the form,
|
<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - \frac{g_0}{a_n}\biggl(\frac{a_n^2 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{d\xi} + \biggl(\frac{a_n^2\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{a_n\xi} \biggr] x </math> |
<math>~=</math> |
<math>~0 \, .</math> |
In addition, given that,
|
<math>~\frac{g_0}{a_n}</math> |
<math>~=</math> |
<math>~4\pi G \rho_c \biggl(-\frac{d \theta}{d\xi} \biggr) \, ,</math> |
and,
|
<math>~\frac{a_n^2 \rho_0}{P_0}</math> |
<math>~=</math> |
<math>~\frac{(n+1)}{(4\pi G\rho_c)\theta} = \frac{a_n^2 \rho_c}{P_c} \cdot \frac{\theta_c}{\theta}\, ,</math> |
we can write,
|
<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4 - (n+1)V(\xi)}{\xi} \biggr] \frac{dx}{d\xi} + \biggl[\omega^2 \biggl(\frac{a_n^2 \rho_c }{\gamma_g P_c} \biggr) \frac{\theta_c}{\theta} - \biggl(3-\frac{4}{\gamma_g}\biggr) \cdot \frac{(n+1)V(x)}{\xi^2} \biggr] x </math> |
<math>~=</math> |
<math>0 \, ,</math> |
where we have adopted the functional notation,
|
<math>~V(\xi)</math> |
<math>~\equiv</math> |
<math>~- \frac{\xi}{\theta} \frac{d \theta}{d\xi} \, .</math> |
As can be seen in the following framed image, this is the same as the radial pulsation equation for polytropic configurations that appears as equation (56) in the detailed discussion of "The Oscillations of Gas Spheres" published by H M. Hurley, P. H. Roberts, & K. Wright (1966, ApJ, 143, 535).
|
Radial Pulsation Equation as Presented by M. Hurley, P. H. Roberts, & K. Wright (1966) |
|---|
Also, as can be seen in the following framed image, this is the form of the polytropic wave equation published by J. O. Murphy & R. Fiedler (1985b, Proc. Astron. Soc. Australia, 6, 222), at the beginning of their discussion of "Radial Pulsations and Vibrational Stability of a Sequence of Two Zone Polytropic Stellar Models." (It should be noted that there is a sign error in the numerator of the second term of their published expression; the definition of the coefficient, <math>~\alpha^*</math>, given in the text of their paper also contains an error.)
|
Polytropic Wave Equation as Presented by J. O. Murphy & R. Fiedler (1985b) |
|---|
Overview
The eigenvector associated with radial oscillations in isolated polytropes has been determined numerically and the results have been presented in a variety of key publications:
- P. LeDoux & Th. Walraven (1958, Handbuch der Physik, 51, 353) —
- R. F. Christy (1966, Annual Reviews of Astronomy & Astrophysics, 4, 353) — Pulsation Theory
- M. Hurley, P. H. Roberts, & K. Wright (1966, ApJ, 143, 535) — The Oscillations of Gas Spheres
- J. P. Cox (1974, Reports on Progress in Physics, 37, 563) — Pulsating Stars
Tables
|
Quantitative Information Regarding Eigenvectors of Oscillating Polytropes <math>~(\Gamma_1 = 5/3)</math> |
||||
|---|---|---|---|---|
|
<math>~n</math> |
<math>~\frac{\rho_c}{\bar\rho}</math> |
Excerpts from Table 1 of Hurley, Roberts, & Wright (1966) <math>~s^2 (n+1)/(4\pi G\rho_c)</math> |
Excerpts from Table 3 of <math>~\sigma_0^2 R^3/(GM)</math> |
<math>\frac{(n+1) *\mathrm{Cox74}}{3 *\mathrm{HRW66}} \cdot \frac{\bar\rho}{\rho_c}</math> |
|
<math>~0</math> |
<math>~1</math> |
<math>~1/3</math> |
<math>~1</math> |
<math>~1</math> |
|
<math>~1</math> |
<math>~3.30</math> |
<math>~0.38331</math> |
<math>~1.892</math> |
<math>~0.997</math> |
|
<math>~1.5</math> |
<math>~5.99</math> |
<math>~0.37640</math> |
<math>~2.712</math> |
<math>~1.002</math> |
|
<math>~2</math> |
<math>~11.4</math> |
<math>~0.35087</math> |
<math>~4.00</math> |
<math>~1.000</math> |
|
<math>~3</math> |
<math>~54.2</math> |
<math>~0.22774</math> |
<math>~9.261</math> |
<math>~1.000</math> |
|
<math>~3.5</math> |
<math>~153</math> |
<math>~0.12404</math> |
<math>~12.69</math> |
<math>~1.003</math> |
|
<math>~4.0</math> |
<math>~632</math> |
<math>~0.04056</math> |
<math>~15.38</math> |
<math>~1.000</math> |
n = 1 Polytrope
Setup
From our derived structure of an n = 1 polytrope, in terms of the configuration's radius <math>R</math> and mass <math>M</math>, the central pressure and density are, respectively,
<math>P_c = \frac{\pi G}{8}\biggl( \frac{M^2}{R^4} \biggr) </math> ,
and
<math>\rho_c = \frac{\pi M}{4 R^3} </math> .
Hence the characteristic time and acceleration are, respectively,
<math>
\tau_\mathrm{SSC} = \biggl[ \frac{R^2 \rho_c}{P_c} \biggr]^{1/2} =
\biggl[ \frac{2R^3 }{GM} \biggr]^{1/2} =
\biggl[ \frac{\pi}{2 G\rho_c} \biggr]^{1/2},
</math>
and,
<math>
g_\mathrm{SSC} = \frac{P_c}{R \rho_c} = \biggl( \frac{GM}{2R^2} \biggr) .
</math>
The required functions are,
- Density:
<math>\frac{\rho_0(\chi_0)}{\rho_c} = \frac{\sin(\pi\chi_0)}{\pi\chi_0} </math> ;
- Pressure:
<math>\frac{P_0(\chi_0)}{P_c} = \biggl[ \frac{\sin(\pi\chi_0)}{\pi\chi_0} \biggr]^2 </math> ;
- Gravitational acceleration:
<math>
\frac{g_0(r_0)}{g_\mathrm{SSC}} = \frac{2}{\chi_0^2} \biggl[ \frac{M_r(\chi_0)}{M}\biggr] =
\frac{2}{\pi \chi_0^2} \biggl[ \sin (\pi\chi_0 ) - \pi\chi_0 \cos (\pi\chi_0 ) \biggr].
</math>
So our desired Eigenvalues and Eigenvectors will be solutions to the following ODE:
<math>
\frac{d^2x}{d\chi_0^2} + \frac{2}{\chi_0} \biggl[ 1 + \pi\chi_0 \cot (\pi\chi_0 ) \biggr] \frac{dx}{d\chi_0} + \frac{1}{\gamma_\mathrm{g}} \biggl\{ \frac{\pi \chi_0}{\sin(\pi\chi_0)} \biggl[ \frac{\pi \omega^2}{2G\rho_c} \biggr] + \frac{2}{\chi_0^2 } (4 - 3\gamma_\mathrm{g}) \biggl[ 1 - \pi\chi_0 \cot (\pi\chi_0 ) \biggr] \biggr\} x = 0 ,
</math>
or, replacing <math>\chi_0</math> with <math>\xi \equiv \pi\chi_0</math> and dividing the entire expression by <math>\pi^2</math>, we have,
<math>
\frac{d^2x}{d\xi^2} + \frac{2}{\xi} \biggl[ 1 + \xi \cot \xi \biggr] \frac{dx}{d\xi} + \frac{1}{\gamma_\mathrm{g}} \biggl\{ \frac{\xi}{\sin \xi} \biggl[ \frac{\omega^2}{2\pi G\rho_c} \biggr] + \frac{2}{\xi^2 } (4 - 3\gamma_\mathrm{g}) \biggl[ 1 - \xi \cot \xi \biggr] \biggr\} x = 0 .
</math>
This is identical to the formulation of the wave equation that is relevant to the (n = 1) core of the composite polytrope studied by J. O. Murphy & R. Fiedler (1985b); for comparison, their expression is displayed, here, in the following boxed-in image.
|
n = 1 Polytropic Formulation of Wave Equation as Presented by Murphy & Fiedler (1985b) |
|---|
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Attempt at Deriving an Analytic Eigenvector Solution
Multiplying the last expression through by <math>~\xi^2\sin\xi</math> gives,
<math>
(\xi^2\sin\xi ) \frac{d^2x}{d\xi^2} + 2 \biggl[ \xi \sin\xi + \xi^2 \cos \xi \biggr] \frac{dx}{d\xi} +
\biggl[ \sigma^2 \xi^3 - 2\alpha ( \sin\xi - \xi \cos \xi ) \biggr] x = 0 \, ,
</math>
where,
|
<math>~\sigma^2</math> |
<math>~\equiv</math> |
<math> ~\frac{\omega^2}{2\pi G\rho_c \gamma_g} \, , </math> |
|
<math>~\alpha</math> |
<math>~\equiv</math> |
<math> ~3-\frac{4}{\gamma_g} \, . </math> |
The first two terms can be folded together to give,
|
<math>~ \frac{1}{\xi^2 \sin^2\xi} \cdot \frac{d}{d\xi}\biggl[ \xi^2 \sin^2\xi \frac{dx}{d\xi} \biggr] </math> |
<math>~=</math> |
<math> ~\frac{1}{\xi^2 \sin\xi} \biggl[ 2\alpha ( \sin\xi - \xi \cos \xi ) - \sigma^2 \xi^3 \biggr] x </math> |
|
|
<math>~=</math> |
<math> ~- \biggl[ \frac{2\alpha}{\xi^2} \biggl( \frac{\xi \cos \xi}{\sin\xi} -1\biggr) + \sigma^2 \biggl( \frac{\xi}{\sin\xi}\biggr) \biggr] x </math> |
|
|
<math>~=</math> |
<math> ~- \biggl[ \frac{2\alpha}{\xi^2} \frac{\xi^2}{\sin\xi} \cdot \frac{d}{d\xi} \biggl( \frac{\sin\xi}{\xi} \biggr) + \sigma^2 \biggl( \frac{\xi}{\sin\xi}\biggr) \biggr] x </math> |
|
|
<math>~=</math> |
<math> ~- \biggl[ \frac{2\alpha}{\xi} \frac{d}{d\xi}\biggl( \frac{\sin\xi}{\xi} \biggr) + \sigma^2 \biggr] \biggl( \frac{\xi}{\sin\xi}\biggr) x \, , </math> |
where, in order to make this next-to-last step, we have recognized that,
|
<math>~ \frac{d}{d\xi} \biggl( \frac{\sin\xi}{\xi} \biggr) </math> |
<math>~=</math> |
<math> ~\frac{\sin\xi}{\xi^2} \biggl[ \frac{\xi \cos\xi}{\sin\xi} - 1 \biggr] \, . </math> |
It would seem that the eigenfunction, <math>~x(\xi)</math>, should be expressible in terms of trigonometric functions and powers of <math>~\xi</math>; indeed, it appears as though the expression governing this eigenfunction would simplify considerably if <math>~x \propto \sin\xi/\xi</math>. With this in mind, we have made some attempts to guess the exact form of the eigenfunction. Here is one such attempt.
First Guess
Let's try,
<math>~x = \frac{\sin\xi}{\xi} \, ,</math>
which means,
|
<math>~x^' \equiv \frac{dx}{d\xi}</math> |
<math>~=</math> |
<math> ~\frac{\sin\xi}{\xi^2} \biggl[ \frac{\xi \cos\xi}{\sin\xi} - 1 \biggr] \, . </math> |
Does this satisfy the governing expression? Let's see. The right-and-side (RHS) gives:
|
RHS |
<math>~=</math> |
<math> ~- \biggl[ \frac{2\alpha}{\xi} \frac{d}{d\xi}\biggl( \frac{\sin\xi}{\xi} \biggr) + \sigma^2 \biggr] \biggl( \frac{\xi}{\sin\xi}\biggr) x = - \biggl[ \frac{2\alpha x^'}{\xi} + \sigma^2 \biggr] \, . </math> |
At the same time, the left-hand-side (LHS) may, quite generically, be written as:
|
LHS |
<math>~=</math> |
<math>~ \frac{x^'}{\xi} \biggl\{ \frac{\xi}{(\xi^2 \sin^2\xi)x^'} \cdot \frac{d[ (\xi^2 \sin^2\xi)x^']}{d\xi} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{x^'}{\xi} \biggl[\frac{d\ln[ (\xi^2 \sin^2\xi)x^']}{d\ln\xi} \biggr] \, . </math> |
Putting the two sides together therefore gives,
|
<math>~ \frac{x^'}{\xi} \biggl[\frac{d\ln[ (\xi^2 \sin^2\xi)x^']}{d\ln\xi} +2\alpha \biggr] </math> |
<math>~=</math> |
<math> ~-\sigma^2 </math> |
|
<math>~ \Rightarrow ~~~~~ \biggl[\frac{d\ln[ (\xi^2 \sin^2\xi)x^']^{1/(2\alpha)}}{d\ln\xi} +1 \biggr] </math> |
<math>~=</math> |
<math> ~- \frac{\sigma^2}{2\alpha } \biggl( \frac{\xi}{x^'} \biggr) </math> |
|
<math>~ \Rightarrow ~~~~~ \frac{d\ln[ (\xi^2 \sin^2\xi)x^']^{-1/(2\alpha)}}{d\ln\xi} </math> |
<math>~=</math> |
<math> ~1 + \frac{\sigma^2}{2\alpha } \biggl( \frac{\xi}{x^'} \biggr) \, . </math> |
[Comment from J. E. Tohline on 6 April 2015: I'm not sure what else to make of this.]
Second Guess
Adopting the generic rewriting of the LHS, and leaving the RHS fully generic as well, we have,
|
<math>~ \frac{x^'}{\xi} \biggl[\frac{d\ln[ (\xi^2 \sin^2\xi)x^']}{d\ln\xi} \biggr] </math> |
<math>~=</math> |
<math> ~- \biggl[ \frac{2\alpha}{\xi} \frac{d}{d\xi}\biggl( \frac{\sin\xi}{\xi} \biggr) + \sigma^2 \biggr] \biggl( \frac{\xi}{\sin\xi}\biggr) x </math> |
|
<math>~\Rightarrow ~~~~~ \frac{x^'}{x} \biggl[\frac{d\ln[ (\xi^2 \sin^2\xi)x^']}{d\ln\xi} \biggr] </math> |
<math>~=</math> |
<math> ~- 2\alpha\biggl( \frac{\xi}{\sin\xi}\biggr) \frac{d}{d\xi}\biggl( \frac{\sin\xi}{\xi} \biggr) ~- \sigma^2\biggl( \frac{\xi^2}{\sin\xi}\biggr) </math> |
|
<math>~\Rightarrow ~~~~~ \frac{d\ln(x)}{d\ln \xi} \biggl[\frac{d\ln[ (\xi^2 \sin^2\xi)x^']}{d\ln\xi} \biggr] </math> |
<math>~=</math> |
<math> ~- 2\alpha\biggl[ \frac{d\ln(\sin\xi/\xi)}{d\ln \xi} \biggr] ~- \sigma^2\biggl( \frac{\xi^3}{\sin\xi}\biggr) \, . </math> |
|
<math> ~\Rightarrow ~~~~ - \sigma^2 </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\sin\xi}{\xi^3}\biggr) \biggl\{\frac{d\ln(x)}{d\ln \xi} \biggl[\frac{d\ln[ (\xi^2 \sin^2\xi)x^']}{d\ln\xi} \biggr] + 2\alpha\biggl[ \frac{d\ln(\sin\xi/\xi)}{d\ln \xi} \biggr] \biggr\} \, . </math> |
[Comment from J. E. Tohline on 6 April 2015: I'm not sure what else to make of this.]
Third Guess
Let's rewrite the polytropic (n = 1) wave equation as follows:
<math> ~\sin\xi \biggl[ \xi^2 x^{} + 2\xi x^' - 2\alpha x \biggr] + \cos\xi \biggl[ 2\xi^2 x^' + 2\alpha \xi x \biggr] +\sigma^2 \xi^3 x = 0 \, . </math>
It is difficult to determine what term in the adiabatic wave equation will cancel the term involving <math>~\sigma^2</math> because its leading coefficient is <math>~\xi^3</math> and no other term contains a power of <math>~\xi</math> that is higher than two. After thinking through various trial eigenvector expressions, <math>~x(\xi)</math>, I have determined that a function of the following form has a chance of working because the second derivative of the function generates a leading factor of <math>~\xi^3</math> while the function itself does not introduce any additional factors of <math>~\xi</math> into the term that contains <math>~\sigma^2</math>:
|
<math>~x</math> |
<math>~=</math> |
<math> ~[a\sin^2(\xi^{5/2}) + b\sin(\xi^{5/2})\cos(\xi^{5/2}) + c\cos^2(\xi^{5/2})] [ A\sin\xi + B\cos\xi] </math> |
|
<math>~\Rightarrow ~~~ x^'</math> |
<math>~=</math> |
<math> ~[a\sin^2(\xi^{5/2}) + b\sin(\xi^{5/2})\cos(\xi^{5/2}) + c\cos^2(\xi^{5/2})] \cdot \frac{d[ A\sin\xi + B\cos\xi]}{d\xi} </math> |
|
|
|
<math> ~+ \frac{d[a\sin^2(\xi^{5/2}) + b\sin(\xi^{5/2})\cos(\xi^{5/2}) + c\cos^2(\xi^{5/2})]}{d\xi} \cdot [ A\sin\xi + B\cos\xi] </math> |
|
|
<math>~=</math> |
<math> ~[a\sin^2(\xi^{5/2}) + b\sin(\xi^{5/2})\cos(\xi^{5/2}) + c\cos^2(\xi^{5/2})] \cdot \frac{d[ A\sin\xi + B\cos\xi]}{d\xi} </math> |
|
|
|
<math> ~+ [ A\sin\xi + B\cos\xi] \biggl\{5a \xi^{3/2} \sin(\xi^{5/2}) \cos(\xi^{5/2}) + b\biggl[ \frac{5}{2} \xi^{3/2}\cos^2(\xi^{5/2}) - \frac{5}{2} \xi^{3/2}\sin^2(\xi^{5/2}) \biggr] - 5c \xi^{3/2} \sin(\xi^{5/2}) \cos(\xi^{5/2}) \biggr\} </math> |
|
|
<math>~=</math> |
<math> ~[a\sin^2(\xi^{5/2}) + b\sin(\xi^{5/2})\cos(\xi^{5/2}) + c\cos^2(\xi^{5/2})] \cdot \frac{d[ A\sin\xi + B\cos\xi]}{d\xi} </math> |
|
|
|
<math> ~+ [ A\sin\xi + B\cos\xi] \biggl\{5(a-c) \xi^{3/2} \sin(\xi^{5/2}) \cos(\xi^{5/2}) + \frac{5b}{2} \xi^{3/2}\biggl[ 1 - 2\sin^2(\xi^{5/2}) \biggr] \biggr\} </math> |
|
<math>~\Rightarrow ~~~ x^{}</math> |
<math>~=</math> |
<math> ~[a\sin^2(\xi^{5/2}) + b\sin(\xi^{5/2})\cos(\xi^{5/2}) + c\cos^2(\xi^{5/2})] \cdot \frac{d^2[ A\sin\xi + B\cos\xi]}{d^2\xi} </math> |
|
|
|
<math>~+ \biggl\{5(a-c) \xi^{3/2} \sin(\xi^{5/2}) \cos(\xi^{5/2}) + \frac{5b}{2} \xi^{3/2}\biggl[ 1 - 2\sin^2(\xi^{5/2}) \biggr] \biggr\} \cdot \frac{d[ A\sin\xi + B\cos\xi]}{d\xi} </math> |
|
|
|
<math> ~+ [ A\sin\xi + B\cos\xi] \biggl\{ \frac{15}{2}(a-c) \xi^{1/2} \sin(\xi^{5/2}) \cos(\xi^{5/2}) +\frac{25}{2}(a-c) \xi^{3} \cos^2(\xi^{5/2}) - \frac{25}{2}(a-c) \xi^{3} \sin^2(\xi^{5/2}) </math> |
|
|
|
<math> + \frac{15b}{4} \xi^{1/2}\biggl[ 1 - 2\sin^2(\xi^{5/2}) \biggr] - 25b \xi^{3}\sin(\xi^{5/2}) \cos(\xi^{5/2}) \biggr\} </math> |
|
|
<math>~=</math> |
<math> ~[a\sin^2(\xi^{5/2}) + b\sin(\xi^{5/2})\cos(\xi^{5/2}) + c\cos^2(\xi^{5/2})] \cdot \frac{d^2[ A\sin\xi + B\cos\xi]}{d^2\xi} </math> |
|
|
|
<math>~+ \biggl\{5(a-c) \xi^{3/2} \sin(\xi^{5/2}) \cos(\xi^{5/2}) + \frac{5b}{2} \xi^{3/2}\biggl[ 1 - 2\sin^2(\xi^{5/2}) \biggr] \biggr\} \cdot \frac{d[ A\sin\xi + B\cos\xi]}{d\xi} </math> |
|
|
|
<math> ~+ [ A\sin\xi + B\cos\xi] \biggl\{ \frac{15}{4}\xi^{1/2} \biggl[ 2(a-c) \sin(\xi^{5/2}) \cos(\xi^{5/2}) + b\biggl( 1 - 2\sin^2(\xi^{5/2}) \biggr) \biggr] </math> |
|
|
|
<math>~+ \frac{25}{2} \xi^3 \biggl[ - 2b \sin(\xi^{5/2}) \cos(\xi^{5/2}) +(a-c) \biggl( 1- 2\sin^2(\xi^{5/2}) \biggr) \biggr] \biggr\} </math> |
[Comment from J. E. Tohline on 9 April 2015: I'm not sure what else to make of this.]
Fourth Guess
Again, working with the polytropic (n = 1) wave equation written in the following form,
<math> ~\sin\xi \biggl[ \xi^2 x^{} + 2\xi x^' - 2\alpha x \biggr] + \cos\xi \biggl[ 2\xi^2 x^' + 2\alpha \xi x \biggr] +\sigma^2 \xi^3 x = 0 \, . </math>
Now, let's try:
<math>~x = a_0 + b_1 \xi \sin\xi + c_2 \xi^2 \cos\xi \, ,</math>
which means,
|
<math>~x^' </math> |
<math>~=</math> |
<math> ~b_1 \sin\xi + b_1 \xi \cos\xi + 2c_2 \xi \cos\xi - c_2\xi^2 \sin\xi </math> |
|
|
<math>~=</math> |
<math> ~(b_1 - c_2\xi^2 ) \sin\xi + (b_1 + 2c_2)\xi \cos\xi \, , </math> |
|
<math>~x^{} </math> |
<math>~=</math> |
<math> ~(- 2c_2\xi ) \sin\xi + (b_1 - c_2\xi^2 ) \cos\xi + (b_1 + 2c_2 )\cos\xi - (b_1 + 2c_2 )\xi \sin\xi </math> |
|
|
<math>~=</math> |
<math> ~-(2c_2+b_1 + 2c_2 ) \xi \sin\xi + (2b_1 + 2c_2 - c_2\xi^2 ) \cos\xi \, . </math> |
The LHS of the wave equation then becomes,
|
LHS |
<math>~=</math> |
<math> ~\sin\xi \biggl\{ \xi^2 \biggl[ -(2c_2+b_1 + 2c_2 ) \xi \sin\xi + (2b_1 + 2c_2 - c_2\xi^2 ) \cos\xi \biggr] + 2\xi \biggl[ (b_1 - c_2\xi^2 ) \sin\xi + (b_1 + 2c_2)\xi \cos\xi \biggr] - 2\alpha \biggl[ a_0 + (b_1 \xi) \sin\xi + (c_2 \xi^2) \cos\xi \biggr] \biggr\} </math> |
|
|
|
<math> + \cos\xi \biggl\{ 2\xi^2 \biggl[ (b_1 - c_2\xi^2 ) \sin\xi + (b_1 + 2c_2)\xi \cos\xi \biggr] + 2\alpha \xi \biggl[ a_0 + (b_1 \xi) \sin\xi + (c_2 \xi^2) \cos\xi \biggr] \biggr\} +\sigma^2 \xi^3 \biggl[ a_0 + b_1 \xi \sin\xi + c_2 \xi^2 \cos\xi \biggr] </math> |
|
|
<math>~=</math> |
<math> ~\sin\xi \biggl\{ \biggl[ -(2c_2+b_1 + 2c_2 ) \xi^3 \sin\xi + (2b_1 + 2c_2 - c_2\xi^2 ) \xi^2\cos\xi \biggr] + \biggl[ 2(b_1 - c_2\xi^2 )\xi \sin\xi + 2(b_1 + 2c_2)\xi^2 \cos\xi \biggr] - 2\alpha \biggl[ a_0 + (b_1 \xi) \sin\xi + (c_2 \xi^2) \cos\xi \biggr] \biggr\} </math> |
|
|
|
<math> + \cos\xi \biggl\{ \biggl[ 2(b_1 - c_2\xi^2 )\xi^2 \sin\xi + 2(b_1 + 2c_2)\xi^3 \cos\xi \biggr] + \biggl[ 2a_0\alpha \xi + 2b_1\alpha \xi^2 \sin\xi + 2c_2 \alpha \xi^3 \cos\xi \biggr] \biggr\} +\sigma^2 \biggl[ a_0\xi^3 + b_1 \xi^4 \sin\xi + c_2 \xi^5 \cos\xi \biggr] </math> |
|
|
<math>~=</math> |
<math> ~\sin\xi \biggl\{- 2\alpha a_0 + \biggl[ -(2c_2+b_1 + 2c_2 ) \xi^3 + 2(b_1 - c_2\xi^2 )\xi - 2\alpha (b_1 \xi) \biggr]\sin\xi + \biggl[ (2b_1 + 2c_2 - c_2\xi^2 ) \xi^2 + 2(b_1 + 2c_2)\xi^2 - 2\alpha (c_2 \xi^2) \biggr] \cos\xi \biggr\} </math> |
|
|
|
<math> + \cos\xi \biggl\{ + 2a_0\alpha \xi + \biggl[ 2(b_1 - c_2\xi^2 )\xi^2 + 2b_1\alpha \xi^2 \biggr] \sin\xi + \biggl[ 2(b_1 + 2c_2)\xi^3 + 2c_2 \alpha \xi^3\biggr] \cos\xi \biggr\} +\sigma^2 \biggl[ a_0\xi^3 + b_1 \xi^4 \sin\xi + c_2 \xi^5 \cos\xi \biggr] </math> |
|
|
<math>~=</math> |
<math> ~\sigma^2 a_0 \xi^3 + \biggl[ -(2c_2+b_1 + 2c_2 ) \xi^3 + 2(b_1 - c_2\xi^2 )\xi - 2\alpha (b_1 \xi) \biggr]\sin^2\xi + \biggl[ 2(b_1 + 2c_2)\xi^3 + 2c_2 \alpha \xi^3\biggr] \biggl(1-\sin^2\xi \biggr) </math> |
|
|
|
<math> + \biggl[ (2b_1 + 2c_2 - c_2\xi^2 ) \xi^2 + 2(b_1 + 2c_2)\xi^2 - 2\alpha (c_2 \xi^2) \biggr] \sin\xi \cos\xi + \biggl[ 2(b_1 - c_2\xi^2 )\xi^2 + 2b_1\alpha \xi^2 \biggr] \sin\xi \cos\xi </math> |
|
|
|
<math> +\sigma^2 \biggl[ b_1 \xi^4 \sin\xi + c_2 \xi^5 \cos\xi \biggr] + 2a_0\alpha \xi\cos\xi - 2\alpha a_0 \sin\xi </math> |
|
|
<math>~=</math> |
<math> ~\biggl[ \sigma^2 a_0 + 2(b_1 + 2c_2) + 2c_2 \alpha \biggr]\xi^3 + \biggl\{+ 2(b_1 )\xi - 2\alpha (b_1 \xi) +[-2c_2 - 2(b_1 + 2c_2) - 2c_2 \alpha -(2c_2+b_1 + 2c_2 )] \xi^3 \biggr\} \sin^2\xi </math> |
|
|
|
<math> + \biggl\{ [ (2b_1 + 2c_2 ) + 2(b_1 + 2c_2) - 2\alpha (c_2 ) + 2(b_1 ) + 2b_1\alpha ] \xi^2 -3c_2\xi^4 \biggr\} \sin\xi \cos\xi </math> |
|
|
|
<math>~+ \sin\xi \biggl[\sigma^2b_1 \xi^4 - 2\alpha a_0 \biggr] + \xi \cos\xi \biggl[\sigma^2 c_2 \xi^4 + 2a_0\alpha \biggr] </math> |
|
|
<math>~=</math> |
<math> ~[ \sigma^2 a_0 + 2(b_1 + 2c_2) + 2c_2 \alpha ]\xi^3 + \biggl\{2 b_1(1-\alpha) - [2c_2(5+\alpha) + 3b_1] \xi^2 \biggr\} \xi \sin^2\xi </math> |
|
|
|
<math> + \biggl\{ 2(3-\alpha)( b_1+c_2 ) -3c_2\xi^2 \biggr\} \xi^2 \sin\xi \cos\xi +\sin\xi \biggl[\sigma^2b_1 \xi^4 - 2\alpha a_0 \biggr] + \xi \cos\xi \biggl[\sigma^2 c_2 \xi^4 + 2a_0\alpha \biggr] \, . </math> |
Fifth Guess
Along a similar line of reasoning, let's try a function of the form,
|
<math>~x</math> |
<math>~=</math> |
<math> ~x_s \sin\xi + x_c \cos\xi + x_1 \sin^2\xi + x_2 \cos^2\xi + x_3 \sin\xi \cos\xi\, , </math> |
where <math>~x_s, x_c, x_1, x_2,</math> and <math>~x_3</math> are five separate, as yet, unspecified (polynomial?) functions of <math>~\xi</math>. This also means that,
|
<math>~x^'</math> |
<math>~=</math> |
<math> ~(x_s^' - x_c)\sin\xi + (x_c^' + x_s)\cos\xi + (x_1^' - x_3)\sin^2\xi + (x_2^' + x_3)\cos^2\xi + (x_3^' + 2x_1 -2x_2)\sin\xi \cos\xi \, ; </math> |
and,
|
<math>~x^{}</math> |
<math>~=</math> |
<math> ~(x_s^{} - 2x_c^{'} - x_s)\sin\xi + (x_c^{} + 2x_s^' -x_c)\cos\xi + (x_1^{} -2x_3^' -2x_1 + 2x_2)\sin^2\xi + (x_2^{} + 2x_3^'+ 2x_1 - 2x_2)\cos^2\xi + (x_3^{} + 4x_1^' -4x_2^' - 4x_3)\sin\xi \cos\xi \, . </math> |
Hence the LHS of the polytropic (n = 1) wave equation becomes,
|
LHS |
<math>~=</math> |
<math> ~~\sin\xi \biggl\{ \xi^2 \biggl[~(x_s^{} - 2x_c^{'} - x_s)\sin\xi + (x_c^{} + 2x_s^' -x_c)\cos\xi + (x_1^{} -2x_3^' -2x_1 + 2x_2)\sin^2\xi + (x_2^{} + 2x_3^'+ 2x_1 - 2x_2)\cos^2\xi + (x_3^{} + 4x_1^' -4x_2^' - 4x_3)\sin\xi \cos\xi \biggr] </math> |
|
|
|
<math> + 2\xi \biggl[~(x_s^' - x_c)\sin\xi + (x_c^' + x_s)\cos\xi + (x_1^' - x_3)\sin^2\xi + (x_2^' + x_3)\cos^2\xi + (x_3^' + 2x_1 -2x_2)\sin\xi \cos\xi \biggr] </math> |
|
|
|
<math> - 2\alpha \biggl[ x_s \sin\xi + x_c \cos\xi + x_1 \sin^2\xi + x_2 \cos^2\xi + x_3 \sin\xi \cos\xi\biggr] \biggr\} </math> |
|
|
|
<math> + \cos\xi \biggl\{ 2\xi^2 \biggl[~(x_s^' - x_c)\sin\xi + (x_c^' + x_s)\cos\xi + (x_1^' - x_3)\sin^2\xi + (x_2^' + x_3)\cos^2\xi + (x_3^' + 2x_1 -2x_2)\sin\xi \cos\xi \biggr] </math> |
|
|
|
<math> + 2\alpha \xi \biggl[ x_s \sin\xi + x_c \cos\xi + x_1 \sin^2\xi + x_2 \cos^2\xi + x_3 \sin\xi \cos\xi\biggr] \biggr\} </math> |
|
|
|
<math> +\sigma^2 \xi^3 \biggl\{ x_s \sin\xi + x_c \cos\xi + x_1 \sin^2\xi + x_2 \cos^2\xi + x_3 \sin\xi \cos\xi \biggr\} </math> |
|
|
<math>~=</math> |
<math> ~\biggl[(x_s^{} - 2x_c^{'} - x_s)\xi^2 + 2\xi (x_s^' - x_c) -2\alpha x_s + \sigma^2 \xi^3 x_1 \biggr]\sin^2\xi + \biggl[(x_c^{} + 2x_s^' -x_c)\xi^2 + 2\xi (x_c^' + x_s) - 2\alpha x_c + 2\xi^2 (x_s^' - x_c) + 2\alpha \xi x_s + \sigma^2 \xi^3 x_3 \biggr] \sin\xi \cos\xi </math> |
|
|
|
<math> +\biggl[ (x_1^{} -2x_3^' -2x_1 + 2x_2)\xi^2 + 2\xi (x_1^' - x_3) - 2\alpha x_1 \biggr] \sin^3\xi + \biggl[(x_2^{} + 2x_3^'+ 2x_1 - 2x_2)\xi^2 + 2\xi (x_2^' + x_3) - 2\alpha x_2 + 2\xi^2 (x_3^' + 2x_1 -2x_2)+ 2\alpha \xi x_3 \biggr]\sin\xi \cos^2\xi </math> |
|
|
|
<math> + \biggl[(x_3^{} + 4x_1^' -4x_2^' - 4x_3)\xi^2 + 2\xi (x_3^' + 2x_1 -2x_2) - 2\alpha x_3 + 2\xi^2 (x_1^' - x_3) + 2\alpha \xi x_1 \biggr] \sin^2\xi \cos\xi </math> |
|
|
|
<math> + \biggl[2\xi^2 (x_c^' + x_s ) + 2\alpha \xi x_c + \sigma^2 \xi^3 x_2 \biggr]\cos^2\xi + \biggl[2\xi^2 (x_2^' + x_3)+ 2\alpha \xi x_2 \biggr]\cos^3\xi + \sigma^2 \xi^3 x_s \sin\xi + \sigma^2 \xi^3 x_c \cos\xi </math> |
|
|
<math>~=</math> |
<math> ~\biggl[(x_s^{} - 2x_c^{'} - x_s)\xi^2 + 2\xi (x_s^' - x_c) -2\alpha x_s + \sigma^2 \xi^3 x_1 \biggr]\sin^2\xi + \biggl[(x_c^{} + 2x_s^' -x_c)\xi^2 + 2\xi (x_c^' + x_s) - 2\alpha x_c + 2\xi^2 (x_s^' - x_c) + 2\alpha \xi x_s + \sigma^2 \xi^3 x_3 \biggr] \sin\xi \cos\xi </math> |
|
|
|
<math> +\biggl[ (x_1^{} -2x_3^' -2x_1 + 2x_2)\xi^2 + 2\xi (x_1^' - x_3) - 2\alpha x_1 + \sigma^2 \xi^3 x_s \biggr] \sin\xi </math> |
|
|
|
<math> + \biggl[(x_2^{} + 2x_3^'+ 2x_1 - 2x_2)\xi^2 + 2\xi (x_2^' + x_3) - 2\alpha x_2 + 2\xi^2 (x_3^' + 2x_1 -2x_2)+ 2\alpha \xi x_3 - (x_1^{} -2x_3^' -2x_1 + 2x_2)\xi^2 - 2\xi (x_1^' - x_3) + 2\alpha x_1 \biggr]\sin\xi \cos^2\xi </math> |
|
|
|
<math> + \biggl[(x_3^{} + 4x_1^' -4x_2^' - 4x_3)\xi^2 + 2\xi (x_3^' + 2x_1 -2x_2) - 2\alpha x_3 + 2\xi^2 (x_1^' - x_3) + 2\alpha \xi x_1 -2\xi^2 (x_2^' + x_3) - 2\alpha \xi x_2 \biggr] \sin^2\xi \cos\xi </math> |
|
|
|
<math> + \biggl[2\xi^2 (x_c^' + x_s ) + 2\alpha \xi x_c + \sigma^2 \xi^3 x_2 \biggr]\cos^2\xi + \biggl[2\xi^2 (x_2^' + x_3)+ 2\alpha \xi x_2 + \sigma^2 \xi^3 x_c \biggr]\cos\xi </math> |
So, the five chosen (polynomial?) functions of <math>~\xi</math> must simultabeously satisfy the following, seven 2nd-order ODEs:
|
<math>~\sin\xi </math> |
: |
<math>~(x_1^{} -2x_3^' -2x_1 + 2x_2)\xi^2 + 2\xi (x_1^' - x_3) - 2\alpha x_1 + \sigma^2 \xi^3 x_s =0</math> |
|
<math>~\sin^2 \xi</math> |
: |
<math>~(x_s^{} - 2x_c^{'} - x_s)\xi^2 + 2\xi (x_s^' - x_c) -2\alpha x_s + \sigma^2 \xi^3 x_1 =0</math> |
|
<math>~\sin^2\xi \cos\xi</math> |
: |
<math>~(x_3^{} + 4x_1^' -4x_2^' - 4x_3)\xi^2 + 2\xi (x_3^' + 2x_1 -2x_2) - 2\alpha x_3 + 2\xi^2 (x_1^' - x_3) + 2\alpha \xi x_1 -2\xi^2 (x_2^' + x_3) - 2\alpha \xi x_2 =0</math> |
|
<math>~\sin\xi \cos\xi</math> |
: |
<math>~(x_c^{} + 2x_s^' -x_c)\xi^2 + 2\xi (x_c^' + x_s) - 2\alpha x_c + 2\xi^2 (x_s^' - x_c) + 2\alpha \xi x_s + \sigma^2 \xi^3 x_3 =0</math> |
|
<math>~\sin\xi \cos^2\xi</math> |
: |
<math>~(x_2^{} + 2x_3^'+ 2x_1 - 2x_2)\xi^2 + 2\xi (x_2^' + x_3) - 2\alpha x_2 + 2\xi^2 (x_3^' + 2x_1 -2x_2)+ 2\alpha \xi x_3 - (x_1^{} -2x_3^' -2x_1 + 2x_2)\xi^2 - 2\xi (x_1^' - x_3) + 2\alpha x_1 =0</math> |
|
<math>~\cos^2\xi</math> |
: |
<math>~2\xi^2 (x_c^' + x_s ) + 2\alpha \xi x_c + \sigma^2 \xi^3 x_2 =0</math> |
|
<math>~\cos\xi</math> |
: |
<math>~2\xi^2 (x_2^' + x_3)+ 2\alpha \xi x_2 + \sigma^2 \xi^3 x_c =0</math> |
Example 1
Let's work on the coefficient of the <math>~\cos\xi</math> term:
|
<math>~x_c</math> |
<math>~=</math> |
<math>~\xi^\beta (A_c)</math> |
|
<math>~x_2</math> |
<math>~=</math> |
<math>~\xi^\beta (C_2 \xi^2)</math> |
|
<math>~x_3</math> |
<math>~=</math> |
<math>~\xi^\beta (B_3 \xi)</math> |
|
<math>~\Rightarrow~</math> Coefficient of "<math>~\cos\xi</math>" term |
<math>~=</math> |
<math>~\xi^\beta [2\xi^2 (2C_2\xi + (B_3 \xi))+ 2\alpha \xi (C_2 \xi^2) + \sigma^2 \xi^3 (A_c)]</math> |
|
|
<math>~=</math> |
<math>~\xi^{\beta+3} [2(2C_2 + B_3 )+ 2\alpha C_2 + \sigma^2 (A_c)]</math> |
|
<math>~\Rightarrow ~~~~ \sigma^2</math> |
<math>~=</math> |
<math>~- \frac{2}{A_c} \biggl[B_3 + (2+\alpha) C_2 \biggr]</math> |
Sixth Guess
Rationale
From our review of the properties of <math>~n=1</math> polytropic spheres, we know that the equilibrium density distribution is given by the sinc function, namely,
|
<math>~\frac{\rho}{\rho_c}</math> |
<math>~=</math> |
<math>~\frac{\sin\xi}{\xi} \, ,</math> |
where,
<math>~\xi \equiv \pi \biggl(\frac{r_0}{R_0} \biggr) \, .</math>
The total mass is,
<math>~M_\mathrm{tot} = \frac{4}{\pi} \cdot \rho_c R_0^3 \, ,</math>
and the fractional mass enclosed within a given radius, <math>~r</math>, is,
|
<math>~\frac{M_r(\xi)}{M_\mathrm{tot}}</math> |
<math>~=</math> |
<math>~\frac{1}{\pi} [\sin\xi - \xi \cos\xi] \, .</math> |
Let's guess that, during the fundamental mode of radial oscillation, the sinc-function profile is preserved as the system's total radius varies. In particular, we will assume that the system's time-varying radius is,
<math>R = R_0 \biggl( 1 + \frac{\delta R}{R_0} \biggr) = R_0 ( 1 + \epsilon_R) \, ,</math>
and seek to determine how the displacement vector, <math>~\epsilon \equiv \delta r/r_0</math>, varies with <math>~r_0</math> in order to preserve the overall sinc-function profile. As is usual, we will only examine small perturbations away from equilibrium, that is, we will assume that everywhere throughout the configuration, <math>~|\epsilon| \ll 1 </math>.
Let's begin by defining a new dimensionless coordinate,
<math>~\eta \equiv \pi \biggl(\frac{r}{R} \biggr) = \pi \biggl[\frac{r_0(1+\epsilon)}{R_0(1+\epsilon_R)} \biggr] \approx \xi (1 + \epsilon) \, ,</math>
and recognize that, in the new perturbed state, the fractional mass enclosed within a given radius, <math>~r</math>, is,
|
<math>~\frac{M_r(\eta)}{M_\mathrm{tot}}</math> |
<math>~=</math> |
<math>~\frac{1}{\pi} [\sin\eta - \eta \cos\eta] \, .</math> |
In order to associate each mass shell in the perturbed configuration with its corresponding mass shell in the unperturbed, equilibrium state, we need to set the two <math>~M_r</math> functions equal to one another, that is, demand that,
|
<math>~\sin\xi - \xi \cos\xi</math> |
<math>~=</math> |
<math>~\sin\eta - \eta \cos\eta</math> |
|
|
<math>~\approx</math> |
<math>~\sin[\xi(1+\epsilon)] - \xi(1+\epsilon) \cos[\xi(1+\epsilon)]</math> |
|
|
<math>~=</math> |
<math>~\biggl[ \sin\xi \cos(\xi\epsilon) + \cos\xi \sin (\xi\epsilon) \biggr] - \xi(1+\epsilon) \biggl[ \cos\xi \cos(\xi\epsilon) - \sin\xi \sin (\xi\epsilon) \biggr]</math> |
|
|
<math>~\approx</math> |
<math>~\sin\xi \biggl[1 - \frac{1}{2}(\xi\epsilon)^2 \biggr] + (\xi\epsilon)\cos\xi - \xi(1+\epsilon) \cos\xi \biggl[1 - \frac{1}{2}(\xi\epsilon)^2 \biggr] + \xi^2 \epsilon(1+\epsilon) \sin\xi </math> |
|
|
<math>~\approx</math> |
<math> ~\sin\xi -\xi\cos\xi - \frac{1}{2}(\xi\epsilon)^2 \sin\xi + (\xi\epsilon)\cos\xi - (\xi \epsilon) \cos\xi + \frac{1}{2} \xi^3 \epsilon^2\cos\xi + \xi^2 \epsilon \sin\xi + (\xi \epsilon)^2\sin\xi </math> |
|
<math>~\Rightarrow~~~~- \xi^2 \epsilon \sin\xi </math> |
<math>~\approx</math> |
<math>~ \frac{(\xi \epsilon)^2}{2} \biggl[\xi \cos\xi+ \sin\xi \biggr] </math> |
|
<math>~\Rightarrow~~~~\frac{1}{\epsilon}</math> |
<math>~\approx</math> |
<math>~- \frac{1}{2} \biggl[\xi \cdot \frac{\cos\xi}{\sin\xi} + 1 \biggr] </math> |
|
<math>~\Rightarrow~~~~\epsilon</math> |
<math>~\approx</math> |
<math>~- 2\biggl[1 + \xi \cdot \frac{\cos\xi}{\sin\xi} \biggr]^{-1} = - 2\sin\xi \biggl[\sin\xi + \xi \cos\xi \biggr]^{-1} \, . </math> |
Resulting Polytropic Wave Equation
So, let's try,
|
<math>~x</math> |
<math>~=</math> |
<math>~ 2\sin\xi \biggl[\sin\xi + \xi \cos\xi \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\sin\xi + \xi \cos\xi \biggr]^{-3} 2\sin\xi \biggl[\sin^2\xi + 2\xi \sin\xi \cos\xi + \xi^2 \cos^2\xi \biggr] \, , </math> |
in which case,
|
<math>~x^'</math> |
<math>~=</math> |
<math>~ 2\cos\xi \biggl[\sin\xi + \xi \cos\xi \biggr]^{-1} -2\sin\xi \biggl[\sin\xi + \xi \cos\xi \biggr]^{-2}\biggl[2\cos\xi - \xi \sin\xi \biggr] </math> |
|
|
<math>~=</math> |
<math>~\biggl[\sin\xi + \xi \cos\xi \biggr]^{-2}\biggl\{ 2\cos\xi \biggl[\sin\xi + \xi \cos\xi \biggr] -2\sin\xi \biggl[2\cos\xi - \xi \sin\xi \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl[\sin\xi + \xi \cos\xi \biggr]^{-2}\biggl[ 2\cos\xi \sin\xi + 2\xi \cos^2\xi -4\sin\xi \cos\xi + 2\xi \sin^2\xi \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 2\biggl[\sin\xi + \xi \cos\xi \biggr]^{-2}\biggl[\xi-\sin\xi \cos\xi \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\sin\xi + \xi \cos\xi \biggr]^{-3} 2 \biggl[\xi \sin\xi + \xi^2 \cos\xi -\sin^2\xi \cos\xi - \xi \sin\xi \cos^2\xi \biggr] \, , </math> |
and,
|
<math>~x^{}</math> |
<math>~=</math> |
<math>~2 \biggl[\sin\xi + \xi \cos\xi \biggr]^{-2}\biggl[1-\cos^2\xi + \sin^2\xi \biggr] - 4\biggl[\sin\xi + \xi \cos\xi \biggr]^{-3}\biggl[\xi-\sin\xi \cos\xi \biggr]\biggl[2\cos\xi - \xi\sin\xi \biggr] </math> |
|
|
<math>~=</math> |
<math>~4 \biggl[\sin\xi + \xi \cos\xi \biggr]^{-3}\biggl\{ \sin^2\xi \biggl[\sin\xi + \xi \cos\xi \biggr] - \biggl[\xi-\sin\xi \cos\xi \biggr]\biggl[2\cos\xi - \xi\sin\xi \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~4 \biggl[\sin\xi + \xi \cos\xi \biggr]^{-3}\biggl[ \sin^3\xi + \xi \sin\xi \cos\xi + \xi^2 \sin\xi -2\xi \cos\xi - \xi\sin^2\xi \cos\xi + 2\sin\xi \cos^2\xi \biggr] </math> |
Graphical Reassessment
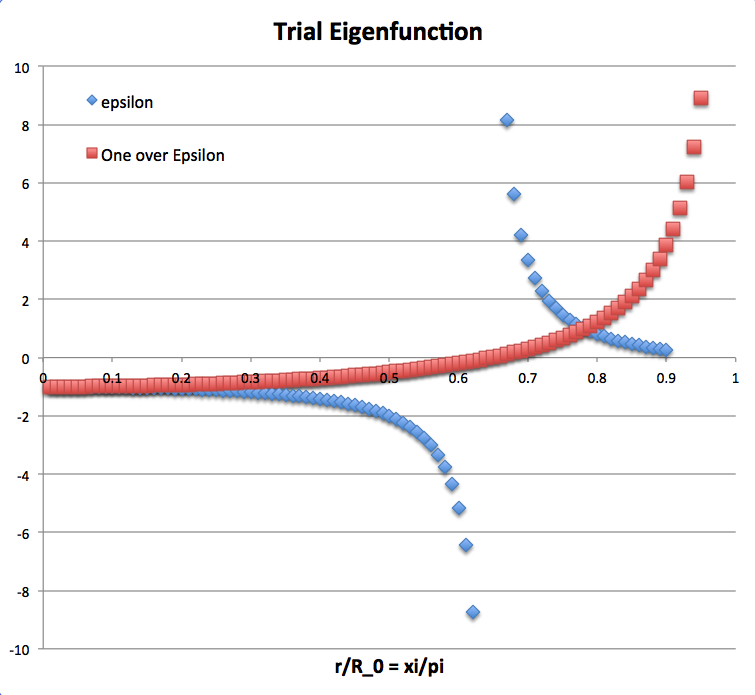
Before plowing ahead and plugging these expressions into the polytropic wave equation, I plotted the trial eigenfunction, <math>~\epsilon(\xi/\pi)</math> (see the blue curve in the accompanying "Trial Eigenfunction" figure), and noticed that it passes through <math>~\pm \infty</math> midway through the configuration. This is a very unphysical behavior. On the other hand, the inverse of this function (see the red curve) exhibits a relatively desirable behavior because it increases monotonically from negative one at the center. As plotted, however, the function has one node. In searching for the eigenfunction of the fundamental mode of oscillation, it might be better to add "1" to the inverse of the function and thereby get rid of all nodes. (Keep in mind, however, that the red curve might be displaying the eigenfunction associated with the first overtone.)
Let's therefore try,
<math>~x = 1 + \frac{1}{\epsilon} = 1 - \frac{1}{2} \biggl[\xi \cdot \frac{\cos\xi}{\sin\xi} + 1 \biggr] = \frac{1}{2} \biggl[1- \xi \cdot \frac{\cos\xi}{\sin\xi} \biggr] \, .</math>
In this case we have,
|
<math>~x^'</math> |
<math>~=</math> |
<math>~ \frac{1}{2}\biggl[\xi - \frac{\cos\xi}{\sin\xi} + \xi \cdot \frac{\cos^2\xi}{\sin^2\xi} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2\sin^2\xi}\biggl[\xi \sin^2\xi - \sin\xi \cos\xi + \xi \cos^2\xi \biggr] \, , </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2\sin^2\xi}\biggl[\xi - \sin\xi \cos\xi \biggr] \, , </math> |
and,
|
<math>~x^{}</math> |
<math>~=</math> |
<math>~ - \frac{\cos\xi}{\sin^3\xi}\biggl[\xi - \sin\xi \cos\xi \biggr] + \frac{1}{2\sin^2\xi}\biggl[1 - \cos^2\xi + \sin^2\xi \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 1 - \frac{\cos\xi}{\sin^3\xi}\biggl[\xi - \sin\xi \cos\xi \biggr] \, . </math> |
Now let's plug these expressions into the polytropic (n = 1) wave equation, namely,
|
<math>~-\sigma^2 \xi^3 x</math> |
<math>~=</math> |
<math>~ \sin\xi \biggl[ \xi^2 x^{} + 2\xi x^' - 2\alpha x \biggr] + \cos\xi \biggl[ 2\xi^2 x^' + 2\alpha \xi x \biggr] \, . </math> |
The first term inside the square brackets on the right-hand-side gives,
|
<math>~\xi^2 x^{} + 2\xi x^' - 2\alpha x </math> |
<math>~=</math> |
<math>~ \xi^2 - \frac{\cos\xi}{\sin^3\xi}\biggl(\xi^3 - \xi^2\sin\xi \cos\xi \biggr) + \frac{1}{\sin^2\xi}\biggl(\xi^2 - \xi \sin\xi \cos\xi \biggr) - \alpha \biggl(1- \xi \cdot \frac{\cos\xi}{\sin\xi} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\sin^3\xi} \biggl[ \xi^2 \sin^3\xi - \cos\xi (\xi^3 - \xi^2\sin\xi \cos\xi ) + \sin\xi (\xi^2 - \xi \sin\xi \cos\xi ) - \alpha (\sin^3\xi - \xi \cos\xi \sin^2\xi ) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{\sin^3\xi} \biggl[ \xi^2 \sin\xi (1-\cos^2\xi) + \xi^2\sin\xi \cos^2\xi - \xi^3 \cos\xi + \xi^2\sin\xi - \xi \sin^2\xi \cos\xi - \alpha \sin^3\xi + \alpha \xi \cos\xi \sin^2\xi \biggr] </math> |
|
|
<math>~=</math> |
<math>~ - \alpha + \frac{1}{\sin^3\xi} \biggl[ 2\xi^2 \sin\xi - \xi^3 \cos\xi - \xi \sin^2\xi \cos\xi + \alpha \xi \cos\xi \sin^2\xi \biggr] \, ; </math> |
and the second term inside the square brackets on the right-hand-side gives,
|
<math>~2\xi^2 x^' + 2\alpha \xi x </math> |
<math>~=</math> |
<math>~ \frac{1}{\sin^2\xi}\biggl(\xi^3 - \xi^2 \sin\xi \cos\xi \biggr) +\frac{\alpha}{\sin\xi} \biggl(\xi \sin\xi - \xi^2 \cos\xi \biggr) \, . </math> |
Put together, then, we have,
|
RHS |
<math>~=</math> |
<math>\frac{1}{\sin^2\xi} \biggl[ 2\xi^2 \sin\xi - \xi^3 \cos\xi - \xi \sin^2\xi \cos\xi + \alpha \xi \cos\xi \sin^2\xi \biggr] + \frac{\cos\xi}{\sin^2\xi}\biggl(\xi^3 - \xi^2 \sin\xi \cos\xi \biggr) -\alpha\sin\xi + \alpha \cdot \frac{\cos\xi}{\sin\xi} \biggl(\xi \sin\xi - \xi^2 \cos\xi \biggr) </math> |
|
|
<math>~=</math> |
<math>\frac{1}{\sin^2\xi} \biggl[ 2\xi^2 \sin\xi - \xi^3 \cos\xi - \xi \sin^2\xi \cos\xi + \alpha \xi \cos\xi \sin^2\xi + \xi^3\cos\xi - \xi^2 \sin\xi \cos^2\xi \biggr] + \frac{\alpha}{\sin\xi} \biggl[ -\sin^2\xi + \xi \sin\xi \cos\xi - \xi^2 \cos^2\xi \biggr] </math> |
|
|
<math>~=</math> |
<math>\frac{\xi}{\sin\xi} \biggl[ 2\xi - \sin\xi \cos\xi - \xi \cos^2\xi \biggr] - \frac{\alpha}{\sin\xi} \biggl[ \sin^2\xi+\xi^2 \cos^2\xi \biggr] </math> |
|
|
<math>~=</math> |
<math>\frac{\xi^2}{\sin\xi} \biggl\{ 2 - \biggl(\frac{\sin\xi}{\xi}\biggr) \cos\xi - \cos^2\xi - \alpha \biggl[ \frac{\sin^2\xi}{\xi^2} +\cos^2\xi \biggr] \biggr\} </math> |
Related Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |