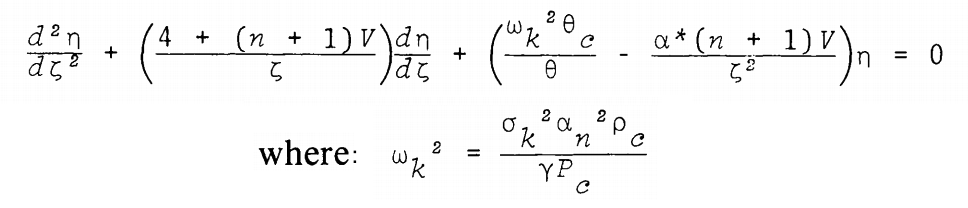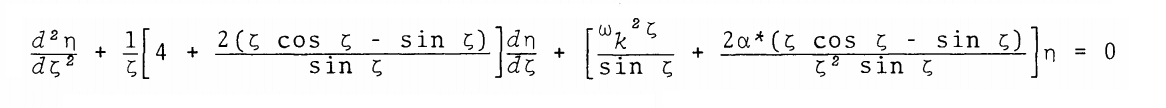User:Tohline/SSC/Stability/Polytropes

Radial Oscillations of Polytropic Spheres

Groundwork

In an accompanying discussion, we derived the so-called,

Adiabatic Wave Equation

<math> \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 \, , </math>

whose solution gives eigenfunctions that describe various radial modes of oscillation in spherically symmetric, self-gravitating fluid configurations. If the initial, unperturbed equilibrium configuration is a polytropic sphere whose internal structure is defined by the function, <math>~\theta(\xi)</math>, then

<math>~r_0</math>	<math>~=</math>	<math>~a_n \xi \, ,</math>
<math>~\rho_0</math>	<math>~=</math>	<math>~\rho_c \theta^{n} \, ,</math>
<math>~P_0</math>	<math>~=</math>	<math>~K\rho_0^{(n+1)/n} = K\rho_c^{(n+1)/n} \theta^{n+1} \, ,</math>
<math>~g_0</math>	<math>~=</math>	<math>~\frac{GM(r_0)}{r_0^2} = \frac{G}{r_0^2} \biggl[ 4\pi a_n^3 \rho_c \biggl(-\xi^2 \frac{d\theta}{d\xi}\biggr) \biggr] \, ,</math>

where,

<math>~a_n</math>

<math>~=</math>

<math>~\biggl[\frac{(n+1)K}{4\pi G} \cdot \rho_c^{(1-n)/n} \biggr]^{1/2} \, .</math>

Hence, after multiplying through by <math>~a_n^2</math>, the above adiabatic wave equation can be rewritten in the form,

<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4}{\xi} - \frac{g_0}{a_n}\biggl(\frac{a_n^2 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{d\xi} + \biggl(\frac{a_n^2\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{a_n\xi} \biggr] x </math>

<math>~=</math>

<math>~0 \, .</math>

In addition, given that,

<math>~\frac{g_0}{a_n}</math>

<math>~=</math>

<math>~4\pi G \rho_c \biggl(-\frac{d \theta}{d\xi} \biggr) \, ,</math>

and,

<math>~\frac{a_n^2 \rho_0}{P_0}</math>

<math>~=</math>

<math>~\frac{(n+1)}{(4\pi G\rho_c)\theta} = \frac{a_n^2 \rho_c}{P_c} \cdot \frac{\theta_c}{\theta}\, ,</math>

we can write,

<math>~\frac{d^2x}{d\xi^2} + \biggl[\frac{4 - (n+1)V(\xi)}{\xi} \biggr] \frac{dx}{d\xi} + \biggl[\omega^2 \biggl(\frac{a_n^2 \rho_c }{\gamma_g P_c} \biggr) \frac{\theta_c}{\theta} - \biggl(3-\frac{4}{\gamma_g}\biggr) \cdot \frac{(n+1)V(x)}{\xi^2} \biggr] x </math>

<math>~=</math>

<math>0 \, ,</math>

where we have adopted the functional notation,

<math>~V(\xi)</math>

<math>~\equiv</math>

<math>~- \frac{\xi}{\theta} \frac{d \theta}{d\xi} \, .</math>

As can be seen in the following framed image, this is the form of the polytropic wave equation published by J. O. Murphy & R. Fiedler (1985b, Proc. Astron. Soc. Australia, 6, 222), at the beginning of their discussion of "Radial Pulsations and Vibrational Stability of a Sequence of Two Zone Polytropic Stellar Models." (It should be noted that there is a sign error in the numerator of the second term of their published expression; the definition of the coefficient, <math>~\alpha^*</math>, given in the text of their paper also contains an error.)

Polytropic Wave Equation as Presented by J. O. Murphy & R. Fiedler (1985b)

Overview

The eigenvector associated with radial oscillations in isolated polytropes has been determined numerically and the results have been presented in a variety of key publications:

• P. LeDoux & Th. Walraven (1958, Handbuch der Physik, 51, 353) —
• R. F. Christy (1966, Annual Reviews of Astronomy & Astrophysics, 4, 353) — Pulsation Theory
• M. Hurley, P. H. Roberts, & K. Wright (1966, ApJ, 143, 535) — The Oscillations of Gas Spheres
• J. P. Cox (1974, Reports on Progress in Physics, 37, 563) — Pulsating Stars

Tables

Quantitative Information Regarding Eigenvectors of Oscillating Polytropes <math>~(\Gamma_1 = 5/3)</math>
<math>~n</math>	<math>~\frac{\rho_c}{\bar\rho}</math>	Excerpts from Table 1 of Hurley, Roberts, & Wright (1966) <math>~s^2 (n+1)/(4\pi G\rho_c)</math>	Excerpts from Table 3 of J. P. Cox (1974) <math>~\sigma_0^2 R^3/(GM)</math>	<math>\frac{(n+1) *\mathrm{Cox74}}{3 *\mathrm{HRW66}} \cdot \frac{\bar\rho}{\rho_c}</math>
<math>~0</math>	<math>~1</math>	<math>~1/3</math>	<math>~1</math>	<math>~1</math>
<math>~1</math>	<math>~3.30</math>	<math>~0.38331</math>	<math>~1.892</math>	<math>~0.997</math>
<math>~1.5</math>	<math>~5.99</math>	<math>~0.37640</math>	<math>~2.712</math>	<math>~1.002</math>
<math>~2</math>	<math>~11.4</math>	<math>~0.35087</math>	<math>~4.00</math>	<math>~1.000</math>
<math>~3</math>	<math>~54.2</math>	<math>~0.22774</math>	<math>~9.261</math>	<math>~1.000</math>
<math>~3.5</math>	<math>~153</math>	<math>~0.12404</math>	<math>~12.69</math>	<math>~1.003</math>
<math>~4.0</math>	<math>~632</math>	<math>~0.04056</math>	<math>~15.38</math>	<math>~1.000</math>

n = 1 Polytrope

Setup

From our derived structure of an n = 1 polytrope, in terms of the configuration's radius <math>R</math> and mass <math>M</math>, the central pressure and density are, respectively,

<math>P_c = \frac{\pi G}{8}\biggl( \frac{M^2}{R^4} \biggr) </math> ,

and

<math>\rho_c = \frac{\pi M}{4 R^3} </math> .

Hence the characteristic time and acceleration are, respectively,

<math> \tau_\mathrm{SSC} = \biggl[ \frac{R^2 \rho_c}{P_c} \biggr]^{1/2} = \biggl[ \frac{2R^3 }{GM} \biggr]^{1/2} = \biggl[ \frac{\pi}{2 G\rho_c} \biggr]^{1/2}, </math>

and,

<math> g_\mathrm{SSC} = \frac{P_c}{R \rho_c} = \biggl( \frac{GM}{2R^2} \biggr) . </math>

The required functions are,

• Density:

<math>\frac{\rho_0(\chi_0)}{\rho_c} = \frac{\sin(\pi\chi_0)}{\pi\chi_0} </math> ;

• Pressure:

<math>\frac{P_0(\chi_0)}{P_c} = \biggl[ \frac{\sin(\pi\chi_0)}{\pi\chi_0} \biggr]^2 </math> ;

• Gravitational acceleration:

<math> \frac{g_0(r_0)}{g_\mathrm{SSC}} = \frac{2}{\chi_0^2} \biggl[ \frac{M_r(\chi_0)}{M}\biggr] = \frac{2}{\pi \chi_0^2} \biggl[ \sin (\pi\chi_0 ) - \pi\chi_0 \cos (\pi\chi_0 ) \biggr]. </math>

So our desired Eigenvalues and Eigenvectors will be solutions to the following ODE:

<math> \frac{d^2x}{d\chi_0^2} + \frac{2}{\chi_0} \biggl[ 1 + \pi\chi_0 \cot (\pi\chi_0 ) \biggr] \frac{dx}{d\chi_0} + \frac{1}{\gamma_\mathrm{g}} \biggl\{ \frac{\pi \chi_0}{\sin(\pi\chi_0)} \biggl[ \frac{\pi \omega^2}{2G\rho_c} \biggr] + \frac{2}{\chi_0^2 } (4 - 3\gamma_\mathrm{g}) \biggl[ 1 - \pi\chi_0 \cot (\pi\chi_0 ) \biggr] \biggr\} x = 0 , </math>

or, replacing <math>\chi_0</math> with <math>\xi \equiv \pi\chi_0</math> and dividing the entire expression by <math>\pi^2</math>, we have,

<math> \frac{d^2x}{d\xi^2} + \frac{2}{\xi} \biggl[ 1 + \xi \cot \xi \biggr] \frac{dx}{d\xi} + \frac{1}{\gamma_\mathrm{g}} \biggl\{ \frac{\xi}{\sin \xi} \biggl[ \frac{\omega^2}{2\pi G\rho_c} \biggr] + \frac{2}{\xi^2 } (4 - 3\gamma_\mathrm{g}) \biggl[ 1 - \xi \cot \xi \biggr] \biggr\} x = 0 . </math>

This is identical to the formulation of the wave equation that is relevant to the (n = 1) core of the composite polytrope studied by J. O. Murphy & R. Fiedler (1985b); for comparison, their expression is displayed, here, in the following boxed-in image.

n = 1 Polytropic Formulation of Wave Equation as Presented by Murphy & Fiedler (1985b)

---

Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
|   Go Home   |

---

Attempt at Deriving an Analytic Eigenvector Solution

Multiplying the last expression through by <math>~\xi^2\sin\xi</math> gives,

<math> (\xi^2\sin\xi ) \frac{d^2x}{d\xi^2} + 2 \biggl[ \xi \sin\xi + \xi^2 \cos \xi \biggr] \frac{dx}{d\xi} + \biggl[ \sigma^2 \xi^3 - 2\alpha ( \sin\xi - \xi \cos \xi ) \biggr] x = 0 \, , </math>

where,

<math>~\sigma^2</math>	<math>~\equiv</math>	<math> ~\frac{\omega^2}{2\pi G\rho_c \gamma_g} \, , </math>
<math>~\alpha</math>	<math>~\equiv</math>	<math> ~3-\frac{4}{\gamma_g} \, . </math>

The first two terms can be folded together to give,

<math>~ \frac{1}{\xi^2 \sin^2\xi} \cdot \frac{d}{d\xi}\biggl[ \xi^2 \sin^2\xi \frac{dx}{d\xi} \biggr] </math>	<math>~=</math>	<math> ~\frac{1}{\xi^2 \sin\xi} \biggl[ 2\alpha ( \sin\xi - \xi \cos \xi ) - \sigma^2 \xi^3 \biggr] x </math>
	<math>~=</math>	<math> ~\biggl[ \frac{2\alpha}{\xi^2} \biggl( 1 - \frac{\xi \cos \xi}{\sin\xi} \biggr) - \sigma^2 \biggl( \frac{\xi}{\sin\xi}\biggr) \biggr] x </math>
	<math>~=</math>	<math> ~- \biggl[ \frac{2\alpha}{\xi} \frac{d}{d\xi}\biggl( \frac{\sin\xi}{\xi} \biggr) + \sigma^2 \biggr] \biggl( \frac{\xi}{\sin\xi}\biggr) x \, , </math>

where, in order to make this last step, we have recognized that,

<math>~ \frac{d}{d\xi} \biggl( \frac{\sin\xi}{\xi} \biggr) </math>

<math>~=</math>

<math> ~\frac{\sin\xi}{\xi^2} \biggl[ \xi \cdot \frac{\cos\xi}{\sin\xi} - 1 \biggr] \, . </math>

It would seem that the eigenfunction, <math>~x(\xi)</math>, should be expressible in terms of trigonometric functions and powers of <math>~\xi</math>. With this in mind, we have made some attempts to guess the exact form of the eigenfunction. Here is one such attempt.

First Guess

Let's try,

<math>~x = A(\xi) \sin\xi + B(\xi)\cos\xi \, .</math>

This means,

<math>~\frac{dx}{d\xi}</math>

<math>~=</math>

<math> ~ \, , </math>

Related Discussions

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation