Difference between revisions of "User:Tohline/Appendix/Ramblings/PPTori"
(→Stability Analyses of PP Tori: correct link to youtube videos) |
(→Blaes85: More introductory presentation of work by Blaes (1985)) |
||
| Line 29: | Line 29: | ||
==Blaes85== | ==Blaes85== | ||
===His Notation=== | |||
[http://adsabs.harvard.edu/abs/1985MNRAS.216..553B Blaes (1985)] adopts a [[User:Tohline/SR#Barotropic_Structure|polytropic equation of state]], | |||
<div align="center"> | |||
<math>~\frac{\rho}{\rho_c} = \Theta_H^n \, ,</math> | |||
</div> | |||
which gives rise to (slim tori) equilibrium structures for which (see his equation 1.3), | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Theta_H</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 - \frac{1}{\beta^2}\biggl[x^2 + x^3(3\cos\theta - \cos^3\theta) + \mathcal{O}(x^4) \biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
He then adopts a related parameter that is constant on isobaric surfaces, namely, | |||
<div align="center"> | |||
<math>\eta^2 \equiv 1 - \Theta_H \, ,</math> | |||
</div> | |||
which is unity at the surface of the torus and which goes to zero at the cross-sectional center of the torus. | |||
===Analytically Prescribed Eigenvector=== | |||
From my initial focused reading of the analysis presented by [http://adsabs.harvard.edu/abs/1985MNRAS.216..553B Blaes (1985)], I conclude that, in the infinitely slender torus case, unstable modes in PP tori exhibit eigenvectors of the form, | From my initial focused reading of the analysis presented by [http://adsabs.harvard.edu/abs/1985MNRAS.216..553B Blaes (1985)], I conclude that, in the infinitely slender torus case, unstable modes in PP tori exhibit eigenvectors of the form, | ||
<div align="center"> | <div align="center"> | ||
| Line 41: | Line 71: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\biggl\{ f_m(\varpi)e^{- | <math>~\biggl\{ f_m(\varpi,\theta)e^{-i[m\phi_m(\varpi) + k\theta]} \biggr\} \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 47: | Line 77: | ||
</div> | </div> | ||
where we written the perturbation amplitude in a manner that conforms with | where we have written the perturbation amplitude in a manner that conforms with the notation that we have used in [[User:Tohline/Appendix/Ramblings/Azimuthal_Distortions#Figure1|Figure 1 of a related, but more general discussion]]. As is summarized in §1.3 of Blaes (1985), for "thick" (but, actually, still quite thin) tori, "exactly one exponentially growing mode exists for each value of the azimuthal wavenumber <math>~m</math>," and its complex amplitude takes the following form (see his equation 1.10): | ||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~f_m(\varpi,\theta)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
~\beta^2 m^2 \biggl[ 2\eta^2 \cos^2\theta - \frac{3\eta^2}{4(n+1)} - \frac{(4n+1)}{4(n+1)^2} | |||
\pm 4i\biggl(\frac{3}{2n+2}\biggr)^{1/2} \eta\cos\theta\biggr] | |||
+ \mathcal{O}(\beta^3) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
=See Also= | =See Also= | ||
Revision as of 22:35, 18 February 2016
Stability Analyses of PP Tori

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
As has been summarized in an accompanying chapter — also see our related detailed notes — we have been trying to understand why unstable nonaxisymmetric eigenvectors have the shapes that they do in rotating toroidal configurations. For any azimuthal mode, <math>~m</math>, we are referring both to the radial dependence of the distortion amplitude, <math>~f_m(\varpi)</math>, and the radial dependence of the phase function, <math>~\phi_m(\varpi)</math> — the latter is what the Imamura and Hadley collaboration refer to as a "constant phase locus." Some old videos showing the development over time of various self-gravitating "constant phase loci" can be found here; these videos supplement the published work of Woodward, Tohline & Hachisu (1994).
Here, we focus specifically on instabilities that arise in so-called (non-self-gravitating) Papaloizou-Pringle tori and will draw heavily from two publications: (1) Papaloizou & Pringle (1987), MNRAS, 225, 267 — The dynamical stability of differentially rotating discs. III. — hereafter, PPIII — and (2) Blaes (1985), MNRAS, 216, 553 — Oscillations of slender tori.
PP III
|
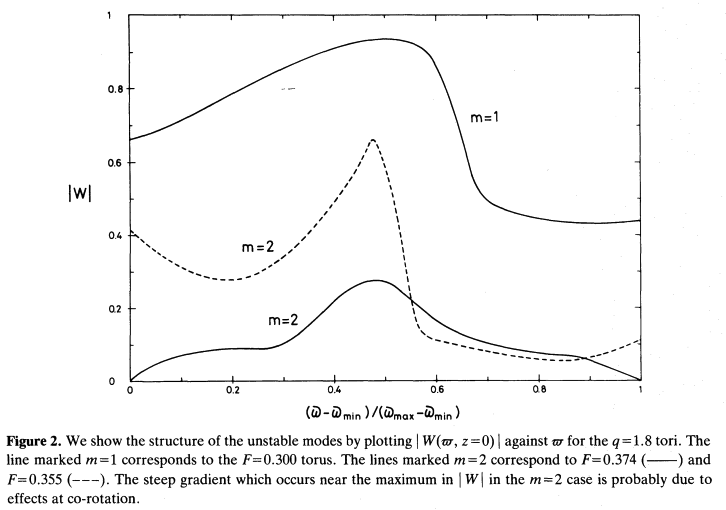
Figure 2 extracted without modification from p. 274 of J. C. B. Papaloizou & J. E. Pringle (1987)
"The Dynamical Stability of Differentially Rotating Discs. III"
MNRAS, vol. 225, pp. 267-283 © The Royal Astronomical Society |
Blaes85
His Notation
Blaes (1985) adopts a polytropic equation of state,
<math>~\frac{\rho}{\rho_c} = \Theta_H^n \, ,</math>
which gives rise to (slim tori) equilibrium structures for which (see his equation 1.3),
|
<math>~\Theta_H</math> |
<math>~=</math> |
<math>~1 - \frac{1}{\beta^2}\biggl[x^2 + x^3(3\cos\theta - \cos^3\theta) + \mathcal{O}(x^4) \biggr] \, .</math> |
He then adopts a related parameter that is constant on isobaric surfaces, namely,
<math>\eta^2 \equiv 1 - \Theta_H \, ,</math>
which is unity at the surface of the torus and which goes to zero at the cross-sectional center of the torus.
Analytically Prescribed Eigenvector
From my initial focused reading of the analysis presented by Blaes (1985), I conclude that, in the infinitely slender torus case, unstable modes in PP tori exhibit eigenvectors of the form,
|
<math>~\biggl[ \frac{W(\eta,\theta)}{C} - 1 \biggr]e^{im\Omega_p t}e^{-y_2 (\Omega_0 t)} </math> |
<math>~=</math> |
<math>~\biggl\{ f_m(\varpi,\theta)e^{-i[m\phi_m(\varpi) + k\theta]} \biggr\} \, ,</math> |
where we have written the perturbation amplitude in a manner that conforms with the notation that we have used in Figure 1 of a related, but more general discussion. As is summarized in §1.3 of Blaes (1985), for "thick" (but, actually, still quite thin) tori, "exactly one exponentially growing mode exists for each value of the azimuthal wavenumber <math>~m</math>," and its complex amplitude takes the following form (see his equation 1.10):
|
<math>~f_m(\varpi,\theta)</math> |
<math>~=</math> |
<math> ~\beta^2 m^2 \biggl[ 2\eta^2 \cos^2\theta - \frac{3\eta^2}{4(n+1)} - \frac{(4n+1)}{4(n+1)^2} \pm 4i\biggl(\frac{3}{2n+2}\biggr)^{1/2} \eta\cos\theta\biggr] + \mathcal{O}(\beta^3) </math> |
See Also
- Imamura & Hadley collaboration:
- Paper I: K. Hadley & J. N. Imamura (2011, Astrophysics and Space Science, 334, 1-26), "Nonaxisymmetric instabilities in self-gravitating disks. I. Toroids" — In this paper, Hadley & Imamura perform linear stability analyses on fully self-gravitating toroids; that is, there is no central point-like stellar object and, hence, <math>~M_*/M_d = 0.0</math>.
- Paper II: K. Z. Hadley, P. Fernandez, J. N. Imamura, E. Keever, R. Tumblin, & W. Dumas (2014, Astrophysics and Space Science, 353, 191-222), "Nonaxisymmetric instabilities in self-gravitating disks. II. Linear and quasi-linear analyses" — In this paper, the Imamura & Hadley collaboration performs "an extensive study of nonaxisymmetric global instabilities in thick, self-gravitating star-disk systems creating a large catalog of star/disk systems … for star masses of <math>~0.0 \le M_*/M_d \le 10^3</math> and inner to outer edge aspect ratios of <math>~0.1 < r_-/r_+ < 0.75</math>."
- Paper III: K. Z. Hadley, W. Dumas, J. N. Imamura, E. Keever, & R. Tumblin (2015, Astrophysics and Space Science, 359, article id. 10, 23 pp.), "Nonaxisymmetric instabilities in self-gravitating disks. III. Angular momentum transport" — In this paper, the Imamura & Hadley collaboration carries out nonlinear simulations of nonaxisymmetric instabilities found in self-gravitating star/disk systems and compares these results with the linear and quasi-linear modeling results presented in Papers I and II.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |