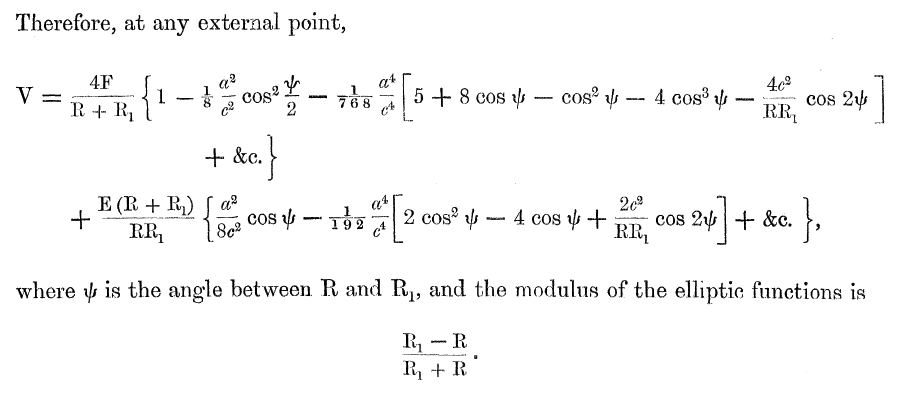Difference between revisions of "User:Tohline/Apps/DysonPotential"
| (44 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
==Overview== | ==Overview== | ||
Our focus, here, is on the pioneering work of [http://adsabs.harvard.edu/abs/1893RSPTA.184...43D F. W. Dyson (1893a, Philosophical Transactions of the Royal Society of London. A., 184, 43 - 95)] and [http://adsabs.harvard.edu/abs/1893RSPTA.184.1041D (1893b, Philosophical Transactions of the Royal Society of London. A., 184, 1041 - 1106)]. He used analytic techniques to determine the approximate equilibrium structure of axisymmetric, uniformly rotating, incompressible tori. [http://adsabs.harvard.edu/abs/1974ApJ...190..675W C.-Y. Wong (1974, ApJ, 190, 675 - 694)] extended Dyson's work, using numerical techniques to obtain more accurate equilibrium structures for incompressible tori having solid body rotation. Since then, [http://adsabs.harvard.edu/abs/1981PThPh..65.1870E Y. Eriguchi & D. Sugimoto (1981, Progress of Theoretical Physics, 65, 1870 - 1875)] and [http://adsabs.harvard.edu/abs/1988ApJS...66..315H I. Hachisu, J. E. Tohline & Y. Eriguchi (1987, ApJ, 323, 592 - 613)] have mapped out the full sequence of Dyson-Wong tori, beginning from a bifurcation point on the Maclaurin spheroid sequence. | |||
The most challenging aspect of each of these studies has been the development of an analytic and/or computational technique that can be used to accurately determine the gravitational potential of toroidal-shaped configurations. With this in mind, it should be appreciated that, in a paper that preceded his 1974 work, [http://adsabs.harvard.edu/abs/1973AnPhy..77..279W C.-Y. Wong (1973, Annals of Physics, 77, 279)] derived an analytic expression for the ''exact'' potential (inside as well as outside) of axisymmetric, uniform-density tori having an arbitrarily specified ratio of the major to minor (cross-sectional) radii, <math>~R/d</math>. This is an outstanding accomplishment that has received little attention in the astrophysics literature and, therefore, has heretofore been under-appreciated. In a [[User:Tohline/Apps/Wong1973Potential#Wong.27s_.281973.29_Analytic_Potential|separate, accompanying discussion]], we detail how Wong accomplished this task. | |||
==External Potential== | ==External Potential== | ||
===His Derived Expression=== | ===His Derived Expression=== | ||
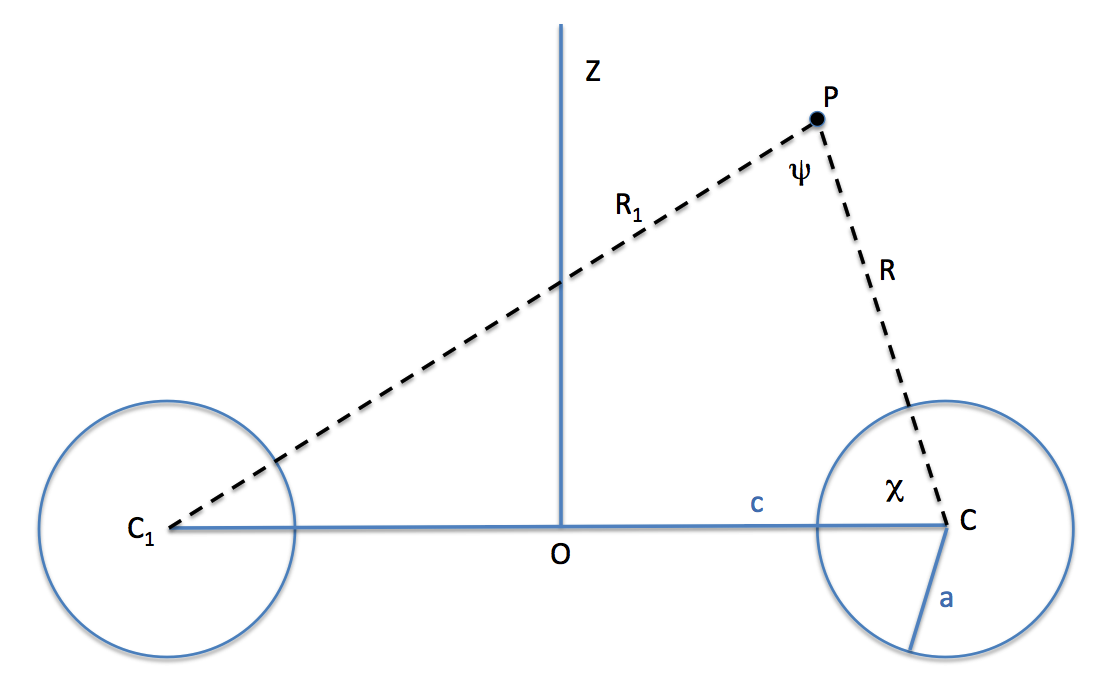
On p. 62 of [http://adsabs.harvard.edu/abs/1893RSPTA.184...43D Dyson (1893a)], we find the following approximate expression for the potential at point "P", anywhere exterior to an [http://www.mathematicsdictionary.com/english/vmd/full/t/torusanchorring.htm anchor ring]: | (See an accompanying [[User:Tohline/Appendix/Ramblings/Dyson1893Part1|''Ramblings Chapter'']] for additional derivation details.) On p. 62, in §8 of [http://adsabs.harvard.edu/abs/1893RSPTA.184...43D Dyson (1893a)], we find the following approximate expression for the potential at point "P", anywhere exterior to an [http://www.mathematicsdictionary.com/english/vmd/full/t/torusanchorring.htm anchor ring]: | ||
<table border="0" cellpadding="10" align="right" width="40%"><tr><td align="center"> | <table border="0" cellpadding="10" align="right" width="40%"><tr><td align="center"> | ||
| Line 17: | Line 20: | ||
<td align="center"> | <td align="center"> | ||
[[File:DysonTorusIllustration03.png|300px|center|Anchor Ring Schematic]]<br /> | [[File:DysonTorusIllustration03.png|300px|center|Anchor Ring Schematic]]<br /> | ||
'''Caption:''' [http://www.mathematicsdictionary.com/english/vmd/full/t/torusanchorring.htm Anchor ring] schematic, adapted from figure near the top of §2 (on p. 47) of Dyson (1893a) | '''Caption:''' [http://www.mathematicsdictionary.com/english/vmd/full/t/torusanchorring.htm Anchor ring] schematic, adapted from figure near the top of §2 (on p. 47) of [http://adsabs.harvard.edu/abs/1893RSPTA.184...43D Dyson (1893a)] | ||
</td> | </td> | ||
</tr> | </tr> | ||
| Line 299: | Line 302: | ||
====Our Attempt to Replicate==== | ====Our Attempt to Replicate==== | ||
First, let's test the accuracy of [http://adsabs.harvard.edu/abs/1893RSPTA.184...43D Dyson's (1893a)] "series expansion" expression for the elliptic integrals, <math>~K(\mu)</math> and <math>~E(\mu)</math>; in the following table, the high-precision evaluations labeled "''Numerical Recipes''" have been drawn from the tabulated data that is provided in our [[User:Tohline/2DStructure/ToroidalCoordinateIntegrationLimits#Evaluation_of_Elliptic_Integrals|accompanying discussion]] of incomplete elliptic integrals. | First, let's test the accuracy of [http://adsabs.harvard.edu/abs/1893RSPTA.184...43D Dyson's (1893a)] "series expansion" expression for the elliptic integrals, <math>~K(\mu)</math> and <math>~E(\mu)</math>; in the following table, the high-precision evaluations labeled "''Numerical Recipes''" have been drawn from the tabulated data that is provided in our [[User:Tohline/2DStructure/ToroidalCoordinateIntegrationLimits#Evaluation_of_Elliptic_Integrals|accompanying discussion]] of incomplete elliptic integrals. Drawing from our [[User:Tohline/Appendix/Equation_templates#Complete_Elliptic_Integrals|accompanying set of Key mathematical relations]] — in which <math>~k</math>, rather than <math>~\mu</math>, represents the function modulus — the relevant series-expansion expressions are: | ||
< | <div align="center"> | ||
{{ User:Tohline/Math/EQ_EllipticIntegral01 }}<br /> | |||
{{ User:Tohline/Math/EQ_EllipticIntegral02 }} | |||
</div> | |||
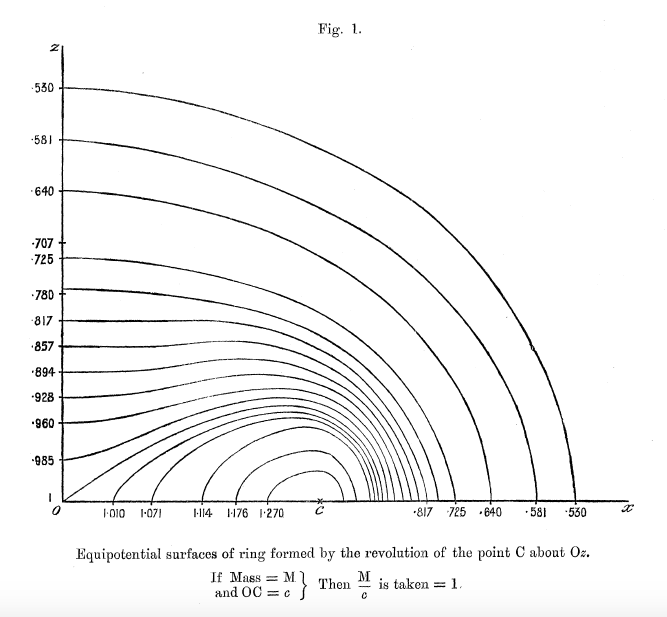
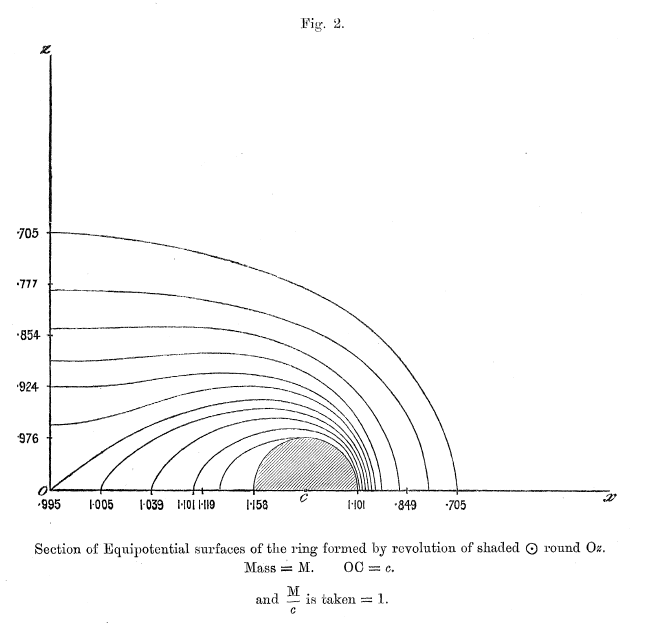
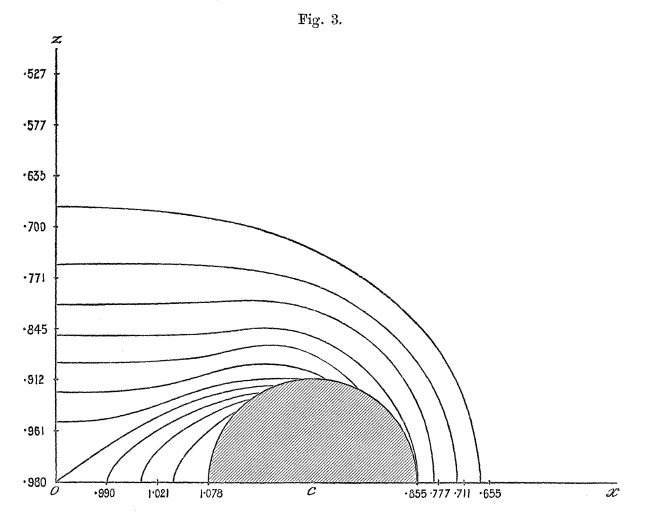
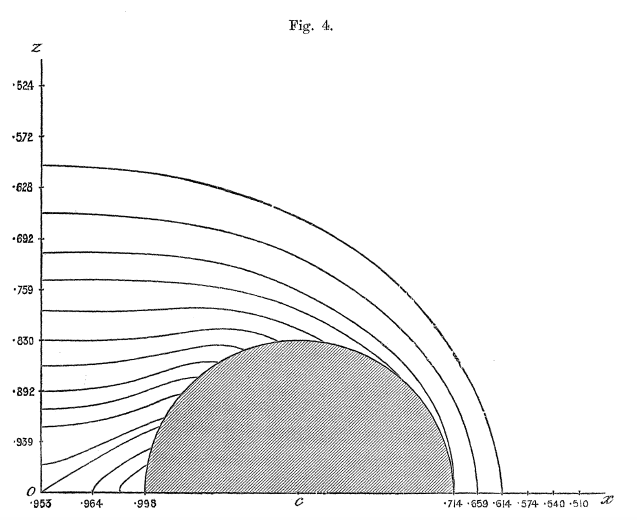
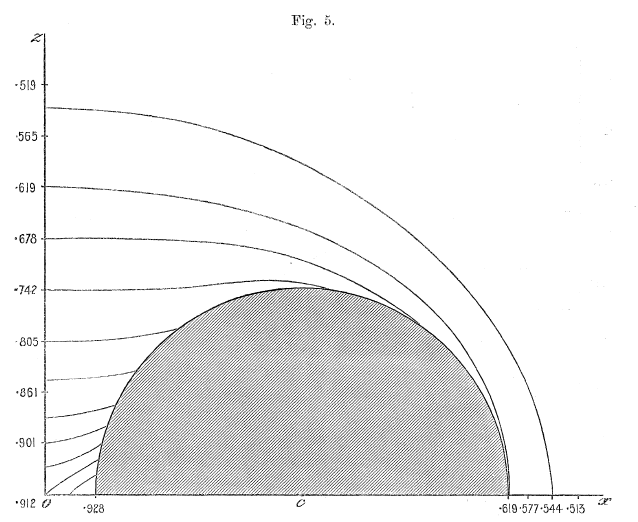
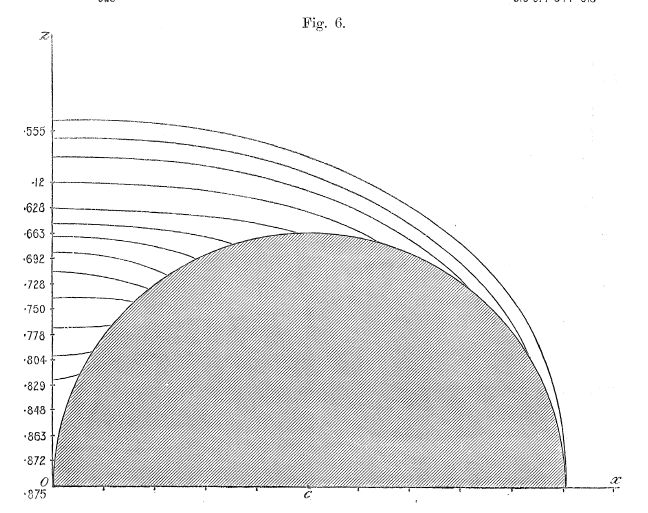
These expressions — up through <math>~\mathcal{O}(\mu^4)</math> — can be found in the middle of p. 58 of [http://adsabs.harvard.edu/abs/1893RSPTA.184...43D Dyson (1893a)]. We strongly suspect that, in constructing the equipotential contours shown in his figures 1-6, Dyson used expressions for <math>~K(\mu)</math> and <math>~E(\mu)</math> that were more accurate than this. For example, we found it necessary to include terms up through <math>~\mathcal{O}(\mu^{10})</math> in order to match to three digits accuracy the potential contour values and coordinate locations reported by Dyson. | These expressions — up through <math>~\mathcal{O}(\mu^4)</math> — can be found in the middle of p. 58 of [http://adsabs.harvard.edu/abs/1893RSPTA.184...43D Dyson (1893a)]. We strongly suspect that, in constructing the equipotential contours shown in his figures 1-6, Dyson used expressions for <math>~K(\mu)</math> and <math>~E(\mu)</math> that were more accurate than this. For example, we found it necessary to include terms up through <math>~\mathcal{O}(\mu^{10})</math> in order to match to three digits accuracy the potential contour values and coordinate locations reported by Dyson. | ||
| Line 2,201: | Line 2,165: | ||
</table> | </table> | ||
Also, we have, | <span id="gammaInverse">Also, we have,</span> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 4,700: | Line 4,664: | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| Line 4,763: | Line 4,727: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl(\frac{a}{c}\biggr) ( | \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) | ||
+ \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) | + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) | ||
~-~\frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 (2~-~ \cos\chi )^2 | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| Line 4,780: | Line 4,743: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3 (3\cos\chi - \cos^3\chi) | |||
\frac{1}{2^ | ~-~ \frac{1}{2^5}\biggl( \frac{a}{c}\biggr)^3 (3-\cos^2\chi) (2~-~ \cos\chi ) | ||
~-~ \frac{1}{2^5}\biggl( \frac{a}{c}\biggr)^3 (3-\cos^2\chi) (2~-~ \cos\chi ) | |||
+~ \frac{1}{2^ | ~+~\frac{1}{2^3\cdot 3}\biggl(\frac{a}{c}\biggr)^3 (2~-~ \cos\chi )^2 (2~-~\cos\chi ) | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 4,797: | Line 4,760: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
~ | ~-~ \frac{1}{2^6}\biggl( \frac{a}{c}\biggr)^4 (3\cos\chi - \cos^3\chi)(2~-~ \cos\chi ) | ||
~ | ~-~ \frac{1}{2^7}\biggl( \frac{a}{c}\biggr)^4 (3-\cos^2\chi) (3-\cos^2\chi) | ||
~ | ~-~ \frac{1}{2^6}\biggl( \frac{a}{c}\biggr)^4 (3\cos\chi - \cos^3\chi)(2~-~ \cos\chi ) | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 4,814: | Line 4,776: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | ~+~ \frac{1}{2^4\cdot 3}\biggl( \frac{a}{c}\biggr)^4 (2~-~ \cos\chi ) (3-\cos^2\chi)(2~-~ \cos\chi ) | ||
\frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^ | +\frac{1}{2^5\cdot 3}\biggl( \frac{a}{c}\biggr)^4 (3-\cos^2\chi) (2~-~ \cos\chi )^2 | ||
+~\frac{1}{2^7}\biggl( \frac{a}{c}\biggr)^4 (- 5 ~+~ 18 \cos^2\chi ~-~ 5 \cos^4\chi ) | |||
- \frac{1}{2^6} \biggl(\frac{a}{c}\biggr)^4(2~-~ \cos\chi )^4 | |||
\frac{1}{2^ | ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | ||
\biggr | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
<tr> | And, | ||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
<math>~~(k')^{2}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{2a}{c}\biggr) \Gamma^{-1} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 4,853: | Line 4,813: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{2a}{c}\biggr) (1+g)^{-1} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 4,864: | Line 4,823: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{2a}{c}\biggr) \biggl\{1 | |||
~-~ g | |||
~+~ g^2 | |||
~-~ g^3 | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 4,882: | Line 4,846: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \biggl( \frac{2a}{c}\biggr) \biggl\{1 | ||
+ \frac{ | ~-~ \biggl[ \biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) | ||
+ \frac{ | + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) | ||
+~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3 (3\cos\chi - \cos^3\chi) | |||
\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl(\frac{a}{ | ~+~ \biggl[\biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) | ||
+ \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) | |||
\biggr]^2 | |||
~-~ \biggl[ \biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) | |||
\biggr]^3 | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 4,915: | Line 4,884: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl(\frac{ | \biggl( \frac{2a}{c}\biggr) \biggl\{1 | ||
~-~ \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) | |||
+ \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2\biggl[ (3-\cos^2\chi) | |||
~+~2(2~-~ \cos\chi )^2 \biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 4,925: | Line 4,897: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3\biggl[ (3\cos\chi - \cos^3\chi) | |||
~+~ (2~-~ \cos\chi )(3-\cos^2\chi) | |||
~-~ (2~-~ \cos\chi )^3 \biggr] | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
And, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~~(k')^{4}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl | \biggl( \frac{2a}{c}\biggr)^2 \Gamma^{-2} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 4,957: | Line 4,933: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{2a}{c}\biggr)^2 (1+g)^{-2} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 4,977: | Line 4,951: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl( \frac{2a}{c}\biggr)^2 \biggl\{1 | |||
~-~ 2g | |||
~+~ 3g^2 | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
1 + \frac{1}{2}\biggl( \ | \biggl( \frac{2a}{c}\biggr)^2 \biggl\{1 | ||
~-~ 2\biggl[ | |||
\biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) | |||
+ \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) | |||
\biggr] | |||
~+~ 3\biggl[ | |||
\biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) | |||
\biggr]^2 | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,005: | Line 4,985: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{ | \biggl( \frac{2a}{c}\biggr)^2 \biggl\{1 | ||
-~\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) | |||
~+~ \frac{1}{2^2} \biggl(\frac{a}{c}\biggr)^2\biggl[ 3(2~-~ \cos\chi )^2 | |||
~-~ (3-\cos^2\chi) \biggr] | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
4\biggl( \frac{a}{c}\biggr)^2 | |||
\biggl(\frac{a}{c}\biggr) | -~\biggl(\frac{a}{c}\biggr)^3 (8~-~ 4\cos\chi ) | ||
~+~ \biggl(\frac{a}{c}\biggr)^4 ( 9 - 12\cos\chi + 4\cos^2\chi ) | |||
~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
===Elliptic Integral Expressions=== | |||
Hence, drawing from our set of [[User:Tohline/Appendix/Equation_templates#Complete_Elliptic_Integrals|Key Expressions for the complete elliptic integral of the first kind]], specifically, | |||
{{User:Tohline/Math/EQ_EllipticIntegral03 }} | |||
we can write, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~K(\mu)</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | \ln \frac{4}{k^'} + \frac{1}{2^2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 | ||
+ \frac{3^2}{2^6} \biggl( \ln\frac{4}{k^'} - \frac{7}{6} \biggr){k'}^4 | |||
\frac{ | + \frac{5^2}{2^8} \biggl( \ln\frac{4}{k^'} - \frac{37}{30} \biggr){k'}^6 + \cdots | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
Now, we recognize that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\biggl(\frac{a}{2}\biggr) \frac{4K(\mu)}{R_1+a}</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl(\frac{a}{2c}\biggr) 4K(\mu) \biggl[\frac{R_1}{c} + \frac{a}{c} \biggr]^{-1} | |||
\biggl | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,077: | Line 5,065: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl(\frac{a}{c}\biggr) 2K(\mu) \biggl(\frac{R_1}{c}\biggr)^{-1}\biggl[1 + \frac{a}{c} \biggl(\frac{R_1}{c}\biggr)^{-1}\biggr]^{-1} | |||
\biggl | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 5,102: | Line 5,083: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl(\frac{R_1}{c}\biggr)^{-1}\biggl[1 + \frac{a}{c} \biggl(\frac{R_1}{c}\biggr)^{-1}\biggr]^{-1}\biggl\{ | \biggl(\frac{a}{c}\biggr) \biggl(\frac{R_1}{c}\biggr)^{-1}\biggl[1 + \frac{a}{c} \biggl(\frac{R_1}{c}\biggr)^{-1}\biggr]^{-1}\biggl\{ 2\ln \frac{4}{k^'} + \frac{1}{2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 \biggr\} \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
<!-- | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~\biggl(\frac{a}{2}\biggr) \frac{4K(\mu)}{R_1+R} = 2K(\mu)\biggl[1 + \frac{R_1}{a}\biggr]^{-1}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~\approx</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl[1 + \frac{R_1}{a}\biggr]^{-1} \biggl\{ 2\ln \frac{4}{k^'} + \frac{1}{2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 \biggr\} | |||
\biggl[\frac{ | |||
\biggl | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,133: | Line 5,115: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl | \biggl[1 + \frac{R_1}{a}\biggr]^{-1} \biggl\{ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{4}\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 2 \biggr] | ||
2^2\biggl( \frac{a}{c}\biggr)\biggl( \frac{R_1}{c}\biggr)^{-1} | |||
\frac{ | \biggl[1 + \frac{a}{c}\cdot \frac{c}{R_1} \biggr]^{-2} \biggr\} | ||
\biggl | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,147: | Line 5,127: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | \biggl[1 + \frac{R_1}{a}\biggr]^{-1} \biggl\{ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 2 \biggr] | ||
\frac{1}{ | \biggl( \frac{a}{c}\biggr)\biggl[ 1 - \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2\biggr]^{-1 / 2} | ||
\biggl | \biggl[1 + \frac{a}{c}\cdot \frac{c}{R_1} \biggr]^{-2} \biggr\} | ||
\biggl | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
--> | |||
Also, drawing from our set of [[User:Tohline/Appendix/Equation_templates#Complete_Elliptic_Integrals|Key Expressions for the complete elliptic integral of the second kind]], specifically, | |||
{{User:Tohline/Math/EQ_EllipticIntegral04 }} | |||
we have, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~E(\mu)</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
2\ln \frac{4}{k | 1 | ||
+ | ~+~ \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 | ||
~+~ \frac{3}{2^4}\biggl( \ln \frac{4}{k'} - 1 - \frac{1}{3\cdot 4}\biggr)(k')^4 | |||
~+~ \frac{3^2\cdot 5}{2^7\cdot 3}\biggl( \ln \frac{4}{k'} - 1 - \frac{1}{2\cdot 3} - \frac{1}{2\cdot 3\cdot 5}\biggr)(k')^6 | |||
~+~ \cdots | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,181: | Line 5,166: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ \biggl(\frac{a}{2}\biggr) \frac{(R_1+R)E(\mu)}{RR_1}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~\approx</math> | <math>~\approx</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
2\ | \frac{1}{2} \biggl[ 1 + \frac{a}{c}\biggl( \frac{R_1}{c}\biggr)^{-1} \biggr] | ||
\biggl\{ 1 + \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 \biggr\} \, . | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
===External Potential at Torus Surface=== | |||
====Initial Low Resolution==== | |||
Hence, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl(\frac{a}{2}\biggr)V_2 </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~\approx</math> | <math>~\approx</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
2\ | \biggl[1 - \frac{1}{8}\biggl(\frac{a^2}{c^2}\biggr) \cos^2\biggl( \frac{\psi}{2}\biggr)\biggr] | ||
\biggl(\frac{a}{c}\biggr) \biggl(\frac{R_1}{c}\biggr)^{-1}\biggl[1 + \frac{a}{c} \biggl(\frac{R_1}{c}\biggr)^{-1}\biggr]^{-1}\biggl\{ 2\ln \frac{4}{k^'} + \frac{1}{2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 \biggr\} | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,216: | Line 5,206: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | + | ||
\biggl[\frac{1}{8}\biggl(\frac{a^2}{c^2}\biggr) \cos\psi \biggr] | |||
\frac{1}{2} \biggl[ 1 + \frac{a}{c}\biggl( \frac{R_1}{c}\biggr)^{-1} \biggr] | |||
\biggr\} | \biggl\{ 1 + \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,230: | Line 5,220: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\Rightarrow ~~~ cV_2 </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~\approx</math> | <math>~\approx</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \biggl[1 - \cancelto{0}{\frac{1}{8}\biggl(\frac{a^2}{c^2}\biggr) \cos^2\biggl( \frac{\psi}{2}\biggr)}\biggr] | ||
\biggl(\frac{R_1}{c}\biggr)^{-1}\biggl[1 + \frac{a}{c} \biggl(\frac{R_1}{c}\biggr)^{-1}\biggr]^{-1}\biggl\{ 4\ln \frac{4}{k^'} + \biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 \biggr\} | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,249: | Line 5,238: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | + | ||
+ | \biggl[\frac{1}{8}\biggl(\frac{a}{c}\biggr) \cos\psi \biggr] | ||
\biggl[ 1 + \frac{a}{c}\biggl( \frac{R_1}{c}\biggr)^{-1} \biggr] | |||
\biggl\{ 1 + \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 \biggr\} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
Hence, | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~ cV_2 </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\approx</math> | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl(\frac{R_1}{c}\biggr)^{-1}\biggl[1 + \frac{a}{c} \biggl(\frac{R_1}{c}\biggr)^{-1}\biggr]^{-1}\biggl\{ 4\ln \frac{4}{k^'} + \biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,291: | Line 5,277: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | + | ||
\biggl[\frac{1}{8}\biggl(\frac{a}{c}\biggr) \cos\psi \biggr] | |||
\biggl[ 1 + \frac{a}{c}\biggl( \frac{R_1}{c}\biggr)^{-1} \biggr] | |||
\biggl\{ 1 + \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,301: | Line 5,290: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~\approx</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl\{ 1 + \frac{1}{2} \biggl(\frac{a}{c}\biggr)\cos\chi | |||
+\biggl( \frac{a}{c}\biggr)^2 \biggl[ | |||
\frac{3}{8}\cos^2\chi -\frac{1}{8}\biggr] \biggr\} | |||
\biggl[1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) + \frac{1}{4} \biggl( \frac{a}{c}\biggr)^2 (1 - \cos\chi)\biggr] | |||
\biggl\{ 2\ln \frac{4}{k^'} + \frac{1}{2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
<td align="right"> | |||
| |||
<tr> | |||
<td align="right"> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | |||
+ \frac{1}{2 | \frac{1}{8}\biggl(\frac{a}{c}\biggr) \cos\psi | ||
+ | \biggl[ 1 + \frac{1}{2}\biggl( \frac{a}{c}\biggr) + \frac{1}{4} \biggl(\frac{a}{c}\biggr)^2\cos\chi \biggr] | ||
\biggl\{ 1 + \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 \biggr\} \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
To order <math>~(a/c)^1</math>, this gives, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\ | <math>~\Rightarrow ~~~ cV_2 </math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\approx</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math>~ | <math>~ | ||
2\ln \frac{4}{k^'} + \frac{1}{2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 | |||
+ \biggl(\frac{a}{c}\biggr)(\cos\chi -1) \ln \frac{4}{k^'} | |||
+ \frac{1}{8}\biggl(\frac{a}{c}\biggr) \cos\psi | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,364: | Line 5,342: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\approx</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math>~ | <math>~ | ||
2\ln \frac{4}{k^'} | |||
+ \biggl(\frac{a}{c}\biggr) \biggl\{ - 1 + \cos\chi \ln \frac{4}{k^'} + \frac{1}{8} \cos\psi | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,382: | Line 5,358: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\approx</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math>~ | <math>~ | ||
2\ln \frac{4}{k^'} | |||
+ \biggl(\frac{a}{c}\biggr) \biggl\{ - 1 + \cos\chi \biggl[ \ln \frac{4}{k^'} - \frac{1}{8} \biggr] | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,399: | Line 5,374: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\approx</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math>~ | <math>~ | ||
\ln\biggl( \frac{2^3c}{a}\biggr) | |||
+ \frac{a}{c}\biggl[ 1- \frac{1}{2} \cos\chi \biggr] | |||
+ \biggl(\frac{a}{c}\biggr) \biggl\{ \frac{1}{2} \cos\chi \biggl[\ln\biggl( \frac{2^3c}{a}\biggr) - \frac{1}{4} \biggr] -1 | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\approx</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math>~ | <math>~ | ||
\ln\biggl( \frac{2^3c}{a}\biggr) | |||
+ | + \frac{a}{c} \biggl\{ 1- \frac{1}{2} \cos\chi + \frac{1}{2} \cos\chi \biggl[\ln\biggl( \frac{2^3c}{a}\biggr) - \frac{1}{4} \biggr] -1 | ||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,443: | Line 5,410: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~ | <math>~\approx</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math>~ | <math>~ | ||
\ln\biggl( \frac{2^3c}{a}\biggr) | |||
+ \frac{1}{2}\biggl(\frac{a}{c}\biggr) \biggl[\ln\biggl( \frac{2^3c}{a}\biggr) - \frac{5}{4} \biggr] \cos\chi \, . | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
---- | |||
We are trying to match equation (6) in [http://adsabs.harvard.edu/abs/1893RSPTA.184.1041D Dyson's (1893b)] "Part II", that is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{V}{2\pi a^2}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | \ln\biggl(\frac{8c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr) \biggl[\ln\biggl(\frac{8c}{a}\biggr) - \frac{5}{4}\biggr] \cos\chi | ||
\biggl\{ \ | + \biggl\{ \frac{1}{16} \biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{5}{2} \biggr] + \frac{3}{16} \biggl[\ln\biggl(\frac{8c}{a}\biggr) +\frac{17}{36} - \frac{72}{36}\biggr]\cos2\chi\biggr\}\biggl(\frac{a^2}{c^2}\biggr) | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,476: | Line 5,452: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | + \biggl\{ \frac{3}{32}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{25}{12}\biggr]\cos\chi + \frac{5}{64}\biggl[ \ln\biggl(\frac{8c}{a}\biggr)+\frac{7}{24} - \frac{48}{24}\biggr]\cos3\chi \biggr\} \biggl(\frac{a^3}{c^3}\biggr) | ||
\biggl\{ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,491: | Line 5,466: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | + \biggl\{ \frac{9}{256}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - 2\biggr] + \frac{7}{128}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{19}{168} - 2\biggr]\cos2\chi | ||
+ \frac{35}{1024} \biggl[ \ln\biggl(\frac{8c}{a}\biggr) - 2 + \frac{19}{120}\biggr]\cos4\chi \biggr\} \biggl(\frac{a^4}{c^4}\biggr) ~+~\cdots | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
====High Resolution==== | |||
<table border="1" width="85%" align="center" cellpadding="8"> | |||
<tr><td align="left"> | |||
<div align="center">'''Summary'''</div> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~2\biggl(\frac{R_1}{c}\biggr)^{-1}</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi | ||
\biggl\{\biggl(\frac{c}{a}\biggr) | + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 \biggl[ 3\cos^2\chi - 1 \biggr] | ||
+ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3\biggl[ 5\cos^3\chi | |||
~-~ 3\cos\chi \biggr] | |||
~+~ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 \biggl[ 3 | |||
~-~ 30 \cos^2\chi | |||
~+~ 35 \cos^4\chi \biggr] | |||
~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, . | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,514: | Line 5,505: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\biggl[1~+~\biggl( \frac{a}{c}\biggr)\biggl(\frac{R_1}{c}\biggr)^{-1}\biggr]^{-1} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 5,521: | Line 5,512: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) | 1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) | ||
~+~ \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^3 ( 2\cos\chi ~-~ 3\cos^2\chi ) | ~+~ \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^3 ( 2\cos\chi ~-~ 3\cos^2\chi ) | ||
| Line 5,551: | Line 5,518: | ||
~+~8\cos^2\chi | ~+~8\cos^2\chi | ||
~-~ 5\cos^3\chi ) | ~-~ 5\cos^3\chi ) | ||
\biggr\ | ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, . | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,558: | Line 5,525: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~t_K</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
1 ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 ( 1 -\cos\chi ) | 1 ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 ( 1 -\cos\chi ) | ||
+ \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 | + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 | ||
( -13~+~12\cos\chi +2 \cos^2\chi ) | ( -13~+~12\cos\chi +2 \cos^2\chi ) | ||
+ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 (-17 + 21\cos\chi - \cos^2\chi ~-~ 2\cos^3\chi ) | + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 (-17 + 21\cos\chi - \cos^2\chi ~-~ 2\cos^3\chi ) | ||
\biggr\ | + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, . | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,578: | Line 5,543: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~1~+~\biggl( \frac{a}{c}\biggr)\biggl(\frac{R_1}{c}\biggr)^{-1} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
1 ~+~\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi | 1 ~+~\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi | ||
~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 | ~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 ( 3\cos^2\chi - 1 ) | ||
~+~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^4 | ~+~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^4 ( 5\cos^3\chi ~-~ 3\cos\chi ) | ||
~-~ 3\cos\chi \ | ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, . | ||
\biggr\ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,598: | Line 5,560: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~t_E</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
-\frac{1}{2^3} \biggl(\frac{a}{c}\biggr)^2\cos\chi | |||
~+~ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 13- 12\cos\chi - 2\cos^2\chi ) | |||
~+~ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^ | ~+~ \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 12 -21 \cos\chi - 2\cos^2\chi - 2\cos^3\chi ) | ||
~+~ \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^ | + f_{E5}\biggl(\frac{a}{c}\biggr)^5 | ||
+ f_{E5}\biggl(\frac{a}{c}\biggr)^ | + \mathcal{O}\biggl(\frac{a^6}{c^6}\biggr) \, . | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
</td></tr> | |||
</table> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{\pi V_\mathrm{Dyson}}{GM/c} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 5,624: | Line 5,592: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
2K(\mu) \biggl | 2K(\mu) \biggl[~2\biggl(\frac{R_1}{c}\biggr)^{-1}\biggr] \biggl[1 + \biggl(\frac{a}{c}\biggr) \biggl(\frac{R_1}{c}\biggr)^{-1} \biggr]^{-1}\biggl\{ t_K \biggr\} | ||
+ | |||
+ \frac{ | E(\mu) \biggl[1 + \biggl(\frac{a}{c}\biggr) \biggl(\frac{R_1}{c}\biggr)^{-1} \biggr] \biggl\{\biggl(\frac{c}{a}\biggr) t_E \biggr\} | ||
+ \frac{ | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,642: | Line 5,604: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | 2K(\mu) \biggl\{ ~2\biggl(\frac{R_1}{c}\biggr)^{-1}\biggr\} | ||
\biggl\{ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,665: | Line 5,622: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\times | |||
\biggl\{ \biggl[1 + \biggl(\frac{a}{c}\biggr) \biggl(\frac{R_1}{c}\biggr)^{-1} \biggr]^{-1} \biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,681: | Line 5,637: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\times | |||
\biggl\{ t_K \biggr\} | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,698: | Line 5,653: | ||
<math>~ | <math>~ | ||
+ | + | ||
E(\mu) \biggl\{ | E(\mu) \biggl\{ 1 + \biggl(\frac{a}{c}\biggr) \biggl(\frac{R_1}{c}\biggr)^{-1} \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,715: | Line 5,667: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\times | |||
\biggl | \biggl\{\biggl(\frac{c}{a}\biggr) t_E \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,727: | Line 5,678: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \frac{1}{2 | 2K(\mu) \biggl\{ | ||
1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi | |||
+ | + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 \biggl[ 3\cos^2\chi - 1 \biggr] | ||
+ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3\biggl[ 5\cos^3\chi | |||
~-~ 3\cos\chi \biggr] | |||
~+~ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 \biggl[ 3 | |||
~-~ 30 \cos^2\chi | |||
~+~ 35 \cos^4\chi \biggr] | |||
\biggr\} | \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,745: | Line 5,700: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\times | |||
1 | \biggl\{ | ||
+ \frac{1}{2^ | 1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) | ||
+ | ~+~ \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^3 ( 2\cos\chi ~-~ 3\cos^2\chi ) | ||
~-~ | ~+~ \frac{1}{2^5} \biggl(\frac{a}{c}\biggr)^4 ( | ||
~+~ \frac{1}{2^ | -~9 \cos\chi | ||
~ | ~+~8\cos^2\chi | ||
~ | ~-~ 5\cos^3\chi ) | ||
\biggr\} | \biggr\} | ||
</math> | </math> | ||
| Line 5,773: | Line 5,728: | ||
\times | \times | ||
\biggl\{ | \biggl\{ | ||
1 - \frac{1 | 1 ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 ( 1 -\cos\chi ) | ||
+ \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 | + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 | ||
( -13~+~12\cos\chi +2 \cos^2\chi ) | |||
+ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 (-17 + 21\cos\chi - \cos^2\chi ~-~ 2\cos^3\chi ) | |||
\biggr\} | |||
\biggr | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,793: | Line 5,746: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \frac{1}{2 | + | ||
\biggl | E(\mu) \biggl\{ | ||
1 ~+~\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi | |||
- | ~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 \biggl[ 3\cos^2\chi - 1 \biggr] | ||
~+~ | ~+~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^4\biggl[ 5\cos^3\chi | ||
\biggr] | ~-~ 3\cos\chi \biggr] | ||
\biggr\} | \biggr\} | ||
</math> | </math> | ||
| Line 5,813: | Line 5,766: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\times | |||
\biggl\{-\frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | |||
~+~ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 12\cos\chi - 2\cos^2\chi ) | |||
~ | ~+~ \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 12 -21 \cos\chi - 2\cos^2\chi - 2\cos^3\chi ) | ||
~ | + f_{E5}\biggl(\frac{a}{c}\biggr)^4 | ||
\biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,828: | Line 5,781: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \frac{1}{2^ | 2K(\mu) \biggl\{ | ||
1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi | |||
~+~ \frac{1}{2^ | + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 \biggl[ 3\cos^2\chi - 1 \biggr] | ||
+ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3\biggl[ 5\cos^3\chi | |||
~-~ 3\cos\chi \biggr] | |||
~+~ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 \biggl[ 3 | |||
~-~ 30 \cos^2\chi | |||
~+~ 35 \cos^4\chi \biggr] | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,848: | Line 5,807: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\times | |||
\biggl\{ | |||
+ | 1 ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 ( 1 -\cos\chi ) | ||
\ | + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 | ||
~ | ( -13~+~12\cos\chi +2 \cos^2\chi ) | ||
+ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 (-17 + 21\cos\chi - \cos^2\chi ~-~ 2\cos^3\chi ) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,862: | Line 5,822: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
- \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^3 ( 1 -\cos\chi ) | |||
- \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4( -13~+~12\cos\chi +2 \cos^2\chi ) | |||
+\frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) - \frac{1}{2^6}\biggl(\frac{a}{c}\biggr)^4(1-\cos\chi )^2 | |||
+ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,885: | Line 5,842: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
~+~ \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^3 ( 2\cos\chi ~-~ 3\cos^2\chi ) | |||
~+~ \frac{1}{2^5} \biggl(\frac{a}{c}\biggr)^4 (-~9 \cos\chi ~+~8\cos^2\chi ~-~ 5\cos^3\chi ) | |||
\biggr\} | |||
+ \frac{1}{2^ | |||
\biggr | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,907: | Line 5,858: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \frac{1}{2^ | + | ||
\biggl[ | E(\mu) \biggl\{ -\frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | ||
+ | \biggl[ 1 ~+~\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi | ||
~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 ( 3\cos^2\chi - 1 ) | |||
~+~ ( | |||
\biggr] | \biggr] | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,927: | Line 5,876: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 12\cos\chi - 2\cos^2\chi ) | ||
\biggl[ 1 ~+~\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi | |||
\biggr] | |||
+ \frac{1}{2 | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,944: | Line 5,892: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 12 -21 \cos\chi - 2\cos^2\chi - 2\cos^3\chi ) | |||
\biggl[ 1 ~+~\frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggr] | |||
~ | + f_{E5}\biggl(\frac{a}{c}\biggr)^4 | ||
\biggr | \biggr\} | ||
~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 5,957: | Line 5,906: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
2K(\mu) \biggl\{ | |||
1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi | |||
~ | + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 \biggl[ 3\cos^2\chi - 1 \biggr] | ||
~ -~ | + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3\biggl[ 5\cos^3\chi | ||
~-~ 3\cos\chi \biggr] | |||
\biggr] | ~+~ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 \biggl[ 3 | ||
~-~ 30 \cos^2\chi | |||
~+~ 35 \cos^4\chi \biggr] | |||
\biggr\} | \biggr\} | ||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\times | |||
1 | \biggl\{ | ||
+ \frac{ | 1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) | ||
+ | +\frac{3}{2^4}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) | ||
~+~ | + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 | ||
\biggr | \biggl[ ( -13~+~12\cos\chi +2 \cos^2\chi ) | ||
~+~ 12 ( 1 -\cos\chi ) | |||
~+~ 48 ( 2\cos\chi ~-~ 3\cos^2\chi ) | |||
\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,005: | Line 5,954: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 | + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 | ||
(- | \biggl[ (-17 + 21\cos\chi - \cos^2\chi ~-~ 2\cos^3\chi ) | ||
- ( -13~+~12\cos\chi +2 \cos^2\chi ) | |||
- 12 (1-\cos\chi )^2 | |||
~+~ 24 (-~9 \cos\chi ~+~8\cos^2\chi ~-~ 5\cos^3\chi ) | |||
\biggr] | |||
\biggr\} | \biggr\} | ||
</math> | </math> | ||
| Line 6,030: | Line 5,977: | ||
E(\mu) \biggl\{ | E(\mu) \biggl\{ | ||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | ||
~ -\frac{1}{2^4} \biggl(\frac{a}{c}\biggr)^2 \cos\chi | |||
~ | ~ -\frac{1}{2^5} \biggl(\frac{a}{c}\biggr)^3 \cos^2\chi | ||
~ -\frac{1}{2^7} \biggl(\frac{a}{c}\biggr)^4 ( 3\cos^3\chi - \cos\chi ) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,045: | Line 5,993: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 12\cos\chi - 2\cos^2\chi ) | |||
\ | ~+~\frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 13- 12\cos\chi - 2\cos^2\chi ) | ||
~+~ \ | ~+~ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 13- 12\cos\chi - 2\cos^2\chi )\cos\chi | ||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,057: | Line 6,005: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 12 -21 \cos\chi - 2\cos^2\chi - 2\cos^3\chi ) | |||
~+~\frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 12 -21 \cos\chi - 2\cos^2\chi - 2\cos^3\chi ) | |||
+ f_{E5}\biggl(\frac{a}{c}\biggr)^4 | |||
\biggr\} | |||
+ \frac{1}{2^ | ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | ||
( - | |||
+ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,078: | Line 6,023: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | 2K(\mu) \biggl\{ | ||
+\frac{ | 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi | ||
+ \frac{1}{2^ | + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 ( 3\cos^2\chi - 1 ) | ||
( - | + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 ( 5\cos^3\chi ~-~ 3\cos\chi ) | ||
~+~ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 ( 3~-~ 30 \cos^2\chi~+~ 35 \cos^4\chi ) | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,099: | Line 6,046: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\times | |||
+ \frac{ | \biggl\{ | ||
1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) | |||
+\frac{3}{2^4}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) | |||
+ \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 | |||
\biggl[ ( -13~+~12\cos\chi +2 \cos^2\chi ) | |||
~+~ ( 12 -12\cos\chi ) | |||
~+~ ( 96\cos\chi ~-~ 144\cos^2\chi ) | |||
\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,115: | Line 6,068: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \frac{1}{2^ | + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 | ||
~ | \biggl[ (-17 + 21\cos\chi - \cos^2\chi ~-~ 2\cos^3\chi ) | ||
+ | + ( 13~-~12\cos\chi -2 \cos^2\chi ) | ||
\biggr\} | + (-12 + 24\cos\chi - 12\cos^2\chi) | ||
~+~ (-~216 \cos\chi ~+~192\cos^2\chi ~-~ 120\cos^3\chi ) | |||
\biggr] | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,135: | Line 6,091: | ||
E(\mu) \biggl\{ | E(\mu) \biggl\{ | ||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | ||
+ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- | + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2\biggl[ ( 13- 12\cos\chi - 2\cos^2\chi ) ~ -12 \cos\chi \biggr] | ||
~ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,150: | Line 6,105: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
~+~ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 12 - | ~+~\frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 \biggl[ | ||
( 13- 12\cos\chi - 2\cos^2\chi ) + ( 12 -21 \cos\chi - 2\cos^2\chi - 2\cos^3\chi ) | |||
~ -~12 \cos^2\chi | |||
\biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~+~ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl[ | |||
( 13\cos\chi - 12\cos^2\chi - 2\cos^3\chi ) | |||
~+~( 12 -21 \cos\chi - 2\cos^2\chi - 2\cos^3\chi ) | |||
~ -~6 ( 3\cos^3\chi - \cos\chi ) | |||
+ 2^8\cdot 3 f_{E5} | |||
\biggr] | |||
\biggr\} | \biggr\} | ||
~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | ||
| Line 6,156: | Line 6,133: | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
That is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~\frac{\pi V_\mathrm{Dyson}}{GM/c} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 6,166: | Line 6,147: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
2K(\mu) | 2K(\mu) \biggl\{ | ||
\biggl\{ | 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi | ||
+ \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 ( 3\cos^2\chi - 1 ) | |||
+\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^ | + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 ( 5\cos^3\chi ~-~ 3\cos\chi ) | ||
~+~ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 ( 3~-~ 30 \cos^2\chi~+~ 35 \cos^4\chi ) | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,183: | Line 6,166: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\times | |||
\biggl\{ | |||
+ | 1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) | ||
+\frac{3}{2^4}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) | |||
+ \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 | |||
( -1 ~+~ 96\cos\chi~-~ 142\cos^2\chi ) | |||
+ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 | |||
(-16 ~-~183\cos\chi ~+~177 \cos^2\chi ~-~ 122\cos^3\chi ) | |||
\biggr\} | |||
+ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 | |||
(-16 ~-~183\cos\chi ~+~177 \cos^2\chi ~-~ 122\cos^3\chi ) | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,258: | Line 6,224: | ||
2K(\mu) | 2K(\mu) | ||
\biggl\{ | \biggl\{ | ||
1 | 1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) | ||
+\frac{1}{2^ | +\frac{3}{2^4}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) | ||
+ \frac{1}{2^ | + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 | ||
( -1 ~+~ 96\cos\chi~-~ 142\cos^2\chi ) | |||
+ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 | |||
(-16 ~-~183\cos\chi ~+~177 \cos^2\chi ~-~ 122\cos^3\chi ) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,274: | Line 6,243: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( - | + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi - \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2\cos\chi | ||
+\frac{3}{2^5}\biggl(\frac{a}{c}\biggr)^3(\cos\chi-\cos^2\chi ) | |||
+ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 | |||
( - \cos\chi ~+~ 96\cos^2\chi~-~ 142\cos^3\chi ) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,289: | Line 6,260: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 ( 3\cos^2\chi - 1 ) | ||
+ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 (1- 3\cos^2\chi ) | |||
~+~\frac{3}{2^7}\biggl(\frac{a}{c}\biggr)^4(1-\cos\chi ) ( 3\cos^2\chi - 1 ) | |||
+ \frac{1}{2^ | |||
~+~\frac{ | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,307: | Line 6,276: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 ( 5\cos^3\chi ~-~ 3\cos\chi ) | |||
\ | ~+~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^4 (3\cos\chi ~-~5\cos^3\chi ) | ||
+ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 ( 3~-~ 30 \cos^2\chi~+~ 35 \cos^4\chi ) | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | |||
<tr> | |||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
2\biggl( \frac{a}{c}\biggr) | + | ||
E(\mu) \biggl\{ | |||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | |||
+ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) | |||
~+~\frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 25- 33\cos\chi - 16\cos^2\chi - 2\cos^3\chi ) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,343: | Line 6,304: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~2\biggl( \frac{a}{c}\biggr)^ | <math>~ | ||
~+~ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 12 -2 \cos\chi - 14\cos^2\chi - 22\cos^3\chi + 2^8\cdot 3 f_{E5} ) | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,363: | Line 6,326: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\biggl | 2K(\mu) | ||
\biggl\{ | |||
1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) | |||
+\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 \biggl[3(1-\cos\chi ) - 4 \cos\chi + 2 ( 3\cos^2\chi - 1 )\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,375: | Line 6,340: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 \biggl[ | |||
36 (\cos\chi-\cos^2\chi ) | |||
+ 24 (1 ~-~ 3\cos\chi - 3\cos^2\chi +5\cos^3\chi ) | |||
+ ( -1 ~+~ 96\cos\chi~-~ 142\cos^2\chi ) | |||
\biggr] | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,387: | Line 6,355: | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{1}{2} | <math>~ | ||
+ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl[ | |||
+ \ | (-16 ~-~183\cos\chi ~+~177 \cos^2\chi ~-~ 122\cos^3\chi ) | ||
~+~18(1-\cos\chi ) ( 3\cos^2\chi - 1 ) | |||
+ ( - \cos\chi ~+~ 96\cos^2\chi~-~ 142\cos^3\chi ) | |||
~+~ 24 (3\cos\chi ~-~5\cos^3\chi ) | |||
+ 6 ( 3~-~ 30 \cos^2\chi~+~ 35 \cos^4\chi ) | |||
\biggr] | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,405: | Line 6,379: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{1}{2} | + | ||
+ \frac{1}{ | E(\mu) \biggl\{ | ||
+ \ | ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | ||
+ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) | |||
~+~\frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 25- 33\cos\chi - 16\cos^2\chi - 2\cos^3\chi ) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,421: | Line 6,397: | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\frac{1}{2} | ~+~ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 12 -2 \cos\chi - 14\cos^2\chi - 22\cos^3\chi + 2^8\cdot 3 f_{E5} ) | ||
+ \ | \biggr\} | ||
~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | <math>~=</math> | ||
</td> | </td> | ||
<td align="left"> | |||
<math>~ | <math>~ | ||
\ | 2K(\mu) | ||
+ \frac{ | \biggl\{ | ||
+ \frac{ | 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) | ||
+\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) | |||
+ \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 (23 ~+~ 60\cos\chi - 250\cos^2\chi +120\cos^3\chi ) | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( -16 ~-~94\cos\chi ~+~147 \cos^2\chi ~-~ 194\cos^3\chi + 210 \cos^4\chi ) | |||
\biggr\} | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
| |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
\ | + | ||
+ | E(\mu) \biggl\{ | ||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | |||
+ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) | |||
~+~\frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 25- 33\cos\chi - 16\cos^2\chi - 2\cos^3\chi ) | |||
</math> | </math> | ||
</td> | </td> | ||
| Line 6,504: | Line 6,468: | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ | ~+~ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 12 -2 \cos\chi - 14\cos^2\chi - 22\cos^3\chi + 2^8\cdot 3 f_{E5} ) | ||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | |||
</math> | </math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | |||
====Insert Expressions for K and E==== | |||
<table border="1" align="center" width="85%" cellpadding="8"> | |||
<tr><td align="left"> | |||
<div align="center"> | |||
'''Summary''' | |||
</div> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~k'</math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
<math>~=</math> | |||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~ | <math>~ | ||
+ \biggl\{ \frac{9}{256}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - 2\biggr] + \frac{7}{128}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{19}{168} - 2\biggr]\cos2\chi | 2\biggl( \frac{a}{c}\biggr)^{1 / 2}\biggl( \frac{R_1}{c}\biggr)^{-1 / 2} | ||
\biggl[1 + \frac{a}{c}\cdot \biggl( \frac{R_1}{c} \biggr)^{-1} \biggr]^{-1} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \frac{4}{k'}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2\biggl( \frac{a}{c}\biggr)^{- 1 / 2}\biggl( \frac{R_1}{c}\biggr)^{1 / 2} | |||
\biggl[1 + \frac{a}{c}\cdot \biggl( \frac{R_1}{c} \biggr)^{-1} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~2\biggl( \frac{c}{a}\biggr)^{1 / 2} | |||
\biggl[ 4 + \biggl( \frac{a}{c}\biggr)^2 - 4\biggl(\frac{a}{c}\biggr)\cos\chi \biggr]^{1 / 4} | |||
\biggl\{ 1 + \frac{a}{c}\cdot \biggl[ 4 + \biggl( \frac{a}{c}\biggr)^2 - 4\biggl(\frac{a}{c}\biggr)\cos\chi \biggr]^{-1 / 2} \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl( \frac{2^3c}{a}\biggr)^{1 / 2} | |||
\biggl[ 1 - \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2 \biggr]^{1 / 4} | |||
\biggl\{ 1 + \frac{a}{2c}\cdot \biggl[ 1 - \biggl(\frac{a}{c}\biggr)\cos\chi + \biggl( \frac{a}{2c}\biggr)^2 \biggr]^{-1 / 2} \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \ln \frac{4}{k'}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) | |||
+ \frac{1}{4}\ln\biggl[ 1 - \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2 \biggr] | |||
+ \ln\biggl\{ 1 + \frac{a}{2c}\cdot \biggl[ 1 - \biggl(\frac{a}{c}\biggr)\cos\chi + \biggl( \frac{a}{2c}\biggr)^2 \biggr]^{-1 / 2} \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) | |||
+ \frac{1}{4}\ln\biggl[ 1 - \biggl(\frac{a}{c}\biggr)\cos\chi \biggr] | |||
+ \ln\biggl[ 1 + \frac{a}{2c} \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) | |||
+ \frac{a}{2c}\biggl[ 1 | |||
- \frac{1}{2} \cos\chi \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr> | |||
</table> | |||
Remember that ([[#Elliptic_Integral_Expressions|see above]]), | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~K(\mu)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\ln \frac{4}{k^'} + \frac{1}{2^2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 | |||
+ \frac{3^2}{2^6} \biggl( \ln\frac{4}{k^'} - \frac{7}{6} \biggr){k'}^4 | |||
+ \frac{5^2}{2^8} \biggl( \ln\frac{4}{k^'} - \frac{37}{30} \biggr){k'}^6 + \cdots | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
And ([[#Elliptic_Integral_Expressions|see above]]), | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~E(\mu)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
1 | |||
~+~ \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 | |||
~+~ \frac{3}{2^4}\biggl( \ln \frac{4}{k'} - 1 - \frac{1}{3\cdot 4}\biggr)(k')^4 | |||
~+~ \frac{3^2\cdot 5}{2^7\cdot 3}\biggl( \ln \frac{4}{k'} - 1 - \frac{1}{2\cdot 3} - \frac{1}{2\cdot 3\cdot 5}\biggr)(k')^6 | |||
~+~ \cdots | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
---- | |||
We are trying to match equation (6) in [http://adsabs.harvard.edu/abs/1893RSPTA.184.1041D Dyson's (1893b)] "Part II", that is, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{V}{2\pi a^2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\ln\biggl(\frac{8c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr) \biggl[\ln\biggl(\frac{8c}{a}\biggr) - \frac{5}{4}\biggr] \cos\chi | |||
+ \biggl\{ \frac{1}{16} \biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{5}{2} \biggr] + \frac{3}{16} \biggl[\ln\biggl(\frac{8c}{a}\biggr) +\frac{17}{36} - \frac{72}{36}\biggr]\cos2\chi\biggr\}\biggl(\frac{a^2}{c^2}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \biggl\{ \frac{3}{32}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{25}{12}\biggr]\cos\chi + \frac{5}{64}\biggl[ \ln\biggl(\frac{8c}{a}\biggr)+\frac{7}{24} - \frac{48}{24}\biggr]\cos3\chi \biggr\} \biggl(\frac{a^3}{c^3}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \biggl\{ \frac{9}{256}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - 2\biggr] + \frac{7}{128}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{19}{168} - 2\biggr]\cos2\chi | |||
+ \frac{35}{1024} \biggl[ \ln\biggl(\frac{8c}{a}\biggr) - 2 + \frac{19}{120}\biggr]\cos4\chi \biggr\} \biggl(\frac{a^4}{c^4}\biggr) ~+~\cdots | + \frac{35}{1024} \biggl[ \ln\biggl(\frac{8c}{a}\biggr) - 2 + \frac{19}{120}\biggr]\cos4\chi \biggr\} \biggl(\frac{a^4}{c^4}\biggr) ~+~\cdots | ||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
---- | |||
=====To First Order===== | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~~(k')^{2}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{2a}{c}\biggr) \biggl\{1 | |||
~-~ \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) | |||
+ \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2\biggl[ (3-\cos^2\chi) | |||
~+~2(2~-~ \cos\chi )^2 \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3\biggl[ (3\cos\chi - \cos^3\chi) | |||
~+~ (2~-~ \cos\chi )(3-\cos^2\chi) | |||
~-~ (2~-~ \cos\chi )^3 \biggr] | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\ln \frac{4}{k'}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\ln \Gamma | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl\{ | |||
\frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) | |||
+ \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) | |||
~-~\frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 (2~-~ \cos\chi )^2 | |||
~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Hence, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\pi V_\mathrm{Dyson}}{GM/c} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2K(\mu) | |||
\biggl\{ | |||
1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) | |||
\biggr\} | |||
+ E(\mu) \biggl\{ | |||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^2}{c^2}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) \biggr] \biggl\{ 2K(\mu) \biggr\} | |||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi \biggl\{~E(\mu) \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl[ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) \biggr] \biggl\{ 2\ln \frac{4}{k'} + \frac{1}{2}\biggl[ \ln\frac{4}{k'} - 1 \biggr] k'^2 \biggr\} | |||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi \biggl\{~1 + \frac{1}{2}\cancelto{0}{\biggl[ \ln\frac{4}{k'} - \frac{1}{2} \biggr] k'^2}\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ 2\ln \frac{4}{k'} + \frac{1}{2}\biggl[ \ln\frac{4}{k'} - 1 \biggr] \biggl(\frac{2a}{c}\biggr) \biggr\} | |||
+ \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) \biggl\{ 2\ln \frac{4}{k'} +\frac{1}{2} \cancelto{0}{\biggl[ \ln\frac{4}{k'} - 1 \biggr] k'^2} \biggr\} | |||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi \biggl\{~1 + \frac{1}{2}\cancelto{0}{\biggl[ \ln\frac{4}{k'} - \frac{1}{2} \biggr] k'^2}\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2\ln \frac{4}{k'} + \biggl(\frac{a}{c}\biggr)\biggl[ \ln\frac{4}{k'} - 1 \biggr] | |||
+ \biggl(\frac{a}{c}\biggr)(\cos\chi - 1) \biggl\{ \ln \frac{4}{k'} \biggr\} | |||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2\ln \frac{4}{k'} + \biggl(\frac{a}{c}\biggr)\biggl[ \ln\frac{4}{k'} - 1 | |||
+ (\cos\chi - 1) \biggl( \ln \frac{4}{k'} \biggr) | |||
~-~ \frac{1}{2^3} \cos\chi \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
2\ln \frac{4}{k'} + \biggl(\frac{a}{c}\biggr)\biggl[ - 1 | |||
+ \cos\chi \biggl( \ln \frac{4}{k'} \biggr) | |||
~-~ \frac{1}{2^3} \cos\chi \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\ln\biggl( \frac{2^3c}{a}\biggr) + | |||
\frac{1}{2}\biggl(\frac{a}{c}\biggr) \biggl\{ (2~-~ \cos\chi ) - 2 | |||
+ \cos\chi \biggl[ \ln\biggl(\frac{2^3c}{a}\biggr)\biggr] | |||
~-~ \frac{1}{4} \cos\chi \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\ln\biggl( \frac{2^3c}{a}\biggr) + | |||
\frac{1}{2}\biggl(\frac{a}{c}\biggr) \biggl[ \ln\biggl(\frac{2^3c}{a}\biggr) | |||
~-~ \frac{5}{4} \biggr]\cos\chi | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
=====To Second Order===== | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\pi V_\mathrm{Dyson}}{GM/c} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) | |||
+\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) | |||
\biggr\} | |||
\biggl\{ | |||
2K(\mu) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ | |||
\biggl\{ | |||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | |||
+ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) | |||
\biggr\} | |||
\biggl\{ | |||
E(\mu) | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) | |||
+\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) | |||
\biggr\} | |||
\biggl\{ | |||
2\ln \frac{4}{k^'} + \frac{1}{2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 | |||
+ \frac{3^2}{2^5} \biggl( \ln\frac{4}{k^'} - \frac{7}{6} \biggr){k'}^4 | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ | |||
\biggl\{ | |||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | |||
+ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) | |||
\biggr\} | |||
\biggl\{ | |||
1 ~+~ \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) | |||
+\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) | |||
\biggr\} | |||
\biggl\{ | |||
2\biggl[\frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\ln \Gamma\biggr] + \frac{1}{2}\biggl[ \frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\ln \Gamma - 1 \biggr]{k'}^2 | |||
+ \frac{3^2}{2^5} \biggl[ \frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\ln \Gamma - \frac{7}{6} \biggr] {k'}^4 | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ | |||
\biggl\{ | |||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | |||
+ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) | |||
\biggr\} | |||
\biggl\{ | |||
1 ~+~ \frac{1}{2}\biggl[ \frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\ln \Gamma - \frac{1}{2}\biggr](k')^2 | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) | |||
+\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) | |||
\biggr\} | |||
\biggl\{ | |||
\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) + \ln \Gamma\biggr] + \frac{1}{2^2}\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) + \ln \Gamma - 2 \biggr] | |||
\biggl( \frac{2a}{c}\biggr) \biggl[ 1 | |||
~-~ \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi )\biggr] | |||
+ \frac{3}{2^6} \biggl[ 3 \ln\biggl( \frac{2^3c}{a}\biggr) + \cancelto{0}{3\ln \Gamma} - 7 \biggr] 4\biggl( \frac{a}{c}\biggr)^2 | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ | |||
\biggl\{ | |||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | |||
+ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) | |||
\biggr\} | |||
\biggl\{ | |||
1 ~+~ \frac{1}{2^2}\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) + \cancelto{0}{\ln \Gamma} - 1 \biggr] | |||
\biggl( \frac{2a}{c}\biggr) \biggl[ 1 | |||
~-~\cancelto{0}{ \frac{1}{2}\biggl(\frac{a}{c}\biggr)} (2~-~ \cos\chi )\biggr] | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) \, , | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\ln\Gamma</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2( -1 ~+~ 4\cos\chi -2\cos^2\chi ) | |||
~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Hence, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\pi V_\mathrm{Dyson}}{GM/c} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) | |||
+\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) | |||
\biggr\} | |||
\biggl\{ | |||
\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2( -1 ~+~ 4\cos\chi -2\cos^2\chi ) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 2 + \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) \biggr] | |||
\biggl[ 1 | |||
~-~ \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi )\biggr] | |||
+ \frac{3}{2^4}\biggl( \frac{a}{c}\biggr)^2 \biggl[ 3 \ln\biggl( \frac{2^3c}{a}\biggr) - 7 \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ | |||
\biggl\{ | |||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | |||
+ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) | |||
\biggr\} | |||
\biggl\{ | |||
1 ~+~ \frac{1}{2}\biggl( \frac{a}{c}\biggr)\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 1 \biggr] | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl\{ | |||
1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) | |||
+\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) | |||
\biggr\} | |||
\biggl\{ | |||
\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2( -1 ~+~ 4\cos\chi -2\cos^2\chi ) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 2 \biggr] | |||
+ \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2 (2~-~ \cos\chi ) | |||
- \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2 \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 2 \biggr] | |||
(2~-~ \cos\chi ) | |||
+ \frac{3}{2^4}\biggl( \frac{a}{c}\biggr)^2 \biggl[ 3 \ln\biggl( \frac{2^3c}{a}\biggr) - 7 \biggr] | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | |||
~+~ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) | |||
~-~ \frac{1}{2^4} \biggl(\frac{a}{c}\biggr)^2\cos\chi \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 1 \biggr] | |||
~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) | |||
~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi | |||
+ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 2 \biggr] | |||
+ \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~+~ \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2( -1 ~+~ 4\cos\chi -2\cos^2\chi ) | |||
+ \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2 (2~-~ \cos\chi ) | |||
- \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2 \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 2 \biggr] | |||
(2~-~ \cos\chi ) | |||
+ \frac{3}{2^4}\biggl( \frac{a}{c}\biggr)^2 \biggl[ 3 \ln\biggl( \frac{2^3c}{a}\biggr) - 7 \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2(\cos\chi - 1) (2~-~ \cos\chi ) | |||
+\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) \ln\biggl( \frac{2^3c}{a}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~+~ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) | |||
~-~ \frac{1}{2^4} \biggl(\frac{a}{c}\biggr)^2\cos\chi \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 1 \biggr] | |||
~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\ln\biggl( \frac{2^3c}{a}\biggr) | |||
+ \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)\biggl\{ 4(2~-~ \cos\chi ) | |||
~-~ \cos\chi | |||
+ \biggl[ 4 \ln\biggl( \frac{2^3c}{a}\biggr) - 8 \biggr] | |||
+ \biggl[ 4\ln\biggl( \frac{2^3c}{a}\biggr) \biggr] (\cos\chi - 1) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ | |||
24( -1 ~+~ 4\cos\chi -2\cos^2\chi ) | |||
+ 48 (2~-~ \cos\chi ) | |||
- 48\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 2 \biggr] | |||
(2~-~ \cos\chi ) | |||
+ 36\biggl[ 3 \ln\biggl( \frac{2^3c}{a}\biggr) - 7 \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 48(\cos\chi - 1) (2~-~ \cos\chi ) | |||
~+~12 (1-7\cos\chi + 6\cos^2\chi ) \ln\biggl( \frac{2^3c}{a}\biggr) | |||
~+~ ( 13- 24\cos\chi - 2\cos^2\chi ) | |||
~-~12\cos\chi \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 1 \biggr] | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\ln\biggl( \frac{2^3c}{a}\biggr) | |||
+ \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)\biggl\{ 4(2~-~ \cos\chi ) | |||
~-~ \cos\chi | |||
+ \biggl[ 4 \ln\biggl( \frac{2^3c}{a}\biggr) - 8 \biggr] | |||
+ \biggl[ 4\ln\biggl( \frac{2^3c}{a}\biggr) \biggr] (\cos\chi - 1) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ (-24 + 96\cos\chi-48\cos^2\chi) | |||
+ (96~-~ 48\cos\chi ) | |||
~+~ \biggl[2- \ln\biggl( \frac{2^3c}{a}\biggr) \biggr] | |||
(96~-~ 48 \cos\chi ) | |||
+ \biggl[ 108 \ln\biggl( \frac{2^3c}{a}\biggr) - 252 \biggr] | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+ 48(3\cos\chi - \cos^2\chi - 2 ) | |||
~+~ (12 - 84\cos\chi + 72\cos^2\chi ) \ln\biggl( \frac{2^3c}{a}\biggr) | |||
~+~ ( 13- 24\cos\chi - 2\cos^2\chi ) ~+~12\cos\chi | |||
~-~12\cos\chi \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - \biggr] | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\ln\biggl( \frac{2^3c}{a}\biggr) | |||
+ \frac{1}{2}\biggl(\frac{a}{c}\biggr)\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) ~-~ \frac{5}{4}\biggr]\cos\chi | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ | |||
-24 ~+~ 96\cos\chi -48\cos^2\chi + 96~-~ 48\cos\chi | |||
+ 192 | |||
- 252 | |||
-96\cos\chi ~+~ ( 13- 12\cos\chi - 2\cos^2\chi ) | |||
+ (144\cos\chi - 48\cos^2\chi -96 ) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
+36 \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr)\biggr]\cos\chi | |||
~+~(12 - 84\cos\chi + 72\cos^2\chi -96 + 108) \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr)\biggr] | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\ln\biggl( \frac{2^3c}{a}\biggr) | |||
+ \frac{1}{2}\biggl(\frac{a}{c}\biggr)\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) ~-~ \frac{5}{4}\biggr]\cos\chi | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
| |||
</td> | |||
<td align="left"> | |||
<math>~~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ | |||
-71 ~+~84\cos\chi -98\cos^2\chi | |||
~+~(24 - 48\cos\chi + 72\cos^2\chi ) \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr)\biggr] | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\ln\biggl( \frac{2^3c}{a}\biggr) | |||
+ \frac{1}{2}\biggl(\frac{a}{c}\biggr)\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) ~-~ \frac{5}{4}\biggr]\cos\chi | |||
~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ | |||
-71 ~+~84\cos\chi -98\cos^2\chi | |||
~+~24\ln\biggl( \frac{2^3c}{a}\biggr)(1 - 2\cos\chi + 3\cos^2\chi ) | |||
\biggr\} | |||
~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
In an effort to compare this expression with equation (6) from Dyson's (1893b) "Part II", we should make the substitutions, | |||
<div align="center"> | |||
<math>~\ln\biggl(\frac{2^3c}{a}\biggr) \rightarrow (\lambda +2)</math> and <math>~2\cos^2\chi \rightarrow 1 + \cos2\chi \, .</math> | |||
</div> | |||
This means, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\pi V_\mathrm{Dyson}}{GM/c}\biggr|_{\mathcal{O}(a^2/c^2)} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ | |||
-71 ~+~84\cos\chi -49(1+\cos2\chi ) | |||
~+~24(\lambda + 2)(1 - 2\cos\chi ) | |||
~+~36(\lambda+2)(1 + \cos2\chi ) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ | |||
-71 ~+~84\cos\chi -49 -49 \cos2\chi | |||
~+~24(\lambda + 2 -2\lambda \cos\chi - 4\cos\chi) | |||
~+~36(\lambda+2 +\lambda\cos 2\chi + 2\cos 2\chi) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ | |||
-71 ~+~84\cos\chi -49 -49 \cos2\chi | |||
~+~24\lambda + 48 -48\lambda \cos\chi - 96\cos\chi | |||
~+~36\lambda+72 +36\lambda\cos 2\chi + 72\cos 2\chi | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ | |||
60\lambda -48\lambda \cos\chi - 12\cos\chi +36\lambda\cos 2\chi + 23\cos 2\chi | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
~+~ \biggl( \frac{a}{c}\biggr)^2\biggl\{ | |||
\frac{5\lambda}{16} - \frac{(4\lambda + 1)}{16}~\cos\chi +\frac{3(\lambda+\tfrac{23}{36})}{16}\cos 2\chi | |||
\biggr\} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
This expression differs from the 2<sup>nd</sup>-order term in Dyson's equation (6) by the amount, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Delta \biggr|_{\mathcal{O}(a^2/c^2)} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\biggl( \frac{a}{c}\biggr)^2\biggl\{ | |||
\frac{5\lambda}{16} - \frac{(4\lambda + 1)}{16}~\cos\chi +\frac{3(\lambda+\tfrac{23}{36})}{16}\cos 2\chi | |||
\biggr\} | |||
- | |||
\biggl(\frac{a}{c}\biggr)^2 \biggl\{ \frac{\lambda - \frac{1}{2}}{16} + \frac{3(\lambda + \frac{17}{36})}{16}\cos2\chi \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{16\cdot 12}\biggl( \frac{a}{c}\biggr)^2\biggl\{ | |||
60\lambda - (48\lambda + 12)~\cos\chi +(36\lambda+23)\cos 2\chi | |||
\biggr\} | |||
- | |||
\frac{1}{16\cdot 12}\biggl(\frac{a}{c}\biggr)^2 \biggl\{ 12\lambda - 6 + (36\lambda + 17) \cos2\chi \biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{16\cdot 12}\biggl( \frac{a}{c}\biggr)^2\biggl\{ | |||
48\lambda + 6 - (48\lambda + 12)~\cos\chi +(6)\cos 2\chi | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2^5}\biggl( \frac{a}{c}\biggr)^2\biggl\{ | |||
(\cos 2\chi -1)- (8\lambda + 2)~(1+\cos\chi) | |||
\biggr\} | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^2\biggl\{ | |||
(\cos\chi - 1)- (4\lambda + 1)~ | |||
\biggr\} (1+\cos\chi) | |||
</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^2 (\cos\chi - 2- 4\lambda ) (1+\cos\chi) | |||
</math> | </math> | ||
</td> | </td> | ||
Latest revision as of 21:04, 16 July 2020
Dyson (1893)

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Overview
Our focus, here, is on the pioneering work of F. W. Dyson (1893a, Philosophical Transactions of the Royal Society of London. A., 184, 43 - 95) and (1893b, Philosophical Transactions of the Royal Society of London. A., 184, 1041 - 1106). He used analytic techniques to determine the approximate equilibrium structure of axisymmetric, uniformly rotating, incompressible tori. C.-Y. Wong (1974, ApJ, 190, 675 - 694) extended Dyson's work, using numerical techniques to obtain more accurate equilibrium structures for incompressible tori having solid body rotation. Since then, Y. Eriguchi & D. Sugimoto (1981, Progress of Theoretical Physics, 65, 1870 - 1875) and I. Hachisu, J. E. Tohline & Y. Eriguchi (1987, ApJ, 323, 592 - 613) have mapped out the full sequence of Dyson-Wong tori, beginning from a bifurcation point on the Maclaurin spheroid sequence.
The most challenging aspect of each of these studies has been the development of an analytic and/or computational technique that can be used to accurately determine the gravitational potential of toroidal-shaped configurations. With this in mind, it should be appreciated that, in a paper that preceded his 1974 work, C.-Y. Wong (1973, Annals of Physics, 77, 279) derived an analytic expression for the exact potential (inside as well as outside) of axisymmetric, uniform-density tori having an arbitrarily specified ratio of the major to minor (cross-sectional) radii, <math>~R/d</math>. This is an outstanding accomplishment that has received little attention in the astrophysics literature and, therefore, has heretofore been under-appreciated. In a separate, accompanying discussion, we detail how Wong accomplished this task.
External Potential
His Derived Expression
(See an accompanying Ramblings Chapter for additional derivation details.) On p. 62, in §8 of Dyson (1893a), we find the following approximate expression for the potential at point "P", anywhere exterior to an anchor ring:
|
|
Equation image extracted without modification from p. 62 of Dyson (1893a)
The Potential of an Anchor Ring, Phil. Trans. Royal Soc. London. A., Vol. 184 |
In Dyson's expression, the leading factor of <math>~F</math> is the complete elliptic integral of the first kind, namely,
|
<math>~F = F(\mu)</math> |
<math>~\equiv</math> |
<math>~\int_0^{\pi/2} \frac{d\phi}{\sqrt{1 - \mu^2 \sin^2\phi}} \, ,</math> |
where, <math>~\mu \equiv (R_1 - R)/(R_1 + R)</math>. Similarly, <math>~E = E(\mu)</math> is the complete elliptic integral of the second kind.
Comparison With Thin Ring Approximation
In the limit of <math>~a/c \rightarrow 0</math>, Dyson's expression gives,
|
<math>~V_\mathrm{Dyson}</math> |
<math>~=</math> |
<math>~\frac{4K(\mu)}{R+R_1} \, ,</math> |
where we have acknowledged that, in the twenty-first century, the complete elliptic integral of the first kind is more customarily represented by the letter, <math>~K</math>. In a separate discussion, we have shown that the gravitational potential of an infinitesimally thin ring is given precisely by the expression,
|
<math>~\biggl[ \frac{\pi}{GM}\biggr] \Phi_\mathrm{TR}</math> |
<math>~=</math> |
<math>~- \frac{2K(k)}{R_1} \, ,</math> |
where, <math>~k \equiv [1-(R/R_1)^2]^{1 / 2}</math>. Is Dyson's expression identical to this one when <math>~a/c = 0</math> ?
Proof
Taking a queue from our accompanying discussion of toroidal coordinates, if we adopt the variable notation,
<math>~\eta \equiv \ln\biggl(\frac{R_1}{R}\biggr) \, ,</math>
then we can write,
|
<math>~\cosh\eta = \frac{1}{2}\biggl[e^\eta + e^{-\eta}\biggr]</math> |
<math>~=</math> |
<math>~\frac{R^2 + R_1^2}{2RR_1} \, ,</math> |
which implies that,
|
<math>~\biggl[ \frac{2}{\coth\eta +1} \biggr]^{1 / 2} = [1 - e^{-2\eta}]^{1 / 2}</math> |
<math>~=</math> |
<math>~\biggl[ 1 - \biggl(\frac{R}{R_1}\biggr)^2 \biggr]^{1 / 2} \, .</math> |
This is the definition of the parameter, <math>~k</math>, in the expression for <math>~\Phi_\mathrm{TR}</math>. Now, if we employ the Descending Landen Transformation for the complete elliptic integral of the first kind, we can make the substitution,
|
<math>~K(k)</math> |
<math>~=</math> |
<math>~ (1 + k_1)K(k_1) \, , </math> |
where, |
<math>~k_1</math> |
<math>~\equiv</math> |
<math>~ \frac{1-\sqrt{1-k^2}}{1+\sqrt{1-k^2}} \, . </math> |
But notice that, <math>~\sqrt{1-k^2} = e^{-\eta}</math>, in which case,
|
<math>~k_1 </math> |
<math>~=</math> |
<math>~ \frac{1-e^{-\eta}}{1+e^{-\eta}} </math> |
<math>~=</math> |
<math>~ \frac{1-R/R_1}{1+R/R_1} </math> |
<math>~=</math> |
<math>~ \frac{R_1-R}{R_1+R} \, , </math> |
which is the definition of the parameter, <math>~\mu</math>, in the expression for <math>~V_\mathrm{Dyson}</math>. Hence, we can write,
|
<math>~\biggl[ \frac{\pi}{GM}\biggr] \Phi_\mathrm{TR}</math> |
<math>~=</math> |
<math>~- \frac{2}{R_1} \biggl[(1+k_1)K(k_1) \biggr] </math> |
|
|
<math>~=</math> |
<math>~- \frac{2K(\mu)}{R_1} \biggl[1+\frac{R_1-R}{R_1+R} \biggr] </math> |
|
|
<math>~=</math> |
<math>~- \frac{4K(\mu)}{R_1+R} \, .</math> |
Aside from the adopted sign convention, this is indeed precisely the expression given by <math>~V_\mathrm{Dyson}</math> when <math>~a/c = 0</math> .
Evaluation
Dyson's Figures
In his effort to illustrate the behavior of equipotential contours in the space exterior to various anchor rings, Dyson evaluated his expression for the potential up through <math>~\mathcal{O}(\tfrac{a^2}{c^2})</math>; that is, he evaluated the function,
|
<math>~V_2 \equiv V_\mathrm{Dyson}\biggr|_{\mathcal{O}(a^2/c^2)}</math> |
<math>~=</math> |
<math>~ \frac{4K(\mu)}{R+R_1}\biggl[1 - \frac{1}{8}\biggl(\frac{a^2}{c^2}\biggr) \cos^2\biggl( \frac{\psi}{2}\biggr)\biggr] + \frac{(R + R_1)E(\mu)}{RR_1}\biggl[\frac{1}{8}\biggl(\frac{a^2}{c^2}\biggr) \cos\psi \biggr] \, . </math> |
Figures 1 - 6 from Dyson (1893a) — replicated immediately below — show his resulting set of contours for six cases: Tori (anchor rings) having aspect ratios of <math>~a/c = 0, 1/5, 2/5, 3/5, 4/5, 1</math>. Click on an image to view the contour plot at higher resolution. In what follows we present results from our own evaluation of this "V2" function for the single case of an anchor ring having <math>~a/c = 2/5</math>.
| |||||||||
Our Attempt to Replicate
First, let's test the accuracy of Dyson's (1893a) "series expansion" expression for the elliptic integrals, <math>~K(\mu)</math> and <math>~E(\mu)</math>; in the following table, the high-precision evaluations labeled "Numerical Recipes" have been drawn from the tabulated data that is provided in our accompanying discussion of incomplete elliptic integrals. Drawing from our accompanying set of Key mathematical relations — in which <math>~k</math>, rather than <math>~\mu</math>, represents the function modulus — the relevant series-expansion expressions are:
|
<math>~\frac{2K(k)}{\pi}</math> |
<math>~=</math> |
<math>~ 1 + \biggl( \frac{1}{2} \biggr)^2k^2 + \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 k^4 + \biggl( \frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2 k^6 + \biggl( \frac{1\cdot 3\cdot 5 \cdot 7}{2^7 \cdot 3}\biggr)^2 k^8 + \cdots + \biggl[ \frac{(2n-1)!!}{2^n n!} \biggr]^2 k^{2n} + \cdots </math> |
|
|
Gradshteyn & Ryzhik (1965), §8.113.1 |
|||
|
<math>~\frac{2E(k)}{\pi}</math> |
<math>~=</math> |
<math>~ 1 - \frac{1}{2^2} ~k^2 - \frac{1^2\cdot 3}{2^2\cdot 4^2}~ k^4 - \biggl(\frac{1\cdot 3\cdot 5}{2^4\cdot 3}\biggr)^2~\frac{ k^6 }{5} - \biggl( \frac{1\cdot 3\cdot 5 \cdot 7}{2^7 \cdot 3}\biggr)^2 \frac{k^8}{7} ~-~ \cdots - \biggl[ \frac{(2n-1)!!}{2^n n!} \biggr]^2 \frac{k^{2n}}{2n-1}
~-~ \cdots </math> |
|
|
Gradshteyn & Ryzhik (1965), §8.114.1 |
|||
These expressions — up through <math>~\mathcal{O}(\mu^4)</math> — can be found in the middle of p. 58 of Dyson (1893a). We strongly suspect that, in constructing the equipotential contours shown in his figures 1-6, Dyson used expressions for <math>~K(\mu)</math> and <math>~E(\mu)</math> that were more accurate than this. For example, we found it necessary to include terms up through <math>~\mathcal{O}(\mu^{10})</math> in order to match to three digits accuracy the potential contour values and coordinate locations reported by Dyson.
| <math>~\mu</math> | Numerical Recipes | Series expansion up through <math>~\mathcal{O}(\mu^4)</math> | Series expansion up through <math>~\mathcal{O}(\mu^{10})</math> | |||
| <math>~K(\mu)</math> | <math>~E(\mu)</math> | <math>~K(\mu)</math> | <math>~E(\mu)</math> | †<math>K(\mu)~</math> | <math>~E(\mu)</math> | |
| 0.34202014 | 1.62002589 | 1.52379921 | 1.6198 | 1.5239 | 1.6200263 | 1.5237989 |
| 0.57357644 | 1.73124518 | 1.43229097 | 1.7239 | 1.4336 | 1.73124518 | 1.43230 |
| 0.76604444 | 1.93558110 | 1.30553909 | 1.8773 | 1.3150 | 1.93558109 | 1.3061 |
| 0.90630779 | 2.30878680 | 1.16382796 | 2.042 | 1.199 | 2.308784 | 1.1700 |
| 0.98480775 | 3.15338525 | 1.04011440 | 2.16 | 1.12 | 3.150 | 1.069 |
|
†We actually used the "descending Landen transformation" to evaluate <math>~K(\mu)</math> through <math>~\mathcal{O}(\mu^{10})</math>. |
||||||
For <math>~c=1</math> and a specification of the ratio, <math>~a/c</math>, take the following steps to map out an equipotential curve that has <math>~V_2 = V_0</math>:
- Choose a value of <math>~R \ge a</math>
- Guess a value of <math>~(c-R) \le R_1 \le (c+R) ~~~\Rightarrow ~~~ \varpi = (R_1^2 - R^2)/(4c)</math> and, <math>~z = \pm \sqrt{ R_1^2 - (c+\varpi)^2}</math>
- Set <math>~ \cos\psi = (R_1^2 + R^2 - 4c^2)/(2RR_1)</math>
- Evaluate the function, <math>~V_2</math>
- If <math>~V_2 \ne V_0</math> to the desired accuracy, loop back up and guess another value of <math>~R_1</math>
- If <math>~V_2 = V_0</math> to the desired accuracy, save the coordinate location, <math>~(\varpi,z)</math>, and loop back up to pick another value of <math>~R</math>
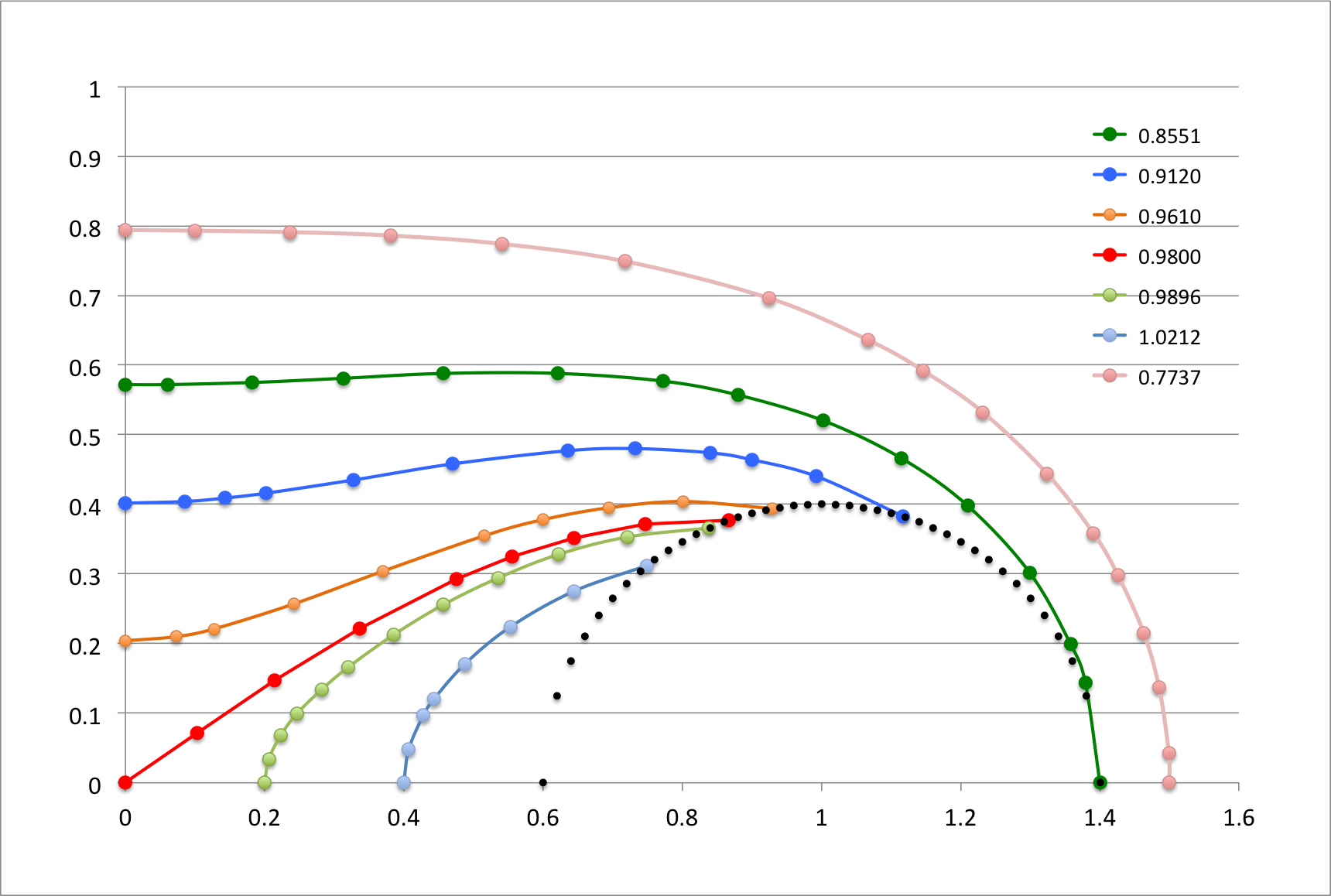 |
Tabulated Data
As the data in the following table documents, we have been able to construct equipotential contours that agree with Dyson, not only qualitatively, but quantitatively. For example:
- The dark green contour has been designed to touch the surface of the torus precisely where its outermost edge cuts through the equatorial plane <math>~(\varpi,z) = (1.4,0)</math>. This means that <math>~R = 0.4</math> and <math>~R_1 = 2.4</math>. (These four coordinate values are highlighted in pink in the second major column of the table.) When we plugged these values of <math>~R</math> and <math>~R_1</math> into Dyson's expression for <math>~V_2</math>, we determined that the value of the potential at this point on the torus surface is 0.8551 — see the yellow-highlighted heading of the second major table column. Compare this to the value of 0.855 that Dyson has printed just below the Figure 3 x-axis where a fiducial identifies the coordinate, <math>~\varpi = 1.4</math>. As has been catalogued at the bottom of table column #2, we have found that this dark-green contour touches the vertical axis at the coordinate location, <math>~(\varpi,z) = (0,0.572)</math>, for which, <math>~R_1 = R = 1.1518</math>.
- By design — see the coordinate values highlighted in pink in table column #1 — our outermost (pink) contour touches the equatorial plane at <math>~(\varpi,z) = (1.5,0) ~\Rightarrow ~ (R,R_1) = (0.5,2.5)</math>. When we plugged these values of <math>~R</math> and <math>~R_1</math> into Dyson's expression for <math>~V_2</math>, we determined that the value of the potential at this point outside the torus is 0.7737 — see the yellow-highlighted heading of table column #1. Compare this to the value of 0.777 that Dyson has printed just below the Figure 3 x-axis where a fiducial identifies the coordinate, <math>~\varpi = 1.5</math>. As has been catalogued at the bottom of table column #1, we have found that this pink contour touches the vertical axis at the coordinate location, <math>~(\varpi,z) = (0,0.794)</math>, for which, <math>~R_1 = R = 1.2766</math>.
- Similarly, we have constructed contours that intersect the equatorial plane at the fiducials marking <math>~\varpi = 0.0</math> (red curve & table column #5), <math>~\varpi = 0.2</math> (light-green curve & table column #6), and <math>~\varpi = 0.4</math> (light-blue curve & table column #7). According to our calculations, they correspond, respectively, to values of the potential, <math>~V_2 = 0.9800</math> (Dyson's corresponding fiducial label is 0.980), <math>~V_2 = 0.9896</math> (Dyson's corresponding fiducial label is 0.990), and <math>~V_2 = 1.0212</math> (Dyson's corresponding fiducial label is 1.021).
- Finally, we constructed two contours (blue and orange) by initially specifying the value of the potential, rather than specifying the coordinate values <math>~(R,R_1)</math>. We used the values of the potential that Dyson associated with the fiducials along the vertical axis at <math>~(\varpi,z) = (0.0,0.4)</math> and at <math>~(\varpi,z) = (0.0,0.2)</math>: Respectively, <math>~V_2 = 0.912</math> — blue contour detailed in our table column #3 — and <math>~V_2 = 0.961</math>— orange contour detailed in our table column #4. We determined that these two contour curves intersected the vertical axis at, respectively, <math>~(\varpi,z) = (0.0, 0.402)</math> and <math>~(\varpi,z) = (0.0, 0.204)</math>, that is, at coordinate locations that were nearly identical to the locations labeled by Dyson.
|
Coordinates of Points that Trace Seven Different Equipotential Contours External to the Anchor Ring With <math>~c/a = 5/2</math> |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Column #1 | Column #2 | Column #3 | Column #4 | Column #5 | Column #6 | Column #7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Intermediate Step
Objective
As has been reprinted above, on p. 62 of Dyson's Part I we find his power-series expression for the external potential, namely,
|
<math>~\frac{\pi V_\mathrm{Dyson}}{GM} \biggr|_{\mathcal{O}(a^4/c^4)}</math> |
<math>~=</math> |
<math>~ \frac{4K(\mu)}{R+R_1}\biggl\{ 1 ~-~ \frac{1}{8}\biggl(\frac{a^2}{c^2}\biggr) \cos^2\biggl( \frac{\psi}{2}\biggr) - \frac{1}{768}\biggl(\frac{a}{c}\biggr)^4 \biggl[ 5 ~+~ 8\cos\psi ~-~ \cos^2\psi ~-~ 4\cos^3\psi ~-~ \frac{4c^2}{RR_1} \cos2\psi \biggr] \biggr\} </math> |
|
|
|
<math>~ + \frac{(R + R_1)E(\mu)}{RR_1}\biggl\{ \frac{1}{8}\biggl(\frac{a}{c}\biggr)^2 \cos\psi ~-~\frac{1}{192} \biggl(\frac{a}{c}\biggr)^4 \biggl[ 2\cos^2\psi ~-~4\cos\psi ~+~ \frac{2c^2}{RR_1}\cos2\psi \biggr] \biggr\} \, , </math> |
where — as in the context of toroidal coordinates — we occasionally will make the substitution, <math>~e^\eta = R_1/R</math>, and therefore,
|
<math>~\mu</math> |
<math>~\equiv</math> |
<math>~\frac{R_1 - R}{R_1+R} = \frac{e^\eta - 1}{e^\eta + 1} \, . </math> |
In order to facilitate matching boundary conditions at the surface of the torus, between the exterior and interior expressions for the gravitational potential, Dyson rewrites this Part I expression for the external potential and — explicitly evaluating it on the torus surface — sets, <math>~R = a</math>. Specifically, on p. 1049 of Dyson's Part II we find equation (6), which reads,
|
<math>~\frac{V}{2\pi a^2}</math> |
<math>~=</math> |
<math>~ \ln\biggl(\frac{8c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr) \biggl[\ln\biggl(\frac{8c}{a}\biggr) - \frac{5}{4}\biggr] \cos\chi + \biggl\{ \frac{1}{16} \biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{5}{2} \biggr] + \frac{3}{16} \biggl[\ln\biggl(\frac{8c}{a}\biggr) +\frac{17}{36} - \frac{72}{36}\biggr]\cos2\chi\biggr\}\biggl(\frac{a^2}{c^2}\biggr) </math> |
|
|
|
<math>~ + \biggl\{ \frac{3}{32}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{25}{12}\biggr]\cos\chi + \frac{5}{64}\biggl[ \ln\biggl(\frac{8c}{a}\biggr)+\frac{7}{24} - \frac{48}{24}\biggr]\cos3\chi \biggr\} \biggl(\frac{a^3}{c^3}\biggr) </math> |
|
|
|
<math>~ + \biggl\{ \frac{9}{256}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - 2\biggr] + \frac{7}{128}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{19}{168} - 2\biggr]\cos2\chi + \frac{35}{1024} \biggl[ \ln\biggl(\frac{8c}{a}\biggr) - 2 + \frac{19}{120}\biggr]\cos4\chi \biggr\} \biggl(\frac{a^4}{c^4}\biggr) ~+~\cdots </math> |
In order to obtain this alternate power-series expression, Dyson …
- Expresses angular variations in terms of the angle, <math>~\chi</math>, instead of the angle, <math>~\psi</math>; these two angles are identified in the above schematic.
- Employs power-series expansions of both elliptic integral functions, <math>~K(\mu)</math> and <math>~E(\mu)</math>.
- Uses the binomial theorem to develop a number of other power-series expressions.
In what follows we will attempt to demonstrate that this second (Part II, equation 6) expression is identical to the first.
The Ratio R1/c
Note that, via the law of cosines,
|
<math>~R_1^2</math> |
<math>~=</math> |
<math>~(2c)^2 + R^2 - 4Rc\cos\chi</math> |
|
<math>~\Rightarrow ~~~\biggl(\frac{R_1}{c}\biggr)^2</math> |
<math>~=</math> |
<math>~4 + \biggl( \frac{R}{c}\biggr)^2 - 4\biggl(\frac{R}{c}\biggr)\cos\chi</math> |
At the surface of the torus, where <math>~R=a</math>, we therefore have,
|
<math>~\frac{R_1}{c}</math> |
<math>~=</math> |
<math>~2\biggl[ 1 - \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2 \biggr]^{1 / 2} \, .</math> |
Low Order
Employing the binomial theorem, we can write,
|
<math>~\biggl(\frac{R_1}{c}\biggr)^{-1}</math> |
<math>~=</math> |
<math>~\frac{1}{2}\biggl[ 1 - \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2 \biggr]^{-1 / 2} </math> |
|
|
<math>~\approx</math> |
<math>~\frac{1}{2}\biggl\{ 1 - \frac{1}{2} \biggl[ - \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2 \biggr] + \frac{3}{8}\biggl[ - \biggl(\frac{a}{c}\biggr)\cos\chi + \cancelto{0}{\frac{1}{4}\biggl( \frac{a}{c}\biggr)^2} \biggr]^2\biggr\}</math> |
|
|
<math>~\approx</math> |
<math>~\frac{1}{2}\biggl\{ 1 + \frac{1}{2} \biggl(\frac{a}{c}\biggr)\cos\chi - \frac{1}{8}\biggl( \frac{a}{c}\biggr)^2 + \frac{3}{8}\biggl(\frac{a}{c}\biggr)^2\cos^2\chi \biggr\}</math> |
|
|
<math>~\approx</math> |
<math>~ \frac{1}{2}\biggl\{ 1 + \frac{1}{2} \biggl(\frac{a}{c}\biggr)\cos\chi +\biggl( \frac{a}{c}\biggr)^2 \biggl[ \frac{3}{8}\cos^2\chi -\frac{1}{8}\biggr] \biggr\} </math> |
|
<math>~\Rightarrow~~~ 1 + \frac{a}{c} \biggl(\frac{R_1}{c}\biggr)^{-1}</math> |
<math>~\approx</math> |
<math>~1 + \frac{1}{2}\biggl( \frac{a}{c}\biggr) + \frac{1}{4} \biggl(\frac{a}{c}\biggr)^2\cos\chi </math> |
|
<math>~\Rightarrow~~~ \biggl[ 1 + \frac{a}{c} \biggl(\frac{R_1}{c}\biggr)^{-1} \biggr]^{-1}</math> |
<math>~\approx</math> |
<math>~1 - \biggl[ \frac{1}{2}\biggl( \frac{a}{c}\biggr) + \frac{1}{4} \biggl(\frac{a}{c}\biggr)^2\cos\chi \biggr] + \biggl[ \frac{1}{2}\biggl( \frac{a}{c}\biggr) + \frac{1}{4} \biggl(\frac{a}{c}\biggr)^2\cos\chi \biggr]^2 </math> |
|
|
<math>~\approx</math> |
<math>~ 1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) + \frac{1}{4} \biggl( \frac{a}{c}\biggr)^2 (1 - \cos\chi) </math> |
Higher Order
Adopting the shorthand notation,
<math>~\gamma \equiv \frac{1}{2}\biggl(\frac{R_1}{c}\biggr) \, ,</math> and <math>~b \equiv - \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2 \, ,</math>
and employing the binomial theorem, we can write,
|
<math>~\gamma = \biggl[ 1 + b \biggr]^{1 / 2}</math> |
<math>~=</math> |
<math>~ 1 + \frac{1}{2}b - \frac{1}{2^3}b^2 + \frac{1}{2^4}b^3 - \frac{3\cdot 5}{2^7\cdot 3}b^4 + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 1 + \frac{1}{2}\biggl[ - \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2 \biggr] - \frac{1}{2^3}\biggl[ - \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2 \biggr]^2 </math> |
|
|
|
<math>~ + \frac{1}{2^4}\biggl[ - \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2 \biggr]^3 - \frac{3\cdot 5}{2^7\cdot 3}\biggl[ - \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2 \biggr]^4 + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 1 ~-~ \frac{1}{2} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 - \frac{1}{2^3}\biggl[\biggl(\frac{a}{c}\biggr)^2\cos^2\chi - \frac{1}{2}\biggl( \frac{a}{c}\biggr)^3 \cos\chi + \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^4 \biggr] </math> |
|
|
|
<math>~ + \frac{1}{2^4}\biggl[ - \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2 \biggr]\biggl[\biggl(\frac{a}{c}\biggr)^2\cos^2\chi - \frac{1}{2}\biggl( \frac{a}{c}\biggr)^3 \cos\chi \biggr] - \frac{3\cdot 5}{2^7\cdot 3}\biggl[ \biggl(\frac{a}{c}\biggr)^4\cos^4\chi \biggr] + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 1 ~-~ \frac{1}{2} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 -~\frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2\cos^2\chi ~+~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3 \cos\chi ~-~ \frac{1}{2^7}\biggl( \frac{a}{c}\biggr)^4 </math> |
|
|
|
<math>~ -~\frac{1}{2^4} \biggl(\frac{a}{c}\biggr)^3\cos^3\chi ~+~ \frac{1}{2^5}\biggl( \frac{a}{c}\biggr)^4 \cos^2\chi + \frac{1}{2^6} \biggl(\frac{a}{c}\biggr)^4\cos^2\chi ~-~ \frac{3\cdot 5}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^4\cos^4\chi ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 1 ~-~ \frac{1}{2} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (1-\cos^2\chi) +~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3 (\cos\chi - \cos^3\chi) +~\frac{1}{2^7}\biggl( \frac{a}{c}\biggr)^4 \biggl[~-~ 1 ~+~ 6 \cos^2\chi ~-~ 5 \cos^4\chi \biggr] ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, . </math> |
Also, we have,
|
<math>~\frac{1}{\gamma} = 2\biggl(\frac{R_1}{c}\biggr)^{-1} = \biggl[ 1 + b \biggr]^{-1 / 2}</math> |
<math>~=</math> |
<math>~ 1 -\frac{1}{2}b + \frac{3}{2^3}b^2 - \frac{3\cdot 5}{2^4\cdot 3}b^3 + \frac{3\cdot 5\cdot 7}{2^7\cdot 3}b^4 + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~1 - \frac{1}{2}\biggl[- \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2\biggr] + \frac{3}{2^3}\biggl[- \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2\biggr]^2 </math> |
|
|
|
<math>~ - \frac{3\cdot 5}{2^4\cdot 3}\biggl[- \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2\biggr]^3 + \frac{3\cdot 5\cdot 7}{2^7\cdot 3}\biggl[- \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2\biggr]^4 + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr)</math> |
|
|
<math>~=</math> |
<math>~1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi - \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 + \frac{3}{2^3}\biggl[\biggl(\frac{a}{c}\biggr)^2\cos^2\chi ~-~ \frac{1}{2} \biggl(\frac{a}{c}\biggr)^3\cos\chi ~+~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^4\biggr] </math> |
|
|
|
<math>~ - \frac{3\cdot 5}{2^4\cdot 3}\biggl[- \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2\biggr] \biggl[\biggl(\frac{a}{c}\biggr)^2\cos^2\chi ~-~ \frac{1}{2} \biggl(\frac{a}{c}\biggr)^3\cos\chi \biggr] + \frac{3\cdot 5\cdot 7}{2^7\cdot 3}\biggl[\biggl(\frac{a}{c}\biggr)^4\cos^4\chi \biggr] + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr)</math> |
|
|
<math>~=</math> |
<math>~1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi - \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 + \frac{3}{2^3}\biggl(\frac{a}{c}\biggr)^2\cos^2\chi ~-~ \frac{3}{2^4}\biggl(\frac{a}{c}\biggr)^3\cos\chi ~+~ \frac{3}{2^7}\biggl( \frac{a}{c}\biggr)^4 </math> |
|
|
|
<math>~ + \frac{3\cdot 5}{2^4\cdot 3} \biggl[\biggl(\frac{a}{c}\biggr)^3\cos^3\chi ~-~ \frac{1}{2} \biggl(\frac{a}{c}\biggr)^4\cos^2\chi \biggr] - \frac{3\cdot 5}{2^6\cdot 3} \biggl[\biggl(\frac{a}{c}\biggr)^4\cos^2\chi\biggr] + \frac{3\cdot 5\cdot 7}{2^7\cdot 3}\biggl[\biggl(\frac{a}{c}\biggr)^4\cos^4\chi \biggr] + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr)</math> |
|
|
<math>~=</math> |
<math>~1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 \biggl[ 3\cos^2\chi - 1 \biggr] + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3\biggl[ 5\cos^3\chi ~-~ 3\cos\chi \biggr] </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 \biggl[ 3 ~-~ 30 \cos^2\chi ~+~ 35 \cos^4\chi \biggr] ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, . </math> |
Hence,
|
<math>~1~+~\biggl( \frac{a}{c}\biggr)\biggl(\frac{R_1}{c}\biggr)^{-1} </math> |
<math>~=</math> |
<math>~1 ~+~\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi ~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 \biggl[ 3\cos^2\chi - 1 \biggr] ~+~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^4\biggl[ 5\cos^3\chi ~-~ 3\cos\chi \biggr] ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, . </math> |
And, adopting the shorthand notation,
<math>~d \equiv \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi ~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 \biggl[ 3\cos^2\chi - 1 \biggr] ~+~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^4\biggl[ 5\cos^3\chi ~-~ 3\cos\chi \biggr]
\, ,</math>
we have,
|
<math>~\biggl[1~+~\biggl( \frac{a}{c}\biggr)\biggl(\frac{R_1}{c}\biggr)^{-1}\biggr]^{-1} </math> |
<math>~=</math> |
<math>~ 1 -d + d^2 - d^3 + d^4 ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~-~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 \biggl[ 3\cos^2\chi - 1 \biggr] ~-~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^4\biggl[ 5\cos^3\chi ~-~ 3\cos\chi \biggr] </math> |
|
|
|
<math>~+~ \biggl\{ \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi ~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 \biggl[ 3\cos^2\chi - 1 \biggr] \biggr\} \biggl\{ \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi ~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 \biggl[ 3\cos^2\chi - 1 \biggr] \biggr\} </math> |
|
|
|
<math>~-~ \biggl[ \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi \biggr] \biggl[ \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi \biggr]^2 ~+~\frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^4 ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~-~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 \biggl[ 3\cos^2\chi - 1 \biggr] ~-~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^4\biggl[ 5\cos^3\chi ~-~ 3\cos\chi \biggr] </math> |
|
|
|
<math>~+~ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggl\{ \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi ~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 \biggl[ 3\cos^2\chi - 1 \biggr] \biggr\} </math> |
|
|
|
<math>~+~ \biggl\{\frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi \biggr\} \biggl\{ \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi \biggr\} ~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 \biggl[ 3\cos^2\chi - 1 \biggr] \biggl\{ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggr\} </math> |
|
|
|
<math>~-~ \biggl[ \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi \biggr] \biggl[ \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi \biggr]^2 ~+~\frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^4 ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~-~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 \biggl[ 3\cos^2\chi - 1 \biggr] ~-~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^4\biggl[ 5\cos^3\chi ~-~ 3\cos\chi \biggr] </math> |
|
|
|
<math>~+~ \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2 ~+~ \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^3\cos\chi ~+~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^4 \biggl[ 3\cos^2\chi - 1 \biggr] ~+~ \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^3\cos\chi +\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^4\cos^2\chi ~+~\frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^4 \biggl[ 3\cos^2\chi - 1 \biggr] </math> |
|
|
|
<math>~-~ \biggl[ \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2 ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^3\cos\chi ~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^4\cos^2\chi \biggr] \biggl[ \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi \biggr] ~+~\frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^4 ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) ~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 \biggl[ 2\cos\chi ~+~2 (\cos\chi -1) ~-~ 2( 3\cos^2\chi - 1 ) \biggr] </math> |
|
|
|
<math> ~+~ \frac{1}{2^5} \biggl(\frac{a}{c}\biggr)^4 \biggl[ ( 3\cos^2\chi - 1 ) + 2\cos^2\chi ~+~( 3\cos^2\chi - 1 ) ~-~2 \cos\chi ~-~ 4 \cos\chi ~+~2 ~-~ ( 5\cos^3\chi ~-~ 3\cos\chi ) \biggr] ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) ~+~ \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^3 ( 2\cos\chi ~-~ 3\cos^2\chi ) </math> |
|
|
|
<math> ~+~ \frac{1}{2^5} \biggl(\frac{a}{c}\biggr)^4 ( -~9 \cos\chi ~+~8\cos^2\chi ~-~ 5\cos^3\chi ) ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, . </math> |
Relationship Between Angles
Drawing on the Law of Cosines, as above, we can state that on the torus surface,
|
<math>~R_1^2</math> |
<math>~=</math> |
<math>~(2c)^2 + a^2 - 4ac\cos\chi</math> |
Alternatively, applying the Law of Cosines to the angle, <math>~\psi</math>, we have,
|
<math>~(2c)^2</math> |
<math>~=</math> |
<math>~R_1^2 + a^2 - 2aR_1\cos\psi</math> |
|
<math>~\Rightarrow ~~~\cos\psi</math> |
<math>~=</math> |
<math>~\frac{R_1^2 + a^2 - 4c^2}{2aR_1} \, .</math> |
Therefore, anywhere along the surface of the torus, we can switch from one of these angles to the other via the relation,
|
<math>~\cos\psi</math> |
<math>~=</math> |
<math>~\frac{1}{2a}\biggl[ 4c^2 + a^2 - 4ac\cos\chi + a^2 - 4c^2\biggr] \biggl[4c^2 + a^2 - 4ac\cos\chi\biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~- \biggl[\cos\chi ~-~ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggr] \biggl[1 - \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi\biggr]^{-1 / 2} \, .</math> |
Cosine ψ Expansion
Employing the binomial theorem, we therefore can write,
|
<math>~\cos\psi</math> |
<math>~=</math> |
<math>~- \biggl[\cos\chi ~-~ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggr] \biggl\{ 1 - \frac{1}{2} \biggl[- \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr] + \frac{3}{8}\biggl[- \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr]^2 </math> |
|
|
|
<math>~ - \frac{5}{2^4}\biggl[- \biggl(\frac{a}{c}\biggr)\biggr]^3 + \frac{5\cdot 7}{2^7}\biggl[- \biggl(\frac{a}{c}\biggr)\biggr]^4 + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~- \biggl[\cos\chi ~-~ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggr] \biggl\{ 1 ~+~ \frac{1}{2} \biggl(\frac{a}{c}\biggr) ~-~ \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 \cos\chi ~+~ \frac{3}{8}\biggl[ \biggl(\frac{a}{c}\biggr)^2 ~-~ \frac{1}{4}\biggl(\frac{a}{c}\biggr)^3 \cos\chi ~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^4 \cos^2\chi \biggr] </math> |
|
|
|
<math>~ +~ \frac{5}{2^4} \biggl(\frac{a}{c}\biggr)^3 ~+~ \frac{5\cdot 7}{2^7} \biggl(\frac{a}{c}\biggr)^4 ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~- \biggl[\cos\chi ~-~ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggr] \biggl\{ 1 ~+~ \frac{1}{2} \biggl(\frac{a}{c}\biggr) ~+~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)^2\biggl[ 3 ~-~ \cos\chi \biggr] +~ \frac{1}{2^5} \biggl(\frac{a}{c}\biggr)^3 \biggl[ 10 ~-~ 3 \cos\chi \biggr]~+~ \frac{1}{2^7} \biggl(\frac{a}{c}\biggr)^4 \biggl[3 \cos^2\chi ~+~ 5\cdot 7 \biggr] ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr\} </math> |
|
<math>~\Rightarrow ~~~ \cos\psi \biggr|_{\mathcal{O}(a^2/c^2)}</math> |
<math>~=</math> |
<math>~- \biggl[\cos\chi ~-~ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggr] \biggl\{ 1 ~+~ \frac{1}{2} \biggl(\frac{a}{c}\biggr) ~+~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)^2\biggl[ 3 ~-~ \cos\chi \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ - \cos\chi \biggl\{ 1 ~+~ \frac{1}{2} \biggl(\frac{a}{c}\biggr) ~+~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)^2\biggl[ 3 ~-~ \cos\chi \biggr] \biggr\} + \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggl\{ 1 ~+~ \frac{1}{2} \biggl(\frac{a}{c}\biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -\cos\chi ~+~ \frac{1}{2} \biggl(\frac{a}{c}\biggr)(1-\cos\chi) ~+~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)^2\biggl[2 - 3\cos\chi + \cos^2\chi \biggr] \, . </math> |
Cosine-Squared Expansion
Letting,
<math>~b \equiv \biggl[- \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr] \, ,</math>
via the binomial theorem we have,
|
<math>~\cos^2\psi</math> |
<math>~=</math> |
<math>~\biggl[\cos\chi ~-~ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggr]^2 \biggl[1 - \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi\biggr]^{-1 } </math> |
|
|
<math>~=</math> |
<math>~\biggl[\cos\chi ~-~ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggr]^2 \biggl\{ 1 - b + b^2 - b^3 + b^4 - \mathcal{O}(b^5) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl[\cos\chi ~-~ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggr]^2 \biggl\{ 1 - \biggl[- \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr] + \biggl[- \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr]^2 </math> |
|
|
|
<math>~ - \biggl[- \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr]^3 + \biggl[- \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr]^4 + \mathcal{O}\biggl( \frac{a^5}{c^5} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl[\cos\chi ~-~ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggr]^2 \biggl\{ 1 + \biggl[\biggl(\frac{a}{c}\biggr) - \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr] + \biggl[\biggl(\frac{a}{c}\biggr)^2 - \frac{1}{2}\biggl(\frac{a}{c}\biggr)^3 \cos\chi + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^4 \cos^2\chi \biggr] </math> |
|
|
|
<math>~ + \biggl[\biggl(\frac{a}{c}\biggr) ~-~ \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr]\biggl[\biggl(\frac{a}{c}\biggr)^2 - \frac{1}{2}\biggl(\frac{a}{c}\biggr)^3 \cos\chi + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^4 \cos^2\chi \biggr] </math> |
|
|
|
<math>~ + \biggl[\biggl(\frac{a}{c}\biggr)^2 - \frac{1}{2}\biggl(\frac{a}{c}\biggr)^3 \cos\chi + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^4 \cos^2\chi \biggr]^2 + \mathcal{O}\biggl( \frac{a^5}{c^5} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl[\cos\chi ~-~ \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggr]^2 \biggl\{ 1 + \biggl(\frac{a}{c}\biggr) - \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi + \biggl(\frac{a}{c}\biggr)^2 - \frac{1}{2}\biggl(\frac{a}{c}\biggr)^3 \cos\chi + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^4 \cos^2\chi </math> |
|
|
|
<math>~ ~+~ \biggl(\frac{a}{c}\biggr)^3 ~-~ \frac{1}{2}\biggl(\frac{a}{c}\biggr)^4 \cos\chi ~-~ \frac{1}{4}\biggl(\frac{a}{c}\biggr)^4 \cos\chi + \biggl(\frac{a}{c}\biggr)^4 + \mathcal{O}\biggl( \frac{a^5}{c^5} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\cos^2\chi ~-~ \biggl( \frac{a}{c}\biggr)\cos\chi ~+~ \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2 \biggr] \biggl\{1 ~+~ \biggl(\frac{a}{c}\biggr) ~+~ \biggl(\frac{a}{c}\biggr)^2\biggl[1 ~-~ \frac{1}{4} \cos\chi \biggr] ~+~ \biggl(\frac{a}{c}\biggr)^3 \biggl[1~-~ \frac{1}{2} \cos\chi \biggr] </math> |
|
|
|
<math>~ + \biggl(\frac{a}{c}\biggr)^4\biggl[1 ~+~ \frac{1}{2^4} \cos^2\chi ~-~ \frac{3}{4} \cos\chi \biggr] + \mathcal{O}\biggl( \frac{a^5}{c^5} \biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \cos^2\chi \biggl\{1 ~+~ \biggl(\frac{a}{c}\biggr) ~+~ \biggl(\frac{a}{c}\biggr)^2\biggl[1 ~-~ \frac{1}{4} \cos\chi \biggr] ~+~ \biggl(\frac{a}{c}\biggr)^3 \biggl[1~-~ \frac{1}{2} \cos\chi \biggr] + \biggl(\frac{a}{c}\biggr)^4\biggl[1 ~+~ \frac{1}{2^4} \cos^2\chi ~-~ \frac{3}{4} \cos\chi \biggr] \biggr\} </math> |
|
|
|
<math> ~-~ \biggl( \frac{a}{c}\biggr)\cos\chi \biggl\{1 ~+~ \biggl(\frac{a}{c}\biggr) ~+~ \biggl(\frac{a}{c}\biggr)^2\biggl[1 ~-~ \frac{1}{4} \cos\chi \biggr] ~+~ \biggl(\frac{a}{c}\biggr)^3 \biggl[1~-~ \frac{1}{2} \cos\chi \biggr] \biggr\} </math> |
|
|
|
<math>~+~ \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2 \biggl\{1 ~+~ \biggl(\frac{a}{c}\biggr) ~+~ \biggl(\frac{a}{c}\biggr)^2\biggl[1 ~-~ \frac{1}{4} \cos\chi \biggr] \biggr\} ~+~ \mathcal{O}\biggl( \frac{a^5}{c^5} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \cos^2\chi ~+~ \biggl(\frac{a}{c}\biggr)\biggl[ \cos^2\chi ~-~\cos\chi \biggr] ~+~ \biggl(\frac{a}{c}\biggr)^2\biggl[ \cos^2\chi ~-~ \frac{1}{4} \cos^3\chi ~-~ \cos\chi ~+~\frac{1}{2^2}\biggr] </math> |
|
|
|
<math> ~+~ \biggl(\frac{a}{c}\biggr)^3\biggl\{ \cos^2\chi \biggl[1~-~ \frac{1}{2} \cos\chi \biggr] ~-~ \cos\chi \biggl[1 ~-~ \frac{1}{4} \cos\chi \biggr]~+~\frac{1}{2^2} \biggr\} </math> |
|
|
|
<math> ~+~\biggl(\frac{a}{c}\biggr)^4 \biggl\{ \cos^2\chi \biggl[1 ~+~ \frac{1}{2^4} \cos^2\chi ~-~ \frac{3}{4} \cos\chi \biggr] ~-~ \cos\chi \biggl[1~-~ \frac{1}{2} \cos\chi \biggr]~+~\frac{1}{2^2} \biggl[1 ~-~ \frac{1}{4} \cos\chi \biggr] \biggr\} ~+~ \mathcal{O}\biggl( \frac{a^5}{c^5} \biggr) </math> |
|
|
<math>~=</math> |
<math>~ \cos^2\chi ~+~ \biggl(\frac{a}{c}\biggr)\biggl[ \cos^2\chi ~-~\cos\chi \biggr] ~+~ \biggl(\frac{a}{c}\biggr)^2\biggl[ \frac{1}{2^2} ~-~ \cos\chi~+~ \cos^2\chi ~-~ \frac{1}{4} \cos^3\chi \biggr] </math> |
|
|
|
<math> ~+~ \biggl(\frac{a}{c}\biggr)^3\biggl[ \frac{1}{2^2}~-~ \cos\chi ~+~ \frac{5}{4} \cos^2\chi ~-~ \frac{1}{2} \cos^3\chi \biggr] ~+~\biggl(\frac{a}{c}\biggr)^4 \biggl[ \frac{1}{2^2} ~-~ \frac{17}{2^4} \cos\chi ~+~ \frac{3}{2} \cos^2\chi ~-~ \frac{3}{4} \cos^3\chi ~+~\frac{1}{2^4} \cos^4\chi \biggr] ~+~ \mathcal{O}\biggl( \frac{a^5}{c^5} \biggr) </math> |
Cosine-Cubed Expansion
Again, letting,
<math>~b \equiv \biggl[- \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr] \, ,</math>
via the binomial theorem we have,
|
<math>~\cos^3\psi</math> |
<math>~=</math> |
<math>~\biggl[\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~-~ \cos\chi \biggr]^3 \biggl[1 - \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi\biggr]^{-3 / 2 } </math> |
|
|
<math>~=</math> |
<math>~\biggl[\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~-~ \cos\chi \biggr]^3 \biggl\{ 1 -\frac{3}{2}\biggl[ b \biggr] + \frac{3\cdot 5}{2^3} \biggl[ b \biggr]^2 - \frac{3\cdot 5\cdot 7}{2^4\cdot 3}\biggl[ b \biggr]^3 + \frac{3\cdot 5\cdot 7\cdot 9}{2^7\cdot 3}\biggl[ b \biggr]^4 + \mathcal{O}(b^5) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl[\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~-~ \cos\chi \biggr]^3 \biggl\{ 1 -\frac{3}{2}\biggl[ - \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr] + \frac{3\cdot 5}{2^3} \biggl[ - \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr]^2 </math> |
|
|
|
<math>~ - \frac{5\cdot 7}{2^4}\biggl[ - \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr]^3 + \frac{5\cdot 7\cdot 9}{2^7}\biggl[ - \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr]^4 + \mathcal{O}(b^5) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl[\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~-~ \cos\chi \biggr]^3 \biggl\{ 1 + \frac{3}{2}\biggl(\frac{a}{c}\biggr) - \frac{3}{2^3}\biggl(\frac{a}{c}\biggr)^2 \cos\chi + \frac{3\cdot 5}{2^3} \biggl[ \biggl(\frac{a}{c}\biggr)^2 - \frac{1}{2} \biggl(\frac{a}{c}\biggr)^3 \cos\chi + \frac{1}{2^4} \biggl(\frac{a}{c}\biggr)^4 \cos^2\chi \biggr] </math> |
|
|
|
<math>~ - \frac{5\cdot 7}{2^4}\biggl[ - \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \cos\chi \biggr] \biggl[ \biggl(\frac{a}{c}\biggr)^2 - \frac{1}{2} \biggl(\frac{a}{c}\biggr)^3 \cos\chi + \frac{1}{2^4} \biggl(\frac{a}{c}\biggr)^4 \cos^2\chi \biggr] </math> |
|
|
|
<math>~ + \frac{5\cdot 7\cdot 9}{2^7}\biggl[ \biggl(\frac{a}{c}\biggr)^2 - \frac{1}{2} \biggl(\frac{a}{c}\biggr)^3 \cos\chi + \frac{1}{2^4} \biggl(\frac{a}{c}\biggr)^4 \cos^2\chi \biggr]^2 + \mathcal{O}(b^5) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl[\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~-~ \cos\chi \biggr]^3 \biggl\{ 1 + \frac{3}{2}\biggl(\frac{a}{c}\biggr) - \frac{3}{2^3}\biggl(\frac{a}{c}\biggr)^2 \cos\chi + \frac{3\cdot 5}{2^3} \biggl[ \biggl(\frac{a}{c}\biggr)^2 - \frac{1}{2} \biggl(\frac{a}{c}\biggr)^3 \cos\chi + \frac{1}{2^4} \biggl(\frac{a}{c}\biggr)^4 \cos^2\chi \biggr] </math> |
|
|
|
<math>~ + \frac{5\cdot 7}{2^4} \biggl(\frac{a}{c}\biggr) \biggl[ \biggl(\frac{a}{c}\biggr)^2 - \frac{1}{2} \biggl(\frac{a}{c}\biggr)^3 \cos\chi \biggr] - \frac{5\cdot 7}{2^6}\biggl(\frac{a}{c}\biggr)^4 \cos\chi + \frac{3^2\cdot 5\cdot 7}{2^7}\biggl(\frac{a}{c}\biggr)^4 + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl[ \cos^2\chi ~-~\biggl( \frac{a}{c}\biggr)\cos\chi + \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2 \biggr] \biggl[\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~-~ \cos\chi \biggr] \biggl\{ 1 + \frac{3}{2}\biggl(\frac{a}{c}\biggr) - \frac{3}{2^3}\biggl(\frac{a}{c}\biggr)^2 \cos\chi + \frac{3\cdot 5}{2^3}\biggl(\frac{a}{c}\biggr)^2 </math> |
|
|
|
<math>~ - \frac{3\cdot 5}{2^4}\biggl(\frac{a}{c}\biggr)^3 \cos\chi + \frac{3\cdot 5}{2^7} \biggl(\frac{a}{c}\biggr)^4 \cos^2\chi + \frac{5\cdot 7}{2^4} \biggl(\frac{a}{c}\biggr)^3 - \frac{5\cdot 7}{2^5} \biggl(\frac{a}{c}\biggr)^4 \cos\chi - \frac{5\cdot 7}{2^6}\biggl(\frac{a}{c}\biggr)^4 \cos\chi + \frac{3^2\cdot 5\cdot 7}{2^7}\biggl(\frac{a}{c}\biggr)^4 + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl\{ -\cos^3\chi + \frac{3}{2}\biggl( \frac{a}{c}\biggr) \cos^2\chi - \frac{3}{2^2}\biggl( \frac{a}{c}\biggr)^2\cos\chi + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^3 \biggr\} </math> |
|
|
|
<math>~\times \biggl\{ 1 + \frac{3}{2}\biggl(\frac{a}{c}\biggr) + \frac{3}{2^3} \biggl(\frac{a}{c}\biggr)^2 \biggl[5 - \cos\chi \biggr] + \frac{5}{2^4} \biggl(\frac{a}{c}\biggr)^3 \biggl[ 7 - 3\cos\chi \biggr] + \frac{5}{2^7} \biggl(\frac{a}{c}\biggr)^4 \biggl[ 3\cos^2\chi - 2^2\cdot 7 \cos\chi - 2\cdot 7 \cos\chi + 3^2\cdot 7 \biggr] + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~-\cos^3\chi \biggl\{ 1 + \frac{3}{2}\biggl(\frac{a}{c}\biggr) + \frac{3}{2^3} \biggl(\frac{a}{c}\biggr)^2 \biggl[5 - \cos\chi \biggr] + \frac{5}{2^4} \biggl(\frac{a}{c}\biggr)^3 \biggl[ 7 - 3\cos\chi \biggr] + \frac{5}{2^7} \biggl(\frac{a}{c}\biggr)^4 \biggl[ 3\cos^2\chi - 2^2\cdot 7 \cos\chi - 2\cdot 7 \cos\chi + 3^2\cdot 7 \biggr] \biggr\} </math> |
|
|
|
<math>~+ \frac{3}{2}\biggl( \frac{a}{c}\biggr) \cos^2\chi \biggl\{ 1 + \frac{3}{2}\biggl(\frac{a}{c}\biggr) + \frac{3}{2^3} \biggl(\frac{a}{c}\biggr)^2 \biggl[5 - \cos\chi \biggr] + \frac{5}{2^4} \biggl(\frac{a}{c}\biggr)^3 \biggl[ 7 - 3\cos\chi \biggr] \biggr\} </math> |
|
|
|
<math>~ - \frac{3}{2^2}\biggl( \frac{a}{c}\biggr)^2\cos\chi \biggl\{ 1 + \frac{3}{2}\biggl(\frac{a}{c}\biggr) + \frac{3}{2^3} \biggl(\frac{a}{c}\biggr)^2 \biggl[5 - \cos\chi \biggr] \biggr\} + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^3 \biggl\{ 1 + \frac{3}{2}\biggl(\frac{a}{c}\biggr) \biggr\} + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~-\cos^3\chi \biggl\{ 1 + \frac{3}{2}\biggl(\frac{a}{c}\biggr) + \frac{3}{2^3} \biggl(\frac{a}{c}\biggr)^2 \biggl[5 - \cos\chi \biggr] + \frac{5}{2^4} \biggl(\frac{a}{c}\biggr)^3 \biggl[ 7 - 3\cos\chi \biggr] + \frac{5}{2^7} \biggl(\frac{a}{c}\biggr)^4 \biggl[ 3\cos^2\chi - 2^2\cdot 7 \cos\chi - 2\cdot 7 \cos\chi + 3^2\cdot 7 \biggr] \biggr\} </math> |
|
|
|
<math>~+ \frac{3}{2} \cos^2\chi \biggl\{ \biggl( \frac{a}{c}\biggr) + \frac{3}{2}\biggl(\frac{a}{c}\biggr)^2 + \frac{3}{2^3} \biggl(\frac{a}{c}\biggr)^3 \biggl[5 - \cos\chi \biggr] + \frac{5}{2^4} \biggl(\frac{a}{c}\biggr)^4 \biggl[ 7 - 3\cos\chi \biggr] \biggr\} </math> |
|
|
|
<math>~ - \frac{3}{2^2} \cos\chi \biggl\{ \biggl( \frac{a}{c}\biggr)^2 + \frac{3}{2}\biggl(\frac{a}{c}\biggr)^3 + \frac{3}{2^3} \biggl(\frac{a}{c}\biggr)^4 \biggl[5 - \cos\chi \biggr] \biggr\} + \frac{1}{2^3} \biggl( \frac{a}{c}\biggr)^3 + \frac{3}{2^4}\biggl(\frac{a}{c}\biggr)^4 </math> |
|
|
|
<math>~ + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
Coefficients of Elliptic Integrals
Rewriting the external potential, as provided in the above-stated objective, and evaluating it at the torus surface,
|
<math>~\frac{\pi V_\mathrm{Dyson}}{GM} \biggr|_{\mathcal{O}(a^4/c^4)}</math> |
<math>~=</math> |
<math>~ \frac{4K(\mu)}{a+R_1}\biggl\{ t_K \biggr\} + \frac{(a + R_1)E(\mu)}{aR_1}\biggl\{ t_E \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{4K(\mu)}{c} \biggl(\frac{R_1}{c}\biggr)^{-1} \biggl[1 + \biggl(\frac{a}{c}\biggr) \biggl(\frac{R_1}{c}\biggr)^{-1} \biggr]^{-1}\biggl\{ t_K \biggr\} + \frac{E(\mu) }{a}\biggl[1 + \biggl(\frac{a}{c}\biggr) \biggl(\frac{R_1}{c}\biggr)^{-1} \biggr] \biggl\{ t_E \biggr\} \, , </math> |
where,
|
<math>~t_K</math> |
<math>~\equiv</math> |
<math>~ 1 ~-~ \frac{1}{8}\biggl(\frac{a^2}{c^2}\biggr) \cos^2\biggl( \frac{\psi}{2}\biggr) - \frac{1}{768}\biggl(\frac{a}{c}\biggr)^4 \biggl[ 5 ~+~ 8\cos\psi ~-~ \cos^2\psi ~-~ 4\cos^3\psi ~-~ \frac{4c^2}{RR_1} \cos2\psi \biggr] \, , </math> |
and,
|
<math>~t_E</math> |
<math>~\equiv</math> |
<math>~ \frac{1}{8}\biggl(\frac{a}{c}\biggr)^2 \cos\psi ~-~\frac{1}{192} \biggl(\frac{a}{c}\biggr)^4 \biggl[ 2\cos^2\psi ~-~4\cos\psi ~+~ \frac{2c^2}{RR_1}\cos2\psi \biggr] \, . </math> |
Given our derived power-series expressions for various trigonometric functions, these coefficients can be rewritten as,
|
<math>~t_K</math> |
<math>~=</math> |
<math>~ 1 ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1 + \cos\psi) + \frac{1}{2^6\cdot 3}\biggl(\frac{a}{c}\biggr)^3 \biggl(\frac{R_1}{c}\biggr)^{-1}(2\cos^2\psi - 1) - \frac{1}{2^8\cdot 3}\biggl(\frac{a}{c}\biggr)^4 \biggl[ 5 ~+~ 8\cos\psi ~-~ \cos^2\psi ~-~ 4\cos^3\psi \biggr] </math> |
|
|
<math>~=</math> |
<math>~ 1 ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 \biggl\{ 1 -\cos\chi ~+~ \frac{1}{2} \biggl(\frac{a}{c}\biggr)(1-\cos\chi) ~+~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)^2\biggl[2 - 3\cos\chi + \cos^2\chi \biggr] \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{2^6\cdot 3}\biggl(\frac{a}{c}\biggr)^3 \biggl(\frac{R_1}{c}\biggr)^{-1}\biggl\{ 2 \biggl[ \cos^2\chi ~+~ \biggl(\frac{a}{c}\biggr)\biggl( \cos^2\chi ~-~\cos\chi \biggr) \biggr] - 1 \biggr\} </math> |
|
|
|
<math>~ - \frac{1}{2^8\cdot 3}\biggl(\frac{a}{c}\biggr)^4 \biggl\{ 5 ~-~ 8\cos\chi ~-~ \cos^2\chi ~+~ 4\cos^3\chi \biggr\} + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 1 ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 \biggl[ 1 -\cos\chi \biggr] ~-~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^3 \biggl[ 1-\cos\chi \biggr] ~-~ \frac{1}{2^7}\biggl(\frac{a}{c}\biggr)^4 \biggl[2 - 3\cos\chi + \cos^2\chi \biggr] </math> |
|
|
|
<math>~ + \frac{1}{2^6\cdot 3} \biggl(\frac{R_1}{c}\biggr)^{-1}\biggl\{ \biggl(\frac{a}{c}\biggr)^3\biggl(2 \cos^2\chi - 1 \biggr) ~+~ 2\biggl(\frac{a}{c}\biggr)^4\biggl( \cos^2\chi ~-~\cos\chi \biggr) \biggr\} </math> |
|
|
|
<math>~ - \frac{1}{2^8\cdot 3}\biggl(\frac{a}{c}\biggr)^4 \biggl\{ 5 ~-~ 8\cos\chi ~-~ \cos^2\chi ~+~ 4\cos^3\chi \biggr\} + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 1 ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 \biggl[ 1 -\cos\chi \biggr] + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^3\biggl\{ \biggl(\frac{R_1}{c}\biggr)^{-1} \biggl(2 \cos^2\chi - 1 \biggr) ~-~ 2\cdot 3 \biggl( 1-\cos\chi \biggr) \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl\{ 2^3 \biggl(\frac{R_1}{c}\biggr)^{-1} \biggl( \cos^2\chi ~-~\cos\chi \biggr) - \biggl[ 5 ~-~ 8\cos\chi ~-~ \cos^2\chi ~+~ 4\cos^3\chi \biggr] ~-~ 2\cdot 3\biggl[2 - 3\cos\chi + \cos^2\chi \biggr] \biggr\} + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 1 ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 ( 1 -\cos\chi ) + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^3\biggl[ \biggl(\frac{R_1}{c}\biggr)^{-1} (2 \cos^2\chi - 1 ) -6~+~6\cos\chi \biggr] </math> |
|
|
|
<math>~ + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl[ 2^3 \biggl(\frac{R_1}{c}\biggr)^{-1} ( \cos^2\chi ~-~\cos\chi ) ~-17 + 26\cos\chi -5 \cos^2\chi ~-~ 4\cos^3\chi \biggr] + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, ; </math> |
and,
|
<math>~t_E</math> |
<math>~=</math> |
<math>~ \frac{1}{8}\biggl(\frac{a}{c}\biggr)^2 \cos\psi ~-~\frac{1}{2^5\cdot 3} \biggl(\frac{a}{c}\biggr)^3 \biggl(\frac{R_1}{c}\biggr)^{-1} \biggl\{ 2 \biggl[\cos^2\psi\biggr] - 1\biggr\} ~-~\frac{1}{2^5\cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl[ \cos^2\psi ~-~2\cos\psi \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{8}\biggl(\frac{a}{c}\biggr)^2 \biggl\{ -\cos\chi ~+~ \frac{1}{2} \biggl(\frac{a}{c}\biggr)(1-\cos\chi) ~+~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)^2\biggl[2 - 3\cos\chi + \cos^2\chi \biggr] \biggr\} </math> |
|
|
|
<math>~ ~-~\frac{1}{2^5\cdot 3} \biggl(\frac{a}{c}\biggr)^3 \biggl(\frac{R_1}{c}\biggr)^{-1} \biggl\{ 2 \biggl[\cos^2\chi ~+~ \biggl(\frac{a}{c}\biggr)\biggl( \cos^2\chi ~-~\cos\chi \biggr)\biggr] - 1\biggr\} ~-~\frac{1}{2^5\cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl[\cos^2\chi ~+~2\cos\chi \biggr] + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ -\frac{1}{2^3} \biggl(\frac{a}{c}\biggr)^2\cos\chi ~+~ \frac{1}{2^4} \biggl(\frac{a}{c}\biggr)^3(1-\cos\chi) ~+~ \frac{1}{2^6} \biggl(\frac{a}{c}\biggr)^4\biggl[2 - 3\cos\chi + \cos^2\chi \biggr] </math> |
|
|
|
<math>~ ~-~\frac{1}{2^5\cdot 3} \biggl(\frac{a}{c}\biggr)^3 \biggl(\frac{R_1}{c}\biggr)^{-1} \biggl[ 2\cos^2\chi ~+~ 2\biggl(\frac{a}{c}\biggr)\biggl( \cos^2\chi ~-~\cos\chi \biggr) - 1\biggr] ~-~\frac{1}{2^5\cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl( \cos^2\chi ~+~2\cos\chi \biggr) + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ -\frac{1}{2^3} \biggl(\frac{a}{c}\biggr)^2\cos\chi ~+~ \frac{1}{2^4} \biggl(\frac{a}{c}\biggr)^3(1-\cos\chi) ~-~\frac{1}{2^5\cdot 3} \biggl(\frac{a}{c}\biggr)^3 \biggl(\frac{R_1}{c}\biggr)^{-1} \biggl( 2\cos^2\chi - 1\biggr) </math> |
|
|
|
<math>~ ~-~\frac{1}{2^4\cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl(\frac{R_1}{c}\biggr)^{-1} \biggl( \cos^2\chi ~-~\cos\chi \biggr) ~+~ \frac{1}{2^6 \cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl[ 6 - 13\cos\chi + \cos^2\chi \biggr] + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ -\frac{1}{2^3} \biggl(\frac{a}{c}\biggr)^2\cos\chi ~+~ \frac{1}{2^5\cdot 3} \biggl(\frac{a}{c}\biggr)^3 \biggl[ 6(1-\cos\chi) ~-~\biggl(\frac{R_1}{c}\biggr)^{-1} ( 2\cos^2\chi - 1 ) \biggr] </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^6 \cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl[ ( 6 - 13\cos\chi + \cos^2\chi ) ~-~4 \biggl(\frac{R_1}{c}\biggr)^{-1} ( \cos^2\chi ~-~\cos\chi ) \biggr] + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, . </math> |
Now, inserting to the appropriate order the above expression for the ratio, <math>~R_1/c</math> — namely,
|
<math>~\biggl(\frac{R_1}{c}\biggr)^{-1}</math> |
<math>~=</math> |
<math>~ \frac{1}{2} + \frac{1}{2^2} \biggl(\frac{a}{c}\biggr)\cos\chi + \mathcal{O}\biggl(\frac{a^2}{c^2}\biggr) \, , </math> |
we have,
|
<math>~t_K</math> |
<math>~=</math> |
<math>~ 1 ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 ( 1 -\cos\chi ) + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^3 \biggl\{ \biggl[ \frac{1}{2} + \frac{1}{2^2} \biggl(\frac{a}{c}\biggr)\cos\chi \biggr] (2 \cos^2\chi - 1 ) -6~+~6\cos\chi \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl\{ 2^2 ( \cos^2\chi ~-~\cos\chi ) ~-17 + 26\cos\chi -5 \cos^2\chi ~-~ 4\cos^3\chi \biggr\} + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 1 ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 ( 1 -\cos\chi ) + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( -13~+~12\cos\chi +2 \cos^2\chi ) + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 (2 \cos^3\chi - \cos\chi ) </math> |
|
|
|
<math>~ + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 (-17 + 22\cos\chi - \cos^2\chi ~-~ 4\cos^3\chi ) + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 1 ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 ( 1 -\cos\chi ) + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( -13~+~12\cos\chi +2 \cos^2\chi ) </math> |
|
|
|
<math>~ + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 (-17 + 21\cos\chi - \cos^2\chi ~-~ 2\cos^3\chi ) + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, ; </math> |
and,
|
<math>~t_E</math> |
<math>~=</math> |
<math>~ -\frac{1}{2^3} \biggl(\frac{a}{c}\biggr)^2\cos\chi ~+~ \frac{1}{2^5\cdot 3} \biggl(\frac{a}{c}\biggr)^3 \biggl\{ 6(1-\cos\chi) ~+~\biggl[ \frac{1}{2} + \frac{1}{2^2} \biggl(\frac{a}{c}\biggr)\cos\chi \biggr] (1- 2\cos^2\chi ) \biggr\} </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^6 \cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl\{ ( 6 - 13\cos\chi + \cos^2\chi ) ~+~2 ( \cos\chi - \cos^2\chi) \biggr\} + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ -\frac{1}{2^3} \biggl(\frac{a}{c}\biggr)^2\cos\chi ~+~ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 13- 12\cos\chi - 2\cos^2\chi ) ~+~ \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^4 (\cos\chi - 2\cos^3\chi ) </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^6 \cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 6 - 11\cos\chi - \cos^2\chi ) + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ -\frac{1}{2^3} \biggl(\frac{a}{c}\biggr)^2\cos\chi ~+~ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 13- 12\cos\chi - 2\cos^2\chi ) </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 12 -21 \cos\chi - 2\cos^2\chi - 2\cos^3\chi ) + \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, . </math> |
Alternate "Small" Argument of Elliptic Integrals
Defining the "small parameter,"
|
<math>~k'</math> |
<math>~\equiv</math> |
<math>~ \sqrt{1-\mu^2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[1 - \biggl( \frac{e^\eta - 1}{e^\eta + 1}\biggr)^2 \biggr]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{(e^\eta + 1)^2 - (e^\eta - 1)^2 }{(e^\eta + 1)^2} \biggr]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{(e^{2\eta} + 2e^\eta+ 1)- (e^{2\eta} - 2e^\eta + 1) }{(e^\eta + 1)^2} \biggr]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{4e^\eta }{(e^\eta + 1)^2} \biggr]^{1 / 2} = \biggl[\frac{4e^{-\eta} }{(1 + e^{-\eta})^2} \biggr]^{1 / 2} </math> |
|
|
<math>~=</math> |
<math>~2\biggl( \frac{R}{R_1}\biggr)^{1 / 2} \biggl[1 + \frac{R}{R_1} \biggr]^{-1} \, . </math> |
At the surface of the torus, where <math>~R=a</math>, we therefore have,
|
<math>~k'</math> |
<math>~=</math> |
<math>~ 2\biggl( \frac{a}{c}\biggr)^{1 / 2}\biggl( \frac{R_1}{c}\biggr)^{-1 / 2} \biggl[1 + \frac{a}{c}\cdot \frac{c}{R_1} \biggr]^{-1} </math> |
|
<math>~\Rightarrow ~~~ \frac{4}{k'}</math> |
<math>~=</math> |
<math>~2\biggl( \frac{a}{c}\biggr)^{- 1 / 2}\biggl( \frac{R_1}{c}\biggr)^{1 / 2} \biggl[1 + \frac{a}{c}\cdot \frac{c}{R_1} \biggr] </math> |
|
|
<math>~=</math> |
<math>~2\biggl( \frac{c}{a}\biggr)^{1 / 2} \biggl[ 4 + \biggl( \frac{a}{c}\biggr)^2 - 4\biggl(\frac{a}{c}\biggr)\cos\chi \biggr]^{1 / 4} \biggl\{ 1 + \frac{a}{c}\cdot \biggl[ 4 + \biggl( \frac{a}{c}\biggr)^2 - 4\biggl(\frac{a}{c}\biggr)\cos\chi \biggr]^{-1 / 2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\biggl( \frac{2^3c}{a}\biggr)^{1 / 2} \biggl[ 1 - \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2 \biggr]^{1 / 4} \biggl\{ 1 + \frac{a}{2c}\cdot \biggl[ 1 - \biggl(\frac{a}{c}\biggr)\cos\chi + \biggl( \frac{a}{2c}\biggr)^2 \biggr]^{-1 / 2} \biggr\} </math> |
|
<math>~\Rightarrow ~~~ \ln \frac{4}{k'}</math> |
<math>~=</math> |
<math>~\frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{4}\ln\biggl[ 1 - \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{4}\biggl( \frac{a}{c}\biggr)^2 \biggr] + \ln\biggl\{ 1 + \frac{a}{2c}\cdot \biggl[ 1 - \biggl(\frac{a}{c}\biggr)\cos\chi + \biggl( \frac{a}{2c}\biggr)^2 \biggr]^{-1 / 2} \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ \frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{4}\ln\biggl[ 1 - \biggl(\frac{a}{c}\biggr)\cos\chi \biggr] + \ln\biggl[ 1 + \frac{a}{2c} \biggr] </math> |
|
|
<math>~\approx</math> |
<math>~ \frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{a}{2c}\biggl[ 1 - \frac{1}{2} \cos\chi \biggr] </math> |
Alternatively, if — as above — we adopt the shorthand notation, <math>~\gamma \equiv R_1/(2c)</math>, we can write,
|
Summary
|
|
<math>~k'</math> |
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr)^{1 / 2} \gamma^{-1 / 2} \biggl[1 + \biggl(\frac{a}{c}\biggr) \frac{1}{2\gamma} \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr)^{1 / 2} \gamma^{-1 / 2} \biggl[1 + \biggl(\frac{a}{c}\biggr) \frac{1}{\gamma} + \biggl(\frac{a}{c}\biggr)^2 \frac{1}{4\gamma^2} \biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr)^{1 / 2} \biggl[\gamma + \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \frac{1}{\gamma} \biggr]^{-1 / 2} </math> |
|
<math>~\Rightarrow ~~~(k')^{2m}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr)^{m } \biggl[\gamma + \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \frac{1}{\gamma} \biggr]^{-m } = \biggl( \frac{2a}{c}\biggr)^{m } \Gamma^{-m} </math> |
|
<math>~\Rightarrow ~~~ \frac{4}{k'}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{2^3c}{a}\biggr)^{1 / 2} \biggl[\gamma + \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \frac{1}{\gamma} \biggr]^{1 / 2} = \biggl( \frac{2^3c}{a}\biggr)^{1 / 2} \Gamma^{1 / 2} </math> |
|
<math>~\Rightarrow ~~~\ln \frac{4}{k'}</math> |
<math>~=</math> |
<math>~ \frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\ln \Gamma \, , </math> |
where,
|
<math>~\Gamma</math> |
<math>~\equiv</math> |
<math>~ \gamma + \biggl(\frac{a}{c}\biggr) + \frac{1}{4}\biggl(\frac{a}{c}\biggr)^2 \frac{1}{\gamma} </math> |
|
|
<math>~=</math> |
<math>~ 1 ~-~ \frac{1}{2} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (1-\cos^2\chi) +~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3 (\cos\chi - \cos^3\chi) +~\frac{1}{2^7}\biggl( \frac{a}{c}\biggr)^4 \biggl[~-~ 1 ~+~ 6 \cos^2\chi ~-~ 5 \cos^4\chi \biggr] ~+~ \biggl(\frac{a}{c}\biggr) </math> |
|
|
|
<math>~ +~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2 \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 \biggl[ 3\cos^2\chi - 1 \biggr] + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3\biggl[ 5\cos^3\chi ~-~ 3\cos\chi \biggr] ~+~ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 \biggl[ 3 ~-~ 30 \cos^2\chi ~+~ 35 \cos^4\chi \biggr] \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 1 + \biggl(\frac{a}{c}\biggr)(1~-~ \frac{1}{2} \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (1-\cos^2\chi) +~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3 (\cos\chi - \cos^3\chi) +~\frac{1}{2^7}\biggl( \frac{a}{c}\biggr)^4 (-~ 1 ~+~ 6 \cos^2\chi ~-~ 5 \cos^4\chi ) </math> |
|
|
|
<math>~ +~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2 + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^3\cos\chi + \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^4 ( 3\cos^2\chi - 1 ) ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 1 + \biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) +~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3 (3\cos\chi - \cos^3\chi) +~\frac{1}{2^7}\biggl( \frac{a}{c}\biggr)^4 (- 5 ~+~ 18 \cos^2\chi ~-~ 5 \cos^4\chi ) ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, . </math> |
Now, if we adopt the shorthand notation,
<math>~g \equiv \biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) +~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3 (3\cos\chi - \cos^3\chi) +~\frac{1}{2^7}\biggl( \frac{a}{c}\biggr)^4 (- 5 ~+~ 18 \cos^2\chi ~-~ 5 \cos^4\chi ) ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, , </math>
we also have,
|
<math>~\ln\Gamma = \ln (1 + g)</math> |
<math>~=</math> |
<math>~ g - \frac{1}{2}g^2 + \frac{1}{3}g^3 - \frac{1}{4}g^4 ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) +~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3 (3\cos\chi - \cos^3\chi) +~\frac{1}{2^7}\biggl( \frac{a}{c}\biggr)^4 (- 5 ~+~ 18 \cos^2\chi ~-~ 5 \cos^4\chi ) </math> |
|
|
|
<math>~ - \frac{1}{2}\biggl[ \biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) +~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3 (3\cos\chi - \cos^3\chi) \biggr]^2 </math> |
|
|
|
<math>~ + \frac{1}{3}\biggl[ \biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) \biggr]^3 - \frac{1}{4}\biggl[ \biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) \biggr]^4 ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) +~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3 (3\cos\chi - \cos^3\chi) +~\frac{1}{2^7}\biggl( \frac{a}{c}\biggr)^4 (- 5 ~+~ 18 \cos^2\chi ~-~ 5 \cos^4\chi ) </math> |
|
|
|
<math>~ - \frac{1}{2} \biggl\{ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2 (2~-~ \cos\chi )^2 + \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3 (3-\cos^2\chi) (2~-~ \cos\chi ) +~ \frac{1}{2^5}\biggl( \frac{a}{c}\biggr)^4 (3\cos\chi - \cos^3\chi)(2~-~ \cos\chi ) </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^3 (3-\cos^2\chi) (1~-~ \frac{1}{2} \cos\chi ) ~+~ \frac{1}{2^6}\biggl( \frac{a}{c}\biggr)^4 (3-\cos^2\chi) (3-\cos^2\chi) ~+~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^4 (3\cos\chi - \cos^3\chi)(1~-~ \frac{1}{2} \cos\chi ) \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{3}\biggl[ \biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) \biggr] \biggl[ \biggl(\frac{a}{c}\biggr)^2 (1~-~ \frac{1}{2} \cos\chi )^2 ~+~ \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^3 (1~-~ \frac{1}{2} \cos\chi ) (3-\cos^2\chi) \biggr] - \frac{1}{2^6} \biggl(\frac{a}{c}\biggr)^4(2~-~ \cos\chi )^4 ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) ~-~\frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 (2~-~ \cos\chi )^2 </math> |
|
|
|
<math>~ +~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3 (3\cos\chi - \cos^3\chi) ~-~ \frac{1}{2^5}\biggl( \frac{a}{c}\biggr)^3 (3-\cos^2\chi) (2~-~ \cos\chi ) ~-~ \frac{1}{2^5}\biggl( \frac{a}{c}\biggr)^3 (3-\cos^2\chi) (2~-~ \cos\chi ) ~+~\frac{1}{2^3\cdot 3}\biggl(\frac{a}{c}\biggr)^3 (2~-~ \cos\chi )^2 (2~-~\cos\chi ) </math> |
|
|
|
<math>~ ~-~ \frac{1}{2^6}\biggl( \frac{a}{c}\biggr)^4 (3\cos\chi - \cos^3\chi)(2~-~ \cos\chi ) ~-~ \frac{1}{2^7}\biggl( \frac{a}{c}\biggr)^4 (3-\cos^2\chi) (3-\cos^2\chi) ~-~ \frac{1}{2^6}\biggl( \frac{a}{c}\biggr)^4 (3\cos\chi - \cos^3\chi)(2~-~ \cos\chi ) </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^4\cdot 3}\biggl( \frac{a}{c}\biggr)^4 (2~-~ \cos\chi ) (3-\cos^2\chi)(2~-~ \cos\chi ) +\frac{1}{2^5\cdot 3}\biggl( \frac{a}{c}\biggr)^4 (3-\cos^2\chi) (2~-~ \cos\chi )^2 +~\frac{1}{2^7}\biggl( \frac{a}{c}\biggr)^4 (- 5 ~+~ 18 \cos^2\chi ~-~ 5 \cos^4\chi ) - \frac{1}{2^6} \biggl(\frac{a}{c}\biggr)^4(2~-~ \cos\chi )^4 ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
And,
|
<math>~~(k')^{2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr) \Gamma^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr) (1+g)^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr) \biggl\{1 ~-~ g ~+~ g^2 ~-~ g^3 \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr) \biggl\{1 ~-~ \biggl[ \biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) +~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3 (3\cos\chi - \cos^3\chi) \biggr] </math> |
|
|
|
<math>~ ~+~ \biggl[\biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) \biggr]^2 ~-~ \biggl[ \biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) \biggr]^3 \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr) \biggl\{1 ~-~ \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2\biggl[ (3-\cos^2\chi) ~+~2(2~-~ \cos\chi )^2 \biggr] </math> |
|
|
|
<math>~ +~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3\biggl[ (3\cos\chi - \cos^3\chi) ~+~ (2~-~ \cos\chi )(3-\cos^2\chi) ~-~ (2~-~ \cos\chi )^3 \biggr] \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
And,
|
<math>~~(k')^{4}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr)^2 \Gamma^{-2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr)^2 (1+g)^{-2} </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr)^2 \biggl\{1 ~-~ 2g ~+~ 3g^2 \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr)^2 \biggl\{1 ~-~ 2\biggl[ \biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) \biggr] ~+~ 3\biggl[ \biggl(\frac{a}{c}\biggr) (1~-~ \frac{1}{2} \cos\chi ) \biggr]^2 \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr)^2 \biggl\{1 -~\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) ~+~ \frac{1}{2^2} \biggl(\frac{a}{c}\biggr)^2\biggl[ 3(2~-~ \cos\chi )^2 ~-~ (3-\cos^2\chi) \biggr] \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 4\biggl( \frac{a}{c}\biggr)^2 -~\biggl(\frac{a}{c}\biggr)^3 (8~-~ 4\cos\chi ) ~+~ \biggl(\frac{a}{c}\biggr)^4 ( 9 - 12\cos\chi + 4\cos^2\chi ) ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
Elliptic Integral Expressions
Hence, drawing from our set of Key Expressions for the complete elliptic integral of the first kind, specifically,
|
<math>~K(\mu)</math> |
<math>~=</math> |
<math>~ \ln \frac{4}{k^'} + \frac{1}{2^2}\biggl( \ln\frac{4}{k^'} - \frac{2}{1\cdot 2} \biggr)(k')^2 + \biggl( \frac{1\cdot 3}{2\cdot 4}\biggr)^2 \biggl( \ln\frac{4}{k^'} - \frac{2}{1\cdot 2} - \frac{2}{3\cdot 4} \biggr)(k')^4 + \biggl( \frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\biggr)^2 \biggl( \ln\frac{4}{k^'} - \frac{2}{1\cdot 2} - \frac{2}{3\cdot 4} - \frac{2}{5\cdot 6} \biggr)(k')^6 ~+~ \cdots </math> |
|
|
Gradshteyn & Ryzhik (1965), §8.113.3 |
|||
|
where: <math>~k^' \equiv (1 - \mu^2)^{1 / 2}</math> |
|||
we can write,
|
<math>~K(\mu)</math> |
<math>~=</math> |
<math>~ \ln \frac{4}{k^'} + \frac{1}{2^2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 + \frac{3^2}{2^6} \biggl( \ln\frac{4}{k^'} - \frac{7}{6} \biggr){k'}^4 + \frac{5^2}{2^8} \biggl( \ln\frac{4}{k^'} - \frac{37}{30} \biggr){k'}^6 + \cdots </math> |
Now, we recognize that,
|
<math>~\biggl(\frac{a}{2}\biggr) \frac{4K(\mu)}{R_1+a}</math> |
<math>~=</math> |
<math>~ \biggl(\frac{a}{2c}\biggr) 4K(\mu) \biggl[\frac{R_1}{c} + \frac{a}{c} \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl(\frac{a}{c}\biggr) 2K(\mu) \biggl(\frac{R_1}{c}\biggr)^{-1}\biggl[1 + \frac{a}{c} \biggl(\frac{R_1}{c}\biggr)^{-1}\biggr]^{-1} </math> |
|
|
<math>~\approx</math> |
<math>~ \biggl(\frac{a}{c}\biggr) \biggl(\frac{R_1}{c}\biggr)^{-1}\biggl[1 + \frac{a}{c} \biggl(\frac{R_1}{c}\biggr)^{-1}\biggr]^{-1}\biggl\{ 2\ln \frac{4}{k^'} + \frac{1}{2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 \biggr\} \, . </math> |
Also, drawing from our set of Key Expressions for the complete elliptic integral of the second kind, specifically,
|
<math>~E(\mu)</math> |
<math>~=</math> |
<math>~ 1 ~+~ \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{1\cdot 2}\biggr)(k')^2 ~+~ \frac{1^2\cdot 3}{2^2\cdot 4}\biggl( \ln \frac{4}{k'} - \frac{2}{1\cdot 2} - \frac{1}{3\cdot 4}\biggr)(k')^4 ~+~ \frac{1^2\cdot 3^2\cdot 5}{2^2\cdot 4^2\cdot 6}\biggl( \ln \frac{4}{k'} - \frac{2}{1\cdot 2} - \frac{2}{3\cdot 4} - \frac{1}{5\cdot 6}\biggr)(k')^6 ~+~ \cdots </math> |
|
|
Gradshteyn & Ryzhik (1965), §8.114.3 |
|||
|
where: <math>~k^' \equiv (1 - \mu^2)^{1 / 2}</math> |
|||
we have,
|
<math>~E(\mu)</math> |
<math>~=</math> |
<math>~ 1 ~+~ \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 ~+~ \frac{3}{2^4}\biggl( \ln \frac{4}{k'} - 1 - \frac{1}{3\cdot 4}\biggr)(k')^4 ~+~ \frac{3^2\cdot 5}{2^7\cdot 3}\biggl( \ln \frac{4}{k'} - 1 - \frac{1}{2\cdot 3} - \frac{1}{2\cdot 3\cdot 5}\biggr)(k')^6 ~+~ \cdots </math> |
|
<math>~\Rightarrow ~~~ \biggl(\frac{a}{2}\biggr) \frac{(R_1+R)E(\mu)}{RR_1}</math> |
<math>~\approx</math> |
<math>~ \frac{1}{2} \biggl[ 1 + \frac{a}{c}\biggl( \frac{R_1}{c}\biggr)^{-1} \biggr] \biggl\{ 1 + \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 \biggr\} \, . </math> |
External Potential at Torus Surface
Initial Low Resolution
Hence,
|
<math>~\biggl(\frac{a}{2}\biggr)V_2 </math> |
<math>~\approx</math> |
<math>~ \biggl[1 - \frac{1}{8}\biggl(\frac{a^2}{c^2}\biggr) \cos^2\biggl( \frac{\psi}{2}\biggr)\biggr] \biggl(\frac{a}{c}\biggr) \biggl(\frac{R_1}{c}\biggr)^{-1}\biggl[1 + \frac{a}{c} \biggl(\frac{R_1}{c}\biggr)^{-1}\biggr]^{-1}\biggl\{ 2\ln \frac{4}{k^'} + \frac{1}{2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 \biggr\} </math> |
|
|
|
<math>~ + \biggl[\frac{1}{8}\biggl(\frac{a^2}{c^2}\biggr) \cos\psi \biggr] \frac{1}{2} \biggl[ 1 + \frac{a}{c}\biggl( \frac{R_1}{c}\biggr)^{-1} \biggr] \biggl\{ 1 + \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 \biggr\} </math> |
|
<math>~\Rightarrow ~~~ cV_2 </math> |
<math>~\approx</math> |
<math>~ \biggl[1 - \cancelto{0}{\frac{1}{8}\biggl(\frac{a^2}{c^2}\biggr) \cos^2\biggl( \frac{\psi}{2}\biggr)}\biggr] \biggl(\frac{R_1}{c}\biggr)^{-1}\biggl[1 + \frac{a}{c} \biggl(\frac{R_1}{c}\biggr)^{-1}\biggr]^{-1}\biggl\{ 4\ln \frac{4}{k^'} + \biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 \biggr\} </math> |
|
|
|
<math>~ + \biggl[\frac{1}{8}\biggl(\frac{a}{c}\biggr) \cos\psi \biggr] \biggl[ 1 + \frac{a}{c}\biggl( \frac{R_1}{c}\biggr)^{-1} \biggr] \biggl\{ 1 + \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 \biggr\} \, . </math> |
Hence,
|
<math>~\Rightarrow ~~~ cV_2 </math> |
<math>~\approx</math> |
<math>~ \biggl(\frac{R_1}{c}\biggr)^{-1}\biggl[1 + \frac{a}{c} \biggl(\frac{R_1}{c}\biggr)^{-1}\biggr]^{-1}\biggl\{ 4\ln \frac{4}{k^'} + \biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 \biggr\} </math> |
|
|
|
<math>~ + \biggl[\frac{1}{8}\biggl(\frac{a}{c}\biggr) \cos\psi \biggr] \biggl[ 1 + \frac{a}{c}\biggl( \frac{R_1}{c}\biggr)^{-1} \biggr] \biggl\{ 1 + \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ \biggl\{ 1 + \frac{1}{2} \biggl(\frac{a}{c}\biggr)\cos\chi +\biggl( \frac{a}{c}\biggr)^2 \biggl[ \frac{3}{8}\cos^2\chi -\frac{1}{8}\biggr] \biggr\} \biggl[1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) + \frac{1}{4} \biggl( \frac{a}{c}\biggr)^2 (1 - \cos\chi)\biggr] \biggl\{ 2\ln \frac{4}{k^'} + \frac{1}{2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 \biggr\} </math> |
|
|
|
<math>~ + \frac{1}{8}\biggl(\frac{a}{c}\biggr) \cos\psi \biggl[ 1 + \frac{1}{2}\biggl( \frac{a}{c}\biggr) + \frac{1}{4} \biggl(\frac{a}{c}\biggr)^2\cos\chi \biggr] \biggl\{ 1 + \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 \biggr\} \, . </math> |
To order <math>~(a/c)^1</math>, this gives,
|
<math>~\Rightarrow ~~~ cV_2 </math> |
<math>~\approx</math> |
<math>~ 2\ln \frac{4}{k^'} + \frac{1}{2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 + \biggl(\frac{a}{c}\biggr)(\cos\chi -1) \ln \frac{4}{k^'} + \frac{1}{8}\biggl(\frac{a}{c}\biggr) \cos\psi </math> |
|
|
<math>~\approx</math> |
<math>~ 2\ln \frac{4}{k^'} + \biggl(\frac{a}{c}\biggr) \biggl\{ - 1 + \cos\chi \ln \frac{4}{k^'} + \frac{1}{8} \cos\psi \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ 2\ln \frac{4}{k^'} + \biggl(\frac{a}{c}\biggr) \biggl\{ - 1 + \cos\chi \biggl[ \ln \frac{4}{k^'} - \frac{1}{8} \biggr] \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{a}{c}\biggl[ 1- \frac{1}{2} \cos\chi \biggr] + \biggl(\frac{a}{c}\biggr) \biggl\{ \frac{1}{2} \cos\chi \biggl[\ln\biggl( \frac{2^3c}{a}\biggr) - \frac{1}{4} \biggr] -1 \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{a}{c} \biggl\{ 1- \frac{1}{2} \cos\chi + \frac{1}{2} \cos\chi \biggl[\ln\biggl( \frac{2^3c}{a}\biggr) - \frac{1}{4} \biggr] -1 \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr) \biggl[\ln\biggl( \frac{2^3c}{a}\biggr) - \frac{5}{4} \biggr] \cos\chi \, . </math> |
We are trying to match equation (6) in Dyson's (1893b) "Part II", that is,
|
<math>~\frac{V}{2\pi a^2}</math> |
<math>~=</math> |
<math>~ \ln\biggl(\frac{8c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr) \biggl[\ln\biggl(\frac{8c}{a}\biggr) - \frac{5}{4}\biggr] \cos\chi + \biggl\{ \frac{1}{16} \biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{5}{2} \biggr] + \frac{3}{16} \biggl[\ln\biggl(\frac{8c}{a}\biggr) +\frac{17}{36} - \frac{72}{36}\biggr]\cos2\chi\biggr\}\biggl(\frac{a^2}{c^2}\biggr) </math> |
|
|
|
<math>~ + \biggl\{ \frac{3}{32}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{25}{12}\biggr]\cos\chi + \frac{5}{64}\biggl[ \ln\biggl(\frac{8c}{a}\biggr)+\frac{7}{24} - \frac{48}{24}\biggr]\cos3\chi \biggr\} \biggl(\frac{a^3}{c^3}\biggr) </math> |
|
|
|
<math>~ + \biggl\{ \frac{9}{256}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - 2\biggr] + \frac{7}{128}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{19}{168} - 2\biggr]\cos2\chi + \frac{35}{1024} \biggl[ \ln\biggl(\frac{8c}{a}\biggr) - 2 + \frac{19}{120}\biggr]\cos4\chi \biggr\} \biggl(\frac{a^4}{c^4}\biggr) ~+~\cdots </math> |
High Resolution
|
Summary
|
|
<math>~\frac{\pi V_\mathrm{Dyson}}{GM/c} </math> |
<math>~=</math> |
<math>~ 2K(\mu) \biggl[~2\biggl(\frac{R_1}{c}\biggr)^{-1}\biggr] \biggl[1 + \biggl(\frac{a}{c}\biggr) \biggl(\frac{R_1}{c}\biggr)^{-1} \biggr]^{-1}\biggl\{ t_K \biggr\} + E(\mu) \biggl[1 + \biggl(\frac{a}{c}\biggr) \biggl(\frac{R_1}{c}\biggr)^{-1} \biggr] \biggl\{\biggl(\frac{c}{a}\biggr) t_E \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 2K(\mu) \biggl\{ ~2\biggl(\frac{R_1}{c}\biggr)^{-1}\biggr\} </math> |
|
|
|
<math>~ \times \biggl\{ \biggl[1 + \biggl(\frac{a}{c}\biggr) \biggl(\frac{R_1}{c}\biggr)^{-1} \biggr]^{-1} \biggr\} </math> |
|
|
|
<math>~ \times \biggl\{ t_K \biggr\} </math> |
|
|
|
<math>~ + E(\mu) \biggl\{ 1 + \biggl(\frac{a}{c}\biggr) \biggl(\frac{R_1}{c}\biggr)^{-1} \biggr\} </math> |
|
|
|
<math>~ \times \biggl\{\biggl(\frac{c}{a}\biggr) t_E \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ 2K(\mu) \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 \biggl[ 3\cos^2\chi - 1 \biggr] + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3\biggl[ 5\cos^3\chi ~-~ 3\cos\chi \biggr] ~+~ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 \biggl[ 3 ~-~ 30 \cos^2\chi ~+~ 35 \cos^4\chi \biggr] \biggr\} </math> |
|
|
|
<math>~ \times \biggl\{ 1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) ~+~ \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^3 ( 2\cos\chi ~-~ 3\cos^2\chi ) ~+~ \frac{1}{2^5} \biggl(\frac{a}{c}\biggr)^4 ( -~9 \cos\chi ~+~8\cos^2\chi ~-~ 5\cos^3\chi ) \biggr\} </math> |
|
|
|
<math>~ \times \biggl\{ 1 ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 ( 1 -\cos\chi ) + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( -13~+~12\cos\chi +2 \cos^2\chi ) + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 (-17 + 21\cos\chi - \cos^2\chi ~-~ 2\cos^3\chi ) \biggr\} </math> |
|
|
|
<math>~ + E(\mu) \biggl\{ 1 ~+~\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi ~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 \biggl[ 3\cos^2\chi - 1 \biggr] ~+~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^4\biggl[ 5\cos^3\chi ~-~ 3\cos\chi \biggr] \biggr\} </math> |
|
|
|
<math>~ \times \biggl\{-\frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi ~+~ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 12\cos\chi - 2\cos^2\chi ) ~+~ \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 12 -21 \cos\chi - 2\cos^2\chi - 2\cos^3\chi ) + f_{E5}\biggl(\frac{a}{c}\biggr)^4 \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 2K(\mu) \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 \biggl[ 3\cos^2\chi - 1 \biggr] + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3\biggl[ 5\cos^3\chi ~-~ 3\cos\chi \biggr] ~+~ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 \biggl[ 3 ~-~ 30 \cos^2\chi ~+~ 35 \cos^4\chi \biggr] \biggr\} </math> |
|
|
|
<math>~ \times \biggl\{ 1 ~-~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 ( 1 -\cos\chi ) + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( -13~+~12\cos\chi +2 \cos^2\chi ) + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 (-17 + 21\cos\chi - \cos^2\chi ~-~ 2\cos^3\chi ) </math> |
|
|
|
<math>~ - \frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^3 ( 1 -\cos\chi ) - \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4( -13~+~12\cos\chi +2 \cos^2\chi ) +\frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) - \frac{1}{2^6}\biggl(\frac{a}{c}\biggr)^4(1-\cos\chi )^2 </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^3 ( 2\cos\chi ~-~ 3\cos^2\chi ) ~+~ \frac{1}{2^5} \biggl(\frac{a}{c}\biggr)^4 (-~9 \cos\chi ~+~8\cos^2\chi ~-~ 5\cos^3\chi ) \biggr\} </math> |
|
|
|
<math>~ + E(\mu) \biggl\{ -\frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi \biggl[ 1 ~+~\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi ~+~ \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 ( 3\cos^2\chi - 1 ) \biggr] </math> |
|
|
|
<math>~ + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 12\cos\chi - 2\cos^2\chi ) \biggl[ 1 ~+~\frac{1}{2}\biggl( \frac{a}{c}\biggr) ~+~ \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2\cos\chi \biggr] </math> |
|
|
|
<math>~ + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 12 -21 \cos\chi - 2\cos^2\chi - 2\cos^3\chi ) \biggl[ 1 ~+~\frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggr] + f_{E5}\biggl(\frac{a}{c}\biggr)^4 \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 2K(\mu) \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 \biggl[ 3\cos^2\chi - 1 \biggr] + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3\biggl[ 5\cos^3\chi ~-~ 3\cos\chi \biggr] ~+~ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 \biggl[ 3 ~-~ 30 \cos^2\chi ~+~ 35 \cos^4\chi \biggr] \biggr\} </math> |
|
|
|
<math>~ \times \biggl\{ 1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) +\frac{3}{2^4}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 \biggl[ ( -13~+~12\cos\chi +2 \cos^2\chi ) ~+~ 12 ( 1 -\cos\chi ) ~+~ 48 ( 2\cos\chi ~-~ 3\cos^2\chi ) \biggr] </math> |
|
|
|
<math>~ + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl[ (-17 + 21\cos\chi - \cos^2\chi ~-~ 2\cos^3\chi ) - ( -13~+~12\cos\chi +2 \cos^2\chi ) - 12 (1-\cos\chi )^2 ~+~ 24 (-~9 \cos\chi ~+~8\cos^2\chi ~-~ 5\cos^3\chi ) \biggr] \biggr\} </math> |
|
|
|
<math>~ + E(\mu) \biggl\{ ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi ~ -\frac{1}{2^4} \biggl(\frac{a}{c}\biggr)^2 \cos\chi ~ -\frac{1}{2^5} \biggl(\frac{a}{c}\biggr)^3 \cos^2\chi ~ -\frac{1}{2^7} \biggl(\frac{a}{c}\biggr)^4 ( 3\cos^3\chi - \cos\chi ) </math> |
|
|
|
<math>~ + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 12\cos\chi - 2\cos^2\chi ) ~+~\frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 13- 12\cos\chi - 2\cos^2\chi ) ~+~ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 13- 12\cos\chi - 2\cos^2\chi )\cos\chi </math> |
|
|
|
<math>~ + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 12 -21 \cos\chi - 2\cos^2\chi - 2\cos^3\chi ) ~+~\frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 12 -21 \cos\chi - 2\cos^2\chi - 2\cos^3\chi ) + f_{E5}\biggl(\frac{a}{c}\biggr)^4 \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 2K(\mu) \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 ( 3\cos^2\chi - 1 ) + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 ( 5\cos^3\chi ~-~ 3\cos\chi ) ~+~ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 ( 3~-~ 30 \cos^2\chi~+~ 35 \cos^4\chi ) \biggr\} </math> |
|
|
|
<math>~ \times \biggl\{ 1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) +\frac{3}{2^4}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 \biggl[ ( -13~+~12\cos\chi +2 \cos^2\chi ) ~+~ ( 12 -12\cos\chi ) ~+~ ( 96\cos\chi ~-~ 144\cos^2\chi ) \biggr] </math> |
|
|
|
<math>~ + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl[ (-17 + 21\cos\chi - \cos^2\chi ~-~ 2\cos^3\chi ) + ( 13~-~12\cos\chi -2 \cos^2\chi ) + (-12 + 24\cos\chi - 12\cos^2\chi) ~+~ (-~216 \cos\chi ~+~192\cos^2\chi ~-~ 120\cos^3\chi ) \biggr] \biggr\} </math> |
|
|
|
<math>~ + E(\mu) \biggl\{ ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2\biggl[ ( 13- 12\cos\chi - 2\cos^2\chi ) ~ -12 \cos\chi \biggr] </math> |
|
|
|
<math>~ ~+~\frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 \biggl[ ( 13- 12\cos\chi - 2\cos^2\chi ) + ( 12 -21 \cos\chi - 2\cos^2\chi - 2\cos^3\chi ) ~ -~12 \cos^2\chi \biggr] </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl[ ( 13\cos\chi - 12\cos^2\chi - 2\cos^3\chi ) ~+~( 12 -21 \cos\chi - 2\cos^2\chi - 2\cos^3\chi ) ~ -~6 ( 3\cos^3\chi - \cos\chi ) + 2^8\cdot 3 f_{E5} \biggr] \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
That is,
|
<math>~\frac{\pi V_\mathrm{Dyson}}{GM/c} </math> |
<math>~=</math> |
<math>~ 2K(\mu) \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 ( 3\cos^2\chi - 1 ) + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 ( 5\cos^3\chi ~-~ 3\cos\chi ) ~+~ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 ( 3~-~ 30 \cos^2\chi~+~ 35 \cos^4\chi ) \biggr\} </math> |
|
|
|
<math>~ \times \biggl\{ 1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) +\frac{3}{2^4}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( -1 ~+~ 96\cos\chi~-~ 142\cos^2\chi ) + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 (-16 ~-~183\cos\chi ~+~177 \cos^2\chi ~-~ 122\cos^3\chi ) \biggr\} </math> |
|
|
|
<math>~ + E(\mu) \biggl\{ ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) ~+~\frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 25- 33\cos\chi - 16\cos^2\chi - 2\cos^3\chi ) </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 12 -2 \cos\chi - 14\cos^2\chi - 22\cos^3\chi + 2^8\cdot 3 f_{E5} ) \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 2K(\mu) \biggl\{ 1 - \frac{1}{2}\biggl( \frac{a}{c}\biggr) +\frac{3}{2^4}\biggl(\frac{a}{c}\biggr)^2(1-\cos\chi ) + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( -1 ~+~ 96\cos\chi~-~ 142\cos^2\chi ) + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 (-16 ~-~183\cos\chi ~+~177 \cos^2\chi ~-~ 122\cos^3\chi ) </math> |
|
|
|
<math>~ + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi - \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2\cos\chi +\frac{3}{2^5}\biggl(\frac{a}{c}\biggr)^3(\cos\chi-\cos^2\chi ) + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( - \cos\chi ~+~ 96\cos^2\chi~-~ 142\cos^3\chi ) </math> |
|
|
|
<math>~ + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 ( 3\cos^2\chi - 1 ) + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 (1- 3\cos^2\chi ) ~+~\frac{3}{2^7}\biggl(\frac{a}{c}\biggr)^4(1-\cos\chi ) ( 3\cos^2\chi - 1 ) </math> |
|
|
|
<math>~ + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3 ( 5\cos^3\chi ~-~ 3\cos\chi ) ~+~ \frac{1}{2^5}\biggl(\frac{a}{c}\biggr)^4 (3\cos\chi ~-~5\cos^3\chi ) + \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 ( 3~-~ 30 \cos^2\chi~+~ 35 \cos^4\chi ) \biggr\} </math> |
|
|
|
<math>~ + E(\mu) \biggl\{ ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) ~+~\frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 25- 33\cos\chi - 16\cos^2\chi - 2\cos^3\chi ) </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 12 -2 \cos\chi - 14\cos^2\chi - 22\cos^3\chi + 2^8\cdot 3 f_{E5} ) \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 2K(\mu) \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) +\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 \biggl[3(1-\cos\chi ) - 4 \cos\chi + 2 ( 3\cos^2\chi - 1 )\biggr] </math> |
|
|
|
<math>~ + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 \biggl[ 36 (\cos\chi-\cos^2\chi ) + 24 (1 ~-~ 3\cos\chi - 3\cos^2\chi +5\cos^3\chi ) + ( -1 ~+~ 96\cos\chi~-~ 142\cos^2\chi ) \biggr] </math> |
|
|
|
<math>~ + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 \biggl[ (-16 ~-~183\cos\chi ~+~177 \cos^2\chi ~-~ 122\cos^3\chi ) ~+~18(1-\cos\chi ) ( 3\cos^2\chi - 1 ) + ( - \cos\chi ~+~ 96\cos^2\chi~-~ 142\cos^3\chi ) ~+~ 24 (3\cos\chi ~-~5\cos^3\chi ) + 6 ( 3~-~ 30 \cos^2\chi~+~ 35 \cos^4\chi ) \biggr] \biggr\} </math> |
|
|
|
<math>~ + E(\mu) \biggl\{ ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) ~+~\frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 25- 33\cos\chi - 16\cos^2\chi - 2\cos^3\chi ) </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 12 -2 \cos\chi - 14\cos^2\chi - 22\cos^3\chi + 2^8\cdot 3 f_{E5} ) \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ 2K(\mu) \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) +\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) + \frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 (23 ~+~ 60\cos\chi - 250\cos^2\chi +120\cos^3\chi ) </math> |
|
|
|
<math>~ + \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( -16 ~-~94\cos\chi ~+~147 \cos^2\chi ~-~ 194\cos^3\chi + 210 \cos^4\chi ) \biggr\} </math> |
|
|
|
<math>~ + E(\mu) \biggl\{ ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) ~+~\frac{1}{2^7\cdot 3} \biggl(\frac{a}{c}\biggr)^3 ( 25- 33\cos\chi - 16\cos^2\chi - 2\cos^3\chi ) </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^8\cdot 3} \biggl(\frac{a}{c}\biggr)^4 ( 12 -2 \cos\chi - 14\cos^2\chi - 22\cos^3\chi + 2^8\cdot 3 f_{E5} ) \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
Insert Expressions for K and E
|
Summary
|
Remember that (see above),
|
<math>~K(\mu)</math> |
<math>~=</math> |
<math>~ \ln \frac{4}{k^'} + \frac{1}{2^2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 + \frac{3^2}{2^6} \biggl( \ln\frac{4}{k^'} - \frac{7}{6} \biggr){k'}^4 + \frac{5^2}{2^8} \biggl( \ln\frac{4}{k^'} - \frac{37}{30} \biggr){k'}^6 + \cdots </math> |
And (see above),
|
<math>~E(\mu)</math> |
<math>~=</math> |
<math>~ 1 ~+~ \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 ~+~ \frac{3}{2^4}\biggl( \ln \frac{4}{k'} - 1 - \frac{1}{3\cdot 4}\biggr)(k')^4 ~+~ \frac{3^2\cdot 5}{2^7\cdot 3}\biggl( \ln \frac{4}{k'} - 1 - \frac{1}{2\cdot 3} - \frac{1}{2\cdot 3\cdot 5}\biggr)(k')^6 ~+~ \cdots </math> |
We are trying to match equation (6) in Dyson's (1893b) "Part II", that is,
|
<math>~\frac{V}{2\pi a^2}</math> |
<math>~=</math> |
<math>~ \ln\biggl(\frac{8c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr) \biggl[\ln\biggl(\frac{8c}{a}\biggr) - \frac{5}{4}\biggr] \cos\chi + \biggl\{ \frac{1}{16} \biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{5}{2} \biggr] + \frac{3}{16} \biggl[\ln\biggl(\frac{8c}{a}\biggr) +\frac{17}{36} - \frac{72}{36}\biggr]\cos2\chi\biggr\}\biggl(\frac{a^2}{c^2}\biggr) </math> |
|
|
|
<math>~ + \biggl\{ \frac{3}{32}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{25}{12}\biggr]\cos\chi + \frac{5}{64}\biggl[ \ln\biggl(\frac{8c}{a}\biggr)+\frac{7}{24} - \frac{48}{24}\biggr]\cos3\chi \biggr\} \biggl(\frac{a^3}{c^3}\biggr) </math> |
|
|
|
<math>~ + \biggl\{ \frac{9}{256}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - 2\biggr] + \frac{7}{128}\biggl[ \ln\biggl(\frac{8c}{a}\biggr) - \frac{19}{168} - 2\biggr]\cos2\chi + \frac{35}{1024} \biggl[ \ln\biggl(\frac{8c}{a}\biggr) - 2 + \frac{19}{120}\biggr]\cos4\chi \biggr\} \biggl(\frac{a^4}{c^4}\biggr) ~+~\cdots </math> |
To First Order
|
<math>~~(k')^{2}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{2a}{c}\biggr) \biggl\{1 ~-~ \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2\biggl[ (3-\cos^2\chi) ~+~2(2~-~ \cos\chi )^2 \biggr] </math> |
|
|
|
<math>~ +~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^3\biggl[ (3\cos\chi - \cos^3\chi) ~+~ (2~-~ \cos\chi )(3-\cos^2\chi) ~-~ (2~-~ \cos\chi )^3 \biggr] \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
<math>~\ln \frac{4}{k'}</math> |
<math>~=</math> |
<math>~ \frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\ln \Gamma </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl\{ \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2 (3-\cos^2\chi) ~-~\frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 (2~-~ \cos\chi )^2 ~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) \biggr\} </math> |
Hence,
|
<math>~\frac{\pi V_\mathrm{Dyson}}{GM/c} </math> |
<math>~=</math> |
<math>~ 2K(\mu) \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) \biggr\} + E(\mu) \biggl\{ ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^2}{c^2}\biggr) </math> |
|
|
<math>~\approx</math> |
<math>~ \biggl[ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) \biggr] \biggl\{ 2K(\mu) \biggr\} ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi \biggl\{~E(\mu) \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ \biggl[ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) \biggr] \biggl\{ 2\ln \frac{4}{k'} + \frac{1}{2}\biggl[ \ln\frac{4}{k'} - 1 \biggr] k'^2 \biggr\} ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi \biggl\{~1 + \frac{1}{2}\cancelto{0}{\biggl[ \ln\frac{4}{k'} - \frac{1}{2} \biggr] k'^2}\biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ \biggl\{ 2\ln \frac{4}{k'} + \frac{1}{2}\biggl[ \ln\frac{4}{k'} - 1 \biggr] \biggl(\frac{2a}{c}\biggr) \biggr\} + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) \biggl\{ 2\ln \frac{4}{k'} +\frac{1}{2} \cancelto{0}{\biggl[ \ln\frac{4}{k'} - 1 \biggr] k'^2} \biggr\} ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi \biggl\{~1 + \frac{1}{2}\cancelto{0}{\biggl[ \ln\frac{4}{k'} - \frac{1}{2} \biggr] k'^2}\biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ 2\ln \frac{4}{k'} + \biggl(\frac{a}{c}\biggr)\biggl[ \ln\frac{4}{k'} - 1 \biggr] + \biggl(\frac{a}{c}\biggr)(\cos\chi - 1) \biggl\{ \ln \frac{4}{k'} \biggr\} ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi </math> |
|
|
<math>~\approx</math> |
<math>~ 2\ln \frac{4}{k'} + \biggl(\frac{a}{c}\biggr)\biggl[ \ln\frac{4}{k'} - 1 + (\cos\chi - 1) \biggl( \ln \frac{4}{k'} \biggr) ~-~ \frac{1}{2^3} \cos\chi \biggr] </math> |
|
|
<math>~\approx</math> |
<math>~ 2\ln \frac{4}{k'} + \biggl(\frac{a}{c}\biggr)\biggl[ - 1 + \cos\chi \biggl( \ln \frac{4}{k'} \biggr) ~-~ \frac{1}{2^3} \cos\chi \biggr] </math> |
|
|
<math>~\approx</math> |
<math>~ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr) \biggl\{ (2~-~ \cos\chi ) - 2 + \cos\chi \biggl[ \ln\biggl(\frac{2^3c}{a}\biggr)\biggr] ~-~ \frac{1}{4} \cos\chi \biggr\} </math> |
|
|
<math>~\approx</math> |
<math>~ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr) \biggl[ \ln\biggl(\frac{2^3c}{a}\biggr) ~-~ \frac{5}{4} \biggr]\cos\chi </math> |
To Second Order
|
<math>~\frac{\pi V_\mathrm{Dyson}}{GM/c} </math> |
<math>~=</math> |
<math>~ \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) +\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) \biggr\} \biggl\{ 2K(\mu) \biggr\} </math> |
|
|
|
<math>~ + \biggl\{ ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) \biggr\} \biggl\{ E(\mu) \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) +\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) \biggr\} \biggl\{ 2\ln \frac{4}{k^'} + \frac{1}{2}\biggl( \ln\frac{4}{k^'} - 1 \biggr){k'}^2 + \frac{3^2}{2^5} \biggl( \ln\frac{4}{k^'} - \frac{7}{6} \biggr){k'}^4 \biggr\} </math> |
|
|
|
<math>~ + \biggl\{ ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) \biggr\} \biggl\{ 1 ~+~ \frac{1}{2}\biggl( \ln \frac{4}{k'} - \frac{1}{2}\biggr)(k')^2 \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) +\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) \biggr\} \biggl\{ 2\biggl[\frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\ln \Gamma\biggr] + \frac{1}{2}\biggl[ \frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\ln \Gamma - 1 \biggr]{k'}^2 + \frac{3^2}{2^5} \biggl[ \frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\ln \Gamma - \frac{7}{6} \biggr] {k'}^4 \biggr\} </math> |
|
|
|
<math>~ + \biggl\{ ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) \biggr\} \biggl\{ 1 ~+~ \frac{1}{2}\biggl[ \frac{1}{2} \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\ln \Gamma - \frac{1}{2}\biggr](k')^2 \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) +\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) \biggr\} \biggl\{ \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) + \ln \Gamma\biggr] + \frac{1}{2^2}\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) + \ln \Gamma - 2 \biggr] \biggl( \frac{2a}{c}\biggr) \biggl[ 1 ~-~ \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi )\biggr] + \frac{3}{2^6} \biggl[ 3 \ln\biggl( \frac{2^3c}{a}\biggr) + \cancelto{0}{3\ln \Gamma} - 7 \biggr] 4\biggl( \frac{a}{c}\biggr)^2 \biggr\} </math> |
|
|
|
<math>~ + \biggl\{ ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) \biggr\} \biggl\{ 1 ~+~ \frac{1}{2^2}\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) + \cancelto{0}{\ln \Gamma} - 1 \biggr] \biggl( \frac{2a}{c}\biggr) \biggl[ 1 ~-~\cancelto{0}{ \frac{1}{2}\biggl(\frac{a}{c}\biggr)} (2~-~ \cos\chi )\biggr] \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) \, , </math> |
where,
|
<math>~\ln\Gamma</math> |
<math>~=</math> |
<math>~ \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2( -1 ~+~ 4\cos\chi -2\cos^2\chi ) ~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) \, . </math> |
Hence,
|
<math>~\frac{\pi V_\mathrm{Dyson}}{GM/c} </math> |
<math>~=</math> |
<math>~ \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) +\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) \biggr\} \biggl\{ \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2( -1 ~+~ 4\cos\chi -2\cos^2\chi ) \biggr] </math> |
|
|
|
<math>~ + \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 2 + \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) \biggr] \biggl[ 1 ~-~ \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi )\biggr] + \frac{3}{2^4}\biggl( \frac{a}{c}\biggr)^2 \biggl[ 3 \ln\biggl( \frac{2^3c}{a}\biggr) - 7 \biggr] \biggr\} </math> |
|
|
|
<math>~ + \biggl\{ ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) \biggr\} \biggl\{ 1 ~+~ \frac{1}{2}\biggl( \frac{a}{c}\biggr)\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 1 \biggr] \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \biggl\{ 1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) +\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) \biggr\} \biggl\{ \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) + \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2( -1 ~+~ 4\cos\chi -2\cos^2\chi ) \biggr] </math> |
|
|
|
<math>~ + \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 2 \biggr] + \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2 (2~-~ \cos\chi ) - \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2 \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 2 \biggr] (2~-~ \cos\chi ) + \frac{3}{2^4}\biggl( \frac{a}{c}\biggr)^2 \biggl[ 3 \ln\biggl( \frac{2^3c}{a}\biggr) - 7 \biggr] \biggr\} </math> |
|
|
|
<math>~ ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi ~+~ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) ~-~ \frac{1}{2^4} \biggl(\frac{a}{c}\biggr)^2\cos\chi \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 1 \biggr] ~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr) (2~-~ \cos\chi ) ~-~ \frac{1}{2^3} \biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2}\biggl( \frac{a}{c}\biggr) \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 2 \biggr] + \frac{1}{2}\biggl(\frac{a}{c}\biggr)(\cos\chi - 1) \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) \biggr] </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^3}\biggl( \frac{a}{c}\biggr)^2( -1 ~+~ 4\cos\chi -2\cos^2\chi ) + \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2 (2~-~ \cos\chi ) - \frac{1}{2^2}\biggl( \frac{a}{c}\biggr)^2 \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 2 \biggr] (2~-~ \cos\chi ) + \frac{3}{2^4}\biggl( \frac{a}{c}\biggr)^2 \biggl[ 3 \ln\biggl( \frac{2^3c}{a}\biggr) - 7 \biggr] </math> |
|
|
|
<math>~ + \frac{1}{2^2}\biggl(\frac{a}{c}\biggr)^2(\cos\chi - 1) (2~-~ \cos\chi ) +\frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^2 (1-7\cos\chi + 6\cos^2\chi ) \ln\biggl( \frac{2^3c}{a}\biggr) </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^6\cdot 3} \biggl(\frac{a}{c}\biggr)^2 ( 13- 24\cos\chi - 2\cos^2\chi ) ~-~ \frac{1}{2^4} \biggl(\frac{a}{c}\biggr)^2\cos\chi \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 1 \biggr] ~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)\biggl\{ 4(2~-~ \cos\chi ) ~-~ \cos\chi + \biggl[ 4 \ln\biggl( \frac{2^3c}{a}\biggr) - 8 \biggr] + \biggl[ 4\ln\biggl( \frac{2^3c}{a}\biggr) \biggr] (\cos\chi - 1) \biggr\} </math> |
|
|
|
<math>~~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ 24( -1 ~+~ 4\cos\chi -2\cos^2\chi ) + 48 (2~-~ \cos\chi ) - 48\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 2 \biggr] (2~-~ \cos\chi ) + 36\biggl[ 3 \ln\biggl( \frac{2^3c}{a}\biggr) - 7 \biggr] </math> |
|
|
|
<math>~ + 48(\cos\chi - 1) (2~-~ \cos\chi ) ~+~12 (1-7\cos\chi + 6\cos^2\chi ) \ln\biggl( \frac{2^3c}{a}\biggr) ~+~ ( 13- 24\cos\chi - 2\cos^2\chi ) ~-~12\cos\chi \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - 1 \biggr] \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)\biggl\{ 4(2~-~ \cos\chi ) ~-~ \cos\chi + \biggl[ 4 \ln\biggl( \frac{2^3c}{a}\biggr) - 8 \biggr] + \biggl[ 4\ln\biggl( \frac{2^3c}{a}\biggr) \biggr] (\cos\chi - 1) \biggr\} </math> |
|
|
|
<math>~~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ (-24 + 96\cos\chi-48\cos^2\chi) + (96~-~ 48\cos\chi ) ~+~ \biggl[2- \ln\biggl( \frac{2^3c}{a}\biggr) \biggr] (96~-~ 48 \cos\chi ) + \biggl[ 108 \ln\biggl( \frac{2^3c}{a}\biggr) - 252 \biggr] </math> |
|
|
|
<math>~ + 48(3\cos\chi - \cos^2\chi - 2 ) ~+~ (12 - 84\cos\chi + 72\cos^2\chi ) \ln\biggl( \frac{2^3c}{a}\biggr) ~+~ ( 13- 24\cos\chi - 2\cos^2\chi ) ~+~12\cos\chi ~-~12\cos\chi \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) - \biggr] \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) ~-~ \frac{5}{4}\biggr]\cos\chi </math> |
|
|
|
<math>~~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ -24 ~+~ 96\cos\chi -48\cos^2\chi + 96~-~ 48\cos\chi + 192 - 252 -96\cos\chi ~+~ ( 13- 12\cos\chi - 2\cos^2\chi ) + (144\cos\chi - 48\cos^2\chi -96 ) </math> |
|
|
|
<math>~ +36 \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr)\biggr]\cos\chi ~+~(12 - 84\cos\chi + 72\cos^2\chi -96 + 108) \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr)\biggr] \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) ~-~ \frac{5}{4}\biggr]\cos\chi </math> |
|
|
|
<math>~~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ -71 ~+~84\cos\chi -98\cos^2\chi ~+~(24 - 48\cos\chi + 72\cos^2\chi ) \biggl[ \ln\biggl( \frac{2^3c}{a}\biggr)\biggr] \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \ln\biggl( \frac{2^3c}{a}\biggr) + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\biggl[ \ln\biggl( \frac{2^3c}{a}\biggr) ~-~ \frac{5}{4}\biggr]\cos\chi ~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ -71 ~+~84\cos\chi -98\cos^2\chi ~+~24\ln\biggl( \frac{2^3c}{a}\biggr)(1 - 2\cos\chi + 3\cos^2\chi ) \biggr\} ~+~ \mathcal{O}\biggl(\frac{a^3}{c^3}\biggr) </math> |
In an effort to compare this expression with equation (6) from Dyson's (1893b) "Part II", we should make the substitutions,
<math>~\ln\biggl(\frac{2^3c}{a}\biggr) \rightarrow (\lambda +2)</math> and <math>~2\cos^2\chi \rightarrow 1 + \cos2\chi \, .</math>
This means,
|
<math>~\frac{\pi V_\mathrm{Dyson}}{GM/c}\biggr|_{\mathcal{O}(a^2/c^2)} </math> |
<math>~=</math> |
<math>~ ~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ -71 ~+~84\cos\chi -49(1+\cos2\chi ) ~+~24(\lambda + 2)(1 - 2\cos\chi ) ~+~36(\lambda+2)(1 + \cos2\chi ) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ ~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ -71 ~+~84\cos\chi -49 -49 \cos2\chi ~+~24(\lambda + 2 -2\lambda \cos\chi - 4\cos\chi) ~+~36(\lambda+2 +\lambda\cos 2\chi + 2\cos 2\chi) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ ~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ -71 ~+~84\cos\chi -49 -49 \cos2\chi ~+~24\lambda + 48 -48\lambda \cos\chi - 96\cos\chi ~+~36\lambda+72 +36\lambda\cos 2\chi + 72\cos 2\chi \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ ~+~ \frac{1}{2^6\cdot 3} \biggl( \frac{a}{c}\biggr)^2\biggl\{ 60\lambda -48\lambda \cos\chi - 12\cos\chi +36\lambda\cos 2\chi + 23\cos 2\chi \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ ~+~ \biggl( \frac{a}{c}\biggr)^2\biggl\{ \frac{5\lambda}{16} - \frac{(4\lambda + 1)}{16}~\cos\chi +\frac{3(\lambda+\tfrac{23}{36})}{16}\cos 2\chi \biggr\} \, . </math> |
This expression differs from the 2nd-order term in Dyson's equation (6) by the amount,
|
<math>~\Delta \biggr|_{\mathcal{O}(a^2/c^2)} </math> |
<math>~=</math> |
<math>~ \biggl( \frac{a}{c}\biggr)^2\biggl\{ \frac{5\lambda}{16} - \frac{(4\lambda + 1)}{16}~\cos\chi +\frac{3(\lambda+\tfrac{23}{36})}{16}\cos 2\chi \biggr\} - \biggl(\frac{a}{c}\biggr)^2 \biggl\{ \frac{\lambda - \frac{1}{2}}{16} + \frac{3(\lambda + \frac{17}{36})}{16}\cos2\chi \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{16\cdot 12}\biggl( \frac{a}{c}\biggr)^2\biggl\{ 60\lambda - (48\lambda + 12)~\cos\chi +(36\lambda+23)\cos 2\chi \biggr\} - \frac{1}{16\cdot 12}\biggl(\frac{a}{c}\biggr)^2 \biggl\{ 12\lambda - 6 + (36\lambda + 17) \cos2\chi \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{16\cdot 12}\biggl( \frac{a}{c}\biggr)^2\biggl\{ 48\lambda + 6 - (48\lambda + 12)~\cos\chi +(6)\cos 2\chi \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2^5}\biggl( \frac{a}{c}\biggr)^2\biggl\{ (\cos 2\chi -1)- (8\lambda + 2)~(1+\cos\chi) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^2\biggl\{ (\cos\chi - 1)- (4\lambda + 1)~ \biggr\} (1+\cos\chi) </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2^4}\biggl( \frac{a}{c}\biggr)^2 (\cos\chi - 2- 4\lambda ) (1+\cos\chi) </math> |
Interior Potential
In equation (9) on p. 1050 of his "Part II", Dyson (1893b) presents the following power-series expression for the gravitational potential at points inside the torus:
|
<math>~V</math> |
<math>~=</math> |
<math>~ 2\pi a^2 \biggl\{ L + \frac{1}{2}\biggl( 1 - \frac{R^2}{a^2}\biggr) + \frac{a}{c}\biggl[ \frac{(L-1)}{2}\biggl(\frac{R}{a}\biggr) - \frac{R^3}{8a^3} \biggr]\cos\chi </math> |
|
|
|
<math>~+~ \frac{a^2}{c^2}\biggl[ - ~\frac{(L - \tfrac{1}{4})}{16} ~+~ \frac{(L-1)}{8} \biggl(\frac{R^2}{a^2} \biggr) ~-~ \frac{3}{64} \biggl( \frac{R^4}{a^4}\biggr) ~+~ \frac{3(L-\tfrac{5}{4})}{16} \biggl(\frac{R^2}{a^2}\biggr) \cos 2\chi ~-~\frac{5}{96} \biggl( \frac{R^4}{a^4}\biggr) \cos 2\chi \biggr] ~+~ \cdots \biggr\} </math> |
where,
|
<math>~L</math> |
<math>~\equiv</math> |
<math>~\ln\biggl(\frac{8c}{a}\biggr) \, .</math> |
Note that, for the example illustrated above, <math>~a/c = 2/5</math> and, hence, <math>~L = \ln(20) = 2.99573</math>. Therefore, at any point on the surface of this example torus,
|
<math>~\frac{V}{2\pi a^2}</math> |
<math>~\approx</math> |
<math>~ \ln(20) + \frac{2}{5}\biggl[ \frac{\ln(20)-1}{2} - \frac{1}{8} \biggr]\cos\chi </math> |
|
|
|
<math>~+~ \frac{2^2}{5^2}\biggl[ - ~\frac{4\ln(20) - 1}{64} ~+~ \frac{\ln(20)-1}{8} ~-~ \frac{3}{64} ~+~ \frac{12\ln(20)-15}{64} \cos 2\chi ~-~\frac{10}{3\cdot 64} \cos 2\chi \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \ln(20) + \frac{2}{40}\biggl[ 4\ln(20)- 5 \biggr]\cos\chi ~+~ \frac{2^2}{2^6\cdot 5^2}\biggl\{ - ~[4\ln(20) - 1] ~+~ [8\ln(20)-8] ~-~ 3 ~+~ [12\ln(20)-15] \cos 2\chi ~-~\biggl(\frac{10}{3} \biggr) \cos 2\chi \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \ln(20) + \frac{1}{20}\biggl[ 4\ln(20)- 5 \biggr]\cos\chi ~+~ \frac{1}{2^4\cdot 5^2}\biggl\{ 4\ln(20)-10 ~+~ \frac{1}{3}\biggl[ 36\ln(20)-55 \biggr] \cos 2\chi \biggr\} </math> |
Red Contour
Let's construct an equipotential contour that extends the red contour into the interior region. Let's begin by evaluating Dyson's interior potential expression at the coordinate location where the red contour touches the surface of the torus. According to Column #5, this point on the surface has coordinates, <math>~(\varpi,z) = (0.867, 0.377)</math>; or, equivalently, <math>~R = a = 0.4</math> and,
|
<math>~\cos\chi</math> |
<math>~=</math> |
<math>~ \frac{1-\varpi}{R} = 0.3325 </math> |
|
<math>~\Rightarrow ~~~ \chi</math> |
<math>~=</math> |
<math>~ \cos^{-1}(0.3325) = 1.2318 \, . </math> |
Hence, for this specific point on the torus surface, we find,
|
<math>~\frac{V}{2\pi a^2}</math> |
<math>~\approx</math> |
<math>~ 3 + \biggl[\frac{7}{20}\biggr]\cos\chi ~+~ \frac{1}{2^4\cdot 5^2}\biggl\{ 2 ~+~ \biggl[ \frac{53}{3} \biggr] \cos 2\chi \biggr\} = 3.0870 \, . </math> |
| Contour (column #) |
<math>~V_2</math> (external) | Surface <math>~\varpi</math> | <math>~\chi</math> (radians) |
|---|---|---|---|
| blue (3) | 0.9120 | 1.117 | 1.8676 |
| orange (4) | 0.961 | 0.929 | 1.392 |
| red (5) | 0.9800 | 0.867 | 1.2318 |
| light green (6) | 0.9800 | 0.838 | 1.1538 |
| light blue (7) | 1.0212 | 0.749 | 0.8925 |
See Also
- T. Fukushima (2016, AJ, 152, article id. 35, 31 pp.) — Zonal Toroidal Harmonic Expansions of External Gravitational Fields for Ring-like Objects
- W.-T. Kim & S. Moon (2016, ApJ, 829, article id. 45, 22 pp.) — Equilibrium Sequences and Gravitational Instability of Rotating Isothermal Rings
- E. Y. Bannikova, V. G. Vakulik & V. M. Shulga (2011, MNRAS, 411, 557 - 564) — Gravitational Potential of a Homogeneous Circular Torus: a New Approach
- D. Petroff & S. Horatschek (2008, MNRAS, 389,156 - 172) — Uniformly Rotating Homogeneous and Polytropic Rings in Newtonian Gravity
|
The following quotes have been taken from Petroff & Horatschek (2008):
§1: "The problem of the self-gravitating ring captured the interest of such renowned scientists as Kowalewsky (1885), Poincaré (1885a,b,c) and Dyson (1892, 1893). Each of them tackled the problem of an axially symmetric, homogeneous ring in equilibrium by expanding it about the thin ring limit. In particular, Dyson provided a solution to fourth order in the parameter <math>~\sigma = a/b</math>, where <math>~a = r_t</math> provides a measure for the radius of the cross-section of the ring and <math>~b = \varpi_t</math> the distance of the cross-section's centre of mass from the axis of rotation."
§7: "In their work on homogeneous rings, Poincaré and Kowalewsky, whose results disagreed to first order, both had made mistakes as Dyson has shown. His result to fourth order is also erroneous as we point out in Appendix B." |
- P. H. Chavanis (2006, International Journal of Modern Physics B, 20, 3113 - 3198) — Phase Transitions in Self-Gravitating Systems
- M. Ansorg, A. Kleinwächter & R. Meinel (2003, MNRAS, 339, 515) — Uniformly Rotating Axisymmetric Fluid Configurations Bifurcating from Highly Flattened Maclaurin Spheroids
- M. Lombardi & G. Bertin (2001, Astronomy & Astrophysics, 375, 1091 - 1099) — Boyle's Law and Gravitational Instability
- W. Kley (1996, MNRAS, 282, 234) — Maclurin Discs and Bifurcations to Rings
- J. W. Woodward, J. E. Tohline, & I. Hachisu (1994, ApJ, 420, 247 - 267) — The Stability of Thick, Self-Gravitating Disks in Protostellar Systems
- I. Bonnell & P. Bastien (1991, ApJ, 374, 610 - 622) — The Collapse of Cylindrical Isothermal and Polytropic Clouds with Rotation
- J. E. Tohline & I. Hachisu (1990, ApJ, 361, 394 - 407) — The Breakup of Self-Gravitating Rings, Tori, and Thick Accretion Disks
- F. Schmitz (1988, Astronomy & Astrophysics, 200, 127 - 134) — Equilibrium Structures of Differentially Rotating Self-Gravitating Gases
- P. Veugelen (1985, Astrophysics & Space Science, 109, 45 - 55) — Equilibrium Models of Differentially Rotating Polytropic Cylinders
- M. A. Abramowicz, A. Curir, A. Schwarzenberg-Czerny, & R. E. Wilson (1984, MNRAS, 208, 279 - 291) — Self-Gravity and the Global Structure of Accretion Discs
- P. Bastien (1983, Astronomy & Astrophysics, 119, 109 - 116) — Gravitational Collapse and Fragmentation of Isothermal, Non-Rotating, Cylindrical Clouds
- Y. Eriguchi & D. Sugimoto (1981, Progress of Theoretical Physics, 65, 1870 - 1875) — Another Equilibrium Sequence of Self-Gravitating and Rotating Incompressible Fluid
- J. E. Tohline (1980, ApJ, 236, 160 - 171) — Ring Formation in Rotating Protostellar Clouds
- T. Fukushima, Y. Eriguchi, D. Sugimoto, & G. S. Bisnovatyi-Kogan (1980, Progress of Theoretical Physics, 63, 1957 - 1970) — Concave Hamburger Equilibrium of Rotating Bodies
- J. Katz & D. Lynden-Bell (1978, MNRAS, 184, 709 - 712) — The Gravothermal Instability in Two Dimensions
- P. S. Marcus, W. H. Press, & S. A. Teukolsky (1977, ApJ, 214, 584- 597) — Stablest Shapes for an Axisymmetric Body of Gravitating, Incompressible Fluid (includes torus with non-uniform rotation)
- Shortly after their equation (3.2), Marcus, Press & Teukolsky make the following statement: "… we know that an equilibrium incompressible configuration must rotate uniformly on cylinders (the famous "Poincaré-Wavre" theorem, cf. Tassoul 1977, &Sect;4.3) …"
- C. J. Hansen, M. L. Aizenman, & R. L. Ross (1976, ApJ, 207, 736 - 744) — The Equilibrium and Stability of Uniformly Rotating, Isothermal Gas Cylinders
- C.-Y. Wong (1974, ApJ, 190, 675 - 694) — Toroidal Figures of Equilibrium
- C.-Y. Wong (1973, Annals of Physics, 77, 279 - 353) — Toroidal and Spherical Bubble Nuclei
- J. Ostriker (1964, ApJ, 140, 1056) — The Equilibrium of Polytropic and Isothermal Cylinders
- J. Ostriker (1964, ApJ, 140, 1067) — The Equilibrium of Self-Gravitating Rings
- J. Ostriker (1964, ApJ, 140, 1529) — On the Oscillations and the Stability of a Homogeneous Compressible Cylinder
- J. Ostriker (1965, ApJ Supplements, 11, 167) — Cylindrical Emden and Associated Functions
- Gunnar Randers (1942, ApJ, 95, 88) — The Equilibrium and Stability of Ring-Shaped 'barred SPIRALS'.
- William Duncan MacMillan (1958), The Theory of the Potential, New York: Dover Publications
- Oliver Dimon Kellogg (1929), Foundations of Potential Theory, Berlin: Verlag Von Julius Springer
- Lord Rayleigh (1917, Proc. Royal Society of London. Series A, 93, 148-154) — On the Dynamics of Revolving Fluids
- F. W. Dyson (1893, Philosophical Transaction of the Royal Society London. A., 184, 1041 - 1106) — The Potential of an Anchor Ring. Part II.
- In this paper, Dyson derives the gravitational potential inside the ring mass distribution
- F. W. Dyson (1893, Philosophical Transaction of the Royal Society London. A., 184, 43 - 95) — The Potential of an Anchor Ring. Part I.
- In this paper, Dyson derives the gravitational potential exterior to the ring mass distribution
- S. Kowalewsky (1885, Astronomische Nachrichten, 111, 37) — Zusätze und Bemerkungen zu Laplace's Untersuchung über die Gestalt der Saturnsringe
- Poincaré (1885a, C. R. Acad. Sci., 100, 346), (1885b, Bull. Astr., 2, 109), (1885c, Bull. Astr. 2, 405). — references copied from paper by Wong (1974)

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |