User:Tohline/Appendix/Ramblings/Dyson1893Part1
Dyson (1893a) Part I: Some Details
This chapter provides some derivation details relevant to our accompanying discussion of Dyson's analysis of the gravitational potential exterior to an anchor ring.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Overview
In his pioneering work, F. W. Dyson (1893a, Philosophical Transactions of the Royal Society of London. A., 184, 43 - 95) and (1893b, Philosophical Transactions of the Royal Society of London. A., 184, 1041 - 1106) used analytic techniques to determine the approximate equilibrium structure of axisymmetric, uniformly rotating, incompressible tori. C.-Y. Wong (1974, ApJ, 190, 675 - 694) extended Dyson's work, using numerical techniques to obtain more accurate — but still approximate — equilibrium structures for incompressible tori having solid body rotation. Since then, Y. Eriguchi & D. Sugimoto (1981, Progress of Theoretical Physics, 65, 1870 - 1875) and I. Hachisu, J. E. Tohline & Y. Eriguchi (1987, ApJ, 323, 592 - 613) have mapped out the full sequence of Dyson-Wong tori, beginning from a bifurcation point on the Maclaurin spheroid sequence.
External Potential in Terms of Angle ψ
Step 1
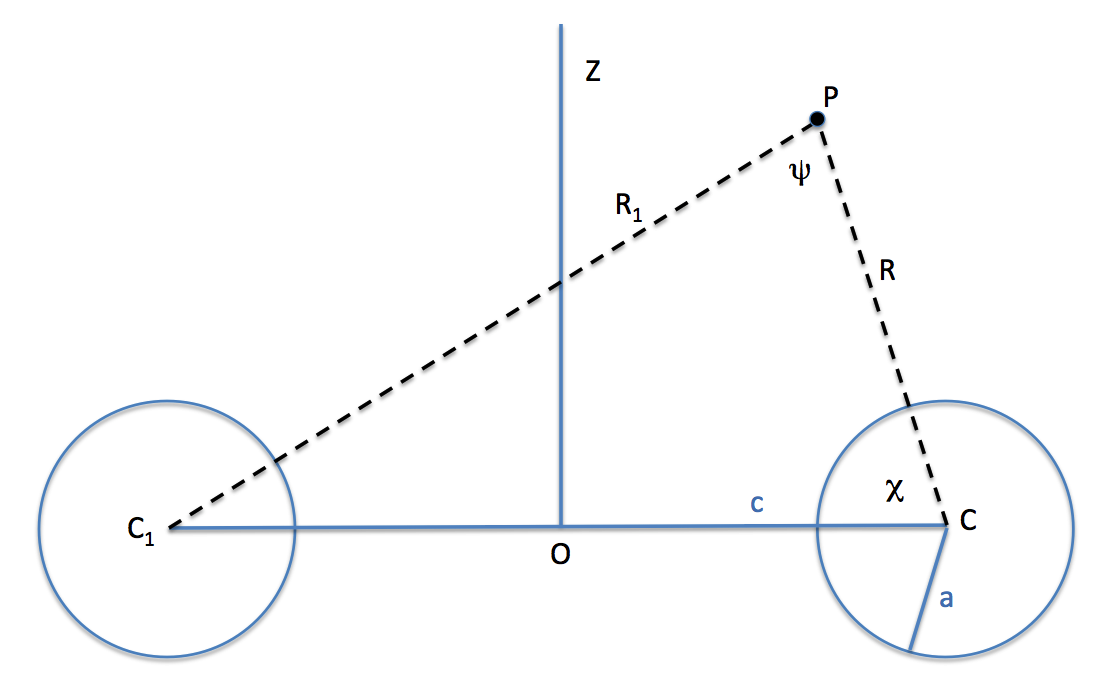
On p. 59, at the end of §6 of Dyson (1893a), we find the following expression for the potential at point "P", anywhere exterior to an anchor ring:
|
<math>~\frac{\pi V(r,\theta)}{M}</math> |
<math>~=</math> |
<math>~ \mathfrak{I}(r,\theta,c) ~+~ \frac{a^2}{2^3} ~\frac{1}{c} \cdot \frac{d}{dc} \biggl[ \mathfrak{I}(r,\theta,c)\biggr] ~-~ \frac{a^4}{2^6\cdot 3} ~\frac{1}{c} \cdot \frac{d}{dc} \biggl\{ \frac{1}{c} \cdot \frac{d}{dc} \biggl[ \mathfrak{I}(r,\theta,c)\biggr]\biggr\} ~+~\cdots </math> |
|
|
|
<math>~ ~+~(-1)^{n+1} \frac{2a^{2n}}{2n+2} \biggl[ \frac{1\cdot 3\cdot 5 \cdots (2n-3)}{2^2\cdot 4^2\cdot 6^2\cdots(2n)^2} \biggr] \biggl( \frac{1}{c}\cdot \frac{d}{dc}\biggr)^n \biggl[ \mathfrak{I}(r,\theta,c)\biggr] ~+~ \cdots </math> |
where (see beginning of §8 on p. 61),
|
|
<math>~\mathfrak{I}(r,\theta,c)</math> |
<math>~\equiv</math> |
<math>~ \int_0^\pi d\phi \biggl[r^2 - 2cr\sin\theta \cos\phi +c^2\biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ 2\int_0^{\pi/2} d\phi \biggl[ R_1^2 - (R_1^2-R^2)\sin^2\phi \biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{2}{R_1}\int_0^{\pi/2} d\phi \biggl[ 1 - \biggl( \frac{R_1^2-R^2}{R_1^2}\biggr) \sin^2\phi \biggr]^{-1 / 2} </math> |
|
|
<math>~=</math> |
<math>~ \frac{2K(k)}{R_1} \, , </math> |
and, where furthermore,
|
<math>~K(k)</math> |
<math>~=</math> |
<math>~ \int_0^{\pi/2} d\phi \biggl[1 - k^2\sin^2\phi \bigg]^{-1 / 2} </math> |
and |
<math>~k</math> |
<math>~\equiv</math> |
<math>~ \biggl[ \frac{R_1^2-R^2}{R_1^2} \biggr]^{1 / 2} \, . </math> |
Step 2
Taking a queue from our accompanying discussion of toroidal coordinates, if we adopt the variable notation,
<math>~\eta \equiv \ln\biggl(\frac{R_1}{R}\biggr) \, ,</math>
then we can write,
|
<math>~\cosh\eta = \frac{1}{2}\biggl[e^\eta + e^{-\eta}\biggr]</math> |
<math>~=</math> |
<math>~\frac{R^2 + R_1^2}{2RR_1} \, ,</math> |
which implies that,
|
<math>~\biggl[ \frac{2}{\coth\eta +1} \biggr]^{1 / 2} = [1 - e^{-2\eta}]^{1 / 2}</math> |
<math>~=</math> |
<math>~\biggl[ 1 - \biggl(\frac{R}{R_1}\biggr)^2 \biggr]^{1 / 2} = k \, .</math> |
Now, if we employ the Descending Landen Transformation for the complete elliptic integral of the first kind, we can make the substitution,
|
<math>~K(k)</math> |
<math>~=</math> |
<math>~ (1 + \mu)K(\mu) \, , </math> |
where, |
<math>~\mu</math> |
<math>~\equiv</math> |
<math>~ \frac{1-\sqrt{1-k^2}}{1+\sqrt{1-k^2}} \, . </math> |
But notice that, <math>~\sqrt{1-k^2} = e^{-\eta}</math>, in which case,
|
<math>~\mu </math> |
<math>~=</math> |
<math>~ \frac{1-e^{-\eta}}{1+e^{-\eta}} </math> |
<math>~=</math> |
<math>~ \frac{1-R/R_1}{1+R/R_1} </math> |
<math>~=</math> |
<math>~ \frac{R_1-R}{R_1+R} \, . </math> |
Hence, we can write,
|
<math>~\mathfrak{I}(r,\theta,c) = \frac{2K(k)}{R_1}</math> |
<math>~=</math> |
<math>~ \frac{2}{R_1} \biggl[(1+\mu)K(\mu) \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{2K(\mu)}{R_1} \biggl[1+\frac{R_1-R}{R_1+R} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{4K(\mu)}{R_1+R} \, .</math> |
This is the expression for <math>~\mathfrak{I}(r,\theta,c) </math> that was adopted by Dyson at the beginning of his §8.
Step 3
Subsequently, Dyson was able to obtain analytic expressions for successive derivatives of the function, <math>~\mathfrak{I}(r,\theta,c) </math>, by first demonstrating that
|
<math>~\frac{dR}{dc}</math> |
<math>~=</math> |
<math>~\frac{4c^2 + R^2 - R_1^2}{4cR} \, ,</math> |
|
<math>~\frac{dR_1}{dc}</math> |
<math>~=</math> |
<math>~\frac{4c^2 + R_1^2 - R^2}{4cR_1} \, ,</math> and, |
|
<math>~\frac{d\mu}{dc}</math> |
<math>~=</math> |
<math>~\frac{\mu}{c} \cos\psi \, ,</math> |
where — as shown above in the Anchor ring schematic — <math>~\psi</math> is the angle between <math>~R</math> and <math>~R_1</math> for which (according to the law of cosines),
|
<math>~\cos\psi</math> |
<math>~=</math> |
<math>~\frac{R^2 + R_1^2 - 4c^2}{2RR_1} \, .</math> |
It will be useful for us to note that,
|
<math>~\frac{d(\cos\psi)}{dc}</math> |
<math>~=</math> |
<math>~ \frac{d}{dc}\biggl[ \frac{R^2 + R_1^2 - 4c^2}{2RR_1} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2RR_1}\frac{d}{dc}\biggl[ R^2 + R_1^2 - 4c^2 \biggr] ~+~(R^2 + R_1^2 - 4c^2) \frac{d}{dc}\biggl[ \frac{1}{2RR_1} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{2RR_1}\biggl[2R\frac{dR}{dc} + 2R_1\frac{dR_1}{dc} - 8c \biggr] ~+~(R^2 + R_1^2 - 4c^2)\biggl[ - \frac{1}{2R^2R_1} \frac{dR}{dc} - \frac{1}{2RR_1^2}\frac{dR_1}{dc} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{4cRR_1}\biggl[ 4c^2 + R^2 - R_1^2 + 4c^2 + R_1^2 - R^2 - 2^4c^2 \biggr] ~-~(R^2 + R_1^2 - 4c^2)\biggl\{ \biggl[ \frac{4c^2 + R^2 - R_1^2}{8cR^3R_1}\biggr] + \biggl[ \frac{4c^2 + R_1^2 - R^2}{8cR_1^3 R} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ -~\frac{2c}{RR_1} ~-~\frac{\cos\psi}{4cR^2 R_1^2} \biggl[4c^2(R_1^2 + R^2) + 2R_1^2 R^2 - R_1^4 - R^4 \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{\cos\psi}{4cR^2 R_1^2} \biggl[ R_1^4 + R^4- 4c^2(R_1^2 + R^2) - 2R_1^2 R^2 \biggr] -~\frac{2c}{RR_1} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{4cR^2 R_1^2}\biggl\{ \cos\psi [R_1^4 + R^4 - 2R_1^2 R^2 - 4c^2(R_1^2 + R^2) ] -~8c^2R R_1 \biggr\} </math> |
But,
|
<math>~[R_1^4 + R^4 - 2R_1^2 R^2 - 4c^2(R_1^2 + R^2)]</math> |
<math>~=</math> |
<math>~ (R_1^2 - R^2)^2 - 4c^2(R_1^2 + R^2) </math> |
|
|
<math>~=</math> |
<math>~ [(R_1+R)(R_1-R)]^2 - 4c^2(R_1^2 + R^2) </math> |
|
|
<math>~=</math> |
<math>~ (R_1^2 + 2R_1 R +R^2)(R_1-R)^2 - 4c^2(R_1^2 + R^2) </math> |
|
|
<math>~=</math> |
<math>~ 2R_1 R(R_1-R)^2 +(R_1^2 + R^2)(R_1-R)^2 - 4c^2(R_1^2 + R^2) </math> |
|
|
<math>~=</math> |
<math>~ 2R_1 R(R_1-R)^2 +(R_1^2 + R^2)[R_1^2 -2R_1 R + R^2 - 4c^2] </math> |
|
|
<math>~=</math> |
<math>~ 2R_1 R[ (R_1-R)^2 +(R_1^2 + R^2)(\cos\psi - 1)] </math> |
|
|
<math>~=</math> |
<math>~ 2R_1 R[ (R_1^2 + R^2)\cos\psi - 2R_1 R] </math> |
|
|
<math>~=</math> |
<math>~ (2R_1 R)^2 \biggl[ \cos^2\psi + \biggl(\frac{2c^2 }{R_1 R}\biggr)\cos\psi - 1 \biggr] </math> |
Hence,
|
<math>~ \frac{d(\cos\psi)}{dc} </math> |
<math>~=</math> |
<math>~\frac{(2R_1 R)^2 }{4cR^2 R_1^2}\biggl\{ \cos\psi \biggl[ \cos^2\psi + \biggl(\frac{2c^2 }{R_1 R}\biggr)\cos\psi - 1 \biggr] -~\frac{8c^2R R_1}{(2R_1 R)^2 } \biggr\} </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{c}\biggl\{ \cos\psi \biggl[ \cos^2\psi + \biggl(\frac{2c^2 }{R_1 R}\biggr)\cos\psi - 1 \biggr] -~\frac{2c^2}{R_1 R } \biggr\} </math> |
|
<math>~ \Rightarrow ~~~ 2c\cdot \frac{d(\cos\psi)}{dc} </math> |
<math>~=</math> |
<math>~ 2\cos\psi \biggl[ \cos^2\psi + \biggl(\frac{2c^2 }{R_1 R}\biggr)\cos\psi - 1 \biggr] -~\frac{4c^2}{R_1 R } </math> |
Step 4
Then, drawing upon known expressions for the derivatives of elliptic integrals, as are now tidily catalogued online in NIST's Digital Library of Mathematical Functions, Dyson showed that,
|
LaTeX mathematical expressions cut-and-pasted directly from
|
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
According to §19.4 of NIST's Digital Library of Mathematical Functions,
where, <math>~k^{\prime} \equiv \sqrt{1 - k^2} \, .</math> |
|
<math>~\frac{d\mathfrak{I}(r,\theta,c)}{dc} = \frac{d}{dc}\biggl[\frac{4K(\mu)}{R_1+R}\biggr]</math> |
<math>~=</math> |
<math>~ 4K(\mu) \frac{d}{dc}\biggl[ R_1 + R \biggr]^{-1} + \frac{4}{(R_1+R)} \biggl[ \frac{E\left(\mu\right)-{\mu^{\prime}}^{2}K\left(\mu\right)}{\mu{\mu^{\prime}}^{2}} \biggr]\frac{d\mu}{dc} </math> |
|
|
<math>~=</math> |
<math>~ -~\frac{4K(\mu)}{(R_1+R)^2} \biggl[ \frac{dR_1}{dc} + \frac{dR}{dc} \biggr] ~-~ \frac{4}{(R_1+R)} \biggl[ \frac{K\left(\mu\right)}{\mu} \biggr]\frac{\mu}{c}\cos\psi + \frac{4}{(R_1+R)} \biggl[ \frac{E\left(\mu\right)}{\mu{\mu^{\prime}}^{2}} \biggr]\frac{\mu}{c}\cos\psi </math> |
|
|
<math>~=</math> |
<math>~ -~\frac{4K(\mu)}{(R_1+R)^2} \biggl[ \frac{4c^2 + R_1^2 - R^2}{4cR_1} + \frac{4c^2 + R^2 - R_1^2}{4cR} \biggr] ~-~ \biggl[ \frac{4K\left(\mu\right)}{c(R_1+R)} \biggr] \cos\psi + \frac{4E\left(\mu\right)}{c(R_1+R)} \biggl[ \frac{(R_1+R)^2}{4RR_1} \biggr]\cos\psi </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(R_1+R)E\left(\mu\right)}{cRR_1}\biggr] \cos\psi ~-~ \biggl[ \frac{4K\left(\mu\right)}{c(R_1+R)}\biggr] \cos\psi ~-~ \frac{4K(\mu)}{4cR_1 R (R_1+R)^2} \biggl[ R(4c^2 + R_1^2 - R^2) + R_1(4c^2 + R^2 - R_1^2) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(R_1+R)E\left(\mu\right)}{cRR_1}\biggr] \cos\psi ~-~ \biggl[ \frac{4K\left(\mu\right)}{c(R_1+R)}\biggr] \cos\psi ~-~ \frac{K(\mu)}{cR_1 R (R_1+R)^2}\biggl[(4c^2 + R_1R)(R_1+R) - (R_1^3 + R^3) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(R_1+R)E\left(\mu\right)}{cRR_1}\biggr] \cos\psi ~-~ \biggl[ \frac{4K\left(\mu\right)}{c(R_1+R)}\biggr] \cos\psi ~-~ \frac{K(\mu)}{cR_1 R (R_1+R)}\biggl[(4c^2 + R_1R) - (R_1^2 + R^2 - R_1R) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(R_1+R)E\left(\mu\right)}{cRR_1}\biggr] \cos\psi ~-~ \biggl[ \frac{4K\left(\mu\right)}{c(R_1+R)}\biggr] \cos\psi ~-~ \frac{K(\mu)}{cR_1 R (R_1+R)}\biggl[4c^2 - (R_1 - R)^2 \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(R_1+R)E\left(\mu\right)}{cRR_1}\biggr] \cos\psi ~-~ \biggl[ \frac{4K\left(\mu\right)}{c(R_1+R)}\biggr] \cos\psi ~-~ \frac{K(\mu)}{c (R_1+R)}\biggl[2(1-\cos\psi) \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(R_1+R)E\left(\mu\right)}{cRR_1}\biggr] \cos\psi~-~\frac{2K(\mu)}{c (R_1+R)}(1+\cos\psi) </math> |
|
<math>~\Rightarrow ~~~\frac{1}{c}\cdot \frac{d\mathfrak{I}(r,\theta,c)}{dc} </math> |
<math>~=</math> |
<math>~ \frac{1}{c^2}\biggl\{\biggl[ \frac{E(\mu)(R+R_1)}{RR_1} \biggr] \cos\psi ~-~\biggl[ \frac{4K(\mu)}{R+R_1} \biggr] \cos^2\frac{\psi}{2} \biggr\} \, . </math> |
This expression appears at the top of Dyson's p. 62.
Step 5
Differentiating a second time gives,
|
<math>~\frac{d}{dc}\biggl[\frac{1}{c}\cdot \frac{d\mathfrak{I}(r,\theta,c)}{dc}\biggr] </math> |
<math>~=</math> |
<math>~ \frac{d}{dc}\biggl\{ \biggl[ \frac{(R_1+R)E\left(\mu\right)}{c^2RR_1}\biggr] \cos\psi~-~\frac{2K(\mu)}{c^2 (R_1+R)}(1+\cos\psi) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ ~-~\frac{2}{c^3}\biggl\{ \biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \cos\psi~-~\frac{2K(\mu)}{ (R_1+R)}(1+\cos\psi) \biggr\} </math> |
|
|
|
<math>~ ~+~\frac{1}{c^2}\cdot \frac{d}{dc}\biggl\{ \biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \cos\psi~-~\frac{2K(\mu)}{ (R_1+R)}(1+\cos\psi) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ ~-~\frac{2}{c^3}\biggl\{ \biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \cos\psi~-~\frac{2K(\mu)}{ (R_1+R)}(1+\cos\psi) \biggr\} </math> |
|
|
|
<math>~ ~+~\frac{1}{c^2}\cdot \frac{d}{dc}\biggl\{ \biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}~-~\frac{2K(\mu)}{ (R_1+R)}\biggr] \cos\psi\biggr\} ~-~\frac{1}{c^2}\cdot \frac{d}{dc}\biggl[ \frac{2K(\mu)}{ (R_1+R)} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ ~-~\frac{2}{c^3}\biggl\{ \biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \cos\psi~-~\frac{2K(\mu)}{ (R_1+R)}(1+\cos\psi) \biggr\} ~+~\frac{1}{c^2}\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}~-~\frac{2K(\mu)}{ (R_1+R)}\biggr] \frac{d(\cos\psi)}{dc} </math> |
|
|
|
<math>~ ~+~\frac{\cos\psi}{c^2}\cdot \frac{d}{dc}\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] ~-~\frac{(1+\cos\psi)}{2c^2}\cdot \frac{d}{dc}\biggl[\frac{4K(\mu)}{ (R_1+R)}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{c^3}\biggl[ \frac{4K(\mu)}{ (R_1+R)}\biggr]\biggl[(1+\cos\psi) - \biggl(\frac{c}{2}\biggr) \frac{d(\cos\psi)}{dc}\biggr] ~-~\frac{2}{c^3}\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl[ \cos\psi - \biggl(\frac{c}{2}\biggr) \frac{d(\cos\psi)}{dc}\biggr] </math> |
|
|
|
<math>~ ~+~\frac{\cos\psi}{c^2}\cdot \frac{d}{dc}\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] ~-~\frac{(1+\cos\psi)}{2c^3} \biggl\{\biggl[ \frac{E(\mu)(R+R_1)}{RR_1} \biggr] \cos\psi ~-~\biggl[ \frac{4K(\mu)}{R+R_1} \biggr] \cos^2\frac{\psi}{2} \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{c^3}\biggl[ \frac{4K(\mu)}{ (R_1+R)}\biggr]\biggl[\frac{(1+\cos\psi)^2}{2^2} + (1+\cos\psi) - \biggl(\frac{c}{2}\biggr) \frac{d(\cos\psi)}{dc}\biggr] </math> |
|
|
|
<math>~ ~-~\frac{2}{c^3}\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl[\frac{(\cos\psi+\cos^2\psi)}{4} ~+~ \cos\psi ~-~ \biggl(\frac{c}{2}\biggr) \frac{d(\cos\psi)}{dc}\biggr] ~+~\frac{\cos\psi}{c^2}\cdot \frac{d}{dc}\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{4c^3}\biggl[ \frac{4K(\mu)}{ (R_1+R)}\biggr]\biggl[5+6\cos\psi + \cos^2\psi - 2c \cdot \frac{d(\cos\psi)}{dc}\biggr] </math> |
|
|
|
<math>~ ~-~\frac{1}{2c^3}\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl[5\cos\psi+\cos^2\psi ~-~ 2c \cdot \frac{d(\cos\psi)}{dc}\biggr] ~+~\frac{\cos\psi}{c^2}\cdot \frac{d}{dc}\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \, . </math> |
Now,
|
<math>~ \frac{d}{dc}\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] </math> |
<math>~=</math> |
<math>~ \biggl[ \frac{(R_1+R)}{RR_1}\biggr]\frac{dE\left(\mu\right)}{d\mu} \cdot \frac{d\mu}{dc} ~+~ E\left(\mu\right)\frac{d}{dc}\biggl[ \frac{(R_1+R)}{RR_1}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(R_1+R)}{RR_1}\biggr]\biggl[\frac{E(\mu) - K(\mu)}{c} \biggr] \cos\psi ~+~ E\left(\mu\right)\biggl\{ \frac{1}{RR_1}\biggl[\frac{dR_1}{dc} + \frac{dR}{dc}\biggr] ~-~ (R_1+R)\biggl[\frac{1}{R R_1^2} \frac{dR_1}{dc} + \frac{1}{R^2 R_1} \frac{dR}{dc}\biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[ \frac{(R_1+R)}{RR_1}\biggr]\biggl[\frac{E(\mu) - K(\mu)}{c} \biggr] \cos\psi ~-~ E\left(\mu\right)\biggl\{ \biggl[\frac{1}{R^2} \frac{dR}{dc}\biggr] ~+~ \biggl[\frac{1}{R_1^2} \frac{dR_1}{dc} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ ~-~K(\mu)\biggl[ \frac{(R_1+R)}{cRR_1}\biggr] \cos\psi +E(\mu)\biggl[ \frac{(R_1+R)}{cRR_1}\biggr] \cos\psi ~-~ E\left(\mu\right)\biggl\{ \biggl[\frac{4c^2 + R^2-R_1^2}{4cR^3}\biggr] ~+~ \biggl[ \frac{4c^2+R_1^2-R^2}{4cR_1^3} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ ~-~K(\mu)\biggl[ \frac{(R_1+R)}{cRR_1}\biggr] \cos\psi +E(\mu)\biggl[ \frac{(R_1+R)}{cRR_1}\biggr] \cos\psi ~+~ E\left(\mu\right)\biggl\{ \biggl[\frac{R_1^2 + R^2-4c^2 }{4cR^3}\biggr] ~-~\biggl[\frac{R^2 }{2cR^3}\biggr] ~+~ \biggl[ \frac{R_1^2 + R^2-4c^2}{4cR_1^3} \biggr] ~-~ \biggl[ \frac{R_1^2}{2cR_1^3} \biggr] \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ ~-~K(\mu)\biggl[ \frac{(R_1+R)}{cRR_1}\biggr] \cos\psi +E(\mu)\biggl[ \frac{(R_1+R)}{cRR_1}\biggr] \cos\psi ~+~ \frac{E\left(\mu\right)}{2cR_1^2R^2} \biggl\{ R_1^3 \cos\psi ~-~R R_1^2 ~+~ R^3\cos\psi ~-~ R_1 R^2 \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ ~-~K(\mu)\biggl[ \frac{(R_1+R)}{cRR_1}\biggr] \cos\psi +E(\mu)\biggl[ \frac{(R_1+R)}{cRR_1}\biggr] \cos\psi ~+~ \frac{E\left(\mu\right)}{2cR_1^2R^2} \biggl\{ (R_1^3 + R^3) \cos\psi ~-~R R_1(R_1 + R) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ ~-~K(\mu)\biggl[ \frac{(R_1+R)}{cRR_1}\biggr] \cos\psi +E(\mu)\biggl[ \frac{(R_1+R)}{cRR_1}\biggr] \cos\psi ~+~ \frac{E\left(\mu\right)(R_1+R)}{2cR_1^2R^2} \biggl\{ (R_1^2 + R^2 - 4c^2) \cos\psi + 4c^2\cos\psi~-~R R_1(1+\cos\psi) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ ~-~K(\mu)\biggl[ \frac{(R_1+R)}{cRR_1}\biggr] \cos\psi +E(\mu)\biggl[ \frac{(R_1+R)}{cRR_1}\biggr] \cos\psi ~+~ \frac{E\left(\mu\right)(R_1+R)}{cR_1 R} \biggl\{ \cos^2\psi ~+~ \frac{2c^2\cos\psi }{R_1R} ~-~\frac{1}{2}(1+\cos\psi) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ ~-~K(\mu)\biggl[ \frac{(R_1+R)}{cRR_1}\biggr] \cos\psi ~+~ \frac{E\left(\mu\right)(R_1+R)}{cR_1 R} \biggl[ \cos^2\psi ~+~\frac{1}{2}(\cos\psi - 1) ~+~ \frac{2c^2\cos\psi }{R_1R} \biggr] \, . </math> |
We therefore have,
|
<math>~\frac{1}{c} \cdot \frac{d}{dc}\biggl[\frac{1}{c}\cdot \frac{d\mathfrak{I}(r,\theta,c)}{dc}\biggr] </math> |
<math>~=</math> |
<math>~ \frac{1}{4c^4}\biggl[ \frac{4K(\mu)}{ (R_1+R)}\biggr]\biggl\{ 5+6\cos\psi + \cos^2\psi ~-~2\cos\psi \biggl[ \cos^2\psi + \biggl(\frac{2c^2 }{R_1 R}\biggr)\cos\psi - 1 \biggr]~+~\frac{4c^2}{R_1 R } \biggr\} </math> |
|
|
|
<math>~ ~-~\frac{1}{2c^4}\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl\{ 5\cos\psi+\cos^2\psi ~-~2\cos\psi \biggl[ \cos^2\psi + \biggl(\frac{2c^2 }{R_1 R}\biggr)\cos\psi - 1 \biggr]~+~\frac{4c^2}{R_1 R } \biggr\} </math> |
|
|
|
<math>~ ~+~\frac{\cos\psi}{c^4} \biggl\{ \frac{E\left(\mu\right)(R_1+R)}{R_1 R} \biggl[ \cos^2\psi ~+~\frac{1}{2}(\cos\psi - 1) ~+~ \frac{2c^2\cos\psi }{R_1R} \biggr] ~-~K(\mu)\biggl[ \frac{(R_1+R)}{RR_1}\biggr] \cos\psi \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{c^4}\biggl[ \frac{K(\mu)}{ (R_1+R)}\biggr]\biggl\{ 5+6\cos\psi + \cos^2\psi ~-~2\cos\psi \biggl[ \cos^2\psi + \biggl(\frac{2c^2 }{R_1 R}\biggr)\cos\psi - 1 \biggr]~+~\frac{4c^2}{R_1 R } \biggr\} </math> |
|
|
|
<math>~ ~-~\frac{1}{2c^4}\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl\{ 5\cos\psi+\cos^2\psi ~-~2\cos\psi \biggl[ \cos^2\psi + \biggl(\frac{2c^2 }{R_1 R}\biggr)\cos\psi - 1 \biggr]~+~\frac{4c^2}{R_1 R } \biggr\} </math> |
|
|
|
<math>~ ~-~\frac{1}{2c^4} \biggl[ \frac{E\left(\mu\right)(R_1+R)}{R_1 R}\biggr] \biggl[ ~-~2\cos^3\psi ~-~\cos^2\psi ~+~ \cos\psi ~-~ \frac{4c^2\cos^2\psi }{R_1R} \biggr] </math> |
|
|
|
<math>~ ~+~\frac{1}{c^4}\biggl[\frac{K(\mu)}{(R_1 + R)}\biggr] \biggl[~-~ \frac{(R_1+R)^2\cos^2\psi}{RR_1}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{c^4}\biggl[ \frac{K(\mu)}{ (R_1+R)}\biggr]\biggl\{ 5 ~+~ 8\cos\psi ~+~ \cos^2\psi ~-~2\cos^3\psi ~+~\frac{4c^2}{R_1 R } ~-~ \biggl[ \frac{R_1^2 + R^2 - 4c^2 }{R_1 R} \biggr]\cos^2\psi ~-~ \biggl[ \frac{2R_1R }{R_1 R} \biggr]\cos^2\psi ~-~ \biggl[ \frac{8c^2 }{R_1 R} \biggr]\cos^2\psi \biggr\} </math> |
|
|
|
<math>~ ~-~\frac{1}{2c^4}\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl\{ 8\cos\psi ~-~4\cos^3\psi ~+~ \biggl(\frac{4c^2 }{R_1 R}\biggr)(1-2\cos^2\psi) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{c^4}\biggl[ \frac{K(\mu)}{ (R_1+R)}\biggr]\biggl\{ 5 ~+~ 8\cos\psi ~-~ \cos^2\psi ~-~4\cos^3\psi ~+~\frac{4c^2}{R_1 R }(1-2\cos^2\psi) \biggr\} </math> |
|
|
|
<math>~ ~-~\frac{1}{c^4}\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl\{ 4\cos\psi ~-~2\cos^3\psi ~+~ \biggl(\frac{2c^2 }{R_1 R}\biggr)(1-2\cos^2\psi) \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{c^4}\biggl[ \frac{K(\mu)}{ (R_1+R)}\biggr]\biggl\{ 5 ~+~ 8\cos\psi ~-~ \cos^2\psi ~-~4\cos^3\psi ~-~\biggl( \frac{4c^2}{R_1 R } \biggr) \cos 2\psi \biggr\} </math> |
|
|
|
<math>~ ~+~\frac{1}{c^4}\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl\{ ~-~4\cos\psi ~+~2\cos^3\psi ~+~ \biggl(\frac{2c^2 }{R_1 R}\biggr)\cos 2\psi \biggr\} \, , </math> |
which exactly matches the second equation from the top of p. 62 in Dyson (1893a).
Step 6 (Summary)
In summary, then,
|
<math>~\frac{\pi V(r,\theta)}{M}</math> |
<math>~=</math> |
<math>~ \mathfrak{I}(r,\theta,c) ~+~ \frac{a^2}{2^3} ~\frac{1}{c} \cdot \frac{d}{dc} \biggl[ \mathfrak{I}(r,\theta,c)\biggr] ~-~ \frac{a^4}{2^6\cdot 3} ~\frac{1}{c} \cdot \frac{d}{dc} \biggl\{ \frac{1}{c} \cdot \frac{d}{dc} \biggl[ \mathfrak{I}(r,\theta,c)\biggr]\biggr\} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{4K(\mu)}{R_1+R} ~+~ \frac{1}{2^3} ~\frac{a^2}{c^2}\biggl\{\biggl[ \frac{E(\mu)(R+R_1)}{RR_1} \biggr] \cos\psi ~-~\biggl[ \frac{4K(\mu)}{R+R_1} \biggr] \cos^2\frac{\psi}{2} \biggr\} </math> |
|
|
|
<math>~ ~-~ \frac{1}{2^6\cdot 3} \frac{a^4}{c^4} \biggl\{ \biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl[ ~-~4\cos\psi ~+~2\cos^3\psi ~+~ \biggl(\frac{2c^2 }{R_1 R}\biggr)\cos 2\psi \biggr] </math> |
|
|
|
<math>~ ~+~ \biggl[ \frac{K(\mu)}{ (R_1+R)}\biggr]\biggl[ 5 ~+~ 8\cos\psi ~-~ \cos^2\psi ~-~4\cos^3\psi ~-~\biggl( \frac{4c^2}{R_1 R } \biggr) \cos 2\psi \biggr] \biggr\} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, . </math> |
In preparation for a comparison between Dyson's expression and the expression derived by Wong (1973), let's regroup terms according to the various trigonometric functions. Keep in mind that,
|
<math>~\cos^2 \frac{\psi}{2}</math> |
<math>~=</math> |
<math>~\frac{1}{2}(1 + \cos\psi) \, ;</math> |
|
<math>~\cos^2 \psi</math> |
<math>~=</math> |
<math>~\frac{1}{2}(1 + \cos2\psi) \, ;</math> |
|
<math>~\cos^3 \psi</math> |
<math>~=</math> |
<math>~\frac{1}{4}(3\cos\psi + \cos3\psi) \, .</math> |
Hence, we have,
|
<math>~\frac{\pi V(r,\theta)}{M}</math> |
<math>~=</math> |
<math>~ \frac{4K(\mu)}{R_1+R} ~+~ \frac{1}{2^3} ~\frac{a^2}{c^2}\biggl\{\biggl[ \frac{E(\mu)(R+R_1)}{RR_1} \biggr] \cos\psi ~-~\biggl[ \frac{2K(\mu)}{R+R_1} \biggr] (1+\cos\psi) \biggr\} </math> |
|
|
|
<math>~ ~-~ \frac{1}{2^6\cdot 3} \frac{a^4}{c^4} \biggl\{ \biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl[ ~-~4\cos\psi ~+~\frac{1}{2}(3\cos\psi + \cos3\psi) ~+~ \biggl(\frac{2c^2 }{R_1 R}\biggr)\cos 2\psi \biggr] </math> |
|
|
|
<math>~ ~+~ \biggl[ \frac{K(\mu)}{ (R_1+R)}\biggr]\biggl[ 5 ~+~ 8\cos\psi ~-~ \frac{1}{2}(1 + \cos2\psi) ~-~(3\cos\psi + \cos3\psi) ~-~\biggl( \frac{4c^2}{R_1 R } \biggr) \cos 2\psi \biggr] \biggr\} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{4K(\mu)}{R_1+R} ~-~\frac{1}{2^3} ~\frac{a^2}{c^2}\biggl[ \frac{2K(\mu)}{R+R_1} \biggr] ~+~ \frac{1}{2^3} ~\frac{a^2}{c^2}\biggl[ \frac{E(\mu)(R+R_1)}{RR_1} \biggr] \cos\psi ~-~\frac{1}{2^3} ~\frac{a^2}{c^2}\biggl[ \frac{2K(\mu)}{R+R_1} \biggr] \cos\psi </math> |
|
|
|
<math>~ ~-~ \frac{1}{2^7\cdot 3} \frac{a^4}{c^4} \biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl[ ~-~5\cos\psi ~+~ \biggl(\frac{4c^2 }{R_1 R}\biggr)\cos 2\psi ~+~ \cos3\psi \biggr] </math> |
|
|
|
<math>~ ~-~ \frac{1}{2^7\cdot 3} \frac{a^4}{c^4} \biggl[ \frac{K(\mu)}{ (R_1+R)}\biggr]\biggl[ 9 ~+~ 10\cos\psi ~-~ \cos2\psi ~-~\biggl( \frac{8c^2}{R_1 R } \biggr) \cos 2\psi ~-~2 \cos3\psi \biggr] ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{2K(\mu)}{R_1+R} \biggl[ 2 ~-~\frac{1}{2^3} ~\frac{a^2}{c^2} ~-~ \frac{3}{2^8} \frac{a^4}{c^4}~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr] </math> |
|
|
|
<math>~ ~+~\biggl\{ ~-~ \frac{5}{2^6\cdot 3} \frac{a^4}{c^4} \biggl[ \frac{K(\mu)}{ (R_1+R)}\biggr] ~+~\frac{1}{2^3} ~\frac{a^2}{c^2}\biggl[ \frac{E(\mu)(R+R_1)}{RR_1} \biggr] ~-~\frac{1}{2^3} ~\frac{a^2}{c^2}\biggl[ \frac{2K(\mu)}{R+R_1} \biggr] ~+~ \frac{5}{2^7\cdot 3} \frac{a^4}{c^4} \biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggr\}\cos\psi </math> |
|
|
|
<math>~ ~+~ \biggl\{ \frac{1}{2^7\cdot 3} \frac{a^4}{c^4} \biggl[ \frac{K(\mu)}{ (R_1+R)}\biggr]\biggl[ 1 ~+~\biggl( \frac{8c^2}{R_1 R } \biggr) \biggr] ~-~ \frac{1}{2^7\cdot 3} \frac{a^4}{c^4} \biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl(\frac{4c^2 }{R_1 R}\biggr) \biggr\} \cos 2\psi </math> |
|
|
|
<math>~ ~+~\biggl\{ \frac{1}{2^6\cdot 3} \frac{a^4}{c^4} \biggl[ \frac{K(\mu)}{ (R_1+R)}\biggr] ~-~ \frac{1}{2^7\cdot 3} \frac{a^4}{c^4} \biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggr\}\cos3\psi ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) </math> |
|
|
<math>~=</math> |
<math>~ \frac{2K(\mu)}{R_1+R} \biggl[ 2 ~-~\frac{1}{2^3} ~\frac{a^2}{c^2} ~-~ \frac{3}{2^8} \frac{a^4}{c^4}~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr] </math> |
|
|
|
<math>~ ~-~\biggl[ \frac{2K(\mu)}{R+R_1} ~-~ \frac{E(\mu)(R+R_1)}{RR_1} \biggr] \biggl[ \frac{1}{2^3} ~\frac{a^2}{c^2} ~+~ \frac{5}{2^7\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr]\cos\psi </math> |
|
|
|
<math>~ ~+~ \biggl\{ \biggl[ \frac{ 2K(\mu)}{ (R_1+R)}\biggr]\biggl[ \frac{1}{2} ~+~\biggl( \frac{4c^2}{R_1 R } \biggr) \biggr] ~-~\biggl[ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl(\frac{4c^2 }{R_1 R}\biggr) \biggr\} \biggl[ \frac{1}{2^7\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr]\cos 2\psi </math> |
|
|
|
<math>~ ~+~ \biggl[ \frac{2K(\mu)}{ (R_1+R)} ~-~ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl[ \frac{1}{2^7\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr)\biggr] \cos3\psi </math> |
|
|
<math>~=</math> |
<math>~ \frac{2K(\mu)}{R_1+R} \biggl[ 2 ~-~\frac{1}{2^3} ~\frac{a^2}{c^2} ~-~ \frac{3}{2^8} \frac{a^4}{c^4}~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr] </math> |
|
|
|
<math>~ ~-~\biggl[ \frac{2K(\mu)}{R+R_1} ~-~ \frac{E(\mu)(R+R_1)}{RR_1} \biggr] \biggl[ \frac{1}{2^3} ~\frac{a^2}{c^2} ~+~ \frac{5}{2^7\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr]\cos\psi </math> |
|
|
|
<math>~ ~+~ \biggl[ \frac{ 2K(\mu)}{ (R_1+R)}~-~\frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl(\frac{4c^2 }{R_1 R}\biggr) \biggl[ \frac{1}{2^7\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr]\cos 2\psi ~+~ \biggl[ \frac{ 2K(\mu)}{ (R_1+R)}\biggr] \biggl[ \frac{1}{2^8\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr]\cos 2\psi </math> |
|
|
|
<math>~ ~+~\biggl[ \frac{2K(\mu)}{ (R_1+R)} ~-~ \frac{(R_1+R)E\left(\mu\right)}{RR_1}\biggr] \biggl[ \frac{1}{2^7\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr)\biggr] \cos3\psi </math> |
Now, drawing from our accompanying discussion of relationships between complete elliptic integrals and relationships between their parameter arguments and, in particular, associating Dyson's parameter, <math>~\mu = (R_1-R)/(R_1+R)</math>, with <math>~k_1</math>, we understand that,
|
<math>~\frac{2E(\mu)}{1+\mu} - (1-\mu)K(\mu)</math> |
<math>~=</math> |
<math>~E(k) \, ,</math> |
where the alternate parameter,
<math>~k = \frac{2\sqrt{\mu}}{1+\mu} = \biggl[1 - \biggr(\frac{R}{R_1}\biggr)^2\biggr]^{1 / 2} = \biggl[ \frac{2}{\coth\eta+1}\biggr]^{1 / 2} = \sqrt{1-e^{-2\eta}} \, .</math>
Hence, we appreciate that,
|
<math>~E(k)</math> |
<math>~=</math> |
<math>~ 2E(\mu) \biggl[ 1 + \frac{R_1-R}{R_1+R} \biggr]^{-1} - \biggl[ 1 - \frac{R_1-R}{R_1+R} \biggr]K(\mu) </math> |
|
|
<math>~=</math> |
<math>~ 2E(\mu) \biggl[ \frac{2R_1}{R_1+R} \biggr]^{-1} - \biggl[ \frac{2R}{R_1+R} \biggr]K(\mu) </math> |
|
|
<math>~=</math> |
<math>~ R \biggl[ \frac{E(\mu)(R_1+R)}{RR_1} - \frac{2K(\mu)}{R_1+R} \biggr] </math> |
As a result, we can rewrite Dyson's expression for the external potential as,
|
<math>~\frac{\pi V(r,\theta)}{M}</math> |
<math>~=</math> |
<math>~ \frac{2K(\mu)}{R_1+R} \biggl[ 2 ~-~\frac{1}{2^3} ~\frac{a^2}{c^2} ~-~ \frac{3}{2^8} \frac{a^4}{c^4}~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr] ~+~\frac{E(k)}{R} \biggl[ \frac{1}{2^3} ~\frac{a^2}{c^2} ~+~ \frac{5}{2^7\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr]\cos\psi </math> |
|
|
|
<math>~ ~-~ \frac{E(k)}{R}\biggl(\frac{4c^2 }{R_1 R}\biggr) \biggl[ \frac{1}{2^7\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr]\cos 2\psi ~+~ \biggl[ \frac{ 2K(\mu)}{ (R_1+R)}\biggr] \biggl[ \frac{1}{2^8\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr]\cos 2\psi </math> |
|
|
|
<math>~ ~-~\frac{E(k)}{R} \biggl[ \frac{1}{2^7\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr)\biggr] \cos3\psi </math> |
|
|
<math>~=</math> |
<math>~ \frac{2K(\mu)}{R_1+R} \biggl\{\biggl[ 2 ~-~\frac{1}{2^3} ~\frac{a^2}{c^2} ~-~ \frac{3}{2^8} \frac{a^4}{c^4}~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr] ~+~\biggl[ \frac{1}{2^8\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr]\cos 2\psi \biggr\} </math> |
|
|
|
<math>~ ~+~\frac{E(k)}{R} \biggl\{ \biggl[ \frac{1}{2^3} ~\frac{a^2}{c^2} ~+~ \frac{5}{2^7\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr]\cos\psi ~-~ \biggl(\frac{4c^2 }{R_1 R}\biggr) \biggl[ \frac{1}{2^7\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \biggr]\cos 2\psi ~-~ \biggl[ \frac{1}{2^7\cdot 3} \frac{a^4}{c^4} ~+~\mathcal{O}\biggl(\frac{a^5}{c^5}\biggr)\biggr] \cos3\psi \biggr\} \, . </math> |
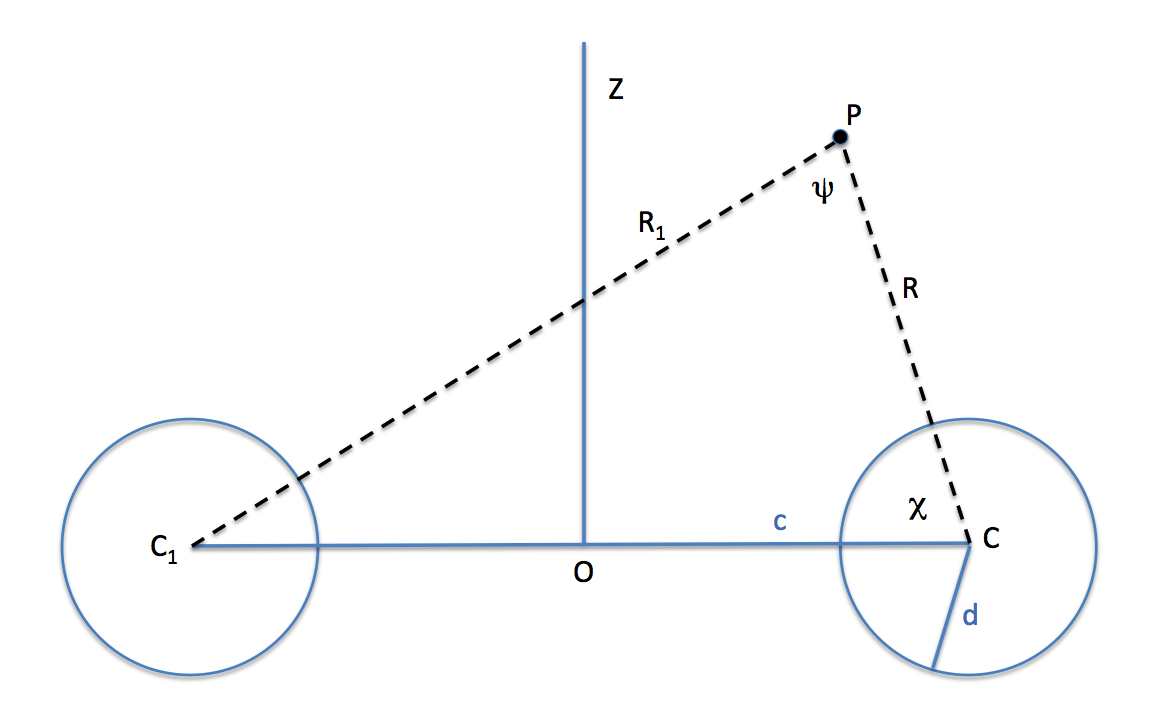
External Potential in Terms of Angle χ
|
Is it relatively straightforward to develop a similar expression for the external potential that is written in terms of the angle, <math>~\chi</math>, instead of (as above) in terms of the angle, <math>~\psi</math> ? This would make the transition to Dyson's Paper II smoother. Initially I have in mind making the transformation via the law of sines, whereby,
|
<math>~\frac{R_1}{\sin\chi}</math> |
<math>~=</math> |
<math>~\frac{2c}{\sin\psi}</math> |
<math>~=</math> |
<math>~\frac{R}{\sin(\pi - \psi - \chi)} \, .</math> |
This means that the following associations may be used as well:
|
<math>~\sin\psi</math> |
<math>~=</math> |
<math>~ \biggl(\frac{2c}{R_1} \biggr)\sin\chi \, ; </math> |
|
<math>~\cos^2\psi = 1 - \sin^2\psi</math> |
<math>~=</math> |
<math>~ 1 - \biggl[\biggl(\frac{2c}{R_1} \biggr)\sin\chi \biggr]^2\, . </math> |
From an accompanying discussion that builds upon the law of cosines, we also may write,
|
<math>~2\biggl(\frac{R_1}{c}\biggr)^{-1} </math> |
<math>~=</math> |
<math>~1 + \frac{1}{2}\biggl(\frac{a}{c}\biggr)\cos\chi + \frac{1}{2^3}\biggl(\frac{a}{c}\biggr)^2 \biggl[ 3\cos^2\chi - 1 \biggr] + \frac{1}{2^4}\biggl(\frac{a}{c}\biggr)^3\biggl[ 5\cos^3\chi ~-~ 3\cos\chi \biggr] </math> |
|
|
|
<math>~ ~+~ \frac{1}{2^7} \biggl( \frac{a}{c}\biggr)^4 \biggl[ 3 ~-~ 30 \cos^2\chi ~+~ 35 \cos^4\chi \biggr] ~+~ \mathcal{O}\biggl(\frac{a^5}{c^5}\biggr) \, . </math> |
Compare Notations Used by Dyson and Wong
|
Dyson's Notation (slightly modified) |
Wong's Notation (slightly modified) |
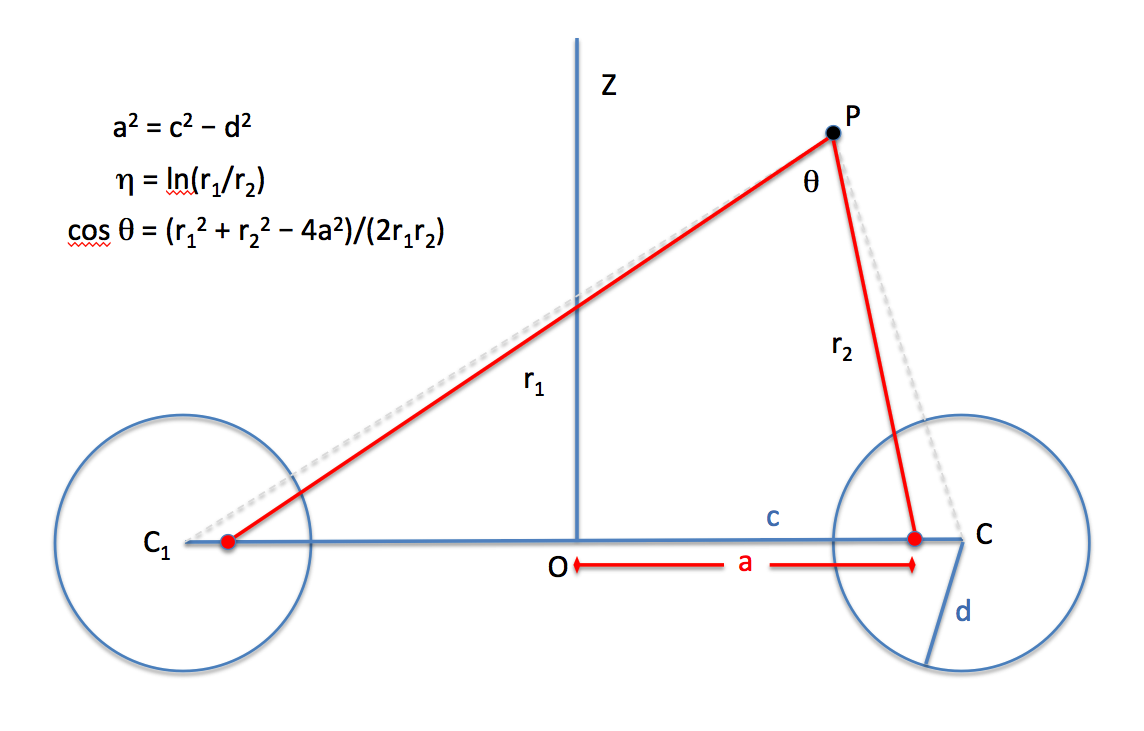
Key relationship, with understanding that, <math>~\epsilon \equiv d/c</math>:
|
<math>~a^2</math> |
<math>~=</math> |
<math>~c^2 (1 - \epsilon^2)</math> |
<math>~\Rightarrow</math> |
<math>~\frac{a}{c}</math> |
<math>~=</math> |
<math>~(1 - \epsilon^2)^{1 / 2} \, .</math> |
Relationship Between Lengths
Subtraction
In both cases, lengths are referenced to the same "external" point whose meridional-plane coordinates are, <math>~(\varpi,z)</math>. Hence,
|
<math>~R^2</math> |
<math>~=</math> |
<math>~z^2 + (c-\varpi)^2 </math> |
|
<math>~r_2^2</math> |
<math>~=</math> |
<math>~z^2 + (a-\varpi)^2</math> |
|
<math>~\Rightarrow~R^2 - r_2^2</math> |
<math>~=</math> |
<math>~(c-\varpi)^2 - (a-\varpi)^2</math> |
|
|
<math>~=</math> |
<math>~(c^2 - 2c\varpi + \varpi^2) - (a^2 -2a\varpi +\varpi^2)</math> |
|
|
<math>~=</math> |
<math>~c^2 - a^2 - 2(c-a)\varpi</math> |
|
<math>~\Rightarrow~\varpi </math> |
<math>~=</math> |
<math>~\frac{c^2 - a^2 + r_2^2 - R^2}{2(c-a)} \, .</math> |
and,
|
<math>~R_1^2</math> |
<math>~=</math> |
<math>~z^2 + (c+\varpi)^2</math> |
|
<math>~r_1^2</math> |
<math>~=</math> |
<math>~z^2 + (a+\varpi)^2</math> |
|
<math>~\Rightarrow ~~~ R_1^2 - r_1^2</math> |
<math>~=</math> |
<math>~(c+\varpi)^2 - (a+\varpi)^2</math> |
|
|
<math>~=</math> |
<math>~(c^2 + 2c\varpi + \varpi^2) - (a^2 + 2a\varpi +\varpi^2)</math> |
|
|
<math>~=</math> |
<math>~c^2 - a^2 + 2(c - a)\varpi </math> |
|
<math>~\Rightarrow ~~~\varpi </math> |
<math>~=</math> |
<math>~ \frac{R_1^2 - r_1^2 - (c^2 - a^2)}{2(c-a)} \, .</math> |
Put together, then,
|
<math>~\frac{c^2 - a^2 + r_2^2 - R^2}{2(c-a)}</math> |
<math>~=</math> |
<math>~\frac{R_1^2 - r_1^2 - (c^2 - a^2)}{2(c-a)}</math> |
|
<math>~\Rightarrow ~~~(R^2 + R_1^2) - (r_1^2 + r_2^2) </math> |
<math>~=</math> |
<math>~2(c^2 - a^2)</math> |
|
|
<math>~=</math> |
<math>~2c^2 - 2c^2(1-\epsilon^2)</math> |
|
|
<math>~=</math> |
<math>~2c^2\epsilon^2</math> |
Multiplication
|
<math>~R^2R_1^2</math> |
<math>~=</math> |
<math>~[z^2 + (c-\varpi)^2][z^2 + (c+\varpi)^2]</math> |
|
<math>~\Rightarrow ~~~ 0</math> |
<math>~=</math> |
<math>~z^4 + z^2[(c-\varpi)^2 + (c+\varpi)^2] + [(c-\varpi)^2(c+\varpi)^2 - R^2R_1^2]</math> |
|
<math>~\Rightarrow~~~ 2z^2</math> |
<math>~=</math> |
<math>~ \pm \biggl[ [(c-\varpi)^2 + (c+\varpi)^2]^2 - 4[(c-\varpi)^2(c+\varpi)^2-R^2R_1^2] \biggr]^{1 / 2} ~-~ [(c-\varpi)^2 + (c+\varpi)^2] </math> |
|
<math>~r_1^2r_2^2</math> |
<math>~=</math> |
<math>~[z^2 + (a-\varpi)^2][z^2 + (a+\varpi)^2]</math> |
|
<math>~\Rightarrow ~~~ 0</math> |
<math>~=</math> |
<math>~z^4 + z^2[(a-\varpi)^2 + (a+\varpi)^2 ] + [(a-\varpi)^2(a+\varpi)^2 - r_1^2r_2^2]</math> |
|
<math>~\Rightarrow~~~ 2z^2</math> |
<math>~=</math> |
<math>~ \pm \biggl[ [(a-\varpi)^2 + (a+\varpi)^2 ]^2 ~-~ 4[(a-\varpi)^2(a+\varpi)^2 - r_1^2r_2^2] \biggr]^{1 / 2} ~-~ [(a-\varpi)^2 + (a+\varpi)^2 ] </math> |
Note: In order to be physically relevant, the quantity, <math>~2z^2</math>, must be positive. Given that the second term on the RHS is always negative, we conclude that only a solution with the superior (plus) sign is physically relevant.
Hence,
|
<math>~ \biggl[ [(c-\varpi)^2 + (c+\varpi)^2]^2 - 4[(c-\varpi)^2(c+\varpi)^2-R^2R_1^2] \biggr]^{1 / 2} ~-~ [(c-\varpi)^2 + (c+\varpi)^2] </math> |
<math>~=</math> |
<math>~ \biggl[ [(a-\varpi)^2 + (a+\varpi)^2 ]^2 ~-~ 4[(a-\varpi)^2(a+\varpi)^2 - r_1^2r_2^2] \biggr]^{1 / 2} ~-~ [(a-\varpi)^2 + (a+\varpi)^2 ] </math> |
Ratios
Let's work with the following (dimensionless) length ratios:
|
<math>~\lambda_2^2 \equiv \frac{R^2}{r_2^2}</math> |
<math>~=</math> |
<math>~\frac{z^2 + (c-\varpi)^2}{z^2 + (a-\varpi)^2} \, ,</math> |
|
<math>~\lambda_1^2 \equiv \frac{R_1^2}{r_1^2}</math> |
<math>~=</math> |
<math>~\frac{z^2 + (c+\varpi)^2}{z^2 + (a+\varpi)^2} \, .</math> |
Solving for <math>~z^2</math> in the first case, we find,
|
<math>~\lambda_2^2 [z^2 + (a-\varpi)^2]</math> |
<math>~=</math> |
<math>~z^2 + (c-\varpi)^2</math> |
|
<math>~\Rightarrow ~~~z^2( \lambda_2^2 - 1) </math> |
<math>~=</math> |
<math>~(c-\varpi)^2 - \lambda_2^2(a-\varpi)^2</math> |
|
<math>~\Rightarrow ~~~z^2 </math> |
<math>~=</math> |
<math>~\frac{(c-\varpi)^2 - \lambda_2^2(a-\varpi)^2}{( \lambda_2^2 - 1)} \, ;</math> |
and in the second case, we find,
|
<math>~\lambda_1^2 [z^2 + (a+\varpi)^2]</math> |
<math>~=</math> |
<math>~z^2 + (c+\varpi)^2</math> |
|
<math>~\Rightarrow ~~~ z^2 (\lambda_1^2 - 1)</math> |
<math>~=</math> |
<math>~(c+\varpi)^2 - \lambda_1^2 (a+\varpi)^2</math> |
|
<math>~\Rightarrow ~~~ z^2 </math> |
<math>~=</math> |
<math>~\frac{(c+\varpi)^2 - \lambda_1^2(a+\varpi)^2}{(\lambda_1^2 - 1)} \, .</math> |
Combined, this gives,
|
<math>~\frac{(c-\varpi)^2 - \lambda_2^2(a-\varpi)^2}{( \lambda_2^2 - 1)} </math> |
<math>~=</math> |
<math>~\frac{(c+\varpi)^2 - \lambda_1^2(a+\varpi)^2}{(\lambda_1^2 - 1)} </math> |
|
<math>~\Rightarrow ~~~ (\lambda_1^2 - 1)[(c-\varpi)^2 - \lambda_2^2(a-\varpi)^2] </math> |
<math>~=</math> |
<math>~( \lambda_2^2 - 1) [ (c+\varpi)^2 - \lambda_1^2(a+\varpi)^2 ]</math> |
|
<math>~\Rightarrow ~~~ (\lambda_1^2 - 1)[(c^2 - 2c\varpi + \varpi^2) - \lambda_2^2(a^2 - 2a\varpi +\varpi^2 )] </math> |
<math>~=</math> |
<math>~( \lambda_2^2 - 1) [ (c^2 + 2c\varpi + \varpi^2) - \lambda_1^2(a^2+ 2a \varpi + \varpi^2) ]</math> |
|
<math>~\Rightarrow ~~~ (\lambda_1^2 - 1)[c^2 - 2c\varpi + \varpi^2 - a^2\lambda_2^2 + 2a\varpi\lambda_2^2 - \varpi^2\lambda_2^2 ] </math> |
<math>~=</math> |
<math>~( \lambda_2^2 - 1) [ c^2 + 2c\varpi + \varpi^2 -a^2\lambda_1^2 - 2a \varpi\lambda_1^2 - \varpi^2\lambda_1^2 ]</math> |
|
<math>~\Rightarrow ~~~ (\lambda_1^2 - 1)[ ( c^2 - a^2\lambda_2^2 ) + ( 2a\lambda_2^2 - 2c )\varpi + \varpi^2(1 - \lambda_2^2 ) ] </math> |
<math>~=</math> |
<math>~( \lambda_2^2 - 1) [ ( c^2 -a^2\lambda_1^2 ) + ( 2c - 2a \lambda_1^2)\varpi + \varpi^2( 1 - \lambda_1^2 ) ]</math> |
|
<math>~\Rightarrow ~~~ (\lambda_1^2 - 1)( c^2 - a^2\lambda_2^2 ) + \varpi^2(1 - \lambda_2^2 )(\lambda_1^2 - 1) + \varpi( 2a\lambda_2^2 - 2c )(\lambda_1^2 - 1) </math> |
<math>~=</math> |
<math>~ ( \lambda_2^2 - 1)( c^2 -a^2\lambda_1^2 ) + \varpi( 2c - 2a \lambda_1^2)( \lambda_2^2 - 1) + \varpi^2( 1 - \lambda_1^2 )( \lambda_2^2 - 1) \, .</math> |
|
<math>~\Rightarrow ~~~ \varpi^2 [(1 - \lambda_2^2 )(\lambda_1^2 - 1) ~-~ ( 1 - \lambda_1^2 )( \lambda_2^2 - 1) ] </math> |
<math>~=</math> |
<math>~ \varpi [ ( 2c - 2a \lambda_1^2)( \lambda_2^2 - 1) ~-~ ( 2a\lambda_2^2 - 2c )(\lambda_1^2 - 1) ] ~+~[ ( \lambda_2^2 - 1)( c^2 -a^2\lambda_1^2 ) ~-~(\lambda_1^2 - 1)( c^2 - a^2\lambda_2^2 ) ] </math> |
Now, because the coefficient of the <math>~\varpi^2</math> term (on the left-hand-side of this last expression) is zero, we find that,
|
<math>~ 2 \varpi </math> |
<math>~=</math> |
<math>~ \frac{ (\lambda_1^2 - 1)( c^2 - a^2\lambda_2^2 ) ~-~( \lambda_2^2 - 1)( c^2 -a^2\lambda_1^2 ) }{ ( c - a \lambda_1^2)( \lambda_2^2 - 1) ~-~ ( a\lambda_2^2 - c )(\lambda_1^2 - 1) } </math> |
|
|
<math>~=</math> |
<math>~ \frac{ (\lambda_1^2 - \lambda_2^2)(c^2 - a^2) }{ (\lambda_1^2 + \lambda_2^2)(c+a) - 2c } \, . </math> |
Relationship Between Key Angles
Law of Cosines:
|
<math>~(2c)^2</math> |
<math>~=</math> |
<math>~ R_1^2 + R^2 - 2RR_1\cos\psi </math> |
|
<math>~(2a)^2</math> |
<math>~=</math> |
<math>~ r_1^2 + r_2^2 - 2r_1 r_2 \cos\theta </math> |
Try Again
Let's transform from Wong's lengths and angles to the ones used by Dyson. (This will permit us to compare Wong's analytic solution to the approximate one presented by Dyson.) Given the coordinate-pair <math>~(\varpi, z)</math> and Dyson's length scale, <math>~c</math>, we have,
|
<math>~\tan\chi_R</math> |
<math>~=</math> |
<math>~\frac{z}{c-\varpi} \, ,</math> |
|
<math>~R^2</math> |
<math>~=</math> |
<math>~z^2 + (c-\varpi)^2 \, .</math> |
From this pair of expressions we can transform from <math>~(R,\chi_R)</math> to <math>~(\varpi,z)</math> as follows:
|
<math>~c-\varpi</math> |
<math>~=</math> |
<math>~z \cot\chi_R</math> |
|
<math>~\Rightarrow ~~~ R^2</math> |
<math>~=</math> |
<math>~z^2 (1 + \cot\chi^2_R) =\biggl[ \frac{z}{\sin\chi_R} \biggr]^{2}</math> |
|
<math>~\Rightarrow ~~~ z</math> |
<math>~=</math> |
<math>~R\sin\chi_R</math> |
|
<math>~\Rightarrow ~~~ \varpi</math> |
<math>~=</math> |
<math>~c - \cot\chi_R \cdot R\sin\chi_R = c - R\cos\chi_R \, .</math> |
Next, given the coordinate-pair <math>~(\varpi, z)</math> and Wong's length scale, <math>~a</math>, we have,
|
<math>~\tan\chi_2</math> |
<math>~=</math> |
<math>~\frac{z}{a-\varpi} \, ,</math> |
|
<math>~r_2^2</math> |
<math>~=</math> |
<math>~z^2 + (a-\varpi)^2 \, ;</math> |
and, combining the two sets gives,
|
<math>~r_2^2</math> |
<math>~=</math> |
<math>~R^2\sin^2\chi_R + [ R\cos\chi_R + (a - c) ]^2 </math> |
|
|
<math>~=</math> |
<math>~R^2\sin^2\chi_R + [ R^2\cos^2\chi_R + 2(a-c)R\cos\chi_R + (a - c)^2 ] </math> |
|
|
<math>~=</math> |
<math>~R^2 + (a - c)^2 - 2(c-a)R\cos\chi_R \, ;</math> |
|
<math>~\tan\chi_2</math> |
<math>~=</math> |
<math>~\frac{R\sin\chi_R}{R\cos\chi_R + (a - c)} \, .</math> |

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |