Difference between revisions of "User:Tohline/ThreeDimensionalConfigurations/ChallengesPt4"
| Line 8: | Line 8: | ||
==The Plan== | ==The Plan== | ||
<font color="red"><b>STEP #1</b></font> | <font color="red"><b>STEP #1</b></font> | ||
First, we present the mathematical expression that describes the intersection between the surface of an ellipsoid and a plane having the following properties: | |||
<ul> | <ul> | ||
<li>The plane cuts through the ellipsoid's z-axis at a distance, <math>~z_0</math>, from the center of the ellipsoid;</li> | <li>The plane cuts through the ellipsoid's z-axis at a distance, <math>~z_0</math>, from the center of the ellipsoid;</li> | ||
| Line 16: | Line 17: | ||
<li>The line that is perpendicular to the plane and passes through the z-axis at <math>~z_0</math> is tipped at an angle, <math>~\theta</math>, to the z-axis.</li> | <li>The line that is perpendicular to the plane and passes through the z-axis at <math>~z_0</math> is tipped at an angle, <math>~\theta</math>, to the z-axis.</li> | ||
</ul> | </ul> | ||
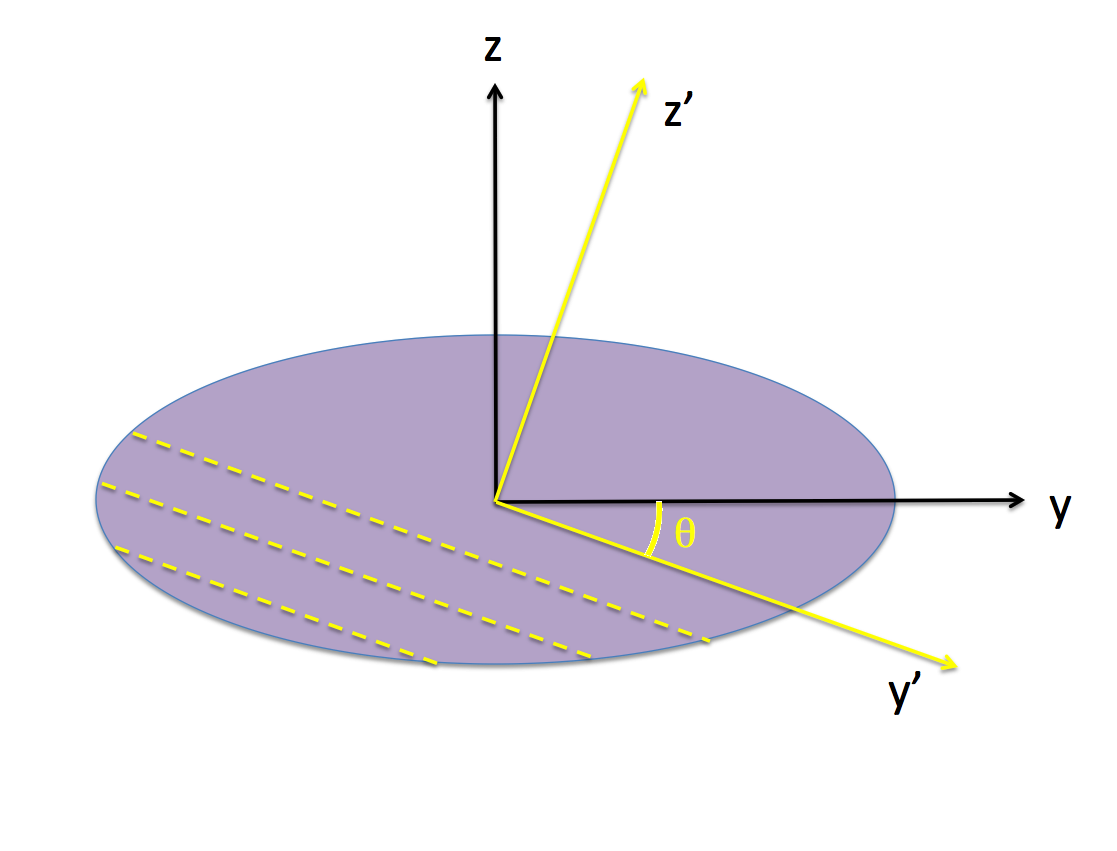
As is illustrated in | As is illustrated in Figure 1, we will use the line referenced in this third property description to serve as the z'-axis of a Cartesian grid that is ''tipped'' at the angle, <math>~\theta</math>, with respect to the ''body'' frame; and we will align the x' axis with the x-axis, so it should be clear that the z'-axis lies in the y-z plane of the ellipsoid. | ||
<table border="1" width="50%" cellpadding="8" align="center"> | |||
<tr> | |||
<td align="center" colspan="3"><b>Figure 1</b></td> | |||
</tr> | |||
<tr> | |||
<td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~x</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~x' \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~y</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
y' \cos\theta - z'\sin\theta | |||
\, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~(z - z_0)</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
z' \cos\theta + y'\sin\theta | |||
\, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td> | |||
<td align="center">[[File:PrimedCoordinates3.png|250px|Primed Coordinates]]</td> | |||
<td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
<tr> | |||
<td align="right"> | |||
<math>~x'</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~x \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | <tr> | ||
<td align=" | <td align="right"> | ||
<math>~y'</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
y \cos\theta + (z - z_0) \sin\theta | |||
\, ,</math> | |||
</td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~ | <math>~z'</math> | ||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 30: | Line 107: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~ | ||
(z-z_0) \cos\theta - y \sin\theta | |||
\, .</math> | |||
</td> | </td> | ||
</tr> | |||
</table> | |||
</td> | |||
</tr> | |||
</table> | |||
As has been shown in [[User:Tohline/ThreeDimensionalConfigurations/ChallengesPt2#Intersection_of_Tipped_Plane_With_Ellipsoid_Surface|our accompanying discussion]], we obtain the following, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="center" colspan="3"><font color="maroon">'''Intersection Expression'''</font></td> | |||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td align="right"> | <td align="right"> | ||
<math>~1 - \frac{x^2}{a^2} </math> | |||
</td> | </td> | ||
<td align="center"> | <td align="center"> | ||
| Line 61: | Line 151: | ||
</tr> | </tr> | ||
</table> | </table> | ||
Rewriting this "intersection expression" in terms of the ''tipped'' (primed) coordinate frame gives us, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~1 - \frac{(x')^2}{a^2} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(y' \cos\theta - z' \sin\theta)^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr] + (y' \cos\theta - z' \sin\theta) \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} \, . </math> | |||
</td> | |||
</tr> | |||
</table> | |||
<font color="red"><b>STEP #2</b></font> | |||
As viewed from the ''tipped'' coordinated frame, the curve that is identified by this intersection should be an | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="center" colspan="3"><font color="maroon">'''Off-Center Ellipse'''</font></td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~1</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[\frac{x'}{x_\mathrm{max}} \biggr]^2 + \biggl[\frac{y' - y_c}{y_\mathrm{max}} \biggr]^2 </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[\frac{x'}{x_\mathrm{max}} \biggr]^2 + \biggl[\frac{(y')^2 - 2y' y_c + y_c^2}{y^2_\mathrm{max}} \biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
that lies in the x'-y' plane — that is, <math>~z' = 0</math>. Let's see if the intersection expression can be molded into this form. | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~1 - \frac{z_0^2}{c^2} - \frac{(x')^2}{a^2} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~(y')^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr]\cos^2\theta + 2y' \biggl[ \frac{z_0 \sin\theta}{c^2} \biggr] </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr]\cos^2\theta \biggl\{ (y')^2 - 2y' \biggl[ \frac{-z_0 \sin\theta}{c^2 \cos^2\theta} \biggr]\biggl[\frac{b^2c^2}{c^2 + b^2\tan^2\theta} \biggr] \biggr\}</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\kappa^2 \biggl[ (y')^2 - 2y' \underbrace{\biggl( \frac{-z_0 \sin\theta}{c^2 \kappa^2} \biggr)}_{y_c} \biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
where, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\kappa^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\equiv</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ | |||
\frac{c^2 \cos^2\theta + b^2 \sin^2\theta}{b^2c^2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Dividing through by <math>~\kappa^2</math>, then adding <math>~y_c^2</math> to both sides gives, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~(y')^2 - 2y' y_c + y_c^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\underbrace{\biggl[ \frac{1}{\kappa^2} - \frac{z_0^2}{c^2 \kappa^2} + y_c^2 \biggr]}_{y^2_\mathrm{max}} - \frac{(x')^2}{a^2\kappa^2} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Finally, we have, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>\frac{1}{y^2_\mathrm{max}} \biggl[ (y')^2 - 2y' y_c + y_c^2 \biggr]</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~1 - (x')^2 \underbrace{\biggl[ \frac{1}{a^2\kappa^2 y_\mathrm{max}^2} \biggr]}_{ 1/x^2_\mathrm{max} } \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
So … the intersection expression can be molded into the form of an off-center ellipse if we make the following associations: | |||
<table border="1" cellpadding="8" align="center" width="60%"><tr><td align="left"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{y_c}{z_0}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~- \frac{\sin\theta}{c^2 \kappa^2} \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~y_\mathrm{max}^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{1}{\kappa^2}\biggl[ 1 - \frac{z_0^2}{c^2 } - \frac{z_0 \sin\theta}{c^2} \biggr] \, ,</math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~x_\mathrm{max}^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~a^2 \biggl[ 1 - \frac{z_0^2}{c^2 } - \frac{z_0 \sin\theta}{c^2} \biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
Note as well that, | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~a^2\kappa^2 = \frac{a^2}{b^2 c^2} \biggl[ c^2 \cos^2\theta + b^2 \sin^2\theta \biggr] \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</td></tr></table> | |||
==Various Coordinate Frames== | ==Various Coordinate Frames== | ||
Revision as of 21:04, 1 May 2021
Challenges Constructing Ellipsoidal-Like Configurations (Pt. 4)
This chapter extends the accompanying chapters titled, Construction Challenges (Pt. 1), (Pt. 2), and (Pt. 3). The focus here is on firming up our understanding of the relationships between various "tilted" Cartesian coordinate frames.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
The Plan
STEP #1
First, we present the mathematical expression that describes the intersection between the surface of an ellipsoid and a plane having the following properties:
- The plane cuts through the ellipsoid's z-axis at a distance, <math>~z_0</math>, from the center of the ellipsoid;
- The line of intersection is parallel to the x-axis of the ellipsoid; and,
- The line that is perpendicular to the plane and passes through the z-axis at <math>~z_0</math> is tipped at an angle, <math>~\theta</math>, to the z-axis.
As is illustrated in Figure 1, we will use the line referenced in this third property description to serve as the z'-axis of a Cartesian grid that is tipped at the angle, <math>~\theta</math>, with respect to the body frame; and we will align the x' axis with the x-axis, so it should be clear that the z'-axis lies in the y-z plane of the ellipsoid.
As has been shown in our accompanying discussion, we obtain the following,
| Intersection Expression | ||
|
<math>~1 - \frac{x^2}{a^2} </math> |
<math>~=</math> |
<math>~y^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr] + y \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} \, , </math> |
as long as z0 lies within the range,
|
<math>~z_0^2</math> |
<math>~\le</math> |
<math>~c^2 + b^2\tan^2\theta \, .</math> |
Rewriting this "intersection expression" in terms of the tipped (primed) coordinate frame gives us,
|
<math>~1 - \frac{(x')^2}{a^2} </math> |
<math>~=</math> |
<math>~(y' \cos\theta - z' \sin\theta)^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr] + (y' \cos\theta - z' \sin\theta) \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} \, . </math> |
STEP #2
As viewed from the tipped coordinated frame, the curve that is identified by this intersection should be an
| Off-Center Ellipse | ||
|
<math>~1</math> |
<math>~=</math> |
<math>~\biggl[\frac{x'}{x_\mathrm{max}} \biggr]^2 + \biggl[\frac{y' - y_c}{y_\mathrm{max}} \biggr]^2 </math> |
|
|
<math>~=</math> |
<math>~\biggl[\frac{x'}{x_\mathrm{max}} \biggr]^2 + \biggl[\frac{(y')^2 - 2y' y_c + y_c^2}{y^2_\mathrm{max}} \biggr] \, ,</math> |
that lies in the x'-y' plane — that is, <math>~z' = 0</math>. Let's see if the intersection expression can be molded into this form.
|
<math>~1 - \frac{z_0^2}{c^2} - \frac{(x')^2}{a^2} </math> |
<math>~=</math> |
<math>~(y')^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr]\cos^2\theta + 2y' \biggl[ \frac{z_0 \sin\theta}{c^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~\biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr]\cos^2\theta \biggl\{ (y')^2 - 2y' \biggl[ \frac{-z_0 \sin\theta}{c^2 \cos^2\theta} \biggr]\biggl[\frac{b^2c^2}{c^2 + b^2\tan^2\theta} \biggr] \biggr\}</math> |
|
|
<math>~=</math> |
<math>~\kappa^2 \biggl[ (y')^2 - 2y' \underbrace{\biggl( \frac{-z_0 \sin\theta}{c^2 \kappa^2} \biggr)}_{y_c} \biggr] \, ,</math> |
where,
|
<math>~\kappa^2</math> |
<math>~\equiv</math> |
<math>~ \frac{c^2 \cos^2\theta + b^2 \sin^2\theta}{b^2c^2} \, . </math> |
Dividing through by <math>~\kappa^2</math>, then adding <math>~y_c^2</math> to both sides gives,
|
<math>~(y')^2 - 2y' y_c + y_c^2</math> |
<math>~=</math> |
<math>~\underbrace{\biggl[ \frac{1}{\kappa^2} - \frac{z_0^2}{c^2 \kappa^2} + y_c^2 \biggr]}_{y^2_\mathrm{max}} - \frac{(x')^2}{a^2\kappa^2} \, .</math> |
Finally, we have,
|
<math>\frac{1}{y^2_\mathrm{max}} \biggl[ (y')^2 - 2y' y_c + y_c^2 \biggr]</math> |
<math>~=</math> |
<math>~1 - (x')^2 \underbrace{\biggl[ \frac{1}{a^2\kappa^2 y_\mathrm{max}^2} \biggr]}_{ 1/x^2_\mathrm{max} } \, .</math> |
So … the intersection expression can be molded into the form of an off-center ellipse if we make the following associations:
Note as well that,
|
Various Coordinate Frames
Tipped Orbit Planes
Summary
In a separate discussion, we have shown that, as viewed from a frame that "tumbles" with the (purple) body of a Type 1 Riemann ellipsoid, each Lagrangian fluid element moves along an elliptical path in a plane that is tipped by an angle <math>~\theta</math> about the x-axis of the body. As viewed from the (primed) coordinates associated with this tipped plane, by definition, z' = constant and dz'/dt = 0, and the planar orbit is defined by the expression for an,
| Off-Center Ellipse | ||
|
<math>~1</math> |
<math>~=</math> |
<math>~\biggl[\frac{x'}{x_\mathrm{max}} \biggr]^2 + \biggl[\frac{y' - y_c(z')}{y_\mathrm{max}} \biggr]^2 \, .</math> |
|
Notice that the offset, <math>~y_c</math>, is a function of the tipped plane's vertical coordinate, <math>~z'</math>. As a function of time, the x'-y' coordinates and associated velocity components of each Lagrangian fluid element are given by the expressions,
|
<math>~x'</math> |
<math>~=</math> |
<math>~x_\mathrm{max}\cos(\dot\varphi t)</math> |
and, |
<math>~y' - y_c</math> |
<math>~=</math> |
<math>~y_\mathrm{max}\sin(\dot\varphi t) \, ,</math> |
|
<math>~\dot{x}'</math> |
<math>~=</math> |
<math>~- x_\mathrm{max}~ \dot\varphi \cdot \sin(\dot\varphi t) = (y_c - y') \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \dot\varphi </math> |
and, |
<math>~\dot{y}' </math> |
<math>~=</math> |
<math>~y_\mathrm{max}~\dot\varphi \cdot \cos(\dot\varphi t) = x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr] \dot\varphi \, .</math> |
We have determined that (numerical value given for our chosen example Type I ellipsoid),
|
<math>~\tan\theta</math> |
<math>~=</math> |
<math>~ - \frac{b^2 \beta \Omega_2}{c^2 \gamma \Omega_3} = -2.43573\, , </math> |
where, as has also been specified in an accompanying discussion,
|
<math>~\beta</math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \frac{\zeta_2}{\Omega_2} = +1.13451 </math> |
and, |
<math>~\gamma</math> |
<math>~=</math> |
<math>~ - \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3}{\Omega_3} = +1.80518\, . </math> |
We also have determined that,
|
<math>~\biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^4</math> |
<math>~=</math> |
<math>~ \frac{a^4 (c^4 \gamma^2 \Omega_3^2 + b^4 \beta^2 \Omega_2^2)}{b^4 c^4(\gamma^2\Omega_3^2 + \beta^2\Omega_2^2)} ~~~\Rightarrow ~~~\frac{x_\mathrm{max}}{y_\mathrm{max}} = 1.26218 \, , </math> |
|
<math>~{\dot\varphi}^4 </math> |
<math>~=</math> |
<math>~ \frac{a^4}{b^4 c^4} \biggl(\gamma^2\Omega_3^2 + \beta^2\Omega_2^2 \biggr) (c^4 \gamma^2 \Omega_3^2 + b^4 \beta^2 \Omega_2^2) ~~~\Rightarrow ~~~ \dot\varphi = 1.59862\, , </math> |
|
<math>~\frac{y_c}{z_0}</math> |
<math>~=</math> |
<math>~ -\sin\theta ~~~\Rightarrow~~~~ \frac{y_c}{z_0} = -0.92507 \, .</math> |
Demonstration
In order to transform a vector from the "tipped orbit" frame (primed coordinates) to the "body" frame (unprimed), we use the following mappings of the three unit vectors:
|
Given that, by design in our "tipped orbit" frame, there is no vertical motion — that is, <math>~\dot{z}' = 0</math> — mapping the (primed coordinate) velocity to the body (unprimed) coordinate is particularly straightforward. Specifically,
|
<math>~\boldsymbol{u'}</math> |
<math>~=</math> |
<math>~ \boldsymbol{\hat\imath'} \dot{x}' + \boldsymbol{\hat\jmath'} \dot{y}' + \boldsymbol{\hat{k}'} \cancelto{0}{\dot{z}'} </math> |
|
|
<math>~~~\rightarrow~~</math> |
<math>~ \boldsymbol{\hat\imath} \dot{x}' + [\boldsymbol{\hat\jmath}\cos\theta + \boldsymbol{\hat{k}}\sin\theta] \dot{y}' </math> |
|
|
<math>~=</math> |
<math>~ \boldsymbol{\hat\imath} \biggl\{ (y_c - y') \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr) \dot\varphi \biggr\} + [\boldsymbol{\hat\jmath}\cos\theta + \boldsymbol{\hat{k}}\sin\theta] \biggl\{ x' \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \dot\varphi \biggr\} \, . </math> |
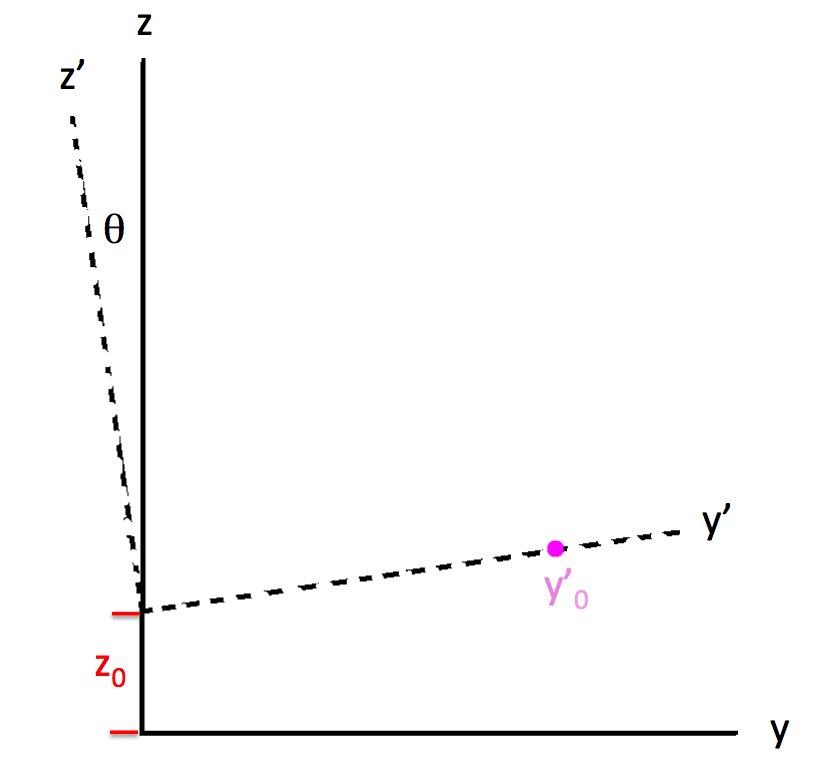
Recognizing, as before, that the relevant coordinate mapping is,
|
 |
|
we have,
|
<math>~\boldsymbol{u'}</math> |
<math>~~~\rightarrow~~~</math> |
<math>~ \boldsymbol{\hat\imath} \dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)\biggl\{y_c - y\cos\theta - (z - z_0)\sin\theta\biggr\} + \boldsymbol{\hat\jmath} \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \biggr\{ x\cos\theta \biggr\} + \boldsymbol{\hat{k}} \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \biggr\{ x\sin\theta \biggr\} \, . </math> |
Therefore, as viewed from the body frame, the individual velocity components are,
|
<math>~\boldsymbol{\hat\jmath} \cdot \boldsymbol{u'}</math> |
<math>~=</math> |
<math>~ \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) x\cos\theta </math> |
|
|
<math>~=</math> |
<math>~x \cdot \biggl\{ \frac{b^4 c^4(\gamma^2\Omega_3^2 + \beta^2\Omega_2^2)}{a^4 (c^4 \gamma^2 \Omega_3^2 + b^4 \beta^2 \Omega_2^2)} \frac{a^4}{b^4 c^4} \biggl(\gamma^2\Omega_3^2 + \beta^2\Omega_2^2 \biggr) (c^4 \gamma^2 \Omega_3^2 + b^4 \beta^2 \Omega_2^2) \biggr\}^{1 / 4} \frac{{c^2 \gamma \Omega_3} }{[c^4 \gamma^2 \Omega_3^2 + b^4\beta^2 \Omega_2^2]^{1 / 2}} </math> |
See Also
- Riemann Type 1 Ellipsoids
- Construction Challenges (Pt. 1)
- Construction Challenges (Pt. 2)
- Construction Challenges (Pt. 3)
- Construction Challenges (Pt. 4)
- Related discussions of models viewed from a rotating reference frame:
- PGE
- NOTE to Eric Hirschmann & David Neilsen... I have moved the earlier contents of this page to a new Wiki location called Compressible Riemann Ellipsoids.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |