Challenges Constructing Ellipsoidal-Like Configurations (Pt. 2)

This chapter extends an accompanying chapter titled, Construction Challenges (Pt. 1). The focus here is on an SCF technique that will incorporate specification of a Lagrangian flow-flied.

Motivation

Where Are We Headed?

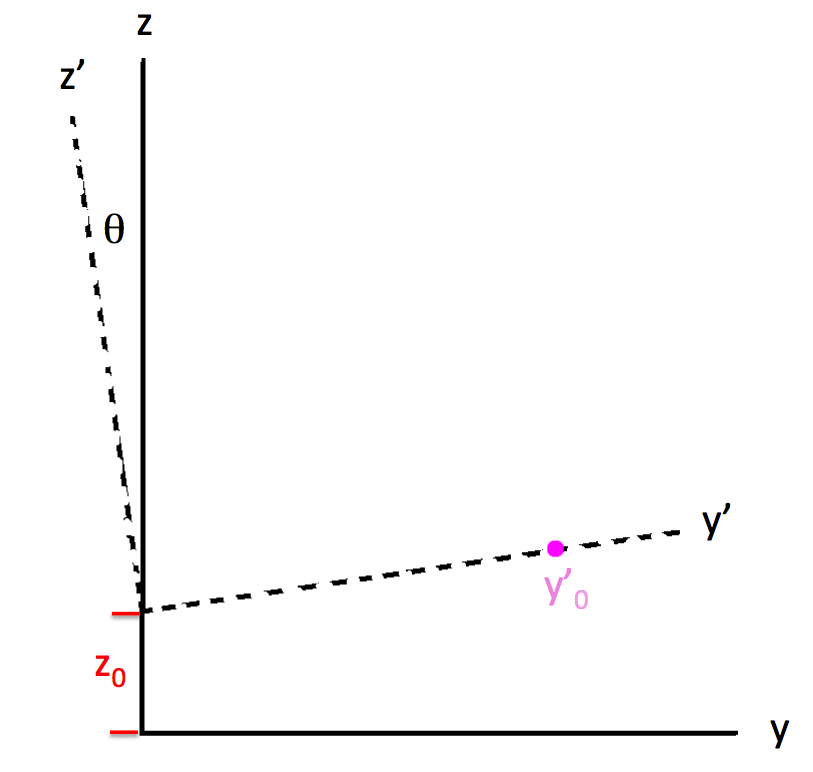
In a separate discussion, we have shown that, as viewed from a frame that "tumbles" with the (purple) body of a Type 1 Riemann ellipsoid, each Lagrangian fluid element moves along an elliptical path in a plane that is tipped by an angle <math>~\theta</math> about the x-axis of the body. (See the yellow-dotted orbits in Figure panels 1a and 1b below). As viewed from the (primed) coordinates associated with this tipped plane, by definition, z' = 0 and dz'/dt = 0, and the planar orbit is defined by the expression for an,

Off-Center Ellipse
<math>~1</math>	<math>~=</math>	<math>~\biggl(\frac{x'}{x_\mathrm{max}} \biggr)^2 + \biggl(\frac{y' - y_0}{y_\mathrm{max}} \biggr)^2 \, .</math>

As a function of time, the x'-y' coordinates and associated velocity components of each Lagrangian fluid element are given by the expressions,

<math>~x'</math>	<math>~=</math>	<math>~x_\mathrm{max}\cos(\dot\varphi t)</math>	and,	<math>~y' - y_0</math>	<math>~=</math>	<math>~y_\mathrm{max}\sin(\dot\varphi t) \, ,</math>
<math>~\dot{x}'</math>	<math>~=</math>	<math>~- x_\mathrm{max}~ \dot\varphi \cdot \sin(\dot\varphi t) = (y_0 - y') \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \dot\varphi </math>	and,	<math>~\dot{y}' </math>	<math>~=</math>	<math>~y_\mathrm{max}~\dot\varphi \cdot \cos(\dot\varphi t) = x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr] \dot\varphi \, .</math>

Notice that this is a divergence-free flow-field:

Divergence

<math>~\nabla \cdot \vec{v'}</math>	<math>~=</math>	<math>~ \frac{\partial \dot{x}'}{\partial x'} + \frac{\partial \dot{y}'}{\partial y'} + \frac{\partial \dot{z}'}{\partial z'} </math>
	<math>~=</math>	<math>~ \frac{\partial }{\partial x'} \biggl[ (y' - y_0) \dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr) \biggr] + \frac{\partial }{\partial y'} \biggl[ x' \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr) \biggr] </math>
	<math>~=</math>	<math>~ 0\, . </math>

Also, along the lines of our accompanying discussion of Riemann S-Type Ellipoids, it is useful to develop the expression for the fluid vorticity as viewed from the rotating- and tipped-reference frame.

Vorticity

<math>~\boldsymbol{\zeta'} \equiv \boldsymbol{\nabla \times}\bold{v'}</math>	<math>~=</math>	<math>~ \boldsymbol{\hat\imath'} \biggl[ \frac{\partial \cancelto{}{\dot{z}'} }{\partial y'} - \frac{\partial \dot{y}'}{\partial z'} \biggr] + \boldsymbol{\hat\jmath'} \biggl[ \frac{\partial \dot{x}'}{\partial z'} - \frac{\partial \cancelto{}{\dot{z}'}}{\partial x'} \biggr] + \bold{\hat{k}'} \biggl[ \frac{\partial \dot{y}'}{\partial x'} - \frac{\partial \dot{x}'}{\partial y'} \biggr] </math>
	<math>~=</math>	<math>~ -\boldsymbol{\hat\imath'} (x' \dot\varphi )\frac{\partial }{\partial z'} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} }\biggr] + \boldsymbol{\hat\jmath'} \biggl\{ \dot\varphi (y_0 - y')\frac{\partial }{\partial z'}\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max} } \biggr] + \dot\varphi \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max} } \biggr] \frac{\partial y_0}{\partial z'} \biggr\} + \bold{\hat{k}'} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} } - \frac{x_\mathrm{max} }{y_\mathrm{max} } \biggr] \dot\varphi \, . </math>

Further evaluation is completed, below, after we determine how <math>~y_0</math> and <math>~[x_\mathrm{max}/y_\mathrm{max}]^{\pm 1}</math> depend on <math>~z_0</math>; and after appreciating that, in order to introduce the functional dependence on <math>~z' \ne 0</math> in every relevant expression, we need to make the replacement, <math>~z_0 \rightarrow (z_0 + z'\cos\theta)</math>. <== Figure this out!

In the subsections of this chapter that follow, we provide analytic expressions for these various quantities — <math>~x_\mathrm{max}, y_\mathrm{max}, y_0, \dot\varphi</math> — in terms of the properties of any chosen Type 1 Riemann ellipsoid.

Intersection of Tipped Plane With Ellipsoid Surface

Body Frame

In a an early subsection of the accompanying discussion, we have pointed out that the intersection of each Lagrangian fluid element's tipped orbital plane with the surface of the (purple) ellipsoidal surface is given by the (unprimed) body-frame coordinates that simultaneously satisfy the expressions,

<math>~\biggl( \frac{x}{a}\biggr)^2 + \biggl( \frac{y}{b}\biggr)^2 + \biggl( \frac{z}{c}\biggr)^2 </math>

and,

<math>~y \tan\theta + z_0 \, ,</math>

where z₀ is the location where the tipped plane intersects the z-axis of the body frame. Combining these two expressions, we see that an intersection between the tipped plane and the ellipsoidal surface will occur at (x, y)-coordinate pairs that satisfy what we will henceforth refer to as the,

Intersection Expression
<math>~1 - \frac{x^2}{a^2} </math>	<math>~=</math>	<math>~\frac{y^2}{b^2} + \biggl[ \frac{y\tan\theta + z_0}{c}\biggr]^2 </math>
	<math>~=</math>	<math>~y^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr] + y \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} \, , </math>

as long as z₀ lies within the range,

<math>~c^2 + b^2\tan^2\theta \, .</math>

Tipped Orbital Plane

A table provided in our accompanying discussion shows how to transform from the body-frame coordinates (unprimed) to the (primed) frame that aligns with the Lagrangian fluid element's orbit. Specifically,

<math>~x</math>	<math>~=</math>	<math>~x' \, ,</math>
<math>~y</math>	<math>~=</math>	<math>~ y' \cos\theta - z'\sin\theta \, ,</math>
<math>~(z - z_0)</math>	<math>~=</math>	<math>~ z' \cos\theta + y'\sin\theta \, .</math>

<math>~x'</math>	<math>~=</math>	<math>~x \, ,</math>
<math>~y'</math>	<math>~=</math>	<math>~ y \cos\theta + (z - z_0) \sin\theta \, ,</math>
<math>~z'</math>	<math>~=</math>	<math>~ (z-z_0) \cos\theta - y \sin\theta \, .</math>

NOTE: <math>~z_0 \rightarrow z_0 + z'\cos\theta \, .</math> <== Figure this out!

Using the 2^nd and 3^rd of these relations, we see from the equation that defines the "tipped plane," that,

<math>~z_0 + z' \cos\theta + y'\sin\theta</math>	<math>~=</math>	<math>~[ y' \cos\theta - z'\sin\theta ]\tan\theta + z_0</math>
<math>~\Rightarrow ~~~z' \biggl[ \cos\theta + \tan\theta \cdot \sin\theta \biggr]</math>	<math>~=</math>	<math>~y' [ \cos\theta \cdot \tan\theta - \sin\theta] </math>
<math>~\Rightarrow ~~~\frac{z'}{\cos\theta} </math>	<math>~=</math>	<math>~0</math>
<math>~\Rightarrow ~~~z' </math>	<math>~=</math>	<math>~0 \, .</math>

Hence, as viewed from the primed coordinate frame, all points of intersection between the tipped plane and the surface of the ellipsoid will be found in the <math>~z' = 0</math> plane, as desired. Inserting the 1^st and 2^nd of these relations into the above-defined Intersection Expression, we find,

<math>~1 - \frac{(x')^2}{a^2} </math>	<math>~=</math>	<math>~\biggl[ y' \cos\theta - \cancelto{0}{z'} \sin\theta \biggr]^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr] + \biggl[ y' \cos\theta - \cancelto{0}{z'} \sin\theta \biggr] \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2}</math>
	<math>~=</math>	<math>~(y')^2\biggl[\frac{c^2 \cos^2\theta + b^2\sin^2\theta}{b^2c^2} \biggr] - 2(y')\biggl[ - \frac{z_0 \sin\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} \, .</math>

Off-Center Ellipse

Now we attempt to transform this last expression into the form of the above-defined equation for an Off-Center Ellipse, which we rewrite here as,

<math>~1 - \frac{(x')^2}{x^2_\mathrm{max}} </math>

<math>~\frac{1}{y^2_\mathrm{max}}\biggl[ (y')^2 - 2(y')y_0 + y_0^2 \biggr] \, .</math>

An initial rearrangement of the relevant "last" expression gives,

<math>~ \frac{c^2 \cos^2\theta + b^2\sin^2\theta}{b^2c^2} \biggl[(y')^2 - 2(y') \underbrace{ \biggl( - \frac{z_0 b^2 \sin\theta}{c^2 \cos^2\theta + b^2\sin^2\theta}\biggr) }_{y_0} \biggr] \, ,</math>

which, as indicated, allows us to identify the appropriate expression for the y-offset, <math>~y_0</math>.

RESULT 1
(compare with Result 2)

<math>~ -\frac{b^2\sin\theta}{c^2\cos^2\theta + b^2\sin^2\theta} = -\frac{\sin\theta}{c^2\kappa^2} </math>

Dividing through by the leading coefficient,

<math>~\kappa^2 \equiv \frac{c^2 \cos^2\theta + b^2\sin^2\theta}{b^2c^2} \, ,</math>

then adding <math>~y_0^2</math> to both sides gives,

<math>~ (y')^2 - 2(y') y_0 + y_0^2 </math>	<math>~=</math>	<math>~ \frac{1}{\kappa^2}\biggl[ 1 - \frac{z_0^2}{c^2} - \frac{(x')^2}{a^2} \biggr] + y_0^2 </math>
	<math>~=</math>	<math>~ \underbrace{\biggl[ \frac{1}{\kappa^2} - \frac{z_0^2}{c^2\kappa^2} + y_0^2 \biggr]}_{y^2_\mathrm{max}} - \frac{(x')^2}{\kappa^2 a^2} \, , </math>

which gives us the appropriate expression for <math>~y_\mathrm{max}^2</math>. Finally, dividing through by <math>~y_\mathrm{max}^2</math> gives,

<math>~ \frac{1}{y_\mathrm{max}^2} \biggl[ (y')^2 - 2(y') y_0 + y_0^2 \biggr] </math>

<math>~ 1 - (x')^2 \underbrace{ \biggl[ \frac{1}{y_\mathrm{max}^2 \kappa^2 a^2} \biggr]}_{1/x^2_\mathrm{max}} \, , </math>

which identifies the appropriate expression for <math>~x^2_\mathrm{max}</math>. As viewed from the "tipped plane" (primed) coordinate frame, then, the equation for the orbit of each Lagrangian fluid element is that of an …

Off-Center Ellipse
<math>~1</math>	<math>~=</math>	<math>~\biggl(\frac{x'}{x_\mathrm{max}} \biggr)^2 + \biggl(\frac{y' - y_0}{y_\mathrm{max}} \biggr)^2 \, ,</math>

with,

<math>~y_0</math>	<math>~\equiv</math>	<math>~- \frac{z_0 b^2 \sin\theta}{c^2 \cos^2\theta + b^2\sin^2\theta} \, ,</math>
<math>~y^2_\mathrm{max}</math>	<math>~\equiv</math>	<math>~ \frac{1}{\kappa^2}\biggl( 1 - \frac{z_0^2}{c^2}\biggr) + y_0^2 </math>
	<math>~=</math>	<math>~ \frac{b^2(c^2 - z_0^2)}{c^2 \cos^2\theta + b^2\sin^2\theta} + \biggl[\frac{z_0 b^2 \sin\theta}{c^2 \cos^2\theta + b^2\sin^2\theta}\biggr]^2 </math>
	<math>~=</math>	<math>~b^2 \biggl\{ \frac{(c^2-z_0^2) ( c^2 \cos^2\theta + b^2\sin^2\theta ) + z_0^2 b^2 \sin^2\theta}{(c^2 \cos^2\theta + b^2\sin^2\theta)^2} \biggr\}\, , </math>
	<math>~=</math>	<math>~ b^2 c^2 \biggl\{ \frac{( c^2 -z_0^2)\cos^2\theta + b^2\sin^2\theta }{(c^2 \cos^2\theta + b^2\sin^2\theta)^2} \biggr\}\, , </math>
<math>~x_\mathrm{max}^2</math>	<math>~\equiv</math>	<math>~a^2 \kappa^2 y_\mathrm{max}^2</math>
	<math>~=</math>	<math>~ a^2\biggl\{ \frac{( c^2 -z_0^2)\cos^2\theta + b^2\sin^2\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr\} \, . </math>

Note that the ratio,

<math>~\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2</math>	<math>~=</math>	<math>~ a^2\biggl[ \frac{( c^2 -z_0^2)\cos^2\theta + b^2\sin^2\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] \frac{1}{b^2 c^2} \biggl[ \frac{(c^2 \cos^2\theta + b^2\sin^2\theta)^2}{( c^2 -z_0^2)\cos^2\theta + b^2\sin^2\theta } \biggr] </math>
	<math>~=</math>	<math>~ \frac{a^2}{b^2c^2} \biggl[ (c^2 \cos^2\theta + b^2\sin^2\theta)\biggr] \, , </math>

which is independent of <math>~z_0</math>.

Velocities

Tipped Orbit Velocities

From the generic expressions for (primed) velocities associated with an off-center elliptical orbit, we expect,

<math>~\frac{\dot{x}'}{\dot\varphi}</math>	<math>~=</math>	<math>~ -x_\mathrm{max} \sin(\dot\varphi t) = - (y' - y_0) \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \, , </math> and,
<math>~\frac{\dot{y}'}{\dot\varphi}</math>	<math>~=</math>	<math>~ y_\mathrm{max} \cos(\dot\varphi t) = x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \, . </math>

Body Frame Velocities

From the already-referenced table provided in our accompanying discussion, we can transform this pair of expressions for the velocity components in the "tipped orbit" frame — remember that the third component, <math>~\dot{z}' = 0</math> — into the (three-component) velocities of the body frame using the expressions,

<math>~\dot{x}</math>	<math>~=</math>	<math>~\dot{x}' \, ,</math>
<math>~\dot{y}</math>	<math>~=</math>	<math>~ \dot{y}' \cos\theta \, ,</math>
<math>~\dot{z}</math>	<math>~=</math>	<math>~ \dot{y}' \sin\theta \, .</math>

<math>~x'</math>	<math>~\rightarrow</math>	<math>~x \, ,</math>
<math>~y'</math>	<math>~\rightarrow</math>	<math>~ y\cos\theta + (z-z_0)\sin\theta \, ,</math>
<math>~z'</math>	<math>~\rightarrow</math>	<math>~ (z-z_0)\cos\theta - y\sin\theta \, .</math>

That is to say,

<math>~\frac{\dot{x}}{\dot\varphi}</math>	<math>~=</math>	<math>~ - (y' - y_0) \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] = \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \biggl\{ y_0 - [y\cos\theta + (z-z_0)\sin\theta] \biggr\} \, , </math>
<math>~\frac{\dot{y}}{\dot\varphi}</math>	<math>~=</math>	<math>~ x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \cos\theta = x \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \cos\theta \, , </math>
<math>~\frac{\dot{z}}{\dot\varphi}</math>	<math>~=</math>	<math>~ x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \sin\theta = x \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \sin\theta \, , </math>

where,

<math>~\biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2</math>

<math>~ \frac{a^2}{b^2 c^2}\biggl[ c^2 \cos^2\theta + b^2\sin^2\theta \biggr] \, . </math>

Notice that the all-important tipping angle, <math>~\theta</math>, is related to these body-frame velocity components via the simple relation,

<math>~\tan\theta</math>

<math>~\biggl( \frac{\dot{z}}{\dot{y}} \biggr) \, .</math>

Vorticity Determination

Given that the ratio, <math>~(x_\mathrm{max}/y_\mathrm{max})</math>, does not depend on <math>~z'</math>, and that, after mapping <math>~z_0 \rightarrow (z_0 + z'\cos\theta)</math>, we find,

<math>~\frac{\partial y_0}{\partial z'} </math>

<math>~ \frac{\partial }{\partial z'} \biggl[ - \frac{(z_0 + z'\cos\theta) b^2 \sin\theta}{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] = - \frac{ b^2 \sin\theta\cos\theta}{c^2 \cos^2\theta + b^2\sin^2\theta} = - b^2 \sin\theta\cos\theta \biggl(\frac{a^2}{b^2c^2}\biggr) \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \, , </math>

the above vorticity expression becomes,

<math>~\boldsymbol{\zeta'} \equiv \boldsymbol{\nabla \times}\bold{v'}</math>	<math>~=</math>	<math>~ -\boldsymbol{\hat\imath'} (x' \dot\varphi ) \cancelto{0}{\frac{\partial }{\partial z'} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} }\biggr]} + \boldsymbol{\hat\jmath'} \biggl\{ \dot\varphi (y_0 - y') \cancelto{0}{\frac{\partial }{\partial z'}\biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max} } \biggr]} + \dot\varphi \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max} } \biggr] \frac{\partial y_0}{\partial z'} \biggr\} + \bold{\hat{k}'} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} } - \frac{x_\mathrm{max} }{y_\mathrm{max} } \biggr] \dot\varphi </math>
	<math>~=</math>	<math>~ - \boldsymbol{\hat\jmath'} \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max} } \biggr] b^2 \sin\theta\cos\theta \biggl(\frac{a^2}{b^2c^2}\biggr) \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2\dot\varphi + \bold{\hat{k}'} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} } - \frac{x_\mathrm{max} }{y_\mathrm{max} } \biggr] \dot\varphi </math>
	<math>~=</math>	<math>~\biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} } \biggr] \dot\varphi \biggl\{ - \boldsymbol{\hat\jmath'} ~\sin\theta\cos\theta \biggl(\frac{a^2}{c^2}\biggr) + \bold{\hat{k}'} \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } \biggr] \biggr\} \, . </math>

Referring back to our aboved-defined tipped plane, we see that the unprimed Cartesian unit vectors are related to the primed unit vectors via the relations …

<math>~\boldsymbol{\hat{\jmath}'}</math>	<math>~=</math>	<math>~ \boldsymbol{\hat{\jmath}}\cos\theta + \boldsymbol{\hat{k}}\sin\theta \, , </math>
<math>~\boldsymbol{\hat{k}'}</math>	<math>~=</math>	<math>~ -\boldsymbol{\hat{\jmath}}\sin\theta + \boldsymbol{\hat{k}}\cos\theta \, . </math>

Hence, from the perspective of the body frame, the expression for the vorticity becomes,

<math>~\boldsymbol{\zeta} </math>	<math>~=</math>	<math>~\biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max} } \biggr] \dot\varphi \biggl\{ - \biggl[ \boldsymbol{\hat{\jmath}}\cos\theta + \boldsymbol{\hat{k}}\sin\theta \biggr] ~\sin\theta\cos\theta \biggl(\frac{a^2}{c^2}\biggr) + \biggl[ -\boldsymbol{\hat{\jmath}}\sin\theta + \boldsymbol{\hat{k}}\cos\theta \biggr] \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } \biggr] \biggr\} </math>
	<math>~=</math>	<math>~\frac{1}{\cos\theta}\biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] \biggl\{ - \boldsymbol{\hat{\jmath}} ~\sin\theta\cos^2\theta \biggl(\frac{a^2}{c^2}\biggr) - \boldsymbol{\hat{k}}~\sin^2\theta\cos\theta \biggl(\frac{a^2}{c^2}\biggr) -\boldsymbol{\hat{\jmath}}\sin\theta \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } \biggr] + \boldsymbol{\hat{k}}\cos\theta \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } \biggr] \biggr\} </math>
	<math>~=</math>	<math>~\biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] \biggl\{ - \boldsymbol{\hat{\jmath}} \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } ~+~\cos^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr]\tan\theta + \boldsymbol{\hat{k}} \biggl[ 1 - \frac{x^2_\mathrm{max} }{y^2_\mathrm{max} } ~-~ \sin^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr] \biggr\} \, . </math>

Now, we appreciate that,

<math>~1 - \frac{x^2_\mathrm{max}}{y^2_\mathrm{max}}</math>

<math>~ 1 - \frac{a^2}{b^2 c^2}\biggl( c^2 \cos^2\theta + b^2\sin^2\theta \biggr) = 1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta \, . </math>

Hence,

<math>~\boldsymbol{\zeta} </math>	<math>~=</math>	<math>~\biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] \biggl\{ - \boldsymbol{\hat{\jmath}} \biggl[ 1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta ~+~\cos^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr]\tan\theta + \boldsymbol{\hat{k}} \biggl[ 1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta ~-~ \sin^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ +~\boldsymbol{\hat{\jmath}} \biggl[ 1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta ~+~\cos^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr] \biggl[ \frac{c^2 \zeta_2}{a^2 + c^2} \biggr] + \boldsymbol{\hat{k}} \biggl[ 1 - \biggl(\frac{a^2}{b^2}\biggr)\cos^2\theta - \biggl(\frac{a^2}{c^2}\biggr)\sin^2\theta ~-~ \sin^2\theta \biggl(\frac{a^2}{c^2}\biggr) \biggr] \biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] </math>
	<math>~=</math>	<math>~ +~\boldsymbol{\hat{\jmath}} \biggl\{ 1 - \biggl( \frac{a^2}{b^2 c^2} \biggr) \biggl[ c^2 \cos^2\theta + b^2\sin^2\theta ~-~b^2 \cos^2\theta \biggr] \biggr\} \biggl[ \frac{c^2 \zeta_2}{a^2 + c^2} \biggr] + \boldsymbol{\hat{k}} \biggl\{ 1 - \biggl( \frac{a^2}{b^2 c^2} \biggr) \biggl[ c^2 \cos^2\theta + b^2\sin^2\theta ~+~ b^2 \sin^2\theta \biggr] \biggr\} \biggl[ \frac{b^2 \zeta_3}{a^2 + b^2} \biggr] </math>
	<math>~=</math>	<math>~ +~\boldsymbol{\hat{\jmath}} \biggl\{ c^2 - \biggl( \frac{a^2}{b^2} \biggr) \biggl[ c^2 \cos^2\theta + b^2\sin^2\theta ~-~b^2 \cos^2\theta \biggr] \biggr\} \biggl[ \frac{\zeta_2}{a^2 + c^2} \biggr] + \boldsymbol{\hat{k}} \biggl\{ b^2 - \biggl( \frac{a^2}{c^2} \biggr) \biggl[ c^2 \cos^2\theta + b^2\sin^2\theta ~+~ b^2 \sin^2\theta \biggr] \biggr\} \biggl[ \frac{\zeta_3}{a^2 + b^2} \biggr] </math>
	<math>~=</math>	<math>~ +~\boldsymbol{\hat{\jmath}} \biggl\{ c^2 - \biggl( \frac{a^2}{b^2} \biggr) \biggl[b^2 + c^2 \cos^2\theta ~-~2b^2 \cos^2\theta \biggr] \biggr\} \biggl[ \frac{\zeta_2}{a^2 + c^2} \biggr] + \boldsymbol{\hat{k}} \biggl\{ b^2 - \biggl( \frac{a^2}{c^2} \biggr) \biggl[c^2 - c^2 \sin^2\theta + 2b^2\sin^2\theta \biggr] \biggr\} \biggl[ \frac{\zeta_3}{a^2 + b^2} \biggr] </math>

Riemann-Derived Velocity Components

Inertial-Frame Expressions

As we have summarized in an accompanying discussion of Riemann Type 1 ellipsoids, [EFE] provides an expression for the velocity vector of each fluid element, given its instantaneous body-coordinate position (x, y, z) = (x₁, x₂, x₃) — see his Eq. (154), Chapter 7, §51 (p. 156). As viewed from the rotating frame of reference, the three component expressions are,

<math>~\dot{x} = u_1</math>	<math>~=</math>	<math>~\biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 y - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 z</math>	<math>~=</math>	<math>~- \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 y + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 z \, ,</math>
<math>~\dot{y} = u_2</math>	<math>~=</math>	<math>~- \gamma \Omega_3 x</math>	<math>~=</math>	<math>~+\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 x \, ,</math>
<math>~\dot{z} = u_3</math>	<math>~=</math>	<math>~+ \beta \Omega_2 x</math>	<math>~=</math>	<math>~- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 x \, ,</math>

where,

<math>~ - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \frac{\zeta_2}{\Omega_2} </math>

and,

<math>~\gamma</math>

<math>~ - \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3}{\Omega_3} \, . </math>

Rotating-Frame Vorticity

<math>~\boldsymbol{\zeta} \equiv \boldsymbol{\nabla \times}\bold{u}</math>	<math>~=</math>	<math>~ \boldsymbol{\hat\imath} \biggl[ \frac{\partial \dot{z} }{\partial y} - \frac{\partial \dot{y}}{\partial z} \biggr] + \boldsymbol{\hat\jmath} \biggl[ \frac{\partial \dot{x}}{\partial z} - \frac{\partial \dot{z}}{\partial x} \biggr] + \bold{\hat{k}} \biggl[ \frac{\partial \dot{y}}{\partial x} - \frac{\partial \dot{x}}{\partial y} \biggr] </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\jmath} \biggl\{ \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 + \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 \biggr\} + \bold{\hat{k}} \biggl\{ \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 + \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \biggr\} </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\jmath} ~\zeta_2 + \bold{\hat{k}} ~\zeta_3 \, . </math>

In the inertial frame, the velocity components are,

<math>~\bold{u}^{(0)} = \bold{u} + \boldsymbol{\Omega \times}\bold{x}</math>	<math>~=</math>	<math>~ ( \boldsymbol{\hat\imath} \dot{x} + \boldsymbol{\hat\jmath} \dot{y} + \bold{\hat{k}} \dot{z} ) + (\boldsymbol{\hat\jmath}\Omega_2 + \boldsymbol{\hat{k}}\Omega_3) \boldsymbol\times (\boldsymbol{\hat\imath} x + \boldsymbol{\hat\jmath}y + \boldsymbol{\hat{k}}z) </math>
	<math>~=</math>	<math>~ ( \boldsymbol{\hat\imath} \dot{x} + \boldsymbol{\hat\jmath} \dot{y} + \bold{\hat{k}} \dot{z} ) + \Omega_2(\boldsymbol{\hat\imath}z -\boldsymbol{\hat{k}} x) + \Omega_3 (\boldsymbol{\hat\jmath}x - \boldsymbol{\hat\imath}y) </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\imath}(\dot{x} + \Omega_2 z - \Omega_3y) + \boldsymbol{\hat\jmath}(\dot{y} + \Omega_3x) + \boldsymbol{\hat{k}}(\dot{z} - \Omega_2 x) </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\imath}\biggl[ \biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 y - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 z + \Omega_2 z - \Omega_3y\biggr] + \boldsymbol{\hat\jmath}\biggr[ - \gamma \Omega_3 x + \Omega_3x \biggr] + \boldsymbol{\hat{k}}\biggl[ + \beta \Omega_2 x - \Omega_2 x \biggr] </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\imath}\biggl\{ \biggl[ \biggl(\frac{a}{b}\biggr)^2 \gamma - 1 \biggr]\Omega_3y + \biggl[ 1 - \biggl(\frac{a}{c}\biggr)^2 \beta\biggr] \Omega_2 z\biggr\} + \boldsymbol{\hat\jmath} ( 1- \gamma ) \Omega_3 x + \boldsymbol{\hat{k}} ( \beta -1 ) \Omega_2 x \, . </math>

Inertial-Frame Vorticity

<math>~\boldsymbol{\zeta}^{(0)} = \boldsymbol{\nabla \times}\bold{u}^{(0)}</math>	<math>~=</math>	<math>~ \boldsymbol{\hat\imath} \biggl[ 0\biggr] + \boldsymbol{\hat\jmath} \biggl\{ \biggl[ 1 - \biggl(\frac{a}{c}\biggr)^2 \beta\biggr] \Omega_2 + (1-\beta)\Omega_2 \biggr\} + \bold{\hat{k}} \biggl\{ (1-\gamma)\Omega_3 + \biggl[1 - \biggl(\frac{a}{b}\biggr)^2 \gamma \biggr]\Omega_3 \biggr\} </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\jmath} \biggl[ 1 - \biggl(\frac{a}{c}\biggr)^2 \beta + (1-\beta) \biggr]\Omega_2 + \bold{\hat{k}} \biggl[ (1-\gamma) + 1 - \biggl(\frac{a}{b}\biggr)^2 \gamma \biggr] \Omega_3 </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\jmath} \biggl[ 2 - \biggl( 1 + \frac{a^2}{c^2} \biggr)\beta \biggr]\Omega_2 + \bold{\hat{k}} \biggl[ 2 - \biggl(1 + \frac{a^2}{b^2} \biggr) \gamma \biggr] \Omega_3 </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\jmath} \biggl[ 2 + \frac{\zeta_2}{\Omega_2} \biggr]\Omega_2 + \bold{\hat{k}} \biggl[ 2 + \frac{\zeta_3}{\Omega_3} \biggr] \Omega_3 </math>
	<math>~=</math>	<math>~ 2\boldsymbol{\Omega} + \boldsymbol{\zeta} \, . </math>

Coefficient Expression in Tipped Plane

In order for our expressions for the body-frame velocity components to align with Riemann's velocity components, we see, first, that,

<math>~\tan\theta</math>

<math>~ \frac{\dot{z}}{\dot{y}} = - \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} \, . </math>

As a result, we find that,

<math>~\frac{b^2 c^2}{a^2}\biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2</math>	<math>~=</math>	<math>~ c^2 \cos^2\theta + b^2\sin^2\theta = \frac{c^2 + b^2\tan^2\theta}{1 + \tan^2\theta} </math>
	<math>~=</math>	<math>~ \biggl[ c^2 + \frac{b^2 \zeta_2^2}{\zeta_3^2} \biggl( \frac{a^2 + b^2}{a^2 + c^2} \biggr)^2 \frac{c^4}{b^4} \biggr] \biggl[1 + \frac{\zeta_2^2}{\zeta_3^2} \biggl( \frac{a^2 + b^2}{a^2 + c^2} \biggr)^2 \frac{c^4}{b^4} \biggr]^{-1} </math>
<math>~\Rightarrow ~~~ \biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2</math>	<math>~=</math>	<math>~a^2 \biggl[ b^2 \zeta_3^2 (a^2 + c^2)^2 + c^2 \zeta_2^2 ( a^2 + b^2)^2 \biggr] \biggl[b^4\zeta_3^2 (a^2 + c^2)^2 + c^4 \zeta_2^2 ( a^2 + b^2 )^2 \biggr]^{-1} \, . </math>

Finally, setting the (square of the) two expressions for the <math>~\dot{y}</math> velocity component equal to one another gives,

<math>~\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 \zeta_3^2 </math>	<math>~=</math>	<math>~{\dot\varphi}^2 \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr]^2 \cos^2\theta</math>
<math>~\Rightarrow ~~~{\dot\varphi}^2 </math>	<math>~=</math>	<math>~ \zeta_3^2\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 \biggl[1 + \tan^2\theta \biggr] </math>
	<math>~=</math>	<math>~ a^2\zeta_3^2\biggl[ \frac{ b^2}{a^2 + b^2} \biggr]^2 \biggl[ b^2 \zeta_3^2 (a^2 + c^2)^2 + c^2 \zeta_2^2 ( a^2 + b^2)^2 \biggr] \biggl[b^4\zeta_3^2 (a^2 + c^2)^2 + c^4 \zeta_2^2 ( a^2 + b^2 )^2 \biggr]^{-1} \biggl\{ 1 + \biggl[ - \frac{\zeta_2}{\zeta_3} \biggl( \frac{a^2 + b^2}{a^2 + c^2} \biggr) \frac{c^2}{b^2} \biggr]^2 \biggr\} </math>
	<math>~=</math>	<math>~ \biggl[ \frac{ a^2 b^4 \zeta_3^2}{(a^2 + b^2)^2} \biggr] \biggl[ b^2 \zeta_3^2 (a^2 + c^2)^2 + c^2 \zeta_2^2 ( a^2 + b^2)^2 \biggr] \biggl[b^4\zeta_3^2 (a^2 + c^2)^2 + c^4 \zeta_2^2 ( a^2 + b^2 )^2 \biggr]^{-1} \biggl\{ \frac{b^4 \zeta_3^2 (a^2 + c^2)^2 + c^4 \zeta_2^2 (a^2 + b^2)^2}{b^4 \zeta_3^2 (a^2 + c^2)^2} \biggr\} </math>
	<math>~=</math>	<math>~ \frac{ a^2 }{(a^2 + b^2)^2(a^2 + c^2)^2} \biggl[ b^2 \zeta_3^2 (a^2 + c^2)^2 + c^2 \zeta_2^2 ( a^2 + b^2)^2 \biggr] </math>

Try Tipped Plane Again

<math>~\frac{\dot{x}'}{\dot\varphi}</math>

<math>~ - (y' - y_0) \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \, , </math> and,

<math>~\frac{\dot{y}'}{\dot\varphi}</math>

<math>~ x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] \, . </math>

<math>~\tan\theta</math>

<math>~ - \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} = - \frac{\beta \Omega_2}{\gamma \Omega_3} \, , </math>

where,

<math>~ - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \frac{\zeta_2}{\Omega_2} </math>

and,

<math>~\gamma</math>

<math>~ - \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3}{\Omega_3} \, . </math>

Also,

<math>~\biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 (1+\tan^2\theta)</math>

<math>~ \frac{a^2}{b^2 c^2} (c^2 + b^2\tan^2\theta) \, , </math>

and,

<math>~{\dot\varphi}^2 </math>

<math>~ \zeta_3^2\biggl[ \frac{b^2}{a^2 + b^2} \biggr]^2 \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^2 \biggl[1 + \tan^2\theta \biggr] \, . </math>

and,

<math>~- \frac{(z_0 + z'\cos\theta) b^2 \sin\theta}{c^2 \cos^2\theta + b^2\sin^2\theta} \, .</math>

<math>~\boldsymbol{\hat{\jmath}}</math>	<math>~=</math>	<math>~ \boldsymbol{\hat{\jmath}'}\cos\theta - \boldsymbol{\hat{k}'}\sin\theta \, , </math>
<math>~\boldsymbol{\hat{k}}</math>	<math>~=</math>	<math>~ \boldsymbol{\hat{\jmath}'}\sin\theta + \boldsymbol{\hat{k}'}\cos\theta \, . </math>
<math>~\Rightarrow~~~\boldsymbol{\Omega} = \boldsymbol{\hat\jmath} \Omega_2 + \boldsymbol{\hat{k}} \Omega_3</math>	<math>~=</math>	<math>~ \Omega_2 ( \boldsymbol{\hat{\jmath}'}\cos\theta - \boldsymbol{\hat{k}'}\sin\theta ) + \Omega_3 ( \boldsymbol{\hat{\jmath}'}\sin\theta + \boldsymbol{\hat{k}'}\cos\theta ) </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\jmath'} (\Omega_2 \cos\theta + \Omega_3\sin\theta) + \boldsymbol{\hat{k}'} (- \Omega_2\sin\theta + \Omega_3\cos\theta) \, . </math>

In the inertial reference frame,

<math>~\bold{u'}^{(0)} = \bold{u'} + \boldsymbol{\Omega \times}\bold{x'}</math>	<math>~=</math>	<math>~ ( \boldsymbol{\hat\imath'} \dot{x}' + \boldsymbol{\hat\jmath'} \dot{y}' + \boldsymbol{\hat{k}'} \cancelto{0}{\dot{z}' }) + [ \boldsymbol{\hat\jmath'} (\Omega_2 \cos\theta + \Omega_3\sin\theta) + \boldsymbol{\hat{k}'} (- \Omega_2\sin\theta + \Omega_3\cos\theta) ] \boldsymbol\times (\boldsymbol{\hat\imath'} x' + \boldsymbol{\hat\jmath'}y' + \boldsymbol{\hat{k'}}z') </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\imath'} \dot{x}' + \boldsymbol{\hat\jmath'} \dot{y}' + [ -\boldsymbol{\hat{k'}} (\Omega_2 \cos\theta + \Omega_3\sin\theta) x'] + [ \boldsymbol{\hat\imath'} (\Omega_2 \cos\theta + \Omega_3\sin\theta) z'] + [ \boldsymbol{\hat\jmath'} (- \Omega_2\sin\theta + \Omega_3\cos\theta)x' ] + [ - \boldsymbol{\hat\imath'} (- \Omega_2\sin\theta + \Omega_3\cos\theta) y'] </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\imath'} \biggl[ \dot{x}' + (\Omega_2\sin\theta - \Omega_3\cos\theta) y' + (\Omega_2 \cos\theta + \Omega_3\sin\theta) z' \biggr] + \boldsymbol{\hat\jmath'} \biggl[ \dot{y}' + (- \Omega_2\sin\theta + \Omega_3\cos\theta)x' \biggr] ~-~\boldsymbol{\hat{k'}} \biggl[ (\Omega_2 \cos\theta + \Omega_3\sin\theta) x' \biggr] \, . </math>

Inertial-Frame Vorticity in Primed Frame

<math>~\boldsymbol{\zeta'}^{(0)} \equiv \boldsymbol{\nabla \times}\bold{u}^{(0)}</math>	<math>~=</math>	<math>~ \boldsymbol{\hat\imath'} \biggl[ \frac{\partial u_z' }{\partial y'} - \frac{\partial u_y'}{\partial z'} \biggr]^{(0)} + \boldsymbol{\hat\jmath'} \biggl[ \frac{\partial u_x'}{\partial z'} - \frac{\partial u_z'}{\partial x'} \biggr]^{(0)} + \bold{\hat{k}'} \biggl[ \frac{\partial u_y'}{\partial x'} - \frac{\partial u_x'}{\partial y'} \biggr]^{(0)} </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\imath'} \biggl[ 0 \biggr] + \boldsymbol{\hat\jmath'} \biggl[\frac{\partial \dot{x}'}{\partial z'} + (\Omega_2 \cos\theta + \Omega_3\sin\theta) + (\Omega_2 \cos\theta + \Omega_3\sin\theta) \biggr] + \bold{\hat{k}'} \biggl[\frac{\partial \dot{y}'}{\partial x'} + (- \Omega_2\sin\theta + \Omega_3\cos\theta) - \frac{\partial \dot{x}'}{\partial y'} - (\Omega_2\sin\theta - \Omega_3\cos\theta) \biggr] </math>
	<math>~=</math>	<math>~2\boldsymbol{\Omega} + \boldsymbol{\hat\jmath'} \biggl[ \frac{\partial \dot{x}'}{\partial z'} \biggr] + \bold{\hat{k}'} \biggl[\frac{\partial \dot{y}'}{\partial x'} - \frac{\partial \dot{x}'}{\partial y'} \biggr] </math>

We appreciate that,

<math>~\frac{\partial \dot{x}'}{\partial z'}</math>

<math>~ \frac{\partial }{\partial z'} \biggl[ (y_0 - y' ) \dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr) \biggr] = \dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr) \frac{\partial y_0}{\partial z'} = -\dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr) \biggl[\frac{b^2 \sin\theta \cos\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] \, . </math>

Hence,

<math>~\boldsymbol{\zeta'}^{(0)} </math>

<math>~2\boldsymbol{\Omega} - \boldsymbol{\hat\jmath'} \dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr) \biggl[\frac{b^2 \sin\theta \cos\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] + \bold{\hat{k}'} \biggl[ \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) + \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr) \biggr]\dot\varphi \, . </math>

Recognizing that,

<math>~{\dot\varphi} \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr] </math>

<math>~ \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \, , </math>

and rearranging terms, we have,

<math>~\boldsymbol{\zeta'}^{(0)} - 2\boldsymbol{\Omega}</math>	<math>~=</math>	<math>~ \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr) \biggl\{ -\boldsymbol{\hat\jmath'} \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr)^2 \biggl[\frac{b^2 \sin\theta \cos\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] + \bold{\hat{k}'} \biggl[ 1+ \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl\{ -\boldsymbol{\hat\jmath'} \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr)^2 \biggl[\frac{b^2 \sin\theta \cos\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] + \bold{\hat{k}'} \biggl[ 1+ \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2 \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \biggl\{ -\boldsymbol{\hat\jmath'} \frac{a^2 }{b^2 c^2} (c^2 \cos^2\theta + b^2\sin^2\theta) \biggl[\frac{b^2 \sin\theta \cos\theta }{c^2 \cos^2\theta + b^2\sin^2\theta} \biggr] + \bold{\hat{k}'} \biggl[ 1+ \frac{a^2 }{b^2 c^2} (c^2 \cos^2\theta + b^2\sin^2\theta) \biggr] \biggr\} </math>
	<math>~=</math>	<math>~ -\boldsymbol{\hat\jmath'} \frac{a^2 }{c^2} \biggl[ \sin\theta \cos\theta\biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \bold{\hat{k}'} \biggl[ 1+ \frac{a^2 }{b^2 c^2} (c^2 \cos^2\theta + b^2\sin^2\theta) \biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\jmath'}~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \cos\theta + \bold{\hat{k}'} \biggl[ 1 \biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \bold{\hat{k}'} \biggl[ \frac{a^2 }{b^2 c^2} (c^2 \cos^2\theta ) \biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \bold{\hat{k}'} \biggl[ \frac{a^2 }{b^2 c^2} (b^2\sin^2\theta) \biggr] \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\jmath'}~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \cos\theta + \bold{\hat{k}'} \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \bold{\hat{k}'} \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta + \bold{\hat{k}'} \biggl[ \tan\theta \biggr] \frac{\zeta_3}{c^2} \biggl[ \frac{a^2 b^2}{a^2 + b^2} \biggr] \sin\theta </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\jmath'}~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \cos\theta + \bold{\hat{k}'} \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \bold{\hat{k}'} \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta - \bold{\hat{k}'} \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \sin\theta </math>
	<math>~=</math>	<math>~ (\boldsymbol{\hat\jmath} \cos^2\theta + \boldsymbol{\hat{k}}\sin\theta \cos\theta )~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] + (-\boldsymbol{\hat\jmath} \sin\theta + \boldsymbol{\hat{k}} \cos\theta )~ \biggl\{ \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta - \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \sin\theta \biggr\} </math>
	<math>~=</math>	<math>~ (\boldsymbol{\hat\jmath} \cos^2\theta )~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] + (-\boldsymbol{\hat\jmath} \sin\theta )~ \biggl\{ \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta - \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \sin\theta \biggr\} </math>
		<math>~ + (\boldsymbol{\hat{k}} \cos\theta )~ \biggl\{ \frac{\zeta_3}{\cos\theta} \biggl[ \frac{b^2}{a^2 + b^2} \biggr] + \biggl[ \frac{a^2 \zeta_3}{a^2 + b^2 } \biggr] \cos\theta - \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \sin\theta \biggr\} +(\boldsymbol{\hat{k}}\sin\theta \cos\theta )~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\jmath} ~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] -\boldsymbol{\hat\jmath}~ \biggl\{ b^2 + a^2 \cos^2\theta \biggr\}\frac{\zeta_3}{a^2 + b^2} \cdot \tan\theta + \boldsymbol{\hat{k}} ~ \biggl\{ b^2 + a^2 \cos^2\theta \biggr\}\frac{\zeta_3}{a^2 + b^2} </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\jmath} ~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] + \boldsymbol{\hat\jmath}~ \biggl\{ b^2 + a^2 \cos^2\theta \biggr\}\frac{\zeta_2}{a^2 + c^2} \cdot \frac{c^2}{b^2} + \boldsymbol{\hat{k}} ~ \biggl\{ b^2 + a^2 \cos^2\theta \biggr\}\frac{\zeta_3}{a^2 + b^2} </math>

<math>~\tan\theta</math>

<math>~ - \frac{\zeta_2}{\zeta_3} \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr] \frac{c^2}{b^2} = - \frac{\beta \Omega_2}{\gamma \Omega_3} \, , </math>

<math>~-\frac{\zeta_3}{c^2} \biggl[ \frac{a^2b^2}{a^2 + b^2} \biggr] \sin\theta</math>	<math>~=</math>	<math>~ \biggl[ \frac{a^2 \zeta_2}{a^2 + c^2} \biggr] \cos\theta </math>
<math>~\Rightarrow~~~\frac{1}{\cos\theta} \biggl[ \frac{\zeta_3b^2}{a^2 + b^2} \biggr] </math>	<math>~=</math>	<math>~ -\biggl[ \frac{c^2 \zeta_2}{a^2 + c^2} \biggr] \frac{1}{\sin\theta} </math>

Example Equilibrium Model

These key parameters have been drawn from [EFE] Chapter 7, Table XIII (p. 170):

<math>~\Omega_2 = 0.3639</math>

<math>~\Omega_3 = 0.6633</math>

As a consequence — see an accompanying discussion for details — the values of other parameters are …

			Example Values
<math>~\tan\theta </math>	<math>~=</math>	<math>~- \frac{\zeta_2 }{ \zeta_3 } \biggl[ \frac{a^2 + b^2}{a^2 + c^2} \biggr]\frac{c^2}{b^2} = -0.344793</math>	<math>~~ \theta =</math>	<math>~- 19.0238^\circ</math>
<math>~ \Lambda </math>	<math>~\equiv</math>	<math> \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 \cos\theta - \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 \sin\theta </math>	<math>~\Lambda =</math>	<math>~-1.332892 </math>
<math>~ \frac{y_0}{z_0} </math>	<math>~=</math>	<math> \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \frac{\zeta_2}{\Lambda} </math>	<math>~\frac{y_0}{z_0} =</math>	<math>~+ 1.400377</math>
<math>~ \frac{x_\mathrm{max}}{ y_\mathrm{max} } </math>	<math>~=</math>	<math>~ \biggl\{ \Lambda \biggl[ \frac{a^2 + b^2}{b^2} \biggr] \frac{\cos\theta}{\zeta_3} \biggr\}^{1 / 2} </math>	<math>~\frac{x_\mathrm{max}}{y_\mathrm{max}} =</math>	<math>~+ 1.025854</math>
<math>~ \dot\varphi </math>	<math>~=</math>	<math>~ \biggl\{ \Lambda \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3 }{\cos\theta} \biggr\}^{1 / 2} </math>	<math>~\dot\varphi =</math>	<math>~+1.299300</math>

COLLADA-Based Representation

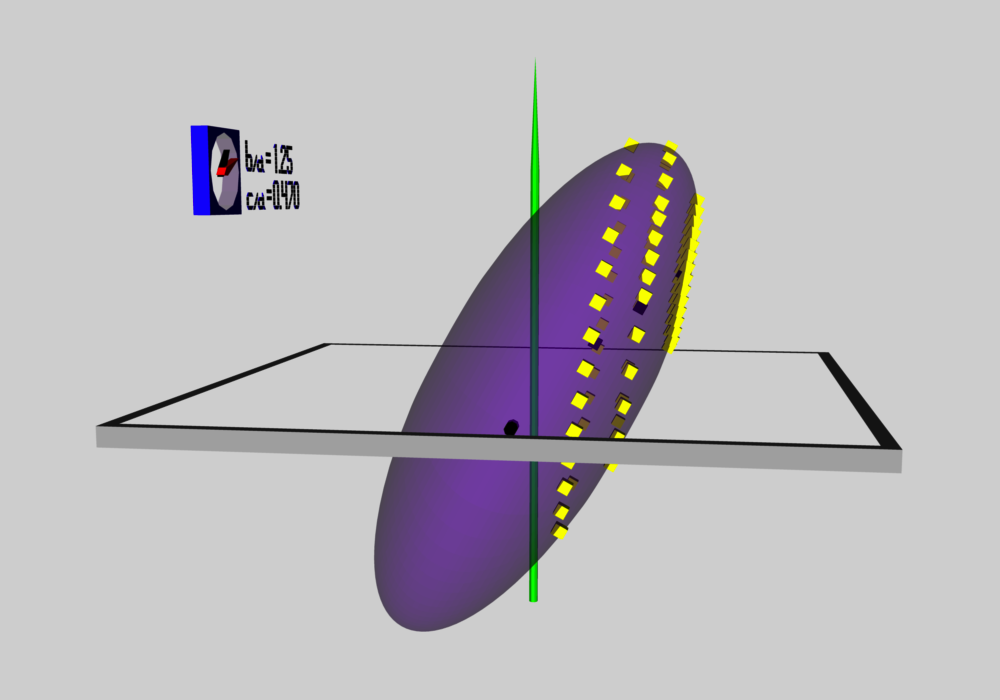
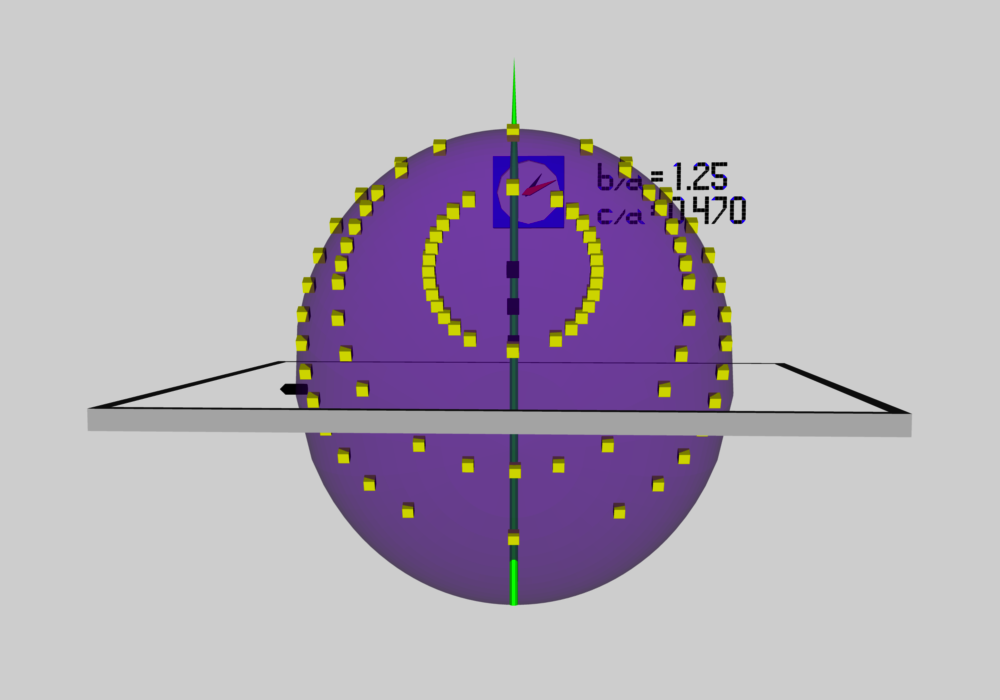
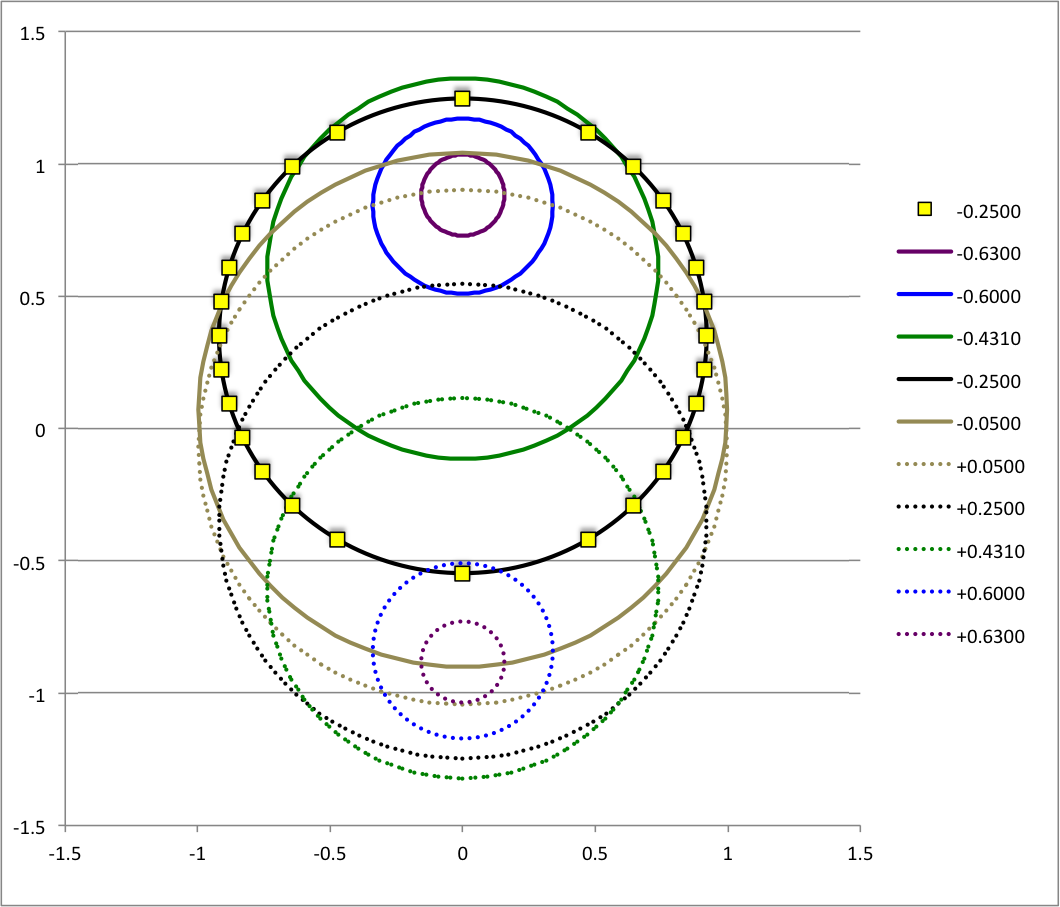
As has been described in an accompanying discussion of Riemann Type 1 ellipsoids, we have used COLLADA to construct an animated and interactive 3D scene that displays in purple the surface of an example Type I ellipsoid; panels a and b of Figure 1 show what this ellipsoid looks like when viewed from two different perspectives. (As a reminder — see the explanation accompanying Figure 2 of that accompanying discussion — the ellipsoid is tilted about the x-coordinate axis at an angle of 61.25° to the equilibrium spin axis, which is shown in green.) Yellow markers also have been placed in this 3D scene at each of the coordinate locations specified in the table that accompanies that discussion. From the perspective presented in Figure 3b, we can immediately identify three separate, nearly circular trajectories; the largest one corresponds to our choice of z₀ = -0.25, the smallest corresponds to our choice of z₀ = -0.60, and the one of intermediate size correspond to our choice of z₀ = -0.4310. When viewed from the perspective presented in Figure 1a, we see that these three trajectories define three separate planes; each plane is tipped at an angle of θ = -19.02° to the untilted equatorial, x-y plane of the purple ellipsoid.

Figure 1a	Figure 1b

↲
Figure 1c
↲

User:Tohline/ThreeDimensionalConfigurations/ChallengesPt2

Contents

Challenges Constructing Ellipsoidal-Like Configurations (Pt. 2)

Motivation

Where Are We Headed?

Intersection of Tipped Plane With Ellipsoid Surface

Body Frame

Tipped Orbital Plane

Off-Center Ellipse

Velocities

Tipped Orbit Velocities

Body Frame Velocities

Vorticity Determination

Riemann-Derived Velocity Components

Inertial-Frame Expressions

Coefficient Expression in Tipped Plane

Try Tipped Plane Again

Example Equilibrium Model

COLLADA-Based Representation

See Also

Navigation menu

Search