User:Tohline/SSC/Virial/PolytropesEmbeddedOutline
Virial Equilibrium of Embedded Polytropic Spheres

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
|
Free-Energy Surfaces for Pressure-Truncated Structures |
|
|---|---|
|
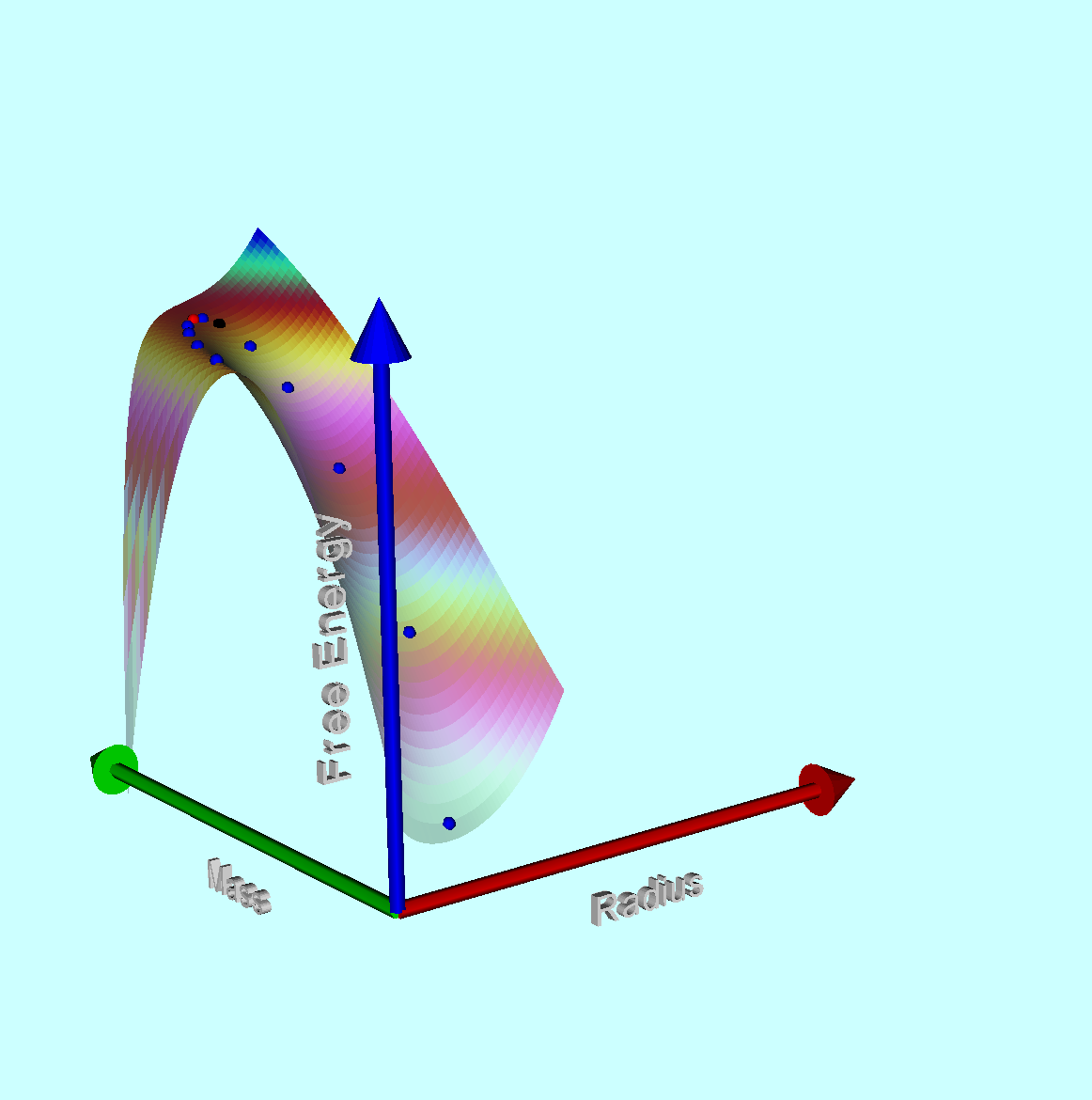
<math>\mathcal{G}(M,R)</math> surface for <math>n = 5</math> polytropic configurations |
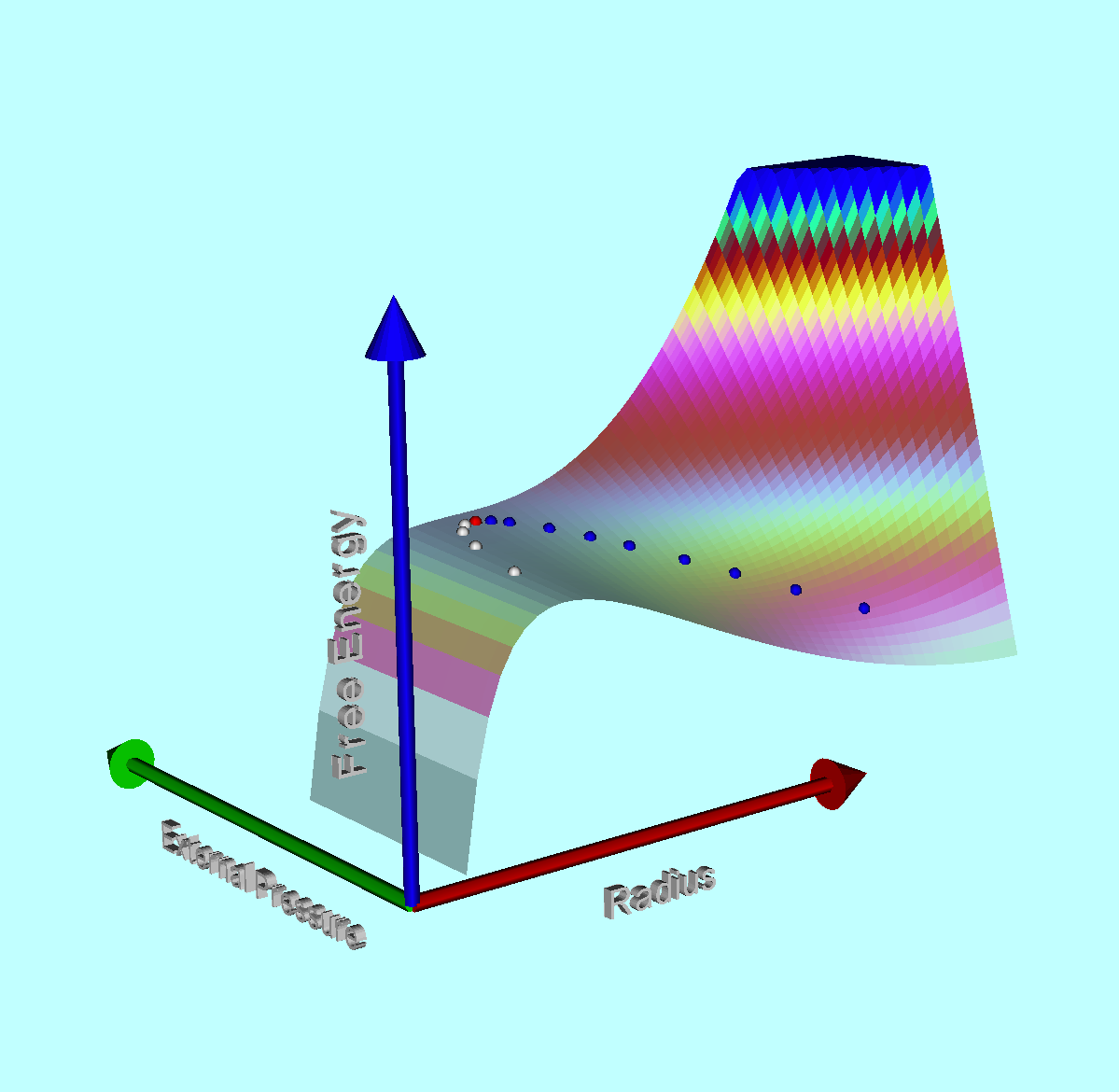
<math>\mathcal{G}(P_e,R)</math> surface for isothermal configurations (see further elaboration below) |
Overview
The free-energy function that is relevant to a discussion of the structure and stability of a pressure-truncated configuration having polytropic index, <math>~n</math>, has the form,
|
<math>~\mathcal{G}(x)</math> |
<math>~=</math> |
<math> -ax^{-1} +b x^{-3/n} + c x^3 + \mathcal{G}_0 \, , </math> |
where <math>~x</math> identifies the size of the configuration and <math>\mathcal{G}_0</math> is an arbitrary constant. (As is explained more fully, below, the lefthand panel of the figure at the top of this page displays a free-energy surface of this form for the case, <math>~n=5</math>.) If the coefficients, <math>~a, b</math>, and <math>~c</math>, are held constant while varying the configuration's size, we see that,
|
<math>~\frac{d\mathcal{G}}{dx}</math> |
<math>~=</math> |
<math> ax^{-2} - \frac{3b}{n}\cdot x^{-(3+n)/n} + 3c x^2 </math> |
|
|
<math>~=</math> |
<math> x^{-2} \biggl[ a - \frac{3b}{n}\cdot x^{(n-3)/n} + 3c x^4 \biggr] \, , </math> |
and,
|
<math>~\frac{d^2\mathcal{G}}{dx^2}</math> |
<math>~=</math> |
<math> x^{-3} \biggl[ -2a + \frac{3(3+n)b}{n^2}\cdot x^{(n-3)/n} + 6c x^4 \biggr] \, . </math> |
Equilibrium Configurations
The size, <math>~x_\mathrm{eq}</math>, of each equilibrium configuration is determined by setting, <math>d\mathcal{G}/dx = 0</math>. Hence, <math>~x_\mathrm{eq}</math> is given by the root(s) of the polynomial expression that is often referred to as the,
Scalar Virial Theorem
|
<math>~x^{(n-3)/n}_\mathrm{eq} </math> |
<math>~=</math> |
<math>\frac{n}{b} \biggl[\frac{a}{3} + c\cdot x^4_\mathrm{eq} \biggr] \, . </math> |
(The equilibrium radii of <math>~n = 5</math> polytropic configurations having a variety of different masses are identified by the sequence of a dozen, small colored spherical dots shown in the lefthand panel of the above figure.)
Stability
The relative stability of each equilibrium configuration is determined by the sign of the second derivative of the free-energy function, evaluated at the specified equilibrium radius. Specifically, the systems being considered here are stable if the second derivative is positive, but they are unstable if the second derivative is negative. Evaluating the second derivative in this manner gives,
|
<math>~\biggl[ x^{3} \cdot \frac{d^2\mathcal{G}}{dx^2}\biggr]_\mathrm{eq}</math> |
<math>~=</math> |
<math> -2a + \frac{3(3+n)}{n} \biggl[\frac{a}{3} + c\cdot x^4_\mathrm{eq} \biggr] + 6c x^4_\mathrm{eq} </math> |
|
|
<math>~=</math> |
<math> -2a + \frac{(3+n)a}{n} + \frac{3(3+n)c}{n} \cdot x^4_\mathrm{eq} + 6c x^4_\mathrm{eq} </math> |
|
|
<math>~=</math> |
<math>\frac{9(n+1)c}{n}\cdot x^4_\mathrm{eq} - \frac{a(n-3)}{n} \, . </math> |
Defining <math>~x_\mathrm{crit}</math> as the equilibrium radius at which this function goes to zero gives,
|
<math>~x_\mathrm{crit} </math> |
<math>~\equiv</math> |
<math> \biggl[ \frac{a(n-3)}{3^2c(n+1)} \biggr]^{1/4} \, . </math> |
(The small red spherical dot in the lefthand panel of the above figure identifies the equilibrium configuration at <math>~x_\mathrm{crit} </math>.) We conclude, therefore, that pressure-truncated, equilibrium polytropic configurations having <math>~n > 3</math> are stable if,
|
<math>~x_\mathrm{eq}</math> |
<math>~></math> |
<math> ~x_\mathrm{crit} \, , </math> |
while they are unstable if,
|
<math>~x_\mathrm{eq}</math> |
<math>~<</math> |
<math> ~x_\mathrm{crit} \, . </math> |
The Physics
The above mathematical statements, ostensibly defining the free-energy function, the scalar virial theorem, and stability, cannot be interpreted in physical terms until the definitions of the various coefficients have been provided. In the discussion that follows, we will focus on sequences of equilibrium configurations that have a polytropic index <math>~n > 3</math> because, as has been foreshadowed in the above overview, such sequences include both stable and unstable equilbria and are therefore of considerable interest in an astrophysical context. Isothermal sequences — corresponding to <math>~n = \infty</math> — are of particular astrophysical interest; however, we will devote a great deal of attention to <math>~n=5</math> configurations because their structures can be defined entirely in terms of analytic expressions.
|
NOTE (copied from here): The following considerations have led us to formally draw a distinction between <math>~M_\mathrm{limit}</math> and the "total" mass, <math>~M_\mathrm{tot}</math>, that we use for normalization. Isolated Polytropes: For isolated polytropes, the limit of integration, <math>~R_\mathrm{limit}</math>, will be the natural edge of the configuration, where the pressure and mass-density drop to zero. In this case, <math>~M_\mathrm{limit}</math> quite naturally corresponds to the total mass of the configuration. Pressure-Truncated Polytropes: But, a configuration embedded in an external medium of pressure, <math>~P_e</math>, will have a (pressure-truncated) surface whose radius, <math>~R_\mathrm{limit}</math>, corresponds to the radial location at which the configuration's internal pressure drops to a value that equals <math>~P_e</math>. In this case as well, one might choose to refer to <math>~M_\mathrm{limit}</math> as the total mass; on the other hand, it might be more useful to distinguish <math>~M_\mathrm{limit}</math> from <math>~M_\mathrm{tot}</math>, continuing to rely on <math>~M_\mathrm{tot}</math> to represent the mass of the corresponding isolated polytrope. BiPolytropes: When discussing bipolytropes, the limit of integration, <math>~R_\mathrm{limit}</math>, will naturally refer to the radial location that defines the outer edge of the configuration's "core" and, at the same time, identifies the radial "interface" between the bipolytrope's core and its envelope. In this case, <math>~M_\mathrm{limit}</math> corresponds to the mass of the core rather than to the total mass of the bipolytropic configuration. |
In order to determine the equilibrium radius, <math>~R_\mathrm{eq}</math>, of any pressure-truncated polytropic configuration, we must specify the configuration's mass, <math>~M_\mathrm{limit}</math>, its polytropic constant, <math>~K</math>, and the pressure, <math>~P_e</math>, of the external medium in which the configuration is embedded, and locate extrema in the resulting <math>~\mathcal{G}(R)</math> function. Then, a sequence of equilibria can be identified if, for example:
- Case P: <math>~P_e</math> is varied while holding <math>~K</math> and <math>~M_\mathrm{limit}</math> fixed; or
- Case M: <math>~M_\mathrm{limit}</math> is varied while holding <math>~K</math> and <math>~P_e</math> fixed.
In the first case, the analysis reveals how <math>~R_\mathrm{eq}</math> varies with the applied external pressure and usually is displayed as a <math>~P_e(R_\mathrm{eq})</math> function. The second case identifies a mass-radius relationship for the polytropic sequence under consideration and is usually displayed as a <math>~M_\mathrm{limit}(R_\mathrm{eq})</math> function. (In the image presented in the lefthand panel of the figure at the top of this page, a "Case M" mass-radius relation for pressure-truncated, <math>~n = 5</math> polytropic configurations is traced by the sequence of a dozen, small colored spherical dots that each reside at an extremum in the displayed free-energy function.)
Whitworth's (1981) Case P Analysis of Uniform-Density Configurations
Coefficient Definitions
Whitworth's (1981) Case P analysis of pressure-truncated polytropic spheres produces the following governing free-energy function — referred to by Whitworth as the "global potential function":
|
Equation extracted without modification from p. 973 of Whitworth (1981)
"Global Gravitational Stability for One-dimensional Polytropes"
Monthly Notices of the Royal Astronomical Society, vol. 195, pp. 967-977 © Royal Astronomical Society |
After setting <math>~\delta_{1\eta} = 0</math>, that is, by choosing to ignore isothermal systems, and after setting <math>~\eta = (n+1)/n</math>, that is, after rewriting his adiabatic exponent <math>~(\eta)</math> in terms of the corresponding polytropic index, Whitworth's free-energy expression becomes,
<math> \frac{2\mathcal{U}}{3M_0 K_1} = -\frac{3}{2} \biggl( \frac{R}{R_\mathrm{rf}}\biggr)^{-1} +~ \frac{2n}{3}\biggl( \frac{R}{R_\mathrm{rf}}\biggr)^{-3/n} +~ \frac{1}{6}\biggl(\frac{P_e}{P_\mathrm{rf}}\biggr) \biggl( \frac{R}{R_\mathrm{rf}}\biggr)^3 \, . </math>
This expression is identical to the free-energy function given above if the following coefficient and variable substitutions are made:
|
Whitworth's (1981) Case P Analysis | |||||||||||||||
|
where (see an accompanying ASIDE),
|
<math>~R_\mathrm{rf}</math> |
<math>~\equiv</math> |
<math> \biggl[ \frac{\pi}{5^n} \biggl( \frac{2^2}{3}\biggr)^{(n+1)} K^{-n} G^{n} M_\mathrm{limit}^{n-1} \biggr]^{1/(n-3)} \, , </math> |
|
<math>~P_\mathrm{rf}</math> |
<math>~\equiv</math> |
<math>~ \biggl[ 2^{-2(5n+1)}\biggl( \frac{3^4\cdot 5^3}{\pi} \biggr)^{n+1} K^{4n} G^{-3(n+1)} M_\mathrm{limit}^{-2(n+1)}\biggr]^{1/(n-3)} \, , </math> |
|
<math>~\mathcal{U}_\mathrm{rf} \equiv (M_0K_1)_\mathrm{Whitworth}</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{3^4\cdot 5^3}{2^8\pi} \biggr) K^n G^{-3} M_\mathrm{limit}^{n-5}\biggr]^{1/(n-3)} \, .</math> |
Virial Equilibrium
Plugging these coefficient assignments into the above mathematical prescription of the virial theorem gives the following relationship between the applied external pressure and the resulting equilibrium radius of pressure-truncated polytropic configurations,
|
<math>~\frac{2}{3}\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{rf}} \biggr)^{(n-3)/n} </math> |
<math>~=</math> |
<math>\frac{1}{2} + \frac{1}{6} \biggl( \frac{P_\mathrm{e}}{P_\mathrm{rf}} \biggr) \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{rf}} \biggr)^4 \, . </math> |
A rearrangement of terms explicitly provides the desired <math>~P_e(R_\mathrm{eq})</math> function, namely,
|
<math>\biggl( \frac{P_\mathrm{e}}{P_\mathrm{rf}} \biggr) </math> |
<math>~=</math> |
<math>~\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{rf}} \biggr)^{-4} \biggl[4\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{rf}} \biggr)^{(n-3)/n} -3\biggr] \, ,</math> |
|
|
<math>~=</math> |
<math>~4\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{rf}} \biggr)^{-3(n+1)/n} -3\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{rf}} \biggr)^{-4} \, ,</math> |
or,
|
<math>~P_e </math> |
<math>~=</math> |
<math>~ 4P_\mathrm{rf} R_\mathrm{rf}^{3(n+1)/n} R_\mathrm{eq}^{-3(n+1)/n} -3P_\mathrm{rf} R_\mathrm{rf}^4 R_\mathrm{eq}^{-4} </math> |
|
|
<math>~=</math> |
<math>~ 4R_\mathrm{eq}^{-3(n+1)/n}\biggl[ 2^{-2(5n+1)}\biggl( \frac{3^4\cdot 5^3}{\pi} \biggr)^{n+1} K^{4n} G^{-3(n+1)} M_\mathrm{limit}^{-2(n+1)}\biggr]^{1/(n-3)} \biggl[ \frac{\pi}{5^n} \biggl( \frac{2^2}{3}\biggr)^{(n+1)} K^{-n} G^{n} M_\mathrm{limit}^{n-1} \biggr]^{3(n+1)/[n(n-3)]} </math> |
|
|
|
<math>~ -3R_\mathrm{eq}^{-4}\biggl[ 2^{-2(5n+1)}\biggl( \frac{3^4\cdot 5^3}{\pi} \biggr)^{n+1} K^{4n} G^{-3(n+1)} M_\mathrm{limit}^{-2(n+1)}\biggr]^{1/(n-3)} \biggl[ \frac{\pi}{5^n} \biggl( \frac{2^2}{3}\biggr)^{(n+1)} K^{-n} G^{n} M_\mathrm{limit}^{n-1} \biggr]^{4/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ 2^2 R_\mathrm{eq}^{-3(n+1)/n}\biggl[ 2^{-2n(5n+1)}\biggl( \frac{3^4\cdot 5^3}{\pi} \biggr)^{n(n+1)} K^{4n^2} G^{-3n(n+1)} M_\mathrm{limit}^{-2n(n+1)}\cdot \frac{\pi^{3(n+1)}}{5^{3n(n+1)}} \biggl( \frac{2^2}{3}\biggr)^{3(n+1)(n+1)} K^{-3n(n+1)} G^{3n(n+1)} M_\mathrm{limit}^{3(n-1)(n+1)} \biggr]^{1/[n(n-3)]} </math> |
|
|
|
<math>~ -3R_\mathrm{eq}^{-4}\biggl[ 2^{-2(5n+1)}\biggl( \frac{3^4\cdot 5^3}{\pi} \biggr)^{n+1} K^{4n} G^{-3(n+1)} M_\mathrm{limit}^{-2(n+1)}\cdot \frac{\pi^4}{5^{4n}} \biggl( \frac{2^2}{3}\biggr)^{4(n+1)} K^{-4n} G^{4n} M_\mathrm{limit}^{4(n-1)} \biggr]^{1/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~ R_\mathrm{eq}^{-3(n+1)/n} \biggl( \frac{3}{2^2\pi}\biggr)^{(n+1)/n} K M_\mathrm{limit}^{(n+1)/n} - R_\mathrm{eq}^{-4} \biggl(\frac{3}{2^2\cdot 5\pi}\biggr) G M_\mathrm{limit}^2 </math> |
|
|
<math>~=</math> |
<math>~K \biggl( \frac{3M_\mathrm{limit}}{4\pi R_\mathrm{eq}^3} \biggr)^{(n+1)/n} - \frac{3GM_\mathrm{limit}^2}{20\pi R_\mathrm{eq}^4} \, .</math> |
Recalling that <math>~\eta \leftrightarrow (n+1)/n</math>, it is clear that this <math>~P_e(R_\mathrm{eq})</math> relation exactly matches equation (5) of Whitworth, which reads:
|
Equation and accompanying sentence extracted without modification from p. 970 of Whitworth (1981)
"Global Gravitational Stability for One-dimensional Polytropes"
Monthly Notices of the Royal Astronomical Society, vol. 195, pp. 967-977 © Royal Astronomical Society |
Stability
Similarly, according to the above-derived stability criterion, pressure-truncated polytropic configurations will only be stable if,
|
<math>~\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{rf}} \biggr)^4 </math> |
<math>~></math> |
<math>\frac{(n-3)}{(n+1)} \biggl( \frac{P_e}{P_\mathrm{rf}} \biggr)^{-1} \, . </math> |
Or, given that <math>~P_\mathrm{rf}R_\mathrm{rf}^4 = (G M_\mathrm{limit}^2)/(20\pi)</math>, the criterion for stability may be written as,
|
<math>~P_e </math> |
<math>~></math> |
<math>~ \frac{(n-3)}{20\pi(n+1)} \biggl( \frac{GM_\mathrm{limit}^2}{R_\mathrm{eq}^4} \biggr) \, . </math> |
ASIDE: Isothermal Configurations
While our focus in this chapter is on polytropic systems, it is advantageous to review Whitworth's (1981) discussion of pressure-truncated isothermal configurations because that discussion includes presentation of a free-energy surface — see, specifically, Whitworth's Figure 2, which is reproduced in the lower-right quadrant of our composite figure, below. Setting <math>~\delta_{1\eta} = 1</math> in Whitworth's free-energy expression (his equation 10, reprinted above) gives,
<math> \frac{2\mathcal{U}}{3\mathcal{U}_\mathrm{rf}} = -\frac{3}{2} \biggl( \frac{R}{R_\mathrm{rf}}\biggr)^{-1} +~ \frac{1}{6}\biggl(\frac{P_e}{P_\mathrm{rf}}\biggr) \biggl( \frac{R}{R_\mathrm{rf}}\biggr)^3 -2\ln\biggl( \frac{R}{R_\mathrm{rf}}\biggr) - \mathcal{G}_0 \, , </math>
where, as earlier, we have inserted the additional constant, <math>\mathcal{G}_0</math>, to accommodate normalization. A segment of the free-energy surface defined by this function is displayed in the righthand panel of the figure shown at the top of this page. In constructing this figure, <math>~\mathcal{G}_0</math> has been set to a value that ensures that <math>~\mathcal{U}</math> is everywhere positive over the displayed domain: <math>~0.1 \le P_e/P_\mathrm{rf} \le 1.1</math> and <math>~0.3 \le R/R_\mathrm{rf} \le 3.0</math>.
For a given choice of <math>~P_e</math>, equilibrium radii are identified by setting <math>~d\mathcal{U}/dR = 0</math>, that is, they are defined by the (scalar virial theorem) relation,
|
<math>~\frac{P_e}{P_\mathrm{rf}} </math> |
<math>~=</math> |
<math>~ \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{rf}}\biggr)^{-4} \biggl[4\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{rf}}\biggr) - 3 \biggr] \, ; </math> |
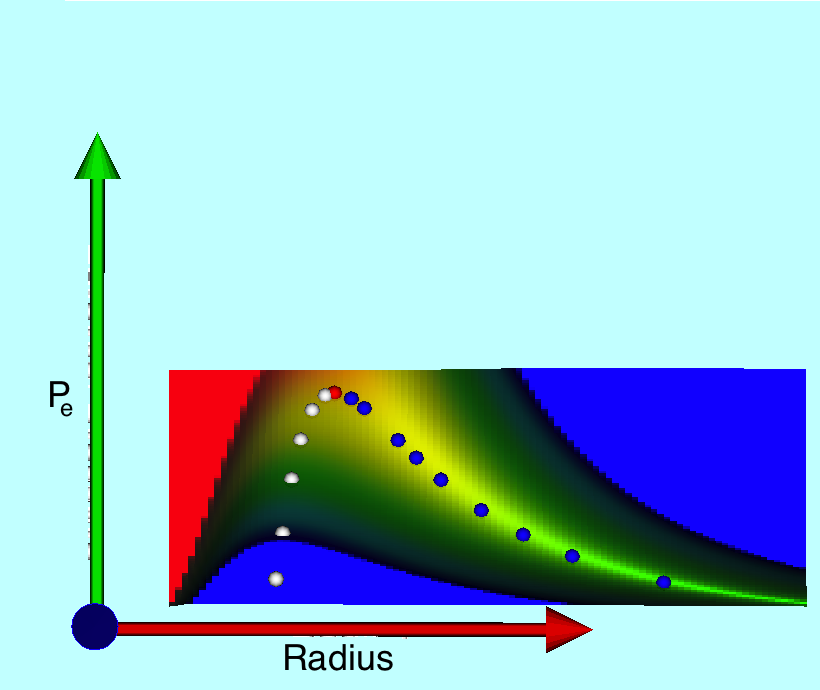
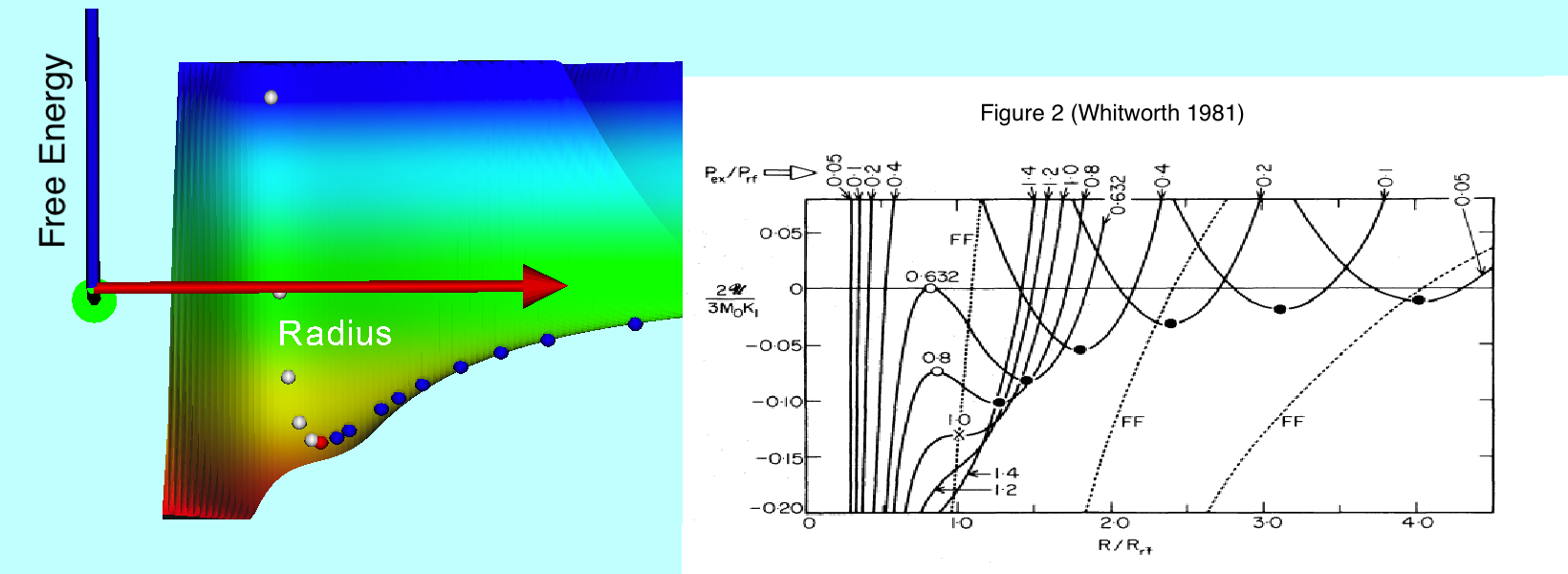
and equilibria are stable — that is, <math>~[d^2\mathcal{U}/dR^2]_\mathrm{eq} > 0</math> — if <math>~R_\mathrm{eq}/R_\mathrm{rf} > 1</math>. For physically realistic systems, of course, <math>~P_e</math> must be positive — which means that all equilibria have <math>~R_\mathrm{eq}/R_\mathrm{rf} > 3/4</math>. But, from this algebraic virial theorem expression, it is also clear that physically realistic equilibrium configurations only exist when <math>~P_e/P_\mathrm{rf} \le 1</math>. The sequence of small, colored spherical dots in the righthand panel of the above figure identify parameter-value pairs, <math>~(R_\mathrm{eq}, P_e)</math>, associated with fourteen different equilibrium configurations: Blue dots — tracing out the valley of the free-energy surface — identify stable configurations; white dots — balanced along the crest of the surface ridge — identify dynamically unstable configurations; and the lone red dot identifies the critical neutral equilibrium state, which is also associated with the maximum allowable value of <math>~P_e</math> along the equilibrium model sequence.
|
The black & white line-drawing in lower-right quadrant of this composite image is … Figure 2 extracted† from p. 973 of Whitworth (1981) "Global Gravitational Stability for One-dimensional Polytropes"Monthly Notices of the Royal Astronomical Society, vol. 195, pp. 967-977 © Royal Astronomical Society | |
|
Graphical depictions of the free-energy surface, <math>~\mathcal{G}(R, P_e) = 2\mathcal{U}/3\mathcal{U}_\mathrm{rf}</math>, associated with pressure-truncated, uniform-density isothermal configurations — see equation (10) of Whitworth (1981) or our restatement of this equation, above.
|
|
|
Properties of Virial Equilibria |
|||
|---|---|---|---|
|
<math>~\frac{P_e}{P_\mathrm{rf}}</math> |
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{rf}}</math> |
<math>~\frac{2\mathcal{U}}{3\mathcal{U}_\mathrm{rf}}</math> |
<math>~\mathcal{G}_0</math> |
|
0.200 |
2.395 |
-0.03205 |
-1.8831 |
|
0.30946 |
2.008 |
-0.04507 |
-1.6786 |
|
0.400 |
1.800 |
-0.05548 |
-1.5646 |
|
0.50364 |
1.622 |
-0.06730 |
-1.4666 |
|
0.632 |
1.452 |
-0.08213 |
-1.3743 |
|
0.72543 |
1.347 |
-0.09327 |
-1.3205 |
|
0.800 |
1.270 |
-0.10252 |
-1.2835 |
|
0.93516 |
1.127 |
-0.12070 |
-1.2263 |
|
0.97564 |
1.071 |
-0.12681 |
-1.2111 |
|
1.000 |
1.000 |
-0.13086 |
-1.2025 |
|
0.9897 |
0.9612 |
-0.12880 |
-1.2061 |
|
0.92636 |
0.9061 |
-0.11370 |
-1.2297 |
|
0.800 |
0.859 |
-0.07423 |
-1.2835 |
|
0.632 |
0.822 |
0.000 |
-1.3743 |
|
0.400 |
0.789 |
+0.17021 |
-1.5646 |
|
0.200 |
0.767 |
+0.47300 |
-1.8831 |
Figure 2 from Whitworth (1981) — reproduced in the lower-right quadrant of the composite image shown immediately above — does an excellent job of conveying many of the essential elements of this isothermal free-energy surface within the constraints imposed by a two-dimensional black & white line plot. In order to construct this compact plot, Whitworth employed a different free-energy normalization parameter for each selected value of the external pressure. Specifically, he used,
<math>~\mathcal{G}_0(P_e) = \frac{2}{3}\biggl[ 1 + \ln\biggl( \frac{P_e}{4P_\mathrm{rf}} \biggr)\biggr] - \frac{3}{2} \biggl( \frac{P_e}{4P_\mathrm{rf}} \biggr)^{1/3} \, .</math>
In an effort to quantitatively compare (and check for accuracy) our results with Whitworth's, we have adopted the same <math>~\mathcal{G}_0(P_e)</math> normalization function when generating the multicolored, three-dimensional free-energy surface that is displayed (with three different projections) in the above composite image, along with the reproduction of Whitworth's Figure 2. Aside from this pressure-dependent normalization parameter, the surface drawn for comparison with Whitworth's Figure 2 is identical to the one displayed in the righthand panel of the figure at the top of this page.
Our Case P Analysis Allowing for Nonuniform Density Structures
Coefficient Definitions
As has been both summarized and detailed in an accompanying discussion, our Case P analysis has demonstrated that the following,
Algebraic Free-Energy Function
<math> \mathfrak{G}^* = -3\mathcal{A} \chi^{-1} +~ n\mathcal{B} \chi^{-3/n} +~ \mathcal{D}\chi^3 \, , </math>
properly governs the equilibrium structure and stability of pressure-truncated polytropic configurations. This algebraic expression is identical to the free-energy function given above if the following coefficient and variable substitutions are made:
|
Our Case P Analysis | |||||||||||||||
|
where — see, for example, our accompanying review,
|
<math>~R_\mathrm{norm}</math> |
<math>~=</math> |
<math>~\biggl[ \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} \biggr]^{1/(n-3)} \, ,</math> |
|
<math>~P_\mathrm{norm}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}} \biggr]^{1/(n-3)} \, , </math> |
|
<math>~E_\mathrm{norm}</math> |
<math>~=</math> |
<math>~ \biggl[ K^n G^{-3}M_\mathrm{tot}^{n-5} \biggr]^{1/(n-3)} \, ,</math> |
and, in terms of the structural form factors, <math>~\tilde\mathfrak{f}_M</math>, <math>~\tilde\mathfrak{f}_A</math>, and <math>~\tilde\mathfrak{f}_W</math>,
|
<math>~\mathcal{A}</math> |
<math>~=</math> |
<math>\frac{1}{5} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^2 \cdot \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \, , </math> |
|
<math>~\mathcal{B}</math> |
<math>~=</math> |
<math> \biggl(\frac{3}{4\pi}\biggr)^{1/n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{(n+1)/n} \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{(n+1)/n}} \, . </math> |
Virial Equilibrium
Plugging these coefficient assignments into the above mathematical prescription of the virial theorem gives the following relationship between the applied external pressure and the resulting equilibrium radius of pressure-truncated polytropic configurations,
|
<math>~\mathcal{B} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^{(n-3)/n} </math> |
<math>~=</math> |
<math>\mathcal{A} + \frac{4\pi}{3} \biggl( \frac{P_\mathrm{e}}{P_\mathrm{norm}} \biggr) \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4 \, , </math> |
which matches the statement of virial equilibrium presented in our accompanying, more detailed analysis. A rearrangement of terms explicitly provides the desired <math>~P_e(R_\mathrm{eq})</math> function, namely,
|
<math>~ \frac{P_\mathrm{e}}{P_\mathrm{norm}} </math> |
<math>~=</math> |
<math>~\frac{3}{4\pi} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^{-4} \biggl[ \mathcal{B} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^{(n-3)/n} -\mathcal{A} \biggr] \, , </math> |
or (see the accompanying derivation for details),
|
<math>~P_e </math> |
<math>~=</math> |
<math>~K \biggl( \frac{3M_\mathrm{limit}}{4\pi R_\mathrm{eq}^3} \biggr)^{(n+1)/n} \cdot \frac{\mathfrak{f}_A}{\mathfrak{f}_M^{(n+1)/n}} - \biggl(\frac{3GM_\mathrm{limit}^2}{20\pi R_\mathrm{eq}^4} \biggr)\cdot \frac{\mathfrak{f}_W}{\mathfrak{f}^2_M} \, .</math> |
Notice that this equilibrium relation exactly matches the one derived by Whitworth — and rederived above — when all three structural form factors are set to unity. This is as it should be because all of Whitworth's results were derived assuming uniform-density configurations. Also notice that, when <math>~P_e \rightarrow 0</math>, this expression reduces to the solution we obtained for an isolated polytrope, expressed in terms of <math>~K</math> and <math>~M_\mathrm{limit}</math> (see the left-hand column of our table titled "Two Points of View").
Stability
Similarly, according to the above-derived stability criterion, pressure-truncated polytropic configurations will only be stable if,
|
<math>~\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4 </math> |
<math>~></math> |
<math>\frac{(n-3)\mathcal{A}}{4\pi(n+1)} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \, . </math> |
Or, given that <math>~P_\mathrm{norm}R_\mathrm{norm}^4 = G M_\mathrm{tot}^2</math>, the criterion for stability may be written as,
|
<math>~P_e </math> |
<math>~></math> |
<math>~ \frac{(n-3)\mathcal{A}}{4\pi(n+1)} \biggl( \frac{GM_\mathrm{tot}^2}{R_\mathrm{eq}^4} \biggr) =\frac{(n-3)}{20\pi(n+1)} \cdot \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \biggl( \frac{GM_\mathrm{limit}^2}{R_\mathrm{eq}^4} \biggr) \, . </math> |
Our Case M Analysis
Coefficient Definitions
As has been detailed in an accompanying discussion, our Case M analysis has demonstrated that the free-energy expression governing the equilibrium structure and stability of pressure-truncated polytropic configurations can also be written as,
|
<math>~\mathfrak{G}^*_\mathrm{SWS}</math> |
<math>~=</math> |
<math>~ -3\mathcal{A}_{M_\ell}\biggl( \frac{n+1}{n}\biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^{2} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-1} +~ n\mathcal{B}_{M_\ell} \cdot \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^{(n+1)/n} \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{-3/n} +~ \frac{4\pi}{3} \cdot \biggl(\frac{R}{R_\mathrm{SWS}}\biggr)^{3} \, . </math> |
Written in this form, the expression highlights the functional dependence on the configuration's mass while assuming that the external pressure is held fixed. Still, the expression is identical to the free-energy function given above, but viewed in this manner the appropriate coefficient and variable substitutions are:
|
Our Case M Analysis | |||||||||||||||
|
where, drawing from Steven W. Stahler's (1983) work — see also our accompanying discussion,
|
<math>~M_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~\biggl( \frac{n+1}{nG} \biggr)^{3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \, ,</math> |
|
<math>~R_\mathrm{SWS}</math> |
<math>~\equiv</math> |
<math>~ \biggl( \frac{n+1}{nG} \biggr)^{1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \, ,</math> |
|
<math>~E_\mathrm{SWS} \equiv \biggl( \frac{n}{n+1}\biggr)\frac{GM_\mathrm{SWS}^2}{R_\mathrm{SWS}} </math> |
<math>~\equiv</math> |
<math>~ \biggl( \frac{n+1}{nG} \biggr)^{3/2} K^{3n/(n+1)} P_\mathrm{e}^{(5-n)/[2(n+1)]} \, ,</math> |
and, in terms of the structural form factors, <math>~\tilde\mathfrak{f}_M</math>, <math>~\tilde\mathfrak{f}_A</math>, and <math>~\tilde\mathfrak{f}_W</math>,
|
<math>~\mathcal{A}_{M_\ell}</math> |
<math>~\equiv</math> |
<math>~ \mathcal{A} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2} = \frac{1}{5} \cdot \frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_M^2} \, ,</math> |
|
<math>~\mathcal{B}_{M_\ell}</math> |
<math>~\equiv</math> |
<math>~\mathcal{B} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{-(n+1)/n} = \biggl( \frac{3}{4\pi}\biggr)^{1/n} \frac{\tilde\mathfrak{f}_A}{\tilde\mathfrak{f}_M^{(n+1)/n}} \, . </math> |
Virial Equilibrium
Plugging these coefficient assignments into the above mathematical prescription of the virial theorem gives the mass-radius relationship for pressure-truncated, polytropic equilibrium configurations, namely,
|
<math>~\mathcal{B}_{M_\ell} \cdot \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^{(n+1)/n} \biggl( \frac{R}{R_\mathrm{SWS}} \biggr)^{(n-3)/n} </math> |
<math>~=</math> |
<math>\mathcal{A}_{M_\ell}\biggl( \frac{n+1}{n}\biggr) \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^{2} + \frac{4\pi}{3} \biggl( \frac{R}{R_\mathrm{SWS}} \biggr)^4 \, , </math> |
which matches the statement of virial equilibrium presented in our accompanying, more detailed analysis.
Stability
Similarly, according to the above-derived stability criterion, pressure-truncated polytropic configurations will only be stable if,
|
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{SWS}} </math> |
<math>~></math> |
<math>\biggl[ \frac{\mathcal{A}_{M_\ell}(n-3)}{4\pi n}\biggr]^{1/4} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{SWS}} \biggr)^{1/2} \, . </math> |
Or, flipped around, the criterion for stability may be written as,
|
<math>~\frac{M_\mathrm{limit}}{M_\mathrm{SWS}} </math> |
<math>~<</math> |
<math>~ \biggl[ \frac{4\pi n}{\mathcal{A}_{M_\ell}(n-3)}\biggr]^{1/2} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^2 \, . </math> |
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Outline of Detailed Investigations Leading to Above Summary
First Effort
My first attempt to analytically define the free energy, and then the virial equilibrium, of pressure-truncated (embedded) polytropic spheres was developed as a direct extension of my description of the virial equilibrium of isolated polytropes. An important outcome of this "first effort" was the unveiling of analytic expressions for the key structural form factors, both for isolated polytropes and, separately, for pressure-truncated polytropic structures.
I am very confident that the form-factor expressions presented for isolated polytropes are all correct because they have been cross-checked with expressions for closely related "integral" parameters discussed by Chandrasekhar [C67]. Although the form-factor expressions derived for pressure-truncated polytropes make some sense — they look very similar to the ones presented for isolated polytropes and seem to behave properly for models which, based on detailed force-balanced analysis, are known to be in equilibrium — I have much less confidence that they are correct. A couple of strategies were developed in an effort to demonstrate the validity and utility of these more general form-factor expressions, resulting in the derivation of a concise virial equilibrium relation,
<math>\Pi_\mathrm{ad} = \chi_\mathrm{ad}^{-3\gamma} - \chi_\mathrm{ad}^{-4} \, ,</math>
that incorporates the newly defined normalization parameters, <math>~R_\mathrm{ad}</math> and <math>~P_\mathrm{ad}</math>. But subsequent derivations aimed at more conclusively demonstrating the correctness of the more general form-factor expressions were messy and got bogged down.
Second Effort
My second attempt to analytically define the free energy, and then the virial equilibrium, of pressure-truncated (embedded) polytropic spheres built upon my first effort and, for a couple of different polytropic indexes, focused on comparing the mass-radius relationship embodied in detailed force-balanced models against the mass-radius relationship implied by the virial theorem. A lot of reasonable results seem to have arisen from a discussion of models (done numerically using Excel) with <math>~n=4</math> polytropic index. And there are some nice aspects of models with an <math>~n=5</math> index, but these models raise some serious concerns related to the fact that two of our "derived" form-factor expressions involve division by the factor, <math>~(5-n)</math>, that is, division by zero.
Third Effort
In an attempt to answer the serious concern(s) raised during our first two efforts, we finally buckled down and performed the integrals necessary to determine expressions for key structural form factors in the cases where the internal structure is known analytically, specifically, for indexes <math>~n=5</math> and <math>~n=1</math>. The result is that the individual expressions derived by direct integration for <math>~\mathfrak{f}_W</math> and for <math>~\mathfrak{f}_A</math> do not match the general form-factor expressions that were rather cavalierly "derived" during our first effort. Oddly enough, as we discovered while fiddling around with the new results, the ratio of these form factors appears to be the same as before, namely,
|
<math>~\frac{\tilde\mathfrak{f}_W}{\tilde\mathfrak{f}_A - \tilde\theta^{n+1}}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{3\cdot 5}{(n+1) \tilde\xi^2 } \biggr] \, . </math> |
It is worth noting that, as a result of this more thorough "third effort" examination, we have confirmed that the third key form factor,
<math>~\mathfrak{f}_M = \frac{\bar\rho}{\rho_c} = \biggl[- \frac{3\tilde\theta^'}{\tilde\xi}\biggr] \, ,</math>
which is the same as before and the same as for isolated polytropes. We also have determined that,
<math>~\biggl(\frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} = \biggl(\frac{\tilde\xi^2 \tilde\theta^'}{\xi_1 \theta^'_1} \biggr)\biggl[- \frac{\tilde\xi}{3\tilde\theta^'}\biggr] = - \frac{\tilde\xi^3 }{3\xi_1 \theta^'_1} \, , </math>
except in the case of <math>~n=5</math> structures, for which we have determined,
<math>~\biggl[\biggl(\frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\mathfrak{f}_M} \biggr]_{n=5} = \ell^3 = \biggl( \frac{\tilde\xi^2}{3} \biggr)^{3/2} \, . </math>
First Effort, Second Time Around
In an accompanying chapter, we reproduce the discussion associated with our "First Effort", as referenced above, but correct expressions for <math>~\mathfrak{f}_W</math> and <math>~\mathfrak{f}_A</math>, as identified in our "Third Effort" and, accordingly, re-derive various affected expressions that follow.
Second Effort, Second Time Around
In an accompanying chapter, we reproduce the discussion associated with our "Second Effort", as referenced above, but revise key sections to incorporate corrected expressions for the structural form factors.
See Also

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |