Difference between revisions of "User:Tohline/SSC/Virial/FormFactors"
(→One Detailed Example (n = 5): Begin showing how appropriate integral gives M_r profile) |
(→Structural Form Factors: Finished carrying out 2nd M_r integral) |
||
| Line 346: | Line 346: | ||
As it should, this expression exactly matches the normalized <math>~M_r</math> profile shown above. | As it should, this expression exactly matches the normalized <math>~M_r</math> profile shown above. | ||
Alternatively, as has been laid out in our [[User:Tohline/SphericallySymmetricConfigurations/Virial#Summary_of_Normalized_Expressions|summary of normalized free-energy | Alternatively, as has been laid out in our [[User:Tohline/SphericallySymmetricConfigurations/Virial#Summary_of_Normalized_Expressions|summary of normalized expressions that are relevant to free-energy calculations]], | ||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 359: | Line 359: | ||
<td align="left"> | <td align="left"> | ||
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) | <math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) | ||
\int_0^{x} 3x^2 \biggl[ \frac{\rho(x)}{\ | \int_0^{x} 3x^2 \biggl[ \frac{\rho(x)}{\rho_0} \biggr] dx \, ,</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
where, <math>~M_\mathrm{limit}</math> is the "total" mass of the polytropic configuration that is truncated at <math>~R_\mathrm{limit}</math>; keep in mind that, here, | |||
<div align="center"> | |||
<math>M_\mathrm{tot} = \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{1/2} \rho_0^{-1/5} \, ,</math> | |||
</div> | |||
is the total mass of the ''isolated'' <math>~n=5</math> polytrope, that is, a polytrope whose ''Lane-Emden'' radius extends all the way to <math>~\xi_1</math>. In our discussions of truncated polytropes, we often will use <math>~\tilde\xi \le \xi_1</math> to specify the truncated radius in terms of the familiar, dimensionless Lane-Emden radial coordinate, so here we will set, | |||
<div align="center"> | |||
<math>~R_\mathrm{limit} = a_5 \tilde\xi ~~~~\Rightarrow ~~~~ x = \frac{r}{R_\mathrm{limit}} = \frac{a_5 \xi}{a_5 \tilde\xi} = \frac{\xi}{\tilde\xi} \, .</math> | |||
</div> | |||
Hence, in terms of the desired integration coordinate, <math>~x</math>, the density profile provided above becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{\rho(x)}{\rho_0}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-5/2} \, ,</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
and the integral defining <math>~M_r(x)</math> becomes, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{M_r(x)}{M_\mathrm{tot}} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) | |||
\int_0^{x} 3x^2 \biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-5/2} dx </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
| |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) | |||
\biggl\{ x^3 \biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-3/2} \biggr\} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
In this case, integrating "all the way out to the surface" means setting <math>~r = R_\mathrm{limit}</math> and, hence, <math>~x = 1</math>; by definition, it also means <math>~M_r(x) = M_\mathrm{limit}</math>. Therefore we have, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~\frac{M_\mathrm{limit}}{M_\mathrm{tot}} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) | |||
\biggl[ 1 + \frac{\tilde\xi^2}{3} \biggr]^{-3/2} </math> | |||
</td> | |||
</tr> | |||
<tr> | |||
<td align="right"> | |||
<math>~\Rightarrow ~~~ \biggl( \frac{\bar\rho}{\rho_c} \biggr)_\mathrm{eq} </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math>~ \biggl[ 1 + \frac{\tilde\xi^2}{3} \biggr]^{-3/2} \, .</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
{{LSU_HBook_footer}} | {{LSU_HBook_footer}} | ||
Revision as of 19:21, 3 January 2015
Structural Form Factors

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
As has been defined in a companion, introductory discussion, three key dimensionless structural form factors are:
|
<math>~\mathfrak{f}_M </math> |
<math>~\equiv</math> |
<math>~ \int_0^1 3\biggl[ \frac{\rho(x)}{\rho_c}\biggr] x^2 dx \, ,</math> |
|
<math>~\mathfrak{f}_W</math> |
<math>~\equiv</math> |
<math>~ 3\cdot 5 \int_0^1 \biggl\{ \int_0^x \biggl[ \frac{\rho(x)}{\rho_c}\biggr] x^2 dx \biggr\} \biggl[ \frac{\rho(x)}{\rho_c}\biggr] x dx\, ,</math> |
|
<math>~\mathfrak{f}_A</math> |
<math>~\equiv</math> |
<math>~ \int_0^1 3\biggl[ \frac{P(x)}{P_c}\biggr] x^2 dx \, ,</math> |
where, <math>~x \equiv r/R_\mathrm{limit}</math>.
One Detailed Example (n = 5)
Here we derive detailed expressions for the above subset of structural form factors in the case of spherically symmetric configurations that obey an <math>~n=5</math> polytropic equation of state. The hope is that this will illustrate, in a clear and helpful manner, how the task of calculating form factors is to be carried out, in practice; and, in particular, to provide one nontrivial example for which analytic expressions are derivable. This should simplify the task of debugging numerical algorithms that are designed to calculate structural form factors for more general cases that cannot be derived analytically. The limits of integration will be specified in a general enough fashion that the resulting expressions can be applied, not only to the structures of isolated polytropes, but to pressure-truncated polytropes that are embedded in a hot, tenuous external medium and to the cores of bipolytropes.
Foundation
We use the following normalizations, as drawn from our more general introductory discussion:
|
Adopted Normalizations <math>~(n=5; ~\gamma=6/5)</math> | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|||||||||||||||||||
|
Note that the following relations also hold: <math>~E_\mathrm{norm} = P_\mathrm{norm} R_\mathrm{norm}^3 = \frac{G M_\mathrm{tot}^2}{ R_\mathrm{norm}} = \biggl( \frac{3}{4\pi} \biggr) M_\mathrm{tot} c_\mathrm{norm}^2</math> | |||||||||||||||||||
As is detailed in our accompanying discussion of bipolytropes — see also our discussion of the properties of isolated polytropes — in terms of the dimensionless Lane-Emden coordinate, <math>~\xi \equiv r/a_{5}</math>, where,
<math> a_{5} =\biggr[ \frac{3K}{2\pi G} \biggr]^{1/2} \rho_0^{-2/5} \, , </math>
the radial profile of various physical variables is as follows:
|
<math>~\frac{r}{[K^{1/2}/(G^{1/2}\rho_0^{2/5})]}</math> |
<math>~=</math> |
<math>~\biggl( \frac{3}{2\pi} \biggr)^{1/2} \xi \, ,</math> |
|
<math>~\frac{\rho}{\rho_0}</math> |
<math>~=</math> |
<math>~\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-5/2} \, ,</math> |
|
<math>~\frac{P}{K\rho_0^{6/5}}</math> |
<math>~=</math> |
<math>~\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3} \, ,</math> |
|
<math>~\frac{M_r}{[K^{3/2}/(G^{3/2}\rho_0^{1/5})]}</math> |
<math>~=</math> |
<math>~\biggl( \frac{2\cdot 3}{\pi } \biggr)^{1/2} \biggl[ \xi^3 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3/2} \biggr] \, .</math> |
Notice that, in these expressions, the central density, <math>~\rho_0</math>, has been used instead of <math>~M_\mathrm{tot}</math> to normalize the relevant physical variables. We can switch from one normalization to the other by realizing that — see, again, our accompanying discussion — in isolated <math>~n=5</math> polytropes, the total mass is given by the expression,
<math>M_\mathrm{tot} = \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{1/2} \rho_0^{-1/5} ~~~~\Rightarrow ~~~~ \rho_0^{1/5} = \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{1/2} M_\mathrm{tot}^{-1} \, .</math>
Employing this mapping to switch to our "preferred" adopted normalizations, as defined in the above boxed-in table, the four radial profiles become,
|
<math>~r^\dagger \equiv \frac{r}{R_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\pi}{2\cdot 3^4} \biggr) \biggl( \frac{3}{2\pi} \biggr)^{1/2} \xi = \biggl( \frac{\pi}{2^3\cdot 3^7} \biggr)^{1/2} \xi \, ,</math> |
|
<math>~\rho^\dagger \equiv \frac{\rho}{\rho_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl( \frac{2^3\cdot 3^6}{\pi} \biggr)^{3/2} \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-5/2} \, ,</math> |
|
<math>~P^\dagger \equiv \frac{P}{P_\mathrm{norm}}</math> |
<math>~=</math> |
<math>~\biggl( \frac{2\cdot 3^4}{\pi} \biggr)^3 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3} \, ,</math> |
|
<math>~\frac{M_r}{M_\mathrm{tot}}</math> |
<math>~=</math> |
<math>~ \biggl( \frac{\pi}{2\cdot 3^4} \biggr)^{1/2} \biggl( \frac{2\cdot 3}{\pi } \biggr)^{1/2} \biggl[ \xi^3 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-3/2} \biggr] = \biggl[\frac{\xi^2}{3}\biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-1}\biggr]^{3/2} \, .</math> |
Mass
While we already know the expression for the <math>~M_r</math> profile, having copied it from our discussion of detailed force-balanced models of isolated polytropes, let's show how that profile can be derived by integrating over the density profile. After employing the norm-subscripted quantities, as defined above, to normalize the radial coordinate and the mass density in our introductory discussion of the virial theorem, we obtained the following integral defining the,
Normalized Mass:
|
<math>~M_r(r^\dagger) </math> |
<math>~=</math> |
<math> M_\mathrm{tot} \int_0^{r^\dagger} 3(r^\dagger)^2 \rho^\dagger dr^\dagger \, . </math> |
Plugging in the profiles for <math>~r^\dagger</math> and <math>~\rho^\dagger</math>, and recognizing that,
<math>~dr^\dagger = \biggl( \frac{\pi}{2^3\cdot 3^7} \biggr)^{1/2} d\xi \, ,</math>
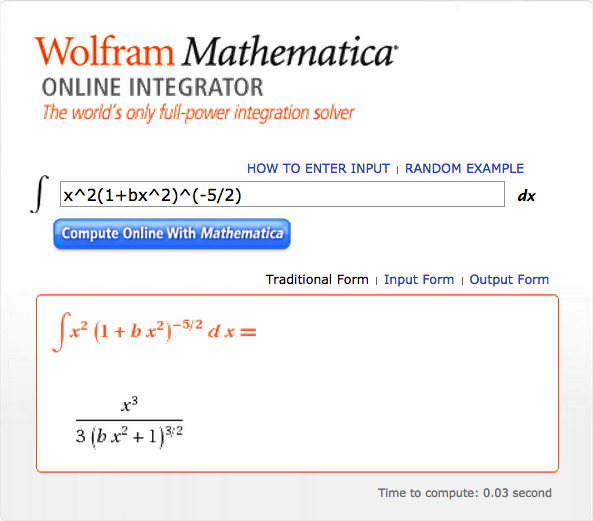
gives, with the help of Mathematica's Online Integrator,
|
<math>~\frac{M_r(\xi)}{M_\mathrm{tot} } </math> |
<math>~=</math> |
<math> 3 \biggl( \frac{\pi}{2^3\cdot 3^7} \biggr)^{3/2} \biggl( \frac{2^3\cdot 3^6}{\pi} \biggr)^{3/2} \int_0^{\xi} \xi^2 \biggl( 1 + \frac{1}{3}\xi^2 \biggr)^{-5/2} d\xi </math> |
|
|
<math>~=</math> |
<math> 3 \biggl( \frac{1}{3} \biggr)^{3/2} \biggl[ \frac{\xi^3}{3}\biggl(1+\frac{\xi^2}{3}\biggr)^{-3/2} \biggr]_0^{\xi} </math> |
|
|
<math>~=</math> |
<math> \biggl[ \frac{\xi^2}{3}\biggl(1+\frac{\xi^2}{3}\biggr)^{-1}\biggr]^{3/2} \, . </math> |
As it should, this expression exactly matches the normalized <math>~M_r</math> profile shown above.
Alternatively, as has been laid out in our summary of normalized expressions that are relevant to free-energy calculations,
|
<math>~\frac{M_r(x)}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \int_0^{x} 3x^2 \biggl[ \frac{\rho(x)}{\rho_0} \biggr] dx \, ,</math> |
where, <math>~M_\mathrm{limit}</math> is the "total" mass of the polytropic configuration that is truncated at <math>~R_\mathrm{limit}</math>; keep in mind that, here,
<math>M_\mathrm{tot} = \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{1/2} \rho_0^{-1/5} \, ,</math>
is the total mass of the isolated <math>~n=5</math> polytrope, that is, a polytrope whose Lane-Emden radius extends all the way to <math>~\xi_1</math>. In our discussions of truncated polytropes, we often will use <math>~\tilde\xi \le \xi_1</math> to specify the truncated radius in terms of the familiar, dimensionless Lane-Emden radial coordinate, so here we will set,
<math>~R_\mathrm{limit} = a_5 \tilde\xi ~~~~\Rightarrow ~~~~ x = \frac{r}{R_\mathrm{limit}} = \frac{a_5 \xi}{a_5 \tilde\xi} = \frac{\xi}{\tilde\xi} \, .</math>
Hence, in terms of the desired integration coordinate, <math>~x</math>, the density profile provided above becomes,
|
<math>~\frac{\rho(x)}{\rho_0}</math> |
<math>~=</math> |
<math>~\biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-5/2} \, ,</math> |
and the integral defining <math>~M_r(x)</math> becomes,
|
<math>~\frac{M_r(x)}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \int_0^{x} 3x^2 \biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-5/2} dx </math> |
|
|
<math>~=</math> |
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \biggl\{ x^3 \biggl[ 1 + \biggl(\frac{\tilde\xi^2}{3}\biggr)x^2 \biggr]^{-3/2} \biggr\} \, .</math> |
In this case, integrating "all the way out to the surface" means setting <math>~r = R_\mathrm{limit}</math> and, hence, <math>~x = 1</math>; by definition, it also means <math>~M_r(x) = M_\mathrm{limit}</math>. Therefore we have,
|
<math>~\frac{M_\mathrm{limit}}{M_\mathrm{tot}} </math> |
<math>~=</math> |
<math>~ \biggl( \frac{\rho_c}{\bar\rho} \biggr)_\mathrm{eq} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \biggl[ 1 + \frac{\tilde\xi^2}{3} \biggr]^{-3/2} </math> |
|
<math>~\Rightarrow ~~~ \biggl( \frac{\bar\rho}{\rho_c} \biggr)_\mathrm{eq} </math> |
<math>~=</math> |
<math>~ \biggl[ 1 + \frac{\tilde\xi^2}{3} \biggr]^{-3/2} \, .</math> |

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |