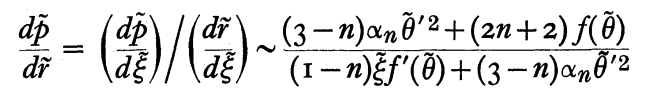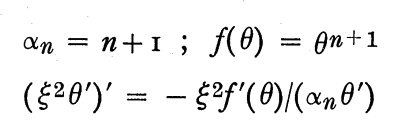User:Tohline/SSC/Structure/PolytropesEmbedded
Embedded Polytropic Spheres
In a separate discussion we have shown how to determine the structure of isolated polytropic spheres. These are rather idealized stellar structures in which the pressure and density both drop to zero at the surface of the configuration. Here we consider how the equilibrium radius of a polytropic configuration of a given <math>~M</math> and <math>~K_\mathrm{n}</math> is modified when it is embedded in an external medium of pressure <math>~P_e</math>. We will begin by reviewing the general properties of embedded (and truncated) polytropes for a wide range of polytropic indexes, principally summarizing the published descriptions provided by Horedt (1970), by Whitworth (1981), by Kimura (1981a), and by Stahler (1983). Then we will focus in more detail on polytropes of index <math>~n</math> = 1 and <math>~n</math> = 5 because their structures can be described by closed-form analytic expressions.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
General Properties
Horedt's Presentation
It appears as though Horedt (1970) was the first to draw an analogy between the mass limit that is associated with bounded isothermal spheres — the so-called Bonnor-Ebert spheres — and the limiting mass that can be found in association with equilibrium sequences of embedded polytropes that have polytropic indexes <math>~n > 3</math>. Using a tilde to denote values of parameters at the (truncated) edge of a pressure-bounded polytropic sphere, Horedt (see the bottom of his p. 83) derives the following set of parametric equations relating the configuration's dimensionless radius, <math>~r_a</math>, to a specified dimensionless bounding pressure, <math>~p_a</math>:
|
<math> ~r_a \equiv \frac{R_\mathrm{eq}}{R_\mathrm{Horedt}} </math> |
<math>~=~</math> |
<math> \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} \, , </math> |
|
<math> ~p_a \equiv \frac{P_\mathrm{e}}{P_\mathrm{Horedt}} </math> |
<math>~=~</math> |
<math> \tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \, , </math> |
where it is understood that, as discussed elsewhere, <math>~\theta_n(\xi)</math> is the solution to the Lane-Emden equation for a polytrope of index <math>~n</math>,
|
<math> \tilde\theta' </math> |
<math>~\equiv~</math> |
<math> \frac{d\theta_n}{d\xi} ~~~\mathrm{evaluated}~\mathrm{at}~\tilde\xi \, , </math> |
|
<math> ~R_\mathrm{Horedt} </math> |
<math>~\equiv~</math> |
<math> \alpha_r \biggl( \frac{\alpha_M}{M} \biggr)^{(1-n)/(n-3)} = \biggl[ \frac{4\pi}{(n+1)^n}\biggl( \frac{G}{K_n} \biggr)^n M^{n-1} \biggr]^{1/(n-3)} \, , </math> |
|
<math> ~P_\mathrm{Horedt} </math> |
<math>~\equiv~</math> |
<math> K_n \biggl( \frac{\alpha_M}{M} \biggr)^{2(n+1)/(n-3)} = K_n^{4n/(n-3)}\biggl[ \frac{(n+1)^3}{4\pi G^3 M^2} \biggr]^{(n+1)/(n-3)} \, . </math> |
Notice that, via these normalizations, Horedt chose to express <math>~R_\mathrm{eq}</math> and <math>~P_\mathrm{e}</math> in terms of <math>~K_\mathrm{n}</math> and the system's total mass, <math>~M</math>.
Whitworth's Presentation
In §5 of his paper, Whitworth (1981) also presents the set of parametric equations that define what the equilibrium radius, <math>~R_\mathrm{eq}</math>, is of an embedded polytrope for a certain imposed external pressure, <math>~P_\mathrm{e}</math>, namely,
|
<math> ~R_\mathrm{eq} </math> |
<math>~=~</math> |
<math> ~R_\mathrm{rf} \biggl\{ \frac{4\eta}{5|\eta-1|} \biggl(\frac{\xi}{3} \biggr)^\eta \biggl|\frac{d\theta_n}{d\xi} \biggr|^{(2-\eta)} \biggr\}_{\xi_e}^{1/(3\eta - 4)} </math> |
|
<math> \Rightarrow ~~~~~ \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{rf}} \biggr)^{(3-n)} </math> |
<math>~=~</math> |
<math> \biggl[ \frac{4(n+1)}{5} \biggr]^{n} \biggl(\frac{\xi_e}{3} \biggr)^{(n+1)} \biggl|\frac{d\theta_n}{d\xi} \biggr|^{(n-1)}_{\xi_e} \, , </math> |
|
<math> ~P_\mathrm{e} </math> |
<math>~=~</math> |
<math> ~P_\mathrm{rf} \biggl\{ 2^{-8/\eta} \biggl(\frac{5|\eta-1|}{\eta} \biggr)^3 \biggl(\frac{3}{\xi} \biggr)^4 \biggl|\frac{d\theta_n}{d\xi} \biggr|^{-2} \biggr\}_{\xi_e}^{\eta/(3\eta - 4)} \theta_n^{\eta/(\eta-1)} </math> |
|
<math> \Rightarrow ~~~~~ \biggl( \frac{P_\mathrm{e}}{P_\mathrm{rf}} \biggr)^{(3-n)} </math> |
<math>~=~</math> |
<math> 2^{-8n}\biggl\{ \biggl(\frac{5}{n+1} \biggr)^3 \biggl(\frac{3}{\xi} \biggr)^4 \theta_n^{(3-n)} \biggl|\frac{d\theta_n}{d\xi} \biggr|^{-2} \biggr\}_{\xi_e}^{(n+1)} \, , </math> |
where, in order to obtain the second line of the two relations we have used the substitution, <math>~\eta \rightarrow (1+1/n)</math>, and, as is detailed in an accompanying ASIDE, Whitworth "referenced" <math>~P_\mathrm{e}</math> and <math>~R_\mathrm{eq}</math> to, respectively,
|
<math> P_\mathrm{rf}^{(4-3\eta)} </math> |
<math>~=~</math> |
<math> 2^{-2(4+\eta)} \biggl( \frac{3^4 \cdot 5^3}{\pi} \biggr)^\eta \biggl[ \frac{K_n^4}{G^{3\eta} M^{2\eta} } \biggr] </math> |
|
<math> \Rightarrow ~~~~~ P_\mathrm{rf}^{(n-3)} </math> |
<math>~=~</math> |
<math> 2^{-2(5n+1)} \biggl( \frac{3^4 \cdot 5^3}{\pi} \biggr)^{(n+1)} \biggl[ \frac{K_n^{4n}}{G^{3(n+1)} M^{2(n+1)} } \biggr] \, , </math> |
|
<math> ~R_\mathrm{rf}^\eta </math> |
<math>~=~</math> |
<math> \frac{2^2}{K_n} \biggl(\frac{GM}{3\cdot 5}\biggr)^\eta P_\mathrm{rf}^{(1-\eta)} </math> |
|
<math> \Rightarrow ~~~~~ R_\mathrm{rf}^{(n+1)} </math> |
<math>~=~</math> |
<math> \biggl( \frac{2^2}{K_n} \biggr)^{n} \biggl(\frac{GM}{3\cdot 5}\biggr)^{(n+1)} P_\mathrm{rf}^{-1} </math> |
|
<math> \Rightarrow ~~~~~ R_\mathrm{rf}^{(3-n)} </math> |
<math>~=~</math> |
<math> \biggl( \frac{2^2}{K_n} \biggr)^{n(3-n)/(n+1)} \biggl(\frac{GM}{3\cdot 5}\biggr)^{(3-n)} P_\mathrm{rf}^{(n-3)/(n+1)} </math> |
|
|
<math>~=~</math> |
<math> \biggl( \frac{2^2}{K_n} \biggr)^{n(3-n)/(n+1)} \biggl(\frac{GM}{3\cdot 5}\biggr)^{(3-n)} \biggl\{2^{-2(5n+1)} \biggl( \frac{3^4 \cdot 5^3}{\pi} \biggr)^{(n+1)} \biggl[ \frac{K_n^{4n}}{G^{3(n+1)} M^{2(n+1)} } \biggr] \biggr\}^{1/(n+1)} </math> |
|
|
<math>~=~</math> |
<math>K_n^{n} ( 2^2 )^{-(n+1)} \biggl(\frac{GM}{3\cdot 5}\biggr)^{(3-n)} \biggl( \frac{3^4 \cdot 5^3}{\pi} \biggr) \biggl[ \frac{1}{G^{3} M^{2} } \biggr] </math> |
|
|
<math>~=~</math> |
<math> 2^{-2(n+1)} \pi^{-1} 3^{n+1} \cdot 5^{n} K_n^n G^{-n} M^{1-n} </math> |
Via these normalizations, Whitworth — as did Horedt (1970) — chose to express <math>~R_\mathrm{eq}</math> and <math>~P_\mathrm{e}</math> in terms of <math>~K_\mathrm{n}</math> and the system's total mass, <math>~M</math>.
To convert from Whitworth's expressions, which use one set of normalization parameters <math>~(R_\mathrm{rf},P_\mathrm{rf})</math>, to Horedt's expressions, which use a somewhat different set of normalization parameters — identified here as <math>~(R_\mathrm{Horedt},P_\mathrm{Horedt})</math> — one simply needs to make use of the relations,
|
<math> \biggl( \frac{R_\mathrm{rf}}{R_\mathrm{Horedt}} \biggr)^{(3-n)} </math> |
<math>~=~</math> |
<math> 3^{(n+1)} \biggl[ \frac{5}{2^2 (n+1)} \biggr]^{n} \, . </math> |
|
<math> \biggl( \frac{P_\mathrm{rf}}{P_\mathrm{Horedt}} \biggr)^{(3-n)} </math> |
<math>~=~</math> |
<math> 2^{8n} \biggl[ \frac{(n+1)^3}{3^4 \cdot 5^3} \biggr]^{(n+1)} \, , </math> |
Kimura's Presentation
At the same time Whitworth's work was being published, Kimura (1981a) also published a derivation of the equations that define the equilibrium properties of embedded, pressure-truncated polytropic configurations. (Note that an erratum has been published correcting typographical errors that appear in a few equations of the original paper.) When compared with, for example, Horedt's published work — which Kimura references — Kimura's set of structural equations are a bit more difficult to digest because they include (a) an equation-of-state index that is different from the traditional polytropic index — specifically (see his equation 6),
<math>~\sigma \equiv (n+1)^{-1} \, </math>
— which was Kimura's effort to more gracefully accommodate discussions of isothermal <math>~(n=\infty)</math> configurations; and (b) an additional integer index, <math>~m</math>, so that a single set of equations can be used to specify the structure of planar <math>~(m = 1)</math> and cylindrical <math>~(m=2)</math> as well as spherical <math>~(m=3)</math> configurations. In the present context, we will fix the value to <math>~m = 3</math>. Kimura also chose to express his structural solutions in terms of a dimensionless radius, <math>~\zeta</math>, instead of the traditional variable, <math>~\xi</math> — note that the two are related via the expression,
<math>~\zeta = (n+1)^{1/2} \xi \, ;</math>
and in terms of a dimensionless gravitational potential, <math>~\phi</math>, instead of the traditional dimensionless enthalpy variable, <math>~\theta_n</math> — note that the two are related via the expression (see Kimura's equation 12),
<math>~\phi = \sigma^{-1}(1 - \theta_n) \, .</math>
Given this relationship, we note as well that,
<math>~\phi^' \equiv \frac{d\phi}{d\zeta} = -\frac{d\theta_n}{d\xi} \cdot \biggl[ \sigma^{-1} \frac{d\xi}{d\zeta} \biggr] = -\frac{d\theta_n}{d\xi} (n+1)^{1/2} \, .</math>
The set of equilibrium equations derived by Kimura (1981a) in what he identifies as "Paper I" — see especially his equations number (16) and (23) — are summarized most succinctly in Table 1 of his "Paper II" (Kimura 1981b). The equations he presents for "radial distance," "pressure," and "fractional mass within <math>~\tilde{\zeta}</math>" are, respectively,
|
<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{Kimura}} </math> |
<math>~=~</math> |
<math> \tilde\zeta = (n+1)^{1/2} \tilde\xi \, , </math> |
|
<math> ~\frac{P_\mathrm{e}}{P_\mathrm{Kimura}} </math> |
<math>~=~</math> |
<math> \tilde\theta_n^{n+1}\, , </math> |
|
<math> ~\frac{M}{M_\mathrm{Kimura}} </math> |
<math>~=~</math> |
<math> \tilde\zeta^2 {\tilde\phi}^' = (n+1)^{3/2} \biggl[ - \xi^2 \frac{d\theta_n}{d\xi} \biggr]_{\tilde\xi} \, , </math> |
where, expressed in terms of the central pressure, <math>~p_*</math>, and the polytropic constant, <math>~K_n, ~[</math>note that, in Kimura's paper, <math>~H = K_n^{n/(n+1)}]</math>, the relevant normalization parameters are,
|
<math> ~R_\mathrm{Kimura} </math> |
<math>~\equiv~</math> |
<math> (4\pi G)^{-1/2} H p_*^{\sigma - 1/2} = (4\pi G)^{-1/2} K_n^{n/(n+1)} p_*^{(1-n)/[2(n+1)]} \, , </math> |
|
<math> ~P_\mathrm{Kimura} </math> |
<math>~=~</math> |
<math> p_* \, , </math> |
|
<math> ~M_\mathrm{Kimura} </math> |
<math>~=~</math> |
<math> (4\pi G)^{-3/2} (4\pi) H^2 p_*^{2\sigma - 1/2} = (4\pi G^3)^{-1/2} K_n^{2n/(n+1)} p_*^{(3-n)/[2(n+1)]} \, . </math> |
In order to compare Kimura's equilibrium expressions for <math>~R_\mathrm{eq}</math> and <math>~P_e</math> with the corresponding expressions presented by Horedt and by Whitworth, we need to replace <math>~p_*</math> by <math>~M</math> in both expressions. Inverting Kimura's expression for <math>~M</math>, we have,
|
<math> ~p_*^{(3-n)/[2(n+1)]} </math> |
<math>~=~</math> |
<math> M (n+1)^{-3/2}( - \tilde\xi^2 \tilde\theta^' )^{-1} (4\pi G^3)^{1/2} K_n^{-2n/(n+1)} \, . </math> |
Hence,
|
<math> ~P_\mathrm{Kimura} </math> |
<math>~=~</math> |
<math> [ M (n+1)^{-3/2}( - \tilde\xi^2 \tilde\theta^' )^{-1} (4\pi G^3)^{1/2} K_n^{-2n/(n+1)} ]^{2(n+1)/(3-n)} \, , </math> |
|
|
<math>~=~</math> |
<math> [ M^{-2} (n+1)^{3}( - \tilde\xi^2 \tilde\theta^' )^{2} (4\pi G^3)^{-1} K_n^{4n/(n+1)} ]^{(n+1)/(n-3)} \, , </math> |
|
|
<math>~=~</math> |
<math>~P_\mathrm{Horedt} [ ( - \tilde\xi^2 \tilde\theta^' )^{2} ]^{(n+1)/(n-3)} </math> |
|
<math>\Rightarrow ~~~~~ P_e</math> |
<math>~=~</math> |
<math>~P_\mathrm{Horedt} ~\tilde\theta^{n+1} ( - \tilde\xi^2 \tilde\theta^' )^{2(n+1)/(n-3)} \, , </math> |
which matches Horedt's expression for <math>~P_e</math>. Also after replacement we obtain,
|
<math> ~R_\mathrm{Kimura} </math> |
<math>~=~</math> |
<math> (4\pi G)^{-1/2} K^{n/(n+1)} [ M (n+1)^{-3/2}( - \tilde\xi^2 \tilde\theta^' )^{-1} (4\pi G^3)^{1/2} K_n^{-2n/(n+1)} ]^{(1-n)/(3-n)} </math> |
|
|
<math>~=~</math> |
<math> M^{(n-1)/(n-3)} ( - \tilde\xi^2 \tilde\theta^' )^{(1-n)/(n-3)} (n+1)^{3(1-n)/2(n-3)} (4\pi)^{[(1-n)-(3-n)]/[2(3-n)]} G^{[3(1-n)- (3-n)]/[2(3-n)]} [ K_n^{n(3-n)-2n(1-n)} ]^{1/[(n+1)(3-n)]} </math> |
|
|
<math>~=~</math> |
<math> M^{(n-1)/(n-3)} ( - \tilde\xi^2 \tilde\theta^' )^{(1-n)/(n-3)} (n+1)^{3(1-n)/2(n-3)} (4\pi)^{1/(n-3)} G^{n/(n-3)} K_n^{-n/(n-3)} </math> |
|
<math>~\Rightarrow ~~~~~ R_\mathrm{eq}</math> |
<math>~=~</math> |
<math>\tilde\xi( - \tilde\xi^2 \tilde\theta^' )^{(1-n)/(n-3)} (n+1)^{[3(1-n)+(n-3)]/2(n-3)} \biggl[ 4\pi \biggl( \frac{G}{K_n} \biggr)^{n} M^{(n-1)} \biggr]^{1/(n-3)} </math> |
|
|
<math>~=~</math> |
<math> R_\mathrm{Horedt}~ \tilde\xi( - \tilde\xi^2 \tilde\theta^' )^{(1-n)/(n-3)} \, , </math> |
which exactly matches Horedt's expression for <math>~R_\mathrm{eq}</math>.
Stahler's Presentation
Similarly, in Appendix B of his work, Steven W. Stahler (1983) states that the mass, <math>~M</math>, associated with the equilibrium radius, <math>~R_\mathrm{eq}</math>, of embedded polytropic spheres is,
|
<math> ~M </math> |
<math>~=~</math> |
<math> M_\mathrm{SWS} \biggl( \frac{n^3}{4\pi} \biggr)^{1/2} \biggl\{ \theta_n^{(n-3)/2} \xi^2 \biggl| \frac{d\theta_n}{d\xi} \biggr| \biggr\}_{\xi_e} </math> |
|
<math> ~R_\mathrm{eq} </math> |
<math>~=~</math> |
<math> R_\mathrm{SWS} \biggl( \frac{n}{4\pi} \biggr)^{1/2} \biggl\{ \xi \theta_n^{(n-1)/2} \biggr\}_{\xi_e} </math> |
where, from his equations (7) and (B3) we deduce,
<math>M_\mathrm{SWS} = \biggl( \frac{n+1}{nG} \biggr)^{3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \, ,</math>
<math> R_\mathrm{SWS} = \biggl( \frac{n+1}{nG} \biggr)^{1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \, . </math>
Notice that, via these two normalizations, Stahler chose to express <math>~R_\mathrm{eq}</math> and <math>~M</math> in terms of <math>~K_\mathrm{n}</math> and the applied external pressure, <math>~P_\mathrm{e}</math>.
Reconciliation
Here we demonstrate that Whitworth's and Stahler's presentations are equivalent to one another. We begin by plugging Stahler's definition of <math>~M_\mathrm{SWS}</math> into his expression for <math>~M</math>, then inverting it to obtain an expression for <math>~P_\mathrm{e}</math> in terms of <math>~M</math> and <math>~K_\mathrm{n}</math>.
|
<math> ~M </math> |
<math>~=~</math> |
<math> \biggl[ \frac{(n+1)^3}{4\pi G^3} \biggr]^{1/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \biggl\{ \theta_n^{(n-3)/2} \xi^2 \biggl| \frac{d\theta_n}{d\xi} \biggr| \biggr\}_{\xi_e} </math> |
|
<math> \Rightarrow ~~~~~ P_\mathrm{e}^{(3-n)} </math> |
<math>~=~</math> |
<math> \biggl[ \frac{4\pi G^3}{(n+1)^3} \biggr]^{(n+1)} K_n^{-4n} M^{2(n+1)} \biggl\{ \theta_n^{(n-3)/2} \xi^2 \biggl| \frac{d\theta_n}{d\xi} \biggr| \biggr\}^{-2(n+1)}_{\xi_e} </math> |
|
|
<math>~=~</math> |
<math> \biggl[ \frac{4\pi G^3 M^2}{(n+1)^3} \biggr]^{(n+1)} K_n^{-4n} \biggl\{ \theta_n^{(3-n)} \xi^{-4} \biggl| \frac{d\theta_n}{d\xi} \biggr|^{-2} \biggr\}^{(n+1)}_{\xi_e} </math> |
Alternatively, plugging Whitworth's definition of <math>~P_\mathrm{rf}</math> into his expression for <math>~P_\mathrm{e}</math> gives,
|
<math> ~P_\mathrm{e}^{(3-n)} </math> |
<math>~=~</math> |
<math> 2^{2(5n+1)} \biggl( \frac{\pi}{3^4 \cdot 5^3} \biggr)^{(n+1)} 2^{-8n} \cdot 3^{4(n+1)} \biggl(\frac{5}{n+1} \biggr)^{3(n+1)} [ G^{3} M^{2} ]^{(n+1)} K_n^{-4n} \biggl\{ \theta_n^{(3-n)}\xi^{-4} \biggl|\frac{d\theta_n}{d\xi} \biggr|^{-2} \biggr\}_{\xi_e}^{(n+1)} </math> |
|
|
<math>~=~</math> |
<math> 2^{2(n+1)} \biggl[ \frac{\pi}{(n+1)^3} \biggr]^{(n+1)} [ G^{3} M^{2} ]^{(n+1)} K_n^{-4n} \biggl\{ \theta_n^{(3-n)}\xi^{-4} \biggl|\frac{d\theta_n}{d\xi} \biggr|^{-2} \biggr\}_{\xi_e}^{(n+1)} \, . </math> |
So Whitworth's and Stahler's relations for <math>~P_\mathrm{e}(M,K_n)</math> are, indeed, identical. Similarly examining Stahler's expression for the equilibrium radius, we find,
|
<math> ~R_\mathrm{eq} </math> |
<math>~=~</math> |
<math> \biggl( \frac{n+1}{4\pi G} \biggr)^{1/2} K_n^{n/(n+1)} \biggl[ \xi \theta_n^{(n-1)/2} \biggr]_{\xi_e} \biggl\{ P_\mathrm{e}^{1/(n+1)} \biggr\}^{(1-n)/2} </math> |
|
|
<math>~=~</math> |
<math> \biggl( \frac{n+1}{4\pi G} \biggr)^{1/2} K_n^{n/(n+1)} \biggl[ \xi \theta_n^{(n-1)/2} \biggr]_{\xi_e} \biggl\{ \biggl[ \frac{4\pi G^3 M^2}{(n+1)^3} \biggr] K_n^{-4n/(n+1)} \biggl[ \theta_n^{(3-n)} \xi^{-4} \biggl| \frac{d\theta_n}{d\xi} \biggr|^{-2} \biggr]_{\xi_e} \biggr\}^{(1-n)/[2(3-n)]} </math> |
|
<math> \Rightarrow ~~~~~ R_\mathrm{eq}^{(3-n)} </math> |
<math>~=~</math> |
<math> \biggl( \frac{n+1}{4\pi G} \biggr)^{(3-n)/2} K_n^{n(3-n)/(n+1)} \xi_e^{3-n} \biggl\{ \biggl[ \frac{4\pi G^3 M^2}{(n+1)^3} \biggr]^{1/2} K_n^{-2n/(n+1)} \biggl[ \xi^{-2} \biggl| \frac{d\theta_n}{d\xi} \biggr|^{-1} \biggr]_{\xi_e} \biggr\}^{(1-n)} </math> |
|
|
<math>~=~</math> |
<math> (n+1)^{[(3-n)-3(1-n)]/2} (4\pi)^{[(n-3) +(1-n)]/2} G^{[(n-3)+3(1-n)]/2} [K_n^{(3-n)+2(n-1)}]^{n/(n+1)} \xi_e^{(3-n)+2(n-1)} M^{(1-n)} \biggl| \frac{d\theta}{d\xi} \biggr|^{(n-1)}_{\xi_e} </math> |
|
|
<math>~=~</math> |
<math> (n+1)^{n} (4\pi)^{-1} G^{-n} K_n^n M^{(1-n)} \biggl[ \xi^{(n+1)} \biggl| \frac{d\theta_n}{d\xi} \biggr|^{(n-1)}\biggr]_{\xi_e} \, . </math> |
And Whitworth's expression becomes,
|
<math> ~R_\mathrm{eq}^{(3-n)} </math> |
<math>~=~</math> |
<math> 2^{-2(n+1)} \pi^{-1} 3^{n+1} \cdot 5^{n} K_n^n G^{-n} M^{1-n} \biggl[ \frac{4(n+1)}{5} \biggr]^{n} \biggl(\frac{\xi_e}{3} \biggr)^{(n+1)} \biggl|\frac{d\theta_n}{d\xi} \biggr|^{(n-1)}_{\xi_e} </math> |
|
|
<math>~=~</math> |
<math> (n+1)^n (4\pi)^{-1} K_n^n G^{-n} M^{1-n} \xi_e^{(n+1)} \biggl|\frac{d\theta_n}{d\xi} \biggr|^{(n-1)}_{\xi_e} \, . </math> |
Hence, Stahler's equilibrium radius, <math>~R_\mathrm{eq}</math>, exactly matches Whitworth's <math>~R_\mathrm{eq}</math>.
Summary
|
Once the function, <math>~\theta_n(\xi)</math>, and its first derivative with respect to the dimensionless radial coordinate, <math>~d\theta_n/d\xi</math>, are obtained via a solution of the Lane-Emden equation, the equilibrium radius, <math>~R_\mathrm{eq}</math>, and total mass, <math>~M</math>, of a pressure-bounded polytrope can be expressed in terms of Stahler's normalizations as follows:
where,
Then, the external pressure, expressed in terms of Whitworth's normalization, is,
and the conversion from Stahler's normalization to Whitworth's normalization of the radius is achieved via the expression,
|
Chieze's Presentation
From equations (8), (10), and (68) in Chapter IV of [C67], we can immediately formulate the following expressions for, respectively, <math>~P_e(\tilde\xi), R_\mathrm{eq}(\tilde\xi)</math>, and <math>~M_\mathrm{tot}(\tilde\xi)</math>:
|
<math>~\frac{P_e}{P_\mathrm{Ch}}</math> |
<math>~=</math> |
<math>~ {\tilde\theta}^{n+1} \, ,</math> |
|
<math>~\frac{R_\mathrm{eq}}{R_\mathrm{Ch}}</math> |
<math>~=</math> |
<math>~\biggl[ \frac{n+1}{4\pi} \biggr]^{1 / 2} \tilde\xi</math> |
|
<math>~\frac{M_\mathrm{tot}}{M_\mathrm{Ch}}</math> |
<math>~=</math> |
<math>~ \biggl[ \frac{(n+1)^3}{4\pi} \biggr]^{1 / 2}(- {\tilde\xi}^2 {\tilde\theta}^') \, , </math> |
where,
|
<math>~P_\mathrm{Ch}</math> |
<math>~\equiv</math> |
<math>~K\rho_c^{(n+1)/n} \, ,</math> |
|
<math>~R_\mathrm{Ch}</math> |
<math>~\equiv</math> |
<math>~\biggl[\biggl(\frac{K}{G}\biggr) \rho_c^{1/n-1}\biggr]^{1 / 2} \, ,</math> |
|
<math>~M_\mathrm{Ch}</math> |
<math>~\equiv</math> |
<math>~\biggl[\biggl(\frac{K}{G}\biggr)^3 \rho_c^{(3-n)/n}\biggr]^{1 / 2} \, .</math> |
In this case, the expressions for the physical variable normalizations have been defined in terms of — in addition to <math>~G</math> and/or <math>~K</math> — the equilibrium configuration's central density, <math>~\rho_c</math>, instead of in terms of <math>~M_\mathrm{tot}</math> or <math>~P_e</math>. These are precisely the expressions for, respectively, <math>~P_s(\xi_s)</math>, <math>~R_s(\xi_s)</math>, and <math>~M_s(\xi_s)</math> that appear in the appendix of J. P. Chieze (1987, A&A, 171, 225-232) — see, respectively, his equations (A7), (A5), and (A6). [Note that, for the polytropic systems of interest to us, here — that is, systems having <math>~0 \le n < \infty</math> — Chieze's parameter <math>~\epsilon \equiv \sgn(n+1) = 1</math>.]
Polytropic Configurations with n = 1
Drawing from the earlier discussion of isolated polytropes, we will reference various radial locations within the spherical configuration by the dimensionless radius,
<math> \xi \equiv \frac{r}{a_\mathrm{n=1}} , </math>
where,
<math> a_\mathrm{n=1} \equiv \biggl[\frac{1}{4\pi G}~ \biggl( \frac{H_c}{\rho_c} \biggr)_{n=1}\biggr]^{1/2} = \biggl[\frac{K}{2\pi G} \biggr]^{1/2} \, . </math>
The solution to the Lane-Emden equation for <math>~n = 1</math> is,
|
<math> ~\theta_1 </math> |
<math>~=~</math> |
<math> \frac{\sin\xi}{\xi} \, , </math> |
hence,
|
<math> \frac{d\theta_1}{d\xi} </math> |
<math>~=~</math> |
<math> \frac{\cos\xi}{\xi} - \frac{\sin\xi}{\xi^2} \, . </math> |
Review
Again, from the earlier discussion, we can describe the properties of an isolated, spherical <math>~n</math> = 1 polytrope as follows:
- Mass:
- In terms of the central density, <math>\rho_c</math>, and <math>~K_\mathrm{n}</math>, the total mass is,
<math>M = \frac{4}{\pi} \rho_c (\pi a_{n=1})^3 = 4\pi^2 \rho_c \biggl[\frac{K}{2\pi G} \biggr]^{3/2} = \rho_c \biggl[\frac{2\pi K^3}{G^3} \biggr]^{1/2}</math> ;
- and, expressed as a function of <math>M</math>, the mass that lies interior to the dimensionless radius <math>\xi</math> is,
<math>\frac{M_\xi}{M} = \frac{1}{\pi} \biggl[ \sin\xi - \xi\cos\xi \biggr] \, ,~~~~~~\mathrm{for}~\pi \ge \xi \ge 0 \, .</math>
- Hence,
<math>M_\xi = \rho_c \biggl[\frac{2K^3}{\pi G^3} \biggr]^{1/2} \biggl[ \sin\xi - \xi\cos\xi \biggr] \, .</math>
- Pressure:
- The central pressure of the configuration is,
<math>P_c = \biggl[ \frac{G^3}{2\pi} \rho_c^4 M^2 \biggr]^{1/3} = \biggl[ \frac{G^3}{2\pi} \rho_c^6 \biggl(\frac{2\pi K^3}{G^3} \biggr) \biggr]^{1/3} = K\rho_c^2</math> ;
- and, expressed in terms of the central pressure <math>P_c</math>, the variation with radius of the pressure is,
<math>P_\xi= P_c \biggl[ \frac{\sin\xi}{\xi} \biggr]^2</math> .
- Hence,
<math>P_\xi= K\rho_c^2 \biggl[ \frac{\sin\xi}{\xi} \biggr]^2</math> .
Extension to Bounded Sphere
Eliminating <math>\rho_c</math> between the last expression for <math>M_\xi</math> and the last expression for <math>P_\xi</math> gives,
<math>P_\xi= \biggl[\frac{\pi}{2} \cdot \frac{G^3 M_\xi^2}{K^2} \biggr] \biggl[ \frac{\sin\xi}{\xi(\sin\xi - \xi \cos\xi )} \biggr]^2</math> .
Now, if we rip off an outer layer of the star down to some dimensionless radius <math>\xi_e < \pi</math>, the interior of the configuration that remains — containing mass <math>M_{\xi_e}</math> — should remain in equilibrium if we impose the appropriate amount of externally applied pressure <math>P_e = P_{\xi_e} </math> at that radius. (This will work only for spherically symmetric configurations, as the gravitation acceleration at any location only depends on the mass contained inside that radius.) If we rescale our solution such that the mass enclosed within <math>\xi_e</math> is the original total mass <math>M</math>, then the pressure that must be imposed by the external medium in which the configuration is embedded is,
<math>P_e= \biggl[\frac{\pi}{2} \cdot \frac{G^3 M^2}{K^2} \biggr] \biggl[ \frac{\sin\xi_e}{\xi_e(\sin\xi_e - \xi_e \cos\xi_e )} \biggr]^2</math> .
The associated equilibrium radius of this pressure-confined configuration is,
<math> R_\mathrm{eq} = \xi_e a_\mathrm{n=1} = \biggl[ \frac{K}{2\pi G} \biggr]^{1/2} \xi_e </math>
Overlap with Whitworth's Presentation
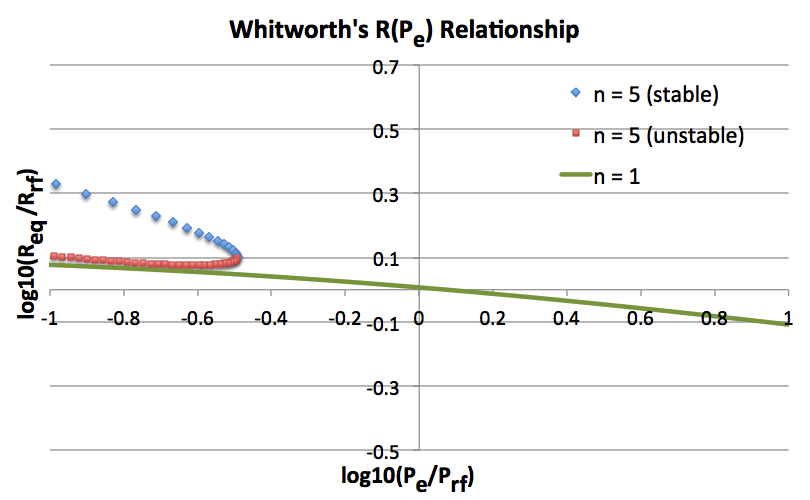
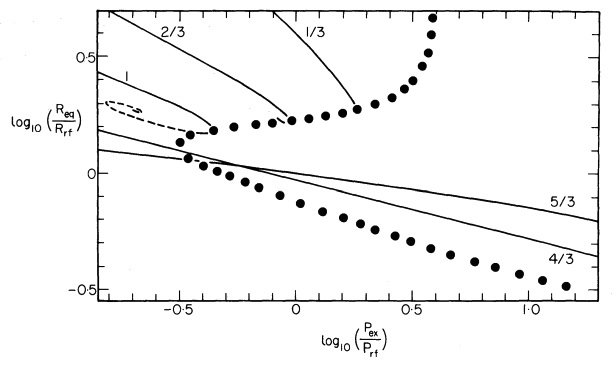
The solid green curve in the two top panels of Figure 1 shows how <math>R_\mathrm{eq}</math> varies with the applied external pressure <math>P_e</math> for this pressure-bounded <math>~n=1</math> model sequence. In the top-right panel, following the lead of Whitworth (1981, MNRAS, 195, 967) — for clarification, read the accompanying ASIDE — these two quantities have been respectively normalized (or, "referenced") to,
<math> R_\mathrm{rf}\biggr|_\mathrm{n=1} \equiv \biggl( \frac{3^2 \cdot 5}{2^4 \pi} \biggr)^{1/2} \biggl(\frac{K}{G}\biggr)^{1/2} ~~~\Rightarrow ~~~ \frac{R_\mathrm{eq}}{R_\mathrm{rf}} = \biggl( \frac{2^3}{3^2 \cdot 5} \biggr)^{1/2} \xi_e \, ; </math>
and,
<math> P_\mathrm{rf}\biggr|_\mathrm{n=1} \equiv \frac{2^6 \pi}{3^4 \cdot 5^3} \biggl(\frac{G^3 M^2}{K^2}\biggr) ~~~\Rightarrow ~~~ \frac{P_e}{P_\mathrm{rf}} = \biggl( \frac{3^4 \cdot 5^3}{2^7} \biggr) \biggl[ \frac{\sin\xi_e}{\xi_e(\sin\xi_e - \xi_e \cos\xi_e )} \biggr]^2 \, . </math>
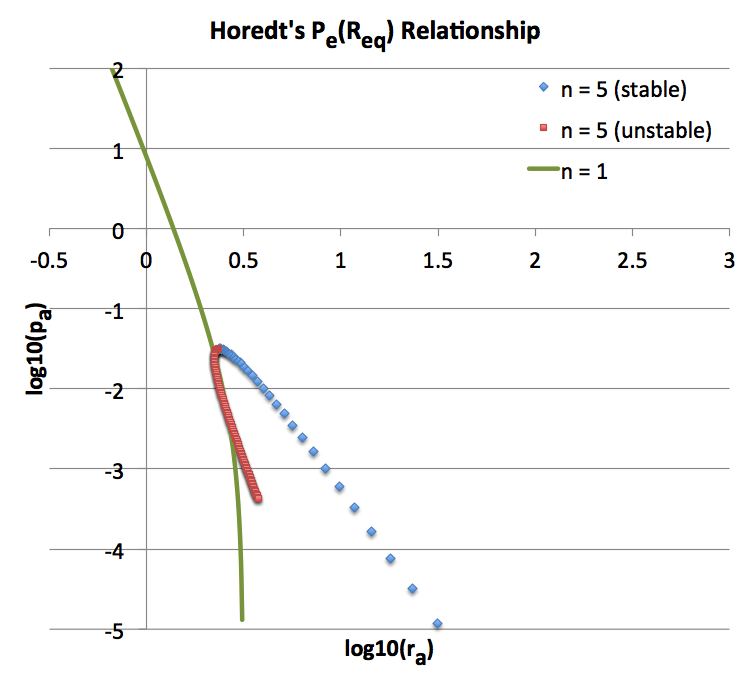
Note that this pair of mathematical expressions has been recorded to the immediate right of Whitworth's name in our <math>~n=1</math> summary table. In the top-left panel of Figure 1, the solid green curve shows the identical sequence, but plotted as <math>~\log(p_a)</math> versus <math>~log(r_a)</math>, for easier comparison with Horedt's work. The pair of mathematical expressions defining <math>~r_a(\xi_e)</math> and <math>~p_a(\xi_e)</math> has been recorded to the immediate right of Horedt's name in the same summary table.
|
Figure 1: Equilibrium R-P Diagram — Referred to by Kimura (1981) as an "M1 Sequence" |
|
|
All of the plots shown in this figure illustrate how the equilibrium radius of a pressure-bounded polytrope varies with the applied external pressure. In the right-hand column, the log-log plots display a normalized <math>~P_e</math> along the horizontal axis and a normalized <math>~R_\mathrm{eq}</math> along the horizontal axis; in the left-hand column, these axes are flipped, and a different normalization is used. One primary intent of all the diagrams is to show that, for polytropic sequences having <math>~n > 3</math> (or, equivalently, sequences having <math>\gamma_g \equiv 1 + 1/n < 4/3),</math> no equilibrium models exist above some limiting external pressure. |
|
|
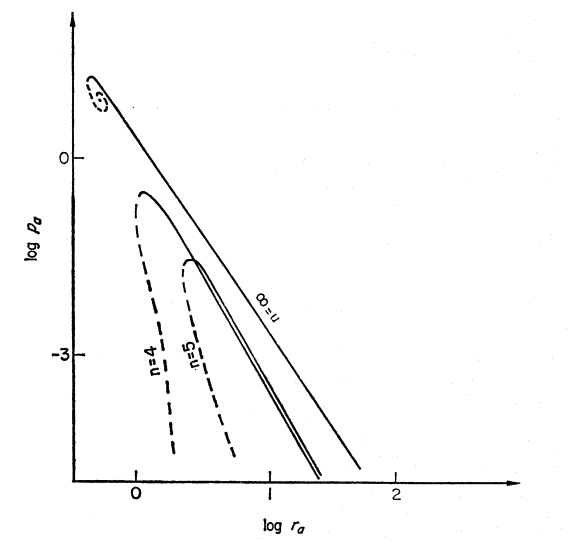
Bottom Left [reproduction of Figure 1 from Horedt (1970)]: All three displayed sequences — <math>~n=4</math> (<math>~\gamma_g = 1.25</math>), <math>~n=5</math> (<math>~\gamma_g = 1.20</math>), and <math>~n=\infty</math> (<math>~\gamma_g = 1</math>, hence, isothermal) — exhibit an upper limit for the bounding pressure. Each sequence displays two segments — a solid segment and a dashed segment — indicating that, below the maximum allowed value of <math>~P_e</math>, it is possible to construct two (or more) equilibrium configurations; models lying along the solid segment of each displayed curve are expected to be dynamically stable while models lying along the dashed segments are unstable. Bottom Right [reproduction of Figure 1b from Whitworth (1981)]: Model sequences are shown for five different effective adiabatic indexes — <math>~\gamma_g = 1/3,~ 2/3,~ 1,~ 4/3,</math> and <math>~ 5/3</math> — corresponding, respectively, to polytropic indexes <math>~n = -2/3, -1/3, \infty, ~3/2, </math> and <math>~3</math>. The three sequences having <math>~\gamma_g < 4/3</math> exhibit an upper limit for the bounding pressure. Both the stable (solid) curve segment and the unstable (dashed) curve segment are drawn for the isothermal <math>~(\gamma_g = 1)</math> sequence, which is also displayed (as the <math>~n=\infty</math> sequence) in Horedt's diagram. Top: Plots that we have generated for direct comparison with Horedt's diagram (left) and with Whitworth's diagram (right). Both plots display only the two sequences that are analytically prescribable: <math>~n=1</math> (<math>~\gamma_g = 2</math>) and <math>~n=5</math> (<math>~\gamma_g = 1.20</math>). Along the <math>~n=1</math> (green) sequence, stable equilibrium models can be constructed for all values of <math>~P_e</math>. Along the <math>~n=5</math> sequence, equilibrium models only exist for values of <math>~P_e</math> less than the critical value, <math>~P_\mathrm{max} = (2^5\cdot 3^9/5^9) P_\mathrm{rf} = (3^{12}/2^{24}) P_\mathrm{Horedt}</math>; below this critical pressure, the sequence has two branches denoted by blue diamonds (stable models) and red squares (unstable models). |
|
Overlap with Stahler's Presentation
We can invert the above expression for <math>~P_e(K,M)</math> to obtain the following expression for <math>~M(K,P_e)</math>:
<math>~M= K \biggl[\frac{2}{\pi} \cdot \frac{P_e}{G^3} \biggr]^{1/2} \biggl[ \frac{\xi_e(\sin\xi_e - \xi_e \cos\xi_e )}{\sin\xi_e} \biggr]</math> .
If, following Stahler's lead, we normalize this expression by <math>~M_\mathrm{SWS}</math> (evaluated for <math>~n=1</math>) and we normalize the above expression for <math>~R_\mathrm{eq}</math> by <math>~R_\mathrm{SWS}</math> (evaluated for <math>~n=1</math>), we obtain,
|
<math> \frac{M}{M_\mathrm{SWS}} </math> |
<math>~=~</math> |
<math> K \biggl[\frac{2}{\pi} \cdot \frac{P_e}{G^3} \biggr]^{1/2} \biggl[ \frac{\xi_e(\sin\xi_e - \xi_e \cos\xi_e )}{\sin\xi_e} \biggr] \biggl[ \biggl( \frac{G}{2} \biggr)^{3/2} K^{-1} P_\mathrm{ex}^{-1/2} \biggr] </math> |
|
|
<math>~=~</math> |
<math> (4\pi)^{-1/2} \biggl[ \frac{\xi_e(\sin\xi_e - \xi_e \cos\xi_e )}{\sin\xi_e} \biggr] \, , </math> |
|
<math> \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} </math> |
<math>~=~</math> |
<math> \biggl[ \frac{K}{2\pi G} \biggr]^{1/2} \xi_e \biggl[ \frac{G}{2K} \biggr]^{1/2} = (4\pi)^{-1/2} \xi_e \, . </math> |
|
Figure 2: Equilibrium Mass-Radius Diagram |
|
|
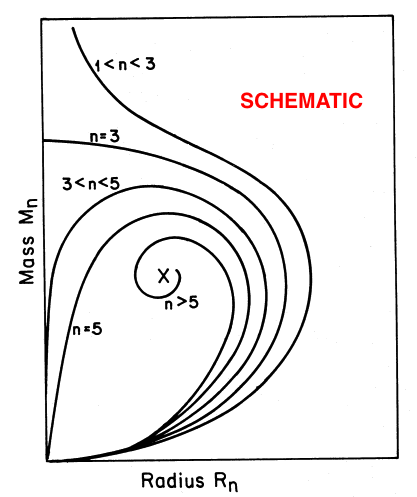
Top: A slightly edited reproduction of Figure 17 in association with Appendix B of Stahler (1983, ApJ, 268, 165). Stahler's figure caption reads, in part, "Mass-radius relation for bounded polytropes (schematic). Each curve is labeled by the appropriate value or range" of <math>~n</math> … "As the cloud density increases from unity, all curves leave the origin with the same slope …"
|
|
Tabular Summary (n=1)
|
Table 1: Properties of <math>~n=1</math> Polytropes Embedded in an External Medium of Pressure <math>~P_e</math>
|
|||||
|---|---|---|---|---|---|
|
|||||
|
Horedt (1970)
|
<math> ~r_a = \frac{R_\mathrm{eq}}{R_\mathrm{Horedt}} = \xi_e </math> |
<math> ~p_a = \frac{P_e}{P_\mathrm{Horedt}} = \biggl[ \frac{\sin\xi_e}{\xi_e(\sin\xi_e - \xi_e \cos\xi_e )} \biggr]^2 </math> |
|||
|
Whitworth (1981)
|
<math> \frac{R_\mathrm{eq}}{R_\mathrm{rf}} = \biggl( \frac{2^3}{3^2 \cdot 5} \biggr)^{1/2} \xi_e </math> |
<math> \frac{P_e}{P_\mathrm{rf}} = \biggl( \frac{3^4 \cdot 5^3}{2^7} \biggr) \biggl[ \frac{\sin\xi_e}{\xi_e(\sin\xi_e - \xi_e \cos\xi_e )} \biggr]^2 </math> |
|||
|
Stahler (1983)
|
<math> \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} = (4\pi)^{-1/2} \xi_e </math> |
<math> \frac{M}{M_\mathrm{SWS}} = (4\pi)^{-1/2} \biggl[ \frac{\xi_e(\sin\xi_e - \xi_e \cos\xi_e )}{\sin\xi_e} \biggr] </math> |
|||
|
NOTE: None of the analytic expressions for the dimensionless radius, pressure, or mass presented in this table explicitly appear in the referenced articles by Horedt, by Whitworth, or by Stahler but, as is discussed fully above, they are straightforwardly derivable from the more general relations that appear in these papers. |
|||||
Polytropic Configurations with n = 5
Drawing from the earlier discussion of isolated polytropes, we will reference various radial locations within a spherical <math>~n</math> = 5 polytrope by the dimensionless radius,
<math> \xi \equiv \frac{r}{a_\mathrm{n=5}} , </math>
where,
<math> a_{n=5} = \biggr[ \frac{(n+1)K}{4\pi G} \rho_c^{(1/n - 1)} \biggr]^{1/2}_{n=5} = \biggr[ \frac{3K}{2\pi G} \biggr]^{1/2} \rho_c^{-2/5} \, . </math>
The solution to the Lane-Emden equation for <math>~n = 5</math> is,
|
<math> ~\theta_5 </math> |
<math>~=~</math> |
<math> \biggl(1+\frac{\xi^2}{3} \biggr)^{-1/2} \, , </math> |
hence,
|
<math> \frac{d\theta_5}{d\xi} </math> |
<math>~=~</math> |
<math> - \frac{\xi}{3}\biggl(1+\frac{\xi^2}{3} \biggr)^{-3/2} \, . </math> |
Review
Again, from the earlier discussion, we can describe the properties of an isolated, spherical <math>~n</math> = 5 polytrope as follows:
- Mass:
- In terms of the central density, <math>\rho_c</math>, and <math>~K_\mathrm{n}</math>, the total mass is,
<math>M = \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{1/2} \rho_c^{-1/5} </math> ;
- and, expressed as a function of <math>M</math>, the mass that lies interior to the dimensionless radius <math>\xi</math> is,
<math> \frac{M_\xi}{M} = \xi^3 (3 + \xi^2)^{-3/2} \, . </math>
- Hence,
<math> M_\xi = \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{1/2} \rho_c^{-1/5} \biggl[ \xi^3 (3 + \xi^2)^{-3/2} \biggr] \, . </math>
- Pressure:
- The central pressure of the configuration is,
<math> P_c = \biggr[ \frac{\pi M^2 G^3}{2\cdot 3^4} \biggr]^{1/3} \rho_c^{4/3} = \biggr[ \frac{\pi G^3}{2\cdot 3^4} \biggr( \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr) \rho_c^{-2/5}\biggr]^{1/3} \rho_c^{4/3} = K\rho_c^{6/5} </math> ;
- and, expressed in terms of the central pressure <math>P_c</math>, the variation with radius of the pressure is,
<math>P_\xi= P_c \biggl[ 1 + \frac{1}{3}\xi^2 \biggr]^{-3}</math> .
- Hence,
<math> P_\xi = K \rho_c^{6/5} \biggl[ 1 + \frac{1}{3}\xi^2 \biggr]^{-3} = 3^3K \rho_c^{6/5} [ 3 + \xi^2 ]^{-3} </math> .
Extension to Bounded Sphere
Eliminating <math>\rho_c</math> between the last expression for <math>M_\xi</math> and the last expression for <math>P_\xi</math> gives,
| <math>~P_\xi</math> | <math>=</math> |
<math> 3^3K [ 3 + \xi^2 ]^{-3} \biggr[ \frac{2\cdot 3^4 K^3}{\pi G^3} \biggr]^{3} M_\xi^{-6} \biggl[ \xi^3 (3 + \xi^2)^{-3/2} \biggr]^6 </math> |
| <math>=</math> |
<math> \biggl( \frac{2^3\cdot 3^{15} K^{10}}{\pi^3 M_\xi^{6} G^9} \biggr) \frac{\xi^{18}}{(3 + \xi^2)^{12}} \, . </math> |
Now, if we rip off an outer layer of the star down to some dimensionless radius <math>\xi_e < \infty</math>, the interior of the configuration that remains — containing mass <math>M_{\xi_e}</math> — should remain in equilibrium if we impose the appropriate amount of externally applied pressure <math>P_e = P_{\xi_e} </math> at that radius. (This will work only for spherically symmetric configurations, as the gravitation acceleration at any location only depends on the mass contained inside that radius.) If we rescale our solution such that the mass enclosed within <math>\xi_e</math> is the original total mass <math>M</math>, then the pressure that must be imposed by the external medium in which the configuration is embedded is,
<math>P_e= \biggr( \frac{2^3\cdot 3^{15} K^{10}}{\pi^3 M^{6} G^9} \biggr) \frac{\xi_e^{18}}{(3 + \xi_e^2)^{12}} </math> .
The associated equilibrium radius of this pressure-confined configuration is,
<math> R_\mathrm{eq} = \xi_e a_\mathrm{n=5} = \biggl[ \frac{3K}{2\pi G} \biggr]^{1/2} \rho_c^{-2/5} \xi_e = \biggl[ \frac{\pi M^4 G^5}{2^3 \cdot 3^7 K^5} \biggr]^{1/2} \frac{(3+\xi_e^2)^3}{\xi_e^5} \, . </math>
Overlap with Whitworth's Presentation
The curve labeled <math>~n=5</math> in the top two panels of Figure 1 shows how <math>R_\mathrm{eq}</math> varies with the applied external pressure <math>P_e</math>; as shown, the curve has two segments — configurations that are stable (blue diamonds) and configurations that are unstable (red squares). Following the lead of Whitworth (1981, MNRAS, 195, 967) — for clarification, read the accompanying ASIDE — these two quantities have been respectively normalized (or, "referenced") to,
<math> R_\mathrm{rf}\biggr|_\mathrm{n=5} \equiv \frac{2^6}{3^3} \biggl( \frac{\pi}{5^5} \biggr)^{1/2} \biggl[ \frac{G^5 M^4}{K^5} \biggr]^{1/2} ~~~\Rightarrow ~~~ \frac{R_\mathrm{eq}}{R_\mathrm{rf}} = \biggl( \frac{5^5}{2^{15}\cdot 3} \biggr)^{1/2} \frac{(3+\xi_e^2)^3}{\xi_e^5} \, ; </math>
and,
<math> P_\mathrm{rf}\biggr|_\mathrm{n=5} \equiv \frac{3^{12} 5^9}{2^{26} \pi^3} \biggl( \frac{K^{10}}{G^9 M^6} \biggr) ~~~\Rightarrow ~~~ \frac{P_e}{P_\mathrm{rf}} = \biggl( \frac{2^{29}\cdot 3^{3} }{5^9} \biggr) \frac{\xi_e^{18}}{(3 + \xi_e^2)^{12}} \, . </math>
We see that this <math>~n=5</math> model sequence bends back on itself. That is to say, for this polytropic index there is an externally applied pressure above which no equilibrium configuration exists. This limiting pressure arises along the curve where,
<math>\frac{dP_e}{dR_\mathrm{eq}} = \biggl( \frac{dP_e}{d\xi_e} \biggr) \biggl( \frac{dR_\mathrm{eq}}{d\xi_e} \biggr)^{-1} = 0 \, .</math>
Evaluation of this expression shows that the limiting pressure occurs precisely at <math>\xi_e = 3</math>, that is,
<math> \biggl( \frac{P_e}{P_\mathrm{rf}} \biggr)_\mathrm{max} = \biggl( \frac{2^{29}\cdot 3^{3} }{5^9} \biggr) \frac{3^{18}}{12^{12}} = \frac{2^5 \cdot 3^9}{5^9} \, , </math>
and the radius of this limiting configuration is,
<math> \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{rf}} \biggr) = \biggl( \frac{5^5}{2^{15}\cdot 3} \biggr)^{1/2} \frac{12^3}{3^5} = \biggl( \frac{5^5}{2^3 \cdot 3^5} \biggr)^{1/2} \, . </math>
On the log-log plot displayed in the top-right panel of Figure 1, the location of this special point is <math>[ \log(P_e/P_\mathrm{rf}) , \log(R_\mathrm{eq}/R_\mathrm{rf}) ] \approx [ -0.49149, +0.10308 ] \, .</math>
We note as well that a conversion from Whitworth's normalizations to the normalizations adopted by Horedt produce the following coordinates for the limiting model configuration:
|
<math> ~p_a|_\mathrm{max} </math> |
<math>~=~</math> |
<math> ~\frac{3^{12}}{2^{24}} \, , </math> |
and, at this bounding pressure, the model has an equilibrium radius,
|
<math> ~r_a </math> |
<math>~=~</math> |
<math> \frac{2^6}{3^3} \, . </math> |
Overlap with Stahler's Presentation
We can invert the above expression for <math>~P_e(K,M)</math> to obtain the following expression for <math>~M(K,P_e)</math>:
<math>M^{6}= \biggr( \frac{2^3\cdot 3^{15} K^{10}}{\pi^3 P_e G^9} \biggr) \frac{\xi_e^{18}}{(3 + \xi_e^2)^{12}} </math> .
If, following Stahler's lead, we normalize this expression by <math>~M_\mathrm{SWS}</math> (evaluated for <math>~n=5</math>) and we normalize the above expression for <math>~R_\mathrm{eq}</math> by <math>~R_\mathrm{SWS}</math> (evaluated for <math>~n=5</math>), we obtain,
|
<math> \frac{M}{M_\mathrm{SWS}} </math> |
<math>~=~</math> |
<math> \biggr( \frac{2^3\cdot 3^{15} K^{10}}{\pi^3 P_e G^9} \biggr)^{1/6} \frac{\xi_e^{3}}{(3 + \xi_e^2)^{2}} \biggl[ \biggl( \frac{2\cdot 3}{5G} \biggr)^{3/2} K^{5/3} P_\mathrm{ex}^{-1/6} \biggr]^{-1} </math> |
|
|
<math>~=~</math> |
<math> \biggr( \frac{3^{2} \cdot 5^3 }{4\pi } \biggr)^{1/2} \frac{\xi_e^{3}}{(3 + \xi_e^2)^{2}} \, , </math> |
|
<math> \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} </math> |
<math>~=~</math> |
<math> \biggl[ \frac{\pi M^4 G^5}{2^3 \cdot 3^7 K^5} \biggr]^{1/2} \frac{(3+\xi_e^2)^3}{\xi_e^5} \biggl[ \biggl( \frac{2\cdot 3}{5G} \biggr)^{1/2} K^{5/6} P_\mathrm{ex}^{-1/3} \biggr]^{-1} </math> |
|
|
<math>~=~</math> |
<math> \biggl[ \biggr( \frac{2^3\cdot 3^{15} K^{10}}{\pi^3 P_e G^9} \biggr)^{1/3} \frac{\xi_e^{6}}{(3 + \xi_e^2)^{4}} \biggr] \biggl[ \frac{\pi G^5}{2^3 \cdot 3^7 K^5} \biggr]^{1/2} \frac{(3+\xi_e^2)^3}{\xi_e^5} \biggl( \frac{5G}{2\cdot 3} \biggr)^{1/2} \biggl[ K^{-5/6} P_\mathrm{ex}^{1/3} \biggr] </math> |
|
|
<math>~=~</math> |
<math> \biggr( \frac{3^{2} \cdot 5}{2^2 \pi } \biggr)^{1/2} \frac{\xi_e}{(3 + \xi_e^2)} \, . </math> |
This set of parametric relations that relate the mass of the truncated configuration to its radius via the parameter, <math>~\xi_e</math>, has been recorded to the immediate right of Stahler's name in our <math>~n=5</math> summary table, below.
Stahler points out (see his equation B13) that, for this particular pressure-bounded polytropic sequence, <math>~\xi_e</math> can be eliminated between the expressions to obtain the following direct algebraic relationship between <math>~M</math> and <math>~R_\mathrm{eq}</math>:
|
<math> \biggl( \frac{M}{M_\mathrm{SWS}} \biggr)^2 - 5 \biggl( \frac{M}{M_\mathrm{SWS}} \biggr)\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr) + \frac{20\pi}{3} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^4 </math> |
<math>~=~</math> |
<math> ~0 \, . </math> |
Viewed as a quadratic equation in the mass, the roots of this expression give,
|
<math> \frac{M}{M_\mathrm{SWS}} </math> |
<math>~=~</math> |
<math> \frac{5}{2} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr) \biggl\{ 1 \pm \biggl[ 1 - \frac{16\pi}{15} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^2 \biggr]^{1/2} \biggr\} \, . </math> |
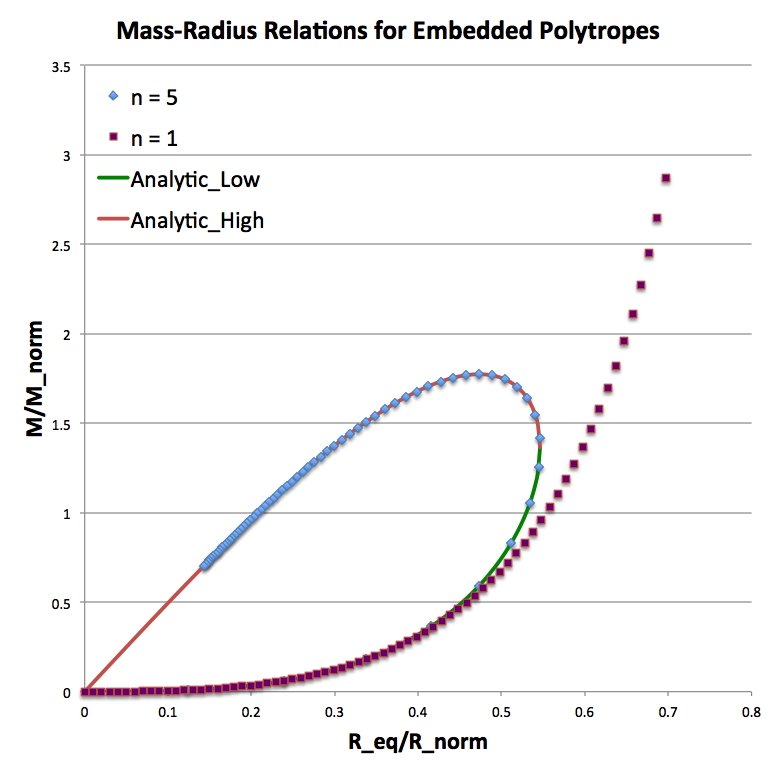
[CORRECTION: Changed factor inside square root from <math>~16\pi/3</math> to <math>~16\pi/15</math> on 24 December 2014.] We have used this expression to generate the complete <math>~n=5</math> sequence shown here in the top panel of Figure 2 — the solid green segment of the curve shows the negative root and the solid red segment of the curve was generated using the positive root.
ASIDE: In his Appendix B, Stahler (1983) claims that the quadratic equation relating <math>~M</math> directly to <math>~R_\mathrm{eq}</math> (his equation B13) can be obtained by analytically integrating the first-order ordinary differential equation presented as his equation B10. I don't think that this is possible without knowing ahead of time how <math>~M</math> relates to <math>~R_\mathrm{eq}</math> through the above-derived parametric relations in <math>~\xi_e</math>.
[29 September 2014 by J. E. Tohline] Now that (I think) I've finished deriving the properly defined virial equilibrium condition for embedded polytropes and have reconciled that equilibrium expression with Horedt's corresponding specification of the equilibrium radius and surface-pressure, it's time to revisit the concern that was expressed in this "ASIDE" regarding the mass-radius relationship for embedded, <math>~n=5</math> polytropes presented by Stahler.
Tabular Summary (n=5)
|
Table 2: Properties of <math>~n=5</math> Polytropes Embedded in an External Medium of Pressure <math>~P_e</math>
|
|||||
|---|---|---|---|---|---|
|
|||||
|
Horedt (1970)
|
<math> ~r_a = \frac{R_\mathrm{eq}}{R_\mathrm{Horedt}} = \biggl\{ 3 \biggl[ \frac{(\xi_e^2/3)^5}{(1+\xi_e^2/3)^{6}} \biggr] \biggr\}^{-1/2} </math> |
<math> ~p_a = \frac{P_e}{P_\mathrm{Horedt}} = 3^3 \biggl[ \frac{(\xi_e^2/3)^3}{(1+\xi_e^2/3)^{4}} \biggr]^3 </math> |
|||
|
Whitworth (1981)
|
<math> \frac{R_\mathrm{eq}}{R_\mathrm{rf}} = \biggl\{ \frac{2^{15}}{5^5} \biggl[ \frac{(\xi_e^2/3)^5}{(1+\xi_e^2/3)^{6}} \biggr] \biggr\}^{-1/2} </math> |
<math> \frac{P_e}{P_\mathrm{rf}} = \frac{2^{29}}{5^9} \biggl[ \frac{(\xi_e^2/3)^3}{(1+\xi_e^2/3)^{4}} \biggr]^3 </math> |
|||
|
Stahler (1983)
|
<math> \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} = \biggl\{ \frac{3\cdot 5}{2^2 \pi} \biggl[ \frac{\xi_e^2/3}{(1+\xi_e^2/3)^{2}} \biggr] \biggr\}^{1/2} </math> |
<math> \frac{M}{M_\mathrm{SWS}} = \biggl[ \biggl( \frac{3 \cdot 5^3}{2^2\pi} \biggr) \frac{(\xi_e^2/3)^3}{(1+\xi_e^2/3)^{4}} \biggr]^{1/2} </math> |
|||
|
<math> \biggl( \frac{M}{M_\mathrm{SWS}} \biggr)^2 - 5 \biggl( \frac{M}{M_\mathrm{SWS}} \biggr)\biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr) + \frac{2^2 \cdot 5 \pi}{3} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^4 = 0 </math> |
|||||
|
NOTE: None of the analytic expressions for the dimensionless radius, pressure, or mass presented in this table explicitly appear in the referenced articles by Horedt, by Whitworth, or by Stahler but, as is discussed fully above, they are straightforwardly derivable from the more general relations that appear in these papers. The final polynomial relating the dimensionless mass to the dimensionless radius does explicitly appear as equation (B13) in Stahler (1983). Additional discussion of Stahler's analytic mass-radius relation is presented in an accompanying chapter. |
|||||
Additional, Numerically Constructed Polytropic Configurations
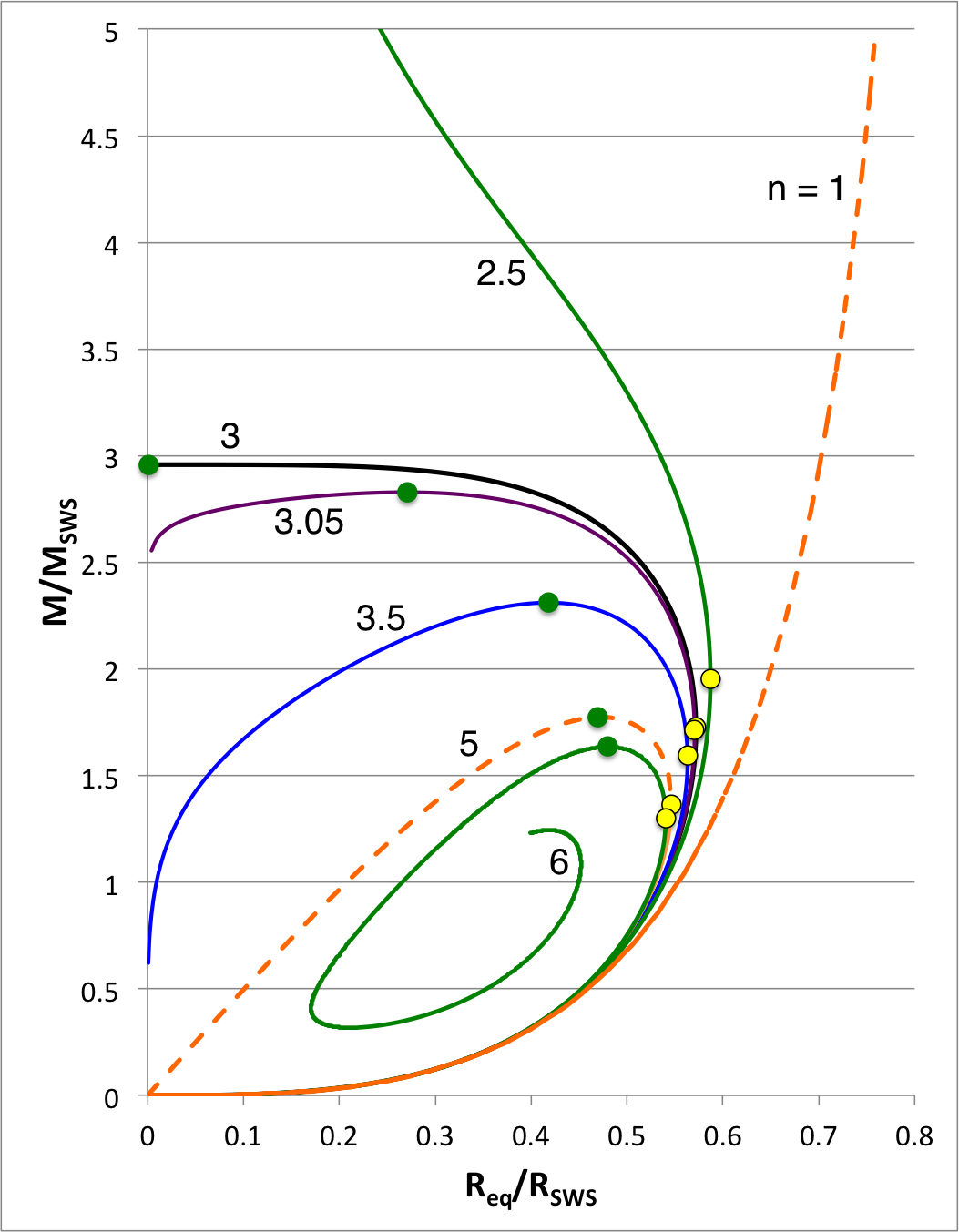
As has been detailed in an accompanying chapter, using numerical techniques we have solved the Lane-Emden equation, and thereby discerned the internal structural profiles, for polytropes having a wide variety of polytropic indexes. The righthand panel of Figure 3 presents a diagram in which the mass-radius "sequences" corresponding to eight different polytropic indexes have been drawn.
Turning Points
Limiting Pressure Along M1 Sequence
As is illustrated in the figures presented above, when an equilibrium sequence is constructed for any bounded (pressure-truncated) configuration having <math>~n > 3</math>, the sequence exhibits multiple "turning points." For example, when moving along the R-P sequence displayed in Figure 1 for <math>~n=5</math> configurations, the external pressure monotonically climbs to a maximum value, <math>~P_\mathrm{max}</math>, then "turns around" and steadily decreases thereafter. Horedt (1970) and Kimura (1981b) separately derived an expression that pinpoints the location of the <math>~P_\mathrm{max}</math> turning point along an R-P sequence — Kimura refers to this as an "M1 sequence" because the configuration's mass is held fixed while the external pressure and the system's corresponding equilibrium radius is varied. The turning point is located along the sequence at the point where,
|
<math> \frac{d P_e}{d R_\mathrm{eq}} \biggr|_M </math> |
<math>~=~</math> |
<math> 0\, , </math> |
or, just as well, where,
|
<math> \frac{d \ln P_e}{d\ln R_\mathrm{eq}} \biggr|_M </math> |
<math>~=~</math> |
<math> 0\, . </math> |
In what follows, we examine the expressions derived by both authors in order to show that they are identical to one another as well as to re-express the result in a form that conforms to our own adopted notation.
Horedt's Derivation
Appreciating that Horedt's notation for the surface pressure of an equilibrium configuration — which equals the applied external pressure <math>~P_e</math> — is <math>~\tilde{p}</math>, and his notation for <math>~R_\mathrm{eq}</math> is <math>~\tilde{r}</math>, the requisite expression from Horedt's paper [see also equation (13) in Viala & Horedt (1974)] is the one displayed in the following boxed image:
|
Excerpt from Horedt (1970) |
|||
|
That is, from Horedt's work we have,
|
<math>~\frac{dP_e}{dR_\mathrm{eq}}\biggr|_M ~~\rightarrow ~~ \frac{d\tilde{p}}{d \tilde{r}}</math> |
<math>~\sim</math> |
<math>~\frac{(3-n)(n+1)(\tilde\theta^')^2 + (2n+2)\tilde\theta^{n+1}}{(1-n)\tilde\xi f^' + (3-n)(n+1)(\tilde\theta^')^2} \, .</math> |
Let's independently derive this relation, starting from Horedt's equilibrium expressions for <math>~\tilde{r}</math> and <math>~\tilde{p}</math>, as summarized above. (For purposes of simplification, we will for the most part drop the tilde notation.)
|
<math>~ \frac{1}{R_\mathrm{Horedt}} \cdot \frac{d\tilde{r}}{d \tilde\xi}</math> |
<math>~=</math> |
<math>~ \frac{d}{d\xi}\biggl[ \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)}\biggr] </math> |
|
|
<math>~=</math> |
<math>~ (-\xi^2\theta^')^{(1-n)/(n-3)}\biggl[ 1 +\frac{(1-n)}{(n-3)} \cdot \xi (-\xi^2\theta^')^{-1} (-\xi^2\theta^')^' \biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{1}{(n-3)(n+1)}\cdot (-\xi^2\theta^')^{(1-n)/(n-3)} \biggl[ (n-3)(n+1) +(n-1)\cdot (\theta^')^{-2} \xi f^'
\biggr] </math> |
|
|
<math>~=</math> |
<math>~\frac{(-\xi^2\theta^')^{(1-n)/(n-3)} }{(3-n)(n+1)(\theta^')^{2}} \biggl[ (3-n)(n+1)(\theta^')^{2} +(1-n) \xi f^' \biggr] \, ; </math> |
|
<math>~ \frac{1}{P_\mathrm{Horedt}} \cdot \frac{d\tilde{p}}{d \tilde\xi}</math> |
<math>~=</math> |
<math>~ \frac{d}{d\xi}\biggl[ \tilde\theta^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ ( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \biggl[ f^' + f \cdot \frac{2(n+1)}{(n-3)}( -\tilde\xi^2 \tilde\theta' )^{-1} ( -\tilde\xi^2 \tilde\theta' )^' \biggr] </math> |
|
|
<math>~=</math> |
<math>~ ( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \biggl[ f^' - \frac{2(n+1)}{(n-3)(n+1)} \cdot \frac{f\cdot f^'}{(\theta^')^2} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{f^' ( -\tilde\xi^2 \tilde\theta' )^{(3n+1)/(n-3)} ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} }{(3-n)(n+1)(\theta^')^2} \biggl[ (3-n)(n+1)(\theta^')^2 + 2(n+1) \theta^{n+1} \biggr] \, . </math> |
The ratio of these two expressions gives,
|
<math>~\frac{R_\mathrm{Horedt}}{P_\mathrm{Horedt}} \cdot \frac{dP_e}{dR_\mathrm{eq}}\biggr|_M </math> |
<math>~=</math> |
<math>~f^' ( -\tilde\xi^2 \tilde\theta' )^{(3n+1)/(n-3)} \biggl\{ \frac{(3-n)(n+1)(\theta^')^2 + 2(n+1) \theta^{n+1}}{(3-n)(n+1)(\theta^')^{2} +(1-n) \xi f^' } \biggr\} \, , </math> |
completing our task, as the term inside the curly braces exactly matches the equation excerpt from Horedt's work, as displayed above.
Kimura's Derivation
Appreciating that Kimura uses the subscript "1," rather than a tilde, to identify equilibrium parameter values, the requisite expression is equation (22) from Kimura's "Paper II," as displayed in the following boxed image:
|
Excerpts (edited) from Kimura (1981b) |
|||
|
Drawing on the additional parameter and variable definitions provided in our discussion of Kimura's presentation, above, we can rewrite this key expression as,
|
<math>~\frac{R_\mathrm{eq}}{P_e} \cdot \frac{dP_e}{dR_\mathrm{eq}}\biggr|_M ~~\rightarrow ~~ \frac{d\ln{p_1}}{d \ln{r_1}}</math> |
<math>~=</math> |
<math>~ \frac{v_G \cdot h_G}{k_G} \, ,</math> |
where,
|
<math>~v_G</math> |
<math>~=</math> |
<math>~\frac{2}{[1-2(n+1)^{-1}]} =\frac{ 2(n+1)}{n-1} \, , </math> |
|
<math>~u_G</math> |
<math>~=</math> |
<math>~(3-1)-\biggl[\frac{1}{1-2(n+1)^{-1}} \biggr] = 2-\frac{(n+1)}{(n-1)} = \frac{(n-3)}{(n-1)} \, , </math> |
|
<math>~h_G</math> |
<math>~=</math> |
<math>~ \frac{1}{u_G} \biggl[ \frac{\zeta \theta^n}{\phi^'} \biggr]_1 - \frac{1}{v_G} \biggl[ \frac{\zeta \phi^'}{\theta} \biggr]_1 = \frac{(n-1)}{(n-3)} \biggl[ \frac{\tilde\xi \tilde\theta^n}{-\tilde\theta^'} \biggr] - \frac{(n-1)}{2(n+1)} \biggl[ \frac{(n+1)\tilde\xi (-\tilde\theta^')}{\tilde\theta} \biggr] </math> |
|
|
<math>~=</math> |
<math>~ \frac{(n-1)\tilde\xi}{2(n+1)(n-3)\tilde\theta (-\tilde\theta^')} \biggl\{ 2(n+1) \tilde\theta^{n+1} + (3-n) (n+1) (-\tilde\theta^')^2 \biggr\} \, , </math> |
|
<math>~k_G</math> |
<math>~=</math> |
<math>~1- \frac{1}{u_G} \biggl[ \frac{\zeta \theta^n}{\phi^'} \biggr]_1 =1- \frac{(n-1)}{(n-3)} \biggl[ \frac{\tilde\xi \tilde\theta^n}{-\tilde\theta^'} \biggr] = \frac{1}{ (n-3) (-\tilde\theta^') } \biggl\{ (n-3)(- \tilde\theta^') - (n-1) \tilde\xi \tilde\theta^n \biggr\} </math> |
|
|
<math>~=</math> |
<math>~ \frac{1}{ (n+1)(n-3) (-\tilde\theta^')^2 } \biggl\{ (n-3)(n+1) (-\tilde\theta^')^2 - (n-1)\tilde\xi [(n+1) \tilde\theta^n (-\tilde\theta^')] \biggr\} \, . </math> |
|
|
<math>~=</math> |
<math>~ \frac{-1}{ (n+1)(n-3) (-\tilde\theta^')^2 } \biggl\{ (3-n)(n+1) (-\tilde\theta^')^2 + (1-n)\tilde\xi [(n+1) \tilde\theta^n (\tilde\theta^')] \biggr\} \, . </math> |
Hence, from Kimura's work we find,
|
<math>~\frac{R_\mathrm{eq}}{P_e} \cdot \frac{dP_e}{dR_\mathrm{eq}}\biggr|_M </math> |
<math>~=</math> |
<math>~ \frac{(n+1)\tilde\xi \tilde\theta^'}{\tilde\theta} \biggl\{ \frac{2(n+1) \tilde\theta^{n+1} + (3-n) (n+1) (\tilde\theta^')^2}{(3-n)(n+1) (\tilde\theta^')^2 + (1-n)\tilde\xi [(n+1) \tilde\theta^n \tilde\theta^'] } \biggr\} \, . </math> |
Appreciating that <math>~f^' = [(n+1)\tilde\theta^n \tilde\theta^']</math>, we see that the expression inside the curly braces here matches exactly the expression inside the curly braces that was obtained through Horedt's derivation, as it should! The prefactor is different in the two expressions only because Kimura's result is for a logarithmic derivative whereas Horedt's derivation is not; the ratio of the two prefactors is, simply, the ratio,
|
<math>~\frac{R_\mathrm{eq}/R_\mathrm{Horedt}}{P_e/P_\mathrm{Horedt}} </math> |
<math>~=</math> |
<math>~\frac{\tilde\xi}{\tilde\theta_n^{n+1}}\cdot ( -\tilde\xi^2 \tilde\theta' )^{[(1-n)-2(n+1)]/(n-3)} </math> |
|
|
<math>~=</math> |
<math>~\frac{\tilde\xi}{\tilde\theta_n^{n+1}}\cdot ( -\tilde\xi^2 \tilde\theta' )^{-(3n+1)/(n-3)} \, . </math> |
In a separate discussion, specifically focused on the <math>~n=5</math> mass-radius relationship, we show how Kimura's analysis of turning points can be usefully applied.
Location of Pressure Limit
Now we can identify the location along the M1 sequence where the turning point set by <math>~P_\mathrm{max}</math> occurs by setting the numerator of this expression equal to zero, specifically,
|
<math>~2(n+1) \tilde\theta^{n+1} + (3-n) (n+1) (\tilde\theta^')^2 </math> |
<math>~=</math> |
<math>~ 0 \, . </math> |
This means that the equilibrium model that sits at the <math>~P_\mathrm{max}</math> turning point will have,
|
<math>~\frac{\tilde\theta^{n+1}}{(\tilde\theta^')^2} </math> |
<math>~=</math> |
<math>~ \frac{(n-3)}{2} \, . </math> |
Other Limits
In a similar fashion, Kimura (1981b) derived mathematical expressions that identify the location of other turning points along equilibrium sequences of bounded polytropic configurations. An M1 sequence — as displayed, for example, in the set of P-R diagrams shown in Figure 1, above — exhibits not only an "extremal of p1" but also an "extremal of r1." As we have just reviewed, the first of these is identified by setting <math>~(d\ln p_1/d\ln r_1)_{M} = 0</math> or, using Kimura's more compact terminology, the first occurs at a location that satisfies the condition,
<math>h_G = 0 \, ,</math> that is, where … <math>~\tilde\theta^{n+1} (\tilde\theta^')^{-2} = (n-3)/2 \, .</math>
Similarly, Kimura points out that an "extremal in r1" along an M1 sequence occurs at a location that satisfies the condition,
<math>k_G = 0 \, ,</math> that is, where … <math>~\tilde\xi \tilde\theta^{n} (-\tilde\theta^')^{-1} = (n-3)/(n-1) \, .</math>
As is illustrated by the plots presented in Figure 2, above, turning points also arise in the mass-radius relationship of bounded polytropic configurations having <math>~n > 3</math>. These are identified by Kimura as "p1 sequences" because the external pressure is held fixed while the system's mass and corresponding equilibrium radius is varied. In §5 of his "Paper II," Kimura points out that the same two conditions — namely, <math>~h_G = 0</math> and <math>~k_G = 0</math> — also identify the location of extrema in M1 along, respectively, p1 sequences and r1 sequences.
We can also identify extrema in r1 along p1 sequences by setting <math>~(\dot{p}_1/p_1) = 0</math> in Kimura's equation (17), then substituting the resulting expression for the function <math>~Z</math>, namely,
<math>~Z = v_1 \, ,</math>
into his equations (15) and (16). The ratio of these two resulting expressions gives,
|
<math>~\frac{d\ln M_1}{d \ln r_1}\biggr|_{p_1}</math> |
<math>~=</math> |
<math>~ \frac{u_1 -(u_G/v_G)v_1}{1 - v_1/v_G} = [u_1 v_G - u_G v_1][v_G - v_1]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \biggl[\frac{2(n+1)}{(n-1)} \cdot \frac{\xi \theta^n}{(-\theta^')} - \frac{(n-3)}{(n-1)} \cdot \frac{(n+1)\xi (-\theta^')}{\theta} \biggr] \biggl[\frac{2(n+1)}{(n-1)} - \frac{(n+1)\xi (-\theta^')}{\theta} \biggr]^{-1} </math> |
|
|
<math>~=</math> |
<math>~ \frac{\xi }{(-\theta^')} \biggl[ \frac{2 \theta^{n+1} - (n-3) (-\theta^')^2 }{2\theta - (n-1)\xi (-\theta^') } \biggr] </math> |
As has just been reviewed, the condition <math>~h_G=0</math> results from setting the numerator of this expression equal to zero and identifies extrema in M1 along p1 sequences. In addition, now, we can identify the condition for extrema in r1 along p1 sequences by setting the denominator to zero. The condition is,
<math>~\frac{\xi (-\theta^')}{\theta} = \frac{2}{(n-1)} \, .</math>
Some Tabulated Values
| Table 3: Turning-Point Locations along M-R Sequences of Pressure-Truncated Polytropes | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | ● Maximum Radius ● | ● Maximum Mass ● | |||||||||||
| <math>~\tilde\xi</math> | <math>~\tilde\theta</math> | <math>~\biggl|\frac{d\theta}{d\xi}\biggr|_\tilde\xi</math> | <math>~\frac{(n-1)}{2}\biggl[ \frac{\xi}{\theta} \biggl|\frac{d\theta}{d\xi}\biggr|~\biggr]_\tilde\xi</math> | <math>~\frac{R}{R_\mathrm{SWS}}</math> | <math>~\frac{M}{M_\mathrm{SWS}}</math> | <math>~\tilde\xi</math> | <math>~\tilde\theta</math> | <math>~\biggl|\frac{d\theta}{d\xi}\biggr|_\tilde\xi</math> | <math>~\frac{(n-3)}{2}\biggl[ \frac{1}{\theta^{n+1}} \biggl(\frac{d\theta}{d\xi}\biggr)^2 \biggr]_\tilde\xi</math> | <math>~\frac{R}{R_\mathrm{SWS}}</math> | <math>~\frac{M}{M_\mathrm{SWS}}</math> | ||
| 3 | 2.172 | 0.5387 | 0.2496 | 1.006 | 0.5717 | 1.726 | 6.89684862 | 0.0 | -0.04242976 | -- | 0.0 | 2.9583456 | |
| 3.05 | 2.162 | 0.5437 | 0.2479 | 1.010 | 0.5704 | 1.715 | 5.034 | 0.1152 | 0.07842 | 0.973 | 0.2707 | 2.829 | |
| 3.5 | 2.050 | 0.5930 | 0.2340 | 1.011 | 0.5630 | 1.594 | 3.910 | 0.2788 | 0.1126 | 0.994 | 0.4180 | 2.311 | |
| 5 | <math>~\sqrt{3}</math> | <math>~\frac{1}{\sqrt{2}}</math> | <math>~\frac{1}{\sqrt{24}}</math> | <math>~1</math> | <math>~\biggl( \frac{3\cdot 5}{2^4\pi}\biggr)^{1 / 2}</math> | <math>~\biggl( \frac{3\cdot 5^3}{2^6\pi}\biggr)^{1 / 2}</math> | <math>~3</math> | <math>~\frac{1}{2}</math> | <math>~\frac{1}{8}</math> | <math>~1</math> | <math>~\biggl( \frac{3^2\cdot 5}{2^6\pi}\biggr)^{1 / 2}</math> | <math>~\biggl( \frac{3^4\cdot 5^3}{2^{10}\pi}\biggr)^{1 / 2}</math> | |
| 6 | 1.6 | 0.7510 | 0.1884 | 1.003 | 0.5404 | 1.301 | 2.7 | 0.5811 | 0.1221 | 0.999 | 0.4802 | 1.635 | |
Related Discussions
- Constructing BiPolytropes
- Analytic description of BiPolytrope with <math>(n_c, n_e) = (5,1)</math>
- Bonnor-Ebert spheres
- Bonnor-Ebert Mass according to Wikipedia
- A MATLAB script to determine the Bonnor-Ebert Mass coefficient developed by Che-Yu Chen as a graduate student in the University of Maryland Department of Astronomy
- Schönberg-Chandrasekhar limiting mass
- Relationship between Bonnor-Ebert and Schönberg-Chandrasekhar limiting masses
- Wikipedia introduction to the Lane-Emden equation
- Wikipedia introduction to Polytropes

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |