Difference between revisions of "User:Tohline/SSC/Structure/LimitingMasses"
(→Mass Upper Limits: Mostly minor edits, but also added a couple of key reference links) |
(→Schönberg-Chandrasekhar Mass: Comment-out image from SC42) |
||
| Line 154: | Line 154: | ||
<tr> | <tr> | ||
<td align="center" colspan="2"> | <td align="center" colspan="2"> | ||
[[Image:SC42excerpt.jpg|600px|center]] | <!-- [[Image:SC42excerpt.jpg|600px|center]] --> | ||
[[Image:AAAwaiting01.png|600px|center]] | |||
</td> | </td> | ||
</tr> | </tr> | ||
Revision as of 18:04, 24 May 2015
Mass Upper Limits

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Spherically symmetric, self-gravitating, equilibrium configurations can be constructed from gases exhibiting a wide variety of degrees of compressibility. When examining how the internal structure of such configurations varies with compressibility, or when examining the relative stability of such structures, it can be instructive to construct models using a polytropic equation of state because the degree of compressibility can be adjusted by simply changing the value of the polytropic index, <math>~n</math>, across the range, <math>~0 \le n \le \infty</math>. (Alternatively, one can vary the effective adiabatic exponent of the gas, <math>~\gamma_g = 1 + 1/n</math>.) In particular, <math>~n = 0 ~~ (\gamma_g = \infty)</math> represents a hard equation of state and describes an incompressible configuration, while <math>~n = \infty ~~(\gamma_g = 1)</math> represents an isothermal and extremely soft equation of state.
Isolated Polytropes
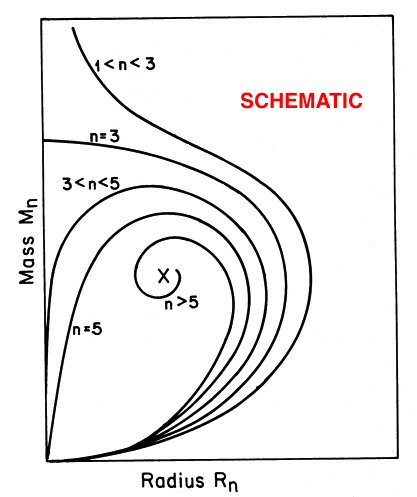
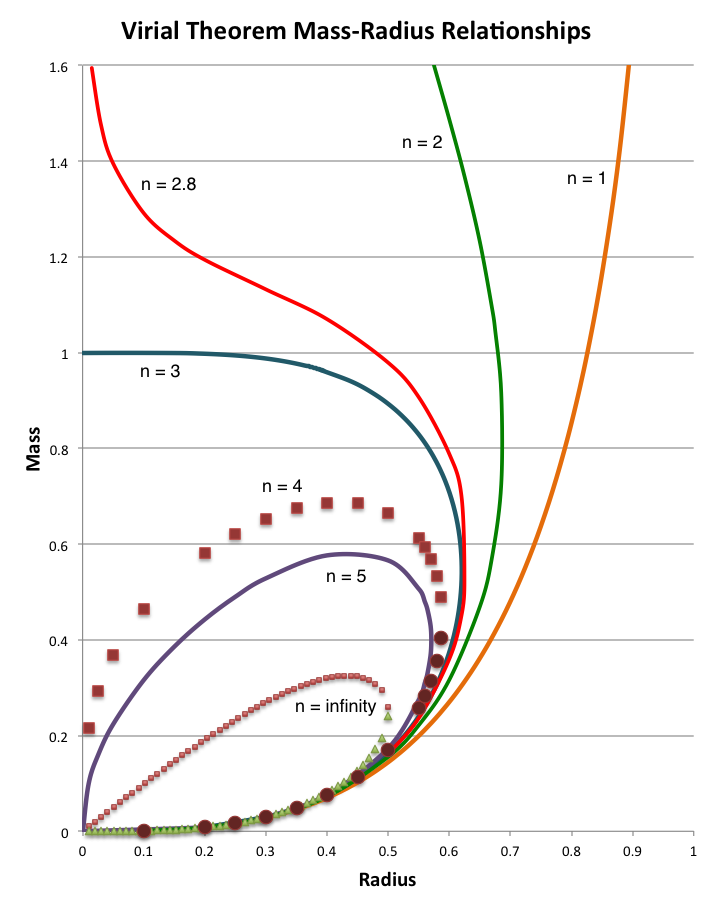
Isolated polytropic spheres exhibit three attributes that are especially key in the context of our present discussion:
- The equilibrium structure is dynamically stable if <math>~n < 3</math>.
- The equilibrium structure has a finite radius if <math>~n < 5</math>.
- The equilibrium structure can be described in terms of closed-form analytic expressions for <math>~n = 0</math>, <math>~n = 1</math>, and <math>~n = 5</math>.
Isothermal Spheres
Isothermal spheres (polytropes with index <math>~n=\infty</math>) are discussed in a wide variety of astrophysical contexts because it is not uncommon for physical conditions to conspire to create an extended volume throughout which a configuration exhibits uniform temperature. But mathematical models of isothermal spheres are relatively cumbersome to analyze because they extend to infinity, they are dynamically unstable, and they are not describable in terms of analytic functions. In such astrophysical contexts, we have sometimes found it advantageous to employ an <math>~n=5</math> polytrope instead of an isothermal sphere. An isolated <math>~n=5</math> polytrope can serve as an effective surrogate for an isothermal sphere because it is infinite in extent and is dynamically unstable, but it is less cumbersome to analyze because its structure can be described by closed-form analytic expressions.
Bounded Isothermal Sphere & Bonnor-Ebert Mass
In the mid-1950s, Ebert (1955) and Bonnor (1956) independently realized that an isothermal gas cloud can be stabilized by embedding it in a hot, tenuous external medium. The relevant mathematical model is constructed by chopping off the isothermal sphere at some finite radius — call it, <math>~\xi_e</math> — and imposing an externally applied pressure, <math>~P_e</math>, that is equal to the pressure of the isothermal gas at the specified edge of the truncated sphere. But for a given mass and temperature, there is a value of <math>~P_e</math> below which the truncated isothermal sphere is dynamically unstable, like its isolated and untruncated counterpart. Viewed another way, given the value of <math>~P_e</math> and the isothermal sound speed, <math>~c_s</math>, a bounded isothermal sphere will be dynamically stable only if its mass is below a critical value,
|
Bonnor-Ebert Mass
|
|
||||||||||||||||||
where <math>~\alpha</math> is a dimensionless coefficient of order unity. This limiting mass is often referred to as the Bonnor-Ebert mass. It appears most frequently in the astrophysics literature in discussions of star formation because that is the arena in which both Bonnor and Ebert were conducting research when they made their discoveries.
As is reviewed in a related discussion and as is documented in the table accompanying the expression for <math>~M_\mathrm{max}</math>, above, Bonnor (1956) used Emden's (1907) tabulated properties of an isothermal sphere to determine that the dimensionless radius of this limiting configuration is <math>\xi_e \approx 6.5</math> and that the leading coefficient, <math>\alpha \approx 1.18</math>. It is worth noting that a global virial analysis of the stability of bounded isothermal spheres produces the same expression for <math>~M_\mathrm{max}</math> with a leading coefficient that has an exact, analytic prescription, namely, <math>\alpha = (3^4 \cdot 5^3/2^{10}\pi)^{1/2} \approx 1.77408</math>. While it can be advantageous to reference this analytic prescription of <math>\alpha</math>, the virial analysis must be considered more approximate than Bonnor's analysis because it does not require the construction of models that are in detailed force balance.
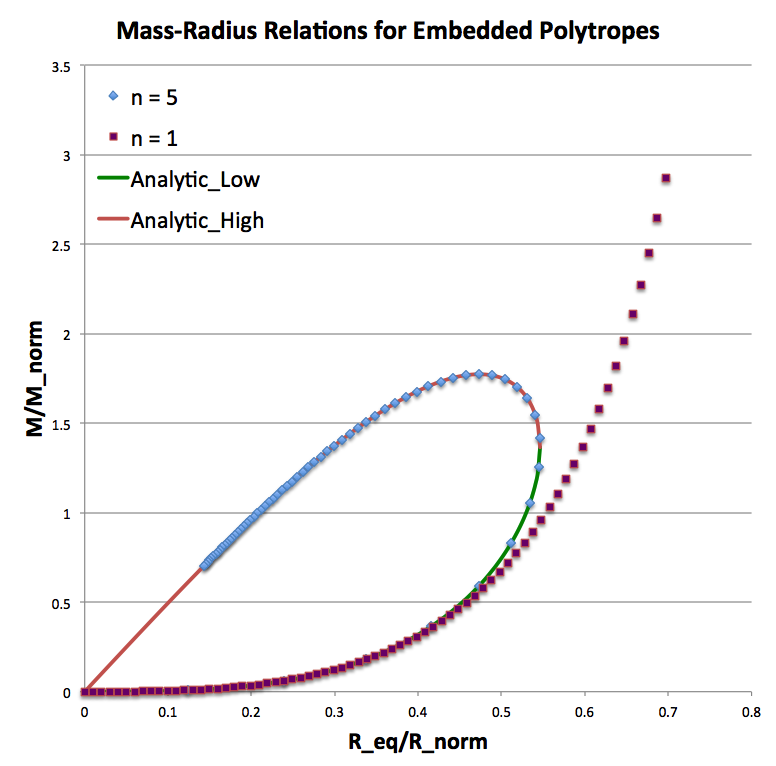
Our detailed force-balance analysis of truncated and pressure-bounded, <math>~n=5</math> polytropes identifies a physically analogous limiting mass. If the average isothermal sound speed, <math>~\bar{c_s}</math>, as defined elsewhere, is used in place of <math>c_s</math>, the mathematical expression for <math>~M_\mathrm{max}</math> has exactly the same form as in the isothermal case. But for the <math>~n=5</math> polytrope we know that the limiting configuration has a dimensionless radius given precisely by <math>~\xi_e = 3</math>; and, as a result, the leading coefficient in the definition of <math>~M_\mathrm{max}</math> is prescribable analytically, namely, <math>~\alpha = 2^{-3/10} \cdot (3^7/2^8 \pi)^{1/2} \approx 1.33943</math>. As is documented in the table accompanying the relation for <math>~M_\mathrm{max}</math>, above, in the case of a truncated <math>~n=5</math> polytrope, the simpler and more approximate virial analysis gives, <math>~\alpha = (3^{19}/2^{12}\cdot 5^7\pi)^{1/2} \approx 1.07523</math>.
Schönberg-Chandrasekhar Mass
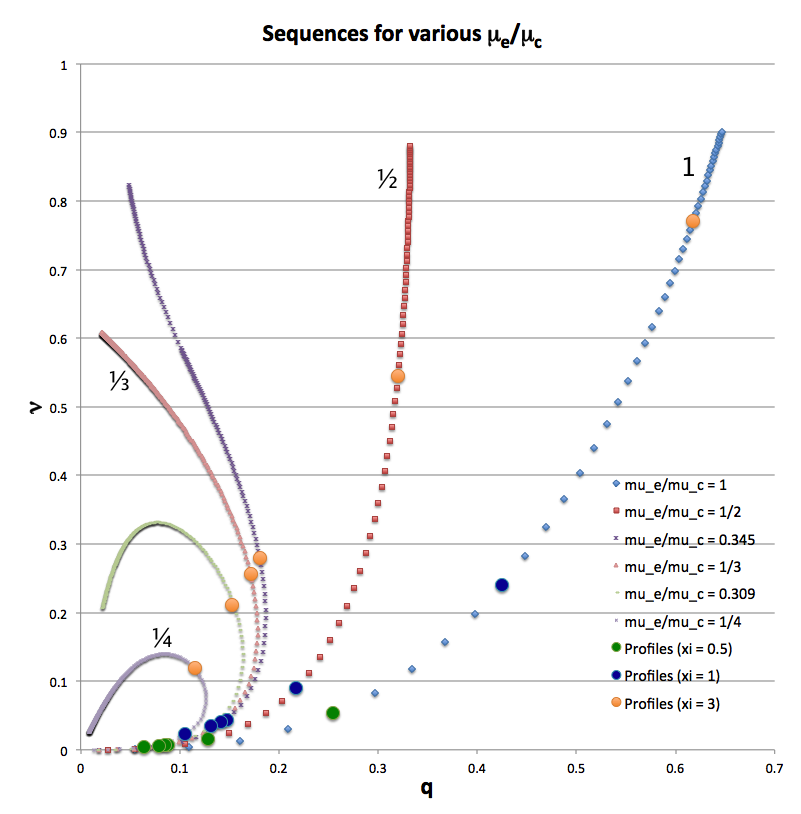
In the early 1940s, Chandrasekhar and his colleagues (see Henrich & Chandraskhar (1941) and Schönberg & Chandrasekhar (1942)) discovered that a star with an isothermal core will become unstable if the fractional mass of the core is above some limiting value. They discovered this by constructing models that are now commonly referred to as composite polytropes or bipolytropes, that is, models in which the star's core is described by a polytropic equation of state having one index — say, <math>~n_c</math> — and the star's envelope is described by a polytropic equation of state of a different index — say, <math>~n_e</math>. In an accompanying discussion we explain in detail how the two structural components with different polytropic indexes are pieced together mathematically to build equilibrium bipolytropes. For a given choice of the two indexes, <math>~n_c</math> and <math>~n_e</math>, a sequence of models can be generated by varying the radial location at which the interface between the core and envelope occurs. As the interface location is varied, the relative amount of mass enclosed inside the core, <math>~\nu \equiv M_\mathrm{core}/M_\mathrm{tot}</math>, quite naturally varies as well.
Henrich & Chandraskhar (1941) built structures of uniform composition having an isothermal core (<math>~n_c = \infty</math>) and an <math>~n_e = 3/2</math> polytropic envelope and found that equilibrium models exist only for values of <math>~\nu \le \nu_\mathrm{max} \approx 0.35</math>. Schönberg & Chandrasekhar (1942) extended this analysis to include structures in which the mean molecular weight of the gas changes discontinuously across the interface. Specifically, they used the same values of <math>~n_c</math> and <math>~n_e</math> as Henrich & Chandrasekhar, but they constructed models in which the ratio of the molecular weight in the core to the molecular weight in the envelope is <math>~\mu_c/\mu_e = 2</math>. This was done to more realistically represent stars as they evolve off the main sequence; they have inert, isothermal helium cores and envelopes that are rich in hydrogen. Note that introducing a discontinuous drop in the mean molecular weight at the core-envelope interface also introduces a discontinuous drop in the gas density across the interface. As the following excerpt from p. 168 of their article summarizes, in these models, Schönberg & Chandrasekhar (1942) found that <math>~\nu_\mathrm{max} \approx 0.101</math>. This is commonly referred to as the Schönberg-Chandrasekhar mass limit, although it was Henrich & Chandrasekhar who were the first to identify the instability.
|
Text excerpt from Schönberg & Chandrasekhar (1942) |
|
In an effort to develop a more complete appreciation of the onset of the instability associated with the Schönberg-Chandrasekhar mass limit, Beech (1988) matched an analytically prescribable, <math>~n_e = 1</math> polytropic envelope to an isothermal core and, like Schönberg & Chandrasekhar, allowed for a discontinuous change in the molecular weight at the interface. [For an even more comprehensive generalization and discussion, see Ball, Tout, & Żytkow (2012, MNRAS, 421, 2713)]. Beech's results were not significantly different from those reported by Schönberg & Chandrasekhar (1942); in particular, the value of <math>~\nu_\mathrm{max}</math> was still only definable numerically because an isothermal core cannot be described in terms of analytic functions.
In an accompanying derivation [see, also, Eggleton, Faulkner, and Cannon (1998, MNRAS, 298, 831)] we have gone one step farther, matching an analytically prescribable, <math>~n_e = 1</math> polytropic envelope to an analytically prescribable, <math>~n_c = 5</math> polytropic core. For this bipolytrope, we show that there is a limiting mass-fraction, <math>~\nu_\mathrm{max}</math>, for any choice of the molecular weight ratio <math>~\mu_c/\mu_e > 3</math> and that the interface location, <math>~\xi_i</math>, associated with this critical configuration is given by the positive, real root of the following relation:
<math> \biggl(\frac{\pi}{2} + \tan^{-1} \Lambda_i\biggr) (1+\ell_i^2) [ 3 + (1-m_3)^2(2-\ell_i^2)\ell_i^2] - m_3 \ell_i [(1-m_3)\ell_i^4 - (m_3^2 - m_3 +2)\ell_i^2 - 3] = 0 \, , </math>
where,
<math> \ell_i \equiv \frac{\xi_i}{\sqrt{3}} \, ; </math> <math> m_3 \equiv 3 \biggl( \frac{\mu_c}{\mu_e} \biggr)^{-1} \, ; </math> and <math> \Lambda_i \equiv \frac{1}{m_3\ell_i} [ 1 + (1-m_3)\ell_i^2] \, . </math>
Relationship Between the Bonnor-Ebert and Schönberg-Chandrasekhar Critical Masses
As we have shown elsewhere, in the limit <math>~m_3 \rightarrow 0</math>, the physically relevant root of the above analytic relation is <math>~\xi_i = 3</math> and the mass contained in the core is,
<math> M_\mathrm{core} = \biggl( \frac{1}{2} \biggr)^{3/10}\biggl( \frac{3^{7}}{2^{8}\pi} \biggr)^{1/2} \biggl( \frac{c_s^8}{G^3 P_e} \biggr)^{1/2} \, .</math>
While the pressure at the base of the envelope in this model is satisfactorily confining the core to a finite radius, the condition <math>~m_3 \rightarrow 0</math> implies that the mass-density at the base of — indeed, throughout — the envelope is zero. As we have pointed out elsewhere, this can be achieved by introducing a temperature discontinuity rather than a molecular weight discontinuity across the interface. Hence, there is no mass in the envelope and the resulting model is, effectively, a truncated <math>~n=5</math> polytrope embedded in a hot, tenuous external medium. It therefore should not come as a surprise that this critical Schönberg-Chandrasekhar-type configuration has a mass that is precisely equal to the Bonnor-Ebert limiting mass, as defined by a "bounded <math>~n=5</math> polytrope." (See the second row from the bottom in the above table.)
It should be clear from this analysis that the Bonnor-Ebert critical mass is not distinct from the Schönberg-Chandrasekhar critical mass. It can be derived from the Schönberg-Chandrasekhar mass in the limit when <math>\mu_e/\mu_c \rightarrow 0</math>. Had Schönberg & Chandrasekhar (1942) examined their model in this limit, they would have "discovered" the Bonnor-Ebert mass a decade prior to both Bonnor's and Ebert's published works.
Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
| Go Home |
Related Discussions
- Polytropes emdeded in an external medium
- Constructing BiPolytropes
- Analytic description of BiPolytrope with <math>(n_c, n_e) = (5,1)</math>
- Bonnor-Ebert spheres
- Bonnor-Ebert Mass according to Wikipedia
- A MATLAB script to determine the Bonnor-Ebert Mass coefficient developed by Che-Yu Chen as a graduate student in the University of Maryland Department of Astronomy
- Schönberg-Chandrasekhar limiting mass
- Relationship between Bonnor-Ebert and Schönberg-Chandrasekhar limiting masses

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |