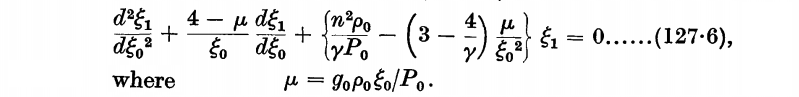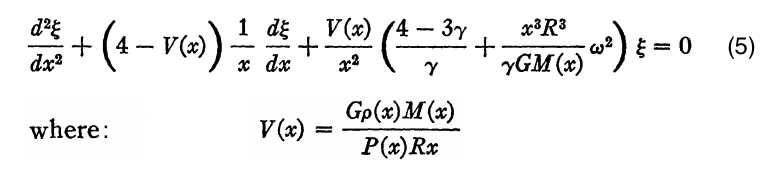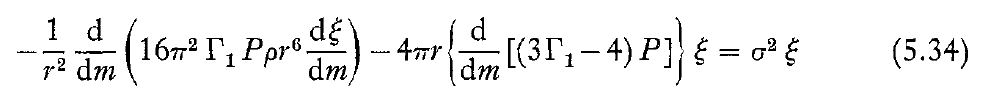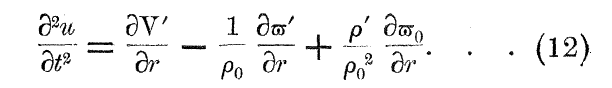Spherically Symmetric Configurations (Stability — Part II)

Suppose we now want to study the stability of one of the spherically symmetric, equilibrium structures that have been derived elsewhere. The identified set of simplified, time-dependent governing equations will tell us how the configuration will respond to an applied radial (i.e., spherically symmetric) perturbation that pushes the configuration slightly away from its initial equilibrium state.

Assembling the Key Relations

Governing Equations

After combining the Euler equation with the Poisson equation in essentially the manner outlined by the "structural solution strategy" we have called Technique 1, the relevant set of time-dependent governing equations is:

Equation of Continuity

<math>\frac{d\rho}{dt} = - \rho \biggl[\frac{1}{r^2}\frac{d(r^2 v_r)}{dr} \biggr] = -\rho \biggl[ \frac{dv_r}{dr} + \frac{2v_r}{r} \biggr] </math>

Euler + Poisson Equations

Adiabatic Form of the
First Law of Thermodynamics

<math>~\frac{d\epsilon}{dt} + P \frac{d}{dt} \biggl(\frac{1}{\rho}\biggr) = 0</math>

where,

<math>v_r \equiv \frac{dr}{dt}</math> ,

and, as before, the mass enclosed inside radius <math>r</math> is,

<math>M_r \equiv \int_0^r dm_r = \int_0^r 4\pi r^2 \rho dr</math> .

Consistent Lagrangian Formulation

The (Lagrangian) time derivatives in these equations define how a given physical parameter — for example, <math>~\rho</math>, <math>~v_r</math>, or <math>~\epsilon</math> — should vary with time in a (Lagrangian) fluid element that is not fixed in space but, rather, is moving along with the flow. However, the radial derivatives describe the spatial variation of various physical parameters as measured at fixed locations in space; that is, as written, the radial derivatives do not track conditions as viewed by a (Lagrangian) fluid element that is moving along with the flow because the position <math>r</math> of each (Lagrangian) fluid element is itself changing with time. A proper Lagrangian representation of the spatial derivatives can be formulated in the case of one-dimensional, spherically symmetric flows by using <math>~M_r</math> (or, equivalently, <math>~m_r</math>) instead of <math>~r</math> as the independent variable. Making the substitution,

in the first two equations above gives, respectively,

and,

Supplemental Relations

As has been discussed elsewhere, in any analysis of time-dependent flows, the principal governing equations must be supplemented by adopting an equation of state for the gas and by specifying initial conditions. Here, initial conditions will be given by the structural properties — for example, <math>~\rho</math><math>(M_r)~</math> and <math>~P</math><math>(M_r)~</math> — of one of our derived, spherically symmetric equilibrium structures — for example, a uniform-density sphere or an <math>~n = 1</math> polytrope. We will adopt an ideal gas equation of state and, specifically, the relation,

<math>~P = (\gamma_\mathrm{g} - 1)\epsilon \rho </math>.

As a result, the adiabatic form of the <math>1^\mathrm{st}</math> law of thermodynamics can be written as,

<math> \rho \frac{dP}{dt} - \gamma_\mathrm{g} P \frac{d\rho}{dt} = 0 . </math>

Summary

In summary, the following three one-dimensional ODEs define the physical relationship between the three dependent variables <math>~\rho</math>, <math>~P</math>, and <math>~r</math>, each of which should be expressible as a function of the two independent (Lagrangian) variables, <math>~t</math> and <math>~M_r</math>:

Equation of Continuity
<math>\frac{d\rho}{dt} = - 4\pi \rho^2 r^2 \frac{d}{dM_r}\biggl(\frac{dr}{dt}\biggr) - \frac{2\rho}{r} \biggl(\frac{dr}{dt}\biggr) </math>
,

Euler + Poisson Equations
<math>\frac{d^2 r}{dt^2} = - 4\pi r^2 \frac{dP}{dM_r} - \frac{GM_r}{r^2} </math>

Adiabatic Form of the
First Law of Thermodynamics
<math> \rho \frac{dP}{dt} - \gamma_\mathrm{g} P \frac{d\rho}{dt} = 0 . </math>

The Eigenvalue Problem

Here we adopt a notation and presentation very similar to what can be found in §38 of Kippenhahn & Weigart (KW94). In particular, we will use <math>~m</math> rather than the more cumbersome <math>~M_r</math> to tag each (Lagrangian) mass shell, both initially and at all later times. As is customary in perturbation studies throughout the field of physics, we will assume that the pressure <math>~P(m,t)</math>, density <math>~\rho(m,t)</math>, and radial position <math>~r(m,t)</math> of each mass shell at any time <math>~t</math> can be written in the form,

<math>~P(m,t)</math>	<math>~=</math>	<math>~P_0(m) + P_1(m,t) = P_0(m) \biggl[1 + p(m) e^{i\omega t} \biggr] \, ,</math>
<math>~\rho(m,t)</math>	<math>~=</math>	<math>~\rho_0(m) + \rho_1(m,t) = \rho_0(m) \biggl[1 + d(m) e^{i\omega t} \biggr] \, ,</math>
<math>~r(m,t)</math>	<math>~=</math>	<math>~r_0(m) + r_1(m,t) = r_0(m) \biggl[1 + x(m) e^{i\omega t} \biggr] \, ,</math>

where the subscript "1" denotes the variation of any variable away from its initial value (subscript 0) as drawn from the derived structure of the selected initial equilibrium model. These expressions encompass the hypothesis that, when perturbations away from the initial equilibrium state are sufficiently small — that is, <math>~|p|</math>, <math>~|d|</math>, and <math>~|x|</math> all <math>~\ll 1</math> — the perturbation can be treated as a product of functions that are separable in <math>~m</math> and <math>~t</math>, and that in general the time-dependent component can be represented by an exponential with an imaginary argument. The task is to solve a linearized version of the coupled set of key relations for the "eigenfunctions" <math>~p_i(m)</math>, <math>~d_i(m)</math>, and <math>~x_i(m)</math> associated with various characteristic "eigenfrequencies" <math>~\omega_i</math> of the underlying equilibrium model.

Linearizing the Key Equations

Adiabatic form of the First Law of Thermodynamics

Plugging the perturbed expressions for <math>~P(m,t)</math> and <math>~\rho(m,t)</math> into the adiabatic form of the First Law of Thermodynamics, we obtain,

<math>~(i\omega) \rho_0(m) \biggl[1 + d(m) e^{i\omega t} \biggr]P_0(m) p(m) e^{i\omega t} - \gamma_\mathrm{g}(i\omega) P_0(m) \biggl[1 + p(m) e^{i\omega t} \biggr] \rho_0(m) d(m) e^{i\omega t}</math>	<math>~=</math>	<math>~0</math>
<math>~\Rightarrow ~~~~~ (i\omega) \rho_0(m)P_0(m) e^{i\omega t} \biggl\{\biggl[1 + d(m) e^{i\omega t} \biggr] p(m) - \gamma_\mathrm{g} \biggl[1 + p(m) e^{i\omega t} \biggr] d(m) \biggr\}</math>	<math>~=</math>	<math>~0 \, .</math>

Because we are seeking solutions that will be satisfied throughout the configuration — that is, for all mass shells <math>~m</math> — the expression inside the curly brackets must be zero. Hence,

<math> ~p(m) - \gamma_\mathrm{g} d(m) + (1 - \gamma_\mathrm{g} ) d(m)p(m) e^{i\omega t} =0 \, . </math>

Also, because we are only examining deviations from the initial equilibrium state in which <math>~|d(m)|</math> and <math>~|p(m)|</math> are both <math>\ll 1</math>, then the third term on the left-hand-side of this equation, which contains a product of these two small quantities, must be much smaller than the first two terms. As is standard in perturbation theory throughout physics, for our stability analysis, we will drop this "quadradic" term and keep only terms that are linear in the small quantities. This leads to the following algebraic relationship between <math>~d(m)</math> and <math>~p(m)</math>:

<math> ~p = \gamma_\mathrm{g} d \, . </math>

Continuity Equation

Adopting the same approach, we will now "linearize" each term in the continuity equation:

<math> ~\frac{d\rho}{dt} </math>	<math> \rightarrow </math>	<math> (i\omega)\rho_0 d~e^{i\omega t} </math>
<math> \frac{\rho}{r} </math>	<math> \rightarrow </math>	<math> \frac{\rho_0}{r_0} \biggl[1 + d e^{i\omega t} \biggr] \biggl[1 + x e^{i\omega t} \biggr]^{-1} \approx \frac{\rho_0}{r_0} \biggl[1 + d ~e^{i\omega t} \biggr]\biggl[1 - x~ e^{i\omega t} \biggr] \approx \frac{\rho_0}{r_0} \biggl[1 + (d - x) ~e^{i\omega t} \biggr] </math>
<math> \frac{dr}{dt} </math>	<math> \rightarrow </math>	<math> (i\omega) r_0 x~e^{i\omega t} </math>
<math> ~\rho^2 r^2 </math>	<math> \rightarrow </math>	<math> \rho_0^2 r_0^2 \biggl[1 + d e^{i\omega t} \biggr]^2 \biggl[1 + x e^{i\omega t} \biggr]^2 \approx \rho_0^2 r_0^2 \biggl[1 + 2d ~e^{i\omega t} \biggr]\biggl[1 + 2x~ e^{i\omega t} \biggr] \approx \rho_0^2 r_0^2 \biggl[1 + 2(d + x) ~e^{i\omega t} \biggr] </math>
<math> \frac{d}{dm}\biggl(\frac{dr}{dt}\biggr) </math>	<math> \approx </math>	<math> \frac{d}{dm}\biggl[(i\omega) r_0 x~e^{i\omega t}\biggr] = (i\omega) e^{i\omega t} \biggl[x\frac{dr_0}{dm} + r_0\frac{dx}{dm} \biggr] = (i\omega) e^{i\omega t} \biggl[\frac{x}{4\pi r_0^2 \rho_0} + r_0\frac{dx}{dm} \biggr] </math>

In the last step of this last expression we have made use of the fact that, in the initial, unperturbed equilibrium model, <math>dr_0/dm = 1/(4\pi r_0^2 \rho_0)</math>. Combining all of these terms and linearizing the combined expression further, the linearized continuity equation becomes,

<math>~(i\omega)\rho_0 d~e^{i\omega t}</math>	<math>~\approx</math>	<math>~- \frac{2\rho_0}{r_0} \biggl[1 + (d - x) ~e^{i\omega t} \biggr] (i\omega) r_0 x~e^{i\omega t} - 4\pi \rho_0^2 r_0^2 \biggl[1 + 2(d + x) ~e^{i\omega t} \biggr](i\omega) e^{i\omega t} \biggl[\frac{x}{4\pi r_0^2 \rho_0} + r_0\frac{dx}{dm} \biggr]</math>
<math>~\Rightarrow ~~~ \rho_0 d </math>	<math>~\approx</math>	<math>~- 3\rho_0 x - 4\pi \rho_0^2 r_0^3 \frac{dx}{dm}</math>
<math>~\Rightarrow ~~~ 4\pi \rho_0 r_0^3 \frac{dx}{dm} </math>	<math>~\approx</math>	<math>~- 3 x - d \, ,</math>

or,

<math> r_0 \frac{dx}{dr_0} \approx - 3 x - d , </math>

where, to obtain this last expression, we have switched back from differentiation with respect to <math>~m</math> to differentiation with respect to <math>~r_0</math>.

Euler + Poisson Equations

Finally, linearizing each term in the combined "Euler + Poisson" equation gives:

<math> \frac{d^2r}{dt^2} </math>	<math> \rightarrow </math>	<math> \frac{d}{dt}\biggl[(i\omega) r_0 x~e^{i\omega t}\biggr] = - \omega^2 r_0 x~e^{i\omega t} </math>
<math> r^2 \frac{dP}{dm} </math>	<math> \rightarrow </math>	<math> r_0^2 \biggl[1 + x~ e^{i\omega t} \biggr]^2 \biggl\{\frac{dP_0}{dm} \biggl[1 + p~ e^{i\omega t} \biggr] + P_0~e^{i\omega t} \frac{dp}{dm} \biggr\} \approx r_0^2 \frac{dP_0}{dm} \biggl[1 + (2x+p)~ e^{i\omega t} \biggr] + P_0 r_0^2~e^{i\omega t} \frac{dp}{dm} </math>
<math> \frac{Gm}{r^2} </math>	<math> \rightarrow </math>	<math> \frac{Gm}{ r_0^2} \biggl[1 + x~ e^{i\omega t} \biggr]^{-2} \approx \frac{Gm}{ r_0^2} \biggl[1 -2 x~ e^{i\omega t} \biggr] \, . </math>

Hence, the combined linearized relation is,

<math> - \omega^2 r_0 x~e^{i\omega t} \approx -4\pi \biggl\{r_0^2 \frac{dP_0}{dm} \biggl[1 + (2x+p)~ e^{i\omega t} \biggr] + P_0 r_0^2~e^{i\omega t} \frac{dp}{dm} \biggr\} - \frac{Gm}{ r_0^2} \biggl[1 -2 x~ e^{i\omega t} \biggr] </math>
<math> \Rightarrow ~~~~~ e^{i\omega t} \biggl\{(2x + p)4\pi r_0^2 \frac{dP_0}{dm}-2x \frac{Gm}{r_0^2} + 4\pi P_0 r_0^2 \frac{dp}{dm} -\omega^2 r_0 x \biggr\} \approx - 4\pi r_0^2 \frac{dP_0}{dm} - \frac{Gm}{r_0^2} </math>
<math> \Rightarrow ~~~~~ 4\pi P_0 r_0^2 \frac{dp}{dm} \approx (4x + p)g_0 + \omega^2 r_0 x \, , </math>

where, in order to obtain this last expression we have made use of the fact that, in the unperturbed equilibrium configuration,

<math> g_0(m) \equiv \frac{Gm}{r_0^2} = - 4\pi r_0^2 \frac{dP_0}{dm} = - \frac{1}{\rho_0} \frac{dP_0}{dr_0} \, . </math>

Switching back from differentiation with respect to <math>~m</math> to differentiation with respect to <math>~r_0</math>, the "Euler + Poisson" combined linearized relation can alternatively be written as,

<math> \frac{P_0}{\rho_0} \frac{dp}{dr_0} \approx (4x + p)g_0 + \omega^2 r_0 x . </math>

Summary

In summary, the following three linearized equations describe the physical relationship between the three dimensionless perturbation amplitudes <math>~p(r_0)</math>, <math>~d(r_0)</math> and <math>~x(r_0)</math>, for various characteristic eigenfrequencies, <math>~\omega</math>:

Linearized
Equation of Continuity
<math> r_0 \frac{dx}{dr_0} = - 3 x - d , </math>

Linearized
Euler + Poisson Equations
<math> \frac{P_0}{\rho_0} \frac{dp}{dr_0} = (4x + p)g_0 + \omega^2 r_0 x , </math>

Linearized
Adiabatic Form of the
First Law of Thermodynamics
<math> p = \gamma_\mathrm{g} d \, . </math>

It is customary to combine these three relations to obtain a single, second-order ODE in terms of the fractional displacement, <math>~x</math> as follows. Using the third expression to replace <math>~d</math> by <math>~p</math> in the first expression, then differentiating the first expression with respect to <math>~r_0</math> generates,

<math>~\frac{d}{dr_0} \biggl[ r_0 \frac{dx}{dr_0}\biggr]</math>	<math>~=</math>	<math>~- \frac{d}{dr_0}\biggl[ 3 x + \frac{p}{\gamma_\mathrm{g}} \biggr]</math>
<math>~\Rightarrow ~~~~~ r_0 \frac{d^2x}{dr_0^2} + 4 \frac{dx}{dr_0}</math>	<math>~=</math>	<math>~- \frac{1}{\gamma_\mathrm{g}} \frac{dp}{dr_0} \, .</math>

Similarly, replacing <math>~p</math> by <math>~d</math> in the second expression, then using the first expression to eliminate <math>~d</math> gives,

<math>~\frac{P_0}{\rho_0} \frac{dp}{dr_0}</math>	<math>~=</math>	<math>~\biggl[4x + \gamma_\mathrm{g}\biggl( -3x -r_0\frac{dx}{dr_0} \biggr) \biggr] g_0 + \omega^2 r_0 x </math>
<math>~\Rightarrow ~~~~~ \frac{1}{\gamma_\mathrm{g}} \frac{dp}{dr_0}</math>	<math>~=</math>	<math>~- \frac{dx}{dr_0} \biggl(\frac{r_0 g_0 \rho_0}{P_0}\biggr) + \biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] \biggl(\frac{r_0 \rho_0}{\gamma_\mathrm{g} P_0} \biggr) x \, .</math>

Finally, then, combining these two expressions gives the desired 2^nd-order ODE,

<math> \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{r_0} \biggr] x = 0 \, . </math>

Classic Papers that Derive & Use this Relation

Eddington (1926)

To our knowledge, a derivation of this governing 2nd-order ODE was first presented by Eddington (1926) in a book titled, The Internal Constitution of the Stars. (This entire book has been digitally scanned and is now available online.) The derived expression, which appears on p. 188 as equation (127.6) of Eddington's book, is presented in the following, framed image.

Pulsation Equation as Derived and Presented by Eddington (1926)

The similarity between Eddington's expression and the governing 2nd-order ODE that we have derived is immediately apparent. Specifically, simply after inserting Eddington's definition of his composite variable, <math>~\mu</math>, and making the substitutions,

<math>~\xi_1 \rightarrow x \, ,</math> <math>\xi_0 \rightarrow r_0 \, ,</math> and <math>n^2 \rightarrow \omega^2 \, ,</math>

Eddington's pulsation equation becomes,

<math>~ \frac{d^2 x}{dr_0^2} + \biggl[ \frac{4}{r_0} - \frac{g_0 \rho_0}{P_0} \biggr] \frac{dx}{dr_0} + \frac{\rho_0}{\gamma P_0} \biggl\{\omega^2 + \biggl(4 - 3\gamma\biggr) \frac{g_0 }{r_0} \biggr\}x </math>

which exactly matches our derived governing relation.

Ledoux and Pekeris (1941)

Historically, by the 1940s, the expression just derived was a relatively familiar one to astrophysicists. For example, the opening paragraph of a 1941 paper by Ledoux & Pekeris (1941, ApJ, 94, 124), reads:

If we divide their equation (1) through by <math>~Xr = \Gamma_1 P r</math> and recognize that,

<math> \frac{dX}{dr} = \frac{dX}{dm}\frac{dm}{dr} = - \Gamma_1 g_0 \rho \, , </math>

we obtain,

<math> \frac{d^2\xi}{dr^2} + \biggl[ \frac{4}{r} - \frac{g_0 \rho}{P} \biggr] \frac{d\xi}{dr} +\frac{\rho}{\Gamma_1 P} \biggl[ \sigma^2 + (4 - 3\Gamma_1) \frac{g_0}{r} \biggr] \xi = 0 \, . </math>

This is clearly the same <math>2^\mathrm{nd}</math>-order, ordinary differential equation as the one we have derived, but with a more general definition of the adiabatic exponent that allows consideration of a situation where the total pressure is a sum of both gas and radiation pressure.

Schwarzschild (1941)

In the same volume of The Astrophysical Journal, Schwarzschild (1941) published work on "Overtone Pulsations for the Standard [Stellar] Model." The following excerpt has been drawn from the first page of this article.

³A. S. Eddington (1930), The Internal Constitution of the Stars, pp. 188 and 192.

The similarity between Schwarzschild's "pulsation equation" and the governing 2nd-order ODE that we have derived is immediately apparent; for example, the eigenfrequency, <math>~\omega</math>, is the same in both,

<math>~\xi_1 \leftrightarrow x</math> and <math>\xi_0 \leftrightarrow r_0 \, .</math>

But the two equations are not exactly the same. To show this, we begin by comparing the last term on the lefthand-side in both expressions and presume that Schwarzschild's <math>~u</math> is related to the state variables in our equation as,

<math>u = \frac{\gamma_g P_0}{\rho_0} \, .</math>

Restricting the discussion to only polytropic equations of state — that is, <math>~P_0 = K\rho_0^{(n+1)/n}</math> — we can write,

<math>~\gamma_g K\rho_0^{1/n} \, ,</math>

which means that,

<math>~\biggl( \frac{\gamma_g K}{n} \biggr) \rho_0^{(1-n)/n} \frac{d\rho_0}{d\xi_0} = \biggl( \frac{\gamma_g}{n+1} \biggr) \frac{1}{\rho_0} \frac{dP_0}{d\xi_0} = - \biggl( \frac{\gamma_g}{n+1} \biggr) g_0 \, ,</math>

where the last step results from recalling that, by our definition above, the unperturbed gravitational acceleration is,

Hence, when considering polytropic configurations, the following substitutions are appropriate between the two equations:

<math>\frac{du}{d\xi_0} \leftrightarrow - \biggl( \frac{\gamma_g}{n+1} \biggr) g_0 </math> and <math>\frac{1}{u} \frac{du}{d\xi_0} \leftrightarrow - \frac{1}{(n+1)} \frac{g_0 \rho_0}{P_0} \, .</math>

Making these substitutions into Schwarzschild's pulsation equation gives,

<math> \frac{d^2x}{dr_0^2} + \biggl[\frac{4}{r_0} - \frac{4}{(n+1)}\biggl(\frac{g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{dr_0} + \biggl(\frac{\rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 - \biggl( \frac{4a\gamma_g}{n+1} \biggr)\frac{g_0}{r_0} \biggr] x = 0 \, . </math>

Appreciating that, in Schwarzschild's expression, <math>~a \equiv - (4-3\gamma_g)/\gamma_g</math>, we see that our expression matches his if and only if <math>~n=3</math>. This is, indeed, precisely the "standard model" that Schwarzschild was considering.

Review Article by Christy (1966)

In the 1966 review by R. F. Christy (1966, Annual Reviews of Astronomy & Astrophysics, 4, 353) titled, Pulsation Theory, this key 2^nd-order ODE appears as equation (5) in the form shown by the following boxed-in (slightly edited) excerpt:

Pulsation Equation as Presented in the Review by R. F. Christy (1966)

Correspondence with our derived equation becomes clear by appreciating that Christy's <math>~x \equiv r_0/R</math> and that,

hence,

<math>V(x) \rightarrow \frac{g_0 \rho_0 r_0}{P_0} \, .</math>

Making these substitutions and multiplying Christy's equation through by <math>~R^{-2}</math> gives,

<math>~ \frac{d^2\xi}{dr_0^2} + \biggl[ \frac{4}{r_0} - \frac{g_0 \rho_0}{P_0} \biggr]\frac{d\xi}{dr_0} + \frac{\rho_0}{\gamma_g P_0 } \biggl[(4-3\gamma_g)\frac{g_0}{r_0} + \omega^2 \biggr] \xi </math>

Review Article by Cox (1974)

In an excellent review of "Pulsating Stars", J. P. Cox (1974, Reports on Progress in Physics, 37, 563) presents a full derivation of, what he refers to as, the adiabatic wave equation. It appears as equation (5.34) in the form displayed in the following boxed-in image:

Adiabatic Wave Equation as derived in the Review by J. P. Cox (1974)

Recognizing the correspondence with our derived expression requires, first, switching the independent variable from <math>~m</math> to <math>~r_0</math> via the relation identified, above, namely,

to obtain,

<math>~ \sigma^2 \xi </math>	<math>~=</math>	<math>~ - \frac{1}{(4\pi \rho_0 r_0^4)}\frac{d}{dr_0}\biggl[ (4\pi \Gamma_1 P_0 r_0^4) \frac{d\xi}{dr_0} \biggr] - \frac{1}{\rho_0 r_0} \biggl\{ \frac{d}{dr_0} [ (3\Gamma_1-4)P_0] \biggr\} \xi </math>
	<math>~=</math>	<math>~ - \frac{\Gamma_1 P_0 }{\rho_0 }\frac{d^2 \xi}{dr_0^2} - \frac{\Gamma_1 }{(\rho_0 r_0^4)} \biggl[4P_0 r_0^3 + r_0^4\frac{dP_0}{dr_0} \biggr] \frac{d\xi}{dr_0} + \frac{(4-3\Gamma_1)}{\rho_0 r_0} \biggl[ \frac{dP_0}{dr_0} \biggr] \xi </math>
<math>~\Rightarrow ~~~~ 0</math>	<math>~=</math>	<math>~ - \frac{\Gamma_1 P_0 }{\rho_0 }\biggl\{ \frac{d^2 \xi}{dr_0^2} + \biggl[\frac{4}{r_0} + \frac{1}{P_0}\frac{dP_0}{dr_0} \biggr] \frac{d\xi}{dr_0} \biggr\} - \biggl\{ \sigma^2 - \frac{(4-3\Gamma_1)}{\rho_0 r_0} \biggl[ \frac{dP_0}{dr_0} \biggr] \biggr\} \xi \, . </math>

Then, using the definition of <math>~g_0</math>, also as provided above, to facilitate the substitution,

<math>~\frac{dP_0}{dr_0} \rightarrow - g_0 \rho_0 \, ,</math>

gives,

<math>~ \frac{d^2 \xi}{dr_0^2} + \biggl[\frac{4}{r_0} - \frac{g_0 \rho_0}{P_0}\biggr] \frac{d\xi}{dr_0} + \frac{\rho_0 }{\Gamma_1 P_0 }\biggl\{ \sigma^2 + \frac{(4-3\Gamma_1)g_0}{r_0} \biggr\} \xi \, , </math>

which, apart from the adoption of different variable names, exactly matches our derived expression.

Bonnor (1957)

In a paper titled, "Jeans' Formula for Gravitational Instability," Bonnor (1957, MNRAS, 117, 104) carried out a linear perturbation analysis, preferring to examine the development of Eulerian fluctuations in the matter density rather than the development of Lagrangian position displacements. Here we show the relationship between his approach to a perturbation analysis and the one that we have focused on, above.

Linearized Equations on a Static Background

First, we examine how Bonnor's (1957) linearized Euler equation (2.7) was derived from the nonlinear Euler equation, numbered (2.1) in his paper.

Bonnor's (1957, MNRAS, 117, 104) Derivation
Original nonlinear Euler Equation	<math>~\rightarrow</math>	Linearized Euler Equation
	<math>~\rightarrow</math>

As has been made clear in our introductory discussions, the

Eulerian Representation
of the Euler Equation,

<math>~\frac{\partial\vec{v}}{\partial t} + (\vec{v}\cdot \nabla) \vec{v}= - \frac{1}{\rho} \nabla P - \nabla \Phi</math>

can be counted among the principal set of equations that govern the dynamics of self-gravitating fluids. Accepting that he uses the boldface variable <math>~\mathbf{u}</math> instead of <math>~\vec{v}</math> to represent the fluid velocity, we see that the lefthand side of Bonnor's equation (2.1) exactly matches the lefthand side of the Euler equation, as we have presented it. The term on the righthand side of Bonnor's equation (2.1) that involves a gradient in the gas pressure also matches ours. What remains is to recognize that, in Bonnor's paper,

<math>~\mathbf{F}</math>

<math>~- \nabla\Phi \, .</math>

This is confirmed by Bonnor's equation (2.6), which presents another one of our identified set of principal governing equations, namely the

Poisson Equation

<math>\nabla^2 \Phi = 4\pi G \rho</math>

in terms of the vector, <math>~\mathbf{F}</math>, specifically,

<math>~\nabla\cdot\mathbf{F}</math>

<math>~= - \nabla^2\Phi =</math>

As we have done in our development of the eigenvalue problem, Bonnor (1957) began the process of linearizing the Euler equation by writing each physical variable in terms of its initial, unperturbed value (denoted by subscript "0") plus a "small quantity." For example, he wrote,

<math>~\mathbf{u}</math>	<math>~=</math>	<math>~\mathbf{u}_0 + \mathbf{u} \, ,</math>
<math>~\mathbf{F}</math>	<math>~=</math>	<math>~\mathbf{F}_0 + \mathbf{F}_1 </math> … and we, furthermore, will write … <math>~\mathbf{F}_0 = -\nabla \Phi_0</math> and <math>~\mathbf{F}_1 = - \nabla \Phi_1 \, ,</math>
<math>~\rho</math>	<math>~=</math>	<math>~\rho_0 + w \, ,</math>
<math>~\rho</math>	<math>~=</math>	<math>~P_0 + q \, .</math>

[For future reference, notice that the perturbation variable names that we introduced for density and pressure — see above — are different from the ones used by Bonner. They are related via the expressions, <math>(\rho_0 d e^{i\omega t}) \leftrightarrow w</math> and <math>(P_0 p e^{i\omega t}) \leftrightarrow q</math>.] He also initially assumed, as have we, that the unperturbed system is in hydrostatic balance, so,

<math>~\mathbf{u}_0</math>	<math>~=</math>	<math>~0 \, ,</math>
<math>~\mathbf{F}_0</math>	<math>~=</math>	<math>~\frac{1}{\rho_0} \nabla P_0 \, .</math>

Notice that — confusion notwithstanding — Bonnor did not affix a subscript to the variable being used to represent the velocity perturbation, at least not initially. So, after setting <math>~\mathbf{u}_0 = 0</math>, the generic velocity vector, <math>~\mathbf{u}</math>, on the lefthand side of his equation (2.1) becomes the small in magnitude velocity perturbation, <math>~\mathbf{u}</math>, on the lefthand side of his equation (2.7); and, in his equation (2.7), the <math>~(\mathbf{u}\cdot \nabla)\mathbf{u}</math> term disappears altogether because it involves the product of two quantities that are both small in magnitude. Although details of the derivation are not presented in Bonnor's (1957) paper, it is reasonable to assume that he took the following steps in linearizing the righthand side of equation (2.1):

RHS of equation (2.1)	<math>~\rightarrow</math>	<math>~\mathbf{F}_0 + \mathbf{F}_1 - \frac{1}{(\rho_0 + w)} \nabla(P_0 + q) </math>
	<math>~=</math>	<math>~\mathbf{F}_0 + \mathbf{F}_1 - \frac{1}{\rho_0} \biggl(1 + \frac{w}{\rho_0} \biggr)^{-1}\nabla(P_0 + q) </math>
	<math>~\approx</math>	<math>~\mathbf{F}_0 + \mathbf{F}_1 - \frac{1}{\rho_0} \biggl(1 - \frac{w}{\rho_0} \biggr)\nabla(P_0 + q) </math>
	<math>~=</math>	<math>~\biggl[ \mathbf{F}_0 - \frac{1}{\rho_0}\nabla P_0 \biggr] + \mathbf{F}_1 - \frac{1}{\rho_0} \nabla q + \biggl(\frac{w}{\rho_0^2} \biggr)\nabla P_0 + \biggl(\frac{w}{\rho_0^2} \biggr)\nabla q</math>
	<math>~\approx</math>	<math>~ \mathbf{F}_1 - \frac{1}{\rho_0} \nabla q + \biggl(\frac{w}{\rho_0^2} \biggr)\nabla P_0 \, .</math>

As is shown in the following framed image, if the discussion is restricted only to fluctuations in the radial coordinate direction of a spherically symmetric configuration, in which case <math>~\nabla \rightarrow \partial/\partial r</math>, this expression exactly matches the righthand side of the linearized Euler equation, derived and presented as equation (12) by James H. Jeans in 1902 (Philosophical Transactions of the royal Society of London. Series A, 199, 1).

Linearized Euler Equation as Derived and Presented by Jeans (1902)

The correspondence between the righthand-sides of equation (12) from Jeans (1902) and our derived expression [using Bonnor's (1957) variable notation] is clear after accepting the following variable mappings:

<math>~\frac{\partial V'}{\partial r}</math>	<math>~~~ \rightarrow ~~</math>	<math>~\mathbf{F}_1= - \nabla \Phi_1</math>
<math>~\varpi_0</math>	<math>~~~ \rightarrow ~~</math>	<math>~P_0</math>
<math>~\varpi'</math>	<math>~~~ \rightarrow ~~</math>	<math>~q</math>
<math>~\rho'</math>	<math>~~~ \rightarrow ~~</math>	<math>~w</math>

The lefthand side of equation (12) from Jeans (1902) also matches the lefthand side of Bonnor's (1957) linearized Euler equation, although this may not be immediately apparent because the variable "u" has been assigned different meanings in the two publications. In Bonnor's paper, <math>~u = \hat{\mathbf{e}}_r \cdot \mathbf{u}</math> is the perturbed velocity in the radial-coordinate direction; while, in the paper by Jeans, <math>~u</math> is the radial displacement itself. Hence,

<math>~\frac{\partial u}{\partial t} \biggr\|_\mathrm{Jeans}</math>	<math>~~~ \rightarrow ~~</math>	<math>~u \biggr\|_\mathrm{Bonner}</math>
<math>~\Rightarrow~~~\frac{\partial^2 u}{\partial t^2} \biggr\|_\mathrm{Jeans}</math>	<math>~~~ \rightarrow ~~</math>	<math>~\frac{\partial u}{\partial t} \biggr\|_\mathrm{Bonner}</math>

Now, in order to morph this last expression into the expression found on the righthand side of Bonnor's equation (2.7), as reprinted above, we need to draw upon the result obtained, above, from linearizing the adiabatic form of the First Law of Thermodynamics. After shifting to Bonnor's variable notation (as clarified in earlier remarks), the relevant result is,

<math>\frac{q}{P_0} \approx \gamma_g \frac{w}{\rho_0} \, .</math>

In addition, we appreciate that,

<math>\gamma_g = \biggl( \frac{d\ln P}{d\ln \rho} \biggr)_0 = \frac{\rho_0}{P_0}\cdot \biggl( \frac{dP}{d\rho} \biggr)_0 \, .</math>

Hence (see also Bonnor's equation 3.7),

<math>q \approx w \biggl( \frac{dP}{d\rho} \biggr)_0 \, ,</math>

which allows us to write the righthand side of the linearized Euler equation as,

RHS of equation (2.1)

<math>~\approx</math>

<math>~ \mathbf{F}_1 - \frac{1}{\rho_0} \biggl\{ \nabla \biggl[ w \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] - \biggl(\frac{w}{\rho_0} \biggr)\nabla P_0\biggr\} \, .</math>

But, given the adopted barotropic equation of state, we can also write,

<math>\nabla P_0 = \biggl(\frac{dP}{d\rho} \biggr)_0 \nabla\rho_0 \, ,</math>

in which case,

RHS of equation (2.1)	<math>~\approx</math>	<math>~ \mathbf{F}_1 - \biggl\{\frac{1}{\rho_0} \nabla \biggl[ w \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] - \biggl(\frac{w}{\rho_0^2} \biggr)\biggl(\frac{dP}{d\rho} \biggr)_0 \nabla\rho_0\biggr\} </math>
	<math>~=</math>	<math>~ \mathbf{F}_1 - \biggl\{ \frac{1}{\rho_0} \nabla \biggl[ w \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] + w\biggl(\frac{dP}{d\rho} \biggr)_0 \nabla\biggl(\frac{1}{\rho_0} \biggr) \biggr\} </math>
	<math>~=</math>	<math>~ \mathbf{F}_1 - \nabla \biggl[ \frac{w}{\rho_0} \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] \, .</math>

This precisely matches the righthand side of the linearized Euler equation derived and presented as equation (2.7) by Bonnor — see the reprinted equation, above.

Reconciliation

It is instructive to explicitly demonstrate that the linearized "Euler + Poisson" equation that we derived and highlighted in our brief summary subsection, above, namely,

<math> \frac{P_0}{\rho_0} \frac{dp}{dr_0} = (4x + p)g_0 + \omega^2 r_0 x \, , </math>

conveys the same physics as Bonnor's (1957) linearized Euler equation when applied to a spherically symmetric system, namely,

<math>\frac{\partial v_r}{\partial t}</math>

<math>~ \hat{\mathbf{e}}_r \cdot \mathbf{F}_1 - \frac{d}{d r_0} \biggl[ \frac{w}{\rho_0} \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] \, .</math>

Step #1: We recognize that, after linearization, <math>~\partial v_r/\partial t = d^2 r/dt^2</math>. So, drawing on our earlier detailed handling of the "Euler + Poisson" equations, we can make the replacement,

<math> \frac{\partial v_r}{\partial t} </math>

<math> \rightarrow </math>

<math> - ~\omega^2 r_0 x~e^{i\omega t} \, . </math>

Step #2: As we have already recognized, swapping between our perturbation notation and Bonnor's leads to the replacement,

<math> w \biggl( \frac{dP}{d\rho} \biggr)_0 </math>

<math> \rightarrow </math>

<math> P_0 p e^{i\omega t} \, . </math>

Hence,

<math> \frac{d}{d r_0} \biggl[ \frac{w}{\rho_0} \biggl( \frac{dP}{d\rho} \biggr)_0 \biggr] </math>	<math> \rightarrow </math>	<math> \frac{d}{d r_0} \biggl[ \biggl( \frac{P_0 p}{\rho_0}\biggr) e^{i\omega t} \biggr] </math>
	<math>~=</math>	<math> e^{i\omega t} \biggl\{ \frac{p}{\rho_0} \frac{d P_0}{d r_0} + P_0 p \frac{d}{d r_0} \biggl( \frac{1}{\rho_0}\biggr) + \frac{P_0}{\rho_0} \frac{d p}{d r_0} \biggr\} </math>
	<math>~=</math>	<math> e^{i\omega t} \biggl\{ \biggl[ \frac{1}{\rho_0} \frac{d P_0}{d r_0} \biggr] (p - d) + \frac{P_0}{\rho_0} \frac{d p}{d r_0} \biggr\} </math>
	<math>~=</math>	<math> e^{i\omega t} \biggl[ (d - p) g_0 + \frac{P_0}{\rho_0} \frac{d p}{d r_0} \biggr] \, . </math>

where we have, again, used the relationship,

<math>\nabla P_0 = \biggl( \frac{dP}{d\rho} \biggr)_0 \nabla \rho_0 = \biggl( \frac{P_0 p}{\rho_o d} \biggr) \nabla \rho_0 </math>

<math>~~~~\Rightarrow~~~~</math>

<math>~ \frac{d}{dr_0} \biggl( \frac{1}{\rho_0}\biggr) = - \frac{1}{\rho_0^2}\frac{d\rho_0}{dr_0} =- \biggl( \frac{d}{P_0 p} \biggr) \biggl[\frac{1}{\rho_0}\frac{dP_0}{dr_0} \biggr] \, .</math>

Step #3: Implementing these first two substitutions, Bonnor's linearized Euler equation becomes,

<math>- ~\omega^2 r_0 x</math>	<math>~=</math>	<math>~ e^{-i\omega t}\hat{\mathbf{e}}_r \cdot \mathbf{F}_1 - \biggl[ (d - p) g_0 + \frac{P_0}{\rho_0} \frac{d p}{d r_0} \biggr] </math>
<math>\Rightarrow ~~~~ \frac{P_0}{\rho_0} \frac{d p}{d r_0} </math>	<math>~=</math>	<math>~ e^{-i\omega t}\hat{\mathbf{e}}_r \cdot \mathbf{F}_1 + (p - d) g_0 + \omega^2 r_0 x\, .</math>

Step #4: In order to map Bonnor's <math>~\mathbf{F}_1</math> to our perturbation notation, we back up to expressions for the gravitational acceleration, as a whole, which establish that, for spherically symmetric systems,

<math>~\hat{\mathbf{e}}_r \cdot \mathbf{F}</math>	<math>~=</math>	<math>~-~\frac{Gm}{r^2}</math>
<math>~\Rightarrow~~~\hat{\mathbf{e}}_r \cdot \biggl[ \mathbf{F}_0 + \mathbf{F}_1 \biggr]</math>	<math>~=</math>	<math>~-~\frac{Gm}{r^2}</math>

Dimensionless Expression

Let's write this governing, 2nd-order ODE and the key physical variables as dimensionless expressions. First, multiply through by <math>~R^2</math> and define the dimensionless radius as,

<math> \chi_0 \equiv \frac{r_0}{R} </math>

to obtain,

<math> \frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0} - \biggl(\frac{R g_0 \rho_0}{P_0}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{R^2 \rho_0}{\gamma_\mathrm{g} P_0} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{R \chi_0} \biggr] x = 0 . </math>

Now normalize <math>~P_0</math> to <math>~P_c</math> and <math>~\rho_0</math> to <math>~\rho_c</math> to obtain,

<math> \frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0} - \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_c}{P_0}\biggr) \biggl(\frac{R g_0 \rho_c}{P_c}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_c}{P_0}\biggr) \biggl(\frac{R^2 \rho_c}{\gamma_\mathrm{g} P_c} \biggr)\biggl[\omega^2 + (4 - 3\gamma_\mathrm{g})\frac{g_0}{R \chi_0} \biggr] x = 0 \, . </math>

The characteristic time for dynamical oscillations in spherically symmetric configurations (SSC) appears to be,

<math> \tau_\mathrm{SSC} \equiv \biggl[ \frac{R^2 \rho_c}{P_c} \biggr]^{1/2} , </math>

and the characteristic gravitational acceleration appears to be,

<math> g_\mathrm{SSC} \equiv \frac{P_c}{R \rho_c} . </math>

So we can write,

<math> \frac{d^2x}{d\chi_0^2} + \biggl[\frac{4}{\chi_0} - \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_0}{P_c}\biggr)^{-1} \biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \biggr] \frac{dx}{d\chi_0} + \biggl(\frac{\rho_0}{\rho_c}\biggr) \biggl(\frac{P_0}{P_c}\biggr)^{-1} \biggl(\frac{1}{\gamma_\mathrm{g}} \biggr)\biggl[\tau_\mathrm{SSC}^2 \omega^2 + (4 - 3\gamma_\mathrm{g})\biggl(\frac{g_0}{g_\mathrm{SSC}}\biggr) \frac{1}{\chi_0} \biggr] x = 0 . </math>

This is the governing relation that we will use to analyze the stability against radial pulsations of spherically symmetric, self-gravitating configurations.

Complementary Approach

Looking back at the set of three, coupled, linearized equations — but using <math>~\Delta</math> to denote the density fluctuation, rather than <math>~d</math>, in order to avoid confusion with the differentiation operators,

Linearized
Equation of Continuity
<math> r_0 \frac{dx}{dr_0} = - 3 x - \Delta , </math>

Linearized
Euler + Poisson Equations
<math> \frac{P_0}{\rho_0} \frac{dp}{dr_0} = (4x + p)g_0 + \omega^2 r_0 x , </math>

Linearized
Adiabatic Form of the
First Law of Thermodynamics
<math> p = \gamma_\mathrm{g} \Delta \, , </math>

let's combine them into a 2^nd-order ODE that governs the eigenfunction of the density perturbation, <math>~\Delta</math>, rather than of the radial displacement, <math>~x</math>. We begin by using the second equation to obtain an expression for <math>~x</math>:

<math>~(4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] \, .</math>

From this, we determine that,

<math>~ (4g_0 + \omega^2 r_0)\frac{dx}{dr_0}</math>	<math>~=</math>	<math>~\frac{d}{dr_0} \biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] + (4g_0 + \omega^2 r_0)\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr]\frac{d}{dr_0}(4g_0 + \omega^2 r_0)^{-1} </math>
	<math>~=</math>	<math>~\frac{P_0}{\rho_0} \frac{d^2p}{dr_0^2} + \frac{dp}{dr_0} \cdot \frac{d}{dr_0} \biggl( \frac{P_0}{\rho_0} \biggr) -p \frac{dg_0}{dr_0} - g_0\frac{dp}{dr_0} - (4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] \biggl[ \omega^2 + 4\frac{dg_0}{dr_0}\biggr] </math>
	<math>~=</math>	<math>~\frac{P_0}{\rho_0} \frac{d^2p}{dr_0^2} + \frac{dp}{dr_0} \biggl\{ -g_0 + \frac{d}{dr_0} \biggl( \frac{P_0}{\rho_0} \biggr) - (4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \biggr] \biggl[ \omega^2 + 4\frac{dg_0}{dr_0}\biggr] \biggr\} + p \biggl\{ (4g_0 + \omega^2 r_0)^{-1}\biggl[ g_0 \biggr] \biggl[ \omega^2 + 4\frac{dg_0}{dr_0}\biggr] -\frac{dg_0}{dr_0} \biggr\} </math>

Next, we substitute this expression for <math>~x</math> into the first equation — gradually replacing <math>~p</math> with <math>~\gamma_g \Delta</math>, as well — and carry out the differentiation:

<math>~ -\Delta - 3\biggl\{(4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - \gamma_g \Delta g_0 \biggr] \biggr\} </math>	<math>~=</math>	<math>~r_0 \frac{d}{dr_0} \biggl\{(4g_0 + \omega^2 r_0)^{-1}\biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] \biggr\} </math>
<math>~ \Rightarrow~~- \Delta \biggl[ \frac{g_0}{r_0} (4 - 3\gamma_g)+ \omega^2 \biggr] - \frac{3P_0}{r_0 \rho_0} \frac{dp}{dr_0} </math>	<math>~=</math>	<math>~ \frac{d}{dr_0} \biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr] - (4g_0 + \omega^2 r_0)^{-1} \biggl[ \frac{P_0}{\rho_0} \frac{dp}{dr_0} - pg_0 \biggr]\frac{d}{dr_0} \biggl[(4g_0 + \omega^2 r_0) \biggr] </math>

User:Tohline/SSC/Perturbations

Contents

Spherically Symmetric Configurations (Stability — Part II)

Assembling the Key Relations

Governing Equations

Consistent Lagrangian Formulation

Supplemental Relations

Summary

The Eigenvalue Problem

Linearizing the Key Equations

Adiabatic form of the First Law of Thermodynamics

Continuity Equation

Euler + Poisson Equations

Summary

Classic Papers that Derive & Use this Relation

Eddington (1926)

Ledoux and Pekeris (1941)

Schwarzschild (1941)

Review Article by Christy (1966)

Review Article by Cox (1974)

Bonnor (1957)

Linearized Equations on a Static Background

Reconciliation

Dimensionless Expression

Complementary Approach

See Also

Navigation menu

Search