User:Tohline/SSC/FreeEnergy/PowerPoint

Supporting Derivations for Free-Energy PowerPoint Presentation

The derivations presented here are an extension of our accompanying free-energy synopsis. These additional details proved to be helpful while developing an overarching PowerPoint presentation.

General Free-Energy Expression

We're considering a free-energy function of the following form:

<math>~\mathfrak{G}^*_\mathrm{type}</math>

<math>~=</math>

<math>~-ax^{-1} + b x^{-3/n} + c x^{-3/j} + \mathfrak{G}_0 \, ,</math>

where,

<math>~x \equiv \frac{R}{R_0} \, .</math>

As we have shown, setting,

<math>~\frac{\partial \mathfrak{G}^*_\mathrm{type}}{\partial x}</math>

<math>~=</math>

<math>~0 \, ,</math>

generates a mathematical statement of virial equilibrium, namely,

<math>~\frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} + \frac{1}{j}\cdot x^{(j-3)/j}_\mathrm{eq} </math>

<math>~=</math>

<math>~ 0 \, .</math>

And equilibrium configurations for which the second (as well as first) derivative of the free energy is zero are found at "critical" radii given by the expression,

<math>~[x_\mathrm{eq}^{(j-3)/j}]_\mathrm{crit} </math>

<math>~=</math>

<math>~ \frac{a}{3^2c}\biggl[ \frac{j^2(n-3)}{n-j} \biggr] \, . </math>

Pressure-Truncated Polytropes

For pressure-truncated polytropes, set <math>~j=-1</math> and let <math>~n</math> be the chosen polytropic index. In this case, the statement of virial equilibrium is,

<math>~\frac{ b}{nc}\cdot x^{(n-3)/n }_\mathrm{eq} - \frac{a}{3c} - x^{4}_\mathrm{eq} </math>

<math>~=</math>

<math>~ 0 \, ;</math>

and the critical equilibrium configuration has,

<math>~[x_\mathrm{eq}]_\mathrm{crit} </math>

<math>~=</math>

<math>~ \biggl[ \frac{a(n-3)}{3^2c (n+1)}\biggr]^{1/4} \, . </math>

Case M

Set <math>~K</math> and <math>~M_\mathrm{tot}</math> constant and examine how the free-energy behaves as a function of the coordinates, <math>~(R,P_e)</math>. In this case (see, for example, here),

<math>~a</math>	<math>~\equiv</math>	<math>~\frac{3}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2}\, , </math>
<math>~b</math>	<math>~\equiv</math>	<math>~n\biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \, , </math>
<math>~c</math>	<math>~\equiv</math>	<math>~\frac{4\pi}{3}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, , </math>

where the structural form factors for pressure-truncated polytropes are precisely defined here. And (see, for example, here),

<math>~R_0 = R_\mathrm{norm}</math>	<math>~\equiv</math>	<math>~\biggl[ \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} \biggr]^{1/(n-3)} \, ,</math>
<math>~P_\mathrm{norm}</math>	<math>~\equiv</math>	<math>~\biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}} \biggr]^{1/(n-3)} \, .</math>

If we set all three structural form-factors to unity, we have,

<math>~\frac{a}{3c}</math>	<math>~=</math>	<math>~\frac{3}{2^2\cdot 5\pi}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \, ,</math>
<math>~\frac{b}{nc}</math>	<math>~=</math>	<math>~\biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} \, .</math>

Virial Equilibrium

Figure 1

So the statement of virial equilibrium becomes,

<math>~ x^{4}_\mathrm{eq} </math>	<math>~=</math>	<math>~\biggl[ \biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} x^{(n-3)/n }_\mathrm{eq} - \frac{3}{2^2\cdot 5\pi}\biggr]\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} </math>
	<math>~=</math>	<math>~\frac{3}{2^2\cdot 5\pi}\biggl[ 5\biggl(\frac{3}{4\pi} \biggr)^{1/n} x^{(n-3)/n }_\mathrm{eq} - 1\biggr]\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} </math>
<math>~ \Rightarrow ~~~ \frac{P_e}{P_\mathrm{norm}}</math>	<math>~=</math>	<math>~\frac{3}{2^2\cdot 5\pi x^{4}_\mathrm{eq} }\biggl[ 5\biggl(\frac{3}{4\pi} \biggr)^{1/n} x^{(n-3)/n }_\mathrm{eq} - 1\biggr] \, . </math>

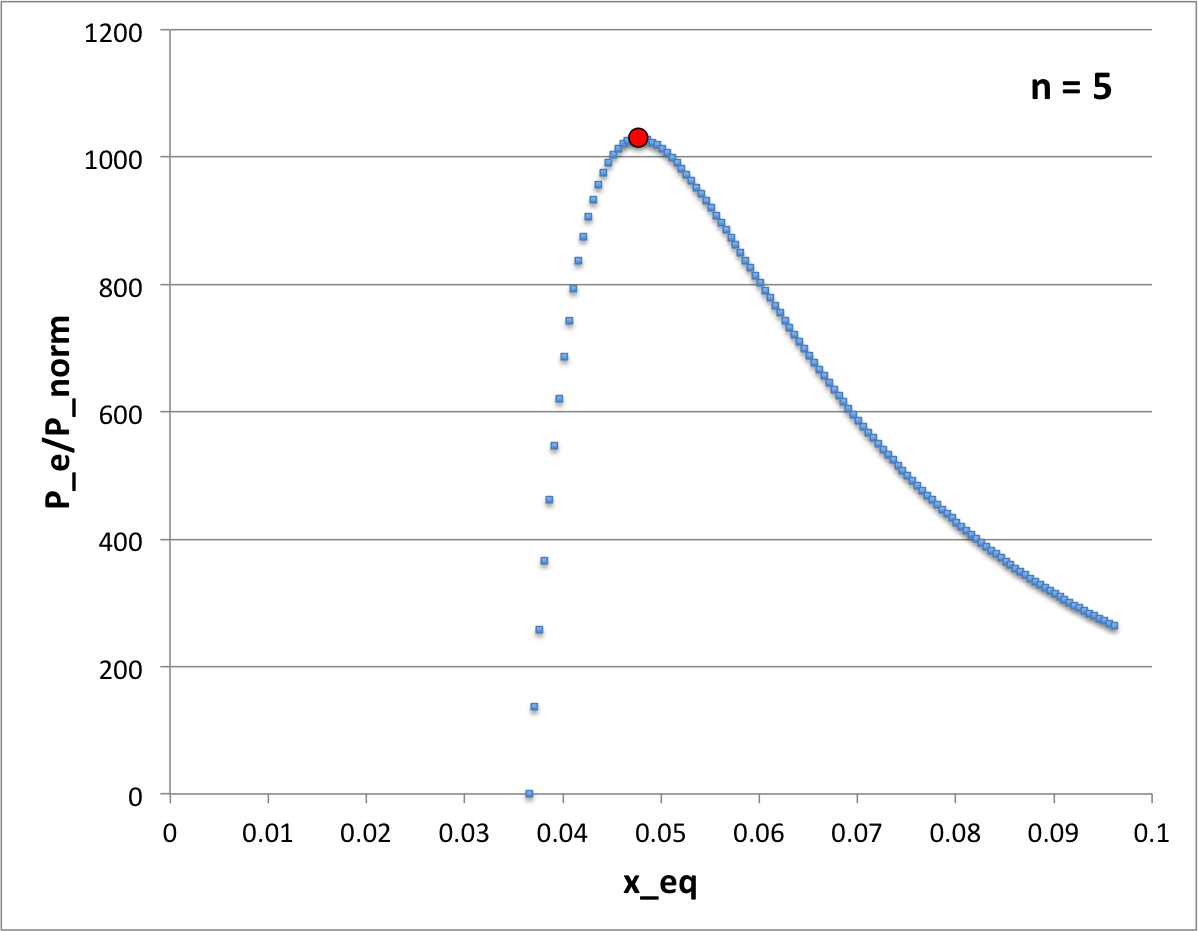
The light-blue dots in Figure 1 trace the equilibrium sequence that is defined by this virial equilibrium function in the case of <math>~n = 5</math>.

Dynamical Instability

Along the "Case M" equilibrium sequence, the transition from stable to unstable configurations occurs at,

<math>~[x_\mathrm{eq}]^4_\mathrm{crit} </math>	<math>~=</math>	<math>~ \biggl[ \frac{(n-3)}{3(n+1)}\biggr] \frac{3}{2^2\cdot 5\pi}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)^{-1} </math>
<math>~\Rightarrow ~~~ \frac{2^2\cdot 5\pi}{3}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)[x_\mathrm{eq}]^4_\mathrm{crit} </math>	<math>~=</math>	<math>~ \biggl[ \frac{(n-3)}{3(n+1)}\biggr] </math>

which, in combination with the virial equilibrium condition gives,

<math>~5\biggl(\frac{3}{4\pi} \biggr)^{1/n} [x_\mathrm{eq}]^{(n-3)/n }_\mathrm{crit} -1</math>	<math>~=</math>	<math>~ \biggl[ \frac{(n-3)}{3(n+1)}\biggr] </math>
<math>~\Rightarrow~~~ [x_\mathrm{eq}]_\mathrm{crit} </math>	<math>~=</math>	<math>~\biggl[ \frac{4n}{3\cdot 5(n+1)} \biggl(\frac{4\pi}{3} \biggr)^{1/n}\biggr]^{n/(n-3)} \, . </math>

The location of this critical configuration along the <math>~n=5</math> equilibrium sequence is marked by the red circular dot in Figure 1.

Turning Point

Let's examine the curvature of the equilibrium sequence.

<math>~ \frac{d}{dx}\biggl( \frac{P_e}{P_\mathrm{norm}} \biggr)</math>	<math>~=</math>	<math>~ - \frac{3}{ 5\pi x^{5} }\biggl[ 5\biggl(\frac{3}{4\pi} \biggr)^{1/n} x^{(n-3)/n } - 1\biggr] + \frac{3(n-3)}{2^2n \pi x^{4} }\biggl(\frac{3}{4\pi} \biggr)^{1/n} x^{-3/n } </math>
	<math>~=</math>	<math>~\frac{3}{ 5\pi x^{5} } + \frac{3}{4\pi}\biggl(\frac{3}{4\pi} \biggr)^{1/n} \biggl[ \frac{(n-3)}{n } - 4\biggr] \frac{x^{(n-3)/n } }{x^5} </math>
	<math>~=</math>	<math>~\frac{3}{ 5\pi x^{5} } - 3\biggl(\frac{3}{4\pi} \biggr)^{(n+1)/n} \biggl[ \frac{n+1}{n } \biggr] \frac{x^{(n-3)/n } }{x^5} \, . </math>

Setting this derivative to zero let's us identify the location of the turning point that identifies <math>~P_\mathrm{max}.</math>

<math>~ [ x_\mathrm{eq}^{(n-3)/n } ]_\mathrm{turn} </math>	<math>~=</math>	<math>~ \frac{1}{ 5\pi }\biggl[ \frac{n }{n+1} \biggr] \biggl(\frac{4\pi}{3} \biggr)^{(n+1)/n} </math>
<math>~\Rightarrow~~~ [ x_\mathrm{eq} ]_\mathrm{turn} </math>	<math>~=</math>	<math>~ \biggl[ \frac{4n}{ 15(n+1)}\biggl(\frac{4\pi}{3} \biggr)^{1/n} \biggr]^{n/(n-3)} \, . </math>

And, returning to the virial equilibrium expression, we find that, associated with this equilibrium radius,

<math>~ \frac{P_\mathrm{max}}{P_\mathrm{norm}}</math>	<math>~=</math>	<math>~\frac{3}{2^2\cdot 5\pi x^{4}_\mathrm{turn} }\biggl[ 5\biggl(\frac{3}{4\pi} \biggr)^{1/n} x^{(n-3)/n }_\mathrm{turn} - 1\biggr] </math>
<math>~ \Rightarrow ~~~2^2\cdot 5\pi x^{4}_\mathrm{turn} \biggl(\frac{P_\mathrm{max}}{P_\mathrm{norm}}\biggr)</math>	<math>~=</math>	<math>~15\biggl(\frac{3}{4\pi} \biggr)^{1/n} \biggl[ \frac{4n}{ 15(n+1)}\biggl(\frac{4\pi}{3} \biggr)^{1/n} \biggr] - 3 </math>
	<math>~=</math>	<math>~\biggl(\frac{n-3}{ n+1} \biggr) </math>
<math>~ \Rightarrow ~~~\frac{P_\mathrm{max}}{P_\mathrm{norm}}</math>	<math>~=</math>	<math>~\frac{1}{20\pi}\biggl(\frac{n-3}{ n+1} \biggr) \biggl[ \frac{ 15(n+1)}{4n}\biggl(\frac{3}{4\pi} \biggr)^{1/n} \biggr]^{4n/(n-3)} \, .</math>

Notice that, under the assumption that all three structural filling-factors are unity, <math>~[x_\mathrm{eq}]_\mathrm{turn} = [x_\mathrm{eq}]_\mathrm{crit}</math>, that is, the location of the turning point coincides precisely with the point along the equilibrium sequence where the transition from stable to unstable equilibrium configurations occurs (marked by the red circular dot in Figure 1).

Case M Summary

Case M
Order-of-Magnitude Analysis: Assume <math>~{\tilde\mathfrak{f}}_M = {\tilde\mathfrak{f}}_W = {\tilde\mathfrak{f}}_A = 1</math>
Virial Equilibrium:	<math>~ \frac{P_e}{P_\mathrm{norm}}</math> <math>~=</math> <math>~\frac{3}{2^2\cdot 5\pi }\biggl(\frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr)^{-4} \biggl[ 5\biggl(\frac{3}{4\pi} \biggr)^{1/n} \biggl(\frac{R_\mathrm{eq}}{R_\mathrm{norm}}\biggr)^{(n-3)/n }_\mathrm{eq} - 1\biggr] </math>
Dynamical Instability: <math>~(n>3)</math>	<math>~\frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr|_\mathrm{crit}</math> <math>~=</math> <math>~\biggl[ \frac{4n}{3\cdot 5(n+1)} \biggl(\frac{4\pi}{3} \biggr)^{1/n}\biggr]^{n/(n-3)} </math>
Turning Point <math>~(P_\mathrm{max} )</math>: <math>~(n>3)</math>	<math>~\frac{P_\mathrm{max}}{P_\mathrm{norm}}</math> <math>~=</math> <math>~\frac{1}{20\pi}\biggl(\frac{n-3}{ n+1} \biggr) \biggl[ \frac{ 15(n+1)}{4n}\biggl(\frac{3}{4\pi} \biggr)^{1/n} \biggr]^{4n/(n-3)} </math> <math>~ \frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr|_\mathrm{turn} </math> <math>~=</math> <math>~ \biggl[ \frac{4n}{ 3\cdot 5(n+1)}\biggl(\frac{4\pi}{3} \biggr)^{1/n} \biggr]^{n/(n-3)} </math>

Case P

Set <math>~K</math> and <math>~P_e</math> constant and examine how the free-energy behaves as a function of the coordinates, <math>~(R,M_\mathrm{tot})</math>. In this case (see, for example, here),

<math>~a</math>	<math>~=</math>	<math>~\frac{3}{5} \cdot \frac{\tilde{\mathfrak{f}}_W}{\tilde{\mathfrak{f}}_M^2} \biggl( \frac{n+1}{n} \biggr)^{n/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{(n-1)/(n-3)} \, , </math>
<math>~b</math>	<math>~=</math>	<math>~n\biggl(\frac{4\pi}{3} \biggr)^{-1/n} \frac{\tilde{\mathfrak{f}}_A}{\tilde{\mathfrak{f}}_M^{(n+1)/n}} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{3(n-1)/[n(n-3)]} \, , </math>
<math>~c</math>	<math>~=</math>	<math>~\frac{4\pi}{3} \biggl( \frac{n+1}{n} \biggr)^{3/(n-3)} \biggl( \frac{M_\mathrm{tot} }{M_\mathrm{SWS}} \biggr)^{(5-n)/(n-3)} \, , </math>
<math>~R_0 = R_\mathrm{SWS} </math>	<math>~\equiv</math>	<math>~\biggl( \frac{n+1}{n} \biggr)^{1/2} G^{-1/2} K_n^{n/(n+1)} P_\mathrm{e}^{(1-n)/[2(n+1)]} \, ,</math>
<math>~M_\mathrm{SWS} </math>	<math>~\equiv</math>	<math>~ \biggl( \frac{n+1}{n} \biggr)^{3/2} G^{-3/2} K_n^{2n/(n+1)} P_\mathrm{e}^{(3-n)/[2(n+1)]} \, .</math>

where the structural form factors for pressure-truncated polytropes are precisely defined here. If we set all three structural form-factors to unity, we have,

<math>~\frac{a}{3c}</math>	<math>~=</math>	<math>~ \frac{3}{20\pi} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} </math>
<math>~\frac{b}{nc}</math>	<math>~=</math>	<math>~ \biggl[ \biggl(\frac{3}{4\pi} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)\biggr]^{(n+1)/n} </math>

Virial Equilibrium

So, the statement of virial equilibrium becomes,

<math>~\biggl[ \biggl(\frac{3}{4\pi} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)\biggr]^{(n+1)/n} x^{(n-3)/n }_\mathrm{eq} - \frac{3}{20\pi} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} - x^{4}_\mathrm{eq} </math>

<math>~=</math>

<math>~ 0 \, .</math>

<math>~\xi_1</math>

Known Analytic Lane-Emden Functions
<math>~n</math>	<math>~\theta_n(\xi)</math>	<math>~-\theta^'_n</math>	<math>~\xi_1</math>
<math>~0</math>	<math>~1-\frac{\xi^2}{6}</math>	<math>~\frac{\xi}{3}</math>	<math>~\sqrt{6}</math>
<math>~1</math>	<math>~\frac{\sin\xi}{\xi}</math>	<math>~\frac{\sin\xi}{\xi^2} - \frac{\cos\xi}{\xi}</math>	<math>~\pi</math>
<math>~5</math>	<math>~\biggl[ 1 + \frac{\xi^2}{3} \biggr]^{-1/ 2}</math>	<math>~\frac{\xi}{3}\biggl[ 1 + \frac{\xi^2}{3} \biggr]^{-3/ 2} </math>	<math>~\infty</math>

Dynamical Instability

Along the "Case P" equilibrium sequence, the transition from stable to unstable configurations occurs at,

<math>~[x_\mathrm{eq}]^4_\mathrm{crit} </math>	<math>~=</math>	<math>~ \frac{(n-3)}{3(n+1)} \biggl[ \frac{3}{20\pi} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} \biggr] </math>
	<math>~=</math>	<math>~ \frac{(n-3)}{20\pi n} \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} = \frac{2^2\pi (n-3)}{3^2\cdot 5 n} \biggl[\frac{3}{4\pi}\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)\biggr]^{2} \, , </math>

which, in combination with the "Case P" virial equilibrium expression gives,

<math>~ 0</math>	<math>~=</math>	<math>~\biggl\{ \biggl[ \frac{3^2\cdot 5 n}{2^2\pi (n-3)} \biggr]^{1/2} x_\mathrm{crit}^2 \biggr\}^{(n+1)/n} x^{(n-3)/n }_\mathrm{crit} - \frac{3}{20\pi} \biggl( \frac{n+1}{n} \biggr) \biggl\{ \biggl[\frac{20\pi n}{(n-3)}\biggr] x^4_\mathrm{crit} \biggr\} - x^{4}_\mathrm{crit} </math>
	<math>~=</math>	<math>~\biggl[ \frac{3^2\cdot 5 n}{2^2\pi (n-3)} \biggr]^{(n+1)/(2n)} x^{(3n-1)/n }_\mathrm{crit} - x^4_\mathrm{crit} \biggl\{ \biggl[\frac{3(n+1)}{(n-3)}\biggr] +1 \biggr\} </math>
	<math>~=</math>	<math>~\biggl[ \frac{3^2\cdot 5 n}{2^2\pi (n-3)} \biggr]^{(n+1)/(2n)} x^{(3n-1)/n }_\mathrm{crit} - \biggl[\frac{4n}{(n-3)}\biggr] x^4_\mathrm{crit} </math>
<math>~\Rightarrow~~~ x^{(n+1)/n}_\mathrm{crit} </math>	<math>~=</math>	<math>~\biggl[\frac{(n-3)}{4n}\biggr] \biggl[ \frac{3^2\cdot 5 n}{2^2\pi (n-3)} \biggr]^{(n+1)/(2n)} </math>

Turning Points

Let's simplify the notation, defining,

<math>~m \equiv \frac{3}{4\pi}\biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr) \, .</math>

The statement of virial equilibrium becomes,

<math>~m^{(n+1)/n} x^{(n-3)/n } - c_0m^2 - x^{4} </math>

<math>~=</math>

<math>~ 0 \, ,</math>

where,

<math>~c_0 \equiv \biggl[ \frac{4\pi(n+1)}{15n} \biggr] \, .</math>

Differentiating gives,

<math>~ 0 </math>	<math>~=</math>	<math>~\biggl(\frac{n+1}{n}\biggr)m^{1/n} x^{(n-3)/n } dm + \biggl(\frac{n-3}{n}\biggr)m^{(n+1)/n} x^{-3/n } dx - 2c_0m dm - 4x^{3} dx </math>
	<math>~=</math>	<math>~\biggl[ (n+1)m^{1/n} x^{(n-3)/n } - 2c_0 n m \biggr] dm + \biggl[ (n-3) m^{(n+1)/n} x^{-3/n } - 4nx^{3} \biggr] dx </math>
<math>~\Rightarrow ~~~\frac{dm}{dx}</math>	<math>~=</math>	<math>~ \frac{4nx^{3} - (n-3) m^{(n+1)/n} x^{-3/n } }{(n+1)m^{1/n} x^{(n-3)/n } - 2c_0 n m} \, . </math>

---

One turning point occurs where the numerator is zero, that is,

<math>~4nx^{3}</math>	<math>~=</math>	<math>~(n-3) m^{(n+1)/n} x^{-3/n } </math>
<math>~\Rightarrow ~~~ 4nx^{3(n+1)/n}</math>	<math>~=</math>	<math>~(n-3) m^{(n+1)/n} </math>
<math>~\Rightarrow ~~~ \frac{m}{x^3}</math>	<math>~=</math>	<math>~\biggl[\frac{4n}{(n-3)}\biggr]^{n/(n+1)} \, .</math>

Plugging this into the virial equilibrium expression gives,

<math>~ 0</math>	<math>~=</math>	<math>~\biggl\{ \biggl[\frac{4n}{(n-3)}\biggr]^{n/(n+1)} x^3 \biggr\}^{(n+1)/n} x^{(n-3)/n } - c_0\biggl\{ \biggl[\frac{4n}{(n-3)}\biggr]^{n/(n+1)} x^3 \biggr\}^2 - x^{4} </math>
	<math>~=</math>	<math>~\biggl[\frac{4n}{(n-3)}\biggr] x^4 - c_0 \biggl[\frac{4n}{(n-3)}\biggr]^{2n/(n+1)} x^6 - x^{4} </math>
<math>~\Rightarrow~~~ c_0 \biggl[\frac{4n}{(n-3)}\biggr]^{2n/(n+1)} x^2 </math>	<math>~=</math>	<math>~\biggl[\frac{4n}{(n-3)}\biggr] - 1 </math>
<math>~\Rightarrow~~~ x^2 </math>	<math>~=</math>	<math>~\biggl[ \frac{15n}{4\pi(n+1)} \biggr]\biggl[\frac{3(n+1)}{(n-3)}\biggr] \biggl[\frac{(n-3)}{4n}\biggr]^{2n/(n+1)} </math>
	<math>~=</math>	<math>~\biggl[ \frac{3^2\cdot 5 n}{4\pi(n-3)} \biggr]\biggl[\frac{(n-3)}{4n}\biggr]^{2n/(n+1)} \, .</math>

The associated mass is,

<math>\biggl( \frac{M_\mathrm{max}}{M_\mathrm{SWS}}\biggr) = \biggl(\frac{4\pi}{3} \biggr)m</math>	<math>~=</math>	<math>~ \frac{4\pi}{3} \biggl[\frac{n-3}{4n}\biggr]^{-n/(n+1)} \biggl[ \frac{3^2\cdot 5 n}{4\pi(n-3)} \biggr]^{3/2}\biggl[\frac{(n-3)}{4n}\biggr]^{3n/(n+1)} </math>
	<math>~=</math>	<math>~ \frac{4\pi}{3} \biggl[\frac{n-3}{4n}\biggr]^{2n/(n+1)} \biggl[ \frac{3^2\cdot 5 n}{4\pi(n-3)} \biggr]^{3/2} \, .</math>

Notice that, for <math>~n=3</math>,

<math>\biggl( \frac{M_\mathrm{max}}{M_\mathrm{SWS}}\biggr)_{n=3}</math>

<math>~=</math>

<math>~ \biggl[\frac{3^4\cdot 5^3 }{2^{8} \pi} \biggr]^{1/2} \, .</math>

---

Another turning point occurs where the denominator is zero, that is,

<math>~(n+1)m^{1/n} x^{(n-3)/n } </math>	<math>~=</math>	<math>~2c_0 n m</math>
<math>~\Rightarrow ~~~ (n+1)x^{(n-3)/n } </math>	<math>~=</math>	<math>~2c_0 n m^{(n-1)/n}</math>
<math>~\Rightarrow ~~~ \frac{x^{n-3}}{ m^{n-1}} </math>	<math>~=</math>	<math>~\biggl[ \frac{2c_0 n}{(n+1)} \biggr]^n</math>
	<math>~=</math>	<math>~\biggl[ \frac{8\pi}{15} \biggr]^n</math>
<math>~\Rightarrow~~~ m</math>	<math>~=</math>	<math>~\biggl[ x^{(n-3)/(n-1)} \biggl( \frac{15}{8\pi} \biggr)^{n/(n-1)}\biggr] \, .</math>

Plugging this into the virial equilibrium expression gives,

<math>~ x^{4} </math>	<math>~=</math>	<math>~\biggl[ x^{(n-3)/(n-1)} \biggl( \frac{15}{8\pi} \biggr)^{n/(n-1)}\biggr]^{(n+1)/n} x^{(n-3)/n } - c_0\biggl[ x^{(n-3)/(n-1)} \biggl( \frac{15}{8\pi} \biggr)^{n/(n-1)}\biggr]^2 </math>
	<math>~=</math>	<math>~\biggl( \frac{15}{8\pi} \biggr)^{(n+1)/(n-1)} x^{(n-3)(n+1)/[n(n-1)]} \cdot x^{(n-3)/n } - c_0 \biggl( \frac{15}{8\pi} \biggr)^{2n/(n-1)} x^{2(n-3)/(n-1)} </math>
	<math>~=</math>	<math>~\biggl( \frac{15}{8\pi} \biggr)^{(n+1)/(n-1)} x^{2(n-3)/(n-1)} - \biggl[ \frac{(n+1)}{2n} \biggr]\biggl( \frac{15}{8\pi} \biggr)^{(n+1)/(n-1)} x^{2(n-3)/(n-1)} </math>
	<math>~=</math>	<math>~\biggl( \frac{15}{8\pi} \biggr)^{(n+1)/(n-1)} x^{2(n-3)/(n-1)} \biggl[1 - \frac{(n+1)}{2n} \biggr] </math>
<math>~\Rightarrow~~~ x^{2(n+1)/(n-1)}</math>	<math>~=</math>	<math>~ \frac{(n-1)}{2n} \biggl( \frac{15}{8\pi} \biggr)^{(n+1)/(n-1)} </math>
<math>~\Rightarrow~~~ \frac{R_\mathrm{max}}{R_\mathrm{SWS}}</math>	<math>~=</math>	<math>~ \biggl[\frac{(n-1)}{2n} \biggr]^{(n-1)/[2(n+1)]} \biggl( \frac{15}{8\pi} \biggr)^{1/2} \, .</math>

And the associated mass is,

<math>~\frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr|_\mathrm{turn}</math>	<math>~=</math>	<math>~\frac{4\pi}{3}\biggl( \frac{15}{8\pi} \biggr)^{n/(n-1)} \biggl\{ \biggl[\frac{(n-1)}{2n} \biggr]^{(n-1)/[2(n+1)]} \biggl( \frac{15}{8\pi} \biggr)^{1/2} \biggr\}^{(n-3)/(n-1)} </math>
	<math>~=</math>	<math>~\frac{4\pi}{3}\biggl( \frac{15}{8\pi} \biggr)^{3/2} \biggl[\frac{(n-1)}{2n} \biggr]^{(n-3)/[2(n+1)]} \, .</math>

Case P Summary

Case P
Order-of-Magnitude Analysis: Assume <math>~{\tilde\mathfrak{f}}_M = {\tilde\mathfrak{f}}_W = {\tilde\mathfrak{f}}_A = 1</math>
Virial Equilibrium:	<math>~\biggl[ \biggl(\frac{3}{4\pi} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)\biggr]^{(n+1)/n} \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^{(n-3)/n } - \frac{3}{20\pi} \biggl( \frac{n+1}{n} \biggr) \biggl( \frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr)^{2} - \biggl( \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr)^{4} </math> <math>~=</math> <math>~ 0 </math>
Dynamical Instability: <math>~(n > 3)</math>	<math>~\frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr|_\mathrm{crit}</math> <math>~=</math> <math>~\biggl[\frac{(n-3)}{4n}\biggr]^{n/(n+1)} \biggl[ \frac{3^2\cdot 5 n}{2^2\pi (n-3)} \biggr]^{1/2} </math>
Turning Point <math>~(M_\mathrm{max} )</math>: <math>~(n>3)</math>	<math>\frac{M_\mathrm{max}}{M_\mathrm{SWS}}</math> <math>~=</math> <math>~ \frac{4\pi}{3} \biggl[\frac{n-3}{4n}\biggr]^{2n/(n+1)} \biggl[ \frac{3^2\cdot 5 n}{4\pi(n-3)} \biggr]^{3/2} </math> <math>~ \frac{R_\mathrm{eq}}{R_\mathrm{SWS}} \biggr|_\mathrm{turn} </math> <math>~=</math> <math>~ \biggl[\frac{(n-3)}{4n}\biggr]^{n/(n+1)} \biggl[ \frac{3^2\cdot 5 n}{2^2\pi(n-3)} \biggr]^{1/2} </math>
Turning Point <math>~(R_\mathrm{max} )</math>: <math>~(n>1)</math>	<math>~ \frac{R_\mathrm{max}}{R_\mathrm{SWS}}</math> <math>~=</math> <math>~ \biggl[\frac{(n-1)}{2n} \biggr]^{(n-1)/[2(n+1)]} \biggl( \frac{15}{8\pi} \biggr)^{1/2} </math> <math>~\frac{M_\mathrm{tot}}{M_\mathrm{SWS}}\biggr|_\mathrm{turn}</math> <math>~=</math> <math>~\frac{4\pi}{3}\biggl( \frac{15}{8\pi} \biggr)^{3/2} \biggl[\frac{(n-1)}{2n} \biggr]^{(n-3)/[2(n+1)]} </math>

Figure 2

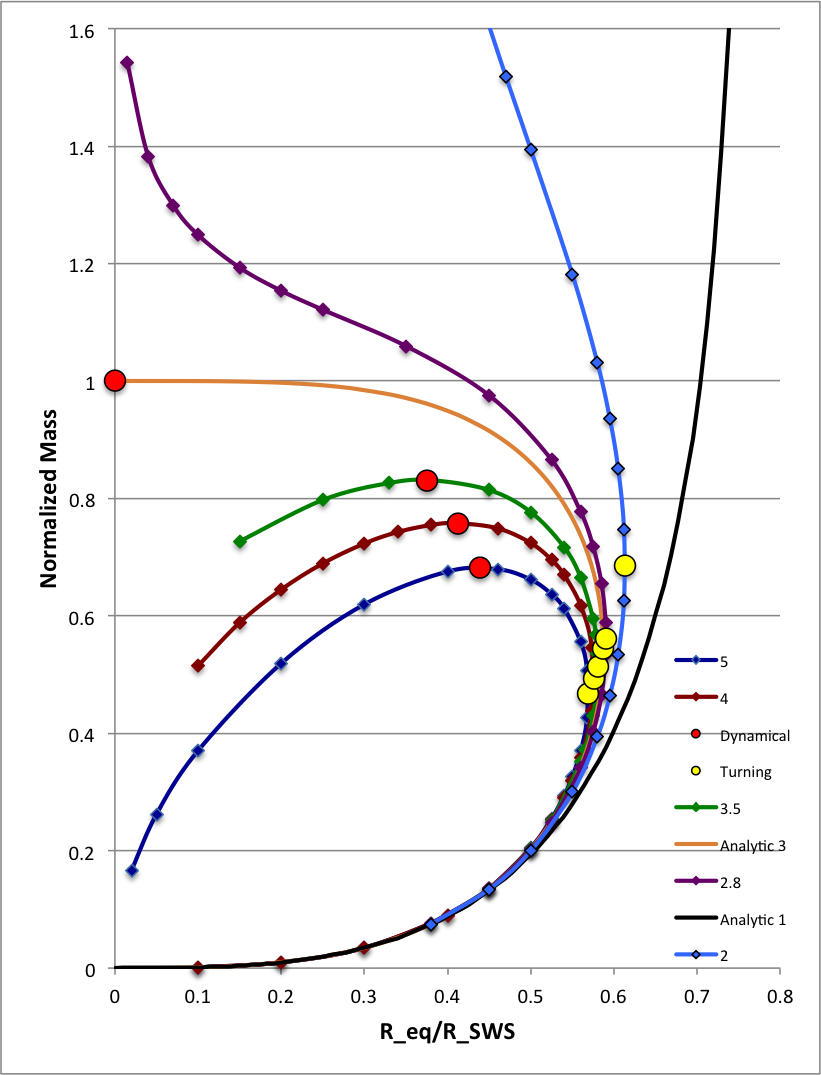
The right-hand panel of Figure 2 presents substantial segments of Case P virial equilibrium sequences for a range of polytropic indexes (n = 1, 2, 2.8, 3, 3.5, 4, 5). For each sequence, the location of the <math>~R_\mathrm{max}</math> and <math>~M_\mathrm{max}</math> turning points — if they exist — are denoted by a yellow or red circular dot, respectively. The point along each <math>~(n \geq 3)</math> sequence at which the transition from dynamically stable to dynamically unstable structures occurs coincides with the location of <math>~M_\mathrm{max}</math> (i.e., with the red circular dot).

For display purposes, all normalized masses <math>~(M_\mathrm{tot}/M_\mathrm{SWS})</math> have been further normalized to the maximum mass on the n = 3 sequence.

Detailed Force-Balance Models

Structural Form Factors

The following table of structural form factors has been drawn from here,

Structural Form Factors for Isolated Polytropes

Structural Form Factors for Pressure-Truncated Polytropes

<math>~\mathfrak{f}_M</math> <math>~=</math> <math>~ \biggl[ - \frac{3\theta^'}{\xi} \biggr]_{\xi_1} </math> <math>\mathfrak{f}_W </math> <math>~=</math> <math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\theta^'}{\xi} \biggr]^2_{\xi_1} </math> <math>\mathfrak{f}_A </math> <math>~=</math> <math> \frac{3(n+1) }{(5-n)} ~\biggl[ \theta^' \biggr]^2_{\xi_1} </math>

<math>~\tilde\mathfrak{f}_M</math> <math>~=</math> <math>~ \biggl( - \frac{3\tilde\theta^'}{\tilde\xi} \biggr) </math> <math>\tilde\mathfrak{f}_W</math> <math>~=</math> <math>\frac{3\cdot 5}{(5-n)\tilde\xi^2} \biggl[\tilde\theta^{n+1} + 3 (\tilde\theta^')^2 - \tilde\mathfrak{f}_M \tilde\theta \biggr] </math> <math>~ \tilde\mathfrak{f}_A </math> <math>~=</math> <math>~\frac{1}{(5-n)} \biggl\{ 6\tilde\theta^{n+1} + (n+1) \biggl[3 (\tilde\theta^')^2 - \tilde\mathfrak{f}_M \tilde\theta \biggr] \biggr\} </math>

and here,

Structural Form Factors for Pressure-Truncated n = 5 Polytropes

<math>~\tilde\mathfrak{f}_M</math> <math>~=</math> <math>~ ( 1 + \ell^2 )^{-3/2} </math> <math>~\tilde\mathfrak{f}_W</math> <math>~=</math> <math>~ \frac{5}{2^4} \cdot \ell^{-5} \biggl[ \ell \biggl( \ell^4 - \frac{8}{3}\ell^2 - 1 \biggr)(1 + \ell^2)^{-3} + \tan^{-1}(\ell ) \biggr] </math> <math>~\tilde\mathfrak{f}_A</math> <math>~=</math> <math>~ \frac{3}{2^3} \ell^{-3} [ \tan^{-1}(\ell ) + \ell (\ell^2-1) (1+\ell^2)^{-2} ] </math> where,       <math>~\ell \equiv \frac{\tilde\xi}{\sqrt{3}}</math>

Equilibrium Conditions

Employing the renormalization factors,

<math>~\frac{R_\mathrm{Horedt}}{R_\mathrm{norm}}</math>	<math>~=</math>	<math>~\biggl[ \frac{4\pi}{(n+1)^n}\biggr]^{1/(n-1)} \, ,</math>
<math>~\frac{P_\mathrm{Horedt}}{P_\mathrm{norm}}</math>	<math>~=</math>	<math>~\biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{(n+1)/(n-1)} \, ,</math>

we find from detailed force-balance analyses that the equilibrium radius and corresponding external pressure for "Case M" configurations are,

<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{norm}} = \frac{R_\mathrm{eq}}{R_\mathrm{Horedt}} \cdot \frac{R_\mathrm{Horedt}}{R_\mathrm{norm}} </math>	<math>~=~</math>	<math>~\biggl[ \frac{4\pi}{(n+1)^n}\biggr]^{1/(n-1)} \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} \, , </math>
<math> ~\frac{P_\mathrm{e}}{P_\mathrm{norm}} = \frac{P_\mathrm{e}}{P_\mathrm{Horedt}} \cdot \frac{P_\mathrm{Horedt}}{P_\mathrm{norm}} </math>	<math>~=~</math>	<math>~\biggl[ \frac{(n+1)^3}{4\pi}\biggr]^{(n+1)/(n-1)} \tilde\theta_n^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \, , </math>

while the equilibrium radius and corresponding configuration mass from a "Case P" analysis are,

<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{SWS} } </math>	<math>~=~</math>	<math> \biggl( \frac{n}{4\pi} \biggr)^{1/2} \tilde\xi {\tilde\theta}_n^{(n-1)/2} \, , </math>
<math> ~\frac{M_\mathrm{tot}}{M_\mathrm{SWS} } </math>	<math>~=~</math>	<math> \biggl( \frac{n^3}{4\pi} \biggr)^{1/2} {\tilde\theta}_n^{(n-3)/2} (-\tilde\xi^2 \tilde\theta^') \, . </math>

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation