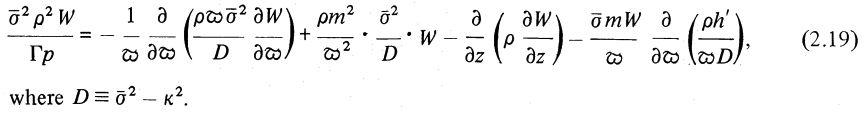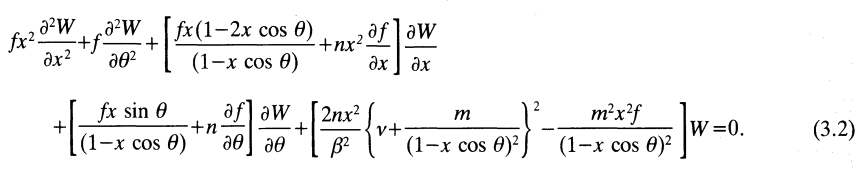Characteristics of Unstable Eigenvectors in Self-Gravitating Tori

In what follows, we will draw heavily from three publications: (1) J. E. Tohline & I. Hachisu (1990, ApJ, 361, 394-407) — hereafter, TH90 — (2) J. W. Woodward, J. E. Tohline, & I. Hachisu (1994, ApJ, 420, 247-267) — hereafter, WTH94 — and (3) K. Hadley & J. N. Imamura (2011, Astrophysics and Space Science, 334, 1) — hereafter, HI11.

Background

Imamura & Hadley Collaboration

Based especially on the analysis provided in Paper I and Paper II of the Imamura & Hadley collaboration, the eigenvectors that have drawn our attention thus far can be categorized as J-modes (as discussed, for example, in §3.2.1, Table 1 & Figure 2 of Paper II) or I-modes. Our initial attempts to construct fits to these eigenvectors empirically have been described in an separate chapter. We begin, here, a more quantitative analysis of the structure of these unstable eigenvectors by borrowing from a subsection of that chapter a table of equilibrium parameter values for the typical P- and E-mode models described in Table 2 of Paper II.

Table 1: P- and E-mode Model Parameters Highlighted in Paper II K. Z. Hadley, P. Fernandez, J. N. Imamura, E. Keever, R. Tumblin, & W. Dumas (2014, Astrophysics and Space Science, 353, 191-222)
Extracted from Table 2 or Table 4 of Paper II						Extracted from Fig. 3 or Fig. 4 of Paper II
Name	<math>~M_*/M_d</math>	<math>~(n, q)</math>^†	<math>~R_-/R_+</math>	<math>~r_\mathrm{outer} \equiv \frac{R_+}{R_\mathrm{max}}</math>	<math>~R_\mathrm{max}</math>	Eigenfunction
E1	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.101</math>	<math>~5.52</math>	<math>~0.00613</math>
E2	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.202</math>	<math>~2.99</math>	<math>~0.0229</math>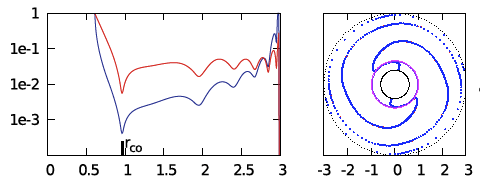
E3	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.402</math>	<math>~1.74</math>	<math>~0.159</math>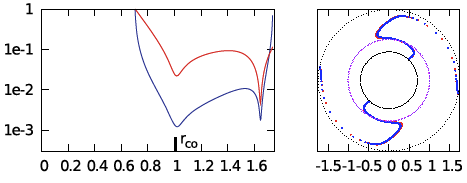
P1	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.452</math>	<math>~1.60</math>	<math>~0.254</math>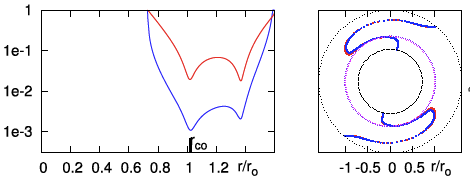
P2	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.500</math>	<math>~1.49</math>	<math>~0.403</math>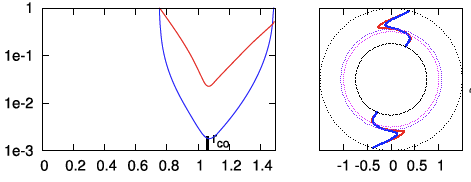
P3	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.600</math>	<math>~1.33</math>	<math>~1.09</math>
P4	<math>~100</math>	<math>~(\tfrac{3}{2}, 2)</math>	<math>~0.700</math>	<math>~1.21</math>	<math>~3.37</math>
^†In all three papers from the Imamura & Hadley collaboration, <math>~q = 2</math> means, "uniform specific angular momentum."

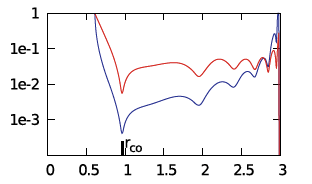
We ask, first, "Can we understand why the radial eigenfunction of, for example, model E2 — re-displayed here, on the right — exhibits a series of sharp dips whose spacing gets progressively smaller and smaller as the outer edge of the torus is approached?"

Radial Modes in Homogeneous Spheres

Before attempting to analyze natural modes of oscillation in a polytropic torus, it is useful to review what is known about radial oscillations in the geometrically simpler, uniform-density sphere. As we have reviewed in a separate chapter, Sterne (1937) was the first to recognize that the set of eigenvectors that describe radial modes of oscillation in a homogeneous, self-gravitating sphere can be determined analytically. In the present context, it is advantageous for us to pull Sterne's solution from a discussion of the same problem presented by Rosseland (1964). As we have summarized in a separate chapter, the relevant eigenvalue problem is defined by the following one-dimensional, 2^nd-order ODE:

<math>~ ( 1-\chi_0^2 ) \frac{\partial^2 \xi}{\partial \chi_0^2} + \frac{2}{\chi_0}\biggl[ 1 - 2\chi_0^2 \biggr] \frac{\partial \xi}{\partial \chi_0} + \biggl(4 - \frac{2}{\chi_0^2} \biggr) \xi</math>

<math>~ - \mathfrak{F} \xi \, , </math>

where, it is understood that the expression for the (spatially and temporally varying) radial location of each spherical shell is,

<math>~r(r_0,t) = r_0 + \delta r(r_0)e^{i\sigma t} \, ,</math>

and in the present context we are adopting the variable notation,

<math>~\chi_0</math>	<math>~\equiv</math>	<math>~\frac{r_0}{R} \, ,</math>
<math>~\xi</math>	<math>~\equiv</math>	<math>~\frac{\delta r}{R} \, ,</math>

and <math>~R</math> is the initial (unperturbed) radius of the sphere. Here, the eigenvalue is related to the physical properties of the homogeneous sphere via the relation,

<math>~\mathfrak{F} \equiv \frac{2}{\gamma_\mathrm{g}} \biggl[\biggl(\frac{3\sigma^2}{4\pi G\rho_0}\biggr) + (4 - 3\gamma_\mathrm{g}) \biggr] \, .</math>

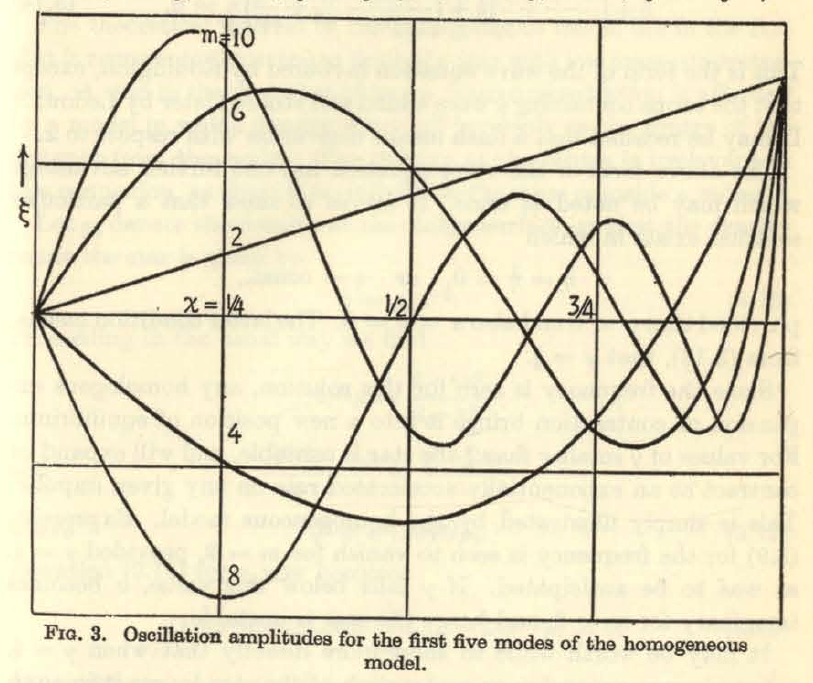
Drawing from Rosseland's (1964) presentation — see his p. 29, and our related discussion — the following table details the eigenvectors (radial eigenfunction and associated eigenfrequency) for the three lowest radial modes (m = 2, 4, 6) that satisfy this wave equation; the figure displayed in the right-most column has been extracted directly from p. 29 of Rosseland and shows the behavior of the lowest five radial modes (m = 2, 4, 6, 8, 10, as labeled) over the interval <math>~0 \le \chi_0 \le 1</math>.

Table 2 Rosseland's (1964) Eigenfunctions for Homogeneous Sphere Figure in the right-most column extracted from p. 29 of Rosseland (1964) "The Pulsation Theory of Variable Stars" (New York: Dover Publications, Inc.)
Mode	Eigenfunction	Square of Eigenfrequency: <math>~3\sigma^2/(4\pi G\rho)</math>
<math>~m</math>	As Published	<math>~\frac{m}{2}(m+1)\gamma - 4</math>
<math>~2</math>	<math>~\xi = -2\chi_0</math>	<math>~3\gamma - 4</math>
<math>~4</math>	<math>~\xi = -\frac{20}{3}\chi_0 + \frac{28}{3}\chi_0^3</math>	<math>~10\gamma-4</math>
<math>~6</math>	<math>~\xi = -14\chi_0 + \frac{252}{5} \chi_0^3 - \frac{198}{5} \chi_0^5</math>	<math>~21\gamma-4</math>

We should point out that, except for the lowest (m = 2) mode, each of the radial eigenfunctions crosses zero at least once at some location(s) that resides between the center <math>~(\chi_0=0)</math> of and the surface <math>~(\chi_0 = 1)</math> of the sphere. More specifically, for each mode, <math>~m</math>, the number of such radial "nodes" is <math>~(m-2)/2</math>. The locations of these nodes is apparent from even a casual inspection of the figure presented in the right-most column of Table 2.

When these radial modes of oscillation are discussed in the astrophysics literature, the conditions that give rise to a dynamical instability are often emphasized. Specifically, each mode becomes unstable when <math>~\sigma^2</math> becomes negative, which translates into a value of <math>~\gamma < \gamma_\mathrm{crit}(m)</math> — see our related discussion of the properties of eigenfunction solutions in the context of Sterne's (1937) analysis of this stability problem. Here we want to emphasize that all of natural modes of oscillation exist even when the configuration is dynamically stable.

Singular Sturm-Liouville Problem

As we have discussed in a separate chapter, there is a class of eigenvalue problems in the mathematical physics literature that is of the "Singular Sturm-Liouville" type. These problems are governed by a one-dimensional, 2^nd-order ODE of the form,

<math>~-(1-x)^{-\alpha}(1+x)^{-\beta} \cdot \frac{d}{dx} \biggl[ (1-x)^{\alpha+1}(1+x)^{\beta+1} \cdot \frac{d\Upsilon(x)}{dx} \biggr]</math>

<math>~ \lambda \Upsilon(x) \, , </math>

where the pair of exponent values, <math>~(\alpha, \beta) </math>, is set by the specific physical problem, while the eigenfunction, <math>~\Upsilon(x)</math>, and associated eigenfrequency, <math>~\lambda</math>, are to be determined. For any choice of the pair of exponents, there is an infinite number <math>~(j = 0 \rightarrow \infty)</math> of analytically known eigenvectors that satisfy this governing ODE; they are referred to as Jacobi Polynomials. Specifically, the j^th eigenfunction is,

<math>~\Upsilon_j(x) = J_j^{\alpha,\beta}(x)</math>

<math>~\equiv</math>

<math>~(1-x)^{-\alpha}(1+x)^{-\beta} \biggl\{ \frac{(-1)^j}{2^j j!} \cdot \frac{d^j}{dx^j}\biggl[ (1-x)^{j+\alpha}(1+x)^{j+\beta} \biggr] \biggr\} \, ;</math>

and the corresponding j^th eigenvalue is,

<math>~\lambda_j^{\alpha,\beta}</math>

<math>~j(j+\alpha+\beta + 1) \, .</math>

Table 3 presents the first three eigenfunctions (j = 0, 1, 2), along with each corresponding eigenfrequency; the figure displayed in the right-most column has been extracted directly from §22 (p. 773) of Abramowitz and Stegun's (1964) Handbook of Mathematical Functions (tenth printing, December 1972, with corrections) and shows the behavior of the lowest five Jacobi polynomials (j = 1, 2, 3, 4, 5, as labeled) over the interval <math>~-1 \le x \le +1</math> and for the specific case of <math>~(\alpha,\beta) = (1.5, - 0.5)</math>.

Table 3: Example Eigenvector Solutions to the Singular Sturm-Liouville Problem
<math>~j</math>	<math>~J_j^{\alpha,\beta}(x)</math>	<math>~\lambda_j^{\alpha,\beta}</math>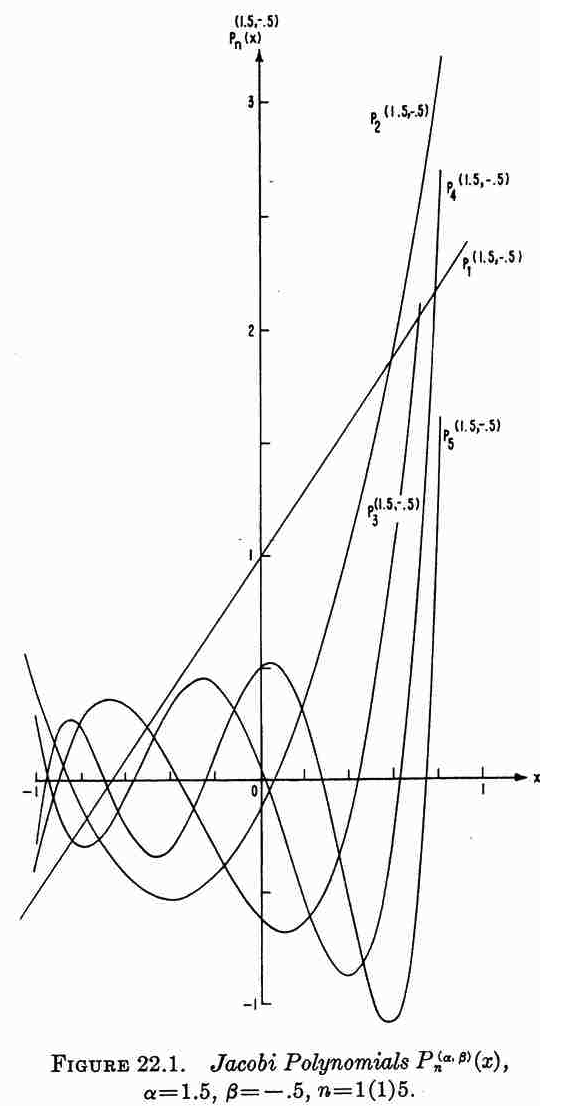
<math>~0</math>	<math>~1</math>	<math>~0</math>
<math>~1</math>	<math>~\tfrac{1}{2}(\alpha+\beta+2)x + \tfrac{1}{2}(\alpha-\beta)</math>	<math>~(\alpha+\beta+2)</math>
<math>~2</math>	<math>~ \tfrac{1}{8}(12+7\alpha + \alpha^2 + 7\beta+\beta^2+ 2\alpha\beta ) x^2 + \tfrac{1}{4}(3\alpha + \alpha^2 - 3\beta-\beta^2) x + \tfrac{1}{8}(-4 - \alpha + \alpha^2-\beta + \beta^2 - 2\alpha\beta) </math>	<math>~2(\alpha+\beta+3)</math>
See also, eqs. (35)-(37) of Wolfram MathWorld; and §22 (p. 773) of Abramowitz and Stegun's (1964) Handbook of Mathematical Functions, from which the illustration on the right has been extracted.

Here we highlight the qualitative similarities between the behavior of the set of Jacobi polynomials [figure extracted from Abramowitz and Stegun (1964) and reprinted here in Table 3] and the set of eigenfunctions that describe normal modes of oscillation in homogeneous, self-gravitating spheres [figure extracted from Rosseland (1964) and reprinted here in Table 2]. As we shall presently see, Jacobi polynomials play an important role in illuminating the structure of normal modes of oscillation in Papaloizou-Pringle tori.

Papaloizou-Pringle Tori

Here we briefly summarize the work (published by several groups in the mid-1980s) that has been done to determine the properties of both stable and unstable, nonaxisymmetric oscillation modes in Papaloizou-Pringle tori. In an accompanying chapter we explain in detail how the two-dimensional, 2^nd-order PDE that governs the behavior of these modes was derived by each research group.

Papaloizou & Pringle (1985)

Performing their linear stability analysis in cylindrical coordinates, Papaloizou & Pringle (1985) considered temporal and spatial variations in, for example, the pressure of the form,

<math>~p(\varpi,\varphi,z,t) = p_0(\varpi,z) + p^'(\varpi,z)e^{i(m\varphi + \sigma t)} \, .</math>

Rather than focusing on <math>~p^'</math>, however, they chose to build the governing PDE around an enthalpy-like perturbation defined as,

<math>~W(\varpi,z) = \frac{p^'}{\rho_0\bar\sigma} \, ,</math>

where, <math>~\bar\sigma \equiv (\sigma + m\Omega)</math>, and <math>~\Omega(\varpi)</math> is the fluid's circular orbital frequency in the initially axisymmetric, equilibrium torus. The governing PDE appears as equation (2.19) in Papaloizou & Pringle (1985); for convenience and clarity, that key equation has been extracted from their paper and displayed in the following framed image.

Equation (2.19) extracted without modification from p. 803 of Papaloizou & Pringle (1985)

"The dynamical stability of differentially rotating discs. II"

Monthly Notices of the Royal Astronomical Society, vol. 213, pp. 799-820 © Royal Astronomical Society

Papaloizou and Pringle (1985, MNRAS, 213, 799)

Note that, in this equation, <math>~\kappa(\varpi)</math> is the (radially dependent) epicyclic frequency in the torus, and <math>~h^'</math> is the radial derivative of the configuration's specific angular momentum. As has been realized by a number of groups — and as we have demonstrated in our accompanying detailed discussion — this governing PDE simplifies considerably when considering only PP tori that have uniform specific angular momentum because both <math>~\kappa^2</math> and <math>~h^'</math> are zero. Hence, also, <math>~D = \bar\sigma^2</math>. For such systems, the governing PDE is,

<math>~\frac{ {\bar\sigma}^2 \rho_0^2 W}{\Gamma p_0 } </math>

<math>~ - \frac{1}{\varpi} \frac{\partial}{\partial\varpi} \biggl[ \rho_0 \varpi \cdot \frac{\partial W}{\partial \varpi} \biggr] + \frac{\rho_0 m^2 W }{\varpi^2} - \frac{\partial}{\partial z} \biggl(\rho_0 \frac{\partial W}{\partial z} \biggr) \, . </math>

Fundamentally, this is the governing PDE that Blaes (1985) used in his examination of the stability of PP tori. But he chose to shift to dimensionless variables and to employ a different meridional-plane coordinate system in his analysis. In an accompanying discussion, we show step-by-step how this expression morphs into the governing PDE that serves as the focus of the Blaes85 analysis. In what follows, we provide a brief summary of this mathematical transformation.

Blaes (1985)

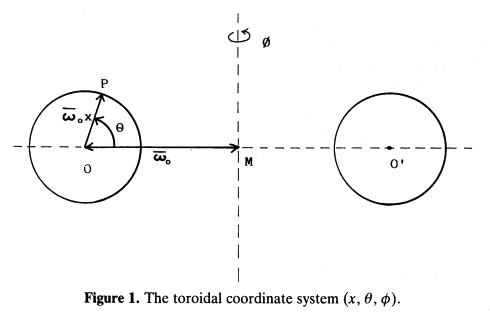
Fig. 1 extracted without modification from p. 554 of Blaes (1985)

"Oscillations of Slender Tori"

Monthly Notices of the Royal Astronomical Society,

As is illustrated in his Figure 1 — which we have reprinted for convenience here, on the right — Blaes (1985) shifted from cylindrical coordinates to a (dimensionless) polar-coordinate <math>~(x,\theta)</math> system whose origin sits at the pressure-maximum of the initial, unperturbed Papaloizou-Pringle torus, a distance, <math>~\varpi_0</math>, from the symmetry axis of the cylindrical coordinate system. Mapping between these two coordinate systems is accomplished via the relations,

<math>~x^2 = \biggl(1-\frac{\varpi}{\varpi_0}\biggr)^2 + \biggl(\frac{z}{\varpi_0}\biggr)^2</math>	and	<math>~\theta = \tan^{-1}\biggl[\frac{\zeta}{1-\chi}\biggr] \, ;</math>
or
<math>~\frac{\varpi}{\varpi_0} = 1 - x\cos\theta</math>	and	<math>~\frac{z}{\varpi_0} = x\sin\theta \, .</math>

Furthermore, he set <math>~\Gamma = (n+1)/n</math>, and rewrote the (initial, unperturbed) equilibrium pressure and density distributions in terms of the dimensionless enthalpy distribution in the PP torus, namely,

<math>~p_0 </math>	<math>~=</math>	<math>~p_\mathrm{max} f^{n+1}\, ,</math>
<math>~\rho_0 </math>	<math>~=</math>	<math>~\rho_\mathrm{max} f^{n}\, ,</math>

where, the two-dimensional dimensionless enthalpy distribution is,

<math>~f(x,\theta) </math>	<math>~=</math>	<math>~1 - \frac{x^2}{\beta^2}\biggl[ 1 + x(3\cos\theta -\cos^3\theta) \biggr] \, ,</math>
<math>~\beta^2</math>	<math>~\equiv</math>	<math>~\frac{2n}{\mathfrak{M}_0^2} \, ,</math>

and <math>~\mathfrak{M}_0</math> is the Mach number of the circular, azimuthal flow at the pressure and density maximum. Then he replaced the perturbation variable, <math>~W</math>, preferred by Papaloizou & Pringle (1985) with an equivalent but dimensionless perturbation variable,

<math>~\delta W</math>

<math>~\equiv \biggl[ \frac{\Omega_0 \rho_\mathrm{max}}{p_\mathrm{max}} \biggr]W \, ,</math>

where <math>~\Omega_0</math> is the angular frequency at the pressure and density maximum. [Actually, Blaes (1985) calls this dimensionless variable <math>~W</math>, rather than <math>~\delta W</math>, so care must be taken when published equations from these separate studies are compared.] After working carefully through these modifications — again, see our accompanying discussion for details — Blaes arrives at the governing PDE (his equation 3.2) that is highlighted in the following bordered box. Notice that, in this published expression, <math>~\nu \equiv \sigma/\Omega_0</math>, represents the azimuthal-mode eigenfrequency, normalized to the system's orbital frequency at the origin of the Blaes85 coordinate system.

Equation (3.2) extracted without modification from p. 558 of Blaes (1985)

"Oscillations of Slender Tori"

User:Tohline/Apps/ImamuraHadleyCollaboration

Contents