Difference between revisions of "User:Tohline/Appendix/CGH/Overview"
| Line 71: | Line 71: | ||
[Z^2 + y_1^2 ]^{1 / 2} \, . | [Z^2 + y_1^2 ]^{1 / 2} \, . | ||
</math> | </math> | ||
</td> | |||
</tr> | |||
</table> | |||
</div> | |||
Notice that, in the definition of <math>~D_j</math>, the expression inside the square brackets involves a term that depends quadratically on the dimensionless length scale, <math>~Y_j/L</math>, as well as a term that depends linearly on this ratio. As discussed below, our expression for the amplitude simplifies nicely in situations where the quadratic term can be ignored. Via a related simplification, we will find that the various natural lengths of this problem are can be related via the expression, | |||
<div align="center"> | |||
<table border="0" cellpadding="5" align="center"> | |||
<tr> | |||
<td align="right"> | |||
<math>~y_1\biggr|_{1^\mathrm{st} \mathrm{fringe}}</math> | |||
</td> | |||
<td align="center"> | |||
<math>~\approx</math> | |||
</td> | |||
<td align="left"> | |||
<math>~\frac{\lambda Z}{w} \, .</math> | |||
</td> | </td> | ||
</tr> | </tr> | ||
Revision as of 04:47, 28 December 2017
CGH: Philosophical Overview

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Slit Diffraction
Single Aperture
|
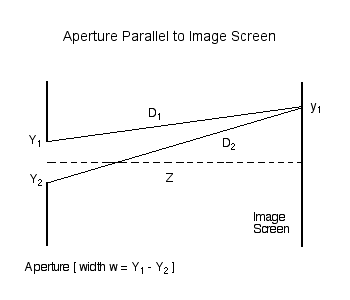
As has been detailed in an accompanying discussion, we consider, first, the amplitude (and phase) of light that is incident at a location <math>~y_1</math> on an image screen that is located a distance <math>~Z</math> from a slit of width <math>~w = (Y_1 - Y_2) = 2c</math>. The amplitude is given by the expression,
|
<math>~A(y_1)</math> |
<math>~=</math> |
<math>~\sum_j a_j \biggl[ \cos\biggl(\frac{2\pi D_j}{\lambda} + \phi_j \biggr) + i \sin\biggl(\frac{2\pi D_j}{\lambda} + \phi_j \biggr) \biggr] \, , </math> |
where,
|
<math>~D_j</math> |
<math>~=</math> |
<math>~ L \biggl[1 - \frac{2y_1 Y_j}{L^2} + \frac{Y_j^2}{L^2} \biggr]^{1 / 2} \, , </math> |
and,
|
<math>~L</math> |
<math>~\equiv</math> |
<math>~ [Z^2 + y_1^2 ]^{1 / 2} \, . </math> |
Notice that, in the definition of <math>~D_j</math>, the expression inside the square brackets involves a term that depends quadratically on the dimensionless length scale, <math>~Y_j/L</math>, as well as a term that depends linearly on this ratio. As discussed below, our expression for the amplitude simplifies nicely in situations where the quadratic term can be ignored. Via a related simplification, we will find that the various natural lengths of this problem are can be related via the expression,
|
<math>~y_1\biggr|_{1^\mathrm{st} \mathrm{fringe}}</math> |
<math>~\approx</math> |
<math>~\frac{\lambda Z}{w} \, .</math> |
See Also
- Tohline, J. E., (2008) Computing in Science & Engineering, vol. 10, no. 4, pp. 84-85 — Where is My Digital Holographic Display? [ PDF ]
- Diffraction (Wikipedia)
- Various Google hits:
- Single Slit Diffraction (University of Tennessee, Knoxville)
- Diffraction from a Single Slit; Young's Experiment with Finite Slits (University of New South Wales, Sydney, Australia)
- Single Slit Diffraction Pattern of Light (University of British Columbia, Canada)
- Fraunhofer Single Slit (Georgia State University)

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |