Challenges Constructing Ellipsoidal-Like Configurations (Pt. 4)

This chapter extends the accompanying chapters titled, Construction Challenges (Pt. 1), (Pt. 2), and (Pt. 3). The focus here is on firming up our understanding of the relationships between various "tilted" Cartesian coordinate frames.

The Plan

Intersection Expression

STEP #1

First, we present the mathematical expression that describes the intersection between the surface of an ellipsoid and a plane having the following properties:

The plane cuts through the ellipsoid's z-axis at a distance, <math>~z_0</math>, from the center of the ellipsoid;
The line of intersection is parallel to the x-axis of the ellipsoid; and,
The line that is perpendicular to the plane and passes through the z-axis at <math>~z_0</math> is tipped at an angle, <math>~\theta</math>, to the z-axis.

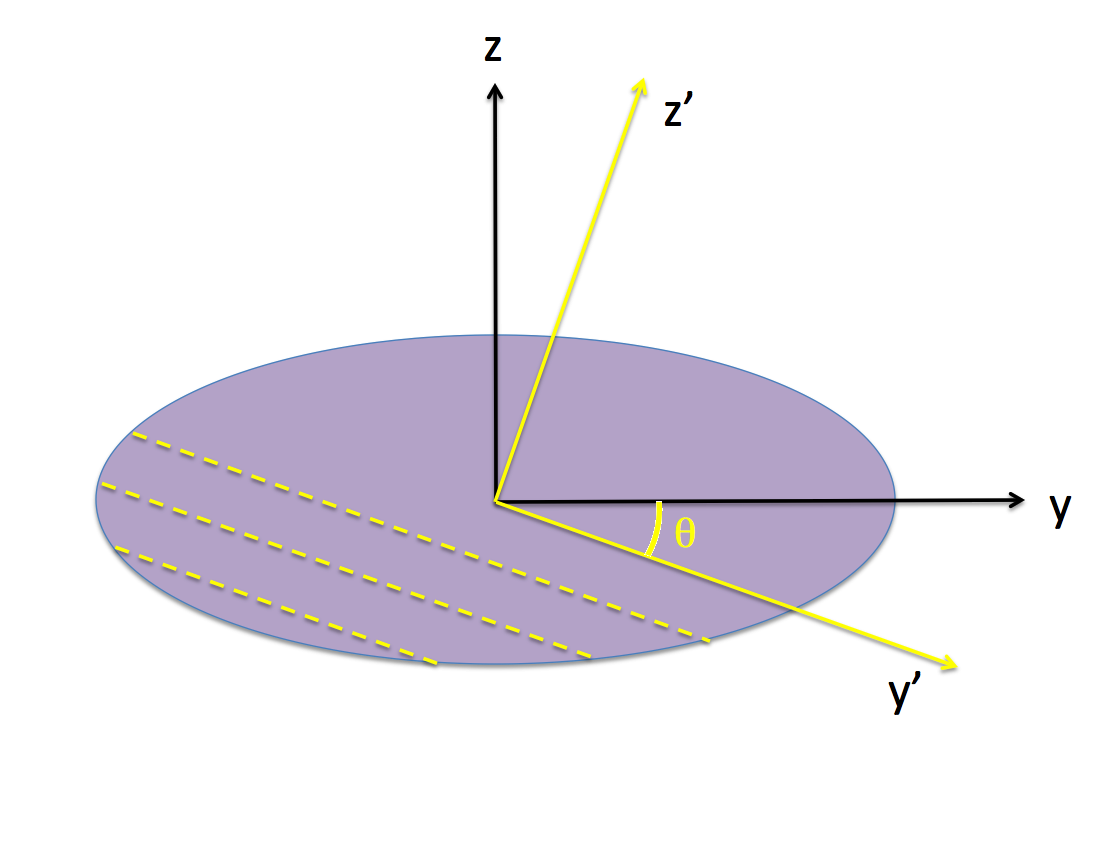
As is illustrated in Figure 1, we will use the line referenced in this third property description to serve as the z'-axis of a Cartesian grid that is tipped at the angle, <math>~\theta</math>, with respect to the body frame; and we will align the x' axis with the x-axis, so it should be clear that the z'-axis lies in the y-z plane of the ellipsoid.

Figure 1

<math>~x</math>	<math>~=</math>	<math>~x' \, ,</math>
<math>~y</math>	<math>~=</math>	<math>~ y' \cos\theta - z'\sin\theta \, ,</math>
<math>~(z - z_0)</math>	<math>~=</math>	<math>~ z' \cos\theta + y'\sin\theta \, .</math>

<math>~x'</math>	<math>~=</math>	<math>~x \, ,</math>
<math>~y'</math>	<math>~=</math>	<math>~ y \cos\theta + (z - z_0) \sin\theta \, ,</math>
<math>~z'</math>	<math>~=</math>	<math>~ (z-z_0) \cos\theta - y \sin\theta \, .</math>

As has been shown in our accompanying discussion, we obtain the following,

Intersection Expression
<math>~1 - \frac{x^2}{a^2} </math>	<math>~=</math>	<math>~y^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr] + y \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} \, , </math>

as long as z₀ lies within the range,

<math>~c^2 + b^2\tan^2\theta \, .</math>

Rewriting this "intersection expression" in terms of the tipped (primed) coordinate frame gives us,

<math>~(y' \cos\theta - z' \sin\theta)^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr] + (y' \cos\theta - z' \sin\theta) \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} \, . </math>

STEP #2

As viewed from the tipped coordinated frame, the curve that is identified by this intersection should be an

Off-Center Ellipse
<math>~1</math>	<math>~=</math>	<math>~\biggl[\frac{x'}{x_\mathrm{max}} \biggr]^2 + \biggl[\frac{y' - y_c}{y_\mathrm{max}} \biggr]^2 </math>
	<math>~=</math>	<math>~\biggl[\frac{x'}{x_\mathrm{max}} \biggr]^2 + \biggl[\frac{(y')^2 - 2y' y_c + y_c^2}{y^2_\mathrm{max}} \biggr] \, ,</math>

that lies in the x'-y' plane — that is, <math>~z' = 0</math>. Let's see if the intersection expression can be molded into this form.

<math>~1 - \frac{z_0^2}{c^2} - \frac{(x')^2}{a^2} </math>	<math>~=</math>	<math>~(y')^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr]\cos^2\theta + 2y' \biggl[ \frac{z_0 \sin\theta}{c^2} \biggr] </math>
	<math>~=</math>	<math>~\biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr]\cos^2\theta \biggl\{ (y')^2 - 2y' \biggl[ \frac{-z_0 \sin\theta}{c^2 \cos^2\theta} \biggr]\biggl[\frac{b^2c^2}{c^2 + b^2\tan^2\theta} \biggr] \biggr\}</math>
	<math>~=</math>	<math>~\kappa^2 \biggl[ (y')^2 - 2y' \underbrace{\biggl( \frac{-z_0 \sin\theta}{c^2 \kappa^2} \biggr)}_{y_c} \biggr] \, ,</math>

RESULT 3
(same as Result 1, but different from Result 2, below)

<math>~ -\frac{\sin\theta}{c^2\kappa^2} </math>

where,

<math>~\kappa^2</math>

<math>~\equiv</math>

<math>~ \frac{c^2 \cos^2\theta + b^2 \sin^2\theta}{b^2c^2} \, . </math>

Dividing through by <math>~\kappa^2</math>, then adding <math>~y_c^2</math> to both sides gives,

<math>~\underbrace{\biggl[ \frac{1}{\kappa^2} - \frac{z_0^2}{c^2 \kappa^2} + y_c^2 \biggr]}_{y^2_\mathrm{max}} - \frac{(x')^2}{a^2\kappa^2} \, .</math>

Finally, we have,

<math>\frac{1}{y^2_\mathrm{max}} \biggl[ (y')^2 - 2y' y_c + y_c^2 \biggr]</math>

<math>~1 - (x')^2 \underbrace{\biggl[ \frac{1}{a^2\kappa^2 y_\mathrm{max}^2} \biggr]}_{ 1/x^2_\mathrm{max} } \, .</math>

So … the intersection expression can be molded into the form of an off-center ellipse if we make the following associations:

<math>~\frac{y_c}{z_0}</math>	<math>~=</math>	<math>~- \frac{\sin\theta}{c^2 \kappa^2} \, ,</math>
<math>~y_\mathrm{max}^2</math>	<math>~=</math>	<math>~\frac{1}{\kappa^2}\biggl[ 1 - \frac{z_0^2}{c^2 } - \frac{z_0 \sin\theta}{c^2} \biggr] \, ,</math>
<math>~x_\mathrm{max}^2</math>	<math>~=</math>	<math>~a^2 \biggl[ 1 - \frac{z_0^2}{c^2 } - \frac{z_0 \sin\theta}{c^2} \biggr] \, .</math>

Note as well that,

<math>~\biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2</math>

<math>~a^2\kappa^2 = \frac{a^2}{b^2 c^2} \biggl[ c^2 \cos^2\theta + b^2 \sin^2\theta \biggr] \, .</math>

Lagrangian Trajectory and Velocities

We presume that the off-center ellipse that is defined by the intersection expression identifies the trajectory of a Lagrangian fluid element. If this is the case, there are a couple of ways that the velocity — both the amplitude and its vector orientation — can be derived.

STEP #3

If the intersection expression identifies a Lagrangian trajectory, then the velocity vector must be tangent to the off-center ellipse at every location. At each <math>~(x', y')</math> coordinate location, the slope of the above-defined off-center ellipse is,

<math>~ \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr)^2 \frac{x'}{(y_c - y')} \, . </math>

From this expression we deduce that the x'- and y'- components of the velocity vector are, respectively,

<math>~\frac{\boldsymbol{\hat\imath'} \cdot \boldsymbol{u'} }{ [\boldsymbol{u'}\cdot \boldsymbol{u'}]^{1 / 2} }</math>

<math>~ \frac{1}{u'_0} \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr) (y_c - y') \, , </math>

and,

<math>~\frac{\boldsymbol{\hat\jmath'} \cdot \boldsymbol{u'} }{ [\boldsymbol{u'}\cdot \boldsymbol{u'}]^{1 / 2} }</math>

<math>~ \frac{1}{u'_0} \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) x' \, , </math>

where the position-dependent — and, hence also, the time-dependent — length scale,

<math>~u'_0</math>	<math>~\equiv</math>	<math>~ \biggl\{ \biggl[ \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr) (y_c - y') \biggr]^2 + \biggl[ \frac{1}{\|u'\|} \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) x' \biggr]^2 \biggr\}^{1 / 2} </math>
	<math>~=</math>	<math>~ \frac{1}{x_\mathrm{max} y_\mathrm{max}} \biggl[ x_\mathrm{max}^4 ( y_c - y')^2 + y_\mathrm{max}^4 (x')^2 \biggr]^{1 / 2} \, . </math>

STEP #4

As a function of time, the x'-y' coordinates and associated velocity components of each Lagrangian fluid element are given by the expressions,

<math>~x'</math>	<math>~=</math>	<math>~x_\mathrm{max}\cos(\dot\varphi t)</math>	and,	<math>~y' - y_c</math>	<math>~=</math>	<math>~y_\mathrm{max}\sin(\dot\varphi t) \, ,</math>
<math>~\dot{x}'</math>	<math>~=</math>	<math>~- x_\mathrm{max}~ \dot\varphi \cdot \sin(\dot\varphi t) = (y_c - y') \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \dot\varphi </math>	and,	<math>~\dot{y}' </math>	<math>~=</math>	<math>~y_\mathrm{max}~\dot\varphi \cdot \cos(\dot\varphi t) = x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr] \dot\varphi \, .</math>

This means that the (dimensional) velocity vector is,

<math>~\boldsymbol{u'}</math>	<math>~=</math>	<math>~ \boldsymbol{\hat\imath'} \dot{x}' + \boldsymbol{\hat\jmath'} \dot{y}' </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\imath'} \biggl[ (y_c - y') \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr) \dot\varphi \biggr] + \boldsymbol{\hat\jmath'} \biggl[ x' \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \dot\varphi \biggr] </math>
<math>~\Rightarrow~~~\boldsymbol{u'} \cdot \boldsymbol{u'}</math>	<math>~=</math>	<math>~ \biggl[ (y_c - y') \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr) \dot\varphi \biggr]^2 + \biggl[ x' \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \dot\varphi \biggr]^2 </math>
	<math>~=</math>	<math>~\frac{\dot\varphi^2}{x_\mathrm{max}^2 y_\mathrm{max}^2} \biggl[ (y_c - y')^2 x_\mathrm{max}^4 + (x')^2 y_\mathrm{max}^4 \biggr] </math>
	<math>~=</math>	<math>~ (u_0')^2 \dot\varphi^2 \, . </math>

Riemann Flow

STEP #5

Example Type I Ellipsoid (see also)
<math>~\frac{b}{a} = \frac{a_2}{a_1}</math>	1.25
<math>~\frac{c}{a} = \frac{a_3}{a_1}</math>	0.4703
<math>~\Omega_2</math>	0.3639
<math>~\Omega_3</math>	0.6633
<math>~\tan^{-1} \biggl[ \frac{\Omega_3}{\Omega_2} \biggr]</math>	61.25°
<math>~\zeta_2</math>	-2.2794
<math>~\zeta_3</math>	-1.9637
<math>~\tan^{-1} \biggl[ \frac{\zeta_3}{\zeta_2} \biggr]</math>	40.74°
<math>~\beta_+</math>	1.13449 (1.13332)
<math>~\gamma_+</math>	1.8052

As we have summarized in an accompanying discussion of Riemann Type 1 ellipsoids — see also our separate discussion — [EFE] provides an expression for the velocity vector of each fluid element, given its instantaneous body-coordinate position (x, y, z) = (x₁, x₂, x₃) — see his Eq. (154), Chapter 7, §51 (p. 156). As viewed from the rotating body coordinate frame, the three component expressions are,

<math>~\dot{x} = u_1 = \boldsymbol{\hat\imath} \cdot \boldsymbol{u}</math>	<math>~=</math>	<math>~\biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 y - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 z</math>	<math>~=</math>	<math>~- \biggl[ \frac{a^2}{a^2 + b^2} \biggr] \zeta_3 y + \biggl[ \frac{a^2}{a^2 + c^2} \biggr] \zeta_2 z \, ,</math>
<math>~\dot{y} = u_2 = \boldsymbol{\hat\jmath} \cdot \boldsymbol{u}</math>	<math>~=</math>	<math>~- \gamma \Omega_3 x</math>	<math>~=</math>	<math>~+\biggl[ \frac{b^2}{a^2 + b^2} \biggr] \zeta_3 x \, ,</math>
<math>~\dot{z} = u_3 = \boldsymbol{\hat{k}} \cdot \boldsymbol{u}</math>	<math>~=</math>	<math>~+ \beta \Omega_2 x</math>	<math>~=</math>	<math>~- \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \zeta_2 x \, ,</math>

where,

<math>~ - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \frac{\zeta_2}{\Omega_2} </math>

and,

<math>~\gamma</math>

<math>~ - \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3}{\Omega_3} \, . </math>

In order to transform Riemann's velocity vector from the body frame (unprimed) to the "tipped orbit" frame (primed coordinates), we use the following mappings of the three unit vectors:

<math>~\boldsymbol{\hat\imath}</math>	<math>~\rightarrow</math>	<math>~\boldsymbol{\hat\imath'} \, ,</math>
<math>~\boldsymbol{\hat\jmath}</math>	<math>~\rightarrow</math>	<math>~\boldsymbol{\hat\jmath'}\cos\theta - \boldsymbol{\hat{k}'}\sin\theta \, ,</math>
<math>~\boldsymbol{\hat{k}}</math>	<math>~\rightarrow</math>	<math>~\boldsymbol{\hat\jmath'}\sin\theta + \boldsymbol{\hat{k}'}\cos\theta \, .</math>

<math>~x</math>	<math>~\rightarrow</math>	<math>~x' \, ,</math>
<math>~y</math>	<math>~\rightarrow</math>	<math>~y' \cos\theta - z' \sin\theta \, ,</math>
<math>~z - z_0</math>	<math>~\rightarrow</math>	<math>~y' \sin\theta + z'\cos\theta \, .</math>

In the tipped frame, we find,

<math>~\boldsymbol{u'}_\mathrm{EFE}</math>	<math>~=</math>	<math>~ \boldsymbol{\hat\imath'} \biggl[ \biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 ( y'\cos\theta - z'\sin\theta ) - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 ( z_0 + y'\sin\theta + z'\cos\theta ) \biggr] + [\boldsymbol{\hat{k}'}\sin\theta -\boldsymbol{\hat\jmath'}\cos\theta ] \biggl[ \gamma \Omega_3 x' \biggr] + [ \boldsymbol{\hat\jmath'}\sin\theta + \boldsymbol{\hat{k}'}\cos\theta] \biggl[ \beta \Omega_2 x' \biggr] </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\imath'} \biggl[ \biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 ( y'\cos\theta - z'\sin\theta ) - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 ( z_0 + y'\sin\theta + z'\cos\theta ) \biggr] + \boldsymbol{\hat\jmath'} \biggl[\beta \Omega_2 x' \cdot \sin\theta - \gamma \Omega_3 x' \cdot \cos\theta \biggr] + \boldsymbol{\hat{k}'}\biggl[ \beta \Omega_2 x' \cdot \cos\theta + \gamma \Omega_3 x' \cdot \sin\theta \biggr] \, . </math>

In order for the <math>~\boldsymbol{k}'</math> component to be zero in the tipped plane, we must choose the tipping angle such that,

<math>~\tan\theta</math>

<math>~ -\frac{\beta\Omega_2}{\gamma \Omega_3} = -0.344793 ~~~\Rightarrow~~~ \theta = -19.0238^\circ \, . </math>

And if we examine the flow only in the tipped x'-y' plane, then we should set <math>~z' = -z_0/\cos\theta</math>. These two constraints lead to the velocity expression,

<math>~\boldsymbol{u'}_\mathrm{EFE}</math>

<math>~ \boldsymbol{\hat\imath'} \biggl[ \biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 ( y'\cos\theta + z_0\tan\theta ) - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 ( y'\sin\theta ) \biggr] + \boldsymbol{\hat\jmath'} \underbrace{\biggl[\beta \Omega_2 \sin\theta - \gamma \Omega_3 \cos\theta \biggr]}_{\dot\varphi y_\mathrm{max}/x_\mathrm{max}}x' \, . </math>

As we have indicated, this <math>~\boldsymbol{\hat\jmath'}</math> component will match our Step #4 velocity expression if,

<math>~\biggl(\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr)\dot\varphi</math>	<math>~=</math>	<math>~ \beta \Omega_2 \sin\theta - \gamma \Omega_3 \cos\theta </math>
	<math>~=</math>	<math>~ \biggl[\frac{1}{1 + \tan^2\theta}\biggr]^{1 / 2} \biggl[\beta\Omega_2 \tan\theta - \gamma\Omega_3\biggr] </math>
	<math>~=</math>	<math>~ -\biggl[\frac{\gamma^2 \Omega_3^2}{\gamma^2 \Omega_3^2 + \beta^2\Omega_2^2}\biggr]^{1 / 2} \biggl[ \frac{\beta^2\Omega_2^2}{\gamma \Omega_3} + \gamma\Omega_3\biggr] </math>
	<math>~=</math>	<math>~ -~\biggl[ \beta^2\Omega_2^2 + \gamma^2\Omega_3^2\biggr]^{1 / 2} \, . </math>

Rewriting the <math>~\boldsymbol{\hat\imath'}</math> component, we have,

<math>~\biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 ( y'\cos\theta + z_0\tan\theta ) - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 ( y'\sin\theta )</math>	<math>~=</math>	<math>~ y' \biggl[ \biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 \cos\theta - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 \sin\theta \biggr] + \biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 ( z_0\tan\theta ) </math>
	<math>~=</math>	<math>~ y' \biggl[ \biggl(\frac{a}{b}\biggr)^2 \gamma \Omega_3 - \biggl(\frac{a}{c}\biggr)^2 \beta \Omega_2 \tan\theta \biggr]\biggl[\frac{1}{1 + \tan^2\theta}\biggr]^{1 / 2} - \biggl(\frac{a}{b}\biggr)^2 \beta \Omega_2 z_0 </math>
	<math>~=</math>	<math>~ y' \biggl[ \biggl(\frac{a}{b}\biggr)^2 \gamma^2 \Omega_3^2 + \biggl(\frac{a}{c}\biggr)^2 \beta^2 \Omega_2^2 \biggr] \biggl[\frac{1}{\gamma^2 \Omega_3^2 + \beta^2\Omega_2^2}\biggr]^{1 / 2} - \biggl(\frac{a}{b}\biggr)^2 \beta \Omega_2 z_0 \, . </math>

Hence,

<math>~\boldsymbol{u'}_\mathrm{EFE}</math>

<math>~ \boldsymbol{\hat\imath'} \biggl\{ y' \underbrace{\biggl[ \biggl(\frac{a}{b}\biggr)^2 \gamma^2 \Omega_3^2 + \biggl(\frac{a}{c}\biggr)^2 \beta^2 \Omega_2^2 \biggr] \biggl[\frac{1}{\gamma^2 \Omega_3^2 + \beta^2\Omega_2^2}\biggr]^{1 / 2}}_{-\dot\varphi x_\mathrm{max}/y_\mathrm{max}} - \biggl(\frac{a}{b}\biggr)^2 \beta \Omega_2 z_0\biggr\} + \boldsymbol{\hat\jmath'} \biggl[ \dot\varphi \biggl(\frac{y_\mathrm{max}}{x_\mathrm{max}} \biggr) \biggr]x' \, . </math>

That is to say, we need to set,

<math>~\dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)</math>

<math>~-~ \biggl[ c^2 \gamma^2 \Omega_3^2 + b^2 \beta^2 \Omega_2^2 \biggr] \biggl[\frac{1}{\gamma^2 \Omega_3^2 + \beta^2\Omega_2^2}\biggr]^{1 / 2} \biggl( \frac{a^2}{b^2 c^2}\biggr) \, . </math>

When this is combined with the constraint set by the <math>~\boldsymbol{\hat\jmath'}</math> component, we find,

<math>~\dot\varphi^2 = \dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr) \cdot \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr)</math>

<math>~+ \biggl[ c^2 \gamma^2 \Omega_3^2 + b^2 \beta^2 \Omega_2^2 \biggr] \biggl( \frac{a^2}{b^2 c^2}\biggr) = (1.29930)^2 \, , </math>

and, hence,

<math>~\biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)^2</math>	<math>~=</math>	<math>~ \biggl[ c^2 \gamma^2 \Omega_3^2 + b^2 \beta^2 \Omega_2^2 \biggr] \biggl[\frac{1}{\gamma^2 \Omega_3^2 + \beta^2\Omega_2^2}\biggr]^{1 / 2} \biggl( \frac{a^2}{b^2 c^2}\biggr) \biggl[ \beta^2\Omega_2^2 + \gamma^2\Omega_3^2\biggr]^{-1 / 2} </math>
	<math>~=</math>	<math>~ \biggl[\frac{c^2 \gamma^2 \Omega_3^2 + b^2 \beta^2 \Omega_2^2 }{\gamma^2 \Omega_3^2 + \beta^2\Omega_2^2}\biggr] \biggl( \frac{a^2}{b^2 c^2}\biggr) = ( 1.02585 )^2 \, . </math>

Finally, then,

<math>~y_c \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr) \dot\varphi</math>	<math>~=</math>	<math>~ -\biggl(\frac{a}{b}\biggr)^2 \beta \Omega_2 z_0 </math>
<math>~\Rightarrow ~~~ \frac{y_c}{z_0} </math>	<math>~=</math>	<math>~ -\biggl(\frac{a}{b}\biggr)^2 \beta \Omega_2 \biggl\{ \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr) \dot\varphi \biggr\}^{-1} </math>
	<math>~=</math>	<math>~ c^2 \beta \Omega_2 \biggl[ c^2 \gamma^2 \Omega_3^2 + b^2 \beta^2 \Omega_2^2 \biggr]^{-1} \biggl[\gamma^2 \Omega_3^2 + \beta^2\Omega_2^2\biggr]^{1 / 2} = 0.19823 \, . </math>

RESULT 2
(different from Result 1 and Result 3, above)

<math>~ -\frac{\sin\theta}{b^2\kappa^2} </math>

Reconcile Results Differences

Before calling upon any of Riemann's model parameters, from geometric considerations alone we should be able to determine exactly what the expression is for any off-center ellipse that results from slicing — at a tipped angle — the chosen ellipsoid.

Figure 1

<math>~x</math>	<math>~=</math>	<math>~x' \, ,</math>
<math>~y</math>	<math>~=</math>	<math>~ y' \cos\theta - z'\sin\theta \, ,</math>
<math>~(z - z_0)</math>	<math>~=</math>	<math>~ z' \cos\theta + y'\sin\theta \, .</math>

<math>~x'</math>	<math>~=</math>	<math>~x \, ,</math>
<math>~y'</math>	<math>~=</math>	<math>~ y \cos\theta + (z - z_0) \sin\theta \, ,</math>
<math>~z'</math>	<math>~=</math>	<math>~ (z-z_0) \cos\theta - y \sin\theta \, .</math>

As has been shown in our accompanying discussion, we obtain the following,

Intersection Expression
<math>~1 - \frac{x^2}{a^2} </math>	<math>~=</math>	<math>~y^2 \biggl[\frac{c^2 + b^2\tan^2\theta}{b^2c^2} \biggr] + y \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} \, , </math>

as long as z₀ lies within the range,

<math>~c^2 + b^2\tan^2\theta \, .</math>

Along the tipped <math>~y'</math> axis, two points will mark the ends of the x'-y' orbit; they are identified by the roots of this Intersection Expression when x = 0. That is, by the roots of,

<math>~y^2 \biggl[\frac{\kappa^2}{\cos^2\theta} \biggr] + y \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \biggl[\frac{z_0^2}{c^2} -1 \biggr] \, ,</math>

where,

<math>~\kappa^2</math>

<math>~\equiv</math>

<math>~ \frac{c^2 \cos^2\theta + b^2 \sin^2\theta}{b^2c^2} \, . </math>

The roots are …

Scratch notes:

<math>~y_\mathrm{edge}</math>

<math>~\frac{B}{2A} \biggl\{\pm \biggl[1 - \frac{4AC}{B^2} \biggr]^{1 / 2} -1 \biggr\}</math>

where,

<math>~ \frac{4AC}{B^2} = \frac{4\kappa^2}{\cos^2\theta} \biggl[\frac{z_0^2}{c^2} -1 \biggr] \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr]^{-2} = \frac{\kappa^2}{\cos^2\theta} \biggl[ \frac{c^2(z_0^2 - c^2)}{z_0^2 \tan^2\theta} \biggr] = \biggl[ \frac{c^2 \kappa^2 (z_0^2 - c^2)}{z_0^2 \sin^2\theta} \biggr] </math>

<math>~y_\mathrm{edge}</math>	<math>~=</math>	<math>~\biggl[ \frac{z_0 \sin\theta \cos\theta}{c^2 \kappa^2} \biggr]\biggl\{\pm \biggl[1 - \frac{c^2 \kappa^2 (z_0^2 - c^2)}{z_0^2 \sin^2\theta} \biggr]^{1 / 2} -1 \biggr\}</math>
	<math>~=</math>	<math>~\biggl[ \frac{\cos\theta}{c^2 \kappa^2} \biggr]\biggl\{\pm \biggl[z_0^2 \sin^2\theta + c^2 \kappa^2 (c^2 - z_0^2 ) \biggr]^{1 / 2} - z_0 \sin\theta \biggr\} \, .</math>

Hereafter we will use <math>~y_p</math> to denote the "plus" root, and <math>~y_m</math> to denote the "minus" root; that is,

<math>~y_p</math>	<math>~\equiv</math>	<math>~\biggl[ \frac{\cos\theta}{c^2 \kappa^2} \biggr]\biggl\{\biggl[z_0^2 \sin^2\theta + c^2 \kappa^2 (c^2 - z_0^2 ) \biggr]^{1 / 2} - z_0 \sin\theta \biggr\} \, ,</math>
<math>~y_m</math>	<math>~\equiv</math>	<math>~- \biggl[ \frac{\cos\theta}{c^2 \kappa^2} \biggr]\biggl\{\biggl[z_0^2 \sin^2\theta + c^2 \kappa^2 (c^2 - z_0^2 ) \biggr]^{1 / 2} + z_0 \sin\theta \biggr\} \, .</math>

The y-coordinate of the center of the orbit will lie halfway between these two "edges". That is,

<math>~y_\mathrm{center}</math>	<math>~=</math>	<math>~\frac{1}{2}\biggl[ y_p - y_m \biggr]</math>
	<math>~=</math>	<math>~ \biggl[ \frac{\cos\theta}{c^2 \kappa^2} \biggr]\biggl[z_0^2 \sin^2\theta + c^2 \kappa^2 (c^2 - z_0^2 ) \biggr]^{1 / 2} \, . </math>

And the x-coordinate line that passes through this "center" location is obtained by plugging <math>~y_\mathrm{center}</math> into the Intersection Expression. That is,

<math>~x_\mathrm{center}</math>

<math>~1 - y^2_\mathrm{center} \biggl[\frac{\kappa^2}{\cos^2\theta} \biggr] + y_\mathrm{center} \biggl[ \frac{2z_0 \tan\theta}{c^2} \biggr] + \frac{z_0^2}{c^2} \, .</math>

Various Coordinate Frames

Tipped Orbit Planes

Summary

In a separate discussion, we have shown that, as viewed from a frame that "tumbles" with the (purple) body of a Type 1 Riemann ellipsoid, each Lagrangian fluid element moves along an elliptical path in a plane that is tipped by an angle <math>~\theta</math> about the x-axis of the body. As viewed from the (primed) coordinates associated with this tipped plane, by definition, z' = constant and dz'/dt = 0, and the planar orbit is defined by the expression for an,

Off-Center Ellipse
<math>~1</math>	<math>~=</math>	<math>~\biggl[\frac{x'}{x_\mathrm{max}} \biggr]^2 + \biggl[\frac{y' - y_c(z')}{y_\mathrm{max}} \biggr]^2 \, .</math>

Tipped Orbit Frame (yellow, primed)

Given that b/a = 1.25 and c/a = 0.4703 for our chosen Example Type I Ellipsoid, we find that, <math>~\theta = - 1.18122 ~\mathrm{rad} = -67.68^\circ</math>.

Notice that the offset, <math>~y_c</math>, is a function of the tipped plane's vertical coordinate, <math>~z'</math>. As a function of time, the x'-y' coordinates and associated velocity components of each Lagrangian fluid element are given by the expressions,

<math>~x'</math>	<math>~=</math>	<math>~x_\mathrm{max}\cos(\dot\varphi t)</math>	and,	<math>~y' - y_c</math>	<math>~=</math>	<math>~y_\mathrm{max}\sin(\dot\varphi t) \, ,</math>
<math>~\dot{x}'</math>	<math>~=</math>	<math>~- x_\mathrm{max}~ \dot\varphi \cdot \sin(\dot\varphi t) = (y_c - y') \biggl[ \frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr] \dot\varphi </math>	and,	<math>~\dot{y}' </math>	<math>~=</math>	<math>~y_\mathrm{max}~\dot\varphi \cdot \cos(\dot\varphi t) = x' \biggl[ \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr] \dot\varphi \, .</math>

We have determined that (numerical value given for our chosen example Type I ellipsoid),

<math>~\tan\theta</math>

<math>~ - \frac{b^2 \beta \Omega_2}{c^2 \gamma \Omega_3} = -2.43573\, , </math>

where, as has also been specified in an accompanying discussion,

<math>~ - \biggl[ \frac{c^2}{a^2 + c^2} \biggr] \frac{\zeta_2}{\Omega_2} = +1.13451 </math>

and,

<math>~\gamma</math>

<math>~ - \biggl[ \frac{b^2}{a^2 + b^2} \biggr] \frac{\zeta_3}{\Omega_3} = +1.80518\, . </math>

We also have determined that,

<math>~\biggl[\frac{x_\mathrm{max}}{y_\mathrm{max}} \biggr]^4</math>	<math>~=</math>	<math>~ \frac{a^4 (c^4 \gamma^2 \Omega_3^2 + b^4 \beta^2 \Omega_2^2)}{b^4 c^4(\gamma^2\Omega_3^2 + \beta^2\Omega_2^2)} ~~~\Rightarrow ~~~\frac{x_\mathrm{max}}{y_\mathrm{max}} = 1.26218 \, , </math>
<math>~{\dot\varphi}^4 </math>	<math>~=</math>	<math>~ \frac{a^4}{b^4 c^4} \biggl(\gamma^2\Omega_3^2 + \beta^2\Omega_2^2 \biggr) (c^4 \gamma^2 \Omega_3^2 + b^4 \beta^2 \Omega_2^2) ~~~\Rightarrow ~~~ \dot\varphi = 1.59862\, , </math>
<math>~\frac{y_c}{z_0}</math>	<math>~=</math>	<math>~ -\sin\theta ~~~\Rightarrow~~~~ \frac{y_c}{z_0} = -0.92507 \, .</math>

Demonstration

In order to transform a vector from the "tipped orbit" frame (primed coordinates) to the "body" frame (unprimed), we use the following mappings of the three unit vectors:

<math>~\boldsymbol{\hat\imath'}</math>	<math>~\rightarrow</math>	<math>~\boldsymbol{\hat\imath} \, ,</math>
<math>~\boldsymbol{\hat\jmath'}</math>	<math>~\rightarrow</math>	<math>~\boldsymbol{\hat\jmath}\cos\theta + \boldsymbol{\hat{k}}\sin\theta \, ,</math>
<math>~\boldsymbol{\hat{k}'}</math>	<math>~\rightarrow</math>	<math>~-\boldsymbol{\hat\jmath}\sin\theta + \boldsymbol{\hat{k}}\cos\theta \, .</math>

Given that, by design in our "tipped orbit" frame, there is no vertical motion — that is, <math>~\dot{z}' = 0</math> — mapping the (primed coordinate) velocity to the body (unprimed) coordinate is particularly straightforward. Specifically,

<math>~\boldsymbol{u'}</math>	<math>~=</math>	<math>~ \boldsymbol{\hat\imath'} \dot{x}' + \boldsymbol{\hat\jmath'} \dot{y}' + \boldsymbol{\hat{k}'} \cancelto{0}{\dot{z}'} </math>
	<math>~~~\rightarrow~~</math>	<math>~ \boldsymbol{\hat\imath} \dot{x}' + [\boldsymbol{\hat\jmath}\cos\theta + \boldsymbol{\hat{k}}\sin\theta] \dot{y}' </math>
	<math>~=</math>	<math>~ \boldsymbol{\hat\imath} \biggl\{ (y_c - y') \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr) \dot\varphi \biggr\} + [\boldsymbol{\hat\jmath}\cos\theta + \boldsymbol{\hat{k}}\sin\theta] \biggl\{ x' \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \dot\varphi \biggr\} \, . </math>

Recognizing, as before, that the relevant coordinate mapping is,

<math>~x</math>	<math>~=</math>	<math>~x' \, ,</math>
<math>~y</math>	<math>~=</math>	<math>~ y' \cos\theta - z'\sin\theta \, ,</math>
<math>~(z - z_0)</math>	<math>~=</math>	<math>~ z' \cos\theta + y'\sin\theta \, .</math>

<math>~x'</math>	<math>~=</math>	<math>~x \, ,</math>
<math>~y'</math>	<math>~=</math>	<math>~ y \cos\theta + (z - z_0) \sin\theta \, ,</math>
<math>~z'</math>	<math>~=</math>	<math>~ (z-z_0) \cos\theta - y \sin\theta \, .</math>

we have,

<math>~\boldsymbol{u'}</math>

<math>~~~\rightarrow~~~</math>

<math>~ \boldsymbol{\hat\imath} \dot\varphi \biggl( \frac{x_\mathrm{max}}{y_\mathrm{max}}\biggr)\biggl\{y_c - y\cos\theta - (z - z_0)\sin\theta\biggr\} + \boldsymbol{\hat\jmath} \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \biggr\{ x\cos\theta \biggr\} + \boldsymbol{\hat{k}} \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) \biggr\{ x\sin\theta \biggr\} \, . </math>

Therefore, as viewed from the body frame, the individual velocity components are,

<math>~\boldsymbol{\hat\jmath} \cdot \boldsymbol{u'}</math>	<math>~=</math>	<math>~ \dot\varphi \biggl( \frac{y_\mathrm{max}}{x_\mathrm{max}}\biggr) x\cos\theta </math>
	<math>~=</math>	<math>~x \cdot \biggl\{ \frac{b^4 c^4(\gamma^2\Omega_3^2 + \beta^2\Omega_2^2)}{a^4 (c^4 \gamma^2 \Omega_3^2 + b^4 \beta^2 \Omega_2^2)} \frac{a^4}{b^4 c^4} \biggl(\gamma^2\Omega_3^2 + \beta^2\Omega_2^2 \biggr) (c^4 \gamma^2 \Omega_3^2 + b^4 \beta^2 \Omega_2^2) \biggr\}^{1 / 4} \frac{{c^2 \gamma \Omega_3} }{[c^4 \gamma^2 \Omega_3^2 + b^4\beta^2 \Omega_2^2]^{1 / 2}} </math>

User:Tohline/ThreeDimensionalConfigurations/ChallengesPt4

Contents

Challenges Constructing Ellipsoidal-Like Configurations (Pt. 4)

The Plan

Intersection Expression

Lagrangian Trajectory and Velocities

Riemann Flow

Reconcile Results Differences

Various Coordinate Frames

Tipped Orbit Planes

Summary

Demonstration

See Also

Navigation menu

Search