User:Tohline/SSC/Stability/BiPolytrope0 0CompareApproaches
Comparing Stability Analyses of Zero-Zero Bipolytropes

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
In separate chapters we have discussed the following interrelated aspects of Bipolytropes that have <math>~(n_c,n_e) = (0,0)</math>:
- Using a detailed force-balance analysis to develop an analytic description of their equilibrium structure
- Using a free-energy analysis to analytically identify the properties of equilibrium structures; see also, an explicit, analytic evaluation of the statement of Virial Equilibrium
- Developing the Linear Adiabatic Wave Equation (LAWE) as it applies separately to the core and to the envelope of zero-zero bipolytropic configurations
- Identifying a method to analytically solve the matching LAWEs for a certain subset of configurations
- A summary of this solution technique, along with the first illustrative analytic specification of an eigenvector
- The derivation of analytically specifiable eigenvectors having a variety of mode quantum numbers
- A free-energy analysis of the global stability of zero-zero bipolytropes
Building on these separate discussions, here we examine what might be learned from a comparison of the two traditional approaches to stability analysis, namely: (1) solutions of the LAWE, and (2) a free-energy analysis.
Key Attributes of Equilibrium Configurations
Aside from specifying its radius, <math>~R</math>, and total mass, <math>~M_\mathrm{tot}</math>, there are three particularly interesting dimensionless parameters that characterize the internal structure of a bipolytrope having <math>~(n_c,n_e) = (0,0)</math>. They are, the radial location of the core/envelope interface,
<math>~q \equiv \frac{r_i}{R} \, ;</math>
the ratio of the density of the envelope material to the density of the core, <math>~0 \le \rho_e/\rho_c \le 1</math>; and the fraction of the total mass that is contained in the core,
<math>~\nu \equiv \frac{M_\mathrm{core}}{M_\mathrm{tot}} \, .</math>
Identifying a unique bipolytropic configuration requires the specification of two of these three dimensionless parameters; the third parameter is, then, necessarily determined via the algebraic relation,
|
<math>~\frac{\rho_e}{\rho_c} </math> |
<math>=</math> |
<math>~\frac{q^3(1-\nu)}{\nu(1-q^3)} \, .</math> |
Our study of equilibrium configurations has shown that once, for example, the pair of parameters, <math>~q</math> and <math>~\rho_e/\rho_c</math>, has been specified, other properties of the associated equilibrium configuration can be succinctly expressed in terms of the function,
|
<math>~g^2</math> |
<math>~\equiv</math> |
<math> 1 + \biggl(\frac{\rho_e}{\rho_0}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_0} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_0} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \, . </math> |
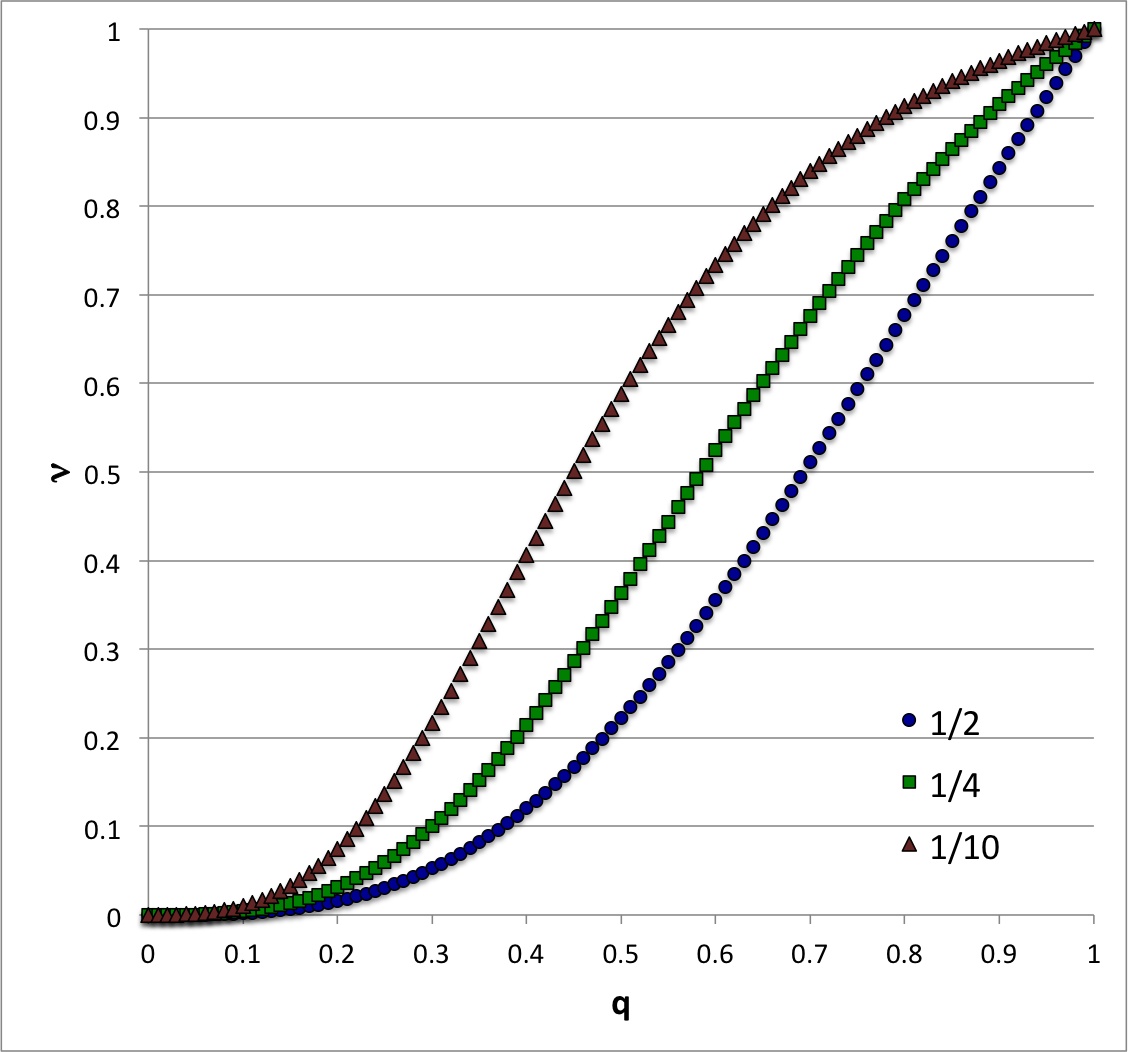
| Figure 1: Equilibrium Sequences of Constant <math>~\rho_e/\rho_c</math> |
Across the two-dimensional, <math>~(q,\nu)</math> parameter space that is defined by the full range of physically viable values of <math>~q</math> and <math>~\nu</math>, namely,
<math>~0 \le q \le 1 \, ,</math> and <math>~0 \le \nu \le 1 \, ,</math>
an equilibrium model sequence can be defined by, for example, specifying that all models along the sequence have the same density jump at the interface. Drawing on the above constraint relation, each choice of <math>~\rho_e/\rho_c</math> will generate a sequence governed by the function,
|
<math>~\nu</math> |
<math>=</math> |
<math>~\biggl[\frac{(1-q^3)}{q^3} \biggl( \frac{\rho_e}{\rho_c} \biggr) + 1\biggr]^{-1} </math> |
|
|
<math>=</math> |
<math>~\frac{q^3}{q^3 + (1-q^3)(\rho_e/\rho_c)} </math> |
Figure 1 displays several such equilibrium sequences across the <math>~(q,\nu)</math> plane — see also a related figure associated with our free-energy determination of stability.
Related Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |