User:Tohline/Appendix/Ramblings/ToroidalCoordinates

Toroidal Configurations and Related Coordinate Systems

Preamble

As I have studied the structure and analyzed the stability of (both self-gravitating and non-self-gravitating) toroidal configurations over the years, I have often wondered whether it might be useful to examine such systems mathematically using a toroidal — or at least a toroidal-like — coordinate system. Is it possible, for example, to build an equilibrium torus for which the density distribution is one-dimensional as viewed from a well-chosen toroidal-like system of coordinates?

I should begin by clarifying my terminology. In volume II (p. 666) of their treatise on Methods of Theoretical Physics, Morse & Feshbach (1953; hereafter MF53) define an orthogonal toroidal coordinate system in which the Laplacian is separable.¹ (See details, below.) It is only this system that I will refer to as the toroidal coordinate system; all other functions that trace out toroidal surfaces but that don't conform precisely to Morse & Feshbach's coordinate system will be referred to as toroidal-like.

I became particularly interested in this idea while working with Howard Cohl (when he was an LSU graduate student). Howie's dissertation research uncovered a Compact Cylindrical Greens Function technique for evaluating Newtonian potentials of rotationally flattened (especially axisymmetric) configurations.^2,3 The technique involves a multipole expansion in terms of half-integer-degree Legendre functions of the <math>2^\mathrm{nd}</math> kind — see NIST digital library discussion — where, if I recall correctly, the argument of this special function (or its inverse) seemed to resemble the radial coordinate of Morse & Feshbach's orthogonal toroidal coordinate system — see more on this, below.

Off-center Circle

In what follows, it will be useful to recall the algebraic expression that defines a circle whose center is not positioned at the origin of a Cartesian coordinate system. Specifically, consider a circle of radius, <math>~r_c</math>, whose center is located a distance <math>~x_0</math> along the plus-x axis. The equation for this circle is,

<math> ~(x-x_0)^2 + y^2 = r_c^2 . </math>

Toroidal Coordinates

Presentation by MF53

The orthogonal toroidal coordinate system <math>(\xi_1,\xi_2,\xi_3=\cos\varphi)</math> discussed by MF53 has the following properties:

<math> ~\frac{x}{a} </math>	<math> ~= </math>	<math> ~\biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr]\cos\varphi \, , </math>
<math> ~\frac{y}{a} </math>	<math> ~= </math>	<math> ~\biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr]\sin\varphi \, , </math>
<math> ~\frac{z}{a} </math>	<math> ~= </math>	<math> ~\frac{(1-\xi_2^2)^{1/2}}{\xi_1 - \xi_2} \, , </math>
<math> ~\frac{\varpi}{a} \equiv \biggl[ \biggl(\frac{x}{a}\biggr)^2 + \biggl(\frac{y}{a}\biggr)^2 \biggr]^{1/2} </math>	<math> ~= </math>	<math> ~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \, , </math>
<math> ~\frac{r}{a} \equiv \biggl[ \biggl(\frac{x}{a}\biggr)^2 + \biggl(\frac{y}{a}\biggr)^2 + \biggl(\frac{z}{a}\biggr)^2\biggr]^{1/2} </math>	<math> ~= </math>	<math> ~\biggl[ \frac{\xi_1 + \xi_2}{\xi_1 - \xi_2} \biggr]^{1/2} \, . </math>

According to MF53, the associated scale factors of this orthogonal coordinate system are:

<math> ~\frac{h_1}{a} </math>	<math> ~= </math>	<math> ~\frac{1}{(\xi_1 - \xi_2)(\xi_1^2 - 1)^{1/2}} \, , </math>
<math> ~\frac{h_2}{a} </math>	<math> ~= </math>	<math> ~\frac{1}{(\xi_1 - \xi_2)(1-\xi_2^2)^{1/2}} \, , </math>
<math> ~\frac{h_3}{a} </math>	<math> ~= </math>	<math> ~\biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr]\frac{1}{\sin\varphi} \, . </math>

That means that, in the meridional plane, an area element should be,

<math> ~d\sigma = (h_1 d\xi_1)(h_2 d\xi_2) = a^2 \biggl[ \frac{d\xi_1}{(\xi_1 - \xi_2)(\xi_1^2 - 1)^{1/2}} \biggr] \biggl[ \frac{d\xi_2}{(\xi_1 - \xi_2)(1-\xi_2^2)^{1/2}} \biggr] \, . </math>

Tohline's Ramblings

My inversion of these coordinate definitions has led to the following expressions:

<math> ~\xi_1 </math>	<math> ~= </math>	<math> \frac{r(r^2 + 1)} {[\chi^2(r^2-1)^2 + \zeta^2(r^2+1)^2]^{1/2}} \, , </math>
<math> ~\xi_2 </math>	<math> ~= </math>	<math> \frac{r(r^2 - 1)}{[\chi^2(r^2-1)^2 + \zeta^2(r^2+1)^2]^{1/2}} \, , </math>

where,

<math> \chi \equiv \frac{\varpi}{a} ~~~;~~~\zeta\equiv\frac{z}{a} ~~~\mathrm{and} ~~~ r=(\chi^2 + \zeta^2)^{1/2} . </math>

Apparently the allowed ranges of the two meridional-plane coordinates are:

<math> +1 \leq \xi_1 \leq \infty ~~~\mathrm{and} ~~~ -1 \leq \xi_2 \leq +1 . </math>

Example Toroidal Surfaces

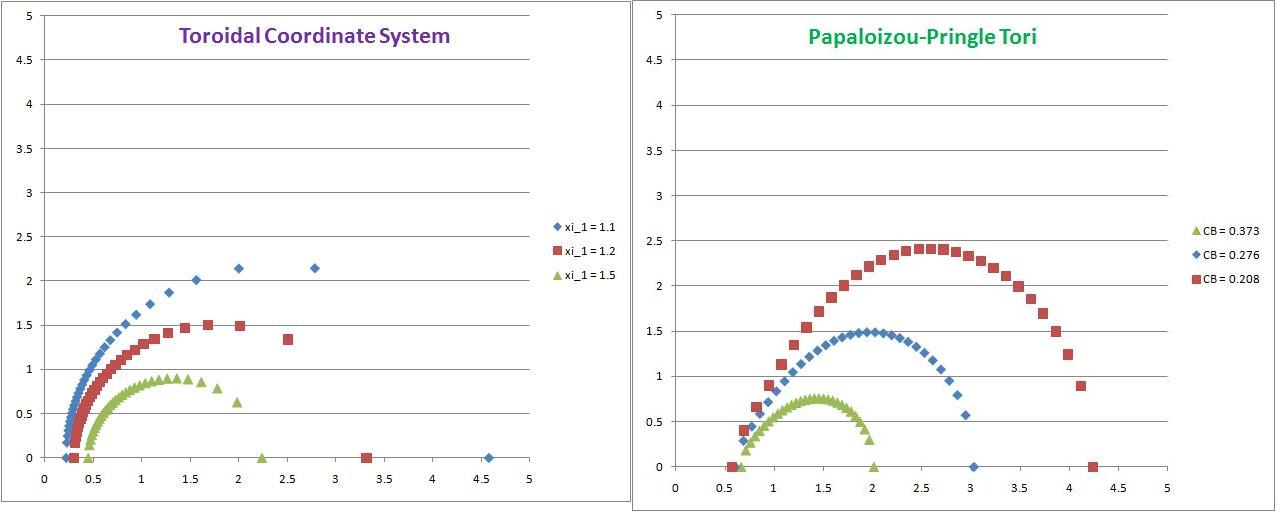
In the accompanying figure labeled "Toroidal Coordinate System," we've outlined three different <math>~\xi_1 = \mathrm{constant}</math> meridional contours for the MF53 toroidal coordinate system. The illustrated values are,

<math> ~\xi_1 </math>	<math>~=</math>	<math>~1.1</math>		<math>~\mathrm{(blue)} \, ;</math>
<math> ~\xi_1 </math>	<math>~=</math>	<math>~1.2</math>		<math>~\mathrm{(red)} \, ;</math>
<math> ~\xi_1 </math>	<math>~=</math>	<math>~1.5</math>		<math>\mathrm{(gold)} \, .</math>

The inner and outer edges of the toroidal surface in the equatorial plane should be determined by setting <math>~\xi_2 = -1</math> (inner) and <math>~\xi_2 = +1</math> (outer). Hence,

<math> ~\chi_\mathrm{inner} </math>	<math>~=</math>	<math> ~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 +1} = \biggl[\frac{(\xi_1 - 1)}{(\xi_1 + 1)} \biggr]^{1/2} </math>
<math> ~\chi_\mathrm{outer} </math>	<math>~=</math>	<math> ~\frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - 1} = \biggl[\frac{(\xi_1 + 1)}{(\xi_1 - 1)} \biggr]^{1/2} </math>

The equatorial-plane location of the "center" of each torus is,

<math> \chi_0 = \frac{1}{2} (\chi_\mathrm{outer} + \chi_\mathrm{inner}) = \frac{\xi_1}{(\xi_1^2 - 1)^{1/2}} , </math>

and the so-called distortion parameter,

<math> \delta \equiv \frac{\chi_\mathrm{outer}-\chi_\mathrm{inner}}{\chi_0}= \frac{2}{\xi_1} . </math>

Properties of <math>\xi_1 = \mathrm{constant}</math> Toroidal Surfaces
Curve in Figure	<math>\xi_1</math>	<math>\chi_\mathrm{inner}</math>	<math>\chi_\mathrm{outer}</math>	<math>\chi_0</math>	<math>\delta</math>
Blue	1.1	0.218	4.583	2.400	1.818
Red	1.2	0.302	3.317	1.809	1.667
Gold	1.5	0.447	2.236	1.342	1.333

What function <math>~\zeta(\varpi)</math> coincides with these <math>~\xi_1 = \mathrm{constant}</math> surfaces? (To be answered!)

Off-center Circle

The curves drawn in the above figure labeled "Toroidal Coordinate System" resemble circles whose centers are positioned a distance <math>~\chi_0</math> away from the origin. Let's examine whether this is the case by drawing on the familiar expression for such a configuration, as presented above. If this is the case, then the circle will have a radius,

<math> ~r_c </math>	<math> ~= </math>	<math> ~\chi_\mathrm{outer} - \chi_0 </math>
	<math> ~= </math>	<math> ~\biggl[\frac{(\xi_1 + 1)}{(\xi_1 - 1)} \biggr]^{1/2} - \frac{\xi_1}{(\xi_1^2 - 1)^{1/2}} </math>
	<math> ~= </math>	<math> ~\frac{1}{(\xi_1^2 - 1)^{1/2}} \, , </math>

and the algebraic expression describing the circle will take the form,

<math> ~(\chi - \chi_0)^2 + \zeta^2 = r_c^2 = (\xi_1^2 - 1)^{-1} . </math>

Let's evaluate the left-hand-side of this expression to see if it indeed reduces to <math>(\xi_1^2 - 1)^{-1}</math>.

<math>~\mathrm{LHS}</math>	<math>~=</math>	<math> ~\biggl\{ \biggl[ \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1 - \xi_2} \biggr] - \frac{\xi_1}{(\xi_1^2 - 1)^{1/2}} \biggr\}^2 + \biggl[ \frac{(1-\xi_2^2)^{1/2}}{\xi_1 - \xi_2} \biggr]^2 </math>
	<math>~=</math>	<math> ~\frac{1}{(\xi_1 - \xi_2)^2 (\xi_1^2 - 1)} \biggl\{ (\xi_1^2 - 1) - \xi_1 (\xi_1-\xi_2) \biggr\}^2 + \frac{(1-\xi_2^2)}{(\xi_1 - \xi_2)^2} </math>
	<math>~=</math>	<math> ~\frac{(\xi_1 \xi_2 - 1)^2}{(\xi_1 - \xi_2)^2 (\xi_1^2 - 1)} + \frac{(1-\xi_2^2)}{(\xi_1 - \xi_2)^2} </math>
	<math>~=</math>	<math> ~\frac{1}{(\xi_1 - \xi_2)^2 (\xi_1^2 - 1)} \biggl[(\xi_1 \xi_2 - 1)^2 + (\xi_1^2 - 1)(1-\xi_2^2) \biggr] </math>
	<math>~=</math>	<math> ~\frac{1}{(\xi_1 - \xi_2)^2 (\xi_1^2 - 1)} \biggl[ \xi_1^2 \xi_2^2 - 2\xi_1 \xi_2 + 1 ) + (\xi_1^2 - 1 -\xi_1^2 \xi_2^2 + \xi_2^2) \biggr] </math>
	<math>~=</math>	<math> ~\frac{\xi_1^2 - 2\xi_1 \xi_2 + \xi_2^2}{(\xi_1 - \xi_2)^2 (\xi_1^2 - 1)} </math>
	<math>~=</math>	<math> ~\frac{1}{(\xi_1^2 - 1)} \, . </math>

Yes! So this means that the <math>~\xi_1 = \mathrm{constant}</math> toroidal contours can be described by the off-center circle expression,

<math> ~(\chi - \chi_0)^2 + \zeta^2 = (\chi_\mathrm{outer} - \chi_0)^2 \, , </math>

or,

<math> ~\biggl[ \chi - \frac{\xi_1}{(\xi_1^2 - 1)^{1/2}} \biggr]^2 + \zeta^2 = \frac{1}{(\xi_1^2 - 1)} \, . </math>

It also means that, while <math>~\xi_1</math> is the official radial coordinate of MF53's toroidal coordinate system, the actual radius of the relevant cross-sectional circle is,

<math> ~r_c </math>

<math> ~= </math>

<math> ~\frac{1}{(\xi_1^2 - 1)^{1/2}} . </math>

Papaloizou-Pringle Tori

Summary of Structure

As derived elsewhere, the accretion tori constructed by Papaloizou & Pringle (1984; hereafter PP84) have the following surface properties. For a given choice of the dimensionless Bernoulli constant, <math>C_\mathrm{B}^'</math>,

<math> ~\chi_\mathrm{inner} </math>	<math>~ =</math>	<math> ~\frac{1}{1 + \sqrt{1-2C_\mathrm{B}^'}} \, ; </math>
<math> ~\chi_\mathrm{outer} </math>	<math>~=</math>	<math> ~\frac{1}{1 - \sqrt{1-2C_\mathrm{B}^'}} \, ; </math>
<math> ~\chi_0 </math>	<math>~=</math>	<math> ~\frac{1}{2} (\chi_\mathrm{outer} + \chi_\mathrm{inner}) = \frac{1}{2C_\mathrm{B}^'} \, ; </math>
<math> ~\delta </math>	<math>~\equiv</math>	<math> ~\frac{\chi_\mathrm{outer} - \chi_\mathrm{inner}}{\chi_0} = 2\sqrt{1-2C_\mathrm{B}^'} \, . </math>

So if I want to construct PP84 tori that are approximately the same size/shape as the MF53 tori illustrated above, I should choose values of the dimensionless Bernoulli constant as follows:

<math> ~{\chi_0}\biggr|_\mathrm{PP84} </math>	<math>~=</math>	<math> ~{\chi_0}\biggr|_\mathrm{MF53} </math>
<math> \Rightarrow~~~~ \frac{1}{2C_\mathrm{B}^'} </math>	<math>~=</math>	<math>~\frac{\xi_1}{(\xi_1^2-1)^{1/2}} </math>
<math> \Rightarrow~~~~ C_\mathrm{B}^' </math>	<math>~=</math>	<math>~\frac{(\xi_1^2-1)^{1/2}}{2\xi_1} \, . </math>

In the accompanying figure labeled "Papaloizou-Pringle Tori," we've drawn three different <math>~C_\mathrm{B}^' = \mathrm{constant}</math> meridional contours for the PP84 tori where the values of the dimensionless Bernoulli constants have been chosen to produce values of <math>~\chi_0</math> that are identical to the values displayed by the three MF53 tori shown above. The following table details properties of these three PP84 tori that have been constructed in an effort to facilitate comparison with the table shown above for MF53 tori.

Properties of <math>C_\mathrm{B}^' = \mathrm{constant}</math> PP84 Toroidal Surfaces
Curve in Figure	<math>C_\mathrm{B}^'</math>	<math>\chi_\mathrm{inner}</math>	<math>\chi_\mathrm{outer}</math>	<math>\chi_0</math>	<math>\delta</math>
Red	0.208	0.567	4.234	2.400	1.528
Blue	0.276	0.599	3.019	1.809	1.338
Gold	0.373	0.665	2.019	1.342	1.009

CCGF Expansion

Cohl & Tohline (1999; hereafter CT99) derive an expression for the Newtonian gravitational potential in terms of a Compact Cylindrical Green's Function expansion. They show, for example, that when expressed in terms of cylindrical coordinates, the axisymmetric potential is,

<math> \Phi(R,z) = - \frac{2G}{R^{1/2}} q_0 , </math>

where,

<math> q_0 = \int (R')^{1/2} \rho(R',z') Q_{-1/2}(\Chi) dR' dz', </math>

and the dimensionless argument of the special function, <math>Q_{-1/2}</math>, is,

<math> \Chi \equiv \frac{R^2 + {R'}^2 + (z - z')^2}{2R R'} . </math>

Note: Here we are using <math>\Chi</math> instead of <math>\chi</math> (as used by CT99) to represent this dimensionless parameter in order to avoid confusion with our use of <math>\chi</math>, above.

Recognition as Circle

If we scale all lengths in this expression to <math>R</math> — in other words, if we set <math>a = R</math> — and, as above, define,

<math> \chi \equiv \frac{R'}{a} ~~~~\mathrm{and}~~~~\zeta \equiv \frac{z-z'}{a} , </math>

we can rewrite the expression in the form,

<math> 2\Chi \chi = \chi^2 + 1 + \zeta^2 , </math>

or,

<math> (\chi - \Chi)^2 + \zeta^2 = (\Chi^2 - 1) . </math>

So, a curve of constant <math>\Chi</math> produces an off-center circle whose center is located at <math>\Chi</math> and whose radius is <math>\sqrt{\Chi^2 - 1}</math>.

Relating CCGF Expansion to Toroidal Coordinates

We see that curves of constant <math>\Chi</math> (as defined in CT99) are in every respect identical to curves of constant <math>\xi_1</math> (as defined in MF53). The association is straightforward:

EUREKA!
<math> \Chi^2 - 1 = \frac{1}{\xi_1^2 - 1} . </math>

But Not Every Circle Will Do

It is very important to appreciate that, although surfaces of constant <math>\Chi</math> (or, equivalently, surfaces of constant <math>\xi_1</math>) are always off-center circles, it is not the case that every off-center circle will prove to be a <math>\Chi= \mathrm{constant}</math> surface in the most relevant toroidal coordinate system. To be more specific, suppose we want to evaluate the potential at some location <math>(R,0)</math> inside or outside of a uniform-density torus whose meridional cross-section is a circle of radius <math>r_c</math> and whose center is located on the <math>x</math>-axis at position <math>x_0</math>. The equation describing the cross-sectional surface of this torus is,

<math> (R' - x_0)^2 - {z'}^2 = r_c^2 . </math>

Dividing through by the square of a (as yet unspecified) scale length, <math>a</math>, gives,

<math> \biggl[ \chi^2 - \frac{x_0}{a} \biggr]^2 - \zeta^2 = \frac{r_c^2}{a^2} . </math>

This dimensionless expression will only describe a <math>\Chi = \mathrm{constant}</math> surface in an MF53 toroidal coordinate system if, simultaneously,

<math> \Chi = \frac{x_0}{a} ~~~~~\mathrm{and}~~~~~ \Chi^2 - 1 = \frac{r_c^2}{a^2} . </math>

That is, only if,

<math> a = (x_0^2 - r_c^2)^{1/2} . </math>

But in the above discussion we were only able to associate the dimensionless argument of the special function in CT99's CCGF expansion with the "radial" coordinate of the MF53 toroidal coordinate system by setting <math>a = R</math>, that is, only by setting the scale length equal to the cylindrical coordinate value <math>R</math> at which the potential is to be evaluated. So the surface of our torus will only align with a <math>\xi_1 = \mathrm{constant}</math> surface in a toroidal coordinate system if,

<math> R = (x_0^2 - r_c^2)^{1/2} . </math>

This is a very tight constraint that usually will not be satisfied.

Multipole Moment in Toroidal Coordinates

While it might not be interesting or useful to impose this constraint in general, it will likely be instructive to evaluate the potential at the location where this constraint is satisfied. That is, we want to evaluate the potential inside a uniform density, circular-cross-section torus at the location,

<math> \Phi[(x_0^2 - r_c^2)^{1/2},0] = - \frac{2G}{(x_0^2 - r_c^2)^{1/4}} q_0 . </math>

Since in this case the argument of <math>Q_{-1/2}</math> can be expressed in terms of the "radial" toroidal coordinate, it is reasonable to write the relevant moment of the mass distribution, <math>q_0</math>, entirely in terms of toroidal coordinates. Specifically,

<math> q_0 = a^{5/2} \int\int \biggl[ \frac{({\xi_1'}^2 - 1)^{1/2}}{\xi_1' - \xi_2'} \biggr]^{1/2} \rho(\xi_1',\xi_2') Q_{-1/2}(\xi_1') \biggl[ \frac{d\xi_1'}{(\xi_1' - \xi_2')({\xi_1'}^2 - 1)^{1/2}} \biggr] \biggl[ \frac{d\xi_2'}{(\xi_1' - \xi_2')(1-{\xi_2'}^2)^{1/2}} \biggr] . </math>

Now suppose that the density distribution is only a function of the radial coordinate, that is, suppose that <math>\rho = \rho(\xi_1')</math>. Then the integral can be written as,

<math> q_0 = a^{5/2} \int \rho(\xi_1') Q_{-1/2}(\xi_1')\biggl[ \frac{d\xi_1'}{({\xi_1'}^2 - 1)^{1/4}} \biggr] \int \biggl[ \frac{d\xi_2'}{(\xi_1' - \xi_2')^{5/2}(1-{\xi_2'}^2)^{1/2}} \biggr] . </math>

Presumably the integral over <math>d\xi_2'</math> can be completed in closed form if the density distribution fills out the entire circular cross-section, that is, if the limits on integration are <math>-1</math> to <math>+1</math>. (Alternatively, write <math>\xi_2'</math> in terms of <math>\cos\theta</math> and integrate from <math>\pi</math> to <math>0</math>.) This needs to be done!

---

Material that appears after this point in our presentation is under development and therefore
may contain incorrect mathematical equations and/or physical misinterpretations.
|   Go Home   |

---

Apparently Irrelevant Material

If we subtract "1" from both sides of this expression, the right-hand-side (RHS) takes on a familiar form:

<math> \chi_\mathrm{CT99}-1 </math>	<math>=</math>	<math> \frac{1}{2R R'} \biggl[ R^2 + {R'}^2 + (z - z')^2 - 2 R R' \biggr] </math>
	<math>=</math>	<math> \frac{1}{2R R'} \biggl[ (R - R')^2 + (z - z')^2 \biggr] . </math>

It appears as though the quantity, <math>[2R R'(\chi_\mathrm{CT99}-1)]^{1/2}</math>, is the radius <math>r_c</math> of a circle whose center is located at either <math>(R,z)</math> or <math>(R',z')</math>, that is, whose center is shifted off the origin of a cylindrical coordinate system. I'm not yet sure how/if we can benefit from recognizing this association.

Case A: Suppose we associate <math>R'</math> with the center of a toroidal cross-section and, at the same time, associate <math>R</math> with the inner edge of a particular toroidal cross-section that is associated with the toroidal coordinate <math>\xi_1</math>. We know that the scale-length <math>a</math> that is associated with the chosen toroidal coordinate system must be given by the ratio,

<math> a = \frac{R'}{\chi_0} . </math>

[NOTE: As I'm doing this, I'm realizing that it may be wiser to associate <math>a</math> directly with the coordinate location <math>R'</math>. But let's play this out first and see.]

Then it also will be true that,

<math> a = \frac{R}{\chi_\mathrm{inner}} = R \biggl[ \frac{\xi_1+1}{\xi_1 - 1} \biggr]^{1/2}. </math>

Hence, we conclude that,

<math> \mathrm{Case~A:}~~~~~\frac{R}{R'} = \frac{\chi_\mathrm{inner}}{\chi_0} = \biggl[\frac{\xi_1 - 1}{\xi_1 + 1}\biggr]^{1/2} \frac{(\xi_1^2 - 1)^{1/2}}{\xi_1} = \frac{(\xi_1 - 1)}{\xi_1} </math>

<math> \Rightarrow~~~~~ \xi_1 = \biggl[1 - \frac{R}{R'} \biggr]^{-1} . </math>

What, then, is the expression for the scale-length <math>a</math> in terms of just <math>R</math> and <math>R'</math>? Well ...

<math> \xi_1 + 1 = \frac{1}{1-(R/R')} +1 = \frac{2 - R/R'}{1-(R/R')} , </math>

and

<math> \xi_1 - 1 = \frac{1}{1-(R/R')} -1 = \frac{R/R'}{1-(R/R')} . </math>

Hence,

<math> a = R \biggl[ \frac{2 - R/R'}{R/R'} \biggr]^{1/2} = ( 2RR' - R^2 )^{1/2}. </math>

Case B: On the other hand, if we associate <math>R'</math> directly with <math>a</math>, then we conclude,

<math> \mathrm{Case~B:}~~~~~\frac{R}{R'} = \chi_\mathrm{inner} = \biggl[\frac{\xi_1 - 1}{\xi_1 + 1}\biggr]^{1/2} . </math>

<math> \Rightarrow~~~~~ (\xi_1 + 1)\biggl(\frac{R}{R'}\biggr)^2 = \xi_1 - 1 . </math>

<math> \Rightarrow~~~~~ \xi_1 \biggl[ 1 - \biggl(\frac{R}{R'}\biggr)^2 \biggr] = \biggl[1 + \biggl(\frac{R}{R'}\biggr)^2 \biggr]. </math>

<math> \Rightarrow~~~~~ \xi_1 = \biggl[1 + \biggl(\frac{R}{R'}\biggr)^2 \biggr]\biggl[ 1 - \biggl(\frac{R}{R'}\biggr)^2 \biggr] ^{-1}. </math>

---

References

1. Morse, P.M. & Feshmach, H. 1953, Methods of Theoretical Physics — Volumes I and II
2. Cohl, H.S. & Tohline, J.E. 1999, ApJ, 527, 86-101
3. Cohl, H.S., Rau, A.R.P., Tohline, J.E., Browne, D.A., Cazes, J.E. & Barnes, E.I. 2001, Phys. Rev. A, 64, 052509

 

© 2014 - 2021 by Joel E. Tohline |   H_Book Home   |   YouTube   | Appendices: | Equations | Variables | References | Ramblings | Images | myphys.lsu | ADS | Recommended citation:   Tohline, Joel E. (2021), The Structure, Stability, & Dynamics of Self-Gravitating Fluids, a (MediaWiki-based) Vistrails.org publication, https://www.vistrails.org/index.php/User:Tohline/citation