Difference between revisions of "User:Tohline/SSC/Virial/PolytropesSummary"
(→Virial Equilibrium of Adiabatic Spheres (Summary): Construct "foreshadowing" equation in first subsection) |
|||
| Line 42: | Line 42: | ||
<td align="left"> | <td align="left"> | ||
<math> | <math> | ||
\tilde\ | \tilde\theta^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} | ||
\biggl[ \frac{(n+1)^3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2}\biggr]^{(n+1)/(n-3)} \, , | \biggl[ \frac{(n+1)^3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2}\biggr]^{(n+1)/(n-3)} \, , | ||
</math> | </math> | ||
| Line 84: | Line 84: | ||
In the expressions for <math>~r_a</math> and <math>~p_a</math>, the tilde indicates that the Lane-Emden function and its derivative are to be evaluated, not at the radial coordinate, <math>~\xi_1</math>, that is traditionally associated with the "first zero" of the Lane-Emden function and therefore with the surface of the ''isolated polytrope,'' but at the radial coordinate, <math>~\tilde\xi</math>, where the internal pressure of the isolated polytrope equals <math>~P_e</math> and at which the ''embedded'' polytrope is to be truncated. The coordinate, <math>~\tilde\xi</math>, therefore identifies the surface of the embedded — or, pressure-truncated — polytrope. We also have taken the liberty of attaching the subscript "limit" to <math>~M</math> in both defining relations because it is clear that Horedt intended for the normalization mass to be the mass of the pressure-truncated object, not the mass of the associated ''isolated'' (and untruncated) polytrope. | In the expressions for <math>~r_a</math> and <math>~p_a</math>, the tilde indicates that the Lane-Emden function and its derivative are to be evaluated, not at the radial coordinate, <math>~\xi_1</math>, that is traditionally associated with the "first zero" of the Lane-Emden function and therefore with the surface of the ''isolated polytrope,'' but at the radial coordinate, <math>~\tilde\xi</math>, where the internal pressure of the isolated polytrope equals <math>~P_e</math> and at which the ''embedded'' polytrope is to be truncated. The coordinate, <math>~\tilde\xi</math>, therefore identifies the surface of the embedded — or, pressure-truncated — polytrope. We also have taken the liberty of attaching the subscript "limit" to <math>~M</math> in both defining relations because it is clear that Horedt intended for the normalization mass to be the mass of the pressure-truncated object, not the mass of the associated ''isolated'' (and untruncated) polytrope. | ||
From these previously published works, it is not obvious how — or even ''whether'' — this pair of parametric equations can be combined to directly show how the equilibrium radius depends on the value of the external pressure. Our examination of the free-energy of these configurations and, especially, an application of the viral theorem shows this direct relationship. | From these previously published works, it is not obvious how — or even ''whether'' — this pair of parametric equations can be combined to directly show how the equilibrium radius depends on the value of the external pressure. Our examination of the free-energy of these configurations and, especially, an application of the viral theorem shows this direct relationship. Foreshadowing these results, we note that, | ||
<div align="center"> | <div align="center"> | ||
<math>~P_e | <table border="0" cellpadding="5"> | ||
<tr> | |||
<td align="right"> | |||
<math>~\biggl(\frac{P_e}{P_\mathrm{norm}}\biggr) \biggl(\frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4 </math> | |||
</td> | |||
<td align="center"> | |||
<math>~=</math> | |||
</td> | |||
<td align="left"> | |||
<math> | |||
\biggl[ \frac{\tilde\theta^{n+1} }{(4\pi)(n+1)( -\tilde\theta' )^{2}} \biggr] | |||
\biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{2} \, . | |||
</math> | |||
</td> | |||
</tr> | |||
</table> | |||
</div> | </div> | ||
==Free Energy Function and Virial Theorem== | ==Free Energy Function and Virial Theorem== | ||
| Line 110: | Line 128: | ||
[[User:Tohline/SSC/Virial/Polytropes#Virial_Equilibrium_of_Adiabatic_Spheres|accompanying detailed analysis of the structure of pressure-truncated polytropes]], we use the virial theorem to show that the equilibrium radii that are identified by extrema in the free-energy function always satisfy the following, | [[User:Tohline/SSC/Virial/Polytropes#Virial_Equilibrium_of_Adiabatic_Spheres|accompanying detailed analysis of the structure of pressure-truncated polytropes]], we use the virial theorem to show that the equilibrium radii that are identified by extrema in the free-energy function always satisfy the following, | ||
<div align="center" id="ConciseVirial"> | <div align="center" id="ConciseVirial"> | ||
<font color="#770000">'''Algebraic Expression of the Virial | <font color="#770000">'''Algebraic Expression of the Virial Theorem'''</font><br /> | ||
<math> | <math> | ||
Revision as of 15:13, 11 October 2014
Virial Equilibrium of Adiabatic Spheres (Summary)
The summary presented here has been drawn from our accompanying detailed analysis of the structure of pressure-truncated polytropes.

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
Detailed Force-Balanced Solution
As has been discussed in detail in another chapter, Horedt (1970), Whitworth (1981) and Stahler (1983) have separately derived what the equilibrium radius, <math>~R_\mathrm{eq}</math>, is of a polytropic sphere that is embedded in an external medium of pressure, <math>~P_e</math>. Their solution of the detailed force-balanced equations provides a pair of analytic expressions for <math>~R_\mathrm{eq}</math> and <math>~P_e</math> that are parametrically related to one another through the Lane-Emden function, <math>~\theta</math>, and its radial derivative. For example — see our related discussion for more details — from Horedt's work we obtain the following pair of equations:
|
<math> ~\frac{R_\mathrm{eq}}{R_\mathrm{norm}} = r_a \cdot \biggl( \frac{R_\mathrm{Horedt}}{R_\mathrm{norm}} \biggr) </math> |
<math>~=~</math> |
<math> \tilde\xi ( -\tilde\xi^2 \tilde\theta' )^{(1-n)/(n-3)} \biggl[ \frac{4\pi}{(n+1)^n} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{n-1} \biggr]^{1/(n-3)} \, , </math> |
|
<math> ~\frac{P_\mathrm{e}}{P_\mathrm{norm}} = p_a \cdot \biggl( \frac{P_\mathrm{Horedt}}{P_\mathrm{norm}} \biggr) </math> |
<math>~=~</math> |
<math> \tilde\theta^{n+1}( -\tilde\xi^2 \tilde\theta' )^{2(n+1)/(n-3)} \biggl[ \frac{(n+1)^3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr)^{-2}\biggr]^{(n+1)/(n-3)} \, , </math> |
where we have introduced the normalizations,
|
<math>~R_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \biggl( \frac{G}{K} \biggr)^n M_\mathrm{tot}^{n-1} \biggr]^{1/(n-3)} \, ,</math> |
|
<math>~P_\mathrm{norm}</math> |
<math>~\equiv</math> |
<math>~\biggl[ \frac{K^{4n}}{G^{3(n+1)} M_\mathrm{tot}^{2(n+1)}} \biggr]^{1/(n-3)} \, .</math> |
In the expressions for <math>~r_a</math> and <math>~p_a</math>, the tilde indicates that the Lane-Emden function and its derivative are to be evaluated, not at the radial coordinate, <math>~\xi_1</math>, that is traditionally associated with the "first zero" of the Lane-Emden function and therefore with the surface of the isolated polytrope, but at the radial coordinate, <math>~\tilde\xi</math>, where the internal pressure of the isolated polytrope equals <math>~P_e</math> and at which the embedded polytrope is to be truncated. The coordinate, <math>~\tilde\xi</math>, therefore identifies the surface of the embedded — or, pressure-truncated — polytrope. We also have taken the liberty of attaching the subscript "limit" to <math>~M</math> in both defining relations because it is clear that Horedt intended for the normalization mass to be the mass of the pressure-truncated object, not the mass of the associated isolated (and untruncated) polytrope.
From these previously published works, it is not obvious how — or even whether — this pair of parametric equations can be combined to directly show how the equilibrium radius depends on the value of the external pressure. Our examination of the free-energy of these configurations and, especially, an application of the viral theorem shows this direct relationship. Foreshadowing these results, we note that,
|
<math>~\biggl(\frac{P_e}{P_\mathrm{norm}}\biggr) \biggl(\frac{R_\mathrm{eq}}{R_\mathrm{norm}} \biggr)^4 </math> |
<math>~=</math> |
<math> \biggl[ \frac{\tilde\theta^{n+1} }{(4\pi)(n+1)( -\tilde\theta' )^{2}} \biggr] \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr)^{2} \, . </math> |
Free Energy Function and Virial Theorem
The variation with size of the normalized free energy, <math>~\mathfrak{G}^*</math>, of pressure-truncated adiabatic spheres is described by the following,
Algebraic Free-Energy Function
<math> \mathfrak{G}^* = -3\mathcal{A} \chi^{-1} +~ \frac{1}{(\gamma - 1)} \mathcal{B} \chi^{3-3\gamma} +~ \mathcal{D}\chi^3 \, . </math>
In this expression, the size of the configuration is set by the value of the dimensionless radius, <math>~\chi \equiv R/R_\mathrm{norm}</math>; as is clarified, below, the values of the coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, characterize the relative importance, respectively, of the gravitational potential energy and the internal thermal energy of the configuration; <math>~\gamma</math> is the exponent (from the adopted equation of state) that identifies the adiabat along which the configuration heats or cools upon expansion or contraction; and the relative importance of the imposed external pressure is expressed through the free-energy expression's third constant coefficient, specifically,
<math>~\mathcal{D} \equiv \frac{4\pi}{3} \biggl( \frac{P_e}{P_\mathrm{norm}} \biggr) \, .</math>
When examining a range of physically reasonable configuration sizes for a given choice of the constants <math>~(\gamma, \mathcal{A}, \mathcal{B}, \mathcal{D})</math>, a plot of <math>~\mathfrak{G}^*</math> versus <math>~\chi</math> will often reveal one or two extrema. Each extremum is associated with an equilibrium radius, <math>~\chi_\mathrm{eq} \equiv R_\mathrm{eq}/R_\mathrm{norm}</math>.
Equilibrium radii may also be identified through an algebraic relation that originates from the scalar virial theorem — a theorem that, itself, is derivable from the free-energy expression by setting <math>~\partial\mathfrak{G}^*/\partial\chi = 0</math>. In our accompanying detailed analysis of the structure of pressure-truncated polytropes, we use the virial theorem to show that the equilibrium radii that are identified by extrema in the free-energy function always satisfy the following,
Algebraic Expression of the Virial Theorem
<math> \Pi_\mathrm{ad} = \frac{(\chi_\mathrm{ad}^{4-3\gamma} - 1)}{\chi_\mathrm{ad}^4} \, , </math>
where, after setting <math>~\gamma = (n+1)/n</math>,
|
<math>~\Pi_\mathrm{ad}</math> |
<math>~=</math> |
<math> ~\mathcal{D} \biggl[ \frac{\mathcal{A}^{3(n+1)}}{\mathcal{B}^{4n}} \biggr]^{1/(n-3)} \, , </math> and, |
|
<math>~\chi_\mathrm{ad}</math> |
<math>~=</math> |
<math> ~\chi_\mathrm{eq} \biggl[ \frac{\mathcal{B}}{\mathcal{A}} \biggr]^{n/(n-3)} \, . </math> |
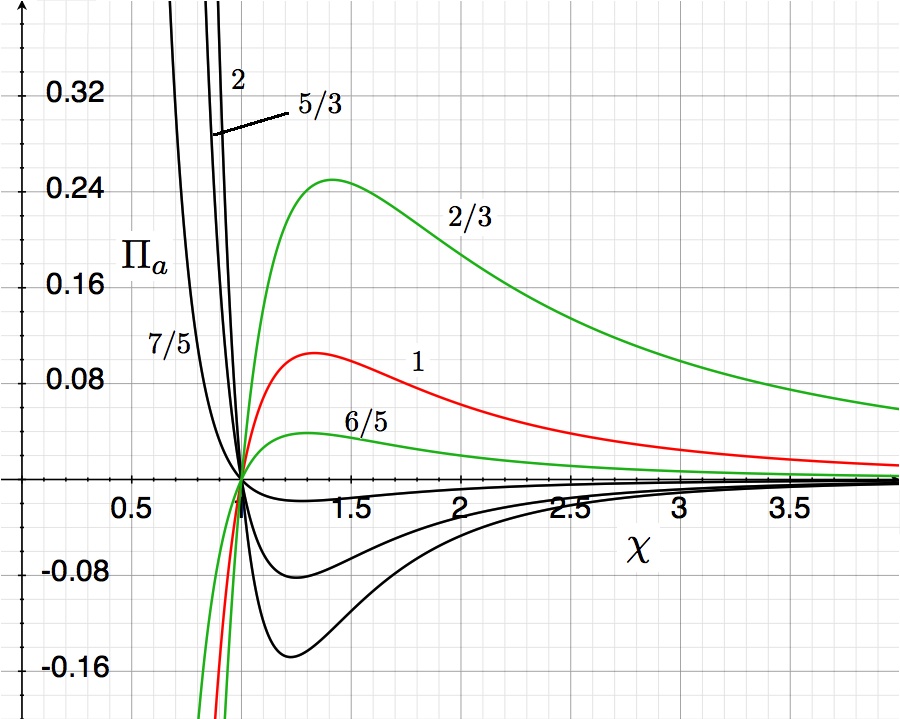
The curves shown in the accompanying "pressure-radius" diagram trace out this derived virial-theorem function for six different values of the adiabatic exponent, <math>~\gamma</math>, as labeled. They show the dimensionless external pressure, <math>~\Pi_\mathrm{ad}</math>, that is required to construct a nonrotating, self-gravitating, adiabatic sphere with a dimensionless equilibrium radius <math>~\chi_\mathrm{ad}</math>. The mathematical solution becomes unphysical wherever the pressure becomes negative.
Relationship to Detailed Force-Balanced Models
Structural Form Factors
In our accompanying detailed analysis, we demonstrate that the expressions given above for the free-energy function and the virial theorem are correct in sufficiently strict detail that they can be used to precisely match — and assist in understanding — the equilibrium of embedded polytropes whose structures have been determined from the set of detailed force-balance equations. In order to draw this association, it is only necessary to realize that, very broadly, the constant coefficients, <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math>, in the above algebraic free-energy expression are expressible in terms of three structural form factors, <math>~\tilde\mathfrak{f}_M</math>, <math>~\tilde\mathfrak{f}_W</math>, and <math>~\tilde\mathfrak{f}_A</math>, as follows:
|
<math>~\mathcal{A}</math> |
<math>~\equiv</math> |
<math>\frac{1}{5} \cdot \biggl[ \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}} \biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]^2 \cdot \tilde\mathfrak{f}_W \, ,</math> |
|
<math>~\mathcal{B}</math> |
<math>~\equiv</math> |
<math> \frac{4\pi}{3} \biggl[ \frac{3}{4\pi} \biggl( \frac{M_\mathrm{limit}}{M_\mathrm{tot}}\biggr) \frac{1}{\tilde\mathfrak{f}_M} \biggr]_\mathrm{eq}^{(n+1)/n} \cdot \tilde\mathfrak{f}_A = \frac{4\pi}{3} \biggl[ \biggl( \frac{P_c}{P_\mathrm{norm}} \biggr)\chi^{3(n+1)/n} \biggr]_\mathrm{eq} \cdot \tilde\mathfrak{f}_A \, ; </math> |
and that, specifically in the context of spherically symmetric, pressure-truncated polytropes, we can write,
|
<math>~\tilde\mathfrak{f}_M</math> |
<math>~=</math> |
<math>~ \biggl[ - \frac{3\tilde\theta^'}{\tilde\xi} \biggr] \, ,</math> |
|
<math>\tilde\mathfrak{f}_W </math> |
<math>~=</math> |
<math>~\frac{3^2\cdot 5}{5-n} \biggl[ \frac{\tilde\theta^'}{\tilde\xi} \biggr]^2 \, ,</math> |
|
<math>\tilde\mathfrak{f}_A </math> |
<math>~=</math> |
<math> \frac{3(n+1) }{(5-n)} ~\biggl[ \tilde\theta^' \biggr]^2 + \tilde\theta^{n+1} \, . </math> |
After plugging these nontrivial expressions for <math>~\mathcal{A}</math> and <math>~\mathcal{B}</math> into the righthand sides of the above equations for <math>~\Pi_\mathrm{ad}</math> and <math>~\chi_\mathrm{ad}</math> and, simultaneously, using Horedt's detailed force-balanced expressions for <math>~r_a</math> and <math>~p_a</math> to specify, respectively, <math>~\chi_\mathrm{eq}</math> and <math>~P_e/P_\mathrm{norm}</math> in these same equations, we find that,
|
<math>~\Pi_\mathrm{ad}</math> |
<math>~=</math> |
<math>~\eta_\mathrm{ad} (1 + \eta_\mathrm{ad})^{-4n/(n-3)} \, ,</math> |
|
<math>~\chi_\mathrm{ad}</math> |
<math>~=</math> |
<math>~(1 + \eta_\mathrm{ad})^{n/(n-3)} \, ,</math> |
where the newly identified, key physical parameter,
|
<math>~\eta_\mathrm{ad} </math> |
<math>~\equiv</math> |
<math>~\frac{(5-n) \tilde\theta^{n+1}}{3(n+1) (\tilde\theta^')^2} \, .</math> |
It is straightforward to show that this more compact pair of expressions for <math>~\Pi_\mathrm{ad}</math> and <math>~\chi_\mathrm{ad}</math> satisfy the virial theorem presented above. This demonstrates that the virial theorem provides the desired algebraic expression relating <math>~R_\mathrm{eq}</math> to <math>~P_e</math>.
Physical Meaning of
Desired Pressure-Radius Relation
Discussion
Physical Meaning of Parameter <math>~\eta_\mathrm{ad}</math>
As defined in our above discussion, <math>~\eta_\mathrm{ad}</math> is the ratio of the two terms that are summed together in the definition of the structural form factor, <math>~\tilde\mathfrak{f}_A</math>. It is worth pointing out what physical quantities are associated with these two terms.
At any radial location within a polytropic configuration, the Lane-Emden function, <math>~\theta</math>, is defined in terms of a ratio of the local density to the configuration's central density, specifically,
<math>\theta \equiv \biggl(\frac{\rho}{\rho_c} \biggr)^{1/n} \, .</math>
Remembering that, at any location within the configuration, the pressure is related to the density via the polytropic equation of state,
<math>P = K\rho^{(n+1)/n} \, ,</math>
we see that,
<math>\frac{P}{P_c} = \theta^{n+1} \, .</math>
Hence, the quantity, <math>~\tilde\theta^{n+1}</math>, which appears as the second term in our definition of <math>~\tilde\mathfrak{f}_A</math>, is the ratio, <math>~(P/P_c)_{\tilde\xi}</math>, evaluated at the surface of the truncated polytropic sphere. But, by construction, the pressure at this location equals the pressure of the external medium in which the polytrope is embedded, so we can write,
<math>\tilde\theta^{n+1} = \frac{P_e}{P_c} \, .</math>
In our accompanying detailed analysis, we have employed the virial theorem expression to demonstrate that the first term in our definition of <math>~\tilde\mathfrak{f}_A</math> provides a measure the configuration's normalized central pressure. Specifically, we show that,
|
<math>~\biggl( \frac{4\pi}{3} \biggr) \frac{P_c R_\mathrm{eq}^4}{G M_\mathrm{tot}^2}</math> |
<math>~=</math> |
<math>~[3 (n+1) (\tilde\theta^')^2]^{-1} \, .</math> |
We conclude, therefore, that quite generally,
|
<math>(5-n) \tilde\mathfrak{f}_A </math> |
<math>~=</math> |
<math> \biggl( \frac{3}{4\pi} \biggr) \frac{G M_\mathrm{tot}^2}{P_c R_\mathrm{eq}^4} + (5-n) \frac{P_e}{P_c} </math> |
|
|
<math>~=</math> |
<math> \biggl( \frac{3}{4\pi} \biggr) \frac{G M_\mathrm{tot}^2}{P_c R_\mathrm{eq}^4} \biggl[1 + \eta_\mathrm{ad} \biggr] \, , </math> |
and that,
|
<math>~\eta_\mathrm{ad} </math> |
<math>~=</math> |
<math>\biggl[ \frac{4\pi (5-n)}{3} \biggr] \frac{P_e R_\mathrm{eq}^4}{G M_\mathrm{tot}^2} \, .</math> |
Model Sequences
After choosing a value for the system's adiabatic index (or, equivalently, its polytropic index), <math>~\gamma = (n+1)/n</math>, the functional form of the virial theorem expression, <math>~\Pi_\mathrm{ad}(\chi_\mathrm{ad})</math>, is known and, hence, the equilibrium model sequence can be plotted. Half-a-dozen such model sequences are shown in the figure near the beginning of this discussion. Each curve can be viewed as mapping out a single-parameter sequence of equilibrium models; "evolution" along the curve can be accomplished by varying the key parameter, <math>~\eta_\mathrm{ad}</math>, over the physically relevant range, <math>0 \le \eta_\mathrm{ad} < \infty</math>.
In the limiting case where <math>~\eta_\mathrm{ad} = 0</math> because <math>~\tilde\theta \rightarrow \theta_{\xi_1} = 0</math>, all curves converge on the same point, that is, <math>~(\chi_\mathrm{ad}, \Pi_\mathrm{ad}) = (1, 0)</math>. This corresponds to the case of no external medium <math>~(P_e = 0)</math> and the familiar isolated polytropic equilibrium configuration.

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |