Difference between revisions of "User:Tohline/SSC/Stability/BiPolytrope0 0CompareApproaches"
(→Sequences: Finished inserting and describing Figure 2) |
(→Key Attributes of Equilibrium Configurations: Finished adding clarifying text) |
||
| Line 23: | Line 23: | ||
===Physical Properties=== | ===Physical Properties=== | ||
Aside from specifying its radius, <math>~R</math>, and total mass, <math>~M_\mathrm{tot}</math>, there are three particularly interesting ''dimensionless'' parameters that characterize the internal structure of a bipolytrope having <math>~(n_c,n_e) = (0,0)</math>. They are, the radial location of the core/envelope interface, | [[File:CommentButton02.png|right|100px|This adopted parameter notation pays tribute to the notation that was introduced by Chandrasekhar and his collaborators in the early 1940s in papers associated with the discovery of the Schönberg-Chandrasekhar mass limit.]]Aside from specifying its radius, <math>~R</math>, and total mass, <math>~M_\mathrm{tot}</math>, there are three particularly interesting ''dimensionless'' parameters that characterize the internal structure of a bipolytrope having <math>~(n_c,n_e) = (0,0)</math>. They are, the radial location of the core/envelope interface, | ||
<div align="center"> | <div align="center"> | ||
<math>~q \equiv \frac{r_i}{R} \, ;</math> | <math>~q \equiv \frac{r_i}{R} \, ;</math> | ||
| Line 31: | Line 31: | ||
<math>~\nu \equiv \frac{M_\mathrm{core}}{M_\mathrm{tot}} \, .</math> | <math>~\nu \equiv \frac{M_\mathrm{core}}{M_\mathrm{tot}} \, .</math> | ||
</div> | </div> | ||
Identifying a unique bipolytropic configuration requires the specification of two of these three dimensionless parameters; the third parameter is, then, necessarily determined via the | Identifying a unique bipolytropic configuration requires the specification of two of these three dimensionless parameters; the third parameter is, then, necessarily determined via what we will refer to as the, | ||
<div align="center"> | |||
<div align="center" id="PrimaryAlgebraicConstraint"> | |||
<font color="#770000">'''Primary Algebraic Constraint'''</font><br /> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 122: | Line 124: | ||
an equilibrium model ''sequence'' can be defined by, for example, specifying that all models along the sequence have the same density jump at the interface. Drawing on the above constraint | an equilibrium model ''sequence'' can be defined by, for example, specifying that all models along the sequence have the same density jump at the interface. Drawing on the above ''[[#PrimaryAlgebraicConstraint|primary algebraic constraint]]'', each choice of <math>~\rho_e/\rho_c</math> will generate a sequence governed by the function, | ||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 146: | Line 148: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\frac{q^3}{q^3 + (1-q^3)(\rho_e/\rho_c)} </math> | <math>~\frac{q^3}{q^3 + (1-q^3)(\rho_e/\rho_c)} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
</div> | </div> | ||
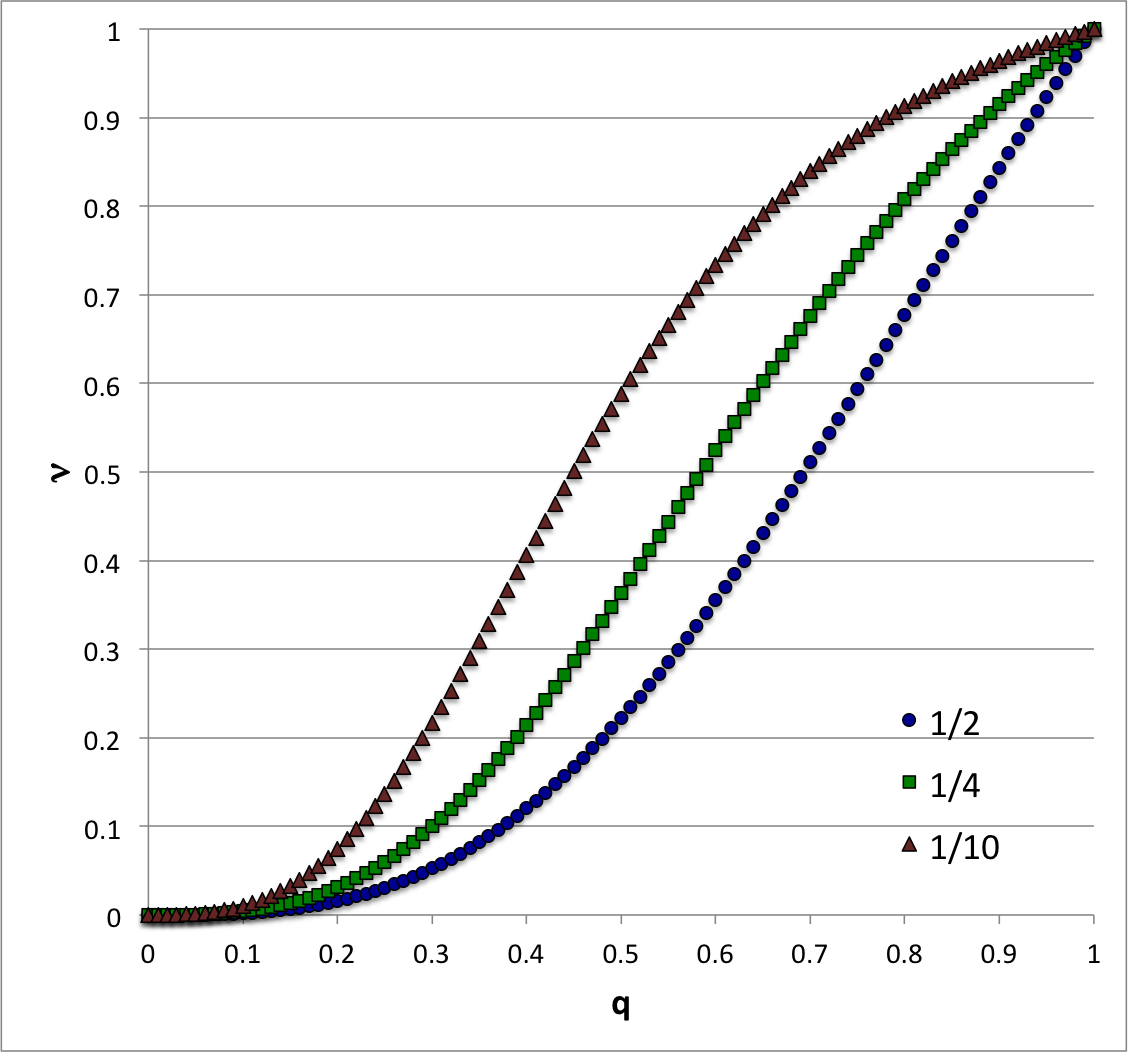
Figure 1 displays several such equilibrium sequences across the <math>~(q,\nu)</math> plane — see also a [[User:Tohline/SSC/Structure/BiPolytropes/Analytic0_0#Illustration|related figure associated with our free-energy determination of stability]]. We have employed a free-energy analysis (see summary, below) to examine whether a transition from stable to unstable configurations is encountered while traversing — that is, while ''evolving'' along — such | Figure 1 displays several such equilibrium sequences across the <math>~(q,\nu)</math> plane — see also a [[User:Tohline/SSC/Structure/BiPolytropes/Analytic0_0#Illustration|related figure associated with our free-energy determination of stability]]. The curves show how <math>~\nu</math> varies with <math>~q</math> along sequences for which the specified density ratio is <math>~\tfrac{1}{2}</math> (blue), <math>~\tfrac{1}{4}</math> (green), and <math>~\tfrac{1}{10}</math> (maroon). We have employed a free-energy analysis (see summary, below) to examine whether a transition from stable to unstable configurations is encountered while traversing — that is, while ''evolving'' along — such sequences. | ||
<table border="0" cellpadding="10" align="left"><tr><td align="center"> | <table border="0" cellpadding="10" align="left"><tr><td align="center"> | ||
| Line 165: | Line 167: | ||
</table> | </table> | ||
</td></tr></table> | </td></tr></table> | ||
In a separate search for eigenvectors that simultaneously satisfy the linear adiabatic wave equation (LAWE) for the core and the LAWE for the envelope (see summary, below), we discovered that eigenvectors for some radial modes of oscillation can be specified ''fully analytically'' along a sequence of equilibrium models that is defined by the | In a separate search for eigenvectors that simultaneously satisfy the linear adiabatic wave equation (LAWE) for the core and the LAWE for the envelope (see summary, below), we discovered that eigenvectors for some radial modes of oscillation can be specified ''fully analytically'' along a sequence of equilibrium models that is defined by what we will refer to as the, | ||
<div align="center"> | |||
<div align="center" id="AnalyticEigenvectorConstraint"> | |||
<font color="#770000">'''Analytic Eigenvector Constraint'''</font><br /> | |||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 184: | Line 188: | ||
</table> | </table> | ||
</div> | </div> | ||
When combined with the above ''[[#PrimaryAlgebraicConstraint|primary algebraic constraint]]'', this is equivalent to demanding that, | |||
<div align="center"> | <div align="center"> | ||
<table border="0" cellpadding="5" align="center"> | <table border="0" cellpadding="5" align="center"> | ||
| Line 213: | Line 217: | ||
</td> | </td> | ||
<td align="left"> | <td align="left"> | ||
<math>~\ | <math>~\frac{2q^3}{1+2q^3} \, .</math> | ||
</td> | </td> | ||
</tr> | </tr> | ||
Revision as of 02:48, 7 January 2017
Comparing Stability Analyses of Zero-Zero Bipolytropes

|
|---|
| | Tiled Menu | Tables of Content | Banner Video | Tohline Home Page | |
In separate chapters we have discussed the following interrelated aspects of Bipolytropes that have <math>~(n_c,n_e) = (0,0)</math>:
- Using a detailed force-balance analysis to develop an analytic description of their equilibrium structure
- Using a free-energy analysis to analytically identify the properties of equilibrium structures; see also, an explicit, analytic evaluation of the statement of Virial Equilibrium
- Developing the Linear Adiabatic Wave Equation (LAWE) as it applies separately to the core and to the envelope of zero-zero bipolytropic configurations
- Identifying a method to analytically solve the matching LAWEs for a certain subset of configurations
- A summary of this solution technique, along with the first illustrative analytic specification of an eigenvector
- The derivation of analytically specifiable eigenvectors having a variety of mode quantum numbers
- A free-energy analysis of the global stability of zero-zero bipolytropes
Building on these separate discussions, here we examine what might be learned from a comparison of the two traditional approaches to stability analysis, namely: (1) solutions of the LAWE, and (2) a free-energy analysis.
Key Attributes of Equilibrium Configurations
Physical Properties
Aside from specifying its radius, <math>~R</math>, and total mass, <math>~M_\mathrm{tot}</math>, there are three particularly interesting dimensionless parameters that characterize the internal structure of a bipolytrope having <math>~(n_c,n_e) = (0,0)</math>. They are, the radial location of the core/envelope interface,
<math>~q \equiv \frac{r_i}{R} \, ;</math>
the ratio of the density of the envelope material to the density of the core, <math>~0 \le \rho_e/\rho_c \le 1</math>; and the fraction of the total mass that is contained in the core,
<math>~\nu \equiv \frac{M_\mathrm{core}}{M_\mathrm{tot}} \, .</math>
Identifying a unique bipolytropic configuration requires the specification of two of these three dimensionless parameters; the third parameter is, then, necessarily determined via what we will refer to as the,
Primary Algebraic Constraint
|
<math>~\frac{\rho_e}{\rho_c} </math> |
<math>=</math> |
<math>~\frac{q^3(1-\nu)}{\nu(1-q^3)} \, .</math> |
It is also relatively straightforward to appreciate that, in dimensional units, the value of the central density is,
|
<math>~\rho_c</math> |
<math>~=</math> |
<math>~\frac{3M_\mathrm{tot}}{4\pi G R^3} \cdot \frac{\nu}{q^3} \, .</math> |
Our study of equilibrium configurations has shown that once, for example, the pair of parameters, <math>~q</math> and <math>~\rho_e/\rho_c</math>, has been specified, other properties of the associated equilibrium configuration can be succinctly expressed in terms of the function,
|
<math>~g^2</math> |
<math>~\equiv</math> |
<math> 1 + \biggl(\frac{\rho_e}{\rho_c}\biggr) \biggl[ 2 \biggl(1 - \frac{\rho_e}{\rho_c} \biggr) \biggl( 1-q \biggr) + \frac{\rho_e}{\rho_c} \biggl(\frac{1}{q^2} - 1\biggr) \biggr] \, . </math> |
For example, the central pressure is given by the expression,
|
<math>~P_c</math> |
<math>~=</math> |
<math>\biggl( \frac{3}{2^3\pi} \biggr) \frac{\nu^2 g^2}{q^4} \biggl[ \frac{GM_\mathrm{tot}^2}{R^4} \biggr] \, .</math> |
Sequences
|
Across the two-dimensional, <math>~(q,\nu)</math> parameter space that is defined by the full range of physically viable values of <math>~q</math> and <math>~\nu</math>, namely,
<math>~0 \le q \le 1 \, ,</math> and <math>~0 \le \nu \le 1 \, ,</math>
an equilibrium model sequence can be defined by, for example, specifying that all models along the sequence have the same density jump at the interface. Drawing on the above primary algebraic constraint, each choice of <math>~\rho_e/\rho_c</math> will generate a sequence governed by the function,
|
<math>~\nu</math> |
<math>=</math> |
<math>~\biggl[\frac{(1-q^3)}{q^3} \biggl( \frac{\rho_e}{\rho_c} \biggr) + 1\biggr]^{-1} </math> |
|
|
<math>=</math> |
<math>~\frac{q^3}{q^3 + (1-q^3)(\rho_e/\rho_c)} \, .</math> |
Figure 1 displays several such equilibrium sequences across the <math>~(q,\nu)</math> plane — see also a related figure associated with our free-energy determination of stability. The curves show how <math>~\nu</math> varies with <math>~q</math> along sequences for which the specified density ratio is <math>~\tfrac{1}{2}</math> (blue), <math>~\tfrac{1}{4}</math> (green), and <math>~\tfrac{1}{10}</math> (maroon). We have employed a free-energy analysis (see summary, below) to examine whether a transition from stable to unstable configurations is encountered while traversing — that is, while evolving along — such sequences.
|
In a separate search for eigenvectors that simultaneously satisfy the linear adiabatic wave equation (LAWE) for the core and the LAWE for the envelope (see summary, below), we discovered that eigenvectors for some radial modes of oscillation can be specified fully analytically along a sequence of equilibrium models that is defined by what we will refer to as the,
Analytic Eigenvector Constraint
|
<math>~g^2</math> |
<math>~\equiv</math> |
<math>~1 + 2\biggl(\frac{\rho_e}{\rho_c}\biggr) - 3\biggl(\frac{\rho_e}{\rho_c}\biggr)^2 \, . </math> |
When combined with the above primary algebraic constraint, this is equivalent to demanding that,
|
<math>~\nu</math> |
<math>~=</math> |
<math>~\tfrac{1}{3}(1+2q^3) \, ,</math> |
and, simultaneously,
|
<math>~\frac{\rho_e}{\rho_c}</math> |
<math>~=</math> |
<math>~\frac{2q^3}{1+2q^3} \, .</math> |
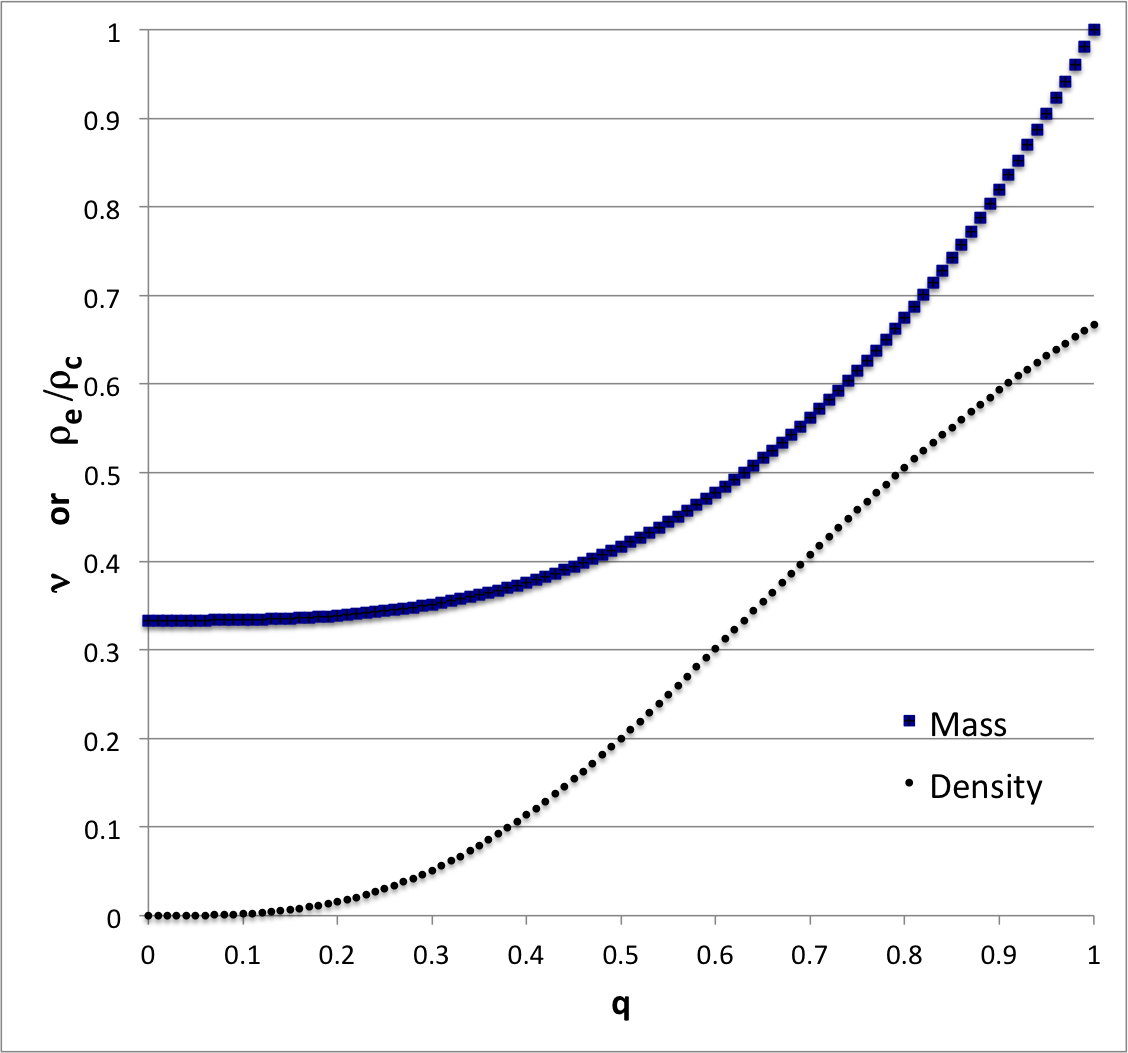
The behavior of these two functions is displayed in Figure 2; the variation of <math>~\nu</math> with <math>~q</math> is traced by the dark blue squares while the variation of <math>~\rho_e/\rho_c</math> with <math>~q</math> is marked by the small, circular black dots.
Related Discussions

|
|---|
|
© 2014 - 2021 by Joel E. Tohline |