A Template for Gravitational Wave Signals from Core-Collapse Supernovae

29 August 2014: The initial content of this chapter has been drawn from a LaTeX document dated 23 December 2009 that J. E. Tohline created while interacting with Cody Arceneaux (at the time, an LSU undergraduate physics major) and Sarah Caudell (at the time, an LSU physics graduate student). I've decided to build on this project foundation that was laid in the 2008 - 2009 time frame.

Introduction

Ott (2009, Classical and Quantum Gravity, 26, 063001)

Our principal objective is to help the gravitational-wave community more fully understand the underlying physics that is fundamentally responsible for the characteristic features that are expected to arise in the signals that are detected from core-collapse supernovae. Building on early, simplified models of nonspherical core collapse presented by Thuan & Ostriker (1974) and by Tohilne (1984), our discussion is intended to supplement and complement published works from the past couple of decades that have focused on analyzing results from large-scale, multidimensional hydrodynamic (or magneto-hydrodynamic and fully relativistic) models, such as the the seminal work of Zwerger and Mueller (1997) and reviews by Ott (2009), Fryer and New (2011) and Logue et al. (2012).

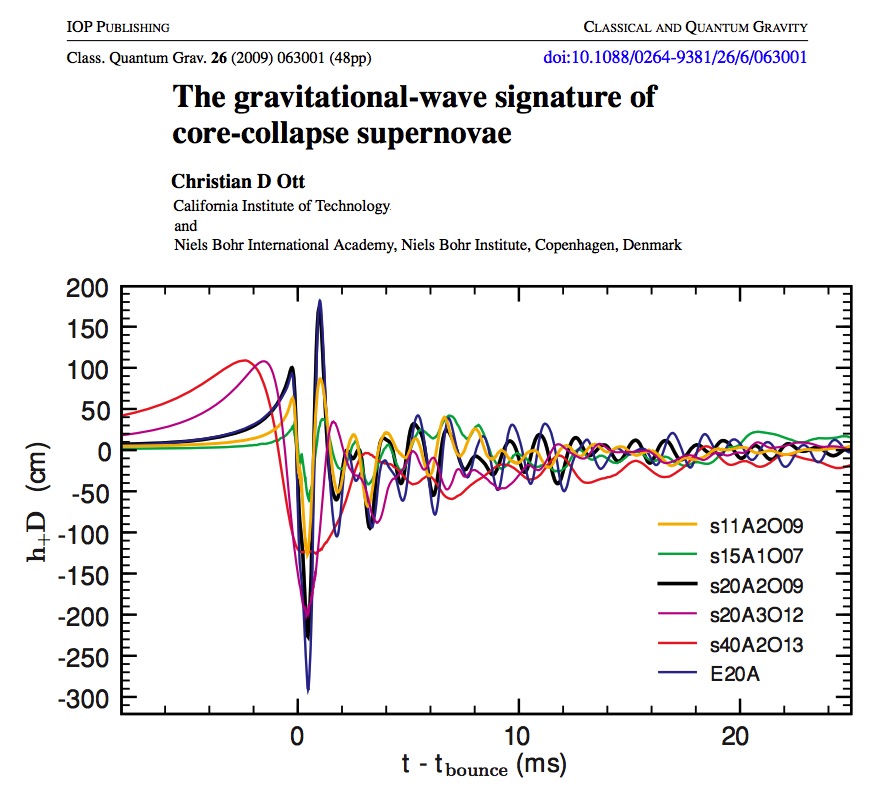
As an example, Figure 2 from Ott (2009) is reprinted here, on the right. Its published caption reads, in part: "Note the generic shape of the waveforms, exhibiting one pronounced spike at core bounce and a subsequent ring down. Very Rapid precollapse rotation … results in a significant slowdown of core bounce, leading to a lower-amplitude and lower-frequency GW burst." As early as 1991, Mönchmeyer et al. (1991) identified four phases of a collapse evolution:

Phase I: Contraction and core flattening. "This phase … is characterized by a growing overall flattening of the density stratification inside and outside [of an] inner core (IC)."
Phase II: Rapid contraction of the IC. "Both the IC and the outer core get strongly deformed during this phase. … The collapse of the IC is finally decelerated and stopped … by either the action of centrifugal forces … or the rise of [the effective adiabatic index] <math>~\Gamma</math> …"
Phase III: Core bounce. "Depending on the stiffness of the [equation of state] and the amount of rotational and kinetic energy the IC overshoots its (rotational) equilibrium position" then bounces back.
Phase IV: Shock propagation and post-bounce oscillations. "… the … IC oscillates [about its equilibrium configuration] with various volume and surface modes. The amplitudes and frequencies of these modes strongly depend on the kinetic energy of the IC at bounce, the stiffness of the [equation of state], and the central and averaged density of the IC …. The IC-oscillations are damped … [on a] time scale [that] strongly depends on the conditions of the shock heated material just outside the IC. After a model dependent number of oscillations, the IC approaches rotational equilibrium …."

Here, we will develop analytic and semi-analytic models that encapsulate the physical phenomena that give rise to and that define the relevant scales of each of these evolutionary phases, then sew the models together to demonstrate how all of the principal features in the core-collapse gravitational-wave signal can be fairly readily understood. We begin with a discussion of the free-fall collapse of rotationally flattened spheroids.

Free-Fall Collapse

Nod to Lynden-Bell's Early Contributions

I want to begin this section by paying tribute to Donald Lynden-Bell who, in 1962 (Mathematical Proceedings of the Cambridge Philosophical Society, vol. 58, pp. 709-711), was the first to appreciate the relatively simple behavior that should be exhibited by the free-fall collapse of a uniformly rotating, uniform-density spheroid. In an article less than two pages in length, Lynden-Bell first noted that the governing dynamical equations (written in cylindrical coordinates) take the form,

<math>~\ddot{R}</math>	<math>~=</math>	<math>~-~ 2A_L(t) R + \frac{h_{LB}^2}{R^3} \, ,</math>
<math>~\ddot{Z}</math>	<math>~=</math>	<math>~-~ 2C_L(t) Z \, ,</math>

where the dots denote differentiation with respect to time, <math>~h_{LB}</math> is a constant and the two time-dependent coefficients, <math>~A(t)</math> and <math>~C(t)</math>, come from the gravitational potential that, according to Lyttleton (1953), has the form,

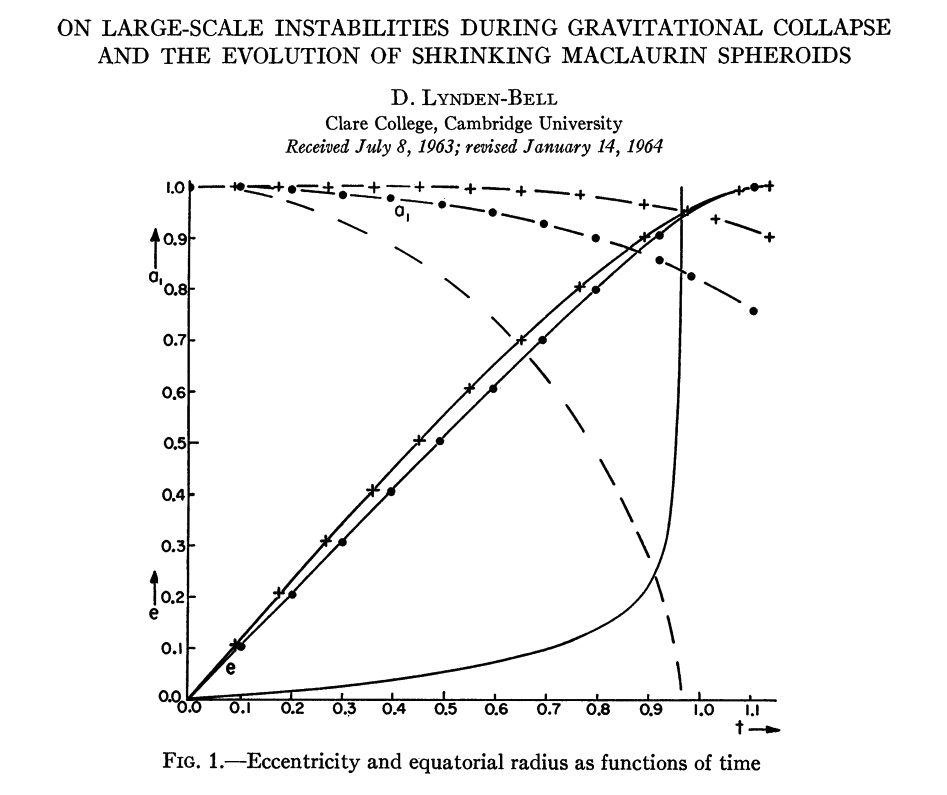
Then Lynden-Bell deduced that, (a) "the result of the motion is merely a change of scales"; (b) the collapsing system "remains uniform [in density], and the boundary remains spheroidal"; and (c) "the collapse … will be through a series of [uniformly rotating] spheroids." Two years later in a separate article, Lynden-Bell (1964, ApJ, 139, 1195) presented results from the numerical integration of this governing set of dynamical equations (see his Figure 1, reprinted to the right, here). The various publications by other authors who also have modeled the free-fall collapse of rotating or nonrotating spheroids in various contexts (see our discussion that follows) have not always acknowledged Lynden-Bell's pioneering analysis of this problem.

Nonrotating, Spherically Symmetric Collapse

When describing the free-fall (pressure-free) collapse from rest of a uniform-density sphere of mass, <math>~M</math>, and initial radius, <math>~r_0</math> — hence, initial density <math>~\rho_0 = 3M/(4\pi r_0^3)</math> — it is convenient to use the Lagrangian radial coordinate, <math>~r(t)</math>, which tracks the radius of the sphere at any time, <math>~t</math>. The relevant equation of motion is (see Lin, Mestel & Shu 1965 or our accompanying discussion),

<math>~\frac{d^2r}{dt^2} </math>	<math>~=</math>	<math>~- \frac{GM}{r^2} = - \frac{G}{r^2} \biggl[ \frac{4\pi}{3} ~r_0^3 \rho_0 \biggr]</math>
<math>~\Rightarrow~~~~\frac{1}{r_0} \frac{d^2r}{dt^2} </math>	<math>~=</math>	<math>~- \frac{4\pi G \rho_0}{3} \biggl( \frac{r_0}{r} \biggr)^2 \, ,</math>

which integrates to give,

where,

<math>~\frac{2}{\pi} \biggl[ \zeta + \frac{1}{2} \sin(2\zeta) \biggr]</math>	<math>~=</math>	<math>~\frac{t}{\tau_\mathrm{ff}} \, ,</math>
<math>~\tau_\mathrm{ff}</math>	<math>~\equiv</math>	<math>~\biggl[ \frac{3\pi}{32 G \rho_0} \biggr]^{1/2} \, .</math>

(Detailed steps through this derivation, as well as an in-depth discussion of the free-fall collapse problem, are provided in an accompanying chapter of this H_Book.) A set of dimensionless expressions drawn from this analytic solution that will prove useful to our discussion of gravitational-wave signals from core-collapse supernovae is provided in the following table. All lengths have been normalized to <math>~r_0</math>, and times have been normalized to the free-fall time, <math>~\tau_\mathrm{ff}</math>. In the lower half of the table, these analytic functions have been evaluated at six different times during the free-fall collapse.

Analytic Solution to Spherical Free-Fall Collapse

<math>~x(\zeta) \equiv \frac{r}{r_0}</math>	<math>~=</math>	<math>~\cos^2 \zeta \, ,</math>
<math>~x'(\zeta) \equiv \biggl( \frac{\tau_\mathrm{ff}}{r_0} \biggr) \frac{dr}{dt}</math>	<math>~=</math>	<math>~-~\frac{\pi}{2} \tan \zeta \, ,</math>
<math>~x(\zeta) \equiv \biggl(\frac{\tau^2_\mathrm{ff}}{r_0} \biggr) \frac{d^2r}{dt^2}</math>	<math>~=</math>	<math>~-~\frac{\pi^2}{8} \cdot \frac{1}{\cos^4 \zeta} = ~-~\frac{\pi^2}{8} \cdot \frac{1}{x^2} \, ,</math>
<math>~\frac{1}{2} \ddot{I} \equiv \frac{1}{2} \biggl(\frac{\tau_\mathrm{ff}}{r_0} \biggr)^2 \frac{d^2(r^2)}{dt^2}</math>	<math>~=</math>	<math>~+~\frac{\pi^2}{8} \cdot (\tan^2\zeta - 1) \, .</math>

<math>~\frac{t}{\tau_\mathrm{ff}}</math>

<math>~-1.24196\times 10^4</math>

Note that the second time-derivative of the moment of inertia, <math>~\ddot{I}</math>, goes through zero when <math>~\zeta = \pi/4</math>, that is, at time,

<math>~\frac{t}{\tau_\mathrm{ff}} = \frac{2}{\pi}\biggl[ \zeta + \frac{1}{2}\sin(2\zeta) \biggr] = \biggl( \frac{1}{2} + \frac{1}{\pi} \biggr) \, .</math>

Nonrotating, Oblate-Spheroidal Collapse

The analogous collapse from rest of a nonrotating, uniform-density, oblate spheroid with equatorial radius, <math>~\varpi_\mathrm{eq}(t)</math>, and polar radius, <math>~Z_p(t)</math>, is governed by the equations,

<math>~\frac{d^2 \varpi_\mathrm{eq}}{dt^2}</math>	<math>~=</math>	<math>~ -~\frac{\partial\Phi}{\partial \varpi} \biggr\|_{\varpi_{eq}} \, , </math>
<math>~\frac{d^2 Z_\mathrm{p}}{dt^2}</math>	<math>~=</math>	<math>~ -~\frac{\partial\Phi}{\partial Z} \biggr\|_{Z_{p}} \, , </math>

where, to within an additive constant,

<math>~\Phi(\varpi,Z)</math>

<math>~ \pi G \rho [ A_1(e) \varpi^2 + A_3(e) Z^2] \, . </math>

We should clarify and emphasize that this expression for the time-dependent gravitational potential has been written in terms of the (time-varying) eccentricity of the spheroid, <math>~e</math>, as measured in the meridional plane. Specifically,

<math>~e </math>	<math>~\equiv</math>	<math>~ \biggl( 1 - \frac{Z_p^2}{\varpi_\mathrm{eq}^2} \biggr)^{1/2} </math>
<math>~\Rightarrow~~~~~ Z_p</math>	<math>~=</math>	<math>~ \varpi_\mathrm{eq} \biggl( 1 - e^2 \biggr)^{1/2} \, , </math>

and, as is derived in our accompanying discussion of the properties of homogeneous ellipsoids,

<math> ~A_1(e) </math>	<math> ~= </math>	<math> ~\frac{1}{e^2} \biggl[ \frac{\sin^{-1}e}{e} - (1-e^2)^{1/2} \biggr] (1-e^2)^{1/2} \, , </math>
<math> ~A_3(e) </math>	<math> ~= </math>	<math> ~\frac{2}{e^2} \biggl[ (1-e^2)^{-1/2} - \frac{\sin^{-1}e}{e} \biggr] (1-e^2)^{1/2} \, . </math>

Hence,

<math> ~\nabla\Phi </math>

<math> ~2\pi G \rho \biggl[ \hat{e}_\varpi A_1(e) + \hat{e}_Z A_3(e) Z \biggr] \, , </math>

and the pair of governing dynamical equations become,

<math>~\frac{d^2 \varpi_\mathrm{eq}}{dt^2}</math>	<math>~=</math>	<math>~ - 2\pi G \rho A_1(e) \varpi_\mathrm{eq} = - \frac{3}{2} \biggl[ \frac{GM}{\varpi_\mathrm{eq} Z_\mathrm{p}} \biggr] A_1(e) \, , </math>
<math>~\frac{d^2 Z_\mathrm{p}}{dt^2}</math>	<math>~=</math>	<math>~ - 2\pi G \rho A_3(e) Z_\mathrm{p} = - \frac{3}{2} \biggl[ \frac{GM}{\varpi_\mathrm{eq}^2} \biggr] A_3(e) \, , </math>

where we have used the relation that is valid for uniform-density, oblate spheoids,

<math> ~\rho = \frac{3M}{4\pi \varpi_\mathrm{eq}^2 Z_\mathrm{p}} \, . </math>

Related Discussions

StellarCollapse.org

User:Tohline/ProjectsUnderway/Core Collapse Supernovae

Contents